E. Quémerais1 - R. Lallement1 - J.-L. Bertaux1 - D. Koutroumpa1 - J. Clarke2 - E. Kyrölä3 - W. Schmidt3
1 - Service d'Aéronomie, Verrières le Buisson, France
2 -
Boston University, Boston, USA
3 -
Finnish Meteorological Institute, Helsinki, Finland
Received 9 March 2006 / Accepted 10 April 2006
Abstract
Aims. Interplanetary Lyman ![]() line profiles are derived from the SWAN H cell data measurements. The measurements cover a 6-year period from solar minimum (1996) to after the solar maximum of 2001. This allows us to study the variations of the line profiles with solar activity.
line profiles are derived from the SWAN H cell data measurements. The measurements cover a 6-year period from solar minimum (1996) to after the solar maximum of 2001. This allows us to study the variations of the line profiles with solar activity.
Methods. These line profiles were used to derive line shifts and line widths in the interplanetary medium for various angles of the LOS with the interstellar flow direction. The SWAN data results were then compared to an interplanetary background upwind spectrum obtained by STIS/HST in March 2001.
Results. We find that the LOS upwind velocity associated with the mean line shift of the IP Lyman ![]() line varies from 25.7 km s-1 to 21.4 km s-1 from solar minimum to solar maximum. Most of this change is linked with variations in the radiation pressure. LOS kinetic temperatures derived from IP line widths do not vary monotonically with the upwind angle of the LOS. This is not compatible with calculations of IP line profiles based on hot model distributions of interplanetary hydrogen. We also find that the line profiles get narrower during solar maximum.
line varies from 25.7 km s-1 to 21.4 km s-1 from solar minimum to solar maximum. Most of this change is linked with variations in the radiation pressure. LOS kinetic temperatures derived from IP line widths do not vary monotonically with the upwind angle of the LOS. This is not compatible with calculations of IP line profiles based on hot model distributions of interplanetary hydrogen. We also find that the line profiles get narrower during solar maximum.
Conclusions. The results obtained on the line widths (LOS temperature) show that the IP line is composed of two components scattered by two hydrogen populations with different bulk velocities and temperature. This is a clear signature of the heliospheric interface on the line profiles seen at 1 AU from the sun.
Key words: interplanetary medium - ultraviolet: solar system - ISM: atoms
The interplanetary background has been used to study the interplanetary hydrogen distribution
since its discovery in the late 1960's (Thomas and Krassa 1970;
Bertaux and Blamont 1970). Lists of previous experimental studies of the interplanetary
Lyman ![]() background can be found in Ajello et al. (1987, 1994) or Quémerais et al. (#Qu&).
background can be found in Ajello et al. (1987, 1994) or Quémerais et al. (#Qu&).
The SWAN instrument on the SOHO spacecraft (Bertaux et al. 1995) is able to study the IP Lyman ![]() line profile using hydrogen absorption cells. These devices are used to scan the line profile
taking advantage of the variation in the Doppler shift between the cells and the interplanetary hydrogen
as the spacecraft rotates on its orbit around the sun. Previous studies of the IP line profile
with H cells were made by the Mars 6 spacecraft (Bertaux et al. 1976)
the Prognoz 5/6 UV photometers (Bertaux et al. 1985) and the ALAE instrument
on ATLAS-1 shuttle mission (Quémerais et al. #Qu&).
line profile using hydrogen absorption cells. These devices are used to scan the line profile
taking advantage of the variation in the Doppler shift between the cells and the interplanetary hydrogen
as the spacecraft rotates on its orbit around the sun. Previous studies of the IP line profile
with H cells were made by the Mars 6 spacecraft (Bertaux et al. 1976)
the Prognoz 5/6 UV photometers (Bertaux et al. 1985) and the ALAE instrument
on ATLAS-1 shuttle mission (Quémerais et al. #Qu&).
IP Lyman ![]() line profiles can also be obtained from high-resolution UV spectrometers in the Earth's orbit.
Clarke et al. (1995, 1998) report measurements made by the GHRS (Goddard High-Resolution Spectrograph)
instrument on Hubble Space Telescope.
More recently, new spectra were obtained from the STIS intrument that replaced GHRS on HST.
line profiles can also be obtained from high-resolution UV spectrometers in the Earth's orbit.
Clarke et al. (1995, 1998) report measurements made by the GHRS (Goddard High-Resolution Spectrograph)
instrument on Hubble Space Telescope.
More recently, new spectra were obtained from the STIS intrument that replaced GHRS on HST.
Studying the IP Lyman ![]() line profiles has proved to be of interest for studying the heliospheric
interface because effects imprinted on the hydrogen distribution at a large distance from the sun are still
visible on Lyman
line profiles has proved to be of interest for studying the heliospheric
interface because effects imprinted on the hydrogen distribution at a large distance from the sun are still
visible on Lyman ![]() line profiles seen at 1 AU. This is due to the fact that the flow of hydrogen in the
heliosphere is collisionless.
line profiles seen at 1 AU. This is due to the fact that the flow of hydrogen in the
heliosphere is collisionless.
Izmodenov et al. (2001) have presented model computations that predict how the hydrogen distribution is affected by the heliospheric interface. The heliospheric interface is the boundary region where the expanding solar plasma interacts with the interstellar plasma. Using the derived hydrogen distributions, Quémerais & Izmodenov (#Qu&) calculated line profiles including a complete model of radiative transfer effects. The derived line shifts and line widths were clearly modified by the heliospheric interface.
In this paper, we continue the work presented by Quémerais et al. (#Qu&) about the line profile reconstruction technique based on the SWAN H cell data. This early work was concentrated on the first year of data. Here we show results obtained from 6 one-year orbits of SOHO around the sun. Some of the details of the data processing are not repeated here and the interested reader should refer to the original paper. Previous analyses of the SWAN H cell data were published by Costa et al. (1999), Lallement et al. (2005), and Koutroumpa et al. (2005).
The first section briefly presents the line profile reconstruction technique and the SWAN data. The following sections give the results obtained for the line shifts and the line widths, as well as the variations during the solar cycle. The last section presents a STIS/HST upwind line profile obtained in March 2001 and compares the derived line shift and line width with the SWAN results.
The SOHO spacecraft was launched in December 1995 from Cape Canaveral. The SWAN instrument started operation in January 1996 and has been active since then except for a few periods of time (June to October 1998 and January 1999).
Characteristics of the SWAN instrument are given
in Bertaux et al. (1995). The SWAN instrument is a UV photometer
with a passband between 110 nm and 160 nm. The instrument is made of two
identical units placed on opposite sides of the SOHO spacecraft
(+Z and -Z sides).
Each unit is equipped with a periscopic scanning mechanism that allows
to point the field of view in any direction of the half sky facing the
side the unit is attached on.
The instantaneous field of view is 5![]() by 5
by 5![]() divided in 25 pixels. Each pixel
has a 1
divided in 25 pixels. Each pixel
has a 1![]() by 1
by 1![]() field of view. Measurements are performed every 15 s,
with at least 13 s of integration time to get a good signal-to-noise ratio.
field of view. Measurements are performed every 15 s,
with at least 13 s of integration time to get a good signal-to-noise ratio.
Each unit is equipped with a hydrogen absorption cell. This cell is placed on the
photon path to the detector. The cell is filled with molecular hydrogen and has MgF2
windows. A tungsten filament passes through the cell. When a current goes through the
filament, H2 is partially dissociated into atomic hydrogen, which creates a small
cloud that can absorb Lyman ![]() photons. Typical values for the optical thickness
of the active cell are around 3 to 5.
Descriptions of the observing programmes and of the various subsets of
data are detailed by Bertaux et al. (1997).
Here we concentrate on the hydrogen absorption cell
measurements obtained between June 1996 and June 2003.
photons. Typical values for the optical thickness
of the active cell are around 3 to 5.
Descriptions of the observing programmes and of the various subsets of
data are detailed by Bertaux et al. (1997).
Here we concentrate on the hydrogen absorption cell
measurements obtained between June 1996 and June 2003.
The most common observation programme of SWAN is the so-called
full-sky observation, during which each sensor unit covers the complete
hemisphere that is on its side by moving a two-mirror
periscope mechanism. One full-sky observation is performed in
one day. The data obtained by both sensors are
then combined into one image of the whole sky at Lyman ![]() .
It must be noted that the areas of the sky viewed by each sensor
overlap, which enables us to compare both sensors on a regular
basis. SWAN performs these observations 4 times per week.
During the first year, one of the four full-sky observations
made each week was made with cyclic activation of the hydrogen
cells. For these observations, we then obtained a full-sky image
at Lyman
.
It must be noted that the areas of the sky viewed by each sensor
overlap, which enables us to compare both sensors on a regular
basis. SWAN performs these observations 4 times per week.
During the first year, one of the four full-sky observations
made each week was made with cyclic activation of the hydrogen
cells. For these observations, we then obtained a full-sky image
at Lyman ![]() as well as a full-sky image of the reduction factor,
which is defined below.
The mechanism is kept fixed during both measurements, cell OFF
and cell ON, before moving to another direction in the sky.
as well as a full-sky image of the reduction factor,
which is defined below.
The mechanism is kept fixed during both measurements, cell OFF
and cell ON, before moving to another direction in the sky.
The reduction factor R used in what follows, is a dimensionless
quantity. It is the ratio of intensities measured in a given direction when
the cell is on (absorption) and when it is off (no absorption).
If we consider an incoming intensity expressed as
![]() where
where
![]() is the wavelength in the cell rest frame and if
we note
is the wavelength in the cell rest frame and if
we note
![]() the transmission function inside the cell,
the reduction factor is defined by
the transmission function inside the cell,
the reduction factor is defined by
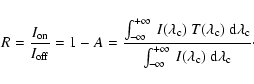 |
(1) |
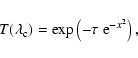 |
(2) |
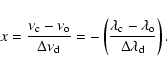 |
(3) |
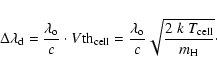 |
(4) |
![\begin{displaymath}W_\lambda = \int_{-\infty}^{+\infty} ~\left[1-T(\lambda_{\rm c})\right]~{\rm d}\lambda_{\rm c} .
\end{displaymath}](/articles/aa/full/2006/33/aa5169-06/img16.gif) |
(5) |
Quémerais et al. (#Qu&) have shown how H cell measurements over a 1-year period can be used to reconstruct the line profiles of the IP glow. The same technique was applied here, and we refer readers to Sect. 3 of Quémerais et al. (#Qu&). We use the same terms and notations as in this paper.
The data used in this work cover a much longer period of time than our previous work which was concentrated on the first year of SWAN data. To reconstruct the line profiles, we need a full rotation of the Earth on its orbit. For each year we selected data from early June of the year until end of May of the following year. For instance, the spectra labelled 2000 were derived from measurements starting in June 2000 and ending in May 2001. The reason for this sampling was the lack of data between June 1998 and October 1998. As a consequence the year 1998 (June 1998 to May 1999) is missing.
As done by Quémerais et al. (#Qu&), we use Eq. (5) to calibrate the absorbing power of the cell. Hydrogen cells are known to age with time. This may be due to ageing of the tungsten filament itself or due to trapping of hydrogen by the glass or even to some leak. This results in a decreasing optical thickness of the cell for a given filament current level. Over a 6-year period, both H cells have aged in very different ways. The H cell in the unit attached to the -Z side of the spacecraft seems to have lost all absorbing power very rapidly in 1999. This suggests that the cell has lost its H2 rather rapidly. The H cell in the other unit (+Z side) still retains most of its H2 cloud as shown by the strong absorption still seen in the 2005 data. However, the optical thickness has decreased with time. This was calibrated by determining the equivalent width of the cell (Eq. (5)) from the data (see Sect. 4.1 of Quémerais et al. #Qu&).
The values for the equivalent width of the +Z hydrogen absorption cell are given in Table 1. Note that we use the transformation into velocity units given by Eq. (11) of Quémerais et al. (#Qu&). These values were used to determine the line profiles as presented in Sect. 4.2 of Quémerais et al. (#Qu&).
Table 1: Equivalent width of the H cells.
This section presents the results found for each of the 6 orbits analysed. As mentioned earlier, each data set starts in June and ends at the end of May of the following year. There is roughly one map per week, which means that about 50 maps are used to derive a line profile in each direction of the sky. In 1996 and 1997, both H cells were active, so we have a full-sky velocity map for both orbits. However, due to the leak in the -Z unit H cell, only the northern ecliptic hemisphere is available from 1999 to 2003. We do not show individual plots of the line profiles. Examples are given in Figs. 5 to 7 of Quémerais et al. (#Qu&).
The line-of-sight (LOS hereafter) velocities shown here correspond to the mean Doppler shifts of the line profile expressed in terms of velocity in the solar rest frame. If the line is not symmetrical, as in Quémerais & Izmodenov (#Qu&) for example, then there is a small difference between the mean Doppler shift and the maximum of the line.
Following Quémerais et al. (#Qu&), we express the relation between velocity v projected on the LOS and
the wavelength in the solar rest frame as
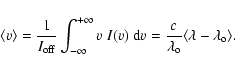 |
(7) |
![\begin{figure}
\par\includegraphics[width=6.7cm,angle=90]{QuemeraisAA5169f01.eps}\end{figure}](/articles/aa/full/2006/33/aa5169-06/Timg34.gif) |
Figure 1: full-sky map of the velocity difference between the 1996 map and the 1997 map. The data are shown in ecliptic coordinates (west ecliptic longitude). The blue color in the upwind side shows that the upwind velocity in 1997 is slightly slower (in modulus), by 0.4 km s-1. |
| Open with DEXTER | |
Quémerais et al. (#Qu&) show the velocity map derived from data obtained in 1996 and early 1997.
This map corresponds to the minimum of activity of cycle 22. In the case of a flow with constant
velocity, the velocity projected on the LOS is simply
![]() ,
where
,
where ![]() is the angle of the LOS with the upwind direction and
is the angle of the LOS with the upwind direction and
![]() is the constant bulk velocity. The actual velocity maps observed by SWAN are more complex
than this simple case.
is the constant bulk velocity. The actual velocity maps observed by SWAN are more complex
than this simple case.
Figure 1 displays the difference between the velocity maps of 1996 and 1997. The variation in the upwind velocity is a deceleration of 0.4 km s-1, with a value of -25.7 km s-1 in 1996 and -25.3 km s-1 in 1997. Considering the uncertainties given in Table 2, the velocity can be considered to be the same. However, a slight deceleration in the solar rest frame is quite possible because of the increase in radiation pressure from the Sun between 1996 and 1997. The LOS (line-of-sight) velocity in the upwind direction is the result of two antagonistic effects. First, selection effects linked to ionization processes increase the mean velocity by ionizing the slower hydrogen atoms. Second, radiation pressure tends to push the atoms away from the sun and slow them down. During most of the solar cycle, radiation pressure is larger than the solar gravitational attraction (Pryor et al. 1998). As the cycle changes from minimum to maximum, the interplanetary hydrogen atoms feel an increasing radiation pressure that becomes more efficient to slow them down in the upwind side of the inner heliosphere.
![\begin{figure}
\par\includegraphics[width=8cm]{QuemeraisAA5169f02.eps}\end{figure}](/articles/aa/full/2006/33/aa5169-06/Timg38.gif) |
Figure 2:
Variation in the LOS velocity as a function of the angle of the LOS
with the upwind direction. Here, the upwind direction is taken to be 252.3 |
| Open with DEXTER | |
The downwind velocity is mostly unchanged with a value equal to
![]() km s-1, which
is not surprising because the hydrogen distribution in the downwind side of the heliosphere is
less affected by variations in radiation pressure.
In this direction, the hydrogen is strongly depleted by ionization effects. A partial filling happens
beyond a few AU from the sun because of the relatively hot temperature of the interplanetary gas.
It is therefore not surprising that radiation pressure plays a lesser role in this direction as
compared to the upwind direction.
km s-1, which
is not surprising because the hydrogen distribution in the downwind side of the heliosphere is
less affected by variations in radiation pressure.
In this direction, the hydrogen is strongly depleted by ionization effects. A partial filling happens
beyond a few AU from the sun because of the relatively hot temperature of the interplanetary gas.
It is therefore not surprising that radiation pressure plays a lesser role in this direction as
compared to the upwind direction.
Figure 2 shows the velocity in the solar rest frame as a function of the angle with the upwind direction.
The upwind direction is the one defined by the isovelocity contours (Quémerais et al. #Qu&) with a longitude of
252.3![]() and a latitude of 8.7
and a latitude of 8.7![]() .
Changes between the two orbits are within the statistical uncertainties of the
velocity values.
.
Changes between the two orbits are within the statistical uncertainties of the
velocity values.
Table 2: Upwind LOS velocity for various orbits.
The SWAN instrument did not operate between the end of June 1998 and October 1998, because of the accidental loss of contact with the SOHO spacecraft. Operations resumed at the end of 1998 but soon were stopped after the failure of the last gyroscope. Normal operations resumed in spring 1999.
In this section, we present maps obtained from measurements made beween June 1999 and June 2003. This period covers the solar activity maximum of 2001 and the beginning of cycle 23. There are no measurements in the southern ecliptic hemisphere because the -Z unit H cell stopped absorbing in 1999 for a reason that is still unclear, while the +Z unit hydrogen cell is still functional in 2006. Table 1 shows the variation in the equivalent width of the cell as a function of orbit year. Between 1997 and 1999, the +Z H cell shows a strong decrease in absorption and after that a steady but slower decrease. The equivalent width in 2002 is only 60% of the post launch value.
Figure 3 shows the difference between the 1996 orbit velocity profile and the five other orbits. The differences are shown as a function of the LOS angle from the upwind direction. First, we note that the 2000 to 2002 orbits yield very similar values, within 1 km s-1 almost everywhere. Since the 1996 and 1997 orbits are also very similar, we see two main regimes for the velocity: one for solar minimum conditions with an upwind LOS velocity around -25.5 km s-1 and one for solar maximum conditions with an upwind LOS velocity around -21.5 km s-1. The 1999 and the missing 1998 ones are intermediary states.
![\begin{figure}
\par\includegraphics[width=8cm]{QuemeraisAA5169f03.eps}\end{figure}](/articles/aa/full/2006/33/aa5169-06/Timg46.gif) |
Figure 3: Difference in LOS velocity between the 1996 orbit and the five other orbits. The velocities are shown as a function of the angle with the upwind direction. The 1996 velocity profile is shown in Fig. 2. The 1997 profile (solid line, top) is very close to the 1996 profile. The 1999 one (solid line bottom) is an intermediary profile, while the 2000 (dotted line), 2001 (dashed line), and 2002 (dash-dot line) profiles are very similar. |
| Open with DEXTER | |
Table 2 gives the numerical values of the upwind velocity for each orbit. The values are slightly different
from those in Fig. 3 because the averaging was done in a different way. In this table, velocities are
averaged within 20![]() of the upwind direction to get better statistics. The apparent variation in upwind velocity can
be explained partially by effects of the radiation pressure; however, detailed calculations will be necessary to see if the
models match the measured variations. The general deceleration observed in the solar rest frame
corresponds to increasing values of radiation pressure as expected from solar Lyman
of the upwind direction to get better statistics. The apparent variation in upwind velocity can
be explained partially by effects of the radiation pressure; however, detailed calculations will be necessary to see if the
models match the measured variations. The general deceleration observed in the solar rest frame
corresponds to increasing values of radiation pressure as expected from solar Lyman ![]() flux measurements
(Rottman et al. 2006).
The change between 1997 and 1999 is very abrupt (3 km s-1) and seems too important for the change of radiation pressure
(+10%) derived from solar flux measurements.
Changes of ionization processes could also be partly responsible for this change of LOS velocity.
Indeed, ionization processes favour fast atoms because slower atoms have a higher probability of being
ionized. This heads to the selection of fast atoms and an increase in the bulk velocity in the inner heliosphere.
However even the fast atoms are ionized with increasing efficiency of the ionization processes.
This means that the atoms contributing to the intensity are farther away from the sun. How this will affect
the line-of-sight velocity is not clear. Only time-dependent calculation of the hydrogen distribution
will allow us to discriminate between the various effects involved here.
flux measurements
(Rottman et al. 2006).
The change between 1997 and 1999 is very abrupt (3 km s-1) and seems too important for the change of radiation pressure
(+10%) derived from solar flux measurements.
Changes of ionization processes could also be partly responsible for this change of LOS velocity.
Indeed, ionization processes favour fast atoms because slower atoms have a higher probability of being
ionized. This heads to the selection of fast atoms and an increase in the bulk velocity in the inner heliosphere.
However even the fast atoms are ionized with increasing efficiency of the ionization processes.
This means that the atoms contributing to the intensity are farther away from the sun. How this will affect
the line-of-sight velocity is not clear. Only time-dependent calculation of the hydrogen distribution
will allow us to discriminate between the various effects involved here.
![\begin{figure}
\par\includegraphics[width=7cm,angle=90]{QuemeraisAA5169f04.eps}\end{figure}](/articles/aa/full/2006/33/aa5169-06/Timg47.gif) |
Figure 4: Difference between the velocity maps of 2001 and 1996. The maximum difference is found in the upwind direction with a value around 4 km s-1. Downwind, the difference is close to zero. Below 10 degrees of latitude, the results are very noisy. Contours of the 1996 velocity map are shifted towards higher latitudes than the contours of the 2001 velocity map. This is due to the existence of anisotropies in the hydrogen distribution of 1996 which create a deviation from the non-isotropic 2001 distribution. |
| Open with DEXTER | |
Figure 4 presents the LOS velocity difference between 2001 and 1996 for all directions in the northern ecliptic hemisphere. The difference in the upwind direction is roughly 4 km s-1, as seen before. The difference in the downwind direction is small, which suggests that changes in radiation pressure over the cycle is not as important with the velocity distribution of hydrogen atoms in the downwind direction. We clearly see a shift between the iso-contours of velocity for 2001 and 1996. This is explained by the changes in the velocity contours induced by anisotropies of the solar ionization fluxes (Lallement et al. 2005; Koutroumpa et al. 2005). In 2001, when solar ionizing fluxes are almost isotropic, the constant velocity contours are well fitted by cones centered on the upwind direction. In 1996, however, due to different ionization fluxes at different heliographic latitudes the resulting iso-velocity contours are elongated towards high latitudes. This is demonstrated in Fig. 4 where the difference of velocity maps shows a maximum that is shifted towards higher ecliptic latitudes.
In this section, we have shown how the LOS velocity of the interplanetary Lyman ![]() line profile changes during the solar cycle.
The amplitude is large, more than 4 km s-1 in the upwind direction. It is also abrupt because we find
a change of 3 km s-1 between 1997 and 1999. The main cause for this variation in the velocity
is the change of radiation pressure during the solar cycle (Pryor et al. 1998).
Other effects linked to ionization processes and their solar cycle variations may also be involved.
line profile changes during the solar cycle.
The amplitude is large, more than 4 km s-1 in the upwind direction. It is also abrupt because we find
a change of 3 km s-1 between 1997 and 1999. The main cause for this variation in the velocity
is the change of radiation pressure during the solar cycle (Pryor et al. 1998).
Other effects linked to ionization processes and their solar cycle variations may also be involved.
This section presents the LOS kinetic temperature maps deduced from the line-profile reconstruction
technique presented in Quémerais et al. (#Qu&). What we call the line-of-sight (LOS) kinetic temperature,
also called apparent temperature in Quémerais & Izmodenov (#Qu&), is actually the line width converted to
temperature units using the relation between thermal velocity
![]() and line width.
and line width.
Using the same notation as before, we have the following expression
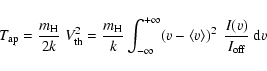 |
(8) |
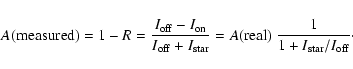 |
(9) |
Figure 5 shows the LOS temperature as a function of the upwind angle derived from
the orbits of 1996 and 1997.
For each orbit, there are 2 curves, one for angles larger than 30![]() and one for angles smaller
than 30
and one for angles smaller
than 30![]() .
Because the upwind direction is very close to the galactic plane, applying a strict
limit on stellar counts for each LOS removes all points within 30
.
Because the upwind direction is very close to the galactic plane, applying a strict
limit on stellar counts for each LOS removes all points within 30![]() from upwind.
However, some lines of sight show a low stellar contamination, of a few percent of the upwind intensity.
Keeping those points, we were able to determine a curve for angles between zero and 30
from upwind.
However, some lines of sight show a low stellar contamination, of a few percent of the upwind intensity.
Keeping those points, we were able to determine a curve for angles between zero and 30![]() .
This second curve shows larger uncertainties. The most striking feature of these two curves is that
they are not monotonic. The temperature reaches a minimum value around 11 000 K for an upwind angle of 60
.
This second curve shows larger uncertainties. The most striking feature of these two curves is that
they are not monotonic. The temperature reaches a minimum value around 11 000 K for an upwind angle of 60![]() .
This feature does not appear in hot model calculations whether they include full radiative transfer
effects on the line profile or simply compute the first-order scattering of photons (Quémerais #Qu&).
For a hot model, the temperature dependence of line profiles from upwind to downwind is always monotonic.
We also find that the upwind LOS temperature is around 14 000 K and the downwind
value is close to 18 000 K. This departure from a monotonic variation with the upwind angle was also
noted by Costa et al. (1999) using a different method.
.
This feature does not appear in hot model calculations whether they include full radiative transfer
effects on the line profile or simply compute the first-order scattering of photons (Quémerais #Qu&).
For a hot model, the temperature dependence of line profiles from upwind to downwind is always monotonic.
We also find that the upwind LOS temperature is around 14 000 K and the downwind
value is close to 18 000 K. This departure from a monotonic variation with the upwind angle was also
noted by Costa et al. (1999) using a different method.
Quémerais (#Qu&) computed LOS temperatures as seen from Earth's orbit for various models
of the hydrogen distribution. What was found is that the LOS temperature of the IP line within
40![]() to 50
to 50![]() in the upwind direction is almost constant. The line width starts to increase for angles larger
than 50
in the upwind direction is almost constant. The line width starts to increase for angles larger
than 50![]() .
This increase in the line width is due to changes of the line shape due to acceleration and
deceleration by radiation pressure and also to selection effects of the fast atoms through ionization processes.
.
This increase in the line width is due to changes of the line shape due to acceleration and
deceleration by radiation pressure and also to selection effects of the fast atoms through ionization processes.
![\begin{figure}
\par\includegraphics[width=8cm]{QuemeraisAA5169f05.eps}\end{figure}](/articles/aa/full/2006/33/aa5169-06/Timg53.gif) |
Figure 5:
LOS kinetic temperature as a function of the upwind angle. The values were obtained for the two orbits
in 1996 and 1997. For each orbit, there are 2 curves, one for angles smaller than 30 |
| Open with DEXTER | |
In that respect, we can argue that the decrease in LOS temperature between 0 to 50![]() is a clear signature
of the existence of two hydrogen populations contributing to the total line profile. Following Izmodenov et al. (2001),
we can divide the hydrogen atoms in the heliosphere into four distinct populations. First, we consider the interstellar
component that has gone through the heliospheric interface without any interaction with the protons. This population at large
distance from the sun has the distribution parameters of the interstellar gas, i.e. a bulk velocity close to 26 km s-1 and
a temperature close to 6000 K. The second population is the one created by charge exchange with protons of the compressed
interstellar plasma. Models predict a strong deceleration and heating of this population. These two populations are the main
contributors to the IP line profile at 1 AU, while the other two populations created by charge exchange with the solar wind
can be neglected here (Quémerais & Izmodenov #Qu&).
is a clear signature
of the existence of two hydrogen populations contributing to the total line profile. Following Izmodenov et al. (2001),
we can divide the hydrogen atoms in the heliosphere into four distinct populations. First, we consider the interstellar
component that has gone through the heliospheric interface without any interaction with the protons. This population at large
distance from the sun has the distribution parameters of the interstellar gas, i.e. a bulk velocity close to 26 km s-1 and
a temperature close to 6000 K. The second population is the one created by charge exchange with protons of the compressed
interstellar plasma. Models predict a strong deceleration and heating of this population. These two populations are the main
contributors to the IP line profile at 1 AU, while the other two populations created by charge exchange with the solar wind
can be neglected here (Quémerais & Izmodenov #Qu&).
A simple model of the two populations is shown in Fig. 6. The profiles are represented by Gaussian functions.
The plots are made in the solar rest frame. One population has the parameters of the interstellar gas,
i.e. a velocity of 30 km s-1 and a temperature of 6000 K. We used a velocity of 30 km s-1 for the primary component to account
for selection of faster atoms by ionization processes (see Quémerais & Izmodenov 2002, Table 4).
The other component is decelerated in the solar rest frame and heated. Its parameters are given by a velocity of 20 km s-1
and a temperature of 14 000 K. We have computed the line shift and line width
of the sum of these two line profiles projected on an LOS with an angle from upwind between zero and 50![]() .
The results
are shown in Table 3. We find values similar to the observations.
.
The results
are shown in Table 3. We find values similar to the observations.
We do not claim that this simple model fits the data. It is just an example to illustrate
why the LOS temperature decreases between 0 and 50![]() ,
i.e. because the Doppler shift between the two
components of the line decreases as the cosine of the angle with the upwind direction. After 50
,
i.e. because the Doppler shift between the two
components of the line decreases as the cosine of the angle with the upwind direction. After 50![]() from upwind,
dynamic effects on the hydrogen distribution make the line width increase again. Actual modeling is required here
to correctly interpret these data.
from upwind,
dynamic effects on the hydrogen distribution make the line width increase again. Actual modeling is required here
to correctly interpret these data.
![\begin{figure}
\par\includegraphics[width=8cm]{QuemeraisAA5169f06.eps}\end{figure}](/articles/aa/full/2006/33/aa5169-06/Timg54.gif) |
Figure 6: Model of the line profile generated for two distinct populations of hydrogen atoms. One has the parameters of the interstellar gas, i.e. velocity of 30 km s-1 (26 km s-1 accelerated by selection effects, see text) and a temperature of 6000 K, the other has parameters reflecting a deceleration and heating due to the heliospheric interface, i.e. velocity of 20 km s-1 and a temperature of 14 000 K. The resulting line profile in the upwind direction has a mean shift of -25 km s-1 and a temperature of a bit less than 14 000 K. The line profiles are shown in the solar rest frame. |
| Open with DEXTER | |
Table 3: LOS velocity and temperature for a 2-population model.
![\begin{figure}
\par\includegraphics[width=8cm]{QuemeraisAA5169f07.eps}\end{figure}](/articles/aa/full/2006/33/aa5169-06/Timg55.gif) |
Figure 7:
LOS temperature as a function of the upwind angle. The values were obtained for the four orbits
from 1999 to 2002. The data from 1999 are shown by crosses, those of 2000 by stars, those of 2001 by squares,
and the data of 2002 are shown by triangles. There are no values for angles smaller than
20 |
| Open with DEXTER | |
Figure 7 shows the LOS temperatures found for the four orbits from 1999 to 2002. The data from these
orbits are noisier due to the degradation of the sensitivity of the sensor units (Quémerais & Bertaux #Qu&).
It was not possible to recover profiles for LOS's within 20![]() of the upwind direction or within
30
of the upwind direction or within
30![]() of the downwind direction. However, two results can be seen from Fig. 7. First, the temperature
minimum around 60
of the downwind direction. However, two results can be seen from Fig. 7. First, the temperature
minimum around 60![]() from upwind has either shifted to lower angle values or even disappeared. This suggests that
the shift between the two components is smaller than in 1996 or that one of the components has become less important
relative to the other giving more weight to the parameters of the other component in the line profile.
Second, the curves show lower temperatures than what was found in 1996 and 1997. The overall decrease is around
1000 K. This feature also suggests that one of the components has become relatively less important, thus yielding
an apparently cooler profile. It is unlikely that the shift between the components has decreased, because this
wouldn't change the LOS temperature for crosswind lines of sight.
from upwind has either shifted to lower angle values or even disappeared. This suggests that
the shift between the two components is smaller than in 1996 or that one of the components has become less important
relative to the other giving more weight to the parameters of the other component in the line profile.
Second, the curves show lower temperatures than what was found in 1996 and 1997. The overall decrease is around
1000 K. This feature also suggests that one of the components has become relatively less important, thus yielding
an apparently cooler profile. It is unlikely that the shift between the components has decreased, because this
wouldn't change the LOS temperature for crosswind lines of sight.
The LOS temperature profiles presented in this section show that the IP line profile is most likely made up
of two components due to distinct hydrogen populations. The first one is composed of unperturbed interstellar
hydrogen atoms getting close to the sun. The second one is composed of hydrogen atoms created after charge exchange with
interstellar protons compressed and heated in the heliospheric interface. The bulk velocity difference explains
why the IP line profile line width decreases when the upwind angle of the LOS goes from zero to 50![]() .
We also find that the profiles appear cooler during solar maximum than during solar minimum.
This could indicate that the increase of the ionization processes but also radiation pressure
with the solar cycle is more effective on one population than the other. The slower population will be more ionized
than the fast one for instance. Consequently, this will result in narrower line profiles. These results will be compared
with model computations in a future work.
.
We also find that the profiles appear cooler during solar maximum than during solar minimum.
This could indicate that the increase of the ionization processes but also radiation pressure
with the solar cycle is more effective on one population than the other. The slower population will be more ionized
than the fast one for instance. Consequently, this will result in narrower line profiles. These results will be compared
with model computations in a future work.
Direct measurements of the Lyman ![]() line profile require a very good spectral resolution which is not
easily obtained with a space instrument. Fortunately, the STIS instrument on the Hubble Space
Telescope has provided a few measurements in June 2000 and March 2001. This section presents the available
upwind spectrum and a comparison with the results obtained from the SWAN H cell data.
line profile require a very good spectral resolution which is not
easily obtained with a space instrument. Fortunately, the STIS instrument on the Hubble Space
Telescope has provided a few measurements in June 2000 and March 2001. This section presents the available
upwind spectrum and a comparison with the results obtained from the SWAN H cell data.
The data presented in this section were obtained with the STIS instrument on-board the Hubble Space Telescope. One measurement was obtained in March 2001 (Upwind LOS).
The main problem for the observation of the interplanetary line profile from Earth's orbit is caused by the existence of the strong emission of the geocorona. At the altitude of the Hubble Space Telescope, the geocoronal emission is 5 to 15 times brighter than the interplanetary line depending on the direction of the LOS. The best time to observe the interplanetary line is when the Doppler-shift between the two lines is at its maximum. For the upwind direction, this is in March when the Earth velocity vector is toward the upwind direction. In that case, the relative motion between the H atoms and the observer is close to 50 km s-1.
Crosswind observations are limited to a relative velocity of 30 km s-1 because their LOS is perpendicular to the velocity vector of the interstellar H atoms. This maximum value is obtained when the Earth velocity vector is perpendicular to the interstellar wind direction, i.e. either when the Earth is upwind from the Sun (early June) or downwind (early December each year).
![\begin{figure}
\par\includegraphics[width=8cm]{QuemeraisAA5169f08.eps}\end{figure}](/articles/aa/full/2006/33/aa5169-06/Timg56.gif) |
Figure 8: Upwind interplanetary spectrum measured by STIS on March, 21, 2001. The geocorona (dash line) is more intense than the IP line (factor of 6) but the two lines are well separated because of the Doppler shift between the H atoms and the Earth. The geocoronal emission has been fitted and removed, leaving a larger uncertainty longward of the interplanetary line. |
| Open with DEXTER | |
The upwind measurement was obtained on March 21, 2001 when the Doppler shift between the interplanetary line and the geocorona is close to its maximum (Position 2). In that case, the two lines are well separated. Figure 8 shows both the geocorona and the interplanetary line. A symmetric line shape fitting the geocorona has been removed from the data. The residual shows the upwind interplanetary line.
We estimated the LOS values of the velocity and the temperature of the line. The results for
apparent velocity corrected for the Earth's motion is
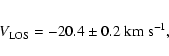
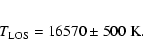
We have used the LSF deduced from the geocorona
to deconvolve the upwind line profile. The result is shown in Fig. 9.
First, the data were fitted to a Voigt function.
Then, this function was deconvolved yielding the spectrum. By assuming that the geocorona
gives the LSF, we have slightly overestimated the actual width of the LSF, as reflected in
the larger uncertainty in the temperature estimate. Future observations of the martian neutral
H atom emission at Lyman ![]() will better estimate the LSF because the martian emission profile has a thermal width
equivalent to a few hundred K (
will better estimate the LSF because the martian emission profile has a thermal width
equivalent to a few hundred K (![]() 200 K).
200 K).
![\begin{figure}
\par\noindent\includegraphics[width=8cm]{QuemeraisAA5169f09.eps}\end{figure}](/articles/aa/full/2006/33/aa5169-06/Timg60.gif) |
Figure 9: Upwind interplanetary spectrum in the solar rest frame. The diamonds show the data, the thin solid line shows a Voigt function fit to the data, the thick solid line shows the deconvolved spectrum obtained from the Voigt function fit assuming that the LSF is given by the geocoronal profile. |
| Open with DEXTER | |
The resulting parameters for the upwind LOS are after deconvolution,
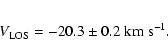
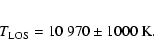
The temperature found from the profile is close to 11 000 K. This value may be slightly
underestimated because the LSF of the STIS instrument is not as wide as the Earth's coronal line. Comparing
with the values shown in Fig. 7, we find correct agreement. This also confirms that
the upwind IP line profile LOS temperature has decreased from 14 000 K to 11 000 K from solar minimum
to solar maximum It also shows that the temperature inflexion seen at 60![]() from upwind at solar minimum
more or less disappeared at solar maximum.
from upwind at solar minimum
more or less disappeared at solar maximum.
This analysis of the SWAN H cell data has allowed us to reconstruct interplanetary Lyman ![]() line profiles
between 1996 and 2003. This period covers the solar activity minimum of 1996 and the maximum of 2001.
line profiles
between 1996 and 2003. This period covers the solar activity minimum of 1996 and the maximum of 2001.
We have found that the mean line shift changes from a LOS velocity of 25.7 km s-1 to 21.4 km s-1 in the solar rest frame. This deceleration is mainly due to changes in radiation pressure with increasing activity, although changes of the ionizing fluxes are also involved. Detailed modelling will be necessary to reproduce this large variation in the mean line shift.
A comparison with a spectrum recorded by STIS on HST yields a good agreement. The STIS line mean shift corresponds to an LOS velocity of 20.3 km s-1 which, given the uncertainties and possible biases involved in both analyses, is quite acceptable. We should also point out that the mean line shift change seen by SWAN is very rapid. We find a variation by 3 km s-1 between 1997 and 1999. This seems hard to explain only by changes in radiation pressure.
The SWAN H cell data were also used to determine line widths (LOS temperature). It is found that the line width variation with upwind angle is not monotonic as is usually found from hot model computations. This can be explained as a proof that the IP line profile is made of two distinct components scattered by populations with different bulk velocities and temperatures. These different components have been theoretically predicted by models of the hydrogen interaction of the heliospheric interface. Here we have an observable effect on the line width which is created by these two populations. Actual model computations of hydrogen distribution and backscattered profiles will be made to test this explanation.
Finally, we found that the LOS temperature profiles are cooler during solar maximum than solar minimum. The line width change corresponds to a decrease in the LOS temperature by 1000 K. A tentative explanation is that the slow hydrogen population component is more effectively ionized than the fast one during solar maximum. This results in a smaller contribution to the total line shape and hence a narrower line profile.
The results obtained in this analysis are summarized by this list
Acknowledgements
SOHO is a mission of international cooperation between ESA and NASA. SWAN was financed in France by the CNES with support from CNRS and in Finland by TEKES and the Finnish Meteorological Institute.