A&A 455, 779-784 (2006)
DOI: 10.1051/0004-6361:20064863
Generation of the magnetic field in jets
V. Urpin1,2
1 - Departament de Física Aplicada, Universitat d'Alacant,
Ap. Correus 99, 03080 Alacant, Spain
2 -
A.F. Ioffe Institute of Physics and Technology and Isaak
Newton Institute of Chili, Branch in St. Petersburg,
194021 St. Petersburg, Russia
Received 16 January 2006 / Accepted 17 April 2006
Abstract
We consider dynamo action under the combined influence of
turbulence and large-scale shear in sheared jets. Shear can stretch
turbulent magnetic field lines in such a way that even turbulent
motions showing mirror symmetry become suitable for generation
of a large-scale magnetic field. We derive the integral induction
equation governing the behaviour of the mean field in jets. The
main result is that sheared jets may generate a large-scale
magnetic field if shear is sufficiently strong. The generated mean
field is mainly concentrated in a magnetic sheath surrounding the
central region of a jet, and it exhibits sign reversals in the
direction of the jet axis. Typically, the magnetic field in a sheath
is dominated by the component along the jet that can reach
equipartition with the kinetic energy of particles. The field
in the central region of jets has a more disordered structure.
Key words: magnetohydrodynamics (MHD) - ISM: jets and outflows - galaxies: jets - ISM: magnetic fields - gravitational lensing - magnetic fields
It is widely believed that magnetic fields play an important
role in the formation and propagation of astrophysical jets providing
an efficient mechanism of collimation through magnetic tension forces
(see, e.g., Hughes 1991; Blandford 1993; Königl & Pudritz 1999).
Polarization observations provide information on the orientation and
degree of order of the magnetic field in jets. It appears that many jets
can develop relatively highly organized magnetic structures
(see, e.g., Cawthorne et al. 1993; Leppänen et al.
1995; Gabuzda 1999). For example, radio emission from the jets of
NGC 4258 indicates that the magnetic field is oriented mainly along
the jet axis but a noticeable toroidal component can also be presented
(Krause & Löhr 2004). The conventional estimate of the magnetic
field strength in jets comes from the minimum energy argument and
corresponds to approximate equipartition between magnetic and jet
particle energy (see, e.g., Laing 1993). Recent observations of jets
in TeV BL Lac objects confirm this estimate (Ghisellini et al. 2005). However, Kataoka & Stawarz (2005)
argue that the powerful jets in quasars and FR II objects can be far
from the minimum energy condition, and the field strength very likely
exceeds the equipartition value. Upper limits to the inverse Compton
radiation of the jet in M 87 imposed by HESS and HEGRA Cerenkov
Telescopes also indicate that the magnetic field cannot be weaker than
the equipartition value (Stawarz et al. 2005).
To explain the observational data, various simplified models of
three-dimensional magnetic structures have been proposed (see, e.g.,
Chan & Henriksen 1980; Laing 1981, 1999). For example, Canvin et al.
(2005) computed emission and polarization for a few different models of
the jets in NGC 315 and concluded that both fully and partially
ordered fields can produce the high fractional polarization observed.
It seems (Laing 1999) that good agreement with observations can be
obtained if the jet is considered as a cylindrical core with more or
less uniform density and pressure surrounded by a shear layer. Possibly,
the core and shear layer are both turbulent (see, e.g., Gabuzda 1999).
The magnetic field has a substantial longitudinal component in the
shear layer, but the field can be random or a transverse component
dominates in the core region. Recent VLBI observations (Hirabayashi
et al. 1998; Gabuzda et al. 2004) indicate that the
transverse field may have a substantial toroidal component in some
objects.
The mechanisms responsible for generation of the magnetic field in
jets are still unclear. Since the origin of jets is probably relevant
to MHD-processes in magnetized plasma, their magnetic fields could be
generated during the process of jet formation (see, e.g., Blandford
& Payne 1982; Romanova & Lovelace 1992; Koide et al. 1998).
However, as mentioned, jets are possibly turbulent, and turbulent
dissipation should lead to a rapid decay of any initially ordered fields
if the mean-field dynamo does not operate. Besides, the toroidal
component becomes dominant as the flow expands (Begelman et al. 1984) and, under certain conditions, this component can be unstable
thereby decollimating the jet (see, e.g., Spruit et al.
1997; Begelman 1998). Therefore, some mechanisms for generating the
magnetic field should certainly be operative in jets. One of these
possibilities has been considered by Honda & Honda (2002), who argued
that the stream can generate a toroidal field that participates in
self-pinching the plasma in a fully relativistic jet consisting of
electrons, positrons, and a small portion of ions.
The magnetic field in jets can also be generated by some dynamo
mechanism. It is plausible that jets are turbulent making the
turbulent dynamo a suitable candidate. This point is argued by
Stawarz et al. (2005) for the particular case of the jet in M 87 where
the field strength is probably stronger than the equipartition value.
The origin of turbulence can be attributed to different instabilities
arising in jets. The classical Kelvin-Helmholtz instability seems to
be the dominating factor of destabilization in the most simplified jet
model with one bulk velocity and a narrow interface with the external
medium. This instability has been studied by many authors both in
linear (e.g., Blandford & Pringle 1976; Ray 1981; Payne & Cohn 1985;
Zhao et al. 1992) and nonlinear regimes (Bodo et al. 1994; Koide et al. 1996; Nishikava et al. 1997; Hardee et al. 1998).
In more refined models, however, other hydrodynamic instabilities can
manifest themselves leading to production of turbulence in jets
(Urpin 2002a; Alloy et al. 2002). Gvaramadze et al. (1984) proposed
the model where the field is generated due to the combined influence
of helical turbulence and regular flow that stretches a seed magnetic
field. In this model, however, the field grows superexponentially only
during the initial stage but decays eventually, sothat a true dynamo is
replaced by a temporal growth of the field.
In this paper, we consider the turbulent dynamo action that can be
responsible for generation of the magnetic field in jets. Our model
is based on the shear-driven dynamo action associated with turbulent
shear flows (see, e.g., Urpin 1999, 2002b). Shear stretches turbulent
magnetic field lines in the direction of a mean flow, which in turn
generates the additional component of the mean electromotive
force, which is proportional to the production of shear and magnetic
field. Plausibly, the flow inside jets is sheared and turbulent, and
the shear-driven dynamo can be in action there. There is observational
evidence that the jet structure is rather complex and that different bulk
velocities can be represented inside the jet; for more details see
the discussion in Hanasz & Sol (1996) and Stawarz & Ostrowski (2002).
Theoretical models of the jet formation also predict the existence of
a nonvanishing transverse gradient in the jet velocity (see, e.g.,
Melia & Königl 1989; Königl & Kartje 1994; Sol et al. 1989).
In the present paper, we show that the shear-driven dynamo can
naturally explain the observed magnetic structure of jets. In Sect. 2,
we derive the main equations governing the magnetic field in sheared
turbulent jets. The geometry and growth rate of the generated field
is then considered in Sect. 3. A brief summary of our results is
finally presented in Sect. 4.
We model the jet as a cylindrical flow in the z-direction with
radius R. Plasma inside the jet has a velocity
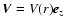 ,
and r,
,
and r, 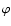 ,
z are the cylindrical coordinates with
,
z are the cylindrical coordinates with
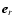 ,
,
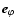 ,
and
,
and
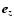 the
corresponding unit vectors. For the sake of simplicity, we assume that
the jet velocity is subrelativistic. Without loss of generality, we
can assume that density
the
corresponding unit vectors. For the sake of simplicity, we assume that
the jet velocity is subrelativistic. Without loss of generality, we
can assume that density 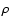 is constant inside the jet. The
Reynolds number is large in jets and, possibly, the plasma of sheared jets
is turbulent. Variations in the flux, which are observed in many
jets, are sometimes interpreted in terms of this turbulence (e.g.,
Marscher et al. 1992; Massaro et al. 1999).
is constant inside the jet. The
Reynolds number is large in jets and, possibly, the plasma of sheared jets
is turbulent. Variations in the flux, which are observed in many
jets, are sometimes interpreted in terms of this turbulence (e.g.,
Marscher et al. 1992; Massaro et al. 1999).
We can represent the magnetic field
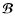 and the velocity
and the velocity
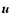 as a sum of the mean and fluctuating parts,
as a sum of the mean and fluctuating parts,
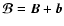 and
and
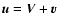 ,
where
,
where 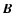 and
and 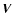 are the mean field and velocity, respectively. We neglect
dissipative effects in the induction equation and assume the field to
be frozen in plasma. Then, averaging the induction equation, we have
for the mean field
are the mean field and velocity, respectively. We neglect
dissipative effects in the induction equation and assume the field to
be frozen in plasma. Then, averaging the induction equation, we have
for the mean field
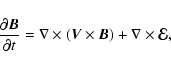 |
(1) |
where
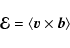 |
(2) |
is the mean electromotive force;
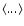 denote ensemble
averaging. In what follows, however, we will need the sign of
dissipative terms to choose the integration path properly when
calculating Fourier integrals. Generally, a weak dissipation in jets
can be provided by either electrical resistivity (if plasma is
collisional) or some plasma mechanisms, such as Landau
damping (if plasma is collisionless).
denote ensemble
averaging. In what follows, however, we will need the sign of
dissipative terms to choose the integration path properly when
calculating Fourier integrals. Generally, a weak dissipation in jets
can be provided by either electrical resistivity (if plasma is
collisional) or some plasma mechanisms, such as Landau
damping (if plasma is collisionless).
We consider the mean electromotive force
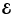 using a
quasilinear approximation. In this approximation, mean quantities are
governed by equations including non-linear effects in fluctuating
terms, whilst the linearized equation is used for the fluctuating
quantities (Krause & Rädler 1980). A quasilinear approximation is
accurate enough, for example, to describe an ensemble of waves
with relatively high frequencies and small amplitudes. Then, the
linearized induction equation for the fluctuating magnetic field
reads
using a
quasilinear approximation. In this approximation, mean quantities are
governed by equations including non-linear effects in fluctuating
terms, whilst the linearized equation is used for the fluctuating
quantities (Krause & Rädler 1980). A quasilinear approximation is
accurate enough, for example, to describe an ensemble of waves
with relatively high frequencies and small amplitudes. Then, the
linearized induction equation for the fluctuating magnetic field
reads
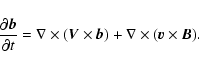 |
(3) |
If
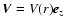 ,
then we have
,
then we have
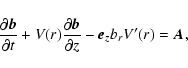 |
(4) |
where
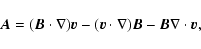 |
(5) |
and
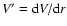 .
.
Equation (4) can be solved by making use of a partial Fourier
transformation. Since coefficients in Eq. (4) do not depend on 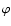 and z we make initial transformations in these
coordinates. The fluctuating magnetic field can be represented as
and z we make initial transformations in these
coordinates. The fluctuating magnetic field can be represented as
where m is an integer. Then,
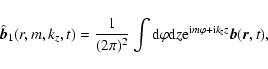 |
(6) |
and the equation for
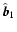 reads
reads
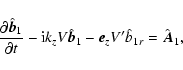 |
(7) |
where
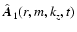 is the corresponding
Fourier amplitude of
is the corresponding
Fourier amplitude of
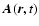 .
Substituting
.
Substituting
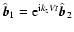 ,
we obtain
the equation for
,
we obtain
the equation for
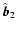 that does not contain the
advective term,
that does not contain the
advective term,
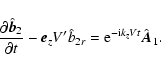 |
(8) |
This equation can be solved by Fourier transformation in t.
Introducing
we obtain the following expression from Eq. (9)
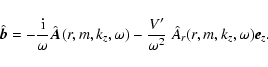 |
(10) |
Expression (10) is not a complete Fourier transform of
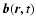 since it depends on the radial coordinate. Note
that, in reality, Eq. (10) does not contain singularities because
neglected dissipative terms would result in small negative imaginary
corrections to
since it depends on the radial coordinate. Note
that, in reality, Eq. (10) does not contain singularities because
neglected dissipative terms would result in small negative imaginary
corrections to 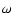 ,
so we would have
,
so we would have
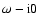 instead of
instead of 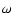 in singular terms. Here,
in singular terms. Here,
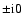 denotes a positive (or
negative)
contribution to
denotes a positive (or
negative)
contribution to 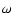 caused by weak dissipative effects. The sign
of this small imaginary term is important when calculating Fourier
integrals.
caused by weak dissipative effects. The sign
of this small imaginary term is important when calculating Fourier
integrals.
The solution for a fluctuating magnetic field reads
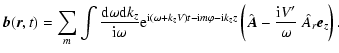 |
|
|
(11) |
Substituting this expression into the definition of
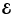 ,
we obtain
,
we obtain
![$\displaystyle \vec{\cal E} = \sum_{m} \int \frac{{\rm d} \omega {\rm d} k_{z}}{...
...c{{\rm i} V'}{\omega}
A_{r}(\vec{r}_{1}, t') \vec{e}_{z} \right] \right\rangle,$](/articles/aa/full/2006/33/aa4863-06/img39.gif) |
|
|
(12) |
where
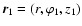 .
Taking into account that
summation over m and integration over dkz yield the corresponding
.
Taking into account that
summation over m and integration over dkz yield the corresponding
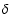 -functions, we can simplify expression (12):
-functions, we can simplify expression (12):
![$\displaystyle \vec{\cal E} = \int \frac{{\rm d} \omega {\rm d}t'}{2 \pi \rm i \...
... t') \vec{e}_{z} \big] \big\rangle
\mid_{\vec{r}' = \vec{r} - \vec{V}(t-t')}\!.$](/articles/aa/full/2006/33/aa4863-06/img42.gif) |
|
|
(13) |
Integrals over d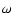 can now be calculated using the known
integrals if we note that
can now be calculated using the known
integrals if we note that 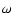 has a small imaginary part caused by
dissipation. We have (see Gradshtein & Ryzhik 1965)
has a small imaginary part caused by
dissipation. We have (see Gradshtein & Ryzhik 1965)
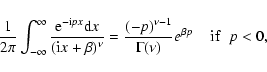 |
(14) |
and 0 if p>0. The parameter 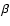 in this integral is small in our
model because it is caused by dissipation. Then, the expression for
in this integral is small in our
model because it is caused by dissipation. Then, the expression for
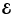 transforms into
transforms into
![$\displaystyle \vec{\cal E} = \int_{-\infty}^{t} {\rm d}t' \langle \vec{v}(\vec{...
..., t') \vec{e}_{z}
\right] \rangle \mid_{\vec{r}' = \vec{r} - \vec{V} (t-t')}\!.$](/articles/aa/full/2006/33/aa4863-06/img45.gif) |
|
|
(15) |
Since
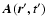 depends on the turbulent velocity
(see Eq. (5)) we can now calculate
depends on the turbulent velocity
(see Eq. (5)) we can now calculate
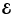 if specifying the
correlation properties of turbulence. For the sake of simplicity, we
assume turbulence to be locally isotropic and homogeneous with the
correlation tensor given by
if specifying the
correlation properties of turbulence. For the sake of simplicity, we
assume turbulence to be locally isotropic and homogeneous with the
correlation tensor given by
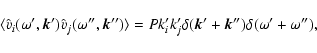 |
(16) |
where
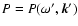 is the spectral function and (i, j)
denote Cartesian components. This correlation tensor corresponds to
acoustic turbulence (see, e.g., Rüdiger 1989), which seems to be
plausible in a supersonic jet flow. For instance, sound waves can be
generated by the Kelvin-Helmholtz instability at the jet boundary and
then propagate through the jet volume generating fluctuations of
the velocity and density (Payne & Cohn 1985).
is the spectral function and (i, j)
denote Cartesian components. This correlation tensor corresponds to
acoustic turbulence (see, e.g., Rüdiger 1989), which seems to be
plausible in a supersonic jet flow. For instance, sound waves can be
generated by the Kelvin-Helmholtz instability at the jet boundary and
then propagate through the jet volume generating fluctuations of
the velocity and density (Payne & Cohn 1985).
Since correlation tensor (16) is of particular simplicity in
Cartesian components, it is convenient to represent the turbulent
velocities
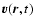 and
and
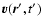 in Eq. (15) in terms of Fourier integrals with Cartesian
wavevectors as
in Eq. (15) in terms of Fourier integrals with Cartesian
wavevectors as
Substituting this expression into Eq. (15), we obtain, after
ensemble averaging,
![$\displaystyle \vec{\cal{E}} = \int_{-\infty}^{t} {\rm d} t' \int {\rm d} \omega...
...\omega', \vec{k}')
[ \vec{E}_{1} - (t-t') V' \vec{e}_{z} \times \vec{E}_{2} ] ,$](/articles/aa/full/2006/33/aa4863-06/img52.gif) |
|
|
(17) |
where
and
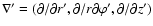 .
Note that
.
Note that 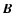 in these expressions is
a function of
in these expressions is
a function of 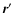 and t'.
and t'.
Since turbulence is locally isotropic and homogeneous in a co-moving
frame, the spectral function
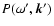 should be an even
function of the frequency
should be an even
function of the frequency
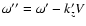 measured in
a co-moving frame, i.e. we have
measured in
a co-moving frame, i.e. we have
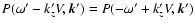 .
Then, denoting
.
Then, denoting
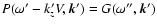 ,
we can transform Eq. (17) into
,
we can transform Eq. (17) into
![$\displaystyle \vec{\cal E}= \int {\rm d} \omega'' {\rm d} \vec{k}' G(\omega'',
...
... (t-t') V' \vec{E}_{2}(\vec{r}',
t')] \vert _{\vec{r}'=\vec{r}- \vec{V}(t-t')}.$](/articles/aa/full/2006/33/aa4863-06/img61.gif) |
|
|
(18) |
Averaging of
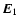 and
and
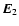 over directions of
over directions of 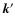 yields
yields
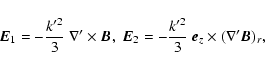 |
(19) |
where
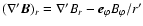 .
Finally, the expression for the mean electromotive
force reads
.
Finally, the expression for the mean electromotive
force reads
![$\displaystyle \vec{\cal{E}} = - \int_{-\infty}^{t} {\rm d}t' F(t-t') [ \nabla' ...
...}_{z} \times (\nabla' \vec{B})_{r}]\vert _{\vec{r}'=
\vec{r} - \vec{V} (t-t')},$](/articles/aa/full/2006/33/aa4863-06/img67.gif) |
|
|
(20) |
where
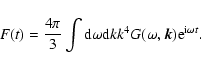 |
(21) |
Note that the mean electromotive force given by Eq. (20) is nonlocal
in our approach since the turbulent magnetic field is determined by
its previous evolution under the influence of shear.
We adopt the simplest model of a jet assuming that shear is
relatively weak in the central region but is stronger in a shear
layer near the jet surface, r=R. If 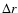 is the thickness of
a shear layer, then the shear-driven dynamo operates in the region
is the thickness of
a shear layer, then the shear-driven dynamo operates in the region
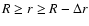 .
Simulations indicate that often the
thickness of a region with strong shear can be much smaller than the
jet radius (see Alloy et al. 1999a,b). At that point, we will not
specify the radial dependence of V(r) because this dependence seems
to be rather uncertain from both theoretical and observational
points of view. However, we show that the proposed mechanism can
generate the magnetic field for any dependence V(r).
.
Simulations indicate that often the
thickness of a region with strong shear can be much smaller than the
jet radius (see Alloy et al. 1999a,b). At that point, we will not
specify the radial dependence of V(r) because this dependence seems
to be rather uncertain from both theoretical and observational
points of view. However, we show that the proposed mechanism can
generate the magnetic field for any dependence V(r).
In a stationary jet, the solution of the mean induction Eq. (1)
can be represented as
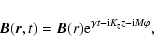 |
(22) |
where Kz is a wavevector of the magnetic field in the
z-direction, M the azimuthal wavenumber, and 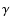 the
growth rate. Solution (22) describes spiral magnetic waves.
the
growth rate. Solution (22) describes spiral magnetic waves.
We are particularly interested in the generation of large-scale fields
with not very large M. Since the thickness of a shear layer is
typically smaller than R, we can neglect terms of the order of 1/r
compared to
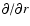 in Eq. (1). Then, the r-component
of Eq. (1) reads
in Eq. (1). Then, the r-component
of Eq. (1) reads
![$\displaystyle \frac{\partial B_{r}}{\partial t} + V(r) \frac{\partial
B_{r}}{\p...
... r' \partial z'}
B_{r}(\vec{r}', t-\xi) \bigg]_{\vec{r}'=\vec{r}- \vec{V} \xi},$](/articles/aa/full/2006/33/aa4863-06/img74.gif) |
|
|
(23) |
where 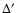 is the Laplacian with the primed coordinates.
Substituting dependence (22) for Br(r), we
obtain
is the Laplacian with the primed coordinates.
Substituting dependence (22) for Br(r), we
obtain
![$\displaystyle [ \gamma- {\rm i} K_{z} V(r)] B_{r}(r) =
\int_{0}^{\infty} {\rm d...
...K_{\perp}^{2} B_{r} + i \xi
V'(r) K_{z} \frac{{\rm d} B_{r}}{{\rm d}r} \right],$](/articles/aa/full/2006/33/aa4863-06/img76.gif) |
|
|
(24) |
where
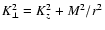 .
Note that the radial
dependence of the azimuthal component of
.
Note that the radial
dependence of the azimuthal component of 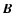 satisfies the same
equation in our model. Integrating Eq. (24) over d
satisfies the same
equation in our model. Integrating Eq. (24) over d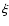 ,
we have
,
we have
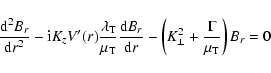 |
(25) |
where
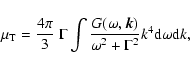 |
(26) |
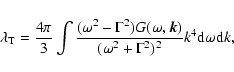 |
(27) |
and
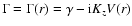 .
The coefficient
.
The coefficient
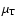 represents a nonlocal magnetic viscosity in a turbulent
shear flow, and the coefficient
represents a nonlocal magnetic viscosity in a turbulent
shear flow, and the coefficient
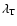 describes a qualitatively
new turbulent kinetic process that can be responsible for the
generation of the mean field. Note that, in our nonlocal model,
turbulent kinetic coefficients depend on the rate of a mean process
that is the principle difference to any local theory like a two-scale
approximation. The kinetic coefficients are complex in our model
since
describes a qualitatively
new turbulent kinetic process that can be responsible for the
generation of the mean field. Note that, in our nonlocal model,
turbulent kinetic coefficients depend on the rate of a mean process
that is the principle difference to any local theory like a two-scale
approximation. The kinetic coefficients are complex in our model
since 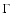 is complex. It is convenient to represent Br(r)
as
is complex. It is convenient to represent Br(r)
as
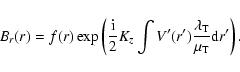 |
(28) |
Then, the equation for f(r) reads
![$\displaystyle \frac{{\rm d}^{2} f}{{\rm d} r^{2}} - \left[K_{\perp}^{2} + \frac...
...rm d}r} \left( V'(r)
\frac{\lambda_{\rm T}}{\mu_{\rm T}} \right) \right] f = 0.$](/articles/aa/full/2006/33/aa4863-06/img87.gif) |
|
|
(29) |
The coefficients
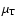 and
and
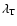 depend on
depend on 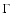 and,
hence, on r, so these dependences are determined by the spectral
function. As mentioned, the origin of turbulent motions, as well
as their spectrum, are rather uncertain in jets. Turbulent motions can
be caused, for example, by acoustic waves generated due to the
Kelvin-Helmholtz instability (see, e.g., Payne & Cohn 1985). In this
paper, we assume as a certainty that turbulence is acoustic and choose
the simplest possible dependence of
and,
hence, on r, so these dependences are determined by the spectral
function. As mentioned, the origin of turbulent motions, as well
as their spectrum, are rather uncertain in jets. Turbulent motions can
be caused, for example, by acoustic waves generated due to the
Kelvin-Helmholtz instability (see, e.g., Payne & Cohn 1985). In this
paper, we assume as a certainty that turbulence is acoustic and choose
the simplest possible dependence of
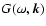 on
on 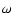 ,
,
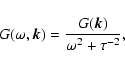 |
(30) |
where 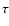 is the characteristic correlation timescale of
turbulence. Dependence (30) corresponds to a velocity correlation
tensor exponentially decreasing with time,
is the characteristic correlation timescale of
turbulence. Dependence (30) corresponds to a velocity correlation
tensor exponentially decreasing with time,
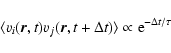 |
(31) |
(see, e.g., Rüdiger 1989). Then, the kinetic coefficients are
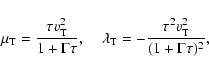 |
(32) |
where 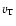 is the characteristic turbulent velocity,
is the characteristic turbulent velocity,
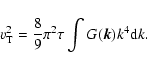 |
(33) |
Substituting expressions (32) into Eq. (29) and taking into
account that
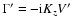 ,
we obtain
,
we obtain
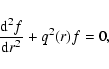 |
(34) |
where
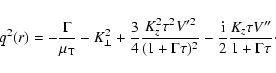 |
(35) |
To solve Eq. (34) one needs the corresponding boundary conditions.
For the sake of simplicity, we assume that plasma inside and outside
of the shear layer is highly conductive and that the mean-field does not
penetrate into the surrounding medium. Then, function f(r)
should be vanishing at r=R and
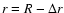 .
The main qualitative
conclusions are the same for other possible boundary conditions.
.
The main qualitative
conclusions are the same for other possible boundary conditions.
To estimate the eigenvalues of Eq. (34), we can use an integral
method similar to the one proposed by Chandrasekhar (1960). Since f is
complex, we multiply Eq. (34) by the complex conjugate function f* and integrate over the whole region where the magnetic field
is generated. Then, we have
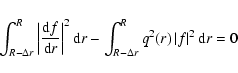 |
(36) |
for the chosen boundary conditions. Both
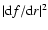 and |f|2
are positive quantities over the integration domain, but q2(r) is
complex. Splitting Eq. (36) into the real and imaginary parts, we
obtain
and |f|2
are positive quantities over the integration domain, but q2(r) is
complex. Splitting Eq. (36) into the real and imaginary parts, we
obtain
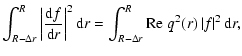 |
|
|
(37) |
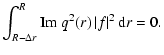 |
|
|
(38) |
By applying the mean value theorem, Eqs. (37) and (38) can be transformed
into
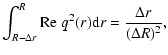 |
|
|
(39) |
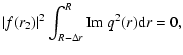 |
|
|
(40) |
where
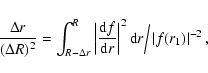 |
(41) |
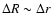 is the characteristic radial lengthscale of
the magnetic field, and r1 and r2 are some mean points within
the shear layer. Equations (39) and (40) can be combined into
is the characteristic radial lengthscale of
the magnetic field, and r1 and r2 are some mean points within
the shear layer. Equations (39) and (40) can be combined into
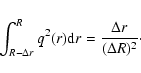 |
(42) |
Substituting expression (35), we obtain the dispersion equation
for dynamo modes
![$\displaystyle \int^{R}_{R-\Delta r} \!\! \left[ \Gamma \tau (1 + \Gamma \tau) \...
...}\! \tau V''}{2 (1 + \Gamma \tau)} \right] {\rm d}r
= -\ell^{2} Q^{2} \Delta r,$](/articles/aa/full/2006/33/aa4863-06/img108.gif) |
|
|
(43) |
where
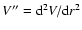 ,
and
,
and
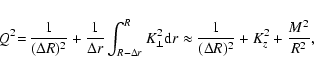 |
(44) |
where Q is the characteristic wavevector of dynamo waves,
and
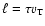 is the lengthscale of turbulence.
is the lengthscale of turbulence.
To estimate the eigenvalues of Eq. (43), we initially consider
the simplest model assuming that shear is approximately linear within
the shear layer,
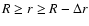 .
In this case, the mean velocity can be represented as
.
In this case, the mean velocity can be represented as
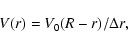 |
(45) |
where V0 is the velocity in the jet core,
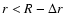 .
Then,
Eq. (43) yields
.
Then,
Eq. (43) yields
![\begin{displaymath}{\rm i}\int^{\tau \Gamma_{\rm e}}_{\tau \Gamma_{\rm i}} \left...
...+ x)^{2}} \right] {\rm d}x
= K_{z} V_{0} \tau \ell^{2} Q^{2},
\end{displaymath}](/articles/aa/full/2006/33/aa4863-06/img114.gif) |
(46) |
where
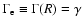 and
and
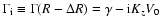 are the values of
are the values of 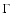 at the outer and inner boundaries of the shear layer. Integrating
Eq. (46), we obtain
at the outer and inner boundaries of the shear layer. Integrating
Eq. (46), we obtain
![$\displaystyle (1 + \gamma \tau)(\gamma - {\rm i} K_{z} V_{0}) + \frac{\rm i}{2}...
...a R)^{2}}{(1 + \gamma \tau)(1 + \gamma \tau -
i \tau K_{z} V_{0})} \right] = 0.$](/articles/aa/full/2006/33/aa4863-06/img117.gif) |
|
|
(47) |
The term proportional to
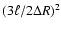 is small in the
mean-field theory and can be neglected compared to 1 in Eq. (47). Then,
the dispersion equation simplifies
is small in the
mean-field theory and can be neglected compared to 1 in Eq. (47). Then,
the dispersion equation simplifies
 |
(48) |
Splitting 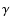 into real and imaginary parts,
into real and imaginary parts,
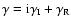 ,
we obtain two equations for
,
we obtain two equations for
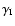 and
and
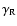 from Eq. (48)
from Eq. (48)
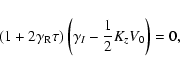 |
(49) |
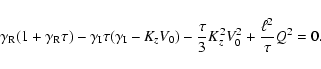 |
(50) |
Equation (49) yields
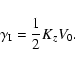 |
(51) |
Then, we have from Eq. (50)
 |
(52) |
The roots of this equation are
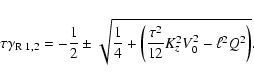 |
(53) |
One of the roots is positive, so the corresponding dynamo
mode is growing if
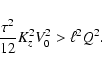 |
(54) |
Estimating
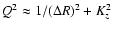 and assuming
that the azimuthal wavelength is much larger than
and assuming
that the azimuthal wavelength is much larger than 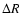 ,
we can
represent Eq. (54) as
,
we can
represent Eq. (54) as
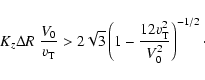 |
(55) |
This condition cannot be fulfilled if
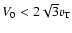 ,
and the dynamo does not operate in such jets. However, it is plausible
that the mean velocity is much larger than the turbulent velocity in jets,
,
and the dynamo does not operate in such jets. However, it is plausible
that the mean velocity is much larger than the turbulent velocity in jets,
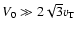 ,
and condition (55) can be satisfied for
a wide range of dynamo modes with
,
and condition (55) can be satisfied for
a wide range of dynamo modes with
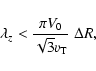 |
(56) |
where
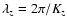 is the wavelength in the z-direction.
Therefore, the maximum longitudinal wavelength of the dynamo-generated
magnetic structure in jets is of the order of
is the wavelength in the z-direction.
Therefore, the maximum longitudinal wavelength of the dynamo-generated
magnetic structure in jets is of the order of
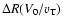 .
.
The generation time,
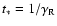 ,
is given by
,
is given by
![\begin{displaymath}t_{*} = 2 \tau \left[ -1 + \sqrt{ 1 + \frac{K_{z}^{2} \tau^{2...
...}^{2}) - \frac{4 \ell^{2}}{(\Delta R)^{2}} }
\right]^{-1}\cdot
\end{displaymath}](/articles/aa/full/2006/33/aa4863-06/img138.gif) |
(57) |
For dynamo waves with a relatively short wavelength,
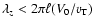 (or
(or
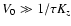 ), the
growth time is
), the
growth time is
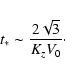 |
(58) |
In the limit of a large wavelength,
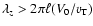 (but still satisfying condition (55)), Eq. (57) yields
(but still satisfying condition (55)), Eq. (57) yields
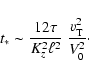 |
(59) |
The dynamo modes with the maximum possible wavelength (
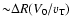 )
grow on the slowest timescale
)
grow on the slowest timescale
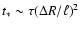 .
.
It is seen from this consideration that generation of the mean-field
is determined by a velocity difference between the boundaries of a shear
layer rather than by the details of the velocity profile. Therefore, our
results can be generalized for any velocity profile in a relatively
simple way. We can split Eq. (43) into the real and imaginary parts and
then obtain equations analogous to Eqs. (51) and (52) by applying the
mean value theorem. The only difference to Eqs. (51) and (52) is that
the equations for a more complicated velocity profile will contain
the value of a flow velocity on some mean point V(r*) (
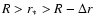 )
instead of V0. Correspondingly, the growth rate
and the generation condition will be given by Eqs. (53) and (54),
respectively, with the replacement
)
instead of V0. Correspondingly, the growth rate
and the generation condition will be given by Eqs. (53) and (54),
respectively, with the replacement
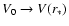 .
Therefore, a particular shape of the velocity profile appears to be
unimportant in our model, and large-scale magnetic fields can be
generated in any jets with a strong shear.
.
Therefore, a particular shape of the velocity profile appears to be
unimportant in our model, and large-scale magnetic fields can be
generated in any jets with a strong shear.
We have considered the turbulent dynamo action in jets. The main
result is that even the simplest turbulent motions showing the mirror
symmetry become suitable for the generation of a large-scale magnetic
field in the presence of shear. An amplification of
the mean field takes place due to non-local terms that appear in the
mean electromotive force and are caused by shear stresses. The
considered mechanism of generation is qualitatively different from
the conventional turbulent alpha-dynamo that, apart from the lack of
the mirror symmetry of turbulence, also requires large-scale
stratification. Due to its simplicity, the proposed mechanism is well
adopted to the physical conditions in jets because the presence of
both shear and turbulence seems to be plausible in a jet flow.
Unfortunately, neither available observational data nor theoretical
modelling provide reliable information concerning the velocity
profile in jets. However, the generation of a large-scale magnetic
field can take place for any velocity profile, which is an attractive
feature of our model. The only necessary condition of the considered
dynamo is the presence of a sufficiently strong shear satisfying
condition (54). This condition can be fulfilled in many jets or,
at least, in a fraction of their volume. This dynamo
mechanism generates the field in jets on a very short timescale that
can be comparable to the turnover time of turbulence 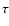 and that
is typically much shorter than the lifetime of jets. Therefore, the
generation can most likely reach a saturation level when the dynamo
works in the nonlinear regime.
and that
is typically much shorter than the lifetime of jets. Therefore, the
generation can most likely reach a saturation level when the dynamo
works in the nonlinear regime.
We considered generation of the radial component of 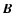 since
this component is the most important one in the shear-driven dynamo.
Generally, two other components can be stronger but their evolution
is determined entirely by the behaviour of Br. We can estimate Bz from the z-component of the mean induction equation, equating
the dissipative and stretching terms. Then,
since
this component is the most important one in the shear-driven dynamo.
Generally, two other components can be stronger but their evolution
is determined entirely by the behaviour of Br. We can estimate Bz from the z-component of the mean induction equation, equating
the dissipative and stretching terms. Then,
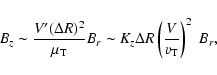 |
(60) |
and the longitudinal magnetic field is always stronger than the
radial one. The azimuthal magnetic field can be estimated from
the divergence condition and can vary within a wide range depending
on the longitudinal wavelength and M. For not very large 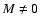 ,
,
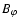 is typically stronger than the radial field. Our
linear analysis does not allow proper estimation of the saturation
magnetic field but, most likely, the strongest field component can
reach equipartition with the kinetic energy of jet particles.
is typically stronger than the radial field. Our
linear analysis does not allow proper estimation of the saturation
magnetic field but, most likely, the strongest field component can
reach equipartition with the kinetic energy of jet particles.
In our model, a dynamo generates a large-scale field in the layer
of the thickness 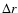 near the jet surface. The shear-driven
dynamo is much less efficient in the core region,
near the jet surface. The shear-driven
dynamo is much less efficient in the core region,
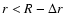 .
However, if the jet is turbulent, the small-scale turbulent dynamo
can amplify small-scale magnetic fields in the core region even if
the shear is negligible. The magnetic Reynolds number is large in jets,
and turbulent motions caused, for example, by instabilities stretch
and distort the field lines increasing thereby the energy of
generated small-scale magnetic fields rapidly (see, e.g., Schekochihin et al.
2001). This random field reaches equipartition with the energy of
turbulent motions on a very short timescale
.
However, if the jet is turbulent, the small-scale turbulent dynamo
can amplify small-scale magnetic fields in the core region even if
the shear is negligible. The magnetic Reynolds number is large in jets,
and turbulent motions caused, for example, by instabilities stretch
and distort the field lines increasing thereby the energy of
generated small-scale magnetic fields rapidly (see, e.g., Schekochihin et al.
2001). This random field reaches equipartition with the energy of
turbulent motions on a very short timescale
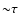 .
Since turbulent motions are less energetic than the mean flow, we can
expect that random fields in the central region are typically weaker
than the large-scale magnetic field in a magnetic sheath surrounding
the jet. The characteristic lengthscale of turbulent
magnetic fields in the central region can be shorter than
.
Since turbulent motions are less energetic than the mean flow, we can
expect that random fields in the central region are typically weaker
than the large-scale magnetic field in a magnetic sheath surrounding
the jet. The characteristic lengthscale of turbulent
magnetic fields in the central region can be shorter than 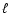 .
.
- Alloy, M. A.,
Ibánez, J. M., Marti, J. M., & Müller, E. 1999a,
ApJS, 122, 151 [NASA ADS] [CrossRef] (In the text)
- Alloy, M. A.,
Ibánez, J. M., Marti, J. M., & Müller, E. 1999b, ApJ,
523, L125 [NASA ADS] [CrossRef]
- Alloy, M. A.,
Ibánez, J. M., Miralles, J. A., & Urpin, V. 2002, A&A,
396, 693 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Begelman, M.
1998, ApJ, 493, 291 [NASA ADS] [CrossRef] (In the text)
- Begelman, M.,
Blandford, R., & Rees, M. 1984, Rev. Mod. Phys., 56, 255 [NASA ADS] [CrossRef] (In the text)
- Blandford, R.
1993, in Astrophysical Jets, ed. D. Burgarella, M. Livio, & C.
P. O'Dea (Cambridge: Cambridge University Press)
(In the text)
- Blandford,
R., & Payne, D. 1982, MNRAS, 199, 883 [NASA ADS] (In the text)
- Blandford,
R., & Pringle, J. E. 1976, MNRAS, 176, 443 [NASA ADS] (In the text)
- Bodo, G., Massaglia,
S., Ferrari, A., & Trussoni, E. 1994, A&A, 283, 655 [NASA ADS] (In the text)
- Canvin, J. R.,
Laing, R. A., Bridle, A. H., & Cotton, W. D. 2005, MNRAS, 363,
1223 [NASA ADS] [CrossRef] (In the text)
- Cawthorne,
T., Wardle, J., Roberts, D., Gabuzda, D., & Brown, L. 1993,
ApJ, 416, 496 [NASA ADS] [CrossRef] (In the text)
- Chan, K. L., &
Henriksen, R. N. 1980, ApJ, 241, 534 [NASA ADS] [CrossRef] (In the text)
-
Chandrasekhar, S. 1960. Proc. Nat. Acad. Sci., 46, 253
(In the text)
- Gabuzda, D. 1999,
in Plasma Turbulence and Energetic Particles in Astrophysics, ed.
M. Ostrowski, & R. Schlickeiser, Krakow: Obserwatorium
Astronomiczne, Universytet Jagiellonski
(In the text)
- Gabuzda, D.,
Murray, E., & Cronin, P. 2004, MNRAS, 351, 89L [NASA ADS] [CrossRef] (In the text)
- Ghisellini,
G., Tavecchio, F., & Chiaberge, M. 2005, A&A, 432, 401 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Gradshtein,
I., & Ryzhik, I. 1965, Table of integrals, series, and
productions (New York: Academic Press)
(In the text)
- Gvaramadze,
V., Lominadze, J., Ruzmaikin, A., Sokoloff, D., & Shukurov, A.
1984, Ap&SS, 140, 165 [NASA ADS] (In the text)
- Hanasz, M., &
Sol, H. 1996, A&A, 315, 355 [NASA ADS] (In the text)
- Hardee, P., Rosen,
A., Hughes, P., & Comer Duncan, G. 1998, ApJ, 500, 599 [NASA ADS] [CrossRef] (In the text)
-
Hirabayashi, H., Hirosawa, H., Kobayashi, H., et al. 1998, Science,
281, 1825 [NASA ADS] [CrossRef] (In the text)
- Honda, M., &
Honda, Y. 2002, ApJ, 569, L39 [NASA ADS] [CrossRef] (In the text)
- Hughes, P. A. 1991,
Beams and Jets in Astrophysics (Cambridge: Cambridge University
Press)
(In the text)
- Kataoka, J.,
& Stawarz, L. 2005, ApJ, 622, 797 [NASA ADS] [CrossRef] (In the text)
- Koide, S., Nishikawa,
K.-I., & Mutel, R.-I. 1996, ApJ, 463, L71 [NASA ADS] [CrossRef] (In the text)
- Koide, S., Shibata,
K., & Kudoh, T. 1998, ApJ, 495, L63 [NASA ADS] [CrossRef] (In the text)
- Königl, A.,
& Kartje, A. 1994, ApJ, 434, 446 [NASA ADS] [CrossRef] (In the text)
- Königl, A.,
& Pudritz, R. 1999, in Protostars and Planets III, ed. V.
Mannings, A. Boss, & S. Russell (Tucson: University of Arizona
Press)
(In the text)
- Krause, F., &
Rädler, K.-H. 1980, Mean-field magnetohydrodynamics and dynamo
theory (Berlin: Akademie-Verlag)
(In the text)
- Krause, M., &
Löhr, A. 2004, A&A, 420, 115 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Laing, R. A. 1981,
ApJ, 248, 87 [NASA ADS] [CrossRef] (In the text)
- Laing, R. A. 1993, in
Astrophysical Jets, ed. D. Burgarella, M. Livio, & C. P. O'Dea
(Cambridge: Cambridge University Press)
(In the text)
- Laing, R. A. 1999, in
Energy Transport in Radio Galaxies and Quasars, ed. P. Hardee, A.
Bridle, & J. Zensus (San Francisco: ASP)
(In the text)
- Leppänen,
K., Zensus, A., & Diamond, P. 1995, AJ, 110, 2479 [NASA ADS] [CrossRef] (In the text)
- Marscher, A.,
Gear, W., & Travis, J. 1992, in Variability of Blazars, ed. E.
Valtaoja, & M. Valtonen (Cambridge: Cambridge University
Press)
(In the text)
- Massaro, E.,
Cipriani, P., Nesci, R., & Tosti, G. 1999, in Plasma Turbulence
and Energetic Particles in Astrophysics, ed. M. Ostrowski, & R.
Schlickeiser, Krakow: Obserwatorium Astronomiczne, Universytet
Jagiellonski
(In the text)
- Melia, F., &
Königl, A. 1989, ApJ, 340, 162 [NASA ADS] [CrossRef] (In the text)
- Nishikawa,
K.-I., Koide, S., Sakai, J., et al. 1998, ApJ, 498, 166 [NASA ADS] [CrossRef]
- Payne, D., &
Cohn, H. 1985, ApJ, 291, 635 [NASA ADS] (In the text)
- Ray, T. 1981, MNRAS, 196,
195 [NASA ADS] (In the text)
- Romanova, M.,
& Lovelace, R. 1992, A&A, 262, 26 [NASA ADS] (In the text)
- Rüdiger, G.
1989, Differential rotation and stellar convection (New York:
Gordon & Breach)
(In the text)
-
Schekochihin, A., Cowley, S., Maron, J., & Malyshkin, L. 2001,
Phys. Rev. E, 65, 6305 (In the text)
- Sol, H., Pelletier, G.,
& Asseo, E. 1989, MNRAS, 237, 411 [NASA ADS] (In the text)
- Spruit, H.,
Foglizzo, T., & Stehle, R. 1997, MNRAS, 288, 333 [NASA ADS] (In the text)
- Stawarz, L.,
& Ostrowski, M. 2002, ApJ, 578, 763 [NASA ADS] [CrossRef] (In the text)
- Stawarz, L.,
Siemiginowska, A., Ostrowski, M., & Sikora, M. 2005. ApJ, 626,
120
(In the text)
- Urpin, V. 1999,
A&A, 347, L47 [NASA ADS] (In the text)
- Urpin, V. 2002a,
A&A, 385, 14 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Urpin, V. 2002b,
Phys. Rev. E, 65, 6301 [NASA ADS]
- Zhao, J.-H., Burus, J.,
Hardee, P., & Norman, M. 1992. ApJ, 387, 69
(In the text)
Copyright ESO 2006
![]() ,
and r,
,
and r, ![]() ,
z are the cylindrical coordinates with
,
z are the cylindrical coordinates with
![]() ,
,
![]() ,
and
,
and
![]() the
corresponding unit vectors. For the sake of simplicity, we assume that
the jet velocity is subrelativistic. Without loss of generality, we
can assume that density
the
corresponding unit vectors. For the sake of simplicity, we assume that
the jet velocity is subrelativistic. Without loss of generality, we
can assume that density ![]() is constant inside the jet. The
Reynolds number is large in jets and, possibly, the plasma of sheared jets
is turbulent. Variations in the flux, which are observed in many
jets, are sometimes interpreted in terms of this turbulence (e.g.,
Marscher et al. 1992; Massaro et al. 1999).
is constant inside the jet. The
Reynolds number is large in jets and, possibly, the plasma of sheared jets
is turbulent. Variations in the flux, which are observed in many
jets, are sometimes interpreted in terms of this turbulence (e.g.,
Marscher et al. 1992; Massaro et al. 1999).
![]() and the velocity
and the velocity
![]() as a sum of the mean and fluctuating parts,
as a sum of the mean and fluctuating parts,
![]() and
and
![]() ,
where
,
where ![]() and
and ![]() are the mean field and velocity, respectively. We neglect
dissipative effects in the induction equation and assume the field to
be frozen in plasma. Then, averaging the induction equation, we have
for the mean field
are the mean field and velocity, respectively. We neglect
dissipative effects in the induction equation and assume the field to
be frozen in plasma. Then, averaging the induction equation, we have
for the mean field
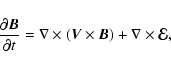
![]() using a
quasilinear approximation. In this approximation, mean quantities are
governed by equations including non-linear effects in fluctuating
terms, whilst the linearized equation is used for the fluctuating
quantities (Krause & Rädler 1980). A quasilinear approximation is
accurate enough, for example, to describe an ensemble of waves
with relatively high frequencies and small amplitudes. Then, the
linearized induction equation for the fluctuating magnetic field
reads
using a
quasilinear approximation. In this approximation, mean quantities are
governed by equations including non-linear effects in fluctuating
terms, whilst the linearized equation is used for the fluctuating
quantities (Krause & Rädler 1980). A quasilinear approximation is
accurate enough, for example, to describe an ensemble of waves
with relatively high frequencies and small amplitudes. Then, the
linearized induction equation for the fluctuating magnetic field
reads
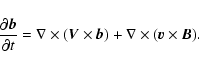
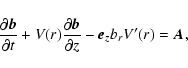
![]() and z we make initial transformations in these
coordinates. The fluctuating magnetic field can be represented as
and z we make initial transformations in these
coordinates. The fluctuating magnetic field can be represented as
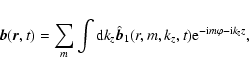
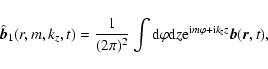
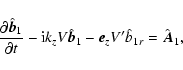
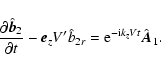
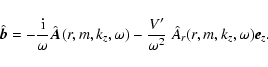
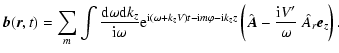
![$\displaystyle \vec{\cal E} = \sum_{m} \int \frac{{\rm d} \omega {\rm d} k_{z}}{...
...c{{\rm i} V'}{\omega}
A_{r}(\vec{r}_{1}, t') \vec{e}_{z} \right] \right\rangle,$](/articles/aa/full/2006/33/aa4863-06/img39.gif)
![$\displaystyle \vec{\cal E} = \int \frac{{\rm d} \omega {\rm d}t'}{2 \pi \rm i \...
... t') \vec{e}_{z} \big] \big\rangle
\mid_{\vec{r}' = \vec{r} - \vec{V}(t-t')}\!.$](/articles/aa/full/2006/33/aa4863-06/img42.gif)
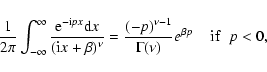
![$\displaystyle \vec{\cal E} = \int_{-\infty}^{t} {\rm d}t' \langle \vec{v}(\vec{...
..., t') \vec{e}_{z}
\right] \rangle \mid_{\vec{r}' = \vec{r} - \vec{V} (t-t')}\!.$](/articles/aa/full/2006/33/aa4863-06/img45.gif)
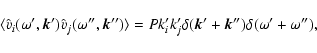
![]() and
and
![]() in Eq. (15) in terms of Fourier integrals with Cartesian
wavevectors as
in Eq. (15) in terms of Fourier integrals with Cartesian
wavevectors as
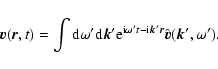
![$\displaystyle \vec{\cal{E}} = \int_{-\infty}^{t} {\rm d} t' \int {\rm d} \omega...
...\omega', \vec{k}')
[ \vec{E}_{1} - (t-t') V' \vec{e}_{z} \times \vec{E}_{2} ] ,$](/articles/aa/full/2006/33/aa4863-06/img52.gif)
![\begin{displaymath}\vec{E}_{1} = -\vec{k}' \times [ {\rm i} k'^{2} \vec{B} +
(\vec{k}' \cdot \nabla') \vec{B} ] ,
\end{displaymath}](/articles/aa/full/2006/33/aa4863-06/img53.gif)
![\begin{displaymath}\vec{E}_{2} = \vec{e}_{z} \times \vec{k}'
\{ {\rm i} k'_{r} (...
... i} k'^{2} B_{r} -
[(\vec{k}' \cdot \nabla' ) \vec{B}]_{r} \},
\end{displaymath}](/articles/aa/full/2006/33/aa4863-06/img54.gif)
![]() should be an even
function of the frequency
should be an even
function of the frequency
![]() measured in
a co-moving frame, i.e. we have
measured in
a co-moving frame, i.e. we have
![]() .
Then, denoting
.
Then, denoting
![]() ,
we can transform Eq. (17) into
,
we can transform Eq. (17) into
![$\displaystyle \vec{\cal E}= \int {\rm d} \omega'' {\rm d} \vec{k}' G(\omega'',
...
... (t-t') V' \vec{E}_{2}(\vec{r}',
t')] \vert _{\vec{r}'=\vec{r}- \vec{V}(t-t')}.$](/articles/aa/full/2006/33/aa4863-06/img61.gif)
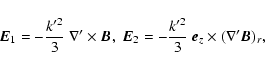
![$\displaystyle \vec{\cal{E}} = - \int_{-\infty}^{t} {\rm d}t' F(t-t') [ \nabla' ...
...}_{z} \times (\nabla' \vec{B})_{r}]\vert _{\vec{r}'=
\vec{r} - \vec{V} (t-t')},$](/articles/aa/full/2006/33/aa4863-06/img67.gif)
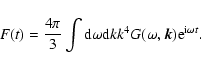
![]() is the thickness of
a shear layer, then the shear-driven dynamo operates in the region
is the thickness of
a shear layer, then the shear-driven dynamo operates in the region
![]() .
Simulations indicate that often the
thickness of a region with strong shear can be much smaller than the
jet radius (see Alloy et al. 1999a,b). At that point, we will not
specify the radial dependence of V(r) because this dependence seems
to be rather uncertain from both theoretical and observational
points of view. However, we show that the proposed mechanism can
generate the magnetic field for any dependence V(r).
.
Simulations indicate that often the
thickness of a region with strong shear can be much smaller than the
jet radius (see Alloy et al. 1999a,b). At that point, we will not
specify the radial dependence of V(r) because this dependence seems
to be rather uncertain from both theoretical and observational
points of view. However, we show that the proposed mechanism can
generate the magnetic field for any dependence V(r).
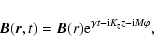
![]() in Eq. (1). Then, the r-component
of Eq. (1) reads
in Eq. (1). Then, the r-component
of Eq. (1) reads
![$\displaystyle \frac{\partial B_{r}}{\partial t} + V(r) \frac{\partial
B_{r}}{\p...
... r' \partial z'}
B_{r}(\vec{r}', t-\xi) \bigg]_{\vec{r}'=\vec{r}- \vec{V} \xi},$](/articles/aa/full/2006/33/aa4863-06/img74.gif)
![$\displaystyle [ \gamma- {\rm i} K_{z} V(r)] B_{r}(r) =
\int_{0}^{\infty} {\rm d...
...K_{\perp}^{2} B_{r} + i \xi
V'(r) K_{z} \frac{{\rm d} B_{r}}{{\rm d}r} \right],$](/articles/aa/full/2006/33/aa4863-06/img76.gif)
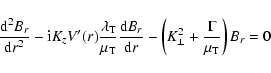
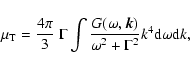
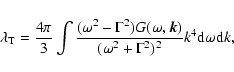
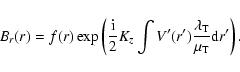
![$\displaystyle \frac{{\rm d}^{2} f}{{\rm d} r^{2}} - \left[K_{\perp}^{2} + \frac...
...rm d}r} \left( V'(r)
\frac{\lambda_{\rm T}}{\mu_{\rm T}} \right) \right] f = 0.$](/articles/aa/full/2006/33/aa4863-06/img87.gif)
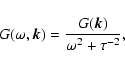
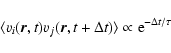
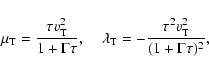
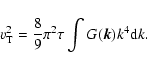
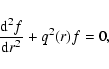
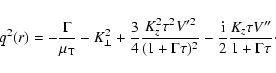
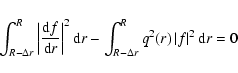
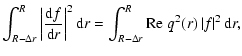
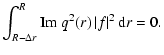
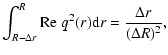
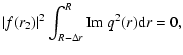
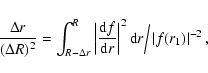
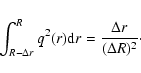
![$\displaystyle \int^{R}_{R-\Delta r} \!\! \left[ \Gamma \tau (1 + \Gamma \tau) \...
...}\! \tau V''}{2 (1 + \Gamma \tau)} \right] {\rm d}r
= -\ell^{2} Q^{2} \Delta r,$](/articles/aa/full/2006/33/aa4863-06/img108.gif)
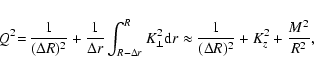
![]() .
In this case, the mean velocity can be represented as
.
In this case, the mean velocity can be represented as
![\begin{displaymath}{\rm i}\int^{\tau \Gamma_{\rm e}}_{\tau \Gamma_{\rm i}} \left...
...+ x)^{2}} \right] {\rm d}x
= K_{z} V_{0} \tau \ell^{2} Q^{2},
\end{displaymath}](/articles/aa/full/2006/33/aa4863-06/img114.gif)
![$\displaystyle (1 + \gamma \tau)(\gamma - {\rm i} K_{z} V_{0}) + \frac{\rm i}{2}...
...a R)^{2}}{(1 + \gamma \tau)(1 + \gamma \tau -
i \tau K_{z} V_{0})} \right] = 0.$](/articles/aa/full/2006/33/aa4863-06/img117.gif)

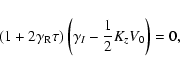
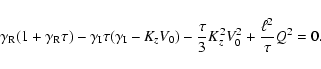
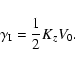

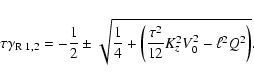
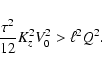
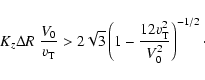
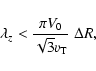
![]() ,
is given by
,
is given by
![\begin{displaymath}t_{*} = 2 \tau \left[ -1 + \sqrt{ 1 + \frac{K_{z}^{2} \tau^{2...
...}^{2}) - \frac{4 \ell^{2}}{(\Delta R)^{2}} }
\right]^{-1}\cdot
\end{displaymath}](/articles/aa/full/2006/33/aa4863-06/img138.gif)
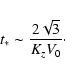
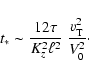
![]() )
instead of V0. Correspondingly, the growth rate
and the generation condition will be given by Eqs. (53) and (54),
respectively, with the replacement
)
instead of V0. Correspondingly, the growth rate
and the generation condition will be given by Eqs. (53) and (54),
respectively, with the replacement
![]() .
Therefore, a particular shape of the velocity profile appears to be
unimportant in our model, and large-scale magnetic fields can be
generated in any jets with a strong shear.
.
Therefore, a particular shape of the velocity profile appears to be
unimportant in our model, and large-scale magnetic fields can be
generated in any jets with a strong shear.
![]() and that
is typically much shorter than the lifetime of jets. Therefore, the
generation can most likely reach a saturation level when the dynamo
works in the nonlinear regime.
and that
is typically much shorter than the lifetime of jets. Therefore, the
generation can most likely reach a saturation level when the dynamo
works in the nonlinear regime.
![]() since
this component is the most important one in the shear-driven dynamo.
Generally, two other components can be stronger but their evolution
is determined entirely by the behaviour of Br. We can estimate Bz from the z-component of the mean induction equation, equating
the dissipative and stretching terms. Then,
since
this component is the most important one in the shear-driven dynamo.
Generally, two other components can be stronger but their evolution
is determined entirely by the behaviour of Br. We can estimate Bz from the z-component of the mean induction equation, equating
the dissipative and stretching terms. Then,
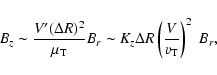
![]() near the jet surface. The shear-driven
dynamo is much less efficient in the core region,
near the jet surface. The shear-driven
dynamo is much less efficient in the core region,
![]() .
However, if the jet is turbulent, the small-scale turbulent dynamo
can amplify small-scale magnetic fields in the core region even if
the shear is negligible. The magnetic Reynolds number is large in jets,
and turbulent motions caused, for example, by instabilities stretch
and distort the field lines increasing thereby the energy of
generated small-scale magnetic fields rapidly (see, e.g., Schekochihin et al.
2001). This random field reaches equipartition with the energy of
turbulent motions on a very short timescale
.
However, if the jet is turbulent, the small-scale turbulent dynamo
can amplify small-scale magnetic fields in the core region even if
the shear is negligible. The magnetic Reynolds number is large in jets,
and turbulent motions caused, for example, by instabilities stretch
and distort the field lines increasing thereby the energy of
generated small-scale magnetic fields rapidly (see, e.g., Schekochihin et al.
2001). This random field reaches equipartition with the energy of
turbulent motions on a very short timescale
![]() .
Since turbulent motions are less energetic than the mean flow, we can
expect that random fields in the central region are typically weaker
than the large-scale magnetic field in a magnetic sheath surrounding
the jet. The characteristic lengthscale of turbulent
magnetic fields in the central region can be shorter than
.
Since turbulent motions are less energetic than the mean flow, we can
expect that random fields in the central region are typically weaker
than the large-scale magnetic field in a magnetic sheath surrounding
the jet. The characteristic lengthscale of turbulent
magnetic fields in the central region can be shorter than ![]() .
.