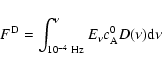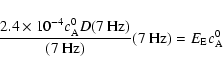A&A 455, 1073-1080 (2006)
DOI: 10.1051/0004-6361:20064816
A mechanism for parallel electric field generation in the MHD limit:
possible implications for the coronal heating problem in the two stage mechanism
D. Tsiklauri
Institute for Materials Research,
University of Salford, Greater Manchester, M5 4WT, UK
Received 5 January 2006 / Accepted 3 April 2006
Abstract
Context. Using Particle-In-Cell simulations i.e. in the kinetic plasma description, the discovery of a new mechanism of parallel electric field generation was recently reported.
Aims. We show that the electric field generation parallel to the uniform unperturbed magnetic field can be obtained in a much simpler framework using the ideal magnetohydrodynamics (MHD) description.
Methods. We solve numerically ideal, 2.5D, MHD equations in Cartesian coordinates, with a plasma beta of 0.0001 starting from the equilibrium that mimics a footpoint of a large curvature radius, solar coronal loop or a polar region plume. On top of such an equilibrium, a purely Alfvénic, linearly polarised, plane wave is launched.
Results. In ideal MHD the electric field parallel to the uniform unperturbed magnetic field appears due to fast magnetosonic waves which are generated by the interaction of weakly non-linear Alfvén waves with the transverse density inhomogeneity. In the context of the coronal heating problem a new two stage mechanism of plasma heating is presented by putting emphasis, first, on the generation of parallel electric fields within an ideal MHD description directly, rather than focusing on the enhanced dissipation mechanisms of the Alfvén waves and, second, dissipation of these parallel electric fields via kinetic effects. It is shown that for a single Alfvén wave harmonic with frequency 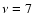 Hz and longitudinal wavelength
Hz and longitudinal wavelength
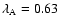 Mm, and a putative Alfvén speed of 4328 km s-1, the generated parallel electric field could account for 10% of the necessary coronal heating requirement. It is also shown that the amplitude of the generated parallel electric field exceeds the Dreicer electric field by about four orders of magnitude, which implies realisation of the run-away regime with associated electron acceleration.
Mm, and a putative Alfvén speed of 4328 km s-1, the generated parallel electric field could account for 10% of the necessary coronal heating requirement. It is also shown that the amplitude of the generated parallel electric field exceeds the Dreicer electric field by about four orders of magnitude, which implies realisation of the run-away regime with associated electron acceleration.
Conclusions. We conjecture that wide spectrum (10
-4-103 Hz) Alfvén waves, based on the observationally constrained spectrum, could provide the necessary coronal heating requirement. The exact amount of energy that could be deposited by such waves through our mechanism of parallel electric field generation can only be calculated once a more complete parametric study is done. Thus, the "theoretical spectrum'' of the energy stored in parallel electric fields versus frequency needs to be obtained.
Key words: Sun: oscillations - Sun: Corona - Sun: solar wind
The coronal heating problem, the puzzle of what maintains the solar corona 200 times
hotter than the photosphere, is one of the main outstanding questions in solar physics
(see e.g. Tsiklauri 2005, for a recent brief review on the subject).
A significant amount of work has been done in the context of heating of open
magnetic structures in the solar
corona (Hood et al. 2002; Tsiklauri et al. 2003; DeMoortel et al. 2000; Nocera et al. 1986; Nakariakov et al. 1997; Parker 1991; Tsiklauri et al. 2002,2001; Tsiklauri & Nakariakov 2002; Botha et al. 2000; Heyvaerts & Priest 1983).
Historically, all phase mixing studies have been performed in the Magnetohydrodynamic (MHD) approximation;
however, since the transverse scales in the Alfvén wave collapse progressively to zero,
the MHD approximation is inevitably violated.
Thus, Tsiklauri et al. (2005b,a) studied the phase mixing effect in the kinetic regime, using Particle-In-Cell simulations, i.e. beyond an MHD approximation, where
a new mechanism for the acceleration of electrons
due to the generation of a parallel electric field in the solar coronal context was discovered.
This mechanism has important implications for various space and laboratory plasmas, e.g. the
coronal heating problem and acceleration of the solar wind.
It turns out that in the magnetosphere a similar parallel electric field generation
mechanism in transversely inhomogeneous plasmas has been reported
(Génot et al. 2004,1999). See also Mottez et al. (2006) and references therein.
This new mechanism occurs when an Alfvén wave moves along the field in
a plasma with a transverse density inhomogeneity. The progressive distortion of the Alfvén wave front due to differences of local Alfvén speed then generates the parallel electric field.
In this work we show that the electric field generation parallel to the uniform unperturbed magnetic field can be obtained in a much simpler framework
using an ideal MHD description, i.e. without resorting to complicated wave particle interaction effects such as ion polarisation drift and resulting space charge separation, which seems to be the fundamental cause of electron acceleration.
See also the Discussion section for a more detailed account of what led us to consider the MHD approximation for parallel electric field generation.
In this paper, we also explore the implications of this effect for the coronal heating problem.
Preliminary results have been reported elsewhere (Tsiklauri 2006).
The present study explores the importance of MHD versus kinetic effects in solar plasmas, which
has recently attracted considerable attention due to apparent difficulties in the coronal heating problem, as well as the natural tendency of
wave heating models to proceed to progressively small spatial scales.
Also, recent observations have indicated further sub-structuring
of the coronal morphology (McEwan & DeMoortel 2006), which is relevant
to our earlier work (Tsiklauri 2005).
Unlike previous studies (Tsiklauri et al. 2005b; Génot et al. 2004; Tsiklauri et al. 2005a; Génot et al. 1999), here we use an ideal MHD description of the problem. We solve numerically ideal, 2.5D, MHD equations in Cartesian coordinates,
with a plasma beta of 0.0001 starting from the following equilibrium
configuration: A uniform magnetic field B0 in the z-direction penetrates plasma with the density inhomogeneity across the x-direction, which varies according to
![\begin{displaymath}%
\rho(x)=\rho_0\left[1+2\left(\tanh(x+10)+\tanh(-x+10)\right)\right].
\end{displaymath}](/articles/aa/full/2006/33/aa4816-06/img9.gif) |
(1) |
This means that the plasma density increases from some reference background value of 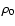 ,
which in our case was fixed at
,
which in our case was fixed at 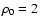

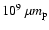 g cm-3 (with a molecular weight of
g cm-3 (with a molecular weight of 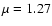 corresponding to the solar coronal conditions 1H:4He = 10:1, Aschwanden (2004) and
corresponding to the solar coronal conditions 1H:4He = 10:1, Aschwanden (2004) and 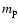 being the proton mass), to
being the proton mass), to 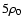 .
Such a density profile across the magnetic field has steep gradients with a half-width of 3 Mm around
.
Such a density profile across the magnetic field has steep gradients with a half-width of 3 Mm around
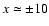 Mm and is essentially flat elsewhere. Such a structure mimics e.g.
the footpoint of a large curvature radius solar coronal loop or a polar
region plume with the ratio of the density inhomogeneity scale and the loop/plume radius of 0.3, which is the median value of the observed range 0.15-0.5 (Goossens et al. 2002). The above quoted values of coordinate x are in dimensionless units. We use the following usual normalisation
Mm and is essentially flat elsewhere. Such a structure mimics e.g.
the footpoint of a large curvature radius solar coronal loop or a polar
region plume with the ratio of the density inhomogeneity scale and the loop/plume radius of 0.3, which is the median value of the observed range 0.15-0.5 (Goossens et al. 2002). The above quoted values of coordinate x are in dimensionless units. We use the following usual normalisation
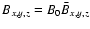 ,
,
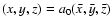 ,
,
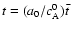 .
Here we fix B0 to 100 G, and hence the dimensional Alfvén speed,
.
Here we fix B0 to 100 G, and hence the dimensional Alfvén speed,
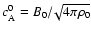 turns out to be 4328 km s-1 = 0.0144 c (c is the speed of light).
The reference length a0 was fixed to 1 Mm, i.e. the dimensionless time of unity corresponds to 0.2311 s. We usually omit the bar on the top of normalised quantities, hence when
numbers are quoted without units, we refer to dimensionless units as defined above.
The dimensionless Alfvén speed (normalised to
turns out to be 4328 km s-1 = 0.0144 c (c is the speed of light).
The reference length a0 was fixed to 1 Mm, i.e. the dimensionless time of unity corresponds to 0.2311 s. We usually omit the bar on the top of normalised quantities, hence when
numbers are quoted without units, we refer to dimensionless units as defined above.
The dimensionless Alfvén speed (normalised to
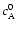 )
is then
)
is then
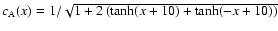 .
The simulation domain spans from -40 Mm to 40 Mm in both x- and z-directions
with the density ramp as described above mimicking a footpoint fragment
of a solar coronal loop or a polar region plume. Our initial equilibrium is depicted in Fig. 1.
.
The simulation domain spans from -40 Mm to 40 Mm in both x- and z-directions
with the density ramp as described above mimicking a footpoint fragment
of a solar coronal loop or a polar region plume. Our initial equilibrium is depicted in Fig. 1.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{4816f1.eps}\end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg23.gif) |
Figure 1:
Dimensionless density (Eq. (1)), solid line, and Alfvén speed, dashed line, profiles across the uniform unperturbed magnetic field (i.e. along x-coordinate) which is
used as an equilibrium configuration in our model of a footpoint of a solar coronal loop or a polar region plume. |
| Open with DEXTER |
The initial conditions for the numerical simulation are
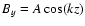 and
and
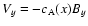 at t=0, which means that a purely
Alfvénic, linearly polarised, plane wave is launched travelling in the
direction of positive zs. The rest of the physical quantities, Vx and Bx (which
would be components of fast magnetosonic waves if the medium were totally homogeneous)
and Vz and Bz (the analogs of slow magnetosonic waves) are initially set
to zero. The plasma temperature is varied as the inverse of Eq. (1) so that the total pressure always remains constant. Boundary conditions used in our simulations are periodic along the z- and the zero gradient along the x-coordinates.
We fixed the amplitude of the Alfvén wave A at 0.05 throughout. This choice makes
the Alfvén wave weakly non-linear. Our motivation for this value was two-fold:
First, this was the value used by Tsiklauri et al. (2005b); Génot et al. (2004), and as one of our
goals here is to show that the parallel electric field generation is also
possible in the MHD limit, we use this value. Tsiklauri et al. (2005b) only used one value of A=0.05, while
Génot et al. (2004) used several values of A and showed that weak non-linearity
(at
at t=0, which means that a purely
Alfvénic, linearly polarised, plane wave is launched travelling in the
direction of positive zs. The rest of the physical quantities, Vx and Bx (which
would be components of fast magnetosonic waves if the medium were totally homogeneous)
and Vz and Bz (the analogs of slow magnetosonic waves) are initially set
to zero. The plasma temperature is varied as the inverse of Eq. (1) so that the total pressure always remains constant. Boundary conditions used in our simulations are periodic along the z- and the zero gradient along the x-coordinates.
We fixed the amplitude of the Alfvén wave A at 0.05 throughout. This choice makes
the Alfvén wave weakly non-linear. Our motivation for this value was two-fold:
First, this was the value used by Tsiklauri et al. (2005b); Génot et al. (2004), and as one of our
goals here is to show that the parallel electric field generation is also
possible in the MHD limit, we use this value. Tsiklauri et al. (2005b) only used one value of A=0.05, while
Génot et al. (2004) used several values of A and showed that weak non-linearity
(at
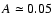 ), in addition to the transverse density inhomogeneity, of
course, is a key factor that facilitates parallel electric field generation.
Smaller As reduced the effect of parallel electric field generation.
Second, the observed values of the Alfvén waves at heights of
), in addition to the transverse density inhomogeneity, of
course, is a key factor that facilitates parallel electric field generation.
Smaller As reduced the effect of parallel electric field generation.
Second, the observed values of the Alfvén waves at heights of
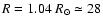 Mm are about 50 km s-1, which for a typical
Alfvén speed of 1000 km s-1 makes A equal to 0.05.
Such observations (see e.g. Banerjee et al. (1998); Moran (2001); Doyle et al. (1998)) indicate that
off limb, heavy element (e.g. Si VIII) line broadening is
beyond the thermal one, and hence mostly undamped, outward
propagating Alfvén waves travel through the stratified plasma with
increasing amplitude (due to the stratification).
Mm are about 50 km s-1, which for a typical
Alfvén speed of 1000 km s-1 makes A equal to 0.05.
Such observations (see e.g. Banerjee et al. (1998); Moran (2001); Doyle et al. (1998)) indicate that
off limb, heavy element (e.g. Si VIII) line broadening is
beyond the thermal one, and hence mostly undamped, outward
propagating Alfvén waves travel through the stratified plasma with
increasing amplitude (due to the stratification).
All previous AC-type models of coronal heating focused
on the mechanisms (e.g. phase mixing or resonant absorption)
that could enhance damping of the Alfvén waves.
However, for the coronal value of shear (Braginskii) viscosity,
by which Alfvén waves damp of about 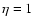 m2 s-1, typical dissipation lengths (e-fold decrease of Alfvén wave amplitude over those lengths) are
m2 s-1, typical dissipation lengths (e-fold decrease of Alfvén wave amplitude over those lengths) are 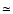 1000 Mm.
Invoking the somewhat ad hoc concept of enhanced (anomalous) resistivity
can reduce the dissipation length to the required value of the
order of the hydrodynamic pressure scale height
1000 Mm.
Invoking the somewhat ad hoc concept of enhanced (anomalous) resistivity
can reduce the dissipation length to the required value of the
order of the hydrodynamic pressure scale height
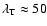 Mm.
In this light (observation of mostly undamped Alfvén waves
and the inability of classical (Braginskii) viscosity to produce a short enough
dissipation length), it seems reasonable to focus rather on the generation
of parallel electric fields which would guarantee plasma heating, should
the energy density of the parallel electric fields be large enough.
In both cases (AC-type MHD models and our model with parallel electric field generation)
the energy comes from Alfvén waves. Therefore observing undamped Alfvén waves could mean two things: (i) the Alfvén waves observed through Doppler line broadening are low frequency ones, while high frequency Alfvén waves produce heating, hence they do not
contribute to the observed line broadening. Clearly one cannot observe waves that have already dissipated; (ii) stratification (increase of Alfvén wave amplitude with height) could be balanced by the damping.
Mm.
In this light (observation of mostly undamped Alfvén waves
and the inability of classical (Braginskii) viscosity to produce a short enough
dissipation length), it seems reasonable to focus rather on the generation
of parallel electric fields which would guarantee plasma heating, should
the energy density of the parallel electric fields be large enough.
In both cases (AC-type MHD models and our model with parallel electric field generation)
the energy comes from Alfvén waves. Therefore observing undamped Alfvén waves could mean two things: (i) the Alfvén waves observed through Doppler line broadening are low frequency ones, while high frequency Alfvén waves produce heating, hence they do not
contribute to the observed line broadening. Clearly one cannot observe waves that have already dissipated; (ii) stratification (increase of Alfvén wave amplitude with height) could be balanced by the damping.
![\begin{figure}
\par\includegraphics[width=5.7cm,clip]{4816f2a.eps}\hspace*{5mm}
...
...c.eps}\hspace*{5mm}
\includegraphics[width=5.7cm,clip]{4816f2d.eps} \end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg31.gif) |
Figure 2:
Intensity plots of Vx and Ez at t=2 and 20 for the case of k=1, 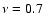 Hz, Hz,
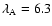 Mm. Mm. |
| Open with DEXTER |
We emphasise parallel electric fields because in the direction parallel
to the magnetic field electrons (and protons) are not constrained.
In the direction perpendicular to the magnetic field,
particles are constrained because of the large classical conductivity
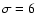
 1016 s-1 (for T=2 MK corona) and inhibited
momentum transport across the magnetic field. The parameter that controls
cross-field transport (flow) is
1016 s-1 (for T=2 MK corona) and inhibited
momentum transport across the magnetic field. The parameter that controls
cross-field transport (flow) is 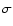 ,
and not plasma
,
and not plasma 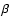 which merely
controls compressibility of the plasma. This is often confused in the literature.
which merely
controls compressibility of the plasma. This is often confused in the literature.
In the ideal, linear MHD limit there are no parallel electric fields associated with the
Alfvén wave. In the single fluid MHD the equation for the electric field
can be obtained by differentiating Ohm's law over time and then using
Maxwell's equations, expressing
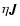 by
by 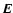 (Krall & Trivelpiece 1973):
(Krall & Trivelpiece 1973):
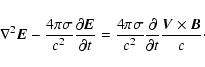 |
(2) |
However, in the coronal plasma conductivity is so large that
a more simple relation (obtained from Eq. (2)) can be used:
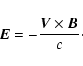 |
(3) |
It is clear from the latter equation that the
parallel electric field is
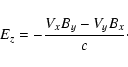 |
(4) |
This means that in the considered system Ez can only be generated if the initial
Alfvén wave (Vy,By) is able to generate
a fast magnetosonic wave (Vx,Bx), which, in turn, is generated due to weak non-linearity and
transverse density inhomogeneity.
Nakariakov et al. (1997) have investigated this possibility of growth
of fast magnetosonic waves in a similar physical system, in a context other
than parallel electric field generation. They used a mostly analytical
approach and focused on the early stages of the system's evolution.
Later, the long-term evolution of the fast magnetosonic wave generation was studied numerically in the case of harmonic (Botha et al. 2000) and Gaussian (Tsiklauri et al. 2001) Alfvénic
initial perturbations. When fast magnetoacoustic perturbations are initially absent
and the initial amplitude of the plane Alfvén wave is small,
the subsequent evolution of the wave, due to the difference in local Alfvén speed
across the x-coordinate, leads to the distortion of the wave
front. This leads to the appearance of transverse (with respect to
the applied magnetic field) gradients, which grow linearly
with time. Nakariakov et al. (1997) have shown that with fairly good accuracy
(which is substantiated by our numerical calculations
presented below) the dynamics of the fast magnetoacoustic
waves can be described by
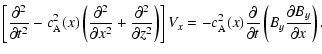 |
|
|
(5) |
Moreover, for small Alfvén wave amplitudes the back-reaction of the generated
fast magnetosonic wave on the Alfvén wave can be neglected and
Eq. (5) can be considered as a linear wave-like equation with
a driver term on the right hand side where By is given by the
travelling wave expression
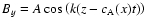 .
The main negative outcome of the studies with the
harmonic (Botha et al. 2000) and Gaussian (Tsiklauri et al. 2001) Alfvénic
initial perturbations was that despite the power-law growth in time of the driver term,
which implies progressive growth of fast magnetosonic wave
amplitude (at least until Vx and Bx reach the same amplitudes
as Vy and By when the the back-reaction can no longer be
neglected, rendering Eq. (5) invalid), the Vx and Bx amplitudes after rapid initial growth tend to saturate due to the destructive wave interference effect (Tsiklauri et al. 2001).
As a self-consistency test, in the next sub-section we present results
of the numerical simulation when the wavenumber of the initial
Alfvén wave is k=1. In dimensional units this corresponds to an Alfvén wave with frequency (
.
The main negative outcome of the studies with the
harmonic (Botha et al. 2000) and Gaussian (Tsiklauri et al. 2001) Alfvénic
initial perturbations was that despite the power-law growth in time of the driver term,
which implies progressive growth of fast magnetosonic wave
amplitude (at least until Vx and Bx reach the same amplitudes
as Vy and By when the the back-reaction can no longer be
neglected, rendering Eq. (5) invalid), the Vx and Bx amplitudes after rapid initial growth tend to saturate due to the destructive wave interference effect (Tsiklauri et al. 2001).
As a self-consistency test, in the next sub-section we present results
of the numerical simulation when the wavenumber of the initial
Alfvén wave is k=1. In dimensional units this corresponds to an Alfvén wave with frequency (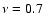 Hz), i.e. longitudinal wave-numbers
Hz), i.e. longitudinal wave-numbers
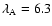 Mm.
Mm.
In Fig. 2 we show two snapshots of Vx and Ez (the latter was reconstructed using Eq. (4))
for the case of k=1, i.e. with 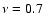 Hz.
The fast magnetosonic wave (Vx) and parallel electric
field (Ez) are both generated in the vicinity of the density gradients
Hz.
The fast magnetosonic wave (Vx) and parallel electric
field (Ez) are both generated in the vicinity of the density gradients
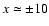 ,
eventually filling the entire density ramp. This means that the generated parallel electric
fields are confined by the density gradients, i.e. the solar coronal loop which the considered
system tries to mimic after about 20 Alfvén periods becomes filled with temporally
oscillating parallel electric fields. Note that this can be a source of polarisation drift of
ions if kinetic effects are considered.
,
eventually filling the entire density ramp. This means that the generated parallel electric
fields are confined by the density gradients, i.e. the solar coronal loop which the considered
system tries to mimic after about 20 Alfvén periods becomes filled with temporally
oscillating parallel electric fields. Note that this can be a source of polarisation drift of
ions if kinetic effects are considered.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4816f3.eps}\end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg42.gif) |
Figure 3:
Time evolution of the amplitudes of
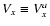 and
and
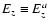 .
Solid lines represent solutions using the linear McCormack code, while
dash-dotted lines with open symbols are the solutions using the non-linear
code Lare2d. Here A=0.05, k=1, .
Solid lines represent solutions using the linear McCormack code, while
dash-dotted lines with open symbols are the solutions using the non-linear
code Lare2d. Here A=0.05, k=1, 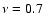 Hz, Hz,
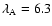 Mm, and both runs have 2000 Mm, and both runs have 2000  2000 spatial grid resolution.
2000 spatial grid resolution. |
| Open with DEXTER |
In Fig. 3 we plot the amplitudes of
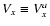 and
and
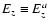 which we
define as the maxima of absolute values of the wave amplitudes along the
which we
define as the maxima of absolute values of the wave amplitudes along the
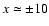 line
(which track the generated wave amplitudes in the strongest density gradient regions)
at a given time step. Solid lines represent solutions using the linear McCormack code, which
solves Eq. (5) with the initial conditions as described above, while
dash-dotted lines with open symbols are the solutions using the non-linear
MHD code Lare2d (Arber et al. 2001). We refer to the McCormac code as linear because
we treat Eq. (5) as a linear wave-like equation with
a driver term on the right hand side where By is given by the
travelling wave form
line
(which track the generated wave amplitudes in the strongest density gradient regions)
at a given time step. Solid lines represent solutions using the linear McCormack code, which
solves Eq. (5) with the initial conditions as described above, while
dash-dotted lines with open symbols are the solutions using the non-linear
MHD code Lare2d (Arber et al. 2001). We refer to the McCormac code as linear because
we treat Eq. (5) as a linear wave-like equation with
a driver term on the right hand side where By is given by the
travelling wave form
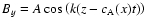 .
Here for both runs we use a 2000
.
Here for both runs we use a 2000  2000 spatial
grid resolution. Note that data with solid lines is plotted with
much smaller time steps than those with dash-dotted lines and open symbols,
which are plotted with the much coarser time step of
2000 spatial
grid resolution. Note that data with solid lines is plotted with
much smaller time steps than those with dash-dotted lines and open symbols,
which are plotted with the much coarser time step of
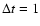 .
This is due to the fact that Lare2d uses MPI parallelisation and hence
tracking time evolution of the solution at
a given point of the simulation domain (which
is split into many parts) is a difficult task.
The linear McCormack code is serial, hence we do not encounter such problems.
The two main observations are:
.
This is due to the fact that Lare2d uses MPI parallelisation and hence
tracking time evolution of the solution at
a given point of the simulation domain (which
is split into many parts) is a difficult task.
The linear McCormack code is serial, hence we do not encounter such problems.
The two main observations are:
- (i)
- We gather from Fig. 3 that as in the previous cases
(Tsiklauri et al. 2001; Botha et al. 2000) the amplitude of Vx initially grows rapidly and then tends to saturate at a level of
A2=0.052=0.0025, as one might expect from the weakly
non-linear theory (cf. Eq. (5)).
- (ii)
- The solutions produced by the fully non-linear MHD code and the
linear McCormack code are similar but not identical. This can be explained
by the fact that the amplitude of A=0.05 is now large enough for the
non-linearity effects to be noticeable. Note that when the amplitude
was much smaller, A=0.001, the deviations between the two
were much smaller (cf. Fig. 6 from Tsiklauri et al. 2001).
In the case of A=0.05 with Lare2d, weak non-linearity of the phase-mixed
Alfvén wave even causes noticeable deviations in the initial
background density, which is an effect previously discussed in the literature.
Figures 2 and 3 corroborate the previous results of Botha et al. (2000) and Tsiklauri et al. (2001).
Here we present results for the case of large wave-numbers, k=10, which in dimensional units
corresponds to an Alfvén wave with 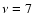 Hz, and
Hz, and
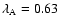 Mm.
This is a regime not investigated before. Figure 4 is similar to Fig. 2 but now k=10, with shaded surface plots given instead of intensity plots. This is due to the
fact that spiky data do not appear clearly using intensity plots.
We gather from this graph that similarly to the results of
Tsiklauri et al. (2005b) and Génot et al. (2004), the generated parallel electric field
is quite spiky, but more importantly, large wavenumbers i.e. short wavelengths now are able to
significantly increase the amplitudes of both the fast magnetosonic waves (Vx) and the parallel electric field Ez. This amplitude growth is beyond a simple A2 scaling (discussed in the previous sub-section). The amplitude growth is presented quantitatively in Fig. 5.
The amplitude of Vx now attains values of 0.01, unlike for moderate ks.
This boost in amplitude growth can be explained qualitatively by analysing Eq. (5).
The driver term (right hand side of Eq. (5)) contains spatial derivatives.
Thus, large wavenumbers (i.e. stronger spatial gradients) seem to boost the values of the driver term which in turn yields larger values for the level of saturation of the Vx amplitude.
In the considered case, Ez now attains values of 0.001.
Mm.
This is a regime not investigated before. Figure 4 is similar to Fig. 2 but now k=10, with shaded surface plots given instead of intensity plots. This is due to the
fact that spiky data do not appear clearly using intensity plots.
We gather from this graph that similarly to the results of
Tsiklauri et al. (2005b) and Génot et al. (2004), the generated parallel electric field
is quite spiky, but more importantly, large wavenumbers i.e. short wavelengths now are able to
significantly increase the amplitudes of both the fast magnetosonic waves (Vx) and the parallel electric field Ez. This amplitude growth is beyond a simple A2 scaling (discussed in the previous sub-section). The amplitude growth is presented quantitatively in Fig. 5.
The amplitude of Vx now attains values of 0.01, unlike for moderate ks.
This boost in amplitude growth can be explained qualitatively by analysing Eq. (5).
The driver term (right hand side of Eq. (5)) contains spatial derivatives.
Thus, large wavenumbers (i.e. stronger spatial gradients) seem to boost the values of the driver term which in turn yields larger values for the level of saturation of the Vx amplitude.
In the considered case, Ez now attains values of 0.001.
Since the amplitude of Vx attains a sizable fraction of the Alfvén wave amplitude rendering weakly non-linear theory inapplicable, we do not plot
solutions obtained from the the linear McCormack code.
Instead, to verify the convergence of the solution, we plot the results of the
numerical run with doubled (4000  4000) spatial resolution.
The match seems satisfactory, which validates the obtained results.
4000) spatial resolution.
The match seems satisfactory, which validates the obtained results.
![\begin{figure}
\par\includegraphics[width=4.8cm,clip]{4816f4a.eps}\hspace*{1.3cm...
...ps}\hspace*{1.3cm}
\includegraphics[width=4.95cm,clip]{4816f4d.eps} \end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg44.gif) |
Figure 4:
Snapshots of Vx and Ez at t=2 and 20 for the case of k=10, 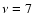 Hz, Hz,
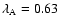 Mm. Mm. |
| Open with DEXTER |
It has been known for decades (Kuperus et al. 1981) that the coronal energy losses that need to be compensated by some additional energy input, to keep the solar corona at the observed temperatures, are (in units of erg cm-2 s-1): 3  105 for the quiet Sun, 8
105 for the quiet Sun, 8  105 for a coronal hole and 107 for an active region. Aschwanden (2004) makes similar estimates for the heating flux per unit area (i.e. in erg cm-2 s-1):
105 for a coronal hole and 107 for an active region. Aschwanden (2004) makes similar estimates for the heating flux per unit area (i.e. in erg cm-2 s-1):
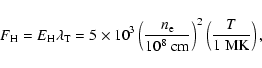 |
(6) |
where
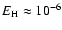 erg cm-3 s-1. This yields an estimate of
erg cm-3 s-1. This yields an estimate of
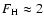
 106 erg cm-2 s-1 in an active region with a typical loop base electron number density of
106 erg cm-2 s-1 in an active region with a typical loop base electron number density of
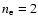
 109 cm-3 and T=1 MK.
109 cm-3 and T=1 MK.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4816f5.eps}\end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg49.gif) |
Figure 5:
Time evolution of the amplitudes of
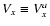 and
and
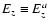 .
Solid lines with stars represent solutions using the Lare2d code with 4000 .
Solid lines with stars represent solutions using the Lare2d code with 4000  4000 resolution, while dash-dotted lines with open symbols are the same but with 2000
4000 resolution, while dash-dotted lines with open symbols are the same but with 2000  2000 resolution. Here A=0.05, k=10,
2000 resolution. Here A=0.05, k=10, 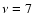 Hz, Hz,
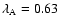 Mm. Mm. |
| Open with DEXTER |
The energy density associated with the parallel electric field Ez is
![\begin{displaymath}%
E_{\rm E}=\frac{\varepsilon E_z^2} {8 \pi}, \;\;\; \left[{\rm erg~cm^{-3} }\right]
\end{displaymath}](/articles/aa/full/2006/33/aa4816-06/img50.gif) |
(7) |
where
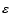 is the dielectric permitivity of plasma. The latter can be conveniently deduced
from the expression for the polarisation current (Krall & Trivelpiece 1973, Appendix I)
is the dielectric permitivity of plasma. The latter can be conveniently deduced
from the expression for the polarisation current (Krall & Trivelpiece 1973, Appendix I)
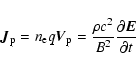 |
(8) |
and Maxwell's equation written as
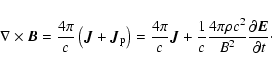 |
(9) |
The result is
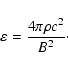 |
(10) |
The latter formula is different from the usual expression for the
dielectric permitivity (Krall & Trivelpiece 1973):
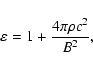 |
(11) |
because the displacement current has been neglected in the above treatment, which is a usual
assumption made in the MHD limit. For the coronal conditions (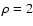

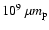 g cm-3,
g cm-3, 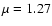 ,
B=100 Gauss) the second term in Eq. (11) is 4.8048
,
B=100 Gauss) the second term in Eq. (11) is 4.8048 
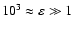 which means that for the coronal conditions
in the energy density Eq. (7) the dominant term is
which means that for the coronal conditions
in the energy density Eq. (7) the dominant term is
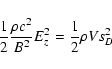 |
(12) |
which is the kinetic energy density associated with the 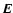

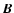 drift (Sturrock 1994, p. 60). In Fig. 5 we saw that electric field amplitude attains a value of
drift (Sturrock 1994, p. 60). In Fig. 5 we saw that electric field amplitude attains a value of 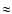 0.001. In order to convert this to dimensional units we use
0.001. In order to convert this to dimensional units we use
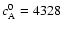 km s-1 and B=100 G and Eqs. (3)-(4) to obtain
km s-1 and B=100 G and Eqs. (3)-(4) to obtain
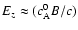
 0.001=0.0014 statvolt cm-1 (in Gaussian units).
Therefore the energy density associated with the parallel electric field Ez (From Eq. (7)) is
0.001=0.0014 statvolt cm-1 (in Gaussian units).
Therefore the energy density associated with the parallel electric field Ez (From Eq. (7)) is
![\begin{displaymath}%
E_E=\varepsilon \times 0.0014^2/(8 \pi)=3.7471 \times 10^{-4}~\left[{\rm erg~cm^{-3} }\right].
\end{displaymath}](/articles/aa/full/2006/33/aa4816-06/img63.gif) |
(13) |
In order to get the heating flux per unit area for a single harmonic with frequency
7 Hz, we multiply the latter expression by the Alfvén speed of 4328 km s-1 (because the fast magnetosonic waves (Vx and Bx) that propagate across the magnetic field and associated parallel electric fields (Ez) are generated in density gradients by the Alfvén waves.
Hence, the flux is carried with the Alfvén speed) to obtain
![\begin{displaymath}%
F_{\rm E}=E_{\rm E} c_{\rm A}^0=1.62\times10^5\;\;\;
\left[{\rm erg~cm^{-2}~s^{-1}}\right],
\end{displaymath}](/articles/aa/full/2006/33/aa4816-06/img64.gif) |
(14) |
which is 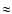 10% of the coronal heating requirement estimate for the same parameters made above using Eq. (6). Note that the latter estimate is for a single harmonic with frequency
7 Hz (see the Discussion section for details when a wide spectrum of Alfvén waves is considered).
10% of the coronal heating requirement estimate for the same parameters made above using Eq. (6). Note that the latter estimate is for a single harmonic with frequency
7 Hz (see the Discussion section for details when a wide spectrum of Alfvén waves is considered).
We now discuss how the energy stored in the generated parallel electric field is dissipated.
We examine the parallel electric field behaviour at a given point in space as a function of
time. In Fig. 6 we plot the time evolution of Ez at a point
(x=10.68,z=0) for the case of k=1, 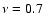 Hz, and
Hz, and
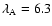 Mm.
Choice of this x-value is such that it captures parallel electric field dynamics at the strongest density gradient point (across x).
Mm.
Choice of this x-value is such that it captures parallel electric field dynamics at the strongest density gradient point (across x).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4816f6.eps}\end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg65.gif) |
Figure 6:
Time evolution of Ez at a point
(x=10.68,z=0). Here k=1, 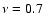 Hz, and Hz, and
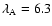 Mm. Mm. |
| Open with DEXTER |
We gather from Fig. 6 that Ez is a periodic (sign-changing) function that is a mixture
of two harmonics with frequencies
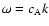 and
and
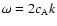 .
This is due to
the fact that Ez is calculated using Eq. (4) where Vy and By at fixed spatial points
vary in time with frequencies
.
This is due to
the fact that Ez is calculated using Eq. (4) where Vy and By at fixed spatial points
vary in time with frequencies
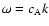 ,
while the generated Vx and Bxvary with frequencies
,
while the generated Vx and Bxvary with frequencies
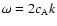 (Nakariakov et al. 1997).
Because of the ideal MHD approximation used in this paper,
the generated electric field cannot accelerate plasma particles or cause Ohmic heating unless kinetic effects are invoked. Let us look at Ohm's law for ideal MHD (Eq. (3)) in more detail denoting physical quantities unperturbed by the waves with subscript 0 and ones associated with the waves by a prime; initial equilibrium implies
(Nakariakov et al. 1997).
Because of the ideal MHD approximation used in this paper,
the generated electric field cannot accelerate plasma particles or cause Ohmic heating unless kinetic effects are invoked. Let us look at Ohm's law for ideal MHD (Eq. (3)) in more detail denoting physical quantities unperturbed by the waves with subscript 0 and ones associated with the waves by a prime; initial equilibrium implies
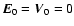 with
with
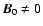 .
For the perturbed state (with Alfvén waves (Vy and By) launched which generate fast magnetosonic waves (Vx and Bx)) we have
.
For the perturbed state (with Alfvén waves (Vy and By) launched which generate fast magnetosonic waves (Vx and Bx)) we have
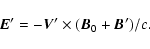 |
(15) |
Note that the projection of
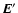 on the full magnetic field (unperturbed
on the full magnetic field (unperturbed 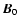 plus the waves
plus the waves
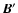 )
is zero by the definition of the cross and scalar product:
)
is zero by the definition of the cross and scalar product:
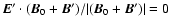 .
Physically this means that in ideal MHD the electric field cannot do any work as it is always perpendicular to the full (background plus wave) magnetic field.
However the projection of
.
Physically this means that in ideal MHD the electric field cannot do any work as it is always perpendicular to the full (background plus wave) magnetic field.
However the projection of
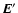 on the unperturbed magnetic field
on the unperturbed magnetic field 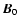 is clearly non-zero
is clearly non-zero
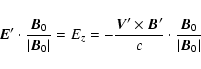 |
(16) |
which exactly coincides with Eq. (4) that was used to calculate Ez.
The crucial next step that is needed to understand how the generated electric fields parallel to the uniform unperturbed magnetic field dissipate must invoke kinetic effects. In our two stage model, in the first stage, bulk MHD motion (waves) generate parallel electric fields, which as we saw cannot accelerate particles if we describe the plasma in the ideal MHD limit. Génot et al. (2004) and Tsiklauri et al. (2005b) showed that when the identical system is
modelled in the kinetic regime particles are accelerated with such parallel fields.
Génot et al. (2004) claimed that electron acceleration is due to the polarisation drift.
They showed that once the Alfvén wave propagates along the density gradient that is
transverse to the magnetic field, a parallel electric field is generated due to
charge separation caused by the polarisation drift associated with the
time-varying electric field of the Alfvén wave. Because the polarisation drift speed is
proportional to the mass of the particle, it is negligible for electrons, hence ions
start to drift. This causes charge separation (the effect that cannot be treated by a MHD description), which results in generation of parallel electric fields, that in turn accelerate electrons. As was shown in Fig. 6, our parallel electric field is also time-varying, hence at the second (kinetic) stage the electron
acceleration can proceed in the same manner through ion polarisation drift and charge separation.
The exact picture of the particle dynamics in this case can no longer be treated with MHD and a kinetic description is more relevant.
The frequencies considered in the kinetic regime (Tsiklauri et al. 2005b),
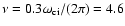
 104 Hz and 0.7-7 Hz (this paper) are different, but we clearly saw that the increase in frequency results in enhancement of the
parallel electric field generation. Various effects of wave-particle interactions will rapidly dampen the parallel electric fields on a time scale much shorter than the MHD time scale.
Génot et al. (2004) clearly demonstrated the role of nonlinearity and kinetic instabilities in the
rapid conversion from the initial low frequency electromagnetic regime to a high frequency
electrostatic one. They identified Buneman and weak beam plasma instabilities in their simulations
(as they studied the time evolution of the system for longer than Tsiklauri et al. 2005b).
Figure 11 from Génot et al. (2004) shows that wave energy is converted into particle energy
on times scales of
104 Hz and 0.7-7 Hz (this paper) are different, but we clearly saw that the increase in frequency results in enhancement of the
parallel electric field generation. Various effects of wave-particle interactions will rapidly dampen the parallel electric fields on a time scale much shorter than the MHD time scale.
Génot et al. (2004) clearly demonstrated the role of nonlinearity and kinetic instabilities in the
rapid conversion from the initial low frequency electromagnetic regime to a high frequency
electrostatic one. They identified Buneman and weak beam plasma instabilities in their simulations
(as they studied the time evolution of the system for longer than Tsiklauri et al. 2005b).
Figure 11 from Génot et al. (2004) shows that wave energy is converted into particle energy
on times scales of
 Alfvén periods.
Perhaps no immediate comparison is possible (because of the different frequencies involved), but still in our case the Alfvén period when sufficient energy is
stored in the parallel electric field is 1/(7 Hz) = 0.14 s, i.e. wave energy is converted into particle energy in a short time.
Alfvén periods.
Perhaps no immediate comparison is possible (because of the different frequencies involved), but still in our case the Alfvén period when sufficient energy is
stored in the parallel electric field is 1/(7 Hz) = 0.14 s, i.e. wave energy is converted into particle energy in a short time.
Yet another important observation can be made by estimating the Dreicer electric field (Dreicer 1959). Dreicer considered dynamics of electrons under the action of two effects: the parallel electric field and friction between electrons and ions.
He noted that the equation describing electron dynamics along the magnetic field can be written as
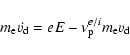 |
(17) |
where 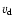 is the electron drift velocity and
is the electron drift velocity and
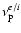 is the electron collision frequency and dot denotes time derivative.
When
is the electron collision frequency and dot denotes time derivative.
When
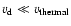 Eq. (17) in the steady state regime, (
Eq. (17) in the steady state regime, (
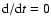 )
allows us to derive the expression for Spitzer resistivity. When
)
allows us to derive the expression for Spitzer resistivity. When
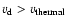 ,
the steady state solution may not apply. In this case, when the right hand side of Eq. (17) is positive i.e. when
,
the steady state solution may not apply. In this case, when the right hand side of Eq. (17) is positive i.e. when
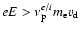 ,
we have electron acceleration. This is the so-called run-away regime. In simple terms, acceleration due to the parallel electric field leads to an increase in
,
we have electron acceleration. This is the so-called run-away regime. In simple terms, acceleration due to the parallel electric field leads to an increase in 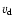 ;
in turn, this leads to a decrease in
;
in turn, this leads to a decrease in
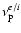 because
because
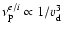 .
Thus, when the electric field exceeds the critical value
.
Thus, when the electric field exceeds the critical value
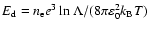 (the Dreicer electric field, which is quoted here in its SI form),
faster drift leads to a decrease in electron-ion friction, which in turn results in even faster drift and hence the run-away regime is reached. Putting coronal values (
(the Dreicer electric field, which is quoted here in its SI form),
faster drift leads to a decrease in electron-ion friction, which in turn results in even faster drift and hence the run-away regime is reached. Putting coronal values (
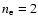
 109 cm-3, T=1 MK and
109 cm-3, T=1 MK and
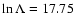 )
in the expression for the Dreicer electric field we obtain 0.0054 V m-1which in Gaussian units is 1.8
)
in the expression for the Dreicer electric field we obtain 0.0054 V m-1which in Gaussian units is 1.8  10-7 statvolt cm-1.
As can be seen from this estimate, the amplitudes of the parallel electric field obtained in this paper exceeds the Dreicer electric field by about four orders of magnitude. This guarantees that the run-away regime would take place leading to electron acceleration and fast conversion of the generated electric field energy into heat.
In Eq. (17) E is constant, while our Ez at the point of strongest density gradient is
time varying. Hence some modification of the Dreicer analysis is expected.
10-7 statvolt cm-1.
As can be seen from this estimate, the amplitudes of the parallel electric field obtained in this paper exceeds the Dreicer electric field by about four orders of magnitude. This guarantees that the run-away regime would take place leading to electron acceleration and fast conversion of the generated electric field energy into heat.
In Eq. (17) E is constant, while our Ez at the point of strongest density gradient is
time varying. Hence some modification of the Dreicer analysis is expected.
After the comment paper by Mottez et al. (2006) we came to the realisation that the electron acceleration seen in both series of works (Tsiklauri et al. 2005b; Génot et al. 2004; Tsiklauri et al. 2005a; Génot et al. 1999) is a non-resonant wave-particle interaction effect. In works by Tsiklauri et al. (2005b,a)
the electron thermal speed was
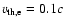 while the Alfvén speed in the strongest density gradient regions was
while the Alfvén speed in the strongest density gradient regions was
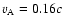 ;
this unfortunate coincidence led us to the conclusion that the electron acceleration by parallel
electric fields was affected by the Landau resonance with the phase-mixed Alfvén wave. In works by Génot et al. (2004,1999) the electron thermal speed was
;
this unfortunate coincidence led us to the conclusion that the electron acceleration by parallel
electric fields was affected by the Landau resonance with the phase-mixed Alfvén wave. In works by Génot et al. (2004,1999) the electron thermal speed was
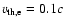 while the Alfvén speed was
while the Alfvén speed was
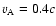 because they considered a more strongly magnetised plasma applicable to Earth magnetospheric conditions. However, the interaction of the Alfvén wave with a transverse density plasma inhomogeneity when the Landau resonance condition
because they considered a more strongly magnetised plasma applicable to Earth magnetospheric conditions. However, the interaction of the Alfvén wave with a transverse density plasma inhomogeneity when the Landau resonance condition
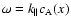 is met can be quite important for the electron acceleration
(Chaston et al. 2000; Hasegawa & Chen 1976). Chaston et al. (2000) assert that the electron acceleration observed in density cavities in aurorae can be explained by the Landau resonance of the cold ionospheric electrons with the Alfvén wave. Hasegawa & Chen (1976) also established that at resonance the Alfvén wave fully converts into the kinetic Alfvén wave with a perpendicular wavelength comparable to the ion gyro-radius. We can then conjecture that because of kinetic Alfvén wave front
stretching (due to phase mixing, i.e. due to the differences in local Alfvén speed),
this perpendicular component gradually realigns with the ambient magnetic field and hence
creates the time varying parallel electric field component. This points to the importance of the Landau resonance for electron acceleration when the resonance condition is met. But as seen in works of Génot et al. (2004,1999),
even when the resonance condition is not met, electron acceleration is still possible.
is met can be quite important for the electron acceleration
(Chaston et al. 2000; Hasegawa & Chen 1976). Chaston et al. (2000) assert that the electron acceleration observed in density cavities in aurorae can be explained by the Landau resonance of the cold ionospheric electrons with the Alfvén wave. Hasegawa & Chen (1976) also established that at resonance the Alfvén wave fully converts into the kinetic Alfvén wave with a perpendicular wavelength comparable to the ion gyro-radius. We can then conjecture that because of kinetic Alfvén wave front
stretching (due to phase mixing, i.e. due to the differences in local Alfvén speed),
this perpendicular component gradually realigns with the ambient magnetic field and hence
creates the time varying parallel electric field component. This points to the importance of the Landau resonance for electron acceleration when the resonance condition is met. But as seen in works of Génot et al. (2004,1999),
even when the resonance condition is not met, electron acceleration is still possible.
There were three main stages that lead to the formulation of the present model:
- (i)
- The realisation that the parallel electric field generation (and particle acceleration) is a non-resonant wave-particle interaction effect lead us to the question: could such parallel electric fields be generated in a MHD approximation?
- (ii)
- If one considers non-linear generation of the fast magnetosonic waves in the transversely inhomogeneous plasma,
then
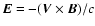 contains a non-zero component
parallel to the ambient magnetic field
Ez = - (Vx By - Vy Bx)/c.
contains a non-zero component
parallel to the ambient magnetic field
Ez = - (Vx By - Vy Bx)/c.
- (iii)
- From previous studies (Tsiklauri et al. 2001; Botha et al. 2000) we knew that the fast magnetosonic waves (Vx and Bx) did not grow to a substantial fraction of the Alfvén wave amplitude. However, after reproducing the old parameter regime (k=1, i.e. a frequency of 0.7 Hz),
the case of k=10, i.e. a frequency of 7 Hz was considered, which showed that fast magnetosonic waves and in turn a parallel electric field were more efficiently generated.
There are two main issues that need to be discussed to address the plausibility of the proposed model: (i) the plausibility of parameters used in the model and (ii) the relation to the observations.
First, the parameter space of the problem is quite large.
The level at which the fast magnetosonic wave (Vx and Bx) and hence the parallel electric field (Ez) amplitudes saturate depends on several parameters. As indicated previously (Tsiklauri et al. 2001; Botha et al. 2000), this level depends on the strength
of the transverse density gradient and the wavelength (width in the case of a Gaussian Alfvénic pulse) of the Alfvén wave. In particular it was found that the stronger density gradients yield lower saturation levels of the fast magnetosonic wave amplitude (due to the fact that destructive wave interference starts earlier when the
density gradients are strong), while shorter wavelengths (width in the case of the Gaussian Alfvénic pulse) of the Alfvén wave generate higher levels (e.g. Figs. 11 and 12 in Tsiklauri et al. 2001). We have not done a full parameter space investigation to demonstrate the effect, but instead we fixed the transverse density gradient guided by observations. In particular, the observed length scale of the density inhomogeneities in loops vary
between 0.15 and 0.5 loop radii (Goossens et al. 2002). In our model the length scale of the density inhomogeneity (half-width) is 3 Mm and the loop radius is 10 Mm (see Fig. 1) which makes the ratio 0.3. This is the median value in the observed range (0.15-0.5).
This eliminates one parameter of variability in the parameter space.
For the Alfvén speed, we used a putative value of 4328 km s-1 and performed two numerical runs for two frequencies, 0.7 and 7 Hz. A full investigation should map a range of frequencies. Such an analysis is pending, but see below for preliminary estimates in the
context of coronal heating.
Second, Alfvén waves as observed in situ in the solar wind always appear to be
propagating away from the Sun and it is therefore natural to assume a solar origin for
these fluctuations. However, the precise origin in the solar atmosphere of the hypothetical
source spectrum for Alfvén waves (turbulence) is unknown, given the impossibility of remote
magnetic field observations above the chromosphere-corona transition region (Velli & Pruneti 1997).
Studies of ion cyclotron resonance heating of the solar corona and high speed winds exist which
provide important spectroscopic constraints on the Alfvén wave spectrum (Cranmer et al. 1999).
Although the spectrum can and is observed at distances of 0.3 AU, it can be projected back to the base of corona using empirical constraints, see e.g. the top line in Fig. 5 from Cranmer et al. (1999) (see also the more elaborate model of Cranmer & van Ballegoouen (2005)).
Using the latter figure we can make the following estimates. Let us look at single harmonic, first. At a frequency of 7 Hz (used in our simulations), the magnetic energy of Alfvénic
fluctuations is
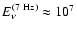 nT2 Hz-1. For a single harmonic
with
nT2 Hz-1. For a single harmonic
with 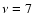 Hz this gives for the energy density
Hz this gives for the energy density
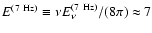
 10-3 G
10-3 G
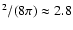
 10-4 erg cm-3. Surprisingly this semi-observational value is quite close to the theoretical value given by Eq. (13). As we saw above, such a single harmonic can provide approximately 10% of the coronal heating requirement. Next let us look at how much energy density is stored in the Alfvén wave spectrum based on the empirically guided top line in Fig. 5 from Cranmer et al. (1999).
Their spectral energy density (which they call "power'') is approximated by the so-called 1/f spectrum, i.e.
10-4 erg cm-3. Surprisingly this semi-observational value is quite close to the theoretical value given by Eq. (13). As we saw above, such a single harmonic can provide approximately 10% of the coronal heating requirement. Next let us look at how much energy density is stored in the Alfvén wave spectrum based on the empirically guided top line in Fig. 5 from Cranmer et al. (1999).
Their spectral energy density (which they call "power'') is approximated by the so-called 1/f spectrum, i.e. 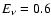

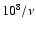 nT2 Hz-1. In proper energy density units this is
nT2 Hz-1. In proper energy density units this is 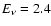

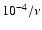 erg cm-3 Hz -1. Thus, the flux carried by Alfvén waves from say 10-4 Hz up to a frequency
erg cm-3 Hz -1. Thus, the flux carried by Alfvén waves from say 10-4 Hz up to a frequency 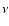 would be
would be
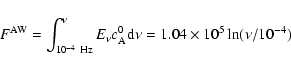 |
(18) |
![$\left[{\rm erg~cm^{-2}~s^{-1}}\right]$](/articles/aa/full/2006/33/aa4816-06/img101.gif) .
It is instructive to look at this equation graphically in Fig. 7: the Alfvén wave spectrum from
.
It is instructive to look at this equation graphically in Fig. 7: the Alfvén wave spectrum from
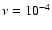 Hz up to about
a few
Hz up to about
a few
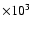 Hz carries a flux that is nearly as much as the coronal heating requirement (Eq. (6)) with T=1 MK. We do not consider higher frequencies because at about 104 Hz, ions become resonant with circularly
polarised Alfvén waves and dissipation proceeds through Landau resonance - a well-studied mechanism, but quite different from our non-resonant mechanism of parallel electric field generation.
Hz carries a flux that is nearly as much as the coronal heating requirement (Eq. (6)) with T=1 MK. We do not consider higher frequencies because at about 104 Hz, ions become resonant with circularly
polarised Alfvén waves and dissipation proceeds through Landau resonance - a well-studied mechanism, but quite different from our non-resonant mechanism of parallel electric field generation.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4816f7.eps}\end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg104.gif) |
Figure 7:
Plot of the flux carried by Alfvén waves from 10-4 Hz up to a frequency 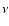 versus that frequency as inferred from the
empirically constrained spectrum of Cranmer et al. (1999). The solid line corresponds to Eq. (18), while the
dashed line shows te coronal heating requirement for a temperature of 1 MK. versus that frequency as inferred from the
empirically constrained spectrum of Cranmer et al. (1999). The solid line corresponds to Eq. (18), while the
dashed line shows te coronal heating requirement for a temperature of 1 MK. |
| Open with DEXTER |
There are several possibilities of how this flux carried by Alfvén waves (fluctuations)
is dissipated. If we consider the regime of frequencies up to 103 Hz, the ion cyclotron resonance condition is not met and hence dissipation is dominated by the mechanism of parallel electric field dissipation formulated in this
paper. However, at this stage it is unclear how much energy could actually be dissipated. This is due to the fact that we
only have two points, 0.7 Hz and 7 Hz, in our "theoretical spectrum''. As we saw, a single Alfvén wave harmonic with frequency 7 Hz can dissipate enough heat to account for 10% of the coronal heating requirement. Equation (18) shows how much flux is carried by the Alfvén waves, while in order to calculate how much of it
is actually dissipated depends on what level FE from Eq. (14) will attain for each harmonic. Hence, the flux dissipation through our mechanism would be
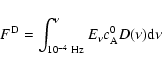 |
(19) |
where 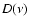 is the "theoretical spectrum'' of the energy stored in
parallel electric fields. For a 7 Hz single harmonic it can be obtained from
is the "theoretical spectrum'' of the energy stored in
parallel electric fields. For a 7 Hz single harmonic it can be obtained from
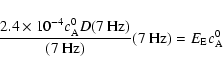 |
(20) |
with
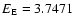
 10-4
10-4
![$\left[{\rm erg~cm^{-3} }\right]$](/articles/aa/full/2006/33/aa4816-06/img109.gif) from Eq. (13) rendering
from Eq. (13) rendering
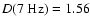 .
For a 0.7 Hz single harmonic EE would be different because as can be seen from Fig. 3
.
For a 0.7 Hz single harmonic EE would be different because as can be seen from Fig. 3
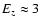
 10-5 (as opposed to
Ez=0.001 for
10-5 (as opposed to
Ez=0.001 for 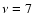 Hz). Since EE scales as Ez2, then
Hz). Since EE scales as Ez2, then
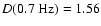

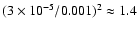
 10-3.
More numerical runs are needed to fully map
10-3.
More numerical runs are needed to fully map 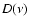 .
This is deferred until further work is done.
.
This is deferred until further work is done.
A clear distinction should be made between our model and the ones that use ion cyclotron resonance damping of Alfvén waves.
Low frequency (0.001-0.1 Hz) Alfvén waves dominate the power spectrum of fluctuations in the solar wind at and beyond 0.3 AU. These waves are able to transport a significant amount of energy (Cranmer et al. 1999). On the contrary, high frequency (10-10 000 Hz) Alfvén waves
are known to damp more easily than their low frequency counterparts, but they are not expected to contain much power. This is problematic for ion cyclotron resonance damping models because Landau resonance of ions occurs at high frequencies (few 104 Hz).
Our model on the contrary is of a non-resonant nature. Thus, it is hoped that it can provide enough heating once the frequency range
10
-4-103 Hz at the base of corona is mapped numerically (i.e. once the level attained by the parallel electric field amplitudes for each frequency is determined).
The proposed wide spectrum idea for Alfvén waves is not as "theoretical-rather-than-demonstrable''
as the one proposed by Tsiklauri & Nakariakov (2001) for the slow magnetosonic waves. One could question the validity of the wide spectrum idea
for the slow magnetosonic waves in coronal loops as predominantly single
harmonics (with periods of 3 and 5 min, etc.) are observed. At the same time it is not possible to observe the high frequency waves that are dissipated already.
However, in the case of Alfvén waves, the presence of a wide spectrum with a frequency range of
10
-4-103 Hz at the base of corona, which is
actually observed at 0.3 AU, seems to be more likely. The possibility of meeting the full coronal heating requirement with the
wide spectrum Alfvén waves via the proposed two stage mechanism of parallel electric field generation needs further investigation.
Acknowledgements
The author acknowledges support from the Nuffield Foundation (UK) through an award to newly
appointed lecturers in Science, Engineering and Mathematics (NUF-NAL 04), from the
University of Salford Research Investment Fund 2005 grant, PPARC (UK) standard grant and
use of the E. Copson Math cluster funded by PPARC
and the University of St. Andrews. The author would like to thank E.R. Priest and K.G. McClements for useful discussions and criticism and the anonymous referee for useful comments and suggestions.
- Arber, T. D., Longbottom,
A. W., Gerrard, C. L., et al. 2001, J. Comput. Phys.,
171, 151 [NASA ADS] [CrossRef] (In the text)
- Aschwanden, M. J. 2004,
Physics of the solar corona an introduction (Chichester, UK: Praxis
Publishing Ltd)
(In the text)
- Banerjee, D.,
Teriaca, L., Doyle, J., et al. 1998, A&A, 339, 208 [NASA ADS]
- Botha, G. J. J., Arber,
T. D., Nakariakov, V. M., et al. 2000, A&A, 363,
1186 [NASA ADS]
- Chaston, C.
C., Carlson, C. W., Ergun, R. E., et al. 2000, Phys.
Scripta, T84, 64 [NASA ADS]
- Cranmer, S. R., & van
Ballegoouen, A. A. 2005, ApJS, 156, 265 [NASA ADS] [CrossRef] (In the text)
- Cranmer, S. R., Field, G.
B., & Kohl, J. L. 1999, ApJ, 518, 937 [NASA ADS] [CrossRef] (In the text)
- DeMoortel, I., Hood, A.
W., & Arber, T. D. 2000, A&A, 354, 334 [NASA ADS]
- Doyle, J., Banerjee, D.,
& Perez, M. 1998, Sol. Phys., 181, 91 [NASA ADS] [CrossRef]
- Dreicer, H. 1959,
Phys. Rev., 115, 238 [NASA ADS] [CrossRef] (In the text)
- Génot, V., Louarn,
P., & Quéau, D. L. 1999, J. Geophys. Res., 104,
22649 [NASA ADS] [CrossRef]
- Génot, V., Louarn,
P., & Mottez, F. 2004, Ann. Geophys., 6, 2081 [NASA ADS]
- Goossens, M., Andries,
J., & Aschwanden, M. J. 2002, A&A, 394, L39 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Hasegawa, A., & Chen,
L. 1976, Phys. Fluids, 19, 1924 [NASA ADS] [CrossRef]
- Heyvaerts, J., &
Priest, E. R. 1983, A&A, 117, 220 [NASA ADS]
- Hood, A. W., Brooks, S.
J., & Wright, A. N. 2002, Proc. Roy. Soc. Lond. A, 458,
2307 [NASA ADS]
- Krall, N. A., &
Trivelpiece, A. W. 1973, Principles of Plasma Physics
(New York: McGraw-Hill)
(In the text)
- Kuperus, M., Ionson, J.
A., & Spicer, D. S. 1981, ARA&A, 19, 7 [NASA ADS] (In the text)
- McEwan, M. P.,
& DeMoortel, I. 2006, A&A, 448, 763 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Moran, T. G. 2001,
A&A, 374, L9 [EDP Sciences] [NASA ADS] [CrossRef]
- Mottez, F., Génot,
V., & Louarn, P. 2006, A&A, 449, 449 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Nakariakov, V. M.,
Roberts, B., & Murawski, K. 1997, Sol. Phys., 175, 93 [NASA ADS] [CrossRef]
- Nocera, L., Priest, E.
R., & Hollweg, J. V. 1986, Geophys. Astrophys. Fl. Dyn.,
35, 111 [NASA ADS]
- Parker, E. N. 1991, ApJ, 376,
355 [NASA ADS] [CrossRef]
- Sturrock, P. A. 1994,
Plasma Physics: an introduction to the theory of astrophysical,
geophysical and laboratory plasmas (Cambridge, UK: Cambridge
University Press)
(In the text)
- Tsiklauri, D. 2005, A&A,
441, 1177 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Tsiklauri, D. 2006, New J.
Phys., 8, 79 (In the text)
- Tsiklauri, D., &
Nakariakov, V. M. 2001, A&A, 379, 1106 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Tsiklauri, D., &
Nakariakov, V. M. 2002, A&A, 393, 321 [EDP Sciences] [NASA ADS] [CrossRef]
- Tsiklauri, D., Arber, T.
D., & Nakariakov, V. M. 2001, A&A, 379, 1098 [EDP Sciences] [NASA ADS] [CrossRef]
- Tsiklauri, D.,
Nakariakov, V. M., & Arber, T. D. 2002, A&A, 395,
285 [EDP Sciences] [NASA ADS] [CrossRef]
- Tsiklauri, D.,
Nakariakov, V. M., & Rowlands, G. 2003, A&A, 400, 1051 [EDP Sciences] [NASA ADS] [CrossRef]
- Tsiklauri, D., Sakai,
J. I., & Saito, S. 2005a, New J. Phys., 7, 79 [CrossRef]
- Tsiklauri, D., Sakai,
J. I., & Saito, S. 2005b, A&A, 435, 1105 [EDP Sciences] [NASA ADS] [CrossRef]
- Velli, M., & Pruneti,
F. 1997, Plasma Phys. Control. Fusion, 39, B317 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{4816f1.eps}\end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=5.7cm,clip]{4816f2a.eps}\hspace*{5mm}
...
...c.eps}\hspace*{5mm}
\includegraphics[width=5.7cm,clip]{4816f2d.eps} \end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg31.gif)
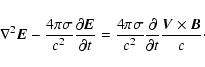
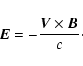
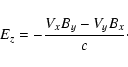
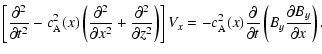
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4816f3.eps}\end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=4.8cm,clip]{4816f4a.eps}\hspace*{1.3cm...
...ps}\hspace*{1.3cm}
\includegraphics[width=4.95cm,clip]{4816f4d.eps} \end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg44.gif)
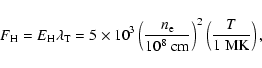
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4816f5.eps}\end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg49.gif)
![\begin{displaymath}%
E_{\rm E}=\frac{\varepsilon E_z^2} {8 \pi}, \;\;\; \left[{\rm erg~cm^{-3} }\right]
\end{displaymath}](/articles/aa/full/2006/33/aa4816-06/img50.gif)
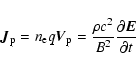
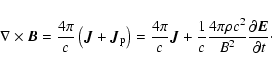
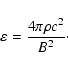
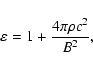
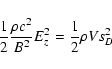
![\begin{displaymath}%
E_E=\varepsilon \times 0.0014^2/(8 \pi)=3.7471 \times 10^{-4}~\left[{\rm erg~cm^{-3} }\right].
\end{displaymath}](/articles/aa/full/2006/33/aa4816-06/img63.gif)
![\begin{displaymath}%
F_{\rm E}=E_{\rm E} c_{\rm A}^0=1.62\times10^5\;\;\;
\left[{\rm erg~cm^{-2}~s^{-1}}\right],
\end{displaymath}](/articles/aa/full/2006/33/aa4816-06/img64.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4816f6.eps}\end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg65.gif)
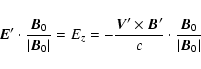
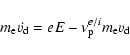
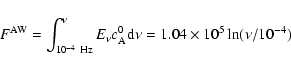
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4816f7.eps}\end{figure}](/articles/aa/full/2006/33/aa4816-06/Timg104.gif)