A&A 455, 791-801 (2006)
DOI: 10.1051/0004-6361:20054717
Three-dimensional reconstruction of the intra-cluster medium
E. Puchwein - M. Bartelmann
Zentrum für Astronomie der Universität
Heidelberg, ITA, Albert-Überle-Str. 2, 69120 Heidelberg,
Germany
Received 19 December 2005 / Accepted 17 May 2006
Abstract
We propose and test a new method based on Richardson-Lucy
deconvolution to reconstruct three-dimensional gas density and temperature
distributions in galaxy clusters from combined X-ray and thermal
Sunyaev-Zel'dovich observations. Clusters are assumed to be axially
symmetric and arbitrarily inclined with respect to the line-of-sight. No equilibrium assumption other than local thermal equilibrium is needed.
We test the algorithm with synthetic observations of analytically
modeled and numerically simulated galaxy clusters and discuss the
quality of the density and temperature reconstructions in idealised
situations and in presence of observational noise, deviations from
axial symmetry and cluster substructure. We find that analytic and
numerical gas density and temperature distributions can be accurately
reconstructed in three dimensions, even if observational noise is
present. We also discuss methods for determining the inclination
angle from data and show that it can be constrained using X-ray
temperature maps. For a realistic cluster and including observational noise the three-dimensional reconstructions reach a level of accuracy of about 15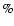 .
.
Key words: galaxies: clusters: general - X-rays: galaxies: clusters - submillimeter
In hierarchical models of structure formation, galaxy clusters are not
only the most massive gravitationally bound objects in the Universe,
but also the most recently forming. Numerous examples show that they
are typically irregularly shaped and occasionally undergoing violent
merger events. Cluster-sized dark-matter halos in simulations can
often be well described as triaxial ellipsoids, but not as spheres
(Jing & Suto 2002).
At the same time, observations of galaxy clusters are often
interpreted based on spherically-symmetric models in hydrostatic
equilibrium. The beta model (Cavaliere & Fusco-Femiano 1976) is still routinely being used for analyses
of the X-ray emission and also of the amplitude of the thermal
Sunyaev-Zel'dovich effect. Given the rapidly improving quality and
diversity of cluster data, it appears timely to search for an
algorithm which avoids the assumption of spherical symmetry and allows
the joint analysis of different types of cluster data.
Several such algorithms have been proposed. Zaroubi et al. (1998) suggested to
base the reconstruction of axisymmetric, three-dimensional
gravitational cluster potentials on the Fourier slice theorem,
extrapolating Fourier modes into the "cone of ignorance''. They
applied their technique to simulated data and showed that it performs
well (Zaroubi et al. 2001). Doré et al. (2001) followed a perturbative approach,
and Lee & Suto (2004) proposed to adapt parameters of triaxial halo
models, all by combining different data sets such as X-ray, (thermal)
Sunyaev-Zel'dovich (SZ) and gravitational-lensing maps. A similar method was applied to data by De Filippis et al. (2005). An alternative
approach based on the iterative Richardson-Lucy deconvolution was
suggested by Reblinsky (2000) and Reblinsky & Bartelmann (2001). It aims at the gravitational potential, assumes only axial
symmetry of the main cluster body, avoids extrapolations in Fourier
space, and can easily be extended to include additional data sets.
In this paper, we develop the latter algorithm further. However, aiming at the
potential would require us to assume a relation between the gas
distribution and the gravitational field, which would be most conveniently
given by hydrostatic equilibrium. But even ignoring this common
equilibrium assumption, it should be possible to reconstruct the
three-dimensional distributions of intra-cluster gas density and
temperature by a joint analysis of X-ray and thermal SZ data.
We demonstrate here that this is indeed possible under the one
simplifying assumption that the underlying three-dimensional
distributions be axially (not spherically!) symmetric. The inclination of the symmetry axis can be arbitrary. We introduce the algorithm in Sect. 2 and apply it to the idealised case of an
analytically modeled, ellipsoidal cluster without substructure in
Sect. 3. Results obtained first without, then with observational noise are
highly promising: both the three-dimensional density and temperature
distributions are accurately reproduced. Noise suggests smoothing, and
we describe a suitable smoothing algorithm.
We study the less-ideal case of a numerically-simulated galaxy cluster
in Sect. 4. Here, axial symmetry is typically violated by the main
cluster body, and substructures are present which further perturb the
symmetry. Yet, faithful reconstructions are possible even in presence
of realistic noise.
Section 5 finally describes how inclination angles can be constrained
using temperature maps, and Sect. 6 summarises and discusses our
results.
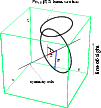 |
Figure 1:
Projection of an axisymmetric distribution of a physical
quantity. The ellipse at the top marks the region where the kernel
function corresponding to the projection along the line-of-sight is
non-zero for fixed R and Z. |
| Open with DEXTER |
2.1 Deprojection of axisymmetric quantities using
Richardson-Lucy deconvolution
As Binney et al. (1990) pointed out, Richardson-Lucy deconvolution
(Lucy 1994,1974) can be used to reconstruct an inclined
axisymmetric three-dimensional distribution of some physical quantity
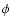 from a two-dimensional map
from a two-dimensional map 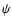 of its projection along the
line-of-sight. In astrophysical applications,
of its projection along the
line-of-sight. In astrophysical applications, 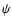 will be data obtained from observations, for example the X-ray flux, the
lensing potential, or the Sunyaev-Zel'dovich decrement of an
approximately axisymmetric galaxy cluster. Because of the assumed
symmetry,
will be data obtained from observations, for example the X-ray flux, the
lensing potential, or the Sunyaev-Zel'dovich decrement of an
approximately axisymmetric galaxy cluster. Because of the assumed
symmetry, 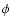 can be written as a function of only two cylindrical
coordinates R and Z, where we choose the symmetry axis as the
Z-axis (see Fig. 1). Then, R is the
distance from the symmetry axis. The projection along the
line-of-sight can be understood as a convolution of
can be written as a function of only two cylindrical
coordinates R and Z, where we choose the symmetry axis as the
Z-axis (see Fig. 1). Then, R is the
distance from the symmetry axis. The projection along the
line-of-sight can be understood as a convolution of 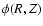 with a
kernel function
P(x,y|R,Z),
with a
kernel function
P(x,y|R,Z),
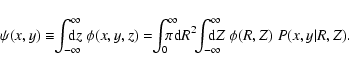 |
(1) |
The kernel function for a given pair (R,Z) is non-zero only on the
ellipse obtained by projecting the ring onto the sky which is
defined by R and Z (see
Fig. 1). It is derived in Appendix A of Binney et al. (1990)
and reads
![\begin{displaymath}P(x,y\vert R,Z) = \frac{\delta[(\frac{y}{\cos i}-Z \tan i)^2-\left(R^2-x^2\right)]}{\pi\cos i},
\end{displaymath}](/articles/aa/full/2006/33/aa4717-05/img34.gif) |
(2) |
where i is the inclination angle of the symmetry axis, defined as
the angle between the symmetry axis and the line-of-sight; see
Fig. 1. The kernel
P(x,y|R,Z) satisfies the
normalisation condition
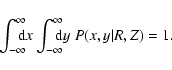 |
(3) |
Assuming that the orientation of the symmetry axis is known and that
one has a two-dimensional map of the projection 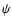 ,
one can
reverse the convolution using the iterative Richardson-Lucy
deconvolution technique (see Lucy 1994,1974) and solve for
,
one can
reverse the convolution using the iterative Richardson-Lucy
deconvolution technique (see Lucy 1994,1974) and solve for 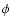 as a function of R
and Z. Starting with an initial guess
as a function of R
and Z. Starting with an initial guess
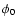 for
for 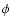 and using the Richardson-Lucy iteration scheme,
and using the Richardson-Lucy iteration scheme,
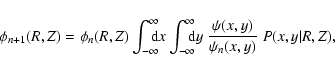 |
(4) |
one can obtain approximations of 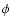 with increasing quality. Here,
with increasing quality. Here,
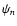 is the projection along the line-of-sight of the
approximation
is the projection along the line-of-sight of the
approximation 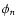 .
If we plug Eq. (2) into
Eq. (4), perform the y integration, and use
the new coordinate
.
If we plug Eq. (2) into
Eq. (4), perform the y integration, and use
the new coordinate 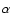 defined by
defined by
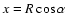 ,
we obtain
(see also Binney et al. 1990; Reblinsky 2000)
,
we obtain
(see also Binney et al. 1990; Reblinsky 2000)
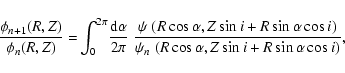 |
(5) |
where the integration follows the ellipse shown in
Fig. 1.
For numerical reconstructions of axisymmetric three-dimensional
distributions, we replace the integral in
Eq. (5) by a sum over points, which are
distributed along the ellipse and equally spaced in 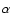 .
To
evaluate the sum, we need to find the ratio
.
To
evaluate the sum, we need to find the ratio
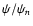 at these
points. We use two grids for the iteration, one in x, y-space for
at these
points. We use two grids for the iteration, one in x, y-space for 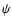 and
and 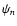 ,
and one in R,Z-space for
,
and one in R,Z-space for 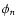 .
First, we
project
.
First, we
project 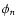 along the line-of-sight on the grid in x,y-space to
find
along the line-of-sight on the grid in x,y-space to
find 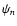 .
We do not use the kernel function for that, but perform
a direct summation using a discretised version of the first equality
in Eq. (1). The projection integral is approximated
by a sum over Nz equally spaced points that cover a section of
length Lz of the line-of-sight. This section is centred on the
z-coordinate of the halo. Then,
.
We do not use the kernel function for that, but perform
a direct summation using a discretised version of the first equality
in Eq. (1). The projection integral is approximated
by a sum over Nz equally spaced points that cover a section of
length Lz of the line-of-sight. This section is centred on the
z-coordinate of the halo. Then, 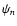 is obtained by
is obtained by
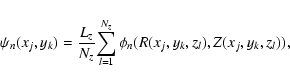 |
(6) |
where xj and yk are the x and y coordinates of the grid point (j,k). The zl are the z coordinates of the Nz points used for the projection. The function
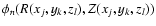 is
approximated by bilinear interpolation from the values of
is
approximated by bilinear interpolation from the values of 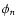 at
neighbouring grid points in R, Z-space. Since we know
at
neighbouring grid points in R, Z-space. Since we know 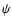 and have
calculated the projection
and have
calculated the projection 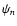 of
of 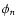 ,
we can find the ratio
,
we can find the ratio
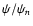 at points on the ellipse by bilinear interpolation from
neighbouring points of the x, y-space grid. This allows us to
approximate the integral in Eq. (5) by a
sum over
at points on the ellipse by bilinear interpolation from
neighbouring points of the x, y-space grid. This allows us to
approximate the integral in Eq. (5) by a
sum over 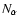 points,
points,
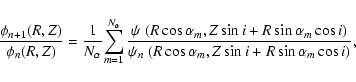 |
(7) |
and find
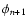 which completes the iteration step. Here
which completes the iteration step. Here
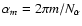 .
.
2.2 Boundary effects, artifacts and regularisation
There is, however, a problem. Assume that Lz corresponds to the
height of the box shown in Fig. 1, and that the area
covered by our map of 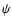 corresponds to its top surface. To
calculate
corresponds to its top surface. To
calculate
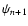 there, we have to know
there, we have to know
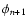 everywhere
in the box. But for finding
everywhere
in the box. But for finding
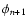 close to the corners of the
box, we have to evaluate Eq. (7) along
ellipses that do not fit into the top surface of the box. This means
that some of the points we have to sum over lie outside our map of
close to the corners of the
box, we have to evaluate Eq. (7) along
ellipses that do not fit into the top surface of the box. This means
that some of the points we have to sum over lie outside our map of 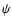 and
and 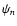 .
As suggested by Reblinsky (2000), we replace
.
As suggested by Reblinsky (2000), we replace
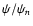 for those points by its value at the closest point at
the perimeter of the map. This leads to some artifacts in the
reconstruction of
for those points by its value at the closest point at
the perimeter of the map. This leads to some artifacts in the
reconstruction of 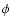 for large R and Z, but yields very good
results in the central region, which we are most interested in.
for large R and Z, but yields very good
results in the central region, which we are most interested in.
To start the iteration, we have to choose a guess or prior
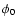 .
We adopt the simplest choice of a flat or constant prior. We
set its value so as to reproduce the average value
.
We adopt the simplest choice of a flat or constant prior. We
set its value so as to reproduce the average value
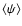 of the map
of the map 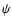 ,
namely
,
namely
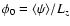 .
.
The algorithm described above can be used to reconstruct axisymmetric
three-dimensional distributions from two-dimensional maps of its
projection along the line-of-sight. However, it runs into problems for
strongly peaked distributions such as the X-ray emissivity of a galaxy
cluster. In order to illustrate that, we reconstructed the X-ray
emissivity from an X-ray flux map, which we obtained by projecting the
emissivity of an analytically modeled, axisymmetric cluster halo. The
halo model is discussed in Sect. 3. For the
projection, we chose an inclination angle of
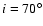 .
We
performed the reconstruction with a rather high number of n=30iterations. In the left panel of Fig. 2, we show the
ratio between the reconstructed and the original X-ray emissivity. One
can clearly see spike-shaped artifacts of the reconstruction. The angle
between these spikes and the symmetry axis is equal to the inclination i. This means that the ellipses corresponding to R and Z values
of points in the spikes pass directly through the halo centre in the
map of
.
We
performed the reconstruction with a rather high number of n=30iterations. In the left panel of Fig. 2, we show the
ratio between the reconstructed and the original X-ray emissivity. One
can clearly see spike-shaped artifacts of the reconstruction. The angle
between these spikes and the symmetry axis is equal to the inclination i. This means that the ellipses corresponding to R and Z values
of points in the spikes pass directly through the halo centre in the
map of 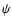 .
.
Richardson-Lucy deconvolution reproduces large structures quickly,
while it converges slowly to small scale structures such as the peak
at the halo centre (see Lucy 1994,1974). This means that, when
starting with a flat prior,
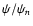 can be quite large close to
the centre even after several iterations. Thus, when we
evaluate (7) for points further out whose ellipses
pass through the halo centre, we find ratios of
can be quite large close to
the centre even after several iterations. Thus, when we
evaluate (7) for points further out whose ellipses
pass through the halo centre, we find ratios of
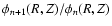 which are too high, and the spike-shaped
artifacts form. They appear already after the first few iterations and
are very stable. In the left panel of Fig. 2, we show
them after 30 iterations, and it would take several hundred more
iterations until they slowly disappear.
which are too high, and the spike-shaped
artifacts form. They appear already after the first few iterations and
are very stable. In the left panel of Fig. 2, we show
them after 30 iterations, and it would take several hundred more
iterations until they slowly disappear.
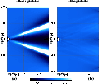 |
Figure 2:
Ratio of the reconstructed to the original X-ray emissivity
after n=30 iteration steps,
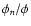 .
The halo centre is at
the centre left of each plot. Panel a) shows the ratio obtained
without regularisation. One can clearly see the spike-shaped artifacts
of the reconstruction. Panel b) shows the ratio for the
reconstruction including the regularisation. It is close to unity
everywhere except very close to the centre, where the algorithm
converges slowly and grid resolution becomes a problem. .
The halo centre is at
the centre left of each plot. Panel a) shows the ratio obtained
without regularisation. One can clearly see the spike-shaped artifacts
of the reconstruction. Panel b) shows the ratio for the
reconstruction including the regularisation. It is close to unity
everywhere except very close to the centre, where the algorithm
converges slowly and grid resolution becomes a problem. |
| Open with DEXTER |
To prevent the formation of such artifacts, we use a regularisation
scheme. First, we calculate an average
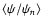 for the points used in the sum in
Eq. (7), which is defined by
for the points used in the sum in
Eq. (7), which is defined by
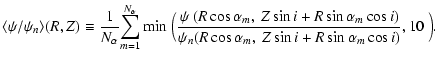 |
|
|
(8) |
Then we set
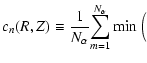 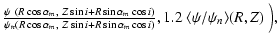 |
|
(9) |
and use
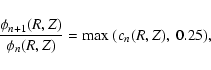 |
(10) |
to calculate
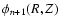 .
This regularisation of the iteration
scheme supresses the formation of the spike-shaped artifacts. It limits
the impact of sharp peaks in
.
This regularisation of the iteration
scheme supresses the formation of the spike-shaped artifacts. It limits
the impact of sharp peaks in 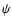 on points that are far away from
the corresponding peaks in
on points that are far away from
the corresponding peaks in 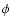 by using an upper limit for
by using an upper limit for
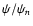 in Eqs. (8) and (9). The effectiveness
of the regularisation scheme is not very sensitive to the exact
numerical values of the upper limits, which we chose by trial and
error, as long as they suppress sharp peaks and are not too
restrictive to allow convergence in a reasonable number of
iterations. The lower limit for the correction factor in
Eq. (10) is introduced just to make sure that
in Eqs. (8) and (9). The effectiveness
of the regularisation scheme is not very sensitive to the exact
numerical values of the upper limits, which we chose by trial and
error, as long as they suppress sharp peaks and are not too
restrictive to allow convergence in a reasonable number of
iterations. The lower limit for the correction factor in
Eq. (10) is introduced just to make sure that
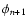 does not change its sign or become very small in the
first few iteration steps, which would potentially cause problems
later.
does not change its sign or become very small in the
first few iteration steps, which would potentially cause problems
later.
We repeated the reconstruction of the X-ray emissivity using this
regularisation. In the right panel of Fig. 2, we show
the ratio of the reconstructed to the original emissivity after 30 iterations. The spikes that are present in the left panel have almost
disappeared. The ratio is close to unity everywhere in the region
shown, except very near the halo centre where grid resolution and the
slow convergence to small-scale structures becomes a problem. Apart
from that, the deprojection works very well. The errors are usually
smaller than 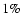 .
.
2.3 Inclination angle
So far, we have assumed that the orientation of the symmetry axis is
known. In reality, when applying this algorithm to observations, this
will not be the case. However, the orientation of the symmetry axis in
the plane of the sky can directly be obtained from the map 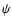 .
Its
inclination i on the other hand can be found in the following
way. First, we repeat the reconstruction as described above, assuming
several different plausible values of i and using a fixed
number
.
Its
inclination i on the other hand can be found in the following
way. First, we repeat the reconstruction as described above, assuming
several different plausible values of i and using a fixed
number
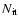 of iterations. Then, we compare the maps
of iterations. Then, we compare the maps
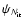 ,
corresponding to the reconstructed
distributions, to the original (or observed) map
,
corresponding to the reconstructed
distributions, to the original (or observed) map 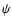 and find the
value of i for which it fits best. This can for example be done by
minimising the penalty function
and find the
value of i for which it fits best. This can for example be done by
minimising the penalty function
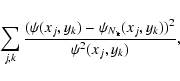 |
(11) |
where, depending on the shape of the distribution one wants to
reconstruct, it may be favourable to sum only over points in the
central region of the map.
2.4 Reconstruction of density and temperature of the ICM from combined X-ray and
thermal Sunyaev-Zel'dovich effect observations
So far, we have discussed how to reconstruct a single
three-dimensional distribution of a physical quantity from a single
two-dimensional map of its projection along the
line-of-sight. However, one can obtain additional information by
combining maps from different observations (see
also Reblinsky & Bartelmann 2001; Reblinsky 2000). Here, we reconstruct several physical
quantities at the same time by combining different observations that
depend on these quantities. Specifically, we will show how to obtain
three-dimensional distributions of the density and temperature of the
intra-cluster medium (ICM) in axisymmetric cluster halos by combining
observations of the (thermal) X-ray emission and the (thermal)
Sunyaev-Zel'dovich effect. The X-ray surface brightness is taken to be
proportional to
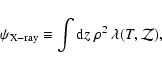 |
(12) |
where 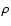 and T are the gas density and temperature,
respectively. The integral extends along the line-of-sight. The
cooling function
and T are the gas density and temperature,
respectively. The integral extends along the line-of-sight. The
cooling function
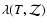 depends on the temperature and
the metallicity
depends on the temperature and
the metallicity 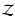 ,
and
,
and 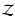 is assumed to be constant
here. The (thermal) Sunyaev-Zel'dovich decrement or increment is
proportional to the Compton y-parameter
is assumed to be constant
here. The (thermal) Sunyaev-Zel'dovich decrement or increment is
proportional to the Compton y-parameter
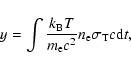 |
(13) |
where the integration also follows the line-of-sight,
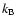 is Boltzmann's constant,
is Boltzmann's constant, 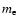 the electron mass, c the speed of
light,
the electron mass, c the speed of
light, 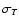 the Thomson cross section, and
the Thomson cross section, and 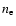 the electron
number density at the position passed by the light ray at time t. For fully ionised gas with constant metallicity, this is also
proportional to
the electron
number density at the position passed by the light ray at time t. For fully ionised gas with constant metallicity, this is also
proportional to
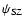 defined by
defined by
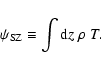 |
(14) |
 and
and
 can be obtained from
observations. For reconstructing the ICM temperature and density, we
start from some initial guess
can be obtained from
observations. For reconstructing the ICM temperature and density, we
start from some initial guess
 and T0(R,Z). In analogy
to Eq. (6), we use discrete approximations of
Eqs. (12) and (14),
and T0(R,Z). In analogy
to Eq. (6), we use discrete approximations of
Eqs. (12) and (14),
to obtain
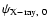 and
and
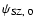 .
In
analogy to Eq. (7), we define
.
In
analogy to Eq. (7), we define
| |
|
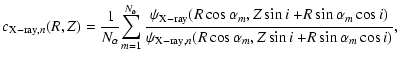 |
(17) |
| |
|
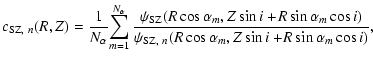 |
(18) |
and use the iteration scheme
| |
|
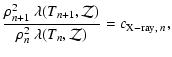 |
(19) |
| |
|
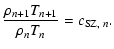 |
(20) |
In order to find the next iterative approximation for the density and
the temperature, we have to solve Eqs. (19)
and (20) for
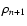 and Tn+1. To include
line emission in the cooling function, one could tabulate
and Tn+1. To include
line emission in the cooling function, one could tabulate
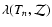 ,
e.g. using the software package XSPEC (see e.g. Arnaud 1996) for a
specific emission model and metallicity, and solve the equations above
numerically. However, since the main focus of this paper is to
demonstrate the deprojection algorithm, we use the simple assumption
of continuous bremsstrahlung,
,
e.g. using the software package XSPEC (see e.g. Arnaud 1996) for a
specific emission model and metallicity, and solve the equations above
numerically. However, since the main focus of this paper is to
demonstrate the deprojection algorithm, we use the simple assumption
of continuous bremsstrahlung,
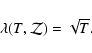 |
(21) |
Then, we obtain from (19) and
(20),
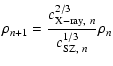 |
|
|
(22) |
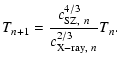 |
|
|
(23) |
Note that for evaluating Eqs. (17) and (18), we also use the regularisation introduced in
Sect. 2.2. Its effectiveness, even when applied to different kinds of data, depends only weakly on the exact values of the numerical constants in Eqs. (8)-(10). Thus we use these equations with the numerical values given there for both the X-ray and SZ data. Again, for points that lie
outside the map of
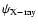 and
and
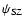 ,
the ratios
,
the ratios
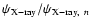 and
and
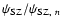 are approximated by their
values at the closest point at the perimeter of the map. In the next
two sections, we shall apply this deprojection algorithm to
axisymmetric analytic halos and to numerically simulated cluster
halos, and discuss its performance.
are approximated by their
values at the closest point at the perimeter of the map. In the next
two sections, we shall apply this deprojection algorithm to
axisymmetric analytic halos and to numerically simulated cluster
halos, and discuss its performance.
3 Deprojection of analytic halos
We use a NFW-like gas density profile to test the deprojection algorithm for axisymmetric, analytic halos. However, for the deprojection to be non-trivial, we prefer to have ellipsoidal iso-density surfaces. We therefore assume that the density of the ICM is a function of
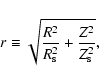 |
(24) |
where 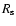 is a scaling radius perpendicular to the symmetry axis,
and
is a scaling radius perpendicular to the symmetry axis,
and 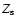 is a scaling distance along the axis. The density of the hot
cluster gas is then taken to be
is a scaling distance along the axis. The density of the hot
cluster gas is then taken to be
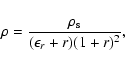 |
(25) |
which differs from the NFW form not only by its ellipsoidal shape but
also by the small constant
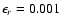 introduced to ensure
that the density does not diverge for
introduced to ensure
that the density does not diverge for
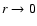 .
This divergence
would cause problems in numerical calculations. For the gas
temperature we use a phenomenological description that roughly
corresponds to the temperature profiles found in the simulated cluster sample that we will use in Sect. 4. Namely, we set
.
This divergence
would cause problems in numerical calculations. For the gas
temperature we use a phenomenological description that roughly
corresponds to the temperature profiles found in the simulated cluster sample that we will use in Sect. 4. Namely, we set
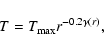 |
(26) |
where
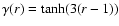 is -1 for
is -1 for 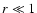 and +1 for
and +1 for 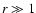 .
The values of the parameters
.
The values of the parameters
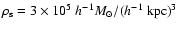 ,
,
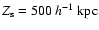 ,
,
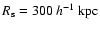 ,
and
,
and
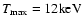 ,
which we use correspond to the gas component of a
massive galaxy cluster. Here, h is the reduced Hubble constant,
which we set to 0.7.
,
which we use correspond to the gas component of a
massive galaxy cluster. Here, h is the reduced Hubble constant,
which we set to 0.7.
Having chosen an inclination angle i, we project the analytic halo
described above on a
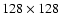 grid with a sidelength of
grid with a sidelength of
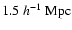 and obtain the X-ray and Sunyaev-Zel'dovich
effect maps,
and obtain the X-ray and Sunyaev-Zel'dovich
effect maps,
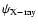 and
and
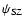 .
We use
the algorithm discussed in Sect. 2.4 with these
maps to reconstruct the gas density and temperature. In
Fig. 3, we compare the results of the
deprojection with the original density and temperature of the analytic
halo for an inclination angle
.
We use
the algorithm discussed in Sect. 2.4 with these
maps to reconstruct the gas density and temperature. In
Fig. 3, we compare the results of the
deprojection with the original density and temperature of the analytic
halo for an inclination angle
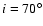 and after n=20iterations. The inclination was assumed to be known in performing the
deprojection. The left and right panels show the density and
temperature ratios,
and after n=20iterations. The inclination was assumed to be known in performing the
deprojection. The left and right panels show the density and
temperature ratios,
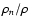 and Tn/T, repsectively. The
star-like pattern of the plots maps the ranges of the R and Zcoordinates occurring in the simulation box used for the
reconstruction (see Fig. 1). In the central region of
the cluster, the reconstruction works very well. Errors are of the
order of
and Tn/T, repsectively. The
star-like pattern of the plots maps the ranges of the R and Zcoordinates occurring in the simulation box used for the
reconstruction (see Fig. 1). In the central region of
the cluster, the reconstruction works very well. Errors are of the
order of 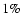 .
Despite the regularisation, one can still see some
remains of the spike-shaped artifacts discussed in
Sect. 2.2. For large R or Z values, close to
the star-shaped boundary of the plots, the quality of the
reconstruction decreases. This is not at all surprising because the
ellipses along which Eqs. (17) and (18)
must be evaluated to reconstruct density and temperature at those
points lie mostly outside of the maps of
.
Despite the regularisation, one can still see some
remains of the spike-shaped artifacts discussed in
Sect. 2.2. For large R or Z values, close to
the star-shaped boundary of the plots, the quality of the
reconstruction decreases. This is not at all surprising because the
ellipses along which Eqs. (17) and (18)
must be evaluated to reconstruct density and temperature at those
points lie mostly outside of the maps of
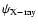 and
and
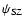 .
.
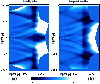 |
Figure 3:
Ratio of the reconstructed to the original density and
temperature for the analytic halo after n=20 iterations. An
inclination angle of
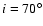 was chosen and assumed to be known
in performing the reconstruction. Panel a) shows the density ratio
was chosen and assumed to be known
in performing the reconstruction. Panel a) shows the density ratio
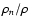 and panel b) the temperature ratio Tn/T. In the
central region, the errors are of the order of
and panel b) the temperature ratio Tn/T. In the
central region, the errors are of the order of 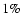 .
We plot the
ratios for all R and Z values possible within the box used for
the reconstruction (see Fig. 1). This causes the
star-like shape of the perimeter of the plot in the R, Z plane. Close to that boundary, at large R or Z values, the
ratios can significantly differ from unity. This is, however,
expected because the ellipses used in the reconstruction
of .
We plot the
ratios for all R and Z values possible within the box used for
the reconstruction (see Fig. 1). This causes the
star-like shape of the perimeter of the plot in the R, Z plane. Close to that boundary, at large R or Z values, the
ratios can significantly differ from unity. This is, however,
expected because the ellipses used in the reconstruction
of 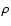 and T at those points lie mostly outside the maps of
and T at those points lie mostly outside the maps of
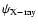 and
and
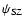 . . |
| Open with DEXTER |
Note that the quality of the reconstruction also depends on the
inclination of the halo's symmetry axis. Of course, best results are
achieved when the symmetry axis is perpendicular to the
line-of-sight. Then the assumption of axial symmetry contains the most
information. If, on the other hand, the symmetry axis is parallel to
the line-of-sight, the axial symmetry just corresponds to the circular
symmetry of the maps
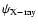 and
and
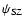 and does not yield any useful additional
information. Figure 4 illustrates this
inclination dependence. It shows the volume-weighted root mean square
(rms) relative errors of the reconstructed gas density and
temperature, computed within a sphere of radius
and does not yield any useful additional
information. Figure 4 illustrates this
inclination dependence. It shows the volume-weighted root mean square
(rms) relative errors of the reconstructed gas density and
temperature, computed within a sphere of radius
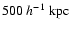 around the halo centre. Again, the knowledge of the
inclination angle i was used in the deprojection. An accuracy of
around the halo centre. Again, the knowledge of the
inclination angle i was used in the deprojection. An accuracy of 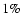 or better is achieved for about two thirds of the analytic halos
in a randomly oriented sample. However, halos that happen to have a
very small inclination angle i are necessarily poorly reconstructed.
or better is achieved for about two thirds of the analytic halos
in a randomly oriented sample. However, halos that happen to have a
very small inclination angle i are necessarily poorly reconstructed.
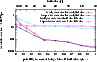 |
Figure 4:
Dependence of the quality of the deprojection on the inclination of the symmetry axis. For the analytic halo, which was deprojected as described above, we show the volume-weighted rms relative errors
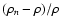 and (Tn-T)/T as functions of the inclination angle i after n=20 iterations. We also show the same errors after n=5 iterations for reconstructions of a numerical halo from maps with observational noise. A detailed description of these reconstructions is given in Sect. 4. The averages of the errors were computed within a sphere of radius
and (Tn-T)/T as functions of the inclination angle i after n=20 iterations. We also show the same errors after n=5 iterations for reconstructions of a numerical halo from maps with observational noise. A detailed description of these reconstructions is given in Sect. 4. The averages of the errors were computed within a sphere of radius
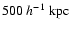 around the halo centre. The quantity
around the halo centre. The quantity 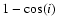 shown on the abscissae is chosen such as to have a flat number-density distribution for randomly oriented halos. The inclination angle i was assumed to be known in performing the deprojection.
shown on the abscissae is chosen such as to have a flat number-density distribution for randomly oriented halos. The inclination angle i was assumed to be known in performing the deprojection. |
| Open with DEXTER |
3.2 Deprojection of analytic halos including observational
noise
So far we have not considered noise that will be present in any real
X-ray or Sunyaev-Zel'dovich effect observation. We will now discuss
the impact it has on the reconstruction of ICM densities and
temperatures.
We model the noise in X-ray observations as follows. First, we
calculate for each pixel (j,k) of the halo's X-ray map
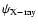 the number of photons
the number of photons
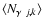 expected from bremsstrahlung, which is
proportional to
expected from bremsstrahlung, which is
proportional to
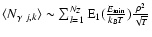 ,
where the sum extends along the line-of-sight represented by the pixel (j,k), and
,
where the sum extends along the line-of-sight represented by the pixel (j,k), and 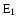 is the exponential
integral function.
is the exponential
integral function.
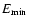 is a lower energy cutoff which
is necessary because the number of photons emitted is infrared
divergent. We choose
is a lower energy cutoff which
is necessary because the number of photons emitted is infrared
divergent. We choose
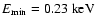 ,
which is a
reasonable lower limit for the photons from galaxy clusters observed
in current X-ray experiments. Next, we normalise the numbers of
expected photons such that they sum up to
,
which is a
reasonable lower limit for the photons from galaxy clusters observed
in current X-ray experiments. Next, we normalise the numbers of
expected photons such that they sum up to
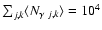 on the entire map. For each pixel (j,k),
we then set the actual number of photon counts
on the entire map. For each pixel (j,k),
we then set the actual number of photon counts
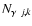 to a
value drawn from a Poisson distribution with expectation value
to a
value drawn from a Poisson distribution with expectation value
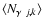 .
We then add the noise to the map
.
We then add the noise to the map
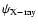 by multiplying
by multiplying
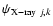 with
with
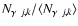 for all pixels.
for all pixels.
For the Sunyaev-Zel'dovich effect, we add noise corresponding to
future ALMA Band 3 observations (see Butler & Wootten 1999). In Band 3 (84
to 116 GHz) and in its compact configuration, ALMA will be able to
achieve a temperature sensitivity of
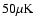 at a spatial
resolution of
at a spatial
resolution of 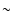 3 arcsec in about four hours of observation. At
an assumed halo redshift of 0.3, this resolution corresponds to the
angular size chosen for the pixels of the map
3 arcsec in about four hours of observation. At
an assumed halo redshift of 0.3, this resolution corresponds to the
angular size chosen for the pixels of the map
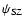 .
We
convert the temperature sensitivity cited above to an error
.
We
convert the temperature sensitivity cited above to an error
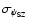 of
of
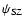 .
Then, for each
pixel, we add noise obtained from a normal distribution with standard
deviation
.
Then, for each
pixel, we add noise obtained from a normal distribution with standard
deviation
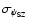 to
to
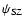 .
.
Richardson-Lucy deconvolution has the nice property of approximating
large-scale features quickly and small-scale noise slowly. Yet, it
turns out that smoothing the noisy maps
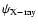 and
and
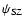 before using them in the deprojection improves
the results considerably. We use the following smoothing scheme. For
the X-ray observations, we assume that in addition to the map
before using them in the deprojection improves
the results considerably. We use the following smoothing scheme. For
the X-ray observations, we assume that in addition to the map
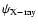 we also know the photon counts
we also know the photon counts
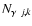 for all pixels. We then calculate for each pixel
(j,k) a radius
for all pixels. We then calculate for each pixel
(j,k) a radius
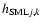 so that we have a fixed number of 100 photons
inside a circle with radius
so that we have a fixed number of 100 photons
inside a circle with radius
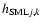 around that pixel. After that we
redistribute the value
around that pixel. After that we
redistribute the value
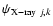 of each pixel on
the grid with a smoothing kernel of width
of each pixel on
the grid with a smoothing kernel of width
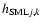 centred on that
pixel. This greatly reduces the fluctuations in the map
centred on that
pixel. This greatly reduces the fluctuations in the map
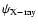 caused by photon noise. In the remainder of the paper we will call this first step of the smoothing scheme "photon-noise smoothing''.
caused by photon noise. In the remainder of the paper we will call this first step of the smoothing scheme "photon-noise smoothing''.
For the smoothing kernel, we take the line-of-sight projection of the
cubic spline SPH kernel
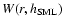 defined in Appendix A of
Springel et al. (2001). It is well suited for this purpose and allows us to use
the same routine for smoothing here and for projecting the numerical
SPH halos we use in Sect. 4. For axisymmetric halos,
the projection should be symmetric about the projected axis. However, the symmetry is broken here by noise. We restore it before performing the deprojection. Since we have oriented the grid
such that it is parallel to and centred on the projected symmetry axis, we can do that by replacing
defined in Appendix A of
Springel et al. (2001). It is well suited for this purpose and allows us to use
the same routine for smoothing here and for projecting the numerical
SPH halos we use in Sect. 4. For axisymmetric halos,
the projection should be symmetric about the projected axis. However, the symmetry is broken here by noise. We restore it before performing the deprojection. Since we have oriented the grid
such that it is parallel to and centred on the projected symmetry axis, we can do that by replacing
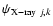 and
and
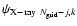 by their arithmetic
mean. Here,
by their arithmetic
mean. Here,
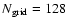 is the dimension of the grid. We
symmetrise
is the dimension of the grid. We
symmetrise
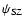 in the same way. After that we perform
one more smoothing operation on
in the same way. After that we perform
one more smoothing operation on
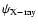 and
and
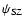 to further reduce fluctuations caused by
noise.
to further reduce fluctuations caused by
noise.
In numerically simulated halos, which we will discuss later, this will
also suppress the effect of subclumps. Since we do not want to smooth
out the peaks in the halo core, we choose a smoothing length
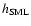 that
depends on the distance r from the halo (or map) centre, namely
that
depends on the distance r from the halo (or map) centre, namely
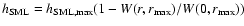 .
It is
zero in the centre of the map and continually increases to
.
It is
zero in the centre of the map and continually increases to
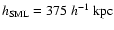 at a radius equal to
at a radius equal to
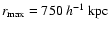 or larger. This yields smallest rms errors. Once we have
calculated
or larger. This yields smallest rms errors. Once we have
calculated
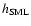 for each pixel, we smooth the maps of
for each pixel, we smooth the maps of
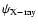 and
and
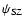 with the projection
of the SPH smoothing kernel mentioned above and with the
position-dependent smoothing length
with the projection
of the SPH smoothing kernel mentioned above and with the
position-dependent smoothing length
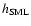 .
Note that roughly 80% of a pixel's value is redistributed within a circle of radius
.
Note that roughly 80% of a pixel's value is redistributed within a circle of radius
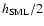 .
We refer to this second step of the smoothing scheme as "radius-dependent smoothing''.
.
We refer to this second step of the smoothing scheme as "radius-dependent smoothing''.
After degrading the analytic halo with noise and applying the
smoothing scheme described above, we perform the iterative
deprojection. The results after n=5 iterations are shown in
Fig. 5. An inclination of
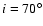 was chosen and assumed to be known in the deprojection. Again, the
left panel shows the ratio of the reconstructed to the original
density, and the right panel the corresponding temperature
ratio. Average errors in the central region are of the order of
was chosen and assumed to be known in the deprojection. Again, the
left panel shows the ratio of the reconstructed to the original
density, and the right panel the corresponding temperature
ratio. Average errors in the central region are of the order of 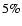 to
to 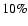 .
As expected, further outside, where the signal-to-noise
ratio becomes small and the ellipses used for the reconstruction lie
mostly outside the maps of
.
As expected, further outside, where the signal-to-noise
ratio becomes small and the ellipses used for the reconstruction lie
mostly outside the maps of
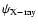 and
and
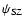 ,
the errors are substantially larger. Note that
at locations where we obtain a too low density, we usually find a too
high temperature and vice versa. This happens because the algorithm
minimises the deviations of the reconstructed from the original X-ray
and SZ-effect maps.
,
the errors are substantially larger. Note that
at locations where we obtain a too low density, we usually find a too
high temperature and vice versa. This happens because the algorithm
minimises the deviations of the reconstructed from the original X-ray
and SZ-effect maps.
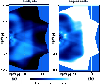 |
Figure 5:
Ratio of the reconstructed to the original density and
temperature for the analytic halo with observational noise after
n=5 iterations. An inclination of
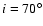 was chosen and
assumed to be known in performing the reconstruction. "Photon-noise'' and "radius-dependent'' smoothing were applied. Panel a) shows the density ratio
was chosen and
assumed to be known in performing the reconstruction. "Photon-noise'' and "radius-dependent'' smoothing were applied. Panel a) shows the density ratio
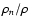 ,
and panel b) the temperature
ratio Tn/T. In the central region, the errors are of the order of ,
and panel b) the temperature
ratio Tn/T. In the central region, the errors are of the order of
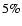 to
to 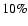 . . |
| Open with DEXTER |
In Fig. 6, we show density and temperature
profiles of the original analytic halo, of the halo reconstructed from
maps without observational noise, and of the halo reconstructed from
smoothed maps which contain observational noise. The reconstructed
halos are the same as shown in Figs. 3 and 5. Without noise, both the temperature
and the density profiles are reproduced very well. With noise, we can
still reproduce density profiles with an accuracy of a few
percent. The errors in the temperature profile are somewhat
larger. Deviations are mainly caused by the noise, but some are also
artifacts of the smoothing scheme we apply. Especially the too high
temperature near
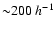 kpc and the too low temperature
near
kpc and the too low temperature
near
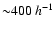 kpc are a consequence of "radius-dependent smoothing''. On the other hand, without such
smoothing we would approximately double the errors in the density and
temperature reconstructions.
kpc are a consequence of "radius-dependent smoothing''. On the other hand, without such
smoothing we would approximately double the errors in the density and
temperature reconstructions.
![\begin{figure}
\scalebox{0.7}
{
\begin{picture}
(0,0)%
\includegraphics{4717fi...
...\strut{} radius $[h^{-1} {\rm kpc}]$ }}%
\end{picture}%
\endgroup
}
\end{figure}](/articles/aa/full/2006/33/aa4717-05/Timg133.gif) |
Figure 6:
Density and temperature profiles of the original and the
reconstructed analytic halos. The upper panel shows the density
(falling curves, left axis) and the temperature profiles (rising
curves, right axis) of the original analytic halo, the halo
reconstructed without observational noise (and without any
smoothing), and the halo reconstructed from maps with
observational noise to which the complete smoothing scheme was applied.
The lower panel shows the profile of the ratio of the reconstructed density 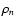 to the original density
to the original density
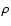 .
The number of iterations used was n=20 in the case without
noise and n=5 in the case with noise. An inclination of .
The number of iterations used was n=20 in the case without
noise and n=5 in the case with noise. An inclination of
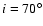 was chosen and assumed to be known in the
reconstruction.
was chosen and assumed to be known in the
reconstruction. |
| Open with DEXTER |
4 Deprojection of numerically simulated cluster halos
So far, we have demonstrated the performance of the algorithm with
axisymmetric analytic halos. We were able to reconstruct their
three-dimensional density and temperature distributions from synthetic
X-ray and (thermal) Sunyaev-Zel'dovich effect observations. Real
galaxy clusters, however, are hardly perfectly axisymmetric. We will
study in this section whether they nonetheless allow accurate density
and temperature reconstructions with the deprojection algorithm
proposed in Sect. 2.4. We use a sample of four
numerically simulated galaxy clusters to investigate into this
question.
The simulations were carried out by Klaus Dolag with GADGET-2
(Springel 2005), a new version of the parallel TreeSPH simulation
code GADGET (Springel et al. 2001). The cluster regions were extracted from
a dissipation-less (dark matter only) simulation with a box size of
479 h-1 Mpc of a flat 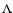 CDM model with
CDM model with
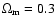 ,
h=0.7,
,
h=0.7,
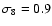 (see Yoshida et al. 2001). They were re-simulated
with higher resolution using the "Zoomed Initial Conditions'' (ZIC)
technique (Tormen 1997). Gas was introduced into the
high-resolution region by splitting each parent particle into a gas
and a dark matter particle, which were then displaced by half the mean
inter-particle distance, such that the centre-of-mass and the momentum
were conserved. The mass ratio of gas to dark matter particles was set
to obtain
(see Yoshida et al. 2001). They were re-simulated
with higher resolution using the "Zoomed Initial Conditions'' (ZIC)
technique (Tormen 1997). Gas was introduced into the
high-resolution region by splitting each parent particle into a gas
and a dark matter particle, which were then displaced by half the mean
inter-particle distance, such that the centre-of-mass and the momentum
were conserved. The mass ratio of gas to dark matter particles was set
to obtain
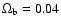 .
The final mass resolution was
.
The final mass resolution was
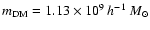 and
and
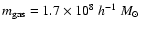 for dark-matter and gas particles within the
high-resolution region, respectively. The simulations we use follow
the dynamics of the dark matter and the adiabatic evolution of the
cluster gas, but they ignore radiative cooling. They are described in
more detail in Puchwein et al. (2005) and Dolag et al. (2005).
for dark-matter and gas particles within the
high-resolution region, respectively. The simulations we use follow
the dynamics of the dark matter and the adiabatic evolution of the
cluster gas, but they ignore radiative cooling. They are described in
more detail in Puchwein et al. (2005) and Dolag et al. (2005).
Our deprojection algorithm requires a symmetry axis, which real
clusters do not generally have. We thus need to choose an axis around
which the numerical clusters have at least a high degree of
symmetry. We do this by calculating the inertial tensor of the cluster
gas inside a sphere of radius
500 h-1 kpc around the cluster
centre and finding its eigenvectors
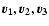 and eigenvalues
and eigenvalues
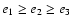 .
We choose the symmetry axis
through the cluster centre and parallel to the eigenvector
.
We choose the symmetry axis
through the cluster centre and parallel to the eigenvector 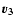 with the smallest eigenvalue if
with the smallest eigenvalue if
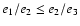 ,
or
parallel to the eigenvector
,
or
parallel to the eigenvector 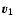 with the largest eigenvalue
otherwise. This means that, if two eigenvalues are very similar, we
choose the axis parallel to the eigenvector corresponding to the third
eigenvalue.
with the largest eigenvalue
otherwise. This means that, if two eigenvalues are very similar, we
choose the axis parallel to the eigenvector corresponding to the third
eigenvalue.
Having chosen a fiducial "symmetry'' axis and a line-of-sight, we can
produce synthetic maps of X-ray and
Sunyaev-Zel'dovich effect
observations. For that purpose, we use the simulated clusters at a
redshift of z=0.3 and project them along the line-of-sight. At z=0.3, the cluster sample spans a mass range between
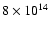 and
and
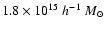 .
.
For now, we do not add any observational noise to the maps. However,
the clusters contain substructures which break axial symmetry and lead
to artifacts in the density and temperature reconstructions. Thus,
depending on the amount of substructure present in a cluster, it may
still be favourable to use "radius-dependent smoothing'' on the X-ray and Sunyaev-Zel'dovich effect
maps prior to reconstruction. In Figs. 7
and 8, we show the results of the deprojection
without any smoothing, and using "radius-dependent smoothing''.
The density reconstruction in the central region reaches an accuracy
of about 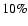 in both cases. For the temperature reconstruction and the density reconstruction at large r, we obtain somewhat better results without smoothing for this rather symmetric cluster. Note, however,
the hyperbolically shaped artifacts in
Fig. 7 which are produced by substructure
clumps in absence of smoothing. They appear at those R and Zvalues which correspond to the line-of-sight passing through such a
clump. The spike-shaped artifacts discussed in
Sect. 2.2 were a special case of the artifacts
found here. For most of the hyperbolae in the left panel of
Fig. 7, one can also see the position of
the clump that produced it in darker colours. The hyperbolae pass
right through them.
in both cases. For the temperature reconstruction and the density reconstruction at large r, we obtain somewhat better results without smoothing for this rather symmetric cluster. Note, however,
the hyperbolically shaped artifacts in
Fig. 7 which are produced by substructure
clumps in absence of smoothing. They appear at those R and Zvalues which correspond to the line-of-sight passing through such a
clump. The spike-shaped artifacts discussed in
Sect. 2.2 were a special case of the artifacts
found here. For most of the hyperbolae in the left panel of
Fig. 7, one can also see the position of
the clump that produced it in darker colours. The hyperbolae pass
right through them.
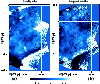 |
Figure 7:
Reconstruction of the simulated cluster g51 without noise and
smoothing. The ratios of the reconstructed to the original density
and temperature are shown. The deprojection was done with n=5 iterations. An inclination angle of
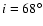 between the
line-of-sight and the principal inertial axis of the cluster gas was
chosen and assumed to be known in the reconstruction. Panel a)
shows the density ratio
between the
line-of-sight and the principal inertial axis of the cluster gas was
chosen and assumed to be known in the reconstruction. Panel a)
shows the density ratio
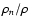 and panel b) the temperature
ratio Tn/T. In the central region, the errors are of the order of
and panel b) the temperature
ratio Tn/T. In the central region, the errors are of the order of
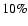 . . |
| Open with DEXTER |
As one can see in Fig. 8, "radius-dependent smoothing'' removes the
hyperbolic artifacts. The subclumps, however, still appear in darker
colours in the density ratio map, which means that the reconstructed
density there is too low. However, this is entirely expected and
inevitable, because they violate axial symmetry and thus cannot be
faithfully reconstructed with this deprojection technique. By
smoothing, we essentially remove the subclumps from the maps and
reconstruct the density and temperature of the main halo without them.
Unfortunately, "radius-dependent smoothing'' also affects the density and temperature
profiles. This can be seen in the "rings'' around the halo centre in
the right panel of Fig. 8. It is further
illustrated in Fig. 10, which shows the density
and temperature profiles of the original cluster g51, after
deprojection without noise but with "radius-dependent smoothing'', and after deprojection
without noise and without smoothing. For
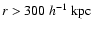 ,
the reconstruction without smoothing yields more accurate density and
temperature profiles. In addition, the profiles for deprojections from
maps including observational noise are shown. They will be discussed
in the next section.
,
the reconstruction without smoothing yields more accurate density and
temperature profiles. In addition, the profiles for deprojections from
maps including observational noise are shown. They will be discussed
in the next section.
Reconstructions along different lines-of-sight and of the three other
clusters in the sample gave similar results. For the most asymmetric
halo, the errors were larger by factors of 1.5 to 2 compared to
the reconstruction of g51 presented above. We can thus conclude that,
although clusters are not strictly axisymmetric and contain
substructure, it is possible to apply the deprojection method proposed
in Sect. 2.4 and successfully reconstruct
three-dimensional density and temperature distributions of the cluster
gas.
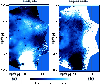 |
Figure 8:
Reconstruction of the simulated cluster g51 without noise but
with "radius-dependent smoothing''. The ratios of the reconstructed
to the original density and temperature are shown. The deprojection
was done with n=5 iterations. An inclination angle of
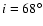 between the line-of-sight and the principal inertial axis of the
cluster gas was chosen and assumed to be known in the
reconstruction. Panel a) shows the density ratio
between the line-of-sight and the principal inertial axis of the
cluster gas was chosen and assumed to be known in the
reconstruction. Panel a) shows the density ratio
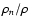 and
panel b) the temperature ratio Tn/T. In the central region, the
errors are of the order of
and
panel b) the temperature ratio Tn/T. In the central region, the
errors are of the order of 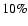 . . |
| Open with DEXTER |
In Sect. 3.2, we studied the impact of
observational noise in the X-ray and Sunyaev-Zel'dovich effect maps on
the quality of the density and temperature reconstruction. We will now
do the same for the numerically simulated cluster halos using the same
noise model, namely Poisson noise corresponding to 104 observed
photons for the X-ray maps and a noise level expected for a four-hour
ALMA Band 3 observation for the Sunyaev-Zel'dovich effect maps. We
also use the smoothing scheme described there.
We show the results of the reconstruction in
Fig. 9. Again, the left panel shows the
ratio of the reconstructed to the original density, and the right
panel the corresponding temperature ratio. In the central region we
achieve an accuracy of about 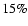 .
Without "radius-dependent smoothing'',
errors would be larger by roughly a factor of 1.5 or even more next to
the halo centre. However, if one is mainly interested in density and
temperature profiles it may still be favourable to leave the "radius-dependent smoothing'' step away. Although the errors are larger without "radius-dependent smoothing'',
they are less biased with respect to the distance from the halo centre
and cancel better when averaging over spherical shells around it,
especially at large radii. Thus depending on the quantity one is finally interested in or the context in which the reconstructions are used, different amounts of smoothing may yield best results. Figure 10 shows the profiles obtained with and without "radius-dependent smoothing''.
.
Without "radius-dependent smoothing'',
errors would be larger by roughly a factor of 1.5 or even more next to
the halo centre. However, if one is mainly interested in density and
temperature profiles it may still be favourable to leave the "radius-dependent smoothing'' step away. Although the errors are larger without "radius-dependent smoothing'',
they are less biased with respect to the distance from the halo centre
and cancel better when averaging over spherical shells around it,
especially at large radii. Thus depending on the quantity one is finally interested in or the context in which the reconstructions are used, different amounts of smoothing may yield best results. Figure 10 shows the profiles obtained with and without "radius-dependent smoothing''.
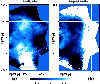 |
Figure 9:
Reconstruction of the simulated cluster g51 with noise and
and the complete smoothing scheme applied. The ratios of the reconstructed to the original density
and temperature are shown. The deprojection was done with n=5 iterations. An inclination angle of
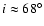 between the
line-of-sight and the principal inertial axis of the cluster gas was
chosen and assumed to be known in the reconstruction. Panel a)
shows the density ratio
between the
line-of-sight and the principal inertial axis of the cluster gas was
chosen and assumed to be known in the reconstruction. Panel a)
shows the density ratio
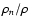 and panel b) the temperature
ratio Tn/T. In the central region, the errors are of the order of
and panel b) the temperature
ratio Tn/T. In the central region, the errors are of the order of
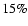 . . |
| Open with DEXTER |
![\begin{figure}
\scalebox{0.7}
{
\begin{picture}
(0,0)%
\includegraphics{4717fi...
...\strut{} radius $[h^{-1} {\rm kpc}]$ }}%
\end{picture}%
\endgroup
}
\end{figure}](/articles/aa/full/2006/33/aa4717-05/Timg169.gif) |
Figure 10:
Gas density and temperature profiles of the original and the
reconstructed cluster g51. The upper panel shows the density
profiles (falling curves, left axis) and the temperature profiles
(rising curves, right axis) of the original cluster, the cluster
reconstructed without observational noise but with "radius-dependent smoothing'', reconstructed without
observational noise and without any smoothing,
reconstructed from maps with observational noise and the complete smoothing scheme applied, and reconstructed
from maps with observational noise but without "radius-dependent smoothing''. The lower panel shows the profile of the ratio of the reconstructed density 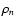 to the original density
to the original density 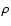 .
The
number of iterations used was n=5 in all cases. An inclination
angle of .
The
number of iterations used was n=5 in all cases. An inclination
angle of
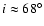 was chosen and assumed to be known in
the reconstruction.
was chosen and assumed to be known in
the reconstruction. |
| Open with DEXTER |
We still need to discuss when the iteration used in the density and
temperature reconstructions should best be
stopped. Figure 11 illustrates the dependence of the
quality of the reconstruction on the number of iterations used. More
precisely, it shows the relative volume-weighted rms
error of the density reconstruction within
r=500 h-1 kpc as a
function of the number of iterations and for different deprojection
schemes, namely for the deprojections of the analytic halo and the
numerically simulated cluster g51 discussed above and shown in
Figs. 3, 5,
8, and 9 after n=20 or
n=5 iterations. The quality of the reconstruction improves quickly
during the first roughly five iterations (first ten for the analytic
halo without noise) and then levels off. In addition, we show the
quality of the reconstruction of g51 from maps with noise but without
using "radius-dependent smoothing''. In this
case, small-scale noise in the maps is not sufficiently
suppressed. The best reconstruction is found after five
iterations. Then, the quality decreases again because the algorithm
starts to approximate small-scale noise. Thus, unless a halo is very
smooth and axisymmetric, such as the analytic halo without noise, we
find that the quality of the reconstruction does not significantly
increase after n=5 iterations and may even decrease if small scale
fluctuations due to noise are not efficiently suppressed. Thus, we
conclude that it is favourable to use this number of iterations for
the deprojection of simulated and real galaxy clusters. Alternatively, one could control the reproduction of small-scale fluctuations with a formal regularisation scheme, such as provided by maximum-entropy methods.
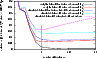 |
Figure 11:
Dependence of the quality of the density reconstruction on
the number of iterations used. We show the volume-weighted relative
rms error
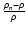 within spheres with
r=500
h-1 kpc radius and for different deprojections of our analytic
halo model and of the numerically simulated cluster g51. The figure legend explains which halo, whether or not noise, and what kind of smoothing were used for the different reconstructions shown. Note that
"photon-noise smoothing'' of the X-ray maps is always and only used for maps with noise.
within spheres with
r=500
h-1 kpc radius and for different deprojections of our analytic
halo model and of the numerically simulated cluster g51. The figure legend explains which halo, whether or not noise, and what kind of smoothing were used for the different reconstructions shown. Note that
"photon-noise smoothing'' of the X-ray maps is always and only used for maps with noise. |
| Open with DEXTER |
In all deprojections of analytic and numerical clusters presented
above, we have assumed that the inclination angle of the "symmetry''
axis is known beforehand. This will usually not be the case for real
observed clusters. In Sect. 2.3, we sketched how
one can obtain inclination angles by comparing the maps obtained by
projecting reconstructed halos to the original maps. One would
reconstruct a cluster assuming different values for i and find the
value for which the maps match best. In principle, we could generalise
this approach to the X-ray and Sunyaev-Zel'dovich effect maps used for
the density and temperature deprojections. That is, we can compare the
original maps
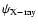 and
and
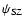 to the
maps
to the
maps
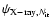 and
and
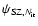 ,
which correspond to the
reconstructed halo after a fixed number
,
which correspond to the
reconstructed halo after a fixed number
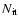 of iterations
and for different values of the inclination angle i used for the
reconstruction.
of iterations
and for different values of the inclination angle i used for the
reconstruction.
We did this for the analytic halo model and for our sample of
numerical clusters and used different inclination angles
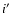 for
projecting these halos to obtain the original maps. However, the
minima in the penalty function (see Eq. (11)) are not well defined. They are
very broad and not always centred on i=i'. Even for the analytic
halo without observational noise, it is hardly possible to find the
correct axis inclination in this way. As one can see from
Eqs. (17) and (18), the iterative
corrections of the deprojection algorithm are determined from the
deviations of the X-ray and Sunyaev-Zel'dovich effect maps, and the
deviations are thereby minimised. Unfortunately, this still works
remarkably well when choosing a wrong inclination angle
for
projecting these halos to obtain the original maps. However, the
minima in the penalty function (see Eq. (11)) are not well defined. They are
very broad and not always centred on i=i'. Even for the analytic
halo without observational noise, it is hardly possible to find the
correct axis inclination in this way. As one can see from
Eqs. (17) and (18), the iterative
corrections of the deprojection algorithm are determined from the
deviations of the X-ray and Sunyaev-Zel'dovich effect maps, and the
deviations are thereby minimised. Unfortunately, this still works
remarkably well when choosing a wrong inclination angle 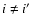 for the deprojection. Thus the X-ray and Sunyaev-Zel'dovich effect
maps are still reproduced well in this case, although the errors of
the density and temperature reconstructions increase significantly.
for the deprojection. Thus the X-ray and Sunyaev-Zel'dovich effect
maps are still reproduced well in this case, although the errors of
the density and temperature reconstructions increase significantly.
We tried to limit the ability of the deprojection algorithm to
reproduce maps well even when the inclination angle is wrong by
reducing its degrees of freedom. For doing so, we used a variant of
the algorithm that only reconstructs the density and uses a constant
but adjustable temperature. This of course also limits the accuracy of
the reconstruction for the correct inclination angle. Thus, the results
of comparing the reconstructed X-ray and Sunyaev-Zel'dovich effect
maps to the original ones for finding the inclination angle were not
significantly better.
On the other hand, leaving the deprojection algorithm as described in
Sect. 2.4, but using additional independent
information for finding the inclination angle of the halo, seems to be
more promising. For the deprojection, we use maps of the X-ray flux of
the clusters, but so far we do not use any spectral information from
the X-ray observations. In Figs. 12 and 13, we assume that in addition to the X-ray flux
maps we also have maps of the emission-weighted temperature
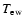 .
We reconstruct the analytic halo and the
numerically simulated cluster g51 from X-ray flux and
Sunyaev-Zel'dovich effect maps as above, but then compare the original
emission-weighted temperature map to one we obtain by projecting the
reconstructed halos. We repeated this for different inclination angles i', chosen for projecting the original maps, and i, chosen in the
reconstruction.
.
We reconstruct the analytic halo and the
numerically simulated cluster g51 from X-ray flux and
Sunyaev-Zel'dovich effect maps as above, but then compare the original
emission-weighted temperature map to one we obtain by projecting the
reconstructed halos. We repeated this for different inclination angles i', chosen for projecting the original maps, and i, chosen in the
reconstruction.
Note, however, when applying this method to real galaxy clusters and projected temperature maps obtained by X-ray spectral fitting of single temperature emission models to observations, it may be favourable to use a more sophisticated projected temperature definition, such as the spectroscopic-like temperature, instead of the emission-weighted temperature (see Mazzotta et al. 2004).
Figure 12 shows the rms relative
error of the reconstructed emission-weighted temperature maps for the
analytic halo without and with noise.
 and no
smoothing were used without noise, and
and no
smoothing were used without noise, and
 and the
complete smoothing scheme were used with noise. The rms error was computed
within a radius of
500 h-1 kpc around the map centre and is
shown for inclinations of
and the
complete smoothing scheme were used with noise. The rms error was computed
within a radius of
500 h-1 kpc around the map centre and is
shown for inclinations of
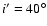 and
and
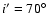 of the
original halo. As desired, the minima of the error curves are at the
correct locations
of the
original halo. As desired, the minima of the error curves are at the
correct locations
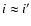 .
.
Note that the curves are only shown for i between 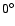 and
and 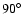 because
because
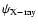 and
and
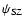 and hence the whole deprojection algorithm is insensitive to what is
the front and what is the back side of the cluster. We thus get the
same reconstruction and the same errors for deprojections which adopt
inclination angles i and
and hence the whole deprojection algorithm is insensitive to what is
the front and what is the back side of the cluster. We thus get the
same reconstruction and the same errors for deprojections which adopt
inclination angles i and
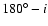 .
There is no way to
distinguish these cases from the X-ray, thermal Sunyaev-Zel'dovich
effect and temperature maps. The error curves are thus symmetric about
.
There is no way to
distinguish these cases from the X-ray, thermal Sunyaev-Zel'dovich
effect and temperature maps. The error curves are thus symmetric about
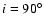 .
Also note that for the halo with noise, we added
observational noise only to the X-ray flux maps and Sunyaev-Zel'dovich
effect maps that were used for the reconstruction, but not to the
.
Also note that for the halo with noise, we added
observational noise only to the X-ray flux maps and Sunyaev-Zel'dovich
effect maps that were used for the reconstruction, but not to the
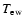 maps which we use for finding the inclination
angle. We do not mimic observational noise in the temperature maps because it can only be realistically modeled when considering instrument response and line emission. In addition to the error curves of the temperature maps, we
also show in Fig. 12 the volume-weighted,
relative rms errors of the density reconstructions in the central
500
h-1 kpc. As expected, the reconstruction works best for
maps which we use for finding the inclination
angle. We do not mimic observational noise in the temperature maps because it can only be realistically modeled when considering instrument response and line emission. In addition to the error curves of the temperature maps, we
also show in Fig. 12 the volume-weighted,
relative rms errors of the density reconstructions in the central
500
h-1 kpc. As expected, the reconstruction works best for
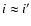 .
.
Figure 13 shows similar quantities as
Fig. 12, but for the numerically simulated
cluster halo g51. Original halo inclinations were set to
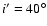 and
and
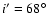 ,
and
,
and
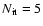 iterations were used. The
error curves are shown for the simulated halo without observational
noise and using "radius-dependent smoothing'', and
including observational noise and using the complete smoothing
scheme. No noise was added to the emission-weighted temperature
maps. The relative rms
iterations were used. The
error curves are shown for the simulated halo without observational
noise and using "radius-dependent smoothing'', and
including observational noise and using the complete smoothing
scheme. No noise was added to the emission-weighted temperature
maps. The relative rms
 error was computed within a
circle of radius
200 h-1 kpc around the map centre, while the
density reconstruction errors were again determined within the central
500 h-1 kpc. Also for this numerical halo the errors are
smallest for
error was computed within a
circle of radius
200 h-1 kpc around the map centre, while the
density reconstruction errors were again determined within the central
500 h-1 kpc. Also for this numerical halo the errors are
smallest for
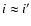 .
.
 |
Figure 12:
Accuracy of emission-weighted temperature
 maps and densities of reconstructed analytic halos. The
deprojections started from maps obtained by projecting the analytic
halo along a line-of-sight with inclination angles of
maps and densities of reconstructed analytic halos. The
deprojections started from maps obtained by projecting the analytic
halo along a line-of-sight with inclination angles of
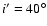 and
and
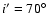 .
Inclination angles i between .
Inclination angles i between  and
and  were used for the reconstruction. As expected, the best
reconstructions are obtained for
were used for the reconstruction. As expected, the best
reconstructions are obtained for
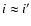 .
The errors are shown
for deprojections from maps without observational noise and from
smoothed maps with observational noise, and were averaged within a
region of radius
500 h-1 kpc around the map or halo centre. .
The errors are shown
for deprojections from maps without observational noise and from
smoothed maps with observational noise, and were averaged within a
region of radius
500 h-1 kpc around the map or halo centre. |
| Open with DEXTER |
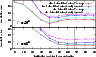 |
Figure 13:
Accuracy of emission weighted temperature
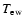 maps and densities for the reconstructed simulated halo g51. Maps
obtained by projecting g51 along a line-of-sight with inclination
angles of
maps and densities for the reconstructed simulated halo g51. Maps
obtained by projecting g51 along a line-of-sight with inclination
angles of
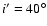 and
and
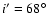 were used. The
reconstruction assumed inclination angles i between
were used. The
reconstruction assumed inclination angles i between  and
and  .
Best reconstructions are obtained for .
Best reconstructions are obtained for
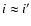 .
The
errors are shown for deprojections from maps without observational
noise but using "radius-dependent smoothing'', and from maps
with observational noise on which the complete smoothing scheme was
applied. The rms relative errors were obtained within a
circle of radius
200 h-1 kpc around the map centre for the Tew maps and inside a sphere of radius
500 h-1 kpc
around the halo centre for the density reconstructions. .
The
errors are shown for deprojections from maps without observational
noise but using "radius-dependent smoothing'', and from maps
with observational noise on which the complete smoothing scheme was
applied. The rms relative errors were obtained within a
circle of radius
200 h-1 kpc around the map centre for the Tew maps and inside a sphere of radius
500 h-1 kpc
around the halo centre for the density reconstructions. |
| Open with DEXTER |
For halos with an original inclination
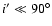 or
or
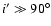 and for the analytic halos without noise, the minima of the
error curves for the emission-weighted temperature and the density
reconstructions are well defined. Thus the quality of the
reconstruction of such halos depends strongly on using the correct
inclination i=i' assumed in the deprojection. However, in such cases, the
inclination angle is better constrained by the emission-weighted
temperature maps. On the other hand, if the "symmetry'' axis of the
original halo is almost perpendicular to the line-of-sight, the minima
of the error curves are usually broad, and finding the precise
inclination i=i' for the reconstruction becomes less important. This
can also be unterstood from the fact that deviations are symmetric around
and for the analytic halos without noise, the minima of the
error curves for the emission-weighted temperature and the density
reconstructions are well defined. Thus the quality of the
reconstruction of such halos depends strongly on using the correct
inclination i=i' assumed in the deprojection. However, in such cases, the
inclination angle is better constrained by the emission-weighted
temperature maps. On the other hand, if the "symmetry'' axis of the
original halo is almost perpendicular to the line-of-sight, the minima
of the error curves are usually broad, and finding the precise
inclination i=i' for the reconstruction becomes less important. This
can also be unterstood from the fact that deviations are symmetric around
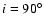 .
For example,
the halo with an inclination of
.
For example,
the halo with an inclination of
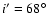 shown in
Fig. 13 should exhibit minima at
shown in
Fig. 13 should exhibit minima at
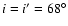 and at
and at
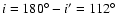 and a maximum in between. However,
because these three extremal points are close to each other, they
start merging into one broad minimum. Note that the emission-weighted
temperature maps can constrain the inclination angle in both cases to
values where the errors of the reconstruction are close to their
minima.
and a maximum in between. However,
because these three extremal points are close to each other, they
start merging into one broad minimum. Note that the emission-weighted
temperature maps can constrain the inclination angle in both cases to
values where the errors of the reconstruction are close to their
minima.
The accuracy of inclination-angle estimates could be improved by using
other independent information in addition to the temperature maps,
such as data from weak and strong-lensing observations. Lensing
observations allow reconstructions of the lensing potential (see
e.g. Cacciato et al. 2005), which is simply the suitably rescaled projection of
the lens' gravitational potential. A natural way to employ this for
finding inclination angles is to assume hydrostatic equilibrium of the
cluster gas in the potential well of the cluster and use the density
and temperature reconstruction described above to obtain the
gravitational potential of the reconstructed cluster halo. Its
projection can then be compared to the lensing potential obtained from
observations. Alternatively, one could use the deprojection algorithm
discussed in Sect. 2.1 to obtain the
three-dimensional gravitational potential from the lensing potential
that was found from observations and compare it to the gravitational
potential corresponding to the density and temperature reconstruction
under the assumption of hydrostatic equilibrium. We shall
explore these possibilities in a forthcoming study.
We propose a new method for deprojecting hot gas in galaxy clusters
which combines X-ray and thermal Sunyaev-Zel'dovich effect
observations and reconstructs three-dimensional density and
temperature distributions. We start from the iterative deprojection
algorithm suggested by Binney et al. (1990) which employs Richardson-Lucy
deconvolution and assumes axial symmetry of the physical quantity
whose three-dimensional distribution shall be reconstructed from
two-dimensional maps of its projection along the line-of-sight.
This approach does not restrict the orientation of the symmetry axis
to be parallel to the line-of-sight, but the inclination angle between
the symmetry axis and the line-of-sight is assumed to be known. This
algorithm runs into problems when it is used to reconstruct strongly
peaked distributions such as the X-ray emissivity of a galaxy
cluster. There, one obtains spike-shaped artifacts through the centre
of the reconstructed halo. We suppress the formation of such artifacts
by introducing a regularisation scheme for the iterative corrections
used in the deprojection. Then, we generalise this algorithm to
simultaneously reconstruct three-dimensional distributions of several
physical quantities by combining two-dimensional maps of projections
which probe these three-dimensional distributions in different ways.
Here, we discuss how three-dimensional density and temperature
distributions of the intra-cluster medium can be reconstructed from
combined X-ray and thermal Sunyaev-Zel'dovich effect observations. We
test the method using synthetic data of analytically modeled and of
numerically simulated galaxy clusters and discuss the quality of the
reconstructions and the impact of observational noise, cluster
substructure and deviations from axial symmetry. For numerical
clusters which are of course not strictly axisymmetric, we use one of
the principal inertial axes as the "symmetry'' axis for the
deprojection.
Our main findings, if we neglect observational noise and assume that
the inclination angle between the symmetry axis and the line-of-sight
is known, are:
- Spike-shaped artifacts of the deprojection are efficiently
suppressed by the regularisation of the iterative corrections.
- Densities and temperatures of the ICM of axisymmetric analytic
clusters can be reconstructed very accurately from X-ray flux and
Sunyaev-Zel'dovich effect maps. Errors are of the order of 1%
unless the angle between the symmetry axis and the line-of-sight is
small.
- The three-dimensional density and temperature distributions of
hot gas in numerically simulated clusters, although not strictly
axisymmetric, can still be reliably reconstructed. Relative errors
reach roughly 10%. Smoothing of the X-ray flux and the
Sunyaev-Zel'dovich effect maps can be used to suppress artifacts
caused by subclumps.
- Accurate gas density and temperature profiles can be obtained
from the reconstructions.
We then add photon noise corresponding to a total number of 104observed photons to the X-ray and observational noise corresponding to
a four-hour ALMA Band 3 observation to the Sunyaev-Zel'dovich effect
maps, respectively. We smooth the maps before repeating the
deprojections to suppress small-scale fluctuations which the algorithm
would otherwise attempt to approximate and thereby reduce the quality of the
reconstructions. From the repeated reconstructions of the analytic and
numerical halos, this time including observational noise, we conclude:
- Gas densities and temperatures of axisymmetric analytic
halos
can also be efficiently reconstructed from maps thatcontain
observational noise. The relative errors of the reconstructions are
about 5% to 10%.
- The three-dimensional structure of the ICM of numerically
simulated clusters can also be reliably reconstructed from X-ray
flux and Sunyaev-Zel'dovich effect maps that contain observational
noise. Relative errors reach roughly 15%.
- Accurate profiles can be obtained from the reconstructions.
- Five iterations are sufficient for the ICM
deprojection. Using a larger number does not increase the quality of the reconstruction.
For these deprojections, we assumed that the inclination angle between
the symmetry axis and the line-of-sight is known beforehand. This will
usually not be the case for observations of real clusters. In
principle, one could try to find the inclination angle by deprojecting
the cluster assuming different values of the inclination angle and
comparing the original X-ray and Sunyaev-Zel'dovich effect maps to
those expected from the reconstructed halo. They should match best if
the correct inclination is used for the deprojection. Unfortunately,
the minima of the deviations of the maps as a function of the
assumed inclination angle are quite broad and not always centred on
the correct value. However additional data which are independent of
the X-ray flux and the Sunyaev-Zel'dovich effect maps, can provide
information on the inclination angle. We show that high-quality
emission-weighted temperature maps which become more and more
routinely available, can constrain the inclination angle of a
cluster's symmetry axis to values for which the quality of the
reconstruction is close to its optimum.
Acknowledgements
We are deeply indebted to Klaus Dolag, who generously provided us access to the numerical simulations of the cluster sample that was used in this work. We also thank Massimo Meneghetti for useful discussions. E.P. is supported by the German Science Foundation under grant number BA 1369/6-1.
- Arnaud, K. A.
1996, Astronomical Data Analysis Software and Systems V, ASP
Conf. Ser., 101, 17
(In the text)
- Binney, J. J.,
Davies, R. L., & Illingworth, G. D. 1990, ApJ, 361,
78 [NASA ADS] [CrossRef] (In the text)
- Butler, B., &
Wootten, A. 1999, ALMA Memo, 276,
http://www.alma.nrao.edu/memos/html-memos/abstracts/abs276.html
(In the text)
- Cacciato, M.,
Bartelmann, M., Meneghetti, M., & Moscardini, L. 2005, A&A,
submitted, preprint [arXiv:astro-ph/0511694]
(In the text)
- Cavaliere, A., &
Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] (In the text)
- De Filippis, E.,
Sereno, M., Bautz, M. W., & Longo, G. 2005, ApJ, 625,
108 [NASA ADS] [CrossRef] (In the text)
- Dolag, K., Vazza, F.,
Brunetti, G., & Tormen, G. 2005, MNRAS, 364, 753 [NASA ADS] [CrossRef] (In the text)
- Doré, O., Bouchet,
F. R., Mellier, Y., & Teyssier, R. 2001, A&A, 375,
14 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Jing, Y. P., &
Suto, Y. 2002, ApJ, 574, 538 [NASA ADS] [CrossRef] (In the text)
- Lee, J., & Suto, Y.
2004, ApJ, 601, 599 [NASA ADS] [CrossRef] (In the text)
- Lucy, L. B. 1974,
AJ, 79, 745 [NASA ADS] [CrossRef]
- Lucy, L. B. 1994,
A&A, 289, 983 [NASA ADS]
- Mazzotta, P., Rasia,
E., Moscardini, L., & Tormen, G. 2004, MNRAS, 354, 10 [NASA ADS] [CrossRef] (In the text)
- Puchwein, E.,
Bartelmann, M., Dolag, K., & Meneghetti, M. 2005, A&A, 442,
405 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Reblinsky, K. 2000,
A&A, 364, 377 [NASA ADS] (In the text)
- Reblinsky, K., &
Bartelmann, M. 2001, in Gravitational Lensing: Recent Progress and
Future Goals, ASP Conf. Ser., 237, 337
(In the text)
- Springel, V. 2005,
MNRAS, 364, 1105 [NASA ADS] [CrossRef] (In the text)
- Springel, V., Yoshida,
N., & White, S. D. M. 2001, New Astron., 6, 79 [NASA ADS] (In the text)
- Tormen, G. 1997, MNRAS,
290, 411 [NASA ADS] (In the text)
- Yoshida, N., Sheth,
R. K., & Diaferio, A. 2001, MNRAS, 328, 669 [NASA ADS] [CrossRef] (In the text)
- Zaroubi, S., Squires,
G., de Gasperis, G., et al. 2001, ApJ, 561, 600 [NASA ADS] [CrossRef] (In the text)
- Zaroubi, S., Squires,
G., Hoffman, Y., & Silk, J. 1998, ApJ, 500, L87 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006

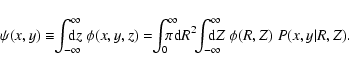
![\begin{displaymath}P(x,y\vert R,Z) = \frac{\delta[(\frac{y}{\cos i}-Z \tan i)^2-\left(R^2-x^2\right)]}{\pi\cos i},
\end{displaymath}](/articles/aa/full/2006/33/aa4717-05/img34.gif)
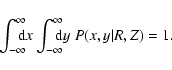
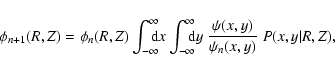
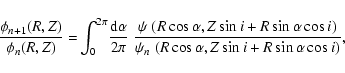
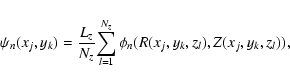
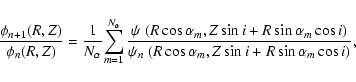

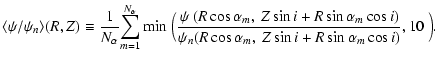
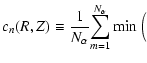
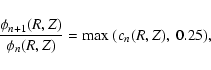
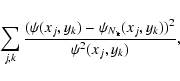
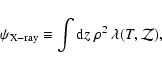
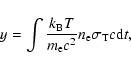
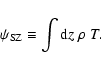
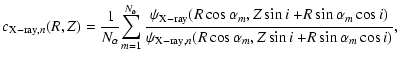
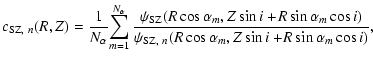
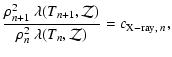
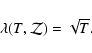
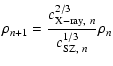
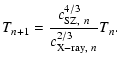
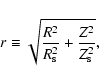
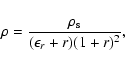
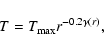



![\begin{figure}
\scalebox{0.7}
{
\begin{picture}
(0,0)%
\includegraphics{4717fi...
...\strut{} radius $[h^{-1} {\rm kpc}]$ }}%
\end{picture}%
\endgroup
}
\end{figure}](/articles/aa/full/2006/33/aa4717-05/Timg133.gif)



![\begin{figure}
\scalebox{0.7}
{
\begin{picture}
(0,0)%
\includegraphics{4717fi...
...\strut{} radius $[h^{-1} {\rm kpc}]$ }}%
\end{picture}%
\endgroup
}
\end{figure}](/articles/aa/full/2006/33/aa4717-05/Timg169.gif)


