A&A 455, 825-834 (2006)
DOI: 10.1051/0004-6361:20054637

On the geometrical evolution of the ionized gas in HII galaxies

F. Cuisinier¹ - P. Westera² - E. Telles³ - R. Buser²

1 - GEMAC - Departamento de Astronomia / Observatório do Valongo, Universidade Federal do Rio de Janeiro, Ladeira do Pedro Antonio 43, 20080-090 Rio de Janeiro RJ, Brazil
2 - Department of Physics and Astronomy, University of Basel, Venusstr. 7, 4102 Binningen, Switzerland
3 - Observatório Nacional/MCT, Rua José Cristino, 77 Rio de Janeiro RJ, 20921-400, Brazil

Received 2 December 2005 / Accepted 28 March 2006

Abstract
Aims. In this paper, we investigate the behaviour of the number of Lyman continuum ionizing photons as compared to the actual number of hydrogen recombinations in HII galaxies.
Methods. We evaluate the number of ionizing photons from the population synthesis of spectra observed in the visible, extrapolating the spectra to the extreme ultraviolet (EUV), beyond the Lyman limit. We check for possible systematic deviations of the predicted ionizing spectra in the EUV by comparing the ratio of the predicted number of ionizing photons to the number of recombinations, as measured in H$\beta$, ${\Delta \log Q\rm (H^0)}$, with the metallicity. We find that, as far as the number of ionizing photons is concerned, no systematic tendency can be detected.

The ${\rm H\beta }$ equivalent width can be understood as a nebular age indicator, decreasing with age, although the observed ${\rm H\beta }$ equivalent width can also be affected by the contribution to the continuum by the accumulation of previous, non-ionizing stellar populations.
Results. We attribute the increase of ${\Delta \log Q\rm (H^0)}$ with the age of the burst to the fact that more and more ionizing photons escape the nebulae when the nebulae get older, because of their increasing, expansion-induced subfragmentation.

Key words: galaxies: starburst - galaxies: ISM - ISM: HII regions - line: formation

1 Introduction

In the giant HII regions present in HII galaxies, photoionization converts ionizing photons of the Lyman continuum in the extreme ultra-violet (EUV) (e.g., with $\lambda \leq 912 ~\AA$ or $E \geq 13.6$ eV) into emission lines, ranging from the ultra-violet to the far infrared; the most prominent ones are recombination lines and collisional lines of atoms, generally in their first and second ionization stages. For photons in the EUV, the radiative world is very different from the one for photons with higher wavelengths. In the latter, small amounts of neutral hydrogen already cause high opacity, and photons are rapidly absorbed.

The EUV part of the ionizing stars in HII regions is poorly known; it is inaccessible observationally and can only be known from stellar atmosphere models. Ionizing stars in HII regions, mainly O and B stars and sometimes Wolf-Rayet stars, possess strong winds, and strong non-ETL effects are present in their atmospheres (Hillier & Miller 1998; Pauldrach 2001; Schaerer & Vacca 1998; Schaerer & de Koter 1997; Smith et al. 2002). In the EUV, various bound-free ionization discontinuities are present, strongly affecting the spectra; however, differences between models by different authors can be significant (Morisset 2004).

The main constraint on these model spectra comes from the reconversion of their energy into emission lines, which are more easily observed. Morisset (2004), for instance, used high ionization stages lines observable in the far infrared to try to constrain the spectral energy distribution of ionizing stars of HII regions in the EUV. This kind of work requires the use of photoionization codes, like CLOUDY (e.g. Ferland 1986), NEBU (e.g. Pequignot 1980), PHOTO (e.g. Stasinska 1978).

However, more basic information can be extracted from just the analysis of hydrogen recombination lines: in the photoionization equilibrium, the number of ionizations of neutral hydrogen is balanced by the number of recombinations. The number of ionizations can easily be calculated from the (theoretical) ionizing spectrum, and the number of recombinations can be counted in hydrogen recombination lines that hardly depend on the plasma parameters (e.g. electronic temperature). The intensity of hydrogen recombination lines should thus simply be proportional to the integrated luminosity of the ionizing spectra in the EUV. This has been known since the pioneering works by Zanstra (1931) on planetary nebulae, but the measurements of EUV luminosities by hydrogen Balmer recombination lines strongly rely on the hypothesis of the optical thickness of the nebulae to Lyman continuum photons. In planetary nebulae, Tylenda & Stasinska (1989) have shown that the optical thickness strongly affects the measurements of their EUV luminosities.

As far as HII regions are concerned, direct measurements of the Lyman continuum for local starburst galaxies show that either they are optically thick or only a low fraction ( ${\lesssim} 10\%$) of ionizing photons are allowed to escape (Leitherer et al. 1995; Heckman et al. 2001; Deharveng et al. 2001; Bergvall et al. 2006). On the other hand, also from direct Lyman continuum measurements, Steidel et al. (2001) found no evidence for the absorption of ionizing photons in high redshift ( $z\simeq3.4$) Lyman Break Galaxies; they estimate a lower limit for their Lyman continuum escaping photons of 50%.

In the local universe, indirect measurements of lower limits of the escaping fraction of ionizing photons are possible from the emission of the diffuse ionized gas (DIG): Zurita et al. (2000) estimate that the luminosity of the DIG in local spiral galaxies can reach 25-70% of their total ${\rm H\alpha}$ luminosity. One has to bear in mind that the actual escaping fraction can be higher, as some photons may leak sideways, perpendicularly to the galactic plane. In the Milky Way, Bland-Hawthorn & Malloney (1999) estimate the upper bound to the leaking fraction of ionizing photons to be only of the order of 10%, from the ionization of clumps in the magellanic stream.

The understanding of the emission lines sequence in HII galaxies can bring some insight into this problem; Stasinska et al. (2001) and Stasinska & Izotov (2003) concluded from the statistical photoionization modelling of large samples (either published catalogues from spectrophotometric surveys or SDSS early data release) that some systematic effect was present in their optical thickness, e.g., that a fraction of HII galaxies was optically thin, and suggested that HII galaxies were becoming thinner with time. Castellanos et al. (2002) reached similar conclusions from the detailed photoionization analysis of 3 giant HII regions in nearby galaxies, e.g., that they were losing a significant fraction of their ionizing photons (between 10-70%).

Photoionization modelling, however, generally does not take into account the presence of dust, which can absorb Lyman continuum photons before they even have a chance to ionize the gas and then re-emits them in the infrared. A significant fraction of the photons that are interpreted as escaping photons may actually be used to heat up the dust. Assuming that no ionizing photon escapes, Inoue (2001) infers from the comparison of radio (gas free-free emission) to infrared (dust emission) luminosities of individual HII regions that the fraction f_iof ionizing photons used for photoionization varies between 0.4 and 0.7. Since he assumes that all ionizing photons are used either to ionize the gas or heat up the dust, the fraction 1-f_i used to heat up the dust should only be considered as an upper limit, as some ionizing photons may simply escape. Nonetheless, this upper limit, of the order of 0.6, is significant. Inoue et al. (2001) and Hirashita et al. (2003) confirmed this result for spiral galaxies, finding upper bounds for 1-f_i ranging from 0.4-0.7 for 1-f_i.

It has to be emphasized that the problem of the optical thickness of the ionized gas in HII galaxies is not restricted to these galaxies. Reionization by the first hypermassive population III stars is a connected question, as the gas ionization responds to the energy input and to the incoming radiation in nearly the same way as in local HII galaxies. Most likely, the gas constituting the intergalactic medium at this stage of the evolution of the Universe is heterogeneous and clumpy. Its interactions with primordial stars can only be understood in terms of complex 3D hydrodynamical and photoionization modelling (Abel et al. 2000), whereas observational constraints are nearly non-existant. HII galaxies might be the closest that we have to a laboratory of the physical conditions of reionization.

Effects originating from the optical thickness, or geometrical effects, are intrinsically hard to distinguish from effects arising from uncertainties concerning the ionizing spectra or from the presence of dust. One way to examine the question is to look at the metallicity of the ionizing clusters. The integrated spectra of an ionizing population should vary with metallicity, partly because of the variation of the metal opacities of the stars that produce the ionizing spectra, but mostly because of the variations of evolutionary tracks due to the metallicity (Schaller et al. 1992; Charbonnel et al. 1993; Schaerer et al. 1993a,b; Mowlavi et al. 1998; Girardi et al. 1996; Fagotto et al. 1994a,b; Bressan et al. 1993). A great part of the opacity in the atmospheres of hot stars in the EUV is due to bound-free transitions of hydrogen and helium - and thus is not affected by metallicity (see Leitherer et al. 1999). The amount of dust is also expected to increase with metallicity (Inoue et al. 2001). Variations of the optical thickness with metallicity (which can easily be measured from oxygen emission lines of the ionized gas) should therefore be indicative of systematic effects of the ionizing spectra, or of the dust, and represent an important check on how to segregate effects of optical thickness from other ones. HII galaxies are actually quite fit for this purpose, because their HII regions are giant, with hundreds or thousands of ionizing stars; in this case, it is much easier to predict the ionizing radiation with a population synthesis code than in normal HII regions, which only possess a few ionizing stars, because the counting noise strongly affects the predicted ionizing spectrum (Cervino & Valls-Gabaud 2003).

In this paper, we investigate effects of optical thickness in a sample of HII galaxies by comparing the number of ionizing photons produced by stars and the number of recombinations. In Sect. 2, we will describe the sample, and our method to evaluate the number of ionizing photons from the stellar spectra. In Sect. 3, we will describe how we can understand statistically the evolution of the (mean) optical thickness with time, e.g., with the nebular age, and how we can check for systematic effects of the model ionizing spectra with metallicity. Finally, Sect. 4 will present the results and a summary.

2 Sample and methodology

Our study is based on the spectrophotometric catalogue of HII galaxies by Kehrig et al. (2004). This catalogue contains homogeneous longslit observations of 188 spectra of individual regions in a sample of 111 HII galaxies. The choice of the regions was made by luminosity, the slit being positioned along the brightest regions. These regions are typically made up of bright knots, generally encompassing several stellar superclusters, with sizes of a few hundreds of pc.

The Kehrig et al. catalogue includes most of the southern hemisphere HII galaxies listed in Terlevich et al. (1991), but with a higher signal/noise. It also includes nearby HII galaxies that have been discovered since the publication of Terlevich et al.'s catalogue. The stellar population content of the galaxies from this catalogue, as derived from their spectra, has already been discussed in Westera et al. (2004).

Westera et al. (2004) based their study on the analysis of modified Lick indices (Worthey 1994; Worthey et al. 1994). What we want to do here is to use a similar population synthesis method, based on a full spectra fitting in the 4000-7000 ${\rm\AA}$ range, with the purpose of predicting the ionizing spectrum in the EUV, for $\lambda \leq 912 ~\AA$.

A best-fit procedure was employed using three different libraries of simple stellar populations (SSPs). The first SSP library (hereafter the "BC99'' library) was produced using the Bruzual and Charlot 2000 Galaxy Isochrone Spectral Synthesis Evolution Library (GISSEL) code (Charlot & Bruzual 1991; Bruzual & Charlot 1993, 2000), implementing the Padova (2000) isochrones (Girardi et al. 2000) combined with the BaSeL 3.1 "Padova 2000'' stellar library (Westera et al. 2001; Westera 2001). The second SSP library, "Starburst'', consists of spectra from the STARBURST99 data package (Leitherer et al. 1999), using the option of including nebular continuum emission (Fig. 1 on the STARBURST99 web site). It implements the BaSeL 2.2 library (Lejeune et al. 1997, 1998), and for stars with strong mass loss, it also takes into account extended model atmospheres by Schmutz et al. (1992), combined with the Geneva isochrones (Meynet et al. 1994; Schaller et al. 1992; Schaerer et al. 1993a,b; Charbonnel et al. 1993). For old populations, the "BC99'' spectrum was used, since the Starburst99 data package only contains spectra up to 900 Myr. In addition to these two libraries - which were already used in Westera et al. (2004) - we also used a library with higher spectral resolution, "BC03'', produced by employing the 2003 version of the GISSEL code (Bruzual & Charlot 2003) and the Padova (1995) isochrones (Fagotto et al. 1994b; Girardi et al. 1996) combined with the STELIB (Le Borgne et al. 2003) stellar library. As the nebular continuum emission is important for the spectral shape of young populations, it was also added to the spectra in the "BC99'' and "BC03'' libraries, in the way described by Leitherer et al. (1999).

Table 1 provides a summary of the evolutionary tracks and stellar libraries used for the three SSP libraries.

Table 1: Evolutionary tracks and stellar libraries used in the SSP libraries.

Since for the present purpose, it is more important to reproduce the shapes of the galaxy spectra than to find the actual parameters of the sub-populations, we fit the full spectra from 3910 Å to 6880 Å instead of single spectral indices, except for those various parts of the spectra showing "contaminations'' from different emission and/or telluric line sources. Table 2 lists all the regions that were not used for the fits.

Table 2: Wavelength ranges that were not used for the spectral fit.

In the present paper, we modelled the actual population as being composed of an old, an intermediate, and a young stellar population (in Westera et al. 2004, we only decomposed the actual population as a young+intermediate one and an old one). The characteristics and free parameters of the three populations are summarised in Table 3.

The spectra were first blueshifted to their rest wavelength. Internal gas extinction was then corrected for, using the observed ${\rm H_{\alpha}/H_{\beta}}$ emission lines ratio. The resolution of our spectra was sufficient ( ${\simeq} 5~ \AA$) to easily deconvolve ${\rm H_{\alpha}}$ from the [NII] doublet at ${\lambda\lambda 6548,6583~ \AA}$ (see Kehrig et al. 2004). As explained in next section, we did not adopt the emission line intensities from Kehrig et al. (2004), but we remeasured them after fitting the stellar continuum by population synthesis. In HII galaxies spectra, ${\rm H_{\alpha}}$ and ${\rm H_{\beta}}$ are present both in absorption (from the stars) and in emission (from the ionized gas); our procedure allowed us to disentangle both components. The repartition of gas and stars inside a galaxy lets them be affected in different manners by extinction (see Calzetti et al. 1994). We dereddened the stellar continuum spectra employing the formulas $E(B - V)=0.665\times C_{\rm H\beta}$ (Sampson 2003) and $E(B - V)_{\rm cont}=0.44\times E(B-V)_{\rm gas}$ (thus, $E(B~-~V)_{\rm cont}=0.2926\times C_{\rm H\beta}$) and the extinction law of Fluks (1994). The factor 0.44 was introduced to correct for systematic differences between the extinction as derived from the stars and from the ionized gas (Calzetti et al. 1994).

The best-fitting population was found by a $\chi^2$ algorithm. To be able to calculate the $\chi^2$ estimator, the empirical and theoretical spectra have to be on the same wavelength grid (at least in the range used for the fit). This was done by rebinning the empirical spectra to the resolution of the theoretical spectra using a Gaussian kernel function with a full width at half maximum (FWHM), corresponding to the resolution of the theoretical spectra (20 Å for "BC99'' and "Starburst'' and 1 Å for "BC03'').

In the end, a selection of acceptable solutions was made. All spectra that had too bad signal-to-noise or a strange shape, indicating calibration problems in the data reduction, were eliminated from the sample. This selection was done by eye. It left us with solutions for 105 spectra of individual regions in 72 galaxies.

The best-fitting population parameters for the fits with the "BC03'' library can be found in Cols. 4 to 8 of Table A.1. Figure 1 shows an example of an observed spectrum and the resulting composite spectra in the wavelength range where the fits were made, and Fig. 2 represents the extrapolations to the UV and EUV.

The introduction of a third partial population again serves the purpose of better reproducing the spectral shapes. In reality, the quality of our spectra is not high enough to determine the parameters (metallicities, ages, and masses) of three sub-populations, so the parameter values given in Table A.1 should be taken with a grain of salt. However, the parameters that can directly be compared with those derived in Westera et al. (2004) agree reasonably well: We obtain the same value for the parameter (M_y+M_i):M_o as for (M_y+i):M_o in Westera et al. (2004) for 38% or 49% of the spectra (depending on the spectral library, see next paragraph), and in another 36% or 28%, these two parameters differ only by one "step'' in the grid. In 49% or 46% the luminosity-weighted (geometrical) mean of ${\rm age}_{y}$ and age_i differs by less than two "steps'' from the age_y+icalculated in Westera et al. (2004), which corresponds to a factor of less than 5 in age_y+i.

Table 3: Possible values of the population parameters.

In Westera et al. (2004), we discussed the differences arising from adopting the Starburst 99 (Leitherer et al. 1999) or the BC93 (Bruzual & Charlot 1993) codes for the young population (the old one being modelled with the BC93 code in both cases). In this paper we enhance these results by modelling both the old and young populations with the BC03 (Bruzual & Charlot 2003) version of their code. Each of these codes, or code versions, has their advantages and inconveniences: Starburst 99 is particularly fit for the study of young populations in the visible/ultraviolet, but does not extend to ages older than 1 Gyr; BC93 is made to model all kinds of populations, but is optimized for old ones. Finally, the BC03 version of the code (Bruzual & Charlot 2003) includes empirical spectral libraries of higher resolution, BC-2000 (Pickles 1998; Bruzual & Charlot 2003) and STELIB (le Borgne et al. 2003), and, therefore, is better suited for calculating Lick indices (because of its higher spectral resolution) than Starburst 99 or BC93. However, it has a poor coverage of parameter space for the ionizing hot stars. Furthermore, the extension of the BC03 version to wide and comprehensive wavelength ranges is made by combining STELIB spectra in the visible, Pickles library (1998) in the UV and IR, and BaSeL theoretical spectra beyond 2.5 $\mu$m of for wavelengths shorter than 1200 ${\rm\AA}$. Comparing the results of different codes or versions, we hope to be able to better assess possible systematic effects.

	Figure 1: Example of a "best fit''. The thin (red) lines represent the empirical spectrum (UM 137(W), taken on August, 18, 1998); the thicker black lines show the best-fitting spectra obtained using the different SSP libraries.
Open with DEXTER

Figure 2: Synthesised spectra over the whole wavelength range. The thin (red) lines represent the empirical spectrum (as in Fig. 1), the solid lines show the best-fitting spectra, and the dashed lines show the decompositions of the best-fitting spectra into young, intermediate, and old populations, respectively. The shaded regions represent the radiation shortward of the Lyman limit (912 Å), which is responsible for the ionization of the surrounding gas. Note that both axes are on a logarithmical scale, in contrast to Fig. 1.

Open with DEXTER

3 Evaluation of the photon loss rate

Figure 3: Illustration of how the H$\beta$ emission line equivalent width was measured through the example of UM137(CentE). In the left panel, the solid line represents the empirical spectrum, whereas the short-dashed line shows the best fit using the BC-2000 stellar library. The shaded region between these two lines (shaded with lines running from the upper left to the lower right) shows the area used to calculate the emission line strength, and the shaded region (lines running from the upper right to the lower left) between the solid line and zero level (the long-dashed line) shows the location of the continuum band. The right panel shows the emission line after subtracting the (rebinned) best fit. The shaded area corresponds to the shaded area between the spectrum and the best fit from the left panel. Here, too, the zero level is shown as a long-dashed line to show the quality of the subtraction.

Open with DEXTER

We evaluate the number of ionizing photons with the method exposed in the previous section from an extrapolation of the ionizing spectrum to the EUV, based on population synthesis. The number of recombinations can also be calculated from a recombination line of hydrogen, like ${\rm H\beta }$. If the number of predicted ionizing photons is correct, in the case of an optically thick ionized nebula, both numbers are equal (in the photoionization equilibrium). In an optically thin nebula, however, not all the ionizing photons will actually be able to ionize the gas, and some will escape. The ratio of the number of (predicted) ionizing photons to the number of recombinations can thus be considered an indicator of optical thickness. We define:

$${\rm\Delta \log {\it Q}(H^0) = \log {\it Q} \left(H^0\right)_{ion} - \log {\it Q} \left(H^0\right)_{rec} ,}$$

where ${Q\rm (H^0)_{ion}}$ is the number of ionizing photons, as determined from the extrapolation of the ionizing spectrum to the EUV, based on population synthesis, and ${Q\rm (H^0)_{rec}}$ is the number of recombinations as calculated from the ${\rm H\beta }$ recombination line, after correction from absorption, as estimated from ${C_{\rm H\beta }}$.

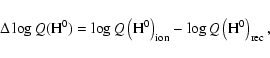
To properly measure the equivalent width of the H$\beta$emission line, we had to correct its strength for the reduction it suffers from the underlying absorption line. For this purpose, we first made a best fit of the continuum in the 3910-6880 ${\rm\AA}$wavelength range, in a similar way to Westera et al. (2004), but putting extra weight on the H$\delta$ index (the wings of the H$\delta$absorption line) and using the theoretical spectra from the BC-2000 stellar library. Although this library only exists for solar metallicity, its resolution is much higher than for the other libraries, and the best-fitting spectra reproduce the shape of the absorption lines better than the fits obtained with the other libraries. Note that these fits were only made for calculating the ${\rm H\beta }$equivalent widths and have nothing to do with the population synthesis described in Sect. 2. After subtracting the (rebinned) best-fitting spectra from the galaxy spectra, we could measure the strength of the emission line and thus calculate the equivalent widths EW(H$_{\beta }$). This is illustrated in Fig. 3. Results are given in Col. 2 of Table A.1.

Using these definitions, ${\Delta \log Q\rm (H^0)}$ will be equal to 0 for optically thick nebulae and increase for nebulae getting optically thinner and thinner. The ${\Delta \log Q\rm (H^0)}$ values of individual spectra can be found in Col. 3 of Table A.1.

As we are more interested here in giant HII regions than in the HII galaxies themselves, we will focus our discussion on the spectra of the individual regions from Kehrig et al.'s (2004) catalogue, and not on the spectra of the individual galaxies. As a matter of fact, we checked if our results were the same considering only the integrated spectra of galaxies, and we found excellent agreement.

We could have some systematical bias due to the fact that we observed the galaxies, or giant HII regions, through apertures defined by the slit, and thus not encompassing the HII regions (galaxies) entirely. As we centred the slit on the brightest regions, we estimate that the quantity of nebular H$\beta$ photons we lose should not exceed a factor of $\simeq$3 (0.5 in logarithm).

3.1 Evaluation of the ionizing spectra

It is intrinsically hard to disentangle effects originating from the ionizing spectra from effects arising from the optical thickness of the nebulae: For a given HII region, an erroneous modelling of the number of ionizing photons can give results equivalent to the ones that would be attributed to an optically thin nebula. The accuracy of the modelling of the stellar spectra in the EUV can be assessed by the comparison of line intensities of ions of different ionization potentials, as in Morisset et al. (2004). Much more basic information can, however, be extracted from systematical tendencies of ${\Delta \log Q\rm (H^0)}$ with metallicity. If the predicted ionizing spectra are wrong for some reason, their systematical excess or deficiency in ionizing photons will vary with metallicity because of the intrinsic change of the integrated ionizing spectra (see Leitherer et al. 1999) and will be seen in ${\Delta \log Q\rm (H^0)}$, if plotted as a function of metallicity. On the other hand, geometrical effects (optical thickness) are not expected to vary with metallicity and will thus just produce a systematical offset in ${\Delta \log Q\rm (H^0)}$.

Figure 4 shows a comparison of ${\Delta \log Q\rm (H^0)}$with the oxygen abundance as derived from emission lines of the gas (Cuisinier et al. 2006). Most giant HII regions have ${\Delta \log Q\rm (H^0)} > 0$, indicating that they let ionizing photons escape, since they are optically thin. A huge scatter exists, however, with some giant HII regions reaching negative values of ${\Delta \log Q\rm (H^0)}$. Nonetheless, as we will show in Sect. 3.3, we believe it to be due to uncertainties in the population synthesis fitting procedure. If we look at the bulk of the giant HII regions, however, they lie at a constant value of ${\Delta \log Q\rm (H^0)}$, around 0.8, with no clear tendency for oxygen abundance.

Another point that could affect our evaluation of the number of ionizing photons is dust absorption. As stated in Sect. 2, we took great care in correcting the observed spectra for absorption before performing any fitting procedure. We did this by measuring the reddening from the observed ${\rm H\alpha/H\beta}$ line ratio. Absorption for the stellar population, however, is not necessarily the same as for the gas phase: the geometrical repartition is not identical in respect to the dust. We applied a correction factor on the reddening for the stellar population to compensate for this effect (Calzetti et al. 1994), but it is important to check that no remaining differential effect exists. Furthermore, dust can absorb high energy ionizing photons, affecting our evaluation of ${\Delta \log Q\rm (H^0)}$.

The dust quantity should increase with metallicity; any effect due to an erroneous evaluation of the absorption should affect the variation of ${\Delta \log Q\rm (H^0)}$ with metallicity, but, as can be seen in Fig. 4, no clear tendency can be detected.

This might seem contradictory to the results by Inoue et al. (2001): from the analysis of the infrared emission of HII regions, due to the dust, and their radio emission, due to the gas, they find that the fraction of Lyman continuum photons absorbed by the dust increases with metallicity (assuming that no photons are leaking). The metallicity range of their HII regions is different, however, and extends to higher metallicities than our HII galaxies, though some overlap exists. A closer inspection of their data shows that at low metallicities, equivalent to the ones we encounter in our sample ( $\rm [0/H]\leq-0.5$), the fraction of Lyman continuum photons used for dust heating 1-f_i is rather constant at $\simeq$0.2. It only increases for higher metallicities. One must bear in mind that, as stated in the introduction, since they do not consider the possibility of photons leaking out, 1-f_i is an upper limit to the fraction of Lyman continuum photons used to heat up the dust.

Thus, from our analysis of the variation of ${\Delta \log Q\rm (H^0)}$ with metallicity, (i) we cannot put into evidence any deficiency from the theoretical ionizing spectra, and (ii) we cannot rule out effects of absorption by the dust, if they are constant with metallicity. Inoue et al. (2001) showed that such an effect exists, but at the metallicities of our HII galaxies sample, it should be lower than 20%.

As a consistency check, in Fig. 5 we compare ${\Delta \log Q(\rm H^0)}$ with the measured ${\rm C_{H\beta}}$values; effects due to the dust, provoking either an erroneous evaluation of the absorption for the stellar population in the visible or an absorption of high energy ionizing photons, should vary with the dust quantity, e.g., the reddening. As can be seen in Fig. 5, no tendency can be detected.

	Figure 4: Logarithmic ratio of the predicted number of ionizing photons to the number of recombinations as a function of the oxygen abundance from the gas.
Open with DEXTER

	Figure 5: Logarithmic ratio of the predicted number of ionizing photons to the number of recombinations as a function of the gas reddening parameter ${C_{\rm H\beta }}$.
Open with DEXTER

   
3.2 Temporal evolution of the optical thickness to the ionizing photons

The equivalent width in ${\rm H\beta }$ is a quantity that monotonically decreases with time within a given HII region, or even within a given star formation episode of an HII galaxy. The number of ionizing photons decreases with time, decreasing the ${\rm H\beta }$ intensity, and the continuum at the same wavelength rises. The equivalent width in ${\rm H\beta }$ has been used extensively as a nebular age indicator by Stasinska et al. (2001), Stasinska & Izotov (2003), Terlevich et al. (2004), and Dottori & Bica (1981), as was first suggested by Dottori (1981).

The underlying non-ionizing population, however, blurs this picture by raising the continuum; the ${\rm H\beta }$ equivalent width anti-correlates with oxygen abundance (though with a huge scatter) (Terlevich et al. 2004), definitely pointing towards a contamination of the continuum by previous populations. Furthermore, stellar population studies (e.g., Westera et al. 2004; Kong et al. 2003; Cid-Fernandes et al. 2003) indicate that stellar formation events last for times of the order of at least 100 Myr, not 10 Myr (which is the photoionization timescale). A stellar formation event in an HII galaxy naturally accumulates an intermediate age population (between 10 and a few 100 Myr) that participates in the continuum budget.

The two effects (i.e. (i) the accumulation of old populations from previous bursts, and (ii) the accumulation of an intermediate age population due to the present burst) have opposite effects in terms of interpreting ${\rm H\beta }$ equivalent widths as star-forming event age indicators. The first one only introduces scatter in the relation, while the second one helps to decrease ${\rm H\beta }$equivalent widths with increasing burst ages. This latter effect happens, however, in a manner that may not be as simple to evaluate as can be naively done by simply comparing with photoionization by single aged stellar populations.

Figure 6 shows a plot of ${\Delta \log Q\rm (H^0)}$versus the equivalent width in ${\rm H\beta }$, as calculated in the previous subsection. As in Fig. 4, we can see a clustering of most data in ${\Delta \log Q\rm (H^0)}$ around a positive value of 0.8. A big scatter exists as well, and as we will explain in Sect. 3.3., we believe that we can explain it just from the uncertainties in the population synthesis process. However, in contrast to Fig. 4, we see a strong correlation of the clustered data with the equivalent width in ${\rm H\beta }$. ${\Delta \log Q\rm (H^0)}$, which can be considered an indicator of the number of ionizing photons escaping the nebulae, increases with the decreasing equivalent width in ${\rm H\beta }$, i.e., time.

	Figure 6: Logarithmic ratio of the predicted number of ionizing photons to the number of recombinations as a function of the equivalent width of  ${\rm H\beta }$.
Open with DEXTER

This result may seem counter-intuitive, as the quantity of matter absorbing the ionizing photons remains the same and the number of ionizing photons decreases with time: the optical thickness should increase with time. However, if we think of HII regions not as homogeneous media, but consider them in their complexity, with all their clumps, filaments, and substructures, we can understand the phenomenon, if we assume that the nebulae are optically thin in some directions, and thick in others. This can be described by a covering factor $f_{\rm c}$, characterizing the fraction of solid angle within which the nebulae are optically thick. The increase of the number of ionizing photons escaping the nebulae with time can thus be understood if the covering factor $f_{\rm c}$ decreases with time. This has already been pointed out by Stasinska et al. (2001) and Stasinska & Izotov (2003), based on other arguments (the time sequence of the intensities of collisional lines in HII galaxies). The decrease of the covering factor $f_{\rm c}$ with time can be understood if the structure of HII regions always becomes more complex with time, continuing to subfragment and thus to form more and more "holes'' in their structure while they expand, always letting more ionizing photons escape. Tenorio-Tagle et al. (2006) reach similar conclusions from the theoretical modelling of the hydrodynamical evolution of giant HII regions under the effect of both photoionization and stellar winds in a clumpy interstellar medium.

Of course, the absorption of ionizing photons by dust would provide an alternative explanation; it would, however, require a mechanism that increases the absorption of ionizing photons by dust with time. As such a mechanism seems rather artificial to us, we prefer to stick to the leaking photons explanation.

The biggest problem with leaking photons is that they are not confirmed by the direct observation of the Lyman continuum in local starburst galaxies, at least in the quantities we predict (Leitherer et al. 1995; Heckman et al. 2001; Deharveng et al. 2001; Bergvall et al. 2006), although is not the case at higher redshifts (Steidel 2001). The total number of galaxies that have been observed in their Lyman continuum is, however, quite small, just a little over 10. These galaxies have been selected on the basis of the intensity of their starbursts. In the explanation we propose, the youngest starbursts, i.e., ones with the highest ${\rm H\beta }$ equivalent widths, which would be interpreted as the ones having the most intense starbursts, have the lowest fraction of escaping ionizing photons. We evaluate this fraction in these galaxies to be $\simeq$70%, i.e., ${\Delta Q\rm (H^0)}\simeq 3$ on a linear scale; one has to take into account that our evaluations of ${\Delta Q\rm (H^0)}$ are certainly systematically over-evaluated by aperture effects by a factor that can be as high as $\simeq$3 (see Sect. 2). Adding some systematic absorption by dust (which we, however, do not believe can be much higher than ${\simeq} 20\%$), we can easily lower the actual escaping fraction of ionizing photons in those galaxies to ${\simeq} 10\%$, which is what is believed to be the upper limit for escaping photons from Lyman continuum observations. This is, however, certainly not the case for the most evolved, lowest ${\rm H\beta }$ equivalent width galaxies in our sample, where ${\Delta Q\rm (H^0)}$reaches values higher than 10.

3.3 Accuracy of the population synthesis modelling

The interpretation of the data presented above highly relies on our ability to evaluate the spectrum in the EUV from a population synthesis over the observed range between 4000-7000 ${\rm\AA}$. Population synthesis is an ill-conditioned problem, subject to all kinds of degeneracies, and it is important to test its ability to recover what we want.

3.3.1 Comparison of the different libraries

We first compared the results given by three different stellar population codes (or combinations), "BC03'', "BC99'', and "Starburst''. The results commented on in Sect. 3.2 are overall consistent with the three different codes, but some differences do exist. It is noteworthy that, as far as the correlations with the ${\rm H\beta }$ equivalent widths are concerned, the best results are obtained with "Starburst'' (Fig. 6). "BC99'' gives nearly as good correlations, and with fewer outliers. Finally, results obtained with "BC03'' do not give any improvement; on the contrary, the correlation presented, though definitely existing, is not as strong as that with the two other libraries, and the number of outliers is higher.

Though this cannot be considered definite evidence, since effects on the number of ionizing photons is what we want to assess, this could be indicative of deficiencies of the BC03 stellar spectra library in the EUV. The BC03 library is made up of the extension of the empirical STELIB library in the visible (Le Borgne et al. 2003) to other wavelengths, with empirical spectra when available, and using theoretical spectra when empirical spectra were not available. The connection of the different spectra of different origins has been based on evaluated physical parameters, or rather, parameter classes, introducing some inconsistency in the process, which is not present in entirely theoretical libraries; one must remember that the EUV part of the spectra is theoretical in all libraries.

3.3.2 Monte-Carlo simulations

As a matter of fact, in our present problem, we are not so much interested in the underlying population parameters, as in our ability to recover a given spectrum from observations over a limited wavelength range.

	Figure 7: Monte Carlo simulation of the logarithmic ratio of the predicted number of ionizing photons to the number of recombinations as a function of the oxygen abundance from the gas for optically thick nebulae.
Open with DEXTER

To do this, we took the synthesised spectra over the whole 91 Å to 160 $\mu$m, corresponding to the population mixtures derived from the population synthesis over the observed range (4000-7000 ${\rm\AA}$). We added Gaussian noise, such that the S/N ratio varied from 2 to 40, corresponding to the observed S/N ratio distribution (see Kehrig et al. 2004), to the fitted synthetic spectrum (assumed to be our true prior), and recovered new synthesised spectra through the same population synthesis process over the 4000-7000 ${\rm\AA}$ range. We assumed the first spectra to give the true number of ionizing photons, giving the number of recombinations counted in ${\rm H\beta }$ under the hypothesis of the nebulae's optical thickness. From the latter spectra, we compute the number of ionizing photons by the population synthesis process, and we obtain ${\Delta \log Q\rm (H^0)}$from the logarithmic difference of both numbers. To obtain reliable statistics, we performed 1620 such Monte-Carlo simulations for each of the three SSP libraries.

Figures 7 and 8 represent ${\Delta \log Q\rm (H^0)}$ as a function of oxygen abundance and ${\rm H\beta }$ equivalent width, respectively. If the population synthesis process were exact, the recovered number of ionizing photons would be equal to the true number of ionizing photons, and in both cases ${\Delta \log Q\rm (H^0)}$ would be constant, equal to 0. The only thing we measure here is the ability of the population synthesis process to recover the number of ionizing photons. As can be seen in Figs. 7 and 8, the dispersion obtained is equivalent to the dispersion observed in Figs. 4 and 6; all the scatter in ${\Delta \log Q\rm (H^0)}$ can simply be explained by the uncertainty introduced by the population synthesis process. However, as can also be seen in Figs. 7 and 8, the population synthesis process does not introduce any systematical bias: most values of ${\Delta \log Q\rm (H^0)}$ lie around 0, and the distribution is fairly symmetric. The systematical clustering of the values of ${\Delta \log Q\rm (H^0)}$ around 0.8 cannot be explained simply by an effect of the population synthesis process, and must be real.

	Figure 8: Monte Carlo simulation of the logarithmic ratio of the predicted number of ionizing photons to the number of recombinations as a function of the equivalent width in ${\rm H\beta }$ for optically thick nebulae.
Open with DEXTER

4 Summary

For a sample of HII galaxies, we compared the number of predicted ionizing photons from the population synthesis of their spectra in the visible to the number of recombinations counted in the observed ${\rm H\beta }$.

Differences between these two numbers can arise (i) because the evaluation of the number of ionizing photons is erroneous, either because the theoretical ionizing spectra are wrong or because the population synthesis algorithm is not able to evaluate the ionizing spectrum correctly, or (ii) because a fraction of the ionizing photons escape since the nebulae is optically thin.

We checked for systematic tendencies depending on metallicity (as measured by the oxygen abundance from the gas) that would be indicative of systematic deviations of the theoretical spectra in the EUV, as far as the number of hydrogen ionizing photons is concerned. We checked this with three different population synthesis libraries, and we did not find any systematic effects for our sample.

Using Monte-Carlo simulations, we checked for the ability of our population synthesis method to recover the actual number of ionizing photons. Though most cases provided great scatter, we did not detect any systematic trend.

Finally, we examined the behaviour of the ratio of the number of predicted ionizing photons to the number of recombinations as a function of ${\rm H\beta }$ equivalent width. Though affected by the presence of older populations, the equivalent width in ${\rm H\beta }$ can be considered a gross indicator of the nebular age, decreasing as the HII nebula becomes older. We found a strong tendency for an increasing number of ionizing photons escape the nebulae as the nebulae get older.

We interpret this as a consequence of the geometrical evolution of the HII regions, which should be optically thick to the ionizing photons in some directions and optically thin in others. We can understand it in terms of a covering factor $f_{\rm c}$ of the ionized gas that should decrease with time. In other words, HII nebulae subfragment more and more as they expand, always letting more ionizing photons escape.

The absorption of ionizing photons by dust would provide an alternative explanation, but we do not favour it, as it would require dust to absorb an always increasing fraction of ionizing photons during the evolution of HII regions.

Acknowledgements

We would like to thank FAPERJ, CNPq, and the Swiss National Foundation for financial support. F. C. wishes to thank the Astronomisches Institut der Universität Basel for hospitality during a stay during which most of this paper was written. We wish to thank the anonymous referee for very helpful comments that helped to clarify and expand the discussion.

References

• Abel, T., Bryan, G. L., & Norman, M. L. 2000, ApJ, 540, 39 [NASA ADS] [CrossRef] (In the text)
• Bergvall, N., Zackrisson, E., Andersson, B.-G., et al. 2006, A&A, 448, 513 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Bland-Hawthorn, J., & Maloney, P. R. 1999, ApJ, 510, L33 [NASA ADS] [CrossRef] (In the text)
• Bressan, A., Fagotto, F., Bertelli, G., & Chiosi, C. 1993, A&AS, 100, 647 [NASA ADS] (In the text)
• Bruzual, A. G., & Charlot, S. 1993, ApJ, 405, 538 [NASA ADS] [CrossRef] (In the text)
• Bruzual, A. G., & Charlot, S. 2000, Galaxy isochrone spectral synthesis evolution library (private communication) (In the text)
• Bruzual, A. G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] (In the text)
• Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [NASA ADS] [CrossRef] (In the text)
• Castellanos, M., Dias, A. I., & Tenorio-Tagle, G. 2002, ApJ, 565, 79 [NASA ADS] [CrossRef] (In the text)
• Cervino, M., & Valls-Gabaud, D. 2003, MNRAS, 338, 481 [NASA ADS] [CrossRef] (In the text)
• Charbonnel, C., Maeder, A., Schaller, G., et al. 1993, A&AS, 101, 415 [NASA ADS] (In the text)
• Charlot, S., & Bruzual, A. G. 1991, ApJ, 367, 126 [NASA ADS] [CrossRef] (In the text)
• Cid Fernandes, R., Leão, J. R. S., & Lacerda, R. R. 2003, MNRAS, 340, 29 [NASA ADS] [CrossRef] (In the text)
• Cuisinier, F., Telles, E., & Kehrig, C. 2006, in preparation (In the text)
• Deharveng, J.-M., Buat, V., Lebrun, V., et al. 2001, A&A, 375, 805 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Dottori, H. 1981, Ap&SS, 80, 267 [NASA ADS] (In the text)
• Dottori, H., & Bica, E. 1981, A&A, 102, 245 [NASA ADS] (In the text)
• Fagotto, F., Bressan, A., Bertelli, G., & Chiosi, C. 1994a, A&AS, 104, 365 [NASA ADS] (In the text)
• Fagotto, F., Bressan, A., Bertelli, G., & Chiosi, C. 1994b, A&AS, 105, 39 [NASA ADS] (In the text)
• Ferland, G. 1986, PASP, 98, 549 [NASA ADS] [CrossRef] (In the text)
• Fluks, M. A., Plez, B., The, P. S., et al. 1994, A&AS, 105, 311 [NASA ADS] (In the text)
• Girardi, L., Bressan, A., Chiosi, C., Bertelli, G., & Nasi, E. 1996, A&AS, 117, 113 [EDP Sciences] [NASA ADS] (In the text)
• Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [EDP Sciences] [NASA ADS] ("Padova 2000'' isochrones) (In the text)
• Heckman, T., Sembach, K., Meurer, G., et al. 2001, ApJ, 558, 56 [NASA ADS] [CrossRef] (In the text)
• Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] (In the text)
• Hirashita, H., Buat, V., & Inoue, A. K. 2003, A&A, 410, 403 (In the text)
• Inoue, A. K. 2001, AJ, 122, 1788 [NASA ADS] [CrossRef] (In the text)
• Inoue, A. K., Hirashita, H., & Kamaya, H. 2001, AJ, 555, 613 [NASA ADS] [CrossRef] (In the text)
• Kehrig, C., Telles, E., & Cuisinier, F. 2004, AJ, 128, 1141 [NASA ADS] [CrossRef] (In the text)
• Kong, X., Charlot, S., Weiss, A., & Cheng, F. 2003, A&A, 403, 877 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Le Borgne, J.-F., Bruzual, A. G., Pelló, R., et al. 2003, A&A, 402, 433 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Leitherer, C., Ferguson, H. C., Heckman, T., & Lowenthal, J. D. 1995, ApJ, 454, L19 [NASA ADS] (In the text)
• Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] (In the text)
• Lejeune, T., Cuisinier, F., & Buser, R. 1997, A&AS, 125, 229 [EDP Sciences] [NASA ADS] (In the text)
• Lejeune, T., Cuisinier, F., & Buser, R. 1998, A&AS, 130, 65 [EDP Sciences] [NASA ADS] (In the text)
• Meynet, G., Maeder, A., Schaller, G., Schaerer, D., & Charbonnel, C. 1994, A&AS, 103, 97 [NASA ADS] (In the text)
• Morisset, C. 2004, ApJ, 601, 558 [NASA ADS] (In the text)
• Mowlavi, N., Meynet, G., Maeder, A., et al. 1998, A&AS, 128, 471 [EDP Sciences] [NASA ADS] (In the text)
• Pauldrach, A. W. A., Hoffmann, T. L., & Lennon, M. 2001, A&A, 375, 161 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Pequignot, D. 1980, A&A, 83, 52 [NASA ADS] (In the text)
• Pickles, A. J. 1998, PASP, 110 863 (In the text)
• Sampson, L. 2003, História de Formação Estelar em Galáxias HII, MSc. dissertation, Observatório Nacional, Brazil (In the text)
• Schaerer, D., & de Koter, A. 1997, A&A, 322, 598 [NASA ADS] (In the text)
• Schaerer, D., & Vacca, W. D. 1998, ApJ, 497, 618 [NASA ADS] [CrossRef] (In the text)
• Schaerer, D., Charbonnel, C., Meynet, G., Maeder, A., & Schaller, G. 1993a, A&AS, 102, 339 [NASA ADS] (In the text)
• Schaerer, D., Meynet, G., Maeder, A., & Schaller, G. 1993b, A&AS, 98, 523 [NASA ADS]
• Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [NASA ADS] (In the text)
• Schmutz, W., Leitherer, C., & Gruenwald, R. 1992, PASP, 104, 1164 [NASA ADS] [CrossRef] (In the text)
• Smith, L. J., Norris, R. P. F., & Crowther, P. A. 2002, MNRAS, 337, 1039 (In the text)
• Stasinska, G. 1978, A&AS, 32, 429 [NASA ADS] (In the text)
• Stasinska, G., & Schaerer, D. 2001, A&A, 370, 1 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Stasinska, G., & Izotov, Y. 2003, A&A, 397, 51 [NASA ADS] (In the text)
• Steidel, C. C., Pettini, M., & Adelberger, K. G. 2001, ApJ, 546, 665 [NASA ADS] [CrossRef] (In the text)
• Tenorio-Tagle, G., Muñoz-Tuñón, C., Silich, S., Pérez, E., & Telles, E. 2006, ApJ, in press (In the text)
• Terlevich, R., Melnick, J., Masegosa, J., Moles, M., & Copetti, M. V. F. 1991, A&AS, 91, 285 [NASA ADS] (T91) (In the text)
• Terlevich, R., Silich, S., Rosa-Gonzales, D., & Terlevich, E. 2004, MNRAS, 348, 1191 [NASA ADS] [CrossRef] (In the text)
• Tylenda, R., & Stasinska, G. 1989, A&A, 217, 209 [NASA ADS] (In the text)
• Westera, P. 2001, The BaSeL 3.1 models: Metallicity calibration of a theoretical stellar spectral library and its application to chemo-dynamical galaxy models, Ph.D. Thesis, Univ. of Basel, 378 (In the text)
• Westera, P., Lejeune, T., Buser, R., Cuisinier, F., & Bruzual, A. G. 2002, A&A, 381, 524 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Westera, P., Cuisinier, F., Telles, E., & Kehrig, C. 2004, A&A, 423, 133 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Worthey, G., Faber, S. M., Jesús González, J., & Burstein, D. 1994, ApJS, 94, 687 [NASA ADS] [CrossRef] (In the text)
• Worthey, G. 1994, ApJS, 95, 107 [NASA ADS] [CrossRef] (In the text)
• Zanstra, H. 1931, Z. Astrophys., 2, 1 [NASA ADS] (In the text)
• Zurita, A., Rozas, M., & Beckman, J. E. 2000, A&A, 363, 9 [NASA ADS] (In the text)

 

  
Online Material

Appendix A: H$_{\beta }$ equivalent widths and population parameters of individual spectra

Table A.1: H$_{\beta }$ equivalent widths, ${\Delta \log Q\rm (H^0)}$ parameters, mass ratios (relative to the total stellar mass), and ages of the individual sub-populations for each spectrum.