A&A 455, 1037-1052 (2006)
DOI: 10.1051/0004-6361:20053792
A. P. Linnell1 - P. Harmanec2,3 -
P. Koubský3,![]() - H. Bozic4 - S. Yang5,
- H. Bozic4 - S. Yang5,![]() -
D. Ruzdjak4 - D. Sudar4 -
J. Libich2,3 - P. Eenens6 -
J. Krpata2 - M. Wolf2 -
P. Skoda3 - M. Slechta3
-
D. Ruzdjak4 - D. Sudar4 -
J. Libich2,3 - P. Eenens6 -
J. Krpata2 - M. Wolf2 -
P. Skoda3 - M. Slechta3
1 -
Department of Physics and Astronomy, Michigan State University,
E. Lansing, MI, 48824 and Affiliate Professor, Department of Astronomy,
University of Washington, Seattle, WA 98195, USA
2 -
Astronomical Institute of the Charles University, Faculty of Mathematics and Physics,
V Holesovickách 2, 180 00 Praha 8, Czech Republic
3 -
Astronomical Institute, Academy of Sciences,
251 65 Ondrejov, Czech Republic
4 -
Hvar Observatory, Faculty of Geodesy, Kaciceva 26,
10000 Zagreb, Croatia
5 -
Department of Physics and Astronomy, University of Victoria,
PO Box 3055 STN CSC, Victoria, B.C., V8W 3P6, Canada
6 -
Dept. of Astronomy, University of Guanajuato,
36000 Guanajuato, GTO, Mexico
Received 7 July 2005 / Accepted 15 May 2006
Abstract
Aims. We include existing photometric and spectroscopic material with new observations in a detailed study of the Be+F binary V360 Lac.
Methods. We used the programs FOTEL and KOREL to derive an improved linear ephemeris and to disentangle the line profiles of both binary components and telluric lines. The BINSYN software suite (described in the paper) is used to calculate synthetic light curves and spectra to fit the ![]() photometry, an
photometry, an ![]() spectrum, blue and red ground-based spectra, and observed radial-velocity curves.
spectrum, blue and red ground-based spectra, and observed radial-velocity curves.
Results. The observations provide evidence of circumstellar matter in the system. The system model shows that the Be primary star is critically rotating, and that the synchronously rotating secondary star fills its Roche lobe. The primary star has a mass of
![]() .
Radial-velocity observations establish a mass ratio of 0.163. Light curve synthesis demonstrates that the observed light curves are controlled largely by tidal distortion and irradiation of the massive primary by the less massive secondary. Synthetic spectra fit both blue and red observed spectra with the exception of spectral lines affected by circumstellar matter in the system. The synthetic spectra allow for gravity darkening and are consistent with critical rotation of the primary. Synthetic spectrum fits to a dereddened
.
Radial-velocity observations establish a mass ratio of 0.163. Light curve synthesis demonstrates that the observed light curves are controlled largely by tidal distortion and irradiation of the massive primary by the less massive secondary. Synthetic spectra fit both blue and red observed spectra with the exception of spectral lines affected by circumstellar matter in the system. The synthetic spectra allow for gravity darkening and are consistent with critical rotation of the primary. Synthetic spectrum fits to a dereddened ![]() spectrum produce a calculated system distance of 512 pc. This distance is
spectrum produce a calculated system distance of 512 pc. This distance is ![]() beyond the Hipparcos distance.
beyond the Hipparcos distance.
Key words: stars: emission-line, Be - binaries: close - binaries: spectroscopic - stars: fundamental parameters - stars: individual: V360 Lac
It is obvious that careful studies of suitably selected Be stars in binaries
with known orbital inclinations may help to solve this long-standing problem.
The danger is, of course, that binary interaction can represent
an additional complication and one can question how representative results
of such studies will be
for the whole population of Be stars. However, since the number
of known binaries among Be stars is growing steadily (see, e.g., the
catalog by Harmanec 2001), such binary studies can at least
be relevant to a large subgroup of Be stars that are members of binary
systems. Notably, the recent estimates of the most probable properties
of ![]() Cas by Harmanec (2002) and
Cas by Harmanec (2002) and ![]() Per by
Harmanec (2003) lead to the conlusion that both of these
stars may be rotating at critical rotation. However, since the inclinations
are not accurately known for these two objects, the conclusions are
uncertain.
Per by
Harmanec (2003) lead to the conlusion that both of these
stars may be rotating at critical rotation. However, since the inclinations
are not accurately known for these two objects, the conclusions are
uncertain.
The situation is much better for V360 Lac.
We have numerous new spectral and ![]() observations of V360 Lac, of
better quality than those available to Hill et al. (1997).
Consequently, we decided to re-analyze the total data set of V360 Lac in
an effort to derive better physical elements of the system.
observations of V360 Lac, of
better quality than those available to Hill et al. (1997).
Consequently, we decided to re-analyze the total data set of V360 Lac in
an effort to derive better physical elements of the system.
The B2e star V360 Lac (14 Lac, HD 216200) is now known as
a double-lined spectroscopic Be+F binary with
an orbital period of 10
![]() 0854 - see Hill et al. (1997)
(hereafter Paper 17).
These authors modelled the light curve using a simple model of a disk,
and derived the first basic binary properties. However Paper 17 gives
no details concerning how the light curve solutions were obtained.
Independently of the Hill et al. paper, Bossi et al. (1998)
analyzed their own photometry and spectroscopy and argued that V360 Lac is
neither an ellipsoidal variable nor an eclipsing binary.
0854 - see Hill et al. (1997)
(hereafter Paper 17).
These authors modelled the light curve using a simple model of a disk,
and derived the first basic binary properties. However Paper 17 gives
no details concerning how the light curve solutions were obtained.
Independently of the Hill et al. paper, Bossi et al. (1998)
analyzed their own photometry and spectroscopy and argued that V360 Lac is
neither an ellipsoidal variable nor an eclipsing binary.
Table 1:
Journal of new ![]() photoelectric observations of V360 Lac.
Observing stations are identified by their file numbers used in
the Praha/Ondrejov data archives (see column "File No.'') as follows:
photoelectric observations of V360 Lac.
Observing stations are identified by their file numbers used in
the Praha/Ondrejov data archives (see column "File No.'') as follows:
1... Hvar 0.65-m reflector, EMI6256 tube;
4... Ondrejov 0.65-m reflector, EMI6256 tube;
30... San Pedro Mártir 0.84-m reflector, Cuenta-pulsos photon-counting
photometer with RCA 31034 tube;
61... Hipparcos satellite Hp broadband photometry transformed
to Johnson V and B magnitudes.
The observational data used in this study consist of all data sets
used in Paper 17 (cf. Table 3 there) plus new
![]() observations secured at Hvar, Ondrejov and
San Pedro Mártir (SPM hereafter) observatories and
observations secured at Hvar, Ondrejov and
San Pedro Mártir (SPM hereafter) observatories and ![]() photometry
secured by
the ESA Hipparcos satellite (Perryman et al. 1997).
Basic information about the new observations is
in Table 1. Throughout the paper we reference epochs in
RJD ("reduced'' Julian date), where
photometry
secured by
the ESA Hipparcos satellite (Perryman et al. 1997).
Basic information about the new observations is
in Table 1. Throughout the paper we reference epochs in
RJD ("reduced'' Julian date), where
These agree very well with the original Johnson et al. (1966) values
A special effort was made to derive improved all-sky values for all comparison stars used, employing carefully standardized
Table 2:
Comparison and check stars used by various photometric observers
of V360 Lac and their ![]() magnitudes adopted here, based on the latest
standardization of Hvar and SPM all-sky
magnitudes adopted here, based on the latest
standardization of Hvar and SPM all-sky ![]() observations.
observations.
Table 3:
Individual ![]() observations of V360 Lac .
Data from individual stations are identified by their numbers
in column "station'', identical to those given in Table 1,
and filters are coded as follows: 3 = V, 4 = B, and
5 = U.
Original (O) observations, smoothed values derived by the HEC13
program (C) and residuals after smoothing (
observations of V360 Lac .
Data from individual stations are identified by their numbers
in column "station'', identical to those given in Table 1,
and filters are coded as follows: 3 = V, 4 = B, and
5 = U.
Original (O) observations, smoothed values derived by the HEC13
program (C) and residuals after smoothing (![]() )
are all tabulated.
)
are all tabulated.
Program HEC13, written by P. Harmanec![]() , was used to remove
long-term variations from the
, was used to remove
long-term variations from the ![]() data, discussed in Sect. 4.1.
This program uses Vondrák's (1969,1977) smoothing technique.
We used the smoothing parameter
data, discussed in Sect. 4.1.
This program uses Vondrák's (1969,1977) smoothing technique.
We used the smoothing parameter
![]() applied to 10-day normals of original data.
Note, however, that after the fit is derived, HEC13 provides individual
smoothed observations on the output. The processed
applied to 10-day normals of original data.
Note, however, that after the fit is derived, HEC13 provides individual
smoothed observations on the output. The processed ![]() data, with long-term
light variations removed, constitute the orbital light curves which we
fit in this paper.
For the convenience of future investigators, we publish all of our
standardized individual
data, with long-term
light variations removed, constitute the orbital light curves which we
fit in this paper.
For the convenience of future investigators, we publish all of our
standardized individual ![]() observations together with their HJDs in
Table 3.
For illustration, we reproduce a short section of Table 3
with the heading and a few first V observations. Note that both
observed and smoothed data are tabulated and that these smoothed values are
not the result of modelling described in this paper.
observations together with their HJDs in
Table 3.
For illustration, we reproduce a short section of Table 3
with the heading and a few first V observations. Note that both
observed and smoothed data are tabulated and that these smoothed values are
not the result of modelling described in this paper.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{3792fig1.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg29.gif) |
Figure 1: KOREL disentangling of the spectrum of the secondary and telluric lines in the region from 6465 to 6529 Å. The corresponding solution 1 is in Table 5. |
| Open with DEXTER | |
Reliable RV determinations for emission-line stars are difficult
because of complications due to circumstellar matter (see
Harmanec 2003 for a detailed discussion on this subject). In
the particular case of V360 Lac, Hill et al. (1997) found
that their RV curve of the Be primary is distorted near the phases
of the RV maxima. This phenomenon, known as the Barr effect, is present in many
emission-line binaries.
The effect produces a false eccentricity with ![]() near
near
![]() in an orbital solution, while the secondary star solution
produces a circular orbit. The following section discusses our treatment of this problem.
in an orbital solution, while the secondary star solution
produces a circular orbit. The following section discusses our treatment of this problem.
We decided to use the largest data set of 23 red spectra covering the region from about 6300 to 6700 Å and proceeded in the following steps:
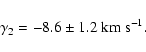 |
(1) |
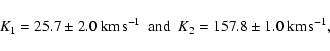 |
(2) |
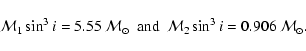 |
(3) |
Table 4: Mean RVs of the primary and secondary from the KOREL solutions, derived via cross-correlation of the disentangled line profiles with the individual spectra.
We
have divided the paper 17 RVs into two groups: one for which we believe the
observations are relatively free of distortion, and one which includes
observations likely affected by distortions.
The paper 17 RVs have an rms error per single observation of
![]() .
By including the new observations of Table 4,
our comparison with theoretical RVs treats the complete set of RVs as three
separate data sets.
Comparison of the observed radial velocities with the system model
is in Sect. 7.
.
By including the new observations of Table 4,
our comparison with theoretical RVs treats the complete set of RVs as three
separate data sets.
Comparison of the observed radial velocities with the system model
is in Sect. 7.
A solution using all available primary and secondary RVs led to
the following ephemeris:
Table 5:
Orbital solutions derived with KOREL (see the text
for details).The orbital period was fixed at 10
![]() 085408
derived in Paper 17.
085408
derived in Paper 17.
![]() denotes the epoch of the superior
conjunction in RJD-52 000.
denotes the epoch of the superior
conjunction in RJD-52 000.
The epoch of the superior conjunction from ephemeris (4) agrees very well with the mean epoch from the KOREL solutions.
We tested the possibility of a secular change of the orbital
period. Splitting the data into two time intervals, we obtained
periods of
![]() and
and
![]() for the older and more recent
RVs, respectively. Considering the associated errors, there is no
compelling reason to assume a variable period on the basis of the
available data. The result formally indicates a slow
secular increase of the orbital period, as would be expected
for a mass-exchanging system with a less massive and
mass-losing secondary. Consequently, we derived a solution with
for the older and more recent
RVs, respectively. Considering the associated errors, there is no
compelling reason to assume a variable period on the basis of the
available data. The result formally indicates a slow
secular increase of the orbital period, as would be expected
for a mass-exchanging system with a less massive and
mass-losing secondary. Consequently, we derived a solution with ![]() as
one of the elements. The solution was
as
one of the elements. The solution was
![]() days per day. This is
a non-significant result and we only use it to set an upper limit
on the rate of mass transfer, assuming that the process is conservative,
i.e. that no mass and angular momentum are lost from the system.
For the masses derived here (see below), we find
days per day. This is
a non-significant result and we only use it to set an upper limit
on the rate of mass transfer, assuming that the process is conservative,
i.e. that no mass and angular momentum are lost from the system.
For the masses derived here (see below), we find
RJD 52 284.440
This result, noted in Paper 17, suggests that a gas stream between the stars, or some other component of the circumstellar matter, affects the blue and ultraviolet light curves.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{3792fg2a.eps}\par\includegraphics[width=8.5cm,clip]{3792fg2b.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg49.gif) |
Figure 2: A plot of V-band and B-band residuals from the orbital variations vs. RJD for all photometric data. Simultaneous cyclic variations in both bands are clearly present. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{3792fg3a.eps}\par\includegraphics[width=8.3cm,clip]{3792fg3b.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg50.gif) |
Figure 3: A time plot of V-band residuals from the orbital variations for the Hipparcos data only: Upper panel: all data. Bottom panel: a subset demonstrating the presence of clear variations on a time scale of days. |
| Open with DEXTER | |
One of the conclusions of Paper 17 was that, in addition to the
orbital light variations and their slightly different phase dependence
at different wavelengths (discussed above), there are also mild cyclic
or possibly periodic light changes on different time scales, one being
322 days.
Long-term light variations are known for
a number of Be stars (cf., e.g. Pavlovski et al. 1997).
The new, standardised ![]() photometry appears to confirm mild long-term
variations of V360 Lac - see Fig. 2.
Most of the photometric data were collected in short
series, covering less than 0.06 d. We have not undertaken a more detailed
characterization of the changes, such as with power spectral analysis.
photometry appears to confirm mild long-term
variations of V360 Lac - see Fig. 2.
Most of the photometric data were collected in short
series, covering less than 0.06 d. We have not undertaken a more detailed
characterization of the changes, such as with power spectral analysis.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3792fig4.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg51.gif) |
Figure 4:
Plot of H |
| Open with DEXTER | |
To demonstrate that the variations are not caused by slight
station-to-station differences and to understand their character
better, we investigated the Hipparcos photometry alone (transformed
to Johnson V). This data set is accurate and homogeneous and its
advantage is that it does not suffer from the usual 1-d aliases.
The plot of all Hipparcos V-band residuals
vs. time gives an impression of systematic long-term
changes - see the upper panel of Fig. 3. However, the scatter
of individual data points indicates more rapid
changes as shown in the bottom panel of the same figure.
A period search in all V-band Hipparcos residuals finds a period
of 9
![]() 8147, with a roughly sinusoidal light curve.
This period is a 1-year alias of the orbital period;
this variation may indicate that the amplitude of orbital light variations
changes with time. An inspection of subsets of the photometric data
gives the same impression. Dedicated, very
accurate photometric observations will be needed to analyze this
phenomenon more precisely.
8147, with a roughly sinusoidal light curve.
This period is a 1-year alias of the orbital period;
this variation may indicate that the amplitude of orbital light variations
changes with time. An inspection of subsets of the photometric data
gives the same impression. Dedicated, very
accurate photometric observations will be needed to analyze this
phenomenon more precisely.
Inspection of the H![]() profiles in Fig. 4 reveals
phase-locked variation of V/R(V/R <1 in phases 0.3-0.4, V/R >1 in phases 0.7-0.8). This
phenomenon is observed in many interacting and Be binaries (cf., e.g.,
previous papers of this series on 88 Her, 4 Her or V832 Cyg).
Tomographic studies of some interacting systems
(Geary & Richards 1996) show that the V/R changes are caused
by a localized enhanced emission region between the components.
A similar region was detected in the Be+F binary CX Dra
(Richards et al. 2000)
which is an analog of V360 Lac but with a lower inclination.
The phase-locked variation is another piece of evidence indicating violation of
axial symmetry in the distribution of circumstellar matter,
discussed in Sect. 3.2.
profiles in Fig. 4 reveals
phase-locked variation of V/R(V/R <1 in phases 0.3-0.4, V/R >1 in phases 0.7-0.8). This
phenomenon is observed in many interacting and Be binaries (cf., e.g.,
previous papers of this series on 88 Her, 4 Her or V832 Cyg).
Tomographic studies of some interacting systems
(Geary & Richards 1996) show that the V/R changes are caused
by a localized enhanced emission region between the components.
A similar region was detected in the Be+F binary CX Dra
(Richards et al. 2000)
which is an analog of V360 Lac but with a lower inclination.
The phase-locked variation is another piece of evidence indicating violation of
axial symmetry in the distribution of circumstellar matter,
discussed in Sect. 3.2.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{3792fig5.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg52.gif) |
Figure 5:
Orbital RV curve of the H |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=11.1cm,clip]{3792fig6.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg53.gif) |
Figure 6: Comparison of rectified synthetic system spectrum, for the preliminary model, with a portion of observed spectrum BXN04816. The continuous line at the top is the system spectrum, superposed on the observed spectrum (grey curve). The middle continuous line is the rectified primary star spectrum. This spectrum has been positioned by adding 0.36 to all ordinates. The bottom line is the rectified secondary star synthetic spectrum, positioned by adding 0.25 to all ordinates. Note that the contribution of the secondary star is much too large, so the preliminary model cannot be correct. See the text for details. |
| Open with DEXTER | |
The Hvar calibrated photometry gives
From standard relations (Becker 1963; Cox 2000) Q=-0.570, E(B-V)=0.270, E(U-B)=0.189, AV=0.908, giving V0=5.00, (B-V)0=-0.187, (U-B)0=-0.700. Using the Hipparcos parallax, MV=-2.58, with an estimated standard error of 0.50, arising from the uncertainty in the Hipparcos parallax.
Paper 17 shows that the primary star is rotating rapidly, with an equatorial
![]() .
Paper 17 also describes a cross-correlation
function study of system spectra at both quadratures. Cross-correlation with a spectral type F8 mask
produced sharp peaks due to the secondary star, establishing
.
Paper 17 also describes a cross-correlation
function study of system spectra at both quadratures. Cross-correlation with a spectral type F8 mask
produced sharp peaks due to the secondary star, establishing
![]() K.
This determination agrees with a separate spectral classification of F9
K.
This determination agrees with a separate spectral classification of F9 ![]() 1 spectral subclass
(Paper 17).
We estimate the limits on this temperature to be
1 spectral subclass
(Paper 17).
We estimate the limits on this temperature to be ![]() 200 K.
(See Table 15.7 of Cox 2000.)
200 K.
(See Table 15.7 of Cox 2000.)
The primary star dominates the spectrum at optical wavelengths (Paper 17), and, based on the
values of (B-V)0, (U-B)0, and
Cox (2000), Table 15.7, the
![]() of the primary star is in the range
16 000 K to 20 000 K. Adopting
of the primary star is in the range
16 000 K to 20 000 K. Adopting
![]() K, Table 3 of Harmanec (1988) assigns a
corresponding mass of
K, Table 3 of Harmanec (1988) assigns a
corresponding mass of
![]() and a radius of
and a radius of
![]() .
Given the value of
.
Given the value of
![]() ,
Eq. (3), we expect a rough value
,
Eq. (3), we expect a rough value
![]() .
.
The rapid rotation of the primary star suggests a mass transfer system in which the secondary star fills its Roche lobe. Subsequent discussion in this paper demonstrates that the secondary star rotates synchronously. We believe that this condition, together with the rapid non-synchronous rotation of the primary star, constitutes clear evidence that the secondary star fills its Roche lobe.
The Hipparcos parallax of V360 Lac (Perryman et al. 1997) is
![]() .
The corresponding
.
The corresponding ![]() distance range is 222 pc to
667 pc.
distance range is 222 pc to
667 pc.
All of our models are based on the BINSYN suite of programs (Linnell & Hubeny 1996).
In the software package, a grid of points and associated photospheric segments defines the
stellar photospheres.
The software, in effect, interpolates a local synthetic spectrum at each photospheric
segment to the local value of
![]() and log g.
The system synthetic spectrum then is calculated as the sum of the
separate contributions, with proper allowance for Doppler shifts and other
sources of line broadening. The interpolation takes
place among
arrays of source synthetic spectra for the two stars,
individually
calculated for single values of
and log g.
The system synthetic spectrum then is calculated as the sum of the
separate contributions, with proper allowance for Doppler shifts and other
sources of line broadening. The interpolation takes
place among
arrays of source synthetic spectra for the two stars,
individually
calculated for single values of
![]() and log g. The program assumes both stars
are rigid rotators described by a Roche model.
and log g. The program assumes both stars
are rigid rotators described by a Roche model.
A visibility key is associated with each segment on the stellar photospheres.
For a given orbital phase and inclination, program routines determine whether
a given segment is visible to the observer and appropriately set the corresponding visibility key.
This information permits evaluation of eclipse effects.
Each segment also receives a
![]() value appropriate to it, based on gravity darkening and
irradiation for the stellar components.
Program routines then integrate over each system component
to calculate flux toward the observer, with due regard for visibility
keys and the
value appropriate to it, based on gravity darkening and
irradiation for the stellar components.
Program routines then integrate over each system component
to calculate flux toward the observer, with due regard for visibility
keys and the
![]() values and limb darkening of the individual segments. A final
calculation sums the component
contributions to provide a system flux toward the observer.
values and limb darkening of the individual segments. A final
calculation sums the component
contributions to provide a system flux toward the observer.
Using the approximate parameters from Sect. 5 and an initial test model, we calculated test V light curves and compared them with the observations. The test system showed deep eclipses, indicating that the value of i was too large.
Table 3 of Harmanec (1988) assigns the radius
![]() to a fairly
large range of stellar masses. We preserved this test radius of the primary star while
varying i and reached an inclination
to a fairly
large range of stellar masses. We preserved this test radius of the primary star while
varying i and reached an inclination
![]() for grazing eclipse. This exercise
required recalculation of the primary star mass as i was changed, to preserve a fit to
the radial velocity curves.
for grazing eclipse. This exercise
required recalculation of the primary star mass as i was changed, to preserve a fit to
the radial velocity curves.
Using this preliminary model to compare with an observed spectrum we met a major problem. A section of the rectified spectrum, compared with observed spectrum BXN04816, is in Fig. 6. In this and subsequent plots that show spectra of individual components, flux has been added to those components to position them conveniently. This action has been necessary to make details visible that otherwise would be lost in a coarser ordinate scale. The contribution of the secondary star is much too large. However, the secondary star absorption line widths in the synthetic spectrum are in good agreement with the observed line widths. This feature confirms that the secondary star is rotating synchronously, and so supports the model in which the secondary star fills its Roche lobe.
Table 6: System parameters used to simulate photometric observations and spectra for the system model.
Could the spectral contribution of the secondary star be reduced by an ad hoc assertion
that the secondary star rotates synchronously but is smaller than its Roche lobe?
In that case there would be no credible explanation for the rapid rotation of the primary
star.
Moreover, if the secondary star once filled its Roche lobe and has
subsequently detached
from it, the secondary would not now rotate synchronously, by conservation of angular momentum.
Can the secondary star
fill its Roche lobe but the temperature of the primary star be increased appropriately?
An increase in the primary star
![]() would produce a more discrepant fit to the
would produce a more discrepant fit to the
![]() spectrum
of the system, described below.
Another alternative would be to reduce the secondary star
spectrum
of the system, described below.
Another alternative would be to reduce the secondary star
![]() .
The
.
The
![]() of the secondary star cannot be reduced by a large amount without destroying
the light curve fit described below. The absorption line strengths of the secondary star are
temperature sensitive and reducing the secondary star
of the secondary star cannot be reduced by a large amount without destroying
the light curve fit described below. The absorption line strengths of the secondary star are
temperature sensitive and reducing the secondary star
![]() actually tends to increase
the intrinsic line
strengths, counteracting the expected gain by reducing the secondary star
actually tends to increase
the intrinsic line
strengths, counteracting the expected gain by reducing the secondary star
![]() .
The direct way to reduce the secondary star
contribution is to increase the size of the primary star while preserving its
.
The direct way to reduce the secondary star
contribution is to increase the size of the primary star while preserving its
![]() .
.
We increased the size of the primary star by reducing ![]() ,
without changing its
polar
,
without changing its
polar
![]() ,
until the
reduced relative spectral contribution of the secondary star matched the observed spectrum,
as determined by eye estimate. The
increased primary star radius required a reduction in i to
,
until the
reduced relative spectral contribution of the secondary star matched the observed spectrum,
as determined by eye estimate. The
increased primary star radius required a reduction in i to
![]() ,
and a corresponding
increase in the
primary star mass to preserve the radial velocity fit. The resulting model represents our system
solution.
The model parameters are in Table 6.
,
and a corresponding
increase in the
primary star mass to preserve the radial velocity fit. The resulting model represents our system
solution.
The model parameters are in Table 6.
![]() and
and ![]() are Roche potentials, with
are Roche potentials, with ![]() set equal to the separately
calculated Roche potential of the inner critical surface. FV1 and
FV2 are rotation rates in units of synchronous rotation, A1 and A2 are bolometric albedos,
set equal to the separately
calculated Roche potential of the inner critical surface. FV1 and
FV2 are rotation rates in units of synchronous rotation, A1 and A2 are bolometric albedos,
![]() and
and ![]() are gravity darkening exponents. The other parameters are self-explanatory.
Equations for calculating gravity and other parameters are in Linnell (1984).
The equator values of
are gravity darkening exponents. The other parameters are self-explanatory.
Equations for calculating gravity and other parameters are in Linnell (1984).
The equator values of
![]() are gravity-darkened
values for an equilibrium structure distorted by rapid rotation and tidally
distorted by the
companion.
Our software uses the theory by Limber (1963) to represent the surface form of the
primary star. The theory considers the general case of nonsynchronous rotation in the presence of
tidal distortion by a companion star. The theory then develops what Limber terms the first approximation.
In this approximation Coriolis forces and gas pressure gradients are neglected.
Also neglected are radiation pressure and
hydrodynamic effects such as
Eddington-Sweet currents (Tassoul 1978).
For the adopted
are gravity-darkened
values for an equilibrium structure distorted by rapid rotation and tidally
distorted by the
companion.
Our software uses the theory by Limber (1963) to represent the surface form of the
primary star. The theory considers the general case of nonsynchronous rotation in the presence of
tidal distortion by a companion star. The theory then develops what Limber terms the first approximation.
In this approximation Coriolis forces and gas pressure gradients are neglected.
Also neglected are radiation pressure and
hydrodynamic effects such as
Eddington-Sweet currents (Tassoul 1978).
For the adopted ![]() ,
critical rotation occurs for
FV1=6.1918755. In view of the physical
approximations of the theory, the Table 6 value of FV1 corresponds to critical rotation.
However, the adopted
,
critical rotation occurs for
FV1=6.1918755. In view of the physical
approximations of the theory, the Table 6 value of FV1 corresponds to critical rotation.
However, the adopted ![]() value depends on an eye estimate of the synthetic spectrum fit
to the secondary
star spectrum. It has an estimated uncertainty as shown in Table 6. A change in
value depends on an eye estimate of the synthetic spectrum fit
to the secondary
star spectrum. It has an estimated uncertainty as shown in Table 6. A change in ![]() also
changes the value of FV1 for critical rotation; the uncertainty in FV1 is dominated
by the
also
changes the value of FV1 for critical rotation; the uncertainty in FV1 is dominated
by the ![]() uncertainty.
uncertainty.
Comparison of the primary star mass with main sequence values, Table 3 of Harmanec (1988)
places
the primary between spectral classes B1 and B2. The corresponding main sequence log
![]() values are 4.418 and 4.364. The polar log
values are 4.418 and 4.364. The polar log
![]() value for V360 Lac is 4.255, and allowing for
temperature variation over the photosphere would reduce this to an average of about 4.17. The main
sequence
radii of B1 and B2 stars are
value for V360 Lac is 4.255, and allowing for
temperature variation over the photosphere would reduce this to an average of about 4.17. The main
sequence
radii of B1 and B2 stars are
![]() and
and
![]() ,
respectively. The Table 6 primary
star polar
radius of
,
respectively. The Table 6 primary
star polar
radius of
![]() identifies this star as larger than a main sequence counterpart, and
thus evolved. The log
identifies this star as larger than a main sequence counterpart, and
thus evolved. The log
![]() value is consistent with an evolved status.
value is consistent with an evolved status.
The radial velocity fit for this model is in
Fig. 7. The theoretical radial velocities are for the stars moving as mass points
in the center of mass system, with ![]() velocities added.
Note that the plotted points are for three data sets.
The standard deviation of the primary star velocity residuals from the first
two data sets is
velocities added.
Note that the plotted points are for three data sets.
The standard deviation of the primary star velocity residuals from the first
two data sets is
![]() and the standard deviation of the secondary star velocity residuals
is
and the standard deviation of the secondary star velocity residuals
is
![]() .
These standard deviations are of the same order as the corresponding
quantities in the various solutions in Paper 17 and are consistent with the parameters determined in
Sect. 3.1.
.
These standard deviations are of the same order as the corresponding
quantities in the various solutions in Paper 17 and are consistent with the parameters determined in
Sect. 3.1.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3792fig7.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg87.gif) |
Figure 7: Fit of theoretical radial velocities ( RVs) to the observed velocities. The filled circles designate mean KOREL disentangled RVs, the open circles designate reliable RVs from paper 17, and the asterisks designate RVs from paper 17 that may be affected by emission lines and are less reliable. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3792fig8.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg88.gif) |
Figure 8: Fit of three theoretical light curves to the observed Vlight curve. The solid line is for a secondary star bolometric albedo of 0.70, the dash line is for a bolometric albedo of 0.90, and the dot-dash line is for a bolometric albedo of 0.50. |
| Open with DEXTER | |
The synthetic V light curve for the system model is sensitive to the primary star rotation parameter, FV1 (see Table 6). Tidal distortion of the primary star by the secondary would be expected to be very small in view of the small mass ratio, as also would irradiation of the 18 000 K primary by the 6000 K secondary. Rapid rotation of the primary, in isolation, produces distortion that is azimuthally constant, and so would have no effect on the light curve. Why, then, is the light curve sensitive to FV1? We return to this point in later paragraphs.
Light curve sensitivity to the
secondary star bolometric albedo is expected, and is present.
The fit of the system model to the Vlight curve, for three values of the bolometric albedo, is in Fig. 8.
In calculating these light curves we used a black body radiation curve at the local
![]() value of each photospheric segment. See Sect. 6 for further details.
The synthetic light curves have been
shifted -0.03 phase units for an optimum match to the observed light curve.
The phase shifts applied to the synthetic
light curves were produced by visual estimates. They are appreciably larger than the
phase displacements
corresponding to the epochs of the deeper
minima in Sect. 3.2, using the first harmonics of the orbital period. This effect represents
a phase difference between the KOREL radial velocity ephemeris and the observed light curves.
We suggest it could be a light curve effect indicating lack of light symmetry of the actual
system about orbital phase 0.0. The model assumes complete symmetry.
value of each photospheric segment. See Sect. 6 for further details.
The synthetic light curves have been
shifted -0.03 phase units for an optimum match to the observed light curve.
The phase shifts applied to the synthetic
light curves were produced by visual estimates. They are appreciably larger than the
phase displacements
corresponding to the epochs of the deeper
minima in Sect. 3.2, using the first harmonics of the orbital period. This effect represents
a phase difference between the KOREL radial velocity ephemeris and the observed light curves.
We suggest it could be a light curve effect indicating lack of light symmetry of the actual
system about orbital phase 0.0. The model assumes complete symmetry.
In Fig. 8 the best fit (solid) line is the theoretical light curve for a bolometric albedo of 0.70, not far from the theoretically-preferred value of 0.60, according to Claret (2001). The formal mean residual, for 834 observations and in light units, is 0.00456 and the standard deviation of the light residuals is 0.01163. Figure 8 shows outliers that are fairly discrepant, with a grouping of negative residuals before phase 0.0 and positive residuals immediately following, as well as a few large positive residuals near phase 0.3. Note that all of the light curve plots have ordinates in light units, not magnitude units.
A synchronously rotating primary star model produces a very discrepant V light curve. Rapid primary star rotation is necessary to produce an acceptable light curve fit; a plot of the light curve contributions of the individual stars is needed to understand why. The V light curve contributions from the separate stellar components and the system light curve are in Fig. 9.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3792fig9.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg89.gif) |
Figure 9: Contributions of the separate stellar components to the V light curve, and the system V light curve. The top curve is the contribution of the secondary star, with 0.95 added to all ordinates. The bottom curve is the contribution of the primary star, with 0.02 added to all ordinates. It is rotating at 6.19 times the synchronous rate. The middle curve is the system V light curve. See the text for details. |
| Open with DEXTER | |
As the primary star rotation
rate increases, equatorial gravity becomes smaller and tidal effects due to the secondary star
become relatively more prominent. The important consideration in the present context is the
effect of gravity darkening. As Table 6 tabulates, the primary star equatorial
![]() values are of order 9000 K less than the polar
values are of order 9000 K less than the polar
![]() ,
and there is appreciable
temperature variation along the equator. In the absence of irradiation by the secondary star, the
"point''
,
and there is appreciable
temperature variation along the equator. In the absence of irradiation by the secondary star, the
"point''
![]() of the primary would be 6869 K (compare with the Table 6 value), based
on the log
of the primary would be 6869 K (compare with the Table 6 value), based
on the log
![]() value of Table 6.
value of Table 6.
As the bottom curve shows in Fig. 9,
the primary star exhibits strong effects of ellipticity and irradiation.
In Fig. 9,
irradiation by the
secondary star (including, importantly, the elevated secondary star inner face temperature
produced by
the primary star)
causes the primary star brightness to be greater at orbital phase 0.0 than at phase 0.5.
The upper curve, Fig. 9, shows the irradiation of
the secondary star "point'' by the primary, producing a constant brightness for an extended
orbital phase around 0.5 rather than a minimum light at orbital phase 0.5.
Note from the caption to Fig. 9 that 0.95 has been added to the secondary star ordinates.
The secondary star contributes about. 0.10 of the V system light. If the contributions
were plotted without change on the Fig. 9 ordinate scale, Fig. 9 would have required more
than the vertical height of a page. A coarser ordinate scale greatly reduces the visibility
of the light variations.
If the illumination by the primary star is reduced in an
attempt to produce a double-humped secondary star light variation, the model quickly produces a
too-bright secondary star, with too strong absorption lines in the synthetic spectrum.
The
system light curve is the resultant superposition of the two individual sources of light variation.
Because of the important primary star contribution to the light curve, the optimum secondary star
bolometric albedo of 0.70 does not represent a significant discrepancy from the theoretical
value of 0.60.
Fits to the ![]() light curves, requiring the primary star to be at critical rotation, are a more
sensitive test than a fit to the Balmer absorption lines.
We stress that the system model fully accounts for gravity darkening. For a
discussion of this point see Cranmer (2005).
light curves, requiring the primary star to be at critical rotation, are a more
sensitive test than a fit to the Balmer absorption lines.
We stress that the system model fully accounts for gravity darkening. For a
discussion of this point see Cranmer (2005).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3792fg10.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg91.gif) |
Figure 10: Fit of the synthetic B light curve to observations. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3792fg11.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg92.gif) |
Figure 11: Fit of the synthetic U light curve to observations. Note the change in ordinate range from the two previous light curve plots. |
| Open with DEXTER | |
The light curves used the limb darkening tables of Wade & Rucinski (1985), interpolated to the local photospheric
values of
![]() and log g. The adopted effective wavelength of the V band was 5500 Å.
We have
iterated the irradiative
interaction twice, in accordance with the prescription of
Wilson (1990). Table 6 includes estimated errors of system parameters. The value listed
for
and log g. The adopted effective wavelength of the V band was 5500 Å.
We have
iterated the irradiative
interaction twice, in accordance with the prescription of
Wilson (1990). Table 6 includes estimated errors of system parameters. The value listed
for
![]() is the nominal value from Paper 17.
is the nominal value from Paper 17.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3792fg12.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg94.gif) |
Figure 12: View of system model projected on the plane of the sky, at orbital phase 0.25. The secondary star fills its Roche lobe Rotational distortion is easily visible for the primary star. It rotates at 6.19 times synchronous rate. The unit of distance for both axes is the semi-major axis of the relative orbit. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{3792fg13.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg95.gif) |
Figure 13:
Fit of system model synthetic spectrum (thin line) to observed (grey curve)
spectral region including
Balmer lines.
The synthetic spectrum fit is reasonably good, including the fits to the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.4cm,clip]{3792fg14.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg96.gif) |
Figure 14: Fit of rectified synthetic spectrum (thin line, top), for system model, to observed spectrum BXN04816 (grey curve). The primary star spectrum has been positioned by adding 0.10 to all ordinates, and the secondary star spectrum haas been positioned by adding 0.67 to all ordinates. The synthetic spectrum identifications are as in Fig. 6, but note the different ordinate scale. Note the generally accurate fit of the secondary star lines to the observations. The fit demonstrates that the secondary star is rotating synchronously. Also note the smearing of the primary star lines that results from rapid stellar rotation. |
| Open with DEXTER | |
The model fit to the B light curve, calculated for an effective wavelength of 4340 Å, is in Fig. 10. The secondary star bolometric albedo is 0.70. The mean residual, for 1172 observations, is 0.00444, in light units, and the standard deviation of the residuals is 0.01151.
The model fit to the U light curve, calculated for an effective wavelength of 3650 Å, is in Fig. 11. The secondary star bolometric albedo is 0.70. The mean residual, for 620 observations, is 0.00798, in light units, and the standard deviation of the residuals is 0.01982.
A projection view of the system model, at orbital phase 0.25, is in Fig. 12. Rotational distortion of the primary star is easily visible. An important point from this analysis is that the primary star is at critical rotation. The term "critical rotation'' requires some discussion. In the case of single stars, critical rotation means such small equatorial gravity that matter may be ejected by, e.g., radiation pressure. Gravity is constant along the equator in single stars. In the present case, the presence of the companion modifies the physical situation. If the primary star rotates synchronously, tidal distortion by the secondary star is nearly negligible. As the model primary star rotates faster, the fixed tidal distortion by the secondary becomes a larger contributor to the decreasing primary star equatorial gravity. Eventually, for sufficiently fast primary star rotation, "gravity'' at the substellar equatorial point on the primary star goes to zero, while gravity at other equatorial points remains larger than zero. By "gravity'' we mean net force directed inward, including gas pressure, radiation pressure, etc. This condition defines "critical rotation''.
Our analysis demonstrates that V360 Lac is a new example of the exotic morphological type first discussed by Wilson (1979) and termed "double-contact binaries''. See also the discussion of the double-contact system RZ Scuti (Wilson et al. 1985) and the review article by Wilson (1994). V360 Lac differs from RZ Scuti in that RZ Scuti is an eclipsing system.
We used Kurucz (1993b) model atmospheres , with the Hubeny program
SYNSPEC (v48)(Hubeny et al. 1985),
to calculate synthetic spectra,
at steps of 1000 K between 7000 K
and 18 000 K,
and for log g values of 2.5, 3.0, and 3.5 for each
![]() .
This set of source spectra was used with the primary star. We also calculated synthetic spectra
at
.
This set of source spectra was used with the primary star. We also calculated synthetic spectra
at
![]() values of 8000 K, 7000 K, 6000 K, 5000 K, and 4000 K and for log g values of
1.5, 2.0, 2.5, and 3.0 for the secondary star. Comparison of these log g values with the
corresponding values in Table 6 shows that only very small regions on the two stars fall
outside the tabulation ranges of the source spectra. If a photospheric segment has a
values of 8000 K, 7000 K, 6000 K, 5000 K, and 4000 K and for log g values of
1.5, 2.0, 2.5, and 3.0 for the secondary star. Comparison of these log g values with the
corresponding values in Table 6 shows that only very small regions on the two stars fall
outside the tabulation ranges of the source spectra. If a photospheric segment has a
![]() or log g outside the tabulation range, BINSYN uses the nearest tabular entry. Since the
outside-range values are at very small log g values, the corresponding photometric segments
are subject to large gravity darkening, and the error in the flux value from using the nearest
tabular log g produces a negligible error.
All spectra were calculated at a wavelength
resolution of 0.1 Å.
We adopted solar composition
(the SYNSPEC default) in all calculations.
The source synthetic spectra tabulate flux as function of wavelength.
In calculating a system synthetic spectrum, BINSYN associates each
source spectrum with a limb darkening coefficient. We have used a standard value of 0.6
and a limb darkening law of the form
or log g outside the tabulation range, BINSYN uses the nearest tabular entry. Since the
outside-range values are at very small log g values, the corresponding photometric segments
are subject to large gravity darkening, and the error in the flux value from using the nearest
tabular log g produces a negligible error.
All spectra were calculated at a wavelength
resolution of 0.1 Å.
We adopted solar composition
(the SYNSPEC default) in all calculations.
The source synthetic spectra tabulate flux as function of wavelength.
In calculating a system synthetic spectrum, BINSYN associates each
source spectrum with a limb darkening coefficient. We have used a standard value of 0.6
and a limb darkening law of the form
![]() ,
where u is the limb darkening
coefficient and
,
where u is the limb darkening
coefficient and ![]() is the cosine of the angle between the surface normal and the line of sight.
is the cosine of the angle between the surface normal and the line of sight.
All observed spectra have been rectified. BINSYN produces synthetic spectra with absolute flux calibrations and so must be rectified for comparison with the observed spectra. To rectify the synthetic spectra, we repeated the spectrum synthesis calculation but with continuum spectra substituted for the source synthetic spectra. (A given SYNSPEC run produces both a synthetic spectrum and a continuum spectrum.) We then divided the output produced with the regular source spectra by the output produced with the continuum spectra, giving a rectified synthetic spectrum. While this procedure gave results that fitted the rectified observed spectra well longward of 3800 Å, the rectified synthetic spectrum required small adjustment short of that wavelength to produce a close fit to the rectified observed spectrum.
The fit of the rectified system synthetic spectrum to a portion of observed spectrum BXN04816 is in
Fig. 14. This is the same observed spectrum as in Fig. 6. Note the
difference in the ordinate scales.
There
now is a very good fit to many of the lines from the secondary star. This fit certifies that the
secondary star is rotating synchronously. More rapid rotation would smear out the synthetic
spectrum lines, while less than synchronous rotation would produce narrower synthetic spectrum
lines.
![\begin{figure}
\includegraphics[width=11.4cm,clip]{3792fg15.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg98.gif) |
Figure 15:
Fit of model synthetic spectrum (thin line, top) to observed (grey curve) spectral
region including H |
| Open with DEXTER | |
Figure 13 shows the synthetic spectrum fit in a spectral region that includes several
Balmer lines. The synthetic spectrum Balmer lines are slightly too shallow for the high series
members.
The secondary star
![]() Ca II line
is prominent. The secondary star
Ca II line
is prominent. The secondary star
![]() Ca II line blends with the primary star
Ca II line blends with the primary star
![]() line.
line.
Figure 15 shows a different spectral region. The fit to the depth of the H![]() line
is quite good. Note the orbital Doppler displacement of
the secondary star from the primary and the intermediate location of the system line, representing
an average of the separate contributions.
line
is quite good. Note the orbital Doppler displacement of
the secondary star from the primary and the intermediate location of the system line, representing
an average of the separate contributions.
The depths of the Balmer lines in the model are sensitive to the rotation parameter FV1. A too small FV1 produces model Balmer lines deeper than observed. In principle, it would be possible to determine FV1 by optimizing the fit to the depths of the Balmer lines. However, as Fig. 15 shows, the quality of fit is not a uniform function of the Balmer series members. We have chosen to use the light curve dependence on FV1 to determine the best value of that parameter.
We now show fits to red spectra at three orbital phases, together with views of the
system. The first group is at orbital phase 0.44, Figs. 17 and 18.
A view of the system is in Fig. 16.
The observed spectrum contains a number of narrow telluric lines near 6300 Å and
near 6500 Å.
The H![]() emission line, with its central reversal, is slightly displaced to the blue relative to the
system synthetic spectrum
absorption line, but aligns accurately with the absorption line in the synthetic spectrum
of the primary star. This result is in agreement with the separately measured radial
velocities of the emission wings described in Sect. 4.2.
The far redward wing appears to be slightly in emission. Also note the emission wings of the
primary star Si II and He I lines. The rotational broadening of the primary star
lines is apparent. Figure 18 shows a detail of Fig. 17. The Doppler shifts
of the secondary star lines are apparent by their displacements from the line identification
markers. Although the synthetic spectrum represents the secondary star reasonably accurately,
there are some differences.
Note the much stronger observed Si II features at 6347.1 and 6371.4 Å than appear in the synthetic
spectrum.
emission line, with its central reversal, is slightly displaced to the blue relative to the
system synthetic spectrum
absorption line, but aligns accurately with the absorption line in the synthetic spectrum
of the primary star. This result is in agreement with the separately measured radial
velocities of the emission wings described in Sect. 4.2.
The far redward wing appears to be slightly in emission. Also note the emission wings of the
primary star Si II and He I lines. The rotational broadening of the primary star
lines is apparent. Figure 18 shows a detail of Fig. 17. The Doppler shifts
of the secondary star lines are apparent by their displacements from the line identification
markers. Although the synthetic spectrum represents the secondary star reasonably accurately,
there are some differences.
Note the much stronger observed Si II features at 6347.1 and 6371.4 Å than appear in the synthetic
spectrum.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{3792fg16.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg102.gif) |
Figure 16:
View of V360 Lac model at orbital phase 0.44. The orbital inclination is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10.6cm,clip]{3792fg17.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg103.gif) |
Figure 17:
Synthetic spectrum (thin line, top) compared with observed spectrum V3L14818
(grey curve) at orbital
phase 0.44 (see Fig. 16). The middle spectrum is the primary star and the bottom
spectrum is the secondary star. The primary star spectrum has been positioned by adding -0.11
to all ordinates, and the secondary star spectrum has been positioned by adding 0.37 to all
ordinates.
Note the decreasing contribution of the primary star and the increasing
contribution of the secondary star with wavelength. Also note
the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10.6cm,clip]{3792fg18.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg104.gif) |
Figure 18:
Detail of Fig. 17. The Doppler shift of the secondary star spectral lines
is clearly evident, since the line identification annotations are positioned at their listed
wavelengths.
Note the emission wings on the Si II doublet. As with H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3792fg19.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg105.gif) |
Figure 19: View of V360 Lac model at orbital phase 0.50. Compare with Fig. 16. This view is associated with the spectra in Figs. 20 and 21. The primary star is nearer the observer and the observer sees the irradiated inner face of the secondary. |
| Open with DEXTER | |
Figure 19 shows the system at orbital phase 0.50, nearly the same phase as Fig. 16.
The Fig. 17 spectrum was taken at RJD 52187.9218, and the Fig. 20 spectrum
was taken at RJD 52309.6070.
The H![]() emission line continues to follow the primary
star. Compare the orbital phase 0.50 Fig. 21 detail spectrum with
Fig. 18 at orbital phase 0.44. The synthetic spectrum shows subtle changes, even
over the short phase interval. The changes in the observed spectrum are different and larger,
indicating temporal variation. Note in
particular the changes in the Si II lines and the Fe I 6400.0 Å line.
emission line continues to follow the primary
star. Compare the orbital phase 0.50 Fig. 21 detail spectrum with
Fig. 18 at orbital phase 0.44. The synthetic spectrum shows subtle changes, even
over the short phase interval. The changes in the observed spectrum are different and larger,
indicating temporal variation. Note in
particular the changes in the Si II lines and the Fe I 6400.0 Å line.
Figure 22 shows the system at orbital phase 0.98. The Fig. 23 spectrum was
observed at RJD 52132.9563.
In Fig. 23, note the greatly increased depth of the H![]() absorption
reversal. In Fig. 24, note the appreciable changes, in both the observed and synthetic
spectrum,
from Fig. 21, especially the stronger absorption line features.
If any mass transfer stream exists,
it would appear projected on the disk of the primary star. We suggest that these enhanced absorption
features may be associated with a mass transfer stream.
absorption
reversal. In Fig. 24, note the appreciable changes, in both the observed and synthetic
spectrum,
from Fig. 21, especially the stronger absorption line features.
If any mass transfer stream exists,
it would appear projected on the disk of the primary star. We suggest that these enhanced absorption
features may be associated with a mass transfer stream.
A single IUE spectrum of the system is available (SWP09204) to download from
the ![]() archive.
Comparison of an initial system synthetic spectrum with one
of the ground-based blue spectra, e.g. BXN04612, shows that
the contribution of the secondary star is a few percent, at most,
in the wavelength range
archive.
Comparison of an initial system synthetic spectrum with one
of the ground-based blue spectra, e.g. BXN04612, shows that
the contribution of the secondary star is a few percent, at most,
in the wavelength range
![]() to
to
![]() .
At IUE wavelengths the contribution of the secondary star is negligible.
We used IUEDAC software to produce a dereddened spectrum, by
application of the
Savage & Mathis procedure (1979), followed by recalibration by the
Massa & Fitzpatrick procedure (2000).
We subjected the synthetic spectrum to Gaussian FWHM broadening to
5.0 Å, using the Hubeny program ROTIN3 (Hubeny et al. 1985), to correspond to the
resolution
of the IUE spectrum.
.
At IUE wavelengths the contribution of the secondary star is negligible.
We used IUEDAC software to produce a dereddened spectrum, by
application of the
Savage & Mathis procedure (1979), followed by recalibration by the
Massa & Fitzpatrick procedure (2000).
We subjected the synthetic spectrum to Gaussian FWHM broadening to
5.0 Å, using the Hubeny program ROTIN3 (Hubeny et al. 1985), to correspond to the
resolution
of the IUE spectrum.
The fit of this model to the IUE spectrum is in Fig. 25. The IUE spectrum
is in physical flux units at the Earth.
The system
synthetic spectrum represents an integration over the visible photospheres,
and is expressed in physical flux units of erg
![]() ,
evaluated at the star.
We determine an empirical scale factor, S, applied to the synthetic spectrum, to superpose the two spectra.
,
evaluated at the star.
We determine an empirical scale factor, S, applied to the synthetic spectrum, to superpose the two spectra.
![\begin{figure}
\includegraphics[width=11cm,clip]{3792fg20.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg109.gif) |
Figure 20:
Synthetic spectrum (thin line, top) compared with observed spectrum V3L00848 (grey curve)
at orbital phase 0.50
(see Fig. 19). Spectra as in Fig. 17. The H |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=11cm,clip]{3792fg21.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg110.gif) |
Figure 21: Detail of Fig. 20. Note the subtle changes, in both the observed and synthetic spectrum, from Fig. 18. The Si II emission wings are present, as in Fig. 18, but the observed absorption component is deeper and narrower. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3792fg22.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg111.gif) |
Figure 22: View of V360 Lac model at orbital phase 0.98. The secondary star is nearer the observer. This view is associated with the spectra in Figs. 23 and 24. |
| Open with DEXTER | |
If the distance to V360 Lac, in cm, is D, then D2=S.
Superposition of the two spectra
corresponds to a distance, formally, of 512 pc. This distance is slightly less than two standard deviations
larger than the Hipparcos distance of 333 pc, which corresponds to a distance of 667 pc.
The fit is reasonably good but the synthetic
spectrum is slightly too hot. If our E(B-V) value were slightly larger, the dereddened ![]() spectrum would be a better fit to the synthetic spectrum and the discrepancy with the Hipparcos
distance would be reduced.
spectrum would be a better fit to the synthetic spectrum and the discrepancy with the Hipparcos
distance would be reduced.
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{3792fg23.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg112.gif) |
Figure 23:
Synthetic spectrum (thin line, top) compared with observed spectrum V3L10685 (grey curve)
at orbital phase 0.98
(see Fig. 22). Spectra as in Fig. 17. Note the much greater depth of the
H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{3792fg24.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg113.gif) |
Figure 24: Detail of Fig. 23. Note the differences from Fig. 21. The Si II emission wings are still present but the absorption component profiles are different from both Figs. 18 and 21. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{3792fg25.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg114.gif) |
Figure 25:
Fit of synthetic spectrum (thin line) to IUE spectrum
SWP09204 (grey curve). The synthetic
spectrum has been divided by
|
| Open with DEXTER | |
Finally, Fig. 26 shows the position of the binary components on
the HR diagram.
![]() of the primary star is -4.13, and,
for the secondary, -0.44. The primary star log
of the primary star is -4.13, and,
for the secondary, -0.44. The primary star log
![]() (averaged over the visible photosphere) is 4.164; the corresponding
secondary star quantity is 3.789. If the primary star were rotating
synchronously, its bolometric magnitude would be -4.58and the secondary star bolometric magnitude would be -0.74.
The corresponding log
(averaged over the visible photosphere) is 4.164; the corresponding
secondary star quantity is 3.789. If the primary star were rotating
synchronously, its bolometric magnitude would be -4.58and the secondary star bolometric magnitude would be -0.74.
The corresponding log
![]() values would be 4.255 and 3.820.
These bolometric magnitudes are for an observer for whom the orbital
inclination is
values would be 4.255 and 3.820.
These bolometric magnitudes are for an observer for whom the orbital
inclination is
![]() .
It is seen that the position of the primary
roughly corresponds to its mass
.
It is seen that the position of the primary
roughly corresponds to its mass![]() while the position of the secondary must obviously be a result of ongoing
mass exchange in the system. That position cannot result from the evolution of
a star with a mass only slightly larger than 1
while the position of the secondary must obviously be a result of ongoing
mass exchange in the system. That position cannot result from the evolution of
a star with a mass only slightly larger than 1 ![]() .
.
In the present system we have shown that there is photometric (Sect. 3.2, 4.1), and
spectroscopic (Sect. 4.2, Fig. 23) evidence
for circumstellar
material. An important point is that
the H![]() emission lines follow the orbital motion of the primary star and show
a strong absorption reversal at orbital phase 0.98, reasonably interpreted as evidence of
a mass transfer stream.
The rapid primary star rotation is most easily explained by mass transfer from the
companion. It is not unreasonable to postulate that an accretion disk surrounds the
primary star.
The disk cannot be a standard accretion disk since the mass transfer stream impacts the
primary star directly, according to Lubow & Shu (1975). (However, see the study by
Kríz (1971).) A conjectural alternative is that the disk results from the splash of the
mass transfer impact on the primary star.
The rapid rotation of the primary star, with
reduced equatorial gravity, facilitates this possibility. The potential well of the primary
star is shallow and the disk must be cold, with a small viscosity
(Frank et al. 1995) and corresponding long decay time against accretion
onto the primary star. Once an accretion disk is formed, further mass transfer will impact
the accretion disk, tending to maintain it.
emission lines follow the orbital motion of the primary star and show
a strong absorption reversal at orbital phase 0.98, reasonably interpreted as evidence of
a mass transfer stream.
The rapid primary star rotation is most easily explained by mass transfer from the
companion. It is not unreasonable to postulate that an accretion disk surrounds the
primary star.
The disk cannot be a standard accretion disk since the mass transfer stream impacts the
primary star directly, according to Lubow & Shu (1975). (However, see the study by
Kríz (1971).) A conjectural alternative is that the disk results from the splash of the
mass transfer impact on the primary star.
The rapid rotation of the primary star, with
reduced equatorial gravity, facilitates this possibility. The potential well of the primary
star is shallow and the disk must be cold, with a small viscosity
(Frank et al. 1995) and corresponding long decay time against accretion
onto the primary star. Once an accretion disk is formed, further mass transfer will impact
the accretion disk, tending to maintain it.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{3792fg26.eps}
\end{figure}](/articles/aa/full/2006/33/aa3792-05/Timg117.gif) |
Figure 26:
Location of individual binary components on a main sequence HR diagram, marked by
the heavy solid line, with ZAMS stellar masses indicated. The rightmost diamond marks
the primary star as affected by
rotation. The leftmost diamond marks the location of the primary star if it were
rotating synchronously. The rightmost triangle marks the secondary, including irradiation
by the rapidly rotating primary star. The leftmost triangle marks the secondary as it
would be located if the primary were rotating synchronously. In the latter case the primary
star is hotter, because of reduced gravitational darkening, and so irradiative heating of the
secondary star is greater. The bolometric magnitudes are as evaluated by an observer for
whom the orbital inclination is
|
| Open with DEXTER | |
The BINSYN package supports analysis of a system with an optically thick accretion disk.
We have tested a large number of possible models and found one which accurately represents all
of the observational data. As with the system model of Table 6, the accretion disk model
requires the primary star to rotate at critical rotation and its individual light curves to
be affected by irradiation
by the secondary star. The orbital inclination, in this model, is
![]() and the primary
star mass is
and the primary
star mass is
![]() .
In this model, secondary minimum is produced in part by
eclipse of the primary star by the accretion disk, extending to the tidal cutoff radius.
.
In this model, secondary minimum is produced in part by
eclipse of the primary star by the accretion disk, extending to the tidal cutoff radius.
A potentially serious objection to this model is that absorption lines might be expected in the spectra due to light from the primary star passing through the accretion disk, assumed to be partially transparent. Detailed calculations would be necessary to determine whether such absorption lines would be easily detectable. During secondary eclipse the obscured upper half of the primary star provides only 17% of that star's light at 5500 Å. Absorption lines produced in the accretion disk will be broadened by Keplerian rotation, and those lines would appear on only a small fraction of the total flux from the primary star.
Without conclusive observational evidence in either direction, it is as likely that an accretion disk will be optically thin as optically thick. At the present time, the observational data demonstrate that circumstellar matter is present, but not enough data are available to constrain a system model.
The model presented in this paper depends strongly on the value of the mass ratio, q.
We take the value q=0.163, from the final solution, Table 6, as a fixed value not subject
to empirical variation in the modelling process.
Earlier attempts at a solution used a variety of q values. A system model for a given
q value is a lengthy, computationally-intensive process. The solution is complicated by the
absence of eclipses, which would permit application of more traditional light curve solution
techniques. In the present instance,
a formal optimization of parameters, either by differential corrections (Wilson & Devinney 1971; Linnell 1989) or by
the simplex method (Kallrath & Linnell 1987), is not possible. Fits, for example, would be required to
the rectified observed
spectrum, by, say, ![]() .
This process would require a setup procedure that is not easily amenable to
automation.
We have simply used visual estimates for Fig. 14
to determine an acceptable fit.
As we have seen in Sect. 7.2, the depths of the model Balmer lines depend on the
rotation parameter FV1 but not in a uniform way with the line sequence.
The observed spectra show cycle-to-cycle variability that would seriously affect the optimization
process. These complexities justify use of visual estimates in selecting a system model.
.
This process would require a setup procedure that is not easily amenable to
automation.
We have simply used visual estimates for Fig. 14
to determine an acceptable fit.
As we have seen in Sect. 7.2, the depths of the model Balmer lines depend on the
rotation parameter FV1 but not in a uniform way with the line sequence.
The observed spectra show cycle-to-cycle variability that would seriously affect the optimization
process. These complexities justify use of visual estimates in selecting a system model.
Because of the V360 Lac time-wise variations, both photometric and spectroscopic, the model
derived in this paper represents a temporal average. Note that the conditions on the solution include
agreement with Eq. (3), an acceptable fit to the ![]() spectrum, fits to the other observed spectra,
accurate representation of the radial velocity
curves, and accurate fits to the
spectrum, fits to the other observed spectra,
accurate representation of the radial velocity
curves, and accurate fits to the ![]() light curves.
light curves.
Our principle results are:
(1) V360 Lac is a binary system in which
the stellar masses are
![]() (primary)
and
(primary)
and
![]() (secondary). The orbital
inclination is near
(secondary). The orbital
inclination is near
![]() .
Observed low amplitude UBV light curves severely constrain possible
system models. There are no stellar eclipses.
.
Observed low amplitude UBV light curves severely constrain possible
system models. There are no stellar eclipses.
(2) The primary star rotates at 6.19 times synchronous rate, corresponding to critical
rotation.
The primary star has a polar
![]() of 18 000 K. The secondary star fills its Roche lobe and has
a polar
of 18 000 K. The secondary star fills its Roche lobe and has
a polar
![]() of 6000 K. V360 Lac is a new example of the morphological type
termed "double-contact'' by Wilson.
of 6000 K. V360 Lac is a new example of the morphological type
termed "double-contact'' by Wilson.
(3) Rapid rotation of the primary star, plausibly produced by mass transfer from the secondary,
leads to reduced equatorial gravity. Associated gravity darkening produces a 9000 K lower
equatorial
![]() than at the pole. The lower equatorial gravity
permits detectable
tidal distortion of the primary star by the secondary star as well as detectable irradiative
heating by the
secondary star.
than at the pole. The lower equatorial gravity
permits detectable
tidal distortion of the primary star by the secondary star as well as detectable irradiative
heating by the
secondary star.
(4) A variety of observations indicate the presence of circumstellar matter moving with the primary star.
(5) Synthetic spectra closely fit an ![]() spectrum and
accurately fit both blue and red
rectified spectra. The synthetic spectra fully allow for gravity darkening and tidal and
rotational distortion of both stellar components.
The
spectrum and
accurately fit both blue and red
rectified spectra. The synthetic spectra fully allow for gravity darkening and tidal and
rotational distortion of both stellar components.
The ![]() spectrum fit indicates a system
distance of approximately 500 pc,
about 2
spectrum fit indicates a system
distance of approximately 500 pc,
about 2![]() beyond the Hipparcos distance.
beyond the Hipparcos distance.
Acknowledgements
We acknowledge the use of Hadrava's programs KOREL and FOTEL and thank Dr. Hadrava for his advice how to use KOREL in more complicated situations. The use of the computerized bibliography from the Strasbourg Astronomical Data Centre is also gratefully acknowledged. Research of PH and MW was supported from the research plan J13/98: 113200004 of Ministry of Education, Youth and Sports. P. Harmanec, P. Koubský P. Skoda and M. Slechta were also supported from the research plans AV 0Z1 003909, 0030501 and project K2043105 of the Academy of Sciences of the Czech Republic. At later stages, this research was supported from the grants GA CR 102/02/1000, GA CR 205/03/0788 and GA CR 205/06/0304 of the Granting Agency of the Czech Republic. The stay of PK at DAO was supported by a grant through the NATO Science Fellowship Programme. PH, PE, MW and JL also acknowledge the support from the Czech-Mexican KONTAKT ME402(2000)/CONACyT E130.734 collaborative project.
We thank the anonymous referee for extensive comments which greatly improved the presentation of this paper.