M. Tafalla¹ - J. Santiago-García¹ - P. C. Myers² - P. Caselli^2,3 - C. M. Walmsley³ - A. Crapsi⁴

1 - Observatorio Astronómico Nacional, Alfonso XII 3, 28014 Madrid, Spain
2 - Harvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge, MA 02138, USA
3 - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
4 - Leiden Observatory, P.O. Box 9513, 2300 RA Leiden, The Netherlands

Abstract
Context. Low mass starless cores present an inhomogeneous chemical composition. Species like CO and CS deplete at their dense interiors, while N₂H⁺ and NH₃ survive in the gas phase. As molecular line observations are used to determine the physical conditions and kinematics of the core gas, chemical inhomogeneities can introduce a serious bias.
Aims. We have carried out a molecular survey towards two starless cores, L1498 and L1517B. These cores have been selected for their relative isolation and close-to-round shape. They have been observed in a number of lines of 13 molecular species in order to determine a self-consistent set of abundance profiles.
Methods. In a previous paper we modeled the physical structure of L1498 and L1517B. Here we use this work together with a spherically-symmetric Monte Carlo radiative transfer code to determine the radial profile of abundance for each species in the survey. Our model aims to fit simultaneously the radial profile of integrated intensity and the emerging spectrum from the core center.
Results. L1498 and L1517B present similar abundance patterns, with most species suffering a significant drop toward the core center. This occurs for CO, CS, CH₃OH, SO, C₃H₂, HC₃N, C₂S, HCN, H₂CO, HCO⁺, and DCO⁺, which we fit with profiles having a sharp central hole. The size of this hole varies with molecule: DCO⁺, HCN, and HC₃N have the smallest holes, while SO, C₂S and CO have the largest holes. Only N₂H⁺ and NH₃ seem present in the gas phase at the core centers.
Conclusions. From the different behavior of molecules, we select SO, C₂S, and CH₃OH as the most sensitive tracers of molecular depletion. Comparing our abundance determinations with the predictions from current chemical models we find order of magnitude discrepancies. Finally, we show how the "contribution function'' can be used to study the formation of line profiles from the different regions of a core.

Key words: ISM: abundances - ISM: clouds - ISM: molecules - stars: formation - ISM: individual objects: L1498 - ISM: individual objects: L1517B

1 Introduction

Recent observations and modelling of low-mass starless cores show that a number of molecular species deplete from the gas phase at the dense interior of these simplest star-forming regions (Kramer et al. 1999; Tafalla et al. 2002; Kuiper et al. 1996; Bergin et al. 2001; Bacmann et al. 2002; Pagani et al. 2005; Willacy et al. 1998; Caselli et al. 1999; Alves et al. 1999). The depletion of molecules in the pre-stellar material has important consequences for the study of the initial conditions of stellar birth. Molecular emission is routinely used to trace the physical properties and the kinematics of the star-forming gas, so the removal of certain species from the gas phase introduces a potential distortion in molecular line observations. Depletion, in addition, systematically increases with time and gas density. Thus, if properly understood, it can provide a reliable clock to time the contraction history of dense cores. Understanding the chemical composition of starless cores has therefore become necessary to reconstruct the earliest phases of low-mass star formation.

Previous studies of core chemical composition show that molecular depletion is a highly selective process. Molecules like CO and CS disappear rapidly from the gas phase, while species like N₂H⁺ and NH₃ survive much longer at high densities (see references above). As a result of this behavior, a core gradually develops a differentiated interior characterized by a center rich in depletion-resistant species surrounded by layers richer in depletion-sensitive molecules. Understanding this abundance pattern is critical to interpret molecular line observations of cores because different species will systematically trace different layers depending both on their response to depletion and their level excitation.

Chemical models already provide an indication of how the different molecular species will be distributed inside a core, but systematic molecular surveys are still needed to obtain a realistic picture of the core chemical composition. Such surveys should be carried out toward starless cores of simple geometry, so the abundances of the different species can be unambiguously derived from observations. In this paper, we present a survey toward two Taurus-Auriga cores, L1498 and L1517B. These two cores are reasonably isolated and present close to round shapes when observed in the millimeter continuum, so they constitute ideal targets for a systematic study. In Tafalla et al. (2004) (Paper I hereafter), we used millimeter continuum data together with C¹⁸O, CS, N₂H⁺, and NH₃ line observations of these cores to derive their radial profiles of density, temperature, turbulent linewidth, and line-of-sight velocity. Now we complement this study with additional observations of a number of molecules, and use the already derived physical models of the cores to determine in a self consistent manner the radial abundance distribution of 13 molecular species.

In the following sections, we present the details of our radiative transfer modeling of the observed lines and the set of abundance profiles derived from this analysis (Sect. 4). Using these abundances, we study the differences and similarities between the two cores, as well as their chemical relation with other cores of well determined abundances (Sects. 5.1-5.3). We also use our data to test core chemical models, in particular the recent work by Aikawa et al. (2005) (Sect. 5.4), and to study the different sensitivity of molecules to depletion (Sect. 5.5). We finish using our chemical determinations and the radiative transfer modeling to study how the different molecular lines originate at the core interior and therefore reflect (or miss) its internal structure when used to trace the core gas (Sect. 5.6). For this analysis we use as a tool the contribution function.

2 Observations

We observed L1498 and L1517B with the IRAM 30m telescope during several runs between 1999 October and 2002 November. We made maps of these cores in the lines shown in Table 1, always observing in frequency switching mode with several receivers simultaneously and a typical sampling of 20''. As a backend, we used a facility autocorrelator that provided a typical velocity resolution of 0.03-0.04 km s^-1. During the observations, the telescope pointing was corrected making frequent cross scans of bright continuum sources, and the atmospheric attenuation was calibrated observing ambient and liquid nitrogen loads. The telescope intensity scale was converted into main beam brightness temperature using standard efficiencies. The FWHM of the telescope beam varied with frequency from 27.7'' at 90 GHz to 11'' at 230 GHz.

We observed L1498 and L1517B in HCO⁺(1-0), H¹³CO⁺(1-0), and HCN(1-0) with the FCRAO 14m telescope in 2001 April. We used the QUARRY array receiver in frequency switching mode together with the facility correlator, which provided a velocity resolution between 0.03 and 0.07 km s^-1. Observations of SiO masers were used to correct the telescope pointing, and an ambient load was used to calibrate the atmospheric attenuation. An efficiency of 0.55 was used to convert the telescope units into mean beam brightness temperature. The typical sampling of the maps was 30'', and the FWHM of the telescope beam at 86-89 GHz was approximately 55''.

**Table 1:** Observed lines and rest frequencies used in this work.
$\begin{table}\begin{displaymath} \begin{array}{lcrrc} \hline \noalign{\smallsk... ...S; (5) JPL; (6) \citet{sch04}; (7) \citet{cas05}; (8) \citet{yam90}. \end{table}$

For the detailed line modeling presented here, accurate rest frequencies are required. We have searched for such frequencies using on-line compilations like the Cologne Database for Molecular Spectroscopy (CDMS, Müller et al. 2001) and the JPL Catalog (Pickett et al. 1998). In most cases, the CDMS and JPL frequencies are consistent with each other, so we have chosen the one quoted as having smaller uncertainty (where possible, we have referred to the original determination). For HCO⁺, however, the values in the two catalogs are inconsistent, probably due to the difficulty measuring frequencies in ions, and we have preferred the JPL value for its better agreement with our line data. For some transitions of CH₃OH and SO, no accurate frequencies were found, and we have determined them by fitting our L1498 spectra assuming an LSR velocity of 7.80 km s^-1 (as measured from the other lines). Fortunately, these few spectra present Gaussian lines, so the astronomical determination is likely to be accurate (about 20 kHz). A summary of the frequencies used in this work is presented in Table 1.

$\begin{figure} \par\resizebox{15.8cm}{!}{\includegraphics{5311fig1.eps}} \end{figure}$

Figure 1: Integrated intensity maps from our molecular survey of L1498. The two top left panels show the 1.2 mm continuum and N₂H⁺(1-0) data presented in Paper I. In contrast with these centrally concentrated distributions, the other molecular-line maps are ring-like or centrally-depressed, and have relative minima at the 1.2 mm/N₂H⁺ peak. This is an indication of a central drop in the abundance of most species (see text). Both IRAM 30 m and FCRAO maps have been convolved with a Gaussian beam of 20-30 arcsec to filter out high-frequency noise, and for all lines, the contours are at 15, 30, ... percent of the peak intensity (peak intensity in K km s^-1 is indicated on the top right corner of each panel). To better compare the survey line maps with the N₂H⁺(1-0) emission, the contour at 75% of the peak is superimposed in red. The dots indicate the original map sampling. Central coordinates are $\alpha_{1950}=4^{\rm h}7^{\rm m}50\hbox{$.\!\!^{\rm s}$ }0$ , $\delta_{1950}=25\degr02'13\hbox{$.\!\!^{\prime\prime}$ }0$ .

3 Overview of the molecular emission

In Figures 1 and 2 we present the integrated intensity maps of all the lines observed toward L1498 and L1517B together with maps of the dust continuum emission and N₂H⁺(1-0) already analyzed in Paper I. For each line, the integrated intensity map reflects the combined effect of excitation, optical depth, and molecular abundance, so its interpretation requires detailed radiative transfer modeling. Even without such an analysis we can appreciate the need for strong abundance variations by noting that most lines are not very optically thick and that their excitation increases with density toward the dust continuum peak. Thus, if the abundance of a molecule were spatially constant, its emission map would present a well-defined maximum at the dust peak. Although this occurs for N₂H⁺ (whose abundance is close to constant, Paper I), it is not the case for the rest of the species.

In the larger and better resolved L1498 core, the maps of C₃H₂, H₂CO, CH₃OH, SO, HCO⁺ (plus isotopes), HCN (plus isotope), HC₃N, and C₂S all present distributions that differ from the centrally concentrated dust or N₂H⁺. In a few species, like CH₃OH, SO, and H₂CO, the emission forms an almost-complete ring around the dust peak. In others, the emission presents discrete peaks, especially to the SW and NE of the dust peak, reminiscent of a broken ring. Such ring-like distributions are also seen in C¹⁸O and CS, and in Paper I it was shown that they reflect the presence of a central depletion hole (see also Kuiper et al. 1996; Willacy et al. 1998). The maps in Fig. 1 show now that depletion holes must be the rule for most species in L1498.

For the more compact L1517B core, the pattern of line emission is similar to that in L1498, although less distinct for some species because of angular resolution. In this core, most molecules present a single emission peak offset to the west from the dust/N₂H⁺ peak, being the most extreme example that of SO. This pattern is again similar to that found in C¹⁸O and CS (Paper I), and for the same reasons as in L1498, it requires a central depletion hole.

A simple inspection of the maps in Figs. 1 and 2 shows that different molecular species have depletion holes of different sizes. Using again the larger L1498 core as a reference, we note that CH₃OH presents a rather prominent hole, while DCO⁺ has a central depression barely resolved by our observations. This variety of hole sizes most likely arises from the different sensitivity to depletion of the different species and from the complex chemical changes resulting from the freeze out of CO, the main source of carbon in the gas phase. The freeze out of CO decreases the abundance of the different C-bearing species by different degree, while it enhances the abundance of deuterium-bearing species (Dalgarno & Lepp 1984). In Sect. 5.2 we will present a quantitative comparison of hole sizes using the results of a radiative transfer analysis.

Given the large effect of depletion in the maps of Figs. 1 and 2, it seems clear that in most species the shape of the emission reflects more the chemical composition of a core than its true physical structure. As chemical inhomogeneities seem the rule in starless cores, this high sensitivity to chemistry of the maps should be carefully considered when deriving physical properties from observations of line emission. The risk of overlooking it is graphically illustrated by the maps of L1498 in species like CH₃OH, SO, or C₃H₂. These maps show highly fragmented distributions with multiple peaks along an approximately elliptical shell, and a naive interpretation of the emission peaks as distinct physical structures would lead to a picture of a highly clumped core. This is of course in contradiction with the the distribution of the most reliable tracers (1.2 mm dust continuum, N₂H⁺, and NH₃), which shows that the core is smooth and centrally concentrated. Any correspondence between map peaks and core substructure, therefore, requires careful consideration core chemistry and a self consistency check using multiple species. The traditional warning against the use of optically thick tracers to infer physical properties of cores should now be expanded to avoid using depletion-sensitive species for the same purpose. Comparing in Figs. 1 and 2 the similar maps of thick and thin tracers like HCO⁺ and H¹³CO⁺ (also HCN and H¹³CN) with the distinct distributions of N₂H⁺ and the dust continuum, we see that the danger of using depletion-sensitive molecules can sometimes exceed that of using thick or even self-absorbed tracers.

4 Abundance analysis

To improve the qualitative abundance analysis of the previous section we need to model the emission of the observed species. Modeling this emission requires first determining the physical structure of each core and then following the transfer of radiation. For the first step, we make a physical model of the core that describes its density, temperature, and gas motions, and we do so assuming spherical symmetry because of the close-to-round shape of the continuum maps. Once the core is modeled, it becomes like a laboratory of known physical conditions where the line intensities can be inverted into abundance estimates. For this second step, we use a non-LTE Monte Carlo code that solves numerically the transfer of the line emission. The details of these two steps are described in the next section.

4.1 Core physical model and Monte Carlo radiation transfer

The physical models of L1498 and L1517B were derived in Paper I from the simultaneous fit of the dust continuum, C¹⁸O/C¹⁷O, CS/C³⁴S, N₂H⁺, and NH₃ emissions. These data constrain the core density, temperature, and kinematics, and here we use the same parameterization for consistency. As mentioned in Paper I, we search for the simplest expressions consistent with the data. We select the core center from the continuum emission, and fit the radial profile of this emission assuming a density profile of the form

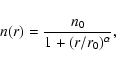
To solve the radiative transfer inside each core we also assume spherical symmetry. In Paper I we saw that the maps of C¹⁸O and CS are not circularly symmetric, in contrast with the maps of more reliable tracers like the mm continuum, N₂H⁺, and NH₃. Figures 1 and 2 show now a similar situation for the species of our survey: in L1498 the emission is systematically brighter towards the SE (some species present a secondary maximum toward the NW), and in L1517B the western half of the core is brighter than the eastern half. These distributions suggest that the abundance of most species is not spherically symmetric, despite the symmetric gas distribution inferred for the two cores. As studied in Paper I, the deviations seem correlated with the velocity of the gas, and this can be understood as the result of differential depletion caused by a non spherical contraction of the cores. Modeling these asymmetric distributions requires a 2D or even 3D radiative transfer code, which exceeds the scope of this paper. In the following discussion we assume spherical symmetry and fit for each species a circular average of the emission. In this way, our abundance estimates represent azimuthal averages over the core and therefore correspond to the result of a mean contraction.

As in Paper I, we solve the radiative transfer inside each core with the non-LTE Monte Carlo code of Bernes (1979), which we have modified to include additional molecules (see Appendix A for a summary of the molecular parameters used in this work). For each molecular species, we run the code together with the core physical model to produce a set of expected intensity distributions for different abundance profiles. These intensity predictions are convolved with the appropriate Gaussian beam and compared with the observed radial profile of integrated intensity and the central emerging spectrum for as many transitions of the species as we have observed (usually two); the best fit model is the one that fits all these constraints simultaneously. As the only free parameter in this process is the abundance profile, observations of one transition are in principle enough to constrain the solution. Fitting at least two transitions simultaneously, as we do, checks the self-consistency of the process.

$\begin{figure} \par\resizebox{14.5cm}{!}{\includegraphics{5311fig3.eps}} \end{figure}$

Figure 3: Radial profiles of integrated intensity and central spectra for all line data observed toward L1498. The squares in the radial profiles and the histograms in the spectra are observed data while the lines represent Monte Carlo model results. The blue dashed lines are models that assume a constant abundance chosen to fit the data at a relatively large fiducial radius (see text), and the red solid lines are the prediction from the best fit model. Note how the constant abundance models over predict the central intensity typically by a factor of 2 or more. The integrated intensities in the radial profiles ( left panels) have a typical 1- $\sigma$ uncertainty of 0.01-0.02 K km s^-1 for the IRAM data (with the exception of the high frequency lines HCN(3-2) and HCO⁺(3-2), which have 1- $\sigma$ uncertainties of 0.06 and 0.09 K km s^-1), 0.02-0.065 K km s^-1 for the FCRAO data, and 0.09 K km s^-1 for the 100 m data. These values are smaller than the internal point-to-point scatter. The spectra in the right panels have been generated from the average of typically 5 spectra within a 20'' radius from the core center (50'' for FCRAO data), in order to produce a relatively high S/N observation. To model this observation, we have generated synthetic spectra for each of the (typically 5) observed radial locations, and we have averaged them as we have done with the data.

4.2 Fitting procedure

As when fitting the core physical parameters, we aim for the simplest abundance profiles consistent with the data. For each species, we start with a constant abundance model that fits the integrated intensity at a fiducial outer radius. This radius is chosen as 75'' for L1498 and 55'' for L1517B and represents a compromise between the need of a large enough radius (to detect central molecular depletion) and the need of a bright enough signal (to make a reliable fit). As shown by the dashed lines in Figs. 3 and 4, the constant abundance models systematically overestimate the intensity toward the core center.

To improve the fit, we decrease the abundance toward the core center by introducing a step-function at $r_{\rm h}$ . The abundance inside $r_{\rm h}$ is taken to be negligible (10^-4 of the outer abundance), and the value of $r_{\rm h}$ is used as a free parameter to improve the quality of the fit. This is the same approach used in Paper I to derive abundance profiles for C¹⁸O and CS, and for most species, it provides a reasonable fit. In a few cases, a slightly different parameterization is needed, and these exceptions are detailed below.

Parameterizing the abundance profiles with a step function is clearly a simplification of the expected depletion behavior of molecules under realistic core conditions (e.g., Aikawa et al. 2005; Bergin & Langer 1997). However, given the fast abundance drops predicted by these models and the finite spatial resolution of our observations, this parameterization is almost as good a description, and it has the advantage of allowing an easy comparison between molecules by comparing the outer abundance and $r_{\rm h}$ values of their fits. In Sect. 5 we will use this approach to study different aspects of the behavior of molecules under high density conditions. In the following paragraphs, we present further details on the fitting procedure of each individual species. Readers not interested in such a detailed view can simply inspect Figs. 3 and 4 and move to Sect. 5.

CH $_{\mathit3}$ OH. Two transitions were observed for each of the A and E forms of this molecule, so we have fitted the two forms independently and determined E/A ratios of 1 for both L1498 and L1517B. As Figs. 3 and 4 show, the constant CH₃OH abundance models fail to fit the central intensity by about a factor of 2, while the models with a central hole provide reasonable fits to all data simultaneously.

SO. SO is the only non C-bearing molecule observed in this survey (N₂H⁺ and NH₃ were studied in Paper I), so its behavior provides information complementary to that of all other species. Three SO transitions were observed toward L1498 and L1517B, but the SO( $\rm JN=12$ -21) line was not detected in either core. Our fits therefore only take into account the emission from SO(32-21) and SO(43-32), as the 12-21 non detection is trivially fitted by all models. Again, the constant abundance models fail to fit the observed SO intensity toward the core centers by a wide margin. Models with a central hole, on the other hand, reproduce the intensities both at large and small radius, and show that this species is one of the most sensitive indicators of molecular depletion (Sect. 5.5).

HC $_{\mathit3}$ N. In L1498, the model with constant HC₃N abundance does not reproduce the observed combination of compact emission and a central hole. Such a pattern requires that the HC₃N abundance increases inwards at intermediate radii, and that it has a sharp depletion hole near the core center. We fit this behavior by introducing an inward jump in the abundance by a factor of 10 at $r = 1.8 \times 10^{17}$ cm (85'' at 140 pc) together with the step central hole used for the other species. This type of profile fits well both the J=4-3 and 10-9 data (Fig. 3), together with the central 12-11 spectrum (not shown). It also agrees with the prediction of the chemical model by Ruffle et al. (1997), who find a late-time HC₃N peak caused by CO depletion. In L1517B the situation is less clear due to the smaller size of this core. A constant abundance model barely fits the data and is inconsistent with the lopsided emission seen in the 4-3 map. To improve the fit, we have introduced a central hole with a small radius ( $r = 4 \times 10^{16}~{\rm cm} = 20''$ ) and a factor of 2 outer abundance drop at $r = 1.25 \times 10^{17}$ cm (60''). This small inner hole, at the limit of our resolution, is consistent with the smaller-than-average hole found in L1498. As will be further discussed in Sect. 5.2, HC₃N seems to survive in the gas phase to higher densities than other species.

C $_{\mathit3}$ H $_{\mathit2}$ . In L1498, C₃H₂ presents the same combination of compact emission and central hole seen in HC₃N. A constant abundance model that reproduces the emission at intermediate radii fails to fit the observations both at large and small radii (Fig. 3). As with HC₃N, we introduce a factor of 10 inward jump in the abundance at $r = 1.8 \times 10^{17}$ cm together with a central hole. This model fits well the emission, including the slightly self-absorbed 2₁₂-1₀₁spectrum towards the core center (Fig. 3). We note that although there are no theoretical predictions for a late-time enhancement of C₃H₂ (Ruffle et al. 1997, do not present results for this species), the chemistry of C₃H₂ and HC₃N seem related (e.g., Cox et al. 1989). It is therefore possible that a single process explains the observed behavior of the C₃H₂ and HC₃N in L1498. Unfortunately, only one C₃H₂ transition was observed toward L1517B. Lacking the brighter 2₁₂-1₀₁transition, we have fitted the C₃H₂ abundance in this core with only a central hole and no abundance jump at intermediate radii. Observations of additional lines of this molecule are needed to clarify the behavior of C₃H₂ in L1517B.

C $_{\mathit2}$ S. Only the $\rm JN=67$ -56 transition was observed toward both cores and, as Figs. 3 and 4 show, its radial distribution is inconsistent with a constant abundance profile. A model with a central abundance hole fits the emission both at large and small radii in both cores and shows that, like SO, C₂S is highly sensitive to depletion. Our model for L1498 also fits nicely the emission of the $\rm JN=21$ -10 (22 GHz), 43-32 (45 GHz), and 87-76 (94 GHz) lines observed by Wolkovitch et al. (1997), who with Kuiper et al. (1996), first found central depletion for this molecule. A detailed comparison with these published data is presented in Appendix C.

HCN and H $^{\mathit{13}}\!$ CN. The HCN(1-0) spectra show evidence for self absorption towards both L1498 and L1517B (see also Sohn et al. 2004). The HCN emission is therefore dominated by the core outer layers and it cannot be used to derive an abundance profile inside the core. We thus base our abundance determination on the thinner H¹³CN(1-0) emission, which clearly shows a need for a central abundance drop in both cores. As in Paper I, we assume a ¹²C/¹³C ratio of 60, and we model the main isotope emission by scaling the H¹³CN abundance profile by that factor. This produces a fit of the HCN(3-2) emission in both cores but underestimates slightly the depth of the 1-0 self absorptions. To improve the fit, we introduce in the constant density envelope that surrounds each core ( $r > 4 \times 10^{17}$ cm) an abundance enhancement of a factor of 4 in L1498 and a factor of 2 in L1517B (the enhancement has no effect on the H¹³CN emission or even on the 3-2 line). It should be noted that $r > 4 \times 10^{17}$ cm corresponds to radii larger than 190'', which are outside the region where our dust-based determination of the density is reliable. For that reason, the outer abundance enhancements should be considered a fitting convenience that corrects the simple core+envelope model that we have used in the Monte Carlo radiative transfer, and not necessarily an indication of an abundance change in the outer core. It is in fact remarkable that such a simple parameterization can simultaneously fit both the radial profiles and the central spectra of lines with such different optical depths as H¹³CN(1-0), HCN(1-0), and HCN(3-2) (Figs. 3 and 4).

H $_{\mathit2}$ CO. Our two H₂CO lines, 2₁₂-1₁₁ and 2₁₁-1₁₀, show evidence for self-absorption and, unfortunately, no thin isotopologue of this species was observed in the survey. Despite this, constant abundance models can be easily ruled out from the shape of the radial profiles, and a central abundance drop is needed to fit simultaneously the inner and outer emission. To properly model the self absorption, we need again an abundance increase in the envelope (r > 190'', and factors 15 and 5 for L1498 and L1517B, respectively), to which the same caveats mentioned for HCN apply. Young et al. (2004) have observed two additional lines towards L1498 (1₁₁-1₁₀ and 3₁₂-2₁₁) and have also concluded that a central abundance drop is needed to fit the data. As shown in Appendix C, our best fit model also fits the H₂CO(3₁₂-2₁₁) data from Young et al. (2004), while it predicts a 1₁₁-1₁₀self-absorption that is weaker than observed. This 1₁₁-1₁₀ absorption originates at the core outer envelope (Appendix C), so the failure in the fit results again from our simplified parameterization of the core outer layers.

HCO⁺, H $^{\mathit{13}}\!$ CO⁺. Both the J=1-0 and 3-2 transitions of HCO⁺ are deeply self absorbed, so our abundance determination relies on the thinner H¹³CO⁺(1-0) line and assumes again a ¹²C/¹³C ratio of 60. As in all other species, a central drop in the HCO⁺abundance is needed to fit the shape of the radial profiles. To fit the HCO⁺ self absorption, we again need to include an outer envelope (r> 190'') abundance enhancement of a factor of 4 in the L1498 model (still the predicted 1-0 line is brighter than observed mostly due to poor modelling of the red component) while no abundance enhancement is needed for L1517B.

DCO⁺. A central abundance hole is also required to fit the DCO⁺ data, but its radius is smaller than the HCO⁺ hole radius. This difference most likely results from a central increase in the deuterium fractionation caused by the CO depletion (e.g., Caselli et al. 1999), which partly compensates the DCO⁺ freeze out at the inner core. The effect is of course incomplete because the DCO⁺ abundance end ups falling at the highest densities. Still, the presence of DCO⁺ inside the CO and HCO⁺ depletion holes suggests that a small amount of CO and HCO⁺ survives at high densities. Comparing the DCO⁺ and HCO⁺ abundances in the outer core, we derive deuteration ratios of 0.02 and 0.03 in the outer layers of L1498 and L1517B, respectively. Each of these values is a factor of 2 lower than the deuteration ratios measured toward the inner core by Crapsi et al. (2005) using N₂H⁺ and N₂D⁺, in good agreement with the expectation of a degree of deuteration that increases toward the core center.

Although the abundance enhancements at large radii required to fit the self absorptions in HCN, H₂CO, and HCO⁺need confirmation using a model of the large-scale structure of the cores, we note that such enhancements are not totally unexpected. Absorption line studies by Lucas & Liszt (1996) and Liszt & Lucas (2001) reveal that species like H₂CO, HCO⁺, and HCN present large column densities in diffuse clouds (but not N₂H⁺, for example). It is therefore possible that the lower density gas surrounding L1498 and L1517B has a chemical composition similar to the diffuse clouds studied by Liszt & Lucas. This would naturally explain the large amounts of low-excitation gas needed to produce the observed self absorptions.

4.3 Ortho-to-para and isotopic ratios: total abundances

For species like NH₃, H₂CO, and C₃H₂, our observations and modeling only determine the abundance of the ortho or para form of the molecule, and we need to assume an ortho-to-para ratio (OPR) to convert our estimate into a total molecular abundance. This OPR depends on the formation history of the molecule, and is therefore somewhat uncertain. Here we assume that the three species are formed by gas-phase reactions, because grain production will require a mechanism to release the products to the gas phase, a difficult task given the strong freeze out observed. (This of course does not imply that NH₃, H₂CO, and C₃H₂ do not form on dust grains, but that the gas-phase chemistry is separate from the dust-grain production, as seen in the models of, e.g., Aikawa et al. 2005.) If this is the case, the OPR should be close to the high-temperature limit, because the energy difference between ortho and para forms (2.4 K for C₃H₂, 15.2 K for H₂CO, and 23.4 K for NH₃) is significantly lower than the energy released during molecule formation (e.g., Dickens & Irvine 1999). Indeed, OPRs close to 3 (high temperature limit) have been found for H₂CO in starless cores, including L1498, by Dickens & Irvine (1999). Takakuwa et al. (2001) measure a C₃H₂ OPR of 2.4 towards TMC1, also close to the high temperature limit. We thus assume OPRs of 3 for H₂CO and C₃H₂ and 1 for NH₃.

In addition to OPRs, we need to assume isotopic ratios to convert rare isotopologue abundances into main species values. Along this paper and in Paper I we have used the standard isotopic ratios of ¹²C/¹³C = 60, ³²S/³⁴S = 22, and ¹⁸O/¹⁷O = 3.65, to which we now add the terrestrial ¹⁶O/¹⁸O ratio of 500. Using these values, we estimate the final main isotopologue abundances presented in Table 2. In the following discussion we will refer only to the main molecular forms, although it should be remembered that most abundances are based on the rare (and optically thin) isotopologues.

**Table 2:** Molecular abundances with respect to H₂
$\begin{table}\begin{displaymath} \begin{array}{lccccc} \hline\hline \noalign{\... ...98) and 2 (L1517B) enhancement for $r > 4 \times 10^{17}$ ~cm. \par\end{table}$

Finally, we stress the dependence of our abundance estimates on the assumed dust parameters. As mentioned in Paper I, the values of the dust temperature and emissivity are still poorly known (e.g., Bianchi et al. 2003; Kramer et al. 2003), and their uncertainty propagates into the determination of the gas density profile and total core column density. These determinations, in turn, affect the abundance estimates through their combined effect on the level excitation and the H₂ column density. For most species, the abundance estimate uses optically thin lines from low-energy levels, so the effect of the density on the excitation is smaller than its effect on the column density. Thus, to first order, we can correct for dust parameter changes with the following simple equation:

5 Discussion

5.1 Comparison between L1498 and L1517B

$\begin{figure} \par\resizebox{8.8cm}{!}{% \includegraphics{5311fig5.eps}} \end{figure}$

Figure 5: Abundance comparison between L1498 and L1517B. Top: ratio between the abundances outside the central hole (X₀) in the two cores (for HC₃N and C₃H₂, X₀ is the abundance between the hole and the outer cutoff). For most species, this ratio is close to 1 (within a factor of 2), indicating a similar pre-freeze out composition. Bottom: ratio between central depletion holes ( $r_{\rm h}$ ). L1498 presents systematically larger hole ratios by a factor of about 1.5, which is consistent with the visual impression from the integrated maps.

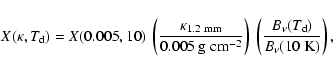
L1498 and L1517B present similarities and differences in their physical properties. They have almost the same kinetic temperature, level of turbulence, and total gas column density, while they differ by a factor of 2 in central density and half maximum density radius (Paper I). Analogously, the two cores present similarities and differences in their chemical composition. To examine them here, we compare the X₀ and $r_{\rm h}$ values derived for the different species.

The top panel of Fig. 5 shows the ratio between the outer molecular abundances derived in L1498 and L1517B for each molecule in our survey (values for C¹⁸O, CS, N₂H⁺, and NH₃ are from Paper I). As can be seen, there is good agreement between the X₀ parameters estimated for the two cores, with most differences being smaller than a factor of 2. The main outliers in the plot are C₂S (4 times more abundant in L1498 than in L1517B) and C¹⁸O (3 times more abundant in L1517B), and although their abundance differences could be real, it should be noted that their X₀ determination is specially prone to error: C₂S is depleted up to such a large radius in L1498 that X₀ is determined using very limited information of the outer core, and the X₀ value for C¹⁸O can be contaminated by the extended emission from the ambient cloud. Given these and other uncertainties, it is rather remarkable that most X₀ values agree within less than a factor of two, and we take this fact as an indication that the two cores share very similar molecular compositions in their outer (undepleted) layers.

The bottom panel of Fig. 5 presents a comparison between the radius of the central abundance holes in L1498 and L1517B. In addition to some scatter, the figure reveals a trend for $r_{\rm h}$ to be larger in L1498 by a factor of about 1.5. This trend agrees with the impression from the maps of Figs. 1 and 2 that L1498 has a larger depletion hole than L1517B for most or all molecular species. Unfortunately, the scatter and the uncertainties in the analysis make it impossible to determine whether the $r_{\rm h}$ ratio varies with molecule.

The similar outer abundances of L1498 and L1517B suggest that both cores have contracted from ambient gas with similar initial compositions. It is unclear however whether the different $r_{\rm h}$ values result from the cores being at different evolutionary stages or from them having followed different contraction paths. L1517B is more centrally peaked, denser at the center, and more circularly symmetric than L1498, so it would seem to be at a more advanced evolutionary stage. If this is the case, and both cores are following the same contraction path, the smaller $r_{\rm h}$ of L1517B would imply that the depletion hole in a core shrinks as it contrasts; this could result from the contraction time scale being shorter than the freeze out time scale during the late stages of contraction. Alternatively, L1517B may have contracted faster than L1498, so its central gas has had less time to freeze out. Further studies of core composition using a larger sample of systems are needed to clarify this important issue.

5.2 Comparison between molecules

$\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{5311fig6.eps}} \end{figure}$

Figure 6: Normalized radius of the abundance hole $r_{\rm h}$ for all molecules in the survey. The red squares represent L1498 data and the blue triangles are L1517B data (normalizing radius is $1.04 \times 10^{17}$ cm for L1498 and $0.66 \times 10^{17}$ for L1517B). Species like CO, SO, and C₂S present larger $r_{\rm h}$ values, while HC₃N, DCO⁺, and HCN have smaller $r_{\rm h}$ values and therefore must remain in the gas phase to higher densities.

The radiative transfer results of Table 2 suggest that different molecules deplete at different radii. In addition to the extreme behavior of N₂H⁺ and NH₃, which do not present abundance holes, several molecules have holes that are systematically smaller or larger than average in both L1498 and L1517B. Identifying these molecules can help better understand the details of depletion. It can also provide a set of tracers to selectively sample cores at different depths.

To compensate for the systematically larger holes in L1498, we normalize the hole radii. We do this by dividing the radius of each species by the average hole radius in the core, which is calculated from the mean radius of all species with small dispersion (i.e., we exclude CO and CS, see below, in addition to N₂H⁺ and NH₃). This normalized hole radius is presented in Fig. 6 for all species in our survey. As the figure illustrates, the hole radii span a range of about a factor of 2. The CO and CS estimates present large scatter, which could result from a real difference between the cores or from artifacts like contamination by the extended cloud in the case of CO and the fact that L1498 the CS analysis is based on the optically thin C³⁴S emission while the analysis in L1517B used the thicker CS line (as C³⁴S was too weak). All other species, on the other hand, present a reasonably low scatter between their L1498 and L1517B results. This low scatter allows distinguishing between species with relatively large and small depletion holes. In the first group we find SO, C₂S, and CH₃OH, which in both cores have larger-than-average abundance holes. In the second group we find HC₃N, DCO⁺, and HCN, whose central holes are more than 50% smaller than the holes in the first group. Such a relatively large difference in $r_{\rm h}$ suggests a corresponding difference in the depletion behavior of these species. It also shows that HC₃N, DCO⁺, and HCN survive in the gas phase up to higher densities than most other species, and this makes them interesting line tracers of the middle layers of dense cores. Recent infall searches in starless cores (Lee et al. 2004; Sohn et al. 2004), do use this property of DCO⁺ and HCN to penetrate deeper than using traditional tracers like CS or HCO⁺ (e.g., Lee et al. 2001). Our L1498 and L1517B analysis, however, shows that HCN and DCO⁺ are no substitute for N₂H⁺ or NH₃, as they end up depleting at densities of about 10⁵ cm^-3.

5.3 Comparison with other starless cores

TMC1 is the core whose chemical composition has been studied with most detail, and its abundances are commonly used as standards for comparison with other low-mass star-forming regions. Current estimates of the TMC1 abundances, however, do not consider the effect of molecular depletion, so a comparison with our L1498 and L1517B estimates can only be approximate. Until a more realistic analysis of TMC1 is available, the most complete study is that of Pratap et al. (1997), who have presented FCRAO observations and analysis of more than a dozen molecular species, 8 of them common to our L1498/L1517B survey. Pratap et al. (1997) normalize their abundances to HCO⁺, and provide values for three positions along the TMC1 filament: the cyanopolyyne peak, the ammonia peak, and the SO peak. To compare with these values, we select the L1498 and L1517B abundances outside the depletion hole and normalize them to HCO⁺. The resulting values agree well with those of TMC1, and in no case the difference exceeds one order of magnitude. The best agreement occurs for the cyanopolyyne peak, where the average ratio between the L1498 and TMC1 abundances for the 8 species is $1.3 \pm 1$ . This position also provides the best match to the L1517B abundances, although the ratio is significantly larger ( $2.3 \pm 2$ ) because our estimate of the HCO⁺ in L1517B is half of that in L1498. Given the very different methods and the uncertainties in the two analysis, the agreement with the TMC1 estimates seems rather good. The fact that the best match to the abundance in the undepleted outer parts of L1498 and L1517B occurs for the cyanopolyyne peak is also in good agreement with the interpretation that this TMC1 position is the most chemically young of the filament (Hirahara et al. 1992; Suzuki et al. 1992). It also suggests that the abundances of TMC1 are not anomalously high (Howe et al. 1996), but representative of the population of dense cores in the Taurus cloud.

A different set of abundance determinations in starless cores has been recently provided by the Texas group using a technique similar to ours: density estimates using continuum (SCUBA) data followed by Monte Carlo modeling of the line emission (Lee et al. 2003; Evans et al. 2001). As a result of this work, Lee et al. (2003) have estimated the abundance of HCO⁺, H¹³CO⁺, and DCO⁺ in L1512, L1544, and L1689 by fitting step functions with non zero value at the core center. Comparing the outer abundances estimated by these authors with those in L1498 and L1517B, we find reasonable (factor of 2) agreement for HCO⁺ in L1512 and L1544, the two Taurus cores, but almost one order of magnitude difference for H¹³CO⁺ and DCO⁺ in the same objects. This result is somewhat surprising, especially for H¹³CO⁺, as our abundance values agree with a standard isotopic ¹²C/¹³C ratio of 60, while the Lee et al. (2003) values imply a ratio one order of magnitude lower. The origin of this discrepancy is not clear, although it most likely results from a combination of a higher dust emissivity, lower gas temperature, and smaller radius coverage by Lee et al. (2003). A similar (factor of 4) discrepancy occurs between our H₂CO abundance determination in L1498 and that by Young et al. (2004) in the same core, despite our model fitting the H₂CO(3₁₂-2₁₁) emission from these authors (Appendix C). This discrepancy most likely arises from a different choice of dust emissivity, which as discussed by Shirley et al. (2005), makes our L1498 models differ from that of the Texas group by a factor of 3 in H₂ column density. Such a systematic discrepancy between models highlights the urgent need for an accurate determination of the dust emissivity at millimeter and submillimeter wavelengths.

Better agreement between our abundance determinations and those in other starless cores occur for N₂H⁺. Caselli et al. (2002a) have estimated an N₂H⁺ abundance of $(2 \pm1) \times 10^{-10}$ for a sample of 25 starless cores assuming virial equilibrium, and this result is in excellent agreement with our determination. Also, Keto et al. (2004) have carried out a detailed analysis of the N₂H⁺ emission in 3 starless cores, one of them being L1517B. They derive for this object a central density within a factor of 2 of ours, and an N₂H⁺ abundance that differs from ours by less than 10%.

Even if the larger abundance differences between cores are real, it seems that in most cases they are well within the factor of 3-4 range. This of course does not imply that starless cores form an homogeneous family. The gradient across TMC1 reveals differences in abundance that are unlikely to be explained simply as the result of differential depletion, and a number of cores are known to have significantly lower abundance of certain late-time species like NH₃ and N₂H⁺ (Suzuki et al. 1992). L1521E, for example, has negligible depletion of C-bearing species and NH₃ and N₂H⁺ abundances one order of magnitude lower than L1498 and L1517B (Hirota et al. 2002; Tafalla & Santiago 2004; Suzuki et al. 1992). Our molecular survey of the L1521E core (in preparation) seems to suggest, however, that most of chemical differences between cores can be explained as a result of differential depletion plus time evolution of the N-bearing species, and that the undepleted abundances in the outer layers do not present extreme (more than a factor few) core to core variations. A systematic survey of a larger sample of cores is still needed to confirm this result.

5.4 Comparison with the Aikawa et al. (2005) chemical model

The chemical evolution of cores as they contract under gravity has been studied by different authors. Bergin & Langer (1997) and Charnley (1997) were first to model the differential depletion of C and N-bearing species as a result of their freeze out onto the dust grains together with a lower binding energy of N₂. More complete chemical networks coupled to realistic contraction physics have been used to improve on this earlier work (Aikawa et al. 2003; Shematovich et al. 2003; Li et al. 2002; Aikawa et al. 2001; Lee et al. 2003). Very recently, (Aikawa et al. 2005, AHRC05 hereafter) have presented the most up-to-date chemical model of starless core contraction. These authors have followed the evolution of two dense cores initially having Bonnor-Ebert density profiles, one subject to a small over-density factor (their $\alpha =1.1$ case, where $\alpha$ is the gravity-to-pressure ratio), and the other highly over dense ( $\alpha=4.0$ ). As intuitively expected, the core with the small over-density factor loses equilibrium and contracts slowly (timescale 1 Myr), while the highly over dense core contracts in one tenth of the time. Due to these very different time scales, the two cores develop significantly different chemical compositions by the time their central densities reach values like those of L1498 and L1517B. The $\alpha =1.1$ core has lost most molecular species at the center, while the $\alpha=4.0$ core still retains a significant fraction of depletion-sensitive molecules in the gas phase. From this dichotomy, AHRC05 argue that the $\alpha =1.1$ model approximates the evolution of quiescent, heavily depleted cores like L1498 and L1517B, while the $\alpha=4.0$ model simulates dense, but not depleted cores like L1521E.

Our molecular survey of L1498 and L1517B can be used to test the predictions of the different chemical models of core contraction. We choose the AHRC05 model because it is the most complete model available and because it presents predictions of both the core velocity field and its chemical composition. To test this model, we have run a series of Monte Carlo radiative transfer calculations using the observed density profiles of L1498 and L1517B together with the abundance and velocity profiles predicted by the AHRC05 models at the time when the core central density reaches $n_0 = 1.5 \times 10^5$ cm^-3 (note that AHRC05 quote densities of H nuclei while we use densities of H₂molecules). At this time, the density profiles of the AHRC05 models are close to those of L1498 and L1517B, although there are still factor-of-2 differences between the density profiles that should be kept in mind when comparing with our observations.

Concerning the velocity field, we find that the $\alpha=4.0$ model predicts for NH₃ lines much broader than observed (0.38 km s^-1 versus 0.2 km s^-1, Paper I), and for species with central depletion like C¹⁸O and CH₃OH, the model predicts spectra with two peaks. These peaks correspond to the front and the back sides of the core, and are separated by 0.4 km s^-1 because each side is moving toward the center with a velocity of about 0.2 km s^-1(Fig. 1e in AHRC05). Such broad, double-peaked profiles are not observed in L1498 or L1517B, and they rule out a fast contraction model for these cores. The $\alpha =1.1$ model, on the other hand, predicts narrower spectra, similar to those observed. In the absence of turbulence, this model predicts the correct NH₃ linewidth toward the center for both L1498 and L1517B (0.2 km s^-1), but for species with central depletion, it predicts lines that have two peaks separated by 0.15 km s^-1, and this is not observed. Although these peaks can be blended into a single feature by adding a small amount of turbulence, the lines are already broader than observed and the extra turbulence further degrades the fit. For the narrow-lined CH₃OH emission, for example, the AHRC05 model without turbulence predicts lines that are broader than measured by 20% in the case of L1517B and by 70% for L1498. This disagreement may be exaggerated by the imperfect match between the density profiles of our cores and the AHRC05 models, but also illustrates the fact that in the AHRC05 $\alpha =1.1$ model, densities like those of L1498 and L1517B are reached at relatively late stages, when the core contraction has started to accelerate. For this reason, the model predicts that the L1498/L1517B phase will only last 10% of the core time life, or just 10⁵ yr, which is too short for a typical starless core (e.g., Lee & Myers 1999). The relatively fast contraction of the model is therefore not supported by the observations. Adding a magnetic field can help to slow down the contraction, but this may introduce additional problems with the chemistry. A long period of slow contraction, for example 1 Myr, would imply CO depletion at densities as low as 10⁴ cm^-3(Léger 1983), which is lower than observed. Accretion of new (undepleted) material from the surrounding molecular cloud may help mitigate this difficulty. An additional problem with chemical models of magnetized clouds is that they predict N₂H⁺ to trace the quiescent and thermally supported core nucleus in contracting starless clouds such as L1544 (Shematovich et al. 2003), in disagreement with observations (Caselli et al. 2002b).

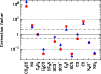$\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{5311fig7.eps}} \end{figure}$

Figure 7: Correction factors needed to make the abundances predicted by the Aikawa et al. (2005) $\alpha =1.1$ model reproduce the observed intensities in the L1498/L1517B molecular survey. The blue triangles (L1517B data) and the red squares (L1498 data) indicate that order of magnitude corrections are needed in a number of species. The comparison between model and observations has been done at the fiducial outer radius defined in Sect. 4.2. The dashed and dotted lines indicate factor of 2 and 10 corrections, respectively.

To test the AHRC05 abundance predictions, we now fix the velocity field of each core to the best fit value determined in Paper I, and we use the Monte Carlo code to estimate predicted radial profiles of integrated intensity for all species observed in L1498 and L1517B and predicted by model $\alpha =1.1$ ( $n_0 = 1.5 \times 10^5$ cm^-3). If the AHRC05 abundance profile does not fit the observations at the fiducial outer radius defined in Sect. 4.2 (75'' for L1498 and 55'' for L1517B), we estimate the global factor by which the model abundance needs to be multiplied to match the data at that radius. This factor measures the deviation of model from the observations, and is shown in Fig. 7 for both the L1498 and L1517B models. As expected from the good agreement between the L1498 and L1517B abundances (Sect. 5.1), the correction factors derived from the two cores agree within a factor of two. This shows that the corrections are almost independent of the exact structure of the core.

The correction factors in Fig. 7 cover more than three orders of magnitude, and this indicates that some species are seriously over or under predicted by the model. Considering all the uncertainties of our fitting procedure, we take any correction smaller than a factor of two as a reasonable match between model and data. This occurs for C₃H₂ (although the model misses the observed outer abundance drop), HCO⁺(although L1498 requires a factor of 3 correction), and CO. Correction factors between 2 and one order of magnitude are considered "clear deviations'' between model and data, and include SO, DCO⁺, C₂S, CS, and N₂H⁺. Interestingly enough, three of these species are S-bearing, and all of them are under predicted by a factor of a few (5-7.5 for CS, and 2-4 for SO and C₂S). This suggests that the model overestimates the depletion of S in its initial atomic conditions by a similar factor. Finally, correction factors larger than one order of magnitude indicate a "serious deviation'' between model and data, and occur for CH₃OH, H₂CO, HCN, and NH₃. Given its large value, the deviation of H₂CO is likely real, although thin isotopologue observations are needed to better quantify the error. On the other hand, the large under production of CH₃OH is not surprising given the lack of a known gas-phase production mechanism for this molecule (Luca et al. 2002). As for HCN, it is possible that the addition of photochemistry to the model may help correct the overproduction of this molecule.

The need for order-of-magnitude corrections does not necessarily imply that the AHRC05 model fails to reproduce all aspects of the chemical structure in cores like L1498 and L1517B. Most abundance profiles, when scaled appropriately, reproduce the shape of the radial distribution of intensity, and this suggests that the model captures at least part of the process of molecular depletion as the core contracts. To study how well the AHRC05 model predicts the radial variation in the abundance of the different species, we compare the shape of the observed intensity profiles with the shape predicted by the model after correcting the abundances by the appropriate global factor. We do this by defining a "concentration factor'' as the ratio between the intensity at the core center and the intensity at a fiducial outer radius (75'' for L1498 and 55'' for L1517B, see Sect. 4.2). Such a factor measures how centrally peaked the emission is, and can be easily estimated both in the model predictions and in the data. The ratio between the model and data concentration factors will equal one in a perfect match, will be larger than one if the model under-predicts the central abundance drop (so its emission is more centrally peaked), and will be less than 1 the other way around.

$\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{5311fig8.eps}} \end{figure}$

Figure 8: Comparison between the concentration ratios predicted by the Aikawa et al. (2005) model and the observations of L1498 (red squares) and L1517B (blue triangles). A value equal to 1 indicates that the model predicts emission with the same central concentration as observed, a value larger than 1 indicates that the model is more concentrated than the data (small central hole), and a value less than 1 indicates a model prediction flatter than the data (too large a hole). There is an overall (factor of 2) agreement between model and data, although the L1517B data seems systematically lower than 1. The model therefore overestimates the central hole seen in L1517B.

Figure 8 presents the ratio of concentration factors (model over data) in both L1498 and L1517B for all available species. For L1498, the AHRC05 model predicts on average the correct size of the central hole, and the average model-to-data ratio is approximately 1. For L1517B, the model over predicts the size of the central hole, as would be expected due to its smaller dimension (Sect. 5.1), and the mean ratio of concentration factors is about 0.75. This systematic over prediction for L1517B reflects a global problem modeling the core, so in the following discussion we concentrate on the L1498 results. As the figure shows, SO and HCN present the largest ratio of all, indicative that the model under predicts their central abundance hole by the largest factor. This occurs in SO because this species has a relatively large hole, while the AHRC05 model predicts an average value. For HCN, the data show a relatively small central hole, but the AHRC05 model predicts negligible depletion at the time when the core has the central density of L1498 and L1517B. (Note that the model correctly predicts a well defined, relatively smaller HCN hole at later times.) DCO⁺, on the other hand, is the species with smallest ratio in the figure, indicating that the AHRC05 model predicts a hole larger than observed. This is most likely due to an under prediction of the central deuterium enhancement, as the model predicts the correct depletion hole for the main isotopologue HCO⁺. Finally, the radial behavior of the two species without central freeze out, N₂H⁺ and NH₃, is well predicted by the model after dividing the N₂H⁺ abundance by a factor of 3.5 and the NH₃abundance by a factor of 20. This general over prediction of N-bearing species probably results from an underestimate of the binding energy to grains (see below), while the improved behavior of NH₃ arises from the new treatment of the N₂H⁺ dissociative recombination thanks to the work by Geppert et al. (2004).

A final problem affecting most current chemical models (including AHRC05, but also Bergin & Langer 1997) is that they owe most of their success in explaining the different depletion behavior of C-bearing and N-bearing species to the assumption that CO and N₂ have significantly different binding energies to grains. Recent laboratory measurements by Öberg et al. (2005) and Bisschop et al. (2006), however, show that the two binding energies differ by less than 10%, and this may seem insufficient to account for the different depletion behavior of CO and N₂H⁺(note however that Aikawa et al. 2001 find differential depletion even when using similar binding energies for CO and N₂). Flower et al. (2005) have proposed an alternative explanation in terms of a lower sticking coefficient for N₂ or N. While the former alternative seems ruled out by laboratory measurements (Bisschop et al. 2006), the latter is still a viable solution, although no laboratory measurements exist yet to confirm or refute the idea. This remaining uncertainty in our understanding of the process behind the differentiation of C-bearing and N-bearing species - the most visible feature of core chemistry - illustrates how it is still premature to use current chemical models to assign contraction ages to cores. A new generation of models is still needed to fulfill the promise of providing core studies with a reliable chemical clock.

5.5 How to best identify depletion (or its absence)

The simplest use of depletion as a qualitative indicator of core age is the classification of cores as chemically evolved if they show evidence for molecular depletion and as chemically young if they do not. Most dense cores, in fact, suffer from severe depletion (e.g., Tafalla et al. 2002; Bacmann et al. 2002), while only a minority seem unaffected by it (Hirota et al. 2002; Tafalla & Santiago 2004). This suggests that young cores are rare, either because they are absent from clouds or because an observational bias limits our ability to recognize them in surveys. In either case, it is of interest identifying the most sensitive tracer of molecular depletion to use it for systematic searches of young cores. Choosing such a tracer requires some consideration. Sensitivity to depletion depends not only on the relative size of the central hole, but on the response of the emission to dense gas and on possible optical depth effects. In this section, we use our radiative transfer analysis of L1498 and L1517B to assess the effect of depletion on the emission of different molecules under realistic core conditions, in order to find the species most sensitive to central depletion.

Strictly speaking, the sensitivity to depletion depends not on the molecule but on its transitions. These may greatly differ in critical density and optical depth, especially in molecules with complex level structure. However, as we will see below, the results tend to agree within a factor of two. To measure quantitatively the sensitivity to depletion of a molecular transition, we compare the intensity toward the core center predicted by our best-fit Monte Carlo model with the prediction from a model of constant abundance equal to the outer value in the best fit (solid and dashed lines in Figs. 3 and 4). The ratio of the constant abundance result over the depletion result measures how much brighter a core with constant abundance would appear compared with the core suffering real depletion.

$\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{5311fig9.eps}} \end{figure}$

Figure 9: Effect of depletion on the different lines and transitions observed in the survey. The y-axis represents the ratio between the central intensities of a constant abundance model and the best fit model for each of the lines observed in L1498 (red squares) and L1517B (blue triangles). Large values indicate a strong effect of the central depletion in the emission from the core center.

Figure 9 presents the depletion sensitivity ratio for all transitions observed toward L1498 (squares) and L1517B (triangles). For most molecules, the L1498 and L1517B values agree within a factor of two even when multiple transitions have been observed. As the figure shows, a sensitivity factor of 2 (dashed line) is common for most species, indicating that molecular depletion typically halves the expected intensity towards the core center. Several species, however, consistently present sensitivity ratios larger than 2. The SO lines reach the highest values of all, and have a mean factor of 4. This behavior is somewhat expected from the systematically larger depletion radius of this molecule (Sect. 5.2) and its moderately large dipole moment (1.55 D), which makes it sensitive to the presence or absence of SO in the inner core. Not surprisingly, the highest SO ratios correspond to the $\rm JN=43$ -32 transition (138 GHz), which has an Einstein A coefficient larger than the other observed SO line, $\rm JN=32{-}21$ at 99.3 GHz. Second in sensitivity to depletion is C₂S, with small scatter and also a mean value of 4. This molecule again combines a larger-than-average depletion radius with lines of relatively large Einstein A. In third position, and with a sensitivity ratio of about 3, lies CH₃OH, which also presents a depletion radius slightly larger than average, sizable A coefficients, and intensities similar to those of the SO lines. Interestingly, the molecule with largest depletion radius, C¹⁸O, has a sensitivity factor marginally better than 2, which results from a combination of a low dipole moment and moderate optical depth. The thinner C¹⁷O (not shown) is significantly more sensitive, although still suffers from contamination by the extended cloud. SO, C₂S, and CH₃OH seem therefore the top three choices for any systematic search of young, undepleted cores.

5.6 Origin of the line emission. Contribution functions

Our L1498 and L1517B models reproduce the observed molecular emission, so they are expected to provide good approximations to the core internal excitation and radiation transfer. We can therefore use them to investigate how the line emission of different molecules is produced inside the core, and how the emission propagates and is distorted by optical depth effects as it travels towards the outside. Understanding these processes is critical when interpreting observations of similar systems for which a full radiative transfer analysis is not available, and can only be done by examining the internal properties of well-calibrated models.

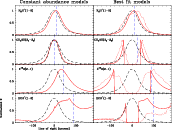$\begin{figure} \par\resizebox{15cm}{!}{\includegraphics{5311fig0.eps}} \end{figure}$

Figure 10: Normalized contribution functions of representative species in L1517B (the observer is at large radius, i.e., to the far right of each panel). The red solid and dotted lines are the contribution functions, while the black dashed lines indicate the normalized density profile shown for reference (the normalized square of the density profile is also shown for CH₃OH). In the best fit models ( right column), the solid line corresponds to our simple abundance step function, while the dotted lines are the contribution functions expected for the abundance profiles predicted by the Aikawa et al. (2005) models (scaled appropriately to fit the L1517B data). In each panel, the vertical dashed lines indicates the radius at which half of the total emission is reached. Note how in the moderately thick C¹⁸O(2-1) and extremely thick HCO⁺(1-0) lines most of the emission arises from the front outer layer of the core.

The general problem of line formation in a core is complex because of the non linear nature of the radiative transfer equation. In this section, we concentrate on the question of how the different layers of a core contribute to the emerging intensity, and on how different molecules can sample (or miss) the internal structure of the core. To quantify the discussion, we make use of the "contribution function'' (CF) commonly used in the study of stellar atmospheres (e.g., Gray 2005; Magain 1986). This function is derived from the formal solution of the radiative transfer equation. According to this solution, the emerging intensity from the core at a given angle and frequency (without the background contribution) is

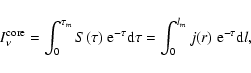
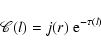
The emergent core intensity is the line-of-sight integral of ${\mathscr C}$ , so the CF is true to its name in the sense that it measures the contribution of a given core element to the observed line intensity. Strictly speaking, the CF depends on wavelength because different regions of the core may contribute to different parts of the line profile. However, because of the small velocity gradients in L1498 and L1517B (Paper I), and for the sake of simplicity, here we will only deal with the frequency-integrated CF, which measures the contribution of a line-of-sight element to the integrated line profile. Also for simplicity, we will only study the central line of sight of the core, although the generalization of the CF for non-zero impact parameters is straightforward. With these assumptions, it can be easily shown that the CF of an optically thin line (where ${\mathscr C} = j$ ) in an isothermal core has two simple limits. If LTE applies ("high density''), the CF is proportional to the density n(r), so the emergent intensity is proportional to the column density. If $A_{ul} \gg C_{ul}$ (where A_ul is the Einstein A coefficient and C_ul is the collision coefficient, "low density'' case), the CF is proportional to n(r)², as each emerging photon is the result of a collision (which has a probability proportional to n(r)²). In this case, the emergent intensity is proportional to the neutral analog of the "emission measure''. Monte Carlo tests using different species and transitions under realistic core conditions show that the CF for a thin line usually lies somewhere between the above two limits.

To illustrate the variety of CFs found during our radiative transfer modeling, we present in Fig. 10 a series of normalized CFs for different species in L1517B (plots for L1498 are similar). Each panel represents a cut along the central impact parameter of the core, has the density peak at r=0, and assumes that the observer is located to the far right of the plot (at $r \to \infty$ ); a normalized density profile in dashed lines indicates the LTE optically thin limit of the CF. Constant abundance models are presented in the left column and best-fit abundance models appear on the right; we first discuss the constant abundance case.

As Fig. 10 shows, the constant abundance model for N₂H⁺(1-0) (and that of NH₃, not presented) has a CF that closely follows the density profile, with a a slight shift to positive radius due to optical depth effects (see below). This good behavior of the CF shows that the N₂H⁺(1-0) emission responds linearly to density and therefore traces faithfully the core structure. To quantify this property, we compare the fraction of integrated CF that arises from the "inner core'' (as defined within the half maximum density radius) to the fraction of gas column density contained in the same region (0.62 for L1517B). For both the N₂H⁺ and NH₃ constant abundance models, we find that the inner core contributes to the emission a percentage indistinguishable from the ideal 62% value. In contrast, the CF of CH₃OH(3₀-2₀) in a constant abundance model (Fig. 10, second left panel) follows closely the n(r)² curve, and is therefore significantly biassed toward the high density gas. For this line, the inner core contributes 85% to the emergent emission, which is almost 40% more than the column density fraction.

The CF for the C¹⁸O constant abundance model shows signs of non negligible optical depth in the form of a forward shift of the peak. This shift indicates that most of the observed C¹⁸O(2-1) emission arises from the front part of the core, and that the emission from the back is heavily attenuated as it travels through the core. In fact, only 15% of the emerging radiation originates from the backside (r<0), and the inner core contributes with only 38% of the emission (a 40% decrease from the ideal value). C¹⁸O, therefore, is a biassed tracer of the core emission despite its LTE excitation, although most of these problems can be minimized using C¹⁷O transitions (but see below for models with depletion). As a final example of a constant abundance model, we consider the heavily self absorbed HCO⁺(1-0) line, although similar results are obtained for CS(2-1). The emission from this line is so dominated by the outer core that half of it originates from radii larger than 90'', and the inner core only contributes 17% of the emergent intensity (23% in the case of CS(2-1)). These numbers illustrate the difficulty of modelling self absorbed lines like HCO⁺(1-0), CS(2-1), or HCN(1-0): the region that dominates the line emission is poorly constrained by the continuum observations that are the basis of our density profile, and its structure is simply guessed using an extrapolation of the central core parameters. These very thick lines are therefore excellent tracers of the outer velocity fields (like infall), but they become poor tools for deriving any line of sight structure, even of the infall velocity, unless there is a very accurate description of the outer core and the surrounding cloud.

The presence of depletion introduces a substantial distortion in the CF. This is illustrated by the right-hand panels of Fig. 10, which are based on the best-fit abundance profiles of Sect. 4. The N₂H⁺ CF is of course the same as in the constant abundance case because no abundance gradient was found for this molecule. The CH₃OH, C¹⁸O, and HCO⁺ CFs, on the other hand, present sharp drops near the core center that correspond to the abundance holes found for these species. Because of these drops, the CF in the inner core vanishes or becomes so small that a negligible part of the emergent emission arises from the dense gas: 5% in HCO⁺(1-0) and less than 1% in both CH₃OH(3₀-2₀) and C¹⁸O(2-1). The spectra towards the core center for these species is therefore overwhelmed by gas outside the core, mostly from an innermost ring if the emission is not very thick (the case of CH₃OH and C¹⁸O) or from the front part of the core in the thicker HCO⁺(1-0) line. Although it can be argued that the abundance drops in our models are artificially steep because of the use of a step function, theoretical considerations of core chemistry still predict very sharp abundance decreases. To test the effect of smoother, but realistic abundance gradients, we have produced a set of CFs using the $\alpha =1.1$ model of Aikawa et al. (2005) corrected by the appropriate scaling factors to match the observed radial profile. The new CFs (shown as dotted lines in the right hand panels of Fig. 10) again present very steep holes toward the core centers and predict inner-core contributions to the emerging intensity of 15% (CH₃OH) and less (C¹⁸O and HCO⁺). The inner core contribution to the emission for these and other depleted species is therefore a minor fraction of the total emergent intensity.

The above small sample of CFs illustrates some of the basic phenomenology of line formation in cores like L1517B. As the plots show, even in the simple case of constant abundance, the emission is not generated at a " $\tau=1$ surface'', but arises from a broad range of radii that in the simplest case (thin LTE) has a weight that mimics the core density distribution, and that in a thick line is strongly biassed toward the front part of the core. When realistic abundance profiles are considered, if the species is sensitive to depletion, all hope of tracing the inner core is lost no matter how much spatial resolution is achieved. Only depletion-resistant species like N₂H⁺ and NH₃ trace the inner gas, at least to densities of a few 10⁵ cm^-3. Among these tracers, N₂H⁺(1-0) seems specially reliable because of a combination of constant abundance, reasonably low optical depth (helped by the hyperfine structure), and well-behaved excitation. Ignoring the NLTE ratios between the J=1-0 hyperfine components (a 10% effect most likely due to a population redistribution), this line consistently produces a CF very close in shape to the density profile. This is somewhat surprising given the significant radial gradient in the excitation temperature of this line (more than a factor of 2 change between center and edge in L1517B), and it results from a population of the J=1 level that follows closely the density law (the population of higher N₂H⁺ levels falls faster than the density law, and the CFs of higher transitions is closer to n(r)²). This fortunate behavior of the N₂H⁺ molecule explains the striking similarity between the mm continuum and N₂H⁺(1-0) maps in many starless cores (e.g., Tafalla et al. 2002; Crapsi et al. 2005; Bacmann et al. 2002; Caselli et al. 1999, this work), and makes the 1-0 line the ideal choice for studying core interiors as long as its optical depth remains low.

6 Conclusions

We have presented observations of 13 molecular species (plus a number of isotopologues) toward the Taurus-Auriga starless cores L1498 and L1517B. Combining Monte Carlo radiative transfer modeling with a physical description of the cores, we have derived a self-consistent set of molecular abundance profiles. From the analysis of these profiles, we have reached the following main conclusions.

References

7 Online Material

Appendix A: Molecular parameters and convergence tests

C $_{\bf 2}$ S. Dicarbon monosulfide is a linear radical with two unpaired electrons (electron spin $\rm S=1$ ), and therefore fine structure in its spectrum. Its rotational levels are characterized by N and J, the quantum numbers of rotational angular momentum and total angular momentum, respectively (e.g., Wolkovitch et al. 1997). We model its radiative transfer using the C₂S molecular parameters from the JPL catalog (Pickett et al. 1998) together with the C₂S-H₂collision rates from Wolkovitch et al. (1997) (downward rates for 10 K together with upward rates derived from detailed balance). We include all energy states up to approximately 60 K, which results in a total of 37 levels and 79 transitions.

CH $_{\bf 3}$ OH. Methanol is a slightly asymmetric top with a hindered internal rotation (Townes & Schawlow 1955). It consists of two symmetry species denoted A and E (e.g., Lees 1973) whose rotation energy levels are characterized by their total angular momentum J and its component along the near symmetry axis k (an additional + or - is required for the A species if $k\ne0$ ). For our calculations, we have used the energy and line strength determinations in the JPL catalog (Pickett et al. 1998) together with the recent CH₃OH-para H₂ collision rates of Pottage et al. (2004) (downward rates for 10 K together with upward rates derived from detailed balance). For both species, we include all energy states up to approximately 70 K, which results in a total of 31 levels and 92 transitions for E-CH₃OH, and 27 levels and 66 transitions for A-CH₃OH.

c-C $_{\bf 3}$ H $_{\bf 2}$ . Cyclopropenylidene, a ring molecule, is an oblate asymmetric top with ortho and para species (Vrtilek et al. 1987). Its rotational levels are characterized by the total angular momentum J and by K_-1 and K₊₁, its two projections on the symmetry axis for the prolate and oblate symmetric top limits (Townes & Schawlow 1955). For our calculations, we have used the C₃H₂ parameters in the JPL catalog (Pickett et al. 1998) together with the C₃H₂-He collision rates for 10 K from Avery & Green (1989) (multiplied by 2^1/2 to simulate collisions with H₂, as recommended by the authors). Only transitions of ortho C₃H₂ were observed, so our modeling is restricted to that species. This modeling includes all states with available collision rates (up to E_u=41 K): 16 levels and 32 transitions.

H $_{\bf 2}$ CO. Formaldehyde is a slightly asymmetric prolate rotor with ortho and para species, and its rotation levels are characterized (like those of C₃H₂) by J, K_-1, and K₊₁. For our calculations, we have used the H₂CO parameters from the on-line Cologne Database for Molecular Spectroscopy (CDMS, Müller et al. 2001), together with the 10 K H₂CO-He collision rates of Green (1991). These collision rates were multiplied by 2.2 to convert them into H₂CO-H₂ rates, as recommended by Green (1991). We only observed lines of ortho H₂CO, so only this species has been modeled. For this, we have taken into account all energy states with energy below 115 K, resulting in a calculation with 14 levels and 19 transitions.

HC $_{\bf 3}$ N. Cyanoacetylene is a linear molecule. Its rotational levels have hyperfine (hf) structure due to the nuclear spin of the nitrogen atom, so they are characterized by the quantum numbers J and F. For our radiative transfer calculation we have used the molecular parameters from Lafferty & Lovas (1978) and the collision rates with He of Green & Chapman (1978) (multiplied by 2^1/2 to simulate collisions with H₂, as recommended by the authors). The calculation treats the hf structure in a simplified manner by solving the equations of statistical equilibrium for the pure rotational levels after dividing by 3 the effect of trapping, to simulate the decrease of optical depth due to the three-fold hf splitting (we find this to be a minor effect). The resulting population of each rotational level is then divided between the hf sub levels assuming LTE to compute the emergent spectrum (see Tafalla et al. 2002 for a discussion of a similar approach with N₂H⁺). All 24 levels up to an energy of 130 K are considered (23 transitions).

HCO⁺ and isotopologues. The formyl cation HCO⁺ and its isotopologues H¹³CO⁺ and DCO⁺ are linear ions. We have modeled their radiative transfer using the parameters in the JPL catalog together with the 10 K HCO⁺-H₂ collision rates of Flower (1999). Our calculation considers a set of 7 levels (6 transitions), up to an equivalent energy of 120 K. To take into account the small additional broadening due to hyperfine structure in H¹³CO⁺, we have artificially broadened this line by an extra 0.133 km s^-1(see Schmid-Burgk et al. 2004).

HCN and H $^{{\bf 13}}$ CN. Hydrogen cyanide is a linear molecule with hyperfine structure due to the nuclear spin of the nitrogen atom. We have modeled its radiative transfer using the molecular parameters in the CDMS together with the HCN-He collision rates of Monteiro & Stutzki (1986) (for J up to 4) and the HCN-He rates of Green & Thaddeus (1974) (remaining levels up to J=7). A factor of 2 was used to convert the He collision rates into H₂ rates. The hyperfine structure of this species (and that of its isotopologue) has been considered explicitly in the calculations, although overlap effects were ignored and the collision rates between hf sub levels with J>4were estimated from the Green & Thaddeus (1974) rates assuming independence of the F number (Guilloteau & Baudry 1981). A total of 22 levels and 39 transitions were included, corresponding to all levels with energy lower than 119 K (up to J=7).

SO. Sulfur monoxide is a diatomic molecule with two unpaired electrons and therefore a fine structure similar to that of C₂S. We have modeled its radiative transfer using the molecular parameters in the CDMS together with the SO-He collision rates from Lique et al. (2005). Following the authors's recommendations, a factor of 1.38 was used to convert the SO-He collision rates into SO-H₂ rates. All 24 levels up to an energy of 85 K and their corresponding 72 transitions were included in the model.

Convergence tests. When solving the radiative transfer, we divide the core in 200 equally spaced shells. We normally use 2000 photon packages to simulate the radiation, and allow 40 iterations for the solution to converge (no radiation reference field was used, see Bernes 1979 for details on the code). To check the convergence of the solution, several tests were carried out. Independence on the initial level population was tested by comparing the results from runs that started with Boltzmann equilibrium at 10 K (kinetic temperature) and at 2.7 K (cosmic background); no differences in the final solution were found. Independence on the internal Monte Carlo parameters was tested by repeating the best fit solutions using 5000 photon packages and 300 iterations. Again, no appreciable differences were found in the predicted intensities.

Appendix B: An additional gas component toward the L1498 core

$\begin{figure}\par\resizebox{8.8cm}{!}{\includegraphics{5311figa.eps}} \end{figure}$

Figure B.1: Spectra towards L1498 illustrating the presence of a red gas component. The bottom (H¹³CN) line shows that the LSR velocity of the cloud is about 7.8 km s^-1(vertical line). The HCN line (next up) shows a deep red self-absorption and a low level red wing, while the CO isotopologue lines show an increasing contribution of the red component with abundance. The coincidence of the red component with the absorption in HCN (also HCO⁺ and CS) suggests that the component lies in front of the L1498 core.

The line of sight toward the L1498 core is complex. In addition to the narrow-line component that corresponds to the core studied in this paper, spectra of abundant species like ¹²CO and ¹³CO show extra emission toward the red extending up to about $V_{\rm LSR} = 9.5$ km s^-1, which is 1.7 km s^-1 higher than the core velocity (Fig. B.1). This additional component has a complex spatial distribution (see also Kuiper et al. 1996). At low velocities ( ${\sim}8.2$ km s^-1), it lies toward the south west of the core (as also found by Lemme et al. 1995), while at high velocities ( ${\sim}9$ km s^-1), it appears toward the NW. This distribution around the L1498 core suggests some relation with the dense gas, although the velocity difference implies that the red gas is not bound to the core. From the C¹⁸O(1-0) spectrum in Fig. B.1 and assuming an excitation temperature of 5-10 K together with a "standard'' C¹⁸O abundance of $1.7\times 10^{-7}$ Frerking et al. (1982), we deduce an approximate H₂ column density for this component of $2 \times 10^{21}$ cm^-2 (less than 10% of the core column density).

Although the red component does not affect the narrow optically thin lines used in our abundance determinations, it can distort the shape of very thick spectra like HCN(1-0), shown in Fig. B.1. These spectra were also modelled in Sect. 4 by assuming standard isotopic ratios, and they sometimes required anomalous abundances in the outer core (Sect. 4.2). As stressed before, these optically thick lines were only fitted to prove self consistency, and not to determine the conditions of the outer core layers. To model these lines, however, some assumptions had to be made about the red component, and a main one was its location along the line of sight with respect to the L1498 core. A foreground position was preferred based on hints from several optically thick spectra, like the HCN( $\rm JF=12$ -01) line shown in Fig. B.1. This spectrum shows a deep self absorption that removes completely the red part of the line and replaces it by a low-level plateau that continues smoothly into the red-component range (from $V_{\rm LSR}$ 8 to 9 km s^-1). Such a feature is best understood if the red component contributes to the absorption of the core emission and therefore arises from gas located in front of the core. To model such a component, we have red-shifted the front outer core layers of L1498 ("envelope'' in Paper I) by 0.35 km s^-1and broadened them to $\Delta V = 0.625$ km s^-1(note that because of a typo, Table 3 in Paper I gives the wrong envelope velocity, which should be 8.15 km s^-1); such a simple parameterization reproduces approximately the shape of most optically thick lines.

Appendix C: Comparison with published data

$\begin{figure}\par\resizebox{8.8cm}{!}{\includegraphics{5311figb.eps}} \end{figure}$

Figure C.1: Comparison of L1498 data taken from the literature (solid squares) with the predictions of the best fit model of Sect. 4.2 (red lines). The top three panels show that the model fits well the C₂S radial profiles generated from the data of Wolkovitch et al. (1997). The bottom two panels show that the model fits well the H₂CO(3₁₂-2₁₁) line of Young et al. (2004), but fails to fit the H₂CO(1₁₁-1₁₀) line (from the same authors), which appears in absorption against the cosmic background. To illustrate the sensitivity of the 1₁₁-1₁₀ absorption to the core low density gas, a model with a backside envelope is shown in blue dashed lines (see text).

We have compared our L1498 model predictions with data for this core available in the literature (no similar data were found for L1517B). Wolkovitch et al. (1997) have presented observations of L1498 in three C₂S transitions, $\rm JN=21$ -01 (22 GHz), $\rm JN=43$ -32 (45 GHz), and $\rm JN=87$ -76 (94 GHz), made with the telescopes of NASA's Deep Space Network and the FCRAO, and having spatial resolutions of about 50''. From the linewidths and peak intensities reported by these authors in their Table 2, we have reconstructed the line integrated intensities for all positions available, and with them, we have generated the radial profile of emission for each transition. When we compare these profiles with the prediction from the best abundance model derived in Sect. 4.2, we find the excellent match illustrated by the three top panels in Fig. C.1. This match shows that our model predictions are fully consistent with the observations of Wolkovitch et al. (1997).

Other L1498 data of interest for our study are those of Young et al. (2004), who have observed L1498 in H₂CO(1₁₁-1₁₀) (6 cm) with the Arecibo telescope and in H₂CO(3₁₂-2₁₁) (1.3 mm) with the CSO (spatial resolutions of 60'' and 32''). To reconstruct the integrated intensities of these lines, we have used the values reported by the authors in their Table 2 (1.3 mm line) and data kindly provided by Kaisa Young and Jeong-Eun Lee (6 cm line). With them, we have generated a set of radial profiles, and in Fig. C.1 we compare them with the predictions from the best fit model of Sect. 4.2. As the figure shows, the model reproduces well the 3₁₂-2₁₁ emission, which is sensitive to the high density gas inside the core. The model, however, fails to reproduce the observed intensity of the 1₁₁-1₁₀ transition, although it agrees with the data in producing an absorption line against the cosmic background. The poor fit occurs because the absorption depends sensitively on the low density gas outside the core, and this gas is not well parameterized by our extrapolation of the inner core model (Sect. 4.2). To illustrate this sensitivity to the low density gas, we have added to the L1498 model an envelope in the back that has the same properties as the front envelope used to simulate the red shifted component (Appendix B). This back envelope doubles the 1₁₁-1₁₀ absorption, and brings the model prediction closer to the observations (blue dashed lines in Fig. C.1). Such strong sensitivity to the low density gas shows that the central core is close to invisible in the 1₁₁-1₁₀ transition (note the flat radial profile), and that improving the fit requires a re-parameterization of the envelope, not the core. Given the few observational constrains of the low density gas, such a parameterization lies outside the scope of this work.

Contents

On the internal structure of starless cores

II. A molecular survey of L1498 and L1517B