A&A 455, 679-684 (2006)
DOI: 10.1051/0004-6361:20065102
On the relevance of Compton scattering for the soft X-ray
spectra of hot DA white dwarfs
V. Suleimanov1,2,5 -
J. Madej3 -
J. J. Drake4 -
T. Rauch1 -
K. Werner1
1 -
Institut für Astronomie und Astrophysik, Universität Tübingen, Sand 1,
72076 Tübingen, Germany
2 -
Kazan State University, Kremlevskaja str., 18, Kazan 420008, Russia
3 -
Warsaw University Observatory, Al. Ujazdowskie 4,
00-478 Warsaw, Poland
4 -
Smithsonian Astrophysical Observatory, MS-3, 60 Garden Street, Cambridge,
MA 02138, USA
5 -
Kazan Branch of Isaac Newton Institute, Santiago, Chile
Received 27 February 2006 / Accepted 7 May 2006
Abstract
Aims. We re-examine the effects of Compton scattering on the emergent spectra of hot DA white dwarfs in the soft X-ray range. Earlier studies have implied that sensitive X-ray observations at wavelengths
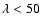 Å might be capable of probing the flux deficits predicted by the redistribution of electron-scattered X-ray photons toward longer wavelengths.
Å might be capable of probing the flux deficits predicted by the redistribution of electron-scattered X-ray photons toward longer wavelengths.
Methods. We adopt two independent numerical approaches to the inclusion of Compton scattering in the computation of pure hydrogen atmospheres in hydrostatic equilibrium. One employs the Kompaneets diffusion approximation formalism, while the other uses the cross-sections and redistribution functions of Guilbert. Models and emergent spectra are computed for stellar parameters representative of HZ 43 and Sirius B, and for models with an effective temperature
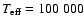 K.
K.
Results. The differences between emergent spectra computed for Compton and Thomson scattering cases are completely negligible in the case of both HZ 43 and Sirius B models, and are also negligible for all practical purposes for models with temperatures as high as
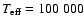 K. Models of the soft X-ray flux from these stars are instead dominated by uncertainties in their fundamental parameters.
K. Models of the soft X-ray flux from these stars are instead dominated by uncertainties in their fundamental parameters.
Key words: radiative transfer - scattering - methods: numerical -
stars: white dwarfs - stars: atmospheres - X-rays: stars
The scattering of radiation by free electrons is one of the dominant
sources of continuous opacity in the atmospheres of hot white dwarfs.
Most model atmosphere calculations adopt the classical Thomson
isotropic scattering approach, whereby only the direction of photon
propagation changes as the result of a scattering event. More
rigorously, finite electron mass instead implies that both momentum
and energy exchange should actually occur.
The effects of Compton scattering on white dwarf model
atmospheres was first investigated in detail by Madej (1994), who
found that pure hydrogen models with
temperatures of 105 K show a significant depression of the X-ray
continuum for wavelengths <50 Å. Effects for models containing
significant amounts of helium, or helium and heavier elements, were
found to be much smaller or negligible, in keeping with expectations
based on the relative importance of electron scattering as an opacity
source as opposed to photoelectric absorption.
In a later paper, Madej (1998) computed the effects of Compton
scattering for a model corresponding to the parameters of the DA white
dwarf HZ 43. Differences between Compton and Thomson scattering model
spectra were apparent for
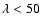 Å, and grew to orders of
magnitude by 40 Å. While current X-ray
instrumentation is not sufficiently sensitive to study the spectra of
even the brightest DA white dwarfs in any detail at wavelengths
Å, and grew to orders of
magnitude by 40 Å. While current X-ray
instrumentation is not sufficiently sensitive to study the spectra of
even the brightest DA white dwarfs in any detail at wavelengths
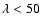 Å, the spectral differences implied by the more
rigorous Compton redistribution formalism will be of interest to more
sensitive future missions. Moreover, the Chandra Low Energy
Transmission Grating Spectrometer (LETG+HRC-S) effective area
calibration is based on observed spectra of HZ 43 and Sirius B at
wavelengths
Å, the spectral differences implied by the more
rigorous Compton redistribution formalism will be of interest to more
sensitive future missions. Moreover, the Chandra Low Energy
Transmission Grating Spectrometer (LETG+HRC-S) effective area
calibration is based on observed spectra of HZ 43 and Sirius B at
wavelengths
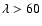 Å (Pease et al. 2003). It is
therefore of current topical interest to re-examine the influence of
Compton scattering for these stars and determine whether any
significant differences might be discernible between Thomson and
Compton scattering in the LETGS bandpass.
Å (Pease et al. 2003). It is
therefore of current topical interest to re-examine the influence of
Compton scattering for these stars and determine whether any
significant differences might be discernible between Thomson and
Compton scattering in the LETGS bandpass.
In this paper, we perform two independent and rigorous tests of the
influence of Compton scattering on the emergent spectra of hot DA
white dwarfs. Our methods of calculation are outlined in
Sect. 2, while results and conclusions are briefly discussed
in Sects. 3-5.
2 Computational methods
In both our numerical approaches, outlined below, we computed model
atmospheres of hot white dwarfs subject to the constraints
of hydrostatic and radiative equilibrium assuming planar geometry
using standard methods (e.g. Mihalas 1978).
The equation of state of an ideal gas used assumes local thermodynamic
equilibrium (LTE), and therefore did not include terms describing the
local radiation field.
The model atmosphere structure for a hot WD is described by the
hydrostatic equilibrium equation,
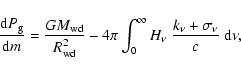 |
(1) |
where 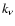 is opacity per unit mass due to free-free, bound-free and
bound-bound
transitions,
is opacity per unit mass due to free-free, bound-free and
bound-bound
transitions,
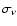 is the electron (Compton) opacity,
is the electron (Compton) opacity, 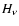 is
Eddington flux,
is
Eddington flux, 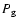 is the gas pressure, and m is the column density
is the gas pressure, and m is the column density
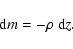 |
(2) |
Variable 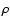 denotes the gas density and z is the vertical distance.
As is obvious from Eq. (1), the structure of the atmosphere is
coupled to the radiation field and the structure and radiative
transfer equations need to be solved simultaneously under the
constraint of radiative equilibrium.
denotes the gas density and z is the vertical distance.
As is obvious from Eq. (1), the structure of the atmosphere is
coupled to the radiation field and the structure and radiative
transfer equations need to be solved simultaneously under the
constraint of radiative equilibrium.
In the Thomson approximation, in which no energy or momentum between
photons and electrons is exchanged,
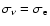 ,
where
,
where
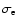 is the classical Thomson opacity.
is the classical Thomson opacity.
In our first approach, Compton scattering is taken into account in
the radiation transfer equation using the Kompaneets operator
(Zavlin & Shibanov 1991; Grebenev & Sunyaev 2002; Kompaneets 1957):
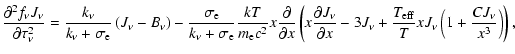 |
|
|
(3) |
where
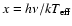 is the dimensionless frequency,
is the dimensionless frequency,
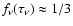 is the variable Eddington factor,
is the variable Eddington factor, 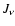 is the mean intensity of radiation,
is the mean intensity of radiation, 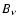 is the black body (Planck)
intensity,
T is the local
electron temperature,
is the black body (Planck)
intensity,
T is the local
electron temperature,
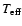 is the effective temperature of WD,
and
is the effective temperature of WD,
and
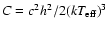 .
The optical
depth
.
The optical
depth
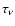 is defined as
is defined as
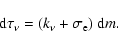 |
(4) |
These equations have to be completed by the energy balance equation
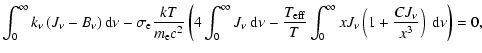 |
|
|
(5) |
the ideal gas law
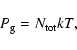 |
(6) |
where
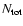 is the number density of all particles, and also
by the particle and charge conservation equations. We assume local
thermodynamical equilibrium (LTE) in our calculations, so the number
densities of all ionisation and excitation states of all elements have
been calculated using Boltzmann and Saha equations.
is the number density of all particles, and also
by the particle and charge conservation equations. We assume local
thermodynamical equilibrium (LTE) in our calculations, so the number
densities of all ionisation and excitation states of all elements have
been calculated using Boltzmann and Saha equations.
For solving the above equations and computing the model atmosphere we
used a version of the computer code ATLAS (Kurucz 1970,1993),
modified to deal with high temperatures; see Ibragimov et al. (2003)
and Swartz et al. (2002) for further details. This code was also
modified to account for Compton scattering.
The scheme of calculations is as follows. First of all, the input
parameters of the WD are defined: the effective temperature
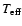 and surface gravity
and surface gravity
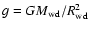 .
Then a
starting model using a grey temperature distribution is calculated.
The calculations are performed with a set of 98 depth points
.
Then a
starting model using a grey temperature distribution is calculated.
The calculations are performed with a set of 98 depth points 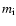 distributed logarithmically in equal steps from
distributed logarithmically in equal steps from
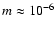 g cm-2 to
g cm-2 to
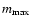 .
The appropriate value of
.
The appropriate value of
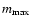 is found from the condition
is found from the condition
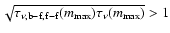 at all frequencies.
Satisfying this equation is necessary for the inner boundary condition
of the radiation transfer.
at all frequencies.
Satisfying this equation is necessary for the inner boundary condition
of the radiation transfer.
For the starting model, all number densities and opacities at all
depth points and all frequencies (we use 300 logarithmically
equidistant frequency points) are calculated. The radiation transfer
Eq. (3) is non-linear and is solved iteratively by the
Feautrier method (Mihalas 1978, see also Zavlin & Shibanov 1991; Pavlov et al. 1991; Grebenev & Sunyaev 2002). We use the last
term of the Eq. (3) in the form
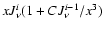 ,
where
,
where
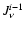 is the mean
intensity from the previous iteration. During the first iteration we
take
is the mean
intensity from the previous iteration. During the first iteration we
take
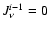 .
Between iterations we calculate the variable
Eddington factors
.
Between iterations we calculate the variable
Eddington factors 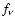 and
and 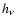 ,
using the formal solution
of the radiation transfer equation in three angles at each frequency.
Usually 2-3 iterations are sufficient to achieve convergence.
,
using the formal solution
of the radiation transfer equation in three angles at each frequency.
Usually 2-3 iterations are sufficient to achieve convergence.
We used the usual condition at the outer boundary
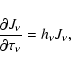 |
(7) |
where
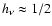 is surface variable Eddington factor.
The inner boundary condition is
is surface variable Eddington factor.
The inner boundary condition is
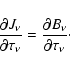 |
(8) |
The outer boundary condition is found from the lack of incoming
radiation at the WD surface, and the inner boundary condition is obtained
from the diffusion approximation
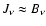 and
and
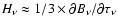 .
.
The boundary conditions along the frequency axis are
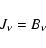 |
(9) |
at the lower frequency boundary (
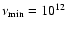 Hz,
Hz,
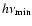
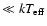 )
and
)
and
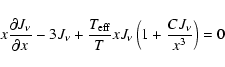 |
(10) |
at the higher frequency boundary (
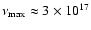 Hz,
Hz,
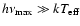 ). Condition (9) means that at the lowest energies the true opacity
dominates the scattering
). Condition (9) means that at the lowest energies the true opacity
dominates the scattering
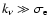 ,
and therefore
,
and therefore
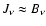 .
Condition (10) means that there is
no photon flux along frequency axis at the highest energy.
.
Condition (10) means that there is
no photon flux along frequency axis at the highest energy.
The solution of the radiative transfer Eq. (3) was checked
for the energy balance Eq. (5) together with the surface
flux condition
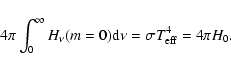 |
(11) |
The relative flux error as a function of depth,
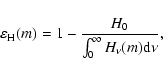 |
(12) |
was calculated, where
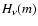 is radiation flux at given depth.
This latter quantity was found from
the first moment of the radiation transfer equation:
is radiation flux at given depth.
This latter quantity was found from
the first moment of the radiation transfer equation:
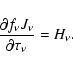 |
(13) |
Temperature corrections were then evaluated using three different
procedures. The first is the integral 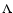 -iteration method,
modified for Compton scattering, based on the energy balance
Eq. (5). It is valid in the upper atmospheric layers. The
second one is the Avrett-Krook flux correction, which uses the
relative flux error, and is valid in the deep layers. And the third
one is the surface correction, which is based on the emergent flux
error. See Kurucz (1970) for a detailed description of the
methods.
-iteration method,
modified for Compton scattering, based on the energy balance
Eq. (5). It is valid in the upper atmospheric layers. The
second one is the Avrett-Krook flux correction, which uses the
relative flux error, and is valid in the deep layers. And the third
one is the surface correction, which is based on the emergent flux
error. See Kurucz (1970) for a detailed description of the
methods.
The iteration procedure is repeated until the relative flux error is
smaller than 1%, and the relative flux derivative error is smaller
than 0.01%. As a result of these calculations, we obtain the
self-consistent WD model atmosphere together with the emergent
spectrum of radiation.
Our method of calculation was tested on a model of bursting neutron
star atmospheres (Pavlov et al. 1991; Madej 1991), and a model DA white
dwarf atmosphere with
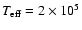 K,
K,
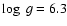 (Madej 1994). Agreement with the earlier calculations is
extremely good. We show the emergent spectrum from the
latter calculation in Fig. 1.
(Madej 1994). Agreement with the earlier calculations is
extremely good. We show the emergent spectrum from the
latter calculation in Fig. 1.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{5102fig1.eps}
\end{figure}](/articles/aa/full/2006/32/aa5102-06/Timg62.gif) |
Figure 1:
Spectra a) and temperature structures
b) of a hot DA white dwarf model
atmosphere with
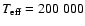 K and K and
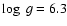 with (solid
line) and without (dashed line) Compton scattering taken into
account.
with (solid
line) and without (dashed line) Compton scattering taken into
account. |
| Open with DEXTER |
Our second approach adopts the equation of transfer for absorption
and scattering presented by Sampson (1959) and Pomraning (1973, see
Eq. (2.167)).
The equation of transfer can be expressed in the form
This transfer equation is written on the monochromatic optical depth
scale d
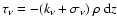 .
The variable
.
The variable 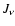 denotes the energy-dependent mean intensity of
radiation. The function
denotes the energy-dependent mean intensity of
radiation. The function
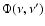 denotes the zeroth angular
moment of the angle-dependent differential cross-section, normalized to unity
(see below).
denotes the zeroth angular
moment of the angle-dependent differential cross-section, normalized to unity
(see below).
Transformation of the equation of transfer by Pomraning (1973) to
Eq. (14) and the definition of required angular approximations
for Compton scattering in a stellar atmosphere was outlined by
Madej (1991,1994) and Madej et al. (2004).
Our equations and theoretical models of Method 2 use detailed differential
cross-sections for Compton scattering,
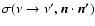 ,
which were taken from Guilbert (1981).
Cross-sections correspond to scattering in a gas of free electrons with
relativistic thermal velocities, and they are also completely valid at low
temperatures.
Differential cross-sections were then integrated numerically to obtain large
grids of Compton scattering opacity coefficients
,
which were taken from Guilbert (1981).
Cross-sections correspond to scattering in a gas of free electrons with
relativistic thermal velocities, and they are also completely valid at low
temperatures.
Differential cross-sections were then integrated numerically to obtain large
grids of Compton scattering opacity coefficients
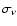
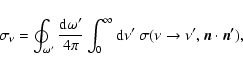 |
(15) |
and grids of angle-averaged Compton scattering redistribution
functions
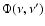
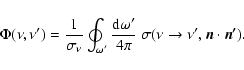 |
(16) |
The scattering frequency redistribution function was introduced by
Pomraning (1973) - see Eq. (7.95) of his book - and it represents
the normalized probability density of scattering from a given frequency 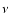 to the outgoing frequency
to the outgoing frequency
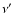 .
.
Note that Eq. (14) also includes stimulated scattering terms,
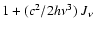 ,
which ensure the physically correct
description of Compton scattering. The actual equations and
calculations used here strongly differ from those in Madej (1998).
The physics of Compton scattering used here is also
fundamentally different to Method 1. Note, that the latter method and that
of Madej (1998)
employ the well-known Kompaneets diffusion approximation to Compton scattering
kernels. The apparent difference between Methods 1 and 2 is that they
use either the differential Kompaneets kernel (Method 1) or kernels given
by integrals over the detailed Compton scattering profiles (Method 2).
,
which ensure the physically correct
description of Compton scattering. The actual equations and
calculations used here strongly differ from those in Madej (1998).
The physics of Compton scattering used here is also
fundamentally different to Method 1. Note, that the latter method and that
of Madej (1998)
employ the well-known Kompaneets diffusion approximation to Compton scattering
kernels. The apparent difference between Methods 1 and 2 is that they
use either the differential Kompaneets kernel (Method 1) or kernels given
by integrals over the detailed Compton scattering profiles (Method 2).
The equation of radiative equilibrium (the energy balance equation) requires
that
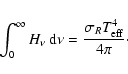 |
(17) |
The above condition is fulfilled in a hot stellar atmosphere, where energy
transport by convective motions can be neglected.
Computing derivatives of both sides of Eq. (17) and using the
equation of transfer, Eq. (14), one can obtain the alternative
energy balance equation
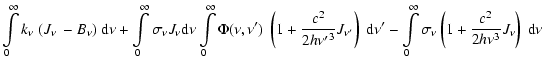 |
|
|
|
![$\displaystyle \int\limits_{0}^{\infty} J_{\nu^\prime}
~ \Phi(\nu,\nu^\prime) ~ ...
...\left[ -{{h(\nu - {\nu^\prime }) }\over {kT}} \right]
~ {\rm d}\nu^\prime = 0 ,$](/articles/aa/full/2006/32/aa5102-06/img78.gif) |
|
|
(18) |
which can be compared with its analog, Eq. (5) of Method 1.
The computer code ATM21 used for the model calculations was
described in detail in Madej & Rózanska (2000) and
Madej et al. (2004). The structure of the code is based on the
partial linearization scheme by Mihalas (1978), in which
corrections of temperature 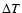 and the function
and the function
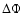 are built into the equation of transfer. The high numerical accuracy
and very good convergence properties of the ATM21 code are vital
for the present paper, and allowed us to compute accurate spectra for
atmospheric parameters appropriate for the white dwarfs HZ 43 and
Sirius B using Method 2, outlined above. These calculations supersede
less accurate X-ray spectra of HZ 43 which were presented in the
earlier paper (Madej 1998).
are built into the equation of transfer. The high numerical accuracy
and very good convergence properties of the ATM21 code are vital
for the present paper, and allowed us to compute accurate spectra for
atmospheric parameters appropriate for the white dwarfs HZ 43 and
Sirius B using Method 2, outlined above. These calculations supersede
less accurate X-ray spectra of HZ 43 which were presented in the
earlier paper (Madej 1998).
For the present research, the ATM21 code included
numerous bound-free LTE opacities of neutral hydrogen and free-free
opacity of ionized hydrogen, which always remains in LTE.
No hydrogen lines were included in the actual computations. In each
temperature iteration the code solves the equation of hydrostatic
equilibrium to obtain stratifications of gas pressure 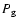 and density
and density 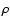 in the model atmosphere. After that the ATM21 code solves
the set of coupled equations of radiative transfer with implicit
temperature corrections and finds the stratification of
in the model atmosphere. After that the ATM21 code solves
the set of coupled equations of radiative transfer with implicit
temperature corrections and finds the stratification of 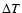 in
the model atmosphere. The equation of radiative transfer was solved
using the
Feautrier method and the technique of variable Eddington factors
(Mihalas 1978). Boundary conditions along the
in
the model atmosphere. The equation of radiative transfer was solved
using the
Feautrier method and the technique of variable Eddington factors
(Mihalas 1978). Boundary conditions along the 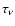 axis were
the same as in Method 1.
Explicit expressions for the temperature corrections,
axis were
the same as in Method 1.
Explicit expressions for the temperature corrections, 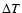 ,
can be
found, e.g., in Madej et al. (2004).
,
can be
found, e.g., in Madej et al. (2004).
3 Computations and results
Using our two independent methods, we investigated the effects of
Compton scattering on the emergent spectra of three pure H white
dwarf models. These were: models appropriate for the well-known DA
white dwarfs Sirius B (assuming
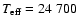 K,
K,
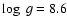 )
and HZ 43 (
)
and HZ 43 (
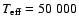 K,
K,
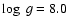 ), together with a significantly hotter
model with
), together with a significantly hotter
model with
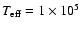 K and
K and
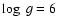 and 8. These
models cover the effective temperature range relevant to pure H DA atmospheres and specifically address the question of whether Compton
scattering might be relevant to the
X-ray bright DA white dwarfs Sirius B and HZ 43 that are central to
the low-energy calibration of Chandra (Pease et al. 2003).
and 8. These
models cover the effective temperature range relevant to pure H DA atmospheres and specifically address the question of whether Compton
scattering might be relevant to the
X-ray bright DA white dwarfs Sirius B and HZ 43 that are central to
the low-energy calibration of Chandra (Pease et al. 2003).
The results of our calculations from both methods are presented in
Figs. 2-5. In Fig. 2a the
spectra of the model atmosphere for the DA white dwarf HZ 43 (
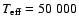 K,
K,
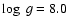 )
computed using Method 1 with (solid
line) and without (dashed line) Compton effects are shown. We also
calculated a non-LTE model atmosphere for HZ 43 using the Tübingen Model
Atmosphere Package (
TMAP) (Werner et al. 2003) and computed the radiation transfer
Eq. (3) with Compton scattering using this non-LTE model
atmosphere structure. The corresponding spectra are shown in
Fig. 2a by the dotted line and by open circles.
)
computed using Method 1 with (solid
line) and without (dashed line) Compton effects are shown. We also
calculated a non-LTE model atmosphere for HZ 43 using the Tübingen Model
Atmosphere Package (
TMAP) (Werner et al. 2003) and computed the radiation transfer
Eq. (3) with Compton scattering using this non-LTE model
atmosphere structure. The corresponding spectra are shown in
Fig. 2a by the dotted line and by open circles.
![\begin{figure}
\par\includegraphics[width=7.3cm,height=10.5cm,clip]{5102fig2.eps}
\end{figure}](/articles/aa/full/2006/32/aa5102-06/Timg87.gif) |
Figure 2:
Spectra a) of the DA white dwarf HZ 43 model atmosphere with (solid line)
and without (dashed line) Compton scattering using Method 1. Also shown are the spectra
of the non-LTE model atmosphere (dotted line) and the spectra of non-LTE
model atmosphere with Compton scattering (open circles). Run b) of
Comptonisation parameter
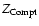 with wavelength (see Eq. (19)).
with wavelength (see Eq. (19)).
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5102fig3.eps}
\end{figure}](/articles/aa/full/2006/32/aa5102-06/Timg88.gif) |
Figure 3:
Emergent X-ray spectra for a pure hydrogen model atmosphere
appropriate for the parameters of HZ 43 computed for classical Thomson
scattering (dashed) and Compton scattering (solid) using Method 2 (the
method of Madej et al. 2004). |
| Open with DEXTER |
Calculations using Method 2 in LTE are illustrated in
Fig. 3. The differences between Compton and Thomson
models in these calculations are very similar to the differences found
in Method 1 in Fig. 2a, and are significant only at
wavelengths <25 Å.
The flux in the
models with Compton scattering (Method 1) is smaller than the flux in the model
without Compton scattering by 0.5% at 50 Å, 1.3% at 40 Å, 7%
at 30 Å, and 40% at 20 Å. Similarly, model computations performed with
Method 2
yield the following differences for HZ 43:
0.5% at 50 Å, 1.4 % at 40 Å, 5% at 30 Å, and 56% at 20 Å.
These results can be understood more clearly if we
consider the Comptonisation parameter
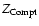 :
:
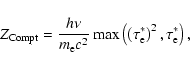 |
(19) |
where
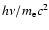 is the relative photon energy lost
during one scattering event off a cool electron,
is the relative photon energy lost
during one scattering event off a cool electron,
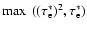 is the number of scattering events the photon
undergoes before escaping,
is the number of scattering events the photon
undergoes before escaping,
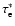 is the Thomson optical depth,
corresponding to the depth where escaping photons of a given frequency
are created. The Comptonisation parameter is, then, a representation
of the influence of Compton down-scattering on the emergent spectrum:
significant Compton effects are expected if the Comptonisation
parameter approaches unity (Rybicki & Lightman 1979). In
Fig. 2b the dependence of
is the Thomson optical depth,
corresponding to the depth where escaping photons of a given frequency
are created. The Comptonisation parameter is, then, a representation
of the influence of Compton down-scattering on the emergent spectrum:
significant Compton effects are expected if the Comptonisation
parameter approaches unity (Rybicki & Lightman 1979). In
Fig. 2b the dependence of
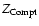 on the
wavelength is shown. It is clear that the Comptonisation parameter is
very small down to 25 Å, and this is indeed reflected in the emergent
spectrum.
on the
wavelength is shown. It is clear that the Comptonisation parameter is
very small down to 25 Å, and this is indeed reflected in the emergent
spectrum.
Similar results were obtained for the DA white dwarf Sirius B
(assuming
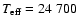 K,
K,
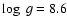 ). The corresponding
spectra and the Comptonisation parameter are shown in
Fig. 4. The effective temperature of this star is smaller,
and the surface gravity is larger, and consequently Compton scattering is
even less significant than for HZ 43. We also calculated a non-LTE
model atmosphere for Sirius B using the TMAP and computed
the radiation transfer Eq. (3) with Compton scattering
using this non-LTE model atmosphere structure, as for HZ 43. The
corresponding spectra are shown in Fig. 4a by the dotted
line and by open circles. Compton scattering changes only very
slightly the emergent spectrum at wavelengths below 20 Å.
). The corresponding
spectra and the Comptonisation parameter are shown in
Fig. 4. The effective temperature of this star is smaller,
and the surface gravity is larger, and consequently Compton scattering is
even less significant than for HZ 43. We also calculated a non-LTE
model atmosphere for Sirius B using the TMAP and computed
the radiation transfer Eq. (3) with Compton scattering
using this non-LTE model atmosphere structure, as for HZ 43. The
corresponding spectra are shown in Fig. 4a by the dotted
line and by open circles. Compton scattering changes only very
slightly the emergent spectrum at wavelengths below 20 Å.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{5102fig4.eps}
\end{figure}](/articles/aa/full/2006/32/aa5102-06/Timg93.gif) |
Figure 4:
The same as Fig. 2 but here for the DA white dwarf Sirius B
LTE model atmosphere. The dotted line lies everywhere under the open circles
(except for hydrogen lines). |
| Open with DEXTER |
In Fig. 5 we present the spectra of the hot DA white
dwarf model atmospheres (
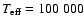 K,
K,
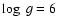 and 8) with and without Compton scattering. It is obvious that Compton
effects are more significant for these hot DA models (especially with
low surface gravity) than for Sirius B and HZ 43, but visible effects
still do not occur for wavelengths >50 Å. Of course,
and 8) with and without Compton scattering. It is obvious that Compton
effects are more significant for these hot DA models (especially with
low surface gravity) than for Sirius B and HZ 43, but visible effects
still do not occur for wavelengths >50 Å. Of course, 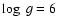 is
not such a realistic value for white dwarfs, but we calculate this model to
demonstrate the dependence of the Compton effect on the surface gravity.
is
not such a realistic value for white dwarfs, but we calculate this model to
demonstrate the dependence of the Compton effect on the surface gravity.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{5102fig5.eps}
\end{figure}](/articles/aa/full/2006/32/aa5102-06/Timg95.gif) |
Figure 5:
Spectra a) of the DA white dwarf
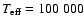 K model
atmospheres with
and without Compton scattering. Solid lines correspond to model with K model
atmospheres with
and without Compton scattering. Solid lines correspond to model with
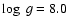 ,
and dashed lines correspond to model with ,
and dashed lines correspond to model with
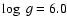 .
Softer high energy tails correspond to models with Compton effect. Run b) of
Comptonisation parameter .
Softer high energy tails correspond to models with Compton effect. Run b) of
Comptonisation parameter
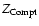 with wavelength.
with wavelength. |
| Open with DEXTER |
The differences we find here between emergent spectra computed using
Thomson and Compton scattering are essentially negligible for practical
purposes. Such differences are in fact much smaller than the
predicted spectral uncertainties resulting from uncertainties in the
current knowledge of the fundamental parameters of DA white
dwarfs - even the best known examples such as HZ 43 and Sirius B.
The spectrum in this Wien tail region is especially sensitive to
uncertainties in the effective temperature.
Comparison of the calculations presented here using both Methods 1 and 2 with the earlier work of Madej (1998) do, however, reveal some
significant differences. For HZ 43, Fig. 3 of Madej (1998)
suggests a large X-ray flux deficit due to Compton scattering of
photons to longer wavelengths, with a precipitous decline in emergent
flux at  40 Å. However, our Figs. 2 and
3 illustrate much smaller effects.
40 Å. However, our Figs. 2 and
3 illustrate much smaller effects.
A careful examination of the Madej (1998) computer code performed
by one of us (JM) has shown that the earlier code (which used
Kompaneets scattering terms) could strongly exaggerate effects of
Compton scattering in cases when they were of only marginal
significance. This is the case for the X-ray spectrum of HZ 43. The
effect was caused by an approximation adopted in the solution of the
transfer equation that was quite valid for the study of X-ray burst
sources, for which the code was primarily developed, but which became
marginally inaccurate for the case of hot DA white dwarf atmospheres.
This problem has been solved by the very stable algorithm of the new code (see
Method 2), described in Madej & Rózanska (2000).
One should note that the differences between this work and that of
Madej (1998) are not related to the numerical approaches adopted
for Compton scattering. Both the Kompaneets diffusion approximation
(Method 1) and the Compton scattering terms of the integral form
(Method 2) satisfactorily describe effects of Compton scattering in
X-ray spectra of hot white dwarf stars. The results of the work
presented here using both methods supersede those of Madej (1998).
At the higher effective temperatures represented by the
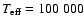 K models, the emergent spectra for Thomson and Compton
scattering begin to diverge at
K models, the emergent spectra for Thomson and Compton
scattering begin to diverge at 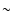 50 Å for the
50 Å for the 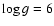 model, and the effects are much larger toward shorter wavelengths than
for the higher gravity
model, and the effects are much larger toward shorter wavelengths than
for the higher gravity 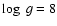 case. It is of course questionable
as to whether any white dwarfs with pure H atmospheres exist with such
high effective temperatures, since in hotter stars radiative
levitation tends to enrich the atmosphere with metals. In atmospheres
with significant metal abundances the electron scattering opacity is
insignificant compared with that due to metals, and Compton
redistribution effects are rendered irrelevant.
case. It is of course questionable
as to whether any white dwarfs with pure H atmospheres exist with such
high effective temperatures, since in hotter stars radiative
levitation tends to enrich the atmosphere with metals. In atmospheres
with significant metal abundances the electron scattering opacity is
insignificant compared with that due to metals, and Compton
redistribution effects are rendered irrelevant.
Our calculations show that even in the hottest pure H atmospheres it
is highly unlikely that future X-ray observations will be sufficiently
sensitive to discern the Compton redistribution effects. Again,
uncertainties in model parameters such as effective temperature and
surface gravity, and abundances of He and trace elements, together
with uncertainties in parameters entering into the modeling calculations
themselves will dominate. Even for models normalised to the same flux
at UV wavelengths a 1% error in
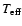 will induce a 20% flux error at 75 Å.
will induce a 20% flux error at 75 Å.
5 Conclusions
New calculations using two independent, rigorous numerical methods
confirm that the effects of Compton energy redistribution in
photon-electron scattering events are completely negligible for the
interpretation of X-ray spectra of DA white dwarfs such as Sirius B
and HZ 43. Differences between emergent spectra of Compton and Thomson
cases are in fact much smaller than the predicted spectral
uncertainties resulting from uncertaintiesin the current knowledge of
the fundamental parameters of stars such as HZ 43. We have found that
differences between Compton effects predicted here for HZ 43 and the
calculations of Madej (1998) are caused by approximations used in
the solution of the transfer equation in the former work; the results
presented here supersede the earlier ones. We conclude that
current non-LTE model atmosphere spectra of hot DA white dwarfs
neglecting Compton scattering can be safely used for the
calibration low energy detectors of X-ray observatories for the
foreseeable future.
Acknowledgements
V.S. thanks DFG for financial support (grant We 1312/35-1) and Russian FBR
(grant 05-02-17744) for partial support of this investigation.
J.M. acknowledges support by the Polish Committee for
Scientific Research grant No. 1 P03D 001 26.
J.J.D. was supported by NASA contract NAS8-39073 to the
Chandra X-ray Center during the course of this research. T.R. is supported by DLR (grant 50 OR 0201).
- Grebenev, S. A., &
Sunyaev, R. A. 2002, Astron. Lett., 28, 150 [NASA ADS] [CrossRef]
- Guilbert,
P. W. 1981, MNRAS, 197, 451 [NASA ADS] (In the text)
-
Ibragimov, A. A., Suleimanov, V. F., Vikhlinin, A., &
Sakhibullin, N. A. 2003, Astron. Rep., 47, 186 [NASA ADS] [CrossRef] (In the text)
-
Kompaneets, A. S. 1957, Sov. Phys. JETP, 4, 730
- Kurucz, R. 1993,
Atomic data for opacity calculations, Kurucz CD-ROMs,
Cambridge, Mass.: Smithsonian Astrophysical Observatory, 1
- Kurucz,
R. L. 1970, SAO Special Rep., 309
- Madej, J. 1991,
ApJ, 376, 161 [NASA ADS] [CrossRef]
- Madej, J. 1994,
A&A, 286, 515 [NASA ADS] (In the text)
- Madej, J. 1998,
A&A, 340, 617 [NASA ADS] (In the text)
-
Madej, J., & Rózanska, A. 2000, A&A, 363, 1055 [NASA ADS] (In the text)
- Madej,
J., Joss, P. C., & Rózanska, A. 2004, ApJ, 602,
904 [NASA ADS] [CrossRef] (In the text)
- Mihalas, D.
1978, Stellar atmospheres, 2nd edition (San Francisco:
W. H. Freeman and Co.)
(In the text)
- Pavlov,
G. G., Shibanov, I. A., & Zavlin, V. E. 1991,
MNRAS, 253, 193 [NASA ADS]
- Pease,
D. O., Drake, J. J., Kashyap, V. L., et al.
2003, in X-Ray and Gamma-Ray Telescopes and Instruments for
Astronomy, ed. J. E. Trümper, & H. D. Tananbaum, Proc.
SPIE, 4851, 157
(In the text)
- Pomraning,
G. C. 1973, The equations of radiation hydrodynamics
(International Series of Monographs in Natural Philosophy, Oxford:
Pergamon Press)
- Rybicki, G. B., &
Lightman, A. P. 1979, Radiative processes in astrophysics (New
York: Wiley-Interscience)
(In the text)
- Sampson,
D. H. 1959, ApJ, 129, 734 [NASA ADS] [CrossRef] (In the text)
- Swartz,
D. A., Ghosh, K. K., Suleimanov, V., Tennant, A. F.,
& Wu, K. 2002, ApJ, 574, 382 [NASA ADS] [CrossRef] (In the text)
- Werner,
K., Deetjen, J. L., Dreizler, S., Nagel, T., Rauch, T., &
Schuh, S. L. 2003, in Stellar Atmosphere Modeling, ASP Conf.
Ser., 288, 31
(In the text)
-
Zavlin, V. E., & Shibanov, Y. A. 1991, Sov. Astron.,
35, 499 [NASA ADS]
Copyright ESO 2006
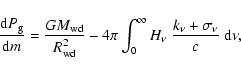
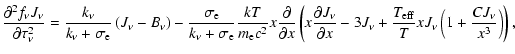
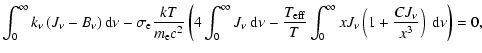
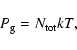
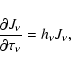
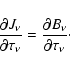
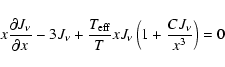
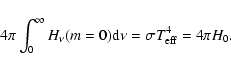
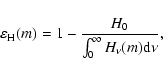
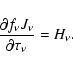
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{5102fig1.eps}
\end{figure}](/articles/aa/full/2006/32/aa5102-06/Timg62.gif)
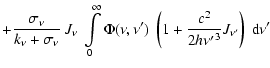
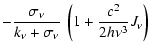
![$\displaystyle \times\int \limits _{0}^{\infty} \Phi (\nu ,\nu ^\prime) J_{\nu ^...
...p \left[ -{{h(\nu - {\nu ^\prime }) }\over {kT}} \right]
~ {\rm d}\nu ^\prime .$](/articles/aa/full/2006/32/aa5102-06/img67.gif)
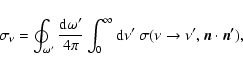
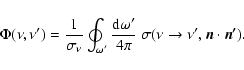
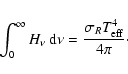
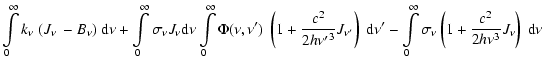
![$\displaystyle \int\limits_{0}^{\infty} J_{\nu^\prime}
~ \Phi(\nu,\nu^\prime) ~ ...
...\left[ -{{h(\nu - {\nu^\prime }) }\over {kT}} \right]
~ {\rm d}\nu^\prime = 0 ,$](/articles/aa/full/2006/32/aa5102-06/img78.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,height=10.5cm,clip]{5102fig2.eps}
\end{figure}](/articles/aa/full/2006/32/aa5102-06/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5102fig3.eps}
\end{figure}](/articles/aa/full/2006/32/aa5102-06/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{5102fig4.eps}
\end{figure}](/articles/aa/full/2006/32/aa5102-06/Timg93.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{5102fig5.eps}
\end{figure}](/articles/aa/full/2006/32/aa5102-06/Timg95.gif)