A&A 455, 259-269 (2006)
DOI: 10.1051/0004-6361:20064829

High-precision elements of double-lined spectroscopic binaries from combined interferometry and spectroscopy

Application to the $\beta~$Cephei star $\beta$ Centauri

M. Ausseloos¹ - C. Aerts^1,2 - K. Lefever¹ - J. Davis³ - P. Harmanec^4,5

1 - Instituut voor Sterrenkunde, Katholieke Universiteit Leuven, Celestijnenlaan 200 B, 3001 Leuven, Belgium
2 - Department of Astrophysics, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
3 - Chatterton Astronomy Department, School of Physics, University of Sydney, NSW 2006, Australia
4 - Astronomical Institute of the Charles University, V Holesovickách 2, 180 00 Praha 8, Czech Republic
5 - Astronomical Institute, Academy of Sciences, 251 65 Ondrejov, Czech Republic

Received 9 January 2006 / Accepted 10 April 2006

Abstract
Aims. We present methodology to derive high-precision estimates of the fundamental parameters of double-lined spectroscopic binaries. We apply the methods to the case study of the double-lined $\beta~$Cephei star $\beta~$Centauri. We also present a detailed analysis of $\beta~$Centauri's line-profile variations caused by its oscillations.
Methods. High-resolution spectral time series and visual or interferometric data with a good phase distribution along the orbital period are required. We point out that a systematic error in the orbital amplitudes, and any quantities derived from them, occurs if the radial velocities of blended component lines are computed without spectral disentangling. This technique is an essential ingredient in the derivation of the physical parameters if the goal is to obtain a precision of only a few percent. We have devised iteration schemes to obtain the orbital elements for systems whose lines are blended throughout the orbital cycle.
Results. We derive the component masses and dynamical parallax of $\beta~$Centauri with a precision of 6% and 4%, respectively. Modelling allowed us to refine the mass estimates to 1% precision resulting in $M_1=10.7\pm 0.1~M_\odot$ and $M_2=10.3\pm 0.1~M_\odot$, and to derive the age of the system as being $(14.1\pm 0.6)\times 10^6$ years. We deduce two oscillation frequencies for the broad-lined primary of $\beta~$Centauri: f₁=7.415 c d^-1 and f₂=4.542 c d^-1 or one of their aliases. The degrees of these oscillation modes are higher than 2 for both frequencies, irrespective of the alias problem. No evidence of oscillations in the narrow-lined secondary was found.
Conclusions. We propose that our iteration schemes be used in any future derivations of the spectroscopic orbital parameters of double-lined binaries with blended component lines to which disentangling can be successfully applied. The combination of parameters resulting from the iteration schemes with high-precision estimates of the orbital inclination and the angular semi-major axis from interferometric or visual measurements allows a complete solution of the system.

Key words: stars: binaries: spectroscopic - stars: individual: $\beta~$Centauri - methods: observational - methods: data analysis - line: profiles - techniques: spectroscopic

   
1 Introduction

Binary stars have long been considered as astrophysical laboratories, providing one of the best tests of stellar structure models (e.g., Maceroni 2005; and Ribas 2005, for recent reviews). This is particularly so for massive binaries because their structure and evolution are not well-understood, while being of great importance for the chemical enrichment and evolution of galaxies. The convective and rotational mixing properties of massive stars with a well-developed convective core are still poorly calibrated, while being the dominant factors determining their evolution (e.g. Maeder & Meynet 2000). While observational capabilities and analysis tools have improved significantly in recent years (e.g. Hilditch 2004a), there is still a lack of ultra-precise fundamental parameter determinations of binaries with an OB-type component (e.g. Hilditch 2004b). Indeed, component mass estimates with a precision better than 2% are available for relatively few such systems, although such a precision is necessary to provide stringent observational tests for stellar structure and evolution models (e.g. Andersen 1991). In this paper, we provide methodology to achieve a high precision for mass estimates from combined interferometric and spectroscopic data of double-lined spectroscopic binaries with merged component lines, and we apply it to the massive binary $\beta~$Cen. The methods are based on spectral disentangling (Hadrava 1995, 1997, 2001, 2004b).

The bright star $\beta~$Cen (HD 122451, HR 5267, B1 III, m_V=0.6) has been known to be variable in velocity since the beginning of the twentieth century. It is the brightest member of the class of $\beta~$Cephei stars, a homogeneous group of oscillating B0-B3 stars (see Stankov & Handler 2005 for a recent review). They have low-degree, low-order pressure and gravity modes with periods of a few hours excited by the $\kappa~$mechanism (Pamyatnykh 1999). They reveal amplitudes of several tens of mmag down to the detection threshold in UBV, so these stars are good potential targets for in-depth seismic studies. Asteroseismology of $\beta~$Cephei stars indeed received a lot of attention lately, after it became clear that their oscillations cannot be explained in terms of standard evolution models. For two prototypical class members, the oscillations revealed differential internal rotation and the occurrence of core convective overshooting (HD 129929: Aerts et al. 2003 and Dupret et al. 2004; $\nu~$Eri: Pamyatnykh et al. 2004 and Ausseloos et al. 2004).

As one of the brightest stars in the southern hemisphere as a whole, $\beta~$Cen has been the subject of numerous studies. We refer to Ausseloos et al. (2002, hereafter Paper I), Davis et al. (2005, hereafter Paper II), and references in these two papers for an overview of these studies, without repeating all of the information here. We summarise only briefly the characteristics of the system that are relevant for our current work.

High-resolution spectra covering 12 years revealed that $\beta~$Cen is a double-lined spectroscopic binary with an orbital period of 357 days and an eccentricity of about 0.81 (Paper I). Interferometric data assembled with the Sydney University Stellar Interferometer (SUSI) and covering 7 years led to similar values for the period and eccentricity and, moreover, to an orbital inclination of $67.4^\circ$ and an angular semi-major axis of 0.0253'', as well as to a brightness ratio of $0.868\pm 0.015$(Paper II). The spectroscopic variability is due not only to the binarity, but also to oscillations of the components with periods of several hours (Paper I). The star is photometrically constant at the level of mmag.

The independent orbital fits to the spectroscopic and interferometric data have four parameters in common: the orbital period ( $P_{\rm orb}$), the epoch of periastron passage (E₀), the eccentricity (e), and the longitude of periastron ($\omega$). The values of these four differed by less than the 1$\sigma$uncertainties such that a fully consistent orbital solution for $\beta$ Cen was achieved (Paper II). The combination of all the available information subsequently led to the conclusion that the system consists of components with equal masses of $M_1=M_2=9.3\pm 0.3~M_\odot$ (i.e., a precision of 3.2%) and that it has a dynamical parallax of $9.78\pm 0.16$ mas.

We show in this work that the masses of the components of $\beta~$Cen were significantly underestimated due to a systematic error in the amplitudes of the spectroscopic orbit. This is a consequence of the inappropriate way in which the radial velocities were estimated from line profiles of merged spectra. A similar conclusion was reached recently by Tango et al. (2006) for the triple system $\lambda~$Sco and occurs for any spectroscopic binary in which both components contribute to the lines used for the orbital radial-velocity (hereafter abbreviated as RV) determination. Earlier attempts to avoid such systematic error can be found in Tomkin et al. (1995) for the $\delta~$Scuti star $\theta^2$ Tauri. In that work, the authors subtracted the lines of the primary by means of spectra of reference stars with the same spectral type before computing the secondary's RV values. We provide analysis schemes based on spectral disentangling to overcome this problem of systematic errors in a more accurate way. Our schemes allow us to eliminate the systematic errors in the physical parameters. We illustrate our method by its application to the case of $\beta~$Cen. Our methodology is applicable to the analysis of any spectroscopic binary whose line profiles can be successfully disentangled. It leads to a significant improvement in the precision of the physical parameters and dynamical parallax of such systems, similar to the case of binaries with emission-line stars (Harmanec 2002).

   
2 Methodology for orbital determination

The data used to illustrate our methodology are the SiIII $\lambda$ 4552.6 Å line profiles of $\beta~$Cen obtained over 12 years with the ESO CAT telescope and with the Swiss Euler telescope, as described in Paper I.

	Figure 1: SiIII $\lambda$ 4552.6 Å line profile obtained by averaging ten spectra measured on 16 May 1988 (solid line). The two vertical lines denote the integration limits which were used in Paper I to calculate the RV of the secondary. The two dotted lines denote the disentangled line profiles of both components.
Open with DEXTER

By means of illustration of the system's lines and of the occurrence of a systematic error in the orbital RV determinations used in Papers I and II, we recall here in quite some detail the way the RVs were obtained. We show in Fig. 1 a typical line profile of the system averaged over one night of data, i.e., a profile in which the oscillatory variations are averaged out. As can be seen, the lines produced by the two components are blended with each other. In none of the available spectra are the two components' lines well separated. Moreover, the oscillations induce deviations from a Gaussian shape for each of the line components (see Fig. 1 in Paper I). For this reason, the RV values of the component with the narrowest line were derived from the line centroid (first moment, see Aerts et al. 1992 for a definition) in Paper I, with the integration limits indicated in Fig. 1 corresponding to a normalised flux value of 0.95.

	Figure 2: SiIII $\lambda$ 4552.6 Å line profile obtained by averaging 39 spectra taken during a period of 12 nights (3-14 August 2000). The vertical lines demonstrate the estimate of the total line width of the broad-lined component.
Open with DEXTER

The orbital RVs for the broad-lined component could not be derived in this way. The following strategy was therefore followed in Paper I. The full width of the line was derived from epochs when the radial velocities of both components did not differ much (see Fig. 2). It was assumed that this width is constant, which is a reasonable approach because rotational broadening is dominant for this component. The centre of the broad line, obtained from averaging spectra over a night (CAT) or over two weeks (Euler), determined by starting from either its left or its right wing, was taken as a good estimate of the RV of the broad-lined component.

We show below that these procedures lead to an underestimation of the true RV values, particularly for the narrow-lined component. We provide the final RV values of both components in Table 1 (only available electronically at the CDS). Hereafter, we will refer to the star producing the deeper and narrower SiIII lines as the secondary and to the other component as the primary. Although this is the opposite of what has been done in the literature so far, we show that the component with the broader lines is indeed the more massive of the two.

   
2.1 KOREL disentangling

Starting from the orbital solution presented in Paper II, we applied KOREL spectral disentangling (Hadrava 1995, 1997, 2001, 2004b). Although KOREL was not developed to treat line-profile variations due to oscillations, Harmanec et al. (2005) showed that the code is able to treat such a complex combination of variability.

KOREL was applied to our $\beta~$Cen CES spectra for many different sets of code input parameters and weights, the CORALIE spectra being too noisy to allow convergence. The resulting disentangled profiles were evaluated each time by visual inspection, paying attention to smoothness, symmetry, and the residual sum of squares. We considered both the situations where line strengths were allowed for and were not taken into account. Moreover, we used several types of weights. Weights proportional to (S/N)² turned out to lead to the most stable solution. The best results were clearly obtained when KOREL was allowed to search through a larger subregion in orbital parameter space than indicated by the uncertainties obtained in Paper II.

The adopted KOREL solution was obtained in four subsequent steps, in which the solution of a particular step was used as the initial guess in the next step. First the light intensities were kept fixed, next the intensity of the primary was allowed to vary, then the intensity of the secondary could vary, and finally the intensities of both components were allowed to vary. This led to a final KOREL orbital solution which was slightly, but significantly, different from the one in Paper II, the largest discrepancy occurring in the value of the semi-amplitude of the secondary's orbit K₂: $63.8 \pm0.6$ km s^-1 (Paper II) versus 68.1 km s^-1 ( KOREL). The present version of KOREL unfortunately does not provide errors in the orbital parameter values given as output.

The dotted lines in Fig. 1 show the disentangled profiles of the primary and secondary shifted to the orbital RV obtained in Paper I. It is obvious from Fig. 1 that the RV estimate of the secondary derived in Paper I is an underestimation of the true RV and that we must take this into account in the derivation of the physical parameters of the components.

In principle, a single application of KOREL disentangling to the blended line profiles should be enough to obtain the final orbital solution. In practice, however, tiny changes in the KOREL input parameters changed the final orbital solution considerably while producing only small changes in the mean disentangled profiles and rms value. For this reason, we devised the iteration schemes discussed below.

2.2 Preliminary update of the orbital solution

	Figure 3: A SiIII $\lambda$ 4552.6 Å line observed on 15 March 1998 (full line) and the secondary's disentangled line profile, which is shifted according to its corresponding orbital RV (dashed line). The residual spectrum obtained by subtracting the shifted disentangled line profile from the original spectrum is shown as dots.
Open with DEXTER

The disentangled line profile of the secondary allows us to improve the orbital solution of the primary. We carried out the following procedure for each of the spectra. We shifted the secondary's disentangled profile according to its orbital RV obtained in Paper I. We subsequently subtracted this shifted disentangled profile from the original blended line profile. This procedure is illustrated in Fig. 3 for one measurement. In this way, we obtain a $\lambda$ 4552.6 Å line profile of the primary whose position and shape is due to the orbital velocity, as well as to the variability due to the oscillations (the dotted line in Fig. 3). This procedure resulted in 402 line profiles $(\lambda, I(\lambda))$which were used to calculate the true RV of the primary. In view of the bumpy profiles, we cannot use a Gaussian fit to compute this true RV. We determine it as follows:

$$v_{\rm rad} = \frac{\int (1-I(\lambda))v_\lambda ~{\rm d}\lambda} {EW},$$ (1)

with EW denoting the equivalent width of the line profile

$${EW} = \int (1-I(\lambda))~{\rm d}\lambda,$$ (2)

and $v_\lambda$ derived by the equation

$$v_\lambda = \frac{\lambda-\lambda_0}{\lambda_0}~c,$$

with c and $\lambda_0$the speed of light and the laboratory wavelength, respectively. What we call the true RV is thus the centroid of the line profile (also termed the first moment, see Aerts et al. 1992, for further extensive discussion of this quantity). Its computation was done by fixing the integration limits interactively for each separate profile, after subtracting the disentangled profile of the secondary. In this way, 402 RV values of the primary were obtained (compared with only 27 values used in Paper I obtained with the procedure described above by means of Fig. 2).

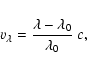
Next, these 402 RV values of the primary were added to the 402 values for the secondary derived in Paper I, and the code FOTEL (Hadrava 1990, 2004a) was applied to this combined RV dataset. The results are quite similar to the ones listed in Paper II, except that the semi-amplitude of the primary's orbit, K₁, is significantly smaller. This is consistent with the KOREL disentangling analysis, which led to a higher value of the semi-amplitude of the secondary, K₂ (compared to the value found in Paper II). Both these results, i.e., a lower K₁ value from KOREL and a higher K₂ value after disentangling the secondary's profile, suggest that the mass ratio M₁/M₂ has been underestimated in Paper II.

Subsequently, a second attempt was undertaken to disentangle the spectra with KOREL by searching through a neighbouring subregion of the orbital parameter space centred around the updated orbital solution with a higher mass ratio. Again, satisfactory results were obtained similar to the orbital solution from FOTEL, except for the values of the semi-amplitudes K₁ and K₂. In comparison with our first attempt to apply KOREL, the residual sum of squares was lower. Figure 4 shows the best disentangled SiIII $\lambda$ 4552.6 Å line profiles of both components at this stage of the process.

	Figure 4: The disentangled SiIII $\lambda$ 4552.6 Å line profiles of the primary (full line) and secondary (dashed line).
Open with DEXTER

2.3 Analysis of the systematic error

We return to Fig. 1. The merged line profile, $I(\lambda)$, is obviously the sum of the primary's average line profile $I_1(\lambda)$ and the secondary's average line profile $I_2(\lambda)$. The primary's disentangled line profile delivers a good approximation of I₁, while the one of the secondary results in an approximation of I₂ (dotted lines in Fig. 1). The 402 RV values for the secondary derived in Paper I were obtained by calculating the centroid of the composite Si III $\lambda$ 4552.6 Å line profile, i.e., from Eq. (1) with $I(\lambda)=I_1(\lambda)+I_2(\lambda)$. To minimize the interfering influence of the primary's line profile $I_1(\lambda)$, the integration limits in Eqs. (1) and (2) were fixed corresponding to a flux value of 0.95 in Paper I, as indicated in Fig. 1. The secondary's RV is, however, given by the centroid of only the secondary's line profile $I_2(\lambda)$. So, calculating the secondary's RVs as was done in Paper I, gives each $v_\lambda$ in the integral (1) too high a weight. When both components have a similar RV, the method adopted in Paper I provides a reasonable approximation of the secondary's RV for the following reasons:

1.

the depth of the secondary's line profile has a significantly larger contribution to the depth of the composite line profile than the depth of the primary's line profile;

2.

the depth of the primary's line profile does not vary much within the integration limits because of the large width of the primary's line profile on the one hand and the fact that both components have a similar radial velocity on the other hand;

3.

the equivalent width in the denominator of Eq. (1) normalises the weighted integral in the numerator.

A systematic error is, however, introduced when the components' RVs are significantly different. This is the case in Fig. 1, as the spectrum shown is observed close to a time at which the primary (secondary) has its minimum (maximum) orbital RV. Indeed, in such cases, the second condition above is not fulfilled, as the depth of the primary's line profile changes considerably within the integration limits. One can derive from Fig. 1 that, within the integration limits, the depth of the primary's line profile decreases monotonically with increasing wavelength so that the additional weight given to each $v_\lambda$ in Eq. (1) strongly varies due to the blending of both line profiles. As lower $v_\lambda$ values systematically get more weight than higher $v_\lambda$ values, the procedure applied so far still underestimates the RV of the secondary. We cannot but conclude that a systematic error has been introduced in Paper I in the calculation of the RVs, due to the fact that the line profiles of both components are so strongly blended with each other.

   
2.4 Iterative determination of the orbital parameters

Since the orbital parameters common to the fit to both the spectroscopic and interferometric data were in agreement with each other, it is appropriate to assume that this spectroscopically determined orbital solution is already close to the true orbit and can hence be considered as a good initial solution to start an iterative process to improve the orbital parameter values. Two different iteration schemes were applied.

   
2.4.1 Iteration scheme I

Figure 5 summarises the features of the first iteration scheme. In each iteration step, a new orbital solution is calculated by applying FOTEL to the combined dataset of new RV values of both the primary and secondary. The new set of the primary's RVs is obtained by calculating the centroid of the "secondary subtracted line profiles''. The latter refer to the spectra obtained by taking the difference between the original spectra and the shifted secondary's disentangled line profile (abbreviated as "secondary's LP'' in Fig. 4). The shift corresponds to the orbital velocity value given by the orbital solution of the previous iteration step. This procedure to determine the secondary subtracted line profiles is illustrated in Fig. 3. A new set of the secondary's RV values is calculated in each iteration step in an analogous manner by means of the primary's disentangled line profile (abbreviated as "primary's LP'' in Fig. 4). The primary's and secondary's disentangled line profiles mentioned above are properly normalised versions of the best disentangled profiles obtained with KOREL. All centroid velocity values were made with fixed integration limits to reduce the noise level. The widths of the primary's and secondary's disentangled line profiles provide us with an objective way to select these fixed integration limits.

   
2.4.2 Iteration scheme II

The second iteration scheme is similar to the first one, but slightly more complicated. For the sake of clarity, the reader is advised to refer to Fig. 6 while reading the following description.

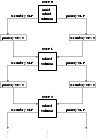	Figure 5: Flowchart diagram of iteration scheme I (see text for details).
Open with DEXTER

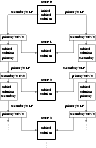	Figure 6: Flowchart diagram of iteration scheme II (see text for details).
Open with DEXTER

In each iteration step, a new orbital solution is again derived on the basis of the combined dataset that consists of the newly derived RV values of both components. Just as in iteration scheme I, the new primary's (secondary's) RVs are derived by calculating the centroid of the "secondary's (primary's) subtracted line profiles'' with fixed integration limits according to the width of the disentangled line profile of either component. The difference between the two iteration schemes lies in the way that these "primary's/secondary's subtracted line profiles'' are constructed. For each original spectrum, both schemes shift the primary's (secondary's) disentangled line profile according to the corresponding orbital velocity that was found in the previous iteration step and subtract it from the original spectrum. While iteration scheme I uses the orbital RV corresponding to the orbital solution derived on the basis of the old RV datasets of both components, iteration scheme II derives the new primary's (secondary's) RV dataset by using the orbital solution derived on the basis of the old secondary's (primary's) RVs.

	Figure 7: Comparison of the results of iteration scheme I (open symbols) and II (filled symbols): evolution of the orbital period $P_{\rm orb}$ ( upper panel), system velocity $v_\gamma$ ( middle panel), and the semi-amplitudes K1 (dots) and K2 (triangles) ( lower panel). The vertical bars denote the errors provided by FOTEL.
Open with DEXTER

Figure 8: Comparison of the results of iteration scheme I (open symbols) and II (filled symbols): evolution of the eccentricity e ( upper panel), epoch of periastron passage $E_{\rm o}$ ( middle panel), and the longitude of periastron $\omega$ ( lower panel). The two horizontal, dotted lines in each panel indicate the corresponding interval estimated from the interferometric measurements taken from Paper II. The vertical bars denote the errors provided by FOTEL.

Open with DEXTER

Figures 7 and 8 show the results of the application of iteration schemes I (open symbols) and II (filled symbols). It reveals only minor differences in the final parameter values obtained with both schemes. Scheme II leads to a slightly higher value of the orbital period, but the differences in the system velocity as well as the semi-amplitudes of both components' orbit are totally negligible. The stability of the semi-amplitudes K₁ and K₂ is of particular importance as these parameters allow an accurate mass determination of both components. The upper panel of Fig. 8 shows that both iteration schemes make the eccentricity converge to a value in excellent agreement with the interferometric value. One can derive from the middle panel of Fig. 8 that iteration scheme II puts the value of the epoch of periastron passage closer to the centre of the interval which was derived for this parameter on the basis of interferometric data than scheme I. The lower panel of Fig. 8 reveals an increase in the value of the longitude of periastron which eliminates the small discrepancy which appeared when applying iteration scheme I.

2.4.3 Evaluation of both iteration schemes

The final orbital solutions derived with iteration schemes I and II are listed in the second and third columns of Table 2, respectively.

To reveal the origin of the small differences between the results obtained with the two iteration schemes, we examined the dataset consisting of the differences between the final RV values derived with iteration schemes II and I:

$$\{\Delta v(t)\}_t = \{v_{\rm rad,~II}(t) - v_{\rm rad,~I}(t)\}_t.$$

This dataset includes two subsets: the primary's and secondary's radial velocity differences between schemes II and I:

$$\{\Delta v(t)\}_t = \{\Delta v_{\rm ~primary}(t)\}_t \cup \{\Delta v_{\rm ~ secondary}(t)\}_t.$$

For each of the above three datasets, the average and the standard deviation were calculated. It is clear from the results, which are listed in Table 3, that the secondary's RVs are in much better agreement than those of the primary. The larger average difference of the $\{\Delta v_{\rm ~primary}(t)\}_t$ dataset is due to the primary's line profile being so strongly rotationally broadened. This implies that the orbital solution derived by means of only the secondary's final RVs is very stable regardless of the applied iteration scheme, while the orbital solution derived on the basis of only the primary's final RVs is somewhat less stable and, hence, causes the small difference between the final results of iteration scheme I and II. We consider the results obtained with iteration scheme II more reliable because they are in better agreement with the interferometrically derived orbital solution on the one hand and, although it is not clear in the rounded values listed in Table 2, the uncertainties in the derived parameters derived with scheme II are all smaller.

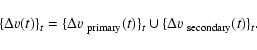
We also note that both iteration schemes lead to smaller error bars on the derived orbital parameter values than the ones obtained in Paper I. Figures 7 and 8 show that the uncertainties in the system velocity, the semi-amplitude of the primary's orbit, and the longitude of periastron have been significantly lowered by the iterative process. The application of iteration scheme II maintains or even improves the compatibility with the interferometric results (see Fig. 8). Therefore, we conclude that the iterative process results in a significant improvement of the orbital solution.

Table 2: Orbital parameters for $\beta$ Cen obtained from KOREL disentangling and by the application of iteration processes to the observed SiIII $\lambda$ 4552.6 Å line profiles listed in Paper I. The errors are 1$\sigma$ estimates resulting from FOTEL assuming the KOREL disentangled profiles to be error-free.

Table 3: Statistical properties of the differences between the final RV values derived with iteration scheme II and I. See text for more information on the three datasets.

The final primary's (open dots) and secondary's (filled dots) RV values that were obtained with iteration scheme II are shown in Fig. 9. The best combined fit to these datasets is denoted as a full (primary's orbit) or dashed (secondary's orbit) line. The fit is satisfying compared to the one obtained in Paper I.

	Figure 9: The orbital curves obtained by means of iteration scheme II. The open and filled dots represent the RVs of, respectively, the primary and secondary components around the centre of mass. The full and dashed lines represent the best-fitting orbits of the primary and secondary, respectively, according to the parameters listed in the column labelled "Scheme II'' in Table 2.
Open with DEXTER

Finally, we applied KOREL again with this new, iteratively derived orbital solution. Indeed, in theory this can result in improved versions of the disentangled profiles of both components and, therefore, allow an iteration process on a higher level. However, the best disentangled profiles that came out of the KOREL analysis were hardly distinguishable from the ones shown in Fig. 4 and, hence, there is no point in repeating the iteration process with these "new'' disentangled profiles. In particular, the small bump in the centre of the primary's disentangled profile in Fig. 4 did not disappear. It is due to the imperfect averaging over the oscillations of the primary by KOREL. This is not surprising in view of its complex multiperiodic high-degree oscillations, which we cannot unravel perfectly from our data (see Sect. 4).

   
3 Physical parameters of the components

The physical parameters of $\beta~$Cen derived in Paper II were obtained without taking into account the systematic effects described here. Their values and errors must clearly be revised. The error estimates were optimistic as they were derived from systematically underestimated RV values.

We first checked that the refined value of the orbital period (which was fixed in deriving the interferometric orbital parameters in Paper II) does not change the values of the orbital inclination and angular semi-major axis. We then followed the same strategy for the computation of the individual component masses as in Paper II, using the refined values of the orbital period and the semi-amplitudes of both components from scheme II, the orbital inclination from the interferometry given in Paper II, and the mean of the spectroscopic and interferometric values for the eccentricity. We also need to take into account the standard errors of these quantities. This is not so straightforward for the parameters resulting from our iteration schemes because their 1$\sigma$ error from FOTEL listed in Table 2 is necessarily an underestimation of the true error. Indeed, these errors were derived under the assumption that the disentangled profiles resulting from KOREL are error-free, which is not the case. We are, unfortunately, unable to propagate the uncertainty induced by the disentangling properly because the current version of KOREL does not provide us with error estimates. Moreover, our schemes implicitly assume that KOREL appropriately treats the effects of the oscillations as random noise in computing the disentangled profiles. For this reason, we adopt a very conservative approach for the error propagation and use 2$\sigma$errors rather than those listed in Table 2 in the derivation of the physical parameters of the system. Following the approach of Paper II, this leads to $M_1 = 11.2 \pm 0.7 ~M_\odot$ and $M_2 = 9.8 \pm 0.7~M_\odot$. Finally, this explains our choice for the revised nomenclature of the primary and secondary.

We attempted to refine these estimates by using all the additional observational information we have at our disposal, such as the CORALIE échelle spectra. We first estimated the effective temperature and gravity of the two components by following the procedure outlined in Uytterhoeven et al. (2005) for the double-lined binary $\kappa~$Sco, i.e., by merging theoretical line profiles of H, He, and Si lines with the appropriate flux ratio according to NLTE predictions made from the latest version of the FASTWIND code (Puls et al. 2005), after using the orbital RVs to shift the profiles. This led us to the conclusion that both components have $T_{\rm eff}=24~000\pm 1000$ K and $\log~g=3.4\pm 0.3$. The large uncertainty in the gravity stems from the difficulty in achieving a proper normalisation of the spectra near the Balmer lines. Since we find the two components to have equal $T_{\rm eff}$ and $\log~g$ within the uncertainties, it is possible to compute photometric estimates of these quantities from multicolour photometry. We did this from Geneva measurements of $\beta~$Cen at our disposal and find $T_{\rm eff}=26~500\pm 500$ K and $\log~g=3.7\pm 0.2$ assuming equal components. This leads us to a safe broad range of $T_{\rm eff}=25~000\pm 2000$ K and $\log~g=3.5\pm 0.4$ for both components.

We subsequently scanned the very extensive database of main-sequence stellar models published by Ausseloos et al. (2004), which have a range in mass from 7 to 13$~M_\odot$ in steps of $0.1~M_\odot$ and a range in Z from 0.012 to 0.030 in steps of 0.002, for each of the three values of the core overshooting parameter of 0.0, 0.1, and 0.2 expressed in local pressure scale heights. The models have X=0.70 and the solar mixture of Grevesse et al. (1996). For a description of the input physics, we refer to Ausseloos et al. (2004). We scanned this database requesting that the masses, effective temperatures, and gravities of $\beta~$Cen's components lie in the appropriate ranges and that the age of the components must be equal to within 1%. This leads us to acceptable ranges for the masses of $M_1\in [10.6,10.8]~M_\odot$ and $M_2\in [10.2,10.4]~M_\odot$, and an age  $\in [13.5,14.7]$ million years.

As an a posteriori check, we computed the allowed mass ratio resulting from the brightness ratio obtained from the interferometry in Paper II and the mass-luminosity relation $\log ~(L_2/L_1)=(3.51\pm 0.14) \log ~(M_2/M_1)$(Griffiths et al. 1988). We thus find the condition $M_2/M_1\in[0.95,0.97]$, which is fulfilled by our solutions for the masses resulting from the spectroscopy and interferometry refined by the modelling.

Finally, the systematic errors in the semi-amplitudes also call for a re-evaluation of the dynamical parallax given in Paper II. Following the same approach as in Paper II and using $2\sigma$ errors for the spectroscopic elements, we find $\pi = 9.3\pm 0.3$, resulting in a distance of $108\pm4$ pc.

4 Analysis of the line-profile variability

Challenging aspects of massive star asteroseismology are the detection of numerous frequencies and their mode identification on the one hand, and the derivation of the fundamental parameters of the targets ( $T_{\rm eff}$, $\log~g$, M) with high precision on the other hand. We succeeded in the latter, and make an attempt to tackle the former challenge now.

4.1 Frequency analysis

Our aim is to find the timescales associated with the short-term line-profile variability and to connect each timescale with the component to which it belongs. This is by no means straightforward because the short-term variations have a significantly lower amplitude than the orbital variations. Moreover, the line profiles of both components are fully blended with each other at all orbital phases. This required a specific non-standard analysis, the details of which are available in Ausseloos (2005). Here, we present only a concise summary of the results. In particular, we point out that the complexity of the profile variations due to the presence of moving subfeatures (see Ausseloos 2005, p. 28, Fig. 2.1 for examples and Fig. 3) does not favour a standard radial-velocity analysis, but requires a search for frequencies across the whole width of the profiles.

We perform an analysis of the intrinsic variability of the primary by using a two-dimensional (2D) frequency analysis method first introduced by Gies & Kullavanijaya (1988) and later defined as the Intensity Period Search (IPS) by Telting et al. (1997). We used a 2D version of the Lomb-Scargle method (Scargle 1982) for the time series of normalised flux values at each wavelength across the profile. As we found a value of 0.0045 c d^-1 for the half-width at half-maximum of the central peak of the window function based on all CES data, and as the 2D frequency analysis is rather time consuming, we adopted a frequency step of 0.001 c d^-1 in a first stage. After having identified the main peak and its aliases, we recomputed the periodograms with a factor 10 smaller frequency step around the dominant peak and its aliases to check if the results remained valid, which was always the case for the relevant frequencies mentioned below.

	Figure 10: Grey-scale representation of the power spectrum obtained at each wavelength position (given in units of the variance) across the SiIII $\lambda$4552.6 Å line profile by the application of the 2D Lomb-Scargle method to all CES spectra.
Open with DEXTER

There exists a small wavelength range centred around 4549 Å, at which only the primary's line profile is present. We first applied the 2D Lomb-Scargle method to the dataset comprising all the CES spectra. A graphical representation of the results is shown in Fig. 10. This figure reveals power excess in the wavelength range between 4550 Å and 4557 Å, which is visible at frequencies below 3 c d^-1. This is caused by the shift of the secondary's line profile due to its orbital motion. However, clearly visible peaks occur between 5 and 9 c d^-1 in the power spectra at wavelengths between 4549 Å and 4550 Å. This excess power can only be due to the primary, proving that this component has short-term periodic variability.

To find the frequencies of the short-term variability of the primary with better significance, we removed the higher-amplitude variability due to its orbital motion around the centre of mass. For this, we used the secondary's disentangled line profile in combination with the orbit. We then computed the periodograms at each wavelength to construct a 2D periodogram. The results for the CES spectra are shown in Fig. 11 (we omitted the CORALIE spectra for this plot due to their larger noise level). We clearly reveal excess power across the whole line profile of the primary at a frequency near 6.4 c d^-1 and its aliases.

We summed all the 1D periodograms (for both the CES and CORALIE spectra) over the range 4549 and 4556.5 Å (Fig. 12). The drawback is that this analysis method removes the secondary's long-term variability, but not its short-term variability. Therefore, the sum of all 1D periodograms shown in Fig. 12 contains a mix of peaks due to the primary's and secondary's short-term variability, if any. The upper panel unquestionably reveals 7.415 c d^-1 as the dominant frequency, although rather strong aliasing still occurs for the whole dataset. We have shown above that this frequency belongs to the primary. The middle panel of Fig. 12 shows the periodogram that is obtained after prewhitening the original data with 7.415 c d^-1. It suggests 4.542 c d^-1, or one of its aliases, as the second frequency. After prewhitening with 7.415 and 4.542 c d^-1, the power spectrum (lower panel) is dominated by peaks at lower frequencies. The highest peak in the interval [3,10] c d^-1 appropriate for $\beta~$Cephei stars occurs at 4.407 c d^-1, but it is not clear at this stage whether this is another intrinsic frequency. We conclude that there is evidence for unexplained additional power.

	Figure 11: Same as Fig. 10, but after subtracting the secondary's disentangled line profile and correcting for the primary's orbital motion.
Open with DEXTER

A study of the secondary's intrinsic temporal behaviour is by no means straightforward. Due to their large width, the primary's line profiles extend over a wavelength range that completely includes the range spanned by the secondary's line profiles during nearly all orbital phases. This makes it very difficult to unravel the secondary's line-profile variations, if any, from the ones of the primary. We applied the following procedure: for each original spectrum, the primary's SiIII $\lambda$ 4552.6 Å disentangled line profile was shifted according to the corresponding orbital velocity and subsequently subtracted from the original spectrum. We then computed a 2D Scargle periodogram as explained above. We subsequently added the power across subintervals of the total wavelength range [4547, 4557] Å. At the same time, we determined the extent of the secondary's line within that wavelength range (see Ausseloos 2005, p. 72, Fig. 2.32 for more details). If the power is only significant in the wavelength range spanned by the secondary, this is considered as a strong indication that the corresponding frequency is associated with that star.

We carried out several tests by considering different subdatasets whose power distribution for candidate frequencies was calculated over different subintervals in wavelength. From all these tests, we conclude that f₂ also belongs to the primary and that no evidence of short-term variability in the line profiles of the secondary was found in our dataset. It has to be stressed that all previously published period analyses of $\beta$ Cen (Breger 1967; Shobbrook & Robertson 1968; Lomb 1975; Robertson et al. 1999; Ausseloos et al. 2002) can no longer be trusted as they all neglect the pulsations of the primary and assume that the component with the deeper and narrower line profiles undergoes the short-term variability.

4.2 Mode identification

An attempt was made to identify the modes of the primary. Given its strongly rotationally-broadened profiles, the Doppler Imaging method was used. This method was introduced by Gies & Kullavanijaya (1988) for the B0.7III star $\varepsilon~$Per, but several authors have elaborated on it since (see, e.g., Telting & Schrijvers 1997, and references therein). Telting & Schrijvers (1997) took a major step forward by making a large Monte-Carlo simulation study from which they derived linear relationships between the degree $\ell$ and the blue-to-red phase difference $\Delta\Psi_f$ of an observed frequency f on the one hand, and between the azimuthal number m and the phase difference of the first harmonic $\Delta\Psi_{2f}$ on the other hand. The errors of the estimates of $\ell$ and m are, respectively, one and two. Telting & Schrijvers (1997) also verified that the method can handle multiperiodic line-profile variations.

	Figure 12: Power spectra resulting from the addition of all the 1D periodograms over the wavelength range between 4549 and 4556.5 Å. The panels correspond to different stages of prewhitening: original periodogram ( upper panel), after prewhitening with 7.415 c d-1 ( middle panel), and after prewhitening with 7.415 and 4.542 c d-1 ( lower panel).
Open with DEXTER

We applied this method to different combinations of alias frequencies (f₁, f₂) with f₁ = 7.415 c d^-1 or one of its adjacent aliases, and f₂ = 5.546 or one of its adjacent aliases and the results are the same for each of them. The resulting phase behaviour for (f₁, f₂) = (7.415, 4.542) c d^-1 is shown in Fig. 13. We obtain smooth phase distributions across the line profile which allow a reliable application of Telting & Schrijvers' (1997) linear relations to estimate $\ell$.

	Figure 13: Phase behaviour across the profile calculated on the basis of all CES and CORALIE data for (f1, f2) = (7.415, 4.542) c d-1. The upper (middle) panel shows the phase behaviour of f1 (f2). The average line profile is given in the lower panel.
Open with DEXTER

For the first frequency f₁ = 7.415 c d^-1, we can read off a blue-to-red phase difference $\Delta\Psi_{f_1}$ of 5$\pi$ radians, irrespective of the value of f₂. This implies that $\ell_1 \in [4,7]$. The phase diagram of 4.542 c d^-1 leads to a phase difference $\Delta\Psi_{f_2} \in [3.5,3.6]~\pi$ radians, hence $\ell_2 \in [3,5]$. These results explain why variations in ground-based photometry are absent because $\ell$ values above two lead to strong cancellation across the visible stellar disk in such data (see, e.g., Dziembowski 1977).

We scanned the database of seismic $\beta~$Cephei star models and their oscillation frequencies computed by Ausseloos et al. (2004) once more, considering the tight limitations on the physical parameters of $\beta~$Cen's primary. Despite the narrow allowed range in the mass, the effective temperature, and the age of the primary, we could find numerous predicted modes with a frequency near f₁ or f₂ for the allowed models. As we have no definitive mode degree for the two frequencies, nor any estimate of their azimuthal orders, we cannot refine the physical parameters of the primary from the oscillations at this stage.

5 Conclusions

We have shown a systematic error to occur in the semi-amplitudes of the velocity curves, due to an underestimation of radial-velocity values in SB2 spectroscopic binaries with merged spectral line profiles. We provide methodological schemes to solve for this systematic error. They are based on spectral disentangling by means of the KOREL code (Hadrava 1997). We suggest that these schemes be used in any future analyses of SB2s whenever their profiles can be successfully disentangled.

In the case of $\beta~$Cen, the systematic underestimation of the spectroscopic orbital semi-amplitudes led to an underestimation of the component masses of about 10%. We refined the component masses of this massive binary by application of our analysis schemes to the available high-resolution spectroscopy, and by combining the spectroscopic results with interferometric measurements across the orbit, leading to a precision of 6%. The accuracy was further improved by stellar modelling taking into account an extensive database of stellar evolution models with wide ranging values of the mass, Z, and core convective overshooting. In this way, we find the component masses of $\beta~$Cen to be $M_1=10.7\pm 0.1~M_\odot$ and $M_2=10.3\pm 0.1~M_\odot$ and its age to be $14.1\pm 0.6$ million years. These mass estimates turn out to be fully compatible with the mass-luminosity relation. The fact that we find $\beta~$Cen to have passed less than half of its main-sequence lifetime is compatible with its high eccentricity and suggests that both components were formed together, rather than having undergone a tidal capture. The absence of an IR excess (Aerts et al. 1999), and of H$\alpha$ emission in the CORALIE spectra, exclude the stars still being in their pre-main-sequence phase. The a posteriori conclusion that the derived fundamental parameters of the components of the system fulfill the tight mass-luminosity relation provides confidence in our high-precision estimates of the masses. The determination of the distance to $\beta~$Cen is also affected by the previous systematic underestimation of the radial-velocity values and has been re-determined from its dynamic parallax to be $108\pm4$ pc.

Next, we performed an in-depth line-profile analysis. All previous frequency analyses were focused on the line-profile variations of the component producing the deeper lines (secondary) and claimed frequencies for this component. We have given compelling evidence that it is actually the component producing the broader lines (primary) which is pulsating, while we did not find any periodic variability that we could link to the secondary. As our dataset is by far the most extensive one so far used for a spectroscopic analysis of $\beta$ Cen, the pulsational nature of the secondary should be regarded as unproven. If the secondary oscillates, its amplitudes must be much smaller than those of the primary because the variations of the combined line profiles of both components are dominated by the variations of the primary's line profile.

We detected two frequencies in the primary's line-profile variations by means of the 2D Lomb-Scargle method, but we were not able to fix their value unambiguously due to aliasing. Notwithstanding the aliasing effect, we were able to restrict the value of the degree $\ell$ to [4, 7] and [3, 5] for the first and second mode, respectively. The detection of only two frequencies and the lack of unique mode identification prevented an in-depth seismic study of the star, despite the fact that its fundamental parameters are so tightly constrained by the binarity. The only conclusion we could draw in this respect is that standard stellar models predict frequencies that are fully compatible with the two detected ones.

Very few accurate masses of $\beta~$Cephei stars are available, notable exceptions being those with a seismic mass estimate (HD 129929: Aerts et al. 2003; 16 Lac: Thoul et al. 2003; $\nu~$Eri: Pamyatnykh et al. 2004; and Ausseloos et al. 2004). The masses we derived here for $\beta~$Cen, together with the estimates for its effective temperature, gravity, and age, constitute a fruitful starting point for future seismic analyses of this massive binary. A distinct short-event photometric variation of $\beta$ Cen with amplitude of about 0.04 mag was observed by Balona (1977) on one night. No period could be derived in these data, however. The lack of other claims of photometric variability of the brightest among all $\beta~$Cephei stars, despite observational efforts (L. A. Balona, private communication), is nicely explained by our detection of pulsation modes with a high degree ( $\ell \ge 3$). This clearly points out that one cannot hope to find a complete frequency spectrum of the p-modes in $\beta~$Cephei stars from ground-based photometry alone. The same conclusion was recently drawn for the fast rotator $\zeta$ Oph on the basis of high-resolution spectroscopy and MOST space photometry (Walker et al. 2005). It is clear that high-precision photometric data from space are necessary to achieve a seismic interpretation of $\beta~$Cen.

Acknowledgements

M.A., C.A., and K.L. are supported by the Fund for Scientific Research of Flanders (FWO) under grant G.0332.06 and by the Research Council of the University of Leuven under grant GOA/2003/04. We are grateful to Dr. P. Hadrava for making his computer source codes FOTEL and KOREL available to us. This study has benefited greatly from the senior fellowship awarded to PH by the Research Council of the University of Leuven, which allowed his three-month stay at the Institute of Astronomy in Leuven. PH was also supported from the research plans J13/98: 113200004 of the Ministry of Education, Youth and Sports, AV 0Z1 003909, GA CR 205/06/0304, and project K2043105 of the Academy of Sciences of the Czech Republic.

References

• Aerts, C., De Pauw, M., & Waelkens, C. 1992, A&A, 266, 294 [NASA ADS] (In the text)
• Aerts, C., De Boeck, I., Malfait, K., & De Cat, P. 1999, A&A, 347, 524 [NASA ADS] (In the text)
• Aerts, C., Thoul, A., Daszynska, J., et al. 2003, Science, 300, 1926 [NASA ADS] [CrossRef] (In the text)
• Andersen, J. 1991, A&AR, 3, 91 [NASA ADS] (In the text)
• Ausseloos, M. 2005, Seismic Studies of Selected $\beta$Cephei Stars: $\beta$Centauri, $\nu$Eridani and 12 Lacertae, Ph.D. Thesis, Katholieke Universiteit Leuven, Belgium (In the text)
• Ausseloos, M., Aerts, C., Uytterhoeven, K., et al. 2002, A&A, 384, 209 [EDP Sciences] [NASA ADS] [CrossRef] (Paper I) (In the text)
• Ausseloos, M., Scuflaire, R., Thoul, A., & Aerts, C. 2004, MNRAS, 355, 352 [NASA ADS] [CrossRef] (In the text)
• Balona, L. A. 1977, Roy. Astron. Soc., Mem., 84, 101 (In the text)
• Breger, M. 1967, MNRAS, 136, 51 [NASA ADS] (In the text)
• Davis, J., Mendez, A., Seneta, E. B., et al. 2005, MNRAS, 356, 1362 [NASA ADS] [CrossRef] (Paper II) (In the text)
• Dupret, M.-A., Thoul, A., Scuflaire, R., et al. 2004, A&A, 415, 215 [NASA ADS] (In the text)
• Dziembowski, W. A. 1977, Acta Astron., 27, 203 [NASA ADS] (In the text)
• Gies, D. R., & Kullavanijaya, A. 1988, ApJ, 326, 813 [NASA ADS] [CrossRef] (In the text)
• Grevesse, N., Noels, A., & Sauval, A. J. 1996, in Proceedings of the sixth annual October Astrophysics Conference in College Park, ed. S. S. Hilt, & G. Sonneborn (ASPC), 99, 117 (In the text)
• Griffiths, S. C., Hicks, R. B., & Milone, E. F. 1988, J. R. Astr. Soc. Canada, 82, 1 [NASA ADS] (In the text)
• Hadrava, P. 1990, Contrib. Astron. Obs. Skal. Pl., 20, 23 [NASA ADS] (In the text)
• Hadrava, P. 1995, A&AS, 114, 393 [NASA ADS] (In the text)
• Hadrava, P. 1997, A&AS, 122, 581 [EDP Sciences] [NASA ADS] (In the text)
• Hadrava, P. 2001, in Astrotomography, Indirect Imaging Methods in Observational Astronomy, ed. H. M. J. Boffin, D. Steeghs, & J. Cuypers, Lecture Notes Phys., 573, 261 (In the text)
• Hadrava, P. 2004a, Publ. Astron. Inst. Czech Acad. Sci., No. 92, 1 (In the text)
• Hadrava, P. 2004b, Publ. Astron. Inst. Czech Acad. Sci., No. 92, 15
• Harmanec, P. 2002, in The Royal Road to the Stars, ed. O. Demircan, & E. Budding (Canakkale Onsekiz Mart University Publications), 3, 221 (In the text)
• Harmanec, P., Uytterhoeven, K., & Aerts, C. 2005, A&A, 422, 1013 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Hilditch, R. W. 2004a, in Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, ed. R. W. Hilditch, H. Hensberge, & K. Pavlovski (ASPC), 318, 3 (In the text)
• Hilditch, R. W. 2004b, in Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, ed. R. W. Hilditch, H. Hensberge, & K. Pavlovski (ASPC), 318, 198
• Lomb, N. R. 1975, MNRAS, 172, 639 [NASA ADS] (In the text)
• Maceroni, C. 2005, in Astrophysics of Variable Stars, ed. C. Sterken, & C. Aerts (ASPC), 349, 41 (In the text)
• Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] (In the text)
• Pamyatnykh, A. A. 1999, Acta Astron., 49, 119 [NASA ADS] (In the text)
• Pamyatnykh, A. A., Handler, G., & Dziembowski, W. A. 2004, MNRAS, 350, 1022 [NASA ADS] [CrossRef] (In the text)
• Puls, J., Urbaneja, M. A., Venero, R., et al. 2005, A&A, 435, 669 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Ribas, I. 2005, in Astrophysics of Variable Stars, ed. C. Sterken, & C. Aerts (ASPC), 349, 55 (In the text)
• Robertson, J. G., Bedding, T. R., Aerts, C., et al. 1999, MNRAS, 302, 245 [NASA ADS] [CrossRef] (In the text)
• Scargle, J. D. 1982, ApJ, 263, 835 [CrossRef] (In the text)
• Shobbrook, R. R., & Robertson, J. W. 1968, PASA, 1, 82 (In the text)
• Stankov, A., & Handler, G. 2005, ApJS, 158, 193 [NASA ADS] [CrossRef] (In the text)
• Tango, W. J., Davis, J., Ireland, M. J., et al. 2006, MNRAS, submitted (In the text)
• Telting, J. H., & Schrijvers, C. 1997, A&A, 317, 723 [NASA ADS]
• Telting, J. H., Aerts, C., & Mathias, P. 1997, A&A, 322, 493 [NASA ADS] (In the text)
• Thoul, A., Aerts, C., Dupret, M. A., et al. 2003, A&A, 406, 287 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Tomkin, J., Pan, X., & McCarthy, J. K. 1995, AJ, 109, 780 [NASA ADS] [CrossRef] (In the text)
• Uytterhoeven, K., Briquet, M., Aerts, C., et al. 2005, A&A, 432, 955 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Walker, G., Kuschnig, R., Matthews, J. M., et al. 2005, ApJ, 623, L145 [NASA ADS] [CrossRef] (In the text)