A&A 455, 349-359 (2006)
DOI: 10.1051/0004-6361:20064806

A new model-independent method to compute magnetic helicity in magnetic clouds

S. Dasso1,2 - C. H. Mandrini1 - P. Démoulin3 - M. L. Luoni1


1 - Instituto de Astronomía y Física del Espacio, IAFE, CC. 67 Suc. 28, 1428 Buenos Aires, Argentina
2 - Departamento de Física, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, Argentina
3 - Observatoire de Paris, LESIA, UMR 8109 (CNRS), 92195 Meudon Cedex, France

Received 3 January 2006 / Accepted 18 April 2006

Abstract
Context. Magnetic clouds are transient magnetic structures expulsed from the Sun that travel toward the external heliosphere carrying a significant amount of magnetic flux and helicity.
Aims. To improve our understanding of magnetic clouds in relation to their solar source regions, we need a reliable method to compute magnetic flux and helicity in both regions. Here we evaluate the sensitivity of the results using different models, methods and magnetic cloud boundaries applied to the same magnetic cloud data.
Methods. The magnetic cloud was observed by the spacecraft Wind on October 18-20, 1995. We analyze this cloud considering four different theoretical configurations (two force free and two non-force free) that have been previously proposed to model cloud fields. These four models are applied using two methods to determine the orientation of the cloud axis: minimum variance and simultaneous fitting. Finally, we present a new method to obtain the axial and azimuthal magnetic fluxes and helicity directly from the observed magnetic field when rotated to the cloud frame.
Results. The results from the fitted models have biases that we analyze. The new method determines the centre and the rear boundary of the flux rope when the front boundary is known. It also gives two independent measurements in the front and back parts for the fluxes and helicity; they are free of model and boundary biases. We deduce that the leading flux of the magnetic cloud had reconnected with the overtaken solar wind magnetic field and estimate the fluxes and helicity present in the full cloud before this reconnection.

Key words: Sun: coronal mass ejections (CMEs) - Sun: magnetic fields - interplanetary medium

  
1 Introduction

  
1.1 Magnetic clouds

Interplanetary Coronal Mass Ejections (ICMEs) are transient solar ejecta that perturb the solar wind. They are expelled from the Sun and travel toward the external heliosphere, reaching the Earth's environment when their trajectories are appropriate. Depending on their magnetic field orientation, they can trigger intense geomagnetic storms.

An important subset of ICMEs is known as interplanetary magnetic clouds (MCs). These huge objects are characterized by a strongly enhanced magnetic field intensity (with respect to ambient values), a smooth and large coherent rotation of the magnetic field vector, and a low proton temperature (e.g., Burlaga et al. 1981; Burlaga 1995; Klein & Burlaga 1982; Burlaga 1991). The global magnetic structure of an MC is a twisted magnetic flux tube; therefore, an MC carries a large amount of magnetic helicity.

   
1.2 The relevance of magnetic helicity

In the Sun, magnetic helicity is generated by the dynamo (helical turbulence and differential rotation) and it does not change its sign with the solar cycle. In the northern hemisphere, magnetic features have preferentially negative (left-handed) helicity, while the southern hemispheric features show a preference for the opposite sign (positive, right-handed helicity), for a recent review see Pevtsov & Balasubramaniam (2003). The magnetic helicity injected in each hemisphere cannot be dissipated on short time scales, such as typical flare durations, nor on the time-scale of the solar cycle (Berger 1984). Apart from the cancellation of helicity by reconnection between the two hemispheres and that carried by the solar wind, the coronal helicity only can be released from the Sun by CMEs. Thus, the accumulation of magnetic helicity in the corona is plausibly the origin of the initiation of CMEs (Zhang et al. 2006; Low 1996; Nindos & Andrews 2004).

The conservation of magnetic helicity is also a key property that allows us to link solar phenomena with their interplanetary counterpart (see, e.g., Mandrini et al. 2005; Luoni et al. 2005). Presently, few works have determined the magnetic helicity in interplanetary flux tubes, such as MCs (e.g., Dasso et al. 2005b,a; Gulisano et al. 2005; Nindos et al. 2003; Nakwacki et al. 2005; Mandrini et al. 2005; Dasso et al. 2003; Luoni et al. 2005).

   
1.3 The analyzed magnetic cloud

In this paper we analyze the magnetic cloud observed by the spacecraft Wind on October 18-20, 1995. This cloud has been studied by several authors (e.g., Janoo et al. 1998; Lepping et al. 1997; Collier et al. 2001; Hidalgo et al. 2002; Larson et al. 1997). The plasma and magnetic data obtained by the Wind spacecraft indicate that the cloud started to cross the spacecraft at 18:58 UT, on October 18, 1995. While the beginning of the cloud is well defined, there is some ambiguity about the position of the end time, taken by several authors as between October 19, 22:54 UT and October 20, 01:38 UT. Lepping et al. (1997) and Hidalgo et al. (2002) considered an end time at 00:00 UT, on October 20, while Janoo et al. (1998) and Collier et al. (2001) took it as 22:54 UT, on October 19, 1995. However, Larson et al. (1997) chose the end time of this cloud at 01:38 UT on October 20.

The orientation and the size of this cloud have been determined by Lepping et al. (1997) and Hidalgo et al. (2002). The physical parameters (free parameters of a magnetic model) have been fitted by Lepping et al. (1997) under the assumption of a linear force-free field model, and by Hidalgo et al. (2002) using a non-force free model. However, a detailed comparison of the results, in particular the magnetic helicity content, using different models has not yet been done.

Complementary information to understand the topology of this cloud can be obtained by studying the electron distribution function. Impulsive electron beams with energies between $\sim$0.1-100 keV are good tracers of the interplanetary magnetic field; they are supposed to come from the corona, indicating a magnetic connection to the Sun. The cloud of October 18-20 presents different topologies: regions magnetically connected to the Sun at both ends, only at one end, and disconnected (Collier et al. 2001). Larson et al. (1997) have estimated the semi-length of the magnetic field lines from in situ observations (at 1 AU) of impulsive electron events ($\sim$1-100 keV) and solar type III radio bursts. From an analysis of the arrival time and the velocity of these electrons, the semi-length of the field lines near the centre of the cloud (i.e., lines practically parallel to the cloud axis) was estimated as $\sim$1.2 AU, a result consistent with a leg still connected to the Sun.

The solar source of this MC was identified as located between two interacting solar active regions (NOAA 7912 and NOAA 7910) by Smith et al. (1997). In a later study, based on the analysis of the coronal soft X-ray evolution, van Driel-Gesztelyi et al. (2000) proposed that the MC was launched from the active region NOAA 7912. This MC was related to a C1.6 long duration event between 5:00 UT and 20:00 UT on October 14, 1995.

   
1.4 The aims of the analysis

The local magnetic configuration of MCs can be modeled using a cylindrical geometry and four different approximations: a linear force-free field (L, Lundquist 1950), a uniformly twisted and non-linear force-free model (G, Gold & Hoyle 1960), a non force-free model with constant current density (H, Hidalgo et al. 2000), and a non force-free model assuming a constant axial component and a linear dependence on the radius for the poloidal component of the current density (C, Cid et al. 2002). These four models provide significantly different helical magnetic configurations with very different distributions of the magnetic twist.

The present work is focused on the determination of the magnetic helicity and flux contained in the MC of October 18-20, 1995, to compare the obtained values when various models and/or methods and/or cloud-sizes are used. We fit the physical parameters for each of the four models (L, G, H, and C). The orientation of the tube is computed with two different methods: a minimum variance (MV) analysis and a simultaneous fitting (SF) of all the parameters. We also present a new method to compute the content of magnetic helicity and flux directly from the magnetic observations, assuming only a cylindrical symmetry for the observed cloud section. We find that the computation of these quantities is very useful to improve the localization of the cloud boundaries. Finally, we explore the sensitivity of the results to variations of the radius of the cloud.

In Sect. 2, we briefly summarize the basic equations. Four models of twisted flux tubes are presented in Sect. 3, where we derive the theoretical expressions for the magnetic helicity and flux. The results of fitting the models to the data are given in Sect. 4. In Sect. 5, we use the new method to directly measure the magnetic helicity and flux of the cloud. We interpret the flux observations in terms of a magnetic shape for the MC, and we analyze the sensitivity of the results to variations of the MC boundaries. In Sect. 6, we give our conclusions.

   
2 Magnetic helicity and fluxes

The relative magnetic helicity within a volume V is obtained by subtracting the helicity of a reference field  $\vec{B}_{\rm ref}$ having the same distribution of the normal component Bn on the surface S surrounding V (Berger & Field 1984):

 \begin{displaymath}% H = \int_{V} \vec{A} \cdot \vec{B} ~ {\ \rm d} V - \int_{V} \vec{A}_{\rm ref} \cdot \vec{B}_{\rm ref} ~ {\ \rm d} V, \end{displaymath} (1)

where $\vec{A}$ is the vector potential of the magnetic field $\vec{B}$. H is gauge invariant (invariant in the transformation $\vec{A}$ to  $\vec{A} + {\nabla} \psi$). H extends the definition of magnetic helicity to magnetic configurations where $B_n \ne 0$ (for example, a section of a twisted flux tube).

Several authors have modeled the local magnetic field of an interplanetary flux tube as a straight cylindrical structure having a magnetic field

 \begin{displaymath}% \vec{B}({r}) = B_\phi(r) ~ \hat{\bf\phi} + B_z(r) ~ \vec{\hat{z}}, \end{displaymath} (2)

(e.g., Hidalgo et al. 2000; Burlaga 1988; Lepping et al. 1990; Hidalgo et al. 2002; Farrugia et al. 1995). The magnetic field lines twist per unit length is:

 \begin{displaymath}% \tau (r) = {\rm d}\phi / {\rm d}z = B_{\phi } / (r B_z). \end{displaymath} (3)

We define two accumulative magnetic fluxes: axial Fz(r) and azimuthal  $F_{\phi}(r)$ for a given length L along the flux tube:
  
    $\displaystyle F_z(r) = 2 \pi \int_{0}^{r} B_z(r') r' {\ \rm d} r'$ (4)
    $\displaystyle F_{\phi}(r) = L \int_{0}^{r} B_{\phi}(r') {\ \rm d} r'.$ (5)

The reference field can be chosen as $\vec{B}_{\rm ref} (r)= B_z(r) \vec{\hat{z}}$ (with null magnetic helicity, since field lines are straight) and the reference vector potential as $\vec{A}_{\rm ref}(r)= A_\phi(r) ~ \hat{\bf\phi} + A_z(r=R) ~ \vec{\hat{z}}$, where R is the radius of the flux tube. Thus, the cumulative helicity per unit length (H/L) can be written as:
 
                          $\displaystyle % \frac {H(r)}{L}$ = $\displaystyle 2 \pi \int_{0}^{r} [B_z A_z + A_\phi B_\phi - A_{{\rm ref},z} B_{{\rm ref},z}] r' {\ \rm d} r'$  
  = $\displaystyle 4 \pi \int_{0}^{r} A_\phi B_\phi ~ r' {\rm d}r'.$ (6)

This last expression can be also directly derived from Eq. (16) of Berger (1999), where $B_\phi$ and Bz are the "closed'' and "open'' field with Bn=0 and $B_n \neq 0$ on the surface S surrounding the cylindrical section of length L, respectively.

The component $A_\phi$ of the vector potential can be written as a function of the magnetic flux (Fz) across a surface perpendicular to the cloud axis as:

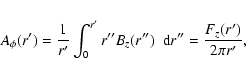
\begin{eqnarray*}A_\phi(r') = \frac{1}{r'} \int_{0}^{r'} r'' B_z(r'') ~ {\ \rm d} r'' = \frac {F_z(r')}{2 \pi r'}, \end{eqnarray*}


and, thus, the relative helicity can be computed as an integral of $B_\phi$, weighted with the accumulative axial flux Fz:

 \begin{displaymath}% \frac {H(r)}{L} = 2 \int_{0}^{r} B_\phi (r') F_z(r') ~ {\rm d}r'. \end{displaymath} (7)

Equation (7) can be used to estimate the helicity directly from the magnetic field observations (Sect. 5.3).

   
3 The four analyzed models

In the magnetohydrodynamic (MHD) framework, the magnetic configuration of an MC can be obtained from the balance between the magnetic Lorentz force and the plasma pressure. Several magneto-static models have been used to describe the magnetic configuration of MCs.

When the plasma pressure is negligible compared to the magnetic pressure, the configuration is called "force-free'' because the magnetic self-force is null (and so, $\vec{B}$ is parallel to the electric current density, $\vec{j}$), and the magnetic pressure is balanced by the tension of the curved magnetic field lines. The "linear-force-free'' field is a sub-set of solutions from the previous set, which satisfies $\nabla \times \vec{B} = \alpha \vec{B}$, with $\alpha$ constant in space. In this section we present four different cylindrical models, two force-free (one linear and one non-linear) and two non force-free.

For the two non force-free models we set the condition Bz(r=R)=0 in order to keep the same number of degrees of freedom as with the force-free models (two degrees of freedom, B0 and $\tau _0$, for a fixed radius of the tube). For a more general case, including $B_z(r=R) \ne 0$, see Dasso et al. (2005b).

   
3.1 Linear force-free field

The axially symmetric magnetic field corresponding to a linear force-free configuration was obtained by Lundquist (1950). It has been shown that this solution is consistent with in situ measurements of interplanetary magnetic flux tubes at 1 AU (Burlaga et al. 1981; Burlaga 1988; Lepping et al. 1990). Thus, the field of MCs is often relatively well modeled by

 \begin{displaymath}% \vec{B}_L = B_{0,L} ~[ J_1(\alpha r) ~ \hat{\bf\phi} + J_0(\alpha r) ~ \vec{\hat{z}}], \end{displaymath} (8)

where Jn is the Bessel function of the first kind of order n, and B0,L is the strength of the field at the MC axis.

The magnetic field line twist per unit length (Eq. (3)) is $\tau_L(r) = J_1(\alpha r) / (r J_0(\alpha r))$. The constant $\alpha$ determines the twist at the flux tube axis, $\tau_{0,L} = \tau_L(0) = \alpha /2$. The axial magnetic flux (Eq. (4)) is given by: $F_{z,L} = 2 \pi B_{0,L} R J_1(\alpha R) ~ /\alpha $. It has been shown that Lundquist's solution extended to the first zero of J0 is enough to describe the magnetic structure of some MCs (e.g., Lepping et al. 1990). In these cases $F_{z,L} \sim 1.4 B_{0,L} R^2$. However, Vandas & Geranios (2001) showed that there are some MCs that seem to be better described using Lundquist's solution beyond the first zero of J0. The azimuthal magnetic flux (Eq. (5)) is given by: $F_{\phi,L} = F_{\phi}(R) = L B_{0,L} ~ (1-J_0(\alpha R)) ~ /\alpha$.

We obtain the relative helicity per unit length from Eq. (6), taking $\vec{A} = \vec{B} / \alpha$:

 
                                   $\displaystyle % \frac{H_{L}}{L}$ = $\displaystyle \frac{4 \pi B_{0,L}^2}{\alpha} \int_{0}^{R} J_1^2(\alpha r) ~ r {\ \rm d} r$  
  = $\displaystyle \frac{4 \pi}{U^2} \left[J_0^2(U)+J_1^2(U)-\frac{2J_0(U)J_1(U)}{U} \right] B_{0,L}^2 R^4 \tau_{0,L},$ (9)

where $U = 2 \tau_{0,L} R$ is a dimensionless quantity. When the boundary of the cloud is such that $\alpha R \sim 2.405$, i.e. the first zero of J0, $H_{L}/L \sim 0.7 B_{0,L} R^3$ (Démoulin et al. 2002). The last expression of Eq. (9) emphasizes that HL/L has the units of a magnetic flux square ( (B0,L R2)2) multiplied by a twist per unit length ( $\tau_{0,L}$).

   
3.2 Uniformly twisted field

A non-linear force-free field with a uniform twist has been used to model interplanetary flux tubes (e.g., Farrugia et al. 1999). For this configuration, $\vec{B}$ is given by Gold & Hoyle (1960):

 \begin{displaymath}% \vec{B}_{G} = B_{0,G} \left[ \frac{b ~ r}{1+b^2 r^2} ~ \hat{\bf\phi} + \frac{1}{1+b^2 r^2} ~ \vec{\hat{z}} \right]. \end{displaymath} (10)

In this magnetic configuration, the twist is independent of r: $\tau_{G}(r) = \tau_{0,G} = b$. The axial flux is: $F_{z,G}=B_{0,G} \pi \ln(1+b^2 R^2)/b^2 $, and the azimuthal flux is: $F_{\phi,G}= B_{0,G} L \ln(1+b^2 R^2)/(2b)$.

From Eq. (6), and

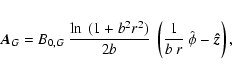
\begin{eqnarray*}\vec{A}_{G} = B_{0,G} ~ \frac{ \ln~(1+ b^2 r^2) }{2 b} ~ \left( \frac{1}{b ~ r} ~ \hat{\bf\phi} - \vec{\hat{z}} \right), \end{eqnarray*}


the relative helicity turns out to be:
 
                              $\displaystyle % \frac{H_{G}}{L}$ = $\displaystyle \frac{\pi B_{0,G}^2}{2 b^3} [\ln~(1+ b^2 R^2)]^2$  
  = $\displaystyle \left( \frac{8\pi [\ln~(1+ U^2/4)]^2 }{U^4} \right) B_{0,G}^2 R^4 \tau_{0,G},$ (11)

where $U = 2 \tau_{0,G} R$ as in the previous model.

   
3.3 Constant current field

A non force-free model has been proposed by Hidalgo et al. (2000,2002) to describe MCs. This model assumes a constant current density such as $\vec{j}(\vec{r}) = j_\phi ~ \hat{\bf\phi} + j_z ~ \vec{\hat{z}}$, where $j_\phi$ and jz are constants. The magnetic field is:

 \begin{displaymath}% \vec{B}_H = B_{0,H} ~[ \tau_{0,H} r ~ \hat{\bf\phi} + (1-r/R) ~ \vec{\hat{z}}], \end{displaymath} (12)

where B0,H is the field at the centre of the tube and  $\tau_{0,H}$ is the magnetic field line twist at the tube centre. Thus, Bz(r=R)=0.

The twist distribution is $\tau_{H}(r)=\tau_{0,H}(1-r/R)^{-1}$. The axial flux is $F_{z,H} = \pi B_{0,H} R^2/3$, and the azimuthal flux is $F_{\phi,H} = B_{0,H} R^2 L \tau_{0,H} /2$. The relative helicity per unit length is:

 \begin{displaymath}% \frac{H_{H}}{L} = \frac{7 \pi }{30} B_{0,H}^2 R^4 \tau_{0,H}. \end{displaymath} (13)

   
3.4 Linear azimuthal current

A cylindrical magnetic configuration with a current density such as: $\vec{j}(\vec{r}) = a r ~ \hat{\bf\phi} + j_z ~ \vec{\hat{z}}$, with a and jz constants, has been proposed for magnetic clouds by Cid et al. (2002). This structure has a magnetic field distribution given by:

 \begin{displaymath}% \vec{B}_C = B_{0,C} ~ [ \tau_{0,C} r ~ \hat{\bf\phi} + (1-r^2/R^2) ~ \vec{\hat{z}}], \end{displaymath} (14)

where B0,C is the field at the centre of the flux tube and  $\tau_{0,C}$ is the twist at the axis.

The twist distribution is $\tau_{C}(r)=\tau_{0,C}(1-r^2/R^2)^{-1}$. The axial flux is $F_{z,C}=B_{0,C} R^2 \pi/2$, and the azimuthal flux is $F_{\phi,C} = B_{0,C} R^2 L \tau_{0,C} /2$. The relative helicity per unit length is:

 \begin{displaymath}% \frac{H_{C}}{L} = \frac{\pi }{3} B_{0,C}^2 R^4 \tau_{0,C}. \end{displaymath} (15)

   
4 Modeling the magnetic cloud

   
4.1 The cloud coordinate system

In situ measurements of the magnetic field vector components are obtained along the trajectory of the spacecraft. Since the speed of an MC is practically in the Sun-Earth direction and it is much larger than the spacecraft speed (which can be supposed to be at rest during the cloud transit time), we assume a rectilinear spacecraft trajectory in the cloud frame. We analyze the three components of the magnetic field measured in GSE (Geocentric Solar Ecliptic) coordinates. In this system of coordinates, $\hat{x}_{\rm GSE}$ corresponds to the Earth-Sun direction, $\hat{z}_{\rm GSE}$ points to the North (perpendicular to the ecliptic plane) and  $\hat{y}_{\rm GSE}$ is such that the system is right handed.

It is useful to define a local system of coordinates linked to the cloud in which $\hat{z}_{\rm cloud}$ is along the cloud axis (with $B_{z, \rm cloud}\!>\!0$ at this axis). To associate the cloud axis direction with the GSE system, we define the latitude angle ($\theta $) between the ecliptic plane and the cloud axis (oriented as $\hat{z}_{\rm cloud}$), as well as the longitude angle ($\varphi $) between the projection of the axis on the ecliptic plane and the Earth-Sun direction ( $\hat{x}_{\rm GSE}$) measured counterclockwise. Accordingly $\theta $ is such that when $\theta $ = 90$^\circ$ ($\theta $ = -90$^\circ$) the cloud axis is parallel to  $\hat{z}_{\rm GSE}$ and it points to the ecliptic North (South). When $\theta $ = 0$^\circ$ the cloud axis is on the ecliptic plane, $\varphi $ = 0$^\circ$ being the case of the axial field pointing toward the Sun, and $\varphi $ = 90$^\circ$ ($\varphi $ = 270$^\circ$) when it points to the terrestrial dusk (dawn).

The rectilinear trajectory of the spacecraft defines a direction $\hat{d}$; then, we define $\hat{y}_{\rm cloud}$ in the direction $\hat{z}_{\rm cloud} \times \hat{d}$ and $\hat{x}_{\rm cloud}$ completes the right-handed orthonormal base ( $\hat{x}_{\rm cloud},\hat{y}_{\rm cloud},\hat{z}_{\rm cloud}$). We also define the impact parameter, p, as the minimum approach distance from the spacecraft to the cloud axis. Then, we construct a rotation matrix from the GSE system to the cloud system, and obtain the components of the observed magnetic field in the cloud coordinates:  $B_{x, \rm cloud}$, $B_{y, \rm cloud}$, $B_{z, \rm cloud}$.

The local system of coordinates is especially useful when p is small compared to the MC radius. In particular, for p=0 and an MC described by a cylindrical magnetic configuration $\vec{B}(r) = B_z(r) \hat{z} + B_\phi(r) \hat{\phi}$, we have $\hat{x}_{\rm cloud} = \hat{r}$ and $\hat{y}_{\rm cloud} = \hat{\phi}$ when the spacecraft leaves the cloud. In this case, the magnetic field data obtained by the spacecraft will show: $B_{x, \rm cloud}=0$, a large and coherent variation of  $B_{y, \rm cloud}$ (with a change of sign), and an intermediate and coherent variation of  $B_{z, \rm cloud}$, from low values at one cloud edge, taking the largest value at its axis and returning to low values at the other edge.

   
4.2 Minimum variance method

It is possible to estimate the orientation of an MC applying the minimum variance (MV) method to the magnetic observations when p is small compared to the cloud radius. This method finds the directions ( $\vec{\hat{n}}$) in which the mean quadratic deviation of the field, $\langle (\vec{B}\cdot\vec{\hat{n}}- \langle\vec{B}\cdot\vec{\hat{n}} \rangle)^2 \rangle$, is minimum and maximum, as well as the orthogonal direction to both. It is possible to show that this is equivalent to finding the eigen-vectors of the covariance matrix Mi,j= $\langle B_iB_j \rangle - \langle B_i \rangle \langle B_j \rangle$ (Sonnerup & Cahill 1967). This symmetric and real matrix has three real eigen-values with orthogonal eigen-vectors.

The MV method determines the MC axis direction, $\vec{\hat{z}}_{\rm cloud}$, as the eigen-vector associated with the intermediate eigen-value. The eigen-vector associated with the lowest eigen-value is expected to be close to the direction that results from the projection of the spacecraft trajectory on the plane perpendicular to  $\vec{\hat{z}}_{\rm cloud}$. In particular, in the cloud analyzed in this paper (see Sect. 4.4) this spacecraft trajectory projection and this eigen-vector differ by less than $\sim$$6^\circ$, compared to the mean value when different boundaries are chosen for the cloud (Sect. 4.6). The eigen-vector associated with the highest eigen-value closes the system such that it is right handed. A more complete discussion of the MV method applied to interplanetary flux tubes can be found in the appendix of Bothmer & Schwenn (1998).

   
4.3 Fitting the physical parameters

From the observed bulk velocity of the interplanetary plasma, we transform the observed time series, $\vec{B}_{\rm obs}(t)$, to a spatial series, $\vec{B}_{\rm obs}(x)$, along $\hat{x}_{\rm GSE}$. Assuming a local invariance by translation along the MC axis and for a given orientation of this axis, the data are transformed to a series along $\hat{x}_{\rm cloud}$. Further, assuming a cylindrical symmetry, and for a given impact parameter p, we can write the field as a function of the spacecraft distance to the MC axis, r, then we obtain the series $\vec{B}_{\rm obs}(r)$. We define a residual function ($\chi ^2$), comparing $\vec{B}_{\rm obs}(r)$ with $\vec{B}_{\rm model}(r)$, for each of the models described in Sect. 3, such that:

 
$\displaystyle % \chi^2 = \frac{1}{N} \sum_{i=1}^{N} [(B^i_{x,{\rm obs}} - B^i_{... ...{\rm obs}}-B^i_{y,{\rm model}})^2 + (B^i_{z,{\rm obs}}-B^i_{z,{\rm model}})^2],$     (16)

where i labels the time and N is the number of data points. We minimize $\chi ^2$ using the standard non-linear least-square fitting Levenberg-Marquardt routine (Press et al. 1992).

We use two methods which differ in the number of free parameters in the $\chi ^2$ minimization. The first method takes the orientation angles, $\theta $ and $\varphi $, from the MV method. The impact parameter p is assumed to be zero and we fit the two free parameters of the models (B0 and $\tau _0$, Sect. 3). The results of this method are labeled simply with MV.

In order to test the validity of the MV method, and to determine p, the second method simultaneously fits (SF) the orientation angles ($\theta $, $\varphi $), the impact parameter (p), and the two physical parameters (B0 and $\tau _0$). The equations for the SF method are given in Hidalgo et al. (2002).


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{4806fig_1.eps}\end{figure} Figure 1: Wind observations for the magnetic cloud observed on 18-20 October, 1995 (one minute cadence). From the upper to the lower panel: radial ( $B_{x, \rm cloud}$), azimuthal ( $B_{y, \rm cloud}$), and axial ( $B_{z, \rm cloud}$) components of the magnetic field (local coordinates, as deduced from the MV), bulk velocity (V), and proton density ($n_{\rm p}$), as a function of time (in hours, after 00:00 UT, October 18, 1995). Dashed lines mark the front boundary of the cloud (18:58 UT, October 18, 1995). Between dash-dotted lines we mark the range of possible ends of the cloud (October 19, 22:54 UT and October 20, 01:38 UT).
Open with DEXTER

   
4.4 The data in the cloud frame

Figure 1 shows the magnetic field components, the bulk velocity and the proton density for an extended range of time around the magnetic cloud. In each panel, the dashed line shows the beginning of the magnetic cloud (18:58 UT, October 18, 1995), while the two dash-dotted lines mark the range of possible final boundaries (from 22:54 UT, October 19 to 01:38 UT, October 20).

We select an end boundary at 00:00 UT on October 20 to apply the MV method; with this boundary we obtain $\theta = -2 ^\circ$ and $\varphi = 288 ^\circ$ (with a radius R=0.13 AU). The flux tube axis is almost on the ecliptic plane and perpendicular to the Sun-Earth direction. Choosing different final boundaries inside the range marked by the two dash-dotted lines in Fig. 1, we obtain very similar orientations for the cloud axis (the angles are modified by less than $5^\circ$).

The MV analysis gives a ratio between the intermediate and the minimum eigen-values $\approx$7, so that the MC axis is well defined. This is confirmed by the SF method which gives a similar orientation (with, at most, $7^\circ$ difference to the MV result).

The fact that $B_{x, \rm cloud}$ in Fig. 1 fluctuates around zero is consistent with a trajectory of Wind almost intersecting the cloud axis ($p \ll R$). In the second and third panels we have the typical behavior of the azimuthal ( $B_{y, \rm cloud}$, global largest variance) and axial ( $B_{z, \rm cloud}$, global intermediate variance) magnetic field components of a cylindrical flux rope, as described in Sect. 4.1.

The bulk velocity profile (fourth panel) shows that this cloud is not expanding, it travels with an almost constant velocity of $\sim$400 km s-1. A shock front is present $\sim$8 h ahead of the cloud (10:42 UT, October 18). This shock was produced because the speed of the leading boundary of the cloud relative to the solar wind is greater than the magneto-acoustic speed (Lepping et al. 1997). Accordingly, the proton density (bottom panel) is high between the shock and the outer front of the cloud implying the consequent accumulation of material at its front. From a 4 minute time cadence analysis, Lepping et al. (1997) showed that there is a tangential discontinuity with a magnetic hole at the leading boundary of the magnetic cloud.


  \begin{figure} \par\includegraphics[width=7.9cm,clip]{4806fig_2.eps}\end{figure} Figure 2: Axial component, $B_{z, \rm cloud}$, of the cloud magnetic field (local coordinate system from MV) as a function of time (in hours, after 18:58 UT, October 18, 1995). Dots correspond to the observed field (temporal cadence of one minute), solid line to the Lundquist model, dashed line to the Gold-Hoyle model, dotted line to the Hidalgo model and dash-dotted line to the Cid model.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.9cm,clip]{4806fig_3.eps}\end{figure} Figure 3: Field component in the direction orthogonal to both the spacecraft trajectory and the MC axis. $B_{y, \rm cloud}$ is the azimuthal component of the magnetic field with the hypothesis of negligible impact parameter. The plotting convention is the same as in Fig. 2.
Open with DEXTER

Table 1: Results from fitting of the geometrical and physical parameters for the magnetic cloud of October 18-20, 1995, choosing the end time as 20-October-1995 00:00 UT (i.e., at t=29 in Figs. 2, 3, 5). The first four rows correspond to the orientation given by the minimum variance method (MV, Sect. 4.2), while the next four to a simultaneous fit (SF, Sect. 4.3). The next two rows are the mean and the maximum deviation from the mean of the parameters found with the eight above models and methods. The bottom three rows give the results of the direct method for the in-bound and out-bound parts of the flux rope, and the full back part of the MC (see Sect. 5.4). L, G, H, C refer to the Lundquist, Gold-Hoyle, Hidalgo et al. and Cid et al. models, respectively, and D to the direct method. The geometrical parameters are: the angle ($\theta $) between the axis of the tube and the ecliptic plane (i.e., its latitude), the angle ($\varphi $) between the projection of the cloud axis on the ecliptic plane and the x-axis of GSE (i.e., its longitude), the flux tube radius (R), and the impact parameter (p) measured in units of R. The two physical parameters of the models are: the twist angle per unit length ($\tau _0$) and the intensity of the field (B0), both computed at the cloud axis. The quality of the fitting is given by the square root of $\chi ^2$ (Eq. (16)). Finally, we give the axial magnetic flux (Fz) and quantities defined per unit length along the cloud axis: the azimuthal magnetic flux and magnetic helicity ($F_\phi /L$ and H/L).

   
4.5 Comparative analysis of the different models

Figures 2 and 3 show the magnetic observations together with the fitted curves corresponding to the four models and the MV method. The curves from the SF (not shown) are similar. Close to the centre of the cloud models L, G, and H overestimate  $B_{z, \rm cloud}$, while model C rather overestimates  $B_{z, \rm cloud}$ near the cloud boundaries. In the case of model H, a triangular profile is present for the magnetic field computed along any rectilinear trajectory that crosses the flux tube axis (p=0, see dotted curve in Fig. 2). In Fig. 3, the two non-force free models (H and C) are represented by the same straight line, which gives only the global behavior of  $B_{y, \rm cloud}$. The two force-free models (L and G) underestimate  $\vert B_{y, \rm cloud}\vert$ near the cloud boundaries.

According to the $\chi ^2$ values (Table 1), the quality of the fit, in decreasing order, is: C, H, L and G models for both MV and SF methods. This confirms the visual inspection of Figs. 2 and 3. However, we have to be cautious when making this comparison because in models L and G, Bz is not forced to be zero at the cloud boundary, while this is the case in models H and C to keep the same degrees of freedom between models. Finally, as expected, a better quality fit is obtained with a SF in all four cases.

The SF method gives a way to estimate the impact parameter p, which is of the order of $10 \%$ of the MC radius, while the orientation remains almost the same. This result, as well as the large angle of rotation of the magnetic vector seen on the variance plane (larger than $\sim$180$^\circ$, not shown), justifies the use of p=0 in the MV method.

The orientation of the magnetic cloud is well determined, being the maximum deviation in $\theta $ of $4^\circ$ and in $\varphi $of $6^\circ$. This, together with an always low impact parameter, implies that the geometry of the crossing is similar in all cases. Then, for fixed MC boundaries, the determined radius varies very little (Table 1).

We compare our results with those of previous works that used the same start and end times. Lepping et al. (1997) found $\theta=-12^\circ$, $\varphi=291^\circ$, p/R=0.08, $\tau _0 = 8.9$ AU-1, B0=25.6 nT, using the linear force-free field model (L) but fitting a magnetic field normalized to unity at each position. These authors fitted hourly averaged magnetic observations and forced Bz to be null at the cloud boundaries. Hidalgo et al. (2002), using model H, found $\theta=-16^\circ$, $\varphi=282^\circ$, p/R=0.15, $\tau _0 = 7.7$ AU-1, B0=24.3 nT, fitting the toroidal and poloidal components of the current (equivalent to our fit of B0 and $\tau _0$). These authors analyzed hourly averaged GSE components of the magnetic field. These small differences between our results and those of previous works are due to the different time cadence and minimization methods used.

From Table 1, we see that the largest difference between models is found for the parameter $\tau _0$, as its relative maximum deviation is $\sim$$38\%$ (compared to $\sim$$23\%$ for B0). However, the magnetic field line twist distribution is strongly model dependent. In the Gold-Hoyle model the twist is constant, in the Lundquist model it is mostly distributed in the periphery of the tube, in the Hidalgo model it depends inversely on the distance to the boundary ( (1-r/R)-1), while in the Cid model it depends on (1-r2/R2)-1. This implies that the obtained values for $\tau _0$, a local quantity, are not directly comparable between different models. A pertinent comparison can only be done using a global quantity, such as the magnetic helicity.

For the estimated fluxes and helicities we have a bias: the largest axial fluxes, Fz, are obtained with the two force-free models, while the largest azimuthal fluxes and helicities are given by the non-force free models. So the estimated global quantities, $F_z, F_\phi/L, H/L$, have a maximum deviation from the mean of 18, 25 and 28%, respectively.


  \begin{figure} \par\includegraphics[width=8cm,clip]{4806fig_4.eps}\end{figure} Figure 4: Axial magnetic field (B0), axial twist per unit length ($\tau _0$), fluxes ($F_\phi /L$ and Fz) and helicity (H/L), for the different chosen end times, as a function of the corresponding estimated MC radius R (see Sect. 4.6). Asterisks and solid line correspond to model L, triangles and dashed line to model G, X-symbol and the dotted line to model H, the O-symbol and dot-dashed line to model C. The vertical dashed line shows the end boundary of the magnetic cloud set on October 19, 22:54 UT. The radius range corresponds to the 21 equi-spaced end boundaries chosen between October 19, 17:31 UT and October 20, 01:38 UT.
Open with DEXTER

   
4.6 Effects of the boundary selection

The end time of this MC is not well defined and different values have been considered (Sect. 1.3). We repeat the fittings (MV and SF) but change the end time from October 19 at 17:31 UT to October 20 at 01:38 UT. We provide the reasons to exploring this extended range of times in Sect. 5. Changing the end time implies some modifications in the cloud orientation and the radius, as well as in the determined physical parameters.

Taking the mean value as reference (for the 4 models), to change the back boundary to the range used in Fig. 4 introduces a maximum relative change of $\pm$35% in $\tau _0$ and of $\pm$20% in B0. The above changes of the fitted parameters have implications for the estimation of the fluxes and helicity, but, since they are extensive quantities, they are more affected by the flux tube radius (which depends directly on the selection of the end time). Both fluxes and helicity show a nearly linear dependence on R (Fig. 4). We find a maximum relative change (relative to the mean value) of $\pm$50% in Fz, $\pm$40% in $F_\phi /L$, and $\pm$75% in H/L. In particular, H depends strongly on the radius (see Eqs. (9), (11), (13), and (15)) and, as found, we expect the largest variations for its value.

The time interval explored for the back boundary is about 3 times larger than the time interval given by the fixed values chosen as the back boundary by the different previous authors (Sect. 1.3). Taking the previous authors' interval, the changes in the magnitudes are about a factor of 2 lower than using our extended time interval (the changes can be seen in Fig. 4 between the dashed line and the right end of the plot). More precisely, for the previous authors' interval we find a relative change of $\sim$$\pm$25% in Fz, $\sim$$\pm$20% in $F_\phi /L$, and $\sim$$\pm$35% in H/L. These variations are comparable to the relative changes introduced when changing fitting methods and models (relative change of $\pm$18% in Fz, $\pm$25% in $F_\phi /L$, and $\pm$28% in H/L from Table 1).

   
5 Helicity and fluxes with the direct method

  
5.1 Determination of the MC centre and boundary directly from observations

Below we use $\nabla \cdot \vec{B}=0$ and the local invariance of $\vec{B}$ along the MC axis to define the centre and rear boundary of the twisted flux tube present in the MC.

Previous investigations of MCs (see Sect. 1), as well as the present one, concluded that they are formed by a twisted magnetic flux tube (or flux rope). Its magnetic field has two components: a longitudinal one (parallel to the MC axis) and an azimuthal one. Let us cut the flux rope once by a generic plane  $\mathcal{P}$, and let us compute the magnetic flux crossing  $\mathcal{P}$. The longitudinal component cuts  $\mathcal{P}$ in only one sense and, thus, its flux contributes a given sign, but the azimuthal component has both positive and negative flux contributions of equal absolute magnitudes across this plane. In order to have only the azimuthal flux and to include the data, below we define $\mathcal{P}$ as that plane formed by the spacecraft trajectory and  $\hat{z}_{\rm cloud}$. Then, we have:

 \begin{displaymath}% \int_{\rm flux~rope} B_{y, \rm cloud} {\ \rm d} x {\ \rm d} z = 0, \end{displaymath} (17)

with x,z being the spatial coordinates in the $\hat{x}_{\rm cloud}$ and  $\hat{z}_{\rm cloud}$ directions, respectively.

The magnetic field is expected to change significantly along the MC axis on a scale of a few AUs, which is much larger than its radius ($\approx$0.1 AU). The global radius of curvature of the MC is also expected to be a few AUs. Then, the hypothesis of a local symmetry by translation along the MC axis is well justified (in particular when data are fitted with models, see Sect. 3). With this hypothesis, Eq. (17) reduces to:

 \begin{displaymath}% \int_{\rm flux~rope} B_{y, \rm cloud} {\ \rm d} x = 0, \end{displaymath} (18)

whatever the precise shape of the MC cross section is (so compared to Sect. 3, we relax the hypothesis of cylindrical symmetry).

If one MC boundary is known, the above flux balance property can be used to find the MC centre and the other boundary as follows. We define the accumulative flux per unit length

 \begin{displaymath}% \frac{F_y(x)}{L} = \int_{X_{\rm in}}^{x} B_{y,{\rm cloud}}(x') {\ \rm d} x', \end{displaymath} (19)

where $X_{\rm in}$ is the position of the known boundary (the front one in the present case). The position where Fy(x) /L has its absolute extremum gives an estimation of the x position of the MC centre. This estimation is more precise as the impact parameter is lower. Then, when Fy(x) /L goes back to zero at $x=X_{\rm out}$, we have the other boundary. The region from $x=X_{\rm in}$ to  $x=X_{\rm out}$ defines the MC flux rope.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4806fig_5.eps}\end{figure} Figure 5: Accumulative flux of $B_{y, \rm cloud}$ (thick solid line) starting from the leading boundary of the cloud. Thin solid line shows $B_{y, \rm cloud}$ as a reference (in arbitrary units). The times of minimum and null flux accumulation are marked with vertical dashed lines.
Open with DEXTER

The accumulative flux Fy/Lis shown in Fig. 5 (thick solid line), together with the observed  $B_{y, \rm cloud}$ component (thin solid line). Vertical dashed lines mark the time at which Fy/L reaches the minimum (October 19, 07:26 UT) and the time when the flux cancels (October 19, 17:37 UT). They correspond to the centre and the rear boundary of the MC flux rope, respectively.

We note that around the time of the defined centre ($\pm$2 h) a well defined sub-structure is present in  $B_{y, \rm cloud}$. This sub-structure is globally anti-symmetric, which is a confirmation of the above determination of the flux rope centre from global flux balance. It also indicates the presence of a specific twist profile in the centre of the main flux rope. Even more striking, the flux balance determines the rear boundary of the flux rope where there is a discontinuity of  $B_{y, \rm cloud}$. This is a confirmation of the rear boundary location since a current sheet, so a discontinuity of $\vec{B}$, is expected at the boundary of two different magnetic structures (e.g. Aly 1990).

An alternative interpretation of this discontinuity has been proposed by Collier et al. (2001). These authors suggested that it is due to an internal shock traveling approximately along the cloud axis. The origin of the shock is supposed to be magnetic reconnection occurring close to the solar surface. With this interpretation, the flux balance determined above is only a coincidence. Our results rather support that this discontinuity is consistent with the presence of a time-dependent current sheet which separates the flux rope from the open field structure at the back part of the cloud. We further justify this below.


  \begin{figure} \par\hspace*{-1.2cm} \includegraphics[width=7cm,clip]{4806fig_6a.eps}\vspace*{2mm} \includegraphics[width=6cm,clip]{4806fig_6b.eps}\end{figure} Figure 6: Schematic 2D view of the magnetic cloud embedded in the solar wind near the Sun ( top) and during the spacecraft passage at 1 AU ( bottom). Because the MC is faster than the surrounding solar wind and their magnetic fields form a large angle (anti-parallel in the scheme), reconnection is forced in front of the MC (see Sect. 5.2). The horizontal dashed line in the bottom figure indicates the spacecraft trajectory.
Open with DEXTER

   
5.2 The structure of the magnetic cloud

The previous analysis of Fy/L shows that this MC is not simply formed by a flux rope. We summarize below the most plausible physical scenario to create such magnetic structure: reconnection between the original flux rope and the solar wind magnetic field. This scenario is coherent with all our results (Sect. 5.4), but we cannot rule out other possibilities such as reconnection closer to the solar surface (coronal observations are not stringent enough, Luoni et al. 2005).

Some of the MC characteristics, such as the low magnetic variance and the low proton temperature, continue well after the rear boundary of the flux rope (Lepping et al. 1997). Indeed, the accumulative Fy/L shows a strong change in the slope at 01:36 UT on October 20 (36 min after the tick at 30 h on the abscissa of Fig. 5), which was almost the back boundary chosen by some authors (Sect. 1.3). The fact that a portion of the back of the MC maintains the characteristics of a classical cloud, as well as a larger unbalanced flux, is unusual and was not noticed in previous works.

We interpret the lack of flux cancellation in the rear portion of the MC as evidence of a magnetic structure connected with solar wind field lines, which in the past formed the periphery of a larger flux rope. The top panel of Fig. 6 shows a 2D scheme of the initial magnetic configuration. It is formed by a flux rope embedded in a solar wind environment having the conditions that favor reconnection at the front of the MC as the flux rope overtakes the wind field. The bottom panel shows a possible result of magnetic reconnection between the MC and the solar wind field lines. Vandas et al. (1995) and Schmidt & Cargill (2003) have done MHD simulations of this process in comparable but different configurations: in a Parker spiral field with an MC axis orthogonal to the ecliptic, and in a radial unipolar solar wind or in a radial current-sheet with an MC, respectively.

The magnetic field in the MC front is mostly directed north-south (Fig. 1 of Janoo et al. 1998). If this field is pushed against a field with a significantly different direction, like the solar wind magnetic field dominant in the ecliptic plane, it will reconnect with it. Indeed, our Fig. 1 shows a sudden change of the bulk velocity at the upstream shock occurring at 10:42 UT on October 18, from $\sim$320 km s-1 before the shock to $\sim$400 km s-1 after, indicating a significant relative velocity between the cloud (plus its sheath) and its environment during the early stage of its travel from the lower corona to 1 AU. This fact favors the reconnection process because its efficiency increases with the relative velocity between the cloud and the solar wind (Schmidt & Cargill 2003). In low density plasmas, such as those found in the interplanetary medium, numerical simulations show that the Hall effect can significantly increase the reconnection rate over the classical rate (e.g., Morales et al. 2005). Furthermore, Farrugia et al. (2001) found that magnetic holes, such as that preceding the cloud analyzed here, can be a signature of magnetic reconnection. Thus, assuming a reconnection process in the cloud front, part of the flux in the front will be removed and will not be observed by a spacecraft crossing the cloud centre. However, the available data do not allow us to localize the reconnection site during the cloud travel from the Sun to the spacecraft.

What are the major implications for the reconnected field lines and the remnant flux rope? First, the magnetic stress is able to decrease because of the propagation of Alfvén waves from the MC into the solar wind along the new reconnected field lines. This decreases $B_{z, \rm cloud}$ at the back of the MC as the reconnected field lines tend to straighten. However, the flux of  $B_{y, \rm cloud}$ cannot decrease since it would need a further reconnection with almost parallel magnetic fields (located further inside the MC). In order to compensate the decrease of  $B_{z, \rm cloud}$ in the magnetic pressure, $B_{y, \rm cloud}$ has to increase. Furthermore, the new reconnected field lines are linked to the solar wind at the back of the MC where a faster stream is present (Lepping et al. 1997). All these effects imply a compression of the back of the MC, with an expected effect also on the back of the remnant flux rope. In conclusion, the front reconnection makes the MC asymmetric, not only in flux but also in field strength.

   
5.3 Quantification of global magnitudes using the direct method

In this section we show how the direct method can be used to compute the magnetic fluxes (axial and azimuthal) and the helicity per unit length directly from the observed magnetic time series. These computations are done as a function of the x coordinate along the projection of the spacecraft trajectory orthogonal to the MC axis. This requires us to transform the magnetic data in the cloud frame (Sect. 4.1). Three hypothesis are needed: the local invariance along the cloud axis, the cylindrical symmetry and a moderately low impact parameter ( $p/R \la 0.3$, see last paragraph of this section).

The centre of the flux rope is defined at the time when Fy/L is minimum (Sect. 5.1, Fig. 5), and we set the coordinate origin there (x=0). Then, we split the time series of $\vec{B}$ in two subseries for  $B_{y, \rm cloud}$ and  $B_{z, \rm cloud}$. The first subseries corresponds to the in-bound path (the path when the spacecraft is going toward the centre of the cloud, x<0) and the second to the out-bound path (when the spacecraft has reached the minimum distance to the cloud axis and is going out the MC, x>0). Differences in the results obtained with these two branches are due to the non-cylindrical symmetry of the flux rope, and also to the systematic bias due to reconnection of part of the MC flux with the solar wind magnetic field (Sect. 5.2).

The spacecraft trajectory approaches the MC axis up to the minimum distance p, so we are only able to evaluate the following quantities on the out-bound path:

   
                                       $\displaystyle F_{z,e}(x) \equiv 2 \pi \int_{0}^{x} B_z(x') x' {\ \rm d} x'$  
    $\displaystyle \hspace*{1cm} = 2 \pi \int_{p}^{r} B_z(r') r' {\ \rm d} r' = F_{z}(r) - F_{z}(p)$ (20)
    $\displaystyle \frac{F_{y,e}(x)}{L} \equiv \int_{0}^{x} B_{y, \rm cloud}(x') {\ \rm d} x'$  
    $\displaystyle \hspace*{1.1cm} = \int_{p}^{r} B_{\phi}(r') {\ \rm d} r' = \frac{F_{\phi}(r) - F_{\phi}(p)}{L}$ (21)
    $\displaystyle \frac{H_{e}(x)}{L} \equiv 2 \int_{0}^{x} B_{y, \rm cloud} (x') F_{z,e}(x') ~ {\rm d}x'$  
    $\displaystyle \hspace*{0.95cm} \approx 2 \int_{p}^{r} B_\phi (r') F_z(r') ~ {\rm d}r' = \frac{H(r)-H(p)}{L},$ (22)

where the position x corresponds to the radius r (taken from the centre of the flux rope). The definitions of Fz,e, Fy,e/L, and He/L (with the symbol $\equiv$) involve only available data in the MC frame. The following equalities (or approximation for He/L) give the interpretation of these quantities supposing a cylindrical symmetry. For the in-bound path the expressions are the same except that integral limits, [0,x], are simply replaced by [x,0] (with x<0).

If the impact parameter is finite, the core of the flux rope is not present in the data, so the fluxes and helicity will be underestimated. Since $Bz \approx B_{0}$ and $B_\phi \approx B_{0} \tau_{0} r$ in the core ($r \ll R$), the relative underestimation of both fluxes given by Eqs. (20) and (21) is of the order of (p/R)2 compared to the fluxes given by Eqs. (4) and (5). If Fz is known, the underestimation of the helicity in the core is of the order of (p/R)4; however, an underestimation of Fz (a cumulative magnitude from r=0) by using Fz,e is present in the integral, and it increases the underestimation to the order (p/R)2. Then, the underestimation of both global fluxes and helicity is of the order of $(p/R)^{2} \approx 1\%$ for the October 18 MC. This is much smaller than the uncertainties present on these quantities (e.g. the difference between the in and out-bound values), and we neglect them below.

We note that, for MCs observed with a higher p/R, a correction can be added by using a fitted model (Sect. 3) as follows. The simultaneous fit of the model parameters to the data lets us estimate the impact parameter p, as well as an extrapolation of the magnetic field in the unobserved core (Sect. 4.3). This extrapolated field can be used to estimate Fz(p), $F_{\phi}(p)$ and H(p) in Eqs. (20)-(22), and so to add a correction for the unobserved core.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4806fig_7.eps}\end{figure} Figure 7: Accumulative azimuthal flux per unit length ( $F_{y,e} /L \approx F_{\phi ,e} /L$, in 1021 Mx/AU), axial flux (Fz,e, in 1021 Mx), and magnetic helicity per unit length (He/L, in 1042 Mx2/AU), as function of |x| where x is the coordinate along the projection of the spacecraft trajectory orthogonal to the MC axis. The location of the MC centre was chosen at 07:26 UT on October 19 (Sect. 5.1). The solid vertical line shows the position of the front of the MC (at $x=X_{\rm in}$) and the dotted vertical line the position of the rear boundary (at $x=X_{\rm out}$) selected to have flux balance in  $B_{y, \rm cloud}$. The dashed vertical line shows the position of the back of the MC (at $x=X_{\rm back}$).
Open with DEXTER

   
5.4 The computed fluxes and helicity values

In this section, we present the results obtained with the direct method applied to the MC of October 18-20, 1995. Each result is first described, and then interpreted within the physical scenario of Sect. 5.2.

The accumulative flux Fy,e(x)/L, shown in Fig. 7, is asymmetric in x between the in-bound (solid line) and the out-bound (dotted line) paths because at the back of the cloud there is a magnetic compression due to the excess of flux (as consequence of the flux reconnected in its front, see Sect. 5.2 and Fig. 6). The vertical solid line marks the well-determined initial boundary of the cloud at $\vert X_{\rm in}\vert=0.101$ AU (note the strong change of the slope of  Fy,e /L). An azimuthal flux $F_{y,e}/L(X_{\rm in})=2.5$ $\times$ 1021 Mx/AU is accumulated in the front part of the flux rope. The vertical dotted line indicates the position  $X_{\rm out}$ (=0.081 AU) where the azimuthal flux cancels the in-bound flux (Fig. 5). Thus, the rear boundary of the flux rope is closer to the centre than its front with an asymmetry factor of $2(X_{\rm out}-\vert X_{\rm in}\vert)/(X_{\rm out}+\vert X_{\rm in}\vert)=0.22$.

Furthermore, in accordance with Fig. 5, there is a strong change of the slope at an out-bound distance $X_{\rm back}=0.147$ AU. Integrating from x=0 up to this extended boundary we obtain $F_{y,e}/L(X_{\rm back})=5.8$ $\times$ 1021 Mx/AU (a factor 2.3 larger than the closed azimuthal flux). Following Sect. 5.2, this flux is interpreted as the total azimuthal flux of the flux rope before its reconnection with the solar-wind magnetic field.

The in- and out-bound Fz,e(x) fluxes are very close, from the centre to about the middle of the central part of the flux rope (Fig. 7). In the outer part the difference has the opposite sign than for Fy,e/L. This is a consequence of the compression of the rear of the flux rope: it enhances $B_{y, \rm cloud}$, but it also flattens the flux rope, extending it in the $\pm y$ directions; then, the Bz flux spreads over a larger area, giving a lower measured Bz for the out-bound (than for the in-bound). The computed fluxes, assuming cylindrical symmetry, are: $F_{z,e}(X_{\rm in})=0.86$ $\times$ 1021 Mx and $F_{z,e}(X_{\rm out})=0.51$ $\times$ 1021 Mx, thus a relative balance of 51% in the flux rope. As with Fy,e/L, a clear change of the Fz,e(x) slope is present at the back of the MC ( $x=X_{\rm back}$). The extra Bz flux at the back of the MC (between  $X_{\rm out}$ and  $X_{\rm back}$) is small: $\Delta F_{z,e}=0.17$ $\times$ 1021 Mx. This was expected in the interpretation of Sect. 5.2 since Alfvén waves transport the Bz component away from the MC on field lines reconnected with the solar wind.

The accumulated magnetic helicity per unit length (He/L) is the most symmetric magnitude (between in- and out-bound paths) of the three quantities shown in Fig. 7. However, there is a strong asymmetry when we consider the amount accumulated at the flux rope boundaries: $H_e/L(X_{\rm in})=2.6$ $\times$ 1042 and $H_e/L(X_{\rm out})= 1.3$ $\times$ 1042 Mx2/AU. There is less helicity at the rear of the flux rope because it is compressed, so Bz is lower.

When considering the full out-bound part of the MC, the asymmetry is reversed, and we get $H_e/L(X_{\rm back})= 5.4$ $\times$ 1042 Mx2/AU so about a factor 2 larger than  $H_e/L(X_{\rm in})$. This shows that taking only the flux rope part of the MC, the magnetic helicity can be significantly underestimated. In fact, even with the full out bound part, the magnetic helicity content before reconnection is still underestimated since part of the helicity is transported away in the reconnected field lines. Thus, part of the mutual helicity associated with $B_\phi$, which encircles the internal Bz flux before reconnection, is lost at the back part due to the propagation of torsional Alfvén waves.

The magnetic helicity found with the full out-bound data, $H/L(X_{\rm back})= 5.4$ $\times$ 1042 Mx2/AU, is within the range found for the models [3.7,6.1] $\times$ 1042 Mx2/AU in Sect. 4.5. These results were obtained fitting the data from  $X_{\rm in}$ to $\sim$ $X_{\rm back}$ (Table 1). This approach also assumes a cylindrical symmetry, but sets the centre in the middle between  $X_{\rm in}$ and  $X_{\rm back}$, which is not the centre of the flux rope (Sect. 5.1). Moreover, the fits introduce model-dependent deviations from the observed data. Then, the estimations from Eqs. (20)-(22) should be more reliable.

Finally, we compare the MC helicity to the helicity variation before and after the solar ejection. The relevant quantity is the total helicity present in the CME/MC before it significantly reconnects with the solar wind magnetic field. Our best estimate is $H/L(X_{\rm back})$. The estimated length of the cloud is $\approx$2 AU (Larson et al. 1997); then, the magnetic helicity content in the MC is, at least, 10 $\times$ 1042 Mx2. This amount is twice the value found by Luoni et al. (2005) ($\approx$5 $\times$ 1042 Mx2) for the difference between the pre- and post-eruption helicity in active region NOAA 7912. This was estimated from a linear force-free field model fitted to best represent the observed coronal loops before and after the solar ejection. This is an indication that the coronal model used underestimates the amount of magnetic helicity present in the corona.

   
6 Conclusions

We have computed the large-scale magnetic fluxes and helicity for the magnetic cloud (MC) observed by Wind on October 18-20, 1995, following two different approaches. The first one fits an analytical model to the observed in situ magnetic field vector. We have tested four models, already proposed in the literature. The second method, introduced in this paper, computes the magnetic fluxes and helicity directly from the observed data, rotated in the MC system of coordinates.

We have determined the MC orientation both from the standard minimum variance analysis (MV) and a simultaneous fitting (SF) of the geometrical and physical parameters. The four different models included in our study are a linear force-free field (L), a uniformly twisted field (G), a field with constant current (H), and a field with a linearly distributed current (C).

The front boundary of the MC is well defined at 18:58 UT on October 18, so we always keep this value. Fixing the back boundary at 00:00 UT on October 20 and considering the different models using MV and SF, we have found a maximum deviation from the mean value of 18% in the axial flux (Fz), of 25% in the azimuthal flux ($F_{\phi}$) and of 28% in the magnetic helicity (H). However, because of the ambiguity present in defining the back boundary, we explore the effects of changing its position. If we restrict the boundary location to the range previously used by several authors (Sect. 1.3), the change of position of the back boundary has an effect comparable to the change when using a different model and method.

The direct integration method takes as input the observed magnetic data transformed to the MC coordinate system (Sect. 4.1). The centre of the flux rope is determined by the extremum of the flux of the azimuthal field (more precisely the flux of the field component both orthogonal to the MC axis and the spacecraft trajectory). This direct method relaxes the need for a model to compute the fluxes and helicity; then, it avoids the biases introduced by a specific model. It also permits two independent measurements on both sides of the flux rope centre: one in the in-bound and another in the out-bound part.

The direct method allows us to determine the centre and the rear boundary of the flux rope present at the time of the observations. The rear boundary is confirmed by the presence of a strong discontinuity of the magnetic field, which implies a current sheet as expected between two magnetic regions of different connectivities. The fluxes and helicity associated with the flux rope are smaller than those estimated from the fitted models, which include a larger part of the MC.

As an outcome of the application of the direct method we can better understand the structure of the MC. We conclude that this MC was most plausibly formed by a large flux rope after its ejection from the Sun, but its front partially reconnects with the solar wind magnetic field. This reconnection removes magnetic flux from the front part of the MC and creates the corresponding amount of open field lines at the back of the MC. At the time of the observations, only the core of the original flux rope remains. The back part no longer belongs to the flux rope but it is still formed by the field and plasma that have some typical characteristics of MCs (low field variance, low proton temperature). We conclude that the direct method provides a better estimate of the fluxes and magnetic helicity in the original flux rope, before reconnection, by using the extended out-bound results (D-MV back in Table 1).

The extended magnetic configuration (flux rope and open field at the back) is more representative of the flux tube expelled from the Sun. Still, magnetic reconnection in the front allows the axial flux and the helicity to go away from the front of the MC, but also partly from its back. So our estimation using the extended out-bound measured values is expected to be only a lower limit. Moreover, we assume a cylindrical symmetry, and with an MC more extended in the transverse direction to the spacecraft trajectory, the axial flux and helicity will be even larger (by a factor roughly proportional to the aspect ratio). Thus, in the October 18 MC we determine a minimum helicity content $\approx$1043 Mx2. This minimum is still a factor of two larger than the coronal helicity variation estimated by Luoni et al. (2005). This indicates that the coronal value is even more underestimated.

Acknowledgements
This research has made use of NASA's Space Physics Data Facility (SPDF). This work was partially supported by the Argentinean grants: UBACyT X329, PIP 6220 (CONICET), and PICTs 03-12187 and 03-14163 (ANPCyT). S.D. and C.H.M. are members of the Carrera del Investigador Científico, CONICET. C.H.M. and P.D. thank CNRS (France) and CONICET (Argentina) for their cooperative science program N0 18302.

References

 
Copyright ESO 2006