A&A 455, 119-129 (2006)
DOI: 10.1051/0004-6361:20054218

3D spectroscopy with VLT/GIRAFFE

II. Are luminous compact galaxies merger remnants?[*]

M. Puech1 - F. Hammer1 - H. Flores1 - G. Östlin2 - T. Marquart3


1 - Laboratoire Galaxies Étoiles Physique et Instrumentation, Observatoire de Paris, 5 place Jules Janssen, 92195 Meudon, France
2 - Stockholm Observatory, AlbaNova University Center, 10691 Stockholm, Sweden
3 - Dept. of Astronomy and Space Physics, Box 515, 75120 Uppsala, Sweden

Received 16 September 2005 / Accepted 3 March 2006

Abstract
Luminous Compact Galaxies (LCGs) are enigmatic sources in many aspects. They can reach the luminosity of the Milky Way within a radius of only a few kpc. They also represent one of the most rapidly evolving populations of galaxies since they represent up to 1/5 of the luminous galaxies at redshift z= 0.7, while being almost absent in the local Universe. The measurement of their dynamics is crucial to our understanding of LCGs since this has the potential of telling us which physical process(es) drive(s) them and ultimately link them to the existing present-day galaxies. Here, we derive the 3-dimensional velocity fields and velocity dispersion ($\sigma $) maps of 17 LCGs selected from the Canada France Redshift Survey and the Hubble Deep Field South with redshifts ranging from z=0.4 to z=0.75. We find that only 18% of them show rotational velocity fields typical of rotating disks while the others show more complex kinematics. Assuming that LCGs are not too far from equilibrium, about half of LCGs then appear to be either non-relaxed objects, or objects that are not supported by velocity dispersion alone. This supports the view that an important fraction of LCGs are probably mergers. It brings additional support to the "spiral rebuilding scenario'' in which LCGs correspond to a previous or post-merger phase before the disk re-building.

Key words: galaxies: evolution - galaxies: formation - Galaxy: kinematics and dynamics - galaxies: bulges

1 Introduction

Luminous Compact Galaxies (LCGs) (MB<-20, \(r_{\rm half}<5~ h_{50}^{-1}\) kpc, and ${\it EW}_0(\rm [OII]) >15$ Å) correspond to the most rapidly evolving population seen in the UV (Lilly et al. 1998): they represent $\sim $20% of the 1>z>0.4 galaxies (Zheng et al. 2005), $\sim $50% of the emission line galaxies (see Paper I, Flores et al. 2006), and almost vanish in the local Universe, with their number density decreasing by factors of 7-10 (Jangren et al. 2004; Garland et al. 2003; Werk et al. 2004). Moreover, LCGs contribute to 40-50% of the increase in the cosmic Star Formation Rate (SFR) density between z=0 and 1, as measured from rest frame UV luminosities (Lilly et al. 1995; Guzman et al. 1997), and 25% in the IR (Zheng et al. 2004). The spectra of LCGs reveal a mixture of old, intermediate, and young stellar populations (Hammer et al. 2001). Apart from their compactness, LCGs have properties surprisingly similar to those of other, more extended luminous IR galaxies and starbursts: they show a similar mix of stellar populations, extinction property distributions, stellar masses, and SFRs (Hammer et al. 2005). This led Hammer et al. (2001) to propose that LCGs are the progenitors of present-day bulges of early type spirals.

Recently, Hammer et al. (2005) proposed the so-called "spiral rebuilding scenario'' to explain the formation of 75% of the most massive local spirals. This scenario is composed of 3 major phases: a "pre-merger phase'' during which two distant spirals merge, the "LCG phase'' where all material from the progenitors fall into the mass barycenter of the system and form a bulge, and the "disk growing phase'' where subsequently accreted material forms a rotating disk. This scenario is partly supported by Östlin et al. (1999 and 2001), who obtained very complex H\(\alpha\) velocity fields for local LCGs, characteristic of what is expected from merging galaxies. Another alternative is the one proposed by Barton & Van Zee (2001): comparing HI and optical emission line widths of nearby LCG candidates, they argued that interactions and minor mergers of disk galaxies may cause apparently compact morphology leading to the formation of a bulge. Both views are not incompatible and can occur during different stages of the "LCG phase'' described by Hammer et al. (2005).

Compact galaxies have been extensively studied in the past. Koo et al. (1995) were the first to propose that some compact galaxies could be the progenitors of local dwarf ellipticals (dE), assuming that they experience a dramatic event of star formation before fading away by up to 5 magnitudes. Guzman et al. (1997) established a distinction between two types of compact galaxies: 60% present properties characteristic of young star-forming HII galaxies (in, e.g., velocity widths, SFRs, and mass-to-light ratios), whereas the remaining 40% constitute a more heterogeneous class of evolved starbursts, similar to local starburst disk galaxies. Philips et al. (1997) then suggested that the HII-like compact galaxies are the best candidates to evolve into dEs. In this paper, we study the most luminous and most actively star-forming fraction of the population of Compact Galaxies (LCGs), i.e., those that contribute most to the increase in the star formation rate density. It is important here to stress that the sample presented in this paper corresponds to the brightest 25% of galaxies in the sample of Blue Compact Galaxies (BCGs) in the Hubble Deep Field (HDF) at 0.1 < z <1.3 studied by Guzman et al. (1997)[*], and would have mostly been classified as SB-disk-like compact galaxies in terms of their criteria. They thus do not correspond to the sub-class of compact galaxies that Guzman et al. (1997) would have considered as possible progenitors of dEs. Notice that for another sub-class of compact galaxies, Philips et al. (1997) found that "one possibility is that they are disks forming from the center outward, and so the radius of the luminous material and enclosed mass are small compared to present-day spirals''.

Whereas the LCGs are important for understanding galaxy evolution below z=1, their nature is still enigmatic. The aim of this paper is to evaluate the nature of their kinematics from a survey of 17 LCGs randomly selected from the CFRS and the HDF-South (HDFS) field at redshifts from z= 0.4 to 0.75 and to investigate whether their dynamics are supported either by rotation or velocity dispersion. Section 2 presents the sample, observations, and the methodology we followed. Kinematical and dynamical results are in Sects. 3 and 4. We discuss our results in Sect. 5, and a conclusion is given in Sect. 6. In the following, we assumed a $\Lambda$-CDM cosmology with H0=70, $\Omega_{\rm m}=0.3$, $\Lambda_0=0.7$, and q0=-0.55.

2 Sample, observations and methodology

To select compact galaxies, we used Hubble Space Telescope (HST) images in the F814W filter (WFPC2, 0.1 arcsec/pix and ACS, 0.05 arcsec/pix), in the CFRS (3 hr and 22 hr fields), and the HDFS field. For one galaxy, however, we used ground-based image obtained by the CFRS team at the CFHT (0.207 arcsec/ pix, see Hammer et al. 2001).

We selected 21 LCGs with \(0.4\leq z\leq 0.75\), following the procedure detailed in Hammer et al. (2001), using the light concentration parameter $\delta$ as a compactness criterion which measures the difference between the luminosities within the 5 and 15 kpc radii (see Table 1). The condition $\delta I < 0.73$allows us to select galaxies with $r_{\rm half} \leq 5~ h^{-1}_{50}$ kpc in a homogeneous way. This value corresponds to $\sim $4.34 kpc in a $\Lambda$-CDM cosmology at $z\sim0.55$. To achieve a homogeneous selection, ACS images were degraded to mimic WFPC2 images using a point spread function (PSF) generated with the Tiny Tim software. This size criterion ensures the selection of relatively small galaxies (see Ravindranath et al. 2004), although not necessarily as compact as those selected by some other authors (e.g., Guzman et al. 1997). Half light radii were then derived by interpolating luminosities enclosed within concentric ellipses using the IRAF polyphot task (see Hammer et al. 2001 for a complete description of the procedure). Inclinations were estimated using Sextractor (Bertin et al. 1996) and the ellipse task of IRAF: we find a mean absolute difference of $\sim $2 degrees between these two methods. Independent measurements were also done by eye and gave similar results as Sextractor to within $\sim $4 degrees. In the following, we will use the estimates from Sextractor and assume an error of $\pm $4 degrees.

Table 1: Main properties of the sample of LCGs: galaxies names, redshifts, isophotal I magnitudes, absolute B and K magnitudes, light concentration, half light radii, inclination.

As part of the Guaranteed Time Observations (GTO) of the Paris Observatory, we obtained observations with the FLAMES/GIRAFFE instrument of the 21 compact galaxies using the deployable integral field units (IFUs), each covering an area of 3 by 2 arcsec2, at 0.52 arcsec/pixel. The complete description of the GTO sample is given in Paper I (Flores et al. 2006). Briefly, we used LR04 and LR05 setups targeting the [OII] doublet ( \(R\sim10~000\)), integration times ranging from 8 to 13 hours, and the seeing was typically \(\sim \)0.6 arcsec during all the observations. Data cubes were reduced using the GIRBLDRS v1.12 package (Blecha et al. 2000), including narrow flat-fielding. Sky was carefully subtracted with our own IDL procedures.

From among these 21 compact galaxies, we selected 17 galaxies for which at least 4 pixels had an [OII] doublet reaching a spectral signal-to-noise ratio (SNR) of 4 (see definition in Paper I). In the following, we focus only on these 17 remaining LCGs (see Table 1). At first sight, it might seem too challenging to derive velocity fields of compact galaxies ( $r_{\rm half} \sim 0.5$ arcsec), using the GIRAFFE/IFU with 0.52 arcsec microlenses. To assess this, we examined how many pixels reached a SNR of 3. Among the sample of LCGs, we found a median value of 11 pixels ($\sim $3 arcsec2) compared to 16 ($\sim $4.3 arcsec2) for a sample of 8 spirals in Paper I (Flores et al. 2006). On average, our LCGs are thus $\sim $30% less extended than spirals. However, the average filling factor of the IFU (20 pixels) for the sample of 17 LCGs is $\sim $55%, which is sufficient to explore the kinematics of these galaxies.

We processed the spectra with a Savitzky-Golay filtering, which has an advantage over the widely used box smoothing in that it conserves the first moment of spectral lines (Press et al. 1989). We identified the [OII] doublet by visual inspection and retained the spectra that reached a sufficient spectral SNR of 3. We then fitted a double Gaussian with the following constraints (where the subscripts denote the two components of the fit): $\lambda _2-\lambda _1=2.783~\AA$(in rest frame wavelength) and $\sigma_1=\sigma _2$. The line ratio was allowed to vary freely except when the fit failed: in these cases we kept the line ratio at a value of 1.4, which was the median value observed in the integrated spectra. This line ratio occurs for pixels with rather low SNR and affects $\sim $10% of the measured pixels; it thus will not significantly affect our results. In all such cases, we checked by eye that the derived fit was acceptable and took this into account during the classification (see below). The complete procedure is described in Paper I.

Figure 1 shows velocity and velocity dispersion ($\sigma $) maps for the 17 LCGs. The $\sigma $-maps were corrected for the instrumental broadening using sky lines. To make the interpretation easier, velocity fields and $\sigma $-maps are presented after a simple $5\times 5$ linear interpolation.

3 Kinematics of LCGs

As in Paper I (Flores et al. 2006), we define 3 kinematical classes: rotating disks (velocity field showing rotation and $\sigma $-map showing a peak at the dynamical center), perturbed rotations (velocity field showing rotation, but $\sigma $-map without peak or with a peak offset from the dynamical center), and complex kinematics (see Fig. 1 and comments on individual objects). This classification relies on the fact that observations with a low spatial resolution integral field spectrograph, such as GIRAFFE, should reveal line widths dominated by the integration of larger scale motions and not by intrinsic random motions: in the case of a rotating disk, $\sigma $ should show a peak near the galaxy dynamical center, where the gradient of the rotation curve is the steepest (e.g., Van Zee & Bryant 1999). This classification has been checked through numerical simulations which are described in detail in Paper I. In these simulations, we assumed that all the observed galaxies are indeed rotating disks (taken as a standard model) and that all the observed large-scale motions in the velocity fields correspond to rotations. In other words, we have tried to force each system to appear as rotational disks and then estimate the discrepancy between the observed system and the adopted standard rotation (see Paper I). Below we comment on the velocity fields of individual objects.


  \begin{figure} \par\includegraphics[width=14.5cm,clip]{4218fg1a.eps}\end{figure} Figure 1: Kinematics of 17 LCGs. From left to right: I band HST imaging (0.1 arcsec/pix, FoV = $3\times 2$ arcsec2) with the IFU bundle superimposed; velocity field ($5\times 5$ interpolation, $\sim $0.1 arcsec/pix), $\sigma $-map ($5\times 5$ interpolation, $\sim $0.1 arcsec/pix), and SNR map (spectral SNR, see Paper I). From top to bottom: LCGs classified as rotating disks (first 3), perturbed (next 5), and complex (last 9). The first 3 galaxies classified as complex (CFRS03.0508, CFRS03.0645, and HDFS5140) are those suspected to be dominated by outflows.
Open with DEXTER


  \begin{figure}\par\includegraphics[width=14.6cm,clip]{4218fg1b.eps}\end{figure} Figure 1: continued.
Open with DEXTER

HDFS4170 Its kinematics is classified as a rotating disk: a rotation is seen in the velocity field and the $\sigma $-map has a clear peak in the center.
HDFS5190 Its kinematics is classified as a rotating disk: a clear rotation is seen in the velocity field and the $\sigma $-map shows a peak near the center.
CFRS03.0619 Its kinematics is classified as a rotating disk: the velocity field shows a clear rotation and the $\sigma $-map has a peak slightly offset from the center of the galaxy, but which can be reproduced by our simulation. We choose to classify this galaxy as a rotating disk rather than a perturbed rotation.
CFRS03.1032 Its kinematics was first classified as complex because the velocity field looked perturbed and the $\sigma $-map has a peak near the edge of the galaxy. Although our simulation cannot reproduce the amplitude of the $\sigma $ peak, this peak is located in the same pixel as the one seen in the observed $\sigma $-map. HST/ACS imaging reveals a very compact structure, completely dominated by the center. This galaxy is the most compact in the sample. We retrieved a FORS slit spectrum from which we found a log ([OIII]/H$_\beta$) ratio of 1.8, which characterizes a Seyfert galaxy spectrum: the high $\sigma $ value of this galaxy might reflect an AGN activity. We choose to re-classify its kinematics as a perturbed rotation, but we note that it somewhat escapes our classification scheme.
CFRS22.0619 Its kinematics is classified as a perturbed rotation: a clear rotation is seen in the velocity field, but the $\sigma $-map has a peak at the edge of the galaxy. Note that this galaxy is seen nearly edge-on.
CFRS03.1349 Its kinematics was first classified as a rotating disk because a clear rotation is seen in the velocity field and a peak is seen near the center of the $\sigma $-map. However, the simulation (see Paper I) cannot reproduce the location of the $\sigma $ peak, although the secondary peak (at the bottom-left of the maximal peak) is reproduced. Zheng et al. (2004) classified this galaxy as Sab with a compact bulge that is relatively blue, compared to the disk. A companion is 20 kpc away at the same redshift, and the distortion in the $\sigma $ map is oriented towards this companion. We suspect that an interaction (gas falling) is responsible for both the star-formation activity and distortion of the kinematics (following the scenario proposed by Barton & Van Zee 2001). We then choose to re-classify its kinematics as a perturbed rotation.

CFRS22.1064 Its kinematics is classified as perturbed: the velocity field shows rotation, but the $\sigma $-map is very perturbed.
HDFS5150 Its kinematics is classified as a perturbed rotation: rotation is seen in the velocity field, but the $\sigma $-map has a peak at the edge of the galaxy. The morphology looks quite irregular.

CFRS03.0508 The velocity field clearly shows an apparent rotation, and the $\sigma $-map has a well-defined peak in the center. Note, however, that the dynamical axis seems almost orthogonal to the photometric axis of the brightest component; this could be a signature of outflows (Veilleux et al. 2005; Bosma, private communication). Hence, its kinematics has been classified complex. From morphological studies, Zheng et al. (2005) classified this galaxy as the relic of an interaction or merger, with a relatively blue color over the whole galaxy.

CFRS03.0645 This galaxy also shows rotation that is orthogonal to the photometric major axis, which may indicate an outflow, and the $\sigma $-map has a peak at the edge of the galaxy. We classified the kinematics as complex. Zheng et al. (2005) found a relatively blue color all over the galaxy and classified it as a probable merger.

CFRS22.0919 Its kinematics is classified as complex: the velocity field is perturbed, and the $\sigma $-map does not show any peak. Note the tails, characteristic of interacting systems, seen in the HST image.

CFRS22.0975 Its kinematics is classified as complex: the velocity field is perturbed, and the $\sigma $-map shows a peak, but not at the galaxy center. HST imaging reveals 3 distinct components. This system is probably just preceding a merger, and the high velocity gradient in Fig. 1 can probably not be attributed to rotation.
CFRS03.0523 Its kinematics is classified as complex: the velocity field and the $\sigma $-map do not show any kind of structure expected from rotation. HST imaging shows a tidal tail, probably indicating ongoing interactions or gas accretion. This galaxy has a central region that is bluer than the outer region (Zheng et al. 2004). The $\sigma $maxima on the outer edges of the galaxy correspond to relatively blue regions (see Zheng et al. 2004).
HDFS4130 Its kinematics is classified as complex: the velocity field shows rotation, but the $\sigma $-map does not have any peak. This galaxy is asymmetric with (spiral?) arms visible on one side only; it may be a distant version of a "tadpole'' galaxy.
HDFS4090 Its kinematics is classified as complex: the velocity field is perturbed, and the $\sigma $-map does not have any peak. The morphology looks like a "peanut''.
HDFS5140 Its kinematics is classified as complex: the velocity field is very perturbed, although the $\sigma $-map has a peak near the center.
HDFS5030 Its kinematics is classified as complex: both the velocity field and the $\sigma $-map appear perturbed.
In the sample, 53% of the LCGs (9 galaxies) present complex kinematics, which are very different from nearby classical spiral galaxies (e.g., Garrido et al. 2002, 2003, 2004) or early-type galaxies (Emsellem et al. 2004), indicating that these LCGs are unrelaxed systems. As Fig. 1 shows, there is no correlation between these dynamical classes and their SNR. Even discarding the lowest SNR pixels would not change the nature of the kinematics; hence the kinematical complexity of a galaxy cannot be attributed to a lower SNR.

Five galaxies, or 29%, have perturbed kinematics, and the remaining three galaxies (18%) look like normal spiral galaxies. Interestingly, among these last eight galaxies (perturbed rotation and rotating disks), all but three (CFRS03.0619, HDFS5150, and HDFS5190) have possible nearby companions which might indicate interactions responsible for their compactness (see Barton & van Zee 2001).

Before concluding on the dynamical nature of LCGs, we have to investigate whether such perturbed/complex velocity fields could be artificial features caused by the low spatial sampling of GIRAFFE. In Flores et al. (2004, 2006), we illustrated the ability of GIRAFFE to recover regular velocity fields of distant rotating disks. The question, then, is to demonstrate the ability of GIRAFFE to recover more complex velocity fields in distant galaxies. To tackle this issue, we used Perot-Fabry observations of a local LCG by Östlin et al. (1999). We redshifted the ESO 400-G43 data cube (see Östlin et al. 1999, 2001) to z=0.6 and simulated the effects of a 0.52 arcsec sampling and a 0.6 arcsec seeing. The result is illustrated in Fig. 2: GIRAFFE smoothes the velocity fields (and thereby underestimates the velocity gradient), but no artificial features are created. Moreover, the simulated velocity field shows some similarities with those of the LCGs in Fig. 1.


  \begin{figure} \par\includegraphics[width=8.4cm,clip]{4218fig2.eps}\end{figure} Figure 2: Simulation of the velocity field of a LCG at z=0.6. Left: redshifted velocity field of ESO400-G43 (see Östlin et al. 1999) with a $\sim $0.1 arcsec pixel (1/5 of a GIRAFFE pixel). Right: velocity field of the same galaxy as could have been seen by GIRAFFE (0.6 arcsec seeing and 0.52 arcsec/pixel) with a simple $5\times 5$interpolation and assuming the same spatial extension. The resolution is dramatically reduced, as well as the velocity gradient (by a factor 4.7), but no artificial features are created.
Open with DEXTER

We can then conclude that LCGs are mainly (53 to 82%, as judged from our rather small number statistics) unrelaxed systems, at least when ionized gas motions are considered. Such complex kinematics have also been observed by Swinbank et al. (2005), who obtained the velocity field of a merger remnant at $z \sim 0.1$, similar to the complex velocity fields of our LCGs. However, this conclusion relies on the kinematics of the gas only: Östlin et al. (2004) showed that, in one local LCG, gas and stars seem dynamically decoupled and that stars seem more relaxed than the gas. In the following section, we attempt to investigate the nature of the LCG kinematics, namely if they are mostly dominated by rotation or by dispersion. The fact that LCGs are not dynamically relaxed systems is a severe limitation for this exercise.

4 Test of the dynamics of LCGs

To investigate energy balances of LCGs, we assume in this section that LCGs are systems that are almost at equilibrium. In this case, one could imagine two possibilities: (1) LCGs are mainly supported by velocity dispersion, or (2) LCGs are mainly supported by rotation. Both options require us to assume that LCGs are dynamically not too far from equilibrium, and we would like to point out that this assumption represents a severe limit in setting up energy balances of LCGs. Moreover, the possibility that LCGs are dominated by rotation requires us, in addition, to identify large-scale motions to rotation, which is even more speculative and will thus be detailed in the appendix.

4.1 Can LCGs be supported by velocity dispersion?

If LCGs were systems at equilibrium and supported by velocity dispersion, then the intensity-weighted mean $\sigma $ and the one derived from their integrated spectra $\sigma _{\rm intg}$ should be in agreement (e.g., Bershady et al. 2004; Östlin et al. 2001).

We constructed integrated spectra by the direct summation of all the spatial elements in the whole IFU. Integrated [OII] lines were fitted in the same way as for IFUs pixels, but due to the influence of larger scale motions (rotation for spirals) that widen integrated lines, about $50\%$ of the integrated spectra could not be fit correctly by a double Gaussian. We then independently summed up the fits of each line of the [OII] doublet over the whole IFU, fitted both by a single Gaussian (corrected from instrumental dispersion), and estimated the integrated velocity dispersion taking the mean of the two velocity dispersions derived independently. We checked that in most cases, these two velocity dispersions were very similar and that when an integrated line fit was possible, both methods gave similar results.

Table 2: Dynamical properties of the sample of LCGs. The column entries are ( from left to right): id, dynamical class (RD = Rotating Disk, PR = Perturbed Rotation, CK = Complex Kinematics), maximal rotational velocity (corrected from inclination, but not from GIRAFFE spatial sampling), intensity-weighted velocity dispersion calculated from the $\sigma $-map, velocity dispersion derived from integrated spectra, and stellar masses derived from photometry (in solar masses). The objects for which the kinematical classification is uncertain are indicated by a star; see individual comments.

Both measurements are presented in Table 2 and Fig. 3. We estimated the error on the sigma measurement to be 10% (median, see Paper I). We thus adopt a 30% relative threshold (3-sigma threshold) between $\sigma $ and $\sigma _{\rm intg}$ to identify the galaxies which could potentially be supported by velocity dispersion. Nine galaxies (roughly 50%) have such a relative difference between $\sigma $ and $\sigma _{\rm intg}$: CFRS03.0523, CFRS03.1032, CFRS22.0919, HDFS4090, HDFS5030, HDFS5150, CFRS03.0645, CFRS22.1064, and HDFS4130 (see Table 2 and Fig. 3). Note that among these galaxies, CFRS03.1032 is a very peculiar case because of both its very high central $\sigma $ and its AGN activity (see individual comments).


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4218fig3.eps}\end{figure} Figure 3: Velocity dispersion $\sigma _{\rm intg}$ derived from integrated spectra vs. intensity weighted, mean velocity dispersion $\sigma $derived from $\sigma $-maps. Encircled blue dots are LCGs classified as rotating disks, encircled green squares are LCGs classified as perturbed, and encircled red triangles are complex LCGs. Blue dots are rotating disks from Paper I (Flores et al. 2006), added for comparison. The dashed line represents the limit where the relative difference between $\sigma $ and $\sigma _{\rm intg}$ is 30%.
Open with DEXTER

4.2 Dynamical support of LCGs

The other possibility for LCGs to be systems at equilibrium is to be supported by rotation. This would imply that the large-scale motions seen in the velocity fields of LCGs are due to rotation, although these motions are not completely relaxed. However, we already know that this is not true, at least for the objects whose dynamical axis are not aligned with the optical one, i.e. for objects suspected of outflows (see individual comments). Nevertheless, in the appendix, we naively assumed that the large-scale motions are precisely due to rotation. Since we assumed that LCGs are at equilibirum, we can then set up energy balance using classical relations linking their kinematics (velocity or dispersion) to their mass, to see if these balances are effectively dominated by the large-scale motions interpreted as rotation. Under such an assumption, one finds that 70% of LCGs have an energy balance effectively consistent with rotation. However, this question can only be properly addressed with the knowledge of the kinematics of stars (see, e.g., Östlin et al. 2004).

To summarize, we find that about 50% of LCGs could be supported by velocity dispersion, assuming they are not too far from equilibrium. Given that 18% of LCGs are classified as RD, one third of LCGs remain for which we cannot exclude the possibility that a rotational support could play a role in their dynamical state. Both large-scale and random motions seem to play an important role in about 40% of LCGs. Such a mix is perfectly compatible with mergers.

5 Stellar vs. dynamical masses

We derive stellar masses M* following Hammer et al. (2005) (see Table 2). Figure 4 compares stellar masses with total dynamical pseudo-equivalent masses derived from integrated spectra, which is the most reliable estimate of the total dynamical mass we can use (see Appendix). Following Conselice et al. (2005), who carried out an extensive study of uncertainties and systematics on stellar masses, we estimate our error on stellar masses to be 0.5 dex. Among the sample of spirals of Paper I (Flores et al. 2006), a mean ratio of dynamical to stellar masses of $\sim $6 (median $\sim $7) was found, which is roughly in agreement with the mean ratio found by Conselice et al. (2005) of $\sim $5 for a sample of $z \sim$ 0.5 disk galaxies. The difference between these two samples of spirals is most probably related to the difference of observational strategy (slit spectroscopy vs. Integral Field Spectroscopy) because the maximal rotational velocity can be largely underestimated when measured by slit spectroscopy, since only a part of the whole kinematics is sampled (see Discussion). On the other hand, we find a mean ratio between dynamical ${\cal M}^E$ and stellar masses of $\sim $2 (median $\sim $1.6) for our sample of LCGs. If the majority of LCGs are merging systems, as suggested by their kinematics, their spectra are then likely to be dominated by unrelaxed motions, which could lead to an underestimation of their total dynamical ${\cal M}^E_{\sigma_{\rm intg}}$.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4218fig4.eps} \end{figure} Figure 4: Stellar masses vs. dynamical ${\cal M}^E$. Encircled blue dots are LCGs classified as rotating disks, encircled green squares are LCGs classified as perturbed, and encircled red triangles are complex LCGs. Blue dots are rotating disks from Paper I (Flores et al. 2006), added for comparison. For convenience, only the median error bar has been plotted.
Open with DEXTER

6 Discussion and conclusion

We have presented GIRAFFE-IFU observations and derived velocity fields and $\sigma $ maps for 17 LCGs. Our main result is that 18% have velocity fields characteristic of rotating disk kinematics, while the rest have perturbed or complex kinematics. This result is unlikely to be affected if we account for the four objects that were discarded because of a too low SNR. Among them, two show (in HST images) tail characteristics of ongoing interactions. Assuming that they are not too far from equilibrium, we find that about half of LCGs could be supported by velocity dispersion. The remaining 32% of LCGs seems to be dominated by large-scale motions. An important fraction of LCGs, between 32 and 82%, are thus probable mergers.

In this sample of 17 LCGs, four have their velocity gradient nearly perpendicular to their main optical axis (CFRS03.0508, CFRS03.0645, CFRS22.0975, and HDFS5140). It suggests that in these galaxies, gas is tracing feedback processes such as outflows, rather than gravitational dynamics: in this case, the dynamical axis should appear off-axis relative to the optical main axis (see Veilleux et al. 2005 and references therein). All of them except CFRS22.0975 have stellar masses lower than $3\times10^{10}~M_\odot$, which is the upper threshold for supernova feedback to drive efficient outflows (Dekel & Birnboim 2006). In CFRS22.0975, the gas velocity field probably traces the relative motion of the merger progenitors (see its morphology in Fig. 1). For CFRS03.0645, we retrieved FORS slit spectra (Hammer et al. 2001) to compare systemic velocities of emission (H$_\beta$, H$_\gamma$, [OII], and [OIII]) and absorption lines (CaII, H, and K) and found no significant shifts between them, which makes the outflow hypothesis uncertain for this galaxy. Note, however, that the slit has been aligned with the apparent (optical) main axis, which could explain why we did not see any shift between emission and absorption lines. The electron density map of CFRS03.0508 is presented in Paper III (Puech et al. 2006b) and supports the outflow hypothesis.

Bershady et al. (2004) used the STIS long slit spectrograph on-board the HST to study the kinematics of 6 LCGs with \(M_B \sim -21\), \(r_{\rm half}\sim2\)  h70-1 kpc, and $\sigma \sim$ 65 km s-1 and found that LCGs are supported by velocity dispersion. Unfortunately, only one galaxy of the present sample (CFRS22.0919) is compact enough to fulfill these selection criteria. Interestingly, it has being pointed out by Hammer et al. (2001) that this galaxy could be a possible progenitor of a dE. Here, we find that this galaxy is a possible candidate for being supported by dispersion. However, given the complexity of most LCGs kinematics presented here, slit spectroscopy should be used with care for this kind of object. A careful inspection of Fig. 1 reveals that with long slit spectroscopy, the real nature of many LCGs presented in this paper would have been misinterpreted. In the case of CFRS03.0645, a slit positioned along the main optical axis would have revealed a rather flat velocity gradient and would have completely missed the velocity gradient. The case of CFRS03.0508 is even more instructive: the same exercise would have revealed a flat velocity gradient and a clear $\sigma $ peak, and this galaxy would then have been classified as being supported by dispersion.

Finally, how can we interpret the compactness of LCGs? Most of perturbed kinematics and rotating LCGs show possible companions with which they could be in interaction. This could explain their compactness as being due to interactions and/or minor mergers, following Barton & van Zee (2001, see introduction). Another conjecture is that of Hammer et al. (2005). They proposed a scenario in which a local massive spiral could form after major mergers in three main phases. The sequence would start by a pre-merging phase during which the system would form a huge number of stars and appear as a LIRG. The second phase would be the LCG phase, where all material falls onto the mass barycenter of the merging system, which could enhance the star-formation activity in the center of these systems, making them look compact. This is consistent with Bergvall & Östlin (2002), who found intense, central starbursts superimposed on low surface-brightness components in four local BCGs. Our results are consistent with this picture, as we found that most LCGs are objects with complex kinematics, as expected from major mergers. During the third phase of the scenario, a disk would grow from material accreted from the IGM. Inflow/outflows are also predicted by this scenario, arising from feedback and gas falling back to form a new disk (see Robertson et al. 2005).

How can we distinguish between minor and major mergers? In a minor merger, the disk cannot be destroyed, and the kinematics of the remnant cannot appear too complex. We should then observe a galaxy still rotating along its main optical axis with a dispersion map peaking outside the center, where the smaller progenitor falls. This could correspond to the LCGs we classified as being perturbed. On the other hand, during a major merger the disk is completely destroyed, or at least strongly perturbed. In this case, we should then observe either a rotation that is significantly misaligned with the optical axis and that is combined with a non-centered dispersion map, or a complex kinematics without any obvious structure. We emphasize that given our spectral resolution, reaching $\sim $10 000, the fact that the [OII] doublet is not always resolved reveals the complexity of some of these galaxies.

LCGs dominate the evolution of the UV luminosity from z=1 to 0. Their role can thus not be negligible in the process of formation and evolution of galaxies during the last 8 Gyr. Our results highly support a hierarchical-type scenario where galaxies form from smaller units. In this scenario, LCGs seem to be a major event, as proposed by Hammer et al. (2005). Although based on small numbers, our sample is nevertheless representative of the galaxy population at \(0.4\leq z\leq 0.75\) (see Paper I). A larger sample is under construction as part of the ESO Large Program IMAGES (P.I.: F. Hammer) and will be a decisive step towards the confirmation of the spiral rebuilding scenario. Recently, it has been shown that major merger remnants may not necessarily be ellipticals, but may also be spirals, depending on the gas abundance (Springel & Hernquist 2005) and/or the Black Hole feedback (Robertson et al. 2005). Comparisons with theoretical simulations will provide crucial tests of the spiral rebuilding scenario and the nature of LCGs.

Acknowledgements
We thank P. Amram and C. Balkowski for their help and very useful comments, and R. Guzman, the referee, for his very useful comments and suggestions. We also thank A. Bosma for his enlightening comment on CFRS03.0508. We are especially indebted to T. J. Cox who provided us with hydrodynamical simulations of a Sbc galaxy. H.F. and M.P. wish to thank the ESO Paranal staff for their reception and their very useful advice during observations. We thank all the team of GIRAFFE at the Paris Observatory, at the Geneva Observatory, and at ESO for the remarkable accomplishments of this unique instrument, without which none of these results could have been obtained.

Appendix A: Energy balance of LCGs

This appendix is devoted to the energy balance of LCGs. It is explicitly assumed that LCGs are systems at equilibrium and supported by rotation. We will thus assume in this appendix that the large-scale motions seen in the velocity fields are associated with rotation, even if the true origin of these large-scale motions is largely uncertain, except for some suspected outflows and those clearly identified as RD from their kinematics (see individual comments and Sect. 4.2). We will nevertheless naively assume that their origin is rotation and see if any contradiction arises. To test this hypothesis, we set up an energy balance in the sample of LCGs. In this balance, we will take into account the contributions from large-scale ordered motions (interpreted as rotation) and from random motions. Energies are estimated in what we call "pseudo equivalent masses'' ( ${\cal M}^E$, i.e., in mass units). It is important to emphasize that these ${\cal M}^E$ can be interpreted as real masses only for galaxies in equilibrium.

A.1 Contribution from rotation

To estimate the mass supported by rotation, we assumed that the maximal rotational velocity is equal to half the maximal gradient of the velocity field, corrected for inclination (see Table 1). Due to the low spatial sampling and large distances to our targets, we have already pointed out that the GIRAFFE/IFU observations will underestimate the maximal rotational velocity (see Fig. 2). Using hydrodynamical simulations of an Sbc (Milky-Way like) galaxy by Cox et al. (2004), we simulated GIRAFFE observations, assuming median atmospherical conditions at ESO VLT (0.81 arcsec seeing at 500 nm and an outer scale for the turbulence of 24 m, see Tokovinin 2002). We scaled this template galaxy ( $V_{\rm rot}=160$ km s-1 and inc=53degrees) to fill boxes of lengths ranging from 0.75 to 6 arcsec to mimic distant galaxies, and then compared the kinematics seen by GIRAFFE with the original simulation (see Fig. A.1). We found that for spiral galaxies with sizes between 2 and 3 arcsec, GIRAFFE is able to correctly recover the maximal rotational velocity, although it is underestimated by $\sim $20%. For more complex kinematics, the correction factor should be larger (see Fig. 2 also): between 2 and 6. However, as we explicitly assume that LCGs are rotating disks in this section, we applied a constant factor of 20% whatever the dynamical class (spiral or perturbed/complex) of LCGs to compute homogeneous estimates.

Table A.1: Dynamical properties of the sample of LCGs. The column entries are ( from left to right): id, dynamical class (RD = Rotating Disk, PR = Perturbed Rotation, CK = Complex Kinematics), intensity-weighted velocity dispersion corrected from GIRAFFE sampling effect (see text), ${\cal M}^E$ supported by rotation (corrected from GIRAFFE sampling effect), ${\cal M}^E$ supported by random motions, total dynamical ${\cal M}^E$, and dynamical ${\cal M}^E$ estimated by integrated velocity dispersion.

Rotational ${\cal M}^E$ are then estimated from (Lequeux 1983):

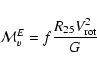
\begin{displaymath}{\cal M}^E_{v}=f{R_{25}V_{\rm rot}^2 \over G} \end{displaymath}

with f=0.6 for a disk with a flat rotation curve and $R_{25}=2r_{\rm half}$, following Phillips et al. (1997). For a purely exponential disk with scale length $r_{\rm d}$, $r_{\rm half}=1.67 r_{\rm d}$. Taking $R_{25}=2r_{\rm half}$ in fact assumes that $r_{\rm half}/r_{\rm d}= 1.6$, since $R_{25}=3.2r_{\rm d}$ (Persic & Salucci 1988). With ${\cal M}^E$ in ${\cal M}_\odot$, $V_{\rm rot}$ in km s-1 and $r_{\rm half}$ in kpc, this becomes:

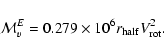
\begin{displaymath}{\cal M}^E_{v}=0.279\times 10^6r_{\rm half}V_{\rm rot}^2. \end{displaymath}

Corrected rotational velocities and ${\cal M}^E$ are given in Table A.1. To estimate our error bars, we took the uncertainties on $r_{\rm half}$ ($\sim $1/2 HST pixel, which represents 0.34 kpc at z=0.6), $V_{\rm rot}$ ($\pm $5 km s-1, determined by repeating the fitting procedure several times), inclination ($\pm $4 degrees, see Sect. 2), and the correction factor on the velocity ($\pm $0.04, see Fig. A.1) into account. Note, however, that the real uncertainty of the inclination is probably higher for unrelaxed systems, as its derivation usually relies on the assumption of a thin disk seen in projection (see Sect. 2). From this, we estimated an median error on ${\cal M}^E_v$ of $\sim $0.16 dex, which is mainly dominated by the uncertainty in the inclination.

A.2 Contribution from velocity dispersion

Following Östlin et al. (2001), we estimated the ${\cal M}^E$ supported by velocity dispersion using ( ${\cal M}^E$ in ${\cal M}_\odot$, $\sigma $ in km s-1and $r_{\rm half}$ in kpc):

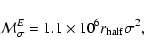
\begin{displaymath}{\cal M}^E_{\sigma}=1.1\times 10^6r_{\rm half}\sigma^2,\end{displaymath}

where $\sigma $is the intensity weighted mean of the $\sigma $-map. Due to the low GIRAFFE spatial sampling, $\sigma $ will tend to be overestimated, since the coarse pixel size integrates large-scale motions (rotation for a spiral galaxy). We used the same hydrodynamical simulation to estimate the increase in $\sigma $ due to large-scale motions and found $\sim $50 km s-1 ( $V_{\rm rot}=160$ km s-1 and inc=53 degrees). We used another simulation to check that the effect approximatively scales with $1/\!\sin(inc)$ (within an error on $\sigma $ of 5 km s-1) and assumed the same scaling with $V_{\rm rot}$. We then corrected the GIRAFFE intensity weighted mean $\sigma $ using this method, and from this estimated the mass supported by velocity dispersion (see Table A.1 and Fig. A.2). For pure rotating disks, a correction roughly equal to the measure is expected, which means that intrinsic velocity dispersion is negligible. Galaxies classified as rotating disks and which fall far from the $\sigma = \sigma _{\rm disk~ model}$region could be galaxies with a significant bulge (e.g., CFRS03.9003, see also Puech et al. 2006b) or could show perturbation in their $\sigma $-map (CFRS03.0619, CFRS22.0504, and HDFS4020). Interestingly, these 4 galaxies (plus CDFS03.1032, but see individual comments) are among those which are the nearest to the $\sigma _{\rm intg}= \sigma$ line in Fig. 3, which supports the idea that their dynamical support could include a substantial contribution coming from dispersion. All points with a correction larger than the measured mean $\sigma $ are spiral galaxies except one (CFRS22.0975) whose velocity gradient is likely due to relative motions between merging components (see its morphology in Fig. 1) rather than rotation. In these few cases, we fixed the corrected value to 10 km s-1, which corresponds to the minimal expected line width due to intrinsic turbulent motions in spiral galaxies (Rozas et al. 1998; Van Zee & Bryant 1999). We estimate a median error on ${\cal M}^E_\sigma$ of $\sim $0.08 dex.
  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4218fgA1.eps}\end{figure} Figure A.1: Correcting factor for the maximal rotational velocity vs. galaxy size. Due to its low spatial sampling, the GIRAFFE IFU leads to an underestimation of $V_{\rm rot}$ by a factor of $1.2\pm 0.04$ for galaxies of sizes between 2 and 3 arcsec. Solid line: tilted view ($\sim $53 degrees). Dashed line: top view ($\sim $25 degrees).


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4218fgA2.eps}\end{figure} Figure A.2: Correction term $\sigma_{\rm disk~ model}$ vs. intensity weighted mean $\sigma $. Encircled blue dots are LCGs classified as rotating disks, encircled green squares are LCGs classified as perturbed, and encircled red triangles are complex LCGs. Blue dots are rotating disks from Paper I (Flores et al. 2006), added for comparison.


  \begin{figure} \includegraphics[width=7.8cm,clip]{4218fgA3.eps} \end{figure} Figure A.3: Dynamical ${\cal M}^E$ derived from integrated spectra vs. dynamical  ${\cal M}^E$ derived from 3D spectroscopy. Encircled blue dots are LCGs classified as rotating disks, encircled green squares are LCGs classified as perturbed, and encircled red triangles are complex LCGs. Blue dots are rotating disks from Paper I (Flores et al. 2006), added for comparison. For convenience, only the median error bar has been plotted.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4218fgA4.eps} \end{figure} Figure A.4: Rotational ${\cal M}^E$ vs. total dynamical ${\cal M}^E$. Encircled symbols are the sample of LCGs. Encircled blue dots are LCGs classified as rotating disks, encircled green squares are LCGs classified as perturbed, and encircled red triangles are complex LCGs. Blue dots are rotating disks from Paper I (Flores et al. 2006), added for comparison. The dashed line represents the limit where ${\cal M}^E_v={\cal M}^E_{\rm dyn}$/2. For convenience, only the median error bar has been plotted. Notice that the high ${\cal M}^E_v$ of CFRS22.0975 (the point at the top right) could not be attributed to a normal rotation since it is an obvious merger.

A.3 Total dynamical ${\cal M}^E$

To estimate total dynamical pseudo-equivalent masses ${\cal M}^E_{\rm dyn}$, we simply added ${\cal M}^E_v$ and ${\cal M}^E_\sigma$. Most authors derive $\sigma $ on integrated spectra (global velocity dispersion) and use the relation of the previous section to estimate the whole dynamical mass ${\cal M}^E_{\sigma_{\rm intg}}$ (Guzman et al. 1996; Phillips et al. 1997). Under assumptions concerning the anisotropy of the kinetic energy tensor and the geometry of the system, this relation can be used to estimate total dynamical masses of rotating and flattened spheroids (Bender et al. 1992). This approach is often employed in studies using slit spectroscopy (Guzman et al. 1997, 2001; Hammer et al. 2001), but the validity of this relation for systems dominated by rotation is uncertain. In the following, we also estimated ${\cal M}^E_{\sigma_{\rm intg}}$, which we compared with ${\cal M}^E_{\rm dyn}$.

Figure A.3 shows the comparison between ${\cal M}^E_{\rm dyn}$ and ${\cal M}^E_{\sigma_{\rm intg}}$. We find a correlation between the two estimates, which seems to validate our estimates and is consistent with the fact that LCGs could be systems not too far from equilibrium. Spiral galaxies are almost equally distributed on both sides of the line where ${\cal M}^E_{\sigma _{\rm intg}}={\cal M}^E_{\rm dyn}$, which is likely due to the fact that ${\cal M}^E_{\sigma_{\rm intg}}$ does not explicitly correct for inclination effects.

In Fig. A.4 we compare ${\cal M}^E_v$ with ${\cal M}^E_{\rm dyn}$to test if the LCGs are dominated by rotation. For comparison, we also plot a sample of 8 rotating disks taken from Paper I (Flores et al. 2006). Clearly, the whole spiral sample falls in the rotation dominated area. At least 70% of the LCGs (12 galaxies) seem to be dominated by rotation, whereas the remaining 30% (5 galaxies) seem to be dominated by velocity dispersion. Note that these five galaxies were already identified as potentially supported by dispersion (see Sect. 4.1): CFRS22.0919, CFRS03.0523, CFRS03.1032 HDF4090, and CFRS22.1064. Interestingly, one of these galaxies (CFRS22.0919) was identified by Hammer et al. (2001) as a potential dwarf progenitor, as discussed by Guzman et al. (1997). Because it is likely that we are underestimating their rotational velocities, we cannot exclude that all LCGs have an energy balance dominated by rotation.

However, we recall that this conclusion relies on the assumptions that large-scale motions in the velocity fields are due to rotation, and that we know that for some systems (e.g., the suspected outflows) this is far from being true. We nevertheless cannot exclude that a possible relation could link most of the LCGs with rotating disks.

References

 
Copyright ESO 2006