A&A 455, 21-43 (2006)
DOI: 10.1051/0004-6361:20053887
S. Colafrancesco1,2 - S. Profumo3 - P. Ullio4,5
1 - INAF - Osservatorio Astronomico di Roma,
via Frascati 33, 00040 Monteporzio, Italy
2 -
Istituto Nazionale di Fisica Nucleare,
Sezione di Roma 2, 00133 Roma, Italy
3 -
Department of Physics, Florida State University,
505 Keen Bldg., Tallahassee, FL 32306, USA
4 -
Scuola Internazionale Superiore di Studi Avanzati,
via Beirut 2-4, 34014 Trieste, Italy
5 -
Istituto Nazionale di Fisica Nucleare,
Sezione di Trieste, 34014 Trieste, Italy
Received 22 July 2005 / Accepted 10 April 2006
Abstract
We study the astrophysical implications of neutralino dark matter annihilations
in galaxy clusters, with a specific application to the Coma cluster. We first address the
determination of the dark halo models for Coma, starting from structure formation models
and observational data, and we discuss in detail the role of sub-halos. We then perform a
thorough analysis of the transport and diffusion properties of neutralino annihilation
products, and investigate the resulting multi-frequency signals, from radio to gamma-ray
frequencies. We also study other relevant astrophysical effects of neutralino
annihilations, like the DM-induced Sunyaev-Zel'dovich effect and the intracluster gas
heating. As for the particle physics setup, we adopt a two-fold approach, resorting both
to model-independent bottom-up scenarios and to benchmark, GUT-motivated frameworks. We
show that the Coma radio-halo data (the spectrum and the surface brightness) can be
nicely fitted by the neutralino-induced signal for peculiar particle physics models and
for magnetic field values, which we outline in detail. Fitting the radio data and moving
to higher frequencies, we find that the multi-frequency spectral energy distributions are
typically dim at EUV and X-ray frequencies (with respect to the data), but show a
non-negligible gamma-ray emission, depending on the amplitude of the Coma magnetic field.
A simultaneous fit to the radio, EUV and HXR data is not possible without violating the
gamma-ray EGRET upper limit. The best-fit particle physics models yields substantial
heating of the intracluster gas, but not sufficient energy injection as to explain the
quenching of cooling flows in the innermost region of clusters. Due to the specific
multi-frequency features of the DM-induced spectral energy distribution in Coma, we find
that supersymmetric models can be significantly and optimally constrained either in the
gamma-rays or at radio and microwave frequencies.
Key words: cosmology: theory - galaxies: clusters - cosmology: dark matter - galaxies: clusters: general
Most of the matter content of the universe is in form of dark matter, whose presence is
indicated by several astrophysical evidences (e.g., gravitational lensing, galaxy
rotation curves, galaxy clusters masses) but whose nature is still elusive.
On the cosmological side, the most recent results of observational
cosmology, i.e. WMAP vs. distant SN Ia, indicate that the matter content
of the universe is
![]() with a baryon
density of
with a baryon
density of
![]() (Spergel et al. 2003).
The combination of the available data on large scale structures (Ly-
(Spergel et al. 2003).
The combination of the available data on large scale structures (Ly-![]() forest
analysis of the SDSS, the SDSS galaxy clustering) with the latest SNe and with the 1st
year WMAP CMB anisotropies can improve the determination of the cosmological parameters
(Seljak et al. 2004) and hence allow us to set a concordance cosmological model.
forest
analysis of the SDSS, the SDSS galaxy clustering) with the latest SNe and with the 1st
year WMAP CMB anisotropies can improve the determination of the cosmological parameters
(Seljak et al. 2004) and hence allow us to set a concordance cosmological model.
We refer, in this paper, to a flat ![]() CDM cosmology with parameters chosen
according to the global best fitting results derived in Seljak et al. (2004) (see their Table 1,
third column): we assume, in fact, that the present matter energy density is
CDM cosmology with parameters chosen
according to the global best fitting results derived in Seljak et al. (2004) (see their Table 1,
third column): we assume, in fact, that the present matter energy density is
![]() ,
that the Hubble constant in units of 100 km s-1 Mpc-1 is h=0.71, that
the present mean energy density in baryons is
,
that the Hubble constant in units of 100 km s-1 Mpc-1 is h=0.71, that
the present mean energy density in baryons is
![]() ,
with the only
other significant extra matter term in cold dark matter
,
with the only
other significant extra matter term in cold dark matter
![]() ,
that our Universe has a flat geometry and a cosmological constant
,
that our Universe has a flat geometry and a cosmological constant ![]() ,
i.e.
,
i.e.
![]() ,
and, finally, that the primordial power
spectrum is scale invariant and is normalized to the value
,
and, finally, that the primordial power
spectrum is scale invariant and is normalized to the value
![]() .
This choice sets our framework, but it is not actually crucial for any of the results
presented in the paper, which can be easily rescaled in case of a re-assessment of
best-fit values of the cosmological parameters, and in particular of the value of
.
This choice sets our framework, but it is not actually crucial for any of the results
presented in the paper, which can be easily rescaled in case of a re-assessment of
best-fit values of the cosmological parameters, and in particular of the value of
![]() (the present concordance cosmological model, while widely used, has been
also criticized and questioned in the light of still unexplored systematics, see, e.g.,
Myers et al. 2003; Sadat et al. 2005; Lieu & Mittaz 2005; Copi et al. 2004)
(the present concordance cosmological model, while widely used, has been
also criticized and questioned in the light of still unexplored systematics, see, e.g.,
Myers et al. 2003; Sadat et al. 2005; Lieu & Mittaz 2005; Copi et al. 2004)
The Coma cluster has been the first astrophysical laboratory for dark matter (DM) since the analysis of F. Zwicky (Zwicky 1933). In this respect, we can consider the Coma cluster as an astrophysical benchmark case-study for DM. Modern observations have led to an increasingly sophisticated exploration of the DM distribution in the universe, now confirmed to be a dominant component (relative to the baryonic material) over scales ranging from those of galaxy halos to that of the particle horizon.
The nature of DM is not yet known and several detection techniques have been used so far. Obviously, direct detection is the cleanest and most decisive discriminant (see e.g. Munoz 2003, for a review). However, it would be interesting if astronomical techniques were to reveal some of the fundamental properties of DM particles. In fact, if DM is supposed to consist of fundamental particles which are weakly interacting, then their own interaction will lead to a number of astrophysical signatures (e.g., high-energy gamma-rays, electrons and positrons, protons and neutrinos and hence by their emission/interaction properties) indicative of their nature and composition.
These facts provide the basic motivations for our study, which is aimed to: i) describe the multi-wavelength signals of the presence of DM through the emission features of the secondary products of neutralino annihilation. These signals are of non-thermal nature and cover the entire electro-magnetic spectrum, from radio to gamma-ray frequencies; ii) indicate the best frequency windows where it will be possible to catch physical indications for the nature of DM; iii) apply this analysis to the largest bound containers of DM in the universe, i.e. galaxy clusters. We shall focus here on the case of the Coma cluster, a particularly rich and suitable laboratory for which an extended observational database is at hand.
Several candidates have been proposed as fundamental DM constituents, ranging from axions to light, MeV DM, from KK particles, branons, primordial BHs, mirror matter to supersymmetric WIMPs (see, e.g., Baltz 2004; Bertone et al. 2004; and Bergstrom 2000, for recent reviews). In this paper we will assume that the main DM constituent is the lightest neutralino of the minimal supersymmetric extension of the Standard Model (MSSM). Although no experimental evidence in favor of supersymmetry has shown up to date, several theoretical motivations indicate that the MSSM is one of the best bets for new physics beyond the Standard Model. Intriguingly enough, and contrary to the majority of other particle physics candidates for DM, supersymmetry can unambiguously manifest itself in future accelerator experiments. Furthermore, provided neutralinos are stable and are the lightest supersymmetric particles, next generation direct detection experiments feature good chances to explore most of the neutralino-proton scattering cross section range predicted by supersymmetry.
A long standing issue in phenomenological studies of low-energy supersymmetry is traced to the parameterization of the supersymmetry breaking terms (see Chung et al. 2003, for a recent review). In this respect, two somehow complementary attitudes have been pursued. On the one hand, one can appeal to a (set of) underlying high energy principles to constrain the form of supersymmetry breaking term, possibly at some high energy (often at a grand unification) scale (see e.g. Baer et al. 2000). The low energy setup is then derived through the renormalization group evolution of the supersymmetry breaking parameters down to the electroweak scale. Alternatively, one can directly face the most general possible low energy realization of the MSSM, and try to figure out whether general properties of supersymmetry phenomenology can be derived (see e.g. Profumo & Yaguna 2004).
In this paper we will resort to both approaches. We will show that the final state products of neutralino pair annihilations show relatively few spectral patterns, and that any supersymmetric configuration can be thought as an interpolation among the extreme cases we shall consider here. The huge number of free parameters of the general MSSM are therefore effectively decoupled, and the only relevant physical properties are the final state products of neutralino pair annihilations, and the mass of the neutralino itself. We will indicate this first strategy as a bottom-up approach (see Sect. 4.1 for details).
Since most phenomenological studies have been so far based on GUT-motivated models, and a wealth of results on accelerator physics, direct and indirect detection has accumulated within these frameworks, we decided to work out here, as well, the astrophysical consequences, for the system under consideration, of a few benchmark models. The latter have been chosen among the minimal supergravity (mSUGRA) models indicated in Battaglia et al. (2004) with the criterion of exemplifying the widest range of possibilities within that particular theoretical setup (see Sect. 3.2 for details).
To make our study quantitative, we will compare the predictions of the above mentioned
neutralino models with the observational set-up of the Coma cluster, which represents the
largest available observational database for a galaxy cluster. The total mass of Coma
found within
10 h-1 Mpc from its center is
![]() (Geller et al. 1999).
The assumption of hydrostatic equilibrium of the thermal intra-cluster gas in Coma
provides a complementary estimate of its total mass enclosed in the radius r. A value
(Geller et al. 1999).
The assumption of hydrostatic equilibrium of the thermal intra-cluster gas in Coma
provides a complementary estimate of its total mass enclosed in the radius r. A value
![]() within
5 h-150 Mpc from the cluster
center has been obtained from X-ray data (Hughes 1989).
within
5 h-150 Mpc from the cluster
center has been obtained from X-ray data (Hughes 1989).
X-ray observations of Coma also yield detailed information about the thermal electrons
population. We know that the hot thermal electrons are at a temperature
![]() keV (Arnaud et al. 2001) and have a central density
keV (Arnaud et al. 2001) and have a central density
![]() cm-3, with a spatial distribution
fitted by a
cm-3, with a spatial distribution
fitted by a ![]() -model,
-model,
![]() ,
with parameters
,
with parameters
![]() and
and
![]() (Briel et al. 1992).
Assuming spherical symmetry and the previous parameter values, the optical depth of the
thermal gas in Coma is
(Briel et al. 1992).
Assuming spherical symmetry and the previous parameter values, the optical depth of the
thermal gas in Coma is
![]() and the pressure due to the
thermal electron population is
and the pressure due to the
thermal electron population is
![]() keV cm-3. The hot
intra-cluster gas produces also a thermal SZ effect (Sunyaev & Zel'dovich 1972; Sunyaev & Zel'dovich 1980; see
Birkinshaw 1999, for a general review) which has been observed over a wide frequency
range, from 32 to 245 GHz (see DePetris et al. 2002, and references therein).
keV cm-3. The hot
intra-cluster gas produces also a thermal SZ effect (Sunyaev & Zel'dovich 1972; Sunyaev & Zel'dovich 1980; see
Birkinshaw 1999, for a general review) which has been observed over a wide frequency
range, from 32 to 245 GHz (see DePetris et al. 2002, and references therein).
Beyond the presence of DM and thermal gas, Coma also shows hints for the presence of
relativistic particles in its atmosphere. The main evidence for the presence of a
non-thermal population of relativistic electrons comes from the observation of the
diffuse radio halo at frequencies
![]() (Deiss et al. 1997;
Thierbach et al. 2003). The radio halo spectrum can be fitted by a power-law spectrum
(Deiss et al. 1997;
Thierbach et al. 2003). The radio halo spectrum can be fitted by a power-law spectrum
![]() in the range 30 MHz-1.4 GHz with a further steepening of
the spectrum at higher radio frequencies.
The radio halo of Coma has an extension of
in the range 30 MHz-1.4 GHz with a further steepening of
the spectrum at higher radio frequencies.
The radio halo of Coma has an extension of
![]() Mpc, and its
surface brightness is quite flat in the inner 20 arcmin with a radial decline at larger
angular distances
(e.g., Colafrancesco et al. 2005).
Mpc, and its
surface brightness is quite flat in the inner 20 arcmin with a radial decline at larger
angular distances
(e.g., Colafrancesco et al. 2005).
Other diffuse non-thermal emissions have been reported for Coma (as well as for a few
other clusters) in the extreme UV (EUV) and in the hard X-ray (HXR) energy bands.
The Coma flux observed in the
65 - 245 eV band (Lieu et al. 1996) is
![]() above the expected flux from the thermal bremsstrahlung emission of the
above the expected flux from the thermal bremsstrahlung emission of the
![]() keV IC gas (Ensslin & Biermann 1998) and it can be modeled with a power-law spectrum with
an approximately constant slope
keV IC gas (Ensslin & Biermann 1998) and it can be modeled with a power-law spectrum with
an approximately constant slope ![]() 1.75, in different spatial regions
(Lieu et al. 1999; Ensslin et al. 1999; Bowyer et al. 2004).
The EUV excess in Coma has been unambiguously detected and it does not depend much on the
data analysis procedure. The integrated flux in the energy band
0.13 - 0.18 keV is
1.75, in different spatial regions
(Lieu et al. 1999; Ensslin et al. 1999; Bowyer et al. 2004).
The EUV excess in Coma has been unambiguously detected and it does not depend much on the
data analysis procedure. The integrated flux in the energy band
0.13 - 0.18 keV is
![]() erg cm-2 s-1 (Bowyer et al. 2004).
According to the most recent analysis of the EUVE data (Bowyer et al. 2004), the EUV
excess seems to be spatially concentrated in the inner region (
erg cm-2 s-1 (Bowyer et al. 2004).
According to the most recent analysis of the EUVE data (Bowyer et al. 2004), the EUV
excess seems to be spatially concentrated in the inner region (
![]() arcmin) of Coma (see also Bonamente et al. 2003). The nature of this excess is not
definitely determined since both thermal and non-thermal models are able to reproduce the
observed EUV flux. However, the analysis of Bowyer et al. (2004) seems to favour a
non-thermal origin of the EUV excess in Coma generated by an additional population of
secondary electrons.
A soft X-ray (SXR) excess (in the energy range
arcmin) of Coma (see also Bonamente et al. 2003). The nature of this excess is not
definitely determined since both thermal and non-thermal models are able to reproduce the
observed EUV flux. However, the analysis of Bowyer et al. (2004) seems to favour a
non-thermal origin of the EUV excess in Coma generated by an additional population of
secondary electrons.
A soft X-ray (SXR) excess (in the energy range
![]() keV) has been also
detected in the outer region (
keV) has been also
detected in the outer region (
![]() )
of Coma
(Bonamente et al. 2003; Finoguenov et al. 2003). The spectral features of this SXR excess
seem to be more consistent with a thermal nature of the SXR emission, while a non-thermal
model is not able to reproduce accurately the SXR data (e.g., Bonamente et al. 2003).
The SXR emission from the outskirts of Coma has been fitted in a scenario in which the
thermal gas at
)
of Coma
(Bonamente et al. 2003; Finoguenov et al. 2003). The spectral features of this SXR excess
seem to be more consistent with a thermal nature of the SXR emission, while a non-thermal
model is not able to reproduce accurately the SXR data (e.g., Bonamente et al. 2003).
The SXR emission from the outskirts of Coma has been fitted in a scenario in which the
thermal gas at
![]() keV with
keV with ![]() 0.1 solar abundance (see, e.g.
Finoguenov et al. 2003 who identify the warm gas with a WHIM component) resides in the
low-density filaments predicted to form around clusters as a result of the evolution of
the large-scale web-like structure of the universe (see Bonamente et al. 2003). It has
been noticed, however, that the WHIM component cannot reproduce, by itself, the Coma SXR
excess because it would produce a SXR emission by far lower (see Mittaz et al. 2004),
and thus one is forced to assume a large amount of warm gas in the outskirts of Coma.
Thus, it seems that the available EUV and SXR data indicate (at least) two different
electron populations: a non-thermal one, likely yielding the centrally concentrated EUV
excess and a thermal (likely warm) one, providing the peripherically located SXR excess.
In this paper, we will compare our models with the EUV excess only, which is intimately
related to Coma being spatially concentrated towards the inner region of the cluster.
0.1 solar abundance (see, e.g.
Finoguenov et al. 2003 who identify the warm gas with a WHIM component) resides in the
low-density filaments predicted to form around clusters as a result of the evolution of
the large-scale web-like structure of the universe (see Bonamente et al. 2003). It has
been noticed, however, that the WHIM component cannot reproduce, by itself, the Coma SXR
excess because it would produce a SXR emission by far lower (see Mittaz et al. 2004),
and thus one is forced to assume a large amount of warm gas in the outskirts of Coma.
Thus, it seems that the available EUV and SXR data indicate (at least) two different
electron populations: a non-thermal one, likely yielding the centrally concentrated EUV
excess and a thermal (likely warm) one, providing the peripherically located SXR excess.
In this paper, we will compare our models with the EUV excess only, which is intimately
related to Coma being spatially concentrated towards the inner region of the cluster.
There is also evidence of a hard X-ray (HXR) emission observed towards the direction of
Coma with the BeppoSAX-PDS (Fusco-Femiano et al. 1999; Fusco-Femiano et al. 2004) and with the
ROSSI-XTE experiments (Rephaeli et al. 1999). Both these measurements indicate an excess over
the thermal emission which amounts to
![]() erg s-1 cm-2 (Fusco-Femiano et al. 2004).
It must be mentioned, for the sake of completeness, that the HXR excess of Coma is still
controversial (see Rossetti and Molendi 2004), but, for the aim of our discussion, it could at worst
be regarded as an upper limit. The nature of the HXR emission of Coma is not yet fully
understood.
erg s-1 cm-2 (Fusco-Femiano et al. 2004).
It must be mentioned, for the sake of completeness, that the HXR excess of Coma is still
controversial (see Rossetti and Molendi 2004), but, for the aim of our discussion, it could at worst
be regarded as an upper limit. The nature of the HXR emission of Coma is not yet fully
understood.
Finally, a gamma-ray upper limit of
![]() pho cm-2 has been derived for Coma from EGRET observations (Sreekumar et al. 1996;
Reimer et al. 2004).
pho cm-2 has been derived for Coma from EGRET observations (Sreekumar et al. 1996;
Reimer et al. 2004).
The current evidence for the radio-halo emission features of Coma has been interpreted as synchrotron emission from a population of primary relativistic electrons which are subject to a continuous re-acceleration process supposedly triggered by merging shock and/or intracluster turbulence (e.g., Brunetti et al. 2004). The EUV and HXR emission excesses are currently interpreted as Inverse Compton scattering (ICS) emission from either primary or secondary electrons. Alternative modeling has been proposed in terms of suprathermal electron bremsstrahlung emission for the HXR emission of Coma (see Ensslin et al. 1999; Kempner & Sarazin 2000, see also Petrosian 2001 for a critical discussion) and in this case the EUV emission should be produced either by a different relativistic electron population or by a warm thermal population both concentrated towards the cluster center. Lastly, models in which the EUV and HXR emission can be reproduced by synchrotron emission from the interaction of Ultra High Energy cosmic rays and/or photons (Timokhin et al. 2004; Inoue et al. 2005) have also been presented. The situation is far from being completely clear and several problems still stand on both the observational and theoretical sides of the issue.
Since DM is abundantly present in Coma and relativistic particles are among the main annihilation products, we explore here the effect of DM annihilation on the multi-frequency spectral energy distribution (SED) of Coma. The plan of the paper is the following. We discuss in Sect. 2 the DM halo models for the Coma cluster, the set of best fitting parameters for the DM distribution, and the role of sub-halos. The annihilation features of neutralinos and the main annihilation products are discussed in Sect. 3. The multi-frequency signals of DM annihilation are presented and discussed in details in Sects. 4 and 5, while the details of the transport and diffusion properties of the secondary particles are described in the Appendix A, together with the derivation of the equilibrium spectrum of relativistic particles in Coma. The conclusions of our analysis and the outline for forthcoming astrophysical searches for DM signals in galaxy clusters are presented in the final Sect. 6.
To describe the DM halo profile of the Coma cluster we refer, as a general setup, to the
![]() CDM model for structure formation, implementing results of galaxy cluster
formation obtained from N-body simulations. Free parameters are fitted against the
available dynamical information and are compared to the predictions of this scheme.
Substructures will play a major role when we will discuss the predictions for signals of
DM annihilations. In this respect, the picture derived from simulations is less clean
and, hence, we will describe in details our set of assumptions.
CDM model for structure formation, implementing results of galaxy cluster
formation obtained from N-body simulations. Free parameters are fitted against the
available dynamical information and are compared to the predictions of this scheme.
Substructures will play a major role when we will discuss the predictions for signals of
DM annihilations. In this respect, the picture derived from simulations is less clean
and, hence, we will describe in details our set of assumptions.
To describe the DM halo profile of the Coma cluster we consider the limit in which the
mean DM distribution in Coma can be regarded as spherically symmetric and represented by
the parametric radial density profile:
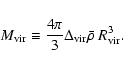 |
(5) |
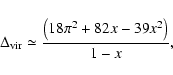 |
(6) |
Since the first numerical results with large statistics became available (Navarro et al. 1996,1997), it
has been realized that, at any given redshift, there is a strong correlation between
![]() and
and
![]() ,
with larger concentrations found in lighter halos. This trend
may be intuitively explained by the fact that mean overdensities in halos should be
correlated with the mean background densities at the time of collapse, and in the
hierarchical structure formation model small objects form first, when the Universe was
indeed denser.
The correlation between
,
with larger concentrations found in lighter halos. This trend
may be intuitively explained by the fact that mean overdensities in halos should be
correlated with the mean background densities at the time of collapse, and in the
hierarchical structure formation model small objects form first, when the Universe was
indeed denser.
The correlation between
![]() and
and
![]() is relevant in our context at two levels:
i) when discussing the mean density profile of Coma and; ii) when including
substructures. Hence, we will review this relevant issue here and we will apply it to the
present case of Coma. Bullock et al. (2001) proposed a model to describe this correlation,
improving on the toy model originally outlined in Navarro et al. (1996,1997). A collapse redshift
is relevant in our context at two levels:
i) when discussing the mean density profile of Coma and; ii) when including
substructures. Hence, we will review this relevant issue here and we will apply it to the
present case of Coma. Bullock et al. (2001) proposed a model to describe this correlation,
improving on the toy model originally outlined in Navarro et al. (1996,1997). A collapse redshift ![]() is assigned, on average, to each halo of mass M at the epoch z through the relation
is assigned, on average, to each halo of mass M at the epoch z through the relation
![]() .
Here it is postulated that a fixed fraction F of M(following Wechsler et al. 2001 we choose F=0.015) corresponds to the typical collapsing
mass
.
Here it is postulated that a fixed fraction F of M(following Wechsler et al. 2001 we choose F=0.015) corresponds to the typical collapsing
mass ![]() ,
as defined implicitly by
,
as defined implicitly by
![]() ,
with
,
with
![]() being the critical overdensity required for collapse
in the spherical model and
being the critical overdensity required for collapse
in the spherical model and ![]() being the present-day rms density fluctuation in
spheres containing a mean mass M (see, e.g., Peebles 1980). An expression
for
being the present-day rms density fluctuation in
spheres containing a mean mass M (see, e.g., Peebles 1980). An expression
for
![]() is given, e.g., in Eke et al. (1996). The rms fluctuation
is given, e.g., in Eke et al. (1996). The rms fluctuation ![]() is
related to the fluctuation power spectrum P(k) (see e.g. Peebles 1993) by
is
related to the fluctuation power spectrum P(k) (see e.g. Peebles 1993) by
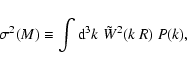 |
(8) |
The toy model of Bullock et al. (2001) prescribes a one to one correspondence between the
density of the Universe at the collapse redshift ![]() of the DM halo and a
characteristic density of the halo at the redshift z; it follows that, on average, the
concentration parameter is given by
of the DM halo and a
characteristic density of the halo at the redshift z; it follows that, on average, the
concentration parameter is given by
![\begin{figure}
\par\includegraphics[width=7cm,clip]{cvir.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg118.gif) |
Figure 1:
The dependence of
|
| Open with DEXTER | |
An alternative toy-model to describe the relation between
![]() and M has been discussed by Eke,
Navarro & Steinmetz (Eke et al. 2001, hereafter ENS model). The relation they propose has a similar
scaling in z, but with a different definition of the collapse redshift
and M has been discussed by Eke,
Navarro & Steinmetz (Eke et al. 2001, hereafter ENS model). The relation they propose has a similar
scaling in z, but with a different definition of the collapse redshift ![]() and a milder dependence
of
and a milder dependence
of
![]() on M. In our notation, they define
on M. In our notation, they define ![]() through the equation
through the equation
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{halofit.eps}\par\vspace*{3mm}
\includegraphics[width=6.5cm,clip]{halofit3.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg126.gif) |
Figure 2:
We show the 1 |
| Open with DEXTER | |
For a given shape of the halo profile we make a fit of the parameters
![]() and
and
![]() against
the available dynamical constraints for Coma. We consider two bounds on the total mass of the cluster
at large radii, as inferred with techniques largely insensitive to the details of the mass profile in
its inner region. In Geller et al. (1999), a total mass
against
the available dynamical constraints for Coma. We consider two bounds on the total mass of the cluster
at large radii, as inferred with techniques largely insensitive to the details of the mass profile in
its inner region. In Geller et al. (1999), a total mass
In our discussion some information on the inner shape of the mass profile in Coma is also important:
we implement here the constraint that can derived by studying the velocity moments of a given tracer
population in the cluster. As the most reliable observable quantity one can consider the projection
along the line of sight of the radial velocity dispersion of the population; under the assumption of
spherical symmetry and without bulk rotation, this is related to the total mass profile M(r) by the
expression (Binney & Mamon 1982):
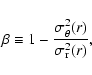 |
(16) |
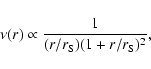 |
(17) |
To compare a model with such datasets, we build a reduced ![]() -like variable of the form:
-like variable of the form:
Nonetheless, we have derived in Fig. 2 the 1![]() ,
2
,
2![]() and
3
and
3![]() contours in the
contours in the
![]() plane for the Navarro et al. halo
profile (Eq. (2) and for the Diemand et al. halo profile (Eq. (3)).
In Fig. 3 we show the analogous contours for the Burkert profile
(Eq. (4)). In all these cases we have performed the fit of the line-of-sight
radial velocity dispersion of E-S0 galaxies assuming that this system has an isotropic
velocity dispersion, i.e. we have taken
plane for the Navarro et al. halo
profile (Eq. (2) and for the Diemand et al. halo profile (Eq. (3)).
In Fig. 3 we show the analogous contours for the Burkert profile
(Eq. (4)). In all these cases we have performed the fit of the line-of-sight
radial velocity dispersion of E-S0 galaxies assuming that this system has an isotropic
velocity dispersion, i.e. we have taken ![]() .
Best fitting values are found at
.
Best fitting values are found at
![]() and
and
![]() (that we
consider, hence, as reference values in the following analysis), not too far from the
mean value expected from models sketching the correlation between these two parameters in
the
(that we
consider, hence, as reference values in the following analysis), not too far from the
mean value expected from models sketching the correlation between these two parameters in
the ![]() CDM picture. We show in Figs. 2 and 3 the
predictions of such correlation in the models of Bullock et al. (solid line) and of
Eke et al. (2001) (dashed line).
CDM picture. We show in Figs. 2 and 3 the
predictions of such correlation in the models of Bullock et al. (solid line) and of
Eke et al. (2001) (dashed line).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{halofit2.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg148.gif) |
Figure 3:
We show here the 1 |
| Open with DEXTER | |
Since the astrophysical signals produced by WIMP pair annihilation scale with the square
of the WIMP density, any local overdensity does play a role (see e.g.
Bergstrom et al. 1999, and references therein). To discuss substructures in the Coma
cluster, analogously to the general picture introduced above for DM halos, we label a
subhalo through its virial mass ![]() and its concentration parameter
and its concentration parameter ![]() (or
equivalently a typical density and length scale,
(or
equivalently a typical density and length scale,
![]() and
and ![]() ). The
subhalo profile shape is considered here to be spherical and of the same form as for the
parent halo. Finally, as for the mean DM density profile, the distribution of subhalos in
Coma is taken to be spherically symmetric. The subhalo number density probability
distribution can then be fully specified through
). The
subhalo profile shape is considered here to be spherical and of the same form as for the
parent halo. Finally, as for the mean DM density profile, the distribution of subhalos in
Coma is taken to be spherically symmetric. The subhalo number density probability
distribution can then be fully specified through ![]() ,
,
![]() and the radial coordinate
for the subhalo position r. To our purposes, it is sufficient to consider the
simplified case when the dependence on these three parameters can be factorized,
i.e.:
and the radial coordinate
for the subhalo position r. To our purposes, it is sufficient to consider the
simplified case when the dependence on these three parameters can be factorized,
i.e.:
![\begin{displaymath}\frac{{\rm d}n_{\rm s}}{{\rm d}M_{\rm s}} = \frac{A(M_{\rm vi...
...t[-\left(\frac{M_{\rm s}}{M_{\rm cut}}\right)^{-2/3}\right]} ,
\end{displaymath}](/articles/aa/full/2006/31/aa3887-05/img153.gif) |
(21) |
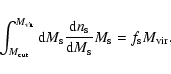 |
(22) |
| (23) |
Finally, we have to specify the spatial distribution of substructures within the cluster.
Numerical simulations, tracing tidal stripping, find radial distributions which are
significantly less concentrated than that of the smooth DM component. This radial bias is
introduced here assuming that:
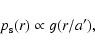 |
(24) |
Having set the reference particle physics framework and specified the distribution of DM
particles, we can now introduce the source function from neutralino pair annihilations. For any stable
particle species i, generated promptly in the annihilation or produced in the decay and
fragmentation processes of the annihilation yields, the source function Qi(r,E) gives the number of
particles per unit time, energy and volume element produced locally in space:
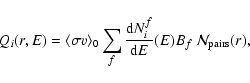 |
(26) |
| |
= | 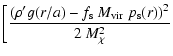 |
|
![$\displaystyle \times \int {\rm d}^3r_{\rm s}\;
\frac{\left(\rho^{\prime}_{\rm s} ~g(r_{\rm s}/a_{\rm s})\right)^2}
{2~M_{\chi}^2} \bigg] \cdot$](/articles/aa/full/2006/31/aa3887-05/img176.gif) |
(27) |
| |
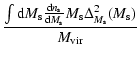 |
(29) | |
| = | 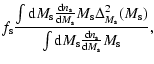 |
(30) |
![\begin{displaymath}\Delta_{M_{\rm s}}^2(M_{\rm s}) \equiv
\frac{\Delta_{\rm vir...
...^{~\prime}~x_{-2})\right]^2}
(c_{\rm s} ^{~\prime}~x_{-2})^3
\end{displaymath}](/articles/aa/full/2006/31/aa3887-05/img182.gif) |
(31) |
![\begin{displaymath}I_n(x) = \int_{0}^{x} {\rm d}y~ y^2 \left[g(y)\right]^n.
\end{displaymath}](/articles/aa/full/2006/31/aa3887-05/img183.gif) |
(32) |
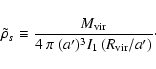 |
(33) |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{delta2ms.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg188.gif) |
Figure 4:
Scaling of the average enhancement in source functions due to a subhalo of mass
|
| Open with DEXTER | |
We show in Fig. 4 the scaling of the average enhancement
![]() in the source function versus the subhalo mass
in the source function versus the subhalo mass ![]() .
We have considered
the three halo models introduced in the previous section, i.e. the N04, D05 and
Burkert profiles, for the two toy models describing the scaling of concentration
parameter with mass, i.e. the Bullock et al. and the ENS schemes, as well as two
sample values for the ratio
.
We have considered
the three halo models introduced in the previous section, i.e. the N04, D05 and
Burkert profiles, for the two toy models describing the scaling of concentration
parameter with mass, i.e. the Bullock et al. and the ENS schemes, as well as two
sample values for the ratio ![]() between the average concentration parameter in subhalos
and that in halos of equal mass. In each setup, going to smaller and smaller values
of
between the average concentration parameter in subhalos
and that in halos of equal mass. In each setup, going to smaller and smaller values
of ![]() ,
the average enhancement
,
the average enhancement
![]() increases and then flattens out at the
mass scale below which all structures tend to collapse at the same epoch, and hence have
equal concentration parameter.
increases and then flattens out at the
mass scale below which all structures tend to collapse at the same epoch, and hence have
equal concentration parameter.
In Fig. 5 we show the scaling of the weighted enhancement ![]() in
the source function due to subhalos versus the ratio between concentration parameter in
subhalos to concentration parameter in halos at equal mass
in
the source function due to subhalos versus the ratio between concentration parameter in
subhalos to concentration parameter in halos at equal mass ![]() ;
we give results for the
usual set of halo profiles considered in our approach. Analogously to the enhancement for
a fixed mass shown in the previous plot,
;
we give results for the
usual set of halo profiles considered in our approach. Analogously to the enhancement for
a fixed mass shown in the previous plot, ![]() is very sensitive to the scaling of
the concentration parameter and hence we find a sharp dependence of
is very sensitive to the scaling of
the concentration parameter and hence we find a sharp dependence of ![]() on
on ![]() .
The fractional contribution per logarithmic interval in subhalo mass
.
The fractional contribution per logarithmic interval in subhalo mass ![]() to
to ![]() is also shown in Fig. 5 for four sample cases. Note that, although the
factorization in the probability distribution for clumps in the radial coordinate and
mass (plus the assumption that
is also shown in Fig. 5 for four sample cases. Note that, although the
factorization in the probability distribution for clumps in the radial coordinate and
mass (plus the assumption that ![]() does not depend on mass) are a crude approximation,
what we actually need in our discussion is
does not depend on mass) are a crude approximation,
what we actually need in our discussion is ![]() and the radial distribution for subhalos
at the peak of the distribution shown in Fig. 5: unfortunately we cannot
read out this from numerical simulations.
and the radial distribution for subhalos
at the peak of the distribution shown in Fig. 5: unfortunately we cannot
read out this from numerical simulations.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{delta2.eps}\hspace*{5mm}
\includegraphics[width=7cm,clip]{delta2int.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg189.gif) |
Figure 5:
Left: scaling of the weighted enhancement in source functions due to subhalos versus the
ratio between concentration parameter in subhalos to concentration parameter in halos at equal mass
|
| Open with DEXTER | |
Figure 6 shows the number density of neutralino pairs (we set here the neutralino mass to
![]() GeV) as a function of the distance from the center of Coma for the three representative
halo profiles introduced here, i.e. the N04, D05 and Burkert profile in their best fit model,
and a sample configuration for the subhalo parameters. For the D05 and N04 profiles, the central
enhancement increases the integrated source function by a factor
GeV) as a function of the distance from the center of Coma for the three representative
halo profiles introduced here, i.e. the N04, D05 and Burkert profile in their best fit model,
and a sample configuration for the subhalo parameters. For the D05 and N04 profiles, the central
enhancement increases the integrated source function by a factor ![]() 6 with respect to the
Burkert profile, but this takes place on such a small angular scale that from the observational point
of view it is like adding a point source at the center of the cluster. The enhancement of the
annihilation signals from subhalos comes instead from large radii. This means that the enhancement
from subhalos largely influences the results when the neutralino source is extended. This is the case
of galaxy clusters, and more specifically of the Coma cluster which is our target in this paper.
6 with respect to the
Burkert profile, but this takes place on such a small angular scale that from the observational point
of view it is like adding a point source at the center of the cluster. The enhancement of the
annihilation signals from subhalos comes instead from large radii. This means that the enhancement
from subhalos largely influences the results when the neutralino source is extended. This is the case
of galaxy clusters, and more specifically of the Coma cluster which is our target in this paper.
The spectral properties of secondary products of DM annihilations depend only, prior to
diffusion and energy losses, on the DM particle mass ![]() and on the branching
ratio
and on the branching
ratio
![]() for the final state f in the DM pair-annihilation.
The DM particle physics model further sets the magnitude of the thermally averaged pair
annihilation cross section times the relative DM particles velocity,
for the final state f in the DM pair-annihilation.
The DM particle physics model further sets the magnitude of the thermally averaged pair
annihilation cross section times the relative DM particles velocity,
![]() at T=0.
at T=0.
The range of neutralino masses and pair annihilation cross sections in the most general supersymmetric DM setup is extremely wide. Neutralinos as light as few GeV (see Bottino et al. 2003) and as heavy as hundreds of TeV (see Profumo 2005) can account for the observed CDM density through thermal production mechanisms, and essentially no constraints apply in the case of non-thermally produced neutralinos.
Turning to the viable range of neutralino pair annihilation cross sections,
coannihilation processes do not allow us to set any lower bound, while on purely
theoretical grounds a general upper limit on
![]() has been recently
set (Profumo 2005). The only general argument which ties the relic abundance of
a WIMP with its pair annihilation cross section is given by the naive relation
has been recently
set (Profumo 2005). The only general argument which ties the relic abundance of
a WIMP with its pair annihilation cross section is given by the naive relation
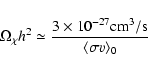 |
(34) |
Since third generation leptons and quarks Yukawa couplings are always much larger than
those of the first two generations, and being the neutralino a Majorana fermion, the
largest
![]() for annihilations into a fermion-antifermion pair are
in most cases
for annihilations into a fermion-antifermion pair are
in most cases![]() into the third generation
final states
into the third generation
final states
![]() ,
,
![]() and
and
![]() .
In the context of
supersymmetry, if the supersymmetric partners of the above mentioned fermions are not
significantly different in mass, the
.
In the context of
supersymmetry, if the supersymmetric partners of the above mentioned fermions are not
significantly different in mass, the
![]() branching ratio will be suppressed,
with respect to the
branching ratio will be suppressed,
with respect to the
![]() branching ratio by a color factor equal to 1/3, plus a
possible further Yukawa coupling suppression, since the two final states share the
same SU(2) quantum number assignment. Further, the fragmentation functions of third
generation quarks are very similar, and give rise to what we will dub in the following as
a "soft spectrum''. A second possibility, when kinematically allowed, is the pair
annihilation into massive gauge bosons
branching ratio by a color factor equal to 1/3, plus a
possible further Yukawa coupling suppression, since the two final states share the
same SU(2) quantum number assignment. Further, the fragmentation functions of third
generation quarks are very similar, and give rise to what we will dub in the following as
a "soft spectrum''. A second possibility, when kinematically allowed, is the pair
annihilation into massive gauge bosons![]() , W+W- and Z0Z0. Again, the fragmentation functions for
these two final states are mostly indistinguishable, and will be indicated as giving a
"hard spectrum''. The occurrence of a non-negligible branching fraction into
, W+W- and Z0Z0. Again, the fragmentation functions for
these two final states are mostly indistinguishable, and will be indicated as giving a
"hard spectrum''. The occurrence of a non-negligible branching fraction into
![]() or into light quarks will generally give raise to intermediate spectra
between the "hard'' and "soft'' case.
or into light quarks will generally give raise to intermediate spectra
between the "hard'' and "soft'' case.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{npairs.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg197.gif) |
Figure 6:
The number density of neutralino pairs (neutralino mass set to
|
| Open with DEXTER | |
Figure 7 shows the spectral shape of the electron source function in the case of the
three sample final states
![]() ,
,
![]() and W+W- for
and W+W- for
![]() GeV, and
clarifies the previous discussion. In what follows we will therefore employ sample DM configurations
making use of either soft (
GeV, and
clarifies the previous discussion. In what follows we will therefore employ sample DM configurations
making use of either soft (
![]() )
or hard (W+W-) spectra, keeping in mind that other
possibilities would likely fall in between these two extrema.
)
or hard (W+W-) spectra, keeping in mind that other
possibilities would likely fall in between these two extrema.
In order to make a more stringent contact with supersymmetry phenomenology, we will
however also resort to realistic benchmark SUSY models: by this we mean thoroughly
defined SUSY setups which are fully consistent with accelerator and other
phenomenological constraints, and whichgive a neutralino thermal relic abundance exactly
matching the central cosmologically observed value. To this extent, we refer to the
so-called minimal supergravity model (Goldberg 1983; Ellis et al. 1983, 1984), perhaps one of the better studied
paradigms of low-energy supersymmetry, which enables, moreover, a cross-comparison with
numerous dedicated studies, ranging from colliders (Baer et al. 2003) to DM
searches (Edsjo et al. 2004; Baer et al. 2004).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{source.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg198.gif) |
Figure 7: The spectral shape of the electron source function in case of three sample final states (see text for details). |
| Open with DEXTER | |
The assumptions of universality in the gaugino and in the scalar (masses and trilinear
couplings) sectors remarkably reduce, in this model, the number of free parameters of the
general soft SUSY breaking Lagrangian (Chung et al. 2003) down to four continuous parameters
(
![]() )
plus one sign (
)
plus one sign (
![]() ). The mSUGRA parameter
space producing a sufficiently low thermal neutralino relic abundance
). The mSUGRA parameter
space producing a sufficiently low thermal neutralino relic abundance
![]() has been shown to be constrained to a handful of "regions'' featuring effective
has been shown to be constrained to a handful of "regions'' featuring effective
![]() suppression mechanisms (Ellis et al. 2003). The latter are
coannihilations of the neutralino with the next-to-lightest SUSY particle
("Coannihilation'' region), rapid annihilations through s channel Higgs exchanges
("Funnel'' region), the occurrence of light enough neutralino and sfermions masses
("Bulk'' region) and the presence of a non-negligible bino-higgsino mixing ("Focus
Point'' region).
suppression mechanisms (Ellis et al. 2003). The latter are
coannihilations of the neutralino with the next-to-lightest SUSY particle
("Coannihilation'' region), rapid annihilations through s channel Higgs exchanges
("Funnel'' region), the occurrence of light enough neutralino and sfermions masses
("Bulk'' region) and the presence of a non-negligible bino-higgsino mixing ("Focus
Point'' region).
With the idea of allowing a direct comparison with the existing research work in a wealth
of complementary fields, we restrict ourselves to the "updated post-WMAP benchmarks
for supersymmetry'' proposed and studied by Battaglia et al. (2004). All of those setups
are tuned so as to feature a neutralino thermal relic density giving exactly the central
WMAP-estimated CDM density![]() .
As a preliminary step, we computed the electrons, neutrinos, gamma-rays and protons
source spectra for all the
13
.
As a preliminary step, we computed the electrons, neutrinos, gamma-rays and protons
source spectra for all the
13
![]() -
-
![]() models. Remarkably
enough, although the SUSY particle spectrum is rather homogeneous throughout the mSUGRA
parameter space, the resulting spectra exhibit at least three qualitatively different
shapes, according to the dominant final state in neutralino pair annihilation processes.
In particular, in the Bulk and Funnel regions the dominant final state is into
models. Remarkably
enough, although the SUSY particle spectrum is rather homogeneous throughout the mSUGRA
parameter space, the resulting spectra exhibit at least three qualitatively different
shapes, according to the dominant final state in neutralino pair annihilation processes.
In particular, in the Bulk and Funnel regions the dominant final state is into ![]() ,
and, with a sub-dominant variable contribution,
,
and, with a sub-dominant variable contribution,
![]() .
The latter channel is
instead dominant, for kinematic reasons, in the stau Coannihilation region. Finally, a
third, and last, possibility is a dominant gauge bosons final state, which is the case
along the Focus Point region. In this respect, in the effort to reproduce all of the
mentioned spectral modes, and to reflect every cosmologically viable mSUGRA region, we
focused on the four models indicated in Table 1, a subset of the
benchmarks of Battaglia et al. (2004) (to which we refer the reader for further details).
We collect in Table 2 the branching ratios for the final states of neutralino
pair annihilations. In the last column of this table we also provide the
thermally-averaged pair annihilation cross section times the relative velocity, at T=0,
.
The latter channel is
instead dominant, for kinematic reasons, in the stau Coannihilation region. Finally, a
third, and last, possibility is a dominant gauge bosons final state, which is the case
along the Focus Point region. In this respect, in the effort to reproduce all of the
mentioned spectral modes, and to reflect every cosmologically viable mSUGRA region, we
focused on the four models indicated in Table 1, a subset of the
benchmarks of Battaglia et al. (2004) (to which we refer the reader for further details).
We collect in Table 2 the branching ratios for the final states of neutralino
pair annihilations. In the last column of this table we also provide the
thermally-averaged pair annihilation cross section times the relative velocity, at T=0,
![]() .
Table 2 is an accurate guideline to interpret the
resulting source spectra for the four benchmarks under consideration here, which are
shown in Figs. 8 and 9. Figure 8
shows in particular the differential electron (left) and photon (right) yields per
neutralino annihilation multiplied by
.
Table 2 is an accurate guideline to interpret the
resulting source spectra for the four benchmarks under consideration here, which are
shown in Figs. 8 and 9. Figure 8
shows in particular the differential electron (left) and photon (right) yields per
neutralino annihilation multiplied by
![]() ,
i.e. the
source function Q(r,E) divided by the number density of neutralino pairs
,
i.e. the
source function Q(r,E) divided by the number density of neutralino pairs
![]() as a function of the particles' kinetic energy. As mentioned above, the Bulk
and Funnel cases are very similar between each other, though in the latter case one has a
heavier spectrum and a larger value of
as a function of the particles' kinetic energy. As mentioned above, the Bulk
and Funnel cases are very similar between each other, though in the latter case one has a
heavier spectrum and a larger value of
![]() .
Figure 9 shows the same quantity for neutrinos and protons.
.
Figure 9 shows the same quantity for neutrinos and protons.
Table 1: The input parameters of the four mSUGRA benchmark models we consider here. The units for the mass parameters are GeV, and the universal trilinear coupling A0 is set to 0 for all models (see Battaglia et al. 2004, for details).
The products of the neutralino annihilation which are more relevant to our discussion are
secondary electrons and pions.
The secondary particles produced by neutralino annihilation are subject to various
physical mechanisms: i) decay (which is especially fast for pions and muons); ii) energy losses which can be suffered by stable particles, like electrons and
positrons; iii) spatial diffusion of these relativistic particles in the atmosphere
of the cluster.
Gamma-rays produced by neutral pion decay,
![]() ,
generate most of the continuum
spectrum at energies
,
generate most of the continuum
spectrum at energies ![]() GeV and this emission is directly radiated since the
GeV and this emission is directly radiated since the
![]() e.m. decay is very fast.
This gamma-ray emission is dominant at high energies,
e.m. decay is very fast.
This gamma-ray emission is dominant at high energies,
![]() of the
neutralino mass, but needs to be complemented by other two emission mechanisms which
produce gamma-rays at similar or slightly lower energies: these are the ICS and the
bremsstrahlung emission by secondary electrons. We will discuss the full gamma-ray
emission of Coma induced by DM annihilation in Sect. 4 below.
Secondary electrons are produced through various prompt generation mechanisms and by the
decay of charged pions (see, e.g., Colafrancesco & Mele 2001).
In fact, charged pions decay through
of the
neutralino mass, but needs to be complemented by other two emission mechanisms which
produce gamma-rays at similar or slightly lower energies: these are the ICS and the
bremsstrahlung emission by secondary electrons. We will discuss the full gamma-ray
emission of Coma induced by DM annihilation in Sect. 4 below.
Secondary electrons are produced through various prompt generation mechanisms and by the
decay of charged pions (see, e.g., Colafrancesco & Mele 2001).
In fact, charged pions decay through
![]() ,
with
,
with
![]() and produce
and produce
![]() ,
muons
and neutrinos.
Electrons and positrons are produced abundantly by neutralino annihilation (see
Fig. 8, left) and are subject to spatial diffusion and energy losses.
Both spatial diffusion and energy losses contribute to determine the evolution of the
source spectrum into the equilibrium spectrum of these particles, i.e. the quantity
which will be used to determine the overall multi-wavelength emission induced by DM
annihilation.
The secondary electrons eventually produce radiation by synchrotron in the magnetized atmosphere of
Coma, Inverse Compton Scattering of CMB (and other background) photons and bremsstrahlung with protons
and ions in the atmosphere of the Coma cluster
(see, e.g., Colafrancesco & Mele 2001; and
Colafrancesco 2003, 2006, for a review). These secondary particles also produce
heating of the intra-cluster gas by Coulomb collisions with the intra-cluster gas particles and SZ
effect (see, e.g. Colafrancesco 2003, 2006).
Other fundamental particles which might have astrophysical relevance are also produced in DM
annihilation.
Protons are produced in a smaller quantity with respect to e
,
muons
and neutrinos.
Electrons and positrons are produced abundantly by neutralino annihilation (see
Fig. 8, left) and are subject to spatial diffusion and energy losses.
Both spatial diffusion and energy losses contribute to determine the evolution of the
source spectrum into the equilibrium spectrum of these particles, i.e. the quantity
which will be used to determine the overall multi-wavelength emission induced by DM
annihilation.
The secondary electrons eventually produce radiation by synchrotron in the magnetized atmosphere of
Coma, Inverse Compton Scattering of CMB (and other background) photons and bremsstrahlung with protons
and ions in the atmosphere of the Coma cluster
(see, e.g., Colafrancesco & Mele 2001; and
Colafrancesco 2003, 2006, for a review). These secondary particles also produce
heating of the intra-cluster gas by Coulomb collisions with the intra-cluster gas particles and SZ
effect (see, e.g. Colafrancesco 2003, 2006).
Other fundamental particles which might have astrophysical relevance are also produced in DM
annihilation.
Protons are produced in a smaller quantity with respect to e![]() (see
Fig. 9, right), but do not loose energy appreciably during their
lifetime while they can diffuse and be stored in the cluster atmosphere. These particles
can, in principle, produce heating of the intra-cluster gas and pp collisions
providing, again, a source of secondary particles (pions, neutrinos,
(see
Fig. 9, right), but do not loose energy appreciably during their
lifetime while they can diffuse and be stored in the cluster atmosphere. These particles
can, in principle, produce heating of the intra-cluster gas and pp collisions
providing, again, a source of secondary particles (pions, neutrinos, ![]() ,
muons,
...) in complete analogy with the secondary particle production by neutralino
annihilation. Neutrinos are also produced in the process of neutralino annihilation (see
Fig. 9, left) and propagate with almost no interaction with the matter
of the cluster. However, the resulting flux from Coma is found to be unobservable by
current experiments.
,
muons,
...) in complete analogy with the secondary particle production by neutralino
annihilation. Neutrinos are also produced in the process of neutralino annihilation (see
Fig. 9, left) and propagate with almost no interaction with the matter
of the cluster. However, the resulting flux from Coma is found to be unobservable by
current experiments.
To summarize, the secondary products of neutralino annihilation which have the most relevant astrophysical impact onto the multi-frequency spectral energy distribution of DM halos are neutral pions and secondary electrons.
Table 2:
The branching ratios into various final states for the four mSUGRA benchmark
models of Table 1; in the last column we also indicate
![]() in units of
in units of
![]() .
.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{E_ele.eps}\hspace*{5mm}
\includegraphics[width=6cm,clip]{E_gam.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg225.gif) |
Figure 8:
Left: The electrons flux
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{E_neu.eps}\hspace*{5mm}
\includegraphics[width=6cm,clip]{E_pro.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg228.gif) |
Figure 9:
Left: the neutrinos flux
|
| Open with DEXTER | |
A complete description of the emission features induced by DM must take, consistently,
into account the diffusion and energy-loss properties of these secondary particles.
These mechanisms are taken into account in the following diffusion equation (i.e.
neglecting convection and re-acceleration effects):
![$\displaystyle \frac{\partial}{\partial t}\frac{{\rm d}n_{\rm e}}{{\rm d}E} = \n...
...[ b(E,\vec{x})
\frac{{\rm d}n_{\rm e}}{{\rm d}E}\right]
+ Q_{\rm e}(E,\vec{x}),$](/articles/aa/full/2006/31/aa3887-05/img229.gif) |
(35) |
In the limit in which electrons and positrons lose energy on a timescale much shorter
than the timescale for spatial diffusion, i.e. the regime which applies to the case
of galaxy clusters, the first term on the r.h.s. of Eq. (A.1) can be neglected,
and the expression for equilibrium number density becomes:
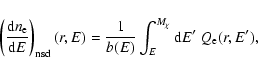 |
(36) |
The derivation of the full solution of the diffusion equation (Eq. (A.1)) and the effects of diffusion and energy losses described in the Appendix A, set us in the position to discuss the multi-frequency emission produced by the DM (neutralino) component of the Coma cluster. We will present the overall DM-induced spectral energy distribution (hereafter SED) from low to high observing frequencies.
We describe here our reference setup for the numerical calculations.
Our reference halo setup is the N04 profile and other parameters/choice of extrapolation schemes as in
Fig. 6.
We consider the predictions of two particle models, one with a branching ratio equal to 1 in ![]() ,
i.e. a channel with a soft production spectrum, and the second one with a branching
ratio equal to 1 into W+ W-, i.e. a channel with hard spectrum.
Since we have previously shown that diffusion is not relevant in a Coma-like cluster of galaxy, we
neglect, in our numerical calculations, the spatial diffusion for electrons and
positrons: this is the limit in which the radial dependence and frequency dependence can
be factorized in the expression for the emissivity.
,
i.e. a channel with a soft production spectrum, and the second one with a branching
ratio equal to 1 into W+ W-, i.e. a channel with hard spectrum.
Since we have previously shown that diffusion is not relevant in a Coma-like cluster of galaxy, we
neglect, in our numerical calculations, the spatial diffusion for electrons and
positrons: this is the limit in which the radial dependence and frequency dependence can
be factorized in the expression for the emissivity.
At radio frequencies, the DM-induced emission is dominated by the synchrotron radiation of the
relativistic secondary electrons and positrons of energy
![]() ,
living in a magnetic
field B(r) and a background plasma with thermal electron density n(r), and in the limit of
frequency
,
living in a magnetic
field B(r) and a background plasma with thermal electron density n(r), and in the limit of
frequency ![]() of the emitted photons much larger than the non-relativistic gyro-frequency
of the emitted photons much larger than the non-relativistic gyro-frequency
![]() Hz and the plasma frequency
Hz and the plasma frequency
![]() Hz. Averaging over the directions of emission, the spontaneously emitted
synchrotron power at the frequency
Hz. Averaging over the directions of emission, the spontaneously emitted
synchrotron power at the frequency ![]() is given by (Longair 1994):
is given by (Longair 1994):
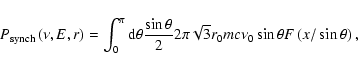 |
(37) |
![\begin{displaymath}x \equiv \frac{2\nu}{3\nu_0 \gamma^2}
\left[ 1+ \left( \frac{\gamma \nu_{\rm p}}{\nu}\right)^2\right]^{3/2} ,
\end{displaymath}](/articles/aa/full/2006/31/aa3887-05/img241.gif) |
(38) |
![\begin{displaymath}F\left(t\right) \equiv t \int_t^\infty {\rm d}z K_{5/3}(z) \simeq
1.25 t^{1/3} \exp{(-t)} \left[ 648 + t^2\right]^{1/12}.
\end{displaymath}](/articles/aa/full/2006/31/aa3887-05/img242.gif) |
(39) |
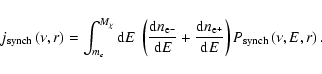 |
(40) |
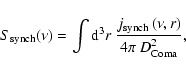 |
(41) |
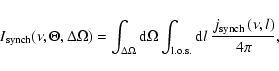 |
(42) |
We started from the full dataset on the radio flux density spectrum
(Thierbach et al. 2003) and minimized the fit with respect to the WIMP mass (with the
bound
![]() GeV for the
GeV for the ![]() case, and mass above threshold for the
W+ W- case), the strength of the magnetic field (with the bound
case, and mass above threshold for the
W+ W- case), the strength of the magnetic field (with the bound
![]() )
and the annihilation rate
)
and the annihilation rate
![]() .
The spectrum predicted by two
models with the lowest values of
.
The spectrum predicted by two
models with the lowest values of ![]() are shown in Fig. 10.
In both cases the best fit corresponds to the lowest neutralino mass allowed, since this
is the configuration in which the fall-off of the flux density at the highest observed
frequency tends to be better reproduced. For the same reason, the fit in the case of a
soft spectrum is favored with respect to the one with a hard spectrum (we have checked
that in case of
are shown in Fig. 10.
In both cases the best fit corresponds to the lowest neutralino mass allowed, since this
is the configuration in which the fall-off of the flux density at the highest observed
frequency tends to be better reproduced. For the same reason, the fit in the case of a
soft spectrum is favored with respect to the one with a hard spectrum (we have checked
that in case of
![]() again does not give a bend-over in the spectrum where
needed).
The values of the annihilation rates required by the fit are fairly large:
again does not give a bend-over in the spectrum where
needed).
The values of the annihilation rates required by the fit are fairly large:
![]() cm3 s-1 for
cm3 s-1 for ![]() case, and about one order
of magnitude smaller,
case, and about one order
of magnitude smaller,
![]() cm3 s-1, for
the W+W- case, despite the heavier neutralino mass, since the best fit values
correspond to different values of the magnetic field of about
cm3 s-1, for
the W+W- case, despite the heavier neutralino mass, since the best fit values
correspond to different values of the magnetic field of about
![]() and
and
![]() ,
respectively.
,
respectively.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{radioflux.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg255.gif) |
Figure 10:
Best fit models for the radio flux density spectrum, in case of a soft spectrum due to a
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{radiobr2.eps}\hspace*{3mm}
\includegraphics[width=6.6cm,clip]{radiobr.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg256.gif) |
Figure 11:
Surface brightness distribution at frequency |
| Open with DEXTER | |
In Fig. 11 we compare the radio-halo brightness data of
Deiss et al. (1997)
with the surface brightness distribution
![]() predicted at
predicted at ![]() GHz,
within a beam equal to the detector angular resolution (HPBW of
GHz,
within a beam equal to the detector angular resolution (HPBW of
![]() ), for the
best fit model with
), for the
best fit model with
![]() GeV. In the left panel we plot the predicted surface
brightness considering the case of a uniform magnetic field equal to
GeV. In the left panel we plot the predicted surface
brightness considering the case of a uniform magnetic field equal to
![]() ,
showing explicitly in this case that the assumption we made of neglecting spatial
diffusion for electrons and positrons is indeed justified, since the results obtained
including or neglecting spatial diffusion essentially coincide. The radial brightness we
derive in this case does not match the shape of the radio halo indicated by the data.
However, it is easy to derive a phenomenological setup with a magnetic field B(r)varying with radius in which a much better fit can be obtained, while leaving unchanged
the total radio flux density
,
showing explicitly in this case that the assumption we made of neglecting spatial
diffusion for electrons and positrons is indeed justified, since the results obtained
including or neglecting spatial diffusion essentially coincide. The radial brightness we
derive in this case does not match the shape of the radio halo indicated by the data.
However, it is easy to derive a phenomenological setup with a magnetic field B(r)varying with radius in which a much better fit can be obtained, while leaving unchanged
the total radio flux density
![]() .
We show in the right panel of
Fig. 11 the predictions for
.
We show in the right panel of
Fig. 11 the predictions for
![]() considering a radial dependence
of the magnetic field of the form:
considering a radial dependence
of the magnetic field of the form:
![\begin{displaymath}B(r) = B_0 \bigg( 1 + {r \over r_{\rm c1}}\bigg)^2 \cdot \bigg[ 1 + \bigg( {r \over r_{\rm c2}}\bigg)^2\bigg]^{-\beta} ,
\end{displaymath}](/articles/aa/full/2006/31/aa3887-05/img260.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{RMComa.ps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg266.gif) |
Figure 12:
The observed absolute RM of background sources in the Coma field
are shown as a function of projected radius |
| Open with DEXTER | |
A decrease of B(r) at large radii is expected by general considerations of the
structure of radio-halos in clusters and, more specifically, for Coma (see
Colafrancesco et al. 2005) and it is also predicted by numerical simulations (see, e.g.,
Dolag et al. 2002): thus it seems quite natural and motivated.
At small radii, the mild central dip of B(r) predicted by the previous formula is what
is phenomenologically required by the specific DM model we worked out in our paper.
Finally, we notice that our specific phenomenological model for the spatial distribution
of B(r) is able to reproduce the spatial distribution of Faraday rotation measures
(RMs) observed in Coma (see Kim et al. 1990), as shown in Fig. 12.
It is evident that models in which B is either constant or decreases monotonically
towards large radii seem to be difficult to reconcile with the available RM data. The RM
data at
![]() arcmin seem to favour, indeed, a model for B(r) with a
slight rise at intermediate angular scales followed by a decrease at large scales, like
the one we adopt here to fit the radio-halo surface brightness of Coma. In this respect,
it seems that our choice for B(r) is, at least, an observationally driven result.
arcmin seem to favour, indeed, a model for B(r) with a
slight rise at intermediate angular scales followed by a decrease at large scales, like
the one we adopt here to fit the radio-halo surface brightness of Coma. In this respect,
it seems that our choice for B(r) is, at least, an observationally driven result.
The synchrotron signal produced by the annihilation of DM depends, given the fundamental physics and
astrophysics framework, on two relevant quantities: the annihilation rate and the magnetic field.
Thus, it is interesting to find the best-fitting region of the
![]() plane which is
consistent with the available dataset for Coma.
plane which is
consistent with the available dataset for Coma.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{bbarmx.eps}\hspace*{3mm}
\includegraphics[width=6cm,clip]{wpwmmx.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg270.gif) |
Figure 13:
Isolevel curves for reduced |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{bbarmxb.eps}\includegraphics[width=6.4cm,clip]{wpwmmxb.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg272.gif) |
Figure 14:
Isolevel curves for minimum reduced |
| Open with DEXTER | |
Since the data on the radio flux density spectrum (Thierbach et al. 2003) is a compilation
of measurements performed with different instruments (possibly with different
systematics), it is difficult to decide a cut on the ![]() value which defines an
acceptable fit. In Fig. 13 we plot sample isolevel curves for
value which defines an
acceptable fit. In Fig. 13 we plot sample isolevel curves for ![]() ,
spotting the shape of the minima of
,
spotting the shape of the minima of ![]() , in the plane
, in the plane
![]() ,
for the two sample annihilation channels and a few sample values of the WIMP
mass (note that values labeling isolevel curves are sensibly different in the two
panels).
In Fig. 14 we show the analogous
,
for the two sample annihilation channels and a few sample values of the WIMP
mass (note that values labeling isolevel curves are sensibly different in the two
panels).
In Fig. 14 we show the analogous ![]() isolevels in the WIMP mass -
annihilation rate plane, and taking at each point the minimum
isolevels in the WIMP mass -
annihilation rate plane, and taking at each point the minimum ![]() while varying
the magnetic field strength between
while varying
the magnetic field strength between
![]() and
and
![]() :
the curves converge to a
maximal value enforced by the lower limit of
:
the curves converge to a
maximal value enforced by the lower limit of
![]() ,
and the upper value does not
enter in defining isolevel curve shapes.
,
and the upper value does not
enter in defining isolevel curve shapes.
In order to assess whether the outlined radio-data preferred regions are or are not compatible with
supersymmetric DM models, we proceed to a random scan of the SUSY parameter space, in the bottom-up
approach which we outline below.
We relax all universality assumptions, and fully scan the low-energy scale MSSM, imposing
phenomenological as well as cosmological constraints on the randomly generated
models![]() . We
take values of
. We
take values of ![]() ,
the ratio between the vacuum expectation values of the two
Higgs doublets, between 1 and 60. The parameters entering the neutralino mass matrix are
generated in the range
,
the ratio between the vacuum expectation values of the two
Higgs doublets, between 1 and 60. The parameters entering the neutralino mass matrix are
generated in the range
![]() ,
and we define
,
and we define
![]() .
To avoid flavor changing effects in the
first two lightest quark generations, we assume that the soft-breaking masses in the
first two generations squark sector are degenerate, i.e. we assume
.
To avoid flavor changing effects in the
first two lightest quark generations, we assume that the soft-breaking masses in the
first two generations squark sector are degenerate, i.e. we assume
![]() .
The scalar masses are scanned over the range
.
The scalar masses are scanned over the range
 |
(43) |
| AU(i) | (44) | ||
| AD(i) | (45) | ||
| AE(i) | (46) |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{grid_soft.eps}\includegraphics[width=7cm,clip]{grid_hard.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg287.gif) |
Figure 15:
A scatter plot of SUSY models, consistent with all available phenomenological constraints, giving a relic abundance in the 2- |
| Open with DEXTER | |
We exclude models giving a relic abundance of neutralinos exceeding
![]() .
Further, we impose the various colliders mass limits on charginos, gluinos,
squarks and sleptons, as well as on the Higgs masses
.
Further, we impose the various colliders mass limits on charginos, gluinos,
squarks and sleptons, as well as on the Higgs masses![]() . Moreover, we also require the BR(
. Moreover, we also require the BR(
![]() )
and all
electroweak precision observables to be consistent with the theoretical and experimental
state-of-the-art (Eidelman et al. 2004).
)
and all
electroweak precision observables to be consistent with the theoretical and experimental
state-of-the-art (Eidelman et al. 2004).
We classify the models according to the branching ratios of the neutralino pair-annihilations final
states, according to the following criteria: we consider a model having a hard spectrum if
 |
(47) |
![\begin{displaymath}\sum_{i=1}^6 \left[{\rm BR}(q_i\bar q_i)+{\rm BR}(q_i\bar q_i
g)\right]+{\rm BR}(gg)>0.8.
\end{displaymath}](/articles/aa/full/2006/31/aa3887-05/img291.gif) |
(48) |
Inverse Compton (IC) scatterings of relativistic electrons and positrons on target cosmic microwave
background (CMB) photons give rise to a spectrum of photons stretching from below the extreme
ultra-violet up to the soft gamma-ray band, peaking in the soft X-ray energy band. Let
![]() be the energy of electrons and positrons,
be the energy of electrons and positrons, ![]() that of the target photons and
that of the target photons and ![]() the energy of the scattered photon. The Inverse Compton power is obtained by folding the differential
number density of target photons with the IC scattering cross section:
the energy of the scattered photon. The Inverse Compton power is obtained by folding the differential
number density of target photons with the IC scattering cross section:
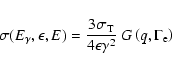 |
(50) |
![\begin{displaymath}G\left(q,\Gamma_{\rm e}\right) \equiv \left[ 2 q \ln q + (1+2...
...q
\right)^2 (1-q)}{2 \left( 1+ \Gamma_{\rm e} q\right)}\right]
\end{displaymath}](/articles/aa/full/2006/31/aa3887-05/img300.gif) |
(51) |
![\begin{displaymath}\Gamma_{\rm e}= 4 \epsilon \gamma / (m_{\rm e} c^2) \;\;\;\;\...
...{\rm e} \left( \gamma m_{\rm e} c^2 - E_\gamma \right)\right].
\end{displaymath}](/articles/aa/full/2006/31/aa3887-05/img301.gif) |
(52) |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{multiflux.eps}\includegraphics[width=6.5cm,clip]{multiflux2.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg305.gif) |
Figure 16:
Multi-wavelength spectrum of the two best fit models for the radio flux shown in
Fig. 10 (see text for details). The halo profile is the best fit
N04 profile:
|
| Open with DEXTER | |
The last relevant contribution to the photon emission of Coma due to relativistic
electrons and positrons is the process of non-thermal bremsstrahlung, i.e. the
emission of gamma-ray photons in the deflection of the charged particles by the
electrostatic potential of intra-cluster gas. Labeling with
![]() the
energy of electrons and positrons, and with
the
energy of electrons and positrons, and with ![]() the energy of the emitted photons,
the local non-thermal bremsstrahlung power is given by:
the energy of the emitted photons,
the local non-thermal bremsstrahlung power is given by:
![$\displaystyle \sigma_j(E_\gamma, E) = \frac{3 \alpha \sigma_T}{8 \pi~ E_\gamma}...
...[\left(1+(1-E_\gamma/E)^2\right)~\phi_1-\frac{2}{3}(1-E_\gamma/E)~\phi_2\right]$](/articles/aa/full/2006/31/aa3887-05/img307.gif) |
(56) |
As we have already mentioned, a hard gamma-ray component arises also from prompt emission in WIMP pair
annihilations, either in loop suppressed two-body final states giving monochromatic photons, or
through the production and prompt decay of neutral pions giving gamma-rays with continuous spectrum.
Since photons propagate on straight lines (or actually geodesics), the gamma-ray flux due to prompt
emission is just obtained by summing over sources along the line of sight; we will consider terms
integrated over volume
We show in Fig. 16 the multi-frequency SED produced by WIMP annihilation in the two models used to fit the radio halo spectrum of Coma, as shown in Fig. 10.
The model with
![]() GeV provides the better fit to the radio halo data because
the relative equilibrium electron spectrum is steeper and shows also the high-
GeV provides the better fit to the radio halo data because
the relative equilibrium electron spectrum is steeper and shows also the high-![]() bending which fits the most recent data (Thierbach et al. 2003). The IC and bremsstrahlung
branches of the SED are closely related to the synchrotron branch (since they depend on
the same particle population) and their intensity ratio depends basically on the value of
the adopted magnetic field. The relatively high value B = 1.2
bending which fits the most recent data (Thierbach et al. 2003). The IC and bremsstrahlung
branches of the SED are closely related to the synchrotron branch (since they depend on
the same particle population) and their intensity ratio depends basically on the value of
the adopted magnetic field. The relatively high value B = 1.2 ![]() G indicated by the
best fit to the radio data implies a rather low intensity of the IC and bremsstrahlung
emission, well below the EUV and hard X-ray data for Coma. Nonetheless, the gamma-ray
emission due to
G indicated by the
best fit to the radio data implies a rather low intensity of the IC and bremsstrahlung
emission, well below the EUV and hard X-ray data for Coma. Nonetheless, the gamma-ray
emission due to
![]() decay predicted by this model could be
detectable with the GLAST-LAT detector, even though it is well below the EGRET upper
limit.
decay predicted by this model could be
detectable with the GLAST-LAT detector, even though it is well below the EGRET upper
limit.
The detectability of the multi-frequency SED worsens in the model with
![]() GeV,
where the flatness of the equilibrium electron spectrum cannot provide an acceptable fit
to the radio data. Moreover, the adopted value of the magnetic field B=8
GeV,
where the flatness of the equilibrium electron spectrum cannot provide an acceptable fit
to the radio data. Moreover, the adopted value of the magnetic field B=8 ![]() G implies a
very low intensity of the IC, bremsstrahlung and
G implies a
very low intensity of the IC, bremsstrahlung and
![]() emission,
which should be not detectable by the next generation HXR and gamma-ray experiments.
emission,
which should be not detectable by the next generation HXR and gamma-ray experiments.
The energetic electrons and positrons produced by WIMP annihilation have other interesting astrophysical effects among which we will discuss specifically in the following the Sunyaev-Zel'dovich (hereafter SZ) effect produced by DM annihilation and the heating of the intracluster gas produced by Coulomb collisions.
The energetic electrons and positrons produced by WIMP annihilation interact with the CMB photons and up-scatter them to higher frequencies producing a peculiar SZ effect (as originally realized by Colafrancesco 2004) with specific spectral and spatial features.
The generalized expression for the SZ effect which is valid in the Thomson limit for a
generic electron population in the relativistic limit and includes also the effects of
multiple scatterings and the combination with other electron population in the cluster
atmospheres has been derived by Colafrancesco et al. (2003). This approach is the one
that should be properly used to calculate the specific SZ![]() effect induced by
the secondary electrons produced by WIMP annihilation. Here we do not repeat the
description of the analytical technique and we refer to the general analysis described in
Colafrancesco et al. (2003). According to these results, the DM induced spectral
distortion is
effect induced by
the secondary electrons produced by WIMP annihilation. Here we do not repeat the
description of the analytical technique and we refer to the general analysis described in
Colafrancesco et al. (2003). According to these results, the DM induced spectral
distortion is
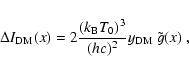 |
(58) |
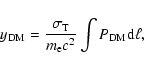 |
(59) |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{sz_coma_tot_mx40_planck.ps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg331.gif) |
Figure 17:
The SZ effect produced by the |
| Open with DEXTER | |
We show in Fig. 17 the frequency dependence of the CMB temperature
change,
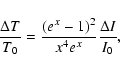 |
(62) |
The presence of a substantial SZ![]() effect is likely to dominate the overall SZ signal at
frequencies
effect is likely to dominate the overall SZ signal at
frequencies
![]() providing a negative total SZ effect. It is, however, necessary to
stress that in such frequency range there are other possible contributions to the SZ effect, like the
kinematic effect and the non-thermal effect which could provide additional biases (see, e.g.,
Colafrancesco et al. 2003).
Nonetheless, the peculiar spectral shape of the
providing a negative total SZ effect. It is, however, necessary to
stress that in such frequency range there are other possible contributions to the SZ effect, like the
kinematic effect and the non-thermal effect which could provide additional biases (see, e.g.,
Colafrancesco et al. 2003).
Nonetheless, the peculiar spectral shape of the
![]() effect is quite different
from that of the kinematic SZ effect and of the thermal SZ effect and this result allows
us to disentangle it from the overall SZ signal.
An appropriate multi-frequency analysis of the overall SZ effect based on observations
performed on a wide spectral range (from the radio to the sub-mm region) is required to
separate the various SZ contributions and to provide an estimate of the DM induced
SZ effect.
In fact, simultaneous SZ observations at low frequencies
effect is quite different
from that of the kinematic SZ effect and of the thermal SZ effect and this result allows
us to disentangle it from the overall SZ signal.
An appropriate multi-frequency analysis of the overall SZ effect based on observations
performed on a wide spectral range (from the radio to the sub-mm region) is required to
separate the various SZ contributions and to provide an estimate of the DM induced
SZ effect.
In fact, simultaneous SZ observations at low frequencies ![]() 30 GHz (where there is
the largest temperature decrement due to SZ
30 GHz (where there is
the largest temperature decrement due to SZ![]() ), at
), at
![]() GHz (where the
SZ
GHz (where the
SZ![]() deepens the minimum in
deepens the minimum in
![]() with respect to the dominant thermal
SZ effect), at
with respect to the dominant thermal
SZ effect), at ![]() 220 GHz (where the SZ
220 GHz (where the SZ![]() dominates the overall SZ effect and
produces a negative signal instead of the expected
dominates the overall SZ effect and
produces a negative signal instead of the expected ![]() null signal) and at
null signal) and at
![]() 250 GHz (where the still negative SZ
250 GHz (where the still negative SZ![]() decreases the overall SZ effect with
respect to the dominant thermal SZ effect) coupled with X-ray observations which
determine the gas distribution within the cluster (and hence the associated dominant
thermal SZ effect) can separate the SZ
decreases the overall SZ effect with
respect to the dominant thermal SZ effect) coupled with X-ray observations which
determine the gas distribution within the cluster (and hence the associated dominant
thermal SZ effect) can separate the SZ![]() from the overall SZ signal, and
consequently, set constraints on the WIMP model.
from the overall SZ signal, and
consequently, set constraints on the WIMP model.
The WIMP model with
![]() GeV produces a temperature decrement which is of the
order of
GeV produces a temperature decrement which is of the
order of ![]() 40 to 15
40 to 15 ![]() K for SZ observations in the frequency range
K for SZ observations in the frequency range ![]() 30 to
150 GHz (see Fig. 17). These signals are still within the actual
uncertainties of the available SZ data for Coma and are below the current SZ sensitivity
of WMAP (see, e.g., Bennet et al. 2003, and the results of the analysis of the WMAP SZ
signals from a sample of nearby clusters performed by Lieu et al. 2005).
Nonetheless, such SZ signals could be detectable with higher sensitivity experiments.
The high sensitivity planned for the future SZ experiments can provide much stringent
limits to the additional SZ effect induced by DM annihilation. In this context, the next
coming sensitive bolometer arrays (e.g., APEX), interferometric arrays (e.g., ALMA) and
the PLANCK-HFI experiment, or the planned OLIMPO balloon-borne experiment, have enough
sensitivity to probe the contributions of various SZ effects in the frequency range
30 to
150 GHz (see Fig. 17). These signals are still within the actual
uncertainties of the available SZ data for Coma and are below the current SZ sensitivity
of WMAP (see, e.g., Bennet et al. 2003, and the results of the analysis of the WMAP SZ
signals from a sample of nearby clusters performed by Lieu et al. 2005).
Nonetheless, such SZ signals could be detectable with higher sensitivity experiments.
The high sensitivity planned for the future SZ experiments can provide much stringent
limits to the additional SZ effect induced by DM annihilation. In this context, the next
coming sensitive bolometer arrays (e.g., APEX), interferometric arrays (e.g., ALMA) and
the PLANCK-HFI experiment, or the planned OLIMPO balloon-borne experiment, have enough
sensitivity to probe the contributions of various SZ effects in the frequency range
![]() GHz, provided that accurate cross-calibration at different frequencies
can be obtained.
The illustrative comparison (see Fig. 17) between the model
predictions and the sensitivity of the PLANCK LFI and HFI detectors at the optimal
observing frequencies (
GHz, provided that accurate cross-calibration at different frequencies
can be obtained.
The illustrative comparison (see Fig. 17) between the model
predictions and the sensitivity of the PLANCK LFI and HFI detectors at the optimal
observing frequencies (![]() and 53 GHz for the LFI detector and
and 53 GHz for the LFI detector and ![]() and
217 GHz for the HFI detector) show that the study of the SZ effect produced by DM
annihilation is actually feasible with the next generation SZ experiments.
We show in Fig. 18 the expected ratio between the DM-induced SZ
effect and the thermal SZ effect for the two WIMP models here considered. It is evident
that while the model with
and
217 GHz for the HFI detector) show that the study of the SZ effect produced by DM
annihilation is actually feasible with the next generation SZ experiments.
We show in Fig. 18 the expected ratio between the DM-induced SZ
effect and the thermal SZ effect for the two WIMP models here considered. It is evident
that while the model with
![]() GeV provides a detectable signal which is a
sensitive fraction of the thermal SZ effect at
GeV provides a detectable signal which is a
sensitive fraction of the thermal SZ effect at ![]() GHz, the SZ signal provided
by the model with
GHz, the SZ signal provided
by the model with
![]() GeV is by far too small to be detectable at any
frequency.
GeV is by far too small to be detectable at any
frequency.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{sz_coma_ratio_multifreq.ps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg344.gif) |
Figure 18:
The ratio between the DM-induced and the thermal SZ effect in Coma is shown for the model
with
|
| Open with DEXTER | |
The spectral properties shown by the SZ![]() for neutralinos depends on the specific
neutralino model as we have shown in Fig. 17: in fact, the SZ effect
is visible for a neutralino with
for neutralinos depends on the specific
neutralino model as we have shown in Fig. 17: in fact, the SZ effect
is visible for a neutralino with
![]() GeV and not visible for a neutralino
with
GeV and not visible for a neutralino
with
![]() GeV. Thus the detailed features of the SZ effect from DM annihilation depends strongly on the mass and composition of the DM particle, and - in
turn - on the equilibrium spectrum of the secondary electrons. Each specific DM model
predicts its own spectrum of secondary electrons and this influences the relative
SZ effect. Models of DM which provide similar electron spectra will provide similar
SZ effects.
GeV. Thus the detailed features of the SZ effect from DM annihilation depends strongly on the mass and composition of the DM particle, and - in
turn - on the equilibrium spectrum of the secondary electrons. Each specific DM model
predicts its own spectrum of secondary electrons and this influences the relative
SZ effect. Models of DM which provide similar electron spectra will provide similar
SZ effects.
Low energy secondary electrons produced by WIMP annihilation might heat the intracluster gas by
Coulomb collisions since the Coulomb loss term dominates the energy losses at ![]() MeV (see
Fig. A.3).
The specific heating rate is given by
MeV (see
Fig. A.3).
The specific heating rate is given by
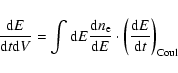 |
(63) |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{heating_mx40_81.ps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg353.gif) |
Figure 19: Left: the specific heating rate is plotted against the radial distance from the center of Coma. Right: the specific heating rate multiplied by the volume element is plotted against the radial distance from the center of Coma. |
| Open with DEXTER | |
This implies, in conclusion, that WIMP annihilation cannot provide most of the heating of
Coma, even in its innermost regions.
Such a conclusion seems quite general and implies that non-singular DM halo models are
not able to provide large quantities of heating at the center of galaxy clusters so to
quench efficiently the cooling of the intracluster gas (with powers of
![]() erg/s).
Only very steep halo profiles (even steeper than the Moore profile) and with the possible adiabatic
growth of a central matter concentration (e.g., a central BH) could provide sufficient power to quench
locally (i.e. in the innermost regions) the intracluster gas cooling (see, e.g.,
Totani 2004).
However, we stress that the spatial diffusion of the secondary electrons in the innermost regions of
galaxy clusters should flatten the specific heating rate in the vicinity of the DM spike and thus
decrease substantially the heating efficiency by Coulomb collisions. In conclusion, we believe that
the possibility to solve the cooling flow problem of galaxy clusters by WIMP annihilation is still an
open problem.
erg/s).
Only very steep halo profiles (even steeper than the Moore profile) and with the possible adiabatic
growth of a central matter concentration (e.g., a central BH) could provide sufficient power to quench
locally (i.e. in the innermost regions) the intracluster gas cooling (see, e.g.,
Totani 2004).
However, we stress that the spatial diffusion of the secondary electrons in the innermost regions of
galaxy clusters should flatten the specific heating rate in the vicinity of the DM spike and thus
decrease substantially the heating efficiency by Coulomb collisions. In conclusion, we believe that
the possibility to solve the cooling flow problem of galaxy clusters by WIMP annihilation is still an
open problem.
WIMP annihilation in galaxy cluster is an efficient mechanism to produce relativistic electrons and high-energy particles which are able, in turn, to produce a wide SED extended over more than 18 orders of magnitude in frequency, from radio to gamma-rays. We discuss here the predictions of two specific models which embrace a vast range of possibilities.
The
![]() model with
model with
![]() GeV and annihilation cross section
GeV and annihilation cross section
![]() provides a reasonable fit to the
radio data (both the total spectrum and the surface brightness radial distribution) with
a magnetic field whose mean value is
provides a reasonable fit to the
radio data (both the total spectrum and the surface brightness radial distribution) with
a magnetic field whose mean value is
![]() G.
We remind here that the quite high value of
G.
We remind here that the quite high value of
![]() is well inside
the range of neutralino masses and annihilation cross-sections provided by the most
general supersymmetric DM setup (see our discussion in Sect. 3.2).
Table 3 provides an illustrative scheme of the radiation mechanisms, of
the particle energies and of the fluxes predicted by this best-fit WIMP model for a wide
range of the physical conditions in the cluster atmosphere.
is well inside
the range of neutralino masses and annihilation cross-sections provided by the most
general supersymmetric DM setup (see our discussion in Sect. 3.2).
Table 3 provides an illustrative scheme of the radiation mechanisms, of
the particle energies and of the fluxes predicted by this best-fit WIMP model for a wide
range of the physical conditions in the cluster atmosphere.
Table 3:
Predicted flux in various frequency ranges for a neutralino
![]() model
with
model
with
![]() GeV and
GeV and
![]() cm3/s. The value of the magnetic field is
cm3/s. The value of the magnetic field is
![]() G.
Eparticle refers to the approximate energy for
G.
Eparticle refers to the approximate energy for ![]() or
or ![]() sourcing the corresponding flux in the monochromatic limit.
sourcing the corresponding flux in the monochromatic limit.
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{multiflux3.eps}\hspace*{5mm}
\includegraphics[width=6.2cm,clip]{bbarmag.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg380.gif) |
Figure 20:
Scaling of the multi-wavelength spectrum and of relative bounds on the particle
physics model with the assumed value for the mean magnetic field in Coma.
Left panel: we
have chosen a few sample values for the magnetic field and varied freely pair
annihilation cross section and WIMP mass to minimize the |
| Open with DEXTER | |
For the best-fit values of
![]() GeV and
GeV and
![]() this model yields EUV and HXR fluxes which are more than one
order of magnitude fainter than the Coma data. The gamma-ray flux produced by this model
is dominated by the continuum
this model yields EUV and HXR fluxes which are more than one
order of magnitude fainter than the Coma data. The gamma-ray flux produced by this model
is dominated by the continuum
![]() component and it is a factor
component and it is a factor
![]() 5 lower than the EGRET upper limit of Coma at its peak frequency (see
Fig. 16, left panel). Such gamma-ray flux could be, nonetheless,
detectable by the GLAST-LAT detector (we will discuss more specifically the
detectability of the gamma-ray WIMP annihilation signals from galaxy clusters in a
dedicated, forthcoming paper (Colafrancesco et al. 2006b).
The rather low neutralino mass
5 lower than the EGRET upper limit of Coma at its peak frequency (see
Fig. 16, left panel). Such gamma-ray flux could be, nonetheless,
detectable by the GLAST-LAT detector (we will discuss more specifically the
detectability of the gamma-ray WIMP annihilation signals from galaxy clusters in a
dedicated, forthcoming paper (Colafrancesco et al. 2006b).
The rather low neutralino mass
![]() GeV of this model makes it rather difficult
to be testable by Cherenkov gamma-ray detectors operating at higher threshold energies.
GeV of this model makes it rather difficult
to be testable by Cherenkov gamma-ray detectors operating at higher threshold energies.
Increasing the neutralino mass does not provide a good fit of the radio-halo spectrum (see Fig. 16, right panel) and yields, in addition, extremely faint EUV, HXR and gamma-ray fluxes, which turn out to be undetectable even by GLAST and/or by the next coming high-energy experiments.
It is possible to recover the EUV and HXR data on Coma with a IC flux by secondary
electrons by increasing the annihilation cross-sections by a factor
![]() (i.e., up
to values
(i.e., up
to values
![]() )
in the
best-fit
)
in the
best-fit
![]() soft WIMP model (at fixed
soft WIMP model (at fixed
![]() GeV). However, in such a
case both the radio-halo flux and the hard gamma-ray flux at
GeV). However, in such a
case both the radio-halo flux and the hard gamma-ray flux at ![]() 1 GeV as produced
by
1 GeV as produced
by ![]() decay should increase by the same factor leading to a problematic picture: in
fact, while the radio-halo data would imply lower values of the magnetic field
decay should increase by the same factor leading to a problematic picture: in
fact, while the radio-halo data would imply lower values of the magnetic field
![]()
![]() G which might still be allowed by the data, the
G which might still be allowed by the data, the
![]() gamma-ray flux at E > 100 MeV should exceed the EGRET limit on Coma. This option is
therefore excluded by the available data.
gamma-ray flux at E > 100 MeV should exceed the EGRET limit on Coma. This option is
therefore excluded by the available data.
Alternatively, it would be possible to fit the EUV and HXR spectra of Coma with the
adopted value of
![]() for
the
for
the
![]() model with
model with
![]() GeV, in the case we sensibly lower the mean
magnetic field. Values of the average magnetic field
GeV, in the case we sensibly lower the mean
magnetic field. Values of the average magnetic field
![]() G are required to
fit the HXR flux of Coma under the constraint to fit at the same time the radio-halo
spectrum (see Fig. 20, left panel), consistently with the general
description of the ratio between the synchrotron and IC emission powers in Coma (see,
e.g., Colafrancesco et al. 2005; Reimer et al. 2004). Magnetic fields as low as
G are required to
fit the HXR flux of Coma under the constraint to fit at the same time the radio-halo
spectrum (see Fig. 20, left panel), consistently with the general
description of the ratio between the synchrotron and IC emission powers in Coma (see,
e.g., Colafrancesco et al. 2005; Reimer et al. 2004). Magnetic fields as low as
![]() G can fit both the HXR and the EUV fluxes of Coma.
However, also in this case the
G can fit both the HXR and the EUV fluxes of Coma.
However, also in this case the
![]() gamma-ray flux predicted by the
same model at E > 100 MeV exceeds the EGRET limit on Coma, rendering untenable this
alternative.
Actually, the EGRET upper limit on Coma set a strong constraint on the combination of
values B and
gamma-ray flux predicted by the
same model at E > 100 MeV exceeds the EGRET limit on Coma, rendering untenable this
alternative.
Actually, the EGRET upper limit on Coma set a strong constraint on the combination of
values B and
![]() (see Fig. 20, right panel)
so that magnetic field larger than
(see Fig. 20, right panel)
so that magnetic field larger than ![]() 0.3
0.3 ![]() G are required for the parameter
setup of the
G are required for the parameter
setup of the
![]() model with
model with
![]() GeV. Figure 20 shows
the upper limits on the value of
GeV. Figure 20 shows
the upper limits on the value of
![]() as a function of the assumed
value of the mean magnetic field of Coma.
According to these results, it is impossible to fit all the available data on Coma for a
consistent choice of the DM model and of the cluster magnetic field. The EUV and HXR data
in particular require extreme conditions, i.e. low values of the magnetic field and/or
high values of the annihilation cross section, which violate the EGRET gamma-ray limit.
Thus, realistic DM models that are consistent with the radio and gamma-ray constraints
predict IC emission which falls short of fitting the EUV and HXR data of Coma.
as a function of the assumed
value of the mean magnetic field of Coma.
According to these results, it is impossible to fit all the available data on Coma for a
consistent choice of the DM model and of the cluster magnetic field. The EUV and HXR data
in particular require extreme conditions, i.e. low values of the magnetic field and/or
high values of the annihilation cross section, which violate the EGRET gamma-ray limit.
Thus, realistic DM models that are consistent with the radio and gamma-ray constraints
predict IC emission which falls short of fitting the EUV and HXR data of Coma.
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{multiflux4.eps}\hspace*{5mm}
\includegraphics[width=6cm,clip]{wpwmmag.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg387.gif) |
Figure 21:
The analogous of Fig. 20, but now for the W+ W- final state
and fixing the WIMP mass to 81 GeV. In the left panel, for each value of the magnetic field, the value
of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{haloscan.eps}\includegraphics[width=6.5cm,clip]{haloscan3.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg388.gif) |
Figure 22:
Scaling of fluxes with the assumptions on the halo model for Coma. In the plane
|
| Open with DEXTER | |
An appealing property of the WIMP model worked out here is that it can reproduce both the
spatial distribution of the radio-halo surface brightness of Coma and, in principle, also
the spatial profile of the EUV emission (see, e.g., Bowyer et al. 2004) which
seems more concentrated than the radio-halo surface brightness.
As for the radio-halo surface brightness profile, it seems necessary for this WIMP model
- due to the shape of the DM halo profile - to invoke a radial distribution of the
magnetic field with a mild decrease towards the Coma center to counterbalance the
centrally peaked DM profile, and with an exponential cutoff at large radii to
counterbalance the effect of the subhalo distribution.
We notice here that such a specific B(r) spatial distribution is - interestingly
enough - able to reproduce the radial distribution of the RMs in Coma (see Sect. 5.1).
While the (Synchrotron) radio surface brightness depends strongly on the magnetic field
radial profile, the (ICS) EUV radial profile only depends on the DM halo profile and on
the secondary electron properties and is, hence, more concentrated (see
Fig. 10 for an example). Thus, the radial distribution of the EUV emission
could be reasonably reproduced by the WIMP model which best fits the radio data but with
a very low value of the magnetic field of order of ![]() 0.15
0.15 ![]() G.
We already noticed, however, that models with values of the average magnetic field in
Coma which are
G.
We already noticed, however, that models with values of the average magnetic field in
Coma which are
![]() G produce a gamma-ray flux which exceeds the EGRET upper
limit of Coma (see Fig. 20), rendering these models untenable.
G produce a gamma-ray flux which exceeds the EGRET upper
limit of Coma (see Fig. 20), rendering these models untenable.
We summarize all the constraints on the neutralino models set by the magnetic field and
by the annihilation cross-section in Figs. 20 and 21.
The available data set constraints on the WIMP annihilation rate. Figures 22 and 23 show the
upper limits on
![]() as a function of the assumed value for the
mean magnetic field in Coma. The EGRET limit proves to be the more constraining at the
moment with respect to the HXR and EUV data. These limits are able to test directly the
annihilation rate since they are independent of the magnetic field value. Nonetheless,
the combination of the gamma-ray and/or HXR constraints with the radio constraints will
be able to determine the full setup of the relevant quantities whose combination is able
to fit the overall Coma SED. In this context, it is clear that the possible GLAST
observations of Coma, combined with the radio data, will increase by far the constraints
in the
as a function of the assumed value for the
mean magnetic field in Coma. The EGRET limit proves to be the more constraining at the
moment with respect to the HXR and EUV data. These limits are able to test directly the
annihilation rate since they are independent of the magnetic field value. Nonetheless,
the combination of the gamma-ray and/or HXR constraints with the radio constraints will
be able to determine the full setup of the relevant quantities whose combination is able
to fit the overall Coma SED. In this context, it is clear that the possible GLAST
observations of Coma, combined with the radio data, will increase by far the constraints
in the
![]() plane.
plane.
The results of our analysis also depend on the assumed DM halo density profile.
Figure 22 shows the scaling of fluxes with the assumptions on the halo
model for Coma. We compare here, for the sake of illustration, the scalings of the N04
and of the Burkert model.
Switching to one of the halo models displayed here is equivalent to shifting all values
of
![]() plotted in the figures to
plotted in the figures to
![]() divided by the scaling value shown here. This analysis allows us to compare correctly the
results of the multi-frequency analysis we have presented in this paper in terms of
substructure enhancement and halo density profile.
divided by the scaling value shown here. This analysis allows us to compare correctly the
results of the multi-frequency analysis we have presented in this paper in terms of
substructure enhancement and halo density profile.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{multiflux5.eps}
\end{figure}](/articles/aa/full/2006/31/aa3887-05/Timg391.gif) |
Figure 23:
Multi-wavelength spectra for the four benchmark models described in the text. The prediction
is shown for the best fit N04 profile, and our reference choice for subhalo parameters, and for a mean
magnetic field equal to
|
| Open with DEXTER | |
Table 4 also shows the typical values for the annihilation
cross-section
![]() and the relative signals expected at different
frequencies for the Coma best-fit model (
and the relative signals expected at different
frequencies for the Coma best-fit model (
![]() neutralino model with
neutralino model with
![]() GeV and B= 1
GeV and B= 1 ![]() G) that we explored in this paper.
Large neutralino pair annihilation cross section will, in general, produce sizable
signals also for other indirect detection techniques, including antimatter searches and
gamma rays from the center of the Milky Way.
Antimatter and gamma-ray fluxes also largely depend on the Milky Way dark-matter halo and
on the specific neutralino model (e.g. through the antimatter yield per neutralino
annihilation). Existing analysis
(Baer & Profumo 2005; Profumo & Ullio 2004; Baer et al. 2005a; Profumo 2005) make it possible to draw
some qualitative estimates of the cross-section,
G) that we explored in this paper.
Large neutralino pair annihilation cross section will, in general, produce sizable
signals also for other indirect detection techniques, including antimatter searches and
gamma rays from the center of the Milky Way.
Antimatter and gamma-ray fluxes also largely depend on the Milky Way dark-matter halo and
on the specific neutralino model (e.g. through the antimatter yield per neutralino
annihilation). Existing analysis
(Baer & Profumo 2005; Profumo & Ullio 2004; Baer et al. 2005a; Profumo 2005) make it possible to draw
some qualitative estimates of the cross-section,
![]() ,
required to produce sensible signals at future DM search experiments. We provide in
Table 4 order-of-magnitude estimates for the value of
,
required to produce sensible signals at future DM search experiments. We provide in
Table 4 order-of-magnitude estimates for the value of
![]() expected to give observable signals in space-based antimatter (AMS-02,
Pamela, GAPS) and gamma-ray search experiments (GLAST), for two extreme choices of the
galactic dark-matter halo: a cuspy profile (such as the N04 profile) and a cored profile
(such as the Burkert profile).
Different search techniques, such as direct detection, or neutrino flux detection from
the core of the Sun induced by the annihilation of captured neutralinos, critically
depend upon the scattering cross section of neutralinos off nucleons, and the resulting
detection rates are therefore unrelated, in general, to the pair annihilation process
discussed here.
expected to give observable signals in space-based antimatter (AMS-02,
Pamela, GAPS) and gamma-ray search experiments (GLAST), for two extreme choices of the
galactic dark-matter halo: a cuspy profile (such as the N04 profile) and a cored profile
(such as the Burkert profile).
Different search techniques, such as direct detection, or neutrino flux detection from
the core of the Sun induced by the annihilation of captured neutralinos, critically
depend upon the scattering cross section of neutralinos off nucleons, and the resulting
detection rates are therefore unrelated, in general, to the pair annihilation process
discussed here.
Table 4:
Order-of-magnitude estimates of the values of the cross-section,
![]() ,
in units of
,
in units of
![]() ,
needed to reproduce the detected
non-thermal emission features in Coma and to produce sizable signals for future indirect
dark matter search experiments in the Milky Way.
,
needed to reproduce the detected
non-thermal emission features in Coma and to produce sizable signals for future indirect
dark matter search experiments in the Milky Way.
We show in Fig. 23 the overall SED of Coma as expected from the four
benchmark models described in the Sect. 3.2. The predictions are shown for the best fit
N04 profile and for our reference choice for subhalo parameters, and for a mean magnetic
field of
![]() .
None of these benchmark model may provide a reasonable fit to the
radio data. Notice, in addition, the quite dim multi-frequency SED predicted for Coma in
these benchmark models. The largest fluxes are, not surprisingly, obtained for the model
lying in the focus point region (
.
None of these benchmark model may provide a reasonable fit to the
radio data. Notice, in addition, the quite dim multi-frequency SED predicted for Coma in
these benchmark models. The largest fluxes are, not surprisingly, obtained for the model
lying in the focus point region (![]() ). In that case, neutralinos mostly annihilate
into gauge bosons, as can be inferred from the spectral shape, which closely resembles
that in Fig. 21. We therefore conclude that the expectation of astrophysical
signatures from neutralino DM annihilations in the Coma cluster (with natural assumptions
on the dark halo profile, substructures and magnetic field of Coma) is not promising in
the context of the commonly discussed minimal supergravity scenario.
). In that case, neutralinos mostly annihilate
into gauge bosons, as can be inferred from the spectral shape, which closely resembles
that in Fig. 21. We therefore conclude that the expectation of astrophysical
signatures from neutralino DM annihilations in the Coma cluster (with natural assumptions
on the dark halo profile, substructures and magnetic field of Coma) is not promising in
the context of the commonly discussed minimal supergravity scenario.
It would be interesting to compare the predictions of the WIMP annihilation for Coma with
the implication of the presence of another population of cosmic rays of different origin
like that, often invoked, produced by acceleration processes in the atmosphere of Coma.
Acceleration scenarios usually produce power-law spectra for the electrons which are
primarily accelerated by shocks or turbulence and are, hence remarkably different from
the source spectra produced by neutralino acceleration. Specifically, acceleration models
do not exhibit a cut-off at the neutralino mass and do not produce the peculiar peaked
![]() gamma-ray emission which remains a distinctive feature of neutralino DM models. A
continuum
gamma-ray emission which remains a distinctive feature of neutralino DM models. A
continuum ![]() gamma-ray emission can be produced in secondary models where the
electrons are produced by proton-proton collision in the cluster atmosphere. But even in
this case the gamma-ray spectrum is likely to be resembled by a power-law shape which
keeps memory of the original acceleration events for the hadrons.
Thus, it will be possible to separate DM annihilation models from acceleration models
based on multi-frequency observations of the hadronic and leptonic components of the
cluster SED.
gamma-ray emission can be produced in secondary models where the
electrons are produced by proton-proton collision in the cluster atmosphere. But even in
this case the gamma-ray spectrum is likely to be resembled by a power-law shape which
keeps memory of the original acceleration events for the hadrons.
Thus, it will be possible to separate DM annihilation models from acceleration models
based on multi-frequency observations of the hadronic and leptonic components of the
cluster SED.
Finally, It should be noticed that the same problem with the consistent fitting of both the synchrotron and IC components to the radio and EUV/HXR data of Coma still remains in both DM and acceleration models, pointing to the fact that these spectral features, if real, have probably different physical origin.
WIMP annihilations in galaxy cluster inevitably produce high-energy secondary particles which are able, in turn, to produce a wide SED extended over more than 18 orders of magnitude in frequency, from radio to gamma-rays.
A consistent analysis of the DM distribution and of its annihilation in the Coma cluster shows that WIMP annihilation is able to reproduce both the spectral and the spatial features of the Coma radio halo under reasonable assumptions for the structure of the intracluster magnetic field. The mild decrease of the magnetic field towards the Coma center, which reproduces the radial trend of the observed RM distribution in Coma, could be better tested with a larger dataset of Faraday rotation measures of background radio sources obtainable with the next generation sensitive radio telescopes (LOFAR, SKA), and with the help of numerical MHD simulations. Radio data are the main constraint, so far, to WIMP models.
The ICS emission produced by the same secondary electrons is able, in principle, to
reproduce both the spectrum and the spatial distribution of the EUV emission observed in
Coma, provided that a quite small average magnetic field
![]()
![]() G is assumed.
Such low value of the B field is also able to make the radio data and the hard X-ray data
of Coma consistent within a Synchrotron/IC model for their origins.
However, such low magnetic field values in Coma produce an unacceptably large gamma-ray flux, which
exceeds the EGRET upper limit. The gamma-ray constraints are thus the most stringent ones for the
analysis of the astrophysical features of DM annihilations.
G is assumed.
Such low value of the B field is also able to make the radio data and the hard X-ray data
of Coma consistent within a Synchrotron/IC model for their origins.
However, such low magnetic field values in Coma produce an unacceptably large gamma-ray flux, which
exceeds the EGRET upper limit. The gamma-ray constraints are thus the most stringent ones for the
analysis of the astrophysical features of DM annihilations.
In conclusion, the viable models of WIMP annihilation which are consistent with the
available data for Coma yield a nice fit to the radio data but produce relatively low
intensity emission at EUV, X-ray and gamma-ray frequencies. The hadronic gamma-ray
emission could be, nonetheless, detected by the GLAST-LAT detector. These models also
produce negligible heating rates for the kind of non-singular halo profile we worked out
in this paper. It is interesting that the best-fit (![]() )
WIMP model with
)
WIMP model with
![]() GeV predicts a detectable SZ effect (with a peculiar spectrum very
different from that of the thermal SZ effect) at the level of
GeV predicts a detectable SZ effect (with a peculiar spectrum very
different from that of the thermal SZ effect) at the level of ![]() 40 to 10
40 to 10 ![]() K in
the frequency range
K in
the frequency range
![]() GHz, which could be observable with the next generation
high-sensitivity bolometric arrays, space and balloon-borne microwave experiments, like
PLANCK, OLIMPO, APEX, ALMA.
GHz, which could be observable with the next generation
high-sensitivity bolometric arrays, space and balloon-borne microwave experiments, like
PLANCK, OLIMPO, APEX, ALMA.
The observational "panorama'' offered by the next coming radio, SZ, and gamma-ray astronomical experiments might produce further constraints on the viable SUSY model for Coma and for other large-scale cosmic structures. Direct DM detection experiments have already explored large regions of the most optimistic SUSY models, and the planned increase in sensitivity of the next-generation experiments will probably be able to explore even the core of the SUSY models. In this context, we have shown that indirect DM detection proves to be not only complementary, but also hardly competitive, especially when a full multi-frequency approach is chosen. When combined with future accelerator results, such multi-frequency astrophysical searches might greatly help us to unveil the elusive nature of dark matter.
Acknowledgements
We thank the Referee for the useful comments and suggestions that allowed us to improve the presentation of our results. S.C. acknowledges support by PRIN-MIUR under contract No.2004027755_003.
To understand quantitatively the role of the various populations of secondary particles
emitting in the Coma cluster, we have to describe in details their transport, diffusion
and energy loss.
We consider the following diffusion equation (i.e. neglecting convection and
re-acceleration effects):
| D = D(E) | (A.2) | ||
| b = b(E) | (A.3) |
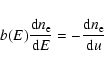 |
(A.4) |
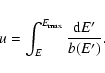 |
(A.5) |
The diffusion equation can be rewritten as
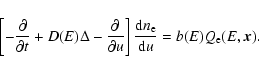 |
(A.6) |
![$\displaystyle \left[-i\omega + D(E) k^2 - {\frac{\partial}{\partial u}} \right]...
...p{ \left[-{\rm i}(\omega t'+\vec{k}\cdot\vec{x}')\right]}
\cdot~ \delta(u-u') ,$](/articles/aa/full/2006/31/aa3887-05/img419.gif) |
(A.7) |
![$\displaystyle \tilde{G} = - \frac{1}{(2\pi)^2} \exp \bigg[-{\rm i}(\omega t'+\v...
...') - i
\omega (u-u')
- k^2~ \int_{u'}^{u} {\rm d}\tilde{u} D(\tilde{u})\bigg] .$](/articles/aa/full/2006/31/aa3887-05/img420.gif) |
(A.8) |
![$\displaystyle G_{\rm free} = - \frac{1}{(4 \pi (v-v'))^{3/2}}~
\exp{\left[-\fra...
...rt\vec{x}-\vec{x}'\vert^2}{4 (v-v')}\right]}
\delta\left((t-t')-(u-u')\right)\;$](/articles/aa/full/2006/31/aa3887-05/img421.gif) |
(A.9) |
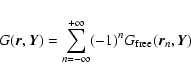 |
(A.10) |
In the limit of time-independence of the source and electron number density that has
already reached equilibrium, Eq. (A.11) takes the form:
Since we have encoded the dependence on the energy loss term and the diffusion
coefficient in the definition of the variable v, we preliminarily study what range of
![]() is relevant in the discussion. To do that, we need to specify D(E) and b(E). For the diffusion coefficient we assume the form:
is relevant in the discussion. To do that, we need to specify D(E) and b(E). For the diffusion coefficient we assume the form:
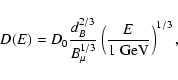 |
(A.15) |
The energy loss term is the sum of effects due to Inverse Compton, synchrotron radiation,
Coulomb losses and Bremsstrahlung:
| b(E) | = | ||
| = | 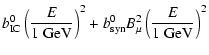 |
||
| (A.16) |
To get a feeling about what is the electron/positron energy range which will be of
interest when considering the radio emissivity, we can resort to the "monochromatic''
approximation, with relativistic particles of a given energy E radiating at a single
frequency, namely the peak frequency:
As a sample case, in Fig. A.1 we consider a WIMP mass
![]() GeV and
sketch the mapping between the energy
GeV and
sketch the mapping between the energy
![]() ,
with E some reference energy
after diffusion, and the square root of
,
with E some reference energy
after diffusion, and the square root of
![]() ,
for a
few values of E and of the mean magnetic field
,
for a
few values of E and of the mean magnetic field ![]() .
We find as largest value
.
We find as largest value
![]() kpc, corresponding to E = 1 GeV and
kpc, corresponding to E = 1 GeV and ![]()
![]() G; the
maximum value of
G; the
maximum value of ![]() diminishes rapidly when increasing E or
diminishes rapidly when increasing E or ![]() .
.
On the right-hand side of Fig. A.1, we plot
![]() as a function of
as a function of
![]() for a few values of the radial coordinate r and in case the DM halo
of Coma is described by a N04 profile. In the very central part of the halo, there are
significant departures of the value of
for a few values of the radial coordinate r and in case the DM halo
of Coma is described by a N04 profile. In the very central part of the halo, there are
significant departures of the value of
![]() from unity, on scales
from unity, on scales
![]() at which, for the given radius r, the mean squared value of the DM profile is
significantly different from the square of the value of the profile at r. Note,
however, that this effect is confined in the innermost region of the cluster,
corresponding to an angular size of
at which, for the given radius r, the mean squared value of the DM profile is
significantly different from the square of the value of the profile at r. Note,
however, that this effect is confined in the innermost region of the cluster,
corresponding to an angular size of
![]() arcmin. We then expect that taking into
account spatial diffusion will modify only slightly the predictions for the radio surface
brightness distribution from moderate to large radial distances in Coma.
arcmin. We then expect that taking into
account spatial diffusion will modify only slightly the predictions for the radio surface
brightness distribution from moderate to large radial distances in Coma.
In Fig. A.2, we plot
![]() as a function of
as a function of
![]() for
the same values of the radial coordinate r as in Fig. A.1 but now in case
the DM halo of Coma is described by a Burkert profile. It is clear that departures from
unity are essentially negligible even in the inner portion of the halo and, hence,
spatial diffusion can be safely neglected for all practical purposes in this case.
for
the same values of the radial coordinate r as in Fig. A.1 but now in case
the DM halo of Coma is described by a Burkert profile. It is clear that departures from
unity are essentially negligible even in the inner portion of the halo and, hence,
spatial diffusion can be safely neglected for all practical purposes in this case.
To get a more physical insight on the reason why spatial diffusion can be neglected, it
is useful to consider the following qualitative solution (see, e.g.,
Colafrancesco 2005) for the average electron density
For E < E*, the condition
![]() (and consistently
(and consistently
![]() )
holds, the diffusion is relevant and the solution of Eq. (A.1) is d
)
holds, the diffusion is relevant and the solution of Eq. (A.1) is d
![]() and shows an energy spectrum
and shows an energy spectrum
![]() which is flatter or equal to the previous case for reasonable values
which is flatter or equal to the previous case for reasonable values
![]() .
This last situation (
.
This last situation (
![]() ,
,
![]() )
applies to
the regime of dwarf galaxies and we will discuss this case more specifically elsewhere
(Colafrancesco et al. 2006).
)
applies to
the regime of dwarf galaxies and we will discuss this case more specifically elsewhere
(Colafrancesco et al. 2006).
Figure A.4 shows the energy shape of the electron equilibrium spectra
derived in our approach for a (![]() )
model with
)
model with
![]() GeV and for a
W+W- model with
GeV and for a
W+W- model with
![]() GeV. The astrophysical predictions of these two
models will be extensively discussed in the following.
GeV. The astrophysical predictions of these two
models will be extensively discussed in the following.