J. Anderson¹ - L. R. Bedin² - G. Piotto³ - R. S. Yadav^3,4 - A. Bellini³

1 - Dept. of Physics and Astronomy, MS-108, Rice University, 6100 Main Street, Houston, TX-77005, USA
2 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
3 - Dipartimento di Astronomia, Università di Padova, 35122 Padova, Italy
4 - Aryabhatta Research Institute of Observational Sciences (ARIES), Nainital 263129, India

Abstract
This paper is the first of a series of papers in which we will apply the methods we have developed for high-precision astrometry (and photometry) with the Hubble Space Telescope (HST) to the case of wide-field ground-based images. In particular, we adapt the software originally developed for WFPC2 to ground-based, wide field images from the WFI at the ESO 2.2 m telescope. In this paper, we describe in details the new software, we characterize the WFI geometric distortion, discuss the adopted local transformation approach for proper-motion measurements, and apply the new technique to two-epoch archive data of the two closest Galactic globular clusters: NGC 6121 (M 4) and NGC 6397. The results of this exercise are more than encouraging. We find that we can achieve a precision of $\sim$ 7 mas (in each coordinate) in a single exposure for a well-exposed star, which allows a very good cluster-field separation in both M 4, and NGC 6397, with a temporal baseline of only 2.8, and 3.1 years, respectively.

Key words: astrometry - globular clusters: individual: NGC 6397 - globular clusters: individual: NGC 6121 (M 4) - techniques: image processing

1 Introduction

Recent investigations have shown that imaging from the cameras onboard the Hubble Space Telescopes (HST) can provide high-precision astrometry for point-like sources (Anderson & King 2000, hereafter AK2000). There are several factors which make imaging astrometry much more accurate from space than from the ground. First, the absence of atmospheric effects allows us to obtain diffraction-limited images, with a point-spread function (PSF) which is nearly constant in time, and therefore amenable to detailed modeling. Also, space-based observatories are free of differential-refraction effects, which plague ground-based images not taken at the zenith. Finally, the weightless environment means that telescope flexure does not lead to large changes in the distortion solution, which means we can model the solution to much higher accuracy.

However, despite all the benefits of imaging astrometry from space, there are some significant limitations as well. First, the need to download all the data taken to the ground puts a major limit on how much data can be collected by HST per hour. For this reason, the largest detectors are 4096 $\;\times\;$ 4096, and almost all of the detectors are undersampled in order to get the maximum sky coverage for the limited number of pixels. Ground-based telescopes suffer no such limitations. They can be made up of dozens of CCDs and can collect Terabytes of information every night. Furthermore each exposure can cover over 400 $\times$ the biggest HST field-of-view. In addition, the fact that HST is undersampled introduces a significant complexity to the data analysis. Special care must be taken to derive exquisitely accurate PSFs (see AK2000), so that the positions measured with them will be free from bias. Ground-based detectors can afford to oversample the stellar image, so that sampling will not be a limitation or complication for our accuracy. Finally, the fact that time on HST is scarce means that it is hard to get space-based observations. By contrast, there are many ground based observatories.

Even with its sampling and field-of-view limitations, the phenomenal astrometric precision possible with HST has allowed us to undertake projects that were simply impossible before, such as:

Our interest in the above applications, in particular in the proper-motion aspects, has stimulated the effort to transfer what we have learned by measuring high-accuracy positions on HST images to wide field, ground-based data. Much attention has been devoted over the years to software that can extract good photometry from ground-based images (DAOPHOT, ROMAPHOT, etc.), but thus far very little attention has been devoted to astrometry. Photometry and astrometry make very different demands on PSF analysis. Photometry concerns itself more with sums of pixels, whereas astrometry keys off of differences between nearby pixel values, but there is no reason that with a good PSF we cannot measure both good fluxes and positions. This paper is one step in that direction.

Over the last few years, several Wide Field Imagers (WFIs) have come on-line at large ground-based telescopes (MPI-ESO 2.2 m, AAT 4 m, CFH 4 m), and their number and their field-of-view are continuously increasing (LBT 2 $\;\times\;$ 8 m, VST 2.5 m, UKIRT 3.8 m, VISTA 4 m, etc.). These WFIs allow us to map completely any open or globular cluster in our Galaxy and their tidal tails, and to get accurate photometry for enormous numbers of stars.

One of the most promising (yet still largely unexplored) opportunities presented by wide-field images involves astrometry. Accurate astrometry over wide fields is important for a variety of reasons. To be sure, an accuracy of 0.2 arcsec or better is usually required to position point-like sources in the increasing number of multi-slit and multi-fiber spectroscopic facilities. But the most promising astrometric applications lie in the ability to measure proper-motions for a large number of stars. In principle, the ground-based WFIs should allow astrometric measurements with an accuracy far better than the nominal 0.2 arcsec. As we will show in Sect. 8, with a baseline of just a few years, images collected with modern WFIs can provide proper motions more accurate than those obtainable with old plates with a baseline of several decades. (Note, though, that these plates will still remain valuable for long-term non-linear astrometry, such as the determination of the orbit of long-period visual binaries, and of course for long-term variation in the light curves.)

In this paper, we apply what we have learned from HST to the case of one particular ground-based wide-field imager: the WFI at the focus of the 2.2 m ESO/MPI telescope, located at La Silla (hereafter we will refer to it as WFI@2.2m). The WFI camera is made up of 8 chips of 2142 $\;\times\;$ 4128 pixels each disposed as illustrated in Fig. 1, with a pixel-scale of 238 mas/pixel.

$\begin{figure} \par\includegraphics[width=8cm,clip]{5004f00.eps} \end{figure}$	Figure 1: WFI@2.2m layout. Dimension of the chips, gaps, and the whole field of view, are expressed in pixels, linear units, and arcsec. Also each chip has different labels, in this paper we will refer to each chip with the numbers going from [1] to [8] as shown in the figures.
Open with DEXTER

$\begin{figure} \par\begin{tabular}{cc} \fbox{\includegraphics[width=6.5cm]{5004f... ...\includegraphics[width=6.5cm]{5004f04.eps}}\\ \end{tabular}\protect\end{figure}$

Figure 2: ( Top-left) one of the images of Baade's window used to calibrate the geometrical distortion of WFI@2.2m. In these images we see the Galactic globular cluster NGC 6528 on chip [8], and NGC 6522 on chip [6]. The dark spot on chip [3] is just a very bright star. Also we over-plot the footprint of a mosaic of 5 WFC/ACS fields available from the archive, that we used to cross check the astrometry obtained with WFI@2.2m (cf. Sect. 6). This image gives a feel for the enormous amount of sky wide-field imagers can cover in a single exposure. ( Top-right) a representative sub-set of the image, which show the homogeneous distribution of stars in Baade's window. ( Bottom-left) zoom-in of 1000 $\;\times\;$ 1000 pixels around the globular cluster NGC 6528. ( Bottom-right) zoom-in of the globular cluster NGC 6522.

Open with DEXTER

The reason for choosing this detector is that the WFI@2.2m camera was one of the first wide field cameras to become available to astronomers. It began its operation in 1999, and today there are in the public archive many multiple-epoch images of star cluster fields, with baselines up to 6 years.

There are clearly some things that only HST can do, namely astrometry and photometry of extremely faint stars or stars in crowded regions, where there truly is no substitute for high resolution. Nevertheless, we show here that many scientifically interesting projects can now be carried out with ground-based imagers, such as the WFI@2.2m (discussed here) or the OMEGACAM (coming on-line in 2007).

In this paper, we will go through the steps that are necessary to get good astrometry with wide-field detectors. In Sect. 2, we will describe the database used for this work. Section 3 will describe the method used to construct accurate PSFs. Section 4 will give details on the fitting procedure, including neighbor subtraction. In Sect. 5 we will discuss the distortion correction, and its stability over time. Section 6 will compare the astrometry obtained with WFI@2.2m with astrometry obtained from HST archive images of the same region. Section 7 will describe the local-transformation approach that allows us to minimize the effects of residuals in the distortion corrections. In Sect. 8 we will apply the method to the case of the two closest globular clusters, namely NGC 6397 and NGC 6121 (M 4). In Sect. 9 we briefly discuss atmospheric effects. Finally, in Sect. 10 we summarize our results, and briefly discuss possible interesting projects for the future.

2 Observations

In this work, we use images for four different fields collected with the WFI@2.2m; details of the data can be found in Table 1.

The first field is located in Baade's Window (see Fig. 2). Although the field contains two small globular clusters (NGC 6522 and NGC 6528), most of the field has a smooth, uniform distribution of Galactic bulge stars. The stars of interest (the $\sim$ 2 mag below saturation in a 60 s V exposure), are typically separated by a few arcseconds, so that there are many in each field, but they are in general well enough separated to allow accurate positions. We took images of this field with a range of offsets so that we could measure the distortion in the detector and evaluate its stability (cf. Sect. 5).

The second field is centered on the open cluster NGC 2477. Several long exposures are taken in almost identical conditions (comparable seeing, no large offsets, identical exposure times). For this reason, and thanks to the ideal stellar density, it has been possible to estimate directly the internal photometric and astrometric errors of our method from analysis of the residuals (cf. Sect. 4.1).

The third field used in this work is centered on NGC 6397. The images were taken at two different epochs separated by 3.1 yr. We will use the two epochs to derive proper motions (Sect. 8.1).

The fourth field covers M 4. Images were taken at two different epochs separated by 2.8 yr. Also for this object we will use the two epochs to derive proper motions and distinguish cluster stars from field stars (Sect. 8.2).

In anticipation of the need to reduce the enormous archive of WFI@2.2m data in an automated way, we developed software specifically for this instrument, though the software can be easily adapted to other CCD mosaics, including OMEGACAM. One particular effort we make to deal with the huge images involved in wide-field surveys is that we take care to do all stages of reduction in a short-integer format. This improves read-in and read-out time, and helps enormously with diskspace considerations (256 Mb compared with $\sim$ 60 Mb once gzipped).

3 Derivation of the PSF

Anderson & King (2000) developed a method to obtain high-accuracy astrometry on under-sampled WFPC2 images. A careful removal of all the sources of systematic errors, such as biases introduced by under-sampling, chip-manufacturing defects (see Anderson & King 1999), and the need for an accurate correction for distortion, led us to arrive at what is more or less the state of the art in imaging astrometry from space.

We found in our treatment of HST images that astrometry is even more sensitive to the PSF model than photometry is. This is because to first order, photometric procedures don't really care where the flux is, so long as it is included within the fitting radius (or aperture). Astrometric procedures, on the other hand, key off of exactly how the flux is distributed among the pixels. We therefore require an accurate PSF to compare the observed pixel distribution with the model, in order to extract a position.

Even though the WFI detectors are not undersampled, our positions are still critically dependent on the accuracy of our PSF models. Thankfully, it is much easier to derive PSFs from well-sampled images than from undersampled ones, so that much of the careful work in AK2000 is not required in this regime. In particular, it is possible to derive a PSF from a single image, without reference to a dithered set. This is good news, since thanks to seeing fluctuations, the ground-based PSF cannot be presumed to be stable from exposure to exposure.

3.1 The empirical PSF model

A PSF model simply tells us what fraction of a star's flux should fall in a pixel located at a given offset from the star's center. The PSF is therefore a two-dimensional function $\psi(\Delta x,\Delta y)$ that returns, for a given $(\Delta x,\Delta y)$ , the fraction of light that would fall in a pixel at that offset.

Unlike DAOPHOT (Stetson 1987) and other photometry routines, our PSF model does not have an analytical-function as a backbone. Rather, we represent the PSF entirely by an empirical grid, a simple look-up table. The entire PSF is represented by an array of 201 $\;\times\;$ 201 grid points. This PSF grid is super-sampled by a factor of 4 with respect to the image pixels, so that the PSF model goes out to a radius of about 25 pixels. The central grid point at (101, 101) tells us what fraction of a star's flux would land in the central pixel of a star that is centered on a pixel. The other grid points tell us what flux would fall in pixels at an array of quarter-pixel offsets from the star's center. Of course, stars can land anywhere within a pixel, and not just at quarter-pixel grid points, so we use a bi-cubic spline to interpolate the value of the PSF in between the grid points.

3.2 Finding the PSF by iteration

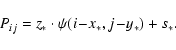
If we have a set of positions and fluxes for a star, we can turn the above equation around to solve for the PSF:

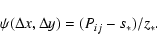
The derivation of an accurate PSF is clearly an iterative procedure. Without a good PSF, we cannot derive good positions and fluxes. Similarly, without good positions and fluxes, we cannot derive an accurate PSF. Thus, our procedure iterates in order to improve both the stellar parameters and the PSF model.

We start with simple centroid positions and aperture-based fluxes. It does not take many iterations to arrive at good models for both the PSF and the stellar parameters. Our iterative procedure here is quite similar to that of AK2000, except that we do not require the second stage of their three-stage iteration. Since our images are well sampled, we do not need to incorporate images taken from other ditherings to remove the star-position/PSF-shape degeneracy inherent in undersampled detectors. This simplifies our reduction procedure significantly, since we can now operate on one exposure at a time.

3.3 Constraints on the PSF

The first constraint we apply is smoothness. Since our detector is well-sampled, the PSF should not change too much from gridpoint to gridpoint. We enforce this by smoothing the PSF with a quadratic smoothing kernel (again, see AK2000). The quadratic kernel fits a quadratic to the gridpoints within the kernel centered on that gridpoint (5 $\;\times\;$ 5 gridpoints, 7 $\;\times$ 7 gridpoints, etc.), then replaces the central value with the value of the quadratic at that point. We experimented and adopted the largest smoothing kernel that was consistent with the star images. (If too much smoothing is done, stars have large residuals at their centers.)

The second constraint we apply is that the PSF has to be centered on the grid. To enforce this, we fit the central 11 $\;\times\;$ 11 pixels of the PSF with a paraboloid, to estimate the apparent center. If this center is not at the center of the grid, then we use bi-cubic interpolation to re-sample the PSF at the locations where the gridpoints should be and replace the PSF with the properly centered model.

The final constraint we apply is normalization. It is nearly impossible to measure all the flux in the PSF. The finite dynamic range of detectors means that stars which are not saturated in their cores are lost in the sky noise beyond about 8 pixels. The saturated stars can be seen well beyond this, but it is hard to determine what fraction of their flux we are seeing, since their central regions are unusable. Our routine does derive a PSF out to 25 pixels using the saturated stars, but it is most accurate within 8 pixels, where it is derived from well-measured bright unsaturated stars. Thus, we normalized the PSF to have a volume of unity within 6 pixels (1.5 arcsec), so that our normalization would not be affected by the uncertainties related to saturation. The WFI@2.2m PSFs typically have 15 percent of their flux beyond this radius, so determining total fluxes will require a simple aperture correction in the calibration process.

3.4 Variability of the PSF with chip position

In the end, we determined that by solving for an array of 15 PSFs in each 2048 $\;\times\;$ 4096-pixel chip (3 across and 5 high), we could capture almost all of the PSF's spatial variability. Our model, then, will feature an independent PSF at each of the locations in Fig. 3.

$\begin{figure} \par\includegraphics[width=8.1cm,clip]{5004f05.eps} \end{figure}$	Figure 3: This figure shows the locations of the 120 fiducial PSFs and the process of interpolation to find a PSF at a particular point on the chip (marked with an $\ast$ ). The dotted lines denote the region of the image used to solve for each PSF.
Open with DEXTER

To construct a model for the PSF in between these fiducial points, we will use simple linear interpolation, in a manner similar to AK2000. To highlight how the PSF changes shape with location in the detector, in Fig. 4 we show the difference of the 120 representative fiducial PSFs and the average PSF across the entire field of view. The PSF comes from one of the U-band Baade's window images. The PSFs are conveniently displayed in order to map their spatial distribution on the detector. Notice how the variations among contiguous PSFs are smooth. The PSFs tend to elongate (mainly due to coma aberration), with the elongation increasing radially as we move out from the principal optical axis (near the center of the detector).

$\begin{figure} \par\includegraphics[width=7.9cm,clip]{5004f06.eps} \end{figure}$	Figure 4: Difference between the local PSF and the average PSF over the entire field. White means more flux in the local PSF than in the average PSF at that location.
Open with DEXTER

It is obvious from Fig. 4 that it would be possible to reparametrize the PSF and reduce the number of degrees of freedom used by taking advantage of the clear radial behavior. But our aim has been to minimize the amount of human intervention required, even at the expense of over-parametrizing the PSFs. (This approach applies to our distortion solution, too). Even though we may use more parameters than necessary, each of our PSFs is still greatly overconstrained, so there is no real advantage in seeking a slightly more efficient parametrization. With our very general parametrization, our routines can operate with a minimum of human oversight.

3.5 Choosing the stars used to model the PSF

The PSF-finding program is designed to require minimal interaction with the user. The user supplies the program with some simple finding criteria (minimum flux, minimum separation from brighter stars), and the program searches the image to find stars that meet the criteria. The program then reports how many stars are available for each PSF-region. If there are more than 150 good stars in a single region (see Fig. 3), then the routine chooses the 150 best stars, based on brightness and isolation from neighbors.

In sparse fields (or equivalently, short exposures), there are not always enough bright stars to use in PSF construction, and we often must make a compromise between the number of stars available to define the PSF and the level of PSF variability we can practically model. For this reason, the program has been set up to allow the determination of: $(3\times5)\times8$ (=120 PSFs), $(3\times3)\times8$ (=72 PSFs), $(2\times3)\times8$ (=48 PSFs), $(2\times2)\times8$ (=24 PSFs), or $(1)\times8$ (=8 PSFs) to cover the detector. Based on the number of bright stars available, the user must determine how finely to model the PSF's spatial variability.

3.6 PSF storage

3.7 Planning for the future

4 Fitting star positions and flux

$\begin{figure} \par\begin{tabular}{cccc} \fbox{\includegraphics[width=3.5cm]{500... ...fbox{\includegraphics[width=3.5cm]{5004f17.eps}} & \\ \end{tabular}\end{figure}$

Figure 5: An image subset of 70 $\;\times\;$ 70 pixels ( ${\sim } 17'' \times 17''$ ) is shown through the various steps of star fitting. On the top, the sky-subtracted image (corrected for CRs and bad pixels) through the iteration 1, 2, 3, and 7. At each step the new difference image (between the corrected and the model images) is calculated using the new detected objects, and the improved positions and fluxes of sources detected in the previous iteration. The star finding at each step is done on the corresponding convolved star-subtracted images (shown in middle line of figures). For comparison, in the bottom are shown, the raw image, the finding chart of the final list of detected objects, and the same area imaged with WFC/ACS HST (data set name j8kce1atq_drz).

Open with DEXTER

Once an array of PSF models has been generated for an image, we can use it to measure all the stars in the image. We designed a simple iterative procedure that seems to work quite well for images with sparse to moderate crowding. Once again, the routine is designed to have minimal input from users. The user simply inputs what the faintest findable star should be (above sky) and how close it can be to brighter neighbors, and the program finds and measures all stars that fit these criteria. Our goal is not to give a line-by-line account here of what the program does, rather we will simply give the general procedure.

Fitting overlapping stellar profiles is clearly an iterative procedure. The routine keeps in memory four images: (1) the raw image, sky-subtracted, and corrected for cosmic rays (CRs) and bad pixels/columns, (2) the model image, which has a properly scaled PSF for each found star, (3) the difference image, and (4) the convolved image.

Our first iteration begins by finding all the saturated stars and measuring fluxes for them. It also identifies all peaks that are 10 times brighter than the threshold and 10 pixels farther than any brighter source, and adds them to the star list. It measures fluxes for all these stars using the PSF, then subtracts the unsaturated stars from the image. It does not subtract the saturated stars, since the PSF is generally not reliable out in the wings, and that would make the subtracted image less useful than the original image. The program then takes this subtracted image and convolves it with the PSF. This allows the signal from fainter stars to be optimally enhanced for finding them. We also generate a model image which contains an estimate of the flux from all the stars, saturated and unsaturated.

The second iteration then finds stars in the convolved image, lowering the threshold to 5 $\times$ the minimum and insisting again that they be isolated from other unfound stars. Any stars found in this iteration must be at least $\sim$ 15% brighter than the model image, so that we can be sure of their authenticity. This requirement prevents us from finding very faint stars next to very bright stars, but this is not a severe limitation, as we could not find such stars reliably anyway. The benefit of the requirement is that we do not end up identifying a lot of undocumented PSF features as stars.

After this second wave of finding, we re-solve for all the stars, using for each star an image that has all its neighbors subtracted. This way, the fits for two nearby stars can quickly converge upon an accurate position and flux for each. We repeat these iterations, lowering the threshold, and incorporating fainter and fainter stars with each iteration.

In Fig. 5 we show the various steps of the fitting procedure. In practice, we often have to run the routine once or so to determine how faint the final threshold should be in order to find and measure the faintest believable stars.

4.1 Direct estimate of internal errors

We used multiple observations of the Galactic open cluster NGC 2477 (6 images of 900s in filter $I_{\char93 853}$ ) to provide a direct estimate of the internal errors. We could not use the Baade's window data-set because of the large offsets (residuals in the geometrical distortion would mask our internal errors).

In the top panel of Fig. 6 we show the rms of the photometry as function of the instrumental magnitude. A horizontal line shows that for well-exposed stars, we attain a single-exposure internal precision of 0.005 mag. In the bottom panel, we show the behavior of the rms in position, taken as the sum in quadrature of the rms along the x, and yaxes of the detectors. That means that the single-exposure precision of the method is ${\sim} 0.04 ~ WFI@2.2m$ pixels, or ${\sim} 10$ mas (i.e. for each coordinate, 0.028 pixels, or 6.7 mas).

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{5004f18.eps} \end{figure}$

Figure 6: Top panel: photometric errors per exposure as a function of the instrumental magnitude defined as $-2.5 \times \log{\rm DN}$ (DN = Digital Numbers), obtained from the 6 archive images in filter $I_{\char93 853}$ , with small off-sets, and identical exposure times. Each star has been measured at least 6 times. In this data set saturation sets in at $\sim$ -14.3, and is indicated by a vertical dotted line. A horizontal line shows the average rms for well-exposed stars (0.005 mag). Bottom panel: for the same data set, astrometric rms both in WFI@2.2m pixels and in mas. Again the dotted vertical line marks the beginning of saturation, and a horizontal line shows the average astrometric rms for well-exposed stars 0.04 pixels, i.e. $\sim$ 10 mas (meaning $\sim$ 6.7 mas for each coordinate). Note how positions are well defined also for moderately saturated stars ( $\sim$ 35 mas).

Open with DEXTER

5 Geometric distortion correction

As we mentioned in the introduction, there is a lot of astrometric potential for these new wide-field ground-based images. Although they can not even approach HST precision, they can cover an enormous field of view, and can go much deeper with a better accuracy than the previous technology of photographic plates. We saw in the previous section that we can measure a reasonably bright star with a precision of about $\sim$ 0.03 pixel ( $\sim$ 7 mas) in a single exposure. These tests involved a local, differential measurement. We still need to determine what limitations distortion will place on our ability to measure positions in a more global sense. In particular, we need to ask: (1) how well we can measure the distortion solution? and (2) how stable the solution is. The answers to these questions will determine what kinds of astrometric projects we can undertake.

When trying to measure the distortion in an instrument, one would ideally like to have reference to a list of the positions of stars in the field in some absolute and accurate system, so that after allowing for a linear transformation, we can see the distortion in our detector by virtue of the position residuals. Unfortunately, we are not aware of the existence of any astrometric standard field that would allow a direct calibration of the distortion in WFI@2.2m. One might be able to use Hipparcos or the USNO B survey to calibrate the most global terms, but to fully calibrate WFI@2.2m, we would really need a field that is at least 0.5 degree on a side, with tens of thousands of stars, each of which should have a position good to better than 5 mas.

We note that Platais et al. (2006) proposed constructing such a frame, and are now in the process of taking observations for it (private communication). Until such a calibrated field is available, we must undertake a self-calibration, similar to what we have done for HST(Anderson & King 2003b). This involves imaging a nicely dense field with a range of telescope offsets. Since we know that the stars have not moved much in the course of the night, we can use their apparent positions in each of our images to solve for the distortion in the detector.

So, to do this, as a back-up program during a non-photometric night, we took several images of the Galactic Bulge, in Baade's Window. We chose this field because it is fairly homogeneous in both spatial and star luminosity distributions, and the crowding is not excessive. This is true across the entire wide field of view (see Fig. 2), with the exception of the cores of two angularly small globular clusters. The exposure time of these images was optimized in order to obtain the necessary number of stars with the needed S/N.

We took 30 images in the V filter, with large dithers following the pattern shown in Fig. 7. The idea was to map the same patch of sky into as many different places on the 8-chip detector as possible. Unfortunately, the focus was unstable, and we had to adjust it from observation to observation. Since we needed to take a large number of images, we did not want to stop to concentrate on the focus, so we simply made small adjustments to the focus between observations based on the FWHM of the proceeding images. This focus variation may well have an effect on the distortion solution, but that is part of what we are trying to study here.

5.1 Finding the average distortion solution

The procedure we followed to derive the correction for geometric distortion is an iterative one. We first parametrized the distortion solution by a look-up table of corrections for each chip that covered each 2048 $\;\times\;$ 4096-pixel chip, sampling every 256 pixels. This resulted in a 9 $\;\times\;$ 17 element array of corrections for each chip. The distortion-corrected position for a star will then be the meta-image position plus the interpolated value from the distortion-correction table:

Before solving for the distortion, we first measured positions and fluxes for all the stars in all the images and cross-identified them using a master list. The challenge in finding an optimal distortion solution is then to find the set of table values which will allow the various star lists to be transformed into each other using only linear transformations. So, we are looking for a single set of table values that can be applied to all the images to minimize the non-linear transformation residuals.

Since our aim is differential astrometry and not absolute astrometry, we use general 6-parameter linear transformations. These allow for offset, rotation, and scale changes, but also allow for the axes to be non-perpendicular and differently scaled. These general linear transformations implicitly remove the first-order atmospheric-refraction terms.

The transformation residuals are constructed as follows. For each pair of images i and j, we find all the stars that are common to both star lists. These N common stars give us N pairs of position associations: (x_i,y_i;x_j,y_j). We first correct these positions using the current best distortion solution, so we have (X_i,Y_i;X_j,Y_j) for each star. We then find the best linear transformation between the frame by least squares.

$\begin{figure} \par\begin{tabular}{cc} \includegraphics[width=5.8cm]{5004f19.eps} &\includegraphics[width=5.8cm]{5004f20.eps}\\ \end{tabular}\end{figure}$	Figure 7: ( Left) dither pattern of the 30 images taken in the Baade's window, in filter V. The coordinates, are in unit of pixels, and referred to the master frame. ( Right) depth-of-coverage map for the same 30 images.
Open with DEXTER

This allows us to compute residuals. For each of the N stars in image i, we have $(x_i,y_i,\delta x_i,\delta y_i)$ , where $\delta x_j$ and $\delta y_j$ correspond to the difference between where the star was found in image i and where its position in image j says it should be in image i (based on the linear transformation). We also have a similar residual for image j, $(x_j,y_j,\delta x_j,\delta y_j)$ . We generate such residuals for each star common to each image pair. This results in many tens of millions of residuals.

Each residual has several contributions: the distortion error in one image, the distortion error in the comparison image, and the inevitable measurement error. If we examine all the residuals from all image pairs for a particular region of the detector, then the average residual will be indicative of the distortion error at that chip location. The other contributions to the residuals will cancel out. Thus, we examine the residuals about each of the distortion-array grid points to determine how the correction at that grid point should change to better approximate the distortion in the image.

We began the solution with a null correction table. We next examined all the residuals in the vicinity of each grid-point and adjusted the correction at that point by half the recommended adjustment. We then smoothed the distortion table with a 5 $\;\times\;$ 5 quadratic smoothing kernel to ensure that our correction table would be smoothly varying. At the end of the iterations we verified that this smoothing did not compromise our solution.

Once we have an initial estimate for the distortion-correction array, we solve once again for the residuals, but this time we include the correction in the computation of the residuals. The residuals get smaller, and now reflect the errors in the distortion solution. We repeat this several times until we converge on a final average solution for the image set. Convergence is reached when the iteration-to-iteration adjustment for the distortion-correction array is less than 0.005 pixel.

The table of distortion corrections is shown graphically in Fig. 8, where the corrections have been exaggerated by a factor of 100. Note that the upper left chip is significantly rotated with respect to the others.

5.2 Stability of the geometrical correction

Comparing two different epochs, separated by $\sim$ 3 years, we find that the geometric distortion can vary up to 0.4 pixel, or $\sim$ 100 mas. Of course, since the 2.2 m ESO/MPI telescope is not fully dedicated to WFI@2.2m, and other instruments can be mounted on the same telescope, manipulation of the camera can easily result in a large variation of the geometrical distortion. In particular we know from other data sets that a rotation of the whole camera by up to few degrees may be present from run to run.

We also found in our data set that filters: V, B, I and $I_{\char93 853}$ share the same distortion solutions down to $\sim$ 0.4 pixels. Filter U is an exception, here the differences may rise up to 5 pixels close to the edges of the field of view. In the present work we are not using the U filter for astrometry. We will calibrate the geometric solution in this filter when a better data-set becomes available.

Thankfully, our proper-motion membership measurements do not require us to know the distortion solution perfectly. We can minimize the impact of distortion errors by using local transformations, which we discuss in Sect. 7.

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{5004f21.eps} \end{figure}$	Figure 8: Map of the geometrical distortion presented in this paper. The corrections are exaggerated by a factor of 100.
Open with DEXTER

6 Comparison with HST

Although the ACS/WFC field of view is only $202'' \times 202''$ , which is just $\sim$ 1% that of the WFI@2.2m, we can still use HSTobservations as a cross check on our measurement precision and distortion correction.

As luck would have it, HST happened to observe the same Baade's window field as we have been analyzing here within a few days of our observations (GO-9690). With the typical motion of a bulge star being $\sim$ 3 mas/yr (Bedin et al. 2003b; Kuijken & Rich 2002), we can assume that the stars are all in the same place, and treat the WFC images as a perfect reference frame against which we can compare our reductions. The footprint of this 5 field WFC/ACS mosaic is superimposed on one WFI image in Fig. 2.

We reduced the WFC images as described in Bedin et al. (2005b) and tied them together, obtaining a huge distortion-free frame covering over 50 contiguous square arcminutes with a global precision of about 1 mas (see Anderson & King 2006). This represents about 5% of the WFI@2.2m field of view.

So, to compare against the HST frame, we cross-identified the stars from our average frame in the previous section with the stars in the HST list. We then transformed the WFI@2.2m measurements into the HST frame using a global linear transformation to construct a measurement residual for each star. Since the HST positions are much better measured than those on ground-based images, these residuals will provide a fundamental test for the WFI@2.2mastrometry.

Figure 9 shows the residuals. In the 4 boxes on the left we show the behavior of the residuals in x and y as function of both the coordinates. In the top right panel we show the spatial distribution of the stars on the WFC/ACS HST-mosaic master frame. Note that there are gaps, which are caused by the fact that we required stars to be detected in 18 out of the 30 V images; the dither pattern ended up placing the same star in the gap for many exposures. The bottom right panel shows the distribution of the residuals.

The fact that the solution appears to get worse over larger distances is consistent with our finding in the previous section that the solution is not stable at the 0.2 pixel level (50 mas), and that most of the variation comes from low-order terms which are worse at the edges. This independent test shows that over distances of 5' or so, an average frame produced with our corrections is accurate to much better than 20 mas ( $\sim$ 0.08 WFI@2.2m pixel). However, this figure and Fig. 6 show that we can clearly measure stars with random errors of less than 10 mas (i.e. 0.04 pixel), so we will have to find some way to minimize these global errors. Local transformations will provide that means.

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{5004f22.eps} \end{figure}$

Figure 9: Left panels: we show the residuals in the distortion solution for y and x vs. dx and dy. Note that residuals are smaller than 20 mas in the common area. Top right: spatial distribution of stars which have measured positions in both the HST and WFI@2.2m data base (one WFC/HST pixel is 50 mas). Bottom right: residuals of positions measured in the WFI@2.2m images and transformed into the HST master frame to cross-check the solutions.

Open with DEXTER

7 Local-transformation approach

7.1 The reference-frame problem

We saw in the previous section that the distortion is not stable at the level of our intrinsic astrometric accuracy ( $\sim$ 0.03 pixel, or $\sim$ 7 mas, in each coordinate). This means that if we want to do high-precision astrometry with our images, we need to find a way to minimize the effect of uncorrected distortion. This led us to investigate a local approach: differential astrometry.

If we want to measure how a star has moved from one epoch to another, we always need to have a frame of reference, in which we can compute a position at one epoch and a position at the other epoch, and a resulting displacement. Now, we do not require an absolute frame of reference here. There are very few stars in a typical field with absolute positions and motions that are known to a useful accuracy.

Thus, our reference frames will necessarily be relative. By this we mean that we will measure our motions with respect to something in our field. We could just use all the stars as a reference and our motions would be with respect to the average motion of all the stars. Typically, however, we will pick a particular population and set its motion to zero and measure motions relative to that population. Since cluster stars tend to have less internal dispersion than the field stars, it is natural to use the cluster as the reference. We will thus identify the obvious cluster-member stars (either by location in the CMD, or iteratively by the motion itself, or both), and use them as the basis for the transformation.

Each star's motion, then, will be measured with respect to the bulk motion of the cluster. Cluster-member stars will by construction have no motion on average, but if our measurements are precise enough to resolve the cluster dispersion, this dispersion will show up as residuals from the average. In the outskirts of clusters, the member density is often extremely low. In these regions, there may not be enough members in each chip to serve as reference stars. Thus, it may be necessary to base the transformations on the non-member stars. In this case, the cluster may show up as a concentration in the motion diagram that is not necessarily at the origin. But this was not necessary for the the present work; even in the outskirts of the clusters there were plenty of member stars to use as reference stars.

We saw in the previous section that all the frames of our images may contain some uncorrected distortion, so we will not have access to a flat global reference frame at any epoch. Rather we have a set of frames, one for each image in each epoch. Each frame has been corrected for distortion as well as possible, but it will invariably have some residual distortion. This residual distortion tends to be of a global nature, in that we can compare nearby stars more accurately than we can compare stars that are farther apart. Thus, if we confine our comparisons to a small region about each star, we can minimize the effects of distortion errors.

In images with HST, the distortion errors are small enough that we can generally define a decent global reference frame and use local transformations to improve positions in this frame. With WFI@2.2m, the distortion errors are larger, and it is more problematic to generate an accurate master frame. For this reason, we decided to treat each frame independently and compute a displacement for each star for each pair of frames. If we have (say) 10 frames in the first epoch and 9 frames in second epoch, this gives us 90 estimates of the inter-epoch displacement. These estimates are not all statistically independent of each other, but simple statistics can tell us how to combine them and estimate the error in the average.

So, there are two steps in our construction of proper motions. The first step is measuring a displacement between each image pair. The second step is combining the many measurements in order to obtain an average displacement from one epoch to another.

7.2 Step 1: measuring displacements between a pair of images

Since we know that the WFI@2.2m frames suffer a distortion error that increases over larger distances, we can minimize the effect of uncorrected distortion on our displacements if we measure the displacements using local transformations. Whereas global transformations use all the stars to compute a single linear transformation between two frames, a separate local transformation will have to be computed for each star we wish to transform from Frame 2 to Frame 1.

We will compute this transformation using a local subset of stars. To do this, we find the closest 55 reference stars to the Frame 1 position, choosing only stars in the same chip as the star in both images. The positions of these stars in both frames give us 55 associations, positions in one image that correspond to the same position in another image. We can use these associations to define a least-squares linear transformation from one frame to the other. We are careful not to use a star in its own transformation, as that would introduce a bias in its displacement (the bias would reduce the true displacement by 1/55).

Figure 10 shows how the positions of reference stars in two frames can allow us to define a transformation that maps the coordinate system of one frame into that of another, so that we can transform a position measured in one frame into that of the other. For clarity, in this figure we only show a few reference stars. In our transformations, we use 55 neighbors.

Now, not all of these stars are as good as the others at specifying this transformation. For one, even though we chose our reference stars to be members based on their location in the CMD, some of them may not be moving with the reference frame, so we automatically reject all stars that are not moving with the "reference population''. There are also some stars that may be poorly measured in one of the frames, or may have an anomalous motion. We do not want these stars to bias our transformation, so we iteratively reject the 10 stars that have the largest transformation residuals.

Once we have the 45 best local stars, they will define a transformation that will allow us to transform (x2_n,y2_n) into the first frame. We can then compute a displacement trivially. This displacement, divided by the time baseline, provides one estimate for the proper motion. This estimate is based solely on positions of stars in the two images being compared.

$\begin{figure} \par\includegraphics[width=8.3cm,clip]{5004f23.eps} \end{figure}$

Figure 10: Visualization of the local-transformation approach. Consider Frame1 and Frame2, observing the same stars (indicated by $\times$ s) but with different orientation and shift. We are trying to transform the position of the star $\ast$ measured in Frame2 into Frame1. In the local approach only the closest stars (highlighted with $\circ$ ) are used to define the 6 parameter linear transformations.

Open with DEXTER

7.3 Step 2: combining the measurements from all pairs

Using the technique in the previous section, we can compute a locally measured displacement for each star for each inter-epoch image pair: $(\Delta x_{ij,n},\Delta y_{ij,n})$ , where i is a first-epoch image and j is a second-epoch image. If there are $\mathcal{I}$ first-epoch images and $\mathcal{J}$ second-epoch images, then we have $\mathcal{I} \times \mathcal{J}$ measured displacements for each star. These displacements are not statistically independent, since each first-epoch image i uses the same $\mathcal{J}$ second-epoch images to construct its displacements.

If we can assume that all the observations are good, then we can take a simple average of these displacement measurements. This average is the best estimate for the inter-epoch displacement. Determining the error in this is trickier.

To estimate the error in our displacemets, we need to estimate the error in each first and second epoch position. We compute intra-epoch displacements in a similar manner to the above inter-epoch displacements by taking all pairs of images from the same epoch. The rms of these displacements (the average will be zero by definition) will give us an estimate of the accuracy of each individual measurement for each epoch, $\sigma_{x_1}$ and $\sigma_{x_2}$ . The error in the average epoch 1 position from this would then be: $\sigma_{\bar{x1}} = \sigma_{x_1} / \sqrt{\mathcal{I}}$ and the error in the epoch 2 position $\sigma_{\bar{x2}} = \sigma_{x_2}/\sqrt{\mathcal{J}}$ . The error in the difference would then be:

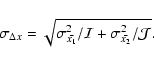
We can also use the intra-epoch analysis to determine if any of the measurements from an epoch are inconsistent with the others. We can look at all the residuals for image i, and if there is one much larger than $\sigma_{x1}$ , then we can reject this observation, and recompute this with $\mathcal{I}-1$ first-epoch measurements. This will lead to a more robust average displacement.

We note that in many projects, we will not need to know the errors of our motion measurements precisely. It is often clear from the diagram itself that we have effected a near-perfect separation between cluster and field, and a precise understanding of the errors is unnecessary. When we are trying to measure internal motions (dispersions), then a proper understanding of the errors will be crucial.

Also, there are some data sets that will have more than two epochs of observation. We can use the above techniques to compute a displacement for each star for each pair of epochs. We can then use a similar approach to combine these displacements into a single proper motion.

$\begin{figure} \par\includegraphics[width=15.2cm,clip]{5004f24.eps} \end{figure}$

Figure 11: ( Top panels) vector point diagrams of displacements of stars in units of WFI@2.2m pixels (238 mas/pixel) after 3.1 years. Since all the reference stars were cluster members, the zero point of the motion is the mean motion of the cluster stars. (Bottom panels) instrumental color magnitude diagrams. The magnitude is calculated as $-2.5 \log{\rm DN}$ , where DN is the total digital counts above the local sky for the considered stars. ( Left) the entire sample; ( center) stars with the same proper motion (within 0.05 pixels) as the MS stars, i.e. with proper motions smaller than 3.8 mas/yr. ( Right) the stars that fell in the bulk of the field distribution. All these plot shows only stars with rms in positions inferior to 0.075 pixels in each coordinate.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=15.1cm,clip]{5004f25.eps} \end{figure}$

Figure 12: Left: color-magnitude diagram for all the stars with positional rms less than 0.05 pixels. Middle: vector point diagrams for the same stars in the corresponding magnitude intervals. A circle in each plot shows the adopted membership criterion for that magnitude interval: from top to bottom: 0.050, 0.055, 0.065, 0.075, and 0.085 pixel in 3 years (i.e. 3.8, 4.2, 5.0, 5.8, 6.5 mas/yr). Note that the proper motions have been corrected for DCR as described in Sect. 9. Right: color-magnitude diagram for the stars assumed to be members.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=14.5cm,clip]{5004f26.eps} \end{figure}$	Figure 13: Additional color-magnitude and color-color diagrams from NGC 6397 WFI reductions and the proper-motion selection from the previous figures.
Open with DEXTER

8 Application

For these reasons, these two clusters are ideal targets to illustrate what can be done with wide field ground-based astrometry. We should note that these images were not taken with astrometry in mind. An ideal astrometric data set would have multiple observations of the same field with a large number of dithers at each epoch, so that we can randomize any distortion errors and improve our random measurement errors by $\sqrt{N_{\rm obs}}$ . These observations were taken with very little dithering, so in some sense, they represent what can be done with the typical archival data set. A properly dithered set at one (or preferably both) epochs would allow to optimize the astrometric measurements.

8.1 NGC 6397

Table 1 lists the data available for NGC 6397. We reduced the images for all four filters (U, B, V, and I), but only use the B and V images for proper-motion analysis. The time baseline is a little over three years.

The first thing to do is determine which stars we will use in the transformations. Since we have multi-color observations, we can use the CMD to select stars that are likely cluster members. We selected stars along the main sequence and red giant branch (RGB), leaving out a few cluster stars (such as blue stragglers or horizontal-branch stars), a fact that will not hamper our results. Also, including a few field stars that happen to lie on the cluster sequence will not affect our measurements, thanks to the rejection criteria in our local transformations.

We started with a list of probable members and used their positions in the images of both epochs to transform (via local transformations) the position of every star in each second-epoch image into the frame of the first-epoch image. We then averaged these displacements as discussed above to arrive at a displacement for each star. In this way, we obtained a set of diagrams similar to those plotted in Fig. 11, which shows a vector-point proper motion diagram, and the members and non-members selection criteria with the resulting CMDs. We then iterated one more time, using as cluster members only those stars that (a) satisfy the above CMD criterion and (b) have a cluster-like motion. This gives us our final motions, which are shown in Fig. 11.

Figure 11 shows the results in an analogous form to the Fig. 1 presented by King et al. (1998) for space-based observations of the same cluster (for comparison, in that work the time base-line was 2.7 years). The cluster-field separation here is nearly as good as the one achieved with HST with the same baseline. Of course we do not go nearly as faint here, but we cover a larger area.

In Fig. 11 we drew the circles which isolate the cluster and field stars by eye. We defined as a cluster member a stars which lies within 0.05 pixels (i.e. 3.8 mas/yr) from the origin of the proper motion axes. The radius has been chosen as the best compromise between losing members with poor proper motions measurements, and including field objects. The internal velocity dispersion of the stars in NGC 6397 is expected to be about 5 km s^-1, or 0.5 mas/yr at the distance of $\sim$ 2 kpc. This should actually be measurable from the ground with a 10-year baseline, or alternately more observations at each epoch.

Since the fainter stars are generally less well measured, we often draw a more generous circle for them. Figure 12 illustrates this. (The proper motions in this figure have been corrected for differential chromatic refraction effects as described in Sect. 9.)

The success of the separation is immediately evident. The relative average motion of the field with respect to the members is $\sim$ 14 mas/yr. This is not the absolute proper motion of the cluster, but only the motion relative to the bulk motion of the field. To get an absolute motion we should either measure the cluster proper motion with respect to background galaxies, or the field proper motion with respect to background galaxies.

Note how the membership is well established even for saturated stars whose instrumental magnitudes are brighter than $V\simeq-14.5$ . Instrumental magnitude is defined here as $-2.5\times \log{DN}$ (Digital Numbers). With our seeing, the central pixel contains no more than 8 percent of the light, and saturation starts at $\sim$ 55 000 DNs. Therefore, saturation begins at an instrumental magnitude of ${\sim}{-}14.5$ [ ${=} {-}2.5 \log{(55~000/0.08)}$ ], for both B, and V. Since our astrometry is done locally, and we need a dense network of reasonably bright stars, it is hard to use the short exposures in the astrometric analysis. However, we can use them easily for the photometry, so for the saturated stars we show the position in the CMD from the short exposures (with a zero-point to match the long exposures) but adopt the astrometry from the deep exposures. (In the next section, we will see that image-motion can significantly affect astrometry in short exposures.)

In Fig. 13 we show how proper motions can be used to clean-up other classical diagrams used in the analysis of stellar populations. The top panels show the color-color (U-B) vs. (B-V)diagram, the middle panels, the color-magnitude diagram with the largest color base-line U vs. (U-I), and finally on the bottom the reddest color-magnitude diagram, the I vs. (V-I).

8.2 M 4 (NGC 6121)

The same exercise has been repeated for the case of M 4 (NGC 6121). In this case, the time base-line is just 2.8 years (see Table 1). The separation based on the proper motion is slightly worse than in the case of NGC 6397, mainly because of worse-than-average seeing (which also affects the photometry). Differential reddening may also be responsible for some of the color broadening. Nevertheless, even with a smaller baseline and poor seeing, we can still successfully separate field from cluster stars (cf. Figs. 14, and 15). The adopted radius for the membership circle is of 0.1 pixels, corresponding to a proper motion of 8.5 mas/yr.

$\begin{figure} \par\includegraphics[width=15.2cm,clip]{5004f27.eps} \end{figure}$	Figure 14: As in Fig. 11 but for M 4. Stars with the same proper motion of the MS stars within 0.08 pixels (2.8 year baseline), are considered members (i.e. the circle centered in the origin includes stars with proper motions smaller than 6.8 mas/yr). All these plots show only stars with rms errors in positions smaller than 0.05 pixels in each coordinate.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=15.4cm,clip]{5004f28.eps} \end{figure}$	Figure 15: As in Fig. 12 but for M 4. A circle in each plot shows the adopted membership criterion for that magnitude interval: from top to bottom: 0.1, 0.1, 0.065, 0.1, and 0.1 pixels.
Open with DEXTER

9 Atmospheric effects

The atmosphere adds several complications to our analysis that we do not have to deal with for HST. The obvious complication is the seeing, which limits our ability to resolve stars and measure precise positions, and makes the PSF change from image to image. This is a random effect, but there are also systematic effects such as: image motion due to isoplanatic patches and differential chromatic refraction.

We must postpone to a future paper of this series a more comprehensive study of the atmospheric effects, when a better data-base will be available. The images here are too few, and taken at a limited range of airmasses. In this section, we will present results from a few tests, to quantify biases and give, a posteriori, some simple corrections.

9.1 Image motion

One of the atmospheric effects we should be aware of is image motion. Atmospheric turbulence introduces perturbations at different scales for different integration times. If we take very short "speckle'' images of a small field, we can get better resolution at the cost of fewer photons. This is because all of the photons go through essentially the same patch of atmosphere and are all shifted the same way by the atmosphere. If longer exposures are taken, the moving packets of air will cause the small field of view to shift up and down together, blurring out the image. As the exposure time goes up, the amplitude of the coherent shifts goes down while the scale of coherence also goes down. Figure 6 in Platais et al. (2002) illustrates the effect of the atmosphere directly.

Lindegren (1980) provides a simple formulation to give us an idea of what we can expect to see from the atmosphere in each coordinate:

9.2 Differential chromatic refraction

The effects of image motion above will average out if we take enough long exposures, but differential chromatic refraction effect is a systematic effect that will not average out with more observations.

Differential chromatic refraction (DCR) causes a shift between the centroid of the blue photons and that of the red photons. This will cause blue stars to have more of a shift towards the zenith than the red stars will have. When we observe through a filter, this effect is lessened, since all of the photons have about the same wavelength, but the details of the spectral distribution through the filter can still affect the centroid of a star's position. This is an effect that will not go away with linear transformations, so we must be careful to calibrate and remove it.

We note that the linearity of CCDs makes it easier to observe and remove this effect. With the old technology of photographic plates, the shape of a star and its apparent centroid depended on its brightness, due to non-linearity effects. Since colors and magnitudes are typically strongly correlated in a CMD, it was difficult to independently remove the atmospheric and photographic effect. The linearity of CCDs allows us to remove much of this degeneracy.

The best way to calibrate the DCR effect is to take multiple observations at a variety of zenith angles, as described in Monet et al. (1992). (See also Stone et al. 2003, and the references therein.) Since the data set examined here was not optimized for calibrated astrometry, we cannot solve for and remove the DCR effect. However, we can still examine it. If there was a difference between the DCR effect at one epoch compared to another, then we would expect the DCR effect to generate an apparent proper motion for blue stars relative to red stars.

In Figs. 16 and 17, we show the proper motion as a function of color for stars on the horizontal and giant branches. Both sets of stars should be moving with the cluster and have no motion relative to the MS stars. Instead, we see that in both clusters there is a color-related displacement of $\sim$ 0.05 pixel ( $\sim$ 12 mas) for M 4, and a displacement of $\sim$ 0.02 pixel ( $\sim$ 5 mas) for NGC 6397.

We made linear fits to the distribution of points shown in Figs. 16 and 17 (upper panels), and removed the DCR contribution from the proper motions. The final, corrected proper motions are shown in Figs. 16 and 17 (bottom right panels). In properly planned observations, this correction can be made for each image, as a function of the airmass of the observations. The correction can also be done all within one epoch, so that we do not need to assume anything about the proper motions.

$\begin{figure} \par\includegraphics[width=7.4cm,clip]{5004f29.eps} \end{figure}$

Figure 16: Bottom-left: in this panel we zoom in the vector point diagram of Fig. 15 for stars in the instrumental B-magnitude between -16 and -14 for NGC 6121 before applying DCR corrections. RGB stars are marked as circles, red HB stars as triangles, and blue HB with squares. Also the average for each group (with error bars) are shown, using a filled symbols. Top: the distribution of displacements as a function of the color is modeled with a linear fit. Bottom-right: the same distribution after the corrections obtained from the linear fit.

Open with DEXTER

10 Conclusion and future applications

In this paper, we have described how the software originally developed by Anderson & King (2000) for high precision relative astrometry and photometry on WFPC2 and ACS HST data has been adapted to ground-based, wide field images from the WFI camera at the ESO 2.2 m telescope. We have also obtained a first approximation solution for the WFI@2.2m geometric distortion, and shown that it is not stable over time. Therefore, to get precise relative proper motions, we need to follow a local-transformation approach, as described in Sect. 7.

As proof of concept, we have applied this new technique on two epochs of data for the two closest Galactic globular clusters: NGC 6121 (M 4) and NGC 6397. The results, though based on data not optimized for high-precision astrometric measurements, are more than encouraging. We have shown that, under average seeing conditions ( ${\sim} 1''$ ) the astrometric precision is of 7 mas in each coordinate, for well exposed stars in a single image, i.e. only $\sim$ 3 (6) times worse than what we are able to obtain with HST using the WFPC2 (WFC/ACS) (which more or less represents the "the state of the art'' in imaging astrometry).

For both clusters, with three-year temporal baseline we have been able to obtain proper-motion measurements that are precise enough to allow a separation between field and cluster stars. We expect to be able to measure the internal proper motions with a precision adequate for stellar dynamics studies with a 10-year baseline and a good number of images at each epoch.

The extension of the AK2000 software to ground-based data makes possible a great number of new projects for the study of the stellar population in Galactic open and globular clusters and their tidal tails, in the Galactic fields, and in nearby galaxies, and represents an important complement to what is presently done with HSTimages. Ground-based facilities are more abundant, allow coverage of much larger fields, and are cheaper and easier to access than HST. HST data are still of fundamental importance for the most crowded regions of star clusters and nearby galaxies.

The forthcoming even-wider-field facilities (e.g. OMEGACAM@VST, VISTA, etc.), and the increased time baseline (when we include archival first-epoch data taken in the mid-90's) will allow further exploitation of this technique here described.

This technique may also be promising in view of the soon-coming multi-conjugated adaptive optics, and non-classical narrow-field astrometric corrections for telescopes larger than 10 meters (Lazorenko & Lazorenko 2004; Lazorenko 2006).

Finally, it is worth mentioning that most of the astrometric and proper-motion measurements on HST and ground-based images are complementary to the data expected from SIM and GAIA. First of all, GAIA is several years away in the future. Realistically, the final catalog will be released not before the end of the second decade of this century, at best. Also the catalog will be limited to magnitudes brighter than $V\sim19$ , and, most importantly, to stars in less crowded regions.

Over the next few years, we will continue to improve these techniques. Specifically, in the next months, we will have WFI@2.2m data for 5 open clusters (60 hours of observing time already scheduled). The new data, properly dithered in order to optimize the astrometric measurements, will allow further improvement of the distortion solution, and more study of atmospheric effects on our astrometry.

$\begin{figure} \par\includegraphics[width=7.6cm,clip]{5004f30.eps} \end{figure}$	Figure 17: As in Fig. 16, but for NGC 6397. This time the stars are the one of the instrumental B-magnitude interval -16--14 of Fig. 12. NGC 6397 has no red HB stars.
Open with DEXTER

Ground-based CCD astrometry with wide field imagers

I. Observations just a few years apart allow decontamination of field objects from members in two globular clusters

1 Introduction

2 Observations

3 Derivation of the PSF

3.1 The empirical PSF model

3.2 Finding the PSF by iteration

3.3 Constraints on the PSF

3.4 Variability of the PSF with chip position

3.5 Choosing the stars used to model the PSF

3.6 PSF storage

3.7 Planning for the future

4 Fitting star positions and flux

4.1 Direct estimate of internal errors

5 Geometric distortion correction

5.1 Finding the average distortion solution

5.2 Stability of the geometrical correction

6 Comparison with HST

7 Local-transformation approach

7.1 The reference-frame problem

7.2 Step 1: measuring displacements between a pair of images

7.3 Step 2: combining the measurements from all pairs

8 Application

8.1 NGC 6397

8.2 M 4 (NGC 6121)

9 Atmospheric effects

9.1 Image motion

9.2 Differential chromatic refraction

10 Conclusion and future applications

References