A&A 454, 609-615 (2006)
DOI: 10.1051/0004-6361:20054792

Modelling chromospheric line profiles in NGC 2808: evidence of mass loss from RGB stars[*]

P. J. D. Mauas1 - C. Cacciari2 - L. Pasquini3


1 - Instituto de Astronomía y Física del Espacio, Buenos Aires, Argentina
2 - INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85749 Garching b. München, Germany

Received 30 December 2005 / Accepted 21 March 2006

Abstract
In this study we test the possibility that the asymmetry in the profiles of the H$\alpha $ and Ca II K lines in red giant stars is due to the presence of an active chromosphere rather than to mass loss. To this end, we compare line profiles computed using relevant model chromospheres to profiles of the H$\alpha $ and Ca II K lines observed in five red giant stars of the globular cluster NGC 2808. The spectra were taken with FLAMES during the science verification, using the UVES mode at high resolution (R=43 000) for the H$\alpha $ line, and GIRAFFE in MEDUSA mode (R=20 000) for the Ca II K line. We find that the observed profiles are better described if a negative (outward) velocity field is included in the model chromospheres. This leads to mass loss rates of a few 10-9 $M_{\odot}$ yr-1, so very close to the requirements of the stellar evolution theory.

Key words: line: profiles - globular clusters: individual: NGC 2808 - stars: atmospheres - stars: mass loss - stars: Population II - techniques: spectroscopic

1 Introduction

It has long been known that the stellar evolution theory requires that some mass ($\sim$0.1-0.2 $M_{\odot}$) be lost by Population II stars during the evolutionary phases preceding the horizontal branch (HB) phase, in order to account for (1) the observed morphologies of the HB in globular clusters (GC), and the maximum luminosity reached by stars on the asymptotic giant branch (Castellani & Renzini 1968; Iben & Rood 1970; Rood 1973; Martinez Roger & Paez 1987; Jorgensen & Thejll 1993; Ferraro et al. 1998; Catelan 2000; Soker et al. 2001), and (2) the pulsational properties of the RR Lyrae variables (Christy 1966; Fusi Pecci et al. 1993; D'Cruz et al. 1996).

Theoretical estimates of mass loss rates at the tip of the red giant branch (RGB) are a few times 10-8 $M_{\odot}$ yr-1 (Fusi Pecci & Renzini 1975, 1976; Renzini 1977). More recently, Mullan & MacDonald (2003) find that the evolution through the "bump'' in the luminosity function of RGB stars might be associated with the onset of a cool massive wind. In a study of RGB stars in the halo of the Milky Way, de Boer (2004) estimates that on average $\sim$0.3 $M_{\odot}$ per star are lost by metal-poor red giants, and would contribute a sizeable fraction of the observed H  I gas falling in from the halo.

As a result, a few tens of solar masses of intracluster matter are expected to be produced in any given GC. This matter should accumulate in the central regions, especially of the more massive clusters, in the absence of sweeping mechanisms between Galactic plane crossings. However, efforts to obtain evidence of intracluster matter have been largely unsuccessful: diffuse gas in GCs was detected only as an upper limit and well below 1 $M_{\odot}$ (Roberts 1988; Smith et al. 1990; Faulkner & Smith 1991; Freire et al. 2001).

Table 1: Physical and atmospheric parameters for the RGB stars in NGC 2808 used for the present study. The temperatures, luminosities, and gravities listed in Cols. 3-5 are derived from the (V-K) colours (see Sect. 2). The expansion velocities and mass loss rates in Cols. 11 and 12 are discussed in Sect. 4.1.

Direct detection of mass loss from individual metal-poor RGB stars, either in the field or in GCs, has been attempted with various observational approaches. Infrared excess, indicative of dusty circumstellar envelopes, has been detected with ISOCAM in $\sim$15% of the globular cluster RGB (or AGB) stars in the $\sim$0.7 mag brightest interval ( $M_{\rm bol} \le -2.5$) (see Origlia et al. 2002, and references therein). Spectroscopic surveys of a few hundred GC red giants (Cohen 1976, 1978, 1979, 1980, 1981; Mallia & Pagel 1978; Peterson 1981, 1982; Cacciari & Freeman 1983; Gratton et al. 1984) revealed H$\alpha $ emission wings in a good fraction of the stars along the uppermost 1.25 mag interval of the RGB. This emission, generally asymmetric and possibly variable on a short-time scale, was initially interpreted as evidence of an extended atmosphere, until Dupree et al. (1984) demonstrated that it could arise naturally in a static stellar chromosphere, in analogy with Reimers' (1975, 1977, 1981) speculations on Population I red giants.

Profile asymmetry and coreshifts of chromospheric lines, such as the Na  I D and Ca II K lines, in addition to H$\alpha $, were then considered as possible indicators of mass motions. Several red giants in GCs were found to exhibit small negative velocity shifts in the cores of these lines (Peterson 1981; Bates et al. 1990, 1993; Dupree et al. 1994; Lyons et al. 1996), as did metal-poor field giants that might be taken as the field counterparts of GC giants (Smith et al. 1992; Dupree & Smith 1995). These coreshifts are all $\le$15 km s-1, i.e. much smaller than the escape velocity from the stellar photosphere ($\sim$50-60 km s-1).

However, in those cases where the Mg II $\lambda$2800 h and k lines were also available for GC RGB or metal-poor field stars (Dupree et al. 1990a, 1990b, 1994; Smith & Dupree 1998), the asymmetries in the Mg  II lines provided, under certain assumptions, some evidence of a stellar wind with a terminal velocity as high as $\sim$50-150 km s-1, exceeding both the stellar photospheric escape velocity and the escape velocity from many cluster cores ($\sim$20-70 km s-1; Webbink 1981). These velocity values, along with appropriate values of stellar radius and chemical abundance, would be consistent with mass loss rates of a few 10-11 to a few 10-9 $M_{\odot}$ yr-1(Dupree et al. 1990b, 1994), leading to a total mass loss of up to $\sim$0.2 $M_{\odot}$ over a time of ${\sim} 2 \times 10^{8}$ yr on the RGB, in general agreement with expectations of the stellar evolution theory.

Further observational evidence of mass outflows from individual metal-poor red giants was provided by Dupree et al. (1992) and Smith et al. (2004) using the He I $\lambda$10830.3 absorption line on five field metal-poor red giants and six RGB stars in the GC M13. This weak line forms higher in the atmosphere than H$\alpha $ or the Ca  II and Mg  II emission cores and is, therefore, a better probe of the outer regions of the atmosphere where the wind begins to accelerate. The study by Smith et al. (2004) has revealed the possible presence of mass outflows in fainter (and hotter) RGB stars than previously monitored by chromospheric lines in the UV and optical ranges.

If we restrict our attention only to studies in the optical range, the most recent study was done by Cacciari et al. (2004, hereafter C04), who used FLAMES (Pasquini et al. 2002) spectra centred on Ca II K, Na  I D, and H$\alpha $ lines of $\sim$100 RGB stars in NGC 2808. Their purpose was to monitor the profiles of these lines along the RGB in search of asymmetries and core shifts, taken to indicate mass motions in the atmospheres. Indeed, a good fraction of the brightest RGB stars was found to show these features, with negative (outward) velocities of $\le$10 km s-1. However, these velocities are quite low and might be accounted for by the presence of local hydrodynamic effects in the chromosphere (Dupree et al. 1984; Smith & Dupree 1988; Dupree & Smith 1995). One could fairly summarise the current status by stating that the long-sought direct evidence of mass loss in Population II RGB stars is still quite elusive.

The purpose of the present study is to compare the observed profiles of the Ca  II K and H$\alpha $ lines in a few RGB stars in the GC NGC 2808 with theoretical profiles from suitable model chromospheres and to verify whether a static chromosphere can account for the observed features or a velocity field needs to be considered. In the latter case, we estimate quantitatively if the adopted field is consistent with the amount of mass loss expected from theory.

In Sects. 2 and 3 we describe the data and the models we have used, in Sect. 4 the results of our analysis are discussed, and Sect. 5 contains a summary of this work and our conclusions.

2 The data

We list in Table 1 the five RGB stars of NGC 2808 selected from the C04 sample for the present analysis. They were selected among the brightest and coolest stars with clear evidence of emission in the H$\alpha $ wings and at the bottom of the Ca  II K absorption core (K2 reversal). The temperatures and luminosities listed in Table 1 are derived from the (V-K) colours, and the gravities assume a mass of 0.85 $M_{\odot}$ for these stars (see C04 and Carretta et al. 2004, for more details). Columns 6 and 8 show the shifts with respect to photospheric lines of the H$\alpha $ and Ca  II K3 absorption line cores, respectively. Columns 7 and 9 show the asymmetry of the H$\alpha $ and K2 emission using the ratio B/R of the respective blue and red wings. As found in all previous studies, the emission wings show the characteristic signature of downflow (i.e. B/R > 1) about as often as that of outflow (B/R < 1), suggesting that the emission could be produced in a locally non-static chromosphere. The consistently negative shifts of the absorption cores should be better indicators of a net outflow; however, the low velocity of these features might also be compatible with normal chromospheric activity.

3 The model chromospheres

For the photospheric temperature distribution we used the model computed by Kurucz (2005) for log(g) = 0.5 and $T_{\rm eff}=4000$ K. Although there are differences in these parameters for the stars in our sample, this model is the closest one in all cases (except perhaps for star 47606, for which the model with $T_{\rm eff}=3750$ K is marginally closer).

On this model, we superimposed a chromospheric rise, with T increasing linearly with negative log(m). In this way, our chromospheric models depend on three free parameters: i) the column mass log(m) where the chromosphere starts, i.e. where the temperature distribution departs from Kurucz' model and where, therefore, the temperature has its minimum value; ii) the slope of the chromospheric T vs. log(m) distribution; and iii) the maximum temperature to which the chromospheric rise extends, which relates directly to the value of log(m) where the chromosphere ends. Upon this chromosphere, we added a "transition region'' where the temperature rises abruptly up to $1.5 \times 10^5$ K, to assure convergence of the calculations. The structure of this "transition region'' has no influence on the computed profiles. As a matter of fact, the computed profiles are unaffected by the structure of the regions where the temperature is higher than $1. \times 10^4$ K, as we see below. Examples of the different models we computed are shown in Fig. 1.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4792f1.ps} \end{figure} Figure 1: Examples of our chromospheric models. The thick line is Kurucz' model for $\log(g) = 0.5$ and $T_{\rm eff}=4000$ K. Different models are shown with different line types for clarity.
Open with DEXTER

For every T vs. log(m) distribution, we solved the non-LTE radiative transfer and the statistical and hydrostatic equilibrium equations, using the program Pandora (Avrett & Loeser 1984). Assuming a gravity log(g) = 0.5, a turbulent velocity varying from 2 to 20 km s-1, and a metallicity [Fe/H] = -1.14 with all elements scaled solar, we self-consistently computed non-LTE populations for 10 levels of H (for details on the atomic models, see Falchi & Mauas 2002), 13 of He  I (see Mauas et al. 2004), 9 of C  I, 15 of Fe  I, 8 of Si  I (see Cincunegui & Mauas 2001), 8 of Ca  I and Na  I, 6 of Al  I (see Mauas et al. 2002), and 7 of Mg  I (see Mauas et al. 1988). In addition, we computed 6 levels of He  II (see Mauas et al. 2004) and Mg  II, and 5 of Ca  II (see Falchi & Mauas 2002).

For every species under consideration we included all the bound-free transitions and the most important bound-bound transitions. Ly-$\alpha $, the Ca  II H and K, and Mg  II h and k lines were all computed with a full partial-redistribution treatment. A test was performed assuming helium abundance Y=0.23 and $\alpha $-element enhancement [Ca/Fe] = +0.3, which are more appropriate for a GC stellar population, and no significant difference was detected in the results discussed in the following section. We also performed several test runs varying the gravity within the observed range, and found that the emitted profiles were not affected.

In our calculations we assumed a plane-parallel atmosphere, for simplicity. However, once the final model was obtained, we computed the emitted profiles assuming a spherically symmetric atmosphere, and we found no significant changes in the emitted profiles with respect to the plane-parallel approximation. The abundances adopted in the present study are taken from the detailed chemical analysis of the same stars performed by Carretta (2006).

4 Analysis and results

The observed profiles for three of our stars (48889, 51454, and 51499) are very similar, differing mainly in the amount of asymmetry in the K2 and H$\alpha $ emission wings. The profiles for the other two stars (37872 and 47606) are also similar and differ mainly in the asymmetry. Furthermore, the asymmetries are not very large and can be considered as a second order change in the profiles. For these reasons, we computed two atmospheric models, one (model A) to fit the profiles of the first three stars and the other (model B) to fit the profiles of the remaining two stars.

Once the models that gave the best fit to the symmetric profiles were obtained, we applied a velocity field to each of them, computed the resulting profiles, and compared them with the observed asymmetries. We modified this velocity field until a satisfactory match between observed and computed profiles was found. The advantage of this approach is that the velocities are not "measured'' from the profiles, but modelled self-consistently along with the rest of the atmospheric parameters, and the region corresponding to each value of the velocity field is well-determined, unlike for other methods such as the bisector.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4792f2.ps} \end{figure} Figure 2: Our chromospheric models: model A (solid line), for the least active stars, and model B (dashed line) for the most active stars (37872 and 47606). These models do not include any velocity field. The approximate depth of formation of the H$\alpha $ core and wings and of the Ca  II K2 and K3 line components are also indicated.
Open with DEXTER

Our two models are shown in Fig. 2, together with the depth of formation of the lines we used as diagnostics, and the velocities obtained are plotted in Fig. 3. The computed H$\alpha $ and Ca  II K line profiles are compared with the observations in Figs. 4 to 8. The observed profiles have been reported to the continuum emission implied by Kurucz's model and shifted by a quantity corresponding to the individual stellar radial velocity (see Table 2 in C04), to report the profiles to their wavelengths at rest. Also shown are the profiles computed for the corresponding model without including the velocity field, as a reference for clarity. These profiles have been superimposed to those with velocity to highlight the asymmetries.


  \begin{figure} \par\includegraphics[width=8cm,clip]{4792f3.ps} \end{figure} Figure 3: The velocity as a function of depth (solid line), derived from the best match with the Ca K (innermost) and H$\alpha $ (outermost) lines, compared to the corresponding escape velocity (dashed line).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4792f4.ps} \end{figure} Figure 4: H$\alpha $ ( top panel) and Ca II K ( bottom panel) observed profiles (dotted lines) for the star 51499, compared with the computed profiles for our model A with no velocity (dashed lines) and with the velocity field shown in Fig. 3 (solid lines).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4792f5.ps} \end{figure} Figure 5: Same as in Fig. 4 for the star 48889.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4792f6.ps} \end{figure} Figure 6: Same as in Fig. 4 for the star 51454.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4792f7.ps} \end{figure} Figure 7: Same as in Fig. 4 for the star 47606. In this case we use model B.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4792f8.ps} \end{figure} Figure 8: Same as in Fig. 4 for the star 37872. In this case we use model B.
Open with DEXTER

One can see in the figures that the agreement between computed and observed profiles is quite good. In fact, the main difference is that the H$\alpha $ computed profiles are broader and slightly deeper in the line core. We point out that in these calculations we are assuming a homogeneous atmosphere and that the broader and deeper core shown by the computed profiles can be due to inhomogeneities in the atmosphere. For example, in Fig. 9 we show the H$\alpha $ profile computed from model A and the profile obtained from an atmosphere with no chromospheric rise (and no velocity field), i.e. a purely photospheric profile. Also shown is the profile obtained by combining 90% of the profile computed from model A and 10% of the profile obtained from the model without chromospheric rise, as a way to simulate an inhomogeneus atmosphere. The resulting profile is narrower and more asymmetric in the centre, and fits the observations much better. We stress that the results discussed below are not affected by this disagreement, since they are mainly based on the asymmetries of the wings.

Also, some of the Ca II photospheric profiles in Figs. 5-8 show a slight mismatch on the blue side of the line, and the model is slightly higher than the observed profile. This is most likely due to the presence of extra photospheric absorption lines in the spectra that are not included in the model, like the Fe I lines at 3930.3 Å and 3929 Å. Some small residual tilt induced by the flat fielding process cannot be excluded (see e.g. the discussion in Pasquini 1992), but this is not relevant to the following discussion. In modelling the Ca II K line, we have been careful to match the chromospheric core intensity, asymmetry, and width (Wilson-Bappu width, Wilson & Bappu 1957). The models tend to produce a higher K3 central intensity with respect to the observed profiles. This is also possibly due to the assumption of a homogeneous chromosphere, since any contribution of a pure photospheric line should be noticed mainly in the line centre. We do not expect a significant contribution of interstellar Ca, since we do not see evidence of it in our spectra, and it could contribute to the Ca  II core profile only if the velocity of the interstellar medium were similar to that of the cluster ($\sim$100 km s-1).


  \begin{figure} \par\includegraphics[width=8cm,clip]{4792f9.ps} \end{figure} Figure 9: H$\alpha $ synthetic profiles computed for our model A (short-dashed line) and for a model with no chromosphere (long-dashed lines). The profile obtained by combining 90% of model A and 10% of the no-chromospheric model (solid line) gives a better fit to the observed profile of star 51499 (dotted line) than the purely chromospheric profile.
Open with DEXTER

In our models, the chromosphere starts (i.e. our model departs from Kurucz' purely photospheric one) at log(m) = 0.8 for the least active stars and at 0.95 for the most active ones. It is this fact that results in stronger emission wings for model B. In both models, the slope of the chromosphere (i.e. T vs. log(m), with T in K and m in g cm-2) is -21 000, and the "transition region'' starts where the temperature reaches 18 000 K.

Regarding the $T_{\rm min}$ region, we found the best agreement in the Ca  II K1 minima with a slightly rounder temperature distribution, which does not show the sharp transition from Kurucz' model to ours, which can be seen in Fig. 1. In fact, the temperature for model B is slightly larger in this region, to account for the more intense K1 minima seen in stars 37872 and 47606.

Regarding the slope of the chromospheric temperature vs. mass, we found that this is the fundamental parameter affecting the H$\alpha $ emission wings: a shallower slope results in no emission wings, and a steeper slope produces too large an emission. In other words, the emission wings are a direct sign of how steep the chromospheric temperature rise is.

With respect to the upper end of the chromosphere, we point out that the temperature distribution above $T \approx 10^4$ K does not affect our observed profiles. Therefore, the influence of this parameter is related to the mass load of the chromosphere, and not to the real temperature.

4.1 Velocity fields and mass loss

We see in the figures that the presence of emission in the H$\alpha $ wings can be reproduced without considering any velocities. However, the asymmetries of these wings and of other features of the profiles can only be reproduced with the inclusion of velocity fields. In all cases, the profiles that include some velocity provide a better fit to the data than those with zero velocity.

The H$\alpha $ line core is the feature that forms higher up in the atmosphere, so we can only infer the velocity up to the height where it is formed, about 1 stellar radius above the photosphere. These are the velocities $V_{\rm exp}$ listed in Table 1. In Fig. 3 we show the full velocity field. For comparison, we also show the corresponding escape velocity, at each height Z from the centre of the star, computed as $V_{\rm esc}=620\ (M/Z)^{1/2}$, where Z and the stellar mass M are in solar units. We assumed a typical mass $M=0.85~ M_{\odot}$ for all the stars.

It can be seen that for one of the stars (48889) the expansion velocity at the most external point estimated from the H$\alpha $ profile is larger than the escape velocity at about 2 stellar radii (from the centre of the star), where the H$\alpha $ core forms. This velocity is reflected in the blue wing of the H$\alpha $profile, which has an absorption feature, whereas the red wing has an emission peak. This is due to the displacement of the line core, which is shallower in the profile with velocity.

This implies that, at least for this star, the material above this level is escaping from the atmosphere. For the other stars, the expansion velocity we estimate for the outermost point for which we have an indication, i.e. where the H$\alpha $ core is formed, is smaller than the escape velocity at that depth. However, there is mass outflow at this height, and the velocity is increasing in all cases, while, of course, the escape velocity is decreasing. Furthermore, there are no signs of a reversal in the velocity field; i.e. there is no material falling back in. Therefore, the most probable situation is that the velocity continues to increase, until eventually it reaches the escape velocity. The particularity of star 48889 is only that it reaches this high level of velocity deep enough to be seen in the H$\alpha $ profile.

We can estimate the mass loss rate for these stars using a simple formulation based on mass outflow:

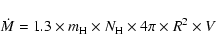
\begin{displaymath}\dot{M} = 1.3 \times m_{\rm H} \times N_{\rm H} \times 4\pi \times R^2 \times V\end{displaymath}

where $m_{\rm H}$ and $N_{\rm H}$ are the mass and the density of hydrogen atoms, R the distance from the stellar centre, and V the velocity of the outermost layer for which we have a determination. The factor 1.3 takes care of the helium abundance Y=0.23. We find that $N_{\rm H}$ is between ${\sim} 1.3\times10^7$ and ${\sim} 2\times10^7$ for all our stars (except 47606 for which the density is ${\sim}1\times10^6$), at about R=2 $R_{\ast}$; the corresponding velocities range from $\sim$10 to 50 km s-1 (see Table 1 Col. 11). The values of $\dot{M}$ thus derived (and listed in Col. 12 of that table) are a few times 10-9 $M_{\odot}$ yr-1 (ten times smaller for the star 47606).

The rates expected from stellar evolution theory can be estimated using Renzini (1977) parameterisation (his Eq. (6.10))

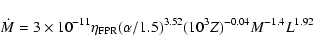
\begin{displaymath}\dot{M} = 3\times10^{-11}\eta_{\rm FPR}(\alpha/1.5)^{3.52} (10^3Z)^{-0.04}M^{-1.4}L^{1.92}\end{displaymath}

assuming $\eta_{\rm FPR} = 6\times10^{-4}$ and $\alpha=1$ (Renzini 1977), and with mass $M=0.85~ M_{\odot}$ and metallicity $Z=1.23\times10^{-3}$ (corresponding to [Fe/H] = -1.14). With these assumptions and approximations, the mass loss rate only depends on luminosity. Compared to the values listed in Table 1 Col. 12, these "evolutionary'' estimates are 2-10 times larger ($\sim$70 times larger for star 47606).

For completeness, we estimated the mass loss rates according to Eq. (4) of Schroeder & Cuntz (2005)

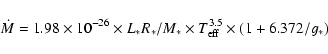
\begin{displaymath}\dot{M} = 1.98 \times 10^{-26} \times L_{\ast}R_{\ast}/M_{\ast} \times T_{\rm eff}^{3.5} \times (1+6.372/g_{\ast})\end{displaymath}

where $L_{\ast}$, $R_{\ast}$, and $M_{\ast}$ are stellar luminosity, radius, and mass in solar units, and $g_{\ast}$ is the stellar surface gravity. This relation is an updated version of Reimers (1975) law $\dot{M} = 4\times10^{-13} \eta L/gR$ derived for Population I K and M giants and supergiants, and includes an additional term related to the stellar temperature that seems to extend its validity also to metal-poor (Population II) stars. The values thus obtained range from 1.5 to $4.1\times 10^{-8}~ M_{\odot}$ yr-1, and represent the average mass loss rates under the assumptions specified by Schroeder & Cuntz for the mass loss mechanism (i.e. cool wind possibly related to Alfvén waves in the chromosphere or underneath). They are about ten times higher than the values we estimate in the present study. These various estimates of mass loss rate may indicate the uncertainty of these determinations.

4.2 Energy requirements

To estimate the energy requirements to sustain the chromosphere, i.e. to constrain the possible heating mechanisms at work, we compute the radiative cooling rate $ \Phi $ (erg cm-3 s-1), namely the net amount of energy radiated at a given depth by the atmosphere, which is given by

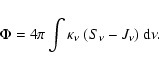
\begin{displaymath}\Phi = 4 \pi \int \kappa_{\nu}\ (S_\nu-J_\nu)\ {\rm d}\nu . \end{displaymath}

In this study we compute the contributions due to H-, H, He  I, Mg  I and II, Ca  I and II, Fe  I, Si  I, Na  I, Al  I and CO. The overall results and the most important individual contributions for model A are presented in Fig. 10. A positive value implies a net loss of energy (cooling), and a negative value represents a net energy absorption (heating).

These rates can be compared with those for dwarf stars of similar $T_{\rm eff}$ (Mauas et al. 1997). It can be seen that the energy required is, as expected, much lower for giant stars: in the mid-chromosphere, where it is largest, it reaches up to 10-4 erg cm-3 s-1 for these giant stars, 5 orders of magnitude smaller than for the dwarfs. However, since the particle density is also 5 orders of magnitude smaller in giants, the energy per particle is within the same order of magnitude.

In the temperature minimum region, the cooling rate is negative. In this case there should be a missing cooling agent, a fact that has already been noted for dwarf stars. However, it should be pointed out that almost all cooling is due to CO, which is the only molecule included in the calculations. It seems reasonable to expect that, should other molecules be computed in detail, the results would show a similar behaviour as the CO calculations, bringing this region closer to radiative balance.

In the mid- and high-chromosphere the energy balance is determined essentially by the hydrogen cooling rate. In this region, the Mg II rate is also important, and it is an order of magnitude higher than the one for Ca  II. Although it is not trivial to compare chromospheric non-radiative losses in different lines, such as Mg  II and Ca  II, observed with different instruments, Pasquini & Brocato (1992) analysed the metal-poor stars observed by Dupree et al. (1994) and found that chromopheric losses in the Mg  II lines are a factor 2-3 higher than in the Ca  II. This, at least qualitatively, agrees with the present analysis.


  \begin{figure} \par\includegraphics[width=8cm,clip]{4792f10.ps} \end{figure} Figure 10: Log$ \Phi $, i.e. the total net radiative cooling rate, as a function of depth for our model A (thick line), and the most important contributions to it.
Open with DEXTER

5 Discussion and conclusions

We can summarise our conclusions as follows:

Acknowledgements

We would like to thank Dr. E.H. Avrett for interesting discussions and comments. C.C. acknowledges the support of the MIUR (Ministero dell'Istruzione, dell'Università e della Ricerca). PM acknowledges the Visiting Scientist programme at ESO-Garching.

References

 
Copyright ESO 2006