A&A 454, 409-414 (2006)
DOI: 10.1051/0004-6361:20054243

On the cosmic microwave background large-scale angular correlations
(Research Note)

A. Bernui - T. Villela - C. A. Wuensche - R. Leonardi - I. Ferreira

Instituto Nacional de Pesquisas Espaciais, Divisão de Astrofísica, Av. dos Astronautas 1758, 12227-010, São José dos Campos, SP - Brazil

Received 23 September 2005 / Accepted 16 January 2006

Abstract
Aims. We study the large-scale angular correlation signatures of the cosmic microwave background (CMB) temperature fluctuations from WMAP data in several spherical cap regions of the celestial sphere, outside the Kp0 or Kp2 cut-sky masks.
Methods. We applied a recently proposed method to CMB temperature maps to permit an accurate analysis of their angular correlations in the celestial sphere through the use of normalized histograms of the number of pairs of such objects with a given angular separation versus their angular separation. The method allows for a better comparison of the results from observational data with the expected CMB angular correlations of a statistically isotropic universe, computed from Monte-Carlo maps according to the WMAP best-fit $\Lambda$CDM model.
Results. We found that the already known, anomalous lack of large-scale power in full-sky CMB maps is mainly due to deficient angular correlations of a quadrupole-like signature. This result is robust with respect to frequency CMB maps and cut-sky masks. Moreover, we also confirm previous results regarding the uneven distribution in the sky of the large-scale power of WMAP data. In a bin-to-bin correlation analyses, measured by the full covariance matrix $\chi ^2$ statistic, we found that the angular correlation signatures in opposite Galactic hemispheres are anomalous at a 98%-99% confidence level.

Key words: cosmology: large-scale structure of Universe - cosmic microwave background - cosmology: observations

1 Introduction

In recent years after the COBE mission, experiments in observational cosmology evolved both in the accuracy and in the angular resolution of the cosmic microwave background (CMB) measurements (see, e.g. Bersanelli et al. 2002, and references therein). However, such experiments were designed to map small patches of the celestial sphere and therefore the study of its properties concerning the large-scale angular correlations was not possible.

This situation changed with the Wilkinson Microwave Anisotropy Probe (WMAP) that produced full-sky CMB maps in five frequency bands (termed K, Ka, Q, V, and W maps), although it does contain different amounts of contaminations from our galaxy (Bennett et al. 2003a). This superb quality data set motivated a number of detailed studies of the CMB properties. As a result, several recent works have reported some anomalies in these data: the low-order multipole values (Bennett et al. 2003a; Efstathiou 2004; Tegmark et al. 2003; Gaztañaga et al. 2003; Slozar et al. 2004; O'Dwyer et al. 2004), the alignment of some low-order multipoles (Tegmark et al. 2003; de Oliveira-Costa et al. 2004; Eriksen et al. 2004b; Bielewicz et al. 2005; Land & Magueijo 2005; Abramo et al. 2006), and an unexpected asymmetric distribution on the sky of the large-scale power of CMB data (Eriksen et al. 2004a, 2005a; Hansen et al. 2004a, 2004b, 2004c; Jaffe et al. 2005; Schwarz et al. 2004; Copi et al. 2005; Bernui et al. 2005).

In this work we focus on the large-scale angular correlations (hereafter termed angular correlations signatures ACS) of the CMB temperature maps from WMAP data. Since the vast majority of the cosmological information is contained in the two-point temperature correlation function, it seems natural to study the ACS by looking at this function (actually, an equivalent of it). Our analyses of the ACS in CMB maps for data outside the region defined by the Kp0 or Kp2 WMAP masks, allowed us to closely inspect two interesting issues. First, we used a full-sky map analysis to investigate the large-scale power in WMAP data and its connection to the low quadrupole moment issue. Second, we use a partial-sky coverage analysis to study the possibly uneven distribution of the CMB's large-scale power on the celestial sphere. The significance of our results were evaluated by comparing these results against those obtained from Monte-Carlo CMB maps produced with the WMAP best-fitting $\Lambda$CDM model properties (Hinshaw et al. 2003b). Finally, using $\chi ^2$ statistics we assess the confidence level of the North/South asymmetry in WMAP data compared to 1000 Monte-Carlo realizations of CMB skies.

2 Analysis method

Recently, Bernui & Villela (2006) introduced a new method to study the large-scale ACS in the distribution of cosmic objects in the sky. This method, called the pair angular separation histogram (PASH) method, consists in first calculating the angular distances between all pairs of cosmic objects, listed in a catalog, and then constructing the normalized histogram of the number of pairs with a given angular separation versus their angular separation (for details on the pair separation histogram method see, for example, Gomero et al. 2002). A catalog with a large number of objects can be divided in a number (say K) of comparable sub-catalogs (i.e. ensembles of iso-number of objects sharing analogous physical properties). After that, one computes a PASH with each one of these sub-catalogs and averages them to obtain the Mean-PASH (MPASH). The difference between the MPASH, caculated using a observational catalog, and the expected-PASH (EPASH), obtained assuming the statistical isotropy hypothesis (hereafter the MPASH-minus-EPASH function), shows the ACS of the cosmic objects in such a catalog.

In the CMB temperature maps the celestial sphere is partitioned in a set of equal-area pixels, where a weighted CMB temperature is assigned to each pixel. To obtain the ACS of a given map, one divides the set of pixels into K=2 sub-maps, one for the negative CMB temperature fluctuations and the other for the positive ones, and then proceeds as before by averaging (K=) 2 PASHs. If, for computational problems, the number of pixels in these sub-maps is too large, one can divide them into, say, K_- and K₊, sub-maps (with iso-number of pixels of analogous temperatures), and proceed by computing the MPASH by averaging the K = K_- + K₊ PASHs. Finally, one plots the MPASH-minus-EPASH function. It can be shown (see Bernui 2005) that the MPASH-minus-EPASH function is independent of the number of sub-maps $K_{-} \ge 1$ and $K_{+} \ge 1$ in which the original CMB map is divided.

The PASH method is also applicable to incomplete sky maps, including disconnected regions such as those resulting from applying the WMAP masks. This method is similar in philosophy to the two-point temperature correlation function, except that the PASH method has zero mean, because the MPASH and EPASH are each normalized histograms. This simple fact allows us to achieve a deeper study of the ACS in CMB temperature maps, such as: the intensity of all their relative mimima and maxima and their corresponding angular scales, their intersections with the horizontal axis (i.e. the zeros of the function), etc. It also leads to calculating the variance $\sigma^2$ of the MPASH-minus-EPASH function f_i (which has zero mean, i.e., $~\sum_{i=1}^{N_{\rm {bins}}} ~ f_i = 0$)

$$\sigma^2 = \frac{1}{N_{\rm {bins}}} \sum_{i=1}^{N_{\rm {bins}}}~ f_i^{~2} .$$

3 CMB data analyses

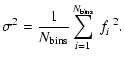In this section we present the ACS of the WMAP data. For these analyses, we used six CMB maps: the individual Q-, V-, and W-band data produced from the (Q₁, Q₂), (V₁, V₂), and (W₁, W₂, W₃, W₄) differential assemblies (DA), respectively, as provided on LAMBDA (Bennett et al. 2003b); the COADDED WMAP map (which combines the eight DA in the Q-, V-, and W-bands using the inverse-variance noise weights as described by Hinshaw et al. 2003b); and the cleaned CMB map (Tegmark et al. 2003, hereafter the TOH map), and the Lagrange internal linear combination (Eriksen et al. 2004b, hereafter the LILC map). It is known that the last two maps are not fully reliable for quantitative analysis because they still have problems with residual foregrounds (Eriksen et al. 2005b); here we use them only as a supporting evidence. After applying the Kp0 or Kp2 WMAP masks to all these six maps, we removed their residual monopole and dipole components, and then corrected them for the dynamic quadrupole.

The examination of the WMAP data performed here includes two types of sky analyses. In both cases we considered data outside the region defined by the Kp0 or the Kp2 mask, to avoid residual foreground contaminations from the beginning (Bennett et al. 2003b; Eriksen et al. 2004b, 2005b; Bielewicz et al. 2004). The first type is the full-sky analysis, and the second the partial-sky analysis carried out through antipodal spherical caps of $45^{\circ }$, $60^{\circ }$, and $90^{\circ }$ of aperture, which means that the maximum angular separation between pixels in each case is twice these angle values.

We used CMB maps with HEALPix (Górski et al. 2005) resolution $N_{\rm {side}}=128$, which amounts to 196 608 pixels. In the following figures we consider the bin width as $0.45^{\circ}$, and the number of bins as $N_{\rm {bins}}=400$; moreover, the shaded areas correspond to 1-sigma confidence regions.

3.1 Full-sky analyses (outside Kp2 or Kp0 masks)

In this subsection we discuss the ACS of the WMAP maps and analyze the CMB data outside the regions defined by the Kp2 and Kp0 masks. The objective of such analysis is to investigate previous claims regarding the lack of power in the large-scale angular correlations in full-sky data (see Bennett et al. 2003a; Efstathiou 2004; Slosar et al. 2004) and its relationship to the low-order multipole values.

First we show the ACS of the WMAP data using the Kp2 mask. In fact, the suitability of using each WMAP mask is well known in the literature, and many works claim that the less severe cut-sky Kp2 could be enough for cosmological purposes (large angular scales). We computed the ACS for both masks, although we only show the ACS for the Kp2 mask case and for all maps under investigation to assert the robustness of our results under different sky cuts.

The results are reported in Fig. 1. In the top panel of Fig. 1 we show the ACS from the six CMB maps investigated here, considering data outside the region determined by the Kp2 mask. For comparison we also plot the average of 1000 MPASH-minus-EPASH functions (termed the expected function) obtained from the same number of Monte-Carlo CMB maps. These realizations were produced using an input power spectrum generated by the CMBFAST code (Seljak & Zaldarriaga 1996) considering the WMAP best-fitting $\Lambda$CDM model properties. The maps were produced using the map-making code SYNFAST from HEALPix. The disagreement observed between the observational data from WMAP and the expected angular correlation function is better appreciated in the bottom panel of Fig. 1, where we plotted the difference of such expected function minus each one of the MPASH-minus-EPASH functions from the six CMB maps. What is revealed in these difference plots is that the ACS lacking in CMB data at large-angular scales correspond to a quadrupole-like angular correlation signature (see, e.g., Bernui 2005). To assess this, we plotted the angular correlation function of a quadrupole (corrected for the Kp2 mask) with moment $C_2 \simeq 670~ \mu$K². Since these curves (bottom panel Fig. 1) represent the lacking ACS in WMAP data to fit the expected function, where $C_2^{\Lambda {\rm\sc cdm}} = 870 ~\mu$K², one finds $C_2^{{\rm\sc wmap}} \simeq 190 \pm 30 ~\mu$K², which is in good agreement with Bielewicz et al. (2004) who obtained $C_2 = 165 \pm 34, 216 \pm 42, 229 \pm 44, 191 \pm 38~ \mu$K², for the Q, V, W, and Coadded maps, respectively). This result, which appears to be robust with respect to the frequency CMB map and to cut-sky mask (we also performed analyses with the Kp0 mask obtaining similar results), proves that the lack of angular power previously found in the two-point temperature correlation function of WMAP data is mainly due to the low quadrupole moment (Efstathiou 2004; Gaztañaga et al. 2003; Slosar et al. 2004).

Figure 1: Top panel: ACS in the six CMB maps: Q (violet line), V (blue line), W (light-blue line), Coadded (green line), TOH (brown line), and LILC (red line), after applying the Kp2 mask. For comparison we also plot the average of 1000 MPASH-minus-EPASH functions obtained from the same number of Monte-Carlo CMB maps (dashed line, also called the expected function). One unit in the vertical axis corresponds to 5460 $\mu$K2. Bottom panel: the differences of the expected function minus the six MPASH-minus-EPASH functions from the top panel, where we observe that these ACS mainly correspond to a quadrupole-like signature. The dashed line here corresponds to the MPASH-minus-EPASH of a quadrupole (corrected for the Kp2 mask) with $C_2 \simeq 670~ \mu$K2. Notice that these curves represent the lacking ACS in WMAP data that is still needed to fit the expected function, which have $C_2^{\Lambda\mbox{\rm\sc cdm}} = 870 ~\mu$K2.

Open with DEXTER

Furthermore, to confirm this result we removed the quadrupole component, after applying the Kp2 mask, and computed the ACS in these maps. The result is shown in Fig. 2 where we also plot the expected function for the case of zero quadrupole compoment for comparison. Again this result is robust with respect to the frequency CMB map analyzed.

	Figure 2: The ACS for the six CMB maps (the nomenclature of the curves follows the same color pattern as before) with the quadrupole component removed. The dashed line is the expected function for the case of a zero quadrupole moment.
Open with DEXTER

Figure 3: The ACS in the $45^{\circ }$-caps in the NGH a) and in the SGH b), and the ACS in the $60^{\circ }$-caps in the NGH c) and in the SGH d), from the six CMB maps (Q, V, W, Coadded, TOH, and LILC), after applying the Kp2 mask. In all plots the dashed line is the average of MPASH-minus-EPASH functions obtained from the corresponding sky regions in 1000 Monte-Carlo maps. The nomenclature of the curves follows the same color pattern as in Fig. 1.

Open with DEXTER

Figure 4: The ACS in the $90^{\circ }$-caps in the NGH a) and in the SGH b), from the six CMB maps (Q, V, W, Coadded, TOH, and LILC), after applying the Kp2 mask. Removing the quadrupole component, after applying the Kp2 mask, in the six CMB maps, we obtain the ACS in the $90^{\circ }$-caps in the NGH c), and in the SGH d). For comparison, the dashed line and the shaded region in panel a) (panel b)) is the same as in panel c) (panel  d)). As before, the nomenclature of all the curves follows the same color pattern as in Fig. 1.

Open with DEXTER

3.2 Partial-sky analyses

The basic idea is to investigate different regions of the celestial sphere, namely spherical caps of various sizes, whose vertices point in the direction of the North Galactic Pole (NGP) and the South Galactic Pole (SGP), with respect to the Galactic coordinate system. Comparison of the ACS in antipodal caps of $45^{\circ }$, $60^{\circ }$, and $90^{\circ }$ of aperture allows a quantitative assessement of the claimed asymmetry in the distribution of the CMB power between the northern and southern hemispheres (Eriksen et al. 2004b).

The resulting ACS are shown in Figs. 3 and 4, where the expected functions result from data on the same patch of the sky from Monte-Carlo CMB maps. In Fig. 3 we present four plots: panels (a) and (b) reveal the ACS in the $45^{\circ }$ NGP-cap and SGP-cap, respectively, while in panels (c) and (d) we show the ACS in the $60^{\circ }$ NGP-cap and SGP-cap, respectively. In Fig. 4, we also show four plots: panels (a) and (b) reveal the ACS in the $90^{\circ }$-cap, outside the Kp2 mask, in the Northern and Southern Galactic hemispheres (NGH, SGH), respectively; panels (c) and (d) show the ACS in the $90^{\circ }$-cap, outside the Kp2 mask, in the NGH and SGH, respectively, but this time we removed the quadrupole component of the CMB maps.

Some interesting features in these plots are evident. The first noticeable result is that, in each one of these figures, the ACS corresponding to the three frequency maps Q, V, and W are practically indistinguishable. It is well known (see Bennett et al. 2003b) that foregrounds have a frequency-band dependence, thus when incorrectly subtracted it is expected to show up at a different level in the frequency maps Q, V, and W. To investigate the robustness of our results with respect to a different sky cut, we computed the ACS for the NGH and SGH (not shown here) for data outside the more severe galactic cut given by the WMAP Kp0 mask (it cuts $\sim$25% of the total data, while the Kp2 mask cuts $\sim$15%), where we found similar results. Thus, one concludes that the ACS found in these maps are remarkably stable compared to both frequency bands and sky cuts, and seem unlikely to be compromised by residual foregrounds.

The second interesting fact is the net asymmetry between the $90^{\circ }$-caps in NGH and SGH: the Northern hemisphere is almost structureless (the variance's square-root for this ACS is $\langle \sigma_N^{Q,V,W} \rangle=0.0054$ while $\sigma^{\rm Expected}= 0.012 \pm 0.006$), whereas the ACS in the Southern hemisphere are relatively intense ( $\langle \sigma_S^{Q,V,W} \rangle = 0.016$ while $\sigma^{\rm Expected}0.015 \pm 0.008$). In this form, the South/North ratio $\sigma_{S/N} \equiv \sigma_{S} / \sigma_{N} = 2.97$quantifies the evident SGH/NGH asymmetry observed in the plots of Fig. 4. The statistical  significance of this result is evaluated in the next section by means of the Monte-Carlo maps and in terms of the standard covariance matrix $\chi ^2$ statistic.

Finally, in order to check the possibility that the low value of the quadrupole moment could be responsible for this peculiar ACS behavior, we removed the quadrupole component, after applying the Kp2 mask, in all six maps, and then again computed the MPASH-minus-EPASH for data in the $90^{\circ }$-caps in the NGH and SGH. Our results can be seen in the Figs. 4c and d, where this time $\langle \sigma_N^{Q,V,W} \rangle=0.0065$ in the NGH, and $\langle \sigma_S^{Q,V,W} \rangle=0.019$ in the SGH. The high value now obtained for the ratio $\sigma_{S/N} = 2.96$ confirms that the North/South asymmetry is not related to the low quadrupole value.

A natural question would be whether the ratio $\sigma_{S/N} \ga 3$ occurs frequently in the ensemble of Monte-Carlo maps. Analyzing the MPASH-minus-EPASH functions for similar NGH and SGH $90^{\circ }$-caps in 1000 Monte-Carlo maps, we found that the corresponding values of $\sigma_{S/N} \in [0.2,5.4]$, with mean $\sigma_{S/N}^{\rm mean} = 1.1 \pm 0.7$. A close inspection of the values in such interval results in less than 2% of them satisfying $\sigma_{S/N} > 3$.

4 Statistical analyses

In this section we present the statistical analysis of the ACS obtained from WMAP data against analogous results derived from the 1000 Monte-Carlo CMB maps. The degree of agreement between the simulations and the observations is quantified in terms of a standard covariance matrix $\chi ^2$ statistic, including all bin-to-bin correlations,

$$\chi^2 = \sum_{i,j=1}^{N_{\rm {bins}}} ( f_i - \langle f_i \rangle ) M^{-1}_{ij} ( f_j - \langle f_j \rangle ) ,$$

where $\langle f_i \rangle$ is the mean of the MPASH-minus-EPASH functions as determined by the Monte-Carlo maps, and $M_{ij} \equiv \langle f_i f_j \rangle - \langle f_i \rangle \langle f_j \rangle$ is the covariance matrix. The results from these computations are reported in Table 1, divided in three groups for the $45^{\circ }$-, $60^{\circ }$-, and $90^{\circ }$-caps, respectively. The first column indicates the CMB map investigated, the second and third ones indicate the frequencies of Monte-Carlo simulations with a lower $\chi ^2$ value than the WMAP data for the NGH and SGH, respectively. The last column indicates the frequency of simulations with a smaller $\chi^2_{\rm SGP} / \chi^2_{\rm NGP}$. These results determine a parameter, the ratio of the $\chi ^2$ values for the NGH and SGH, that is used to quantify the degree of asymmetry between both hemispheres (Eriksen et al. 2004a, 2005a).

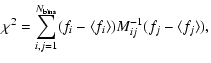The results reported in Table 1 are as follows. In all cases, the NGH and SGH indepedently show acceptable values of probability (frequency of simulated maps, given the model, where the MPASH-minus-EPASH function of such maps has a lower $\chi ^2$ value than the WMAP data). However, data in the third column says that the antipodal $90^{\circ }$-caps are marginally consistent internally (when considered simultaneously one is opposite to the other): for the Q, V, W, and Coadded maps the mean of the $\chi^2_{S/N}$ values is $\ga$0.98, or equivalently $\chi^2_{N/S} \la 0.02$, which means that $\la$2% of the simulations have a smaller ratio of $\chi ^2$. It is worth noticing that these results appearing in the $90^{\circ }$-caps are shown to be robust with respect to frequency (the same result for Q, V, W, and Coadded CMB maps). Therefore, we conclude that there is a significant discrepancy, at the $\ga$98% CL, between WMAP data and the ACS expected in a statistically isotropic universe.

Table 1: $\chi ^2$-test for the ACS in different caps. The first column indicates the CMB map investigated, the second and third ones indicate the frequency of Monte-Carlo simulations with a lower $\chi ^2$ value than the WMAP data. The last column indicates the frequency of simulations with a smaller $\chi ^2_{{\rm SGH}}/\chi ^2_{{\rm NGH}}$.

5 Conclusions

Here we have shown through full-sky analyses of the ACS of the WMAP data (outside the Kp0 or Kp2 sky cuts) that the "anomalous'' lack of power at large angular scales is mainly explained by the low quadrupole-moment value (see Efstathiou 2004; Gaztañaga et al. 2003; and Slosar et al. 2004, for more detailed discussions; see also Bielewicz et al. 2004, for complete calculations, in particular in similar band maps). We confirmed this result by also analyzing the WMAP data after removing the quadrupole component, obtaining a better (but not exact) agreement with what is expected in a $\Lambda$CDM model with zero quadrupole.

We also performed partial-sky coverage analyses and showed that there is significative evidence at the $98\%{-}99\%$ CL of an anomalous distribution of the CMB power in opposite Galactic hemispheres. In fact, in less than 2% of the Monte-Carlo CMB maps analyzed, data in opposite hemispheres present analogous bin-to-bin correlations to those shown by the $90^{\circ }$-caps with WMAP data. More interestingly, the excess of correlations in the comparison of opposite antipodal caps is manifestly observed at the South/North $90^{\circ }$-caps, but it is not seen in examination of either the antipodal $45^{\circ }$- or $60^{\circ }$-caps.

The fact that the South/North asymmetry persists at a significant level in several frequency bands (the Q, V, and W CMB maps) and with different sky cuts (the Kp0 and Kp2 masks) excludes a simple explanation based on systematic effects and foregrounds (see Hinshaw et al. 2003a; Eriksen et al. 2004a, 2004b; Hansen et al. 2004b).

Acknowledgements

We acknowledge use of the Legacy Archive for Microwave Background Data Analysis (LAMBDA), and use of the TOH map (Tegmark et al. 2003). Thanks go to M. J. Rebouças, K. Land, and P. Bielewicz for useful comments. We are grateful to H. K. Eriksen for valuable suggestions. T.V. and C.A.W. acknowledge CNPq grants 305219/2004-9 and 307433/2004-8, respectively, and a FAPESP grant 00/06770-2. R.L. and I.F. acknowledge CAPES fellowships, and A.B. thanks a PCI/7B-CNPq fellowship. Some of the results in this paper were derived using the HEALPix package (Górski et al. 2005).

References

• Abramo, L. R., Bernui, A., Ferreira, I., Villela, T., & Wuensche, C. A. 2006 [arXiv:astro-ph/0604346] (In the text)
• Bennett, C. L., Halpern, M., Hinshaw, G., et al. 2003a, ApJS, 148, 1 [NASA ADS] [CrossRef] (In the text)
• Bennett, C. L., Hill, R. S., Hinshaw, G., et al. 2003b, ApJS, 148, 97 [NASA ADS] [CrossRef] (In the text)
• Bernui, A. 2005, Braz. J. Phys., 35 - 4B, 1185 (In the text)
• Bernui, A., & Villela, T. 2006, A&A, 445, 795 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Bernui, A., Mota, B., Rebouças, M. J., & Tavakol, R. 2005 [arXiv:astro-ph/0511666] (In the text)
• Bersanelli, M., Maino, D., & Mennella, A. 2002, Riv. del Nuovo Cim., 25(9), 1 (In the text)
• Bielewicz, P., Gorski, K. M., & Banday, A. J. 2004, MNRAS, 355, 1283 [NASA ADS] [CrossRef] (In the text)
• Bielewicz, P., Eriksen, H. K., Banday, A. J., Górski, K. M., & Lilje, P. B. 2005 [arXiv:astro-ph/0507186] (In the text)
• Copi, C. J., Huterer, D., Schwarz, D. J., & Starkman, G. D. 2005 [arXiv:astro-ph/0508047] (In the text)
• de Oliveira-Costa, A., Tegmark, M., Zaldarriaga, M., & Hamilton, A. J. S. 2004, Phys. Rev. D, 69, 063516 [NASA ADS] [CrossRef] (In the text)
• Efstathiou, G. 2004, MNRAS, 348, 885 [NASA ADS] [CrossRef] (In the text)
• Eriksen, H. K., Hansen, F. K., Banday, A. J., Górski, K. M., & Lilje, P. B. 2004a, ApJ, 605, 14 [NASA ADS] [CrossRef]; Errat. 2004, 609, 1198 (In the text)
• Eriksen, H. K., Banday, A. J., Górski, K. M., & Lilje, P. B. 2004b, ApJ, 612, 633 [NASA ADS] [CrossRef] (In the text)
• Eriksen, H. K., Banday, A. J., Górski, K. M., & Lilje, P. B. 2005a, ApJ, 622, 58 [NASA ADS] [CrossRef] (In the text)
• Eriksen, H. K., Banday, A. J., Górski, K. M., & Lilje, P. B. 2005b [arXiv:astro-ph/0508196] (In the text)
• Gaztañaga, E., Wagg, J., Multamäki, T., Montaña, A., & Hughes, D. H. 2003, MNRAS, 346, 47 [NASA ADS] [CrossRef] (In the text)
• Gomero, G. I., Teixeira, A. F. F., Rebouças, M. J., & Bernui, A. 2002, Int. J. Mod. Phys. D, 11, 869 [NASA ADS] (In the text)
• Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] (In the text)
• Hansen, F. K., Cabella, P., Marinucci, D., & Vittorio, N. 2004a, ApJ, 607, L67 [NASA ADS] [CrossRef] (In the text)
• Hansen, F. K., Banday, A. J., & Górski, K. M. 2004b, MNRAS, 354, 641 [NASA ADS] [CrossRef] (In the text)
• Hansen, F. K., Balbi, A., Banday, A. J., & Górski, K. M. 2004c, MNRAS, 354, 905 [NASA ADS] [CrossRef] (In the text)
• Hinshaw, G., Barnes, C., Bennett, C. L., et al. 2003a, ApJS, 148, 63 [NASA ADS] [CrossRef] (In the text)
• Hinshaw, G., Spergel, D. N., Verde, L., et al. 2003b, ApJS, 148, 135 [NASA ADS] [CrossRef] (In the text)
• Jaffe, T. R., Banday, A. J., Eriksen, H. K., Gorski, K. M., & Hansen, F. K. 2005, ApJ, 629, L1 [NASA ADS] [CrossRef] (In the text)
• Land, K., & Magueijo, J. 2005, , 95, 071301 (In the text)
• O'Dwyer, I. J., Eriksen, H. K., Wandelt, B. D., et al. 2004, ApJ, 617, L99 [NASA ADS] [CrossRef] (In the text)
• Seljak, U., & Zaldarriaga, M. 1996, ApJ, 469, 437 [NASA ADS] [CrossRef] (In the text)
• Slosar, A., Seljak, U., & Makarov, A. 2004, Phys. Rev. D, 69, 123003 [NASA ADS] [CrossRef] (In the text)
• Schwarz, D. J., Starkman, G. D., Huterer, D., & Copi, C. J. 2004, , 93, 221301 (In the text)
• Tegmark, M., de Oliveira-Costa, A., & Hamilton, A. J. S. 2003, Phys. Rev. D, 68, 123523 [NASA ADS] [CrossRef] (In the text)