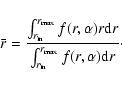A&A 454, 537-542 (2006)
DOI: 10.1051/0004-6361:20052758
Non-thermal pulsed X-ray emission from rotation-powered pulsars
L. Zhang1,2 - Z. J. Jiang2
1 - National Astronomical Observatories/Yunnan Observatory,
Chinese Academy of Sciences, PO Box 110, Kunming, China
2 -
Department of Physics, Yunnan University, Kunming, China
Received 25 January 2005 / Accepted 28 March 2006
Abstract
We study the properties of the pulsed component of hard (>2 keV) X-ray emission from pulsars based on the new version of
the outer-gap model proposed by Zhang et al. (2004). In this outer-gap model, high-energy photons emitted by relativistic charged
particles produce e pairs through magnetic-pair production
on their way from the outer gap to the neutron-star surface, and
these pairs produce the bulk of pulsed X-rays by the synchrotron
radiation. The X-ray luminosity of rotation-powered pulsars is a
function not only of the period and magnetic field strength, but
also of the magnetic inclination angle. Application of this model to
the observed pulsed X-ray emission of normal pulsars by ASCA shows a
better consistence. Further, the inclination angles of these pulsars
are estimated using the observed X-ray data, and the predicted
conversion efficiencies of high-energy
pairs through magnetic-pair production
on their way from the outer gap to the neutron-star surface, and
these pairs produce the bulk of pulsed X-rays by the synchrotron
radiation. The X-ray luminosity of rotation-powered pulsars is a
function not only of the period and magnetic field strength, but
also of the magnetic inclination angle. Application of this model to
the observed pulsed X-ray emission of normal pulsars by ASCA shows a
better consistence. Further, the inclination angles of these pulsars
are estimated using the observed X-ray data, and the predicted
conversion efficiencies of high-energy  -rays for seven confirmed
-rays for seven confirmed
 -ray pulsars are consistent with the observed data.
-ray pulsars are consistent with the observed data.
Key words: pulsars: general - radiation mechanisms: non-thermal -
X-rays: stars
It is believed that hard (>2 keV) pulsed X-ray emission from a
pulsar comes from a pulsar magnetosphere and is dominated by
non-thermal radiation. Einstein data indicate a relationship between
the X-ray luminosity  and spin-down power
and spin-down power
 (erg/s) of
pulsars as
(erg/s) of
pulsars as
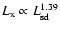 (Seward & Wang 1988).
Observation of ROSAT and ASCA have given the observed
data of more and more rotation-powered pulsars at the X-ray band.
Becker & Trümper (1997) examined the correlation by using 27 spin-down pulsars observed by ROSAT in soft X-ray band
(0.1-2.4 keV) and found that
(Seward & Wang 1988).
Observation of ROSAT and ASCA have given the observed
data of more and more rotation-powered pulsars at the X-ray band.
Becker & Trümper (1997) examined the correlation by using 27 spin-down pulsars observed by ROSAT in soft X-ray band
(0.1-2.4 keV) and found that
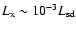 .
Furthermore,
using the data from ASCA (2-10 keV), Saito (1998) gives the
correlation between the X-ray luminosity and the spin-down
luminosity and concludes that at the hard X-ray band
.
Furthermore,
using the data from ASCA (2-10 keV), Saito (1998) gives the
correlation between the X-ray luminosity and the spin-down
luminosity and concludes that at the hard X-ray band
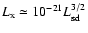 .
Possenti et al. (2002) have obtained a
relation
.
Possenti et al. (2002) have obtained a
relation
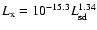 through a re-examination of
39 pulsars. Recently, Cheng et al. (2004) investigated hard X-ray
emission from the non-accreting pulsars using ASCA data, including
non-thermal, non-pulsed, and pulsed X-ray components. They collected
23 X-ray pulsars (19 normal X-ray pulsars plus 4 millisecond X-ray
pulsars) that have been resolved with both pulsed and non-pulsed
components obtained from the ASCA, and found that the best fit
between
through a re-examination of
39 pulsars. Recently, Cheng et al. (2004) investigated hard X-ray
emission from the non-accreting pulsars using ASCA data, including
non-thermal, non-pulsed, and pulsed X-ray components. They collected
23 X-ray pulsars (19 normal X-ray pulsars plus 4 millisecond X-ray
pulsars) that have been resolved with both pulsed and non-pulsed
components obtained from the ASCA, and found that the best fit
between 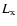 and
and
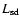 for the pulsed components of these X-ray
pulsars is
for the pulsed components of these X-ray
pulsars is
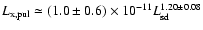 .
.
Two kinds of pulsar models can explain the non-thermal X-ray
emission from the pulsars, one is polar cap models (e.g. Zhang &
Harding 2000); the other outer gap models (e.g. Halpern & Ruderman
1993; Zhang & Cheng 1997; Wang et al. 1998; Cheng et al. 1998;
Hirotani & Shibata 2001). Based on the outer gap model of Zhang &
Cheng (1997), the X-ray properties of rotation-powered pulsars were
studied in detail (Cheng et al. 1998; Cheng & Zhang 1999).
Recently, we revised the outer gap model of Zhang & Cheng (1997)
(Zhang et al. 2004); as an approximation, a vacuum solution for the
acceleration electric field and a non-vacuum particle density are
assumed for explaining the high-energy photon flux.
In this revised model, three important effects have been taken into
account. The first is the effect of the inclination angle (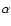 )
in determining the size of the outer gap; the second discards the
assumption that the typical radiation region of the outer gap is at
half of the light cylinder, and an appropriate average over the
entire outer gap is used instead. This effect is particularly
important for old pulsars. When the gap size at this region is
larger than unity, the outer gap is assumed to be turned off; and
the third effect is that the outer gap still exists as long as the
fractional size of the outer gap at the inner boundary is less than
unity. This effect allows some pulsars with the appropriate
combination of
)
in determining the size of the outer gap; the second discards the
assumption that the typical radiation region of the outer gap is at
half of the light cylinder, and an appropriate average over the
entire outer gap is used instead. This effect is particularly
important for old pulsars. When the gap size at this region is
larger than unity, the outer gap is assumed to be turned off; and
the third effect is that the outer gap still exists as long as the
fractional size of the outer gap at the inner boundary is less than
unity. This effect allows some pulsars with the appropriate
combination of 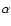 ,
P, and B, to maintain their outer gaps
until they are a few million years old. Here, we use a new version
of the outer gap model proposed by Zhang et al. (2004) to study the
properties of the pulsed X-ray component of the normal pulsars, and
compare model results with the observed pulsed X-ray luminosity of
the 19 X-ray pulsars collected by Cheng et al. (2004). In Sect. 2 we
present the outer-gap model for describing non-thermal X-ray
radiation from rotation-powered pulsars. In Sect. 3 we apply the model
to 19 known X-ray pulsars, and compare with the observed data by
ASCA. Finally we briefly give our discussions and conclusions in
Sect. 4.
,
P, and B, to maintain their outer gaps
until they are a few million years old. Here, we use a new version
of the outer gap model proposed by Zhang et al. (2004) to study the
properties of the pulsed X-ray component of the normal pulsars, and
compare model results with the observed pulsed X-ray luminosity of
the 19 X-ray pulsars collected by Cheng et al. (2004). In Sect. 2 we
present the outer-gap model for describing non-thermal X-ray
radiation from rotation-powered pulsars. In Sect. 3 we apply the model
to 19 known X-ray pulsars, and compare with the observed data by
ASCA. Finally we briefly give our discussions and conclusions in
Sect. 4.
In the outer-gap model of Zhang et al. (2004), a criterion for the
existence of an outer gap is given in terms of the fractional size
of the outer gap, f. Inside the outer gap, the curvature photons
interact with the thermal X-rays from the stellar surface to produce
e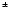 pairs through a photon-photon pair production process,
thereby sustaining the outer gap. This pair-production condition is
pairs through a photon-photon pair production process,
thereby sustaining the outer gap. This pair-production condition is
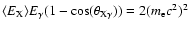 ,
where
,
where
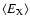 is the average X-ray energy and
is the average X-ray energy and
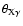 the angle
between the emission directions of curvature photons and the thermal
X-rays. In the self-sustained outer gap model of Zhang et al.
(2004), the thermal X-ray come from the bombardment of the
relativistic particles from the outer gap. For a given
the angle
between the emission directions of curvature photons and the thermal
X-rays. In the self-sustained outer gap model of Zhang et al.
(2004), the thermal X-ray come from the bombardment of the
relativistic particles from the outer gap. For a given  -ray
pulsar with period, magnetic field, and inclination angle, f is a
function of P, B, and radial distance r, which is
-ray
pulsar with period, magnetic field, and inclination angle, f is a
function of P, B, and radial distance r, which is
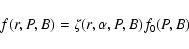 |
(1) |
where
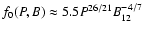 is the
fractional size of the outer gap by ignoring the effect of the
inclination angle (Zhang & Cheng 1997). The function
is the
fractional size of the outer gap by ignoring the effect of the
inclination angle (Zhang & Cheng 1997). The function
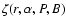 contains the effect of inclination angle, which can
be expressed as
contains the effect of inclination angle, which can
be expressed as
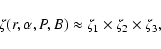 |
(2) |
where
![\begin{displaymath}\zeta_1=\left[{2\sqrt{1-{3\over4}{r\over R_{\rm L}}a(\alpha)}...
...lpha)}+ \sqrt{1-{r\over R_{\rm L}}
a(\alpha)}} \right]^{4/7} ,
\end{displaymath}](/articles/aa/full/2006/29/aa2758-05/img26.gif) |
(3) |
![\begin{displaymath}\zeta_2=\left[{4\over 3}{(1-{3\over 4} {r\over R_{\rm L}}
a(\...
...er 2} {r\over R_{\rm L}}
a(\alpha))\cos\alpha} \right]^{1/7} ,
\end{displaymath}](/articles/aa/full/2006/29/aa2758-05/img27.gif) |
(4) |
and
![\begin{displaymath}\zeta_3=\left(\ln{r\over R}\right)^{{1\over21}} \left({r\over...
...-{3\over 4}{r\over R_{\rm L}}a(\alpha)
\right]^{-{3\over14}} ,
\end{displaymath}](/articles/aa/full/2006/29/aa2758-05/img28.gif) |
(5) |
and
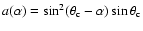 .
It should be
noted that
.
It should be
noted that
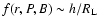 ,
where h represents the vertical
height of the outer gap, which is controlled by the photon-photon
pair production (Cheng et al. 1986, hereafter CHR; Zhang
& Cheng 1997; Cheng et al. 2000).
,
where h represents the vertical
height of the outer gap, which is controlled by the photon-photon
pair production (Cheng et al. 1986, hereafter CHR; Zhang
& Cheng 1997; Cheng et al. 2000).
Obviously, the present model is a modified version of the original
outer gap model (CHR), i.e. a vacuum gap. On the assumption of
slab-like geometry, CHR solved the Poisson equation and found that
the inner boundary is located close to the null charge surface.
Therefore, the outer gap in the CHR model extends from the null
charge surface to the light cylinder with a constant f. The main
difference in the gap structure between the CHR model and our model
is that the CHR model is a one-dimensional gap structure in which
the vertical height of the outer gap is constant, while our model is
a two-dimensional model in which the gap extends along both the
magnetic field lines and trans-field direction; i.e. f is the
function of position. Based on physical considerations, Zhang et al.
(2004) assumed that  -ray luminosity
-ray luminosity 
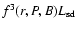 for any rotation-powered pulsar does not exceed the spin-down power;
that is, the fractional size of the outer gap at any position within
the gap must not be larger than unity,
for any rotation-powered pulsar does not exceed the spin-down power;
that is, the fractional size of the outer gap at any position within
the gap must not be larger than unity,
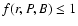 .
From Eq. (1), f(r,P,B) reaches a minimum at the radius (
.
From Eq. (1), f(r,P,B) reaches a minimum at the radius (
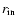 )
of the
inner boundary, and then increases with radius for a given pulsar.
)
of the
inner boundary, and then increases with radius for a given pulsar.
For a given pulsar, if
f(r,P,B)<1 at the inner boundary, the range
of the outer gap is from the inner boundary to light cylinder, if
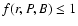 at
at 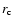 ,
or to the radius
,
or to the radius
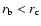 of some surface
if
f(r,P,B)=1 at
of some surface
if
f(r,P,B)=1 at 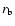 ,
where
,
where 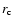 is the radial distance where
the last open field line is the tangent to the light cylinder(
is the radial distance where
the last open field line is the tangent to the light cylinder(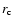 increases with the magnetic inclination angle,
increases with the magnetic inclination angle,
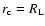 for aligned
rotator), and
for aligned
rotator), and 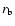 is determined by
is determined by
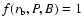 .
Therefore, a
self-sustained outer-gap accelerator does not exist if
.
Therefore, a
self-sustained outer-gap accelerator does not exist if
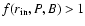 ;
otherwise, the outer gap exists and the radius
of its outer boundary is
;
otherwise, the outer gap exists and the radius
of its outer boundary is
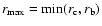 .
In our model, the
parallel electric field,
.
In our model, the
parallel electric field,
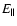 ,
can be estimated when fis given
,
can be estimated when fis given
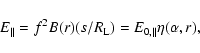 |
(6) |
where
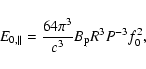 |
(7) |
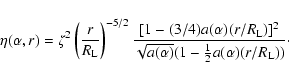 |
(8) |
Obviously,
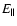 is a function of
is a function of 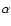 and r and
decreases with r for a given pulsar. In Fig. 1, we show the
variations of
and r and
decreases with r for a given pulsar. In Fig. 1, we show the
variations of
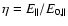 and
and
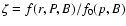 with a radial distance for
with a radial distance for
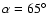 and Vela pulsar's parameters; the former
decreases with radius, but the latter increases with radius.
and Vela pulsar's parameters; the former
decreases with radius, but the latter increases with radius.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{2758fig1.eps}
\end{figure}](/articles/aa/full/2006/29/aa2758-05/Timg46.gif) |
Figure 1:
Variations of
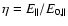 and
and
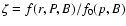 with radial distance for
with radial distance for
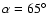 and Vela pulsar's parameters. Solid and dashed
lines represent
and Vela pulsar's parameters. Solid and dashed
lines represent 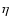 and
and 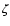 ,
respectively. Tow vertical
dotted-dash lines represent the inner and outer boundaries of the
outer gap. ,
respectively. Tow vertical
dotted-dash lines represent the inner and outer boundaries of the
outer gap. |
| Open with DEXTER |
It should be pointed out that our model gives an approximate
estimation of the outer gap and electric field within the outer gap.
Strictly speaking, an electrodynamic study is necessary in order to
determine the structure of the outer gap and electric field within
the outer gap. Hirotani & Shibata (1999a,b) propose a
one-dimensional non-vacuum outer gap model (also see Hirotani &
Shibata 2001a,b; Hirotani et al. 2003) in which the
electrodynamics of the outer gap is studied in detail. In this
one-dimensional electrodynamical model, the trans-field thickness
(i.e. f(r,P,B) in our model) is assumed to be a constant and is
considered as a parameter to be determined by the observed flux (in
the sense we cannot compare our model with this one-dimensional
model).
Because this model neglected important trans-field effects caused by
the curvature of the field lines that affect the electrodynamics,
Takata et al. (2004) propose a two-dimensional outer gap model with
trans-field structure (also see, Takata et al. 2006). After
complicated calculations (solving Poisson equation, particle's
continuity equations with pair creation model, etc.), they obtained
a vacuum and non-vacuum solution with the dipole magnetic field. For
the vacuum case, their result indicates the same feature as one of
CHR-the inner boundary is located near the null surface-and this
feature does not depend on the location of the outer boundary. In
this two-dimensional model, one important result for the gap
structure is that the gap width relates to trans-field thickness;
i.e. large gap width corresponds to a small trans-field thickness,
at least for the vacuum case, and vice versa (see Figs. 2 and 7
in Takata et al. 2004). Such a feature is similar in our model: a
high
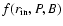 results in a low value for
results in a low value for 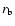 because f(r,P,B) increases with r for a given pulsar, and vice versa.
Obviously, there are many differences between our model and the
two-dimensional model of Takata et al. (2004). Further detailed study
is needed, and is planned for our next paper.
because f(r,P,B) increases with r for a given pulsar, and vice versa.
Obviously, there are many differences between our model and the
two-dimensional model of Takata et al. (2004). Further detailed study
is needed, and is planned for our next paper.
According to Zhang et al. (2004), the Lorentz factor of the primary
electrons/positrons at the radius r of the outer gap is
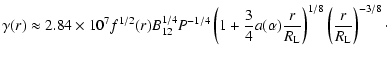 |
|
|
(9) |
They will lose their energy through curvature radiation, and the
characteristic energy of the  -ray photons in the outer gap
can be approximated as
-ray photons in the outer gap
can be approximated as
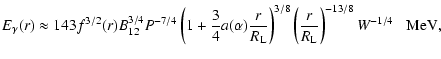 |
|
|
(10) |
where
![$W(r)={4\over 3}\left[1-{3\over 4}a(\alpha){r\over
R_{\rm L}}\right]^{3/2}\!/\!\sqrt{a(\alpha)}\left(1-{1\over2}a(\alpha){r\over R_{\rm L}}\right)$](/articles/aa/full/2006/29/aa2758-05/img50.gif) .
.
In the outer-gap model, half of the primary electrons/positrons in
the outer gap will move toward the star and lose their energy
through curvature radiation. The return particle flux can be
approximated by
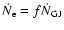 ,
where
,
where
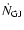 is
the Goldreich-Julian current, which is roughly
is
the Goldreich-Julian current, which is roughly
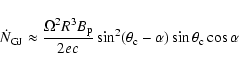 |
(11) |
in polar coordinates. In such a geometry,
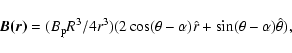 |
(12) |
where 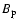 is estimated by
is estimated by
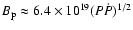 G, R is the stellar radius, and
G, R is the stellar radius, and 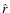 and
and
 are the unit vectors of radial and polar angle
directions, respectively. Halpern & Ruderman (1993) pointed out
that these primary electrons/positrons will radiate most of their
energies during the motion from the inner boundary of the outer gap
toward the neutron star surface. The inner boundary of the outer gap
can be described by (
are the unit vectors of radial and polar angle
directions, respectively. Halpern & Ruderman (1993) pointed out
that these primary electrons/positrons will radiate most of their
energies during the motion from the inner boundary of the outer gap
toward the neutron star surface. The inner boundary of the outer gap
can be described by (
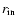 ,
,
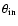 ), which are
), which are
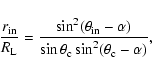 |
(13) |
and
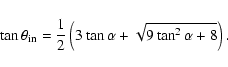 |
(14) |
According to Zhang & Cheng (1997), return relativistic particles in
the outer gap lose their energy via curvature radiation. We assume
that
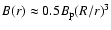 is a reasonable approximation near
the surface of the neutron star. In the neutron star's strong
magnetic field, these curvature photons will convert into secondary
pairs through magnetic-pair production at the distance
is a reasonable approximation near
the surface of the neutron star. In the neutron star's strong
magnetic field, these curvature photons will convert into secondary
pairs through magnetic-pair production at the distance 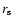 ,
which
is
,
which
is
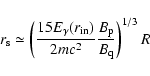 |
(15) |
where R is the neutron-star radius and
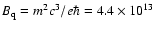 G. These pairs quickly lose
their momentum, which is perpendicular to the local magnetic field
by synchrotron radiation with the characteristic energy
G. These pairs quickly lose
their momentum, which is perpendicular to the local magnetic field
by synchrotron radiation with the characteristic energy
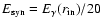 (Cheng et al. 1998).
If the energy of synchrotron photons is high enough, they will
convert further into e
(Cheng et al. 1998).
If the energy of synchrotron photons is high enough, they will
convert further into e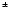 in the strong magnetic field until
their energy reduces to
in the strong magnetic field until
their energy reduces to 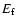
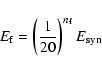 |
(16) |
where 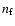 is the generation number, and this will form a cascade.
The position
is the generation number, and this will form a cascade.
The position 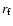 where the pair-production stops is given by
(Cheng & Zhang 1999)
where the pair-production stops is given by
(Cheng & Zhang 1999)
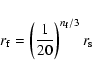 |
(17) |
and then non-thermal X-rays develop. An electromagnetic cascade
will take place until the energy of synchrotron photons is 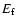 .
According to Zhang & Cheng (1997), the total number of
secondary electron/positron pairs created in the electromagnetic
cascade is
.
According to Zhang & Cheng (1997), the total number of
secondary electron/positron pairs created in the electromagnetic
cascade is
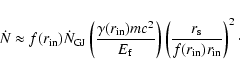 |
(18) |
Therefore the luminosity of non-thermal X-rays produced by the
cascade is given by
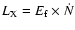 .
Using Eq. (1), we have
.
Using Eq. (1), we have
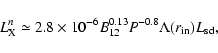 |
(19) |
and
![$\displaystyle \Lambda(r_{\rm in})=a(\alpha)\zeta^{1/2}(r_{\rm in})\cos\alpha\le...
...rm L}}\right]^{3/8} \left({r_{\rm in}\over R_{\rm L}}\right)^{-83/24}W^{-1/6} .$](/articles/aa/full/2006/29/aa2758-05/img75.gif) |
|
|
(20) |
Obviously, for a
given pulsar, its X-ray luminosity is a function of the magnetic
inclination angle (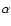 ).
).
In order to determine the spectrum of non-thermal X-rays from a
pulsar, we need to estimate the minimum (
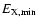 )
and maximum
(
)
and maximum
(
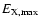 )
energies of these non-thermal X-rays, which are
)
energies of these non-thermal X-rays, which are
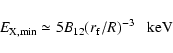 |
(21) |
and
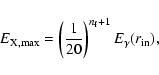 |
(22) |
respectively, where 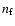 is the generation number. Assuming
is the generation number. Assuming
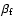 is the spectral index at position
is the spectral index at position 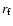 ,
,
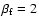 when
the cascade approaches infinity, so we assume that
when
the cascade approaches infinity, so we assume that
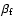 is
generally less than 2. The spectrum of non-thermal X-rays with a
spectral index of
is
generally less than 2. The spectrum of non-thermal X-rays with a
spectral index of
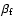 distributes between
distributes between
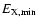 and
and
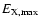 ,
and the differential luminosity of these non-thermal
X-rays from the X-ray pulsar is given by
,
and the differential luminosity of these non-thermal
X-rays from the X-ray pulsar is given by
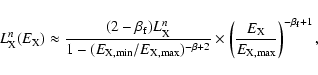 |
(23) |
where
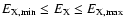 .
For the luminosity of
non-thermal X-rays with energy ranges from E1 to E2, we have
.
For the luminosity of
non-thermal X-rays with energy ranges from E1 to E2, we have
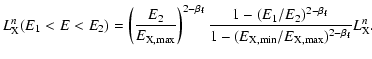 |
|
|
(24) |
Table 1:
Pulsed X-ray properties of rotation-powered pulsars.
Comparison of model X-ray luminosity (
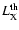 )
(assuming
)
(assuming
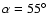 )
with observed pulsed X-ray luminosity
(
)
with observed pulsed X-ray luminosity
(
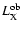 )
for each X-ray pulsars.
)
for each X-ray pulsars.
Cheng et al. (2004) have collected the pulsed X-ray data of 23 X-ray
pulsars by ASCA, including 19 normal pulsars and 4 millisecond
pulsars (see their Table 1). Here we only consider the hard-pulsed
X-ray emission of 19 normal pulsars. The best fit of the observed
pulsed X-ray luminosity of the 19 pulsars is
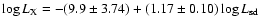 .
Because the fractional
size of the outer gap is the function of magnetic inclination angle
.
Because the fractional
size of the outer gap is the function of magnetic inclination angle 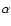 but
but 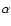 is not known well (see Zhang et al. 2004 in
detail), we use the inclination angle as a parameter. In Table 1,
the typical parameters and expected values for 19 pulsars with
is not known well (see Zhang et al. 2004 in
detail), we use the inclination angle as a parameter. In Table 1,
the typical parameters and expected values for 19 pulsars with
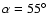 are given.
are given.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{2758fig2.eps}
\end{figure}](/articles/aa/full/2006/29/aa2758-05/Timg91.gif) |
Figure 2:
Plot
of the X-ray pulsar luminosity vs. the spin-down luminosity for 19 pulsars. The data points are represented by filled symbols (after
Cheng et al. 2004), while model values are represented by open
symbols. Pulsars with detected  -ray emission are marked by
circles and those with no -ray emission are marked by
circles and those with no  -rays detected are marked by
squares. -rays detected are marked by
squares. |
| Open with DEXTER |
In estimating the X-ray luminosity in the range of 2-10 keV using
this model, at first, the fractional size of the outer gap, the
typical energy of  -rays at the inner boundary of the outer
gap and the distance
-rays at the inner boundary of the outer
gap and the distance 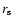 have been calculated for each X-ray
pulsar, then the spectral index for the X-ray spectrum and the
minimum and maximum X-ray energies of each X-ray pulsar are
determined. For each X-ray pulsar, the generation number and
spectral index
have been calculated for each X-ray
pulsar, then the spectral index for the X-ray spectrum and the
minimum and maximum X-ray energies of each X-ray pulsar are
determined. For each X-ray pulsar, the generation number and
spectral index
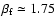 can be determined based on the
can be determined based on the
 -ray energy at the inner boundary. In Fig. 1, the data points
from Cheng et al. (2004) are reproduced with the corresponding model
values, pulsars with detected
-ray energy at the inner boundary. In Fig. 1, the data points
from Cheng et al. (2004) are reproduced with the corresponding model
values, pulsars with detected  -ray emission and the pulsars
with no detected
-ray emission and the pulsars
with no detected  -ray emission. The model results with
-ray emission. The model results with
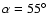 for 19 pulsars are also shown in Fig. 2, and
the best fit is
for 19 pulsars are also shown in Fig. 2, and
the best fit is
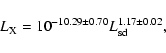 |
(25) |
which is consistent with the observed data. From Fig. 2, the
relationship between 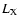 (2-10 keV) and
(2-10 keV) and
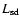 in this model
satisfies
in this model
satisfies
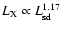 ,
which is similar to
,
which is similar to
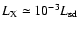 (Becker & Trümper 1997) and
(Becker & Trümper 1997) and
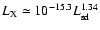 (Possenti et al. 2002), but is
different from
(Possenti et al. 2002), but is
different from
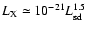 (Saito 1998).
(Saito 1998).
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{2758fig3.eps}
\end{figure}](/articles/aa/full/2006/29/aa2758-05/Timg99.gif) |
Figure 3:
X-ray
luminosity of the Vela pulsar versus the inclination angle. Two
horizonal dashed lines represent the upper and lower limits of the
observed pulsed X-ray luminosity of the Vela pulsar. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{2758fig4.eps}
\end{figure}](/articles/aa/full/2006/29/aa2758-05/Timg100.gif) |
Figure 4:
X-ray
luminosity of the Geminga pulsar versus the inclination angle. Two
horizonal dashed lines represent the upper and lower limits of the
observed pulsed X-ray luminosity of the Geminga pulsar. |
| Open with DEXTER |
It can be seen from Fig. 2, as pointed out by Cheng et al. (1998),
that discrepancies between the observed and the model values of 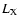 result from the actual value of the inclination angle.
Therefore, the actual distribution of inclination angles is probably
broader, which would automatically imply wider scatter in the X-ray
luminosity. In fact, we can show the change in
result from the actual value of the inclination angle.
Therefore, the actual distribution of inclination angles is probably
broader, which would automatically imply wider scatter in the X-ray
luminosity. In fact, we can show the change in 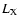 with the
inclination angle for each pulsar. For example, we show the change
of
with the
inclination angle for each pulsar. For example, we show the change
of 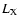 with
with 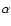 of Vela and Geminga pulsars in Figs. 3 and 4,
respectively. It can be seen that the non-thermal X-ray luminosity
increases with the inclination angle. Such a feature makes it
possible to estimate the inclination angle for each pulsar using the
observed data. We fit the observed data of 19 X-ray pulsars by
changing the inclination angle for each pulsar. Following Possenti
et al. (2002), we grouped these pulsars into four classes:
Crab-like, Vela-like, Geminga-like, and old pulsars. For the
Crab-like pulsars (Crab, PSR B1509-58, PSR B0540-69, PSR B1853+01,
PSR B0537-69, and PSR J1846-0258), the inclination angles are large (
of Vela and Geminga pulsars in Figs. 3 and 4,
respectively. It can be seen that the non-thermal X-ray luminosity
increases with the inclination angle. Such a feature makes it
possible to estimate the inclination angle for each pulsar using the
observed data. We fit the observed data of 19 X-ray pulsars by
changing the inclination angle for each pulsar. Following Possenti
et al. (2002), we grouped these pulsars into four classes:
Crab-like, Vela-like, Geminga-like, and old pulsars. For the
Crab-like pulsars (Crab, PSR B1509-58, PSR B0540-69, PSR B1853+01,
PSR B0537-69, and PSR J1846-0258), the inclination angles are large (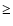
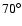 ), the main reason being not knowing the
non-thermal X-rays produced in the outer gap through synchrotron and
inverse-Compton scattering (Cheng et al. 2000). For the Vela-like
pulsars (Vela, PSR J0631+1036, PSR J1811-1925, PSR B1706-44, PSR
B1046-58, PSR B1953+01, and PSR J1846-0258), the inclination angles
change from
), the main reason being not knowing the
non-thermal X-rays produced in the outer gap through synchrotron and
inverse-Compton scattering (Cheng et al. 2000). For the Vela-like
pulsars (Vela, PSR J0631+1036, PSR J1811-1925, PSR B1706-44, PSR
B1046-58, PSR B1953+01, and PSR J1846-0258), the inclination angles
change from
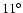 for PSR J2229+6114 to
for PSR J2229+6114 to 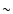
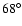 for
PSR B1046-58, which indicates a trend of the inclination angle to
increase with the pulsar's age. For Geminga-like pulsars (Geminga,
PSR B1055-52, PSR B1951+32, and PSR B0656+14), the ranges of the
inclination angle are from
for
PSR B1046-58, which indicates a trend of the inclination angle to
increase with the pulsar's age. For Geminga-like pulsars (Geminga,
PSR B1055-52, PSR B1951+32, and PSR B0656+14), the ranges of the
inclination angle are from
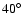 for the Geminga pulsar to
for the Geminga pulsar to 
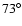 for PSR B0656+14; and we noted that the distances
of PSR B0656+14 and PSR B1055-52 used by Cheng et al. (2004) are 0.76 kpc and 1.53 kpc, respectively (also see Table 1), which are
about twice the present distances (0.3 kpc and 0.75 kpc) of these
two pulsars (De Luca et al. 2004). When the new distances are used,
the inclination angles for PSR B1055-52 and PSR B0656+14 are
for PSR B0656+14; and we noted that the distances
of PSR B0656+14 and PSR B1055-52 used by Cheng et al. (2004) are 0.76 kpc and 1.53 kpc, respectively (also see Table 1), which are
about twice the present distances (0.3 kpc and 0.75 kpc) of these
two pulsars (De Luca et al. 2004). When the new distances are used,
the inclination angles for PSR B1055-52 and PSR B0656+14 are 
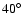 and
and 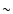
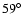 ,
respectively. The inclination
angles for two old pulsars of PSR B1929+10 and PSR B0950+08 are
estimated as
,
respectively. The inclination
angles for two old pulsars of PSR B1929+10 and PSR B0950+08 are
estimated as 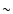
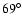 and
and 
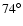 ,
respectively.
,
respectively.
Table 2:
Comparison of observed and theoretical  -ray
luminosity for confirmed high-energy
-ray
luminosity for confirmed high-energy  -ray pulsars.
-ray pulsars.
Once the inclination angle of a pulsar is given, we can estimate its
high-energy  -ray emission. Seven pulsars have been confirmed
as emitting high-energy (
-ray emission. Seven pulsars have been confirmed
as emitting high-energy ( 100 MeV)
100 MeV)  -rays (Hartman et al. 1999; Kaspi et al. 2000), and 19 plausible associations between
the unidentified EGRET sources and the observed radio pulsars have
been found (Camilo et al. 2000; Torres et al. 2001; Kramer et al.
2003). To explain the average properties of high-energy photon
emission from the outer gap, Zhang et al. (2004) assumed that
high-energy emission at a average radius
-rays (Hartman et al. 1999; Kaspi et al. 2000), and 19 plausible associations between
the unidentified EGRET sources and the observed radio pulsars have
been found (Camilo et al. 2000; Torres et al. 2001; Kramer et al.
2003). To explain the average properties of high-energy photon
emission from the outer gap, Zhang et al. (2004) assumed that
high-energy emission at a average radius 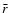 represents the
typical emission of high-energy photons from a pulsar, the average
radius is
represents the
typical emission of high-energy photons from a pulsar, the average
radius is
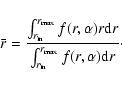 |
(26) |
The radius 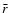 for a pulsar with a given inclination angle
(
for a pulsar with a given inclination angle
(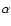 )
can be determined, which is a function of P, B, and
)
can be determined, which is a function of P, B, and 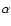 .
Therefore the typical
.
Therefore the typical  -ray luminosity of pulsars
is
-ray luminosity of pulsars
is
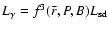 ,
where
,
where
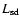 is the
pulsar spin-down power. When the pulsar's inclination angles are
given, we can estimate the conversion efficiency from rotation power
to
is the
pulsar spin-down power. When the pulsar's inclination angles are
given, we can estimate the conversion efficiency from rotation power
to  -ray power for the pulsar (
-ray power for the pulsar (
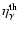 ), which
is defined as
), which
is defined as
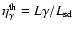 .
Using our
estimate of the inclination angles, we calculated the conversion
efficiencies of seven confirmed
.
Using our
estimate of the inclination angles, we calculated the conversion
efficiencies of seven confirmed  -ray pulsars and compared
them with the observed data (
-ray pulsars and compared
them with the observed data (
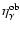 ), where a solid
angle of
), where a solid
angle of  -ray beam is assumed to be 1 sr when
-ray beam is assumed to be 1 sr when
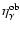 is determined (Fierro 1995). We show our
results in Table 2, where it can be seen that the model results are
consistent with the observed data.
is determined (Fierro 1995). We show our
results in Table 2, where it can be seen that the model results are
consistent with the observed data.
Based on a new version of the outer-gap model proposed by Zhang et al. (2004), we study the pulsed non-thermal X-ray emission from
normal pulsars. In this model, the effects of magnetosphere geometry
and inclination angle are taken into account, so the fractional size
of the outer gap is a function of period, magnetic field strength,
inclination angle, and the distance to the neutron star.
In our model, both outward and inward gamma-rays are produced in the
outer gaps, but inward and/or outward X-rays depend on the pair-
production processes in the outer-magnetosphere. For most pulsars
except for the crab-like pulsars, the optical depth due to
photon-photon pair production at the typical distance of the outer
gap is small, so only a small portion of the outward gamma-rays
materializes due to photon-photon pair production and most
high-energy outward gamma-rays can escape from the outer gap (see
Zhang & Cheng 2002). Because most of the inward gamma-rays
materialize due to magnetic pair production for the normal pulsars,
in particular for large inclination angles, resulting in inward
X-ray luminosity is three order of magnitude larger than the outward
ones for the mature pulsars (Cheng et al. 2000),
gamma-ray emission are dominated by the outward gamma-rays but
non-thermal X-ray emission are dominated by inward X-rays except for
the crab-like pulsars.
We applied this model to 19 normal X-ray pulsars whose pulsed X-ray
components in the energy band of 2-10 keV have been detected by
ASCA (see Table 1). For simplicity, we assumed that
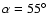 in our calculations although different pulsars
may have different inclination angles. The predicted X-ray
luminosity for these pulsars are shown in Fig. 2, where they are
shown to be consistent with the observed data. Further, our model
indicates that X-ray luminosity for each pulsar increases with the
inclination angle of this pulsar (see Figs. 3 and 4), so using X-ray
data of these pulsars and this feature of our model, we estimated
the approximate inclination angles of these pulsars, and then
calculated high-energy
in our calculations although different pulsars
may have different inclination angles. The predicted X-ray
luminosity for these pulsars are shown in Fig. 2, where they are
shown to be consistent with the observed data. Further, our model
indicates that X-ray luminosity for each pulsar increases with the
inclination angle of this pulsar (see Figs. 3 and 4), so using X-ray
data of these pulsars and this feature of our model, we estimated
the approximate inclination angles of these pulsars, and then
calculated high-energy  -ray conversion efficiencies for the
confirmed
-ray conversion efficiencies for the
confirmed  -ray pulsars, which are consistent with the
observed data (see Table 2).
-ray pulsars, which are consistent with the
observed data (see Table 2).
The differences between the model of Cheng et al. (1998) (also see
Cheng & Zhang 1999) and this model are (i) Cheng et al. (1998) use
the average fractional size of the outer gap, which does not depend
on the inclination angle (i.e. f=f0), but the fractional size of
the outer gap in this model is a function of the inclination angle,
i.e.
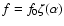 ;
and (ii) they assume that the cascade
stops when the final energy of synchrotron radiation is
;
and (ii) they assume that the cascade
stops when the final energy of synchrotron radiation is 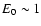 MeV, but here is
MeV, but here is
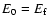 .
Although there are these differences,
both models have similar results. The former gives
.
Although there are these differences,
both models have similar results. The former gives
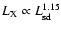 for the pulsed X-ray luminosity of 14 pulsars (Cheng
& Zhang 1999), the latter gives
for the pulsed X-ray luminosity of 14 pulsars (Cheng
& Zhang 1999), the latter gives
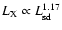 for the
pulsed X-ray luminosity of 19 pulsars, indicating that the previous
model for X-ray emission from pulsars (for example Cheng & Zhang
1999) is reasonable.
for the
pulsed X-ray luminosity of 19 pulsars, indicating that the previous
model for X-ray emission from pulsars (for example Cheng & Zhang
1999) is reasonable.
From Fig. 2, there is a certain difference between the different
observed data with model results for each pulsar. According to this
model, the difference could possibly come from (i) the actual value
of the inclination angle and viewing angle and/or from (ii) ignoring
the contribution of the non-thermal X-rays indirectly emitted from
the outer gap for the Crab-like pulsars (Cheng et al. 2000; Zhang &
Cheng 2000). It should be pointed out that our estimate of pulsar
inclination angle depends on the pulsar distance, but some pulsar's
distances are not well-determined, which introduces a bigger
uncertainty for the estimate of the inclination angle.
Acknowledgements
We thank the anonymous referee for his very
constructive comments and K.S. Cheng for his helpful suggestions.
This work is partially supported by "Hundred Talents Program of
CAS'', Grant for Distinguished Young Scientists from NSFC (10425314), Grand from NSFC (10463002), and Grant from Yunnan Province
(2004PY01).
- Becker, W.,
& Trümper, J. 1997, A&A, 326, 682 [NASA ADS] (In the text)
- Camilo, F.,
Bell, J. F., Manchester, R. N., et al. 2001, ApJ, 557, L51 [NASA ADS] [CrossRef]
- Cheng, K. S.,
& Zhang, L. 1999, ApJ, 515, 337 [NASA ADS] [CrossRef] (In the text)
- Cheng, K. S.,
Ruderman, M., & Zhang, L. 2000, ApJ, 537, 964 [NASA ADS] [CrossRef] (In the text)
- Cheng, K. S.,
Gil, J., & Zhang, L. 1998, ApJ, 493, L35 [NASA ADS] [CrossRef] (In the text)
- Cheng, K. S.,
Taam, R. E., & Wang, W. 2006, ApJ, 641, 427 [NASA ADS] [CrossRef]
- De Luca, A.,
Caraveo, P. A., Mereghetti, S., et al. 2005, ApJ, 623, 1051 [NASA ADS] [CrossRef]
- Fierro, J. M.
1995, Ph.D. Thesis, Stanford Univ.
(In the text)
- Halpern, J.
P., & Ruderman, M. A. 1993, ApJ, 415, 286 [NASA ADS] [CrossRef] (In the text)
- Hartman, R.
C., Bertsch, D. L., Bloom, S. D., et al. 1999, ApJS, 123, 79 [NASA ADS] [CrossRef] (In the text)
- Hirotani,
K., & Shibata, S. 1999a, MNRAS, 308, 54 [NASA ADS] [CrossRef] (In the text)
- Hirotani,
K., & Shibata, S. 1999b, MNRAS, 308, 67 [NASA ADS] [CrossRef]
- Hirotani,
K., & Shibata, S. 2001a, MNRAS, 325, 1228 [NASA ADS] [CrossRef] (In the text)
- Hirotani,
K., & Shibata, S. 2001b, ApJ, 558, 216 [NASA ADS] [CrossRef]
- Hirotani,
K., Harding, A. K., & Shibata, S. 2003, ApJ, 591, 334 [NASA ADS] [CrossRef] (In the text)
- Kaspi, V. M.,
Lackey, J. R., Mattox, J., et al. 2000, ApJ, 528, 445 [NASA ADS] [CrossRef] (In the text)
- Kramer, M.,
Bell, J. F., Manchester, R. N., et al. 2003, MNRAS, 342, 1299 [NASA ADS] [CrossRef] (In the text)
- Possenti,
A., Cerutti, R., Colpi, M., et al. 2002, A&A, 387, 993 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Saito, Y. 1998,
Ph.D. Thesis, Univ. of Tokyo
(In the text)
- Seward, F. D.,
& Wang, Z. 1988, ApJ, 332, 199 [NASA ADS] [CrossRef] (In the text)
- Takata, J.,
shibata, S., & Hirotani, K. 2004, MNRAS, 354, 1120 [NASA ADS] [CrossRef] (In the text)
- Takata, J.,
shibata, S., Hirotani, K., & Chang, H.-K. 2006, MNRAS, 366,
1310 [NASA ADS] (In the text)
- Torres, D. F.,
Butt, Y. M., & Camilo, F. 2001, ApJ, 560, L155 [NASA ADS] [CrossRef] (In the text)
- Wang, F. Y.-H.,
Ruderman, M., Halpern, J. P., & Zhu, T. 1998, ApJ, 498,
373 [NASA ADS] [CrossRef] (In the text)
- Zhang, B., &
Harding, A. K. 2000, ApJ, 532, 1150 [NASA ADS] [CrossRef] (In the text)
- Zhang, L., &
Cheng, K. S. 1997, ApJ, 487, 370 [NASA ADS] [CrossRef] (In the text)
- Zhang, L.,
& Cheng, K. S. 2000, A&A, 363, 575 [NASA ADS] (In the text)
- Zhang, L., &
Cheng, K. S. 2002, ApJ, 579, 716 [NASA ADS] [CrossRef] (In the text)
- Zhang, L., Cheng,
K. S., Jiang, Z. J., & Leung, P. 2004, ApJ, 604, 317 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
![\begin{displaymath}\zeta_1=\left[{2\sqrt{1-{3\over4}{r\over R_{\rm L}}a(\alpha)}...
...lpha)}+ \sqrt{1-{r\over R_{\rm L}}
a(\alpha)}} \right]^{4/7} ,
\end{displaymath}](/articles/aa/full/2006/29/aa2758-05/img26.gif)
![\begin{displaymath}\zeta_2=\left[{4\over 3}{(1-{3\over 4} {r\over R_{\rm L}}
a(\...
...er 2} {r\over R_{\rm L}}
a(\alpha))\cos\alpha} \right]^{1/7} ,
\end{displaymath}](/articles/aa/full/2006/29/aa2758-05/img27.gif)
![\begin{displaymath}\zeta_3=\left(\ln{r\over R}\right)^{{1\over21}} \left({r\over...
...-{3\over 4}{r\over R_{\rm L}}a(\alpha)
\right]^{-{3\over14}} ,
\end{displaymath}](/articles/aa/full/2006/29/aa2758-05/img28.gif)
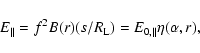
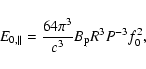
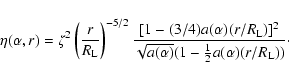
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{2758fig1.eps}
\end{figure}](/articles/aa/full/2006/29/aa2758-05/Timg46.gif)
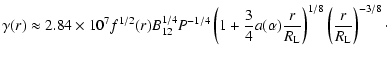
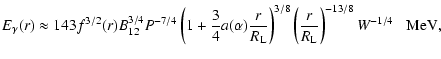
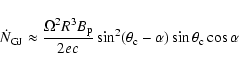
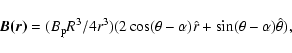
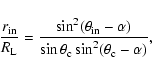
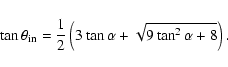
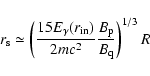
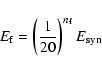
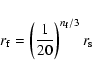
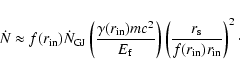
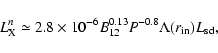
![$\displaystyle \Lambda(r_{\rm in})=a(\alpha)\zeta^{1/2}(r_{\rm in})\cos\alpha\le...
...rm L}}\right]^{3/8} \left({r_{\rm in}\over R_{\rm L}}\right)^{-83/24}W^{-1/6} .$](/articles/aa/full/2006/29/aa2758-05/img75.gif)
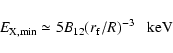
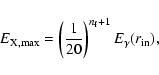
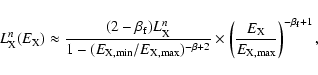
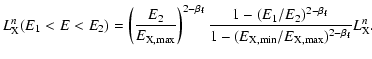
![\begin{figure}
\par\includegraphics[width=6cm,clip]{2758fig2.eps}
\end{figure}](/articles/aa/full/2006/29/aa2758-05/Timg91.gif)
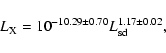
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{2758fig3.eps}
\end{figure}](/articles/aa/full/2006/29/aa2758-05/Timg99.gif)
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{2758fig4.eps}
\end{figure}](/articles/aa/full/2006/29/aa2758-05/Timg100.gif)