A&A 454, 213-219 (2006)
DOI: 10.1051/0004-6361:20053533
S. D. Philipp1 - D. C. Lis2 - R. Güsten1 - C. Kasemann1 - T. Klein1 - T. G. Phillips2
1 - Max-Planck-Institut für Radioastronomie, Auf dem
Hügel 69, 53121 Bonn, Germany
2 - California Institute of Technology, Downs Laboratory
of Physics 320-47, Pasadena, CA 91125, USA
Received 30 May 2005 / Accepted 16 March 2006
Abstract
We present ![]() 15 arcsecond resolution single-dish
imaging of the Horsehead nebula in the C I (1-0) and CO (4-3)
lines, carried out using the CHAMP array at the Caltech Submillimeter
Observatory (CSO). The data are used together with supporting
observations of the (2-1) transitions of the CO isotopologues to
determine the physical conditions in the atomic and molecular gas via
Photon Dominated Region (PDR) modeling. The CO (4-3)/(2-1) line
ratio, which is an excellent tracer of the direction of the incoming
UV photons, increases at the western and northern edges of the nebula,
confirming that the illumination is provided mostly by the stars
15 arcsecond resolution single-dish
imaging of the Horsehead nebula in the C I (1-0) and CO (4-3)
lines, carried out using the CHAMP array at the Caltech Submillimeter
Observatory (CSO). The data are used together with supporting
observations of the (2-1) transitions of the CO isotopologues to
determine the physical conditions in the atomic and molecular gas via
Photon Dominated Region (PDR) modeling. The CO (4-3)/(2-1) line
ratio, which is an excellent tracer of the direction of the incoming
UV photons, increases at the western and northern edges of the nebula,
confirming that the illumination is provided mostly by the stars
![]() and
and ![]() Orionis. The observed line intensities are
consistent with PDR models with an H nuclei volume density of
Orionis. The observed line intensities are
consistent with PDR models with an H nuclei volume density of
![]() cm-3. The models predict a kinetic temperature of
cm-3. The models predict a kinetic temperature of
![]() 12 K and a C18O fractional abundance with respect to H atoms
of
12 K and a C18O fractional abundance with respect to H atoms
of
![]() in the shielded region, which in turn imply a
total molecular mass of
in the shielded region, which in turn imply a
total molecular mass of ![]() 24 M
24 M![]() in the C18O filament. The
outer halo, devoid of C18O, but traced by the C I emission has a
comparable density and contributes additional
in the C18O filament. The
outer halo, devoid of C18O, but traced by the C I emission has a
comparable density and contributes additional ![]() 13 M
13 M![]() of
material, resulting in an upper limit of
of
material, resulting in an upper limit of ![]() 37 M
37 M![]() for the
total molecular mass of the nebula.
for the
total molecular mass of the nebula.
Key words: ISM: individual: objects: Horsehead nebula - ISM: molecules - ISM: structure - ISM: abundances - ISM: clouds - stars: formation
PDRs are surface layers of interstellar molecular clouds exposed to
intense fluxes of FUV photons from external sources, e.g. nearby
hot OB stars or clusters. These regions are strong sources of
far-infrared atomic fine-structure line emission of singly ionized
carbon (C II) and neutral oxygen (O I), molecular hydrogen (H2)
ro-vibrational transitions, as well as infrared continuum
emission. Deeper into the transition region, at
![]() mag of visual extinction, as the FUV flux is gradually
attenuated by the intervening dust, strong emission of fine-structure
lines of neutral atomic carbon (C I) appears, along with carbon
monoxide (CO) rotational lines. The CO emission defines the regions
referred to as molecular clouds, which harbor all known sites of
ongoing star formation in the Milky Way. In recent years, PDRs have
been subjects of numerous observational studies, as well as
theoretical modeling aimed at deriving the physical conditions and
chemical abundance profiles of the atomic and molecular species as a
function of visual extinction (see Hollenbach & Tielens 1997, 1999,
for recent reviews).
mag of visual extinction, as the FUV flux is gradually
attenuated by the intervening dust, strong emission of fine-structure
lines of neutral atomic carbon (C I) appears, along with carbon
monoxide (CO) rotational lines. The CO emission defines the regions
referred to as molecular clouds, which harbor all known sites of
ongoing star formation in the Milky Way. In recent years, PDRs have
been subjects of numerous observational studies, as well as
theoretical modeling aimed at deriving the physical conditions and
chemical abundance profiles of the atomic and molecular species as a
function of visual extinction (see Hollenbach & Tielens 1997, 1999,
for recent reviews).
The Horsehead, best known from its stunning optical images, is located
in the H II region IC 434 in Orion. It is a dense clump of molecular
material at the periphery of the L1630 molecular cloud, protruding
into the H II region and illuminated by the FUV radiation from
![]() Orionis, an O 9.5 V star located at a projected distance of
Orionis, an O 9.5 V star located at a projected distance of
![]() 4 pc. The region has been a subject of several recent and
ongoing studies at millimeter wavelengths. Pound et al. (2003)
presented high-angular resolution CO (1-0) observations of the region
and found that the CO emission closely matches the outline of the dark
patch seen at visual wavelengths. They also showed that the molecular
cloud exhibits a pronounced velocity gradient of 5 km s-1 pc-1 from
the NE to the SW and derived a total mass of the molecular material of
27 M
4 pc. The region has been a subject of several recent and
ongoing studies at millimeter wavelengths. Pound et al. (2003)
presented high-angular resolution CO (1-0) observations of the region
and found that the CO emission closely matches the outline of the dark
patch seen at visual wavelengths. They also showed that the molecular
cloud exhibits a pronounced velocity gradient of 5 km s-1 pc-1 from
the NE to the SW and derived a total mass of the molecular material of
27 M![]() .
The presence of several near-infrared and IRAS sources in
the vicinity of the Horsehead (Reipurth & Bouchet 1984; Sandell et al. 1985) provides direct evidence for recent star formation in the
region. Yamauchi et al. (2000) report a detection of a faint X-ray
point source using ASCA with a luminosity of
.
The presence of several near-infrared and IRAS sources in
the vicinity of the Horsehead (Reipurth & Bouchet 1984; Sandell et al. 1985) provides direct evidence for recent star formation in the
region. Yamauchi et al. (2000) report a detection of a faint X-ray
point source using ASCA with a luminosity of
![]() erg s-1 (0.5-10 keV), which are also interpreted to be young stellar objects.
erg s-1 (0.5-10 keV), which are also interpreted to be young stellar objects.
Zhou et al. (1993) derive a mean H nuclei density in the Horsehead
nebula of ![]()
![]() cm-3 and an incident UV flux
of 20-100 Habing units (Habing 1968) based on their observations of
CO, 13CO, CS, and C II emission. Kramer et al. (1996) derive a
similar density of
cm-3 and an incident UV flux
of 20-100 Habing units (Habing 1968) based on their observations of
CO, 13CO, CS, and C II emission. Kramer et al. (1996) derive a
similar density of
![]() cm-3 from various CO line ratios.
The Horsehead can be identified with the CS (2-1) clump 42 in the
survey of Lada et al. (1991), who derive a virial mass of 35 M
cm-3 from various CO line ratios.
The Horsehead can be identified with the CS (2-1) clump 42 in the
survey of Lada et al. (1991), who derive a virial mass of 35 M![]() and an effective radius of 0.17 pc, leading to an H nuclei density of
and an effective radius of 0.17 pc, leading to an H nuclei density of
![]() cm-3, if the cloud is in virial equilibrium.
Mid-infrared emission from the Horsehead (Abergel et al. 2002, 2003;
also the recent analysis of Habart et al. 2005, published after this
manuscript has been submitted) reveals a sharp filament at the
illuminated edge of the nebula. A comprehensive study of small carbon
chains and rings in this region was presented by Teyssier et al.
(2004) and Pety et al. (2005).
cm-3, if the cloud is in virial equilibrium.
Mid-infrared emission from the Horsehead (Abergel et al. 2002, 2003;
also the recent analysis of Habart et al. 2005, published after this
manuscript has been submitted) reveals a sharp filament at the
illuminated edge of the nebula. A comprehensive study of small carbon
chains and rings in this region was presented by Teyssier et al.
(2004) and Pety et al. (2005).
Here we present high-angular resolution single-dish observations of the Horsehead in the C I (1-0) and CO (4-3) emission, together with supporting observations of the (2-1) transitions of the CO isotopologues. The data are used to derive the physical conditions in the molecular gas through PDR modeling.
The submm observations discussed here were performed using CHAMP at the CSO in two observing periods in January and September 2001. The complementary C18O (2-1) (219.56 GHz) and CO (2-1) (230.54 GHz) data were obtained at the IRAM 30m with the Heterodyn Receiver Array HERA (Schuster et al. 2002) in May 2003.
CHAMP, the "Carbon Heterodyne Array of the MPIfR'' was operated at the CSO until June 2003. The CHAMP array
consists of ![]() elements, with
elements, with
![]() spacing of
the pixels on the sky, where
spacing of
the pixels on the sky, where
![]() is the FWHM beam size
(see, e.g., Güsten et al. 1998, for a design description). The tuning
range of the receiver covered the 625
is the FWHM beam size
(see, e.g., Güsten et al. 1998, for a design description). The tuning
range of the receiver covered the 625 ![]() m atmospheric window
(
m atmospheric window
(![]() 450-495 GHz, limited by the local oscillator), including the
J = 4-3 transition of excited warm CO (461.06 GHz) as well as the
fine-structure transition of atomic carbon [C I] (492.16 GHz).
Cold optics and a Martin-Puplett interferometer serving as a
single-sideband filter, that terminated the image band on a 15 K
absorber, allowed for SSB-system temperatures well below 1000 K in
good atmospheric conditions. The frontend was linked to a flexible
autocorrelator backend, with a maximum bandwidth of 2 GHz (2048 channels) per frontend pixel. For the Horsehead observations we
operated the spectrometer in one of its higher resolution mode,
providing a resolution of 0.15 km s-1 per channel. A network of
fast Digital Signal Processors with optimized Fast Fourier Transform
algorithms processed the correlator raw data realtime.
450-495 GHz, limited by the local oscillator), including the
J = 4-3 transition of excited warm CO (461.06 GHz) as well as the
fine-structure transition of atomic carbon [C I] (492.16 GHz).
Cold optics and a Martin-Puplett interferometer serving as a
single-sideband filter, that terminated the image band on a 15 K
absorber, allowed for SSB-system temperatures well below 1000 K in
good atmospheric conditions. The frontend was linked to a flexible
autocorrelator backend, with a maximum bandwidth of 2 GHz (2048 channels) per frontend pixel. For the Horsehead observations we
operated the spectrometer in one of its higher resolution mode,
providing a resolution of 0.15 km s-1 per channel. A network of
fast Digital Signal Processors with optimized Fast Fourier Transform
algorithms processed the correlator raw data realtime.
The instrument control could handle total power, frequency and wobble
switch observations in pointing, raster and on-the-fly-modes, allowing
to adopt the optimal observing strategy for a given source. The
Horsehead observations were performed in frequency-switched (at 1 Hz
switch frequency) on-the-fly scanning mode. The symmetric switch throw
was set to ![]() 15-25 MHz and the mapping was performed both in RA
and Dec directions with a sampling of 8''. The array was kept in its
orientation with respect to the sky using the de-rotator of the
cryostat.
15-25 MHz and the mapping was performed both in RA
and Dec directions with a sampling of 8''. The array was kept in its
orientation with respect to the sky using the de-rotator of the
cryostat.
Pointing was established by scans across the planets to an accuracy of
a few arcsec rms, the CHAMP beams were diffraction limited (15'' at
464 GHz and 14.5'' at 492 GHz). Calibration of the antenna
temperature scale was performed by the standard chopper wheel method,
coupling efficiencies were determined by flux measurements of the
planets. The efficiencies determined on Jupiter and Mars were
![]() and 0.45, respectively, with max 10% variation
between the pixels. The actual zenith sky opacity during observations
was between 0.06 and 0.11 at 225 GHz.
and 0.45, respectively, with max 10% variation
between the pixels. The actual zenith sky opacity during observations
was between 0.06 and 0.11 at 225 GHz.
The complementary observations of the C18O (2-1) and CO (2-1) lines
with the HEterodyne Receiver Array (HERA) on the
IRAM 30 m telescope on Pico Veleta, Spain were obtained in total power
on-the-fly scanning mode, again with a sampling of 8'' and mapping
performed in both, RA and Dec directions. The array was inclined
18.5
![]() to the equatorial frame using HERA's derotation system. For
details of the set-up and instrument description we refer to Schuster
et al. (2002). Pointing was established on Saturn and the nearby
quasar 0420-014, for calibration we assumed a main-beam coupling
efficiency of 0.52. We estimate the calibration uncertainty to be
to the equatorial frame using HERA's derotation system. For
details of the set-up and instrument description we refer to Schuster
et al. (2002). Pointing was established on Saturn and the nearby
quasar 0420-014, for calibration we assumed a main-beam coupling
efficiency of 0.52. We estimate the calibration uncertainty to be
![]() 20%. The observations were performed under average to good
weather conditions with zenith opacities of
20%. The observations were performed under average to good
weather conditions with zenith opacities of
![]() .
.
In addition, supporting observations of the 13CO(2-1) (220.40 GHz)
transition, with 31'' angular resolution, were carried out, as
a bad weather backup observing program, using the CSO facility
receiver and the CHAMP autocorrelator backend.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{3533fig1.ps}
\end{figure}](/articles/aa/full/2006/28/aa3533-05/Timg30.gif) |
Figure 1:
Distribution of the CO (2-1) integrated intensity, convolved
to 14'' resolution, in the Horsehead in the 8.2-11.7 km s-1 and
11.7-13.8 km s-1 velocity intervals (color-scale image and white
contours, respectively). The low-velocity interval includes most of
the emission from the Horsehead. The C18O (2-1) emission (black
contours, 9.2-11.7 km s-1 velocity interval, also convolved to 14''resolution) reveals a narrow filament running through the center of
the head, referred to as the neck, and a bright hammer-like structure
on the top of the head. A compact high-velocity CO clump, most likely
unrelated to the head is located |
| Open with DEXTER | |
Figure 1 shows the overall morphology of the Horsehead
nebula as traced by the CO (2-1) and C18O (2-1) emission observed
with HERA with 11
![]() angular resolution, smoothed to 16
angular resolution, smoothed to 16
![]() .
Figure 2 shows the CO (4-3) emission overlaid on
the corresponding mosaic of the NOAO Star Formation Survey Data 1997
by J. Bally (private communication) in H
.
Figure 2 shows the CO (4-3) emission overlaid on
the corresponding mosaic of the NOAO Star Formation Survey Data 1997
by J. Bally (private communication) in H![]() emission.
emission.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.9cm,clip]{3533fig2.ps}
\end{figure}](/articles/aa/full/2006/28/aa3533-05/Timg31.gif) |
Figure 2:
Distribution of the CO (4-3) integrated intensity in the
Horsehead in the 8.9-11.7 km s-1 velocity interval (contours as in
Fig. 1) overlaid on the corresponding mosaic of the
NOAO Star Formation Survey Data 1997 by J. Bally (private
communication) in H |
| Open with DEXTER | |
The CO data, both (2-1) and (4-3), show the characteristic outline
of the nebula as seen in the optical images of the region, while the
C18O emission is confined to a narrow filament running through the
center of the head (black contours in Fig. 1;
hereafter referred to as the neck). In addition, a bright, hammer-like
C18O structure is seen near the top of the head. The CO emission
associated with the Horsehead is confined to velocities in the range
8.2-11.7 km s-1 (color image, Fig. 1). Two compact CO
clumps are seen at higher velocities (11.7-14 km s-1), one of them
just ![]() 45
45
![]() south of the brightest C18O peak in the neck
(white contours in Fig. 1). This is either a
background or a foreground source, kinematically distinct from the
head. No C18O or 13CO for which we observed some snapshots using
the CSO, emission in this velocity range has been detected. Therefore,
they appear to be a relatively low column density condensation
(see Sect. 6).
south of the brightest C18O peak in the neck
(white contours in Fig. 1). This is either a
background or a foreground source, kinematically distinct from the
head. No C18O or 13CO for which we observed some snapshots using
the CSO, emission in this velocity range has been detected. Therefore,
they appear to be a relatively low column density condensation
(see Sect. 6).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{3533fig3.ps}
\end{figure}](/articles/aa/full/2006/28/aa3533-05/Timg32.gif) |
Figure 3:
Distribution of the C I integrated intensity in the
8.9-11.7 km s-1 velocity interval (color-scale) and the CO (4-3)
emission (black contours). White contours outline the distribution of
the 350 |
| Open with DEXTER | |
Figure 3 shows the distribution of the C I (1-0) and
CO (4-3) emission observed with CHAMP at ![]() 20 and 16
20 and 16
![]() angular resolution (color image and black contours, respectively). The
CO (4-3) emission is quite uniform, with the exception of a bright
patch near the top of the head. The C I emission is much less
enhanced in this region, compared to CO (4-3), and the brightest C I peak is found instead in the middle of the neck, at the SW end of a
compact 350
angular resolution (color image and black contours, respectively). The
CO (4-3) emission is quite uniform, with the exception of a bright
patch near the top of the head. The C I emission is much less
enhanced in this region, compared to CO (4-3), and the brightest C I peak is found instead in the middle of the neck, at the SW end of a
compact 350 ![]() m continuum source (white contours; D. Dowell, private
communication). The white circles and the dotted polygon in
Fig. 3 mark the location of regions selected for
detailed PDR modeling (Sect. 4). The distribution of the
C I (1-0) emission is strikingly different from that of the C II 158
m continuum source (white contours; D. Dowell, private
communication). The white circles and the dotted polygon in
Fig. 3 mark the location of regions selected for
detailed PDR modeling (Sect. 4). The distribution of the
C I (1-0) emission is strikingly different from that of the C II 158
![]() m emission, as imaged by Zhou et al. (1993) with the FIFI
instrument aboard the Kuiper Airborne Observatory, with a beam size of
each detector of 55
m emission, as imaged by Zhou et al. (1993) with the FIFI
instrument aboard the Kuiper Airborne Observatory, with a beam size of
each detector of 55
![]() in the
in the ![]() array. The
velocity-integrated C II emission (Fig. 2 of Zhou et al. 1993) shows
two peaks north and south of the C I peak in the neck and an
east-west filament just north of the C18O neck. These differences
may be partially attributed to the low spectral resolution of the
C II data, which does not allow for separating emission associated
with the Horsehead from the bright high-velocity emission from the
edge of the L1630 molecular cloud (white contours in
Fig. 1; see also Fig. 1 of Pound et al. 2003).
array. The
velocity-integrated C II emission (Fig. 2 of Zhou et al. 1993) shows
two peaks north and south of the C I peak in the neck and an
east-west filament just north of the C18O neck. These differences
may be partially attributed to the low spectral resolution of the
C II data, which does not allow for separating emission associated
with the Horsehead from the bright high-velocity emission from the
edge of the L1630 molecular cloud (white contours in
Fig. 1; see also Fig. 1 of Pound et al. 2003).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{3533fig4.ps}
\end{figure}](/articles/aa/full/2006/28/aa3533-05/Timg34.gif) |
Figure 4: Sample spectra at the (85, 3) and (82, -37) positions (position A and the high velocity clump, respectively). |
| Open with DEXTER | |
Figure 4 shows example spectra towards the C I peak and
the high-velocity clump positions, with offsets of (85, 3) and
(82, -37) arcsec, respectively, with respect to our nominal reference
position
![]() ,
,
![]() ). The excitation of the high-velocity gas is
different from the Horsehead nebula gas proper and the two are likely
physically not associated. Figure 5 displays the
CO (2-1) and C18O (2-1) velocity channel maps. We confirm the
pronounced velocity gradient along the neck, previously seen by Pound
et al. (2003; 5 km/s/pc), with the horse's nose being most redshifted.
). The excitation of the high-velocity gas is
different from the Horsehead nebula gas proper and the two are likely
physically not associated. Figure 5 displays the
CO (2-1) and C18O (2-1) velocity channel maps. We confirm the
pronounced velocity gradient along the neck, previously seen by Pound
et al. (2003; 5 km/s/pc), with the horse's nose being most redshifted.
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{3533fig5.ps}
\end{figure}](/articles/aa/full/2006/28/aa3533-05/Timg37.gif) |
Figure 5: Velocity channel maps of the C18O (2-1) and CO (2-1) emission (color image and white contours, respectively). Contour levels are 5 to 20 K, with an interval of 5 K. The center velocity of each channel is shown in the upper right corner, channel width 0.5 km s-1. |
| Open with DEXTER | |
The C I and CO isotopologue emission from the Horsehead nebula
have been modeled using the Meudon PDR code (Abgrall et al. 1992; Le
Bourlot et al. 1993; Le Bourlot 2000 and more recently Pety et
al. 2005). This model treats the PDR as a one-dimensional
plane-parallel slab (similar to the one shown in Fig. 1 of Sternberg
2005), with hydrogen density ![]() and an incident radiation
field G0 (in Draine units,
and an incident radiation
field G0 (in Draine units,
![]() erg/s/cm2; one
Draine unit equals 1.7 Habing units). Most of the models presented
here assume a constant density. A comparison with isobaric models is
presented in Sect. 4.2. The chemical network uses 450 chemical species
and roughly 5000 reactions. "Standard'' abundances used for the most
abundant elements are are C/H =
erg/s/cm2; one
Draine unit equals 1.7 Habing units). Most of the models presented
here assume a constant density. A comparison with isobaric models is
presented in Sect. 4.2. The chemical network uses 450 chemical species
and roughly 5000 reactions. "Standard'' abundances used for the most
abundant elements are are C/H =
![]() ,
O/H =
,
O/H =
![]() ,
N/H =
,
N/H =
![]() with isotopic abundances
13C/H =
with isotopic abundances
13C/H =
![]() ,
18O/H =
,
18O/H =
![]() .
The photodissociation of the CO isotopomeres is treated in details.
For a detailed description of the code, we refer the interested reader
to Le Petit et al. (2006).
.
The photodissociation of the CO isotopomeres is treated in details.
For a detailed description of the code, we refer the interested reader
to Le Petit et al. (2006).
In order to characterize the physical conditions in the neck, away
from the narrow, limb-brightened filament on the top of the head,
we have selected three positions. Position A corresponds to the
location of the C I peak in the neck, at the SW end of the 350 ![]() m continuum source. Position B represents the average envelope emission,
m continuum source. Position B represents the average envelope emission,
![]() 70
70
![]() south of the C18O filament (see the dotted polygon
in Fig. 3); this region is characterized by relatively
uniform emission in all the tracers studied here. Finally, position C
corresponds to a CO and C I peak in the "mouth'' region. We assume
that the cloud geometry is that of a roughly cylindrical filament
attached to the main molecular cloud at the bottom of the neck. The
FUV illumination is provided primarily by
south of the C18O filament (see the dotted polygon
in Fig. 3); this region is characterized by relatively
uniform emission in all the tracers studied here. Finally, position C
corresponds to a CO and C I peak in the "mouth'' region. We assume
that the cloud geometry is that of a roughly cylindrical filament
attached to the main molecular cloud at the bottom of the neck. The
FUV illumination is provided primarily by ![]() Orionis (equivalent
Orionis (equivalent
![]() ,
e.g. Pety et al. 2005). The top of the head is
directly exposed to the stellar radiation, while the neck is
illuminated indirectly by the radiation scattered and reprocessed by
the dust. In the models for the neck area (positions A-C), we
assume double-sided illumination with the same FUV intensity on the
front and back side of the cloud, characterized by an enhancement
factor G0 over Draine's value. The only parameters adjusted in the
models are: G0, the hydrogen volume density,
,
e.g. Pety et al. 2005). The top of the head is
directly exposed to the stellar radiation, while the neck is
illuminated indirectly by the radiation scattered and reprocessed by
the dust. In the models for the neck area (positions A-C), we
assume double-sided illumination with the same FUV intensity on the
front and back side of the cloud, characterized by an enhancement
factor G0 over Draine's value. The only parameters adjusted in the
models are: G0, the hydrogen volume density, ![]() (assumed
to be uniform in our constant density models) or the gas
pressure (in our isobaric models, Sect. 4.2), and the total visual
extinction through the cloud,
(assumed
to be uniform in our constant density models) or the gas
pressure (in our isobaric models, Sect. 4.2), and the total visual
extinction through the cloud, ![]() .
The dust extinction curve toward
.
The dust extinction curve toward
![]() Ori has not been measured. We thus use the dust extinction
curve parameters derived by Fitzpatrick & Massa (1990) toward
HD 37903, the star illuminating the nearby NGC 2023 reflection nebula.
The HD 37903 extinction curve is relatively similar to the standard
Galactic extinction curve (Seaton 1979).
Ori has not been measured. We thus use the dust extinction
curve parameters derived by Fitzpatrick & Massa (1990) toward
HD 37903, the star illuminating the nearby NGC 2023 reflection nebula.
The HD 37903 extinction curve is relatively similar to the standard
Galactic extinction curve (Seaton 1979).
The model parameters are listed in Table 1. The integrated
line intensities, computed assuming a face-on geometry and a turbulent
velocity dispersion of 0.8 km s-1 (FWHM), roughly consistent with the
observed line widths of the 13CO (2-1) and C I emission, are also
listed for each model, along with the observed line intensities. The
last column in Table 1 gives the reduced ![]() per
degree of freedom for each model,
per
degree of freedom for each model,
![]() ,
where
,
where
![]() and
and
![]() are the observed and model line intensities integrated over all
velocities,
are the observed and model line intensities integrated over all
velocities,
![]() is the uncertainty of the observed
intensities (assumed to be 20% for all transitions) and N is the
number of grid points. The transitions included in the fit are
CO (2-1), CO (4-3), CO (6-5), 13CO(2-1), C18O (2-1), and
C I (1-0). CO (6-5) has been observed at a position 27
is the uncertainty of the observed
intensities (assumed to be 20% for all transitions) and N is the
number of grid points. The transitions included in the fit are
CO (2-1), CO (4-3), CO (6-5), 13CO(2-1), C18O (2-1), and
C I (1-0). CO (6-5) has been observed at a position 27
![]() away of
the C I peak (position A) (M. Gerin, private communication; observed
using the CSO) and we assume that the CO (4-3)/(6-5) ratio there is
the same as at the C I peak. CO (6-5) has not been observed toward
positions B and C, and is thus not included in the fit at this
location.
away of
the C I peak (position A) (M. Gerin, private communication; observed
using the CSO) and we assume that the CO (4-3)/(6-5) ratio there is
the same as at the C I peak. CO (6-5) has not been observed toward
positions B and C, and is thus not included in the fit at this
location.
Table 1: PDR models of the Horsehead nebula.
The observed line intensities at position A are well reproduced by
model A1, with G0 =25,
![]() cm-3, and
cm-3, and
![]() .
The extinction is tightly constrained to fit the C18O
line intensity. With the uncertainties of the dust emission
coefficients and temperature, the derived extinction is
consistent with the 1.2 mm continuum flux given in the literature
(S = 44 mJy; D. Tessier priv. comm., Ph.D. Thesis).
.
The extinction is tightly constrained to fit the C18O
line intensity. With the uncertainties of the dust emission
coefficients and temperature, the derived extinction is
consistent with the 1.2 mm continuum flux given in the literature
(S = 44 mJy; D. Tessier priv. comm., Ph.D. Thesis).
Models A2 and A3 show how the output intensities vary
with the gas density. High-J, means high excitation CO lines
are most affected (compare model A2 vs. A3 and
A4 vs. A5, respectively). In particular, the
CO (6-5)/(2-1) ratio increases by a factor of ![]() 2 for the
density increasing from
2 for the
density increasing from
![]() to
to
![]() cm-3.
Subthermally excited, high-J CO lines are thus excellent density
tracers in PDRs (the density effect is even stronger for the high-Jlines of optically thin CO isotopologues). On the other hand, line
intensities of the low-J transitions of the CO isotopologues, as well
as the CI line are little affected by the gas density.
Models A4 and A5 show the effect of G0 on the model
line intensities. All line intensities increase with G0, with C I and CO (6-5) being most affected. Finally, model A6 shows the
effect of
cm-3.
Subthermally excited, high-J CO lines are thus excellent density
tracers in PDRs (the density effect is even stronger for the high-Jlines of optically thin CO isotopologues). On the other hand, line
intensities of the low-J transitions of the CO isotopologues, as well
as the CI line are little affected by the gas density.
Models A4 and A5 show the effect of G0 on the model
line intensities. All line intensities increase with G0, with C I and CO (6-5) being most affected. Finally, model A6 shows the
effect of ![]() on the computed line intensities. Only the C18O intensity is affected, increasing with
on the computed line intensities. Only the C18O intensity is affected, increasing with ![]() .
All the line intensities
in Table 1 are computed assuming a 0
.
All the line intensities
in Table 1 are computed assuming a 0![]() inclination
angle between the line of sight and the line normal to the PDR
surface. Increasing the inclination angle affects primarily
intensities of the optically thin lines, namely C I and C18O. As is
clear from this comparison, the different model parameters affect the
computed line intensities of different transitions and a good fit can
be generally obtained for different locations in the Horsehead.
inclination
angle between the line of sight and the line normal to the PDR
surface. Increasing the inclination angle affects primarily
intensities of the optically thin lines, namely C I and C18O. As is
clear from this comparison, the different model parameters affect the
computed line intensities of different transitions and a good fit can
be generally obtained for different locations in the Horsehead.
The observed line intensities at position B are relatively well
reproduced by model B1 with a hydrogen density of
![]() cm-3, somewhat lower than that derived at position A, and a low
value of
cm-3, somewhat lower than that derived at position A, and a low
value of
![]() .
The low C I line intensity is a direct
consequence of the low G0 value. As illustrated by model B2,
increasing the value of G0 to 2 results in a C I intensity
.
The low C I line intensity is a direct
consequence of the low G0 value. As illustrated by model B2,
increasing the value of G0 to 2 results in a C I intensity ![]() 40% higher than the observed value. Therefore, this part of the neck
appears to be well shielded from the FUV photons.
40% higher than the observed value. Therefore, this part of the neck
appears to be well shielded from the FUV photons.
Model C1 gives the best fit to the observed line intensities in
the mouth area, position C. The derived gas density at this location,
![]() cm-3 is the same as at the C I peak in the neck
(position A), and
cm-3 is the same as at the C I peak in the neck
(position A), and
![]() is intermediate between the value at
positions A and B. This suggests that the mouth is also partially
shielded from the FUV photons, although not as well as the back of the
neck. This region may be partially illuminated by the radiation from
is intermediate between the value at
positions A and B. This suggests that the mouth is also partially
shielded from the FUV photons, although not as well as the back of the
neck. This region may be partially illuminated by the radiation from
![]() Ori to the north.
Ori to the north.
The volume density and visual extinction values derived from the PDR
modeling at positions A and B correspond to the line-of-sight depths
of ![]() 230 and 70
230 and 70
![]() ,
respectively, assuming a distance of
400 pc (Lada et al. 1991). These values are comparable to the width of
the nebula in the plane of the sky, confirming our initial assumption
of a roughly cylindrical geometry of the neck.
,
respectively, assuming a distance of
400 pc (Lada et al. 1991). These values are comparable to the width of
the nebula in the plane of the sky, confirming our initial assumption
of a roughly cylindrical geometry of the neck.
Interestingly, a good fit to the observed line intensities assuming a
face-on geometry can also be obtained at position D, on the top
of the head (model D1). In this case a somewhat higher gas
density of
![]() cm-3 is required and the FUV illumination
assumed in this model is that of an O 9.5 V star at a distance of
4 pc, the parameters corresponding to those of
cm-3 is required and the FUV illumination
assumed in this model is that of an O 9.5 V star at a distance of
4 pc, the parameters corresponding to those of ![]() Ori (see
Fig. 1 of Pound et al. 2003). The angular resolution of our data is
insufficient to resolve the PDR layer in its fine details, but the
density we derive from our excitation model for the shielded region is
comparable to the density of
Ori (see
Fig. 1 of Pound et al. 2003). The angular resolution of our data is
insufficient to resolve the PDR layer in its fine details, but the
density we derive from our excitation model for the shielded region is
comparable to the density of
![]() cm-3 derived by
Habart et al. (2005) from their high-resolution IR-spectroscopy of the
H2 fluorescent emission and CO lines.
cm-3 derived by
Habart et al. (2005) from their high-resolution IR-spectroscopy of the
H2 fluorescent emission and CO lines.
PDR models A3 and D1 predict face-on C II 158 ![]() m line intensities of
m line intensities of
![]() and
and
![]() erg cm-2 s-1 sr-1, respectively. These are in reasonably
good agreement with the observed values of the head (see Fig. 3 of
Zhou et al. 1993). The low spatial (55'') and spectral (50 km s-1)
resolution of the C II data make a more quantitative comparison
difficult. Future missions (like SOFIA and Herschel/HIFI) will
provide the complementary data required for a more detailed analysis.
erg cm-2 s-1 sr-1, respectively. These are in reasonably
good agreement with the observed values of the head (see Fig. 3 of
Zhou et al. 1993). The low spatial (55'') and spectral (50 km s-1)
resolution of the C II data make a more quantitative comparison
difficult. Future missions (like SOFIA and Herschel/HIFI) will
provide the complementary data required for a more detailed analysis.
All the models presented above assume a constant density
distribution throughout the cloud. Given the strong temperature
gradient, this assumption results in the gas pressure increasing
rapidly toward the surface. Habart et al. (2005) presented a
high-resolution study of the Horsehead nebula and based on their PDR
modeling concluded that the interface region is well described by a
constant pressure model, with
![]() K cm-3. We
therefore run a series of isobaric models equivalent to our model D1
using the Meudon PDR code. The results are shown in Table 1, models
D2-D4.
K cm-3. We
therefore run a series of isobaric models equivalent to our model D1
using the Meudon PDR code. The results are shown in Table 1, models
D2-D4.
The intensity of the CO (6-5) line is most sensitive to the
value of the pressure in the isobaric models and a good fit to
the observed line intensities is obtained for
![]() K cm-3. This is within a factor of 2 from the value
derived by Habart et al. (2005). Given all the modeling and
calibration uncertainties, this can be considered as good
agreement. We note that the value of
K cm-3. This is within a factor of 2 from the value
derived by Habart et al. (2005). Given all the modeling and
calibration uncertainties, this can be considered as good
agreement. We note that the value of ![]() is the same in our best
fit constant-density and constant-pressure models. The resulting
column density and mass estimates are thus not affected.
is the same in our best
fit constant-density and constant-pressure models. The resulting
column density and mass estimates are thus not affected.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{3533fig6.ps}
\end{figure}](/articles/aa/full/2006/28/aa3533-05/Timg68.gif) |
Figure 6:
CO (4-3)/CO (2-1) ratio map at 16
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{3533fig7.eps}
\end{figure}](/articles/aa/full/2006/28/aa3533-05/Timg69.gif) |
Figure 7:
Peak line intensities of various CO transitions in the PDR
model D1 as a function of distance from the ionization front
(assuming a line-of-sight depth of 120''). The CO (4-3)/(2-1)
ratio is shown as a double line (right axis). Ratios of order unity,
corresponding to the maximum observed value in Fig. 6,
are only present in the outer
|
| Open with DEXTER | |
Figure 6 shows the CO (4-3)/(2-1) intensity ratio at
16
![]() angular resolution. The ratio is relatively uniform across
the nebula, with a marked increase at the northern (red rim,
Fig. 6) and western edge. Figure 7 shows
edge-on peak line intensities of various CO transitions as a function
of distance from the ionization front, computed from PDR model
D1 for a 120
angular resolution. The ratio is relatively uniform across
the nebula, with a marked increase at the northern (red rim,
Fig. 6) and western edge. Figure 7 shows
edge-on peak line intensities of various CO transitions as a function
of distance from the ionization front, computed from PDR model
D1 for a 120
![]() line-of-sight depth. The line intensities
are computed from the molecular level population given by the PDR
model that are assumed to be constant along each line of sight and to
vary only with the distance from the ionization front. The gas kinetic
temperature is also shown, along with the CO (4-3)/(2-1) line ratio
(double line, right axis). The CO (4-3)/(2-1) ratio in the model
increases toward the edge of the PDR owing to the difference in
optical depth between the two transitions in the region with a steep
temperature gradient. This ratio is thus an excellent tracer of the
direction of incoming UV photons. In the case of the Horsehead, the
illumination comes primarily from the west (
line-of-sight depth. The line intensities
are computed from the molecular level population given by the PDR
model that are assumed to be constant along each line of sight and to
vary only with the distance from the ionization front. The gas kinetic
temperature is also shown, along with the CO (4-3)/(2-1) line ratio
(double line, right axis). The CO (4-3)/(2-1) ratio in the model
increases toward the edge of the PDR owing to the difference in
optical depth between the two transitions in the region with a steep
temperature gradient. This ratio is thus an excellent tracer of the
direction of incoming UV photons. In the case of the Horsehead, the
illumination comes primarily from the west (![]() Ori),
as suggested by the sharp increase of the CO (4-3)/(2-1)
ratio, as well as the bright H2 fluorescent emission and PAH emission
(Habbart et al. (2005). However the observed increase in the CO (4-3)/(2-1)
ratio on the north side of the neck may suggest additional illumination from
Ori),
as suggested by the sharp increase of the CO (4-3)/(2-1)
ratio, as well as the bright H2 fluorescent emission and PAH emission
(Habbart et al. (2005). However the observed increase in the CO (4-3)/(2-1)
ratio on the north side of the neck may suggest additional illumination from
![]() Ori
Ori![]() at a projected distance of 30
at a projected distance of 30![]() to the north.
The back of the neck, on the other hand, appears well shielded from the UV
photons. This conclusion is consistent with the results of our PDR modeling
(Sect. 4).
to the north.
The back of the neck, on the other hand, appears well shielded from the UV
photons. This conclusion is consistent with the results of our PDR modeling
(Sect. 4).
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{3533fig8.ps}
\end{figure}](/articles/aa/full/2006/28/aa3533-05/Timg70.gif) |
Figure 8:
Temperature structure (double line, right
scale) and abundance profiles as a function of |
| Open with DEXTER | |
The main result of the PDR modeling described above, in addition to
constraining the gas density, is the determination of the kinetic
temperature and C18O and Carbon abundance in the shielded region.
With this information, we can accurately determine the molecular mass
of the cloud. From the best fit model for the C I peak in the neck,
A1, we derive a fractional C18O abundance (with respect to H
nuclei) of
![]() and a kinetic temperature of
and a kinetic temperature of ![]() 12 K in the shielded region (Fig. 8). This C18O fractional abundance can be compared with the value of
12 K in the shielded region (Fig. 8). This C18O fractional abundance can be compared with the value of
![]() and
and
![]() derived by Teyssier et al. (2004)
and Pety et al. (2005) ("CO-peak'' and "Cloud'' positions,
respectively). Based on LVG models with an H nuclei density of
derived by Teyssier et al. (2004)
and Pety et al. (2005) ("CO-peak'' and "Cloud'' positions,
respectively). Based on LVG models with an H nuclei density of
![]() cm-3 and a kinetic temperature of 12 K, we derive a
conversion factor from the C18O (2-1) integrated line intensity to
the C18O column density of
cm-3 and a kinetic temperature of 12 K, we derive a
conversion factor from the C18O (2-1) integrated line intensity to
the C18O column density of
![]() cm-2 (K km s-1)-1. This conversion factor is not
sensitive to the volume density and varies by
cm-2 (K km s-1)-1. This conversion factor is not
sensitive to the volume density and varies by ![]() 17% for kinetic
temperatures between 10 and 15 K. Under these assumptions, and using a
distance of 400 pc, we derive the total mass contained in the C18O filament to be 24 M
17% for kinetic
temperatures between 10 and 15 K. Under these assumptions, and using a
distance of 400 pc, we derive the total mass contained in the C18O filament to be 24 M![]() ,
slightly lower than the value derived by
Pound et al. (2003) based on their CO (1-0) interferometric
observations (27 M
,
slightly lower than the value derived by
Pound et al. (2003) based on their CO (1-0) interferometric
observations (27 M![]() ).
).
As seen in Fig. 8, C18O is photo-dissociated in the
outer PDR layers with
![]() ,
hence does not trace these outer
layers. However, the C I emission is an excellent tracer of this
region. In fact, the C abundance drops just as the C18O abundance
increases and the two tracers can thus be considered complementary.
The C fractional abundance, with respect to H nuclei, in the outer
envelope reaches a maximum of
,
hence does not trace these outer
layers. However, the C I emission is an excellent tracer of this
region. In fact, the C abundance drops just as the C18O abundance
increases and the two tracers can thus be considered complementary.
The C fractional abundance, with respect to H nuclei, in the outer
envelope reaches a maximum of
![]() at an
at an
![]() and decreases to
and decreases to
![]() at an
at an
![]() .
The gas
kinetic temperature in this region is between 45 and 15 K. The atomic
carbon column density can be computed from the LTE formula
.
The gas
kinetic temperature in this region is between 45 and 15 K. The atomic
carbon column density can be computed from the LTE formula
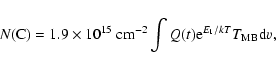 |
(1) |
We derive a peak C I column density of
![]() cm-2 toward the high velocity CO clump south of the neck
(Fig. 1), corresponding to an H nuclei column density
of
cm-2 toward the high velocity CO clump south of the neck
(Fig. 1), corresponding to an H nuclei column density
of
![]() cm-2. No C18O emission is detected at
this location, confirming that this is a low column density fragment
poorly shieldedfrom the UV field. The total molecular mass of this
clump, based on the C I emission, is only
cm-2. No C18O emission is detected at
this location, confirming that this is a low column density fragment
poorly shieldedfrom the UV field. The total molecular mass of this
clump, based on the C I emission, is only ![]() 0.2 M
0.2 M![]() .
.
The C I and CO isotopologue line intensities observed toward the
Horsehead nebula are consistent with PDR models assuming FUV
illumination primarily from ![]() Orionis. Our models indicate an
average density of H nuclei of
Orionis. Our models indicate an
average density of H nuclei of ![]() 3 (shielded neck) to
3 (shielded neck) to
![]() cm-3 (top of the head). The models predict a kinetic
temperature of
cm-3 (top of the head). The models predict a kinetic
temperature of ![]() 12 K and a C18O fractional abundance with
respect to H of
12 K and a C18O fractional abundance with
respect to H of
![]() in the shielded region traced by
the C18O emission. Towards the PDR layers facing the ionizing
star(s), temperatures increase to
in the shielded region traced by
the C18O emission. Towards the PDR layers facing the ionizing
star(s), temperatures increase to ![]() 50 K at an
50 K at an ![]() of 1 (nicely
reflected in the enhanced CO (4-3)/(2-1) line ratio). Using these
parameters, we derive a total molecular mass of 24 M
of 1 (nicely
reflected in the enhanced CO (4-3)/(2-1) line ratio). Using these
parameters, we derive a total molecular mass of 24 M![]() in the
C18O filament. The outer halo devoid of C18O emission, but traced
by the C I emission contributes additional 13 M
in the
C18O filament. The outer halo devoid of C18O emission, but traced
by the C I emission contributes additional 13 M![]() of material,
leading to upper limit of
of material,
leading to upper limit of ![]() 37 M
37 M![]() for the total mass of the
nebula.
for the total mass of the
nebula.
Acknowledgements
This research has been supported by NSF grant AST 22-09008 to the Caltech Submillimeter Observatory. We thank D. Dowell for providing us with the 350
m SHARC II image prior to publication and J. Bally for the mosaic on the horsehead of the NOAO Star Formation Survey Data 1997 in H
emission, J. Le Bourlot and E. Roueff for their assistance with the Meudon PDR code, and M. Gerin, K. M. Menten, P. Schilke and M. Walmsley for stimulating discussions. Also we like to thank the CSO staff for their help and support during the CHAMP campaigns.