A&A 454, 37-53 (2006)
DOI: 10.1051/0004-6361:20052733
A. von der Linden 1,2 - T. Erben 1 - P. Schneider 1 - F. J. Castander 3
1 - Argelander-Institut für Astronomie![]() ,
Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
,
Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
2 -
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str. 1, Postfach 1317,
85741 Garching, Germany
3 -
Institut d'Estudis Espacials de Catalunya/CSIC,
Gran Capita 2-4, 08034 Barcelona, Spain
Received 20 January 2005 / Accepted 10 March 2006
Abstract
Using HST WFPC2 mosaic imaging, deep Chandra observations, and the
original CFHT imaging, we investigate the case for the dark clump candidate
originally presented by (Erben et al. 2000, A&A, 355, 23).
We show that the original detection is well reproducible in the CFHT data,
and can confirm the presence of an alignment signal at the dark clump
position in the HST data. The HST signal strength, however, is weaker than in
the ground-based data.
A comparison of the ellipticity measurements from the space-based HST data
and the ground-based CFHT data on an object-by-object basis shows a remarkable agreement on average, demonstrating that weak lensing studies from high-quality ground-based
observations can yield reliable results. In the vicinity of the
dark clump position, however, there is a notable disagreement in the
ellipticity measurements tangential to it, which leads to the discrepant
lensing results. Despite a detailed investigation,
the cause of this disagreement remains unclear.
In the deep HST observations, we find a significant number overdensity of
galaxies close to the dark clump, but due to lacking redshift estimates it
is unclear whether this corresponds to a coherent structure.
Deep Chandra observations of the dark clump fail to reveal significant
extended emission, in contrast to the original putative ROSAT detection.
Altogether, the current data render the hypothesis of a dark matter halo
similar to that of a massive cluster unlikely. Yet there remains evidence
that the alignment signal is caused not solely by intrinsic galaxy
ellipticities. Likely explanations are thus a superposition of the lensing
signal of a less massive system with a noise peak, or a filament along the
line-of-sight.
Key words: gravitational lensing - cosmology: dark matter - galaxies: clusters: general
In the currently favored cosmological model, structure formation in the universe is dominated by collisionless Cold Dark Matter (CDM). The model of structure formation by gravitational collapse in a pressure-less fluid is able to successfully reproduce the filamentary large scale structure observed in the universe (e.g. Peacock 1999). However, for the formation of galaxies and galaxy clusters, gas dynamics play an important role. It seems obvious that galaxy formation is triggered when gas falls into the potential wells of dark matter concentrations. We therefore expect to find galaxies at the high-density peaks of the dark matter distribution. In the CDM scenario, small halos collapse earlier and merge to larger halos later. For galaxy formation, this implies that the large galaxies we see today formed from mergers of protogalaxies. Observations support this theory: we see more irregular, small galaxies at higher redshifts and many merger systems and galaxies showing evidence for recent mergers. This bottom-up scenario also calls for galaxy clusters to build up through the merger of smaller halos.
While it may be possible to (temporarily) drive gas from galaxy-sized halos, when such halos merge to form cluster-sized objects, the majority of them should contain galaxies and/or hot gas, so that the resulting massive halo is expected to contain a substantial amount of luminous matter. A cluster-sized halo very poor of luminous matter (dark clump) would require a mechanism to drive the gas out of all the smaller halos from which it assembled or from the massive halo itself. Both cases are highly unlikely: the first is very improbable, the second very difficult due to the high mass of the object. At the moment, there are no well-motivated physical processes to explain either scenario.
The discovery of a dark clump would therefore call for a critical reevaluation of our current understanding of structure formation in the universe. Currently, the only tool available to search for such objects is gravitational lensing, as it probes matter concentrations independent of their nature.
In the course of a weak lensing study, Erben et al. (2000) announced
the possible discovery of a dark clump, about
![]() south of the
galaxy cluster Abell 1942. This assertion is based on
significant alignment signals seen in two independent high-quality images, taken with the MOCAM and UH8K cameras at the CFHT. There is no associated apparent galaxy overdensity
visible in these images nor in deep H-band images analyzed by
Gray et al. (2001). There is faint X-ray emission about
south of the
galaxy cluster Abell 1942. This assertion is based on
significant alignment signals seen in two independent high-quality images, taken with the MOCAM and UH8K cameras at the CFHT. There is no associated apparent galaxy overdensity
visible in these images nor in deep H-band images analyzed by
Gray et al. (2001). There is faint X-ray emission about
![]() from
the lensing centroid detected by the ROSAT survey, but it is unclear
whether this could be associated with a lensing object. If the alignment
signal is due to a lensing mass at a similar redshift as the cluster,
z=0.223, this halo would have a mass of the order of
from
the lensing centroid detected by the ROSAT survey, but it is unclear
whether this could be associated with a lensing object. If the alignment
signal is due to a lensing mass at a similar redshift as the cluster,
z=0.223, this halo would have a mass of the order of
![]() .
At a higher redshift (0.8-1.0), it would
require a mass of the order of
.
At a higher redshift (0.8-1.0), it would
require a mass of the order of
![]() .
.
There are currently three more such dark clump candidates in the literature:
However, the noise in weak lensing analyses due to intrinsic ellipticities of galaxies can have a profound effect on the statistics of the number of halos detected per area. Intrinsic ellipticities may mimic tangential alignment, thereby causing false peaks or boosting the significance of lensing signals (e.g. Hamana et al. 2004).
To determine the nature of the dark clump near Abell 1942, we obtained a set of HST observations of the field (General Observer Program, Proposal ID 9132, PI Erben). The HST probes fainter and thus more distant galaxies, for which the distortions of a foreground lensing mass are larger; additionally, due to the lack of seeing, its shape measurements should be more reliable. If the alignment signal seen in the ground-based data is due to a lensing mass, it should thus be even more significant in the HST data.
The structure of this paper is as follows. In Sect. 2 we present the optical data available to us, namely the CFHT images of the original detection and the HST data, along with our data reduction methods to extract object catalogs suitable for lensing studies. Section 3 gives a brief overview of the weak lensing methods employed in this paper. In Sect. 4 we present a re-analysis of the I-band image of the CFHT data. Our weak lensing analysis of the HST data, which confirms the alignment signal, but not its strength, is described in Sect. 5. In Sect. 6 we use a deep Chandra image to show that the ROSAT source is likely to be a spurious detection. The appendices illustrate various tests for systematics (Appendix A) and a comparison of the individual shape measurements of objects common to the CFHT and HST datasets (Appendix B).
The goal of this work is to understand the origin of the lensing signal seen by Erben et al. (2000). We therefore consider both the ground-based dataset used in the original discovery as well as the HST data. Such a treatment also allows for a direct comparison of the ellipticity measurements of objects detected in both datasets.
Our analysis concentrates on the same I-band image as used in
Erben et al. (2000), as this covers most of the area imaged by the HST. We use Chip 3 of a mosaic
observation of Abell 1942 taken with the UH8K camera, with a pixel scale of
![]() .
9 exposures of 1200 s went into the final
image, which has a seeing of
.
9 exposures of 1200 s went into the final
image, which has a seeing of
![]() .
Unfortunately, a photometric calibration is missing.
.
Unfortunately, a photometric calibration is missing.
Our HST data is a WFPC2 mosaic (approximately 5
![]()
![]()
![]() )
of six pointings, each
consisting of 12 dithered exposures with an exposure time of 400 s each, taken between May 20th and June 1st, 2001. The position of the mosaic with respect to the
I-band image from the CFHT is shown in Fig. 1 The filter
employed was F702W.
)
of six pointings, each
consisting of 12 dithered exposures with an exposure time of 400 s each, taken between May 20th and June 1st, 2001. The position of the mosaic with respect to the
I-band image from the CFHT is shown in Fig. 1 The filter
employed was F702W.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{2733_01.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg58.gif) |
Figure 1: The outlines of the six HST pointings superposed on the CFHT I-band image. The center of Abell 1942 lies in the top half of the CFHT image, the HST mosaic is centered on the dark clump position. |
| Open with DEXTER | |
Our reduction of the HST data is based largely on the dither package (Fruchter & Hook 2002) for IRAF. Each of the six pointings was reduced separately. Simultaneous processing of the four individual chips is done automatically by the dither routines. Due to their better signal-to-noise behavior, only the chips of the Wide Field Camera, namely Chips 2, 3, and 4 of WFPC2, were used for the later analysis. The dither pattern of the images allows us to achieve a higher resolution in the coadded image via the drizzle algorithm (Gonzaga et al. 1998).
The steps of the reduction are outlined in the following:
![\begin{figure}
\par\includegraphics[width=17.35cm,clip]{2733_02.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg59.gif) |
Figure 2:
The HST mosaic with an illustration of the various dark clump centroids cited in the
text: the centroid we found in the ground-based data ( |
| Open with DEXTER | |
For both datasets, we used a similar process to build the object catalogs. Differences in the procedure arise mainly from the small field-of-view and mosaic nature of the HST data.
We manually updated the astrometric information of the ground-based image until its bright objects coincide with their positions as given in the USNO-A2 catalog (Monet et al. 1998). This step is not necessary for the lensing analysis of the ground-based image, but provides us with a reference catalog for the astrometric calibration of the HST mosaic.
The HST images are aligned roughly with sky coordinates, but since each chip
is read out along a different chip border, the individual images are rotated
with respect to each other. To avoid
confusion, we first rotate the images of Chips 2 and 4 by
![]() ,
respectively, such that north is up and east to the left (approximately).
This is performed solely as a rearrangement of pixel values to avoid
any additional resampling process.
,
respectively, such that north is up and east to the left (approximately).
This is performed solely as a rearrangement of pixel values to avoid
any additional resampling process.
In order to avoid noise signals and distorted ellipticity measurements, we mask out bright stars and the artefacts they cause (diffraction spikes, blooming, CTE trails, a ripple-like structure at the eastern edge of the I-band image, and brightening of the background along columns of the HST chips in two cases). In the HST image, we also mask the bright galaxy in the field.
We use SExtractor (Bertin & Arnouts 1996) to identify objects in the
image. SExtractor considers N connected pixels that are at a level
![]() above the sky background as an object, with
above the sky background as an object, with
![]() being the standard deviation of the background noise. For the CFHT image, we use N = 3 and k=1.0. These are very low
thresholds, but since we later want to correlate objects present in both
datasets, we strive to obtain a high number density of objects. For the HST images we use N = 3 and k=1.5.
being the standard deviation of the background noise. For the CFHT image, we use N = 3 and k=1.0. These are very low
thresholds, but since we later want to correlate objects present in both
datasets, we strive to obtain a high number density of objects. For the HST images we use N = 3 and k=1.5.
HST: astrometric and photometric calibration
The astrometric calibration plays an important role for a mosaic dataset such as our HST images, as it gives the position of the images with respect to each other. Indeed, the positions on the sky will be used later on in the lensing analysis rather than x and y position on the chip.
For a reference catalog, we had extracted a catalog of bright objects from the astrometrically calibrated ground-based I-band image (see Sect. 2.3.1). We match the entries of the reference catalog to objects found in the HST images. This allows the determination of the pointing and the distortion of the image. Objects that are detected both in the I-band and the HST image can then be identified by sky coordinates.
The photometric calibration is done based on the relevant keywords of the HST image headers.
For the objects in the SExtracted catalogs, we measure the ellipticities using a modified version of the imcat software, following the method of Kaiser et al. (1995). We used the half-light radius as measured by SExtractor as the radius of the weight function with which the brightness profile is weighted.
The measured image ellipticity
![]() is related to the source
ellipticity
is related to the source
ellipticity
![]() by
by
To correct for the anisotropy induced by the telescope-detector system, we
measure the ellipticities of the stars present in the field; for these
Eq. (1) simplifies to
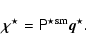 |
(2) |
Thus, we obtain anisotropy-corrected ellipticity measurements:
Since the PSF cannot be described analytically across chip-borders, the anisotropy correction for a mosaic has to be applied to the single chips. With the small field of view of the WF chips, we have the added difficulty that for each image, there are only about five stars that could be used for the polynomial fitting, obviously not enough. Since the images were taken consecutively, we can assume that the PSF does not change considerably between the six pointings. We therefore apply an anisotropy correction for each chip based upon all the stars that were found in the six images taken by that chip.
The 18 single-chip catalogs are combined to three catalogs, one for each chip. Because there are still few stars even in these catalogs, the stellar sequence is selected manually. For each catalog, a third-order polynomial is fitted.
The anisotropy correction of the HST images is further discussed in Appendix A.1.
After the anisotropy correction, the second step in retrieving an estimate
of the local shear from
ellipticity measurements is the correction for the
![]() tensor.
It is a combination of
tensor.
It is a combination of
![]() and the shear polarizability
tensor
and the shear polarizability
tensor
![]() :
:
The basic assumption of weak lensing studies is that the average source
ellipticities vanish, i.e.
![]() .
We also assume
that
.
We also assume
that
![]() ,
so by averaging
Eq. (1) we obtain:
,
so by averaging
Eq. (1) we obtain:
![]() is an almost diagonal tensor with
similar elements on the diagonal. In fact, in the absence of a weight
function and a PSF its elements would be:
is an almost diagonal tensor with
similar elements on the diagonal. In fact, in the absence of a weight
function and a PSF its elements would be:
![]() ,
,
![]() .
We can therefore approximate the
tensor
.
We can therefore approximate the
tensor
![]() by a scalar quantity:
by a scalar quantity:
We therefore use a variant of Eq. (5) as our estimate of the local
shear at each galaxy's position:
The ellipticities were measured with respect to the x-axis of each
image, which for all images runs approximately along the east axis. However,
the lensing analyses are done in sky coordinates. We therefore need to
transform the ellipticity measurements so that their position angle is
measured relative to the right ascension axis. This is done with the
transformation
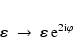
After this step, the 18 single-image catalogs of the HST data are merged into one catalog.
To describe the reliability of its shape measurement, we want to assign
a weight to each galaxy, based on its noise properties. Since our shear
estimates are gained from averages over ellipticities, a good weight
estimate is
After the weighting, we remove objects with
![]() .
Such objects
would dominate the shear signal, but
these are also the objects that are most afflicted by noise in the
.
Such objects
would dominate the shear signal, but
these are also the objects that are most afflicted by noise in the
![]() tensor. Additionally, we use only objects for which
tensor. Additionally, we use only objects for which
![]() .
This leaves about 2000 objects in both catalogs, which
corresponds to 20 galaxies/arcmin2 for the I-band image and 65 galaxies/arcmin2 for the HST image.
.
This leaves about 2000 objects in both catalogs, which
corresponds to 20 galaxies/arcmin2 for the I-band image and 65 galaxies/arcmin2 for the HST image.
Weak lensing analyses are based on using estimates of the local shear
![]() to reconstruct information on the convergence
to reconstruct information on the convergence ![]() ,
which is a dimensionless measure of the surface mass density. In the weak lensing regime,
,
which is a dimensionless measure of the surface mass density. In the weak lensing regime,
![]() ,
so that
,
so that
![]() .
.
Both the shear
![]() and the convergence
and the convergence ![]() are linear
combinations of second derivatives of the lensing potential, so that it is
possible to express
are linear
combinations of second derivatives of the lensing potential, so that it is
possible to express ![]() as an integral over
as an integral over
![]() via the
Kaiser-Squires Inversion (Kaiser & Squires 1993).
This method is usually not applied directly, as the shot noise introduced by
summing over individual galaxies (shear measurements) produces infinite
noise. This can be avoided by first smoothing the shear measurements;
however, such a smoothing scale introduces correlated errors. Another
problem arises from the limited field-of-view of any
observations. Seitz & Schneider (2001) express this as a von Neumann boundary problem, leading to
the so-called finite-field inversion. We rely on this method for
mass reconstructions throughout the paper.
via the
Kaiser-Squires Inversion (Kaiser & Squires 1993).
This method is usually not applied directly, as the shot noise introduced by
summing over individual galaxies (shear measurements) produces infinite
noise. This can be avoided by first smoothing the shear measurements;
however, such a smoothing scale introduces correlated errors. Another
problem arises from the limited field-of-view of any
observations. Seitz & Schneider (2001) express this as a von Neumann boundary problem, leading to
the so-called finite-field inversion. We rely on this method for
mass reconstructions throughout the paper.
The mass-aperture, or
![]() ,
Statistics, developed by
Schneider (1996), provides a method with defined noise properties to identify
mass concentrations. It is based upon the relation
,
Statistics, developed by
Schneider (1996), provides a method with defined noise properties to identify
mass concentrations. It is based upon the relation
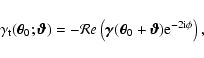 |
(10) |
Equation (9) is intuitively clear: a lens
most often deforms images so they align tangentially to the center of
mass. An average over the tangential components of galaxy ellipticities must therefore be a measure of the surface mass. With this interpretation,
![]() is a useful quantity in
its own right even if the weak lensing assumption,
is a useful quantity in
its own right even if the weak lensing assumption,
![]() ,
breaks down or if part of the weight function lies
outside the field.
,
breaks down or if part of the weight function lies
outside the field.
The imaginary shear component is the cross component:
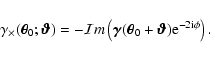 |
(11) |
With the weighting scheme introduced in Eq. (8),
this becomes:
Any
![]() value is incomplete without an estimate of its significance,
i.e. how it compares to the typical noise level of the
value is incomplete without an estimate of its significance,
i.e. how it compares to the typical noise level of the
![]() estimator.
The signal-to-noise ratio is given by
estimator.
The signal-to-noise ratio is given by
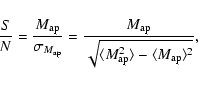 |
(14) |
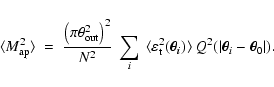 |
(15) |
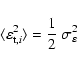 |
(16) |
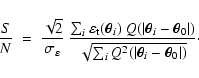 |
(17) |
With this in mind, we reconsider Eq. (18). Such randomizations
represent a possible ensemble average, which we denote by
![]() .
For each realization, the ellipticity modulus remains the same, only the orientation changes. In this
case, the weights also remain the same and we can simplify the expression:
.
For each realization, the ellipticity modulus remains the same, only the orientation changes. In this
case, the weights also remain the same and we can simplify the expression:
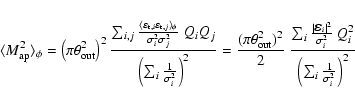
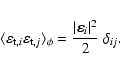
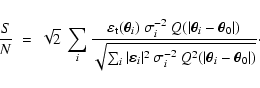 |
(19) |
Table 1: Summary of the differences of the object catalogs used for the lensing analyses of Erben et al. (2000) and this work. The brightness key refers to the magnitude bins used to split the sample (note that the magnitudes are not calibrated).
In Table 1, we summarize the differences between the analyses of Erben et al. (2000) and this work.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2733_03.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg140.gif) |
Figure 3:
The filter function U (solid line) we used and its
corresponding weight function Q (dashed line) shown in units of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.8cm,clip]{2733_04.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg141.gif) |
Figure 4:
Mass reconstruction of the CFHT I-band image according to
Seitz & Schneider (2001). Solid (dashed) lines give positive (negative) |
| Open with DEXTER | |
In order to apply the finite-field inversion (Sect. 3.1), we further cut the I-band image to avoid the ripple-like reflection artefact at the eastern edge altogether. This narrows the available field, but avoids problems at the boundaries. A resulting mass reconstruction is shown in Fig. 4.
Abell 1942 shows up prominently in the top half of the field, with the peak
of the mass map centered approximately on the cD galaxy. In the lower half
of the image, there is a second, albeit lower peak at the same position as
detected in Erben et al. (2000). Relative to the peak ![]() of A1942, our dark
clump signal is slightly larger than given by Erben et al. (2000). However, north
of the dark clump, there is a "hole'' - a region of significantly negative
of A1942, our dark
clump signal is slightly larger than given by Erben et al. (2000). However, north
of the dark clump, there is a "hole'' - a region of significantly negative
![]() values. Although this is a somewhat disconcerting result, it must be stressed that
values. Although this is a somewhat disconcerting result, it must be stressed that ![]() is underestimated in the whole field due to the mass sheet
degeneracy and the cluster in the field (two of the three field boundaries
close to the cluster and well within its extent display nearly vanishing
is underestimated in the whole field due to the mass sheet
degeneracy and the cluster in the field (two of the three field boundaries
close to the cluster and well within its extent display nearly vanishing
![]() values). Unfortunately, the original analysis of Erben et al. (2000)
only investigates regions of positive
values). Unfortunately, the original analysis of Erben et al. (2000)
only investigates regions of positive ![]() ,
so that this result cannot
be compared.
,
so that this result cannot
be compared.
![\begin{figure}
\par\includegraphics[width=17.25cm,clip]{2733_05.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg142.gif) |
Figure 5:
Results of a weighted
|
| Open with DEXTER | |
We perform the
![]() analysis as described in
Sect. 3.2 and evaluate the
analysis as described in
Sect. 3.2 and evaluate the
![]() statistic on a grid with
grid spacings of 2
statistic on a grid with
grid spacings of 2
![]() .
The result is shown in Fig. 5.
The dark clump signal is seen significantly at all filter scales, but it is
particularly strong for the 120
.
The result is shown in Fig. 5.
The dark clump signal is seen significantly at all filter scales, but it is
particularly strong for the 120
![]() filter, where it reaches a peak significance of 5
filter, where it reaches a peak significance of 5![]() .
In the other filters, the
significance is at the 3.5
.
In the other filters, the
significance is at the 3.5![]() level, as in Erben et al. (2000).
level, as in Erben et al. (2000).
Abell 1942 is detected only weakly for large filter scales, a result that is
consistent with Erben et al. (2000). The mass reconstruction from the previous
paragraph demonstrates why the dark clump reaches a much higher
![]() significance than the cluster: at the dark clump position, the negative part
of the filter function (Fig. 3) is evaluated largely at the position
of the hole, thereby boosting the signal. The same in reverse is true for
the hole itself: its significance is boosted by its proximity to the Dark
Clump. Yet its significance remains lower than that of the dark clump.
significance than the cluster: at the dark clump position, the negative part
of the filter function (Fig. 3) is evaluated largely at the position
of the hole, thereby boosting the signal. The same in reverse is true for
the hole itself: its significance is boosted by its proximity to the Dark
Clump. Yet its significance remains lower than that of the dark clump.
![\begin{figure}
\par\includegraphics[width=17.25cm,clip]{2733_06.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg143.gif) |
Figure 6: The same as the previous figure (Fig. 5), but with the galaxies divided into three magnitude bins and only positive contours. White contours correspond to the brightest galaxies, gray contours to those of medium brightness, and black contours to the faintest. |
| Open with DEXTER | |
On average, the more distant a galaxy, the fainter it is. By introducing magnitude cuts we split the galaxy sample into three parts of about 660 galaxies each with different mean redshift. This is a very crude redshift distinction, but should reveal any trend of lens strength with redshift.
The results of this analysis are shown in Fig. 6. We see that the dark clump signal stems mostly from faint galaxies, which supports the notion that this is a high-redshift object. However, these are also those objects that are most subject to noise effects.
At the 120
![]() filter scale, there is also a 3
filter scale, there is also a 3![]() contribution
from bright galaxies. Assuming that the lensing mass is indeed a high
redshift object, these bright galaxies are unlikely to be at higher
redshifts. Thus, this is probably not a lensing signal.
Yet, this "contamination'' can explain the high signal-to-noise ratio we
see at this filter scale.
contribution
from bright galaxies. Assuming that the lensing mass is indeed a high
redshift object, these bright galaxies are unlikely to be at higher
redshifts. Thus, this is probably not a lensing signal.
Yet, this "contamination'' can explain the high signal-to-noise ratio we
see at this filter scale.
For Abell 1942, there is a strong signal at the smallest filter scale, centered on the cD galaxy which exhibits a strong lensing arc. It may well be that at these radii we are not in the weak lensing regime any more and the tangential alignment is already rather distinct. In the other filter radii, there is no particularly strong signal. This might be due to the generic weight function which is not adapted to the NFW profile.
Our plot does not show the negative
![]() contours to avoid
overcrowding. Unlike to the dark clump, all three magnitude bins contribute
to the "hole''.
contours to avoid
overcrowding. Unlike to the dark clump, all three magnitude bins contribute
to the "hole''.
In Sect. 3.2, we argued that
![]() ,
i.e.
,
i.e.
![]() calculated with the cross component of the shear instead
of the tangential one, must vanish. By
checking the validity of this assumption in the dataset, we can
identify possible problems.
calculated with the cross component of the shear instead
of the tangential one, must vanish. By
checking the validity of this assumption in the dataset, we can
identify possible problems.
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{2733_07.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg144.gif) |
Figure 7:
Results of a
|
| Open with DEXTER | |
The results are shown in Fig. 7. Particularly at
small filter scales, there are some positive and negative peaks
with significances
![]() (negative values are indicated by negative
signal-to-noise ratios). However, most of the peaks are at the edge of
the field, where a part of the weight function lies outside the
field. While (the real part of)
(negative values are indicated by negative
signal-to-noise ratios). However, most of the peaks are at the edge of
the field, where a part of the weight function lies outside the
field. While (the real part of)
![]() retains its justification
at these places as being simply a measure of the tangential alignment,
we can no longer assume that
retains its justification
at these places as being simply a measure of the tangential alignment,
we can no longer assume that
![]() vanishes.
vanishes.
There is no peak with a significance larger than 2![]() in the
vicinity of the dark clump, so the detection passes this test well.
in the
vicinity of the dark clump, so the detection passes this test well.
Despite several differences to the lensing analysis of Erben et al. (2000), the
![]() results agree at least qualitatively. We are curious whether we
can also reproduce the radial dependence of the mean tangential ellipticity shown in
Fig. 9 of Erben et al. (2000).
results agree at least qualitatively. We are curious whether we
can also reproduce the radial dependence of the mean tangential ellipticity shown in
Fig. 9 of Erben et al. (2000).
We determine the position of the dark clump from the
![]() peak at the
120
peak at the
120
![]() filter scale, where the signal is strongest. We find it to be
filter scale, where the signal is strongest. We find it to be
![]() ,
which is at a distance of
,
which is at a distance of
![]() from the
position given by Erben et al. (2000), and thus just at the 1
from the
position given by Erben et al. (2000), and thus just at the 1![]() level they
give for the uncertainty of the centroid's position.
level they
give for the uncertainty of the centroid's position.
The tangential ellipticity relative to this position is calculated for each
galaxy within 200
![]() .
They are then binned according to their distance
from the dark clump and the weighted mean is calculated for each bin. To
estimate the standard deviation, we randomize the position angles of
these galaxies 1000 times and calculate the mean tangential
ellipticity each time, thus gaining an estimate for the standard deviation.
This analysis is done for the complete
galaxy sample as well as the three samples split according to brightness.
The results are shown in Fig. 8.
.
They are then binned according to their distance
from the dark clump and the weighted mean is calculated for each bin. To
estimate the standard deviation, we randomize the position angles of
these galaxies 1000 times and calculate the mean tangential
ellipticity each time, thus gaining an estimate for the standard deviation.
This analysis is done for the complete
galaxy sample as well as the three samples split according to brightness.
The results are shown in Fig. 8.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2733_08.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg149.gif) |
Figure 8:
The mean tangential ellipticity
|
| Open with DEXTER | |
Particularly for the faintest galaxies, we find positive values out to 120
![]() .
This agrees well with the strong shear signal seen for these
galaxies. We can also identify the cause of the signal seen for bright
galaxies at the 120
.
This agrees well with the strong shear signal seen for these
galaxies. We can also identify the cause of the signal seen for bright
galaxies at the 120
![]() filter scale: the two significantly positive
bins at 90
filter scale: the two significantly positive
bins at 90
![]() and 110
and 110
![]() (the filter function employed
assigns the highest weight around a radius
(the filter function employed
assigns the highest weight around a radius
![]() ).
For the medium bright galaxies
).
For the medium bright galaxies
![]() is largely consistent
with zero.
is largely consistent
with zero.
Compared to Erben et al. (2000), who measure
![]() at 100
at 100
![]() ,
we find a higher value (
,
we find a higher value (![]() 0.1). On the other
hand, we find positive values only out to
120
0.1). On the other
hand, we find positive values only out to
120
![]() rather than 150
rather than 150
![]() .
And since the centroid positions do
not coincide, the inner two bins are not comparable. Yet, we can also be
confident that the signal is not caused just by a few galaxies.
.
And since the centroid positions do
not coincide, the inner two bins are not comparable. Yet, we can also be
confident that the signal is not caused just by a few galaxies.
Table 2:
Overview of the
![]() values and signal-to-noise ratios of
the peaks found in the analyses of the CFHT data. We also give
the number of galaxies located in the aperture (N), and the (weighted) average galaxy ellipticity dispersion
values and signal-to-noise ratios of
the peaks found in the analyses of the CFHT data. We also give
the number of galaxies located in the aperture (N), and the (weighted) average galaxy ellipticity dispersion
![]() ,
as well as the
offset to the assumed centroid position, measured in the
sky coordinate system. In two cases, there was no
,
as well as the
offset to the assumed centroid position, measured in the
sky coordinate system. In two cases, there was no
![]() peak in the
vicinity of the dark clump - we then quote the values at the reference
position (in italics).
peak in the
vicinity of the dark clump - we then quote the values at the reference
position (in italics).
We have successfully confirmed the weak lensing signal seen in two sets of CFHT observations (our re-analysis of the V-band data are not shown here but agree well with Erben et al. 2000). We show that the alignment signal comes from faint galaxies, which supports the hypothesis that it is caused by a lensing mass at high redshifts. One must keep in mind, however, that these are also those objects most affected by noise.
With several variations of the catalog that enters the
![]() analysis,
we tested that the detection of the dark clump is resistant against these and
consistently recovered at all filter scales. It
reaches a peak significance of about 5
analysis,
we tested that the detection of the dark clump is resistant against these and
consistently recovered at all filter scales. It
reaches a peak significance of about 5![]() ,
although this signal is
contaminated by a tangential alignment of bright objects, which is unlikely
to be a lensing effect.
,
although this signal is
contaminated by a tangential alignment of bright objects, which is unlikely
to be a lensing effect.
The HST catalog extends to fainter and thus more distant galaxies than the ground-based catalog. If the alignment signal found in the ground-based data does indeed stem from a mass concentration, its lens strength should increase with source redshift. Additionally, since the HST is space-based and thus not afflicted by atmospheric seeing, its ellipticity measurements are more reliable than those from ground-based telescopes. If the ground-based signal is not just a noise peak, the signal should therefore be even stronger in the HST images.
Figure 9 shows the results of a mass reconstruction of the inner rectangle of the HST data field. The dark clump shows up prominently, slightly westward of the position found in the ground-based analyisis.
The results of the weighted
![]() analysis of the complete catalog is shown
in Fig. 10 and summarized in Table 3. Indeed, we find a peak at approximately the same position as in the ground-based images in the 120
analysis of the complete catalog is shown
in Fig. 10 and summarized in Table 3. Indeed, we find a peak at approximately the same position as in the ground-based images in the 120
![]() filter, but with only 2.9
filter, but with only 2.9![]() significance it is considerably weaker.
At the smallest filter scale used (
significance it is considerably weaker.
At the smallest filter scale used (
![]() ), this peak diminishes and
dissolves into two peaks.
), this peak diminishes and
dissolves into two peaks.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2733_09.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg158.gif) |
Figure 9:
The mass density map of the inner region of the HST image
reconstructed according to the method given in
Seitz & Schneider (2001). Shown are |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12.7cm,clip]{2733_10.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg159.gif) |
Figure 10:
Results of the
|
| Open with DEXTER | |
Just as for the ground-based data, we split the catalog into three bins
according to brightness to probe the redshift dependence of the lens
strength. With cuts at m=25.46 and m=26.43, the three samples contain
approximately equal numbers of galaxies. The respective
![]() analyses are
shown in Fig. 11.
The alignment signal is carried by the galaxies in the bright and in the
faint bin, but there is a lack of signal in the
medium-bright bin. The galaxies that were detected in the ground-based
image should be mostly contained in the HST's bright bin. Although the
analyses are
shown in Fig. 11.
The alignment signal is carried by the galaxies in the bright and in the
faint bin, but there is a lack of signal in the
medium-bright bin. The galaxies that were detected in the ground-based
image should be mostly contained in the HST's bright bin. Although the
![]() values differ by a factor of about 2, the measurement in the
bright bin therefore confirms that there is tangential
alignment around the dark clump candidate. However, the
lack of alignment in the medium bin is difficult to explain with the lensing
hypothesis.
values differ by a factor of about 2, the measurement in the
bright bin therefore confirms that there is tangential
alignment around the dark clump candidate. However, the
lack of alignment in the medium bin is difficult to explain with the lensing
hypothesis.
![\begin{figure}
\par\includegraphics[width=13.3cm,clip]{2733_11.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg160.gif) |
Figure 11:
The same as the previous figure (Fig. 10), but
with the galaxies divided into three bins. White contours correspond to the
brightest galaxies, gray contours to those of medium brightness, and black
contours to the faintest. The contours start at 1.5 |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=13.3cm,clip]{2733_12.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg161.gif) |
Figure 12:
The
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{2733_13.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg162.gif) |
Figure 13:
The same as Fig. 12, but with the galaxies split into
three samples according to brightness. The color coding is identical to
that of Fig. 11. The contours start at
|
| Open with DEXTER | |
Table 3:
Overview of the
![]() values and signal-to-noise ratios of
the peaks found in the analyses of the HST data.
We also give the number of galaxies located
in the aperture (N), and the (weighted) average galaxy ellipticity
values and signal-to-noise ratios of
the peaks found in the analyses of the HST data.
We also give the number of galaxies located
in the aperture (N), and the (weighted) average galaxy ellipticity
![]() ,
as well as the offset to the assumed centroid position, measured in the
sky coordinate system. For the smallest filter scale (
,
as well as the offset to the assumed centroid position, measured in the
sky coordinate system. For the smallest filter scale (
![]() ), the anlysis of all galaxies yields two peaks in the vicinity of the dark clump position, both of which are listed. For the medium bright
bin, there is no peak close to the dark clump in the largest two filter
scales - we then quote the values at the reference position (in italics).
), the anlysis of all galaxies yields two peaks in the vicinity of the dark clump position, both of which are listed. For the medium bright
bin, there is no peak close to the dark clump in the largest two filter
scales - we then quote the values at the reference position (in italics).
As described in Appendix A.1, it is difficult to judge the quality
of the anisotropy
correction of the HST data. A faulty anisotropy correction is likely to
cause a non-vanishing
![]() component. Also the CTE problem of the
camera might do so. We therefore calculate
component. Also the CTE problem of the
camera might do so. We therefore calculate
![]() with the shear cross component
instead of the tangential component; the result of this analysis is
shown in Fig. 12.
with the shear cross component
instead of the tangential component; the result of this analysis is
shown in Fig. 12.
Indeed, there is a 3![]() peak roughly coincident with the group of galaxies
close to the dark clump, and one close to the border of the image. For
the latter one, a large part of the aperture is evaluated outside of
the field, so that
peak roughly coincident with the group of galaxies
close to the dark clump, and one close to the border of the image. For
the latter one, a large part of the aperture is evaluated outside of
the field, so that
![]() is not necessarily expected to vanish in
this case. This argument applies only weakly to the first one, which
is affected only by masks of stars.
is not necessarily expected to vanish in
this case. This argument applies only weakly to the first one, which
is affected only by masks of stars.
The stellar anisotropy increases with distance from the center of the chips,
cf. Fig. A.4. At the edges of the chips we also
expect the largest deviations of the fit from the actual values. Therefore,
the quality of the anisotropy correction should decrease withincreasing
distance from the chip center. To test this effect, we reject those objects
which are more than
700 pixels from the center of their chip (343 objects) and repeat the
![]() analysis. The result differs only very little from the
previous one.
analysis. The result differs only very little from the
previous one.
We also calculate the
![]() cross component for the three brightness bins,
Fig. 13. We find that the
cross component for the three brightness bins,
Fig. 13. We find that the
![]() peaks
are caused solely by the bright galaxies.
If they were caused by an insufficient anisotropy correction, we would expect these peaks to show up
for all three bins. Additionally, as the brightest objects are generally
also the largest, the effect of the anisotropy correction is smallest for
these.
peaks
are caused solely by the bright galaxies.
If they were caused by an insufficient anisotropy correction, we would expect these peaks to show up
for all three bins. Additionally, as the brightest objects are generally
also the largest, the effect of the anisotropy correction is smallest for
these.
These results indicate that the
![]() peaks are unlikely to be
caused by a poor anisotropy correction. Rather, they seem to be caused by an intrinsic alignment of some of the bright galaxies.
peaks are unlikely to be
caused by a poor anisotropy correction. Rather, they seem to be caused by an intrinsic alignment of some of the bright galaxies.
Just as described in Sect. 4.3, we calculate the
average tangential ellipticity
![]() as a function of the distance from the Dark
Clump position. The position of the strongest lensing signal is
as a function of the distance from the Dark
Clump position. The position of the strongest lensing signal is
![]() ,
as measured from the peak in the 120
,
as measured from the peak in the 120
![]() filter of the
complete sample. This is
filter of the
complete sample. This is
![]() from the position we measured in the ground-based data
and
from the position we measured in the ground-based data
and
![]() from the position originally cited by Erben et al. (2000).
from the position originally cited by Erben et al. (2000).
The radial profile is shown in Fig. 14. For the complete
sample of galaxies,
![]() is positive or very close to
zero between 20
is positive or very close to
zero between 20
![]() and 140
and 140
![]() radii. For this range, it is
inconsistent with zero only for
radii between 60
radii. For this range, it is
inconsistent with zero only for
radii between 60
![]() and 100
and 100
![]() .
.
For bright galaxies, there is some excess
![]() between 20
between 20
![]() and 100
and 100
![]() ,
which is clearly the cause of
the peak we find.
For the medium bright
galaxies,
,
which is clearly the cause of
the peak we find.
For the medium bright
galaxies,
![]() is largely consistent with zero within in the
is largely consistent with zero within in the
![]() error bars. However, the value is positive only in two bins. For
the faintest galaxies,
error bars. However, the value is positive only in two bins. For
the faintest galaxies,
![]() is positive over a fairly
large range of radii, but with varying significance and no clear
resemblance of a shear profile.
is positive over a fairly
large range of radii, but with varying significance and no clear
resemblance of a shear profile.
We also calculate the radial profile around the dark clump center we found
in the ground-based images; it is shown in Fig. 15. For the
complete galaxy sample, it is largely consistent with zero but with a trend to positive values. But for the bright galaxies,
![]() follows a typical shear profile between 20
follows a typical shear profile between 20
![]() and 100
and 100
![]() ,
with
,
with
![]() at
at
![]() Erben et al. (2000) use the radial profile, namely
Erben et al. (2000) use the radial profile, namely
![]() at
at
![]() ,
to deduce a mass estimate of the Dark Clump. This further illustrates the difference of a factor of 2 between the signal strengths in the ground-based and space-based image, which relates directly to the mass estimate.
,
to deduce a mass estimate of the Dark Clump. This further illustrates the difference of a factor of 2 between the signal strengths in the ground-based and space-based image, which relates directly to the mass estimate.
However, for the medium bright and faint galaxies, there is no obvious NFW-like trend in the profile.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2733_14.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg173.gif) |
Figure 14:
The mean tangential ellipticity
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2733_15.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg174.gif) |
Figure 15: Same as Fig. 14, but with the distance measured relative to the position of the dark clump (as measured in the ground-based data). |
| Open with DEXTER | |
Neither Erben et al. (2000, I-band) nor Gray et al. (2001, <)998#>H-band# find a significant overdensity of galaxies which could be associated with the Dark Clump. With the substantially deeper HST data, we can probe the galaxy number density to fainter magnitudes. In Fig. 16, we present surface number densities for the complete galaxy sample, as well as split up according to brightness, as done before for the lensing analysis.
The bin of brightest HST galaxies corresponds roughly to those objects detected also in the ground-based image. It is quite puzzling that rather than an overdensity of galaxies at the dark clump, the galaxies seem to form a ring around that position. However, this is hardly significant.
The most significant feature we find is a ![]() galaxy overdensity in
the bin of medium bright galaxies, located about
galaxy overdensity in
the bin of medium bright galaxies, located about
![]() from the Dark Clump. Given that these objects are fainter than the ones that carry the
lensing signal in the ground-based data, this is rather unlikely to be
associated with a lensing mass. However, it could explain the alignment
signal seen in the faintest HST bin. It would be highly interesting to
investigate whether this overdensity is present also in color space;
unfortunately, the currently available data sets are not deep enough.
from the Dark Clump. Given that these objects are fainter than the ones that carry the
lensing signal in the ground-based data, this is rather unlikely to be
associated with a lensing mass. However, it could explain the alignment
signal seen in the faintest HST bin. It would be highly interesting to
investigate whether this overdensity is present also in color space;
unfortunately, the currently available data sets are not deep enough.
We have shown that we also detect tangential alignment around the dark clump in the HST data. However, it is considerably less significant than in the ground-based data. It is particularly intriguing that we do not detect alignment in the medium bright HST galaxies.
We refrain from trying to deduce a mass for the dark clump from these measurements, as it is obvious that our results are not unambiguous. As an upper limit, the HST data suggest that the mass estimate of the dark clump has to be corrected at least by a factor of 1/2 compared to the original value.
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{2733_16.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg176.gif) |
Figure 16:
Projected number density of galaxies in the HST image. The upper
left image shows contours of surface densities, smoothed with a Gaussian
of width
|
| Open with DEXTER | |
In Appendix B, we carry out a detailed comparison of the
ground-based and space-based ellipticity measurements. We find that, on
average, the ellipticity measurements of both components
![]() and
and
![]() correlate very well, and thus justify ground-based lensing
studies. The scatter of this correlation is about 15%, so that this is not
valid for single objects, but only for ensembles. However, if the ellipticity measurement is expressed as the tangential ellipticity with respect to the dark clump position, there is a significant offset, which results in the discrepant lensing results. Despite a careful investigation, we are not able to isolate the cause of this.
correlate very well, and thus justify ground-based lensing
studies. The scatter of this correlation is about 15%, so that this is not
valid for single objects, but only for ensembles. However, if the ellipticity measurement is expressed as the tangential ellipticity with respect to the dark clump position, there is a significant offset, which results in the discrepant lensing results. Despite a careful investigation, we are not able to isolate the cause of this.
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{2733_17.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg179.gif) |
Figure 17:
A part of the Chandra image overlaid on the HST image. The point sources
were removed from the image, and it was smoothed with a Gaussian of
|
| Open with DEXTER | |
If the dark clump is a virialized massive dark matter concentration,
one would expect that the baryons trapped by the potential well and
not in galaxies would have been shock-heated in the gravitational
collapse and therefore would emit in X-rays. Erben et al. (2000) present the
analysis of the ROSAT HRI image of the A1942 field. They found a hardly
significant X-ray detection at a position
![]() away from
the weak lensing mass peak position reported in that paper.
away from
the weak lensing mass peak position reported in that paper.
Since then, the field of A1942 was imaged by the Chandra X-ray
observatory in March 2002 (PI: Garmire). It was observed for
58 ks with the ACIS-I detector configuration. We retrieved the
observation from the archive and analyzed it using standard techniques
with the CIAO v3.1 package![]() . and recipes from
the "ACIS Recipes: Clean the Data'' web
page
. and recipes from
the "ACIS Recipes: Clean the Data'' web
page![]() .
We use the standard set of event grades (0, 2, 3, 4, 6) and restrict our
analysis to the 0.5-8.0 keV energy band. We detect sources with
CIAO's WAVDETECT routine using wavelet scales 1, 2, 4, 8 and 16. Only
two sources are detected within
.
We use the standard set of event grades (0, 2, 3, 4, 6) and restrict our
analysis to the 0.5-8.0 keV energy band. We detect sources with
CIAO's WAVDETECT routine using wavelet scales 1, 2, 4, 8 and 16. Only
two sources are detected within
![]() of the CFHT data lensing
of the CFHT data lensing
![]() centroid. These two sources are found to be point sources with
clear optical counterparts in the optical data.
centroid. These two sources are found to be point sources with
clear optical counterparts in the optical data.
Visual inspection does not reveal any obvious extended source at the
position of the dark clump. Nevertheless, in order to check if there
really is any extended source, we created a diffuse emission image
from our original image excising the data where WAVDETECT detected
sources and filling the holes according to CIAO's threads. We also
created a "blank-sky'' background image to better estimate the
background contribution at the position of the dark clump. We smoothed
the point-source-removed image with and without background subtraction
with various algorithms and scales but no obvious extended source was
detected. The most significant source consistent with the broad
position of the dark clump is a 1.5![]() source (in a circular
aperture of radius
source (in a circular
aperture of radius
![]() )
whose coordinates are
)
whose coordinates are
![]() .
We measure a count-rate of
.
We measure a count-rate of
![]()
![]() 10-4 counts/s in the 0.5-8.0 keV energy range in a circular aperture of
radius
10-4 counts/s in the 0.5-8.0 keV energy range in a circular aperture of
radius
![]() which corresponds to a unabsorbed flux of
which corresponds to a unabsorbed flux of
![]()
![]() 10-15 erg cm-2 s-1 assuming an incident spectrum
of T=3 keV and a local hydrogen column density of
10-15 erg cm-2 s-1 assuming an incident spectrum
of T=3 keV and a local hydrogen column density of
![]()
![]() 1020 cm-2. We also measure the count rate in various
apertures centered at the positions of the CFHT and HST data lensing
centroids. The measurements are of lower significance compared to the
previous one. We have fitted a standard beta profile (Cavaliere & Fusco-Femiano 1978) to the
azimuthally average radial profile
centered at the position of this potential source. The best values we obtain
for the core radius and beta parameter (slope decline at large
radius) are
1020 cm-2. We also measure the count rate in various
apertures centered at the positions of the CFHT and HST data lensing
centroids. The measurements are of lower significance compared to the
previous one. We have fitted a standard beta profile (Cavaliere & Fusco-Femiano 1978) to the
azimuthally average radial profile
centered at the position of this potential source. The best values we obtain
for the core radius and beta parameter (slope decline at large
radius) are
![]() and 0.55, respectively. These values indicate that if
there really is an extended source, it is rather compact with a small
core radius. However, one has to keep in mind that these best fit
parameters are highly uncertain due to the low number of counts.
The total count rate predicted integrating the best-fit model would be
9.4
and 0.55, respectively. These values indicate that if
there really is an extended source, it is rather compact with a small
core radius. However, one has to keep in mind that these best fit
parameters are highly uncertain due to the low number of counts.
The total count rate predicted integrating the best-fit model would be
9.4 ![]() 10-4 counts/s.
10-4 counts/s.
Erben et al. (2000) reported a hardly significant (![]() ) detection
of X-ray emission in the dark clump area in the ROSAT HRI image of
this field. We have measured the flux in the Chandra image at the same
position, which is very close (
) detection
of X-ray emission in the dark clump area in the ROSAT HRI image of
this field. We have measured the flux in the Chandra image at the same
position, which is very close (
![]() away) to the previously reported
source. We find an unabsorbed flux of
away) to the previously reported
source. We find an unabsorbed flux of
![]()
![]() 10-15 erg cm-2 s-1 in a
10-15 erg cm-2 s-1 in a
![]() aperture. This value is slightly higher than the previous one only due to the inclusion in the aperture
of another faint source situated at the NE and not included in the
mesurement at the previous position. Therefore, we do not confirm the flux
measurement of the ROSAT HRI source.
aperture. This value is slightly higher than the previous one only due to the inclusion in the aperture
of another faint source situated at the NE and not included in the
mesurement at the previous position. Therefore, we do not confirm the flux
measurement of the ROSAT HRI source.
Given the faintness and measured uncertainties of our possible detection, there is little point in speculating about its luminosity and gas mass. Even if this source was real and its real flux was the highest allowed by the data, it would not have enough mass to be considered a rich cluster by its X-ray properties. Overall, the Chandra image of this source indicates that if there is a dark matter concentration producing the lensing signal, this concentration does not contain the expected mass of hot gas that would be expected for its lensing signal if it were similar to the clusters of galaxies we have observed so far.
Tangential alignment around the dark clump has been detected in three datasets, which differ in the filter, camera, and telescope used. It can therefore be ruled out that the alignment is caused by instrument-specific systematics. However, the significance of the detection is lowest in the space-based dataset. If the alignment were due to lensing by a matter concentration, the highest alignment signal would be expected in the HST data, as it extends to more distant galaxies which should be more affected by the distortions due to lensing.
The significant alignment signal in the ground-based data is caused mainly by faint galaxies, for which the individual shape measurement are uncertain due to background noise. We show in Appendix B that the shape measurements agree very well on average when comparing ground-based and space-based data. Thus, also the amplitude of an alignment signal should be comparable. Considering the high alignment signal in the two ground-based datasets, it seems unlikely that background noise boosted the signal in both cases. Yet, for the I-band image, there is some indication of such a "conspiracy'', as the average tangential ellipticity toward the dark clump of the objects compared is significantly larger for the ground-based measurements (see B.4).
There are several issues involved which make weak lensing analyses difficult to apply to HST data (small field-of-view, complicated PSF structure). But various tests (Appendices A and B.4) have not revealed any bias these problems might cause to the ellipticity measurements. The weaker alignment signal in the HST data is therefore not a result of these systematics.
For the original detection claim, further evidence for a lensing mass was lent by the detection of X-ray emission in a ROSAT HRI image. However, follow-up observations with Chandra measure only a tenth of the flux originally measured in the ROSAT data, making this more likely to be a spurious detection. Thus, if it is a lensing mass, the dark clump would be truly "dark'', not just in the optical.
In the discovery paper, Erben et al. (2000) argue that the alignment signal they measure is the lensing signal of a dark matter halo with the mass of a typical galaxy cluster, but with an unusually low baryon density. The lower significance of the alignment in the HST data we present in this paper substantially weakens this hypothesis.
While the HST data confirm the existence of an alignment signal, its lower
amplitude and significance could indicate that this is not a lensing signal,
but rather a chance alignment of the intrinsic galaxy
ellipticities. Several studies of simulated ![]() -maps have shown that
even for high detection thresholds the rate of lensing peaks which cannot be
associated with a cluster is non-negligible. White et al. (2002) find
that in a high-quality single-band ground-based survey about 20% (80%) of
the peaks with a significance of
-maps have shown that
even for high detection thresholds the rate of lensing peaks which cannot be
associated with a cluster is non-negligible. White et al. (2002) find
that in a high-quality single-band ground-based survey about 20% (80%) of
the peaks with a significance of ![]()
![]() in a
in a
![]()
![]() filter do not
correspond to a mass peak above
filter do not
correspond to a mass peak above
![]() .
Hamana et al. (2004) find that 15% / 44% / 72% of the lensing
peaks with a significance of
.
Hamana et al. (2004) find that 15% / 44% / 72% of the lensing
peaks with a significance of ![]() /
/![]() /
/![]() do not correspond
to a
do not correspond
to a ![]()
![]() mass overdensity.
These numbers show that the lower significance we find for the dark clump
question the existence of a very massive structure.
mass overdensity.
These numbers show that the lower significance we find for the dark clump
question the existence of a very massive structure.
The simulations cited above assume a weak lensing survey observed in one band. Hennawi & Spergel (2005) show that the efficiency of such a survey can be significantly improved by observing in at least three bands, thus providing crude photometric redshifts. Although we do have three bands (CFHT V and I, HST F702W), the coverage and depth of the three datasets are too inhomogeneous to be meaningfully combined and used for the lensing analysis. Additionally, they cover adjacent bands in spectral range, and are thus not well suited for determining photometric redshifts.
It has also been shown that with imaging in multiple bands, the derived photometric redshifts are accurate enough to provide three-dimensional lensing maps (lensing tomography). Such datasets have been used to confirm galaxy clusters discovered by their lensing signal (Wittman et al. 2001; Wittman et al. 2003), and a distant cluster located behind a foreground cluster (Taylor et al. 2004). A similar study of the dark clump region could thus provide the crucial test whether the alignment signal measured can be associated with a mass concentration.
It must also be pointed out that the dark clump was detected not as part of a survey, but serendipitously in a pointed observation. This may well play a role; i.e. possibly the dark signal is the combination of a cluster subclump and a noise peak. The statistics of statistical flukes found from simulations of surveys are thus not directly applicable to this case.
So far the largest compilation of purely weak-lensing-selected cluster
candidates is the GaBoDS survey (Schirmer et al. 2003), which comprises 20 square degrees of data from the
Wide Field Imager at the 2.2 m MPG/ESO telescope at La Silla drawn from the ESO archive. Of the 100 peaks detected at a significance threshold of ![]()
![]() ,
45 are unclear
or dark (Schirmer 2004). This is in a surprising agreement with the
contamination level estimated by Hamana et al. (2004), particularly since the
latter assumes a deeper survey than GaBoDS actually is.
,
45 are unclear
or dark (Schirmer 2004). This is in a surprising agreement with the
contamination level estimated by Hamana et al. (2004), particularly since the
latter assumes a deeper survey than GaBoDS actually is.
Both White et al. (2002) and Hamana et al. (2004) suggest that the most likely cause of
a high alignment signal that does not correspond to a real cluster is a lensing signal of a less massive dark matter halo (![]()
![]() )
superposed with a noise peak caused by the intrinsic galaxy
ellipticities. This may well be the case here, given the detected alignment
signal, and the galaxy overdensity detected in the HST image.
)
superposed with a noise peak caused by the intrinsic galaxy
ellipticities. This may well be the case here, given the detected alignment
signal, and the galaxy overdensity detected in the HST image.
A definite answer to the question of the nature of this dark clump candidate thus still remains to be given. While our analysis yields the hypothesis of a dark matter halo of the size of a galaxy cluster unlikely, it is still unclear whether the dark clump corresponds to a (less massive) halo, is caused by chance alignment of intrinsic galaxy ellipticities, or is a combination of the two.
Acknowledgements
We are very grateful to Ludovic van Waerbeke for many helpful discussions and suggestions, and to Jörg Dietrich and Tim Schrabback for providing help and new ideas at various points of this work. We thank Yannick Mellier for his collaboration on this project, and Richard Ellis and Meghan Gray for their support of the HST follow-up observations. We also thank the anonymous referee for thoroughly reading our paper and for helpful comments.
This work was supported by the German Ministry for Science and Education (BMBF) through DESY under the project 05AE2PDA/8, and by the Deutsche Forschungsgemeinschaft under the project SCHN 342/3-1.
![\begin{figure}
\par\parbox{7.8cm}{\includegraphics[width=7.8cm,clip]{2733a02a.ps...
...mm}
\parbox{9.5cm}{\includegraphics[width=9.5cm,clip]{2733a02b.ps}}
\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg197.gif) |
Figure A.2: Same as Fig. A.1, but for Chip 3. 31 objects out of 930 were used for the fit. |
![\begin{figure}
\par\parbox{7.8cm}{\includegraphics[width=7.8cm,clip]{2733a03a.ps...
...mm}
\parbox{9.5cm}{\includegraphics[width=9.5cm,clip]{2733a03b.ps}}
\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg198.gif) |
Figure A.3: Same as Fig. A.1, but for Chip 4. 30 objects out of 770 were used for the fit. |
Despite the lack of seeing due to the Earth's atmosphere, weak lensing analyses cannot be applied straightforwardly to HST data. Due to the small field-of-view, there are only few stars available for the anisotropy correction; the pixels of the WFPC2 camera undersample the PSF, and the camera has a notable charge transfer inefficiency. In the following, we investigate the effects and possible bias from these problems.
Hoekstra et al. (1998) showed that a better anisotropy correction (Eq. (3)) of WFPC2 images can be achieved if the weight function applied to the stellar images is adapted to the size of the object to be corrected.
However, in practice, the ellipticity measurements become increasingly noisy for larger radii of the weight function. Along with the low number of stars, this causes fits to the anisotropy kernel to be both noisy and ill-described by a simple polynomial.
We tested three possible methods of correcting for the anisotropy as measured from the stars:
The anisotropy patterns produced by these methods are indeed notably
different. But the resulting shear estimates
![]() differ only on a percent level. Accordingly, the
differ only on a percent level. Accordingly, the
![]() measurements change only minutely
with a different anisotropy correction. We used the third method as a compromise solution.
measurements change only minutely
with a different anisotropy correction. We used the third method as a compromise solution.
The fits to
![]() are illustrated in
Figs. A.1-A.3.
For each chip, about 30 stars are available for the anisotropy
correction. This is a very small number, and as can be seen from the
Figures, they are not evenly distributed over the chip. It is therefore
difficult to judge the quality of the anisotropy correction.
are illustrated in
Figs. A.1-A.3.
For each chip, about 30 stars are available for the anisotropy
correction. This is a very small number, and as can be seen from the
Figures, they are not evenly distributed over the chip. It is therefore
difficult to judge the quality of the anisotropy correction.
Alternatives? It is common to use globular cluster fields for the anisotropy correction rather than the few stars contained in the field itself. With the large number of stars, the anisotropy can be very well determined. Such fields have to be chosen carefully: they should have been taken temporally close to our field, have a similar dither pattern, and should have been taken in the same filter. However, as the filter F702W is used mainly for extragalactic studies, there are no observations of dense stellar fields available in this filter.
Instead, we retrieved images of a field within the globular cluster 47 Tuc (NGC 104) taken in the F606W filter on Oct. 19th, 2002. We found the anisotropy patterns of these images to be similar to the ones in our images, but with some notable differences. Using these patterns for the anisotropy correction did not reduce the ellipticity dispersion of the stars (see Fig. A.4). At least for the centers of the images, the previous method is therefore superior. However, due to a lack of stars, the anisotropy correction is largely extrapolated toward the edges of each chip. These are also the areas with the largest anisotropy (as apparent from the figures), so that we are uncertain of the quality of the anisotropy correction applied to them.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{2733a04.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg201.gif) |
Figure A.4: Anisotropy correction of Chip 3. In the top left field, we plot the ellipticities of the 33 stars from the stellar sequence (as in Fig. A.2). Their ellipticity components are shown in the bottom left panel. In the top middle panel, we evaluate the anisotropy kernel as found from these 33 stars on a grid. The residual ellipticities of the stars after correction are shown in the bottom middle panel. In the top right panel, the correction polynomial found from 372 stars in a star cluster field is shown. Applying this polynomial to our data yields the residual ellipticities shown in the lower right panel. |
WFPC2 has a considerable Charge Transfer Efficiency (CTE) problem. Stars bright enough to show diffraction spikes also show typical "CTE tails'' in the direction opposite to the read-out direction. In fainter objects, these tails are not distinguishable by eye. Unfortunately, this effect is difficult to compensate for and has been studied only little for extended objects (Riess 2000).
The imperfect CTE of WFPC2 could potentially
bias the measured ellipticities, since it results in charge being
depleted in some pixels and added into others. Unlike for the photometry
of point sources, there is not yet a correction procedure to account
for this effect for shape measurements. According to Riess (2000),
for extended objects, the
deficient CTE causes charge loss in the pixels
closer to the read-out amplifier but adds this charge to the pixels
farther from the amplifier. To first order, this just causes a slight
displacement of the galaxy's centroid. But since depletion and
addition cannot be expected to be symmetric, it may also distort the
galaxy's shape. If so, it would bias the
![]() components, as this is
measured along rows and columns.
components, as this is
measured along rows and columns.
From studies on how CTE affects photometry it is known that it increases with distance from the read-out amplifier. This is also visible in our images: stars with large y-coordinates have more pronounced CTE trails. Also, the charge loss due to CTE depends on the background level of the image. A high background effectively suppresses CTE losses. The images of our dataset have a background corresponding to about 35 electrons per pixel, which reduces CTE loss significantly, at least for photometry. Lastly, the relative CTE losses are largest for faint objects.
To investigate any possible bias due to CTE, we divide the galaxy
catalog into four bins according to the original y position, which
gives its distance from the amplifier. Unlike for the lensing analysis, we
are not interested in the ellipticity with respect to the right ascension axis,
but to the original x-axis of the image. We denote these with
![]() .
For
each bin, we calculate the weighted mean of
.
For
each bin, we calculate the weighted mean of
![]() and
and
![]() .
The results are shown in Fig. A.5.
.
The results are shown in Fig. A.5.
If the CTE would affect galaxies similar to stars, i.e. it causes them
to trail and thus elongates them in the
![]() direction, we
would expect that
direction, we
would expect that
![]() is consistent with zero for the
first bin and then decreases with increasing distance from the amplifier.
This is clearly not the case for any of the brightness bins.
The scatter in
is consistent with zero for the
first bin and then decreases with increasing distance from the amplifier.
This is clearly not the case for any of the brightness bins.
The scatter in
![]() about zero is comparable to that
in
about zero is comparable to that
in
![]() ,
which should not be affected by CTE. The
deviations from zero in some bins may well be due to the fact that
there is some degree of tangential alignment in the field, so that
,
which should not be affected by CTE. The
deviations from zero in some bins may well be due to the fact that
there is some degree of tangential alignment in the field, so that
![]() and
and
![]() are not necessarily
zero. Yet, Fig. A.5 excludes a notable bias due to CTE.
are not necessarily
zero. Yet, Fig. A.5 excludes a notable bias due to CTE.
With the two datasets - the I-band image and the HST image - we have the opportunity to directly compare shape measurements from the ground to those from space. Ground-based shape determinations rely on an accurate compensation of the smearing due to the Earth's atmosphere, while the HST observations are hampered by the small image size, and the undersampling of the PSF. We confirmed with the HST data the presence of tangential alignment around the dark clump candidate, which implies that ellipticity measurements are to some degree comparable. However, we failed to confirm the amplitude of the alignment signal.
A direct comparison of the objects common to both catalogs tests the reliability of ground-based shape measurements and may also help to identify any systematics in either dataset. The ultimate goal of this comparison is to find the cause of the discrepancy in the significance of the alignment signal between the two datasets.
As the HST data was astrometrically calibrated by using a reference catalog extracted from the I-band image, objects present in both images can be identified by their sky coordinates.
To correlate the catalogs, we searched for objects within
![]() of
objects detected in the respective other catalog. This radius was found to
be the optimal balance between a high number of matched objects and a low rate of double detections.
of
objects detected in the respective other catalog. This radius was found to
be the optimal balance between a high number of matched objects and a low rate of double detections.
The catalogs used are the same as those for the lensing analysis, except
that objects with
![]() in the ground-based catalog are also
considered.
in the ground-based catalog are also
considered.
Within the field covered by the HST mosaic, there are 507 objects in the I-band catalog. We find one HST counterpart for 350 of these objects, and two or three counterparts for 17 objects, as the HST is able to resolve very close objects which were identified as single objects in the ground-based data. For 140 objects, no counterpart was found. For most of these, this results from the large areas that were masked in the HST images.
Figure B.1 illustrates the matched objects in an
![]() diagram of the ground-based data. There is no apparent trend as to for
which objects we are
more likely to find a counterpart in the space-based data. In particular, it
is not less likely to do so for faint objects. This shows that the catalog
was only very little contaminated by noise detections. Since close
objects are often unresolved in the ground-based image, objects with
two HST counterparts have on average a larger radius than those with
one counterpart.
diagram of the ground-based data. There is no apparent trend as to for
which objects we are
more likely to find a counterpart in the space-based data. In particular, it
is not less likely to do so for faint objects. This shows that the catalog
was only very little contaminated by noise detections. Since close
objects are often unresolved in the ground-based image, objects with
two HST counterparts have on average a larger radius than those with
one counterpart.
The basis of weak lensing analyses are the shape measurements of faint galaxy images. But the fainter an object is, the more difficult the shape determination is. Our dataset provides an ideal opportunity to test the reliability of shape measurements of ground-based data compared to space-based measurements.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2733b02a.ps}\hspace*{3.5mm}
\includegraphics[width=8cm,clip]{2733b02b.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg212.gif) |
Figure B.2:
Comparison of the ellipticity measurements from the HST images to
the I-band image. Objects for which
|
In Fig. B.2, we compare the ellipticity measurements in the
space-based data to those of the ground-based data. To these points, we fit a linear function
(algorithm fitexy from Press et al. 1992, to account for errors in both
coordinates), where we employ the
same weighting scheme as applied to the lensing analysis. We find:
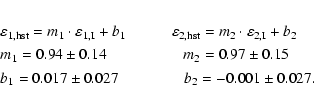
The scatter seen in the correlation of both components is of a similar
order of magnitude, so that the deviations in the ellipticity
measurements cannot be attributed to a single component.
For simplicity, we therefore reduce the difference of the
ellipticity measurements to a one-dimensional quantity:
For the lensing analyses, the galaxy catalogs were split into three parts according to brightness to investigate their contribution to the lensing signal. The division was chosen such that each sample contained an equal number of galaxies. With the merged catalog, we can now examine how these samples compare in the two datasets.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2733b03.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg215.gif) |
Figure B.3: Magnitude measured in the HST data vs. magnitude measured in the I-band image for the matched objects. The symbol coding is identical to that of Fig. B.2. The dashed lines indicate the cuts used to divide the respective catalogs into three samples. |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2733b04.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg216.gif) |
Figure B.4:
The ellipticity correction factor
|
Figure B.3 illustrates the magnitudes measured of the matched objects. Most of the objects found in the I-band image are considered "bright'' objects in the HST data. The fact that we also detected tangential alignment in the bright HST bin confirms the lensing signal seen in the ground-based image.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2733b05.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg217.gif) |
Figure B.5: The signal-to-noise ratios snr and weights of the I-band objects in the HST field. The symbol-coding is identical to that of Fig. B.4. |
As would be expected, the shape measurements agree best for the brighter objects, while they are inconsistent for most of the faint objects.
One quality attribute we used previously to classify objects was the
factor
![]() by which the smearing due to the PSF was
corrected. In Fig. B.4
we plot an
by which the smearing due to the PSF was
corrected. In Fig. B.4
we plot an
![]() diagram of the objects found in the I-band
image within the field covered by the HST mosaic. There is only a slight
indication that ellipticity measurements with
diagram of the objects found in the I-band
image within the field covered by the HST mosaic. There is only a slight
indication that ellipticity measurements with
![]() are less
reliable than others.
are less
reliable than others.
Two other criteria for the reliability of a shape measurement are the
signal-to-noise ratio of a detection and the
weight it was assigned. The latter one was taken to be inversely
proportional to the variance ![]() of the ellipticities of a galaxy
ensemble with similar noise properties (see
Sect. 2.3.9). Figure B.5 shows the
signal-to-noise ratios and weights of the I-band objects in the
HST field. As expected, the ellipticity measurements deviate for those objects with a low signal-to-noise ratio. These are in general down-weighted, although the
weight itself is not a clear indicator of the reliability. The weighting
scheme could therefore be improved.
of the ellipticities of a galaxy
ensemble with similar noise properties (see
Sect. 2.3.9). Figure B.5 shows the
signal-to-noise ratios and weights of the I-band objects in the
HST field. As expected, the ellipticity measurements deviate for those objects with a low signal-to-noise ratio. These are in general down-weighted, although the
weight itself is not a clear indicator of the reliability. The weighting
scheme could therefore be improved.
The lensing signal in the ground-based data was carried by faint
galaxies with a signal-to-noise ratio of less than about 4. These are
precisely those galaxies for which the space-based measurements give
different ellipticities. It is therefore not surprising that the amplitude
of the
![]() signal is different in the two datasets.
signal is different in the two datasets.
As mentioned before, we cannot judge the quality of the anisotropy
correction of the HST images due to the small number of stars in the
images. With the
correlated catalogs, we have another test of the correction: if it is faulty,
then we expect to see a systematic variation of the ellipticity
differences
![]() and
and
![]() between the three chips and/or with position on the chip. We reduce
the latter one to a one-dimensional quantity by considering the distance rfrom the respective chip center; this is motivated by the observation that
the anisotropy seen in the HST chips is largest at the edge (see
Fig. A.4).
between the three chips and/or with position on the chip. We reduce
the latter one to a one-dimensional quantity by considering the distance rfrom the respective chip center; this is motivated by the observation that
the anisotropy seen in the HST chips is largest at the edge (see
Fig. A.4).
In Fig. B.6 we plot
![]() and
and
![]() as a function of r, where we distinguish between the three chips.
Clearly, an object's position in the HST mosaic is not the main cause of discordance in the ellipticity measurement. However, there are trends visible such as a slight overestimation of
as a function of r, where we distinguish between the three chips.
Clearly, an object's position in the HST mosaic is not the main cause of discordance in the ellipticity measurement. However, there are trends visible such as a slight overestimation of
![]() for small r in Chip 4 and an underestimation of
for small r in Chip 4 and an underestimation of
![]() for
small r in Chip 3. To quantify these, we fit a linear function
for
small r in Chip 3. To quantify these, we fit a linear function
![]() ,
for each chip.
We weight the
,
for each chip.
We weight the
![]() values by the same weighting scheme as
before, but do not assign error bars to the distance. The results are:
values by the same weighting scheme as
before, but do not assign error bars to the distance. The results are:
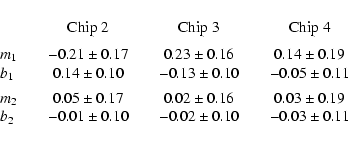
Considering that
![]() is on average constant at zero, but also
that
is on average constant at zero, but also
that
![]() is consistent with zero for a large number of objects
(
400 < r< 800), strengthens our assumption that the anisotropy
correction worked properly.
is consistent with zero for a large number of objects
(
400 < r< 800), strengthens our assumption that the anisotropy
correction worked properly.
Since the ellipticity measurements agree on average, one can assume that the lensing analysis of our set of matched objects should yield similar results. However, the individual analyses indicate otherwise: the faint galaxies in the ground-based data, which caused most of the lensing signal, correspond to the bright (and medium bright) galaxies in the HST data, which gave only a weak signal.
In order to directly evaluate the correlation (or discrepancy) between the
ellipticity measurements and the lensing analysis, we perform several
![]() analyses of the matched galaxies (see Table B.1 for a quantitative summary).
analyses of the matched galaxies (see Table B.1 for a quantitative summary).
As a reference, we perform a
![]() analysis of the 350 matched objects using once
the ground-based ellipticity measurements and once the space-based
measurements (Fig. B.7). It is quite remarkable how well
the
analysis of the 350 matched objects using once
the ground-based ellipticity measurements and once the space-based
measurements (Fig. B.7). It is quite remarkable how well
the
![]() contours agree for these; however, for the dark clump peak, the space-based
values reach only half the amplitude of the ground-based.
contours agree for these; however, for the dark clump peak, the space-based
values reach only half the amplitude of the ground-based.
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{2733b08.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg228.gif) |
Figure B.8:
|
Restricting the galaxy sample to those for which
![]() further
highlights the agreement, as is expected (left hand side of
Fig. B.8). These are mainly the galaxies considered
"bright'' also in the ground-based image (see Fig. B.3), which
contribute to the lensing signal found there.
Even for these, the
further
highlights the agreement, as is expected (left hand side of
Fig. B.8). These are mainly the galaxies considered
"bright'' also in the ground-based image (see Fig. B.3), which
contribute to the lensing signal found there.
Even for these, the
![]() values of the dark clump peak are a factor of 1.4 higher for the
ground-based ellipticity measurements.
values of the dark clump peak are a factor of 1.4 higher for the
ground-based ellipticity measurements.
For the
![]() scale, the
discrepancy in the
scale, the
discrepancy in the
![]() measurements at the dark clump position is even larger for those
objects with
measurements at the dark clump position is even larger for those
objects with
![]() (right hand side of
Fig. B.8). In the ground-based data, there is a >
(right hand side of
Fig. B.8). In the ground-based data, there is a >![]() peak slightly to the right of the dark clump position, while the
peak slightly to the right of the dark clump position, while the
![]() values in the space-based data are comparable to the
values in the space-based data are comparable to the
![]() sample, with a significance of
sample, with a significance of ![]()
![]() .
At the dark clump position, the
amplitudes in the ground-based values are on average a factor 3 larger than
the space-based ones for all filter scales. Interestingly, for the smallest
two filter scales, the highest significance found in the vicinity of
the dark clump is equivalent in the two datasets. However, this is
based only on a very small number of galaxies.
.
At the dark clump position, the
amplitudes in the ground-based values are on average a factor 3 larger than
the space-based ones for all filter scales. Interestingly, for the smallest
two filter scales, the highest significance found in the vicinity of
the dark clump is equivalent in the two datasets. However, this is
based only on a very small number of galaxies.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2733b09.ps}\end{figure}](/articles/aa/full/2006/28/aa2733-05/Timg231.gif) |
Figure B.9:
A comparison of the weights assigned to the matched objects
in the HST catalog and the ground-based catalog. Again, solid points
denote objects with
|
Table B.1:
Overview of the
![]() analyses discussed in this appendix. Shown
are the results at the position of the dark clump as measured in the
ground-based data, since we want to determine the cause of the high
analyses discussed in this appendix. Shown
are the results at the position of the dark clump as measured in the
ground-based data, since we want to determine the cause of the high
![]() amplitude in the ground-based data at this position. We list the ellipticity dispersion, the
amplitude in the ground-based data at this position. We list the ellipticity dispersion, the
![]() value
itself, and the signal-to-noise ratio. For those analyses of the 350 matched objects, we give both the results of using the ground-based and
of using the space-based data. For the second block from the bottom of the table, the
ground-based analysis uses the space-based weights and vice versa. For the last block, the
value
itself, and the signal-to-noise ratio. For those analyses of the 350 matched objects, we give both the results of using the ground-based and
of using the space-based data. For the second block from the bottom of the table, the
ground-based analysis uses the space-based weights and vice versa. For the last block, the
![]() component of the HST measurements is modified by applying the inverse of the linear fit between space-based and ground-based ellipticities.
Evaluating
component of the HST measurements is modified by applying the inverse of the linear fit between space-based and ground-based ellipticities.
Evaluating
![]() only at the ground-based dark clump position biases the result in favor of larger
ground-based values. For a better comparison of the general values, we quote the highest
significance found in the vicinity of this position in parentheses.
only at the ground-based dark clump position biases the result in favor of larger
ground-based values. For a better comparison of the general values, we quote the highest
significance found in the vicinity of this position in parentheses.
As there is a
![]() peak in all these samples, we can be sure that there is
some tangential alignment around the dark clump candidate. But it is still
unclear why it is measured to be so much larger in the ground-based image.
peak in all these samples, we can be sure that there is
some tangential alignment around the dark clump candidate. But it is still
unclear why it is measured to be so much larger in the ground-based image.
For the lensing analysis, the entries in the ground-based and space-based catalogs differ mainly in the shape measurements and in the weights assigned to each object. We have shown that the ellipticity measurements agree on average, but we have not yet considered the different weights assigned.
In Fig. B.9, we directly compare the weights assigned to the matched objects. Certainly, objects which were down-weighted in the ground-based data have higher weights in the HST catalog. But else, the scatter is fairly large.
To test the influence of the weights on the lensing analyses, we perform an analysis where we interchange the weights, i.e. we assign to each object in the ground-based image
the weight of its counterpart in the HST image and vice versa. The
results are listed in Table B.1. It is interesting to note that at most filter
scales, this causes the ground-based value to decrease and the space-based
value to increase.
But the
![]() values are within the error bars of the ones
with the original weights and are therefore only slightly
dependent on the weights.
values are within the error bars of the ones
with the original weights and are therefore only slightly
dependent on the weights.
We noted earlier that the linear fit applied to the
![]() components of the
matched objects yields a y-intercept with almost
components of the
matched objects yields a y-intercept with almost ![]() significance
(Sect. B.2.1). This might point to a problem of the HST data
related to its CTE or the drizzle procedure.
significance
(Sect. B.2.1). This might point to a problem of the HST data
related to its CTE or the drizzle procedure.
Earlier, the ellipticity measurements from all three chips were considered. The ellipticities compared were those defined with respect to the right ascension axis. However, any problem regarding the CTE would bias the ellipticity measurements with respect to the read-out direction, which is different for all three chips. Also, the effect of the anisotropy correction is likely to be different for each chip.
Therefore, we repeat the ellipticity comparison for the matched
objects separated according to which HST chips they were measured in (Fig. B.10). The
linear fits yield (with the same definition of the fit-parameters as in
Sect. B.2.1):

We modify the HST measurements by the relation
The results of a lensing analysis of the matched objects with these
modified ellipticities are listed in Table B.1. Indeed, this transformation yields
![]() values 25% larger than the original ones for the smallest two filter scales. For the
values 25% larger than the original ones for the smallest two filter scales. For the
![]() filter scale, the effect is
smaller, and for the
filter scale, the effect is
smaller, and for the
![]() filter scale it is negligible.
filter scale it is negligible.
If the height of the
![]() peak were uncorrelated with the systematic
deviation in the ellipticity measurement, the modification would only
add noise to the
peak were uncorrelated with the systematic
deviation in the ellipticity measurement, the modification would only
add noise to the
![]() statistic, as most ellipticities are amplified
due to mi < 1. The
statistic, as most ellipticities are amplified
due to mi < 1. The
![]() value of the peak therefore would not be
significantly altered, as is the case at least for the largest
filter scale. For the other filter scales, there is a slight increase
in both
value of the peak therefore would not be
significantly altered, as is the case at least for the largest
filter scale. For the other filter scales, there is a slight increase
in both
![]() and SNR value. But the change is at most
and SNR value. But the change is at most
![]() ,
so the variations are still within the standard deviation of the
original measurement.
,
so the variations are still within the standard deviation of the
original measurement.
The results of a lensing analysis of the complete HST catalog with this modification of the ellipticity are very similar to the original one. But as the linear fit which was the basis of this modification applies only to bright objects in the HST catalog, it is very speculative to extrapolate this to fainter objects.
As this modification alone is not able to reproduce the large lensing
signal seen in the ground-based data, particularly at the
![]() filter scale, the offset of the space-based ellipticities is
not the cause of the discrepancy in the
filter scale, the offset of the space-based ellipticities is
not the cause of the discrepancy in the
![]() measurements.
measurements.
For the lensing analysis of the HST data, we had divided the galaxy
sample into three magnitude bins of equal numbers of object. About half of the
objects in the brightest bin were also detected in the I-band image
and are used in the comparisons presented in this chapter. For these,
we have confirmed the presence of tangential alignment, even though
the
![]() amplitude differs in the two datasets. But
we fail to detect alignment in the medium bright HST bin.
amplitude differs in the two datasets. But
we fail to detect alignment in the medium bright HST bin.
The completion limit of the ground-based image falls within the brightest HST bin (cf. Fig. B.3), and so a number of objects in the latter, though of similar brightness, were not detected in the ground-based image. To test how much the additional objects in the HST image contribute to the lensing signal, we rearrange the HST brightness bin: instead of the magnitude cut between the brightest and medium bin, we split the galaxies according to whether or not they are a counterpart of an object detected in the I-band image. From the latter sample the faintest bin is split with the same magnitude cut as before. This effectively moves several objects from the bright into the medium bin and only a few the other way. The faint bin remains almost unaltered.
In Fig. B.11, we present the signal-to-noise contours of a
![]() analysis of these three bins. The medium bin, i.e. galaxies brighter
than m=26.5 that were not detected in the ground-based image
contains the most galaxies (835 compared to 350 in the bright bin and 594 in the faint bin), so that the noise is smallest. Yet,
the
analysis of these three bins. The medium bin, i.e. galaxies brighter
than m=26.5 that were not detected in the ground-based image
contains the most galaxies (835 compared to 350 in the bright bin and 594 in the faint bin), so that the noise is smallest. Yet,
the
![]() values in the vicinity of the dark clump are compatible
with zero within
values in the vicinity of the dark clump are compatible
with zero within ![]() .
.
Apparently, there is no tangential alignment present in the objects
that were moved from the bright bin to the medium bin. This is
compliant with the observation that for those objects also detected in
the I-band image, the signal-to-noise ratio of the
![]() peak is
larger than for the bright magnitude bin (cf. Fig. 11).
peak is
larger than for the bright magnitude bin (cf. Fig. 11).
Intriguingly, this implies that of the faint galaxies at the completion limit of the I-band image, those with a tangential alignment to the dark clump were preferentially detected. However, the fact that there is no tangential alignment for about half of the objects in the HST image, which are neither at the bright nor the faint end of the magnitude distribution, clearly disfavors the hypothesis that the tangential alignment in the brighter galaxies is caused by a lensing mass.
So far, we have not found any systematic that could be the single cause for the discrepancy in the lensing analyses. However, it is clear that for the faint galaxies which mainly caused the lensing signal in the ground-based image, the ellipticities agree with the HST measurements only on average, but not on an object-to-object basis. This is not surprising as the noise in the ground-based image is likely to influence the shape measurements. Yet, it is unlikely that noise can cause (or amplify) tangential alignment around a certain point.
In Fig. B.12 we compare the tangential ellipticity
![]() of the matched objects with respect to the dark clump centroid found
in the ground-based data. Only objects within
of the matched objects with respect to the dark clump centroid found
in the ground-based data. Only objects within
![]() of that
position are shown. Evidently, most objects in the ground-based data have a positive
of that
position are shown. Evidently, most objects in the ground-based data have a positive
![]() .
The scatter is comparable to the comparison of the individual
ellipticity components (Sect. B.2.1). Likewise, we fit
a linear function, where we distinguish between the
complete sample of matched galaxies and how well the ellipticity
measurements agree (as before, the fit is expressed such that the
ground-based data are the independent variable):
.
The scatter is comparable to the comparison of the individual
ellipticity components (Sect. B.2.1). Likewise, we fit
a linear function, where we distinguish between the
complete sample of matched galaxies and how well the ellipticity
measurements agree (as before, the fit is expressed such that the
ground-based data are the independent variable):
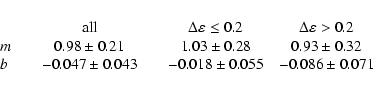
On the basis of the correlation of the individual measurements of the
tangential ellipticity, the agreement between the two datasets is
comparable to that of the ellipticity components, as would be
expected. Yet, the mean tangential ellipticity is different: for the
ground-based data, it is
![]()
![]() 0.017, for
the space-based
data,
0.017, for
the space-based
data,
![]()
![]() 0.017. These are very similar to the
results of the
0.017. These are very similar to the
results of the
![]() analysis at the same position at the
analysis at the same position at the
![]() filter scale,
filter scale,
![]()
![]() 0.019 and
0.019 and
![]()
![]() 0.019 (compare Table B.1). This again demonstrates that the coherent
alignment is present over a range of distance from the dark clump, as
the
0.019 (compare Table B.1). This again demonstrates that the coherent
alignment is present over a range of distance from the dark clump, as
the
![]() statistics is a weighted average tangential ellipticity,
where the weight is dependent on the distance.
statistics is a weighted average tangential ellipticity,
where the weight is dependent on the distance.
Within the standard deviations of the cited values, the two analyses are compatible with
each other. However, these errors are not independent, as they are based
on the ellipticities of the same galaxies. To estimate the
significance with which the ground-based mean is larger than the
space-based mean, we perform a bootstrap analysis, i.e. from the 195 galaxies in the sample, we draw at random 195 objects, with replacement. From these
we calculate
![]() and
and
![]() and repeat the
procedure 1 000 000 times. The result is shown in Fig. B.13. We
find that the space-based mean exceeds the ground-based mean in only
176 cases, i.e. the latter one is larger with
and repeat the
procedure 1 000 000 times. The result is shown in Fig. B.13. We
find that the space-based mean exceeds the ground-based mean in only
176 cases, i.e. the latter one is larger with
![]() confidence.
confidence.
This analysis is biased in the way that the reference position is the
dark clump position as measured in the ground-based data. Therefore,
we repeat the analysis for the centroid found in the space-based
data. Even for this case, the ground-based mean value exceeds the
space-based mean with
![]() confidence.
confidence.
It is quite puzzling that despite the general agreement of the ellipticity measurements, the mean tangential alignment can differ so much. As yet, we have no explanation for the cause of this.
In Fig. B.14, we present clippings of some of these galaxies from
the two images to convey a visual impression on how they compare in the
images and how the shape measurements relate to the image, especially
for the ground-based image. We find that in the HST image, the
measured ellipticity very well represents the shape of the
object. This is to be expected as all these objects are detected with
a high signal-to-noise ratio in the HST image. In the I-band image,
these objects have a low signal-to-noise ratio and the ellipticity
measurements only vaguely reflect the shape of the objects.
About 10% of the objects are actually two or more objects which were not
resolved in the ground-base image; for about 20% a nearby (though
resolved) object seems to influence the ellipticity measurement.
It is especially striking that for many, the ellipticity modulus
![]() is
clearly overestimated.
is
clearly overestimated.
We have shown that on average, ground-based and space-based ellipticity measurements agree very well. This justifies the assumption that weak lensing analyses based on ground-based data yield reliable results despite the smearing of object shapes by the Earth's atmosphere.
For the HST ellipticities, we have found only little evidence that they might be biased due to the CTE problem, the PSF undersampling, or the anisotropy correction. This holds at least for bright objects, for fainter ones we have no possibility of comparison. Yet, previous analyses (Sect. A.2) have shown that these problems have little influence.
The fainter an object, the less reliable its shape measurement is
(Fig. B.3). The strong lensing signal seen in the
ground-based data is caused mainly by faint objects, for which the
ellipticity measurements in the two datasets deviate. In both datasets,
there is a
![]() peak at the position of the dark clump, but the
degree of tangential alignment is much stronger in the ground-based
data. For many of
these objects, the ellipticity modulus
peak at the position of the dark clump, but the
degree of tangential alignment is much stronger in the ground-based
data. For many of
these objects, the ellipticity modulus
![]() is overestimated in the
ground-based measurements, and many of these seem to be accidentally
tangentially aligned to the dark clump, thus causing a high
is overestimated in the
ground-based measurements, and many of these seem to be accidentally
tangentially aligned to the dark clump, thus causing a high
![]() signal.
signal.