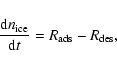A&A 453, L47-L50 (2006)
DOI: 10.1051/0004-6361:20065569
LETTER TO THE EDITOR
Spatial mapping of ices in the Ophiuchus-F core
A direct measurement of CO depletion and the formation of CO2
K. M. Pontoppidan1,2
1 - California Institute of Technology, Division for Geological and Planetary Sciences, MS 150-21, Pasadena, CA 91125, USA
2 -
Leiden Observatory, PO Box 9513, 2300 RA, Leiden, The Netherlands
Received 9 May 2006 / Accepted 22 May 2006
Abstract
Aims. Ices in dense star-forming cores contain the bulk of volatile molecules apart from H2 and thus represent a large fraction of dark cloud chemistry budget. Mm observations of gas provide indirect evidence for significant freeze-out of CO in the densest cores. To directly constrain the freeze-out profile of CO, the formation route of CO2 and the carrier of the 6.8  m band, the spatial distribution of the CO/CO2 ice system and the 6.8
m band, the spatial distribution of the CO/CO2 ice system and the 6.8  m band carrier are measured in a nearby dense core.
m band carrier are measured in a nearby dense core.
Methods. VLT-ISAAC, ISOCAM-CVF and Spitzer-IRS archival mid-infrared (3-20  m) spectroscopy of young stellar objects is used to construct a map of the abundances of CO and CO2 ices in the Oph-F star-forming core, probing core radii from
m) spectroscopy of young stellar objects is used to construct a map of the abundances of CO and CO2 ices in the Oph-F star-forming core, probing core radii from
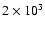 to
to
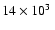 AU or densities from
AU or densities from
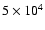 to
to
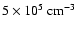 with a resolution of
with a resolution of
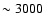 AU.
AU.
Results. The line-of-sight averaged abundances relative to water ice of both CO and CO2 ices increase monotonously with decreasing distance to the core center. The map traces the shape of the CO abundance profile between freeze-out ratios of 5-60%. and shows that the CO2 ice abundance increases by a factor of 2 as the CO freezes out. It is suggested that this indicates a formation route of CO2 on a CO ice surface to produce a CO2 component dilute in CO ice, in addition to a fraction of the CO2 formed at lower densities along with the water ice mantle. It is predicted that the CO2 bending mode band profile should reflect a high CO:CO2 number ratio in the densest parts of dark clouds. In contrast to CO and CO2, the abundance of the carrier of the 6.8  m band remains relatively constant throughout the core. A simple freeze-out model of the CO abundance profile is used to estimate the binding energy of CO on a CO ice surface to
m band remains relatively constant throughout the core. A simple freeze-out model of the CO abundance profile is used to estimate the binding energy of CO on a CO ice surface to
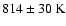 .
.
Key words: astrochemistry - molecular processes - ISM: molecules - infrared: ISM
Theory has long predicted that molecules freeze out onto dust grains in dense molecular clouds causing gas-phase abundances
to drop by orders of magnitude. A series of recent measurements of the gas-phase abundances of volatile molecules such as CO and N2H+in dense cores have corroborated this conjecture (e.g. Tafalla et al. 2004; Bacmann et al. 2002; Caselli et al. 1999). CO ice has also been
observed directly along
a growing sample of isolated lines of sight toward both embedded young stellar objects as well as background stars,
showing that the CO molecules taken from the gas-phase re-appears in the solid phase (Pontoppidan et al. 2003; Chiar et al. 1994).
CO ice is an excellent tracer of
freeze-out processes because it is the only abundant ice species known to form initially in the gas-phase before adsorbing to
a grain surface.
Pontoppidan et al. (2004) introduced the technique of ice mapping
at high (
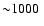 AU) spatial resolution - comparable to that of gas-phase maps. The procedure was demonstrated by
constructing a map of the distribution of water and methanol ices in the outer envelope of the
class 0 protostar SMM 4 in the
Serpens star-forming cloud. The ice map of SMM 4 was used to show that the water ice abundace remained constant over a relatively wide
range of densities, while the methanol abundance increased sharply by at least a factor of ten within 10 000 AU of the center of SMM 4.
In principle, ices are best mapped toward field stars located behind the cloud. However, such background stars are typically
extremely faint in the mid-infrared wavelength region. Therefore, disk sources embedded in their parent molecular cloud core
offer a convenient infrared continuum against which the ices in the core can be mapped, with appropriate caveats on the
interpretation of the derived ice abundances.
AU) spatial resolution - comparable to that of gas-phase maps. The procedure was demonstrated by
constructing a map of the distribution of water and methanol ices in the outer envelope of the
class 0 protostar SMM 4 in the
Serpens star-forming cloud. The ice map of SMM 4 was used to show that the water ice abundace remained constant over a relatively wide
range of densities, while the methanol abundance increased sharply by at least a factor of ten within 10 000 AU of the center of SMM 4.
In principle, ices are best mapped toward field stars located behind the cloud. However, such background stars are typically
extremely faint in the mid-infrared wavelength region. Therefore, disk sources embedded in their parent molecular cloud core
offer a convenient infrared continuum against which the ices in the core can be mapped, with appropriate caveats on the
interpretation of the derived ice abundances.
Direct mapping of CO ice abundances is highly
complementary to mapping of gas phase abundances, because ice maps are sensitive to depletion fractions as low as 5%, while
gas-phase abundance maps trace high depletion factors (
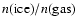 )
of
)
of
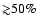 (Caselli et al. 1999).
Furthermore, the depletion fraction as a function of gas density
in a core is strongly dependent on the properties of the dust grain surfaces. Direct maps of CO ice in a dense core
therefore enables an independent measure of surface binding energies.
(Caselli et al. 1999).
Furthermore, the depletion fraction as a function of gas density
in a core is strongly dependent on the properties of the dust grain surfaces. Direct maps of CO ice in a dense core
therefore enables an independent measure of surface binding energies.
This letter presents the first spatial map of CO and CO2 ices in a dense molecular core. It will be demonstrated
that by directly measuring the relation between ice abundances and gas densities, the following quantities can be constrained: 1)
the dependence of CO depletion on gas density with a large dynamical range, 2) the CO-CO binding energy, 3) the formation route
of CO2 and the 6.8  m band carrier.
The case study is the F core in the Ophiuchus molecular cloud complex (Motte et al. 1998). Embedded within this region are at least
8-10 infrared-bright young stars. The lines of sight toward 5 of these young stars are used to probe the ices
in front of each star in order to obtain a profile of ice abundances across the minor axis of the core.
m band carrier.
The case study is the F core in the Ophiuchus molecular cloud complex (Motte et al. 1998). Embedded within this region are at least
8-10 infrared-bright young stars. The lines of sight toward 5 of these young stars are used to probe the ices
in front of each star in order to obtain a profile of ice abundances across the minor axis of the core.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{5569fig1.ps}
\end{figure}](/articles/aa/full/2006/27/aa5569-06/Timg12.gif) |
Figure 1:
Overview of the H2O, CO, 6.8  m and CO2 ice bands ( ordered left to right) used to construct the ice map of the
Oph-F core. The 3.08 m and CO2 ice bands ( ordered left to right) used to construct the ice map of the
Oph-F core. The 3.08  m
water ice bands shown on the left-most panel are ordered according to optical depth, for clarity, as indicated in the panel. In the remaining
panels, the sources are ordered according to projected distance to the core center, with the source furthest from the center (IRS 46) at the
top. No. 5-8 m
water ice bands shown on the left-most panel are ordered according to optical depth, for clarity, as indicated in the panel. In the remaining
panels, the sources are ordered according to projected distance to the core center, with the source furthest from the center (IRS 46) at the
top. No. 5-8  m spectrum is available for IRS 46. Note also that the 6.8 m spectrum is available for IRS 46. Note also that the 6.8  m band of IRS 42 is filled in by emission likely due to PAHs.
All the spectra have been shifted vertically, for clarity. m band of IRS 42 is filled in by emission likely due to PAHs.
All the spectra have been shifted vertically, for clarity. |
| Open with DEXTER |
The individual spectra are taken from van Dishoeck et al. (2003) and Pontoppidan et al. (2003) of the 3.08  m and 4.67
m and 4.67  m stretching modes
of solid H2O and CO,
obtained with the Infrared Spectrometer And Array Camera (ISAAC) on the Very Large Telescope
(VLT)
m stretching modes
of solid H2O and CO,
obtained with the Infrared Spectrometer And Array Camera (ISAAC) on the Very Large Telescope
(VLT)![[*]](/icons/foot_motif.gif) . The solid CO2 component is probed along the same lines of sight using the InfraRed Spectrograph (IRS) on the
Spitzer Space Telescope (AOR IDs 0009346048 and 0009829888
. The solid CO2 component is probed along the same lines of sight using the InfraRed Spectrograph (IRS) on the
Spitzer Space Telescope (AOR IDs 0009346048 and 0009829888 ![[*]](/icons/foot_motif.gif) )
(Lahuis et al. 2006; Pontoppidan et al. 2005)
as well as 5-16.3
)
(Lahuis et al. 2006; Pontoppidan et al. 2005)
as well as 5-16.3  m spectra obtained with
ISOCAM-CVF (TDTs 29601715 and 29601813)
(Alexander et al. 2003)
m spectra obtained with
ISOCAM-CVF (TDTs 29601715 and 29601813)
(Alexander et al. 2003)![[*]](/icons/foot_motif.gif) . The Spitzer spectra were taken as part of the
Cores to Disks Legacy program (Evans et al. 2003).
Combining these facilities, high quality 3-16
. The Spitzer spectra were taken as part of the
Cores to Disks Legacy program (Evans et al. 2003).
Combining these facilities, high quality 3-16  m spectra are available for 5 sources within a radius of
15 000 AU from the center of the pre-stellar core, defined to be the 850
m spectra are available for 5 sources within a radius of
15 000 AU from the center of the pre-stellar core, defined to be the 850  m peak of Oph-F MM2 (
m peak of Oph-F MM2 (
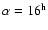 27 24.3,
27 24.3,
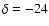
 40 35, J2000) (Motte et al. 1998). Only IRS 46 has no suitable spectrum between 5 and 10
40 35, J2000) (Motte et al. 1998). Only IRS 46 has no suitable spectrum between 5 and 10  m.
m.
To determine the optical depths of the various ice bands continua were fitted using low-order polynomials. The CO and CO2 bands
are sufficiently narrow to make the continuum determination relatively straight-forward and unbiased. For the 3.08  m water ice band
a continuum is fitted to points between 3.8 to 4.0
m water ice band
a continuum is fitted to points between 3.8 to 4.0  m and a K-band photometric point from the 2MASS
catalogue. Finally, a local continuum between 5.5 and 8.0
m and a K-band photometric point from the 2MASS
catalogue. Finally, a local continuum between 5.5 and 8.0  m is used to extract optical depth spectra of the 6.8
m is used to extract optical depth spectra of the 6.8  m band.
In consideration of the uncertainties in the continuum determination,
care was taken to use the same "ice-free'' regions and second-order polynomials for
all sources. Further discussion of the determination of continua
for extracting ice optical depth spectra can be found in e.g. Gerakines et al. (1995); Dartois et al. (2002) and Keane et al. (2001).
The ice spectra are shown on an optical depth scale in Fig. 1, while the
locations of the sources relative to an 850
m band.
In consideration of the uncertainties in the continuum determination,
care was taken to use the same "ice-free'' regions and second-order polynomials for
all sources. Further discussion of the determination of continua
for extracting ice optical depth spectra can be found in e.g. Gerakines et al. (1995); Dartois et al. (2002) and Keane et al. (2001).
The ice spectra are shown on an optical depth scale in Fig. 1, while the
locations of the sources relative to an 850  m JCMT-SCUBA map obtained by the COMPLETE collaboration (Ridge et al. 2006) are shown
in Fig. 2.
m JCMT-SCUBA map obtained by the COMPLETE collaboration (Ridge et al. 2006) are shown
in Fig. 2.
The CO ice column densities have been determined in Pontoppidan et al. (2003). For the water 3.08  m band and the CO2
15.2
m band and the CO2
15.2  m band, band strengths of
m band, band strengths of
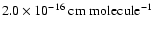 and
and
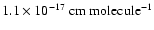 are used,
respectively (Gerakines et al. 1995). For the 6.8
are used,
respectively (Gerakines et al. 1995). For the 6.8  m band, a band strength of
m band, a band strength of
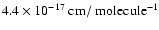 is assumed,
appropriate for NH4+ (Schutte & Khanna 2003).
The ice column densities are summarized in Table 1.
is assumed,
appropriate for NH4+ (Schutte & Khanna 2003).
The ice column densities are summarized in Table 1.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5569fig2.ps}
\end{figure}](/articles/aa/full/2006/27/aa5569-06/Timg19.gif) |
Figure 2:
The locations (triangles) of the sources used to construct the ice map plotted on the SCUBA 850  m map.
The star symbol indicates the center of the core. m map.
The star symbol indicates the center of the core. |
| Open with DEXTER |
Table 1:
Line-of-sight averaged ice abundances in the Oph-F core.
3 Abundance profiles of CO and CO2 ice
The basic ice map is constructed by determining the ice column densities along each line of sight and ratioing with the water ice column
density. The implicit assumption is that the 3.08  m water ice band traces the total H2 column density (see Pontoppidan et al. (2004) for a discussion).
This yields CO and CO2 line-of-sight averaged ice abundances relative to H2O ice as a function
of projected distance to the center of the core. The radial map is shown in Fig. 3.
m water ice band traces the total H2 column density (see Pontoppidan et al. (2004) for a discussion).
This yields CO and CO2 line-of-sight averaged ice abundances relative to H2O ice as a function
of projected distance to the center of the core. The radial map is shown in Fig. 3.
It is seen that the abundances of pure CO,
water-rich CO and CO2 all increase toward the center of the core, while the 6.8  m band carrier decreases slightly in abundance.
The sharp rise in CO ice abundance is expected for CO freezing
out from the gas-phase at high densities in the central parts of the core.
Assuming a constant water ice abundance of
m band carrier decreases slightly in abundance.
The sharp rise in CO ice abundance is expected for CO freezing
out from the gas-phase at high densities in the central parts of the core.
Assuming a constant water ice abundance of
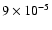 relative to H2 in accordance
with a model of the CRBR 2422.8-3423 line of sight of Pontoppidan et al. (2005), the average abundance of pure CO ice is seen to rise from
relative to H2 in accordance
with a model of the CRBR 2422.8-3423 line of sight of Pontoppidan et al. (2005), the average abundance of pure CO ice is seen to rise from
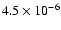 to
to
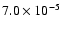 ,
and the total CO and CO2 abundances from
,
and the total CO and CO2 abundances from
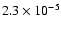 to
to
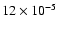 .
This corresponds to a total CO depletion ranging from 12% to 60%, assuming an initial CO gas-phase
abundance of
.
This corresponds to a total CO depletion ranging from 12% to 60%, assuming an initial CO gas-phase
abundance of
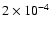 .
.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5569fig3.ps}
\end{figure}](/articles/aa/full/2006/27/aa5569-06/Timg27.gif) |
Figure 3:
Radial map of CO and CO2 ices of the Oph-F core. Ice
abundances relative to H2O ice toward young stars are plotted as functions of projected distance to the center of the core as
described in the text. The CO ice has been split into a "pure'' and "water-rich'' component following Pontoppidan et al. (2003). |
| Open with DEXTER |
The increase by roughly a factor two in CO2 ice abundance is particularly interesting. Since
CO2 molecules are formed on the grain surfaces, the increase in CO2 ice abundance along with the CO freeze out is a direct
indication of a formation route associated with CO. A significant amount of CO2 is present in
the outer parts of the Oph-F core where the densities are not yet high enough for the CO to freeze out.
This can be interpreted as evidence for two distinct eras for CO2 ice formation: The first takes place at roughly the same time
as the bulk of the water ice is formed, which is known to happen as soon as the extinction, AV, into the cloud reaches a specific,
relatively low, threshold of roughly 3-5 magnitudes (Whittet et al. 1988). This domain is not probed by the Oph-F ice map.
The second takes place during the catastrophic freeze-out of CO that occurs at
densities of a few
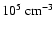 (Jørgensen et al. 2005) in which an almost pure CO ice mantle forms. This second phase of CO2 molecules should be easily detectable in the shape of the 15.2
(Jørgensen et al. 2005) in which an almost pure CO ice mantle forms. This second phase of CO2 molecules should be easily detectable in the shape of the 15.2  m CO2 bending mode absorption band, which is highly sensitive to the
molecular environment of the CO2 molecules. Specifically, the new CO2 molecules should be found to be dilute in the CO ice
with an average fraction
of 1:5, as determined by the relative CO and CO2 abundance increases in the Oph-F core. Since the CO freeze-out rate is
a very strongly increasing function of density, it is expected that the CO2:CO ratio will decrease in denser parts of the core. Thus,
one would expect to find components with a range of CO2:CO ratios in the CO2 bending mode in the centers of dense clouds.
The spectral resolution of the ISOCAM-CVF spectra (
m CO2 bending mode absorption band, which is highly sensitive to the
molecular environment of the CO2 molecules. Specifically, the new CO2 molecules should be found to be dilute in the CO ice
with an average fraction
of 1:5, as determined by the relative CO and CO2 abundance increases in the Oph-F core. Since the CO freeze-out rate is
a very strongly increasing function of density, it is expected that the CO2:CO ratio will decrease in denser parts of the core. Thus,
one would expect to find components with a range of CO2:CO ratios in the CO2 bending mode in the centers of dense clouds.
The spectral resolution of the ISOCAM-CVF spectra (
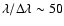 )
is not sufficiently high to search for such band shape
changes in the current data.
)
is not sufficiently high to search for such band shape
changes in the current data.
Since the young stars that are used to estimate ice abundances in the core
material are embedded in the core, significant caveats apply. Heating of the core material may desorb CO ice within a radius of a
few hundred AU of each source, depending on the luminosity. However,
since the projected size of the core is 30 000 AU, desorption is likely to play only a minor role. A possible exception
to this is IRS 46, which contains a significant component of warm molecular gas along the line of sight (Lahuis et al. 2006).
Also, the sources may be surrounded by remnant envelopes with different ice abundances than the surrounding core.
The ice absorption toward CRBR 2422.8-3423 was shown by Pontoppidan et al. (2005) to be dominated by cold core material, although a fraction
of the water, CO2 and 6.8  m ices are likely located in the disk. However, it
was found that the CO ice observed in this line of sight could not originate in the disk.
m ices are likely located in the disk. However, it
was found that the CO ice observed in this line of sight could not originate in the disk.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{5569fig4.ps}
\end{figure}](/articles/aa/full/2006/27/aa5569-06/Timg30.gif) |
Figure 4:
Observed and modeled CO ice abundance for Oph-F. The curve shows the simple
freeze-out model for the best-fitting CO binding energy of dH/k=814 K. The "solid CO'' abundance is the sum of the pure CO, CO in water
and the CO2 ice excess abundances. This assumes that one CO molecule is used to produce each CO2 molecule. The error bars indicate a 20% uncertainty. |
| Open with DEXTER |
The CO depletion profile in Fig. 3 is modeled using a simplified freeze-out model, assuming a static core and
that only thermal desorption occurs. For the purposes of this letter, the model presented is intended as a demonstration of
the method, rather than achieving very accurate results. The rate of ice mantle build-up is then given by:
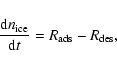 |
(1) |
where
![$R_{\rm des}=\nu_0 \exp[-dH/kT]\times n_{\rm CO,ice}\times \beta$](/articles/aa/full/2006/27/aa5569-06/img32.gif) is the desorption rate and
is the desorption rate and
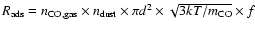 is the adsorption rate.
is the adsorption rate.
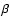 is a factor taking into account that CO only desorbs from the top monolayer (i.e. 1st order desorption for
sub-monolayer coverage and 0th order desorption for multilayers).
is a factor taking into account that CO only desorbs from the top monolayer (i.e. 1st order desorption for
sub-monolayer coverage and 0th order desorption for multilayers).
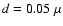 m is the grain radius, f=1 is the sticking coefficient,
m is the grain radius, f=1 is the sticking coefficient, 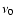 is the frequency of the CO stretching mode and
is the frequency of the CO stretching mode and
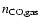 and
and
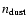 are the number densities of CO gas and dust particles. Solving for
are the number densities of CO gas and dust particles. Solving for
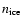 yields a time dependent
ice density given a gas density and (assumed identical) gas and dust temperature. This rate equation reaches an equilibrium on
relatively short time scales (
yields a time dependent
ice density given a gas density and (assumed identical) gas and dust temperature. This rate equation reaches an equilibrium on
relatively short time scales (
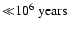 ). Therefore, given a temperature and density structure, one can in principle
solve for the binding energy of CO, dH.
For the density profile of the core, a Bonnor-Ebert sphere with a central density of
). Therefore, given a temperature and density structure, one can in principle
solve for the binding energy of CO, dH.
For the density profile of the core, a Bonnor-Ebert sphere with a central density of
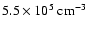 is used
with a temperature of 15 K as suggested by Motte et al. (1998) and references therein. This simple procedure yields a CO on CO binding energy
of
is used
with a temperature of 15 K as suggested by Motte et al. (1998) and references therein. This simple procedure yields a CO on CO binding energy
of 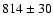 K. The uncertainty reflects different
results obtained if varying the central density and water ice abundance by 50%. Additionally, the derived binding energy scales
linearly with the assumed dust temperature. Considering the simplified analysis, this result
is consistent with that recently found by Bisschop et al. (2006) from laboratory experiments.
K. The uncertainty reflects different
results obtained if varying the central density and water ice abundance by 50%. Additionally, the derived binding energy scales
linearly with the assumed dust temperature. Considering the simplified analysis, this result
is consistent with that recently found by Bisschop et al. (2006) from laboratory experiments.
The radial map constitutes the first direct observation of the freeze-out profile of CO on dust grains in a prestellar core previously
inferred indirectly from observations of millimetre lines of molecules. Additionally
the observed increase in CO2 ice abundance toward the center is the first quantitative observational evidence of the formation
of CO2 from CO on the surfaces of dust grains. These are observations that would not have been possible with single lines of sight.
Acknowledgements
This work was supported by a Spinoza grant. The author gratefully acknowledges discussions with Helen Fraser and Ewine van Dishoeck. The
850  m map of Oph-F from the COMPLETE survey was supplied by Doug Johnstone.
m map of Oph-F from the COMPLETE survey was supplied by Doug Johnstone.
- Alexander,
R. D., Casali, M. M., André, P., Persi, P., &
Eiroa, C. 2003, A&A, 401, 613 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Bacmann, A.,
Lefloch, B., Ceccarelli, C., et al. 2002, A&A, 389,
L6 [EDP Sciences] [NASA ADS] [CrossRef]
- Bisschop,
S. E., Fraser, H. J., Öberg, K. I., van
Dishoeck, E. F., & Schlemmer, S. 2006, A&A, 449,
1297 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Caselli, P.,
Walmsley, C. M., Tafalla, M., Dore, L., & Myers,
P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef]
- Chiar, J. E.,
Adamson, A. J., Kerr, T. H., & Whittet,
D. C. B. 1994, ApJ, 426, 240 [NASA ADS] [CrossRef]
- Dartois, E.,
d'Hendecourt, L., Thi, W., Pontoppidan, K. M., & van
Dishoeck, E. F. 2002, A&A, 394, 1057 [EDP Sciences] [NASA ADS] [CrossRef]
- Evans, N. J.,
Allen, L. E., Blake, G. A., et al. 2003, PASP, 115,
965 [NASA ADS] [CrossRef] (In the text)
- Gerakines,
P. A., Schutte, W. A., Greenberg, J. M., & van
Dishoeck, E. F. 1995, A&A, 296, 810 [NASA ADS]
-
Jørgensen, J. K., Schöier, F. L., & van
Dishoeck, E. F. 2005, A&A, 435, 177 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Keane, J. V.,
Tielens, A. G. G. M., Boogert, A. C. A.,
Schutte, W. A., & Whittet, D. C. B. 2001,
A&A, 376, 254 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Lahuis, F., van
Dishoeck, E. F., Boogert, A. C. A., et al.
2006, ApJ, 636, L145 [NASA ADS] [CrossRef]
- Motte, F., Andre, P.,
& Neri, R. 1998, A&A, 336, 150 [NASA ADS] (In the text)
-
Pontoppidan, K. M., Fraser, H. J., Dartois, E.,
et al. 2003, A&A, 408, 981 [EDP Sciences] [NASA ADS] [CrossRef]
-
Pontoppidan, K. M., van Dishoeck, E. F., & Dartois,
E. 2004, A&A, 426, 925 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Pontoppidan, K. M., Dullemond, C. P., van Dishoeck,
E. F., et al. 2005, ApJ, 622, 463 [NASA ADS] [CrossRef]
- Ridge, N. A.,
Di Francesco, J., Kirk, H., et al. 2006, AJ, in
press
(In the text)
- Schutte,
W. A., & Khanna, R. K. 2003, A&A, 398, 1049 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Tafalla, M.,
Myers, P. C., Caselli, P., & Walmsley, C. M. 2004,
A&A, 416, 191 [EDP Sciences] [NASA ADS] [CrossRef]
- van Dishoeck,
E. F., Dartois, E., Pontoppidan, K. M., et al. 2003,
The Messenger, 113, 49 [NASA ADS] (In the text)
- Whittet,
D. C. B., Bode, M. F., Longmore, A. J.,
et al. 1988, MNRAS, 233, 321 [NASA ADS] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{5569fig1.ps}
\end{figure}](/articles/aa/full/2006/27/aa5569-06/Timg12.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5569fig2.ps}
\end{figure}](/articles/aa/full/2006/27/aa5569-06/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5569fig3.ps}
\end{figure}](/articles/aa/full/2006/27/aa5569-06/Timg27.gif)
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{5569fig4.ps}
\end{figure}](/articles/aa/full/2006/27/aa5569-06/Timg30.gif)