A&A 453, 1059-1066 (2006)
DOI: 10.1051/0004-6361:20054771
The polar wind of the fast rotating Be star Achernar
VINCI/VLTI interferometric observations of an elongated polar envelope
P. Kervella1 -
A. Domiciano de Souza2,3
1 - LESIA, CNRS UMR 8109, Observatoire de Paris-Meudon, 5
place Jules Janssen, 92195 Meudon Cedex, France
2 -
Lab. Univ. d'Astrophysique de Nice (LUAN), CNRS UMR 6525, UNSA, Parc Valrose,
06108 Nice, France
3 -
Observatoire de la Côte d'Azur, CNRS UMR 6203, Département GEMINI,
BP 4229, 06304 Nice Cedex 4, France
Received 23 December 2005 / Accepted 20 February 2006
Abstract
Context. Be stars show evidence of mass loss and circumstellar envelopes (CSE) from UV resonance lines, near-IR excesses, and the presence of episodic hydrogen emission lines. The geometry of these envelopes is still uncertain, although it is often assumed that they are formed by a disk around the stellar equator and a hot polar wind.
Aims. We probe the close environment of the fast rotating Be star Achernar at angular scales of a few milliarcseconds (mas) in the infrared, in order to constrain the geometry of a possible polar CSE.
Methods. We obtained long-baseline interferometric observations of Achernar with the VINCI/VLTI beam combiner in the H and K bands, using various telescope configurations and baseline lengths with a wide azimuthal coverage.
Results. The observed visibility measurements along the polar direction are significantly lower than the visibility function of the photosphere of the star alone, in particular at low spatial frequencies. This points to the presence of an asymmetric diffuse CSE elongated along the polar direction of the star. To our data, we fit a simple model consisting of two components: a 2D elliptical Gaussian superimposed on a uniform ellipse representing the distorted photosphere of the fast rotating star.
Conclusions. We clearly detected a CSE elongated along the polar axis of the star, as well as rotational flattening of the stellar photosphere. For the uniform-ellipse photosphere we derive a major axis of
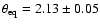 mas and a minor axis of
mas and a minor axis of
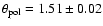 mas. The relative near-IR flux measured for the CSE compared to the stellar photosphere is
mas. The relative near-IR flux measured for the CSE compared to the stellar photosphere is
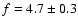 %. Its angular dimensions are loosely constrained by the available data at
%. Its angular dimensions are loosely constrained by the available data at
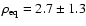 mas and
mas and
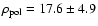 mas. This CSE could be linked to free-free emission from the radiative pressure driven wind originating from the hot polar caps of the star.
mas. This CSE could be linked to free-free emission from the radiative pressure driven wind originating from the hot polar caps of the star.
Key words: techniques: high angular resolution - techniques:
interferometric - stars: emission-line, Be - stars: mass-loss -
stars: rotation - stars: individual: Achernar
The southern star Achernar (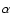 Eridani, HD 10144)
is the brightest of all Be stars (V =0.46 mag). Depending on the
author (and the technique used) the spectral type of Achernar
ranges from B3-B4IIIe to B4Ve (e.g., Slettebak 1982;
Balona et al. 1987).
The estimated projected rotation velocity
Eridani, HD 10144)
is the brightest of all Be stars (V =0.46 mag). Depending on the
author (and the technique used) the spectral type of Achernar
ranges from B3-B4IIIe to B4Ve (e.g., Slettebak 1982;
Balona et al. 1987).
The estimated projected rotation velocity 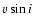 ranges from 220 to 270 km s-1 and the effective
temperature
ranges from 220 to 270 km s-1 and the effective
temperature
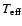 from 15 000 to 20 000 K (e.g., Vinicius et al. 2006; Rivinius,
priv. comm.; Chauville et al. 2001).
The difficulty in deriving these parameters more precisely is a
direct consequence of the rapid rotation of Achernar. Such rapid
rotation (
from 15 000 to 20 000 K (e.g., Vinicius et al. 2006; Rivinius,
priv. comm.; Chauville et al. 2001).
The difficulty in deriving these parameters more precisely is a
direct consequence of the rapid rotation of Achernar. Such rapid
rotation (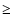
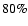 of the critical velocity) induces mainly two effects
on the star structure:
a rotational flattening and a gravity
darkening, which can be described by the von Zeipel effect (von Zeipel 1924).
of the critical velocity) induces mainly two effects
on the star structure:
a rotational flattening and a gravity
darkening, which can be described by the von Zeipel effect (von Zeipel 1924).
Table 1:
Relevant parameters of the calibrators used for VINCI
observations of Achernar (continued in Table 2).
Domiciano de Souza et al. (2003, hereafter D03) measured the apparent
rotational flattening of Achernar using the Very Large Telescope Interferometer (VLTI).
They showed that the flattening ratio measured on this star
cannot be explained in the Roche approximation, especially when taking
the von Zeipel effect into account.
Recently, this effect was revealed in two other rapidly
rotating stars thanks to interferometric observations:
Altair (A7V, Ohishi et al. 2004;
Domiciano de Souza et al. 2005) and
Regulus (B7V, McAlister et al. 2005).
Rapid rotation and gravity darkening seem to be important keys to
explaining the two-component circumstellar environment (CSE) of Be
stars: (1) a dense (particle densities
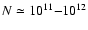 cm-3), high mass-loss (
cm-3), high mass-loss (
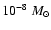 /yr) and low
radial velocity (
/yr) and low
radial velocity (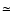 10-100 km s-1) equatorial envelope and (2) a rarefied (
10-100 km s-1) equatorial envelope and (2) a rarefied (
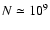 cm-3), low mass-loss
(
cm-3), low mass-loss
(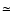
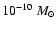 /yr) and fast (
/yr) and fast (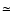 1000 km s-1) polar
wind (e.g. Damineli Neto & de Freitas Pacheco 1982; Waters et al. 1987, and references therein).
This picture of a two-component CSE is based on many observations of
Be stars performed in the past few decades. For example,
optical/IR data have shown emission lines and IR excesses that
essentially probe the denser regions of the CSE (e.g. Waters 1986;
Dougherty et al. 1994), while UV resonance lines of highly ionized
species can probe regions of lower density (e.g. Snow 1981; Peters 1982).
Gehrz et al. (1974) showed that the near-IR
excess measured in Be stars is due to free-free radiation.
1000 km s-1) polar
wind (e.g. Damineli Neto & de Freitas Pacheco 1982; Waters et al. 1987, and references therein).
This picture of a two-component CSE is based on many observations of
Be stars performed in the past few decades. For example,
optical/IR data have shown emission lines and IR excesses that
essentially probe the denser regions of the CSE (e.g. Waters 1986;
Dougherty et al. 1994), while UV resonance lines of highly ionized
species can probe regions of lower density (e.g. Snow 1981; Peters 1982).
Gehrz et al. (1974) showed that the near-IR
excess measured in Be stars is due to free-free radiation.
The disk-like shape of the dense equatorial CSE has been directly
measured by interferometric observations in the radio and
optical/IR (e.g. Dougherty & Taylor 1992; Stee et al. 1995;
Quirrenbach et al. 1997). In a recent work,
Tycner et al. (2005) explore
the relationship between the angular size of the H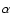 emitting region
(measured by interferometry) and the net H
emitting region
(measured by interferometry) and the net H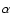 emission measured spectroscopically
for seven Be stars. They find an interesting correlation between the two quantities,
which they attribute to an optically thick emission
proportional to the effective area of the emitting disk.
Because the equatorial disks are denser (
emission measured spectroscopically
for seven Be stars. They find an interesting correlation between the two quantities,
which they attribute to an optically thick emission
proportional to the effective area of the emitting disk.
Because the equatorial disks are denser (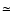 100 times) than
the polar winds and because the free-free emissivity is proportional to the
density squared, the equatorial disk dominates the near-IR continuum
emission when it is present.
100 times) than
the polar winds and because the free-free emissivity is proportional to the
density squared, the equatorial disk dominates the near-IR continuum
emission when it is present.
However, it is still not clear if this free-free radiation comes
only from the equatorial envelope or if it can also be formed, at
least partially, in the polar wind. Modern high angular resolution
techniques have the resolving power and sensitivity required to
map the spatial distribution of the near-IR emission.
In the present paper we investigate this issue by using all
available interferometric observations of Achernar obtained with
the VINCI/VLTI near-IR instrument (Sect. 2).
These observations were performed during a phase where the equatorial
disk was nearly absent. The adopted analytical model is presented in
Sect. 3 and our results discussed in
Sect. 4.
2 Interferometric observations
The European Southern Observatory's VLTI
(Glindemann et al. 2000, 2004) has been in operation on top
of the Cerro Paranal, in Northern Chile since March 2001. For the observations reported in this
paper, the light coming from two test siderostats (0.35 m aperture) or two Unit Telescopes (8 m aperture)
was recombined coherently in VINCI, the VLT INterferometer Commissioning Instrument
(Kervella et al. 2000, 2003). We used either a K band (
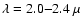 m)
or H band (
m)
or H band (
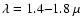 m) filter, depending on the beam combiner. In the K band, we
relied on the MONA beam combiner, based on fluoride glass optical fibers, while in the H band,
we employed the IONIC integrated optics beam combiner
(Berger et al. 2001; Kervella et al. 2003; Lebouquin et al. 2004).
A total of nine VLTI baselines were used for this program, including five out of the six possible Unit
Telescope baselines. Considering the transmission of the instrument and the average effective temperature
of Achernar, the effective wavelength of our observations was
m) filter, depending on the beam combiner. In the K band, we
relied on the MONA beam combiner, based on fluoride glass optical fibers, while in the H band,
we employed the IONIC integrated optics beam combiner
(Berger et al. 2001; Kervella et al. 2003; Lebouquin et al. 2004).
A total of nine VLTI baselines were used for this program, including five out of the six possible Unit
Telescope baselines. Considering the transmission of the instrument and the average effective temperature
of Achernar, the effective wavelength of our observations was
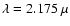 m in the K band
and
m in the K band
and
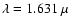 m in the H band. The uncertainty on these wavelengths (
m in the H band. The uncertainty on these wavelengths (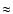 0.2%) is
negligible compared to the accuracy of our measurements.
0.2%) is
negligible compared to the accuracy of our measurements.
The raw data processing was achieved using a wavelet-based
algorithm, integrated in an automated data reduction pipeline
(Kervella et al. 2004a). The general principle is similar to the
original FLUOR algorithm (Coudé du Foresto et al. 1997), but
instead of the classical Fourier analysis, we implemented a
wavelet-based time-frequency analysis (Ségransan et al. 1999).
The output of this pipeline is a single value of the squared coherence factor 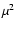 for each series of 500 interferograms and the associated bootstrapped error bar.
We obtained a total of 49 500 interferograms of Achernar in the
K band and 9500 in the H band, among which 32 394 and 3029
were reduced by the pipeline, respectively.
The lower proportion of processed interferograms
in the H band is explained by the fact that only one interferometric
output is available in the IONIC component, instead of two for the MONA
beam combiner. In both cases, two photometric outputs are present.
This resulted in a total of 99 squared visibility measurements in the K band,
and 19 in the H band, with their associated statistical and calibration uncertainties.
for each series of 500 interferograms and the associated bootstrapped error bar.
We obtained a total of 49 500 interferograms of Achernar in the
K band and 9500 in the H band, among which 32 394 and 3029
were reduced by the pipeline, respectively.
The lower proportion of processed interferograms
in the H band is explained by the fact that only one interferometric
output is available in the IONIC component, instead of two for the MONA
beam combiner. In both cases, two photometric outputs are present.
This resulted in a total of 99 squared visibility measurements in the K band,
and 19 in the H band, with their associated statistical and calibration uncertainties.
We used a number of calibrators taken mainly from the Bordé
et al. (2002) catalogue, which is an adaptation of the
Cohen et al. (1999) catalogue for interferometric
observations. The observations of these stars were used
to estimate the point source response of the interferometer
immediately before or after the Achernar observations. Their
properties are listed in Tables 1 and 2. The choice of the calibrators is an important
step in the preparation of interferometric observations, as
significant departures of their actual visibilities from the
expected model can propagate into biases on the calibrated
visibilities of the scientific target. Among the possible reasons
for such departures, binarity (or multiplicity) and deviations
from sphericity (due, for instance, to fast rotation or
gravitational interaction) are the most critical. All stars in the
Bordé et al. (2002) catalogue were carefully scrutinized
by these authors for the presence of companions, and are currently
regarded as single stars. With respect to fast rotation, the
values of 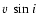 are generally low for all our calibrators.
Spectroscopic measurements of the projected rotational velocities
are missing for some of our calibrators; but as they are giant
stars, we assume that they are small and, therefore, that the
deformation of these stars can be neglected.
are generally low for all our calibrators.
Spectroscopic measurements of the projected rotational velocities
are missing for some of our calibrators; but as they are giant
stars, we assume that they are small and, therefore, that the
deformation of these stars can be neglected.
One of our calibrators, 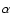 PsA (Fomalhaut), is a moderately fast rotating dwarf
(A3V,
PsA (Fomalhaut), is a moderately fast rotating dwarf
(A3V,
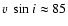 km s-1, from Glebocki et al. 2000).
We considered carefully the visibilities that were computed using this calibrator,
and they show no deviation from the other measurements, in particular those calibrated
by
km s-1, from Glebocki et al. 2000).
We considered carefully the visibilities that were computed using this calibrator,
and they show no deviation from the other measurements, in particular those calibrated
by 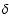 Phe that were obtained on the same baseline.
Moreover, Di Folco et al. (2004) have measured
the angular diameter of this star along the same projected baseline azimuth as during our
observations of Achernar. Therefore, we do not expect any difference in terms of
angular diameter.
In any case, we considered a conservative
Phe that were obtained on the same baseline.
Moreover, Di Folco et al. (2004) have measured
the angular diameter of this star along the same projected baseline azimuth as during our
observations of Achernar. Therefore, we do not expect any difference in terms of
angular diameter.
In any case, we considered a conservative 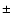 0.07 mas (
0.07 mas (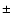 3%)
uncertainty on the asumed angular diameter of
3%)
uncertainty on the asumed angular diameter of 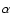 PsA.
PsA.
The resulting calibrated squared visibilities are listed in Tables 3a-d.
For each measurement, the calibrator
is listed. No systematic deviation of the visibility was observed for any of our calibrators
at a 1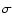 level.
level.
Table 2:
Relevant parameters of the calibrators used for VINCI
observations of Achernar (continued from
Table 1). The references are the same as in
Table 1.
3 Model fitting
3.1 Polar and equatorial visibilities
In order to define a plausible model for the light distribution of Achernar,
we examine here the shape of the polar and equatorial visibility functions.
The orientation of the minor axis of Achernar on the plane of the
sky relative to the North was obtained by D03 using a subset of the
data discussed in the present paper. Using a simplified analysis of the dependence
of the equivalent uniform disk angular diameter with the azimuth
of the projected baseline, they obtained an orientation of the
minor axis of Achernar (assumed to be the polar axis) of
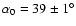 east of North.
east of North.
To visualize the polar visibility function of Achernar, we extracted
the interferometric measurements
with azimuth angles between 10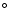 and 70
and 70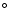 ,
i.e.
,
i.e.
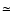
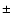
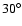 from the sky-projected polar axis of the star.
As shown in Fig. 2 (left), it appears that the
distribution of the measured visibilities does not follow that of
a uniform disk, and there is a clear deficit of visibility at low spatial frequencies.
Fitting a simple uniform disk model (through a classical least-square
minimization) to these data leads to
from the sky-projected polar axis of the star.
As shown in Fig. 2 (left), it appears that the
distribution of the measured visibilities does not follow that of
a uniform disk, and there is a clear deficit of visibility at low spatial frequencies.
Fitting a simple uniform disk model (through a classical least-square
minimization) to these data leads to
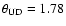 mas, but the reduced
mas, but the reduced 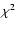 of 6.2 is characteristic of a
poor fit. The deficit of visibility at low spatial frequencies
is typical of the presence of an extended, incoherent
source that is already resolved by the interferometer on the short
baselines. In other words, a diffuse and extended envelope appears to
be present along the polar axis of the star.
of 6.2 is characteristic of a
poor fit. The deficit of visibility at low spatial frequencies
is typical of the presence of an extended, incoherent
source that is already resolved by the interferometer on the short
baselines. In other words, a diffuse and extended envelope appears to
be present along the polar axis of the star.
The equatorial visibility function can be
evaluated by restricting our sample to the visibility measurements obtained
in the azimuth range
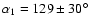 .
As shown in
Fig. 1, we do not have as many
measurements at high spatial frequencies along this range of
azimuth, due to the limitations in the available VLTI baselines during
commissioning. Figure 2 (right) shows the distribution of
squared visibilities observed in this azimuth range as a function
of the spatial frequency. In this case, the fit of a simple
uniform disk model with
.
As shown in
Fig. 1, we do not have as many
measurements at high spatial frequencies along this range of
azimuth, due to the limitations in the available VLTI baselines during
commissioning. Figure 2 (right) shows the distribution of
squared visibilities observed in this azimuth range as a function
of the spatial frequency. In this case, the fit of a simple
uniform disk model with
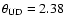 mas produces
satisfactory results with a reduced
mas produces
satisfactory results with a reduced 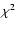 of only 0.6. In this
case, we conclude that we do not detect any significant diffuse
envelope along the equatorial plane of the star.
of only 0.6. In this
case, we conclude that we do not detect any significant diffuse
envelope along the equatorial plane of the star.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4771fig1.eps}
\end{figure}](/articles/aa/full/2006/27/aa4771-05/Timg67.gif) |
Figure 1:
Coverage of the (u,v) plane for the VINCI observations of Achernar.
The K band observations (MONA beam combiner) are represented using circles
(open for siderostat observations, solid for the Unit Telescopes), and the H band
observations are represented using crosses.
The scales are in units of 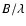 ,
expressed in cycles/arcsec. ,
expressed in cycles/arcsec. |
| Open with DEXTER |
Table 3:
(a) Squared visibilities of Achernar in the K band from VINCI, ordered by
increasing azimuth angle of the projected baseline.
The calibrators are named using their HR number, when no Bayer designation is available.
The stated Julian date JD0 is JD
 .
The azimuth is counted in degrees clockwise from North (
.
The azimuth is counted in degrees clockwise from North (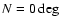 ,
,
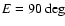 ),
and B is the projected baseline in meters.
The squared visibilities are followed in subscript by the statistical and calibration uncertainties.
),
and B is the projected baseline in meters.
The squared visibilities are followed in subscript by the statistical and calibration uncertainties.
Table 3:
(b) Squared visibilities of Achernar in the K band from
VINCI (continued from Table 3a).
Table 3:
(c) Squared visibilities of Achernar in the K band from
VINCI (continued from Table 3b).
Table 3:
(d) Squared visibilitiess of Achernar in the H band from VINCI, equipped with
the IONIC integrated optics beam combiner.
![\begin{figure}
\par\includegraphics[width=16.6cm,clip]{4771fig2.eps}
\end{figure}](/articles/aa/full/2006/27/aa4771-05/Timg188.gif) |
Figure 2:
Left: squared visibilities V2 measured on
Achernar and corresponding to projected baseline azimuth angles
around the polar direction (values between 10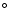 and
70
and
70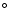 ). Right: V2 corresponding to projected
baseline azimuth angles around the equatorial direction (values
between 100 ). Right: V2 corresponding to projected
baseline azimuth angles around the equatorial direction (values
between 100 and 160
and 160 ).
The solid squares and crosses represent K and H band data, respectively.
The solid curves represent
theoretical V2 along the pole ( left) and the equator ( right)
obtained from the 2D fit of our two-component model
(Sect. 3) to all measured V2(Tables 3a-d.
Note
also the V2 outliers along the polar direction, which were not
included in the fit (see text for details). ).
The solid squares and crosses represent K and H band data, respectively.
The solid curves represent
theoretical V2 along the pole ( left) and the equator ( right)
obtained from the 2D fit of our two-component model
(Sect. 3) to all measured V2(Tables 3a-d.
Note
also the V2 outliers along the polar direction, which were not
included in the fit (see text for details). |
| Open with DEXTER |
As discussed in Sect. 3.1, it appears that a diffuse envelope,
confined to the direction of its polar axis, is present around
Achernar. In order to study the
flux contribution of this envelope, we need to define a simple model to fit the observed
visibility data. For this purpose, we considered the following components:
- the stellar photosphere is represented by a uniform ellipse.
The parameters are the equatorial and polar angular sizes
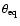 and
and
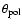 and the azimuth
orientation of the equatorial axis on the sky
and the azimuth
orientation of the equatorial axis on the sky 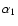 ;
;
-
the diffuse envelope is represented by a bidimensional elliptical
Gaussian. It is parametrized by its full widths at half maximum
(FWHM) along the polar and equatorial axes of the star
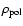 and
and
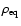 ,
and its integrated flux relative to
the stellar flux f. We make the assumption that its principal
axes are aligned with the principal axes of the stellar
photosphere.
,
and its integrated flux relative to
the stellar flux f. We make the assumption that its principal
axes are aligned with the principal axes of the stellar
photosphere.
Using a simple uniform ellipse model is naturally a very
simplified approximation of the photospheric light distribution of
Achernar. In reality, the rapid rotation of the star
causes significant brightening of the polar
caps of the star as a consequence of its
flattening. Though numerical models can accurately predict
the distribution of light on the photosphere of
uniformly rotating stars (see e.g. Domiciano de Souza et al. 2002), the underlying Roche approximation is not
necessarily verified for Achernar. In particular, Jackson et al. (2004) show that stellar
models of Achernar including differential internal rotation result
in better agreement with the interferometric profile obtained by D03. Though there are
good prospects for differential rotation being constrained
observationally by spectro-interferometry (Domiciano de Souza et al. 2004), the current uncertainties on the light
distribution of the photosphere lead us to prefer the simple
approach of a uniform ellipse.
We also make the hypothesis that the axes of the envelope are
aligned with the principal axes of the stellar photosphere. Due to
the limited coverage of our data set in terms of azimuth angle at
intermediate baselines, we choose this approach in order to reduce
the number of fitted parameters, and therefore improve the
stability of the convergence of the 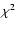 minimization.
minimization.
3.3 Photospheric visibility function
The visibility function of a uniform ellipse can be derived from the classical
visibility function of a circular uniform disk with an angular diameter
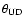 :
:
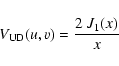 |
(1) |
where
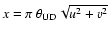 ,
with u and v the spatial frequency
coordinates in units of
,
with u and v the spatial frequency
coordinates in units of 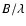 .
In order to obtain the visibility function of the ellipse, we use a rotation
of the (u,v) axes and a scaling of the (u,v) variables:
.
In order to obtain the visibility function of the ellipse, we use a rotation
of the (u,v) axes and a scaling of the (u,v) variables:
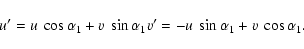 |
(2) |
The visibility of the uniform ellipse with a major axis
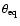 ,
a minor axis
,
a minor axis
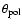 ,
and a major
axis orientation relative to the u axis
,
and a major
axis orientation relative to the u axis 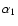 is
therefore:
is
therefore:
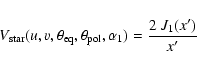 |
(3) |
where
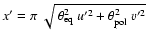 .
.
3.4 Envelope visibility function
As in Sect. 3.3, we can obtain the
visibility function of an elliptical Gaussian brightness
distribution from the circularly symmetric case for which we have
![\begin{displaymath}V_{\rm Gauss}(u,v)=\exp\left[ -\frac{\left( \pi~ \rho \sqrt{u^2 + v^2} \right)^2}{4~\ln 2} \right]
\end{displaymath}](/articles/aa/full/2006/27/aa4771-05/img200.gif) |
(4) |
where 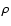 is the FWHM. In the elliptical case, we therefore obtain
is the FWHM. In the elliptical case, we therefore obtain
![\begin{displaymath}V_{\rm env}(u,v,\rho_{\rm eq},\rho_{\rm pol},\alpha_1) =\exp\...
...q}^2 u'^2 + \rho_{\rm pol}^2
v'^2} \right)^2}{4~\ln 2} \right]
\end{displaymath}](/articles/aa/full/2006/27/aa4771-05/img202.gif) |
(5) |
with the same expression of u' and v' as in
Sect. 3.3, as we assume that the axes of the
Gaussian envelope are aligned with the axes of the photosphere.
The indexes "eq'' and "pol'' refer to the equator and pole
of the central star.
Combining the visibility expressions presented in Sects. 3.3 and 3.4, we obtain the following expression for our simple model
of an elongated ellipse with a superimposed Gaussian envelope:
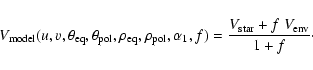 |
(6) |
To derive the six free parameters of our model, we proceed through a classical
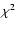 minimization process, with
minimization process, with
![\begin{displaymath}\chi^2_{\rm tot} (\theta_{\rm eq},\theta_{\rm pol},\rho_{\rm ...
...ft[V_i^2 - V_{\rm model}^2(u_i,v_i,...) \right]^2}{\sigma_i^2}
\end{displaymath}](/articles/aa/full/2006/27/aa4771-05/img204.gif) |
(7) |
where Vi2 is one of the VINCI squared-visibility
measurements, and
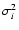 its associated total variance.
The expression of the reduced
its associated total variance.
The expression of the reduced 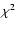 is:
is:
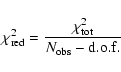 |
(8) |
where
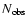 is the number of individual observations
and
is the number of individual observations
and
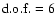 the numbers of degrees of freedom,
considering that we fit a total of six parameters.
the numbers of degrees of freedom,
considering that we fit a total of six parameters.
Table 4:
Best fit parameters (and corresponding uncertainties)
of our simple model consisting in a Gaussian elliptical envelope
superimposed on a uniform ellipse representing the central star.
The fit was computed on our complete H and K band
data set.
The minimum
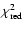 of 0.79 is reached for the
parameters listed in Table 4. This low value is
characteristic of a good correspondence of our model to the
interferometric data. The best-fit visibility function is a
two-dimensional V2(u,v) map. Figure 2 shows the
cuts of this best-fit V2(u,v) map along the stellar pole and
the equator (solid curves). Note that the rapid visibility
decrease observed at low spatial frequencies in the polar
direction is reproduced well by the presence of the elongated
polar envelope in the model.
of 0.79 is reached for the
parameters listed in Table 4. This low value is
characteristic of a good correspondence of our model to the
interferometric data. The best-fit visibility function is a
two-dimensional V2(u,v) map. Figure 2 shows the
cuts of this best-fit V2(u,v) map along the stellar pole and
the equator (solid curves). Note that the rapid visibility
decrease observed at low spatial frequencies in the polar
direction is reproduced well by the presence of the elongated
polar envelope in the model.
A graphical representation of the star and its polar
envelope based on the best-fit parameters is presented in
Fig. 3. We emphasize that this figure is not a
true image of the star, but only the representation of the
best-fit light distribution with the a priori hypothesis that the
star can be described by a uniform ellipse surrounded by an
elliptical Gaussian envelope aligned with its principal axes.
This intensity distribution reproduces the observed
visibilities well, but several others could also fit. In particular,
we cannot determine if the envelope is symmetric relative to
the star, due to the baseline orientation ambiguity of 180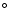 .
.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4771fig3.eps}
\end{figure}](/articles/aa/full/2006/27/aa4771-05/Timg216.gif) |
Figure 3:
Graphical representation of the best-fit model intensity
distribution of Achernar. The relative flux contributions from the star and
the envelope are not to scale. This illustration
should not be considered as a true image of the star. |
| Open with DEXTER |
In the fitting process, we chose to exclude the four data
points obtained on the UT1-UT4 baseline (see
Table 3b).
With a position angle of 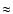 46 deg for the
projected baseline, they correspond to a measurement that is almost
aligned with the pole of the star (
46 deg for the
projected baseline, they correspond to a measurement that is almost
aligned with the pole of the star (
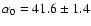 deg).
Although they satisfy the data
quality criteria that we applied to the other data points, they
are located
deg).
Although they satisfy the data
quality criteria that we applied to the other data points, they
are located
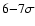 away from the best-fit model.
It should be noted that the 114 remaining data points are in excellent
agreement with our CSE model, and the residuals of the fit
present satisfactory statistical properties (see Sect. 3.7).
away from the best-fit model.
It should be noted that the 114 remaining data points are in excellent
agreement with our CSE model, and the residuals of the fit
present satisfactory statistical properties (see Sect. 3.7).
An instrumental origin for these outliers
cannot be formally excluded, especially
as these data points were obtained on the very first night of
VLTI operations of the UT1-UT4 baseline. However,
no particular technical problem was reported, and the
other stars observed on this night showed consistent results.
As we could not distinguish these measurements from the rest of our
data, we chose to publish them all together for the sake of homogeneity.
A possible astrophysical cause for these low visibilities would be
a stellar eruption that could have suddenly increased the CSE
brightness and/or angular extension.
3.7 Comparison with other models and residuals of the fit
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{4771fig4a.eps}\par\vspace*...
...\par\vspace*{2mm}
\includegraphics[width=6.8cm,clip]{4771fig4c.eps}
\end{figure}](/articles/aa/full/2006/27/aa4771-05/Timg219.gif) |
Figure 4:
Residuals of the visibility fit in units of V2 standard deviation 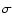 ,
as a function of azimuth angle, for
a uniform disk ( top), a uniform ellipse ( middle), and our uniform ellipse with CSE model ( bottom).
The H band data are shown with crosses. The four outliers
(open diamonds) were not included in the fit.
The dashed and dot-dashed lines represent, respectively, the
polar and equatorial directions of the models, including a uniform ellipse. ,
as a function of azimuth angle, for
a uniform disk ( top), a uniform ellipse ( middle), and our uniform ellipse with CSE model ( bottom).
The H band data are shown with crosses. The four outliers
(open diamonds) were not included in the fit.
The dashed and dot-dashed lines represent, respectively, the
polar and equatorial directions of the models, including a uniform ellipse. |
| Open with DEXTER |
In order to assess the level of adequation of our star+CSE model to the data,
we also tried to fit them with two simpler models: a circular uniform disk
and a uniform ellipse.
The residuals for each of the three models
are presented in Fig. 4 as
a function of the projected baseline azimuth angle.
We obtained in the first case a uniform disk angular diameter
of
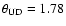 mas, with the large
mas, with the large
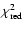 of 4.9 characteristic
of a bad fit. Fitting a uniform ellipse results in the following best-fit values:
of 4.9 characteristic
of a bad fit. Fitting a uniform ellipse results in the following best-fit values:
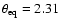 mas,
mas,
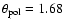 mas, and
mas, and
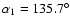 .
Again, the
.
Again, the
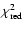 of 3.2 shows poor agreement of this model to our data.
It thus appears that our star+Gaussian CSE model is a much better fit to our
data set (
of 3.2 shows poor agreement of this model to our data.
It thus appears that our star+Gaussian CSE model is a much better fit to our
data set (
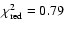 )
than the models without CSE.
)
than the models without CSE.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4771fig5a.eps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{4771fig5b.eps}
\end{figure}](/articles/aa/full/2006/27/aa4771-05/Timg224.gif) |
Figure 5:
Residuals of the visibility fit as a function of projected baseline
length ( top) and date of observation ( bottom).
The symbols are the same as in Fig. 4. |
| Open with DEXTER |
As shown in Fig. 4 (bottom), the residuals of our star+CSE
fit appear to be homogeneous with respect to azimuth angle.
Similarly, we do not detect any significant residual either with respect
to projected baseline length or with time (Fig. 5).
The H and K band data sets do not show any systematic deviation,
which justifies a posteriori our combined treatment of these two data sets.
Due to the relatively small number of measurements in the H band and their
lower accuracy compared to the K band, their influence on the best-fit parameters
is very limited. However, they are overall in
excellent agreement with the best-fit model, with a specific reduced 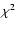 of only 0.2. Considering the limited amount of H band data,
we currently cannot investigate the wavelength dependence of the CSE properties,
but additional observations with the AMBER instrument of the VLTI in the J and H bands will soon allow such studies. It should be noted that
interferometric observations of the bright
B0IVpe star
of only 0.2. Considering the limited amount of H band data,
we currently cannot investigate the wavelength dependence of the CSE properties,
but additional observations with the AMBER instrument of the VLTI in the J and H bands will soon allow such studies. It should be noted that
interferometric observations of the bright
B0IVpe star 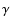 Cas in the visible have shown that
the apparent size of this star can vary considerably with wavelength
(Stee et al. 1998).
The scatter appears to be slightly larger along the polar direction than along
the equator of the star (Fig. 5, top). This could be caused by
deviations from our simple star-CSE model on small
angular scales. For instance, the presence of clumps in the CSE could
create this apparent instability of the visibility function. However,
our data set is still too limited to constrain their properties significantly.
Cas in the visible have shown that
the apparent size of this star can vary considerably with wavelength
(Stee et al. 1998).
The scatter appears to be slightly larger along the polar direction than along
the equator of the star (Fig. 5, top). This could be caused by
deviations from our simple star-CSE model on small
angular scales. For instance, the presence of clumps in the CSE could
create this apparent instability of the visibility function. However,
our data set is still too limited to constrain their properties significantly.
4 Nature of the CSE of Achernar
As listed in Table 4, the angular sizes of the axes
of the photosphere ellipse (
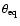 and
and
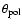 )
are well constrained, as is the flux ratio
)
are well constrained, as is the flux ratio
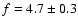 % between the star and the polar envelope. However, the
angular dimensions of the envelope itself are poorly constrained.
In particular, as visible in Fig. 2, we lack very short
baseline measurements to estimate the total extension of the envelope in
the polar direction. Considering our data, it could be much more
extended than the derived
% between the star and the polar envelope. However, the
angular dimensions of the envelope itself are poorly constrained.
In particular, as visible in Fig. 2, we lack very short
baseline measurements to estimate the total extension of the envelope in
the polar direction. Considering our data, it could be much more
extended than the derived
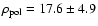 mas, which
should be considered as a lower limit. The angular extension of
the envelope in the equatorial direction is also rather poorly
constrained by our data, but appears to be small,
and could be approximately the size of the star itself.
mas, which
should be considered as a lower limit. The angular extension of
the envelope in the equatorial direction is also rather poorly
constrained by our data, but appears to be small,
and could be approximately the size of the star itself.
From the fit of our two-component model, we obtained a
photospheric major- over minor-axis ratio of
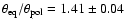 ,
while
D03 measured a value of
,
while
D03 measured a value of
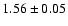 ,
using part of the current data set. The 2.3
,
using part of the current data set. The 2.3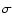 difference between these two values can be explained by the difference
in adopted model between these two approaches.
D03 estimated the uniform disk equivalent angular diameter for
each available azimuth and fitted an ellipse on the resulting
values. In the present work, we directly fitted our two-component
model to the visibilities in the (u,v) plane. In addition, D03
used a single-disk model that does not take the
presence of the envelope into account.
difference between these two values can be explained by the difference
in adopted model between these two approaches.
D03 estimated the uniform disk equivalent angular diameter for
each available azimuth and fitted an ellipse on the resulting
values. In the present work, we directly fitted our two-component
model to the visibilities in the (u,v) plane. In addition, D03
used a single-disk model that does not take the
presence of the envelope into account.
Both approaches are valid and have their limitations and
advantages. The important point where the main objective concerns
the study of the flattening of the star is to compare the results
to a physically realistic model including (at least) rotational
deformation and gravity darkening, as was done by D03.
In a future work we intend to perform a complete astrophysical
analysis of the available interferometric and spectroscopic data
on Achernar, including rotational effects (flattening and gravity darkening)
and the CSE, both in the polar and equatorial directions.
From the measured flattening ratio, the polar temperature of
Achernar could be higher than 20 000 K. In this context, the
radiation pressure reaches very high values. As was demonstrated in
the case of the luminous blue variable star 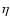 Carinae by Van Boekel et al. (2003), a stellar wind ejected
from the poles can have a detectable signature in the
interferometric visibilities in the near infrared.
Recently, Meilland et al. (2006) showed that an
elongated polar wind should be included with a thin disk
in order to explain the near-IR VLTI/AMBER (e.g., Petrov et al. 2003) observations of
Carinae by Van Boekel et al. (2003), a stellar wind ejected
from the poles can have a detectable signature in the
interferometric visibilities in the near infrared.
Recently, Meilland et al. (2006) showed that an
elongated polar wind should be included with a thin disk
in order to explain the near-IR VLTI/AMBER (e.g., Petrov et al. 2003) observations of 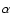 Arae, another Be star that is very
similar to Achernar (rotation velocity, spectral type). Although
the central stars are similar, one important difference is that
Arae, another Be star that is very
similar to Achernar (rotation velocity, spectral type). Although
the central stars are similar, one important difference is that 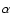 Arae presented hydrogen lines in
strong emission during the interferometric observations, while they
were absent from the spectrum of Achernar.
Both stars show an elongated polar wind responsible for a free-free and
free-bound near-IR continuum emission, while only one of them
(
Arae presented hydrogen lines in
strong emission during the interferometric observations, while they
were absent from the spectrum of Achernar.
Both stars show an elongated polar wind responsible for a free-free and
free-bound near-IR continuum emission, while only one of them
(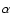 Arae) shows a dense equatorial disk (resolved by
VLTI/AMBER) where hydrogen emission lines are formed.
This indicates that a significant (in terms of size and near-IR
emission) polar wind exists independently if the star is in a normal B or in a Be phase; i.e., the polar wind does not seem to be
completely related to the existence of a denser equatorial envelope.
Arae) shows a dense equatorial disk (resolved by
VLTI/AMBER) where hydrogen emission lines are formed.
This indicates that a significant (in terms of size and near-IR
emission) polar wind exists independently if the star is in a normal B or in a Be phase; i.e., the polar wind does not seem to be
completely related to the existence of a denser equatorial envelope.
In the hypothesis that the observed polar CSE near-IR emission is
mostly caused by free-free radiation, we can roughly estimate the
mean electron density as
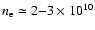 cm-3 for
the H and K bands. This value was obtained from the free-free
emissivity (e.g. Allen 1973) by considering an electron
temperature of 20 000 K (the result does not depend strongly on
this value) and by using the CSE parameters derived in this work
(Table 4).
cm-3 for
the H and K bands. This value was obtained from the free-free
emissivity (e.g. Allen 1973) by considering an electron
temperature of 20 000 K (the result does not depend strongly on
this value) and by using the CSE parameters derived in this work
(Table 4).
In a recent paper, Vinicius et al. (2006) estimated the
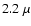 m continuum emission based on a residual emission detected
in the H
m continuum emission based on a residual emission detected
in the H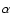 absorption profile measured contemporaneously to
the VINCI/VLTI campaign on Achernar. They proposed an explanation for
the strong flattening measured on Achernar (Domiciano de Souza et al. 2003) by adopting the hypothesis that the residual H
absorption profile measured contemporaneously to
the VINCI/VLTI campaign on Achernar. They proposed an explanation for
the strong flattening measured on Achernar (Domiciano de Souza et al. 2003) by adopting the hypothesis that the residual H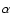 emission and the associated near-IR continuum emission are formed in
the remaining equatorial disk. However, considering the results from
the present work, a significant fraction of the near-IR
emission appears to originate in the polar envelope.
emission and the associated near-IR continuum emission are formed in
the remaining equatorial disk. However, considering the results from
the present work, a significant fraction of the near-IR
emission appears to originate in the polar envelope.
We have detected a diffuse circumstellar envelope around
the bright Be star Achernar, which accounts for approximately 5%
of the flux of the star in the near-IR (H and K bands). This
envelope presents clear asymmetry with a significantly larger
extension along the polar direction of the star. The photosphere of
the star itself is distorted by the fast rotation with a larger equatorial angular
diameter. The elongation of the CSE points to a significant polar wind, most
probably powered by the hot temperature at the stellar poles (von
Zeipel effect). Its total extension is loosely constrained by our observations,
and it could reach large distances from the star.
It appears that a complete astrophysical model able to simultaneously
explain all observations (spectroscopic and interferometric) of
Achernar is required. We are also confident that
spectro-interferometric observations of Achernar with the VLTI/AMBER
instrument will bring new insight into
the gravity darkening, actual
shape and relative intensity of the central star and its immediate
circumstellar environment.
Acknowledgements
The interferometric measurements were obtained using the
VINCI instrument installed at the VLTI. The VLTI is operated by
the European
Southern Observatory at Cerro Paranal, Chile. These
data were obtained under an unreferenced P70 shared-risk
programme and during the technical commissioning of the
interferometer. Their processing made use of the wavelet-based
technique developed by D. Ségransan (Observatoire de
Genève) and integrated into the VINCI pipeline. Observations with
the VLTI are only made possible through the efforts of the VLTI
team, for which we are grateful. The VINCI public commissioning
data reported in this paper were retrieved from the
ESO/ST-ECF Archive (Garching, Germany). This research made use
of the SIMBAD and VIZIER databases at the CDS, Strasbourg (France),
and NASA's Astrophysics Data System Bibliographic Services. We
thank Drs. O. Chesneau and J. A. de Freitas Pacheco for their
enlightening suggestions.
- Allen, C. W. 1973,
Astrophysical quantities (London: University of London, Athlone
Press), 3rd edn.
(In the text)
- Balona, L. A.,
Engelbrecht, C. A., & Marang, F. 1987, MNRAS, 227, 123 [NASA ADS] (In the text)
- Berger, J.-P.,
Haguenauer, P., Kern, P., et al. 2001, A&A, 376, 31 [NASA ADS] [CrossRef] (In the text)
- Bordé, P.,
Coudé du Foresto, V., Chagnon, G., & Perrin, G. 2002,
A&A, 393, 183 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Chauville,
J., Zorec, J., Ballereau, D., et al. 2001, A&A, 378, 861 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Claret, A.,
Diaz-Cordovez, J., & Gimenez, A. 1995, A&AS, 114, 247 [NASA ADS]
- Claret, A. 2000,
A&A, 363, 1081 [NASA ADS]
- Cohen, M., Walker, R.
G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef] (In the text)
- Coudé du Foresto,
V., Ridgway, S., & Mariotti, J.-M. 1997, A&AS, 121,
379 [EDP Sciences] [NASA ADS] (In the text)
- Di Folco, E.,
Thévenin, F., Kervella, P., et al. 2004, A&A, 426,
601 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Damineli Neto,
A., & de Freitas-Pacheco, J. A. 1982, MNRAS, 198, 659 [NASA ADS] (In the text)
- Domiciano de
Souza, A., Vakili, F., Jankov, S., Janot-Pacheco, E., & Abe, L.
2002, A&A, 393, 345 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Domiciano de
Souza, A., Kervella, P., Jankov, S., et al. 2003, A&A, 407,
L47 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Domiciano de
Souza, A., Zorec, J., Jankov, S., et al. 2004, A&A, 418,
781 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Domiciano de
Souza, A., Kervella, P., Jankov, S., et al. 2005, A&A, 442,
567 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Dougherty, S.
M., & Taylor, A. R. 1992, Nature, 359, 808 [NASA ADS] [CrossRef] (In the text)
- Dougherty, S.
M., Waters, L. B. F. M., Burki, G., et al. 1994, A&A, 290,
609 [NASA ADS] (In the text)
- Dyck, H. M., van Belle,
G. T., & Thompson, R. R. 1998, AJ, 116, 981 [NASA ADS] [CrossRef]
- Gehrz, R. D.,
Hackwell, J. A., & Jones, T. W. 1974, ApJ, 191, 675 [NASA ADS] [CrossRef] (In the text)
- Glebocki, R.,
Gnacinski, P., & Stawikowski, A. 2000, Acta Astron., 50,
509 [NASA ADS] (In the text)
- Glindemann,
A., Abuter, R., Carbognani, F., et al. 2000, SPIE, 4006, 2 [NASA ADS] (In the text)
- Glindemann,
A., Albertsen, M., Avila, G., et al. 2004, SPIE, 5491, 447 [NASA ADS] (In the text)
- Jackson, S.,
MacGregor, K. B., & Skumanich, A. 2004, ApJ, 606, 1196 [NASA ADS] [CrossRef] (In the text)
- Kervella, P.,
Coudé du Foresto, V., Glindemann, A., & Hofmann, R. 2000,
SPIE, 4006, 31 [NASA ADS] (In the text)
- Kervella, P.,
Gitton, Ph., Ségransan, D., et al. 2003, SPIE, 4838, 858 [NASA ADS] (In the text)
- Kervella, P.,
Ségransan, D., & Coudé du Foresto, V. 2004a, A&A,
425, 1171 [NASA ADS] (In the text)
- Kervella, P.,
Thévenin, F., Di Folco, E., & Ségransan, D. 2004b,
A&A, 426, 297 [EDP Sciences] [NASA ADS] [CrossRef]
- Lebouquin,
J.-B., Rousselet-Perraut, K., Kern, P., et al. 2004, A&A, 424,
719 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- McAlister, H.
A., ten Brummelaar, T. A., Gies, D. R, et al. 2005, ApJ, 628,
439 [NASA ADS] [CrossRef] (In the text)
- Meilland, A.,
Stee, Ph., Vannier, M., et al. 2006, A&A, submitted
(In the text)
- Ohishi, N.,
Nordgren, T. E., & Hutter, D. J. 2004, ApJ, 612, 463 [NASA ADS] [CrossRef] (In the text)
- Peters, G. J. 1982,
ApJ, 253, L33 [NASA ADS] [CrossRef] (In the text)
- Petrov, R. G.,
& Amber Consortium, The 2003, EAS Publications Series,
Observing with the VLTI, ed. G. Perrin, & F. Malbet, 6,
111
(In the text)
-
Quirrenbach, A., Bjorkman, K. S., Bjorkman, J. E., et al. 1997,
ApJ, 479, 477 [NASA ADS] [CrossRef] (In the text)
- Richichi, A.,
& Percheron, I. 2005, A&A, 434, 1201 [EDP Sciences] [NASA ADS] [CrossRef]
-
Ségransan, D., Forveille, T., Millan-Gabet, C. P. R., &
Traub, W. A. 1999, in ASP Conf. Ser., 194, 290
(In the text)
- Slettebak, A.
1982, ApJS, 50, 55 [NASA ADS] [CrossRef] (In the text)
- Stee, Ph., de Araujo,
F. X., Vakili, F., et al. 1995, A&A, 300, 219 [NASA ADS] (In the text)
- Stee, Ph., Vakili, F.,
Bonneau, D., & Mourard, D. 1998, A&A, 332, 268 [NASA ADS] (In the text)
- Snow, T. P. 1981, ApJ,
251, 139 [NASA ADS] [CrossRef] (In the text)
- Tycner, C., Lester,
J. B., Hajian, A. R., et al. 2005, ApJ, 624, 359 [NASA ADS] [CrossRef] (In the text)
- Van Boekel,
R., Kervella, P., Schöller, M., et al. 2003, A&A, 410,
37 [NASA ADS] [CrossRef] (In the text)
- Vinicius, M. M.
F., Zorec, J., Leister, N. V., & Levenhagen, R. S. 2006,
A&A, 446, 643 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- von Zeipel,
H. 1924, MNRAS 84, 665
(In the text)
- Waters, L. B. F. M.
1986, A&A, 162, 121 [NASA ADS] (In the text)
- Waters, L. B. F.
M., Cote, J., & Lamers, H. J. G. L. M. 1987, A&A, 185,
206 [NASA ADS] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4771fig1.eps}
\end{figure}](/articles/aa/full/2006/27/aa4771-05/Timg67.gif)
![\begin{figure}
\par\includegraphics[width=16.6cm,clip]{4771fig2.eps}
\end{figure}](/articles/aa/full/2006/27/aa4771-05/Timg188.gif)
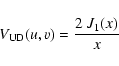
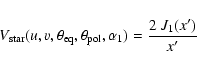
![\begin{displaymath}V_{\rm Gauss}(u,v)=\exp\left[ -\frac{\left( \pi~ \rho \sqrt{u^2 + v^2} \right)^2}{4~\ln 2} \right]
\end{displaymath}](/articles/aa/full/2006/27/aa4771-05/img200.gif)
![\begin{displaymath}V_{\rm env}(u,v,\rho_{\rm eq},\rho_{\rm pol},\alpha_1) =\exp\...
...q}^2 u'^2 + \rho_{\rm pol}^2
v'^2} \right)^2}{4~\ln 2} \right]
\end{displaymath}](/articles/aa/full/2006/27/aa4771-05/img202.gif)
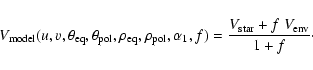
![\begin{displaymath}\chi^2_{\rm tot} (\theta_{\rm eq},\theta_{\rm pol},\rho_{\rm ...
...ft[V_i^2 - V_{\rm model}^2(u_i,v_i,...) \right]^2}{\sigma_i^2}
\end{displaymath}](/articles/aa/full/2006/27/aa4771-05/img204.gif)
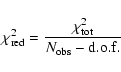
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4771fig3.eps}
\end{figure}](/articles/aa/full/2006/27/aa4771-05/Timg216.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{4771fig4a.eps}\par\vspace*...
...\par\vspace*{2mm}
\includegraphics[width=6.8cm,clip]{4771fig4c.eps}
\end{figure}](/articles/aa/full/2006/27/aa4771-05/Timg219.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4771fig5a.eps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{4771fig5b.eps}
\end{figure}](/articles/aa/full/2006/27/aa4771-05/Timg224.gif)