A&A 453, 943-947 (2006)
DOI: 10.1051/0004-6361:20054736

Electron temperature fluctuations in H II regions

The feasibility of t2 estimates from point-to-point observations[*]

M. V. F. Copetti

Laboratório de Análise Numérica e Astrofísica, Departamento de Matemática, Universidade Federal de Santa Maria, 97119-900 Santa Maria, RS, Brazil

Received 20 December 2005 / Accepted 24 February 2006

Abstract
Context. The spatial electron temperature fluctuations in ionized nebulae that were initially proposed to explain the discrepancies among temperatures obtained from different sensors have been pointed to as the cause of huge inconsistencies among abundances of heavy elements calculated from recombination and forbidden emission lines. Recently, there have been some attempts of direct detection and quantification of spatial temperature fluctuations with point-to-point temperature measurements across the nebula.
Aims. In this paper, we assess the feasibility of estimating the temperature fluctuation parameter t2, the total variance of the spatial distribution of temperature relative to the mean, from the distribution of temperatures measured on the plane of the sky with different sensors.
Methods. Point-to-point measurements of the electron temperature at a series of contiguous and equally spaced rectangular apertures along a radius of homogeneous and spherically symmetric nebulae were numerically simulated for six different temperature sensors.
Results. Variances of projected temperature distributions were obtained and compared with total t2 for different values for the density, ionization parameter and temperature of the ionizing star. The projected profiles of electron temperature obtained from indicators associated with ions occurring at large fractions of the nebula, such as [O III] ( $\lambda 4959 + \lambda 5007)/\lambda 4363$, [Ar III]  $(\lambda 7136 + \lambda 7751)/\lambda 5192$, and the Balmer jump $(I_{\lambda} (3646^-) - I_{\lambda} (3646^+))$/H$\beta$, are good tracers of the internal gradient of temperature. The variances $t^2_{\rm s}$ of the projected temperature distributions measured from these sensors correspond to significant fractions of the total temperature variance, for typical nebulae of the order of $t^2_{\rm s}/t^2 \approx $ 30%, 25%, and 15% for the Balmer jump and the [O III] and [Ar III] ratios, in that order. On the other hand, the temperature profiles obtained from sensors corresponding to low ionization ions, such as [N II] ( $\lambda 6548 + \lambda 6584)/\lambda 5755$, [O I]  $(\lambda 6300 + \lambda 6364)/\lambda 5577$, and [C I]  $(\lambda 9823 + \lambda 9849)/\lambda 8728$, are almost constant at the values of temperature of the outer parts of the nebula, fail to reproduce the true temperature gradient, and have a $t^2_{\rm s}$ that is always less than 10% and is usually around 1-3% of t2.

Key words: ISM: H II regions - ISM: planetary nebulae: general

1 Introduction

The theory of photoionized nebulae very successfully explains most of the features observed in the spectra of H II regions and planetary nebulae. This fact has supported the intensive use of these objects as probes of the chemical composition of galaxies. Traditionally, the abundances of heavy elements in ionized nebulae have been obtained from their strong, collisionally excited emission lines. The recent developments in astronomical instruments have made the determination of the abundances of the C, N, and O elements from their weak recombination lines possible. However, huge discrepancies between the abundances obtained from collisionally excited and recombination lines have been found, which cast doubt on the accuracy of the abundance determinations in gaseous nebulae. For example, Liu et al. (1995) determined abundances of C, N, and O in the planetary nebula NGC 7009 by recombination lines and found that they are about 5 times higher than those derived from forbidden lines.

The existence of spatial temperature fluctuations in the nebulae has been suggested as one of the most probable explanations of the inconsistency among abundances calculated from forbidden and recombination lines (Peimbert et al. 1995). Originally, large temperature fluctuations had been proposed by Peimbert (1967) to explain the discrepancies between the values of electron temperature obtained from different indicators.

The magnitude of the temperature fluctuations are usually quantified by the parameter t2 defined by Peimbert (1967) as

 \begin{displaymath} t^2 = \frac{ \int{(T_{\rm e}- T_0)^2 N_{\rm i} N_{\rm e} {\rm d}V }} { T_0^2 \int{N_{\rm i} N_{\rm e} {\rm d}V }}, \end{displaymath} (1)

with

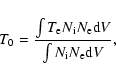\begin{displaymath}T_0 = \frac{ \int{T_{\rm e} N_{\rm i} N_{\rm e} {\rm d}V }} { \int{N_{\rm i} N_{\rm e} {\rm d}V }}, \end{displaymath} (2)

where $N_{\rm i}$ is the density of the ion used to measure the temperature, and where the integrals are calculated over the volume V of the nebula. Essentially, T0 and t2 are the mean and the relative variance of the temperature distribution weighted by the square of the local density.

However, the magnitudes of the temperature fluctuations needed to reconcile the recombination line metallicities with those based on collisionally excited lines or the electron temperature measurements from different line ratios of planetary nebulae and H II regions of the order $t^2 \approx 0.02{-}0.10$ (Luridiana et al. 1999; Esteban et al. 1999b,1998; Peimbert et al. 1995; Esteban et al. 1999a; Dinerstein et al. 1985; Gonzalez-Delgado et al. 1994; Liu & Danziger 1993) are considerably higher than those predicted by standard photoionisation models (Pérez 1997; Kingdon & Ferland 1995; Gruenwald & Viegas 1995), which are typically in the range of $t^2 \leq 0.02$. Besides, the physical mechanisms that could possibly explain the large temperature fluctuations presumed are unknown. Recently, an alternative solution to the abundance problem has been proposed and supported based on the assumption of the presence of hydrogen-deficient and very cold clumps inside the nebula, which, even if they were to make up only a few percent of the total mass, would be largely responsible for the emission of recombination lines of heavy elements (Liu et al. 2000; Tsamis et al. 2004; Tsamis & Péquignot 2005). So, the question of the existence of substantial spatial variations of electron temperature in nebulae has became a key issue in the study of H II regions and planetary nebulae.

There have been some attempts of estimating the magnitude of the temperature fluctuations from point-to-point measurements of the temperature in planetary nebulae and H II regions (Krabbe & Copetti 2002; Rubin et al. 2002; O'Dell et al. 2003; Liu 1998; Rubin et al. 2003). As a direct estimator for t2, Liu (1998) has proposed the use of

 \begin{displaymath} t_{\rm s}^2=\frac{ \sum_{i=1}^{N}{(T_{\rm e}^i-T_0)^2 F_{\r... ... H}\beta)}} { T_0^2 \sum_{i=1}^{N}{F_{\rm i}({\rm H}\beta)}}, \end{displaymath} (3)

where $T_{\rm e}^i$ and $F_{\rm i}({\rm H}\beta)$ are the electron temperature and the H$\beta$ flux obtained for the aperture i, respectively, and where N is the total number of apertures. Clearly, this parameter is a biased estimator of t2. We have that  $t^2_{\rm s} \leq t^2$, since the temperature measured at any aperture is a mean value inside a cylinder through the nebula. So, any line of sight or small-scale temperature fluctuation would be smoothed out by this kind of observation. For this reason, it is clear that  $t^2_{\rm s}$ can only give a lower limit to t2. In the present paper, by means of model simulations, we assess the feasibility and discuss the limitations of the t2 estimations based on point-to-point measurements of the electron temperature in ionized nebulae.

   
2 The models

Table 1: Electron temperature indicators and symbols.

We have numerically simulated a point-to-point measurement of the electron temperature at a series of contiguous and equally spaced rectangular apertures along the radius of a homogeneous and spherically symmetric nebula. Six different electron temperature sensors were considered, including the most commonly used [O III] $(\lambda 4959 + \lambda 5007)/\lambda 4363$, [N II] $(\lambda 6548 + \lambda 6584)/\lambda 5755$, and the Balmer jump at 3646 Å relative to H$\beta$ (see Table 1 for the complete list and for the symbols used for the derived temperatures). The photoionization code Cloudy 95.03 (Ferland et al. 1998) was used to calculate the thermal and ionization structure of the nebula. An inner radius of 10% of the outer nebular radius was assumed. The non-LTE CoStar stellar atmosphere models (Schaerer et al. 1996a; Schaerer & Koter 1997; Schaerer et al. 1996b) for zero age main sequence stars were used. The solar chemical composition was adopted. We ran models with the effective temperature of the ionizing star varying from 38 500 to 50 000 K, corresponding to spectral type from O8 to O3, according to the calibration of Vacca et al. (1996), an with an ionization parameter in the range $-3.5 \leq \log U \leq -2$ and a hydrogen density $1.5 \leq \log N_{\rm H}~{\rm (cm^{-3})} \leq 4$. Also, to test the effects of spatial resolution on the simulations, we varied the number of apertures in the range $5 \leq N \leq 1000$.

The emissivities of the emission lines involved were calculated with an n-level atom programme ( $5 \leq n \leq 10$) that we wrote using the atomic parameters from the IRAF/STSDAS 3.0/nebular package database. For the fainter lines (e.g. [O III] $\lambda 4363$ or [N II] $\lambda 5755$), we considered the contributions to the emissivities due to recombination and charge transfer effects, since they are significant at some parts of the nebula. The emissivity of the Balmer jump was calculated from $T_{\rm e}$ (in K units) and the H$\beta$ emissivity predicted by the code Cloudy by the expression

 \begin{displaymath} \frac{j_\nu({\rm Bac})}{j_{{\rm H}\beta}} = 2.00 \times 10^{... ...0^{424 / T_{\rm e}} T_{\rm e}^{-0.517} ~~~ ({\rm in~Hz^{-1}}), \end{displaymath} (4)

deduced from the approximations given by Aller (1984, p. 76 and 99). The emissivities were integrated within the apertures and along the line of sight to produce the emission line intensities. The simulated line ratios and the Balmer discontinuity were used to derive the "observed'' electron temperature in each aperture using the same n-level atom models and numerically solving Eq. (4) for $T_{\rm e}$(Bac).

3 Results and discussions

In Fig. 1, the comparison between the true electron temperature radial gradient and the spatial profiles of temperature obtained from different sensors is shown for a typical example of the simulations described in Sect. 2. This figure shows that the temperature indicators can be divided into two groups. The electron temperature profiles derived from indicators associated with ions occurring at large fractions of the nebula, such as $T_{\rm e}$(Bac), $T_{\rm e}$(O III), and $T_{\rm e}$(Ar III), tend to follow the true internal temperature variation fairly well. On the other hand, the spatial profiles of temperatures obtained from line ratios of low ionization ions, $T_{\rm e}$(N II), $T_{\rm e}$(O I), and $T_{\rm e}$(C I), are almost constant, at values representative of the higher temperatures predicted for the outskirts of the nebula, and badly fail to reproduce the inner part of the electron temperature gradient, essentially because the low ionization ions are concentrated in the outer and hotter parts of the nebula.

Using expression (3), we calculated the relative variance $t^2_{\rm s}$ of the temperature profile for each temperature sensor considered, then compared them with the value of t2. The level of dependency of  $t^2_{\rm s}$ on the number of apertures N is summarised in Table 2, which shows the range of the percentage values of  $t^2_{\rm s}$ for N = 5, 10, and 20, relative to  $t^2_{\rm s}$ for N = 100, found in the simulations. We verified that $t^2_{\rm s}$ calculated from $T_{\rm e}$(Bac), $T_{\rm e}$(O III), and $T_{\rm e}$(Ar III) are little dependent on the number of apertures, especially for $N \geq 10$. Even for as a small number as N = 5, these sensors produce reasonable results, with  $t^2_{\rm s}$ at least 60% of the value for N = 100. This is a consequence of the fact that the photoionization models predict a fairly smooth gradient of temperature with steep spatial variations only at the outer border of the nebula (see Fig. 1).


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4736fg01.eps} \end{figure} Figure 1: Comparison between the true electron temperature radial gradient (solid line) and the "observed'' spatial profiles of temperature obtained from different sensors with a very large number of apertures, N = 1000 (broken lines), and with a small one, N = 20 (marks). The input parameters for this model were: $T_{\rm eff} = 43~560$ K, $\log U = -3$, and $N_{\rm e} = 100$ cm-3. The spike in the $T_{\rm e}$(N II) profile at the outskirts of the nebula, which is the consequence of a strong enhancement of the [N II] $\lambda 5755$ emission line by charge transfer effects in a more than 95% neutral thin layer, is impractical to observe, because the corresponding [N II] lines are extremely weak, and has a negligible effect on the value calculated for $t^2_{\rm s}$(N II), due to the flux weighting.
Open with DEXTER

Figures 2 and 3 show the dependence of the electron temperature fluctuation parameter t2 on the ionization parameter U for a fixed stellar temperature, $T_{\rm eff} = 43~560$ K, and on the effective temperature of the ionizing star for a fixed ionization parameter, $\log U = -3$, and for 6 different values of hydrogen density in the range $1.5 \leq \log N_{\rm H}~{\rm (cm^{-3})} \leq 4$, respectively. These figures illustrate the kind of relationships between t2, U, $T_{\rm eff}$, and $N_{\rm H}$ found in the complete set of models. The t2 parameter ranges from 0.001 to 0.05, with little dependency on the stellar effective temperature, but strong dependency on the hydrogen density for $\log N_{\rm H}~{\rm (cm^{-3})} \la 3$. According to the models, denser objects would have more homogeneous temperature structures, and consequently lower values of t2. The increase of temperature in the outer parts of the nebula (see Fig. 1), caused by the hardening of the ionizing radiation as the distance to the centre increases, which is due to the preferential absorption of low-energy photons in the photoionization process, is more pronounced in rarefied objects, for which the ionizations are essentially produced by photons coming directly from the stars. For denser objects, the much softer diffuse radiation field plays a more important role in the ionization of the nebula.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4736fg02.eps} \end{figure} Figure 2: Temperature fluctuation parameter t2 vs. the ionization parameter U for $T_{\rm eff} = 43~560$ K and six different values of hydrogen density in the range $1.5 \leq \log N_{\rm H}~({\rm cm^{-3}}) \leq 4$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4736fg03.eps} \end{figure} Figure 3: Temperature fluctuation parameter t2 vs. the effective temperature $T_{\rm eff}$ of the ionizing star for an ionization parameter $\log U = -3$ and six different values of hydrogen density in the range $1.5 \leq \log N_{\rm H}~({\rm cm^{-3}}) \leq 4$ (indicated by the same line types used in Fig. 2).
Open with DEXTER

Table 2: Dependency of $t^2_{\rm s}$ on the number of apertures N.

In Figs. 4 to 15, we summarise the results of our simulated evaluation of the spatial variance of the electron temperature obtained from point-to-point measurements of temperature. In these figures, the $t^2_{\rm s}$ parameter for each of the six electron temperature sensors listed in Table 1 is shown as a function of the ionization parameter U (for $T_{\rm eff} = 43~560$ K) or stellar temperature (for $\log U = -3$) for a number of apertures N = 100 and different values of electron density. For all temperature sensors considered, the ratio $t^2_{\rm s}/t^2$ showed little dependence on the stellar temperature, especially for $T_{\rm eff} \ga 43~000$ K. Again, the electron temperature sensors can be divided into two groups. The temperature variances  $t^2_{\rm s}$ from $T_{\rm e}$(Bac), $T_{\rm e}$(O III), and $T_{\rm e}$(Ar III) correspond to a significant fraction of t2 of the order of 20-40%, 8-40%, and 5-22%, in that order. On the other hand, for the sensors associated with low ionization ions, $T_{\rm e}$(N II), $T_{\rm e}$(O I), and $T_{\rm e}$(C I), $t^2_{\rm s}$ is always less than 10% and is usually around 1-3% of t2.

To show the potential use of the present simulations, we have estimated the global t2 from the measured values of $t^2_{\rm s}(O {\sc iii})$ for 30 Doradus and the Orion Nebulae. From the calibration of the ionization parameter with the line ratio $[S {\sc ii}](\lambda 6717 + \lambda 6731)/[S {\sc iii}](\lambda 9069 + \lambda 9532)$ by Diaz et al. (1991), and the observed line ratios from Kennicutt et al. (2000), we estimate a value of $\log U \approx - 3.2$ for both of these objects. The electron density is $\log N_{\rm e}~{\rm (cm^{-3})} = 3.7 \pm 0.2$ (Esteban et al. 1998) in the Orion Nebula and $\log N_{\rm e}~{\rm (cm^{-3})} = 2.5 \pm 0.1$ (Peimbert 2003) in 30 Doradus. The spectral type of the main ionizing stars is O6 or O7 V in the Orion Nebula (Conti & Alschuler 1971; Copetti & Bica 1983) and O3 in 30 Doradus (Massey & Hunter 1998), which correspond to $T_{\rm eff} \approx 40~000$ K and 50 000 K, respectively, according to the calibration of Vacca et al. (1996). From Fig. 5, we verify that $t^2_{\rm s}(O {\sc iii})$ is 24% of t2 for the 30 Doradus Nebula and 28% of t2 for the Orion Nebula.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4736fg04.eps} \end{figure} Figure 4: Temperature fluctuation parameter of the simulated measurements of $T_{\rm e}$(O III) (in percentages of t2 in the upper panel and absolute value in the lower panel) vs. the ionization parameter U for N = 100 apertures, $T_{\rm eff} = 43~560$ K, and six different values of hydrogen density in the range $1.5 \leq \log N_{\rm H}~({\rm cm^{-3}}) \leq 4$ (indicated by the same line types used in Fig. 2).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4736fg05.eps} \end{figure} Figure 5: Temperature fluctuation parameter of the simulated measurements of $T_{\rm e}$(O III) (in percentages of t2 in the upper panel and absolute value in the lower panel) vs. the effective temperature $T_{\rm eff}$ of the ionizing star for N = 100 apertures, ionization parameter U=-3, and six different values of hydrogen density in the range $1.5 \leq \log N_{\rm H}~({\rm cm^{-3}}) \leq 4$ (indicated by the same line types used in Fig. 2).
Open with DEXTER

From point-to-point measurements in three different directions on the plane of 30 Doradus Nebula, Krabbe & Copetti (2002) found a fairly homogeneous spatial distribution of [O III] electron temperature, corresponding to $t^2_{\rm s}(O {\sc iii})= 0.0025$. Therefore, we estimate a value of t2 = 0.010 for this nebula, which is very close to the value of t2 = 0.014 predicted by the photoionization model with appropriate parameters. Similar observations by Tsamis et al. (2003) confirmed that the spatial variation of temperature is very small in this nebula. However, based on the comparisons among electron temperatures obtained from forbidden lines and from the Balmer continuum, as well as among O+, O++, and C+ ionic abundances obtained from forbidden and recombination lines, Peimbert (2003) estimated $t^2 = 0.033 \pm 0.005$ for 30 Doradus.

For the Orion Nebula, from the value of $t^2_{\rm s}(O {\sc iii}) = 0.0079$ measured by O'Dell et al. (2003), we derive t2 = 0.028, which is the same value as that obtained by O'Dell et al. (2003) using a completely different approach. They evaluated the temperature fluctuation for the whole nebula from the projected [O III] temperature distribution, based essentially on the fraction of the nebular volume occupied by the O++ zone and on the difference between the mean temperatures in the O+ and O++ zones. Through long-slit spectroscopy, Rubin et al. (2003) have obtained eight independent estimates of  $t^2_{\rm s}(O {\sc iii})$ for four different $52\hbox{$^{\prime\prime}$ }\times 0.5\hbox{$^{\prime\prime}$ }$ areas over the Orion Nebula, finding values from 0.00682 to 0.0176, which correspond to t2 varying from 0.024 to 0.062, according to our models. The two highest values for  $t^2_{\rm s}(O {\sc iii})$ were found for the fainter areas, consequently from data with poorer S/N. The median of their estimates from brighter areas, $t^2_{\rm s}(O {\sc iii}) = 0.0098$, is probably more representative of the whole nebula, and it leads to t2=0.035. Esteban et al. (1998) estimated $t^2 = 0.024 \pm 0.004$ from the comparison of O++ abundances from collisionally excited and recombination lines.

Although a more profound discussion about the existence of significant temperature fluctuations in ionized nebulae is beyond the scope of this paper, we observe that two different conclusions were attained from the above comparisons. For the 30 Doradus Nebula, we estimate a value of t2, compatible with that predicted by photoionization models, but too small to invoke the temperature fluctuations as the cause of the discrepancy between the abundances derived from collisionally excited and recombination lines. On the other hand, for the Orion Nebula, we obtain a magnitude for the temperature fluctuation that could explain the abundance problem, but it is much higher than the predictions of photoionization models for homogeneous nebulae. If the projected temperature variance observed in the Orion Nebula is confirmed (the knotty task is the discount of the pure error variance), it would leave no doubt that the classic temperature fluctuations play an important role in the interpretation of the spectra of H II regions. 2D mapping of temperature with different indicators for a significant sample of objects would be of help to settle the question.

4 Conclusions

Through model simulations, we have assessed the feasibility of quantifying the global spatial temperature fluctuation parameter t2, based on point-to-point measurements of the electron temperature across the nebula with different temperature sensors. The main conclusions are:

1.
The projected profiles of electron temperature obtained from sensors associated with ions occurring in large fractions of the nebula, such as $T_{\rm e}$(Bac), $T_{\rm e}$(O III), and $T_{\rm e}$(Ar III), are good tracers of the internal gradient of temperature. On the other hand, the temperature profiles obtained from temperature sensors corresponding to low ionization ions, such as $T_{\rm e}$(N II), $T_{\rm e}$(O I), and $T_{\rm e}$(C I), are almost constant, at values corresponding to the temperatures of the outer parts of the nebula, and fail to reproduce the true temperature gradient.

2.
The variances $t^2_{\rm s}$ of the distributions of the temperatures $T_{\rm e}$(Bac), $T_{\rm e}$(O III), and $T_{\rm e}$(Ar III), measured on the plane of the sky, correspond to a significant fraction of the total temperature fluctuation t2. For typical H II regions ( $40~000 \la T_{\rm eff} \la 50~000$ K, $N_{\rm e} \approx 100{-}1000$ cm-3, and $\log U \approx -3$), $t^2_{\rm s}/t^2 \approx 30$%, 25%, and 15% for the distributions of $T_{\rm e}$(Bac), $T_{\rm e}$(O III), and $T_{\rm e}$(Ar III), in that order. On the other hand, for the sensors associated with low ionization ions, $T_{\rm e}$(N II), $T_{\rm e}$(O I), and $T_{\rm e}$(C I), $t^2_{\rm s}/t^2 \approx 2\%$.

Acknowledgements
This work was partially supported by the Brazilian institutions CNPq and FAPERGS. We thank the anonymous referee for helpful comments and suggestions.

References

 

  
Online Material


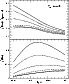  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics*{4736fg06.eps}}\end{figure} Figure 6: The same as in Fig. 4, except for temperature $T_{\rm e}$(Bac).
Open with DEXTER


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics*{4736fg07.eps}}\end{figure} Figure 7: The same as in Fig. 5, except for temperature $T_{\rm e}$(Bac).
Open with DEXTER


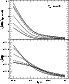  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics*{4736fg08.eps}}\end{figure} Figure 8: The same as in Fig. 4, except for temperature $T_{\rm e}$(N II).
Open with DEXTER


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics*{4736fg09.eps}}\end{figure} Figure 9: The same as in Fig. 5, except for temperature $T_{\rm e}$(N II).
Open with DEXTER


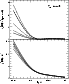  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics*{4736fg10.eps}}\end{figure} Figure 10: The same as in Fig. 4, except for temperature $T_{\rm e}$(O I).
Open with DEXTER


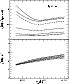  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics*{4736fg11.eps}}\end{figure} Figure 11: The same as in Fig. 5, except for temperature $T_{\rm e}$(O I).
Open with DEXTER


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics*{4736fg12.eps}}\end{figure} Figure 12: The same as in Fig. 4, except for temperature $T_{\rm e}$(Ar III).
Open with DEXTER


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics*{4736fg13.eps}}\end{figure} Figure 13: The same as in Fig. 5, except for temperature $T_{\rm e}$(Ar III).
Open with DEXTER


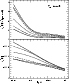  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics*{4736fg14.eps}}\end{figure} Figure 14: The same as in Fig. 4, except for temperature $T_{\rm e}$(C I).
Open with DEXTER


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics*{4736fg15.eps}}\end{figure} Figure 15: The same as in Fig. 5, except for temperature $T_{\rm e}$(C I).
Open with DEXTER


Copyright ESO 2006