A&A 453, 1037-1040 (2006)
DOI: 10.1051/0004-6361:20054616
Recent timing studies on RXTE observations of 4U 1538-52
(Research Note)
A. Baykal1 - S. Ç. Inam2 - E. Beklen1,3
1 - Physics Department, Middle East Technical University, 06531 Ankara, Turkey
2 - Department of Electrical and Electronics Engineering, Baskent University, 06530 Ankara, Turkey
3 - Physics Department, Süleyman Demirel University, 32260 Isparta, Turkey
Received 30 November 2005 / Accepted 2 April 2006
Abstract
The high mass X-ray binary pulsar 4U 1538-52 was observed between
July 31 and August 7, 2003. Using these observations, we
determined new orbital epochs for both circular and elliptical orbit
models. The orbital epochs for both orbit solutions
agreed with each other and yielded an orbital period derivative
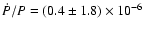 yr-1.
This value is consistent with the earlier
measurement of
yr-1.
This value is consistent with the earlier
measurement of
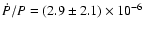 yr-1
at the
yr-1
at the 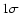 level and gives only an upper limit to the
orbital period decay.
Our determination
of the pulse frequency showed that the source spun up at an average rate
of
level and gives only an upper limit to the
orbital period decay.
Our determination
of the pulse frequency showed that the source spun up at an average rate
of
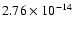 Hz s-1 between 1991 and 2003.
Hz s-1 between 1991 and 2003.
Key words: X-rays: binaries - stars: neutron - pulsars: individual: 4U 1538-52 -
accretion, accretion disks
The source 4U 1538-52 was discovered using the Uhuru satellite
(Giacconi et al. 1974). X-ray pulsations with a period of 529 s
were detected from two independent satellite experiments:
Ariel 5 (Davidson 1977) and OSO-8 (Becker et al. 1977).
OSO-8 observations also revealed a clear orbital modulation at
3.7 days and evidence of an eclipse lasting 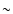 0.51 days.
The optical companion of 4U 1538-52 was identified to be the B0 I giant
QV Nor (Parkes et al. 1978).
BATSE observations of this source permitted the construction
of long-term pulse frequency and intensity histories (Rubin et al. 1997). In the pulse frequency history, Rubin et al. (1997) found
short-term pulse frequency changes of either sign, and a
power density spectrum
of fluctuations of the pulse frequency derivative that is consistent
with white torque noise on timescales from 16 to 1600 days.
0.51 days.
The optical companion of 4U 1538-52 was identified to be the B0 I giant
QV Nor (Parkes et al. 1978).
BATSE observations of this source permitted the construction
of long-term pulse frequency and intensity histories (Rubin et al. 1997). In the pulse frequency history, Rubin et al. (1997) found
short-term pulse frequency changes of either sign, and a
power density spectrum
of fluctuations of the pulse frequency derivative that is consistent
with white torque noise on timescales from 16 to 1600 days.
From RXTE observations,
Clark (2000) obtained new orbital
parameters of the source that provided marginal evidence of
orbital decay, i.e., they found
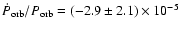 yr-1.
In this work, we present new orbital epoch and pulse frequency measurements
based on our analysis of archival RXTE observations of 4U 1538-52.
yr-1.
In this work, we present new orbital epoch and pulse frequency measurements
based on our analysis of archival RXTE observations of 4U 1538-52.
The observations of 4U 1538-52 took place between July 31 and
August 7, 2003 (MJD 52851-52858) and accumulated a total nominal
exposure of 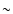 75 ks. The results presented
here are based on data collected with the Proportional Counter Array (PCA,
Jahoda et al. 1996). The PCA instrument consists of an array of five
collimated xenon/methane multianode proportional counters. The total effective
area is approximately 6250 cm2 and the field of view is
75 ks. The results presented
here are based on data collected with the Proportional Counter Array (PCA,
Jahoda et al. 1996). The PCA instrument consists of an array of five
collimated xenon/methane multianode proportional counters. The total effective
area is approximately 6250 cm2 and the field of view is
 FWHM. The nominal energy range of the PCA extends from 2 to 60 keV.
FWHM. The nominal energy range of the PCA extends from 2 to 60 keV.
![\begin{figure}
\par\includegraphics[angle=-90,width=14.4cm,clip]{4616fig1.eps}\end{figure}](/articles/aa/full/2006/27/aa4616-05/Timg9.gif) |
Figure 1:
2-30 keV RXTE-PCA light curve of 4U 1538-52
between July 31 and August 7, 2003. Two 26 s binned  3 ks samples
of this light curve corresponding to single RXTE orbits are presented on the
upper left and the upper right. 3 ks samples
of this light curve corresponding to single RXTE orbits are presented on the
upper left and the upper right. |
| Open with DEXTER |
Table 1:
Orbital parameters of 4U 1538-52.
Background light curves and X-ray spectra were generated by using background
estimator models based on the rate of very large events (VLE),
detector activation, and cosmic X-ray background.
The background light curves were subtracted from the source light curve
obtained from the binned Good Xenon data. For 4U 1538-52, X-ray emission coming from the galactic ridge is only a few percent of the total X-ray emission which should not affect our timing analysis (see Makishima et al. 1987), so we did not include an estimation of the galactic ridge emission in our analysis. In Fig. 1, we present
the background subtracted light curve. Although the number of
active PCUs varied from 1 to 4 during the observations,
Fig. 1 shows count rates
adjusted as if 5 PCUs had been active using the "correctlc'' tool in
HEASOFT 6. For the timing analysis, we corrected
the light curve to the barycenter of the solar system.
We also corrected this barycentered
light curve for binary orbital motion using
both circular and elliptical orbital models given in Table 1 (see also
Clark 2000). Then a template pulse profile
was created by folding the light curve into one master profile.
Pulse profiles were also made from each of the 12 independent
RXTE observations seen in Fig. 1.
In order to find the pulse frequency and a new orbital epoch, we
obtained
12 pulse arrival times through the  2 binary orbits
using a cross-correlation technique.
In the pulse timing analysis, we used the method of
harmonic representation of pulse profiles, which was proposed by
Deeter
2 binary orbits
using a cross-correlation technique.
In the pulse timing analysis, we used the method of
harmonic representation of pulse profiles, which was proposed by
Deeter  Boynton (1985). In this method, the pulse profiles
for each orbit and the master profile are expressed in terms of harmonic
series. We used 10-term unweighted harmonic series to
cross-correlate
the template pulse profile with the pulse profiles for each
RXTE observation. The maximum value
of the cross-correlation is analytically well-defined and does not depend
on the phase binning of the pulses.
Boynton (1985). In this method, the pulse profiles
for each orbit and the master profile are expressed in terms of harmonic
series. We used 10-term unweighted harmonic series to
cross-correlate
the template pulse profile with the pulse profiles for each
RXTE observation. The maximum value
of the cross-correlation is analytically well-defined and does not depend
on the phase binning of the pulses.
The source 4U 1538-52 has a variable pulse profile which
affects the pulse timing. In order to estimate
the errors in the arrival times,
the light curve of each RXTE observation was
divided into approximately 4-5 equal
subsets and new arrival times were estimated.
The standard deviation of the arrival times obtained
from each subset of the observation was taken to be the
uncertainty in the arrival time for that observation.
Table 2:
Orbital epochs by pulse timing analysis.
Arrival time delays may arise from the
change of the pulse frequency during the observation (or
intrinsic pulse frequency derivative) and from the differences
between the assumed and actual orbital and pulse parameters
(Deeter et al. 1981),
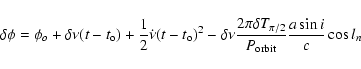 |
(1) |
where
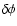 is the pulse phase offset
deduced from the pulse
timing analysis,
is the pulse phase offset
deduced from the pulse
timing analysis, 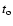 is the mid-time of the observation,
is the mid-time of the observation,
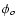 is the residual phase offset at
is the residual phase offset at 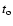 ,
,
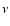 is the pulse frequency at time t0,
is the pulse frequency at time t0,
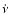 is the pulse frequency derivative of the source,
is the pulse frequency derivative of the source,
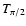 is the orbital epoch when the mean orbital
longitude is equal to 90 degrees,
is the orbital epoch when the mean orbital
longitude is equal to 90 degrees,
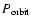 is the orbital period
and
is the orbital period
and
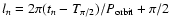 is the mean orbital
longitude at tn.
Corrected values of
orbital and pulse parameters
is the mean orbital
longitude at tn.
Corrected values of
orbital and pulse parameters
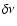 ,
,
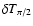 and
and 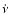 were estimated from
the fits of the above expression to pulse phase residuals.
were estimated from
the fits of the above expression to pulse phase residuals.
Table 1 presents the result of fits for both orbital and pulse parameters.
We also reestimated the orbital epochs by varying the
projected orbital radius
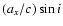 in the range of its uncertainty (
in the range of its uncertainty (
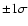 )
and
found that the resulting orbital epochs are consistent with the best fit
value at the 1
)
and
found that the resulting orbital epochs are consistent with the best fit
value at the 1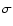 level. The error in the orbital epoch
due to an error in
level. The error in the orbital epoch
due to an error in
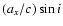 may
also be expressed (Deeter et al. 1981) as
may
also be expressed (Deeter et al. 1981) as
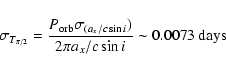 |
(2) |
where
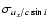 is the uncertainty in the
projected orbital radius. This value is small relative to our
error estimate for the orbital epoch (see Table 1).
In Fig. 2, we present the arrival
time delay, the best fit elliptical orbit model,
and arrival time residuals.
is the uncertainty in the
projected orbital radius. This value is small relative to our
error estimate for the orbital epoch (see Table 1).
In Fig. 2, we present the arrival
time delay, the best fit elliptical orbit model,
and arrival time residuals.
As seen from Table 1, the
orbital epochs for circular and elliptical orbital models agree with
each other at the 1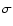 level. In order to check our
technique, we extracted observations of 4U 1538-52 done in
1997 (MJD 50449.93-50453.69) and estimated orbital epochs for
those observations. The results agreed with the orbital epochs
given by Clark (2000).
level. In order to check our
technique, we extracted observations of 4U 1538-52 done in
1997 (MJD 50449.93-50453.69) and estimated orbital epochs for
those observations. The results agreed with the orbital epochs
given by Clark (2000).
In Table 2, we present the orbital epoch measurements from
different observatories and orbital cycle number (n).
In Fig. 3, we present observed minus calculated values
of orbital epochs
(
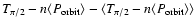 )
relative to the
constant orbital period (
)
relative to the
constant orbital period (
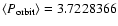 days).
A quadratic fit to the epochs from all experiments yielded
an estimate of the rate of period change
days).
A quadratic fit to the epochs from all experiments yielded
an estimate of the rate of period change
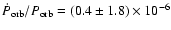 yr-1.
In Fig. 4, we display the long-term pulse frequency history of the source.
yr-1.
In Fig. 4, we display the long-term pulse frequency history of the source.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{4616fig2.ps}\end{figure}](/articles/aa/full/2006/27/aa4616-05/Timg37.gif) |
Figure 2:
( Top) Pulse arrival time delays
and best-fit
elliptical orbital model given in Table 1.
(Note that pulse profiles are obtained
with respect to the reference time 52855.0585 MJD.)
( Below) Residuals after removing best orbital model. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{4616fig3.ps}\end{figure}](/articles/aa/full/2006/27/aa4616-05/Timg39.gif) |
Figure 3:
The phase residuals of orbital epoch for 4U 1538-52.
The orbital phases are estimated relative the constant
orbital period
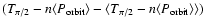 ,
where n is the
orbital cycle number (see Table 2).
The rightmost point
corresponds to the most recent RXTE observation of ID 80016. ,
where n is the
orbital cycle number (see Table 2).
The rightmost point
corresponds to the most recent RXTE observation of ID 80016. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{4616fig4.ps}\end{figure}](/articles/aa/full/2006/27/aa4616-05/Timg40.gif) |
Figure 4:
Pulse frequency history of 4U 1538-52.
The rightmost point
corresponds to the most recent RXTE observation of ID 80016. |
| Open with DEXTER |
Before CGRO observations, 4U 1538-52 had been found to have a long-term
spin down trend. A linear fit to pre-CGRO pulse frequency history gives
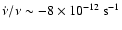 and a linear fit to
CGRO and our RXTE result yields
and a linear fit to
CGRO and our RXTE result yields
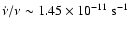 .
Rubin et al. (1997) constructed the power spectrum of pulse frequency
derivative fluctuations. Their analysis showed that the pulse frequency
derivative fluctuations can be explained on timescales from 16 to 1600 days
with an average white noise strength of
.
Rubin et al. (1997) constructed the power spectrum of pulse frequency
derivative fluctuations. Their analysis showed that the pulse frequency
derivative fluctuations can be explained on timescales from 16 to 1600 days
with an average white noise strength of
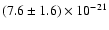 (Hz s-1)2 Hz-1. A random walk in pulse frequency
(or white noise in pulse frequency derivative) can be explained
as a sequence of steps in pulse frequency with an rms value
of
(Hz s-1)2 Hz-1. A random walk in pulse frequency
(or white noise in pulse frequency derivative) can be explained
as a sequence of steps in pulse frequency with an rms value
of
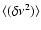 which occur
at a constant rate R. Then the rms variation
of the pulse frequency scales with elapsed time
which occur
at a constant rate R. Then the rms variation
of the pulse frequency scales with elapsed time 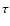 as
as
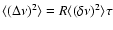 (Hz),
where
(Hz),
where
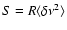 is defined as noise strength.
Then, rms scaling for the pulse frequency derivatives
can be obtained as
is defined as noise strength.
Then, rms scaling for the pulse frequency derivatives
can be obtained as
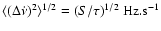 .
As seen from Table 1, in our fits, upper limits on
intrinsic pulse frequency derivatives are 7-10 times higher than
the long-term spin up rates. If white noise in the pulse
frequency derivative can be interpolated to a few days, then the upper limit on the change of frequency derivative obtained from a
.
As seen from Table 1, in our fits, upper limits on
intrinsic pulse frequency derivatives are 7-10 times higher than
the long-term spin up rates. If white noise in the pulse
frequency derivative can be interpolated to a few days, then the upper limit on the change of frequency derivative obtained from a 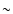 1 week observation should
typically have a magnitude that can be estimated from
1 week observation should
typically have a magnitude that can be estimated from
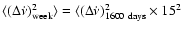 .
This value is 15/7-15/10 times higher than the measured upper limit values. Therefore the measured upper limits on the intrinsic pulse frequency derivatives for 1 week are consistent with the values from the extrapolation of the power spectrum within a factor of a few.
.
This value is 15/7-15/10 times higher than the measured upper limit values. Therefore the measured upper limits on the intrinsic pulse frequency derivatives for 1 week are consistent with the values from the extrapolation of the power spectrum within a factor of a few.
The previous marginal measurement of change in the orbital period
was
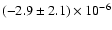 yr-1 (Clark 2000), and our new
value for the orbital period change,
yr-1 (Clark 2000), and our new
value for the orbital period change,
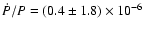 yr-1,
are consistent with zero.
These two measurements are consistent with each other in
yr-1,
are consistent with zero.
These two measurements are consistent with each other in
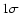 level.
level.
In most of the X-ray binaries with accretion powered pulsars,
the evolution of the orbital period seems to be too slow to be detectable.
Yet there are still some such systems in which this evolution was
measured and 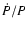 were reported.
These systems include Cen X-3 with
were reported.
These systems include Cen X-3 with
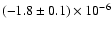 yr-1(Kelley et al. 1983; Nagase et al. 1992),
Her X-1 with
yr-1(Kelley et al. 1983; Nagase et al. 1992),
Her X-1 with
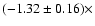 10-8 yr-1 (Deeter et al. 1991),
SMC X-1 with
10-8 yr-1 (Deeter et al. 1991),
SMC X-1 with
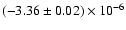 yr-1 (Levine et al. 1993),
Cyg X-3 with
yr-1 (Levine et al. 1993),
Cyg X-3 with
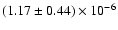 yr-1 (Kitamoto et al. 1995),
4U 1700-37 with
yr-1 (Kitamoto et al. 1995),
4U 1700-37 with
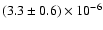 yr-1 (Rubin et al. 1996),
and LMC X-4 with
yr-1 (Rubin et al. 1996),
and LMC X-4 with
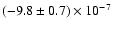 yr-1
(Levine et al. 2000). Change in the orbital period of Cyg X-3 was associated
with the mass loss rate from the Wolf-Rayet companion star. For 4U 1700-37,
the major cause of orbital period change was also thought to be
mass loss from the companion star. For Her X-1, mass loss and mass
transfer from the companion were proposed to be the reasons for the change in
the orbital period of the system.
yr-1
(Levine et al. 2000). Change in the orbital period of Cyg X-3 was associated
with the mass loss rate from the Wolf-Rayet companion star. For 4U 1700-37,
the major cause of orbital period change was also thought to be
mass loss from the companion star. For Her X-1, mass loss and mass
transfer from the companion were proposed to be the reasons for the change in
the orbital period of the system.
On the other hand, for the high mass X-ray binary systems
Cen X-3, LMC X-4 and SMC X-1, the major cause of change
in the orbital period is likely to be tidal interactions
(Kelley et al. 1983; Levine et al. 2000; Levine et al. 1993).
For these three systems, the orbital period decreases
(i.e. the derivative of the orbital period is negative).
Our new measurement of orbital period change
(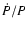 )
gives the value of about -10-6 yr-1 which is
similar to the observed values of SMC X-1 and Cen X-3. Further observations
can give more information about the orbital period change of this source.
)
gives the value of about -10-6 yr-1 which is
similar to the observed values of SMC X-1 and Cen X-3. Further observations
can give more information about the orbital period change of this source.
Acknowledgements
We thank the anonymous referee for useful suggestions and comments. A.B. and S.C.I. acknowledge research project TBAG 106T040 of the Scientific and Technological Research Council of Turkey (TUBITAK).
- Becker, R. H.,
Swank, J. H., Bold, E. A., et al. 1977, ApJ, 216, L11 [NASA ADS] [CrossRef]
- Clark, G. W. 2000,
ApJ, 542, L133 [NASA ADS] (In the text)
- Corbet, R. H. D.,
Woo, J. W., & Nagase, F. 1993, A&A, 276, 52 [NASA ADS]
- Deeter, J. E.,
Boynton, P. E., & Pravdo, S. H. 1981, ApJ, 247, 1003 [NASA ADS] [CrossRef] (In the text)
- Deeter, J. E.,
& Boynton, P. E. 1985, in Proc. Inuyama Workshop on Timing
Studies of X-ray Sources, ed. S. Hayakawa, & F. Nagase (Nagoya:
Nagoya Univ.), 29
(In the text)
- Deeter, J. E.,
Boynton, P. E., Miyamoto, S., et al. 1991, ApJ, 383, 324 [NASA ADS] [CrossRef] (In the text)
- Giacconi, R.,
Murray, S., Gursky, H., et al. 1974, ApJS, 27, 37 [NASA ADS] [CrossRef] (In the text)
- Jahoda, K., Swank,
J. H., Giles, A. B., et al. 1996, Proc. SPIE, 2808, 59 [NASA ADS]
- Kelley, R. L.,
Rappaport, G., Clark, G. W., & Petro, L. D. 1983, ApJ, 268,
790 [NASA ADS] [CrossRef] (In the text)
- Kitamoto, S.,
Hirano, A., Kawashima, K., et al. 1995, PASJ, 47, 233 [NASA ADS] (In the text)
- Levine, A.,
Rappaport, S., Deeter, J. E., et al. 1993, ApJ, 410, 328 [NASA ADS] [CrossRef] (In the text)
- Levine, A. M.,
Rappaport, S. A., & Zojcheski, G. 2000, ApJ, 541, 194 [NASA ADS] [CrossRef] (In the text)
- Makishima,
K., Koyama, K., Hayakawa, S., & Nagase, F. 1987, ApJ, 314,
619 [NASA ADS] [CrossRef] (In the text)
- Nagase, F., Corbet,
R. H. D., Day, C. S. R., et al. 1992, ApJ, 396, 147 [NASA ADS] [CrossRef] (In the text)
- Parkes, G. E.,
Murdin, P. G., & Mason, K. O. 1978, MNRAS, 184, 73 [NASA ADS] (In the text)
- Rubin, B. C., Finger,
M. H., Harmon, B. A., et al. 1996, ApJ, 459, 259 [NASA ADS] [CrossRef] (In the text)
- Rubin, B. C., Finger,
M. H., Scott, D. M., et al. 1997, ApJ, 488, 413 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[angle=-90,width=14.4cm,clip]{4616fig1.eps}\end{figure}](/articles/aa/full/2006/27/aa4616-05/Timg9.gif)
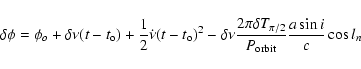
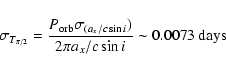
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{4616fig2.ps}\end{figure}](/articles/aa/full/2006/27/aa4616-05/Timg37.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{4616fig3.ps}\end{figure}](/articles/aa/full/2006/27/aa4616-05/Timg39.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{4616fig4.ps}\end{figure}](/articles/aa/full/2006/27/aa4616-05/Timg40.gif)