A&A 453, 1027-1036 (2006)
DOI: 10.1051/0004-6361:20054225
Low compressibility accretion disc formation in close binaries:
the role of physical viscosity
G. Lanzafame1 - G. Belvedere2 - D. Molteni3
1 - INAF - Osservatorio Astrofisico di Catania, via S. Sofia
78, 95123 Catania, Italy
2 -
Dipartimento di Fisica e Astronomia dell'Universitá - Sezione
Astrofisica, via S. Sofia 78, 95123 Catania, Italy
3 -
Dipartimento di Fisica e Tecnologie Relative, Universitá di
Palermo, Viale delle Scienze, 90128 Palermo, Italy
Received 19 September 2005 / Accepted 9 March 2006
Abstract
Aims. Physical viscosity naturally hampers gas dynamics (rarefaction or compression). Such a role should support accretion disc development inside the primary gravitation potential well in a close binary system, even for low compressibility modelling. Therefore, from the astrophysical point of view, highly viscous accretion discs could exist even in the low compressibility regime showing strong thermal differences to high compressibility ones
Methods. We performed simulations of stationary Smooth Particle Hydrodynamics (SPH) low compressibility accretion disc models for the same close binary system. Artificial viscosity operates in all models. The absence of physical viscosity and a supersonic high mass transfer characterize the first model. Physical viscosity and the same supersonic high mass transfer characterize the second model, whilst physical viscosity and a subsonic low mass transfer characterize the third model. The same binary system parameters, such as stellar masses and their separation, have been adopted, as well as the same polytropic index
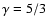 .
Thus we investigated the role of physical viscosity in mass and angular momentum transport in the two viscid models and compare them to the inviscid model. An initial value of the parameter
.
Thus we investigated the role of physical viscosity in mass and angular momentum transport in the two viscid models and compare them to the inviscid model. An initial value of the parameter
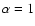 has been considered for the physically viscous models, according to the well-known Shakura and Sunjaev formulation, but simulations were carried out also for
has been considered for the physically viscous models, according to the well-known Shakura and Sunjaev formulation, but simulations were carried out also for
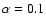 and
and
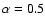 in the case of a supersonic mass transfer. Physical viscosity is represented by the viscous force contribution expressed by the divergence of the symmetric viscous stress tensor in the Navier-Stokes equation, while the viscous energy contribution is given by a symmetric combination of the symmetric shear tensor times the particle velocity.
in the case of a supersonic mass transfer. Physical viscosity is represented by the viscous force contribution expressed by the divergence of the symmetric viscous stress tensor in the Navier-Stokes equation, while the viscous energy contribution is given by a symmetric combination of the symmetric shear tensor times the particle velocity.
Results. The results show that physical viscosity supports and favours accretion disc formation despite the very low compressibility assumed. On the contrary, in the inviscid case no evident disc structure appears. In all models neither shock fronts nor extended clear spirals in the radial flow develop.
Key words: accretion, accretion discs - stars: binaries: close - stars: dwarf novae,
white dwarfs - methods: numerical - methods: N-body simulations
Since the eighties, the existence of spiral patterns and radial shocks in physically
inviscid accretion discs in close binaries has been discussed. According to some authors,
i.e. Chakrabarti (1992), Bisikalo et al. (1999), spiral patterns do not appear if a
polytropic index (appearing in the perfect gas state equation)
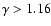 is adopted.
According to some others, such as Sawada et al. (1987), Spruit et al. (1987), Kaisig (1989), Matsuda et al. (1992,1990),
Ichikawa & Osaki (1992,1994), Sawada & Matsuda (1992), Savonije et al. (1994), Yukawa et al. (1997), Makita et al. (2000), spiral
patterns and radial shocks always exist whatever the
is adopted.
According to some others, such as Sawada et al. (1987), Spruit et al. (1987), Kaisig (1989), Matsuda et al. (1992,1990),
Ichikawa & Osaki (1992,1994), Sawada & Matsuda (1992), Savonije et al. (1994), Yukawa et al. (1997), Makita et al. (2000), spiral
patterns and radial shocks always exist whatever the 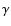 is and the initial kinematic
conditions are. Tidal effects should be responsible for spirals and spiral shock development
in the disc bulk, starting from the outer disc edge. Recently some papers
(Lanzafame et al. 2000; Lanzafame & Belvedere 2001; Belvedere & Lanzafame 2002; Lanzafame et al. 2001; Lanzafame & Belvedere 2005) conclude, through 2D and 3D SPH simulations, that initial conditions, such
as angular momentum and energy, are crucial in spiral shock formation. These studies were
performed as a consequence of the fact that in some previous papers of our group (Molteni et al. 1991; Lanzafame et al. 1992)
we did not obtain spirals, both in low compressibility
models (
is and the initial kinematic
conditions are. Tidal effects should be responsible for spirals and spiral shock development
in the disc bulk, starting from the outer disc edge. Recently some papers
(Lanzafame et al. 2000; Lanzafame & Belvedere 2001; Belvedere & Lanzafame 2002; Lanzafame et al. 2001; Lanzafame & Belvedere 2005) conclude, through 2D and 3D SPH simulations, that initial conditions, such
as angular momentum and energy, are crucial in spiral shock formation. These studies were
performed as a consequence of the fact that in some previous papers of our group (Molteni et al. 1991; Lanzafame et al. 1992)
we did not obtain spirals, both in low compressibility
models (
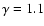 and
and
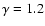 )
and in a high compressibility model (
)
and in a high compressibility model (
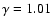 ). Instead, we found spiral patterns, mainly close to the disc outer edge, in Lanzafame & Belvedere (1998,1997)
by considering different injection conditions. In Molteni et al. (1991) and in Lanzafame et al. (1992) no well bound
and defined accretion discs were found in the case of low compressibility models (
). Instead, we found spiral patterns, mainly close to the disc outer edge, in Lanzafame & Belvedere (1998,1997)
by considering different injection conditions. In Molteni et al. (1991) and in Lanzafame et al. (1992) no well bound
and defined accretion discs were found in the case of low compressibility models (
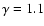 and
and
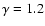 ). The investigation carried out in this paper arose as a consequence of the
idea that physical viscosity naturally hampers the gas dynamics (rarefaction or compression).
Such a role should support accretion disc development inside the primary gravitation potential
well, even for low compressibility modelling. In the case of a well bound and defined physically
viscous accretion disc, we also investigated the possibility of spiral shock front development
from its outer edge in spite of the physical viscosity degradation effect on gas dynamics and
shock front discontinuities. Spiral shock fronts coming out in the disc radial flow have
clearly been shown in a previous paper (Lanzafame 2003) for
). The investigation carried out in this paper arose as a consequence of the
idea that physical viscosity naturally hampers the gas dynamics (rarefaction or compression).
Such a role should support accretion disc development inside the primary gravitation potential
well, even for low compressibility modelling. In the case of a well bound and defined physically
viscous accretion disc, we also investigated the possibility of spiral shock front development
from its outer edge in spite of the physical viscosity degradation effect on gas dynamics and
shock front discontinuities. Spiral shock fronts coming out in the disc radial flow have
clearly been shown in a previous paper (Lanzafame 2003) for
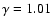 in the case of a
physically viscous disc. In this paper a
in the case of a
physically viscous disc. In this paper a
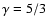 polytropic index has been adopted and
a comparison among three stationary SPH accretion disc models has been performed, adopting
the same binary system parameters such as stellar masses and their separation. The here
adopted
polytropic index has been adopted and
a comparison among three stationary SPH accretion disc models has been performed, adopting
the same binary system parameters such as stellar masses and their separation. The here
adopted
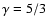 value is common in the literature. Even higher
value is common in the literature. Even higher 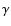 s up to 2
have been chosen by various authors (e.g. Bisikalo et al. 1999). However in most papers the
gas chemical composition is unknown or not specified. This means that the
s up to 2
have been chosen by various authors (e.g. Bisikalo et al. 1999). However in most papers the
gas chemical composition is unknown or not specified. This means that the 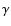 value does
not have any strict relation to the traditional adiabatic index built using specific heats.
value does
not have any strict relation to the traditional adiabatic index built using specific heats.
In this paper the first model (model a)) is of a physically inviscid accretion disc and adopts
a supersonic high mass transfer condition at the inner Lagrangian point L1. The second one
(model b)) is a physically viscous disc with the same supersonic mass trasfer condition at L1.
The third one (model c)) is a physically viscous disc and adopts a subsonic low mass transfer
condition at L1. The well-known Shakura and Sunyaev viscosity prescription (Shakura 1972; Shakura & Sunyaev 1973) has
been adopted with
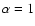 .
.
The SPH formulation of viscous contributions in the Navier-Stokes and energy equations has been
developed by Flebbe et al. (1994,1992). Such a formulation could also describe molecular and
turbulent viscosity effects (Landau & Lifshitz 1959). These goals are not obtained by
artificial viscosity which is, however, introduced in both models to resolve shocks numerically
and to avoid spurious heating. Artificial viscosity vanishes when the limit value of the
particle interpolation domain goes to zero. Drimmel (1993), Meglicki et al. (1993), Murray (1996) demonstrated that the linear
component of artificial viscosity itself, in the continuum limit, yields a viscous shear force.
In particular the last two authors have explicitly formulated such an artificial viscosity
contribution in the momentum and energy equations. Murray (1996) found an analogy between the shear
viscosity generated by the linear artificial viscosity term and the well-known Shakura and Sunyaev
shear viscosity, in the continuum limit. These conclusions do not disagree with our goals. The SPH
method, like other finite difference schemes, is far from the continuum limit; moreover we need the
quadratic (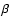 )
artificial viscosity term to handle strong shocks. In conclusion, we compare
three SPH accretion disc models where artificial viscosity is necessarily included. Some models
also include physical viscosity, but one does not. In this paper, the viscous force contribution is
represented by the divergence of the symmetric viscous stress tensor in the Navier-Stokes equation. A
symmetric combination of the symmetric shear tensor times the particle velocity has been added
to the energy equation as a viscous heating contribution. The bulk physical viscosity
contribution has not been considered for the sake of simplicity.
)
artificial viscosity term to handle strong shocks. In conclusion, we compare
three SPH accretion disc models where artificial viscosity is necessarily included. Some models
also include physical viscosity, but one does not. In this paper, the viscous force contribution is
represented by the divergence of the symmetric viscous stress tensor in the Navier-Stokes equation. A
symmetric combination of the symmetric shear tensor times the particle velocity has been added
to the energy equation as a viscous heating contribution. The bulk physical viscosity
contribution has not been considered for the sake of simplicity.
Notice that our analysis and results are somewhat different from those by Flebbe et al. (1994,1992), who
used the same SPH viscous formulation in the equations and applied the code to
similar numerical tests. However, they adopted a shear component of the stress tensor
proportional to the 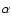 Shakura and Sunjaev parameter times the gas pressure and excluded
any artificial viscosity contribution. Bisikalo et al. (2000), adopting
Shakura and Sunjaev parameter times the gas pressure and excluded
any artificial viscosity contribution. Bisikalo et al. (2000), adopting
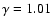 ,
an
Eulerian finite difference method and various physical viscosities, found self-consistent
solutions showing the absence of a shock impact between the stream flowing from L1 and the disk
body at its outer edge. They also found a similarity of the flow patterns even adopting
different disc viscosities.
,
an
Eulerian finite difference method and various physical viscosities, found self-consistent
solutions showing the absence of a shock impact between the stream flowing from L1 and the disk
body at its outer edge. They also found a similarity of the flow patterns even adopting
different disc viscosities.
In Sect. 2 of this paper we briefly present the SPH formulation of the models. In Sect. 3
we describe the adopted boundary conditions and the physical characteristics of the disc gas,
while in Sect. 4 we discuss our results.
As for non-viscous gas hydrodynamics, the relevant equations to our model are:
 |
(1) |
![\begin{displaymath}% latex2html id marker 284
\frac{{\rm d} \underline{v}}{{\rm ...
...\nabla \Phi_{\rm grav}]
\hspace*{1cm} \mbox{momentum equation}
\end{displaymath}](/articles/aa/full/2006/27/aa4225-05/img22.gif) |
(2) |
 |
(3) |
 |
(4) |
Here most symbols have the usual meaning,
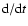 stands for the Lagrangian derivative,
stands for the Lagrangian derivative, 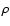 is the gas density,
is the gas density, 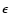 is the thermal energy per unit mass,
is the thermal energy per unit mass,
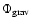 is the
effective gravitational potential generated by the two stars and
is the
effective gravitational potential generated by the two stars and
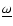 is the
angular velocity of the rotating reference frame, corresponding to the rotational period of
the binary system. Self gravitation has not been included, as it appears irrelevant. The
adiabatic index
is the
angular velocity of the rotating reference frame, corresponding to the rotational period of
the binary system. Self gravitation has not been included, as it appears irrelevant. The
adiabatic index 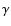 is a numerical parameter whose value lies in the range between 1 and
5/3, in principle.
is a numerical parameter whose value lies in the range between 1 and
5/3, in principle.
The SPH method is a Lagrangian scheme that discretizes the fluid into moving interacting and
interpolating domains called "particles''. All particles move according to pressure and body
forces. The method makes use of a kernel W useful to interpolate a physical quantity
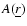 related to a gas particle at position
related to a gas particle at position
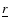 according to:
according to:
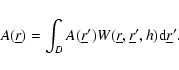 |
(5) |
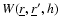 ,
the interpolation kernel, is a continuous function - or
two connecting continuous functions whose derivatives are continuous even at the connecting
point - defined in the spatial range 2h, whose limit for
,
the interpolation kernel, is a continuous function - or
two connecting continuous functions whose derivatives are continuous even at the connecting
point - defined in the spatial range 2h, whose limit for
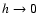 is the Dirac delta
distribution function. All physical quantities are described as extensive properties smoothly
distributed in space and computed by interpolation at
is the Dirac delta
distribution function. All physical quantities are described as extensive properties smoothly
distributed in space and computed by interpolation at
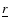 .
In SPH terms we write:
.
In SPH terms we write:
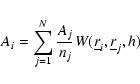 |
(6) |
where the sum is extended to all particles included in the domain D,
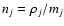 is the number density relative to the jth particle and
is the number density relative to the jth particle and
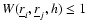 is the adopted interpolation kernel whose value is determined by the relative
distance between particles i and j.
is the adopted interpolation kernel whose value is determined by the relative
distance between particles i and j.
In the SPH formalism, Eqs. (2) and (3) take the form:
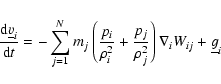 |
(7) |
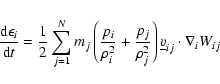 |
(8) |
where
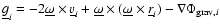 ,
,
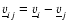 and
mj is the mass of the jth particle. Alternatively, Eq. (8) can
also be written:
and
mj is the mass of the jth particle. Alternatively, Eq. (8) can
also be written:
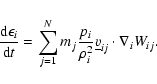 |
(9) |
In this scheme the continuity equation takes the form:
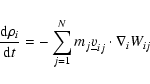 |
(10) |
or it can also be written as:
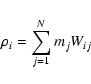 |
(11) |
which identifies the natural space interpolation of particle densities
according to Eq. (6).
The pressure term includes the artificial viscosity contribution
given by (Monaghan 1985,1992) and Monaghan & Lattanzio (1985), with an appropriate thermal diffusion term which
reduces shock fluctuations. It is given by:
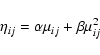 |
(12) |
where
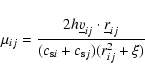 |
(13) |
with
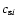 being the sound speed of the ith particle,
being the sound speed of the ith particle,
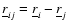 ,
,
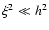 ,
,
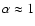 and
and
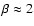 .
These
.
These 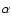 and
and
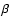 parameters of the order of unity are usually adopted to damp
oscillations past high Mach number shock fronts developed by
non-linear instabilities (Boris & Book 1973). These
parameters of the order of unity are usually adopted to damp
oscillations past high Mach number shock fronts developed by
non-linear instabilities (Boris & Book 1973). These 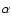 and
and
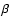 values were also adopted by Lattanzio et al. (1986). Lower
values were also adopted by Lattanzio et al. (1986). Lower
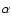 and
and 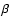 values, as adopted by Meglicki et al. (1993),
would develop more turbulence in the disc and possibly only one shock
front at the impact zone between the infalling particle stream and the
returning particle stream at the disc outer edge. In the physically
inviscid SPH gas dynamics, angular momentum transport is mainly due to
the artificial viscosity included in the pressure terms as:
values, as adopted by Meglicki et al. (1993),
would develop more turbulence in the disc and possibly only one shock
front at the impact zone between the infalling particle stream and the
returning particle stream at the disc outer edge. In the physically
inviscid SPH gas dynamics, angular momentum transport is mainly due to
the artificial viscosity included in the pressure terms as:
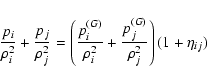 |
(14) |
where p(G) is the intrinsic gas pressure.
In the Lagrangian SPH modelling of physically viscous gas dynamics, we
have to add the viscous force term to the right side of
momentum Eq. (2). The resulting Navier-Stokes equation is:
![\begin{displaymath}\frac{{\rm d} \underline{v}}{{\rm d}t} = - \frac{\nabla p}{\r...
...abla \Phi_{\rm grav}] +
\frac{1}{\rho} \nabla \cdot {\vec t}.
\end{displaymath}](/articles/aa/full/2006/27/aa4225-05/img53.gif) |
(15) |
Here, the viscous stress tensor
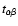 includes the
positive first and second viscosity coefficients
includes the
positive first and second viscosity coefficients 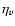 and
and
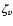 which are velocity independent and describe shear and
tangential viscosity stresses (
which are velocity independent and describe shear and
tangential viscosity stresses (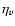 ), and compressibility
stresses (
), and compressibility
stresses (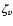 ):
):
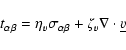 |
(16) |
where the shear
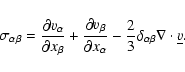 |
(17) |
In these equations the indexes 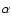 and
and 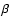 are spatial
indexes while tensors are written in bold characters. For simplicity we
assume
are spatial
indexes while tensors are written in bold characters. For simplicity we
assume
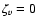 ,
however our code also allows
different choices. As in Flebbe et al. (1994,1992), defining
,
however our code also allows
different choices. As in Flebbe et al. (1994,1992), defining
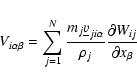 |
(18) |
as the SPH formulation of
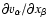 ,
the SPH equivalent of the shear is:
,
the SPH equivalent of the shear is:
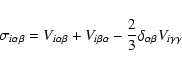 |
(19) |
therefore, the SPH momentum equation equivalent is:
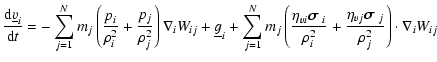 |
|
|
(20) |
and the energy balance equation for the total energy
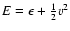 is:
is:
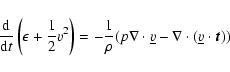 |
(21) |
which has the SPH equivalent:
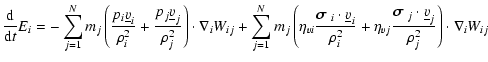 |
|
|
(22) |
where
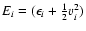 .
.
A full justification of this SPH formalism can be found in Flebbe et al. (1994,1992).
The characteristics of the binary system are determined by the
masses of the two companion stars and their separation. We
chose to model a system in which the mass M1 of the primary
compact star and the mass M2 of the secondary normal star are
equal to one 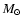 and the distance between their centres is
and the distance between their centres is
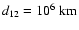 .
The injection gas velocity at L1
is fixed to
.
The injection gas velocity at L1
is fixed to
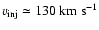 for our
inviscid first model (a)) and our viscous second model (b))
and to
for our
inviscid first model (a)) and our viscous second model (b))
and to
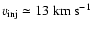 as for the viscous third
model (c)) while the injection gas temperature at L1 is fixed to
as for the viscous third
model (c)) while the injection gas temperature at L1 is fixed to
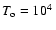 K. Such a temperature value is slightly higher
than the value corresponding to a normal
K. Such a temperature value is slightly higher
than the value corresponding to a normal
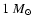 star because,
even as a first approximation, the radiative heating of the secondary
surface due to lightening of the disc is taken into account. Gas
compressibility is fixed by the adiabatic index
star because,
even as a first approximation, the radiative heating of the secondary
surface due to lightening of the disc is taken into account. Gas
compressibility is fixed by the adiabatic index 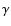 of 5/3. In
models a) and b) we chose a highly supersonic injection velocity at L1,
to verify whether, by adopting a high angular momentum injection
condition, spiral structures and shocks in the radial flow would appear in
low compressibility 3D modelling, as shown by Lanzafame et al. (2000,2001) in
2D, and by Lanzafame (2003) in 3D, high compressibility models.
We and other authors (Yukawa et al. 1997; Meglicki et al. 1993) have found that spirals and shock fronts
in the radial flow do not develop in high compressibility 3D SPH accretion disc
models if subsonic injection conditions at L1 are adopted, in spite of the fact
that tidally induced spiral patterns should develop (Murray 1996; Truss et al. 2001; Blondin 2000; Truss et al. 2000),
at least in 2D modelling. Therefore, our assumption of strongly supersonic mass
inflow could be effective enough to allow spirals to form in spite of the
artificial viscosity degradation. In our models the unknowns are: pressure,
density, temperature, velocity, so we solve the continuity, momentum,
energy and state (perfect gas) equations.
of 5/3. In
models a) and b) we chose a highly supersonic injection velocity at L1,
to verify whether, by adopting a high angular momentum injection
condition, spiral structures and shocks in the radial flow would appear in
low compressibility 3D modelling, as shown by Lanzafame et al. (2000,2001) in
2D, and by Lanzafame (2003) in 3D, high compressibility models.
We and other authors (Yukawa et al. 1997; Meglicki et al. 1993) have found that spirals and shock fronts
in the radial flow do not develop in high compressibility 3D SPH accretion disc
models if subsonic injection conditions at L1 are adopted, in spite of the fact
that tidally induced spiral patterns should develop (Murray 1996; Truss et al. 2001; Blondin 2000; Truss et al. 2000),
at least in 2D modelling. Therefore, our assumption of strongly supersonic mass
inflow could be effective enough to allow spirals to form in spite of the
artificial viscosity degradation. In our models the unknowns are: pressure,
density, temperature, velocity, so we solve the continuity, momentum,
energy and state (perfect gas) equations.
In order to make our equations dimensionless, we adopted the
following normalization factors:
M = M1 + M2 for masses,
d12 = 1011 cm for lengths,
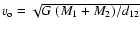 for speeds, so that the orbital period is
normalized to
for speeds, so that the orbital period is
normalized to 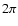 ,
,
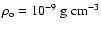 for the
density,
for the
density,
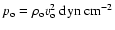 for
pressure,
for
pressure,
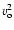 for thermal energy per unit mass and
for thermal energy per unit mass and
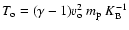 for
temperature, where
for
temperature, where 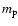 is the proton mass and
is the proton mass and 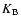 is the
Boltzman constant. The adopted kernel width in the SPH interpolations
is h = 0.005 and the geometrical domain including moving disc
particles is a sphere of radius 0.6, centred on the primary. The
rotating reference frame is centred on the compact primary and its
rotational period equals the orbital one. We simulated the physical
conditions at the inner and at the outer edges as follows:
is the
Boltzman constant. The adopted kernel width in the SPH interpolations
is h = 0.005 and the geometrical domain including moving disc
particles is a sphere of radius 0.6, centred on the primary. The
rotating reference frame is centred on the compact primary and its
rotational period equals the orbital one. We simulated the physical
conditions at the inner and at the outer edges as follows:
a) Inner edge:
The free inflow condition is realized by eliminating particles flowing
inside the sphere of radius 4h, centred on the primary. It follows
that disc structure and dynamics are altered within a few h values of the
inner edge, adopting a fixed h SPH code, but these alterations in
disc behaviour are relatively small because they are counterbalanced
by a higher particle concentration close to the inner edge in the
supersonic injection models.
b) Outer edge:
The injection of "new'' particles from L1 towards the interior of the
primary Roche Lobe is simulated by generating them in fixed points,
called "injectors'', symmetrically placed within an angle having
L1 as a vertex and an aperture of
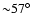 .
The initial
injection particle velocity is radial with respect to L1. In
order to simulate a constant and smooth gas injection, a "new''
particle is generated in the injectors whenever "old'' particles leave
an injector free, inside a small sphere with radius h, centred on
the injector itself.
.
The initial
injection particle velocity is radial with respect to L1. In
order to simulate a constant and smooth gas injection, a "new''
particle is generated in the injectors whenever "old'' particles leave
an injector free, inside a small sphere with radius h, centred on
the injector itself.
The formulation adopted for the 3D SPH accretion disc model
including physical viscosity is the well-known Shakura (1972); Shakura & Sunyaev (1973) 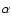 parametrization:
parametrization:
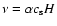 ,
where
,
where 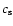 is the sound velocity,
is the sound velocity,
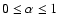 is the Shakura and Sunyaev parameter and
is the Shakura and Sunyaev parameter and
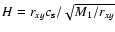 is a dimensionless estimate of
the standard disc thickness, where
is a dimensionless estimate of
the standard disc thickness, where
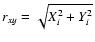 is the cylindrical radial coordinate of the ith particle.
In this paper we chose to adopt
is the cylindrical radial coordinate of the ith particle.
In this paper we chose to adopt
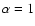 as an initial value to point out
evident differences in disc structure and dynamics between our SPH
disc models.
as an initial value to point out
evident differences in disc structure and dynamics between our SPH
disc models.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{4225fig1.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg88.gif) |
Figure 1:
XY plots for the inviscid model a) with
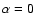 ( bottom) and the two physically viscous models with
( bottom) and the two physically viscous models with
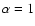 ( middle - model b) and top - model c)). The final time T and total
particle number N, as well as the injection velocity from the inner
Lagrangian point L1, are also reported.
( middle - model b) and top - model c)). The final time T and total
particle number N, as well as the injection velocity from the inner
Lagrangian point L1, are also reported. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{4225fig2.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg89.gif) |
Figure 2:
rXYZ plots for the inviscid model a) with
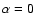 ( bottom) and the two physically viscous models with
( bottom) and the two physically viscous models with
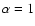 ( middle -
model b) and top - model c)). The final time T and total particle number
N, as well as the injection velocity from the inner Lagrangian point L1, are also
reported.
( middle -
model b) and top - model c)). The final time T and total particle number
N, as well as the injection velocity from the inner Lagrangian point L1, are also
reported. |
| Open with DEXTER |
We carried out our simulations until a time
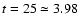 orbital periods, namely until fully stationary configurations. This means that particles
injected into the primary potential well (which is not deep, due to the primary small mass) are
statistically balanced by particles accreted onto the primary itself and by particles ejected from the
outer disc edge. In the present simulations, in the fully stationary statistical equilibrium
configurations, particles number only a few thousands ranging from about 3000 to about 13 000. There is no
way to obtain a higher number of particles with the adopted value of h=0.005, which is a small enough
value and historically confirmed since our first papers on accretion discs in 1991. Other authors
have adopted such a good compromise h value in SPH accretion disc modelling. However, here the problem is
not the total number of particles, but rather their concentration, namely whether the
fluid properties (density, pressure gradients, etc.) are computed accurately enough. This will be
extensively discussed below (Sect. 4.2).
orbital periods, namely until fully stationary configurations. This means that particles
injected into the primary potential well (which is not deep, due to the primary small mass) are
statistically balanced by particles accreted onto the primary itself and by particles ejected from the
outer disc edge. In the present simulations, in the fully stationary statistical equilibrium
configurations, particles number only a few thousands ranging from about 3000 to about 13 000. There is no
way to obtain a higher number of particles with the adopted value of h=0.005, which is a small enough
value and historically confirmed since our first papers on accretion discs in 1991. Other authors
have adopted such a good compromise h value in SPH accretion disc modelling. However, here the problem is
not the total number of particles, but rather their concentration, namely whether the
fluid properties (density, pressure gradients, etc.) are computed accurately enough. This will be
extensively discussed below (Sect. 4.2).
The mass transfer injection rates from L1
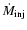 ,
accretion rates
,
accretion rates
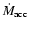 and ejection
rates
and ejection
rates
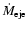 are of the order of
are of the order of
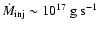 ,
,
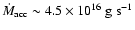 and
and
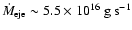 for inviscid model a),
for inviscid model a),
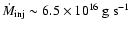 ,
,
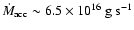 and
and
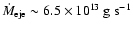 for viscous disc model b) and
for viscous disc model b) and
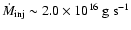 ,
,
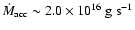 and
and
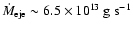 for
viscous disc model c). Both physically viscous disc models (b) and c)) show
mass ejection rates lower than or equal to
for
viscous disc model c). Both physically viscous disc models (b) and c)) show
mass ejection rates lower than or equal to
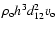 ,
which is the
conversion factor from particle/time to
,
which is the
conversion factor from particle/time to
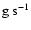 .
For this reason we believe that the two
viscous mass ejection rates may be considered as higher limits.
.
For this reason we believe that the two
viscous mass ejection rates may be considered as higher limits.
Figure 1 shows XY and XZ plots of the physically inviscid disc
(bottom-left side) and the two physically viscous discs (top side).
While the latter plots clearly show well bound structures
with a definite disc outer edge, the first plot shows that the particle
dispersion is too high as to get a well bound and a well defined disc. This
result was obtained by Lanzafame et al. (1992); Molteni et al. (1991), adopting lower polytropic indexes
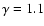 and
and
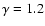 and a subsonic injection condition at L1. Here we adopt the
value
and a subsonic injection condition at L1. Here we adopt the
value
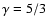 which represents the correct adiabatic index of a monoatomic gas.
which represents the correct adiabatic index of a monoatomic gas.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{4225fig3.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg104.gif) |
Figure 3:
Plots of the radial Mach number Mr as a function of
the radial distance for the inviscid model a) (
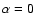 )
and for the two
physically viscous models: model b) for )
and for the two
physically viscous models: model b) for
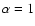 , ,
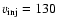 km s-1 and
model c) for km s-1 and
model c) for
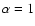 , ,
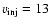 km s-1. Here three radial shells have been
considered. The thickness of each radial shell is km s-1. Here three radial shells have been
considered. The thickness of each radial shell is
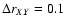 ,
as shown
in each plot by looking at rXY. ,
as shown
in each plot by looking at rXY. |
| Open with DEXTER |
Figure 2 shows the rXYZ for all three accretion disc models
obtained by folding all disc bulk particles onto a plane containing the Z
axis and being perpendicular to the XY orbital plane. An evident latitudinal
spread appears for the inviscid model a), differently from the viscous models b)
and c). Moreover, comparing models b) and c) shows a small but clear dependence
on the mass transfer injection speed at L1. Latitudinal angular
spreads computed for all three disc models are
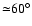 ,
,
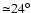 and
and
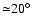 for disc models a), b) and c) respectively.
Therefore, a more stretched and slim structure characterizes physically viscous
discs due to the more effective particle radial velocity transport and channeling
towards the primary.
for disc models a), b) and c) respectively.
Therefore, a more stretched and slim structure characterizes physically viscous
discs due to the more effective particle radial velocity transport and channeling
towards the primary.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{4225fig4.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg109.gif) |
Figure 4:
Plots of the work made by the pressure forces Wp and
by the viscosity forces Wv per unit mass (here
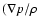 and
and
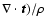 )) as a function of the disc radial distance for model b) -
( top two panels) and model c) - ( bottom two panels). )) as a function of the disc radial distance for model b) -
( top two panels) and model c) - ( bottom two panels). |
| Open with DEXTER |
Physical viscosity naturally works where the particle mutual velocity (and
separation) change in time, namely when a mutual acceleration exists contrasting
gas dynamics (rarefaction or compression) and converting kinetic energy into
thermal energy. Such a mechanism clearly supports the development of well bound
accretion discs inside the primary potential well, in spite of the low
compressibility, at least for
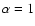 .
No spirals and shock fronts exist in the inviscid accretion disc bulk or
at its outer edge, as shown in Figs. 1 and 2. The mean particle
concentration is too low to allow us to have a reliable particle statistics for
such an inviscid model. Because of this statistical limitation,
we should be able to see spirals in a better defined physically
viscous disc structure and especially in accretion disc model b) where a
supersonic mass transfer injection condition has been adopted at L1, but it
is not so. Figure 3 shows the profile of the radial Mach number Mr as a
function of the radial distance for all three accretion disc models. For a
better understanding of such behaviour, a selection of particles included in
three suitable cylindrical radial shells has been made for each model.
Figure 3 shows that no shock fronts and spiral structures develop in all three
accretion disc models. This is not surprising for models b) and c). Indeed,
physical viscosity, slowing down the radial flow and
heating the gas particles (so increasing the local sound speed), reduces the
Mach number and the radial Mach number, although a more ordered radial transport, and some radial and
azimuthal ripples, are clearly shown. However, we cannot conclude that spirals and shock fronts should
not appear in the inviscid accretion disc since model a) is not well resolved because of the lack of
reliable particle statistics. The lack of resolution is due not only to the low particle
concentration but also to the artificial viscosity smoothing effect which is heavy in 3D simulations.
This investigation shows that spirals and shock fronts may not develop in low compressibility
physically viscous discs in a binary system with low mass stars and a mass ratio of the order of the
unity. Our work is essentially concerned with viscid discs, the inviscid case being of minor
importance. This is also the reason why 2D SPH simulations (where artificial viscosity is less
important) are not totally overcome. On the contrary, often 2D simulations are complementary.
.
No spirals and shock fronts exist in the inviscid accretion disc bulk or
at its outer edge, as shown in Figs. 1 and 2. The mean particle
concentration is too low to allow us to have a reliable particle statistics for
such an inviscid model. Because of this statistical limitation,
we should be able to see spirals in a better defined physically
viscous disc structure and especially in accretion disc model b) where a
supersonic mass transfer injection condition has been adopted at L1, but it
is not so. Figure 3 shows the profile of the radial Mach number Mr as a
function of the radial distance for all three accretion disc models. For a
better understanding of such behaviour, a selection of particles included in
three suitable cylindrical radial shells has been made for each model.
Figure 3 shows that no shock fronts and spiral structures develop in all three
accretion disc models. This is not surprising for models b) and c). Indeed,
physical viscosity, slowing down the radial flow and
heating the gas particles (so increasing the local sound speed), reduces the
Mach number and the radial Mach number, although a more ordered radial transport, and some radial and
azimuthal ripples, are clearly shown. However, we cannot conclude that spirals and shock fronts should
not appear in the inviscid accretion disc since model a) is not well resolved because of the lack of
reliable particle statistics. The lack of resolution is due not only to the low particle
concentration but also to the artificial viscosity smoothing effect which is heavy in 3D simulations.
This investigation shows that spirals and shock fronts may not develop in low compressibility
physically viscous discs in a binary system with low mass stars and a mass ratio of the order of the
unity. Our work is essentially concerned with viscid discs, the inviscid case being of minor
importance. This is also the reason why 2D SPH simulations (where artificial viscosity is less
important) are not totally overcome. On the contrary, often 2D simulations are complementary.
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{4225fig5.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg111.gif) |
Figure 5:
Neighbours histograms for the inviscid model a) with
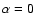 ( bottom) and the two physically viscous models with
( bottom) and the two physically viscous models with
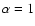 ( middle - model b) and top - model c)). These histograms show the percentage
distribution of particles
( middle - model b) and top - model c)). These histograms show the percentage
distribution of particles
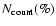 having a given number of neighbours
having a given number of neighbours
 .
The
average value .
The
average value
 ,
the final time T, as well as the injection velocity and from the
inner Lagrangian point L1, are also reported. ,
the final time T, as well as the injection velocity and from the
inner Lagrangian point L1, are also reported. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17.3cm,clip]{4225fig6.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg112.gif) |
Figure 6:
XY and rXYZ plots for the physically viscous models with
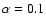 ( left side) and with
( left side) and with
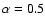 ( right side). The final time T and total particle number
N, as well as the injection velocity from the inner Lagrangian point L1, are also
reported.
( right side). The final time T and total particle number
N, as well as the injection velocity from the inner Lagrangian point L1, are also
reported. |
| Open with DEXTER |
The present conclusions do not disagree with our previous results, related to differently
structured binary systems. Lanzafame & Belvedere (2005) showed in
a 2D SPH simulation that, even in the low compressibility regime, spirals and shock
fronts do exist in accretion discs around supermassive black holes of
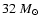 or more, where a
or more, where a
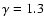 and a stellar mass ratio
M1/M2
> 50 were adopted. Similar results for 2D SPH modelling, but much less evident,
were also shown in Lanzafame & Belvedere (2001) and in Belvedere & Lanzafame (2002). As explained in these three papers, the
strong impact of the massive injected accreting stream (strongly accelerated in the deep
primary potential well) with the outer disc edge determines the onset of spiral shocks.
Indeeed, for a massive primary star whose mass
and a stellar mass ratio
M1/M2
> 50 were adopted. Similar results for 2D SPH modelling, but much less evident,
were also shown in Lanzafame & Belvedere (2001) and in Belvedere & Lanzafame (2002). As explained in these three papers, the
strong impact of the massive injected accreting stream (strongly accelerated in the deep
primary potential well) with the outer disc edge determines the onset of spiral shocks.
Indeeed, for a massive primary star whose mass
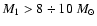 and for a
stellar mass ratio
M1/M2 > 10, the gravitational acceleration of the
massive primary dominates over both
and for a
stellar mass ratio
M1/M2 > 10, the gravitational acceleration of the
massive primary dominates over both
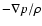 and
and
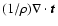 terms.
terms.
A comparison of the absolute values of the pressure and viscosity forces per
unit mass (here
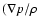 and
and
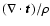 )
is shown in
Fig. 4 as a function of the radial distance for models b) and c) for all disc
particles (with
)
is shown in
Fig. 4 as a function of the radial distance for models b) and c) for all disc
particles (with
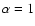 ). These plots show that the work made by the pressure
forces Wp is of the same order as the viscous one Wv. This result
suggests that physically viscous
). These plots show that the work made by the pressure
forces Wp is of the same order as the viscous one Wv. This result
suggests that physically viscous
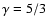 low compressibility accretion disc
models are meaningful if we adopt
low compressibility accretion disc
models are meaningful if we adopt
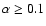 .
.
A reasonable SPH
accuracy is related to the number of space neighbours of each SPH particle. Problems about
spatial resolution and SPH accuracy may exist for our physically inviscid accretion disc
model. This model is a "reference model''. Indeed, it is very hard to perform low
compressibility gas dynamic simulations when attractive force fields are not dominant with
respect to repulsive pressure forces. In the inviscid case, there is no way to obtain a
particle concentration higher than 5-10 particle neighbours, even by changing the h value
in the range from its half to its double. Here, we do not want to challenge the SPH particle
resolution required (commonly about 30-50 neighbours per particle in 3D simulations), but
only to indicate that a problem exists in the astrophysical context of inviscid low
compressibility modelling, when thermal energies are of the order of gravitational energies
(generally of any binding energies) or larger. From a strictly mathematical point of view,
the minimum condition of at least 3 non-coplanar neighbours SPH particles is statistically
satisfied even in our "starting'' inviscid disc model, following Ben Moussa & Vila (2000).
See the neighbours histograms in Fig. 5, showing the percentage distribution of
particles
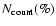 having a given number of neighbours
having a given number of neighbours
 (and the average value
(and the average value
 )
for all three a), b) and c) models.
)
for all three a), b) and c) models.
However, our work is much more concerned with the introduction of physical viscosity. The
main interest of this paper is the demonstration that, even in the case of very low
compressibility, a strong physical viscosity allows the formation of a well bound accretion disc
within the primary Roche Lobe. In some astrophysical situations, numerical simulations
(e.g. Katz et al. 1996; Lanzafame & Belvedere 2001; Hernquist & Katz 1989; Spruit et al. 1987; Bate & Burkert 1997; Nelson & Papaloizou 1994) show a high particle concentration with 30
to 50 particle neighbours or more. According to the neighbours histograms shown in Fig. 7, we
have an average number of 25.51 neighbours for the
 high injection speed model
(model b)) and 25.32 for the
high injection speed model
(model b)) and 25.32 for the
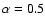 high injection speed model, the latter being a
further simulation carried out to investigate the role of
high injection speed model, the latter being a
further simulation carried out to investigate the role of 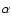 ,
as shown below. These numbers
seem to have a reasonable SPH accuracy.
,
as shown below. These numbers
seem to have a reasonable SPH accuracy.
Adopting
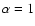 stresses differences in disc structure and dynamics with respect to the
physically inviscid model. However, values of
stresses differences in disc structure and dynamics with respect to the
physically inviscid model. However, values of 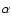 less than unity may be more realistic
according to some thin disc analytical models (Lasota 2001; Pringle et al. 1986). In order to
examine the role of the physical viscosity strength, we carried out simulations with
less than unity may be more realistic
according to some thin disc analytical models (Lasota 2001; Pringle et al. 1986). In order to
examine the role of the physical viscosity strength, we carried out simulations with
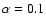 and
and
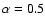 with supersonic injection.
with supersonic injection.
The mass transfer injection rates from L1
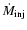 ,
accretion rates
,
accretion rates
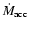 and
ejection rates
and
ejection rates
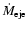 for the
for the
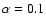 and
and
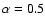 models, are respectively
models, are respectively
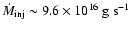 ,
,
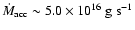 and
and
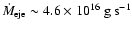 and
and
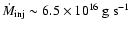 ,
,
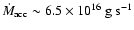 and
and
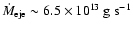 .
.
Figure 6 shows XY and rXYZ plots for these simulations, while Fig. 7 shows their neighbour histograms. For the
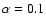 case no evident
differences appear with respect to the inviscid reference model. A similar result was also reported
in Lanzafame (2003). Instead, a well bound accretion disc is seen for the
case no evident
differences appear with respect to the inviscid reference model. A similar result was also reported
in Lanzafame (2003). Instead, a well bound accretion disc is seen for the
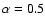 case. These results show that in the low compressibility regime a value of
case. These results show that in the low compressibility regime a value of 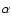 less or equal
to 0.1 should not be effective. Low alpha values of the order of 0.1 are found in Pringle et al. (1986) and in
Lasota (2001) in the thin disc approximation where hydrostatic equilibrium along the Z
direction is assumed, a case different from ours, where turbulence plays a role also along the Z-axis.
Therefore, we think that the
less or equal
to 0.1 should not be effective. Low alpha values of the order of 0.1 are found in Pringle et al. (1986) and in
Lasota (2001) in the thin disc approximation where hydrostatic equilibrium along the Z
direction is assumed, a case different from ours, where turbulence plays a role also along the Z-axis.
Therefore, we think that the
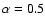 supersonic injection model is a good compromise and so can
be considered as our reference viscid model. Statistically, the total number of particles is
(slightly) larger than for the
supersonic injection model is a good compromise and so can
be considered as our reference viscid model. Statistically, the total number of particles is
(slightly) larger than for the
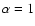 model b). This result in our opinion is mainly due to a
(slightly) lower particle radial transport toward the compact primary for the
model b). This result in our opinion is mainly due to a
(slightly) lower particle radial transport toward the compact primary for the
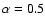 (less
viscosity) than for the
(less
viscosity) than for the
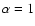 model b). The computed injection, accretion and ejection rates
for these two models are in practice the same after
model b). The computed injection, accretion and ejection rates
for these two models are in practice the same after 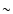 4 orbital periods (stationary conditions).
Here, no finer distinction can be made as the percentage computing errors are of the same order as
the percentage difference in the number of particles.
4 orbital periods (stationary conditions).
Here, no finer distinction can be made as the percentage computing errors are of the same order as
the percentage difference in the number of particles.
Our physical viscosity is only a shear viscosity. For simplicity no bulk viscosity has been
considered, as explicitly said in the paper. A value
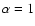 for the bulk viscosity should be
too high.
for the bulk viscosity should be
too high.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{4225fig7.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg124.gif) |
Figure 7:
Neighbours histograms for the physically viscous models
with
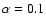 ( bottom) and with
( bottom) and with
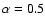 ( top). These histograms show the
percentage distribution of particles
( top). These histograms show the
percentage distribution of particles
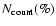 having a given number of neighbours
having a given number of neighbours
 .
The average value .
The average value
 ,
the final time T, as well as the injection velocity from the inner
Lagrangian point L1, are also reported. ,
the final time T, as well as the injection velocity from the inner
Lagrangian point L1, are also reported. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4225fig8.eps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg125.gif) |
Figure 8:
Logarithmic plots of angular momentum radial distributions for the inviscid
model a) with
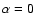 ( bottom) and the two physically viscous models with
( bottom) and the two physically viscous models with
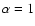 ( middle - model b) and top - model c)). The final time T as well as the injection
velocity from the inner Lagrangian point L1, are also reported.
( middle - model b) and top - model c)). The final time T as well as the injection
velocity from the inner Lagrangian point L1, are also reported. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{4225fig9.eps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg126.gif) |
Figure 9:
Logarithmic plots of temperature radial distributions for the inviscid
model a) with
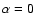 ( bottom) and the two physically viscous models with
( bottom) and the two physically viscous models with
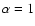 ( middle - model b) and top - model c)). The final time T as well as the injection
velocity from the inner Lagrangian point L1, are also reported.
( middle - model b) and top - model c)). The final time T as well as the injection
velocity from the inner Lagrangian point L1, are also reported. |
| Open with DEXTER |
Figures 8 and 9 show in a logarithmic scale the angular momentum and
temperature radial distribution respectively, for models a), b) and c).
The logarithmic angular momentum and temperature radial distributions,
the radial profiles of pressure and viscosity forces, as well as the azimuthal profiles of the radial
Mach number for
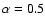 are similar to those for
are similar to those for
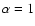 model b) and, therefore, are
not reported here.
model b) and, therefore, are
not reported here.
The angular momentum radial distribution for the viscous models is very close to that of the standard
model
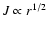 .
This can be explained considering that in stationary
conditions an accretion disc redistributes the angular momentum injected at the
outer edge into the disc bulk according to outer edge boundary conditions only,
as already shown in Belvedere et al. (1993) and in Lanzafame et al. (1993).
Physical viscosity plays a role in regions where particle velocity gradients
are significant. This means that physical viscosity plays a relevant role mainly
in the radial transport, while it has little influence on the tangential dynamics.
A strong difference appears when looking at the temperature radial distribution. The heating
effect of the physical viscosity is particularly evident in the disc inner zones. The disc itself is
in an equilibrium stationary state in which the heated particles are directly accreted towards the
primary. This as for particle advection. As for conduction, although much less important,
the temperature decreases towards the exterior, thus heat is dispersed outside. However, discs could
also radiate energy. In disc models without explicit inclusion of radiative terms in the energy
equation (almost all models, since, such an inclusion complicates the analysis), the effect of
radiative cooling is better simulated with
.
This can be explained considering that in stationary
conditions an accretion disc redistributes the angular momentum injected at the
outer edge into the disc bulk according to outer edge boundary conditions only,
as already shown in Belvedere et al. (1993) and in Lanzafame et al. (1993).
Physical viscosity plays a role in regions where particle velocity gradients
are significant. This means that physical viscosity plays a relevant role mainly
in the radial transport, while it has little influence on the tangential dynamics.
A strong difference appears when looking at the temperature radial distribution. The heating
effect of the physical viscosity is particularly evident in the disc inner zones. The disc itself is
in an equilibrium stationary state in which the heated particles are directly accreted towards the
primary. This as for particle advection. As for conduction, although much less important,
the temperature decreases towards the exterior, thus heat is dispersed outside. However, discs could
also radiate energy. In disc models without explicit inclusion of radiative terms in the energy
equation (almost all models, since, such an inclusion complicates the analysis), the effect of
radiative cooling is better simulated with 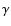 less than 5/3. Thus, we cannot neglect the
possibility that the non-appearance of shocks in viscid discs may be a consequence of the lack of
an efficient radiative cooling in the simulations.
less than 5/3. Thus, we cannot neglect the
possibility that the non-appearance of shocks in viscid discs may be a consequence of the lack of
an efficient radiative cooling in the simulations.
The main consequences of the viscous heating,
which implies a more efficient particle radial transport toward the primary, in the case
of low compressibility accretion disc modelling, are the following: disc bounding
inside the primary Roche lobe, disc thinning as far as their latitudinal spread is concerned, disc
heating and its increasing in temperature radial gradient. Therefore, in viscous
discs particles are hotter and much better accreted (see the comparison between the values of the
accretion rate for models b) and c)).
Indeed, for the first time, our results show that physical viscosity
supports the development of a well bound accretion disc in the primary potential
well, even in the case of low compressibility. However, no spirals and shocks appear, although the
disc structure is well defined and statistically meaningful, but this may be a consequence of the lack of
an efficient radiative cooling, as said before. Such results mean that the initial angular momentum
injection conditions at the disc outer edge are responsible for the disc tangential dynamics, while
viscosity is mainly responsible for the thermodynamical disc properties, even for low compressibility
disc models (
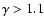 ,
here
,
here
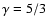 ). Indeed, physical viscosity implies a degradation and
smoothing effect both on dynamical and thermodynamical discontinuities, so disfavouring shocks. As shown
in Lanzafame (2003), high compressibility (
). Indeed, physical viscosity implies a degradation and
smoothing effect both on dynamical and thermodynamical discontinuities, so disfavouring shocks. As shown
in Lanzafame (2003), high compressibility (
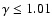 )
is a quite favourable condition
to develop spirals and shock fronts in the radial flow according to some suitable dynamical and
thermodynamical initial outer edge conditions at L1. Accretion disc models around massive black holes, as
in Lanzafame & Belvedere (2005), are an exception. For such objects, spirals and shock fronts develop
anyway due to the strong impact of the flow injected from L1. In this case both dynamical and
thermodynamical disc properties are mainly a consequence of the primary strong gravitational field.
)
is a quite favourable condition
to develop spirals and shock fronts in the radial flow according to some suitable dynamical and
thermodynamical initial outer edge conditions at L1. Accretion disc models around massive black holes, as
in Lanzafame & Belvedere (2005), are an exception. For such objects, spirals and shock fronts develop
anyway due to the strong impact of the flow injected from L1. In this case both dynamical and
thermodynamical disc properties are mainly a consequence of the primary strong gravitational field.
Acknowledgements
We are grateful to the anonymous referee for helpful comments and suggestions.
- Bate, M. R., & Burkert, A.
1997, MNRAS, 288, 1060 [NASA ADS]
- Belvedere, G., Lanzafame, G.,
& Molteni, D. 1993, A&A, 280, 525 [NASA ADS] (In the text)
- Belvedere, G., & Lanzafame,
G. 2002, PASJ, 54, 781 [NASA ADS]
- Ben Moussa, B., & Vila, J.
P. 2000, SIAM, J. Numer. Anal., 37, 863
(In the text)
- Bisikalo, D. V., Boyarchuk, A.
A., Chechetkin, V. M., Kutznetsov, O. A., & Molteni, D. 1999,
Astro. Rep., 43, 797 [NASA ADS] (In the text)
- Bisikalo, D. V., Boyarchuk, A.
A., Kutznetsov, O. A., & Chechetkin, V. M. 2000, Astronomy
Rep., 44, 26 [NASA ADS] (In the text)
- Blondin, J. M. 2000, New
Astron., 5, 53 [NASA ADS]
- Boris, J. P., & Book, D. L.
1973, J. Comput. Phys., 12, 1198 (In the text)
- Chakrabarti, S. K. 1992, MNRAS,
259, 410 [NASA ADS] (In the text)
- Drimmel, R. 1993, MNRAS, 282,
982 [NASA ADS] (In the text)
- Flebbe, O., Münzel, H.,
Riffert, H., & Herold, H. 1992, Mem. Soc. Astr. It., 65,
1049 [NASA ADS]
- Flebbe, O., Münzel, H.,
Herold, H., Riffert, H., & Ruder, H. 1994, ApJ, 431, 754 [NASA ADS] [CrossRef]
- Hernquist, L., & Katz, N.
1989, ApS, 70, 419 [NASA ADS]
- Ichikawa, S., & Osaki, Y.
1992, PASJ, 44, 15 [NASA ADS]
- Ichikawa, S., & Osaki, Y.
1994, PASJ, 46, 621 [NASA ADS]
- Kaisig, M. 1989, 2003,
A&A, 218, 102 [NASA ADS] (In the text)
- Katz, N., Weinberg, D. H.,
& Hernquist, L. 1996, ApJS, 105, 19 [NASA ADS] [CrossRef]
- Landau, L. D., &
Lifshitz, E. M. 1959, Course of Theoretical Physics, Vol. VI: Fluid
Mechanics (Pergamon Press)
(In the text)
- Lanzafame, G. 2003, A&A,
403, 593 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Lanzafame, G., &
Belvedere, G. 1997, MNRAS, 284, 957 [NASA ADS]
- Lanzafame, G., &
Belvedere, G. 1998, MNRAS, 295, 618 [NASA ADS] [CrossRef]
- Lanzafame, G., &
Belvedere, G. 2001, JKAS, 34, S313 [NASA ADS]
- Lanzafame, G., &
Belvedere, G. 2005, ApJ, 632, 499 [NASA ADS] [CrossRef]
- Lanzafame, G., Belvedere, G.,
& Molteni, D. 1992, MNRAS, 258, 152 [NASA ADS] (In the text)
- Lanzafame, G., Belvedere, G.,
& Molteni, D. 1993, MNRAS, 263, 839 [NASA ADS] (In the text)
- Lanzafame, G., Maravigna, F.,
& Belvedere, G. 2000, PASJ, 52, 515 [NASA ADS]
- Lanzafame, G., Maravigna, F.,
& Belvedere, G. 2001, PASJ, 53, 139 [NASA ADS]
- Lasota, J. P. 2001, New Astr.
Rev., 45, 449 [NASA ADS]
- Lattanzio, J. C., Monaghan,
J. J., Pongracic, H., & Schwarz, M. P. 1986, SIAM J. Sci. Stat.
Comput., 7, 591 [CrossRef] (In the text)
- Makita, M., Miyawaki, K.,
& Matsuda, T. 2000, MNRAS, 316, 906 [NASA ADS] [CrossRef] (In the text)
- Matsuda, T., Sekino, N.,
Shima, E., Sawada, K., & Spruit, H. 1990, A&A, 235,
211 [NASA ADS]
- Matsuda, T., Ishii, T.,
Sekino, N., et al. 1992, MNRAS, 255, 183 [NASA ADS]
- Meglicki, Z., Wickramasinghe,
D., & Bicknell, G. V. 1993, MNRAS, 264, 691 [NASA ADS] (In the text)
- Molteni, D., Belvedere, G.,
& Lanzafame, G. 1991, MNRAS, 249, 748 [NASA ADS] (In the text)
- Monaghan, J. J. 1985, Comp.
Phys. Rep., 3, 71 [CrossRef]
- Monaghan, J. J. 1992,
ARA&A, 30, 543 [NASA ADS]
- Monaghan, J. J., &
Lattanzio, J. C. 1985, A&A, 149, 135 [NASA ADS] (In the text)
- Murray, J. R. 1996, MNRAS,
279, 402 [NASA ADS] (In the text)
- Nelson, R. 1994, Mem. S.A.
It, 65, 1161 [NASA ADS]
- Nelson, R. P., &
Papaloizou, J. C. B. 1994, MNRAS, 270, 1 [NASA ADS]
- Pringle, J. E., Verbunt, F.,
& Wade, R. A. 1986, MNRAS, 221, 169 [NASA ADS]
- Savonije, G. J., Papaloizou,
J. C. B., & Lin, D. N. C. 1994, MNRAS, 268, 13 [NASA ADS] (In the text)
- Sawada, K., Matsuda, T.,
Inoue, M., & Hachisu, I. 1987, MNRAS, 224, 307 [NASA ADS] (In the text)
- Sawada, K., & Matsuda, T.
1992, MNRAS, 255, 17p [NASA ADS] (In the text)
- Shakura, N. I. 1972, Astron.
Zh., 49, 921 [NASA ADS] (English tr.: 1973, Sov. Astron., 16, 756)
- Shakura, N. I., &
Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS]
- Springel, V., Yoshida,
N., & White, S. D. M. 2001, New Astr., 6, 79 [NASA ADS]
- Spruit, H. C., Matsuda, T.,
Inoue, M., & Sawada, K. 1987, MNRAS, 229, 517 [NASA ADS] (In the text)
- Truss, M. R., Murray, J. R.,
Wynn, G. A., & Edgar, R. G. 2000, MNRAS, 319, 467 [NASA ADS] [CrossRef]
- Truss, M. R., Murray, J. R.,
& Wynn, G. A. 2001, MNRAS, 324, L1 [NASA ADS] [CrossRef]
- Yukawa, H., Boffin, H. M. J.,
Matsuda, T., & Inoue, M. 1997, MNRAS, 292, 321 [NASA ADS] (In the text)
Copyright ESO 2006

![\begin{displaymath}% latex2html id marker 284
\frac{{\rm d} \underline{v}}{{\rm ...
...\nabla \Phi_{\rm grav}]
\hspace*{1cm} \mbox{momentum equation}
\end{displaymath}](/articles/aa/full/2006/27/aa4225-05/img22.gif)

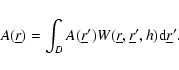
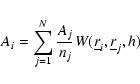
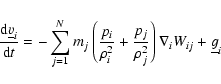
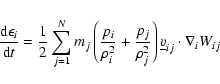
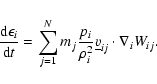
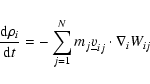
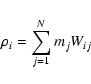
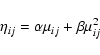
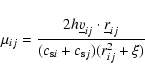
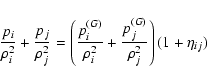
![\begin{displaymath}\frac{{\rm d} \underline{v}}{{\rm d}t} = - \frac{\nabla p}{\r...
...abla \Phi_{\rm grav}] +
\frac{1}{\rho} \nabla \cdot {\vec t}.
\end{displaymath}](/articles/aa/full/2006/27/aa4225-05/img53.gif)
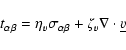
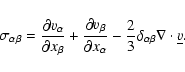
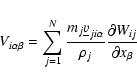
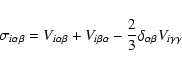
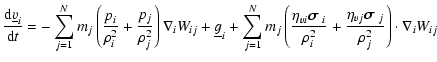
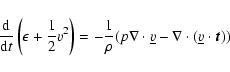
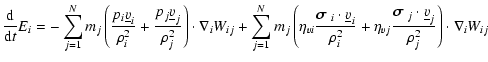
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{4225fig1.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{4225fig2.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg89.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{4225fig3.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg104.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{4225fig4.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg109.gif)
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{4225fig5.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg111.gif)
![\begin{figure}
\par\includegraphics[width=17.3cm,clip]{4225fig6.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg112.gif)
![\begin{figure}
\par\includegraphics[width=6cm,clip]{4225fig7.ps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg124.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4225fig8.eps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg125.gif)
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{4225fig9.eps}\end{figure}](/articles/aa/full/2006/27/aa4225-05/Timg126.gif)