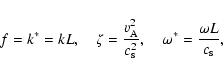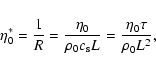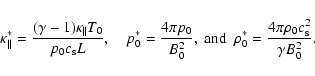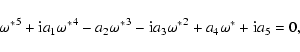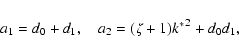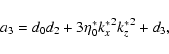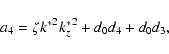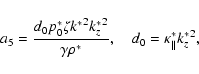A&A 453, 1067-1078 (2006)
DOI: 10.1051/0004-6361:20054141
Coronal heating by MHD waves
N. Kumar1 - P. Kumar1,2 - S. Singh2
1 - Department of Mathematics, K.G.K.(P.G.) College, Moradabad 244001
(UP), India
2 -
Department of Physics, Hindu College, Moradabad 244001 (UP), India
Received 2 September 2005 / Accepted 26 January 2006
Abstract
Aims. We study the possible role of magnetohydrodynamic (MHD) waves in the heating of solar corona and magnetic coronal loops.
Methods. Taking into account viscosity and thermal conductivity, we obtained a general fifth order dispersion relation for MHD waves propagating in a homogeneous, magnetically structured, compressible low-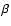 plasma. The general fifth order dispersion relation has been solved numerically, and we discuss its application to magnetic coronal loops with the help of data provided by the NIXT mission.
plasma. The general fifth order dispersion relation has been solved numerically, and we discuss its application to magnetic coronal loops with the help of data provided by the NIXT mission.
Results. The dispersion relation results in three modes, namely slow, fast, and thermal. The damping of both slow- and fast-mode waves depends upon the plasma density, the temperature, the magnetic field strength, and the angle of propagation relative to the background magnetic field. Slow-mode waves contribute to the heating of the solar corona, if one considers that they are generated in the corona by turbulent motions at magnetic reconnection sites. Calculations of wave damping rates determined from the dispersion relation indicate that slow-mode waves with periods of less than 60 s damp sufficiently rapidly and dissipate enough energy to balance the radiative losses, whereas the fast-mode waves with periods of less than 3 s may damp at rates great enough to balance the radiative losses in active regions. In the case of magnetic coronal loops, it is observed that slow-mode waves with frequencies greater than 0.003 Hz and fast mode waves with frequencies greater than 0.28 Hz (high frequency) are needed for coronal heating and to balance the radiative losses in active regions.
Key words: magenohydrodynamics (MHD) - plasmas - Sun: corona - waves
The temperature of solar corona within 1-2  is of the order of
is of the order of
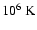 (Hassler et al. 1990; Saba & Strong 1991; Young et al. 1999). Plasma at the above-quoted temperature is bound to lose energy through optically thin emission and thermal conduction to the transition region. There must be a steady heat source to balance energy losses and to maintain the coronal temperatures. Except for transient heating mechanisms like nano-, micro-, or large flares, we can make a rough classification of steady heating mechanisms, such as hydrodynamic and magnetic ones, which are responsible for heating the corona to such a high temperature. Recent review articles on coronal heating (Narain & Ulmschneider 1990,1996; Gomez 1990; Zirker 1993) explore the various theoretical models in detail. Most of the current theories of coronal heating deal with different mechanisms to speed up dissipation (Parker 1972,1983; Heyvaerts & Priest 1983). It is accepted that Joule dissipation is a natural candidate for the energy dissipation in the solar atmosphere. Parker (1972) indicated that a large-scale magnetic field develops tangential discontinuities (current sheets) between regions of dissimilar twisting, and suggested that the Joule heating and magnetic reconnection occur at these sheets. Giovanelli (1946,1947) first recognized the importance of magnetic reconnection processes in cosmic plasma, such as in the Sun, and Dungey (1958) indicated its importance in the magnetosphere. There has been a great deal of work on magnetic reconnection in astrophysical plasma (Sweet 1958; Parker 1963,1979,1988; Petschek 1964; Priest 1985; Forbes & Priest 1987). In particular, Parker (1988) pointed out that the corona is heated by small flare-like events called "nano-flares''. Parker noted that photospheric motions result in currents in the magnetic field, and the dissipation of these currents leads to Joule heating of the plasma. The reconnection of these current sheets could result in nano-flares that heat the corona. Sturrock (1999) suggested that when two different bipoles (current elements) of opposite magnetic polarity are brought together in a network region, reconnection can occur. This reconnection event in the chromosphere leads to the generation of high frequency waves that propagate into the corona causing chromospheric and coronal heating. Based on the Doppler shift observations of UV emission lines, Bruner (1978) and Athay & White (1978) ruled out the possibility that the corona is heated by a flux of waves generated below it. It seems that magnetic reconnection events occurring within the corona are likely to develop MHD turbulence, which may be expected to generate both slow- and fast-mode waves. In the numerical simulation of line-tied magnetic reconnection, Forbes & Priest (1982) and Priest (1986) suggested that when the central current sheet in an "impulsive bursty regime'' grows too long, it becomes unstable and begins to tear and coalesce. The impulsive bursty regime exhibits a more rapid energy release in a series of bursts as the islands coalesce; it may be one possible mechanism of wave generation at reconnection sites.
(Hassler et al. 1990; Saba & Strong 1991; Young et al. 1999). Plasma at the above-quoted temperature is bound to lose energy through optically thin emission and thermal conduction to the transition region. There must be a steady heat source to balance energy losses and to maintain the coronal temperatures. Except for transient heating mechanisms like nano-, micro-, or large flares, we can make a rough classification of steady heating mechanisms, such as hydrodynamic and magnetic ones, which are responsible for heating the corona to such a high temperature. Recent review articles on coronal heating (Narain & Ulmschneider 1990,1996; Gomez 1990; Zirker 1993) explore the various theoretical models in detail. Most of the current theories of coronal heating deal with different mechanisms to speed up dissipation (Parker 1972,1983; Heyvaerts & Priest 1983). It is accepted that Joule dissipation is a natural candidate for the energy dissipation in the solar atmosphere. Parker (1972) indicated that a large-scale magnetic field develops tangential discontinuities (current sheets) between regions of dissimilar twisting, and suggested that the Joule heating and magnetic reconnection occur at these sheets. Giovanelli (1946,1947) first recognized the importance of magnetic reconnection processes in cosmic plasma, such as in the Sun, and Dungey (1958) indicated its importance in the magnetosphere. There has been a great deal of work on magnetic reconnection in astrophysical plasma (Sweet 1958; Parker 1963,1979,1988; Petschek 1964; Priest 1985; Forbes & Priest 1987). In particular, Parker (1988) pointed out that the corona is heated by small flare-like events called "nano-flares''. Parker noted that photospheric motions result in currents in the magnetic field, and the dissipation of these currents leads to Joule heating of the plasma. The reconnection of these current sheets could result in nano-flares that heat the corona. Sturrock (1999) suggested that when two different bipoles (current elements) of opposite magnetic polarity are brought together in a network region, reconnection can occur. This reconnection event in the chromosphere leads to the generation of high frequency waves that propagate into the corona causing chromospheric and coronal heating. Based on the Doppler shift observations of UV emission lines, Bruner (1978) and Athay & White (1978) ruled out the possibility that the corona is heated by a flux of waves generated below it. It seems that magnetic reconnection events occurring within the corona are likely to develop MHD turbulence, which may be expected to generate both slow- and fast-mode waves. In the numerical simulation of line-tied magnetic reconnection, Forbes & Priest (1982) and Priest (1986) suggested that when the central current sheet in an "impulsive bursty regime'' grows too long, it becomes unstable and begins to tear and coalesce. The impulsive bursty regime exhibits a more rapid energy release in a series of bursts as the islands coalesce; it may be one possible mechanism of wave generation at reconnection sites.
One can not rule out the possibility that the above-mentioned heating mechanisms are all at work simultaneously in the solar corona. The problem of MHD wave dissipation in the solar corona has been widely explored under various assumptions in different regimes of the solar corona. It is necessary to study the accumulating evidence for the presence of MHD waves in the corona. One possible way of transferring energy, apart from macroscopic mechanisms, is through microscopic mechanisms called dissipation via viscosity, resistivity, and thermal conduction. Dissipative processes cause the damping of MHD waves (e.g., Braginskii 1965). Osterbrock (1961) studied the heating of the solar chromosphere and corona by MHD waves in detail and pointed out that the upper chromosphere is mainly heated by slow-mode shocks, while the corona is probably heated by Alfvén waves. Without making any assumptions on damping, Field (1965) derived a general dispersion relation for MHD waves in the absence of viscosity. Gordon & Hollweg (1983) investigated the damping of surface waves and trapped body waves by calculating the wave properties in the absence of dissipation. They then estimated the damping lengths from these ideal MHD wave quantities. They pointed out that the surface waves are linearly compressive and dissipated by ion viscosity and electron heat conduction, so they are able to heat the corona. Ruderman (1991) investigated the viscous damping of surface waves at a magnetic interface without taking thermal conduction into account, and using a small damping approximation. Roberts (1991) showed that slow and fast magnetoacoustic surface waves propagating in a region with a sharp magnetic field gradient readily dissipate their energies by resonant absorption. Davila (1991) described the resonant absorption theory for a plasma with a turbulent magnetic field, shear viscosity, resistive dissipation, compressive viscosity, and nonlinear wave-wave interaction. Steinolfson & Davila (1993) studied the heating of a compressible, low-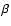 ,
and resistive plasma that is trapped in active region coronal loops by the resonant absorption of MHD waves. They concluded that the dissipation occurs primarily in a thin resonance layer, and the thickness of the layer varies with the loop density ratio. Thus, MHD waves play an important role in heating the solar corona. Braginskii (1965) estimated the damping rates of MHD waves in the weak-damping approximation and obtained the rate of energy dissipation due to Joule heating, viscosity, and thermal conduction.
,
and resistive plasma that is trapped in active region coronal loops by the resonant absorption of MHD waves. They concluded that the dissipation occurs primarily in a thin resonance layer, and the thickness of the layer varies with the loop density ratio. Thus, MHD waves play an important role in heating the solar corona. Braginskii (1965) estimated the damping rates of MHD waves in the weak-damping approximation and obtained the rate of energy dissipation due to Joule heating, viscosity, and thermal conduction.
We concentrate only on the damping of magnetoacoustic waves and ignore the Alfvén waves because Alfvén waves are incompressible and can only be damped ohmically or by shear viscosity, which in corona, are much less efficient damping mechanisms than ion-compressive viscosity and electron-thermal conduction. Moreover, Alfvén waves are described as notoriously difficult to dissipate (Hollweg 1991). Porter et al. (1994) have considered magnetoacoustic wave damping in a homogeneous plasma permeated by a uniform magnetic field. They made no assumptions about the strength of the damping. They claimed that if magnetoacoustic waves generate in the solar corona by turbulent motions at magnetic reconnection sites, the slow-mode waves can contribute to heating in active regions. Porter et al. pointed out that the fast-mode waves are also potential agents for heating the solor corona. Pekünlü et al. (2001) studied magnetoacoustic wave damping in an inhomogeneous plasma permeated by dipole-like magnetic loops. They found that if a fast magnetoacoustic wave generated from the coronal base propagates upwards into the corona, it dissipates its mechanical energy as heat. They further indicated that slow-mode waves cannot propagate in the solar corona.
Our main objective in the present study is to see the exact behaviour of dissipative MHD waves in the solar atmosphere and to examine their role in the heating of the solar corona, taking the homogeneous background magnetic field into account. We shall also examine the role of MHD waves in coronal loop heating, with the help of data provided by the NIXT mission. The assumption about a homogeneous magnetic field may be reasonable for the large region of the quiet Sun, but the active corona contains many bright loop inhomogeneous structures. Therefore, the assumption of a homogeneous magnetic field in the solar corona does not imply appropriate results in coronal heating. However, this assumption of a homogeneous magnetic field provides us with a relatively simple mathematical model with which to study the facts involved in coronal heating and the variation of the damping rate of MHD waves. Several authors (see, e.g., Zweibel 1979; Ibanez et al. 1993; Laing & Edwin 1995; Nakariakov et al. 2000; Zaqarashvili et al. 2004; Carbonell et al. 2004) used homogeneous magnetic field to study MHD waves in different regions of the solar atmosphere. The coronal heating by MHD waves with an inhomogeneous magnetic field is still an unsolved problem on which work is currently in progress.
In Sect. 2, we describe ion-compressive viscosity and electron-thermal conduction as possible damping mechanisms for MHD waves. The basic equations governing plasma motion are given in Sect. 3, and a general dispersion relation for the complex frequency as a function of the real wavenumber is also derived in this section. The solution of the dispersion relation yields wave damping rates and is presented in different approximations in Sect. 4. In Sect. 5, the dispersion relation is solved numerically and discussed to examine how wave damping depends upon plasma density, temperature, and magnetic field strength. Section 6 deals with the application of results to three types of magentic coronal loops. In Sect. 7, we briefly discuss all the results obtained.
Studies of solar coronal dynamics usually assume scalar pressure and ignore viscosity and thermal conductivity. However, there are many studies on coronal heating in which coronal viscosity and thermal conductivity play significant roles in heating. Thus, neglect of these dissipative processes may lead to misleading results. It is, therefore, important to take into account viscosity and thermal conductivity dissipative mechanisms.
Piddington (1955) calculated the Joule loss of hydromagnetic waves from the conductivity transport equation and found that it is negligible in the solar atmosphere. The effect of viscosity, which causes absorption and hence heating, has been considered by Van de Hulst (1949). The ratio of viscosity loss to Joule loss calculated by Van de Hulst is
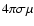 ,
which is greater than unity for solar coronal plasma, where
,
which is greater than unity for solar coronal plasma, where 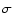 is electrical conductivity and
is electrical conductivity and 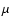 is the kinematic viscosity. He also indicated that viscous heating alone is not sufficient to maintain the coronal plasma at such a high temperature.
is the kinematic viscosity. He also indicated that viscous heating alone is not sufficient to maintain the coronal plasma at such a high temperature.
Gorden & Hollweg (1983) and Steinolfson et al. (1986) concluded that the viscous damping of coronal surface waves can heat the corona only if the magnetic field strength is of the order of a few Gauss. Steinolfson et al. (1986) also examined the viscous damping of Alfvén waves both analytically and numerically using incompressible MHD, and they determined that the viscous decay rate is always about two orders of magnitude larger than the resistive decay rate. Finally, they concluded that the viscous damping of surface waves might be capable of causing coronal heating, particularly at higher frequencies. Ruderman (1991) studied the viscous damping of MHD surface waves on a magnetic interface in a cold plasma and showed that the waves with periods less than a few tens of seconds can damp in the corona if magnetic field strength is not larger than 10 G.
De Azevedo et al. (1991) calculated the coronal loop heating rate for various possible processes and compared their results with the observed value reported by Hollweg (1985), which is of the order
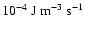 .
For the discrete Alfvén wave (DAW), the energy density rate is given by
.
For the discrete Alfvén wave (DAW), the energy density rate is given by
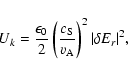 |
(1) |
and the power dissipation density rate in a steady-state situation is given by
![\begin{displaymath}%
P_k = 2I_m[\omega_k]U_k,
\end{displaymath}](/articles/aa/full/2006/27/aa4141-05/img21.gif) |
(2) |
where
![$I_m[\omega_k]$](/articles/aa/full/2006/27/aa4141-05/img22.gif) is the damping rate for the DAW due to any collisional or collisionless mechanism. The damping coefficients calculated for various possible dissipation processes, namely Joule, magnetic field diffusion, two ion species friction, cyclotron, and Chernkov effects are small since
is the damping rate for the DAW due to any collisional or collisionless mechanism. The damping coefficients calculated for various possible dissipation processes, namely Joule, magnetic field diffusion, two ion species friction, cyclotron, and Chernkov effects are small since 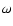
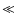
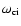 and
and 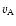

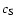 ,
where
,
where
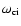 is the cyclotron frequency. To obtain the numerical value for Pk, they used the active coronal loop parameters and estimated the wave damping and the quality factor due to the viscosity:
is the cyclotron frequency. To obtain the numerical value for Pk, they used the active coronal loop parameters and estimated the wave damping and the quality factor due to the viscosity:
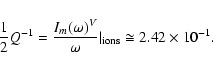 |
(3) |
Assuming that
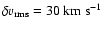 (Hollweg 1985), where
(Hollweg 1985), where
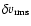 is related to the wave magnetic field by the expression
is related to the wave magnetic field by the expression
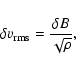 |
(4) |
and where
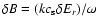 ,
De Azevedo et al. obtained the spectral energy density Uk = 4.4
,
De Azevedo et al. obtained the spectral energy density Uk = 4.4 
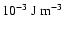 and the heating density rate Pk = 3.0
and the heating density rate Pk = 3.0 
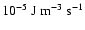 .
When they compared the heating density rate with the power density rate
.
When they compared the heating density rate with the power density rate
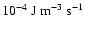 obtained by Hollweg (1985), needed to keep the coronal plasma hot, they concluded that the viscosity could be responsible for at least 30
obtained by Hollweg (1985), needed to keep the coronal plasma hot, they concluded that the viscosity could be responsible for at least 30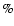 of the required coronal energy density rate.
of the required coronal energy density rate.
The relative importance of viscosity and thermal conductivity can be characterised by the relation
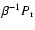 ,
where
,
where
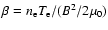 measures the relative importance of plasma pressure and magnetic pressure, and where
measures the relative importance of plasma pressure and magnetic pressure, and where
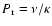 is the Prandtl number and
is the Prandtl number and 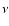 and
and 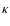 are the viscosity and thermal coefficients (Melrose 1989; Ruderman et al. 1996). In the coronal active region,
are the viscosity and thermal coefficients (Melrose 1989; Ruderman et al. 1996). In the coronal active region,
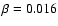 and
and
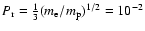 ,
so that
,
so that
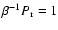 .
This implies that viscosity and thermal conductivity are of the same importance. The magnetic Prandtl number
.
This implies that viscosity and thermal conductivity are of the same importance. The magnetic Prandtl number 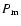 can characterise the relative importance of the viscosity and resistivity. By substituting the parameter values for an active region of the corona into
can characterise the relative importance of the viscosity and resistivity. By substituting the parameter values for an active region of the corona into
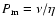 ,
Ruderman (1996) obtained
,
Ruderman (1996) obtained
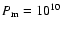 ,
where
,
where 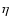 is the coefficient of resistivity. This estimate shows that dissipation caused by resistivity can be neglected in comparison to dissipation caused by viscosity. Ruderman et al. (2000) studied the damping of slow surface waves in plasma with anisotropic viscosity and thermal conductivity. They found that for typical conditions in the upper chromosphere, the damping is mainly due to resonant absorption, whereas the corresponding estimates in solar corona are quite different. They pointed out that the structure of the dissipation and damping for
realistic wave properties can be determined by compressional viscosity and parallel thermal conductivity. Moreover, Nakariakov et al. (1999) observed that loop oscillations will favour coronal heating by viscous dissipation, if the classical value of viscosity is enhanced.
is the coefficient of resistivity. This estimate shows that dissipation caused by resistivity can be neglected in comparison to dissipation caused by viscosity. Ruderman et al. (2000) studied the damping of slow surface waves in plasma with anisotropic viscosity and thermal conductivity. They found that for typical conditions in the upper chromosphere, the damping is mainly due to resonant absorption, whereas the corresponding estimates in solar corona are quite different. They pointed out that the structure of the dissipation and damping for
realistic wave properties can be determined by compressional viscosity and parallel thermal conductivity. Moreover, Nakariakov et al. (1999) observed that loop oscillations will favour coronal heating by viscous dissipation, if the classical value of viscosity is enhanced.
We present some estimations to substantiate the model for describing the wave propagation in the active region of the corona. We take the values of solar coronal parameters to be as follows:
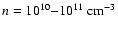 ,
T=2-3
,
T=2-3 
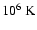 ,
and
,
and
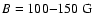 (Thomas 1993; Schmelz et al. 1992), where n, T, and B are the electron concentration, the temperature, and the magnetic field strength respectively. The scale height in the corona is of the order of 1010 cm. Plasma can be considered to be homogeneous only if the characteristic wave length is much smaller than the scale height. The wave period in the corona is equal to its wave length divided by the phase velocity. The phase velocity of MHD disturbances is approximately of the order of Alfvén velocity
(Thomas 1993; Schmelz et al. 1992), where n, T, and B are the electron concentration, the temperature, and the magnetic field strength respectively. The scale height in the corona is of the order of 1010 cm. Plasma can be considered to be homogeneous only if the characteristic wave length is much smaller than the scale height. The wave period in the corona is equal to its wave length divided by the phase velocity. The phase velocity of MHD disturbances is approximately of the order of Alfvén velocity 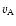 .
For
.
For
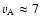
 107 cm/s, we obtain the charateristic periods of disturbances smaller than 150 s. Therefore, we consider waves with periods up to 100 s.
107 cm/s, we obtain the charateristic periods of disturbances smaller than 150 s. Therefore, we consider waves with periods up to 100 s.
Since we have
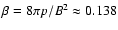 ,
where p is the pressure, the plasma may be considered low-
,
where p is the pressure, the plasma may be considered low-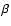 plasma or cold plasma. The ratio of energy losses due to Joule dissipation to energy losses due to viscosity is of the order of
plasma or cold plasma. The ratio of energy losses due to Joule dissipation to energy losses due to viscosity is of the order of
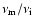 ,
where
,
where
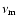 and
and
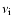 are the coefficients of magnetic and ion viscosity respectively. Estimations give
are the coefficients of magnetic and ion viscosity respectively. Estimations give
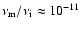 ,
so the Joule dissipation can be neglected in comparision to the ion viscosity.
,
so the Joule dissipation can be neglected in comparision to the ion viscosity.
The volumetric heating rate due to viscosity is given by (Braginskii 1965):
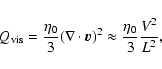 |
(5) |
where L is the characteristic length scale, V is the plasma velocity, and 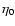 is the ion compressive viscosity coefficient.
is the ion compressive viscosity coefficient.
The volumetric heating rate due to Joule dissipation is
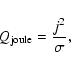 |
(6) |
where j is current density and 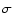 is resistivity. To estimate
is resistivity. To estimate
 ,
we take
,
we take
which, when substituted into Eq. (6) gives:
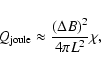 |
(7) |
where
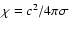 is the magnetic diffusivity and
is the magnetic diffusivity and 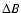 is the magnetic field change over the distance L.
is the magnetic field change over the distance L.
From Eqs. (5) and (6), we obtain
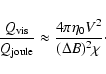 |
(8) |
Numerically,
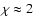

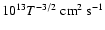 (Priest 1982), where T is the temperature. Thus we have, from Eq. (8)
(Priest 1982), where T is the temperature. Thus we have, from Eq. (8)
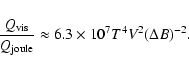 |
(9) |
For typical coronal values
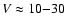 km s-1,
km s-1,
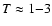

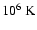 ,
and
,
and
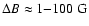 ,
we find
,
we find
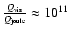 ,
that is,
,
that is,
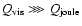 .
Thus, for coronal conditions, Joule dissipation is not significant in comparision to viscous dissipation. However, viscous heating is comparable to heating by electron heat conduction. The ratio of energy losses due to electron thermal conduction to the energy losses due to viscosity is of the order of
.
Thus, for coronal conditions, Joule dissipation is not significant in comparision to viscous dissipation. However, viscous heating is comparable to heating by electron heat conduction. The ratio of energy losses due to electron thermal conduction to the energy losses due to viscosity is of the order of
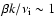 .
.
The volumetric heating rate due to electron thermal conduction is
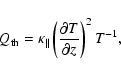 |
(10) |
where
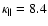
 10-7 T5/2 is the heat conductivity along the magnetic field
10-7 T5/2 is the heat conductivity along the magnetic field  .
The temperature gradient
.
The temperature gradient
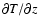 is, in general, difficult to estimate. For linear long-period waves, the temperature fluctuations can be approximately adiabatic. So,
is, in general, difficult to estimate. For linear long-period waves, the temperature fluctuations can be approximately adiabatic. So,
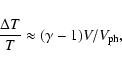 |
(11) |
where
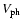 is the wave phase velocity and
is the wave phase velocity and 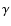 is the ratio of specific heats. Thus, we finally have
is the ratio of specific heats. Thus, we finally have
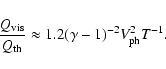 |
(12) |
If
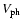 is the Alfvén speed,
is the Alfvén speed,
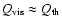 in the corona.
in the corona.
Furthermore, ion viscosity is dominated by electron viscosity by a factor of
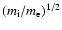 ,
while electron thermal conduction is dominated by ion thermal conduction by the same factor (Braginskii 1965). Since
,
while electron thermal conduction is dominated by ion thermal conduction by the same factor (Braginskii 1965). Since
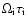
 1 in the corona, the viscous stress tensor is highly anisotropic, and compressive viscosity dominates shear viscosity by a factor of
1 in the corona, the viscous stress tensor is highly anisotropic, and compressive viscosity dominates shear viscosity by a factor of
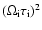 or 10 to 12 orders of magnitude. The terms associated with the four other viscosity coefficients in the viscous stress tensor will be ignored because two of them,
or 10 to 12 orders of magnitude. The terms associated with the four other viscosity coefficients in the viscous stress tensor will be ignored because two of them, 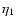 and
and 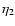 ,
are smaller than
,
are smaller than 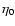 and are reduced by factors of the order of
and are reduced by factors of the order of
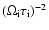 (where
(where
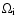 is the ion cycltron frequency and
is the ion cycltron frequency and
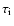 is the ion-collision time); the remaining terms
is the ion-collision time); the remaining terms 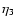 and
and 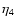 ,
are reduced from
,
are reduced from 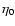 by factors of
by factors of
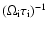 .
Similarly, the coefficient of thermal conduction along the magnetic field dominates over the perpendicular heat conduction by a factor of
.
Similarly, the coefficient of thermal conduction along the magnetic field dominates over the perpendicular heat conduction by a factor of
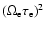 ,
where
,
where
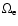 is the electron cyclotron frequency and
is the electron cyclotron frequency and
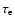 is the electron collision time. Hence, we only consider the thermal conduction parallel to the field.
is the electron collision time. Hence, we only consider the thermal conduction parallel to the field.
We consider the propagation of MHD disturbances in a homogeneous, magnetically structured, compressible, and low- 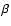 plasma. We describe the plasma dynamics by an equation of continuity (13), an equation of momentum (14), an energy Eq. (15), an equation of state (16), and an induction Eq. (17) as follows:
plasma. We describe the plasma dynamics by an equation of continuity (13), an equation of momentum (14), an energy Eq. (15), an equation of state (16), and an induction Eq. (17) as follows:
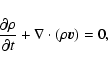 |
(13) |
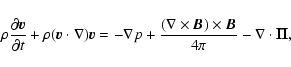 |
(14) |
![\begin{displaymath}%
\frac{D p}{Dt}-\frac{\gamma p}{\rho}\frac{D \rho}{D t}=(\gamma-1)\left[Q_{{\rm th}}+Q_{{\rm vis}}-Q_{\rm rad}\right],
\end{displaymath}](/articles/aa/full/2006/27/aa4141-05/img100.gif) |
(15) |
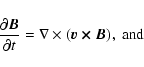 |
(16) |
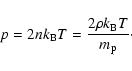 |
(17) |
Here,
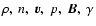 ,
and T are the total mass density, the electron number density, the velocity, the total pressure, the magnetic field vector, the ratio of specific heats and the temperature, respectively.
,
and T are the total mass density, the electron number density, the velocity, the total pressure, the magnetic field vector, the ratio of specific heats and the temperature, respectively.
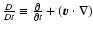 represents the material derivative for time variations.
represents the material derivative for time variations. 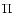 is the viscosity tensor,
is the viscosity tensor, 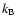 is the Boltzman constant, and
is the Boltzman constant, and 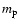 is the proton mass. In the present analysis, the effects of the coriolis force and the gravitational force on wave propagation are assumed to be negligible, and therefore are not included in the equation of motion.
is the proton mass. In the present analysis, the effects of the coriolis force and the gravitational force on wave propagation are assumed to be negligible, and therefore are not included in the equation of motion.
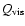 denotes the rate of viscous heating per unit volume, while
denotes the rate of viscous heating per unit volume, while
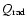 stands for the radiative loss rate per unit volume. More precisely,
stands for the radiative loss rate per unit volume. More precisely,
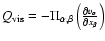 (Braginskii 1965) and
(Braginskii 1965) and
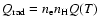 (Bray et al. 1991). Ohmic dissipation has not been taken into account, as it is insignificant for coronal conditions.
(Bray et al. 1991). Ohmic dissipation has not been taken into account, as it is insignificant for coronal conditions.
Assuming a uniform background magnetic field and homogeneous background plasma, we consider small deviations of the physical quantities of the medium from their equilibrium values as
p=p0+p1,
where the subscripts "0'' and "1'' refer to the equilibrium and perturbed quantities. The equilibrium magnetic field is considered along the z-axis, i.e.
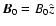 ,
and the y-axis is considered to be perpendicular to both
,
and the y-axis is considered to be perpendicular to both
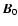 and the wave vector
and the wave vector
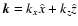 .
Linearizing Eqs. (13)-(17), we get
.
Linearizing Eqs. (13)-(17), we get
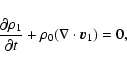 |
(19) |
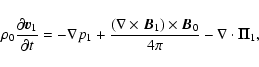 |
(20) |
![\begin{displaymath}%
\frac{\partial p_1}{\partial t}-\frac{\gamma p_0}{\rho_0}\f...
...gamma-1)\left[Q_{{\rm th}}+Q_{{\rm vis}}-Q_{{\rm rad}}\right],
\end{displaymath}](/articles/aa/full/2006/27/aa4141-05/img120.gif) |
(21) |
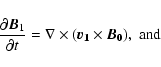 |
(22) |
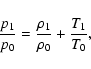 |
(23) |
where
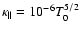 .
We then, consider the perturbations that are proportional to
.
We then, consider the perturbations that are proportional to
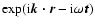 which, when inseted into Eqs. (19)-(23), gives:
which, when inseted into Eqs. (19)-(23), gives:
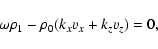 |
(24) |
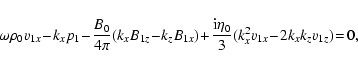 |
(25) |
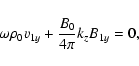 |
(26) |
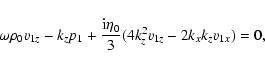 |
(27) |
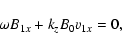 |
(28) |
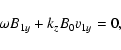 |
(29) |
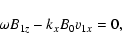 |
(30) |
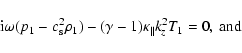 |
(31) |
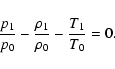 |
(32) |
Equations (26) and (29), for variables v1y and B1y, are decoupled from the rest and describe Alfvén waves. The rest of the equations, for variables
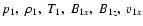 ,
and v1z, describe damped magnetoacoustic waves. Then, setting the determinant of the coefficients of the system of algebraic equations equal to zero yields the dispersion relation
,
and v1z, describe damped magnetoacoustic waves. Then, setting the determinant of the coefficients of the system of algebraic equations equal to zero yields the dispersion relation
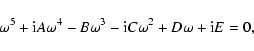 |
(33) |
where
Here, all units are considered in cgs. It should be noted that our dispersion relation (33) differs from the dispersion relations (3.6) obtained by Porter et al. (1994) and (6) obtained by Dwivedi & Pandey (2003). The calculations by Porter et al. (1994) and by Dwivedi & Pandey (2003) seem to be in error as sixth order polynomials in 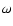 .
The dispersion relations should be fifth order polynomials in
.
The dispersion relations should be fifth order polynomials in 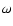 instead of sixth order polynomials, as has been shown in previous studies under certain limiting conditions (see, e.g., Carbonell et al. 2004). This fact is in agreement with the works of Carbonell et al. (2004), De Moortel et al. (2003), and Field (1965).
instead of sixth order polynomials, as has been shown in previous studies under certain limiting conditions (see, e.g., Carbonell et al. 2004). This fact is in agreement with the works of Carbonell et al. (2004), De Moortel et al. (2003), and Field (1965).
Carbonell et al. (2004) found a fifth order dispersion relation for 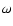 in optically thin plasma in which only thermal conduction is taken into account as a dissipative process. They found that the dispersion relation results in three wave modes, namely slow, fast, and thermal. They obtained one purely imaginary root corresponding to the thermal or condensational mode, whereas Porter et al. (1994) obtained two thermal modes. De Moortel et al. (2003) studied the damping of slow MHD waves in the solar corona with two different damping mechanisms, namely thermal conduction and compressive viscosity, and obtained a dispersion relation that is cubic in the frequency
in optically thin plasma in which only thermal conduction is taken into account as a dissipative process. They found that the dispersion relation results in three wave modes, namely slow, fast, and thermal. They obtained one purely imaginary root corresponding to the thermal or condensational mode, whereas Porter et al. (1994) obtained two thermal modes. De Moortel et al. (2003) studied the damping of slow MHD waves in the solar corona with two different damping mechanisms, namely thermal conduction and compressive viscosity, and obtained a dispersion relation that is cubic in the frequency 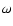 .
Their dispersion relation gives three roots in which one purely imaginary root implies a thermal mode, whereas the other roots represent the slow-mode waves. In the study of thermal instabilities, Field (1965) has shown that there is only one thermal or condensational mode corresponding to thermal conduction, whereas the other roots represents two wave modes: slow- and fast-mode waves.
.
Their dispersion relation gives three roots in which one purely imaginary root implies a thermal mode, whereas the other roots represent the slow-mode waves. In the study of thermal instabilities, Field (1965) has shown that there is only one thermal or condensational mode corresponding to thermal conduction, whereas the other roots represents two wave modes: slow- and fast-mode waves.
Thus, it can be concluded that there is only one thermal mode in the solar atmosphere, and that it is purely imaginary when viscosity and thermal conductivity are taken into account. This implies that the dispersion relation giving slow
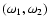 modes, fast
modes, fast
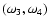 modes, and one purely imaginary thermal
modes, and one purely imaginary thermal
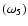 mode should be a fifth order polynomial in
mode should be a fifth order polynomial in 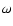 ,
even in the presence of viscosity and thermal conductivity. Hence, the sixth order dispersion relation in
,
even in the presence of viscosity and thermal conductivity. Hence, the sixth order dispersion relation in 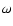 obtained by Porter et al. and implying two thermal modes seems to be in error. Moreover, the agreement of our results with the results obtained by Williams et al. (2001) justifies the accuracy of our dispersion relation (33). Equation (33) gives one purely imaginary root corresponding to the thermal or condensation mode, while the rest of the roots correspond to two modes, of which one represents the slow wave, whereas the other represents the fast wave. For each wave mode, the damping rate is given by the imaginary part of
obtained by Porter et al. and implying two thermal modes seems to be in error. Moreover, the agreement of our results with the results obtained by Williams et al. (2001) justifies the accuracy of our dispersion relation (33). Equation (33) gives one purely imaginary root corresponding to the thermal or condensation mode, while the rest of the roots correspond to two modes, of which one represents the slow wave, whereas the other represents the fast wave. For each wave mode, the damping rate is given by the imaginary part of 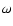 and the period of the wave is
and the period of the wave is
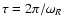 .
Since the thermal mode does not represent a propagating wave and since thermal instabilities due to this mode were already extensively studied by Field (1965), we have decided not to study this mode.
.
Since the thermal mode does not represent a propagating wave and since thermal instabilities due to this mode were already extensively studied by Field (1965), we have decided not to study this mode.
We first discuss approximate analytical expressions for the wave damping rates of slow and fast mode waves in the limit of weak damping. The expressions obtained by Braginskii (1965) are useful for explaining the dependence of the damping on the physical parameters. For the coronal condition
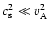 ,
where
,
where 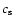 is the speed of sound and
is the speed of sound and 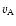 is the Alfvén speed, the slow wave represents the acoustic wave distorted by a magnetic field, and it propagates with the frequency
is the Alfvén speed, the slow wave represents the acoustic wave distorted by a magnetic field, and it propagates with the frequency
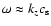 ,
where v1z is very much larger than v1x. The fast-mode wave propagates with frequency
,
where v1z is very much larger than v1x. The fast-mode wave propagates with frequency 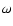 approximately equal to
approximately equal to
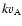 ,
where
,
where
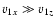 .
.
If the damping is small, the mean volumetric heating rate due to both ion viscosity and electron thermal conduction can be expressed in terms of wave quantities obtained from ideal MHD theory and can be set to be equal to the product of the mean energy density of the wave
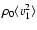 and the wave energy damping rate
and the wave energy damping rate
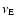 .
This yields the expression for the damping rate.
Since the energy of the wave (integrated over volume) is proportional to the square of the perturbed velocity amplitude,
.
This yields the expression for the damping rate.
Since the energy of the wave (integrated over volume) is proportional to the square of the perturbed velocity amplitude,
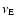 will be twice as large as the amplitude damping rate
will be twice as large as the amplitude damping rate
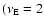 Im
Im 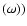 .
.
For coronal active regions, the ideal MHD expressions for the damping rate of slow- and fast-mode waves, in terms of wavenumber and frequency, were calculated by Braginskii (1965) and Porter et al. (1994). These calculations will be explained in the folowing sections.
According to have (Braginskii 1965), if the wave is dissipated only by ion viscous damping, the damping rate obtained will be
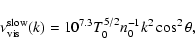 |
(34) |
or, in terms of frequency, it can be rewritten as
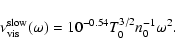 |
(35) |
The damping rate of slow-mode waves is given by Porter et al. (1994) as
![$\displaystyle %
\nu_{{\rm vis}}^{{\rm slow}}(k) \approx 10^{7.3} T_0^{5/2}n_0^{...
...t)^2 \sin^2\theta\right]}{\left[1+\left(\frac{v_{1x}}{v_{1z}}\right)^2\right]},$](/articles/aa/full/2006/27/aa4141-05/img156.gif) |
|
|
(36) |
or as a function of frequency,
![$\displaystyle %
\nu_{{\rm vis}}^{{\rm slow}}(\omega) \approx 10^{0.54} T_0^{3/2...
...os^2\theta}\right]\left[1\!+\!\left(\frac{v_{1x}}{v_{1z}}\right)^2\right]}\cdot$](/articles/aa/full/2006/27/aa4141-05/img157.gif) |
|
|
(37) |
It can be shown that, for values of
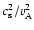 less than 0.9,
less than 0.9,
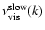 given by Eq. (36) differs slightly from that given by Eq. (34). However,
given by Eq. (36) differs slightly from that given by Eq. (34). However,
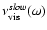 given by Eq. (37) should be replaced by Eq. (35) for values of
given by Eq. (37) should be replaced by Eq. (35) for values of
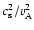 less than 0.18.
less than 0.18.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg1a.eps}\vspace*{2mm}
\includegraphics[width=8cm,clip]{4141fg1b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg162.gif) |
Figure 1:
Damping rate as a function of wavenumber for a) slow-mode waves and b) fast-mode waves, for n0= 1.0 
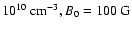 ,
and T0= 2.0 ,
and T0= 2.0 
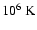 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg2a.eps}\vspace*{2mm}
\includegraphics[width=8cm,clip]{4141fg2b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg164.gif) |
Figure 2:
Damping rate as a function of wavenumber for a) slow-mode waves and b) fast-mode waves, for n0= 1.0 
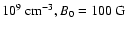 ,
and T0= 2.0 ,
and T0= 2.0 
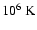 . . |
| Open with DEXTER |
The damping rate of the fast-mode wave, according to Porter et al. (1994), is
![$\displaystyle %
\nu_{{\rm vis}}^{{\rm fast}}(k) \approx 10^{7.3} T_0^{5/2}n_0^{...
...t)^2 \cos^2\theta\right]}{\left[1+\left(\frac{v_{1z}}{v_{1x}}\right)^2\right]},$](/articles/aa/full/2006/27/aa4141-05/img165.gif) |
|
|
(38) |
or as a function of frequency,
![$\displaystyle %
\nu_{{\rm vis}}^{{\rm fast}}(\omega) \approx 10^{-15.1} T_0^{5/...
...\beta \cos^2\theta}\right]\left[1+\left(\frac{v_{1z}}{v_{1x}}\right)^2\right]},$](/articles/aa/full/2006/27/aa4141-05/img166.gif) |
|
|
(39) |
whereas, the viscous damping rate of fast-mode waves given by Braginskii (1965) is
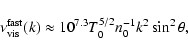 |
(40) |
or in terms of frequency,
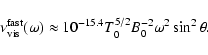 |
(41) |
Equations (38) and (39) should be used in place of Eqs. (40) and (41) when
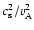 exceeds the value of about 0.02.
exceeds the value of about 0.02.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{4141fg3a.eps}\hspace*{2mm}...
...c.eps}\hspace*{2mm}
\includegraphics[width=6.8cm,clip]{4141fg3d.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg171.gif) |
Figure 3:
Damping rate as a function of wavenumber with n0=1.0 
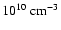 and
and
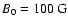 for a) slow-mode waves, b) fast-mode waves for T0=3.0
for a) slow-mode waves, b) fast-mode waves for T0=3.0 
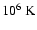 ,
c) slow-mode waves with different background temperatures, and d) fast-mode waves with different background temperatures. ,
c) slow-mode waves with different background temperatures, and d) fast-mode waves with different background temperatures. |
| Open with DEXTER |
Since the corona loses energy through optically thin emission and thermal conduction to the transition region, the minimum required damping rates for slow- and fast-mode waves to heat the corona can be determined by equating the volumetric wave heating rate to the optically thin radiative cooling rate as
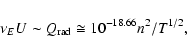 |
(42) |
where 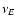 is the energy decay rate and U is the mean energy density of the wave. The wave energy damping rate
is the energy decay rate and U is the mean energy density of the wave. The wave energy damping rate 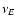 is twice the wave-amplitude damping rate, Im
is twice the wave-amplitude damping rate, Im 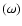 .
The mean energy density of the waves can be calculated as the product of the equilibrium mass density
.
The mean energy density of the waves can be calculated as the product of the equilibrium mass density 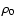 and the square of the rms velocity amplitude. We assume a rms velocity amplitude of 40 km s-1, well within the range of 25-60 km s-1 reported from coronal line-broadening observations (Saba & Strong 1991). Taking n0 = 1
and the square of the rms velocity amplitude. We assume a rms velocity amplitude of 40 km s-1, well within the range of 25-60 km s-1 reported from coronal line-broadening observations (Saba & Strong 1991). Taking n0 = 1 
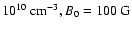 ,
and T0 = 2
,
and T0 = 2 
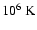 ,
we find that the required damping rate is 2.89
,
we find that the required damping rate is 2.89 
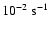 ,
which is shown by the horizontal line in Figs. 1 to 6 and is labeled as the "Required Rate Line''.
,
which is shown by the horizontal line in Figs. 1 to 6 and is labeled as the "Required Rate Line''.
We first study the solutions obtained from the dispersion relation (33) for slow- and fast-mode waves by examining different physical parameters, i.e. plasma density, temperature, magnetic field strength, and angle of propagation relative to the magnetic field. For the coronal conditions, we take n0 = 1 
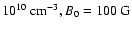 ,
and T0 = 2
,
and T0 = 2 
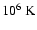 .
For each wave mode, we assign four different values to the angle of propagation relative to the magnetic field. Furthermore, to see the influence of different parameters on the damping rate of the slow and fast waves, the values of the density, the magnetic field, and the temperature are modified within a range of typical coronal conditions. The effect of viscosity and thermal conductivity are shown in Fig. 6.
.
For each wave mode, we assign four different values to the angle of propagation relative to the magnetic field. Furthermore, to see the influence of different parameters on the damping rate of the slow and fast waves, the values of the density, the magnetic field, and the temperature are modified within a range of typical coronal conditions. The effect of viscosity and thermal conductivity are shown in Fig. 6.
The dependence of the damping rate of slow- and fast-mode waves on different physical parameters is discussed below.
Figures 1a and 1b show slow and fast mode damping rates for the density n0=1 
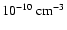 ,
the magnetic field strength of
,
the magnetic field strength of
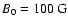 ,
and the temperature of T0=2
,
and the temperature of T0=2 
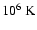 .
These figure indicate that the damping rate increases with wavenumber, as is to be expected from the analytical expressions (34) and (40).
.
These figure indicate that the damping rate increases with wavenumber, as is to be expected from the analytical expressions (34) and (40).
The damping rates for slow and fast modes are shown as a function of wavenumber in Figs. 2a and 2b by taking n0 = 1 
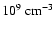 ,
,
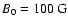 ,
and T0 = 2
,
and T0 = 2 
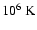 .
It can be seen from Figs. 1 and 2 that the damping rate of slow and fast modes at a fixed wavenumber decreases with the increase in density, as observed from the analytical expressions (34) and (40). Furthermore, the slow mode damping rate increases with density, depending upon the angle of propagation for wavenumbers lying in the range 6
.
It can be seen from Figs. 1 and 2 that the damping rate of slow and fast modes at a fixed wavenumber decreases with the increase in density, as observed from the analytical expressions (34) and (40). Furthermore, the slow mode damping rate increases with density, depending upon the angle of propagation for wavenumbers lying in the range 6  10-9 to 3
10-9 to 3 
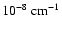 ,
whereas the damping rate of fast waves at a fixed wavenumber is expected to vary as n0-1 and always decreases with the increase in density.
,
whereas the damping rate of fast waves at a fixed wavenumber is expected to vary as n0-1 and always decreases with the increase in density.
To explain this difference, we examine how the density influences the damping rates at a fixed wavenumber when ion viscosity and electron thermal conduction are taken together and separately. Analytical theory suggests that the damping of both slow- and fast-mode waves due to ion viscosity varies inversely with density for all wavenumbers. Figures 6a and 6b show the plots of damping rate versus wavenumber for thermal conduction and viscosity, separately. It can also be observed from the Eqs. (34) and (40) that the viscous damping for slow and fast modes exhibits k2 dependence. Similarly, the thermal conduction damping for slow and fast modes also exhibits k2 dependence. However, it is interesting to note that the damping rate for slow-mode waves goes on decreasing after the wavenumber k=1.145 
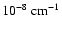 .
This indicates that the slow-mode waves with lower density (coronal condition) are capable of heating the corona.
.
This indicates that the slow-mode waves with lower density (coronal condition) are capable of heating the corona.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg4a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg4b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg181.gif) |
Figure 4:
Damping rate as a function of wavenumber with n0=1.0 
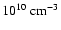 and T0=2.0
and T0=2.0 
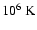 for a) fast-mode waves for
for a) fast-mode waves for
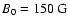 and b) fast-mode waves with different background magnetic fields.
and b) fast-mode waves with different background magnetic fields. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg5a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg5b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg182.gif) |
Figure 5:
Damping rate as a function of wavenumber with modern viscosity and thermal conductivity for a) slow-mode waves and b) fast-mode waves for n0=1.0 
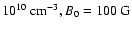 ,
and T0=2.0 ,
and T0=2.0 
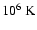 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg6a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg6b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg183.gif) |
Figure 6:
Damping rate as a function of wavenumber with viscosity and thermal conductivity for a) slow-mode waves and b) fast-mode waves for n0=1.0 
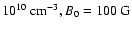 ,
and T0=2.0 ,
and T0=2.0 
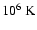 . . |
| Open with DEXTER |
Figures 3a and 3b show the variation of damping rate with wavenumber for slow and fast mode waves with n0 = 1 
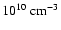 ,
,
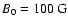 ,
and T0 = 3
,
and T0 = 3 
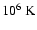 .
For both waves, the damping rate always increases very rapidly with temperature, which is fully consistent with the analytical theory. It is worth mentioning that for a fixed wavenumber, as the temperature increases by a factor of 5, the damping rate increases by a factor of about 50-60.
.
For both waves, the damping rate always increases very rapidly with temperature, which is fully consistent with the analytical theory. It is worth mentioning that for a fixed wavenumber, as the temperature increases by a factor of 5, the damping rate increases by a factor of about 50-60.
Figure 4a represents the fast mode damping rate for n0 =1.0 
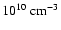 ,
,
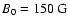 ,
and T0 = 2.0
,
and T0 = 2.0 
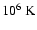 .
Figures 4a and 1b show that the damping of fast mode decreases with the increase in magnetic field strength. This fact may be justified by analytical expressions (35) and (41), which suggest that the damping of fast-mode waves varies inversely with the square of the magnetic field strength, whereas the damping of slow-mode waves does not depend upon the magnetic field. Figure 4b represents the variation of the damping rate of fast waves with wavenumbers for different background magnetic field strengths. It can be seen from Fig. 4b that the damping rate increases linearly with the wavenumber up to
.
Figures 4a and 1b show that the damping of fast mode decreases with the increase in magnetic field strength. This fact may be justified by analytical expressions (35) and (41), which suggest that the damping of fast-mode waves varies inversely with the square of the magnetic field strength, whereas the damping of slow-mode waves does not depend upon the magnetic field. Figure 4b represents the variation of the damping rate of fast waves with wavenumbers for different background magnetic field strengths. It can be seen from Fig. 4b that the damping rate increases linearly with the wavenumber up to
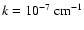 ,
and thereafter, the damping rate corresponding to a strong magnetic field goes on increasing in comparison to the damping rate corresponding to a weak magnetic field. For wavenumber k=5
,
and thereafter, the damping rate corresponding to a strong magnetic field goes on increasing in comparison to the damping rate corresponding to a weak magnetic field. For wavenumber k=5 
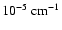 ,
the damping rates for different field strength (50 G, 100 G, and 200 G) are almost same, and thereafter, the damping rate corresponding to a strong magnetic field increases more rapidly with the wavenumber than with the weak magnetic field. It may also be observed from analytical expression (41) that the damping of fast-mode waves increases with frequency. Since wave frequency is proportional to wavenumber, the term
,
the damping rates for different field strength (50 G, 100 G, and 200 G) are almost same, and thereafter, the damping rate corresponding to a strong magnetic field increases more rapidly with the wavenumber than with the weak magnetic field. It may also be observed from analytical expression (41) that the damping of fast-mode waves increases with frequency. Since wave frequency is proportional to wavenumber, the term 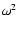 in Eq. (41) must dominate over B0-2 for a large wavenumber. It can be seen from the Figs. that for a fixed wavenumber, the damping rate of fast-mode waves decreases by a factor of 1.2 as the field strength increases by a factor of 5 to 10.
in Eq. (41) must dominate over B0-2 for a large wavenumber. It can be seen from the Figs. that for a fixed wavenumber, the damping rate of fast-mode waves decreases by a factor of 1.2 as the field strength increases by a factor of 5 to 10.
Table 1:
Parameter values for the coronal loop taken bY NIXT in cgs units.
For slow-mode waves, we find that the damping rate at a fixed wavenumber always decreases with an increase in the angle of propagation. This fact is fully justified by analytical theory because of
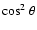 dependence in both viscous and thermal conduction damping. For fast-mode waves, the damping rate at fixed wavenumbers always increases with the angle of propagation, as is to be expected from analytical theory, due to
dependence in both viscous and thermal conduction damping. For fast-mode waves, the damping rate at fixed wavenumbers always increases with the angle of propagation, as is to be expected from analytical theory, due to
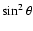 dependence in viscous damping.
dependence in viscous damping.
The recent observations from the Skylab show that the emission of X-ray wavelengths from the solar corona tends to be concentrated in certain loop-like structures. It is widely believed that these coronal loop structures correspond to magnetic flux tubes with ends rooted in the photosphere (Bray et al. 1991). A high resolution image from the NIXT rocket (Golub et al. 1990) shows that these magnetic loops are a widespread feature of the X-ray corona. The coronal portion of an active region is formed by an arcade of loops of different sizes and height, with footpoints anchored in regions of opposite magnetic polarity. In general, small compact loops have a higher temperature and a higher magnetic field strength than large compact loops.
The recent pictures of the corona taken by the NIXT telescope in the soft X-ray range offer very high spatial resolution and reveal that coronal loops are thinner than was previously thought. Data taken by NIXT is shown in Table 1. Here, we consider a coronal loop to be a static, straight plasma slab, with half-length L and thickness "a''. The coronal loop dimension is measured
from a number of X-ray pictures and lies in the ranges
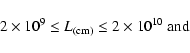
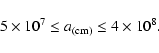
Based on the loop parameters, we can derive the minimum required damping rates for slow and fast modes to sustain the coronal loops at such high temperature and density. This can be done by equating the volumetric wave-heating rate with the optically thin radiative-cooling rate given by Eq. (42).
Table 2:
Physical parameters for three different coronal loops (the short dense loop, the intermediate loop, and the long rarefied loop).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg7a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg7b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg220.gif) |
Figure 7:
Variation of damping rate with parameter f for a) slow-mode waves and b) fast-mode waves for n0=1.0 
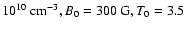 
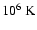 ,
and L=1.0 ,
and L=1.0 
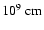 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg8a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg8b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg222.gif) |
Figure 8:
Variation of damping rate with parameter f for a) slow-mode waves and b) fast-mode waves for n0=3.0 
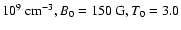 
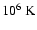 ,
and L=3.0 ,
and L=3.0 
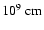 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg9a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg9b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg225.gif) |
Figure 9:
Variation of damping rate with parameter f for a) slow-mode waves and b) fast-mode waves for n0=1.0 
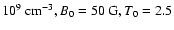 
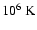 ,
and L=1.0 ,
and L=1.0 
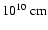 . . |
| Open with DEXTER |
In accordance with Beaüfume et al. (1992), coronal loops may be divided into three types: short dense, intermediate, and long rarefied loops. The typical parameters for each type of loop is given in Table 2. The wave periods are calculated using the formula
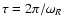 ,
and the damping rate is calculated from Eq. (42).
Columns (2)-(5) give the typical parameters for three types of coronal magnetic loops. Column (6) gives the resonant wave periods. Column (7) represents the radiative losses in coronal loops. Column (8) gives the minimum values of the required damping rate.
,
and the damping rate is calculated from Eq. (42).
Columns (2)-(5) give the typical parameters for three types of coronal magnetic loops. Column (6) gives the resonant wave periods. Column (7) represents the radiative losses in coronal loops. Column (8) gives the minimum values of the required damping rate.
We examine the results obtained in Sects. 3 and 4 for the three types of magnetic loops observed by NIXT (Golub et al. 1990) and calculate the wave periods and damping rates for these loops. To calculate the wave periods and damping rates, we make Eq. (33) dimensionless by the following transformations:
Here, L is the typical coronal loop length from the coronal base, and R is the Reynolds number.
Using the transformations described above, Eq. (33) can be written as:
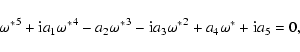 |
(43) |
where
We have numerically computed all the roots of the fifth degree polynomial in 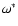 (Eq. (43)) for different values of parameter f, taking
(Eq. (43)) for different values of parameter f, taking
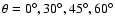 ,
and
,
and
 .
In Figs. 7-9, we have plotted damping rate (Im(
.
In Figs. 7-9, we have plotted damping rate (Im(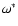 )) versus parameter f for slow- and fast-mode waves. These figure show the same pattern of variation for damping rates with f for three different loops. Figures 7a-9a show that the damping rate for slow-mode waves increases linearly with f up to a value of 5. Thereafter, it increases slowly for large values of f, whereas Figs. 7b-9b indicate that the the damping of fast-mode waves increases linearly with f, and the increasing pattern remains same for large values of f. It is also observed from all the figures that the damping of slow-mode waves is larger than the damping of fast-mode waves for any fixed value of f. It can be seen from figures that the damping of slow-mode waves decreases with the angle of propagation, whereas the damping of fast-mode waves increases with the angle of propagation.
)) versus parameter f for slow- and fast-mode waves. These figure show the same pattern of variation for damping rates with f for three different loops. Figures 7a-9a show that the damping rate for slow-mode waves increases linearly with f up to a value of 5. Thereafter, it increases slowly for large values of f, whereas Figs. 7b-9b indicate that the the damping of fast-mode waves increases linearly with f, and the increasing pattern remains same for large values of f. It is also observed from all the figures that the damping of slow-mode waves is larger than the damping of fast-mode waves for any fixed value of f. It can be seen from figures that the damping of slow-mode waves decreases with the angle of propagation, whereas the damping of fast-mode waves increases with the angle of propagation.
For short dense coronal loops, slow-mode waves attain the minimum required damping rate (0.7047 in units of
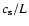 or 2.188
or 2.188 
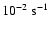 )
at wavenumbers k= 4.93
)
at wavenumbers k= 4.93 
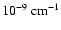 for
for
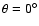 ,
k=5.69
,
k=5.69 
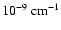 for
for
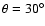 ,
k=6.988
,
k=6.988 
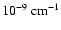 for
for
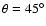 ,
and k=9.98
,
and k=9.98 
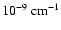 for
for
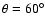 ,
whereas the fast-mode waves attain the minimum required damping rate at wavenumbers k=5.99
,
whereas the fast-mode waves attain the minimum required damping rate at wavenumbers k=5.99 
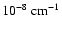 for
for
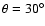 ,
k= 4.27
,
k= 4.27 
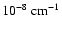 for
for
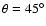 ,
k=3.527
,
k=3.527 
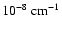 for
for
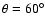 ,
and k=3.093
,
and k=3.093 
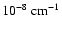 for
for
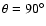 .
The frequencies of the slow- and fast-mode waves propagating in a short dense loop are calculated numerically.
For slow-mode waves, the frequency is 0.022 Hz for all angles of propagation. For fast-mode waves, the frequencies are 6.24 Hz for
.
The frequencies of the slow- and fast-mode waves propagating in a short dense loop are calculated numerically.
For slow-mode waves, the frequency is 0.022 Hz for all angles of propagation. For fast-mode waves, the frequencies are 6.24 Hz for
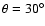 ,
4.45 Hz for
,
4.45 Hz for
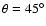 ,
3.67 Hz for
,
3.67 Hz for
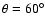 ,
and 3.3 Hz for
,
and 3.3 Hz for
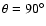 .
.
For intermediate coronal loops, the slow-mode waves attain the minimum required damping rate (0.74 in units of
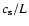 or 7.09
or 7.09 
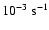 )
at wavenumbers k=1.81
)
at wavenumbers k=1.81 
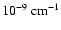 for
for
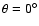 ,
k=2.09
,
k=2.09 
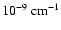 for
for
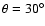 ,
k=2.56
,
k=2.56 
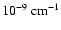 for
for
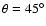 ,
and k=3.6258
,
and k=3.6258 
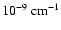 for
for
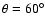 ,
whereas fast-mode waves attain the minimum required damping rate at wavenumbers k=2.262
,
whereas fast-mode waves attain the minimum required damping rate at wavenumbers k=2.262 
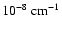 for
for
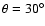 ,
k=1.614
,
k=1.614 
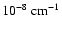 for
for
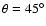 ,
k=1.333
,
k=1.333 
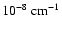 for
for
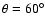 ,
and k=1.17
,
and k=1.17 
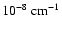 for
for
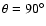 .
The frequencies of slow- and fast-mode waves that can provide adequate coronal heating are 0.0076 Hz for slow-mode waves and 2.15 Hz for
.
The frequencies of slow- and fast-mode waves that can provide adequate coronal heating are 0.0076 Hz for slow-mode waves and 2.15 Hz for
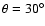 ,
1.53 Hz for
,
1.53 Hz for
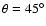 ,
1.26 Hz for
,
1.26 Hz for
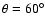 ,
and 1.11 Hz for
,
and 1.11 Hz for
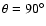 for fast-mode waves. From Figs. 7-8 it is also observed that the damping and wave periods for slow- and fast-mode waves in an intermediate loop are larger than those in a short dense loop.
for fast-mode waves. From Figs. 7-8 it is also observed that the damping and wave periods for slow- and fast-mode waves in an intermediate loop are larger than those in a short dense loop.
For long rarefied loops, the minimum required damping rate (0.9866 in units of
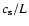 or 2.59
or 2.59 
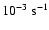 )
is obtained for slow-mode waves at wavenumbers k=7.74
)
is obtained for slow-mode waves at wavenumbers k=7.74 
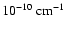 for
for
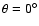 ,
k=8.95
,
k=8.95 
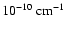 for
for
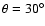 ,
k=1.095
,
k=1.095 
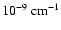 for
for
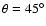 ,
and k=1.55
,
and k=1.55 
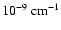 for
for
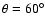 ,
whereas for fast-mode waves the minimum required damping rate is obtained at wavenumbers k=9.53
,
whereas for fast-mode waves the minimum required damping rate is obtained at wavenumbers k=9.53 
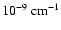 for
for
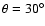 ,
k=6.84
,
k=6.84 
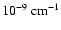 for
for
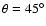 ,
k=5.737
,
k=5.737 
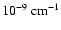 for
for
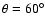 ,
and k=9.53
,
and k=9.53 
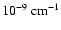 for
for
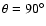 .
The frequency of slow-mode waves is 0.003 Hz; for fast-mode waves the frequencies are 0.52 Hz for
.
The frequency of slow-mode waves is 0.003 Hz; for fast-mode waves the frequencies are 0.52 Hz for
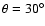 ,
0.375 Hz for
,
0.375 Hz for
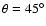 ,
0.315 Hz for
,
0.315 Hz for
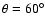 ,
and 0.28 Hz for
,
and 0.28 Hz for
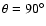 .
Figures 7-9 indicate that the damping and wave periods for slow- and fast-mode waves in long rarefied loops are much larger than those in short dense and intermediate loops.
.
Figures 7-9 indicate that the damping and wave periods for slow- and fast-mode waves in long rarefied loops are much larger than those in short dense and intermediate loops.
In this paper, we have analyzed the time damping of linear magnetoacoustic waves by the joint effect of viscosity and thermal conduction. We have also examined whether the damping of slow- and fast-mode waves can contribute significantly to the heating of the solar corona. To this end, we have numerically solved the dispersion relation for MHD waves in uniform magnetised plasma and studied the behaviour of the damping rate of slow- and fast-mode waves for different physical parameters.
The main conclusions that can be drawn from our study are as follows:
- 1.
- Our results indicate that the slow-mode waves with periods less than 40 s damp to dissipate enough energy to balance radiative losses in active regions, if one considers classical viscosity and thermal conductivity. On the other hand, if we consider modern values for viscosity and thermal conductivity, the slow-mode waves with periods of about 55 s dissipate enough energy to balance the radiative losses in active regions (Figs. 1a and 5a).
- 2.
- Fast-mode waves with very small periods of less than 0.40 s damp sufficiently to balance radiative losses, if we consider classical values for viscosity and thermal conductivity. Fast-mode waves with periods of about 3 s are enough to balance the radiative losses in active regions, if we consider the modern values for viscosity and thermal conductivity (Figs. 1b and 5b). The fast-mode waves with periods less than 0.77 s are needed in the strong field regions of the active corona to balance the raditive losses (Fig. 4).
- 3.
- We have also studied the behaviour of damping rates, wave periods, and frequencies of slow- and fast-mode waves propagating in three different loops, i.e. short dense, intermediate, and long rarefied. For short dense loops, it is observed that the slow-mode waves with periods of less than 45 s and fast-mode waves with periods of less than 0.3 s are needed to balance the radiative losses. In the cases of intermediate and long rarefied loops, the periods of slow-mode waves are 130 s and 330 s, and for fast-mode waves, the periods are less than 0.9 s and 3.5 s, respectively. Our results are nearly in agreement with Williams et al. (2001), but differ from those of Porter et al. (1994). We have shown that slow-mode waves with frequencies greater than 0.003 Hz and fast-mode waves with frequencies in excess of 0.28 Hz are needed for coronal loop heating, whereas Williams et al. have reported coronal loop oscillations with frequencies greater than 0.16 Hz.
Thus, slow- and fast-mode waves generated by MHD turbulence through magnetic reconnection events within the corona are capable of heating the solar corona. Slow-mode waves generated at such reconnection sites would damp rapidly, causing localized heating, which would lead to the evaporation of material from the chromosphere, resulting in a density enhancement along the magnetic field lines. This may be the origin of coronal loops. Since the damping of fast-mode waves increases more rapidly than that of slow-mode waves as temperature increases, it is possible that the dissipation of fast-mode waves contributes to heating of the loop, provided that the wavenumbers are low enough to damp in the presence of the magnetic field in active regions. Finally, the sixth order dispersion relations (3.6) and (6) obtained by Porter et al. (1994) and Dwivedi & Pandey (2003), respectively, are in error and should be replaced by our fifth order dispersion relation (33). This discrepancy can be quantified by solving Eqs. (13)-(32), and it leads to a modification of the results obtained by Porter et al. (1994) concerning coronal heating by MHD waves. In the case of coronal loop heating, our results nearly match those obtained by Williams et al. (2001).
Acknowledgements
We would like to thank M. S. Ruderman for helpful discussions and suggestions related to this work. P.K. thanks CSIR, New Delhi for financial support under grant No. (8/ 483(1) EMR-1). N.K. acknowledges support from IUCAA, Pune, and University Grants Commission, New Delhi.
- Athay, R. G., &
White, O. R. 1978, ApJS, 39, 333 [NASA ADS] [CrossRef] (In the text)
- Braginskii, S.
I. 1965, Rev. Plasma Phys., 1, 205 [NASA ADS] (In the text)
- Beaüfume, P.,
Coppi, B., & Golub, L. 1992, ApJ, 393, 396 [NASA ADS] [CrossRef] (In the text)
- Bray, R. J., Cram, L. E.,
Durrant, C. J., & Loughhead, R. E. 1991, Plasma Loops in the
Solar Corona (Cambridge: Cambridge Univ. Press), Chap. 5
(In the text)
- Bruner, E. C. 1978,
ApJ, 226, 1140 [NASA ADS] [CrossRef] (In the text)
- Carbonell, M.,
Oliver R., & Ballester, J. L. 2004, A&A, 415, 739 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Davila, J. M. 1991, in
Mechanisms of Chromospheric and Coronal Heating, ed. P.
Ulmschneider, E. R. Priest, & R. Rosner (Berlin:
Springer-Verlag), 464
(In the text)
- Dungey, J. W. 1958,
Cosmic Electrodynamics (Cambridge: Cambridge Univ. Press)
(In the text)
- De Azevedo, C. A., De
Assis, A. S., Shigueoka, H., & Sakanaka, P. H. 1991, Sol.
Phys., 136, 295 [NASA ADS] [CrossRef] (In the text)
- De Moortel, I., &
Hood, A. W. 2003, A&A, 408, 755 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Dwivedi, B. N., &
Pandey, V. S. 2003, Sol. Phys., 216, 59 [NASA ADS] [CrossRef] (In the text)
- Field, G. B. 1965, ApJ,
142, 531 [NASA ADS] [CrossRef] (In the text)
- Forbes, T. G.,
& Priest, E. R. 1982, Sol. Phys., 81, 303 [NASA ADS] [CrossRef] (In the text)
- Forbes, H. P.,
& Priest, E. R. 1987, Rev. Geophys., 25, 1583 [NASA ADS] (In the text)
- Giovanelli, R. G.
1946, Nature, 158, 51 (In the text)
- Giovanelli, R. G.
1947, MNRAS, 107, 338 [NASA ADS]
- Golub, L., Herant, M.,
Kalata, K., et al. 1990, Nature, 344, 842 [NASA ADS] [CrossRef] (In the text)
- Gomez, D. O. 1990, Fund.
Cosmic Phys., 14, 361 (In the text)
- Gorden, B. E., &
Hollweg, J. V. 1983, ApJ, 266, 373 [NASA ADS] [CrossRef] (In the text)
- Hassler, D. M., &
Rottman, G. J. 1990, ApJ, 348, L77 [NASA ADS] [CrossRef] (In the text)
- Heyvaerts, J.,
& Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] (In the text)
- Hollweg, J. V. 1985,
in Advances in Space Plasma Physics, ed. B. Buti (Singapore: World
Scientific), 77
(In the text)
- Hollweg, J. V.
1991, in Mechanisms of Chromospheric and Coronal Heating, ed. P.
Ulmschneider, E. R. Priest, & R. Rosner (Berlin:
Springer-Verlag), 423
(In the text)
- Ibanez, M. H., &
Escalona, O. B. 1993, ApJ, 415, 335 [NASA ADS] [CrossRef] (In the text)
- Laing, G. B., &
Edwin, P. M. 1995, 157, 103
(In the text)
- Melrose, D. B. 1989,
Instabilities in Space and Laboratory Plasma (Cambridge: Cambridge
Univ. Press)
(In the text)
- Nakariakov, V.
M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M.
1999, Science, 285, 862 [NASA ADS] [CrossRef] (In the text)
-
Nakariakov, V. M., Mendoza-Briceno, C.A., & Ibanez, M. H. 2000,
ApJ, 528, 767 [NASA ADS] [CrossRef] (In the text)
- Narain, U., &
Ulmschneider, P. 1990, Space Sci. Rev., 54, 377 [NASA ADS] (In the text)
- Narain, U., &
Ulmschneider, P. 1996, Space Sci. Rev., 75, 453 [NASA ADS] [CrossRef]
- Osterbrock, D.
E. 1961, ApJ, 134, 347 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N. 1963,
ApJS, 8, 77 [NASA ADS] (In the text)
- Parker, E. N. 1972,
ApJ, 174, 499 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N. 1979,
Cosmical Magnetic Fields (Oxford: Clarendon)
(In the text)
- Parker, E. N. 1983,
ApJ, 264, 642 [NASA ADS] [CrossRef]
- Parker, E. N. 1988,
ApJ, 330, 474 [NASA ADS] [CrossRef]
- Pekünlü, E.
R., Cakirli, Ö., & Özetken, E. 2001, MNRAS, 326,
675 [NASA ADS] [CrossRef] (In the text)
- Petschek, H. E.
1964, in The Physics of Solar Flares, ed. W. N. Hess (NASACP-50)
Washington; NASA, 425
(In the text)
- Piddington, J.
H. 1955, MNRAS, 115, 671 [NASA ADS] (In the text)
- Porter, L. J.,
Klimchuk, J. A., & Sturrock, P. A. 1994, ApJ, 435, 482 [NASA ADS] [CrossRef] (In the text)
- Priest, E. R. 1982,
Solar Magnetohydrodynamics (Reidel: Dordrecht)
(In the text)
- Priest, E. R. 1985,
Rep. Prog. Phys., 48, 955 [NASA ADS] [CrossRef] (In the text)
- Priest, E. R. 1986,
Mitt. Astron. Ges., 65, 41 [NASA ADS] (In the text)
- Roberts, B. 1991,
in Mechanisms of Chromospheric and Coronal Heating, ed. P.
Ulmschneider, E. R. Priest, & R. Rosner (Berlin:
Springer-Verlag), 494
(In the text)
- Ruderman, M. S.
1991, Sol. Phys., 131, 11 [NASA ADS] [CrossRef] (In the text)
- Ruderman, M.
S., Verwichte, E., Erdelyi, R., & Goossens, M. 1996, J. Plasma
Phys., 56, 285 (In the text)
- Ruderman, M.
S., Oliver, R., Erdelyi, E., Ballester, J. L., & Goossens, M.
2000, A&A, 354, 261 [NASA ADS] (In the text)
- Saba, J. L. R., &
Strong, K. T. 1991, ApJ, 375, 789 [NASA ADS] [CrossRef] (In the text)
- Schmelz, J. T.,
Holman, G. D., Brosius, J. W., & Gonzales, R. D. 1992, ApJ,
399, 733 [NASA ADS] [CrossRef] (In the text)
- Steinolfson,
R. S., & Davila, J. M. 1993, ApJ, 415, 354 [NASA ADS] [CrossRef] (In the text)
-
Steinolfson, R. S., Priest, E. R., Poedts, S., Nocera, L., &
Goossens, M. 1986, ApJ, 304, 526 [NASA ADS] [CrossRef] (In the text)
- Sturrock, P. A.
1999, ApJ, 521, 451 [NASA ADS] [CrossRef] (In the text)
- Sweet, P. A. 1958, in
Electromagnetic Phenomena in Cosmical Physics, ed. B. Lehnart
(Cambridge: Cambridge Univ. Press), IAU Symp., 6, 123
(In the text)
- Thomas, R. J. 1993,
BASS, 25, 3 (In the text)
- Van de Hulst, H. C. 1949,
in IUTAM and IAU Symp. 6, Problems of Cosmical Aerodynamics
(Dayton: Ohio) Paris
(In the text)
- Williams, D. R.,
Phillips, K. J. H., Rudawy, P., et al. 2001, MNRAS, 326, 428 [NASA ADS] [CrossRef] (In the text)
- Young, P. R., Klimchuk,
J. A., & Mason, H. E. 1999, A&A, 350, 286 [NASA ADS] (In the text)
- Zaqarashvili, T. V.,
Oliver, R., & Ballester, J. L. 2004, In Proc. of SOHO 13, Waves
Oscillations and Small-Scale Transient Events in the Solar
Atmosphere: A Joint View from SOHO and TRACE, Palma de Mallorca,
Spain, ESASP-547
(In the text)
- Zirker, J. B. 1993,
Sol. Phys., 148, 43 [NASA ADS] [CrossRef] (In the text)
- Zweibel, E. 1979,
Sol. Phys., 66, 305 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
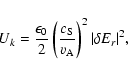
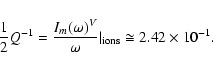
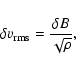
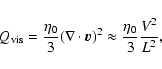
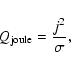
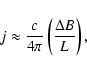
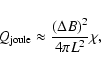
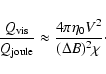
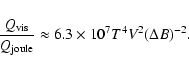
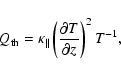
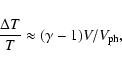
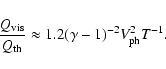
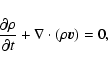
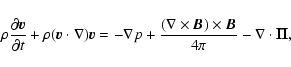
![\begin{displaymath}%
\frac{D p}{Dt}-\frac{\gamma p}{\rho}\frac{D \rho}{D t}=(\gamma-1)\left[Q_{{\rm th}}+Q_{{\rm vis}}-Q_{\rm rad}\right],
\end{displaymath}](/articles/aa/full/2006/27/aa4141-05/img100.gif)
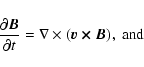
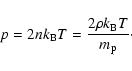
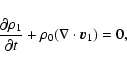
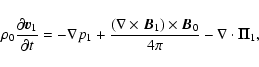
![\begin{displaymath}%
\frac{\partial p_1}{\partial t}-\frac{\gamma p_0}{\rho_0}\f...
...gamma-1)\left[Q_{{\rm th}}+Q_{{\rm vis}}-Q_{{\rm rad}}\right],
\end{displaymath}](/articles/aa/full/2006/27/aa4141-05/img120.gif)
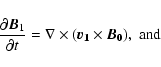
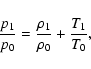
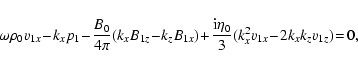
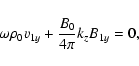
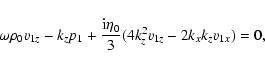
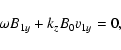
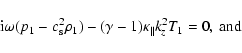
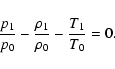
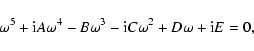
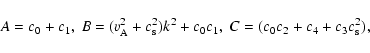
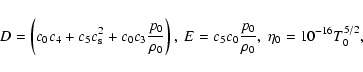
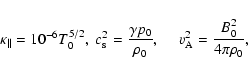
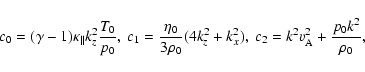
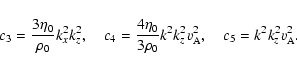
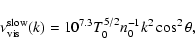
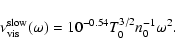
![$\displaystyle %
\nu_{{\rm vis}}^{{\rm slow}}(k) \approx 10^{7.3} T_0^{5/2}n_0^{...
...t)^2 \sin^2\theta\right]}{\left[1+\left(\frac{v_{1x}}{v_{1z}}\right)^2\right]},$](/articles/aa/full/2006/27/aa4141-05/img156.gif)
![$\displaystyle %
\nu_{{\rm vis}}^{{\rm slow}}(\omega) \approx 10^{0.54} T_0^{3/2...
...os^2\theta}\right]\left[1\!+\!\left(\frac{v_{1x}}{v_{1z}}\right)^2\right]}\cdot$](/articles/aa/full/2006/27/aa4141-05/img157.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg1a.eps}\vspace*{2mm}
\includegraphics[width=8cm,clip]{4141fg1b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg162.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg2a.eps}\vspace*{2mm}
\includegraphics[width=8cm,clip]{4141fg2b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg164.gif)
![$\displaystyle %
\nu_{{\rm vis}}^{{\rm fast}}(k) \approx 10^{7.3} T_0^{5/2}n_0^{...
...t)^2 \cos^2\theta\right]}{\left[1+\left(\frac{v_{1z}}{v_{1x}}\right)^2\right]},$](/articles/aa/full/2006/27/aa4141-05/img165.gif)
![$\displaystyle %
\nu_{{\rm vis}}^{{\rm fast}}(\omega) \approx 10^{-15.1} T_0^{5/...
...\beta \cos^2\theta}\right]\left[1+\left(\frac{v_{1z}}{v_{1x}}\right)^2\right]},$](/articles/aa/full/2006/27/aa4141-05/img166.gif)
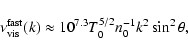
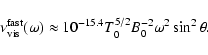
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{4141fg3a.eps}\hspace*{2mm}...
...c.eps}\hspace*{2mm}
\includegraphics[width=6.8cm,clip]{4141fg3d.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg171.gif)
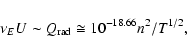
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg4a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg4b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg181.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg5a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg5b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg182.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg6a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg6b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg183.gif)
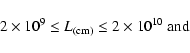
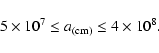
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg7a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg7b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg220.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg8a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg8b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg222.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4141fg9a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{4141fg9b.eps}\end{figure}](/articles/aa/full/2006/27/aa4141-05/Timg225.gif)