A&A 453, 729-736 (2006)
DOI: 10.1051/0004-6361:20054665

Solar bursts gyrosynchrotron emission from three-dimensional sources

P. J. A. Simões1,2 - J. E. R. Costa1,2


1 - Instituto Nacional de Pesquisas Espaciais - INPE, Av. dos Astronautas, 1758 J. da Granja 515, 12227-010 São José dos Campos SP, Brazil
2 - Centro de Rádio Astronomia e Astrofísica Mackenzie - CRAAM, Rua da Consolação, 896, Ed. Amantino Vassão, 01302 São Paulo SP, Brazil

Received 8 December 2005 / Accepted 23 February 2006

Abstract
Aims. In this study we have analyzed the spectral and spatial characteristics of gyrosynchrotron emission and the polarization of solar bursts in a highly inhomogeneous medium. Our main goal was to investigate the effects of the geometry of the source on the resulting spectrum.
Methods. The SOHO/EIT and TRACE high resolution images revealed structured magnetic configurations in detail over solar active regions. In our method, we represent the magnetic field geometry by three-dimensional structures obtained from magnetic field extrapolation, tomography, or any geometry that resembles the observed structures. The gyrosynchrotron radiation was numerically calculated through a modified version of Ramaty's code.
Results. We calculated the radiation produced by non-thermal electron distributions in this complex environment and solved the radiative transfer equation. The results, presented in brightness distribution maps, polarization maps, and spectra, are discussed. Our numerical results agree with statistical analyses of observed spectra present in the literature. We note a spectral broadening due to the spatial and intensity inhomogeneity of the magnetic field and no center-to-limb variations, which cannot be explained by homogeneous source models. The computed maps revealed a non uniform brightness distribution, with small-scale structures, and different spatial characteristics in each frequency. Also, we found different spectral characteristics at different regions of the emitting source. Polarization maps reveal its high dependence on geometry and on the position of the source on the solar disk.

Key words: Sun: flares - Sun: radio radiation - Sun: activity - Sun: magnetic fields - Sun: particle emission

1 Introduction

The theory of synchrotron radiation generated by highly relativistic electrons was first used in the interpretation of solar bursts by Takakura (1960). However, the ultra-relativistic approach was not enough to explain the solar case, in contrast to the cases of the majority of the cosmic objects (Ginzburg 1964). An extensive review of this topic was presented by Takakura (1967). The gyrosynchrotron radiation is produced by mildly relativistic electrons moving in a magnetic field, and the microwave emission from solar flares is typically generated by non-thermal electron distributions, commonly described as a power law distribution. The complete formalism for the theory of the gyrosynchrotron radiation for homogeneous sources was presented by Ramaty (1969), and has been applied since then to solar bursts.

Once solar observations had begun with high spatial resolution in diverse bands of the electromagnetic spectrum, it became evident that the solar atmosphere is highly inhomogeneous and structured by complex magnetic fields. Observations with high resolution in radio, for example with the Westerbork Synthesis Radio Telescope, WSRT (Alissandrakis & Kundu 1978), and the Very Large Array, VLA (Kundu et al. 1981), had identified brightness structures in the low corona on the order of 1''. Other works also suggest the existence of compact and complex sources (Raulin et al. 1998; Correia et al. 1995). Observations in soft and hard X-rays had shown that the bursts occur in magnetic arcs with a typical size of 10''-20'', with clear evidence of different sources, in size and position, in the several bands of photon energy. Several other works suggest the inhomogeneous nature of the explosive sources in the solar atmosphere (Lee et al. 1994; Stähli et al. 1989; Schoechlin & Magun 1979; Wiehl et al. 1985). Source models with simplified geometric configurations have been proposed to analyze the characteristics of the gyrosynchrotron radiation (Alissandrakis & Preka-Papadema 1984; Klein et al. 1986; Preka-Papadema & Alissandrakis 1988; Dulk & Dennis 1982; Petrosian 1982). In the majority of the analyses of observed events, however, homogeneous source models were used for calculating the emissions. Some exceptions are the studies presented by Nindos et al. (2000) and Kundu et al. (2001a), who both propose a simple loop geometry to define the magnetic field lines.

Solar active regions are structured by complex magnetic fields where the magnetic induction and the surrounding density vary in space. These magnetic fields play an important role in flares. First, the magnetic energy, released through magnetic reconnection, is believed to accelerate the ambient electrons; second, the magnetic field structure holds the electrons trapped in the field lines and may shape the spectrum by its magnitude and direction. Concerning this scenario, the geometric structure of the emitting sources can be an important aspect to consider while studying the dynamics of the electron population, as well as the produced radiation.

A typical scenario in the main impulsive phase of solar bursts is constituted by magnetic arcs where a fraction of the accelerated particles is trapped, while another fraction precipitates to lower regions of the solar corona. The trapped fraction gyrates around the field lines, emitting microwave radiation, and the precipitating fraction collides with the dense plasma in the lower atmosphere, emitting both X-rays by a bremsstrahlung mechanism and microwaves by gyrosynchrotron (Costa & Rosal 2005). The dynamic of the flaring electrons mainly depends on their pitch-angle distribution function (e.g. Lee & Gary 2000a) and also on the magnetic geometry (e.g. Lee et al. 2000). The anisotropic pitch-angle distributions may also affect the produced microwave spectrum, as concluded by Fleishman & Melnikov (2003). Hence, the gyrosynchrotron spectra must be formed by the contributions of regions with different physical parameters and be viewed under different angles for an observer.

In radio wavelengths, gyrosynchrotron emission is governed by the intensity and direction of the magnetic field, as well as by the density of non-thermal electrons and the extent of the source. Detailed analysis of the radiation produced in solar bursts would require a complete knowledge of the magnetic induction and geometry of the fields. The recent results of the observations in X-rays by the SXT/HXT on board Yohkoh and in extreme ultraviolet (EUV) by SOHO and TRACE instruments prove the highly complex geometry of the coronal magnetic arcs. However, magnetic induction information is mainly restricted to photospheric magnetograms obtained through the Zeeman effect in spectral lines. Coronal and chromospheric magnetic fields are commonly extrapolated using force-free models (Sakurai 1981; Amari et al. 1999; Nakagawa & Raadu 1972; Amari et al. 1997). Some techniques have been proposed to obtain the three-dimensional topology of coronal fields using the observational images of quiescent active regions (Simões & Costa 2003; Aschwanden et al. 1999b,2000). Aurass et al. (2005) have developed and applied a method of probing the magnetic field intensity and its 3D structure from fiber burst analysis and from comparison to soft X-ray and EUV loop images.

The interpretation of observed events also demands detailed calculations of the radiative transfer for the emission in radio wavelengths (which are optically thick at low frequencies). The inhomogeneity of solar burst sources must be considered in the generation of the emission, as well in the wave propagation. Calculations based on homogeneous sources are the simplest but are not the best approach for analyzing of solar events. We present in this paper the result of calculations of the gyrosynchrotron radiation produced by a population of accelerated electrons and the radiative transfer considering the three-dimensional complexity of the magnetic fields of the explosive regions. This method makes it possible to evaluate the emission and its polarization for the whole source, as well as for some specific regions, with a given spatial resolution.

2 Description of the method

In this section, we describe our method for calculating the gyrosynchrotron emission produced in three-dimensional sources. The procedure may be divided into three steps: description of the emitting source (magnetic field and ambient electron density), calculation of emission and self-absorption coefficients, and evaluation of the radiative transfer through the source.

2.1 Description of the source

Precise knowledge of coronal/chromospheric magnetic fields is unlikely to be achieved. However, this information is an input parameter, so our method does not rely on a specific technique to obtain the geometry and induction of the magnetic fields. To represent inhomogeneous sources, we defined a three-dimensional discrete space, in which a set of voxels (volume elements) defines the magnetic geometry. Each voxel, considered here as a homogeneous source, is assigned with numerical values representing magnetic induction and ambient density as a function of space, represented by its Cartesian coordinates (i,j,k). The composition of this set of voxels constitutes an inhomogeneous source with spatial variation in both magnetic field and ambient density. The ambient density is also an input parameter, and any model can be applied, such as an atmosphere in hydrostatic equilibrium. The angle $\theta$ between the observer's line of sight and a magnetic field line is found by applying the scalar product between the direction of the field in each voxel, given by a three-element vector, and the line of sight direction (k), aligned with the z-axis of the reference coordinate system.

Once the source parameters (magnetic field - B and $\theta$ - and ambient density N) that control the gyrosynchrotron emission are defined as a function of the discrete space (i,j,k), the emission and self-absorption coefficients can be computed.

2.2 Calculations of emission and self-absorption coefficients

The complete formalism of gyrosynchrotron radiation, as applied to homogeneous sources, was presented by Ramaty (1969). Current knowledge of radio burst emission is based mainly on this formalism. Since in our method each voxel is a homogeneous source, we used Ramaty's code[*] (Ramaty 1969; Ramaty et al. 1994) to calculate the emission $j_\nu$ and self-absorption $\kappa_\nu$ coefficients for the ordinary and extraordinary magneto-ionic modes. The expressions for $j_\nu$ and  $\kappa_\nu$ are given in Ramaty (1969).

The coefficients are calculated by numerical integration using the Gauss-Legendre method. Bessel functions are calculated using the IDL[*] BESELJ function and recursive relations for the derivatives. We assumed a cold and collisionless plasma permeated by a static and uniform (in each voxel) magnetic field.

As described in the previous section, each homogeneous voxel has different values for magnetic field $\vec{B}$ and ambient density N, so each voxel has different characteristics for emission and absorption.

2.3 Radiative transfer

The frequency spectrum (F) of gyrosynchrotron emission, produced by an electron distribution with a power-law energy spectrum, typically shows an optically thick part, with F rising with frequency, and an optically thin part, with Ffalling with frequency. In analysis based on homogeneous source models, it is usually assumed that the spectral maximum occurs at a frequency where $\tau \approx 1$, where $\tau$ is the optical depth of the source. When considering 3D source models, this may not be assumed so easily.

Our method for solving the radiative transfer equation is based on the assumption that the voxels are homogeneous regions, so we can use its analytical solution. It is important to note that, while each voxel is treated as a homogeneous region, the voxels are individually different from each other, having different values of magnetic field and ambient density. We also assumed that the ray paths are straight lines, since the refractive index varies slowly in space for microwave wavelengths. The voxel-volume where the field lines are defined is rotated and the coordinate system is redefined with the z-axis aligned with the line-of-sight, thus the magnetic structure becomes oriented as viewed by the observer. Once all the coefficients are calculated, these values are associated with their respective voxel (i,j,k). Using the analytical solution for a homogeneous source, the radiative transfer equation is

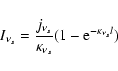\begin{displaymath}% I_{\nu_s} = \frac{j_{\nu_s}}{\kappa_{\nu_s}}(1-{\rm e}^{-\kappa_{\nu_s} l}) \end{displaymath} (1)

where $I_{\nu_s}$ is the radiation produced in the sth voxel (the index s indicates the voxel number in the line of sight, from the farthest to the nearest layer of voxels) and l is the voxel depth. This emission becomes the input of the next voxel according to

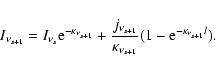\begin{displaymath}% I_{\nu_{s+1}} = I_{\nu_s} {\rm e}^{-\kappa_{\nu_{s+1}}}+ \... ...s+1}}}{\kappa_{\nu_{s+1}}}(1-{\rm e}^{-\kappa_{\nu_{s+1}} l}). \end{displaymath} (2)

This proceeds until the end of the source, i.e. the nearest layer to the observer, resulting in a bi-dimensional flux density map, considering the voxel solid angle  $\Delta\Omega$. Each column of voxels of the source volume forms a pixel in the resulting map image, after the radiative transfer calculation. The total emission (integrated in space) of the whole source can be easily obtained summing all the pixels, containing flux density values. This procedure is applied independently for the ordinary and extraordinary wave modes. The total flux and polarization maps are then obtained by the sum and subtraction of the extraordinary and ordinary emission maps, respectively.

3 Numerical results

Using the method described, we computed the gyrosynchrotron radiation produced by non-thermal electrons in an idealized three-dimensional source configuration. In order to verify the characteristics of the emission in this proposed environment, the resulting spectra were compared with the well-known characteristics of the emission from homogeneous models.

3.1 Source model

The adopted geometry of the magnetic field is an idealized set of 30 circular arcs, with a random variation of the height (values between 1 and 2 $\times $ 109), inclination ($\pm$$5^\circ$), and azimuth ($\pm$$5^\circ$) values for each arc, in relation to the local vertical, resulting in a similar configuration of the magnetic structures typically identified by EUV emission. This configuration is shown in Fig. 1.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4665fig1.eps} \end{figure} Figure 1: The adopted three-dimensional magnetic field structure: perspective view and three orthogonal projections.
Open with DEXTER

The magnetic induction B for this structure was calculated using a simple dipole approximation. The dipole parameters were chosen to set the magnetic field strength of about 1000 G at the magnetic loop feet and 100 G at the loop top. Moreover, magnetic field values as high as 2000 G have been reported for chromospheric and low coronal regions (Akhmedov et al. 1982; White et al. 1991; Shibasaki et al. 1994). Our intention here was not to model the magnetic field as accurately as possible, but rather to define a general field description, in order to investigate the geometric implications in the flare emission. Force-free field (linear or non-linear) extrapolations may be used when studying a specific flare, even to test if the extrapolation method can successfully describe the magnetic field under flare conditions.

The electron ambient density N was calculated using an exponential function with height h:

 \begin{displaymath}% N(h) = N_0 {\rm e}^{\frac{-h}{H}} \end{displaymath} (3)

where N0 is the density at the bottom layer of the source volume and H is the scale height. Usually, the scale height is treated as a function of the temperature, as in Aschwanden et al. (1999b); however, in this work, the ambient density was chosen to verify the Razin suppression, associated with the ratio of the gyro-frequency  $\nu_{\rm B}$ to the plasma frequency  $\nu_{\rm P}$ through the Razin parameter:

 \begin{displaymath}% \alpha_{\rm R} = \frac{3}{2} \nu_{\rm B} / \nu_{\rm P}. \end{displaymath} (4)

Thus, we assumed that H is an independent parameter. We evaluated the calculations for two ambient density profiles, with an exponential function with height (Eq. (3)). We set a low ambient density profile (with $N_0=10^{11}~{\rm cm}^{-3}$) and a high density profile (with $N_0=10^{12}~{\rm cm}^{-3}$), both with the same scale height H = 5 $\times $ $10^8~{\rm cm}$. In terms of the Razin parameter (Eq. (4)), the gyrosynchrotron emission from an electron of Lorentz factor $\gamma$is suppressed at low frequencies if $\alpha_{\rm R}\gamma<1$, and it is not affected if $\alpha_{\rm R}\gamma>1$ (Ramaty 1969,1968).

In this steady-state solution, we also assumed a homogeneous density of the non-thermal electrons along the magnetic arcs. For a more realistic spatial distribution of the non-thermal electrons, one must consider magnetic mirroring effects and its relation with pitch angle distributions, along with energy and pitch-angle variations due, mainly, to Coulomb collisions, requiring a time-dependent analysis. When considering these effects, isotropic pitch-angle distributions are likely to become anisotropic; electrons with small pitch angles should precipitate in the loss cone, while electrons with larger pitch angles would remain trapped longer. Moreover, initial anisotropic electrons distributions are necessary to explain the spectral evolution observed by Lee & Gary (2000a), suggesting that there are some accelerations processes that inject highly beamed electrons into the magnetic loops. This anisotropy may affect the radiation produced by these electrons. Fleishman & Melnikov (2003) conclude that anisotropic pitch-angle distributions affect the gyrosynchrotron emission produced in its intensity, polarization, and spectral index. On the other hand, the simple spatial distribution that we employed does not generate unknown effects in the produced radiation, thus the field geometry effects can be clearly noted. We will improve this analysis to include the time evolution of the non-thermal electrons, which will be presented in the near future.

The momentum distribution function of the non-thermal electrons may be separated into an energy distribution u(E) and a pitch angle distribution $g(\phi)$ (Ramaty 1969). The energy spectrum of non-thermal electrons is usually described as a power-law function:

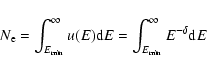\begin{displaymath}% N_{\rm e} = \int_{E_{{\rm min}}}^\infty u(E) {\rm d}E = \int_{E_{{\rm min}}}^\infty E^{-\delta} {\rm d}E \end{displaymath} (5)

where $E_{\rm min}$ is the energy lower limit. In numerical approaches, the upper limit of the integral is usually replaced for a practical limit by $E_{\rm max}$. In all our calculations, we set these limits as $E_{\rm min}=10$ keV and $E_{\rm max}=100$ MeV to avoid effects of low and high energy cutoffs in the resulting spectra (Holman 2003). We used a typical value for the energy spectral index, $\delta = 3$ (Silva et al. 2000; Stähli et al. 1989; Alissandrakis 1986; Lim et al. 1992), and $N_{\rm e}=6$ $\times $ 107 cm-3 for the non-thermal electron density, uniformly distributed along the magnetic arcs, as discussed above.

The description of the accelerated electron population dynamics in this complex magnetic environment is not an easy task. For simplicity, we assumed an isotropic pitch angle distribution $g(\phi)= 1/4\pi$, as typically done in the literature (e.g. Alissandrakis & Preka-Papadema 1984).

3.2 Spectral analysis

3.2.1 Center-to-limb variations

Gyrosynchrotron emission models based on homogeneous sources indicate some dependence of the radiation on the viewing angle $\theta$. Even in slightly inhomogeneous models, one may expect directivity effects on gyrosynchrotron spectra (Takakura & Scalise 1970). These are 1) a slight increase in the intensity with the increase of $\theta$, 2) the peak frequency shifts to higher frequencies for higher values of $\theta$, and 3) the optically thin spectral index is independent of the viewing angle $\theta$. Since microwave emission from flares is believed to be produced by the same electron population that produces hard X-ray emission, center-to-limb variations were investigated for both bands. Statistical analysis of hard X-rays flares have shown no center-to-limb variations, in low energy bands (<100 keV) (Vestrand et al. 1987; Li 1994) as well as in high energy bands (Trottet 1994). These reported results indicate that hard X-rays emission have no significant directivity; i.e., the emission characteristics do not depend on the flare's position on the solar disk. Furthermore, spectral parameters of microwave flare emission, such as optically thin spectral index, peak frequency, and flux at spectral maximum also have no directivity, as reported by Kosugi (1985), when studying flare emissions up to 17 GHz, and by Silva & Valente (2002), when covering frequencies up to 50 GHz. Thus, these observational results cannot be fully understood by homogeneous source models, which result in a $\theta$ dependence, as described above.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{4665fig2.eps} \end{figure} Figure 2: Source heliographic positions: 20$^\circ $S 0$^\circ $W (center), 20$^\circ $S 40$^\circ $W and 20$^\circ $S 80$^\circ $W (near limb). The arcs were scaled by a factor 15 larger to be visible in this figure.
Open with DEXTER

In order to examine the existence of center-to-limb variations in the emission produced in a 3D inhomogeneous source, we computed gyrosynchrotron emission in the previously described source positioned in three different locations on the solar disc: 20$^\circ $S 0$^\circ $W (center), 20$^\circ $S 40$^\circ $W, and 20$^\circ $S 80$^\circ $W (near limb), as shown in Fig. 2. We also computed the microwave emission from homogeneous sources, using these results as a reference to analyze the inhomogeneous source emission spectra, with viewing angles $\theta$ ranging from 10$^\circ $ to 80$^\circ $, in 10$^\circ $ steps. As in the inhomogeneous source, we set an isotropic pitch-angle distribution $g(\phi)= 1/4\pi$ and two ambient density values, represented by the Razin parameter  $\alpha_{\rm R}$: 3 and 0.59, for the low and high density models, respectively. The other parameters are energy spectral index $\delta = 3$, magnetic field B=500 G, energy range $E_{\rm min}-E_{\rm max}=10~{\rm keV}{-}100~{\rm MeV}$, non-thermal electron density $N_{\rm e}=6$ $\times $ $10^7~{\rm cm}^{-3}$, source depth $l=10^9~{\rm cm}$, and source solid angle  $\Omega=13''$. In Fig. 3 we plotted the spectral index, peak frequency, and peak flux as functions of the viewing angle $\theta$, for the homogeneous (continuous lines) and inhomogeneous sources. In the homogeneous case, the peak frequency and flux show high dependence on the viewing angle, while spectral index showed no dependence. In our inhomogeneous case, the spectral parameters found agreed with statistical results (Silva & Valente 2002). We interpreted this behavior as a result of the source geometry: each segment of the magnetic loops is seen by an observer with a different angle that varies from $0^\circ$ to $90^\circ$ in the same loop, reducing the spectral dependence on the source's heliographic position.


  \begin{figure} \par\includegraphics[width=7cm,clip]{4665fig3.eps} \end{figure} Figure 3: Center-to-limb variations of spectral parameters: a), b) spectral index $\alpha _{\rm thin}$, c), d) peak frequency  $\nu _{\rm peak}$, and e), f) flux density at  $\nu _{\rm peak}$. The homogeneous source model results are indicated by continuous lines and our inhomogeneous models by dash-dotted lines. The left and right columns show the results for low and high ambient density profiles, respectively.
Open with DEXTER

3.3 Spectral shape

The optically thick spectral shape is commonly interpreted based on self-absorption, Razin effect, or plasma frequency cutoff. Concerning homogeneous source models, these effects, in general, do not reflect an optically thick spectral index  $\alpha _{\rm thick}$ lower than 2 (Guidice & Castelli 1975). Observational results, however, have shown values between 0.4 and 10 (or even higher) (Stähli et al. 1989; Schoechlin & Magun 1979).

The Razin effect is believed to result in rather high spectral slopes ( $\alpha_{\rm thick}>3$), while the lower values resulting in a broader spectrum can be due to source sizes varying with frequency (Kocharov et al. 1994; Schoechlin & Magun 1979; Gary & Hurford 1990; Kucera et al. 1994; Dulk & Marsh 1982) or also caused by multiple emitting sources (Klein et al. 1986). In a statistical study, Schoechlin & Magun (1979) found a non-Gaussian distribution of optically thick spectral indices with a mean value of 1.8 $\pm$ 0.1. A histogram of the $\alpha _{\rm thick}$ values presented in Fig. 2 of Schoechlin & Magun (1979) shows two peaks: a higher peak around 1.4 and another at 2.5. Since homogeneous sources cannot produce $\alpha_{\rm thick}<2.5$, the authors associated the $\alpha_{\rm thick}<2.5$ with spatially inhomogeneous sources, which may cause the source size variation with frequency. In Table 1 we present the resulting $\alpha _{\rm thick}$ from our calculated spectra, presented in Fig. 4. Note that all values are lower than 2 for these inhomogeneous sources, which agrees with observational analysis from Schoechlin & Magun (1979) and Dulk & Marsh (1982). This spectral broadening is likely to be larger in cases where magnetic field inhomogeneity is along the line of sight.

Table 1: Spectral index $\alpha _{\rm thick}$ results.

As pointed out by Schoechlin & Magun (1979), and independently by Dulk & Marsh (1982), this spectral broadening may be due to variations in the source emitting area with frequency. In Fig. 5, we plotted the emitting area A for the calculated flux maps, and these results show the approximate relation $A \propto \nu^b$, with b between -0.9and -1.7, for our computations. This relation between source area and frequency comes from the magnetic field geometry. Compact loop systems, or more efficient electron trapping may display less variations in the emitting area. Similar spectra were observed in flares at OVSA (Lim et al. 1994; Wang et al. 1994).


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4665fig4.eps} \end{figure} Figure 4: Calculated spectra for our source models at three solar longitudes: $\rm0^\circ W$ (continuous), $\rm 40^\circ W$ (dashed), and  $\rm 80^\circ W$ (dash-dotted). a) Low ambient density source; b) high ambient density source.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4665fig5.eps} \end{figure} Figure 5: Emitting area (at half power) as a function of frequency.
Open with DEXTER

An unusual characteristic that we found when dealing with inhomogeneous sources is the effect of Razin suppression on spectral shape. We verify the importance of Razin effect on spectra through the Razin frequency (Eq. (6)), where the emission with frequency $\nu < \nu_{\rm R}$ is strongly suppressed.

 \begin{displaymath}% \nu_{\rm R} = \frac{2}{3}\frac{\nu_{\rm p}^2}{\nu_{\rm B} \sin \theta}\cdot \end{displaymath} (6)

For our source model, the Razin effect is not important for the low ambient density profile, because the highest Razin frequency found is lower than our minimum calculated frequency (2.8 GHz). For the high density profile, the Razin frequency reached higher values, up to 20 GHz in most of the source voxels. In homogeneous sources, Razin suppression affects the shape of the optically thick part of the spectrum, increasing its slope. In our source, the Razin effect has a spatial dependence, which is reflected in the whole spectrum (see Fig. 4b). The loop in the center of the solar disk had its emission suppressed mainly in the range 5 to 10 GHz, resulting in a non typical spectral shape. The $\rm 40^\circ W$ loop was also affected in a similar way, but in the range 4 to 9 GHz. The limb-loop presented a more typical spectral shape, but we found an optically thick slope of about 2, which was the steepest value found in all of our computations. From this analysis, we concluded that unusual observed spectral shapes might be due to the Razin effect, as it may affect different regions of spectrum, not only the low frequency part, as commonly inferred from homogeneous source models.

3.4 Flux density maps

Our calculated emission maps showed the same main features as those commonly seen in spatially resolved observations: lower frequencies revealed the extended sources, associated with looptop emission, and the higher frequencies revealed one or two compact emitting sources associated with footpoints (Shevgaonkar & Kundu 1985; Nindos et al. 2000; Marsh & Hurford 1980; Lee & Gary 2000b; Wang et al. 1995; Kundu et al. 1989,2001b,a; Alissandrakis et al. 1993; Nishio et al. 1997). This result also agrees with two-dimensional model computations performed by Alissandrakis & Preka-Papadema (1984) and also by Klein & Trottet (1984). In Fig. 6, emission maps for 3 GHz and 10 GHz, calculated for both ambient density profiles, are illustrated.

The maps were normalized for the maximum intensity in each map. The contours show the normalized flux at 10, 30, 50, 70, and 90% of the maximum. The 3 GHz emission comes mainly from the looptop, while the 10 GHz emission comes from the footpoint. This is due to the magnetic field values in those regions. At the limb sources, positioned as presented in Fig. 2, the eastern footpoint may overlap the western one. Nevertheless, the western emission also contributes to the total emission; for each column of volume voxels, the optical regime can be thick or thin, thus some parts of the eastern footpoint are optically thin and the western footpoint emission contributes. However, if the former is optically thick, it covers the western emission.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4665fig6.eps} \end{figure} Figure 6: Flux density maps calculated for the low density source model at center ( left) and limb ( right); the top row shows 3 GHz maps and bottom row shows 10 GHz. The contour levels are 10, 30, 50, 70, and 90% of normalized flux. The 10'' $\times $ 10'' dashed lined boxes indicate the regions taken to simulate high spatial resolution spectra. In the maps presented in this work, the north is up and west is to the right.
Open with DEXTER

The ambient density might change the emission intensity, but no significant spatial morphology is noted. Comparing the maps calculated for the two ambient density profiles, the high ambient density maps had their emission drastically reduced due to the Razin effect, as can be seen in Fig. 4. The angular resolution in this analysis is given by the resolution of the magnetic structure, and thus, by the method in which the structure is obtained. In this work, using an idealized loop system, the map resolution was chosen to be $0.25\hbox{$^{\prime\prime}$ }$.

We also simulated observations with moderate angular resolution instead of summing the entire emission map. This can be done in specific regions of desired size, even just one pixel. To illustrate this procedure, we took two 10'' $\times $ 10'' (40 $\times $ 40 pixels) boxes in each map, one centered at the looptop and the other at a footpoint. The resulting spectra for looptop and footpoint are shown in Fig. 7. For the source at the disk center, the looptop spectrum peaks at 4.8 GHz, while the footpoint spectrum peaks at 8.8 GHz. This difference arises from different effective magnetic induction values in each region. The optically thin spectral index for both spectra was found to be closer to the value found for the spectrum of the whole region, $\alpha_{\rm thin} \approx -1.5$. For the limb source, the looptop and footpoint frequency peak was 3.6 and 12.5 GHz, respectively, revealing the local magnetic field values. In this case, geometry constraints are also important: the looptop segment is seen by the observer with angles between $0^\circ$ and $20^\circ$. The gyrosynchrotron emission is much less efficient for this range of viewing angles, thus the emission is weaker. In the footpoint, the viewing angles lie between $70^\circ$ and $90^\circ$, resulting in a stronger emission. Spectral differences in separated regions of the same emitting source had been reported by Lim et al. (1994), Wang et al. (1994), and Costa & Rosal (2005). We also applied an equation derived by Costa & Rosal (2005) (Eq. (1) in their paper) that relates the peak frequency to the effective magnetic field value in those 10'' $\times $ 10'' spectra. We found mean values of $B_{\rm top}=660$ G and $B_{\rm foot}=1060$ G, which give the mirror ratio $B_{\rm foot}/B_{\rm top}=1.8$, typically found in the literature (e.g. Costa & Rosal 2005; Aschwanden et al. 1999a). Thus, the spatial variation of the magnetic intensity adopted in this work should not be considered inappropriate (1000 G in footpoints falling to 100 G in looptop) to solar burst sources.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4665fig7.eps} \end{figure} Figure 7: Looptop (continuous lines) and footpoint (dash-dotted) spectra for the low (thin lines) and high (thick) density source models at a) center and b) limb positions.
Open with DEXTER

3.5 Polarization

In the previous sections, we discussed the characteristics of total flux produced in a three-dimensional source. While the total flux is simply the sum of the emitted flux in ordinary and extraordinary modes, for the other Stokes parameters (Q, U and V) that define the emission polarization, propagation effects must be taken into account. The Faraday rotation couples the transfer equations of the four Stokes' parameters I, Q, U, and V(Pacholczyk 1977). Assuming the limit of strong Faraday rotation, these four equations can be reduced to two uncoupled ones in the intensity of the ordinary and extraordinary magneto-ionic modes (Ramaty 1969). In active regions, the intrinsic polarization, i.e. without propagation effects, will depend on the sign of the longitudinal component of the magnetic field. In our calculations, the sign of the longitudinal magnetic field component is represented in Fig. 8, as viewed by an observer. The black regions (south magnetic polarity) indicates a negative component, while gray regions (north magnetic polarity) show a positive component. One can note that the signs of the magnetic components are geometry dependent: the center source (Fig. 8, left panel) has opposite signs on each side of the loop; the limb source (right panel) has a positive component in the looptop and negative in footpoints. From the magneto-ionic theory (Ratcliffe 1959; Cohen 1960) and considering propagation with large Faraday rotation (as happens in the solar corona), the circular polarization can be evaluated considering two approximations: quasi-longitudinal (QL) and quasi-transversal (QT) cases. The QL approximation is valid when

 \begin{displaymath}% \frac{\nu^2-\nu_{\rm p}^2}{\nu \nu_{\rm B}} \gg \frac{1}{2}\frac{\sin^2\theta}{\vert\cos \theta\vert}\cdot \end{displaymath} (7)

Nevertheless, in practice, this approximation is not valid only when $\theta \approx 90^\circ$ (quasi-transversal approximation); linear polarization should appear in this case, forcing the evaluation of radiative transfer of all Stokes parameters for a correct analysis of polarization. On the other hand, in QL approximation, the circular polarization is given by $V = {\rm sign}(\cos \theta)(I_+ - I_-)$, where I+ and I-represent the intensity of the ordinary and extraordinary modes, respectively. In the QL approximation, the wave modes propagate uncoupled; i.e., the sense of polarization is preserved. Since extraordinary mode emission is usually stronger than ordinary emission (e.g. Kundu & Alissandrakis 1984; Nindos et al. 2000), we might expect right-hand circular polarization (RCP) from regions of a positive component of magnetic field, and left-hand circular polarization (LCP) from negative component regions. These results are indeed obtained, as can be seen in Fig. 9. Circular polarization maps at 3 and 10 GHz of the center and limb sources (with low ambient density) are displayed. In the center disk source (left column), the eastern side of the loop system (associated with the negative magnetic polarity) produced LCP, while the western side (positive magnetic polarity) resulted in RCP. The limb source (right column) also revealed the expected sense of polarization: positive magnetic component showed RCP (looptop) and negative component showed LCP (footpoints). Since the validity of the QL approximation (Eq. (7)) depends on ambient plasma density (plasma frequency  $\nu_{\rm p}$) and on the magnetic field (gyrofrequency  $\nu_{\rm B}$ and viewing angle $\theta$), QT regions occurred only where $\theta \approx 90^\circ$, which corresponds just to a few pixels near the dashed-line in each map (Fig. 9). Those pixels were discarded when evaluating the integrated polarization degree, without changing the final results significantly, given the few occurrences of QT pixels.


  \begin{figure} \par\includegraphics[width=7cm,clip]{4665fig8.eps} \end{figure} Figure 8: Longitudinal component of the magnetic field. Black region shows negative field and gray regions shows positive field. The dashed line indicates the QT line, where the magnetic field invert its sign.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4665fig9.eps} \end{figure} Figure 9: Circular polarization maps for 3 GHz ( top row) and 10 GHz ( bottom). The dashed contours are left-handed circular polarization (LCP), and continuous contours are right-handed circular polarization (RCP) at 10, 30, 50, 70, and 90% levels. The dashed line indicates the inversion of the circular polarization due to the inversion of the longitudinal component of the magnetic field sign.
Open with DEXTER

Nevertheless, one must be careful when studying the polarization of observed flares; the geometric structure of the magnetic field and the ambient plasma density are very difficult to infer from observations, thus the analysis of wave propagation and its effect of the sense of polarization can be even more difficult to accomplish.

As discussed before, extraordinary mode emission is expected to be stronger than the ordinary emission; however, the 3 GHz maps (top row) revealed small regions near the footpoints with an opposite sense of the expected polarization. As mode coupling was not considered in our computations, the ordinary mode is stronger in those regions than extraordinary mode. This is more likely to occur when optical depth ( $\kappa_\nu l$) is large (e.g. Nindos et al. 2000).


  \begin{figure} \par\includegraphics[width=5.5cm,clip]{4665fig10.eps} \end{figure} Figure 10: Polarization degree (RCP - LCP) of the whole source. The polarization for the three source positions are shown for the low ambient density model.
Open with DEXTER

In Fig. 10, the polarization degree (RCP - LCP) of the emitting sources were computed by summing up all the pixels in polarization maps. We can note that the source at the disk center appears practically unpolarized. When summing the opposite senses of polarization on each side of the loop, given the adopted symmetric geometry, the difference is almost null. At the other positions ( $\rm 40^\circ W$ and  $\rm 80^\circ W$), the lower frequencies produced mainly at looptop (viewed as a positive magnetic field) show right-handed polarization. The higher frequencies coming from loop legs and footpoint sources, which are seen as a negative magnetic field, reveal a higher degree of left-handed circular polarization. The observed polarization shows a high dependence on magnetic field geometry/polarity and also on source heliographic position. Moreover, we would like to point out that, in the high ambient density cases, the QL approximation (Eq. (7)) was not valid for a wider range of $\theta$ values, thus larger areas of the source require the radiative transfer solution for each Stokes parameter and for their coupling, while propagating through a 3D source. This complete solution was not implemented in this work, given the complexity of evaluating the four transfer equations of the Stokes' parameters and the changes in the polarization by mode coupling. When waves propagate through a QT region, the sense of polarization reverses if the modes are weakly coupled; however, if they are strongly coupled, the polarization is unchanged. In fact, it is also necessary to identify if the waves are generated or just propagate in a QT region, since the polarization effects will be different for each case (Cohen 1960).

4 Summary

We have presented the computational results of gyrosynchrotron emission produced in a three-dimensional source. The source structure is given by the magnetic field geometry; our method does not impose any reconstruction or modeling technique to describe the magnetic field, so that force-free field extrapolation from photospheric magnetograms, tomographic reconstructions, or even idealized models can be applied. The numerical results can be expressed by emission spectra (with any desired spectral resolution), intensity and polarization maps (angular resolution is limited by the magnetic field structure knowledge), after the solution of the radiative transfer through the source.

Our results reveal that geometric aspects of the source play an important role in the spectral shape and in the observed polarization. Analyzing center-to-limb variations, our results agree with statistical studies (Silva & Valente 2002), which had found no directivity in observed solar microwave bursts. This lack of directivity could not be explained from homogeneous source models. We also found agreement with the spectral broadening that is typically reported (e.g. Schoechlin & Magun 1979). Our conclusion on spectral broadening, reinforcing other authors' findings (Klein & Trottet 1984; Takakura 1972; Dulk & Marsh 1982), is caused by the inhomogeneity of the magnetic field, but also by the field geometry, only revealed by including the radiative transfer in the calculations.

The spatial morphology of the emission evidently has a relation to the magnetic field geometry; nevertheless, this emission morphology, for each frequency, will also be governed by magnetic field intensity and, less important, by ambient density. It is important to note, however, that direct comparisons to observations must be made with care, since in this analysis, we applied a simple spatial distribution of the non-thermal electrons in the flaring loops. Time-dependent analysis is required to better evaluate the electron spatial distribution along the loops.

The observed polarization from solar bursts, in addition to photospheric magnetograms and optical data from active regions, may give some clues to the magnetic field geometry. Mode coupling of the magneto-ionic modes, governed by weak Faraday rotation, might change the polarization in wave propagation through the source and above, and it is usually evoked to (qualitatively) explain unusual observed polarization maps (e.g. Nindos et al. 2000). If the quasi-longitudinal approximation is valid, mode coupling should not occur in radio wavelengths (Cohen 1960). Thus, the sense of the intrinsic polarization is preserved.

In quasi-transversal propagation, especially when ambient density and magnetic field intensity are both low, as in the high solar corona, the sense of polarization might change; thus, polarization should be analyzed carefully. From the analysis presented here, we conclude that the geometric aspects of the emitting source should be considered for a better diagnostic of the physical properties of the source and of the accelerated particles.

Acknowledgements
We thank the anonymous referee for the interesting suggestions and corrections. P. J. A. Simões would also like to thank FAPESP for supporting this work, under process No. 03/01406-6.

References

 
Copyright ESO 2006