A&A 453, 219-227 (2006)
DOI: 10.1051/0004-6361:20054370
The ZZ Ceti star G 185-32: new insight from asteroseismology
D. Pech - G. Vauclair
Université Paul-Sabatier, Observatoire Midi-Pyrénées, CNRS/UMR5572, 14 Av. Edouard Belin, 31400 Toulouse, France
Received 18 October 2005 / Accepted 29 January 2006
Abstract
One of the brightest pulsating DA white dwarfs (ZZ Ceti stars), G 185-32, shows 19 periods in its power spectrum, from 71 s to 651 s. Its short periods are among the shortest ones observed in a ZZ Ceti star.
The one at 141.9 s shows an amplitude which does not vary with wavelength, in contrast with what the linear theory predicts for  or
or  non-radial g-modes. The mass and
non-radial g-modes. The mass and
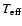 of G 185-32
are well constrained by spectroscopic observations and parallax measurement.
The aim of the present paper is to take advantage of this rich observational background to derive the fundamental parameters of the star
from asteroseismology.
We computed a grid of realistic models for G 185-32 and the periods of their
adiabatic
of G 185-32
are well constrained by spectroscopic observations and parallax measurement.
The aim of the present paper is to take advantage of this rich observational background to derive the fundamental parameters of the star
from asteroseismology.
We computed a grid of realistic models for G 185-32 and the periods of their
adiabatic  and
and  non-radial g-modes.
We determined the model which fits best the observations.
We identify 14 periods as real modes and determine their
non-radial g-modes.
We determined the model which fits best the observations.
We identify 14 periods as real modes and determine their  ,
k, and m values. We show that the remaining 5 periods are linear combinations.We find
that G 185-32 oscillates mostly according to
,
k, and m values. We show that the remaining 5 periods are linear combinations.We find
that G 185-32 oscillates mostly according to  modes.
We present a new hypothesis to account for the peculiar behaviour of
the 141.9 s mode's amplitude and suggest that it is a true mode interfering with higher
modes.
We present a new hypothesis to account for the peculiar behaviour of
the 141.9 s mode's amplitude and suggest that it is a true mode interfering with higher  degree modes, involving a possible triplet resonance.
We determine the main parameters of G 185-32: its total mass
M*=0.638 (
degree modes, involving a possible triplet resonance.
We determine the main parameters of G 185-32: its total mass
M*=0.638 (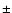 0.007)
0.007) 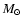 ,
its hydrogen mass fraction
,
its hydrogen mass fraction
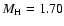 (
(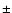 0.10)
0.10)
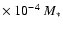 ,
which implies a helium mass fraction of
,
which implies a helium mass fraction of 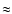 10-2 M*, its
10-2 M*, its
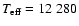 (
(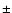 )80 K,
and estimate its rotation period to be 14.5 h.
)80 K,
and estimate its rotation period to be 14.5 h.
Key words: stars: fundamental parameters - stars: white dwarfs - stars: oscillations - stars: individul: ZZ Ceti G 185-32
The DA white dwarf G 185-32 (PY Vul or WD1935+279) was discovered to pulsate as a ZZ Ceti star by Mc Graw et al. (1981). It is
one of the brightest known ZZ Ceti stars (V=12.97 mag), and it exhibits many low-amplitude pulsation frequencies,
making the star a good candidate for a detailed asteroseismological analysis.
Bergeron et al. (1995, 2004)
determined its full mass and effective temperature of
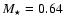 (
(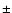 0.03)
0.03) 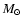 and
and
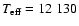 (
(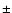 200) K, from high resolution, high signal/noise spectroscopy and from a model atmosphere using the
ML2 version of the mixing length theory with
200) K, from high resolution, high signal/noise spectroscopy and from a model atmosphere using the
ML2 version of the mixing length theory with
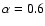 .
This
.
This
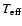 places G 185-32 close to the blue edge
of the ZZ Ceti instability strip.
places G 185-32 close to the blue edge
of the ZZ Ceti instability strip.
Photometric observations of G 185-32 were obtained during the 1992 Whole Earth Telescope (WET, Nather et al.
1990) campaign XCOV8
(photometry in the visible wavelength range) and by Kepler et al. (2000) with the
HST Faint Object Camera (UV and far blue photometry). From these observations, 19 periodicities have been detected between 71 s and 651 s.
With periods as short as 70 s, G185-32 is
the shortest-period ZZ Ceti pulsator confirmed so far![[*]](/icons/foot_motif.gif) .
In addition, time-resolved spectroscopy has been obtained
by Thomson et al. (2004) with one Keck telescope.
.
In addition, time-resolved spectroscopy has been obtained
by Thomson et al. (2004) with one Keck telescope.
Castanheira et al. (2004, hereafter CKM) present a preliminary study of G 185-32 based on the
WET and HST observations. They tried to discriminate the true pulsation modes from their linear combinations.
They also proposed an identification of the spherical degree,  ,
for most of the observed periods by using their amplitude variation with wavelength as predicted by linear
theory for
,
for most of the observed periods by using their amplitude variation with wavelength as predicted by linear
theory for  and
and  non-radial g-modes. The power spectrum of G 185-32 shows one puzzling
period at 141.9 s whose amplitude does not increase toward the UV
contrarily to what is predicted for g-modes pulsation of degree
non-radial g-modes. The power spectrum of G 185-32 shows one puzzling
period at 141.9 s whose amplitude does not increase toward the UV
contrarily to what is predicted for g-modes pulsation of degree  or
or  (Robinson et al. 1982, 1995; Kepler 1984).
As a consequence, they conclude that it should be a false mode, probably the subharmonic of the 70.9 s period.
Accordingly, this suggestion implies that the 70.9 s is a real mode, so their study relies on the assumption
that it is the
(Robinson et al. 1982, 1995; Kepler 1984).
As a consequence, they conclude that it should be a false mode, probably the subharmonic of the 70.9 s period.
Accordingly, this suggestion implies that the 70.9 s is a real mode, so their study relies on the assumption
that it is the  ,
k=1 mode.
Thompson et al. (2004) propose a different hypothesis for the peculiar behaviour of the 141.9 s period. They
suggest that it could be an
,
k=1 mode.
Thompson et al. (2004) propose a different hypothesis for the peculiar behaviour of the 141.9 s period. They
suggest that it could be an 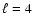 mode whose amplitude is predicted as not changing significantly with wavelength.
mode whose amplitude is predicted as not changing significantly with wavelength.
These interpretations of the observational data do not use any model computations. Such a modelling
is the next step in checking whether one model, or set of models, could realistically fit the observed frequencies. It is
also useful when trying to recognize true pulsation modes from their linear combinations, since such linear combinations
might actually be genuine modes involved in true resonances.
In addition, they did not consider
the rotational splitting effect and thus did not take the impact of stellar rotation on the observed modes into account.
This context strongly motivated us to undertake an independent study following a different approach,
preferably based on modelling. This is the next step in deciphering
the power spectrum of G 185-32 and trying to derive its fundamental parameters.
In Sect. 2, we summarize the main observational data on G 185-32. In Sect. 3, we discuss our
strategy for modelling the star and obtaining a best-fitting model. In Sect. 4 we present a first identification of the degree
 and order kof the observed modes and discuss the cases of the ambiguous frequencies; for each of them, we find out whether they are
a linear combination or a true mode. Section 5 introduces the effect of the rotational splitting that enables us
to complete the
modes identification with the azimuthal number m. In Sect. 6, we discuss our identifications and focus on the
case of the mysterious 141.9 s period for which we present a new hypothesis. Section 7 summarizes our work.
and order kof the observed modes and discuss the cases of the ambiguous frequencies; for each of them, we find out whether they are
a linear combination or a true mode. Section 5 introduces the effect of the rotational splitting that enables us
to complete the
modes identification with the azimuthal number m. In Sect. 6, we discuss our identifications and focus on the
case of the mysterious 141.9 s period for which we present a new hypothesis. Section 7 summarizes our work.
The available data on G 185-32 are described in CKM. Table 1 lists the 19 significant periods
detected in its power spectrum, following their analysis. The question mark indicates periods that
were marginally detected, either in the WET or in the HST data sets, or, in the case of the 285.1 s period, was
only detected by Thomson et al. (2004).
The exclamation mark indicates frequencies that are implied in a linear
combination (or a true resonance), so that their identification as real modes is doubtful.
The asterisk outlines the enigmatic 141.9 s period whose
amplitude remains constant with wavelength.
A first examination of Table 1 suggests that the G 185-32 pulsation spectrum seems to exhibit partial multiplets.
That is the case for the pairs of periods: 299.8 s-301.4 s; 264.2 s-266.2 s, and the potential triplet 72.5 s-72.9 s-70.9 s. Those groups
have periods that are close enough to be considered a priori as members of the same multiplet generated by rotational or magnetic splitting.
Let us consider the case of the magnetic splitting first. Since the expected frequency shift is proportional to m2, the ratio of the frequency differences between
the m=2 and the m=1 components and the m=1 and the m=0 components should be 4, if this triplet corresponds to the m=0, 1, 2 components of an  mode.
The observed ratio is
mode.
The observed ratio is
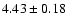 from the WET data, where we use the frequency resolution of the WET campaign as an upper limit to the frequency
uncertainty. This is close enough to the expected value of 4 to make the assumption of magnetic splitting appealing. However, according to Jones et al. (1989)
a magnetic field largely in excess of 105 G would be required in order to reproduce the observed frequency shift of 70
from the WET data, where we use the frequency resolution of the WET campaign as an upper limit to the frequency
uncertainty. This is close enough to the expected value of 4 to make the assumption of magnetic splitting appealing. However, according to Jones et al. (1989)
a magnetic field largely in excess of 105 G would be required in order to reproduce the observed frequency shift of 70 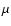 Hz between the presumed m=0 and m=1components with periods 72.9 s and 72.5 s. Since Schmidt & Smith (1995) reported only an upper limit of
Hz between the presumed m=0 and m=1components with periods 72.9 s and 72.5 s. Since Schmidt & Smith (1995) reported only an upper limit of
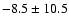 kG for the magnetic field of G 185-32, one
can safely reject the magnetic splitting as being responsible for the observed multiplets. We conclude that the observed multiplets are the components of modes
split by rotation.
kG for the magnetic field of G 185-32, one
can safely reject the magnetic splitting as being responsible for the observed multiplets. We conclude that the observed multiplets are the components of modes
split by rotation.
Table 1:
Observed periods in G 185-32.
Pech et al. (2006, hereafter PVD), show in the case of HL Tau 76 how far it was possible to constrain
the internal structure of a ZZ Ceti star from asteroseismology. The chosen method relies on building
a grid of static models and comparing the observed modes with
the synthetic spectrum computed for each of them.
The grid of models was built in a 3-dimensional parameter space by varying the total mass, the fractional mass of the hydrogen layer, and the effective
temperature. The fractional mass of the helium layer was constrained by the mass of the hydrogen layer, on one hand, and by considerations of the
absence of observed carbon in the spectra of ZZ Ceti stars on the other. A similar grid of models was built for the purpose of the present paper
in the range of parameters suitable for
G 185-32.
The strategy used to constrain the model of HL Tau 76 was based on an
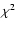 test that selects the model that fits best the observations. The strength
of this method is to take all the observed modes into account, after removal of the linear combinations.
Its efficiency depends on the richness of the observed spectrum.
Its weakness, however, is to be sensitive to a preliminary identification of the modes according to their
test that selects the model that fits best the observations. The strength
of this method is to take all the observed modes into account, after removal of the linear combinations.
Its efficiency depends on the richness of the observed spectrum.
Its weakness, however, is to be sensitive to a preliminary identification of the modes according to their
 degree.
Actually, if the identification of
degree.
Actually, if the identification of  is uncertain for many modes, the
is uncertain for many modes, the 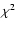 algorithm may link computed and
observed modes of different degrees and result in a wrong-fitting model. However, if the star exhibits a large enough
number of
modes, some errors in the preliminary determination of
algorithm may link computed and
observed modes of different degrees and result in a wrong-fitting model. However, if the star exhibits a large enough
number of
modes, some errors in the preliminary determination of  (due to observational uncertainties) do not threaten
the reliability of the deduced best-fit model. That was the case for the cool ZZ Ceti star HL Tau 76 (PVD), which exhibits
as much as
(due to observational uncertainties) do not threaten
the reliability of the deduced best-fit model. That was the case for the cool ZZ Ceti star HL Tau 76 (PVD), which exhibits
as much as 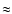 40 independent modes (Dolez et al. 2006).
In the case of G 185-32, a smaller amount of periods (19) is available, making the
40 independent modes (Dolez et al. 2006).
In the case of G 185-32, a smaller amount of periods (19) is available, making the
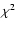 method risky. It is even more so, since some of them (at least three) are suspected to be
false modes involved in linear combinations. That is why we decided to use another strategy.
method risky. It is even more so, since some of them (at least three) are suspected to be
false modes involved in linear combinations. That is why we decided to use another strategy.
The first step is to consider a reference mode with a secure identification in the frequency spectrum.
It has to be selected among the shortest periods
since there are those which constrain the model more unambiguously.
There are actually 3 periods to choose from 70.9 s, 72.5 s, and 72.9 s. The 72.5 s-72.9 s pairs could be considered at
this stage as two possible components of a multiplet. The status of the 70.9 s is ambiguous, since it could be a true mode or
the first harmonics of the 141.9 s period.
For this reason, we did not take it as our reference mode, in contrast to CKM,
but chose the shortest period of the pair at 72.5 s.
The visibility
of a mode of a given  degree decreases rapidly with increasing values of
degree decreases rapidly with increasing values of  and depends on the inclination angle of the pulsation axis of symmetry on the
line of sight (see for instance Dziembowski 1977; Robinson et al. 1982; Brassard et al. 1995).
Brassard et al. (1995) have computed the expected visibility of pulsation modes of degree
and depends on the inclination angle of the pulsation axis of symmetry on the
line of sight (see for instance Dziembowski 1977; Robinson et al. 1982; Brassard et al. 1995).
Brassard et al. (1995) have computed the expected visibility of pulsation modes of degree 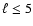 for ZZ Ceti stars through
various photometric bandpasses. They show that for the typical white light WET photometry, the visibility of
for ZZ Ceti stars through
various photometric bandpasses. They show that for the typical white light WET photometry, the visibility of 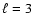 modes relative to
modes relative to  modes
is reduced by a factor
modes
is reduced by a factor
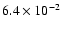 by taking into account the geometrical cancellation effect resulting from the integration on the stellar disk
of the Legendre polynomial associated to the spherical harmonics and assuming that all the modes of various
by taking into account the geometrical cancellation effect resulting from the integration on the stellar disk
of the Legendre polynomial associated to the spherical harmonics and assuming that all the modes of various  values have the same intrinsic amplitudes.
The
values have the same intrinsic amplitudes.
The 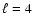 modes' visibility is reduced even more by a factor
modes' visibility is reduced even more by a factor
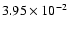 .
As a result it is generally admitted that modes with degrees
.
As a result it is generally admitted that modes with degrees
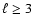 are unlikely to be observed. Thus, the expected value for the degree of the modes corresponding to the periods at 72.9 s, 72.5 s, or 70.9 s should be either
are unlikely to be observed. Thus, the expected value for the degree of the modes corresponding to the periods at 72.9 s, 72.5 s, or 70.9 s should be either
 or
or  .
Identifying these periods either as
.
Identifying these periods either as  ,
,
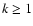 or as
or as  ,
,
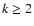 would
imply a mass of G 185-32
close to the Chandrashekar limit, which strongly disagrees with the mass of
would
imply a mass of G 185-32
close to the Chandrashekar limit, which strongly disagrees with the mass of
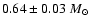 deduced from spectroscopy (Bergeron et al.
1995, 2004).
As a consequence, our reference period of 72.5 s is necessarily the
deduced from spectroscopy (Bergeron et al.
1995, 2004).
As a consequence, our reference period of 72.5 s is necessarily the  ,
k=1 mode. Modelling will confirm this assertion later.
We checked whether the 70.9 s could, however, be an
,
k=1 mode. Modelling will confirm this assertion later.
We checked whether the 70.9 s could, however, be an 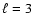 mode. Note that it would imply that it should have an intrinsic amplitude at the stellar surface
that is at least 15 times larger than the
mode. Note that it would imply that it should have an intrinsic amplitude at the stellar surface
that is at least 15 times larger than the  modes in order to exhibit a comparable, observed amplitude. We think that this is quite unlikely, but
as the intrinsic amplitudes at the stellar surface are unknown,
we cannot formally disprove such a possibility. We extended our grid of models to find what should the stellar mass be, in order to have its
modes in order to exhibit a comparable, observed amplitude. We think that this is quite unlikely, but
as the intrinsic amplitudes at the stellar surface are unknown,
we cannot formally disprove such a possibility. We extended our grid of models to find what should the stellar mass be, in order to have its 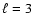 ,
k=1, or k=2mode with a 70.9 s period. We found 0.5
,
k=1, or k=2mode with a 70.9 s period. We found 0.5 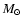 for the case k=1 and a mass in excess of 0.9
for the case k=1 and a mass in excess of 0.9 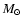 in the case k=2. Both masses are far outside
the range of mass allowed by spectroscopy.
We conclude that the 70.9 s is not an
in the case k=2. Both masses are far outside
the range of mass allowed by spectroscopy.
We conclude that the 70.9 s is not an 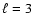 mode on an asteroseismology basis.
mode on an asteroseismology basis.
In their paper, CKM also conclude that the shortest period observed in G 185-32 has to be the  ,
k=1 mode
and identified this mode as the 70.9 s period. In the next sections, we alternatively explore the possibility of accounting
for the period distribution observed in G 185-32 by identifying the 72.5 s with this mode.
,
k=1 mode
and identified this mode as the 70.9 s period. In the next sections, we alternatively explore the possibility of accounting
for the period distribution observed in G 185-32 by identifying the 72.5 s with this mode.
Once the reference mode is selected, the goal was to search for potential solutions in the
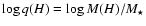 vs.
vs.
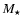 plane, where M(H) is the mass of the hydrogen outer layers. Our method consists in determining
a series of couples (
plane, where M(H) is the mass of the hydrogen outer layers. Our method consists in determining
a series of couples (
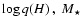 )
for which the resulting model
presents the
)
for which the resulting model
presents the  ,
k=1 mode with a period of 72.5 s (
,
k=1 mode with a period of 72.5 s (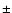 0.7 s), i.e. within an allowed 1% uncertainty.
Our model grid scanned the whole range of total mass allowed by spectroscopy (i.e. from 0.61
0.7 s), i.e. within an allowed 1% uncertainty.
Our model grid scanned the whole range of total mass allowed by spectroscopy (i.e. from 0.61 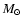 up to
0.67
up to
0.67 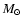 ). Then, the hydrogen mass fraction for each model was adjusted
so as to obtain the right period for the
). Then, the hydrogen mass fraction for each model was adjusted
so as to obtain the right period for the  ,
k=1 mode.
,
k=1 mode.
Our model grid is built as described in PVD. They are static models with
a pure, degenerate carbon core.
Convection in the outer H/He layers is computed according to the ML2 version of the mixing
length theory with
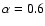 .
The remaining free parameters were kept constant because they do not influence the
fundamental (
.
The remaining free parameters were kept constant because they do not influence the
fundamental ( ,
k=1) mode enough to alter its period noticeably.
Brassard et al.
(1992) showed that the periods of pulsation are almost insensitive to the helium mass fraction.
Thus this parameter was kept constant at
,
k=1) mode enough to alter its period noticeably.
Brassard et al.
(1992) showed that the periods of pulsation are almost insensitive to the helium mass fraction.
Thus this parameter was kept constant at
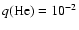 .
The input parameters for the model calculations are the total mass of the white dwarf, the hydrogen and helium fractional masses, and the luminosity. The other
global parameters are derived from the model calculated, i.e. the
.
The input parameters for the model calculations are the total mass of the white dwarf, the hydrogen and helium fractional masses, and the luminosity. The other
global parameters are derived from the model calculated, i.e. the
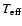 and the radius. The model with the appropriate value of
and the radius. The model with the appropriate value of
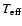 is obtained
by iterating on the value of the luminosity.
is obtained
by iterating on the value of the luminosity.
We checked the impact of changing the effective temperature of the models on the period of the reference mode.
To do this, we built up 8 models
with 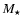 close to the mass of G 185-32 as deduced from spectroscopy. These models have
close to the mass of G 185-32 as deduced from spectroscopy. These models have
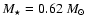 ,
,
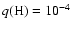 ,
and
,
and
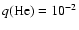 .
Their
.
Their
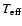 varies within the spectroscopic range (from 11 930 K to 12 330 K).
For each model, the adiabatic
varies within the spectroscopic range (from 11 930 K to 12 330 K).
For each model, the adiabatic  ,
k=1 and
,
k=1 and  ,
k=10 modes were computed. Table 2 lists the periods
of these modes.
While the period of the
,
k=10 modes were computed. Table 2 lists the periods
of these modes.
While the period of the  ,
k=10 mode
increases by 14 s when
,
k=10 mode
increases by 14 s when
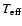 varies within this range, the period of the
varies within this range, the period of the  ,
k=1 mode increases by only 0.2 s. We must
emphasize here that since our models are static models, it is not possible to infer the rate of change of the period. To calculate such a rate of
change would require a fully evolutionary sequence. The goal of these additional model calculations is to evaluate
the sensitivity of the periods of the
,
k=1 mode increases by only 0.2 s. We must
emphasize here that since our models are static models, it is not possible to infer the rate of change of the period. To calculate such a rate of
change would require a fully evolutionary sequence. The goal of these additional model calculations is to evaluate
the sensitivity of the periods of the  ,
k=1, and k=10modes to the location of the star within the error box in the H-R diagram. Accordingly, the period variation of 0.2 s that we find for the
,
k=1, and k=10modes to the location of the star within the error box in the H-R diagram. Accordingly, the period variation of 0.2 s that we find for the  ,
k=1 mode
for a variation of
,
k=1 mode
for a variation of
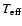 of 370 K is not a measure of the rate of change for the period expected for a decrease in 370 K along a cooling sequence.
Checking that the period of the reference mode does not change much in the allowed range of
of 370 K is not a measure of the rate of change for the period expected for a decrease in 370 K along a cooling sequence.
Checking that the period of the reference mode does not change much in the allowed range of
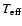 is important since the validity of the possible solutions in the
is important since the validity of the possible solutions in the 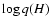 vs.
vs. 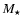 plane strongly relies on the
quasi-constancy of that period. Table 2 guarantees that one may consider
plane strongly relies on the
quasi-constancy of that period. Table 2 guarantees that one may consider
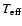 as a degenerate
parameter in a first step.
as a degenerate
parameter in a first step.
The spectroscopic range for 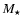 was covered with a step of 0.005
was covered with a step of 0.005 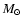 from 0.610
from 0.610 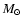 to
0.670
to
0.670 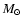 ,
and q(H) was fit so each model kept the fundamental mode with a period of 72.5 s
(
,
and q(H) was fit so each model kept the fundamental mode with a period of 72.5 s
(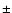 1%). Then
1%). Then
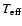 was fixed at 12 130 K and q(He) at 10-2.
was fixed at 12 130 K and q(He) at 10-2.
Table 2:
Impact of
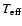 variation on the
variation on the  ,
k=1 and
,
k=1 and  ,
k=10 modes.
,
k=10 modes.
Then we tried a rough identification of the modes observed in the G 185-32 spectrum from the adiabatic spectra calculated for
each model. Table 3 gives the results: 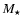 ,
,
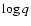 (H), the number of correctly identified modes, and the
respective
(H), the number of correctly identified modes, and the
respective 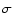 for each of the 13 models. Table 3 shows that the model with
for each of the 13 models. Table 3 shows that the model with
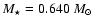 and
and
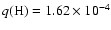 has a spectrum that fits the observed modes with the best accuracy (lowest deviation).
It is also one of those that identify the larger number of observed modes.
Consequently, the mass of G 185-32 and its hydrogen mass fraction should be close to
this couple of values.
The second step of the process is now to perform a fine determination of these two parameters around this pair of values.
has a spectrum that fits the observed modes with the best accuracy (lowest deviation).
It is also one of those that identify the larger number of observed modes.
Consequently, the mass of G 185-32 and its hydrogen mass fraction should be close to
this couple of values.
The second step of the process is now to perform a fine determination of these two parameters around this pair of values.
Table 3:
Potential solutions in the 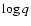 (H) vs.
(H) vs. 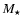 plane derived from the reference mode with
plane derived from the reference mode with
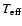 and q(He) constant.
and q(He) constant.
The models in the second sharper grid have masses around 0.640 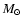 ,
with a variation step of
0.002
,
with a variation step of
0.002 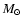 between two consecutive models. The H mass fraction is adjusted accordingly to keep the period
of the reference mode constant. The
between two consecutive models. The H mass fraction is adjusted accordingly to keep the period
of the reference mode constant. The
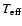 is maintained at 12 130 K for all the models.
The best fit with the
observed power spectrum of G 185-32 is found for the couple
is maintained at 12 130 K for all the models.
The best fit with the
observed power spectrum of G 185-32 is found for the couple
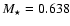 (
(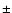 0.007)
0.007) 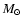 and
and
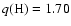 (
(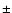 0.10)
0.10)
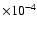 .
The uncertainty on
.
The uncertainty on 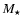 is an estimate of how necessary it is to change the mass from the best-fit value
(0.638
is an estimate of how necessary it is to change the mass from the best-fit value
(0.638 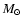 )
to increase the deviation
)
to increase the deviation 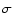 of the resulting model by 10%.
The uncertainty on q(H) corresponds to the minimum variation from the best-fit value (
of the resulting model by 10%.
The uncertainty on q(H) corresponds to the minimum variation from the best-fit value (
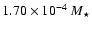 )
necessary to exceed the 1% tolerance allowed on the reference period.
For a best-fit model with
)
necessary to exceed the 1% tolerance allowed on the reference period.
For a best-fit model with
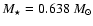 ,
it is the variation of q(H)
that pushes the period of the
,
it is the variation of q(H)
that pushes the period of the  ,
k=1 mode outside the range 71.8 s-73.2 s.
,
k=1 mode outside the range 71.8 s-73.2 s.
The value derived for q(H) confirms that the initial choice for the He mass fraction was optimal since such a
thick hydrogen envelope implies that
 must be close to
must be close to
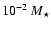 .
The last free parameter to constrain is
.
The last free parameter to constrain is
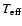 .
We calculated the power spectra for a series of models with
.
We calculated the power spectra for a series of models with
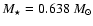 and
and
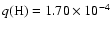 ,
varying their
,
varying their
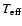 within the spectroscopic interval (11 920 K-12 320 K) by 40 K steps. For each model, we
evaluated its deviation
within the spectroscopic interval (11 920 K-12 320 K) by 40 K steps. For each model, we
evaluated its deviation 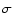 .
The impact of changing
.
The impact of changing
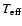 on the pulsation periods is very weak.
However, the value of
on the pulsation periods is very weak.
However, the value of 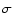 indicates that the model with
indicates that the model with
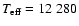 K gives the best fit. A variation of 80 K around this
value does not change the quality of the fit significantly. We conclude that the most probable
effective temperature is
K gives the best fit. A variation of 80 K around this
value does not change the quality of the fit significantly. We conclude that the most probable
effective temperature is
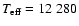 (
(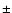 80) K.
This best-fit model gives
80) K.
This best-fit model gives
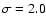 s, with an average relative error of 0.63% on the periods.
The details of this fit are discussed in the next section.
s, with an average relative error of 0.63% on the periods.
The details of this fit are discussed in the next section.
The model fit procedure
described in Sect. 3.2 results in the determination of the main structural parameters of G 185-32:
its total mass
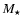 ,
its H and He mass fractions, its luminosity, its
,
its H and He mass fractions, its luminosity, its
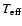 ,
and its radius. These parameters are summarized in Table 4.
,
and its radius. These parameters are summarized in Table 4.
Table 4:
Structural parameters for the best fitting model.
Table 5:
 modes for the best fitting model.
modes for the best fitting model.
Table 6:
 modes for the best fitting model.
modes for the best fitting model.
During the process described in the previous section,
we computed the adiabatic  and
and  pulsation modes for the best-fit model on a period interval encompassing
the range of periods observed in G 185-32. The periods of those modes are listed in Table 5 for the
pulsation modes for the best-fit model on a period interval encompassing
the range of periods observed in G 185-32. The periods of those modes are listed in Table 5 for the  modes
and in Table 6 for the
modes
and in Table 6 for the  ones.
This enables us to perform a preliminary identification of
the observed pulsations. It also allows us to distinguish for ambiguous cases whether the observed periods are true modes
or linear combinations. At this stage, we do not yet consider the impact of the stellar rotation on the pulsation spectrum,
so that those periods are for the m=0 component of each mode.
ones.
This enables us to perform a preliminary identification of
the observed pulsations. It also allows us to distinguish for ambiguous cases whether the observed periods are true modes
or linear combinations. At this stage, we do not yet consider the impact of the stellar rotation on the pulsation spectrum,
so that those periods are for the m=0 component of each mode.
Table 7 shows the comparison between the observed periods and the periods calculated in the best-fit model.
The average deviation for this preliminary identification is
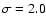 s and the average relative difference is
s and the average relative difference is
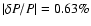 .
These two indicators reveal a satisfactory fit between observed and computed spectra. This
fit will be refined later and completed when the azimuthal number m is taken into account.
.
These two indicators reveal a satisfactory fit between observed and computed spectra. This
fit will be refined later and completed when the azimuthal number m is taken into account.
Using the preliminary identification of the modes given in Table 7, one can check which frequencies must correspond
to real modes and which ones are linear combinations of parent modes. Some of the observed periods cannot be recovered
by the synthetic spectrum of the best fit model, which implies that they should be false modes.
Let us consider first the mysterious 141.9 s period. The model spectrum has its  ,
k=2 mode at a period of
142.1 s. This suggests that the pair 141.2 s-141.9 s is part of the
quintuplet generated by the
,
k=2 mode at a period of
142.1 s. This suggests that the pair 141.2 s-141.9 s is part of the
quintuplet generated by the  ,
k=2 mode split by rotation. Accordingly, the 141.9 s is a true mode and the
70.9 s should consequently be its harmonic, thus a false mode (
,
k=2 mode split by rotation. Accordingly, the 141.9 s is a true mode and the
70.9 s should consequently be its harmonic, thus a false mode (
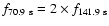 with
with
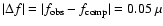 Hz, where
Hz, where
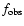 is the observed frequency and
is the observed frequency and
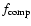 the computed
frequency).
the computed
frequency).
The 148.5 s period does not correspond to any computed mode. This confirms its identification as a linear combination
satisfying the relation:
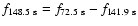 ,
as suggested by CKM.
,
as suggested by CKM.
The 181.9 s period is marginally detected only in the HST data set where
it appears with a low S/N ratio (about 3.6), close to the detection limit that CKM fixed at
3.3 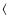 A
A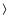 , where
, where 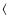 A
A is the average noise level.
Had they chosen a more conservative detection limit (4
is the average noise level.
Had they chosen a more conservative detection limit (4  A
A for instance), this pulsation would
have remained unnoticed and regarded as noise. As a consequence, we are not surprised that the synthetic spectrum
derived from
our best-fit model fails to reproduce this period. We conclude that the 181.9 s is not a true pulsation mode.
for instance), this pulsation would
have remained unnoticed and regarded as noise. As a consequence, we are not surprised that the synthetic spectrum
derived from
our best-fit model fails to reproduce this period. We conclude that the 181.9 s is not a true pulsation mode.
The period at 651.7 s might be a linear combination, since
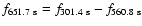 with
with
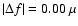 Hz. CKM also note that this frequency might be involved in a linear combination, which
they expressed
as
Hz. CKM also note that this frequency might be involved in a linear combination, which
they expressed
as
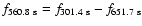 .
The 651.7 s period is not exactly predicted by the model
(Table 7). The calculated (m=0) modes with the closest periods are the
.
The 651.7 s period is not exactly predicted by the model
(Table 7). The calculated (m=0) modes with the closest periods are the  ,
k=11 at 637.5 s and the
,
k=11 at 637.5 s and the  ,
k=22at 672.3 s.
However, when
the rotational splitting is taken into account in the matching process, as discussed in the next section,
this period can be better identified with one mode of the synthetic
spectrum of the model. In addition, if we look at the amplitudes of these 3 pulsations in the 3 data sets available
(WET, HST UV and HST far blue), we note that the 560.7 s is undetected in the WET data. At first glance,
that would
suggest that there are 2 real modes: the 301.4 s and the 651.7 s periods. Then, when the HST data alone are examined,
the three periodicities are detected and
the 651.7 s period may be
seen as a linear combination since it has the smallest amplitude. The
compatibility between these two different conclusions is therefore ensured if we consider that the three modes are real.
This also agrees with our analysis since the three periods are correctly reproduced by our model.
Accordingly, we conclude that these three modes are an illustration of a true resonance. Furthermore, the 301.4 s
mode must be a component of a multiplet with the 299.8 s mode.
,
k=22at 672.3 s.
However, when
the rotational splitting is taken into account in the matching process, as discussed in the next section,
this period can be better identified with one mode of the synthetic
spectrum of the model. In addition, if we look at the amplitudes of these 3 pulsations in the 3 data sets available
(WET, HST UV and HST far blue), we note that the 560.7 s is undetected in the WET data. At first glance,
that would
suggest that there are 2 real modes: the 301.4 s and the 651.7 s periods. Then, when the HST data alone are examined,
the three periodicities are detected and
the 651.7 s period may be
seen as a linear combination since it has the smallest amplitude. The
compatibility between these two different conclusions is therefore ensured if we consider that the three modes are real.
This also agrees with our analysis since the three periods are correctly reproduced by our model.
Accordingly, we conclude that these three modes are an illustration of a true resonance. Furthermore, the 301.4 s
mode must be a component of a multiplet with the 299.8 s mode.
The 212.8 s and 215.7 s periodicities also deserve close examination. Table 7 shows that these periods cannot be well reproduced with any
real mode of the best-fit model.
The period of the closest mode ( ,
k=5, m=0) is 11.4 s and 8.5 s away, respectively. This suggests that those periods
should be false modes from a linear combination. However, none of the observed pulsations,
properly recognized as true modes in the best-fit model, are able to reproduce these periods by any of their
linear combinations.
A close inspection of Tables 5 and 6 reveals a perfect coincidence between the
,
k=5, m=0) is 11.4 s and 8.5 s away, respectively. This suggests that those periods
should be false modes from a linear combination. However, none of the observed pulsations,
properly recognized as true modes in the best-fit model, are able to reproduce these periods by any of their
linear combinations.
A close inspection of Tables 5 and 6 reveals a perfect coincidence between the  ,
k=6
and the
,
k=6
and the  ,
k=12 modes, which pulsate at the same period of 397.0 s. This similarity in periods
is within a probable uncertainty close
to 0.5 s due to modelling internal errors. These two modes should interfere. Since this period is not detected in the
data, it means that the beating period might be quite long
and that the two modes must have been in a situation of destructive interference during the observational campaigns.
However, this double 397.0 s period, although not seen during the observations, might be present in the star as truly
excited modes
able to generate a linear combination with another parent mode. We note that
,
k=12 modes, which pulsate at the same period of 397.0 s. This similarity in periods
is within a probable uncertainty close
to 0.5 s due to modelling internal errors. These two modes should interfere. Since this period is not detected in the
data, it means that the beating period might be quite long
and that the two modes must have been in a situation of destructive interference during the observational campaigns.
However, this double 397.0 s period, although not seen during the observations, might be present in the star as truly
excited modes
able to generate a linear combination with another parent mode. We note that
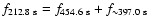 with
with
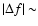 20.0
20.0 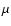 Hz and that
Hz and that
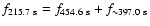 with
with
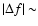 83.0
83.0 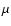 Hz.
Note also that these frequency mismatches might be reduced if the proposed linear combinations involve one of the components of
the multiplets induced by rotational splitting on the modes at
397.0 s, rather than their m=0 component. This will be discussed in the next section.
The impossibility of properly matching the 212.8 s and 215.7 s periods with any of the computed modes and the possibility of accounting for
them as linear combinations involving a beat phenomenon suggests that they are false modes.
Our interpretation could be tested by further observations since we suggest that there should be two modes of different degree at the same period of
397.0 s that were
not observed, because they were in destructive interference. There should be circumstances where they are in constructive interference and where that period could be
detected.
Hz.
Note also that these frequency mismatches might be reduced if the proposed linear combinations involve one of the components of
the multiplets induced by rotational splitting on the modes at
397.0 s, rather than their m=0 component. This will be discussed in the next section.
The impossibility of properly matching the 212.8 s and 215.7 s periods with any of the computed modes and the possibility of accounting for
them as linear combinations involving a beat phenomenon suggests that they are false modes.
Our interpretation could be tested by further observations since we suggest that there should be two modes of different degree at the same period of
397.0 s that were
not observed, because they were in destructive interference. There should be circumstances where they are in constructive interference and where that period could be
detected.
This preliminary modes identification allows us to conclude that the 70.9 s, 148.5 s, 181.9 s, 212.8 s, and 215.7 s
periods do not correspond to real modes.
A few modes in the frequency spectrum of G 185-32 can be used to estimate the rotational splitting and derive the
rotation rate of the star. Some pairs of modes have periods that are close
enough to imply that they must be components of a multiplet induced by stellar rotation. As can be seen from Tables
5 and 6, the adiabatic calculations
for the  and
and  modes show that at the periods of those
pairs of modes there is no coincidence of periods between modes with different spherical
degrees. Thus the existence of these pairs of modes can only be interpreted as the result of rotational splitting, where
only two components of the multiplets are seen.
From the previous analysis, we identify as such multiplet components the following pairs:
modes show that at the periods of those
pairs of modes there is no coincidence of periods between modes with different spherical
degrees. Thus the existence of these pairs of modes can only be interpreted as the result of rotational splitting, where
only two components of the multiplets are seen.
From the previous analysis, we identify as such multiplet components the following pairs:
A(299.8 s, 301.4 s), B(264.2 s, 266.2 s), C(141.2 s, 141.9 s) and D(72.5 s, 72.9 s).
All are identified as  modes.
These modes have short periods, which
implies that the rotational splitting cannot be determined very precisely. In the following, we consider that the
rotation affects all the modes uniformly, whatever their period range. This simplifying hypothesis is justified
since a differential rotation, if present, has a weak impact on the pulsation periods.
In this case and after assuming slow rotation, the pulsation frequencies in the rotating case,
modes.
These modes have short periods, which
implies that the rotational splitting cannot be determined very precisely. In the following, we consider that the
rotation affects all the modes uniformly, whatever their period range. This simplifying hypothesis is justified
since a differential rotation, if present, has a weak impact on the pulsation periods.
In this case and after assuming slow rotation, the pulsation frequencies in the rotating case,
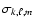 ,
are related to the frequencies in the non-rotating case (
,
are related to the frequencies in the non-rotating case (
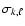 )
by
)
by
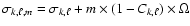 ,
where
,
where
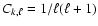 in the asymptotic limit (Brickhill, 1975)
and
in the asymptotic limit (Brickhill, 1975)
and 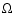 is the angular rotation velocity.
is the angular rotation velocity.
Table 7:
Preliminary identification of the modes observed in G 185-32.
The first column
gives the observed periods, the second one the spherical degree ( )
of the mode, the third its radial order (k), the fourth gives the value of the corresponding period
computed from the best-fit model,
the fifth gives the absolute difference between the two periods, and the sixth their
relative difference.
)
of the mode, the third its radial order (k), the fourth gives the value of the corresponding period
computed from the best-fit model,
the fifth gives the absolute difference between the two periods, and the sixth their
relative difference.
To estimate the rotational splitting, one considers the frequency shift between the components of the
four pairs of  modes identified above.
We get
modes identified above.
We get
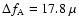 Hz for the pair A,
Hz for the pair A,
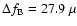 Hz for B,
Hz for B,
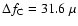 Hz for C, and
Hz for C, and
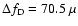 Hz for D. Within the asymptotic regime, one should have
Hz for D. Within the asymptotic regime, one should have
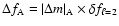 ,
,
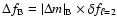 and
and
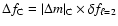 ,
where
,
where
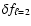 is the predicted frequency shift
for two consecutive components of a quintuplet in the asymptotic regime
and
is the predicted frequency shift
for two consecutive components of a quintuplet in the asymptotic regime
and
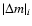 is the absolute difference between the azimuthal number of the components in each pair i.
is the absolute difference between the azimuthal number of the components in each pair i.
According to theory, the asymptotic regime may not be
verified for the pair C (k=2). However, the asymptotic relation
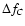 =
=
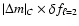 appears surprisingly well satisfied, as seen below.
But the asymptotic regime is not
verified for the pair D, as expected for a k=1 mode.
appears surprisingly well satisfied, as seen below.
But the asymptotic regime is not
verified for the pair D, as expected for a k=1 mode.
As
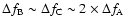 ,
the possible solutions for
,
the possible solutions for
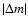 are:
are:
- either
 and
and
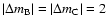 ,
which involves a frequency shift for the
,
which involves a frequency shift for the
 modes:
modes:
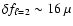 Hz;
Hz;
- or
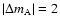 and
and
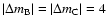 ,
which implies a frequency shift for the
,
which implies a frequency shift for the
 modes:
modes:
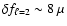 Hz.
Hz.
The pair D allows to remove this indetermination because
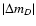 should be of the order of
should be of the order of
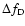 /
/
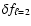 .
A value
for
.
A value
for
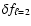 close to 8
close to 8 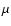 Hz can be rejected since it would imply
Hz can be rejected since it would imply
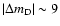 ,
i.e.
,
i.e.
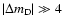 ,
which contradicts the
,
which contradicts the  identification.
With
identification.
With
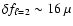 Hz,
then
Hz,
then
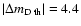 (
(
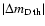 stands for the expected value of
stands for the expected value of
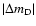 in
the asymptotic limit).
As this approximation is not valid for this doublet (with k=1), one
must have:
in
the asymptotic limit).
As this approximation is not valid for this doublet (with k=1), one
must have:
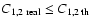 and thus
and thus
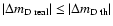 .
One deduces
that
.
One deduces
that
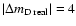 .
.
As a conclusion, we find that there is only one possible value of the frequency
shift for the  modes that satisfies the frequency differences among the four partial quintuplets
observed in
G 185-32:
modes that satisfies the frequency differences among the four partial quintuplets
observed in
G 185-32:
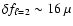 Hz.
Hz.
We take advantage of our evaluation of the frequency shift for the  modes to derive the frequency shift for
the
modes to derive the frequency shift for
the  modes since
modes since
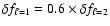 ,
within the asymptotic limit. Accordingly,
,
within the asymptotic limit. Accordingly,
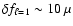 Hz. This value will
be useful to complete the identification, with their azimuthal number m, of the observed modes
that our model identify as
Hz. This value will
be useful to complete the identification, with their azimuthal number m, of the observed modes
that our model identify as  modes.
modes.
The value derived for
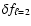 implies an average rotation period close to 14.5 h. This rotation
rate is similar for G 226-29 (about 9 h), for which
implies an average rotation period close to 14.5 h. This rotation
rate is similar for G 226-29 (about 9 h), for which
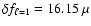 Hz (Kepler et al. 1995).
Dolez
et al. (2006) derived a value of
Hz (Kepler et al. 1995).
Dolez
et al. (2006) derived a value of
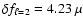 Hz for HL Tau 76.
Therefore G185-32 rotates about 4 times
faster than HL Tau 76.
Hz for HL Tau 76.
Therefore G185-32 rotates about 4 times
faster than HL Tau 76.
Considering the pair D, the value
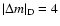 confirms that the 70.9 s period cannot
correspond to a component of the quintuplet generated by the
confirms that the 70.9 s period cannot
correspond to a component of the quintuplet generated by the  ,
k=1 mode. The frequency difference between
the 70.9 s period and the next one at 72.5 s is 313
,
k=1 mode. The frequency difference between
the 70.9 s period and the next one at 72.5 s is 313 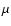 Hz, about 20 times the value of
Hz, about 20 times the value of
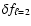 .
As a consequence, the 2 periods 70.9 s and 72.5 s cannot belong to the same multiplet. This reinforces our
previous conclusion that the 70.9 s period should be the harmonics of the 141.9 s mode, with
f
.
As a consequence, the 2 periods 70.9 s and 72.5 s cannot belong to the same multiplet. This reinforces our
previous conclusion that the 70.9 s period should be the harmonics of the 141.9 s mode, with
f
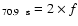
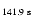 .
.
From Table 7, we could not identify the 651.7 s period at first sight. Taking the rotational splitting into account
with
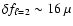 Hz, we can now identify this mode with the m=-2 component of the
Hz, we can now identify this mode with the m=-2 component of the
 ,
k=21, m=0 mode at 633.8 s (Table 6), which we find at a period of 646.9 s, with a relative error of
0.7%.
,
k=21, m=0 mode at 633.8 s (Table 6), which we find at a period of 646.9 s, with a relative error of
0.7%.
CKM identify the 299.8 s and 301.4 s periods as  modes. Our analysis offers an
alternative identification as
modes. Our analysis offers an
alternative identification as  modes. Our model spectrum can only match these periods with the
modes. Our model spectrum can only match these periods with the  ,
k=8
mode with a period at 300.7 s. The pair 299.8 s, 301.4 s is equidistant from the closest computed
,
k=8
mode with a period at 300.7 s. The pair 299.8 s, 301.4 s is equidistant from the closest computed
 modes at 281.2 s for the k=3 mode and at 322.0 s for the k=4 mode. This confirms that the 299.8 s
and 301.4 s periods must be
modes at 281.2 s for the k=3 mode and at 322.0 s for the k=4 mode. This confirms that the 299.8 s
and 301.4 s periods must be  modes.
modes.
We suggested in the previous section that these two periods may result from a linear combination of the mode observed at 454.6 s with the two
interfering and undetected modes at 397.0 s predicted as  and
and  modes in our best-fit model.
Note that it is usually postulated that in order to be identified as the linear combination of two parent mode frequencies f1 and f2, a frequency f3such that
modes in our best-fit model.
Note that it is usually postulated that in order to be identified as the linear combination of two parent mode frequencies f1 and f2, a frequency f3such that
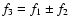 should be visible only when its two parents are also detected and its amplitude in the Fourier spectrum should be smaller than their
respective amplitude. In the present case, the situation is different since one of the two parent modes itself results from two modes interfering at the same frequency,
and could be either in a regime
of destructive or constructive interference. Considering now that these two interfering modes are split by rotation, with the value of the rotational splitting derived
from
section 5.1, we find that the linear combination of the observed mode
at 454.6 s with the
should be visible only when its two parents are also detected and its amplitude in the Fourier spectrum should be smaller than their
respective amplitude. In the present case, the situation is different since one of the two parent modes itself results from two modes interfering at the same frequency,
and could be either in a regime
of destructive or constructive interference. Considering now that these two interfering modes are split by rotation, with the value of the rotational splitting derived
from
section 5.1, we find that the linear combination of the observed mode
at 454.6 s with the  ,
k=12, m=-1 component has a period of 212.6 s, at 0.2 s of the observed period 212.8 s, and with the m=-2 component has a period of
213.3 s, at 2.4 s of the observed period at 215.7 s. The linear combination with the
,
k=12, m=-1 component has a period of 212.6 s, at 0.2 s of the observed period 212.8 s, and with the m=-2 component has a period of
213.3 s, at 2.4 s of the observed period at 215.7 s. The linear combination with the  ,
k=6, m=-1 component would explain the 212.8 s period
(at 212.3 s) almost as well but would not provide any solution for the 215.7 s.
,
k=6, m=-1 component would explain the 212.8 s period
(at 212.3 s) almost as well but would not provide any solution for the 215.7 s.
Our estimate of the frequency shift for the  modes allows us to complete the former preliminary identification
of the periods given in Table 7 by introducing the value of the azimuthal number m. When no unique
interpretations were possible for some periods, i.e. when two distinct modes with a different
modes allows us to complete the former preliminary identification
of the periods given in Table 7 by introducing the value of the azimuthal number m. When no unique
interpretations were possible for some periods, i.e. when two distinct modes with a different
 degree could match the observed period, we selected the solution that resulted in the least
relative (and absolute) error. The value of m was chosen so as to induce the most
constant value of
degree could match the observed period, we selected the solution that resulted in the least
relative (and absolute) error. The value of m was chosen so as to induce the most
constant value of
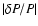 within the components of a multiplet.
Table 8 gives the complete identification of the modes observed in G 185-32.
Taking the rotational splitting into account improves
the quality of the global fit to
within the components of a multiplet.
Table 8 gives the complete identification of the modes observed in G 185-32.
Taking the rotational splitting into account improves
the quality of the global fit to
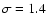 s. The average relative error
decreases to 0.5% and one additional mode (the 651.7 s period) is successfully identified.
s. The average relative error
decreases to 0.5% and one additional mode (the 651.7 s period) is successfully identified.
Our strategy to constrain the internal structure of the ZZ Ceti star G 185-32, based on studying its
pulsation modes, resulted in obtaining a best-fit model. From this model one derives its main structural parameters:
its total mass 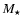 ,
H and He mass fractions,
,
H and He mass fractions,
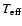 ,
radius, and luminosity. We were also able
to distinguish the real modes from their linear combinations and harmonics among the observed periods.
Then we deduce the degree, the order, and the azimuthal number of the real modes by using the additional
information on the rotational
splitting induced by the stellar rotation.
In the following, we compare our results with the previous analyses by CKM and by Thomson et al. (2004).
,
radius, and luminosity. We were also able
to distinguish the real modes from their linear combinations and harmonics among the observed periods.
Then we deduce the degree, the order, and the azimuthal number of the real modes by using the additional
information on the rotational
splitting induced by the stellar rotation.
In the following, we compare our results with the previous analyses by CKM and by Thomson et al. (2004).
CKM propose an identification of the  value for 14 of the modes observed in G 185-32. They based this
identification
on the different variations in the modes amplitude with wavelength according to their
value for 14 of the modes observed in G 185-32. They based this
identification
on the different variations in the modes amplitude with wavelength according to their  value.
For those periods that we identify as real modes in our analysis, we find some
value.
For those periods that we identify as real modes in our analysis, we find some  identifications that
disagree with CKM.
Our identifications agree with
CKM for the 72.5 s, 72.9 s, 264.2 s, 266.2 s, and 651.7 s modes, but they disagree
for the 299.8 s, 301.4 s, 370.2 s, 454.6 s, and 560.8 s periods. However, the
disagreement may not be that significant. In the UV, the predicted
theoretical amplitude difference between
identifications that
disagree with CKM.
Our identifications agree with
CKM for the 72.5 s, 72.9 s, 264.2 s, 266.2 s, and 651.7 s modes, but they disagree
for the 299.8 s, 301.4 s, 370.2 s, 454.6 s, and 560.8 s periods. However, the
disagreement may not be that significant. In the UV, the predicted
theoretical amplitude difference between  and
and  modes is the same order of magnitude as
the uncertainties on the HST data as shown by the error
bars on the mode amplitudes given by CKM. As a consequence, distinguishing
modes is the same order of magnitude as
the uncertainties on the HST data as shown by the error
bars on the mode amplitudes given by CKM. As a consequence, distinguishing  from
from  modes with
this method would require a much higher S/N ratio in the UV.
We also argue that some of the periods that CKM identify as real modes should instead be linear combinations.
modes with
this method would require a much higher S/N ratio in the UV.
We also argue that some of the periods that CKM identify as real modes should instead be linear combinations.
A few cases where we find different identifications deserve a more detailed discussion.
According to the periods of the  and
and  modes in our best-fit model, as listed in Tables 5 and 6,
there could be two possible
identifications for 2 of the observed modes at 370.2 s and 454.6 s.
The 370.2 s mode could be:
modes in our best-fit model, as listed in Tables 5 and 6,
there could be two possible
identifications for 2 of the observed modes at 370.2 s and 454.6 s.
The 370.2 s mode could be:
- either the
 ,
k=11, and m=2 mode, for which we find a period of 369.8 s, which matches the observed period
with a relative error
,
k=11, and m=2 mode, for which we find a period of 369.8 s, which matches the observed period
with a relative error
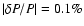 ;
;
- or the
 ,
k=5, and m=-1 mode, for which we find a period of 365.6 s, which matches the observed period
with a relative error
,
k=5, and m=-1 mode, for which we find a period of 365.6 s, which matches the observed period
with a relative error
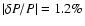 .
.
Our identification criterium selects the identification that minimizes the relative error,
so we selected the first identification. The second solution is still satisfactory,
although less pertinent, and agrees with the  identification of CKM. However, the first identification
gives a better fit with the data.
identification of CKM. However, the first identification
gives a better fit with the data.
Similarly, the 454.6 s mode could be identified as:
- either the
 ,
k=14, and m=0 mode, with a period of 455.2 s and a relative error
,
k=14, and m=0 mode, with a period of 455.2 s and a relative error
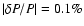 ;
;
- or the
 ,
k=7, m=1 mode, with a of 459.4 s and a relative error of
,
k=7, m=1 mode, with a of 459.4 s and a relative error of
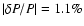 .
.
Once again, the first identification fits the data best, while the second one, which agrees for the  value with CKM, cannot be absolutely rejected.
value with CKM, cannot be absolutely rejected.
Table 8:
Full identification of the observed modes in G 185-32.
We justified above the identification of the pair of periods at 299.8 s and 301.4 s as  modes.
It fits the observed periods with a very
small relative error (
modes.
It fits the observed periods with a very
small relative error (
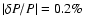 ). This disagrees with CKM, who identify
those periods as
). This disagrees with CKM, who identify
those periods as  modes.
modes.
CKM propose an identification of the 212.8 s periodicity as an  mode and of the 215.7 s one as an
mode and of the 215.7 s one as an  mode.
We argue above that, by considering the beating
that occurs between two modes of degree
mode.
We argue above that, by considering the beating
that occurs between two modes of degree  and
and  with a similar period of 397.0 s,
we could explain the 212.8 s and 215.7 s periods as resulting from a linear combination of those modes at 397.0 s, split by rotation, with the 454.6 s mode.
In addition, the inability of the synthetic spectrum
to reproduce those two periods strengthens this hypothesis.
Provided that the 212.8 s and 215.7 s pulsations are factitious modes,
the problem of their
with a similar period of 397.0 s,
we could explain the 212.8 s and 215.7 s periods as resulting from a linear combination of those modes at 397.0 s, split by rotation, with the 454.6 s mode.
In addition, the inability of the synthetic spectrum
to reproduce those two periods strengthens this hypothesis.
Provided that the 212.8 s and 215.7 s pulsations are factitious modes,
the problem of their  identification vanishes.
identification vanishes.
Among the various singularities detected in the power spectrum of G 185-32, the most enigmatic is the 141.9 s
period whose amplitude does not vary with wavelength, contrary to what is expected from theory for  or
or
 non-radial g-modes. Several scenarii have been proposed to explain this peculiar behaviour.
non-radial g-modes. Several scenarii have been proposed to explain this peculiar behaviour.
For CKM, this atypical behaviour is the signature of a non-linear effect, and thus the 141.9 s
period is not a true pulsation mode. This implies that the 70.9 s period is a real mode and, consequently, that the
141.9 s is its sub-harmonics. We have proposed an alternative hypothesis,
considering that the 70.9 s period
and the pair of periods at 72.5 s and 72.9 s are all genuine modes is problematic. If these three periods
are real modes,
either they belong to the same multiplet generated by rotation
(since we have dismissed magnetic splitting as a possible explanation)
or the 70.9 s period, one one hand, and the pair
72.5 s-72.9 s, on the other, correspond to
distinct modes with different  degrees, either
degrees, either  or
or  .
The value we derived for the frequency shift
(
.
The value we derived for the frequency shift
(
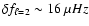 )
excludes the first possibility. The frequency difference between the 70.9 s period
and the 72.5 s one is by far too large to be compatible with
)
excludes the first possibility. The frequency difference between the 70.9 s period
and the 72.5 s one is by far too large to be compatible with
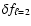 .
Since the 72.5 s and 72.9 s periods
are identified as components of a
.
Since the 72.5 s and 72.9 s periods
are identified as components of a  mode, the result is that the 70.9 s period has to be an
mode, the result is that the 70.9 s period has to be an  (and obviously the k=1) mode
according to the second alternative, if one excludes the possibility of
(and obviously the k=1) mode
according to the second alternative, if one excludes the possibility of
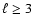 because of the geometrical cancellation
effect. This second hypothesis would imply a mass of G 185-32 close to the Chandrashekar limit, since only
such a very massive ZZ Ceti star could exhibit an
because of the geometrical cancellation
effect. This second hypothesis would imply a mass of G 185-32 close to the Chandrashekar limit, since only
such a very massive ZZ Ceti star could exhibit an  ,
k=1 mode with such a short period.
,
k=1 mode with such a short period.
As already pointed
out by CKM, this disagrees
with the mass derived from spectroscopic observations and parallax, which is about 0.64 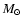 .
As a result,
the assumption that the 70.9 s is a real mode, and the 141.9 s period consequently a false one, appears very doubtful.
Alternatively, we showed that identifying the 70.9 s with an
.
As a result,
the assumption that the 70.9 s is a real mode, and the 141.9 s period consequently a false one, appears very doubtful.
Alternatively, we showed that identifying the 70.9 s with an 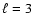 mode would imply that it has an intrinsic amplitude at the stellar surface
at least 15
mode would imply that it has an intrinsic amplitude at the stellar surface
at least 15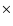 larger than the
larger than the  mode. The mass of G 185-32 which we derived if the 70.9 s is identified as either a k=1 or k=2
mode. The mass of G 185-32 which we derived if the 70.9 s is identified as either a k=1 or k=2 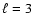 mode is outside the
range of the spectroscopic mass. Furthermore, if our best-fit model does satisfactorily represent G 185-32, it does not have any
mode is outside the
range of the spectroscopic mass. Furthermore, if our best-fit model does satisfactorily represent G 185-32, it does not have any 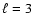 mode with period
close to 70.9 s. This value falls in between the k=1 mode at 50.9 s and the k=2 mode at 101.2 s.
mode with period
close to 70.9 s. This value falls in between the k=1 mode at 50.9 s and the k=2 mode at 101.2 s.
Thompson et al. (2004) do not exclude the possibility that the 141.9 s period could be a genuine mode, but they
do suggest that it is an 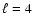 non
radial g-mode. Linear theory predicts that the amplitude for the
non
radial g-mode. Linear theory predicts that the amplitude for the 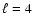 g-modes does not vary
significantly with wavelength from the UV to the visible, which is precisely what is observed for the 141.9 s period.
However,
they did not compute relevant models and their non-radial g-modes to check
whether a suitable
g-modes does not vary
significantly with wavelength from the UV to the visible, which is precisely what is observed for the 141.9 s period.
However,
they did not compute relevant models and their non-radial g-modes to check
whether a suitable 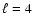 mode could match the observed 141.9 s pulsation, as well as the other periods
observed in G 185-32.
Considering the
mode could match the observed 141.9 s pulsation, as well as the other periods
observed in G 185-32.
Considering the 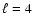 modes in the best-fit model that could best approach the 141.9 s, we find the k=4 mode at 145.6 s, at 3.7 s of the observed period.
By taking into account the rotational splitting, which should be
modes in the best-fit model that could best approach the 141.9 s, we find the k=4 mode at 145.6 s, at 3.7 s of the observed period.
By taking into account the rotational splitting, which should be 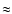 18.2
18.2 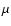 Hz for the
Hz for the 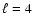 modes if it is 16
modes if it is 16 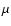 Hz for the
Hz for the  ,
we find
that the m=4component at 144.07 s could marginally fit the observed period within 2.17 s (1.5%). On this argument alone, we cannot dismiss the possibility that the 141.9 s could be
an
,
we find
that the m=4component at 144.07 s could marginally fit the observed period within 2.17 s (1.5%). On this argument alone, we cannot dismiss the possibility that the 141.9 s could be
an 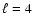 mode. However, the visibility of such modes is problematic, since the amplitude ratio of
mode. However, the visibility of such modes is problematic, since the amplitude ratio of 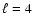 modes relative to
modes relative to  modes is reduced
by at least a factor of 25 (Brassard et al. 1995). It would require that the intrinsic amplitudes at the stellar surface be
at least 25 times larger for the
modes is reduced
by at least a factor of 25 (Brassard et al. 1995). It would require that the intrinsic amplitudes at the stellar surface be
at least 25 times larger for the 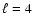 modes than for the
modes than for the  in order to be observed with comparable amplitudes, which we consider as improbable.
in order to be observed with comparable amplitudes, which we consider as improbable.
We suggest another scenario to account for the peculiarity of the 141.9 s period.
We found the  ,
k=2, m=0 mode in our best-fit model to have a period of 142.1 s. We conclude that the 141.9 s period can be
identified with
this mode. However, if this identification allows us to recognize
the 141.9 s period as a true mode, the strange behaviour of its amplitude with wavelength still needs to be understood.
In computing the
,
k=2, m=0 mode in our best-fit model to have a period of 142.1 s. We conclude that the 141.9 s period can be
identified with
this mode. However, if this identification allows us to recognize
the 141.9 s period as a true mode, the strange behaviour of its amplitude with wavelength still needs to be understood.
In computing the 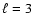 ,
,
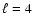 and
and 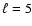 non-radial g-modes in our best-fit model, whose periods
are close to 140 s,
we found that the
non-radial g-modes in our best-fit model, whose periods
are close to 140 s,
we found that the 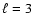 ,
k=4 mode has a period of 139.9 s, the
,
k=4 mode has a period of 139.9 s, the 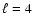 ,
k=6 a period of 145.6 s and the
,
k=6 a period of 145.6 s and the 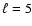 ,
k=9 a period of 143.0 s. One then notices that
,
k=9 a period of 143.0 s. One then notices that
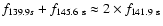 with
with
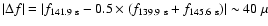 Hz and that
Hz and that
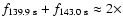
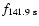 with
with
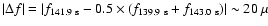 Hz.
Hz.
These relations suggest that the  ,
k=2 mode accounting for the observed 141.9 s period might be affected
by two potential true resonances, each implying modes with 3 different
,
k=2 mode accounting for the observed 141.9 s period might be affected
by two potential true resonances, each implying modes with 3 different  degrees,
degrees,  ,
3, 4 for the first one and
,
3, 4 for the first one and  ,
3, 5 for the second one. The frequency differences
,
3, 5 for the second one. The frequency differences
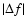 are not strong concerns because they can be easily justified by the internal errors inherent to modelling and mode computation,
which cannot lead to better precision on the computed periods than about 0.5 s. This is even truer for
the second potential frequency resonance for which
are not strong concerns because they can be easily justified by the internal errors inherent to modelling and mode computation,
which cannot lead to better precision on the computed periods than about 0.5 s. This is even truer for
the second potential frequency resonance for which
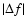 is the same order of magnitude than
the frequency resolution derived from the HST data set.
is the same order of magnitude than
the frequency resolution derived from the HST data set.
It is also possible that modes with degree
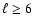 could potentially
induce true resonances with the
could potentially
induce true resonances with the  ,
k=2 mode. However, the radial density and pressure
perturbations decrease with increasing
,
k=2 mode. However, the radial density and pressure
perturbations decrease with increasing  ,
making the probability of interfering with the central mode
,
making the probability of interfering with the central mode
 ,
k=2 of the resonant triplet less probable, or at least strongly reducing its detectability.
As a consequence, we consider only the two
former frequency relations as able to account for a true resonance involving the observed (
,
k=2 of the resonant triplet less probable, or at least strongly reducing its detectability.
As a consequence, we consider only the two
former frequency relations as able to account for a true resonance involving the observed ( ,
k=2) 141.9 s mode.
,
k=2) 141.9 s mode.
It is hardly surprising not to detect the two other modes involved in these resonant
triplets since the visibility of the modes decreases rapidly with increasing  .
For the same reason, the results of the linear combinations
[
.
For the same reason, the results of the linear combinations
[
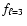
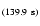 +
+
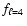
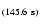 ]
or [
]
or [
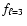
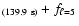
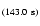 ]
would probably remain undetected if they did not combine with the
]
would probably remain undetected if they did not combine with the  ,
k=2, 141.9 s mode.
,
k=2, 141.9 s mode.
As a consequence, we suggest that the 141.9 s pulsation might be the result of a three-mode resonance,
due to the coincidence between the frequency of a  mode
and the frequency of the linear combination generated by two parent modes of higher degrees, either
mode
and the frequency of the linear combination generated by two parent modes of higher degrees, either 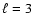 and
and
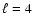 or
or 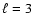 and
and 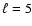 .
This
may explain why the amplitude of the resulting pulsation does
not follow the wavelength dependence predicted by linear theory for the amplitude of a single, isolated
.
This
may explain why the amplitude of the resulting pulsation does
not follow the wavelength dependence predicted by linear theory for the amplitude of a single, isolated  mode.
One may anticipate that if such a triplet resonance occurs, the amplitude of the
mode.
One may anticipate that if such a triplet resonance occurs, the amplitude of the  mode might be strongly
disturbed by its interaction with the other modes.
It is still necessary to prove that the wavelength dependence of the resuling pulsation agrees with the observations, which is
beyond the scope of the present paper.
mode might be strongly
disturbed by its interaction with the other modes.
It is still necessary to prove that the wavelength dependence of the resuling pulsation agrees with the observations, which is
beyond the scope of the present paper.
One may even go further than this hypothesis to also suspect that this resonant triplet is affected by the
non-linear
effect of frequency-lock or, at least, is in the situation of the intermediate regime discussed by Goupil et al.
(1998). They showed
that, if three modes of different  degrees have frequencies very close to resonance, i.e. such as
f1+f3
degrees have frequencies very close to resonance, i.e. such as
f1+f3 
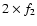 ,
then they are frequency-locked.
It means that,
when the frequencies are near the exact resonance, the resonant coupling resulting from their non-linear interaction
forces the three frequencies to be
equidistant even if they are not so in the frame of linear theory. Note that in this case the actual frequencies
of the modes
involved by the frequency-lock differ from the values computed for the modes in our model since our calculations rely
on linear theory.
However, Goupil & Buchler (1994) have established that such a non-linear effect must comply with some selection
rules. In particular, for the resonant coupling to occur, the sum of the spherical degrees of all the involved modes
must be even. For the first
potential resonance, the sum of the degrees is 11 (
,
then they are frequency-locked.
It means that,
when the frequencies are near the exact resonance, the resonant coupling resulting from their non-linear interaction
forces the three frequencies to be
equidistant even if they are not so in the frame of linear theory. Note that in this case the actual frequencies
of the modes
involved by the frequency-lock differ from the values computed for the modes in our model since our calculations rely
on linear theory.
However, Goupil & Buchler (1994) have established that such a non-linear effect must comply with some selection
rules. In particular, for the resonant coupling to occur, the sum of the spherical degrees of all the involved modes
must be even. For the first
potential resonance, the sum of the degrees is 11 (
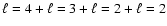 ), so this solution
is not eligible for non-linear coupling. The second potential resonance satisfies the selection criterium
since it implies an even sum of degrees (12):
), so this solution
is not eligible for non-linear coupling. The second potential resonance satisfies the selection criterium
since it implies an even sum of degrees (12):
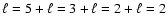 .
It is the only
possibility for a non-linear coupling to occur either in a frequency-lock or in an intermediate regime.
The probability of a non-linear coupling to occur increases with decreasing frequency mismatch
.
It is the only
possibility for a non-linear coupling to occur either in a frequency-lock or in an intermediate regime.
The probability of a non-linear coupling to occur increases with decreasing frequency mismatch
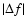 .
Here,
.
Here,
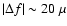 Hz and the frequencies of the three modes are almost equidistant:
[
Hz and the frequencies of the three modes are almost equidistant:
[
![$f_{(141.9~\rm s)} -f_{(143.0~\rm s)}] \sim[f_{(139.9~\rm s)}-f_{(141.9~\rm s)}$](/articles/aa/full/2006/25/aa4370-05/img141.gif) ].
].
Goupil et al. (1998) have shown that the amplitude of the three modes resulting from a frequency-lock depends on
the modes growth rate (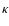 )
and on some non-linear coupling coefficients. It is then possible that the triplet
configuration favours the amplitude of the central component, i.e. the 141.9 s observed mode, and also not surprising
that the amplitude of this mode does not vary with wavelength as suggested by linear theory. To settle this
hypothesis unambiguously, it will be necessary to estimate the growth rate
)
and on some non-linear coupling coefficients. It is then possible that the triplet
configuration favours the amplitude of the central component, i.e. the 141.9 s observed mode, and also not surprising
that the amplitude of this mode does not vary with wavelength as suggested by linear theory. To settle this
hypothesis unambiguously, it will be necessary to estimate the growth rate  of the involved modes by performing
non-adiabatic calculations. According to the value derived for
of the involved modes by performing
non-adiabatic calculations. According to the value derived for  ,
it will be possible to check
whether the triplet resonance is in the frequency-lock regime, i.e. if
,
it will be possible to check
whether the triplet resonance is in the frequency-lock regime, i.e. if
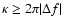 ,
or in the intermediate regime, if
,
or in the intermediate regime, if
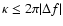 .
This is a promising direction to explore but
is also out of the scope of this paper.
This suggestion could also be checked observationally since the resonant coupling induces amplitude and frequency variations,
whose amplitudes and timescales depend
on the status of the coupling, i.e. on whether it is in a frequency-locked or in an intermediate regime. Those predictions could be tested
by long-term observations if they provide the required frequency and amplitude accuracy. The WET data are
presently the only data providing the required accuracy on the frequencies (but may be not on the amplitudes) for only one season. More observations
are necessary to test the validity of
this assumption.
.
This is a promising direction to explore but
is also out of the scope of this paper.
This suggestion could also be checked observationally since the resonant coupling induces amplitude and frequency variations,
whose amplitudes and timescales depend
on the status of the coupling, i.e. on whether it is in a frequency-locked or in an intermediate regime. Those predictions could be tested
by long-term observations if they provide the required frequency and amplitude accuracy. The WET data are
presently the only data providing the required accuracy on the frequencies (but may be not on the amplitudes) for only one season. More observations
are necessary to test the validity of
this assumption.
By comparing the observed periods with the periods of the non-radial g-modes of a set of models,
we were able to select a model that
fits best the ZZ Ceti star G 185-32 and to constrain its main physical parameters.
It was then possible to identify the periods detected in its power spectrum and to distinguish the real
modes from their linear
combinations. We also estimated the rotational splitting, which allowed a more complete mode identification.
We proposed a new hypothesis to explain the singularity of the 141.9 s mode.
Relying on the 72.5 s period, which we identify as the  ,
k=1 mode as a reference mode,
the modelling process resulted in a best-fit model whose
synthetic spectrum fits the observed modes of G 185-32 with an average relative error of 0.5%, which we
consider as a very good fit. The main structural properties of the model are: a full mass
,
k=1 mode as a reference mode,
the modelling process resulted in a best-fit model whose
synthetic spectrum fits the observed modes of G 185-32 with an average relative error of 0.5%, which we
consider as a very good fit. The main structural properties of the model are: a full mass
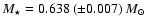 ,
a thick hydrogen envelope as massive as
,
a thick hydrogen envelope as massive as
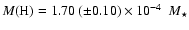 ,
and an effective temperature
,
and an effective temperature
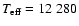 (
( 80) K. These values
confirm that G 185-32 is located near the blue edge of the ZZ Ceti instability strip.
Its hydrogen mass
fraction is close to the one derived for the cooler ZZ Ceti star
HL Tau 76:
80) K. These values
confirm that G 185-32 is located near the blue edge of the ZZ Ceti instability strip.
Its hydrogen mass
fraction is close to the one derived for the cooler ZZ Ceti star
HL Tau 76:
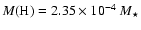 (PVD, 2006).
(PVD, 2006).
The presence of partial multiplets in the pulsation spectrum of G 185-32 allowed us to evaluate the rotational
splitting for the  modes,
modes,
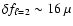 Hz. It implies an average rotation period of 14.5 hr, roughly 3
or 4 times faster than HL Tau 76. This rotation period is comparable to the one for G 226-29
(approximatively 9 h).
Hz. It implies an average rotation period of 14.5 hr, roughly 3
or 4 times faster than HL Tau 76. This rotation period is comparable to the one for G 226-29
(approximatively 9 h).
The computed  and
and  modes for the best-fit model enabled us to determine the nature of some ambiguous
periods, especially when they are marginally detected, as in the case of the 181.9 s period, for example, or when the
mode satisfies a
linear combination relation. Thus, our modelling finds that the 70.9 s, 148.5 s, 181.9 s, 212.8 s, and 215.7 s
periods are false modes.
modes for the best-fit model enabled us to determine the nature of some ambiguous
periods, especially when they are marginally detected, as in the case of the 181.9 s period, for example, or when the
mode satisfies a
linear combination relation. Thus, our modelling finds that the 70.9 s, 148.5 s, 181.9 s, 212.8 s, and 215.7 s
periods are false modes.
We compared our  identification with the one proposed
by CKM. Our analysis globally agrees with CKM except in the following cases:
the pair of periods 299.8 s-301.4 s, which CKM identify as an
identification with the one proposed
by CKM. Our analysis globally agrees with CKM except in the following cases:
the pair of periods 299.8 s-301.4 s, which CKM identify as an  mode, are
mode, are  modes; the 370.2 s
and 454.6 s periods, which CKM also identify as
modes; the 370.2 s
and 454.6 s periods, which CKM also identify as  modes, are found to fit the observations better if they are
modes, are found to fit the observations better if they are
 modes.
We note that G 185-32 oscillates more often in
modes.
We note that G 185-32 oscillates more often in  modes, like HL Tau 76 (PVD 2006)
and BPM 37093 (Kanaan et al. 2005).
modes, like HL Tau 76 (PVD 2006)
and BPM 37093 (Kanaan et al. 2005).
Finally, we propose a new working hypothesis to explain why the amplitude of the enigmatic 141.9 s period does not vary
with wavelength from the UV to the visible, contrary to what the linear theory predicts for  or
or  modes.
To account
for this phenomenon, CKM considered that this period was not a true mode, while Thompson et al. (2004)
propose associating this period with an
modes.
To account
for this phenomenon, CKM considered that this period was not a true mode, while Thompson et al. (2004)
propose associating this period with an 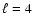 mode. We suggest another scenario based on calculation of the
mode. We suggest another scenario based on calculation of the
 ,
3, 4, and 5 modes
in our best fit model. The 141.9 s could result from the superposition of a real
,
3, 4, and 5 modes
in our best fit model. The 141.9 s could result from the superposition of a real  mode with a linear
combination generated by two parent modes of degrees
mode with a linear
combination generated by two parent modes of degrees 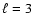 and
and 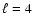 or
or 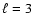 and
and 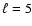 .
As a
result, the amplitude of the genuine
.
As a
result, the amplitude of the genuine  mode would be altered by its interference with the linear combination
whose frequency
coincides exactly with its frequency. Accordingly, it is not surprising that the amplitude variation with wavelength
of the resulting period does not comply
with the theoretical predictions of an isolated, undisturbed mode. Furthermore, this resonant triplet,
induced by the non-linear interaction between the three modes, may be
in a frequency-lock regime or in a situation of intermediate regime. However, such a resonance is possible
only between the
mode would be altered by its interference with the linear combination
whose frequency
coincides exactly with its frequency. Accordingly, it is not surprising that the amplitude variation with wavelength
of the resulting period does not comply
with the theoretical predictions of an isolated, undisturbed mode. Furthermore, this resonant triplet,
induced by the non-linear interaction between the three modes, may be
in a frequency-lock regime or in a situation of intermediate regime. However, such a resonance is possible
only between the  ,
3, and 5 modes because of selection rules. This non-linear coupling, if it
occurs, could explain the strangeness of the 141.9 s mode, since it perturbs both the frequency
and the amplitude of each mode involved in the resonant triplet.
,
3, and 5 modes because of selection rules. This non-linear coupling, if it
occurs, could explain the strangeness of the 141.9 s mode, since it perturbs both the frequency
and the amplitude of each mode involved in the resonant triplet.
- Bergeron, P., Wesemael,
F., Lamontagne, R., et al. 1995, ApJ, 449, 258 [NASA ADS] [CrossRef] (In the text)
- Bergeron, P., Fontaine,
G., Billères, M., Boudreault, S., & Green, E.M. 2004, ApJ,
600, 404 [NASA ADS] [CrossRef] (In the text)
- Brassard, P., Fontaine,
G., Wesemael, F., & Tassoul, M. 1992, ApJS, 81, 747 [NASA ADS] [CrossRef] (In the text)
- Brassard, P., Fontaine,
G., & Wesemael, F. 1995, ApJS, 96, 545 [NASA ADS] [CrossRef] (In the text)
- Brickhill, A. J. 1975,
MNRAS, 170, 405 [NASA ADS] (In the text)
- Castanheira, B. G.,
Kepler, S. O., Moskalik, P., et al. 2004, A&A, 413, 623 [EDP Sciences] [NASA ADS] [CrossRef]
(CKM)
(In the text)
- Dolez, N., Vauclair,
G., Kleinman, S. J., et al. 2006, A&A, 446, 237 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Dziembowski, W. 1977,
Acta Astr., 27, 203 [NASA ADS] (In the text)
- Goupil, M.-J., &
Buchler, J. R. 1994, A&A, 291, 481 [NASA ADS] (In the text)
- Goupil, M.-J.,
Dziembowski, W. A., & Fontaine, G. 1998, Baltic Astronomy, 7,
21 [NASA ADS] (In the text)
- Jones, P. W., Pesnell,
W. D., Hansen, C. J., & Kawaler, S. D. 1989, ApJ, 336, 403 [NASA ADS] [CrossRef] (In the text)
- Kanaan, A., Nitta, A.,
Winget, D. E., et al. 2005, A&A, 432, 219 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kepler, S. O. 1984,
ApJ, 278, 754 [NASA ADS] [CrossRef] (In the text)
- Kepler, S. O.,
Giovannini, O., Wood, M. A., et al. 1995, ApJ, 447, 874 [NASA ADS] [CrossRef] (In the text)
- Kepler, S. O.,
Robinson, E. L., Koester, D., et al. 2000, ApJ, 539,379
(In the text)
- Mc Graw, J. T.,
Fontaine, G., Lacombe, P., et al. 1981, ApJ, 250, 349 [NASA ADS] [CrossRef] (In the text)
- Mukadam, A., et al.
2006, ApJ, in press [arXiv:astro-ph/0507425]
- Nather, R. E., Winget,
D. E., Clemens, J. C., et al. 1990, ApJ, 361, 309 [NASA ADS] [CrossRef] (In the text)
- Pech, D., Vauclair, G.,
& Dolez, N. 2006, A&A, 446, 223 [EDP Sciences] [NASA ADS] [CrossRef] (PVD)
(In the text)
- Robinson, E. L.,
Kepler, S. O., & Nather, R. E. 1982, ApJ, 259, 219 [NASA ADS] [CrossRef] (In the text)
- Robinson, E. L.,
Mailloux, T. M., Zhang, E., et al. 1995, ApJ, 438, 908 [NASA ADS] [CrossRef] (In the text)
- Schmidt, G. D., &
Smith, P. S. 1995, ApJ, 448, 305 [NASA ADS] [CrossRef] (In the text)
- Thomson, S. E.,
Clemens, J. C., van Kerkwijk, M. H., et al. 2004, ApJ, 610,
1001 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006