A&A 453, 321-327 (2006)
DOI: 10.1051/0004-6361:20054055
Neoclassical bootstrap current in solar plasma loops
B.-L. Tan1,2 -
G.-L. Huang1
1 - Purple Mountain Observatory, the Chinese Academy of Sciences, Nanjing, 210008, PR China
2 -
Graduate School of the Chinese Academy of Sciences, Beijing, 100871, PR China
Received 16 August 2005 / Accepted 26 February 2006
Abstract
From the similarities in magnetic configurations and plasma
behaviors between tokamaks and solar current-carrying plasma
loops, we apply the theory of neoclassical bootstrap current in
tokamaks to the solar plasma loops. We present a simplified
expression of the bootstrap current in the solar plasma loops and
find that there may be a considerable component of the
neoclassical bootstrap current in some compact current-carrying
solar flare loops; e.g. the fraction of the bootstrap current is
up to 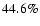 of a flare loop of the event that occurred on Aug. 25, 1999. We suggest that the neoclassical effect changes the current distribution and affects the instability of solar plasma
loops. Based on the data analysis of SXT/Yohkoh, HXT/Yohkoh, GOES,
and NoRP, we find that the timescale of the neoclassical tearing
modes is consistent with the rising time of the impulsive phase
during the event, while the timescale of the classical tearing
modes is much longer than that of the event, which may provide
important evidence of the bootstrap current and help us understand
the mechanisms of the eruptive events, such as solar flares,
prominence, and CMEs.
of a flare loop of the event that occurred on Aug. 25, 1999. We suggest that the neoclassical effect changes the current distribution and affects the instability of solar plasma
loops. Based on the data analysis of SXT/Yohkoh, HXT/Yohkoh, GOES,
and NoRP, we find that the timescale of the neoclassical tearing
modes is consistent with the rising time of the impulsive phase
during the event, while the timescale of the classical tearing
modes is much longer than that of the event, which may provide
important evidence of the bootstrap current and help us understand
the mechanisms of the eruptive events, such as solar flares,
prominence, and CMEs.
Key words: Sun: evolution - plasmas - Sun: magnetic fields
After many years of intensively studying of solar eruptive events
(such as solar flares, prominence, and CMEs), there are still many
unsolved problems for solar physics. The most essential questions
include energy storage and release processes. About forty years
ago, Alfvén & Carlqvist (1967) stressed the importance of
electric currents in the processes of solar flares. Recent
observations show that current-carrying plasma loops may play an
important role in the study of the solar eruptive events (Strong
1994; Spadaro 2003; Ashbourn & Woods 2004). The technique of
vector magnetograms proved the existence of the electric current
and showed that the total current is about  1010-1012 A (Severny 1964; Canfield et al. 1993). People think that such a current comes from the photospheric convective motion. Since we know that the loop current and its distribution dominate the
plasma instabilities, evolution, energy storage, and release in
solar plasma loops, studies of the origin and distribution of the
current become a fundamental task (Sen & White 1972; Zaitsev & Stepanov 1992).
1010-1012 A (Severny 1964; Canfield et al. 1993). People think that such a current comes from the photospheric convective motion. Since we know that the loop current and its distribution dominate the
plasma instabilities, evolution, energy storage, and release in
solar plasma loops, studies of the origin and distribution of the
current become a fundamental task (Sen & White 1972; Zaitsev & Stepanov 1992).
On the other hand, some theoretical studies from the early 1970s
predicted that the effects of the finite toroidal orbit might lead
to the generation of a new current, called the neoclassical
bootstrap current, in the presence of the gradients of plasma
density and temperature in toroidal plasma devices (Bickerton et al. 1971; Zarnstorff & Prager 1986; Hirshman 1988; Peeters et al. 2000). Then, the experiments in many toroidal devices (in particular, tokamaks, toroidal multipoles, and stellarators) have
confirmed the existence of the self-generated current (reviewed by
Kikuchi & Azumi 1995). Recently, a direct measurement of
neoclassical bootstrap current in laboratory was made by Petty et al. (2005). By comparing magnetic configurations and plasma
behaviors between tokamaks and solar current-carrying plasma
loops, we suggest in this work that, besides the convective
current, the bootstrap current may be an important component in
solar current-carrying plasma loops.
In Sect. 2 we compare the magnetic configurations and plasma
behavior in tokamaks and solar plasma loops. The derivations of
bootstrap current in tokamaks and solar current-carrying plasma
loops are given in Sect. 3. A solar flare event is studied with
analysis of bootstrap current in Sect. 4, and the conclusion and
discussions are summarized in Sect. 5.
There are a lot of similarities in the plasma and magnetic
configurations between tokamaks and solar current-carrying plasma
loops, which we presents in details.
The magnetic field is composed of a toroidal component and a poloidal component in the tokamak. The toroidal component,
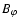 is the main part in the total magnetic field. The
poloidal magnetic field,
is the main part in the total magnetic field. The
poloidal magnetic field,
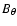 is induced by the plasma current flowing along the toroidal direction in the main coils, and
is induced by the plasma current flowing along the toroidal direction in the main coils, and
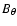 depends on the distribution of the plasma
current,
depends on the distribution of the plasma
current,
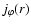 .
From Fig. 1, we may clearly get insight of the configuration. Figure 1a shows that the magnetic lines stretch along the toroidal direction, rotate along the poloidal direction, and form a series of nested magnetic flux surfaces. Figure 1b shows the spatial distribution of the magnetic field lines on a magnetic flux surface. Generally,
.
From Fig. 1, we may clearly get insight of the configuration. Figure 1a shows that the magnetic lines stretch along the toroidal direction, rotate along the poloidal direction, and form a series of nested magnetic flux surfaces. Figure 1b shows the spatial distribution of the magnetic field lines on a magnetic flux surface. Generally,
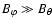 ,
the total magnetic field can be approximately
simplified to:
,
the total magnetic field can be approximately
simplified to:
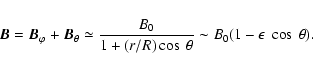 |
(1) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{Figure1.eps} \end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg8.gif) |
Figure 1:
Sketch maps of the magnetic configuration of the tokamak:
a) the magnetic field lines form a series of nested magnetic
flux surfaces; b) the spatial distribution of the magnetic
field lines on a flux surface. |
| Open with DEXTER |
The maximum and minimum magnetic field strength on the magnetic
flux surface are
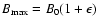 and
and
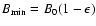 ,
respectively, here B0 is the
value on the toroidal axis of tokamaks, r the cross-section
radius of the flux surface, R the main radius of tokamaks, and
,
respectively, here B0 is the
value on the toroidal axis of tokamaks, r the cross-section
radius of the flux surface, R the main radius of tokamaks, and
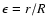 is the inverse aspect ratio of the flux surface. A magnetic line passes strong and weak magnetic field regions alternately, while it stretches in the toroidal direction and
rotates in the poloidal direction in the tokamaks. The strong
field region is near the inside part of the flux surface, while
the weak field region is near the outside part of the flux
surface. Thus a localized magnetic mirror forms, spreads on the
magnetic surface, stretches in the toroidal direction, and rotates
in the poloidal direction. The magnetic mirror ratio is:
is the inverse aspect ratio of the flux surface. A magnetic line passes strong and weak magnetic field regions alternately, while it stretches in the toroidal direction and
rotates in the poloidal direction in the tokamaks. The strong
field region is near the inside part of the flux surface, while
the weak field region is near the outside part of the flux
surface. Thus a localized magnetic mirror forms, spreads on the
magnetic surface, stretches in the toroidal direction, and rotates
in the poloidal direction. The magnetic mirror ratio is:
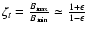 .
.
Because of the existence of the localized magnetic mirror, the
electrons in tokamaks may be classified into two groups: trapped
and passing electrons. The trapped electrons cannot pass through
the strong field region, so they only move and bounce back and
forth along the banana orbit in the mirror. The magnetic mirror
ratio
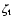 is an important factor, which dominates the
fraction of banana particles (i.e. trapped particles) relative to
the total particles, and affects the magnitude of the bootstrap
current.
is an important factor, which dominates the
fraction of banana particles (i.e. trapped particles) relative to
the total particles, and affects the magnitude of the bootstrap
current.
Besides the configuration of localized magnetic mirror, the
occurrence of the bootstrap current needs another two conditions:
banana regime and pressure gradient. The banana regime depends on
the plasma collisions. We may define a factor g as a characteristic of the plasma collision,
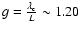
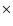
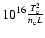 ,
here
,
here
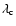 is the electron mean free path, L the scale length of the loops,
is the electron mean free path, L the scale length of the loops,
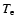 the electron temperature, the unit of
the electron temperature, the unit of 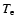 is eV, and
is eV, and
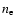 the electron density with unit of
the electron density with unit of
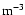 .
When g>1,
most of the trapped particles can finish one or more while bounces
before de-trapping due to a scattering collision in the magnetic
mirror; then the plasma situates in banana regime, and this
condition is satisfied in most of modern tokamaks. And the gradient of the plasma
pressure also exists in practice.
.
When g>1,
most of the trapped particles can finish one or more while bounces
before de-trapping due to a scattering collision in the magnetic
mirror; then the plasma situates in banana regime, and this
condition is satisfied in most of modern tokamaks. And the gradient of the plasma
pressure also exists in practice.
The solar plasma loop is current-carrying in most cases (Ashbourn
et al. 2004). Its magnetic field is also composed of a loop
component and a poloidal component, which is similar to that of
tokamaks. Figure 2 shows the magnetic configuration of solar
current-carrying plasma loops. The poloidal component is induced
by the electric current in the loops, while the current may come
from the mass convection of the photosphere and sub-photosphere.
The magnetic field lines rotate around the axis of the loop, while
they stretch along the loop, and also form a series of nested
magnetic flux surfaces similar to those of tokamaks.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Figure2.eps}\end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg21.gif) |
Figure 2:
Sketch maps of the magnetic configuration in the solar
current-carrying plasma loops and the banana orbit spread of the
trapped particles (green lines), here red lines indicate the
magnetic field lines. |
| Open with DEXTER |
The loop component of the magnetic field in the solar plasma loop
is changeable and different from the one in tokamaks. The magnetic
field in foot-point is stronger than that in loop-top. The
magnetic field
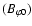 at foot-point can be obtained from
the observation of vector magnetograms, and the one at loop-top
can be extrapolated from certain models. The following is a simple
extrapolated expression:
at foot-point can be obtained from
the observation of vector magnetograms, and the one at loop-top
can be extrapolated from certain models. The following is a simple
extrapolated expression:
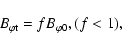 |
(2) |
where
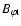 is the loop magnetic field at the loop-top,
f a extrapolated function related with the loop parameters (such
as height h, distance d between the two foot-points of the
loop, etc.). Thus, there are two strong magnetic field regions at
two foot-points and a weak region at the loop-top, which forms a local magnetic mirror.
is the loop magnetic field at the loop-top,
f a extrapolated function related with the loop parameters (such
as height h, distance d between the two foot-points of the
loop, etc.). Thus, there are two strong magnetic field regions at
two foot-points and a weak region at the loop-top, which forms a local magnetic mirror.
Let a0 and 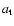 refer to the cross-section radii of the
foot-points and the loop-top, respectively. Based on the
conservation of magnetic flux along the loop (
refer to the cross-section radii of the
foot-points and the loop-top, respectively. Based on the
conservation of magnetic flux along the loop (
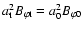 ), we have the relation:
), we have the relation:
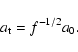 |
(3) |
On a flux surface with the cross-section radius r at the foot-
points and r' at the loop-top (
r'=f-1/2r), the poloidal
magnetic field is estimated by
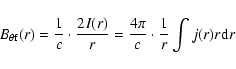 |
(4) |
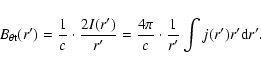 |
(5) |
Here
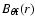 and
and
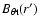 are the poloidal
magnetic field at foot-points and loop-top, respectively, and I(r) (j(r)) and I(r') (j(r')) are the total current (density) at foot-points and loop-top, respectively. The total
current may be estimated from the solar observations of vector
magnetograms (Canfield et al. 1993), which are obtained in the
solar photosphere; thus, only the vertical electric current can be
determined. However, with the assumption of a force-free field
(
are the poloidal
magnetic field at foot-points and loop-top, respectively, and I(r) (j(r)) and I(r') (j(r')) are the total current (density) at foot-points and loop-top, respectively. The total
current may be estimated from the solar observations of vector
magnetograms (Canfield et al. 1993), which are obtained in the
solar photosphere; thus, only the vertical electric current can be
determined. However, with the assumption of a force-free field
(
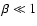 and
and 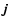
 ), we may
estimate the magnitude of the total current from the vector
magnetic field as:
), we may
estimate the magnitude of the total current from the vector
magnetic field as:
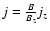 ,
B=(Bx2
+By2+Bz2)1/2. The total current I is obtained by
integrating j(r). Since the coronal loops are always in
steady-state during a relatively long period, we may suppose that
the distribution of total current is dominated by the pinch effect
(Bennett 1934), with expressions such as:
,
B=(Bx2
+By2+Bz2)1/2. The total current I is obtained by
integrating j(r). Since the coronal loops are always in
steady-state during a relatively long period, we may suppose that
the distribution of total current is dominated by the pinch effect
(Bennett 1934), with expressions such as:
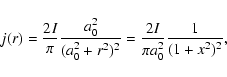 |
(6) |
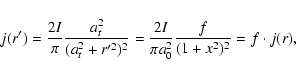 |
(7) |
where x=r/a0, and I refers to the total current in the
loop. Substituting Eqs. (6) and (7) into Eqs. (4) and (5), we may
get the poloidal magnetic field at foot-points and loop-top,
respectively:
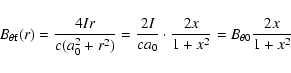 |
(8) |
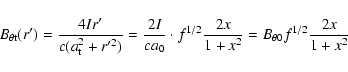 |
(9) |
with the relation:
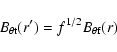 |
(10) |
where
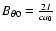 is the maximum of poloidal
magnetic field strength at the foot-point. When
is the maximum of poloidal
magnetic field strength at the foot-point. When
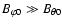 and
and
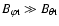 ,
the total
magnetic fields at the foot-points and the loop-top can be
expressed respectively as follows:
,
the total
magnetic fields at the foot-points and the loop-top can be
expressed respectively as follows:
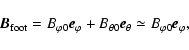 |
(11) |
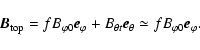 |
(12) |
Then the magnetic mirror ratio of solar current-carrying plasma
loops can be written as:
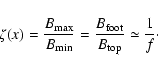 |
(13) |
As a result, electrons in solar current-carrying plasma loops can
also be classified into trapped and passing electrons due to the
existence of a localized magnetic mirror, similar to those in tokamaks.
In fact, there are two possible kinds of magnetic traps in the
coronal loops. The first case is considered in the above
paragraphs, where the cross-section is changeable along the loop
axis. The second case is connected with the loop-type which the
cross-section does not change, and its high values of magnetic
field on the internal (with respect to the loop curvature center)
surface of current-carrying loops and the horizontal
stratification of plasma will also create magnetic traps. This
kind of trap is more similar to that of tokamaks, and it will
probably play an important role in the neoclassical effect. In
practice, the first case of traps is more prevalent in the solar
atmosphere. So we limit our discussion of the first case of traps
in this work. As for the second case of traps, its analysis is
similar to the first case, so we do not present a detailed
description.
We estimate the plasma collision based on the data from the book
by Bray et al. (1991). The magnitude of the electron
mean free path about 1.0 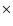 102-1.0
102-1.0 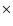 108 m, and
factor g is about
10-5-10. We see that some of the loops
satisfy the condition of the banana regime. For example, when
108 m, and
factor g is about
10-5-10. We see that some of the loops
satisfy the condition of the banana regime. For example, when
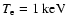 ,
,
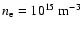 ,
the electron mean free path
is 1.2
,
the electron mean free path
is 1.2 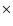
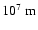 .
In this case, if the loop has the scale
L<1.2
.
In this case, if the loop has the scale
L<1.2 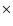
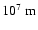 ,
the condition g>1 is satisfied. Note that
the plasma loops we considered here mainly refers to the flare
loops. Observations show that the flare loops with the above
parameters are possible. For example, many solar flare loops have
a temperature up to 1 KeV and higher (Tanaka 1982; Bray et al.
1991). Moreover, the plasma pressure gradient exists due to the
pinch effect with distribution:
,
the condition g>1 is satisfied. Note that
the plasma loops we considered here mainly refers to the flare
loops. Observations show that the flare loops with the above
parameters are possible. For example, many solar flare loops have
a temperature up to 1 KeV and higher (Tanaka 1982; Bray et al.
1991). Moreover, the plasma pressure gradient exists due to the
pinch effect with distribution:
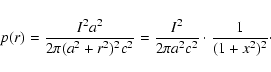 |
(14) |
Note that a is the radius of the cross-section with different
values at the foot-points and the loop-top. Then, we get the
pressure gradient as:
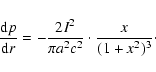 |
(15) |
However, the difference between tokamaks and solar plasma loops is
obvious. In tokamaks, the banana orbit is generated from the
magnetic field curvature and the inhomogeneity in the direction of
main radius R, while the banana orbit of the solar plasma loop
is generated mainly from the inhomogeneity at the loop direction
of 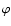 .
On the other hand, Tokamaks are annular symmetrical
systems, while the solar plasma loops seem to be a semicircular
loop. We regard the solar plasma loop as composed of two parts.
The first part is above the photosphere and includes loop-top and
its vicinity, and is located in the corona with low plasma density
and high temperature. The plasma is completely ionized, the
electron mean free path has a large value, and it can be treated
as non-collision. The magnetic mirror is mainly localized in this
part. The second part is localized in the photosphere and in the
low transition region with high plasma density and low temperature
and is partially ionized, while the electron mean free path is
very small. As the plasma in the second part is partially ionized,
it is a good conductor for the electric current. The two parts
constitute integral circuit where the electric current can flow
from one part to the other. The idea that the current exists in
narrow channels passing through the solar atmosphere and is closed
in the photosphere was mentioned first by Alfvén & Carlqvist
(1967). This property is very important for the work of the
neoclassical bootstrap current in the solar plasma loops.
.
On the other hand, Tokamaks are annular symmetrical
systems, while the solar plasma loops seem to be a semicircular
loop. We regard the solar plasma loop as composed of two parts.
The first part is above the photosphere and includes loop-top and
its vicinity, and is located in the corona with low plasma density
and high temperature. The plasma is completely ionized, the
electron mean free path has a large value, and it can be treated
as non-collision. The magnetic mirror is mainly localized in this
part. The second part is localized in the photosphere and in the
low transition region with high plasma density and low temperature
and is partially ionized, while the electron mean free path is
very small. As the plasma in the second part is partially ionized,
it is a good conductor for the electric current. The two parts
constitute integral circuit where the electric current can flow
from one part to the other. The idea that the current exists in
narrow channels passing through the solar atmosphere and is closed
in the photosphere was mentioned first by Alfvén & Carlqvist
(1967). This property is very important for the work of the
neoclassical bootstrap current in the solar plasma loops.
When conditions for the neoclassical bootstrap current are
satisfied, trapped electrons move along the banana orbit and
bounce back and forth in the mirrors, and electrons will have a net momentum when they finish a whole bounce. The net momentum will transfer to passing electrons while the trapped electrons
collide with the passing electrons. Consequently, an electric
current occurs as the bootstrap current, which is carried by
passing electrons in the direction parallel to the magnetic field lines.
In tokamaks, when the condition of the banana regime is satisfied,
the critical incidence angle
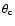 can be identified from
the expression
can be identified from
the expression
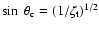 .
If the
incidence angle
.
If the
incidence angle
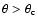 ,
electrons cannot pass through
the stronger magnetic region and bounce back to the weak region
before they reach the stronger region. When
,
electrons cannot pass through
the stronger magnetic region and bounce back to the weak region
before they reach the stronger region. When
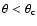 ,
they become passing electrons, and we may get the critical
parallel velocity of the passing electrons:
,
they become passing electrons, and we may get the critical
parallel velocity of the passing electrons:
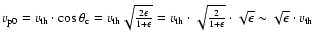 ,
where
,
where
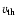 is the thermal
velocity. In the case of a straight cylinder,
is the thermal
velocity. In the case of a straight cylinder,
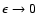 ,
,
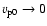 ;
then all the particles
become passing particles, and no magnetic mirror exists. The
fraction of trapped electrons is about
;
then all the particles
become passing particles, and no magnetic mirror exists. The
fraction of trapped electrons is about
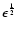 .
The canonical toroidal angular momentum of the trapped particles
.
The canonical toroidal angular momentum of the trapped particles
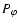 is an invariant:
is an invariant:
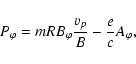 |
(16) |
where
 is the toroidal component of the vector
potential, and
is the toroidal component of the vector
potential, and
 ,
,
 .
Then the width of trapped particle orbits is approximately
.
Then the width of trapped particle orbits is approximately
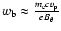 ,
where
,
where 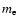 is
the electron mass. The net momentum generated by the density
gradient in the banana orbit is:
is
the electron mass. The net momentum generated by the density
gradient in the banana orbit is:
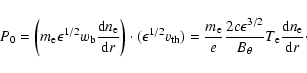 |
(17) |
Here the trapped electrons will collide not only with the passing
electrons, but also with the ions. When they collide with the
passing electrons, they diffuse in the direction of magnetic field
lines, and the scattering over an angle
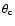 in velocity
space takes place with a typical efficiency of
in velocity
space takes place with a typical efficiency of
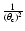 .
The trapped electrons are localized to a part
.
The trapped electrons are localized to a part
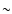
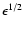 of velocity space. The characteristic time of
such diffusion is about
of velocity space. The characteristic time of
such diffusion is about
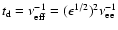 .
The momentum exchange in unit time between passing
and trapped electrons is
.
The momentum exchange in unit time between passing
and trapped electrons is
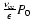 .
In the
meantime the collision between the passing electrons and the ions
make an anti-directional drift velocity
.
In the
meantime the collision between the passing electrons and the ions
make an anti-directional drift velocity 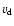 to the passing
electrons. The momentum change in unit time related to the
anti-directional drift is
to the passing
electrons. The momentum change in unit time related to the
anti-directional drift is
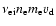 .
Equating
these two expressions for momentum exchange of the passing
electrons, we get:
.
Equating
these two expressions for momentum exchange of the passing
electrons, we get:
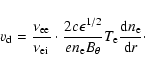 |
(18) |
This net momentum will result in a electric current as:
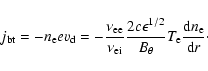 |
(19) |
Since
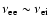 ,
the bootstrap current in tokamaks
can be expressed approximately as
,
the bootstrap current in tokamaks
can be expressed approximately as
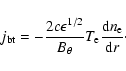 |
(20) |
This expression (20) is consistent with the results of Bickerton
(1971), Cordey (1988) etc., here
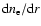 refers to the plasma
density gradient. The unit of the temperature
refers to the plasma
density gradient. The unit of the temperature 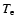 is eV.
From Table 1 we know that the bootstrap current is detected with a maximal value up to 0.85 MA, and the fraction
is eV.
From Table 1 we know that the bootstrap current is detected with a maximal value up to 0.85 MA, and the fraction
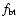 has been up to 77
has been up to 77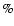 in several large tokamak devices since 1988 (Wesson 1997), here
in several large tokamak devices since 1988 (Wesson 1997), here
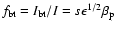 ,
I is
the total current, s a constant around 1/3,
,
I is
the total current, s a constant around 1/3,
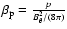 the plasma poloidal
the plasma poloidal 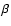 value, and the plasma pressure
value, and the plasma pressure
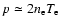 .
.
Table 1:
Experimental results of bootstrap current in tokamak devices.
The bootstrap current theory is widely accepted in the field of
nuclear fusions. It is one of the most important bases for
designing the next step of advanced tokamaks, e.g. ITER. In fact,
the bootstrap current occurs not only in tokamaks, but also in
stellarators (Peeters 2000) and toroidal multipoles (Zarnstorff
& Prager 1986).
From Sect. 2, we show that there are a lot of similarities between
tokamaks and solar current-carrying plasma loops. Both of them are
current-carrying plasma loops, all have localized magnetic mirror
configurations, all charged particles may be classified into two groups (trapped and passing particles), all have plasma pressure
gradient, and in some of the solar flare loops, the plasma is
situated in the banana regime. Thus, it is reasonable to suppose
that bootstrap currents possibly occur in solar current-carrying
plasma loops. We suppose that the total current of solar plasma
loops is composed of two parts: convectional current 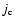 and
neoclassical bootstrap current
and
neoclassical bootstrap current 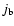 .
With the magnetic mirror
ratio
.
With the magnetic mirror
ratio 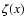 ,
we write the critical incidence angle
,
we write the critical incidence angle
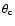 and the paralleled velocity of passing electrons as
and the paralleled velocity of passing electrons as
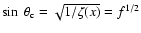 and
and
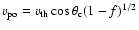 ,
respectively.
,
respectively.
Then the fraction of trapped electrons is
(1-f)1/2. The
expression of bootstrap current density in solar current-carrying
plasma loops is written in comparison with Eq. (20) as
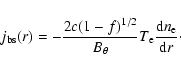 |
(21) |
The appearance of bootstrap current will disturb the equilibrium
of the magnetic tube and result in a redistribution of pressure.
As the bootstrap current is coupled strongly with the distribution
of total current, we may suppose that the distribution of total
current is approximately dominated by the pinch effect, with
expressions in Eqs. (6) and (7). We adopt Eqs. (14), (15) as the
equilibrium distribution of the plasma pressure and Eqs. (8), (9) as
the equilibrium distribution of the poloidal magnetic field,
substitute Eqs. (15), (9), and the relation
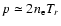 into Eq. (21), we rewrite the expression of bootstrap current
density in solar current-carrying plasma loops:
into Eq. (21), we rewrite the expression of bootstrap current
density in solar current-carrying plasma loops:
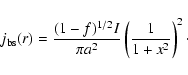 |
(22) |
The bootstrap current is
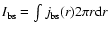 .
From
Eqs. (6) or (7), we obtain the fraction of bootstrap current in the
total current:
.
From
Eqs. (6) or (7), we obtain the fraction of bootstrap current in the
total current:
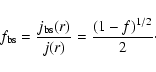 |
(23) |
Equations (22) and (23) vary with the extrapolated model of magnetic
field, i.e. the function of f. Here we quote a extrapolated
expression as follows (Takakura 1972; Huang et al. 1999):
Then the fraction of bootstrap current is about:
![\begin{displaymath}%
f_{{\rm bs}}=\frac{1}{2}[1-(1+h/d)^{-3}]^{1/2}.
\end{displaymath}](/articles/aa/full/2006/25/aa4055-05/img101.gif) |
(25) |
The bootstrap current will induce a magnetic field in the same way
as the conductive current, and of course it satisfies Ampère's Law. The occurrence of bootstrap current changes both the current density profile and the poloidal magnetic field distribution, and
affects the evolution of magnetic reconnection and the tearing
mode instability in plasma loops. When the bootstrap current 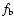 becomes large enough, a new kind of MHD instability, the neoclassical tearing mode (NTM), will be triggered. The growth
rate is obtained first by Qu & Callen (1985), and modified by
Tan (2003):
becomes large enough, a new kind of MHD instability, the neoclassical tearing mode (NTM), will be triggered. The growth
rate is obtained first by Qu & Callen (1985), and modified by
Tan (2003):
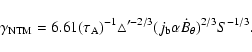 |
(26) |
Its reciprocal indicates the growth time
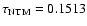
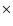
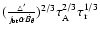 ,
here S is the magnetic Reynolds number,
,
here S is the magnetic Reynolds number,
 ,
,
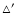 is the tearing mode instability factor,
is the tearing mode instability factor, 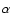 the mode number,
the mode number,
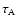 the Alfvén time scale, and
the Alfvén time scale, and
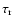 the resistive diffusive time.
The first observation of NTM is obtained by Chang et al. (1995).
As a contrast, the growth rate of classical tearing mode (CTM) is
derived by Furth et al. (1963, 1973) as:
the resistive diffusive time.
The first observation of NTM is obtained by Chang et al. (1995).
As a contrast, the growth rate of classical tearing mode (CTM) is
derived by Furth et al. (1963, 1973) as:
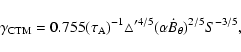 |
(27) |
and its growth time is
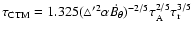 .
For solar
plasma
.
For solar
plasma
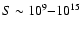 ,
if the bootstrap current occurs in
solar plasma loop and trigger NTM, then
,
if the bootstrap current occurs in
solar plasma loop and trigger NTM, then
 .
This shows that the growth rate of NTM
is much higher than that of CTM, which may cause much fast
eruptive events, and the plasma loops may become even more
unstable. Using this mechanism, we can explain some features of
solar eruptive events.
.
This shows that the growth rate of NTM
is much higher than that of CTM, which may cause much fast
eruptive events, and the plasma loops may become even more
unstable. Using this mechanism, we can explain some features of
solar eruptive events.
We may roughly classify the typical solar plasma loops into two groups: hot loops and cold loops. The first and second columns in Table 2 are the parameters in typical coronal loops (Bray et al. 1991) and calculating results. As an approximation, we let
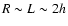 .
The typical values of total current are estimated from the combination of the model of Zaitsev et al. (1998) and the observations of vector magnetography (Khodachenko et al. 2003).
.
The typical values of total current are estimated from the combination of the model of Zaitsev et al. (1998) and the observations of vector magnetography (Khodachenko et al. 2003).
Table 2:
The loop's parameters (from Bray et al. 1991) and the bootstrap current calculating results.
From Table 2, we find that bootstrap current is negligible in
typical solar plasma loops. With average parameters of the typical
solar plasma loops in Table 2, the factor 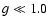 and the
plasma beyond the banana regime, so it is impossible to get a meaningful value for the bootstrap current.
and the
plasma beyond the banana regime, so it is impossible to get a meaningful value for the bootstrap current.
However, the parameters of solar plasma loops vary in a broad
range. For example, plasma density 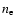 may change from
may change from
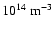 to
to
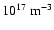 ,
and temperature
,
and temperature 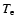 change
from 105 K to several 107 K, loop radius R,L from 5000 km to 50 000 km, etc. The range of the
change
from 105 K to several 107 K, loop radius R,L from 5000 km to 50 000 km, etc. The range of the
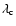 magnitude is about 1.0
magnitude is about 1.0 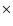 102-1.0
102-1.0 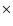
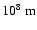 ,
and the factor g is about
10-5-20. If the plasma at
,
and the factor g is about
10-5-20. If the plasma at
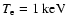 ,
,
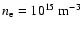 ,
we find g>1 when
,
we find g>1 when 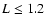
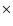
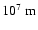 .
Likewise,
some of solar loops satisfy the conditions of the banana regime.
In this case, it is reasonable to suppose that the neoclassical
effect is measurable in these loops. A flare event with a plasma
loop is selected in comparison with the conditions of the
bootstrap current as follows.
.
Likewise,
some of solar loops satisfy the conditions of the banana regime.
In this case, it is reasonable to suppose that the neoclassical
effect is measurable in these loops. A flare event with a plasma
loop is selected in comparison with the conditions of the
bootstrap current as follows.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Figure3.eps} \end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg146.gif) |
Figure 3:
An M 3.6 flare loop of YOHKOH/SXT overlaid by SOHO/MDI
on 25 Aug. 1999. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{Figure4.eps} \end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg147.gif) |
Figure 4:
The temporal profile of GOES X-rays of the loop flare
on 25 Aug. 1999. |
| Open with DEXTER |
The third column in Table 2 shows an M 3.6 GOES flare event on 25 Aug. 1999 from 01:32 UT to 01:40 UT, with the maximum at 01:36 UT in AR8674 (Huang et al. 2003). Figure 3 is the flare loop of
YOHKOH/SXT overlaid by the magnetic map of SOHO/MDI, in which we
can estimate the geometrical parameters of the loop in Table 2.
The loop radius R and section radius a are measured by the
contour with 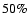 of the maximum intensity in the image of YOHKOH/SXT.
of the maximum intensity in the image of YOHKOH/SXT.
From the third column of Table 2, we find that the fraction of
bootstrap current is about
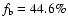 ,
and the total bootstrap
current is about 4.46
,
and the total bootstrap
current is about 4.46 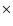
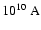 in the above flare loop,
and this value is even larger than that of many tokamaks (Table 1). As the neoclassical effect is proportional to
in the above flare loop,
and this value is even larger than that of many tokamaks (Table 1). As the neoclassical effect is proportional to 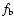 ,
it will be very obvious in the above loop.
,
it will be very obvious in the above loop.
Moreover, NTM may occur in the above loop, in which the magnetic
Reynolds number is S=2.349 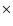 1015, and the growing
timescale of NTM is
1015, and the growing
timescale of NTM is
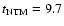
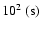 ,
while
,
while
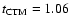
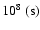 ,
so,
,
so,
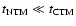 .
Figure 4 shows
the X-ray temporal profile of GOES 8, which reflects the thermal
emission feature in the flare. The rising phase in this profile is
about 3 min. Figures 5 and 7 are the time profiles,
respectively, of radio emissions (NoRP) and hard X-rays (Yohkoh/
HXT), which reflect the features of non-thermal emissions, with
the thermal features at lower frequencies and energies. The
duration of the impulsive phase is about minute, so, the NTM
growing timescale fits the observations much better than those of CTM.
.
Figure 4 shows
the X-ray temporal profile of GOES 8, which reflects the thermal
emission feature in the flare. The rising phase in this profile is
about 3 min. Figures 5 and 7 are the time profiles,
respectively, of radio emissions (NoRP) and hard X-rays (Yohkoh/
HXT), which reflect the features of non-thermal emissions, with
the thermal features at lower frequencies and energies. The
duration of the impulsive phase is about minute, so, the NTM
growing timescale fits the observations much better than those of CTM.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{Figure5.eps} \end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg156.gif) |
Figure 5:
Temporal profile of radio emission (NoRP) on 25 Aug. 1999. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{Figure6.eps} \end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg157.gif) |
Figure 6:
The contour of 17 GHz (NoRH) overlaid on Yohkoh/SXT of
the flare event on 25 Aug. 1999. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{Figure8.eps} \end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg159.gif) |
Figure 8:
The contour of Yohkoh/HXT overlaid on Yohkoh/SXT for
the flare event on 25 Aug. 1999. |
| Open with DEXTER |
In fact, the flare loop in this event looks like a single loop.
With Figs. 4 and 7, the temporal profiles are composed of a pre-phase and a main phase. The main phase occurs 3 min later than the pre-phase. The total duration of the pre-phase and main phase is about 3 min (from 01:33 to 01:36), which is comparable to the duration of the rising phase in Fig. 4, as well as to the growing time of NTM. From the left panels of
Figs. 3, 6, and 8, the pre-phase takes place in a large area
within the loop and near the loop top, and the main phase takes
place near one foot-point from the right panels of Figs. 3, 6,
and 8. These results may support the existence of bootstrap
current, the NTM instability, and magnetic reconnection may take
place inside the loop, not only in the area above the loop top,
which is a hint that the bootstrap current and NTM may provide a new mechanism for the plasma heating and particle acceleration.
Based on the similarities in magnetic configurations and plasma
behaviors between tokamaks and solar current-carrying plasma
loops, we suggest that the neoclassical effect does work in some
of the solar plasma loops. In typical coronal loops, the
neoclassical effect is too weak to be considered, while in some
flare loops with high temperature, the neoclassical effect is very
strong and the bootstrap current really exists. For example, in
the flare loop that occurred during the event on 25 Aug. 1999, the
fraction of bootstrap current in total current (
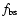 )
may
reach
)
may
reach 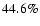 .
.
From derivations in Sect. 3, we can know that the fraction of
banana particles (trapped particles) relative to the total amount
of particles is an important parameter for the bootstrap current.
In tokamaks the fraction of trapped particles is about
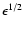 ,
while in solar current-carrying plasma loops
(1-f) 1/2. Based on the parameters from the book by Bray et al. (1991),
the fraction is about
,
while in solar current-carrying plasma loops
(1-f) 1/2. Based on the parameters from the book by Bray et al. (1991),
the fraction is about 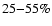 and
and 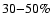 in typical cool and
hot coronal loops respectively, while in the solar flare loop, the
fraction is about 50-90%. As a comparison, in typical modern
tokamaks, the inverse aspect ratio
in typical cool and
hot coronal loops respectively, while in the solar flare loop, the
fraction is about 50-90%. As a comparison, in typical modern
tokamaks, the inverse aspect ratio
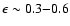 ,
the
fraction of trapped particles is about 55-75%.
,
the
fraction of trapped particles is about 55-75%.
Because of the low values of plasma beta in the solar corona, the
force-free magnetic field is widely accepted in solar coronal
loops. Based on the data from Bray et al. (1991) and the
expression from the book by Priest & Forbes (2000), the beta
value in solar flare loops is about
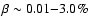 ,
while
in tokamaks, the maximum value is about 8% for the case of
circular magnetic surface, and the typical value is about
,
while
in tokamaks, the maximum value is about 8% for the case of
circular magnetic surface, and the typical value is about 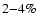 (Boozer 2004). In both of the above cases,
(Boozer 2004). In both of the above cases,
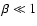 ,
all of
them are low beta plasma. We may regard them as a force-free
field, approximately. In the derivation of the bootstrap current,
the neoclassical tearing modes, and other instabilities of the
circular magnetic surface, we may use the assumption of force-free
field, i.e., low beta and
,
all of
them are low beta plasma. We may regard them as a force-free
field, approximately. In the derivation of the bootstrap current,
the neoclassical tearing modes, and other instabilities of the
circular magnetic surface, we may use the assumption of force-free
field, i.e., low beta and 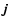
 (Bickerton et al. 1971; Qu & Callen 1985; Peeters et al.
2000). Thus, some properties of the solar flare loops are similar
to tokamaks with a circular magnetic surface.
(Bickerton et al. 1971; Qu & Callen 1985; Peeters et al.
2000). Thus, some properties of the solar flare loops are similar
to tokamaks with a circular magnetic surface.
However, in some modern tokamaks, magnetic surfaces are always
non-circular and the beta value may exceed 10%. In such cases, it
isn't suitable to deal with the derivation of bootstrap current
under the assumption of a force-free field. The bootstrap current
may occur in the plasma torus not only with the force-free field,
but also with the non-force-free field. And the high beta plasma
is one of the intended targets in magnetic confinement fusion
(MCF). In fact, when we analyze the current penetration, edged
localized modes, and the nonlinear evolution of the plasma
instabilities in modern tokamaks, the localized beta value may
exceed 10% where we should consider the non-force-free field. In
this work, we simply use a simplified way to study the possibility
of a bootstrap current in the solar plasma loops, but will make a further effort in our forthcoming work.
The bootstrap current is a new possible complement to the current
model in solar magnetic current-carrying plasma loops. With such a consideration of the new current profile, we may investigate the
evolution of tearing mode instability and the magnetic
reconnection in the loops. The occurrence of bootstrap current
changes the profile of current density and poloidal magnetic
field. When it becomes large enough, the neoclassical tearing mode
will be triggered in the whole loop to cause a fast magnetic
reconnection, which may provide an effective mechanism of the
solar plasma heating and particle acceleration.
Electric currents in magnetic plasma loops governs the total
amount of energy stored in the loops and released in the process
of magnetic reconnection. In the meantime, the tearing modes may
result in the plasma current redistribution and lead to the
formation of magnetic islands, while plasma loops may change into
filaments along the magnetic field lines. With this analysis, we
can explain the observations of the low filling factors of hot
coronal plasma loops (Martens et al. 1985).
In our forthcoming work, we will try to apply the concept of the
disruptive instability in tokamaks to solar current-carrying
plasma loops as a new model for explaining the process of the
solar and stellar eruptive events. It is emphasized that the
magnetic reconnection triggered by the tearing modes takes place
in the whole loop, and is not only localized in the current sheet
above the loop top. And this will be more effective for the plasma
heating and particle acceleration. With the high-resolution
observations of RHESSI and other instruments, we may be able to
distinguish the fine structure of loops in plasma temperature,
density, magnetic field, and their distribution to better
understand the solar eruptive events.
Acknowledgements
The authors would like to thank the anonymous referee very much
for the helpful and significant comments on our paper. We are
grateful for the useful discussions with Prof. Wang D. Y., Dr. Ji
H. S., and Dr. WuD. J. at the Purple Mountain Observatory, and with
Prof. Dong J. Q. at the Southwestern Institute of Physics, Chengdu,
China. This study is supported by the NFSC projects No. 10333030
and 10273025, and "973'' program with No. G2000078403.
- Alfvén H.,
& Carlqvist, P. 1967, Sol. Phys., 1, 220 [NASA ADS] [CrossRef] (In the text)
- Ashbourn, J. M.
A., & Woods, L. C. 2004, ApJ, 602, 1021 [NASA ADS] [CrossRef] (In the text)
- Bennett, W. H.
1934, Phys. Rev., 45, 90 [NASA ADS]
- Bickerton, R.
J., Connor, J. W., & Taylor, J. B. 1971, Nature Phys. Sci.,
229, 110 [NASA ADS] (In the text)
- Boozer, A. H. 2004,
Rev. Mod. Phys., 76, 1071 [NASA ADS] [CrossRef] (In the text)
- Bray, R. J., Cram, L.
E., Durrant, C. J., & Loughhead, R. E. 1991, Plasma Loops in
the Solar Coroma (New York: Cambridge University Press)
(In the text)
- Canfield, R.
C., De La Beaujardiere, J. F., Fan, Y., et al. 1993, ApJ, 411,
362 [NASA ADS] [CrossRef] (In the text)
- Chang, Z., Callen, J.
D., & Fridrickson, E. D. 1995, Phys. Rev. Let., 74, 4663 [NASA ADS] (In the text)
- Coenelis, D. J.
1988, Astrophys. Space Sci., 144, 319
- Cordey, J. G.,
Challis, C. D., & Stubberfield, P. M. 1988, Plasma phys.
Control. Fusion, 30, 1625 [NASA ADS] [CrossRef]
- Furth, H. P.,
Killeen, J., & Rosenbluth, M. N. 1963, Phys. Fluids, 6,
459 [CrossRef] (In the text)
- Furth, H. P.,
Rutherford, P. H., & Selberg, H. 1973, Phys. Fluids, 16,
1054 [CrossRef] (In the text)
- Huang, G. L., Fu, Q.
J., & Qin, Z. H. 1999, Astrophys. Space Sci., 266, 389 [NASA ADS] [CrossRef] (In the text)
- Huang, G. L., Wu, H.
A., Grechnev, V. V., Sych, R. A., & Altyntsev, A. T. 2003, Sol.
Phys., 213, 341 [NASA ADS] [CrossRef] (In the text)
- Hirshman, S. P.
1988, Phys. Fluids, 31, 3150 [NASA ADS] [CrossRef] (In the text)
-
Khodachenko, M., Haerendel, G., & Rucker, H. O. 2003, A&A,
401, 721 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kikuchi, M.,
& Azumi, M. 1995, Plasma Phys. Control. Fusion, 37, 1215 [NASA ADS] [CrossRef] (In the text)
- Martens, P. C.
H., Van Den Oord, G. H. J., & Hoyng, P. 1985, Sol. Phys., 96,
253 [NASA ADS] [CrossRef] (In the text)
- Peeters, A. G.
2000, Plasma Phys. Control. Fusion, 42, B231 [NASA ADS] [CrossRef] (In the text)
- Petty, C. C.,
Politzer, P. A., & Lin-Liu, Y. R. 2005, Plasma Phys. Control.
Fusion, 47, 1077 [NASA ADS] [CrossRef] (In the text)
- Priest, E., &
Forbes, T. 2000, Magnetic Reconnection-MHD Theory and Applications
(Cambridge: Cambridge University Press)
(In the text)
- Qu, W. X., & Callen, J.
D. 1985, UWPR-85-5, University of Wisconsin, Wisconsin
(In the text)
- Schuller, F. C.
1995, Plasma phys. Control. Fusion, A135, 37
- Sen, H. K., & White,
M. L. 1972, Sol. Phys., 23, 146 [NASA ADS] [CrossRef] (In the text)
- Severny, A. B.
1964, Space Sci. Rev., 3, 451 [NASA ADS] [CrossRef] (In the text)
- Spadaro, D. 2003,
Mem. S. A. It. Suppl., 3, 30 (In the text)
- Strong, K. T.,
& the Yohkoh team 2003, Space Sci. Rev., 70, 133 [NASA ADS] [CrossRef]
- Takatura, T.
1972, Sol. Phys., 77, 151 [NASA ADS]
- Tan, B. L. 2003, MA
thesis (in Chinese), Southwestern Institute of Physics, Chengdu,
China
(In the text)
- Tanaka, K.,
Watanabe, T., & Nishi, K. 1982, ApJ, 254, L59 [NASA ADS] [CrossRef] (In the text)
- Wesson, J. 1997,
Tokamak, 2nd ed. (Oxford: Claarendon Press)
(In the text)
- Zaitsev, V. V.,
& Stepanov, A. V. 1992, Sol. Phys., 139, 343 [NASA ADS] [CrossRef] (In the text)
- Zaitsev, V. V.,
Stepanov, A. V., Urpo, S., & Pohjolainen, S. 1998, A&A,
337, 887 [NASA ADS] (In the text)
- Zarnstorff,
M. C., & Prager, S. C. 1986, Phys. Fluids, 29, 308 [NASA ADS] (In the text)
Copyright ESO 2006
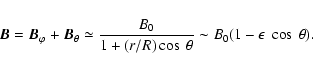
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{Figure1.eps} \end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg8.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Figure2.eps}\end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg21.gif)
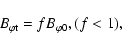
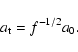
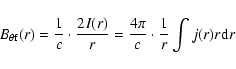
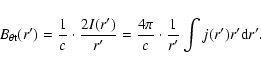
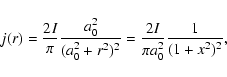
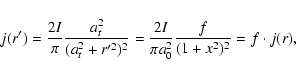
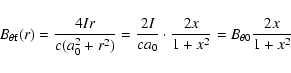
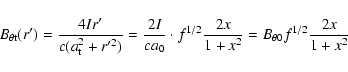
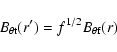
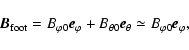
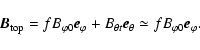
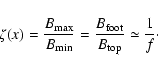
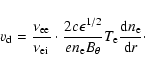
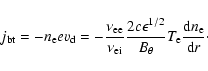
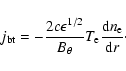
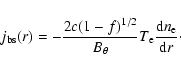
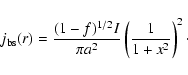
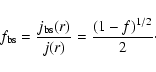
![\begin{displaymath}%
f_{{\rm bs}}=\frac{1}{2}[1-(1+h/d)^{-3}]^{1/2}.
\end{displaymath}](/articles/aa/full/2006/25/aa4055-05/img101.gif)
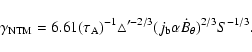
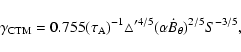
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Figure3.eps} \end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg146.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{Figure5.eps} \end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg156.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{Figure7.eps} \end{figure}](/articles/aa/full/2006/25/aa4055-05/Timg158.gif)