A&A 452, 751-762 (2006)
DOI: 10.1051/0004-6361:20054612
S. Fromang1,2 - J. Papaloizou2
1 - Astronomy Unit, Queen Mary, University of London,
Mile End Road, London E1 4NS, UK
2 -
Department of Applied Mathematics
and Theoretical Physics, University of Cambridge, Centre for
Mathematical Sciences, Wilberforce Road, Cambridge, CB3 0WA, UK
Received 30 November 2005 / Accepted 25 February 2006
Abstract
Aims. In this paper, we study the effect of MHD turbulence on the dynamics of dust particles in protoplanetary disks. We vary the size of the particles and relate the dust evolution to the turbulent velocity fluctuations.
Methods. We performed numerical simulations using two Eulerian MHD codes, both based on finite difference techniques: ZEUS-3D and NIRVANA. These were local shearing box simulations incorporating vertical stratification. Both ideal and non ideal MHD simulations with midplane dead zones were carried out. The codes were extended to incorporate different models for the dust as an additional fluid component. Good agreement between results obtained using the different approaches was obtained.
Results. The simulations show that a thin layer of very small dust particles is diffusively spread over the full vertical extent of the disk. We show that a simple description obtained using the diffusion equation with a diffusion coefficient simply expressed in terms of the velocity correlations accurately matches the results. Dust settling starts to become apparent for particle sizes of the order of 1 to 10 centimeters for which the gas begins to decouple in a standard solar nebula model at 5.2 AU. However, for particles which are 10 centimeters in size, complete settling toward a very thin midplane layer is prevented by turbulent motions within the disk, even in the presence of a midplane dead zone of significant size.
Conclusions. These results indicate that, when present, MHD turbulence affects dust dynamics in protoplanetary disks. We find that the evolution and settling of the dust can be accurately modelled using an advection diffusion equation that incorporates vertical settling. The value of the diffusion coefficient can be calculated from the turbulent velocity field when that is known for a time of several local orbits.
Key words: accretion, accretion disks - magnetohydrodynamics (MHD) - methods: numerical - planets and satellites: formation
Dust particles are very likely to be the basic building blocks that need to be assembled to make planets.
In the "core-accretion'' model for the formation of giant planets
(Mizuno 1980; Pollack et al. 1996), the growth of their solid cores
proceeds through the accretion of objects ranging from
micron sized dust particles to planetesimals of radius ![]() 10 km
to eventually reach about
10 km
to eventually reach about
![]() .
Dust is also one of the main observational
tracers of the structure of protoplanetary accretion disks
(D'Alessio et al. 2001; Adams et al. 1987). A detailed knowledge of its
dynamics is therefore needed both in order to make theoretical models and to give
the best interpretation of the observations.
.
Dust is also one of the main observational
tracers of the structure of protoplanetary accretion disks
(D'Alessio et al. 2001; Adams et al. 1987). A detailed knowledge of its
dynamics is therefore needed both in order to make theoretical models and to give
the best interpretation of the observations.
The key ingredient that drives the evolution of dust particles is the drag force they feel from the gas (Weidenschilling 1977). Gas must be present if a giant planet is to form subsequently. Drag is responsible for example for the radial migration of solid bodies toward the inner parts of a disk for which the pressure decreases radially outwards. The timescale for this migration is so rapid for centimeter and meter size bodies that it has become a problem for standard planet formation theories (Weidenschilling 1977), a resolution of which might involve the particles accumulating close to pressure maxima possibly at the center of vortices.
Another important aspect of dust dynamics is the tendency to settle towards the midplane of the disk, which increases with particle size. Because of this, centimeter and metre sized bodies accumulate close to the disk midplane. As argued by Goldreich & Ward (1973), a gravitational instability in the dust sub-disk in triggered when the dust density becomes high enough (see also Safronov 1969; and, as remarked in a note in proof by Goldreich & Ward 1973; Gurevich & Lebedinsky 1950). At this point, larger bodies known as planetesimals form.
However, because the pressure force acts only on the gas, a velocity shear between the dust sub-disk and the upper layers of the gas disk develops. This can lead to the so called "shear-induced'' turbulence that may be able to mix the dust layer enough to prevent enough gravitational settling to satisfy the condition for gravitational instability (Gómez & Ostriker 2005; Garaud et al. 2004). However, the onset of this shear induced turbulence depends on the vertical profile of the dust sub-disk which is quite difficult to calculate. Indeed, this is determined as the result of the interplay between various physical processes, such as dust coagulation, Brownian motions and turbulent mixing (Dullemond & Dominik 2005). The purpose of this paper is to investigate the behaviour of the dust disk when just one of these operates, namely MHD turbulence, from first principles.
Turbulence in protoplanetary disks is believed to be the result of the magnetorotational instability (MRI). More than a decade of analytical and numerical work (see a review by Balbus & Hawley 1998) has shown that this is capable of leading to sustained turbulence, and magnetic field with associated stresses that transport angular momentum outwards. More and more of its properties have been analysed thanks to the increased computational power currently available. However, little work has focused on the effects of MHD turbulence on dust dynamics. Carballido et al. (2005) and Johansen & Klahr (2005) analysed the radial diffusion of small particles and calculated the effective Schmidt number, which is the ratio between the anomalous turbulent viscosity and the anomalous diffusion coefficient. They found different results which could be due to their different initial setup. Johansen et al. (2006) and Fromang & Nelson (2005) studied the radial migration of centimeter and meter size bodies in turbulent disk models and found that dust trapping in local pressure maxima could be an important confining effect. Very recently, Turner et al. (2006) investigated the dispersion of a passive scalar in stratified disk models by releasing particles at high altitude in the disk. They interpreted the effect of MHD turbulence in terms of a damped wave equation. However their analysis was restricted to infinitely small particles. They did not consider the vertical settling that begins to occur for larger particles. Thus in their case stratification is only significant for the gas, being felt by the dust particles only through their strong coupling to the gas.
A first attempt to study vertical settling numerically was made through global SPH calculations by Barrière-Fouchet et al. (2005). They confirmed earlier analytical results regarding settling in a quiescent disk (Garaud & Lin 2004). However, the question of the effect of MHD turbulence was left unanswered. In this paper, we tackle this problem by means of local MHD simulations that use Eulerian finite difference codes. Our goal is to relate the dust dynamics to the properties of the turbulence. and also to characterise the amount of settling as a function of the particle size. Because of the complexity of this problem, we neglect dust coagulation and only consider populations of particles with a single specified size.
The plan of the paper is as follows: in Sect. 2, we review the characteristics of dust-gas interaction and describe a simple model to account for the dispersion of a passive scalar in a turbulent medium with random velocity field. In Sect. 3, we present the numerical methods we used together with the basic disk model which exhibits sustained MHD turbulence. We go on to study of the diffusion of very small dust particles in Sect. 4. Their evolution is analysed in the context of the simple diffusion model discussed in Sect. 2. We then show in Sect. 5 that larger dust particles start to decouple from the gas and settle toward the midplane of the disk. In this case the evolution is found to be well described using an advection diffusion equation incorporating settling together with the same diffusion coefficient that applied to the very small particles. In Sect. 6, we investigate the effect a dead zone is likely to have on these processes by setting up non-ideal MHD calculations that result in a significant midplane centered dead zone. However, gas motions are effective at preventing complete settling for 10 cm sized particles in this case too. Finally, we discuss our results in Sect. 7.
We adopt a two fluid model of the dust and gas circulating in a protoplanetary accretion disk. The basic equations are those of MHD applied to the gas component together with those of hydrodynamics applied to the dust component. The model allows the two fluids to have different flow velocities and consequently exchange momentum through drag forces.
The basic equations for the gas component
are the continuity, momentum conservation and induction
equations. In a frame rotating with angular velocity
![]() ,
with
,
with
![]() being the unit vector in the fixed direction of rotation, here called the vertical direction and
being the unit vector in the fixed direction of rotation, here called the vertical direction and ![]() being the magnitude of the angular velocity, these take the form
being the magnitude of the angular velocity, these take the form
The equations for the dust are
The dust interacts
with the gas through drag.
In this paper, we consider only dust particles that are small enough in
size that they are in the
Epstein regime (Weidenschilling 1977). The drag force
![]() acting on a single particle then takes the form
acting on a single particle then takes the form
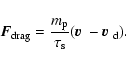 |
(6) |
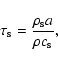 |
(7) |
When ![]() is taken to be the Keplerian angular velocity
at some disk radius,
the size of the particles there
can be measured in terms of the dimensionless parameter
is taken to be the Keplerian angular velocity
at some disk radius,
the size of the particles there
can be measured in terms of the dimensionless parameter
![]() through the relation
through the relation
Using an approach based on Boltzmann averaging,
Garaud et al. (2004) argued that the evolution of the dust particle
distribution can be
accurately determined by modelling it as a pressureless fluid as long as the
dimensionless parameter
![]() is less than unity. This is
the case for the dust particles over most of the
disk domains considered in this
paper. Accordingly we adopt the two fluid description in preference
to, for example a much more computationally demanding N-body
approach. We also assume throughout this paper that the dust particles
remain electrically neutral so that they do not react to the
magnetic field.
is less than unity. This is
the case for the dust particles over most of the
disk domains considered in this
paper. Accordingly we adopt the two fluid description in preference
to, for example a much more computationally demanding N-body
approach. We also assume throughout this paper that the dust particles
remain electrically neutral so that they do not react to the
magnetic field.
We here note that in the limit
![]() the
two fluid description can be reduced to one of a single fluid
with MHD together with an advection diffusion equation describing the evolution of the
dust. To see this we introduce a density
the
two fluid description can be reduced to one of a single fluid
with MHD together with an advection diffusion equation describing the evolution of the
dust. To see this we introduce a density
![]() and a velocity
and a velocity
![]() associated with the combined fluid.
These are defined through
associated with the combined fluid.
These are defined through
| (15) |
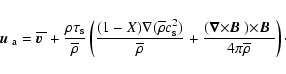 |
(18) |
The above analysis suggests that the dust mass fraction is advected
as a passive scalar. When the gas is turbulent part of the velocity
field will be turbulent. The characteristic correlation
time associated with the turbulence is expected to be a fraction
of an orbital period (see below), whereas the underlying settling
takes place on a significantly longer timescale ![]()
![]() Thus we separate the effects of turbulent diffusion and settling
and
consider the simplest case of the dispersion of a
passive scalar in steady state, homogeneous and isotropic
turbulence. This means that effects related to the imperfect coupling
between dust and gas such as turbulent enhancement of grain-grain
collisions are neglected (Morfill 1985; Voelk et al. 1980). It is well
known (Batchelor 1949; Taylor 1921) that the mean
square displacement of the scalar from its location
at some initial time can be expressed in terms of the fluid
velocity fluctuations. We adopt a Lagrangian approach and for simplicity
consider only the vertical z-direction. Extension to consider the
other coordinate directions is straightforward but uninformative in our case.
Thus we separate the effects of turbulent diffusion and settling
and
consider the simplest case of the dispersion of a
passive scalar in steady state, homogeneous and isotropic
turbulence. This means that effects related to the imperfect coupling
between dust and gas such as turbulent enhancement of grain-grain
collisions are neglected (Morfill 1985; Voelk et al. 1980). It is well
known (Batchelor 1949; Taylor 1921) that the mean
square displacement of the scalar from its location
at some initial time can be expressed in terms of the fluid
velocity fluctuations. We adopt a Lagrangian approach and for simplicity
consider only the vertical z-direction. Extension to consider the
other coordinate directions is straightforward but uninformative in our case.
Let
z(z0,t) be the position of a particle which was located at z=z0 at t=0. Its displacement Z(z0,t) is given by
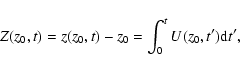 |
(19) |
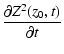 |
= | 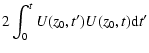 |
|
| = | 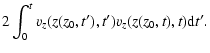 |
(20) |
| (23) |
The calculation of the velocity correlation described above
is greatly simplified if the integral in (21)
can be performed at a fixed location using Eulerian velocity components,
such that
![]() is replaced by
is replaced by
![]() with z0 being fixed.
This is possible when the distance moved by a particle during the
turbulence correlation time is small compared to the characteristic
scale of the turbulence (Biferale et al. 1995) as would always be
the case if the turbulent velocities were reduced in magnitude
while retaining their spatial and temporal characteristics. This situation
seems to be a reasonable approximation in the case of the MRI where
the turbulence is subsonic and we note that it would be even better
in dead zones where the turbulent velocity fluctuations are reduced in
magnitude. In this case Szz simply scales down as the square of
the velocity amplitude. Furthermore for the turbulence we consider,
there is no preferred location or particles
in the above ensemble averages and all fixed locations can be assumed
to get complete information about all particle realisations.
Then it is reasonable to replace the
ensemble average over all possible particle realisations as a function
of time, by one over all possible fixed locations using the
velocities there at that time. Therefore, from now on, we adopt
with z0 being fixed.
This is possible when the distance moved by a particle during the
turbulence correlation time is small compared to the characteristic
scale of the turbulence (Biferale et al. 1995) as would always be
the case if the turbulent velocities were reduced in magnitude
while retaining their spatial and temporal characteristics. This situation
seems to be a reasonable approximation in the case of the MRI where
the turbulence is subsonic and we note that it would be even better
in dead zones where the turbulent velocity fluctuations are reduced in
magnitude. In this case Szz simply scales down as the square of
the velocity amplitude. Furthermore for the turbulence we consider,
there is no preferred location or particles
in the above ensemble averages and all fixed locations can be assumed
to get complete information about all particle realisations.
Then it is reasonable to replace the
ensemble average over all possible particle realisations as a function
of time, by one over all possible fixed locations using the
velocities there at that time. Therefore, from now on, we adopt
In this context we comment that the modelling of dust spreading using a diffusion coefficient obtained by the above procedure, on account of the averaging involved, of necessity only describes evolution occurring on time scales significantly longer than the correlation time associated with the turbulence. Behaviour occurring on the correlation time scale or faster cannot be meaningfully considered in this approach.
In this paper, we use two well known finite difference codes: ZEUS-3D
(Stone & Norman 1992a,b) and NIRVANA
(Ziegler & Yorke 1997). Both are
used here to solve the
MHD equations in the shearing sheet approximation
(Goldreich & Lynden-Bell 1965), including vertical stratification.
In this approximation a small region of the disk is considered
in the neighbourhood of some point rotating in circular
orbit with the local Keplerian angular
velocity. Local Cartesian coordinates are used with the x axis
along the line connecting the origin to the central mass but pointing away from it, and
the y axis directed in the direction of orbital motion.
When dust is absent the equations solved are (1)-(3)
with
![]() adapted to the shearing sheet
by taking
adapted to the shearing sheet
by taking
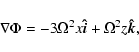 |
(28) |
In the two codes, we employ two different algorithms to describe the evolution of the dust particles that are the main focus of this paper. ZEUS-3D was extended to describe the dust particle evolution by means of a second, pressureless fluid (Fromang & Nelson 2005) using Eqs. (4), (5) together with appropriate drag forces in the low X limit. Because of the short stopping time of the dust particles, the effect of these is computed implicitly.
On the other hand, NIRVANA solved the MHD Eqs. (12), (13)
together with (3). Consistent with the low X limit the mean
flow velocity
![]() was used in (3).
The evolution of the dust mass fraction was calculated by solving
Eq. (17) but with the use of an advection
velocity limiter. This was applied such as to restrict the settling velocity
was used in (3).
The evolution of the dust mass fraction was calculated by solving
Eq. (17) but with the use of an advection
velocity limiter. This was applied such as to restrict the settling velocity
![]() to be less than
to be less than
![]() in magnitude.
This is required in the low density upper layers where dust gas coupling becomes weak and where the theoretical description breaks down.
However, because it applies only in the upper layers, calculations
of settling dust are insensitive to this cut off that is required for numerical reasons.
in magnitude.
This is required in the low density upper layers where dust gas coupling becomes weak and where the theoretical description breaks down.
However, because it applies only in the upper layers, calculations
of settling dust are insensitive to this cut off that is required for numerical reasons.
In this section, we describe the underlying disk model we used and highlight some of the properties of the MHD turbulence that are of importance for the dynamics of the dust that we go on to study.
The initial disk setup in the absence of dust is very similar to the model of
Stone et al. (1996). The parameters are those of the
standard shearing box. The equation of state for the gas is isothermal,
![]() .
Because of the vertical stratification, the initial density
distribution is given by:
.
Because of the vertical stratification, the initial density
distribution is given by:
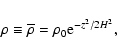 |
(29) |
In ZEUS-3D, we therefore made the vertical gravitational force
continuous at the boundary by
writing the gravitational potential as
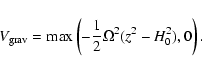 |
(30) |
In NIRVANA, we further checked for the existence
of numerically generated fluctuations
by applying the additional procedure of making the vertical
gravitational acceleration continuous throughout.
To do this the usual acceleration was applied for
![]() This was then reduced to zero in
This was then reduced to zero in ![]() [2.25H ,2.4 H]
by means of linear interpolation and
set to zero for |z|> 2.4H. As indicated below, similar results were
obtained with both codes.
[2.25H ,2.4 H]
by means of linear interpolation and
set to zero for |z|> 2.4H. As indicated below, similar results were
obtained with both codes.
In both cases the computational box is initially threaded by a magnetic field
with zero net flux, being of the form
| (31) |
We describe here simulation results, focusing on those
obtained with ZEUS-3D. The results obtained using NIRVANA were
very similar and accordingly only a few need to be illustrated here.
As expected, the initial set up is unstable to the MRI.
Its early growth is illustrated in
Fig. 1. Corresponding results obtained with NIRVANA
are plotted in Fig. 2. Both figures show the
time history of the
volume averaged Maxwell stress (upper solid line) and Reynolds
stress (lower solid line), normalised by the average midplane
pressure P0. They are respectively defined as
| |
= | 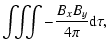 |
(32) |
| = | (33) |
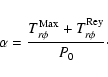 |
(34) |
In Sect. 2.3, we argued that the diffusion of small dust
particles depends on velocity fluctuations in the disk. In
Fig. 4, we plot their vertical profile normalised by the
sound speed. The dashed
curve corresponds to the radial velocity fluctuations, while the
azimuthal and vertical fluctuations are respectively given by the solid
and dotted curves. The midplane values given by this plot are
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4612fig1.ps}\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg123.gif) |
Figure 1: Time history of the total stress ( dashed line), the sum of the Maxwell ( upper solid line) and the Reynolds stresses ( lower solid line) obtained with ZEUS-3D. All stresses are normalised by the midplane pressure. After the linear growth of the MRI, the total stress reaches a nonzero quasi-steady state, showing that the turbulence is sustained. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4612fig2.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg124.gif) |
Figure 2: As in Fig. 1 but obtained with NIRVANA. |
| Open with DEXTER | |
| |
Figure 3: Gas distribution in the (r,z) plane. Density fluctuations across the disk are clearly visible, showing that the entire disk is turbulent at this stage. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4612fig4.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg126.gif) |
Figure 4: Velocity dispersion as a function of height, normalised by the sound speed. The three curves corresponds to the radial ( dashed line), azimuthal ( solid line) and vertical ( dotted line) velocity dispersions. |
| Open with DEXTER | |
In this section, we present the results we obtained for very small
particles using ZEUS-3D. For a given disk model, simulations of dust
evolution are defined by the
value of
![]() .
This is actually a function of gas density.
To obtain a fixed parameter defining a given simulation,
.
This is actually a function of gas density.
To obtain a fixed parameter defining a given simulation,
![]() is
evaluated using the initial uniform midplane disk gas density. Where
this is not stated explicitly it should be taken as read. We focus here
on particles for which
is
evaluated using the initial uniform midplane disk gas density. Where
this is not stated explicitly it should be taken as read. We focus here
on particles for which
![]() in the midplane of the
initial disk. Equation (9) indicates that this
corresponds to micron size particles. This small value of
in the midplane of the
initial disk. Equation (9) indicates that this
corresponds to micron size particles. This small value of
![]() means that the dust particles are very well coupled
to the gas and behave almost like a passive scalar.
means that the dust particles are very well coupled
to the gas and behave almost like a passive scalar.
![\begin{figure}
\par\mbox{\includegraphics[scale=0.15]{4612fig5a.ps}\includegraph...
...g5d.ps}\hspace{0.5cm}
\includegraphics[scale=0.15]{4612fig5e.ps} }\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg128.gif) |
Figure 5: The first four snapshots show the dust distribution in the (r,z) plane obtained with ZEUS-3D at times t=3, 5, 10 and 15 orbits after the dust is introduced ( from left to right). The last snapshot on the right represents the gas distribution at t=15 orbits. At that time, the micron-sized dust particles are well mixed in the entire disk. The dust density distribution is also seen to be well correlated with the gas density. |
| Open with DEXTER | |
The dust is initially distributed in a thin layer around the disk
midplane. Initially, the vertical profile of
![]() is taken to be a
Gaussian with a thickness
is taken to be a
Gaussian with a thickness
![]() .
Under the effects of MHD turbulence,
this small layer broadens with time. We found that its precise
evolution depends largely on the particular time at
which the dust particles are released in the disk. In order to improve
the statistics, we computed nine simulations,
by restarting the disk model described in Sect. 3.2 at
times t=40, 45, 50, 55, 60, 65, 70, 75 and 80 orbits.
.
Under the effects of MHD turbulence,
this small layer broadens with time. We found that its precise
evolution depends largely on the particular time at
which the dust particles are released in the disk. In order to improve
the statistics, we computed nine simulations,
by restarting the disk model described in Sect. 3.2 at
times t=40, 45, 50, 55, 60, 65, 70, 75 and 80 orbits.
Figure 5 illustrates the typical evolution of such a model. From left to right, the first four snapshots on the left show the dust density distribution in the (r,z) plane at time t=3, 5, 10 and 15 orbits (measured after the dust has been introduced). The last snapshot shows the corresponding gas distribution at t=15 orbits. The dust is seen to spread quite rapidly. At 15 orbits, it is almost filling the entire vertical extend of the disk. At later times, this distribution does not change qualitatively. By comparing the dust and the gas distribution at t=15 orbits, one can also see that they are very well correlated. We also found that the initial distribution of the dust has very little effect on this final state: starting with an initial dust distribution such that the gas-to-dust ratio is uniform gives an end product almost indistinguishable from the last two snapshots of Fig. 5.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4612fig6.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg131.gif) |
Figure 6:
Time history of the function
|
| Open with DEXTER | |
In order to make a more quantitative comparison between the
results of these simulations and the simple theory presented in
Sect. 2.3, we computed the functions Szz and ![]() according to Eqs. (24) and (25). To
calculate the former, we first volume averaged the velocity product
in radius and azimuth. The vertical average is taken only within Haround the disk equatorial plane. Indeed, the behaviour of the
turbulence away from the midplane is likely to depart very much from
being homogeneous and isotropic
and may be influenced by the vertical boundary conditions.
To reduce the statistical noise, the result
is then averaged over the nine different models we computed. The resulting
function
according to Eqs. (24) and (25). To
calculate the former, we first volume averaged the velocity product
in radius and azimuth. The vertical average is taken only within Haround the disk equatorial plane. Indeed, the behaviour of the
turbulence away from the midplane is likely to depart very much from
being homogeneous and isotropic
and may be influenced by the vertical boundary conditions.
To reduce the statistical noise, the result
is then averaged over the nine different models we computed. The resulting
function
![]() is plotted in Fig. 6 using the
solid line. The dotted line represents the time variation of the function
is plotted in Fig. 6 using the
solid line. The dotted line represents the time variation of the function
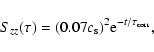 |
(35) |
Integrating Szz over time gives
![]() .
The left panel of
Fig. 7 shows the time evolution of
.
The left panel of
Fig. 7 shows the time evolution of
![]() .
Figure 8 gives results of similar calculations done
from runs with NIRVANA (see below).
.
Figure 8 gives results of similar calculations done
from runs with NIRVANA (see below). ![]() is first observed to rise
at early times. This is in good agreement with
Eq. (26). In fact, the prediction given by
Eq. (26) is represented by the dashed line on the
right panel of Fig. 7, which is an enlargement of the
left panel at small times. It uses
is first observed to rise
at early times. This is in good agreement with
Eq. (26). In fact, the prediction given by
Eq. (26) is represented by the dashed line on the
right panel of Fig. 7, which is an enlargement of the
left panel at small times. It uses
![]() ,
as
obtained in Sect. 3.2. This early linear rise of the
diffusion coefficient was also observed by
Carballido et al. (2005). Here, we see that it is naturally understood in
terms of the fluid velocity correlations. After this initial rise,
,
as
obtained in Sect. 3.2. This early linear rise of the
diffusion coefficient was also observed by
Carballido et al. (2005). Here, we see that it is naturally understood in
terms of the fluid velocity correlations. After this initial rise,
![]() is observed to reach a roughly constant value of
is observed to reach a roughly constant value of
![]() .
This value nicely compares with the naïve estimate of
Eq. (27). Indeed, taking the value of
.
This value nicely compares with the naïve estimate of
Eq. (27). Indeed, taking the value of
![]() and
and
![]() derived above, one obtain
derived above, one obtain
![]() ,
a value which is surprisingly close to the result of
the numerical simulations. This analytical estimate is represented by
the dashed line in Fig. 7.
,
a value which is surprisingly close to the result of
the numerical simulations. This analytical estimate is represented by
the dashed line in Fig. 7.
If the dust distribution undergoes diffusive evolution as indicated
by the simple theory,
![]() should
satisfy a diffusion equation of the form
should
satisfy a diffusion equation of the form
The comparison between the analytical solution of Eq. (36) and the results of the numerical simulations is shown in Fig. 9. It is illustrated by nine panels. They correspond, from top left to bottom right, to times t=0.48, 0.80, 1.12, 1.44, 1.76, 2.08, 2.40, 2.72 and 3.04 orbits (measured after the dust was introduced into the disk). On each panel, there are four curves. The solid line shows the vertical profile of the dust-to-gas ratio, averaged between the nine models we ran and normalised by the value in the equatorial plane at t=0. The three dashed curves are the solutions of Eq. (36) using the three diffusion coefficients mentioned above. Of course, the smaller the value of D, the less the dust is spread across the disk at a given time.
The agreement between the numerical results and the simple model is fairly
good. In all panels, the solid line is seen to have the best agreement
with the middle dashed curve, calculated using
![]() .
The
agreement is especially good at low altitude (typically z<H). This
was to be expected: first, this is the region in space where we
performed the volume average used to calculate
the function Szz. Second, the theory supposes that
the turbulence is homogeneous and isotropic. This results in only possibly reasonable
modelling near the
midplane. The anisotropy of the turbulence is expected to increase
away from the midplane, as the density stratification becomes
stronger. From Fig. 9, there are some indications
that the estimated diffusion coefficient might increase with
height. Indeed, at late times, for
z>H, the solid line shows better agreement with the dashed curve
computed using
.
The
agreement is especially good at low altitude (typically z<H). This
was to be expected: first, this is the region in space where we
performed the volume average used to calculate
the function Szz. Second, the theory supposes that
the turbulence is homogeneous and isotropic. This results in only possibly reasonable
modelling near the
midplane. The anisotropy of the turbulence is expected to increase
away from the midplane, as the density stratification becomes
stronger. From Fig. 9, there are some indications
that the estimated diffusion coefficient might increase with
height. Indeed, at late times, for
z>H, the solid line shows better agreement with the dashed curve
computed using
![]() than at lower altitudes, indicating that
dust particles are spread more efficiently than the simple theory
suggests. This is also supported by results of runs performed with NIRVANA
to test the simple diffusion theory. As with ZEUS-3D we considered
runs restarted from the basic disk model after 33, 40, and 60 orbits. We evaluated the function
than at lower altitudes, indicating that
dust particles are spread more efficiently than the simple theory
suggests. This is also supported by results of runs performed with NIRVANA
to test the simple diffusion theory. As with ZEUS-3D we considered
runs restarted from the basic disk model after 33, 40, and 60 orbits. We evaluated the function
![]() by performing ensemble averages both over grid points
such that |z| < H, and for grid points such that
H <|z| < 2Hand then averaging over the models. Results are shown in Fig. 8. The indication is, in agreement with ZEUS, that for |z| < H,
by performing ensemble averages both over grid points
such that |z| < H, and for grid points such that
H <|z| < 2Hand then averaging over the models. Results are shown in Fig. 8. The indication is, in agreement with ZEUS, that for |z| < H, ![]() approaches
approaches ![]()
![]() but for
H < |z| < 2H,
but for
H < |z| < 2H, ![]() is
is ![]() 4 times larger.
4 times larger.
![\begin{figure}
\par\includegraphics[width=5.75cm,clip]{4612fig7a.ps}\hspace*{4mm}
\includegraphics[width=5.85cm,clip]{4612fig7b.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg142.gif) |
Figure 7:
Diffusion coefficient as a function of time, normalised by
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4612fig8.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg143.gif) |
Figure 8:
As in Fig. 7 but for runs performed
with NIRVANA. The lower curve applies for |z| < H, and
the upper curve for
H < |z| < 2H. In the former case the diffusion
coefficient is observed to attain
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.3cm,clip]{4612fig9.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg144.gif) |
Figure 9:
Vertical profile of the dust to gas ratio as a function of
time. The different panels correspond, from top to bottom and from
left to right, to t=0.48, 0.80, 1.12, 1.44, 1.76, 2.08,
2.40, 2.72 and 3.04 orbits. On
each panels, the solid line is the result of the simulations
performed with ZEUS-3d,
averaged over the nine models described in the text. Three dashed
curves are plotted. They
show the solution of Eq. (36), computed using
|
| Open with DEXTER | |
In the previous section, we have studied the effect of MHD turbulence on very small dust particles, which behave essentially like passive scalars. In this section, we will focus on larger particles for which the settling processes described in the introduction are fast in the absence of turbulence.
We focus on three sizes, for which the parameter
![]() is
respectively 0.001, 0.01 and 0.1 in the midplane of the initial
disk. Using Eq. (9), these values correspond respectively
to 1 mm, 1 cm and 10 cm. In the absence of turbulence, the
typical settling timescale can be written (Dullemond & Dominik 2004)
is
respectively 0.001, 0.01 and 0.1 in the midplane of the initial
disk. Using Eq. (9), these values correspond respectively
to 1 mm, 1 cm and 10 cm. In the absence of turbulence, the
typical settling timescale can be written (Dullemond & Dominik 2004)
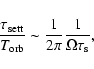 |
(37) |
At t=40 orbits, we introduced the particles into the turbulent disk
model with the
same vertical distribution as for the small particles discussed in
Sect. 4. Their evolution was then followed until the
vertical profile of the dust-to-gas ratio reaches a steady
state. Once again, by running models in which the initial
dust-to-gas ratio is uniform, we checked that this final
distribution does not depend on the initial conditions.
| |
Figure 10:
Dust distribution in the (r,z) plane, obtained with ZEUS-3D,
after a quasi-steady
state has been reached. From left to right, the different panels
correspond to
|
| Open with DEXTER | |
The results obtained with ZEUS-3D are illustrated in
Fig. 10. This
shows the typical distribution of the dust particles in the (r,z) plane after they have reached a steady state. From left to right, the
snapshots corresponds to
![]() ,
0.01 and 0.1. While the smallest dust particles are still efficiently spread
across the disk (compare with the fourth panel of
Fig. 5), there are some signs of vertical settling
for the larger particles. This is obvious in particular for the
largest particles. But note however that turbulence is quite
efficient at preventing the complete settling of these
particles. As discussed above, a very thin dust subdisk would
form in just a few orbits in a quiescent disk. We have confirmed
that very similar results for the degree of settling
as a function of
,
0.01 and 0.1. While the smallest dust particles are still efficiently spread
across the disk (compare with the fourth panel of
Fig. 5), there are some signs of vertical settling
for the larger particles. This is obvious in particular for the
largest particles. But note however that turbulence is quite
efficient at preventing the complete settling of these
particles. As discussed above, a very thin dust subdisk would
form in just a few orbits in a quiescent disk. We have confirmed
that very similar results for the degree of settling
as a function of
![]() (evaluated in the midplane) are
obtained with NIRVANA which employed
an advection diffusion treatment of the dust mass fraction.
Steady state distributions corresponding to those shown in
Fig. 10 are plotted in Fig. 11.
Again these are found to be initial condition independent for distributions initiated
in the midplane regions.
(evaluated in the midplane) are
obtained with NIRVANA which employed
an advection diffusion treatment of the dust mass fraction.
Steady state distributions corresponding to those shown in
Fig. 10 are plotted in Fig. 11.
Again these are found to be initial condition independent for distributions initiated
in the midplane regions.
![\begin{figure}
\par\includegraphics[scale=0.43]{4612fig11a.ps}\includegraphics[scale=0.43]{4612fig11b.ps}\includegraphics[scale=0.43]{4612fig11c.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg149.gif) |
Figure 11: As in Fig. 10 but for results obtained with NIRVANA. |
| Open with DEXTER | |
Once again, we can make use of the simple theory developed in
Sect. 2.3 to interpret these results. However, in this case the full
advection diffusion Eq. (17) incorporating settling must be used
with an anomalous diffusion coefficient. Neglecting Lorentz forces, in the low X
or
![]() limit
this gives (Schräpler & Henning 2004; Dubrulle et al. 1995).
limit
this gives (Schräpler & Henning 2004; Dubrulle et al. 1995).
All the results presented so far in this paper suppose that gas and magnetic field are perfectly coupled throughout the entire vertical extent of the disk. However, protoplanetary disks are probably cold and dense enough that this perfect coupling is unlikely, at least in some regions of the disk. This situation has generated the "layered accretion'' paradigm (Gammie 1996) in which the gas is turbulent only in the upper layers of the disk, while a quiescent (or "dead'') zone exists around the midplane. The extent of this dead zone is very uncertain, since it depends on the ionising source and on the chemistry (Ilgner & Nelson 2006; Sano et al. 2000; Fromang et al. 2002), but its existence is likely. In this section, we investigate how the presence of a dead zone would influence the results described in the previous sections.
The problem of layered
turbulence in local numerical simulations of stratified disks has
already been studied by Fleming & Stone (2003). In this section, we
reproduce one of their disk models by allowing the resistivity ![]() to be a
function of position. We choose the vertical profile of
to be a
function of position. We choose the vertical profile of ![]() such that our model is identical to the "larger dead
zone'' model of Fleming & Stone (2003):
such that our model is identical to the "larger dead
zone'' model of Fleming & Stone (2003):
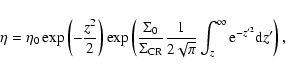 |
(39) |
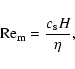 |
(40) |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4612fig12.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg159.gif) |
Figure 12:
Steady state vertical profile of the dust-to-gas ratio when
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4612fig13.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg160.gif) |
Figure 13:
Same as Fig. 12, but for the case
|
| Open with DEXTER | |
Using this new underlying disk model and introducing dust particles, we used
ZEUS-3D to recalculate the models described in
Sect. 5 for which
![]() and
and
![]() .
After a few orbits, the dust distribution reaches
a new equilibrium state. It is represented in
Fig. 15 (for
.
After a few orbits, the dust distribution reaches
a new equilibrium state. It is represented in
Fig. 15 (for
![]() )
and
Fig. 16 (for
)
and
Fig. 16 (for
![]() ). In both cases,
the solid line shows the vertical profile of the dust-to-gas ratio in the
nonideal case with a dead zone, while the dashed line corresponds to the fully
turbulent case. As expected, the thickness of the dust
sub-disk is smaller in the former case.
). In both cases,
the solid line shows the vertical profile of the dust-to-gas ratio in the
nonideal case with a dead zone, while the dashed line corresponds to the fully
turbulent case. As expected, the thickness of the dust
sub-disk is smaller in the former case.
It is possible to compare these results to those obtained using the simple
model presented in Sect. 2.3. To do so, we first note
that close to the midplane, the stopping time
![]() is nearly constant. A
steady-state solution to Eq. (38) can be
written in that case as
is nearly constant. A
steady-state solution to Eq. (38) can be
written in that case as
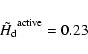 |
(43) |
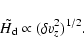 |
(44) |
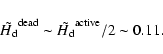 |
(45) |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{4612fig14.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg170.gif) |
Figure 14: Same as Fig. 4, but for the "larger dead zone'' model of Fleming & Stone (2003). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{4612fig15.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg171.gif) |
Figure 15:
Steady state vertical profile of the dust to gas ratio in
the ideal MHD case ( dashed line) and when a dead zone is
present around the equatorial plane of the disk ( solid
line). The parameter
|
| Open with DEXTER | |
The same procedure was followed in the model for which
![]() .
In that case, we found
.
In that case, we found
![]() and
and
![]() .
The dust-to-gas ratio vertical profiles
derived using these two values are plotted in
Fig. 15 with dotted lines. The agreement with
the solid line is quite good. However, there is a poor agreement with
the dashed line. This is because the dust is spread to higher altitudes
in that case. The hypothesis that
.
The dust-to-gas ratio vertical profiles
derived using these two values are plotted in
Fig. 15 with dotted lines. The agreement with
the solid line is quite good. However, there is a poor agreement with
the dashed line. This is because the dust is spread to higher altitudes
in that case. The hypothesis that
![]() is a constant which we used
to derive Eqs. (41) and (42)
starts to break down, which explain the discrepancy with the
numerical result.
is a constant which we used
to derive Eqs. (41) and (42)
starts to break down, which explain the discrepancy with the
numerical result.
In this paper, we studied the effects of MHD turbulence on dust
settling by means on local numerical simulations
performed using ZEUS-3D and NIRVANA, being Eulerian MHD codes using
finite differences.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{4612fig16.ps}
\end{figure}](/articles/aa/full/2006/24/aa4612-05/Timg174.gif) |
Figure 16:
Same as Fig. 15, but for the case
|
| Open with DEXTER | |
We first investigated the case of very small particles which are strongly
coupled to the gas. Turbulent velocity fluctuations were found to
cause an initially thin dust sub-disk to spread. The time evolution of the
vertical profile for the dust-to-gas ratio can be well modelled
by a diffusion equation, with a diffusion coefficient Dthat can be expressed in terms of turbulent velocity correlations. We found that
a simple analytical estimate of D can be obtained in terms of
the mean square amplitude of the
velocity fluctuations
![]() and their correlation time
and their correlation time
![]() both of which are properties of the turbulence alone:
both of which are properties of the turbulence alone:
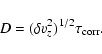 |
(46) |
A standard procedure in this type of analysis is to determine the value of the
Schmidt number ![]() ,
defined as the ratio between the anomalous viscosity
and the diffusion coefficient. The standard approach in dust diffusion
modelling is to take
,
defined as the ratio between the anomalous viscosity
and the diffusion coefficient. The standard approach in dust diffusion
modelling is to take
![]() (Ilgner et al. 2004; Schräpler & Henning 2004; Dullemond & Dominik 2004). In
non zero net flux local simulations of radial dust diffusion,
Carballido et al. (2005) found
(Ilgner et al. 2004; Schräpler & Henning 2004; Dullemond & Dominik 2004). In
non zero net flux local simulations of radial dust diffusion,
Carballido et al. (2005) found
![]() ,
while Johansen & Klahr (2005)
reported
,
while Johansen & Klahr (2005)
reported
![]() for vertical diffusion in zero net flux
simulations. Turner et al. (2006) also reported a near unity Schmidt
number in their calculations. It is worth comparing these values to the
Schmidt number we can derive from our simulations. By averaging
the total stress represented in Fig. 1 between 20 and 100 orbits, one obtains
for vertical diffusion in zero net flux
simulations. Turner et al. (2006) also reported a near unity Schmidt
number in their calculations. It is worth comparing these values to the
Schmidt number we can derive from our simulations. By averaging
the total stress represented in Fig. 1 between 20 and 100 orbits, one obtains
![]() .
This, together with the value of the diffusion coefficient
obtained from the velocity fluctuations gives
.
This, together with the value of the diffusion coefficient
obtained from the velocity fluctuations gives
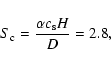 |
(47) |
When dust particles grow to centimeter sizes, we found that they
start to decouple from the turbulence and settle towards the
midplane. The steady state profile of the
dust-to-gas ratio is well approximated by the solution of an
advection-diffusion equation. Even for particles as
large as 10 cm, we found that the dust sub-disk is significantly spread
since its semi-thickness ![]() equals 0.23H, while the settling
timescale in a quiescent disk is very short in that case (1.6 orbits). We note however that radial migration is important for
particles of this size and the interplay between that migration and
MHD turbulence in a stratified disk could lead to complex phenomena, such as local
enhancement of the dust density
(Fromang & Nelson 2005) that might affect this picture.
equals 0.23H, while the settling
timescale in a quiescent disk is very short in that case (1.6 orbits). We note however that radial migration is important for
particles of this size and the interplay between that migration and
MHD turbulence in a stratified disk could lead to complex phenomena, such as local
enhancement of the dust density
(Fromang & Nelson 2005) that might affect this picture.
Because they are cold and dense, protoplanetary disks are unlikely to have adequate ionisation to be turbulent everywhere. Therefore we also investigated the effect of the presence of a dead zone around the midplane. As expected, we found thinner dust sub-disks in that case. Similarly to previous studies (Fleming & Stone 2003), we found the dead zone is able to maintain significant activity (excited by the turbulent velocity fluctuations of the active zone). This activity is able to prevent the complete settling of 10 cm size particles. However, we want to emphasise that for computational reasons, our analysis was limited to a case in which the mass of the dead zone roughly equals the mass of the active zone. We expect our result to be modified in cases where the mass of the dead zone is much larger than that of the active zone and therefore only apply them to dead zones that involve a modest fraction of the local surface density.
Nonetheless for conditions appropriate to a minimum mass solar nebula, the work presented here that considered MHD turbulence, taken together with that of eg. Gómez & Ostriker (2005) indicates that gravitational instability of the dust layer is unlikely and that the formation of objects of planetesimal size may depend on phenomena such as densification in vortices operating together with vertical settling.
For practical reasons, we neglected grain growth in this work. This is an important simplification, as dust particles are likely to grow at the same time as they settle toward the equatorial plane of the disk (Cuzzi et al. 1996; Dullemond & Dominik 2005). Simulations of the evolution of an entire dust population through grain growth and turbulent stirring, that take account of both radial and vertical disk structure, are very challenging with present day computational capabilities, but will have to be performed in the future.
Acknowledgements
Some of the simulations presented in this paper were performed on the QMUL High Performance Computing Facility purchased under the SRIF initiative.