A&A 452, 795-802 (2006)
DOI: 10.1051/0004-6361:20053921
Enrichment of the ICM of galaxy clusters due to ram-pressure stripping
W. Domainko1 - M. Mair1 - W. Kapferer1 - E. van Kampen1 - T. Kronberger2,1 - S. Schindler1 - S. Kimeswenger1 - M. Ruffert3 - O. E. Mangete3
1 - Institut für Astro- und Teilchenphysik, Leopold-Franzens Universität
Innsbruck, Technikerstraße 25, 6020 Innsbruck, Austria
2 -
Institut für Astrophysik, Universität Göttingen,
Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
3 -
School of Mathematics, University of Edinburgh, Edinburgh EH9 3JZ, Scotland, UK
Received 26 July 2005 / Accepted 22 February 2006
Abstract
We investigate the impact of galactic mass loss
triggered by ram-pressure stripping of cluster galaxies on the evolution of the
intra-cluster medium (ICM).
We use combined N-body and hydrodynamic simulations together with a phenomenological galaxy formation model and a prescription of the effect of ram-pressure stripping on the galaxies. We analyze the effect of galaxy - ICM interaction for different model clusters with different
masses and different merger histories.
Our simulations show that ram-pressure stripping can account for
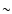 10% of the overall observed level of enrichment in the ICM
within a radius of 1.3 Mpc. The efficiency of metal ejection of cluster galaxies depends in the first few Gyr of the simulation mainly on the cluster mass and is significantly increased
during major merger events. Additionally we show that ram-pressure
stripping is most efficient in the center of the galaxy cluster and the level of enrichment drops quite fast at larger radii. We present emission-weighted metallicity maps of the
ICM which can be compared with X-ray observations. The resulting distribution
of metals in the ICM shows a complex pattern with stripes and plumes of metal-rich material.
The metallicity maps can be used to trace the
present and past interactions between the ICM and cluster galaxies.
10% of the overall observed level of enrichment in the ICM
within a radius of 1.3 Mpc. The efficiency of metal ejection of cluster galaxies depends in the first few Gyr of the simulation mainly on the cluster mass and is significantly increased
during major merger events. Additionally we show that ram-pressure
stripping is most efficient in the center of the galaxy cluster and the level of enrichment drops quite fast at larger radii. We present emission-weighted metallicity maps of the
ICM which can be compared with X-ray observations. The resulting distribution
of metals in the ICM shows a complex pattern with stripes and plumes of metal-rich material.
The metallicity maps can be used to trace the
present and past interactions between the ICM and cluster galaxies.
Key words: galaxies: clusters: general - galaxies: abundances -
galaxies: interactions - galaxies: ISM -
X-rays: galaxies: clusters
The presence of an embedding medium has an influence on the evolution of
galaxies. This effect will be most important in high density environments
like those of galaxy clusters. One mechanism by which galaxies can lose part of
their inter-stellar medium (ISM) due to interaction with their surroundings is
ram-pressure stripping (Gunn & Gott 1972). Observations show that
this mechanism is at work in several galaxies in the Virgo cluster
(e.g. Cayatte et al. 1990; Kenney et al. 2004; Vollmer et al. 2004) and in the Coma cluster (Bravo-Alfaro et al. 2000,
2001). Galaxies subject to ram-pressure stripping will
lose part of their ISM which has been enriched with heavy elements by their
stars. This will have an impact on the chemical abundance of the surrounding
intra-cluster medium (ICM). X-ray observations
revealed that the ICM is highly enriched with heavy elements (about 0.3 solar
in iron: e.g. Fukazawa et al. 1998).
With the recent X-ray satellites Chandra and XMM it is even
possible to study the 2D distribution of the heavy elements (e.g. Schmidt et al.
2002; Furusho et al. 2003; Sanders et al. 2004;
Fukazawa et al. 2004; Hayakawa et al. 2004).
As heavy elements cannot be produced in the ICM itself, part of this medium
seems to originate from cluster galaxies. Although
ram-pressure stripping of cluster galaxies will contribute to the chemical
enrichment of the ICM, several other mechanisms like galactic winds
(de Young 1978), galaxy-galaxy interaction (e.g. Kapferer et al.
2005a) or intra-cluster supernovae (Domainko et al.
2004) will also play an important role.
Each mechanism will result in a characteristic distribution of metal rich
material in the ICM, so with the distribution of heavy elements the origin of the
metals can be constrained. Observational evidence for some
chemical enrichment due to ram-pressure stripping has been found: high
metallicity regions in the ICM of the galaxy cluster Abell 1060 stripped from cluster
galaxies were measured (Hayakawa et al. 2004).
Indeed it has been argued that ram-pressure stripping can act as an enrichment agent over a long period of cluster evolution (Finoguenov et al. 2000)
and at low redshifts (Oosterloo & van Gorkom 2005).
Hence metals are a good tracer of the present and past interaction processes between
galaxies and the ICM.
The high level of enrichment in the ICM has triggered much discussion about
the origin of these metals. Several groups here investigated the chemical evolution
of the ICM with extensive numerical simulations. De Lucia et al.
(2004) and Nagashima et al. (2005) investigated this
problem using N-body simulations combined with semi-analytic galaxy formation
and evolution. They conclude that most of the metals are ejected by supernova-driven
galactic winds mainly from the most massive galaxies and they find
that there has been a mild chemical evolution since z = 1. They do not predict the
distribution of the metals in the ICM. Tornatore et al. (2004) use a smooth
particle hydrodynamic simulation and emphasize the contribution of
different supernova types to the enrichment but do not investigate in detail
the influence of different ejection mechanisms. Their results
indicate that the simulations still lack a feedback mechanism that quenches
star formation and transports metals at low redshifts.
In contrast to these papers, our calculations emphasize the
transport mechanisms of the enriched
material and we use a shock capturing method for the hydrodynamic treatment
(see also Schindler et al. 2005; Domainko et al. 2005).
Furthermore we are able to
trace the distribution of the enriched material lost by the cluster
galaxies. In this paper we investigate the
impact of the enrichment of the ICM by ram-pressure stripping of cluster
galaxies. Other processes are studied elsewhere (e.g. Kapferer et al.
2006, 2005b).
The effect of ram-pressure stripping on individual galaxies has been studied
analytically and numerically by
several groups. A first analytical criterion for ram-pressure stripping
was given by Gunn & Gott (1972). According to this criterion
galaxies lose material if the force due to ram-pressure stripping exceeds the
restoring gravitational force of the galaxy. One result of this consideration is
the presence of a stripping radius in ram-pressure affected galaxies outside of
which the galactic gravitational potential is too shallow to prevent the ISM from
being stripped. Various authors studied this stripping radius with respect
to ram-pressure and galaxy properties (e.g. Abadi et al. 1999;
Vollmer et al. 2001; Roediger & Hensler 2005). In
general these authors found a reasonable agreement between the analytically
estimated stripping radius and the stripping radius determined by numerical
simulations. Additionally Roediger & Hensler (2005) discussed the most
appropriate analytical description with respect to the numerical results. These
authors adapt the estimate used by Mori & Burkert (2000)
which compares the thermal ISM pressure with ram pressure. For the case of a constant ram pressure acting on the galaxy, Roediger & Hensler (2005) found the closest coincidence between analytical description and numerical simulation for the estimate introduced by Mori & Burkert
(2000). For the case of a time-dependent ram pressure as is the
case for galaxies moving on non-circular orbits through a galaxy cluster,
Vollmer et al. (2001) concluded that the Gunn & Gott (1972)
criterion adapted to the galactic inclination angle can explain the HI deficiency of the galaxies in the Virgo cluster. Further numerical simulations for ram-pressure stripping on galaxy scales were presented in several papers (e.g. Abadi et al. 1999; Quilis et al.
2000; Mori & Burkert 2000; Vollmer et al. 2001;
Toniazzo & Schindler 2001; and Roediger &
Hensler 2005). In contrast to those papers we present
simulations showing the impact of ram-pressure stripping
of all cluster galaxies on the ICM. We obtain simulations on galaxy cluster scales and compute
the efficiency and time dependence of galactic mass loss triggered by
ram-pressure stripping. In this paper we focus on the effect of
ram-pressure stripping on the metal enrichment of the ICM. The effect on
the galaxies will be shown in van Kampen et al. (in prep.).
This paper is organized as follows: in Sect. 2 we present the
numerical method used. In Sect. 3 we describe the general simulation
setup and the properties of the model clusters. In Sect. 4 we show
our results. In Sect. 5 we summarize and discuss the
results obtained.
2 Numerical method
We use the same general simulation setup as described in Schindler et al.
(2005).
2.1 N-body simulations
Our starting point is a model for the dark matter distribution within and
around the cluster, for which we use N-body simulations.
The N-body code is that of Barnes & Hut (1986), adapted to include a halo formation recipe that prevents over merging on small scales
(van Kampen et al. 1999). This paper assumes
a 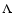 CDM cosmology, with
CDM cosmology, with
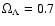 ,
,
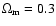 ,
h=0.7, and
,
h=0.7, and
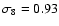 .
Initial conditions are produced using the constrained random field method of Hoffman & Ribak (1991), as implemented by van de Weygaert & Bertschinger
(1996). Constraints are put on the smoothed density field in the
form of peak heights for a Gaussian window of 6 Mpc, which produce
a rich cluster in the center of the box for peaks above three times the rms density fluctuation at that scale. The N-body simulations are obtained within a box
of 46 Mpc (for H0 = 70 km s-1 Mpc-1) with 643 particles.
The softening length of the N-body simulation is 20 kpc which is also the
resolution of the dark matter distribution.
The whole cluster is described by tens of thousands of dark matter
particles, which can easily resolve the radial structure of the cluster as well as substructures.
The halos of the galaxies are represented by groups of particles with a minimum of 10 particles
with a half-mass radius of the smallest halo of 30 kpc.
For these galactic halos we assume an isothermal profile. The galactic dark matter halo
gravitation is treated without any spatial detail by simply applying the gravitational potential.
.
Initial conditions are produced using the constrained random field method of Hoffman & Ribak (1991), as implemented by van de Weygaert & Bertschinger
(1996). Constraints are put on the smoothed density field in the
form of peak heights for a Gaussian window of 6 Mpc, which produce
a rich cluster in the center of the box for peaks above three times the rms density fluctuation at that scale. The N-body simulations are obtained within a box
of 46 Mpc (for H0 = 70 km s-1 Mpc-1) with 643 particles.
The softening length of the N-body simulation is 20 kpc which is also the
resolution of the dark matter distribution.
The whole cluster is described by tens of thousands of dark matter
particles, which can easily resolve the radial structure of the cluster as well as substructures.
The halos of the galaxies are represented by groups of particles with a minimum of 10 particles
with a half-mass radius of the smallest halo of 30 kpc.
For these galactic halos we assume an isothermal profile. The galactic dark matter halo
gravitation is treated without any spatial detail by simply applying the gravitational potential.
2.2 Hydrodynamic treatment
For the hydrodynamic part of the simulation we use a shock capturing, grid
based scheme (PPM, Collela & Woodward 1984; Fryxell et al.
1989). PPM is a higher order version of the Riemann solver based Godunov method
(Godunov 1959). This allows us to
study all the dynamical effects in the ICM connected to subcluster mergers
with high accuracy. To achieve high resolution at the cluster center
where most of the stripping is expected to happen and also to trace infalling gas-rich
galaxies from outside the cluster, we compute our simulation on multiple
refined grids (Ruffert 1992).
Radiative cooling of the ICM is treated according to the cooling
functions given by Sutherland & Dopita (1993).
Metallicity is used as a tracer to follow the gas which
is lost by the cluster galaxies. Metallicity is handled as a single
quantity therefore we do not distinguish between different chemical
elements (like iron and  elements) but assume solar composition.
Additionally to the bulk motion of the ICM, diffusion should also further disperse the
stripped gas. In the presented paper we are mainly interested in the distribution of the
enriched material, therefore only the effect of diffusion on heavy nuclei is investigated.
Diffusion strongly depends on the mass and the charge of the nuclei involved (see Lang
1999, Chapter 3.1.2 and 3.1.5). The most
prominent detection of metals in the ICM is connected to the presence of iron.
Diffusion will spread iron in the ICM within the Hubble time on length scales of less than 100 kpc. Therefore this process is inefficient in further distributing iron on galaxy cluster scales.
elements) but assume solar composition.
Additionally to the bulk motion of the ICM, diffusion should also further disperse the
stripped gas. In the presented paper we are mainly interested in the distribution of the
enriched material, therefore only the effect of diffusion on heavy nuclei is investigated.
Diffusion strongly depends on the mass and the charge of the nuclei involved (see Lang
1999, Chapter 3.1.2 and 3.1.5). The most
prominent detection of metals in the ICM is connected to the presence of iron.
Diffusion will spread iron in the ICM within the Hubble time on length scales of less than 100 kpc. Therefore this process is inefficient in further distributing iron on galaxy cluster scales.
2.3 Galaxy formation
The halo formation recipe that is part of the N-body code allows us to
easily generate halo merging histories, and also the merging histories of the galaxies
occupying the halos. Simple prescriptions for gas cooling, star formation and feedback
mechanisms make up our phenomenological galaxy formation model, which is an improved
version of the model of van Kampen et al. (1999).
We include a disk model, which is similar to that of Mo et al. (1998), but with the inclusion of an observed threshold for star formation in disks (Kennicut 1989;
Martin & Kennicutt 2001).
The adoption of the Mo et al. approximations produce a gas and stellar
disk with the same exponential scale-length, but different cut-off radii and central
densities. Our modeling of the metallicity evolution is described in two papers: in
Kapferer et al. (2006) the coupled circuit of the evolution of the stellar, cold
and hot gas components is given; the chemical evolution of the stellar populations
can be found in van Kampen et al. (1999).
The star formation history of each galaxy is constrained by its merger history.
Halo-halo mergers and galaxy-galaxy mergers trigger short bursts of star formation.
Metals that are produced in disk stars can either be added to the cold gas disk or can be
ejected directly into the hot gas, or into the ICM
for cluster galaxies that have their hot gas halos stripped.
We choose the extreme scenario to add metals produced in disk stars to the
cold gas in the disk which can then be stripped off through ram-pressure stripping.
We do not replenish the stellar disk with stellar ejecta along the path of a galaxy:
star formation is truncated "forever'' if the whole gas disk is stripped, and the galaxy
ends up as an S0 if the stellar disk is prominent enough, and as an elliptical if
it is not. In reality, some stellar mass loss will also occur after
star formation has ended. Intermediate mass stars will eject material in the form of AGB winds
and supernova Ia ejecta.
2.4 Ram-pressure stripping
To calculate the mass loss of cluster galaxies due to ram-pressure stripping
we follow the classical Gunn & Gott (1972) criterion
because Vollmer et al. (2001) concluded that for non
circular orbits the Gun & Gott (1972) criterion additionally extended
for the inclination angle of the galaxy can explain the HI deficiency of galaxies
located in the Virgo cluster. According to
this criterion, material is lost by a galaxy if the force due to ram-pressure
exceeds the restoring gravitational force.
The Gunn & Gott (1972) criterion is given by:
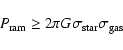 |
(1) |
with
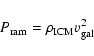 |
(2) |
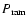 is the ram-pressure, G is the gravitational constant,
is the ram-pressure, G is the gravitational constant,
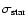 is the stellar surface density,
is the stellar surface density,
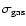 is the surface density of the gas,
is the surface density of the gas,
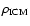 is the density of the ICM and
is the density of the ICM and
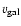 is the velocity of the galaxy
relative to the ICM. We calculate the mass loss of the cold ISM disks of
spiral galaxies. We assume that the galaxies consist of an exponential stellar disk and an exponential gas disk. Due to the phenomenological galaxy formation model (see Sect. 2.3) the scale length of the stellar disk and gas disk are equal but the central
densities are different:
is the velocity of the galaxy
relative to the ICM. We calculate the mass loss of the cold ISM disks of
spiral galaxies. We assume that the galaxies consist of an exponential stellar disk and an exponential gas disk. Due to the phenomenological galaxy formation model (see Sect. 2.3) the scale length of the stellar disk and gas disk are equal but the central
densities are different:
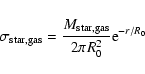 |
(3) |
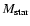 is the mass of the stars,
is the mass of the stars,
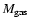 is the mass of the gas and R0 is the disk scale length. With these assumptions we can analytically determine a stripping radius
is the mass of the gas and R0 is the disk scale length. With these assumptions we can analytically determine a stripping radius
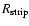 :
:
 |
(4) |
with
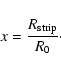 |
(5) |
Material which is located outside this stripping radius is then lost by the
galaxy. The validity of this treatment was shown with numerical simulations
and with comparisons with Virgo cluster galaxies by Abadi et al. (1999).
The amount of cold gas that can be kept by the galaxy (
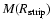 ) is:
) is:
![\begin{displaymath}%
M(R_{\rm strip}) = M_{\rm gas}
\left[ 1- \left( x+1 \right)
{\rm e}^{-x} \right].
\end{displaymath}](/articles/aa/full/2006/24/aa3921-05/img22.gif) |
(6) |
Consequently the amount of gas
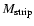 which is stripped off the
galaxy is then:
which is stripped off the
galaxy is then:
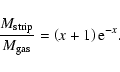 |
(7) |
Mass loss due to ram-pressure stripping should in principle also be influenced by the
inclination angle of the affected galaxy. The impact of the inclination angle of the galaxy
on the stripping process was investigated by Quilis et al. (2000) with numerical simulations. Those authors find that there is only slight dependence of the effectiveness of ram-pressure stripping on inclination angle for galaxies
that move close to face-on through the ICM. For example, a galaxy moving at an inclination of 20 to the direction of motion suffers as much stripping as face-on encounters (Quilis et al. 2000).
However, there are also arguments that suggest a certain impact of the inclination angle on the
stripping process. The column density of the gas that has to be pushed by the momentum transfer
from the ICM grows with the cosine of the inclination angle.
Also the area of ram pressure that is acting on the unit area of an inclined galaxy scales with the same factor. In this work, due to the lack of more elaborate considerations and for simplicity,
mass loss of galaxies moving inclined as opposed to face-on through the ICM is scaled by
the cosine of the inclination angle with respect to the mass loss derived for an uninclined galaxy.
Stripped material is added locally to the ICM and is removed from the galaxies.
Note that this treatment can be regarded as an upper limit of the galactic mass
loss due to ram-pressure stripping as it was shown that a minor fraction of stripped
material might be re-accreated by the stripped galaxy (see Vollmer et al.
2001). The stripping condition is evaluated at each time step of the cluster-scale
hydrodynamic simulation. The mass loss of the galaxies is calculated according to the
actual properties of the galaxies as derived by the galaxy evolution model (see Sect. 2.3). We also assume that the gas disk remains truncated after
a stripping event. This means that galaxies are only further stripped when they
experience increasing ram-pressure. The stripped ISM in the outer part of the disks in principle should be replaced by supernovae and stellar winds. However, observations show that star
formation is truncated in ram-pressure affected cluster galaxies (e.g. Koopmann & Kenney
2004). Hence only a passively aging stellar population with a significantly reduced mass loss is present in regions of the galactic disk where the ISM is stripped off.
Although as already mentioned in Sect. 2.3, intermediate mass stars will
eject some enriched material, we do not take this additional effect into account.
to the direction of motion suffers as much stripping as face-on encounters (Quilis et al. 2000).
However, there are also arguments that suggest a certain impact of the inclination angle on the
stripping process. The column density of the gas that has to be pushed by the momentum transfer
from the ICM grows with the cosine of the inclination angle.
Also the area of ram pressure that is acting on the unit area of an inclined galaxy scales with the same factor. In this work, due to the lack of more elaborate considerations and for simplicity,
mass loss of galaxies moving inclined as opposed to face-on through the ICM is scaled by
the cosine of the inclination angle with respect to the mass loss derived for an uninclined galaxy.
Stripped material is added locally to the ICM and is removed from the galaxies.
Note that this treatment can be regarded as an upper limit of the galactic mass
loss due to ram-pressure stripping as it was shown that a minor fraction of stripped
material might be re-accreated by the stripped galaxy (see Vollmer et al.
2001). The stripping condition is evaluated at each time step of the cluster-scale
hydrodynamic simulation. The mass loss of the galaxies is calculated according to the
actual properties of the galaxies as derived by the galaxy evolution model (see Sect. 2.3). We also assume that the gas disk remains truncated after
a stripping event. This means that galaxies are only further stripped when they
experience increasing ram-pressure. The stripped ISM in the outer part of the disks in principle should be replaced by supernovae and stellar winds. However, observations show that star
formation is truncated in ram-pressure affected cluster galaxies (e.g. Koopmann & Kenney
2004). Hence only a passively aging stellar population with a significantly reduced mass loss is present in regions of the galactic disk where the ISM is stripped off.
Although as already mentioned in Sect. 2.3, intermediate mass stars will
eject some enriched material, we do not take this additional effect into account.
After the stripping radius is reached, the mass loss continues due to
Kelvin-Helmholz instabilities (Mori & Burkert 2000). Since Roediger
& Hensler (2005) argued that the contribution to the mass loss
caused by Kelvin-Helmholz instabilities is small, we do not account for
this mass loss in our further calculations.
Observations of nearby spiral galaxies show that abundance
gradients are present in their disks (see e.g. Henry & Worthey
1999). The slopes of the gradients depend on the morphology of the
galaxy (Henry & Worthey 1999). This feature influences
the enrichment of the surrounding medium due to ram-pressure stripping.
For the case of galactic metallicity gradients that flatten in the outer parts of the
galaxy we expect only a limited effect on the proposed enrichment process. In this case the mean
abundance of the gas is close to the abundance of the bulk of the gas which is
located at large galactic radii. This issue demands further analysis.
As a first approach we do not consider galactic abundance gradients in our
simulations. In future, more refined, studies we will investigate the
impact of galactic abundance gradients on the ICM enrichment.
In our simulations, several galaxies move with a velocity relative to the
embedding medium which is higher than the local sound velocity. In this
case of supersonic galaxies, the classical Gunn & Gott (1972)
approach has to be modified. Supersonic galaxies will form bow shocks in front
of them and the stripping criterion has to be applied to the conditions behind
these bow shocks. Hydrodynamic quantities behind the bow shocks can be
calculated as functions
of the quantities in front of the bow shock according to the Rankine-Hugoniot
conditions for all Mach numbers M > 1.
Using the equation of continuity at the bow shock we can calculate
the ratio between densities and velocities in front of and behind the bow
shock:
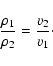 |
(8) |
Here  are the densities, v are the velocities and subscript 1 stands
for quantities in front of the shock and subscript 2 stands for quantities
behind the shock. For the ram-pressure in front of and behind the shock this
leads to:
are the densities, v are the velocities and subscript 1 stands
for quantities in front of the shock and subscript 2 stands for quantities
behind the shock. For the ram-pressure in front of and behind the shock this
leads to:
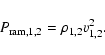 |
(9) |
As the velocities behind the shock are smaller than the velocities in front
of the shock the ram-pressure also will be smaller behind the shock due to its
dependence on the square of the velocity. This means that for supersonic
galaxies ram-pressure stripping is less efficient than the classical
Gunn & Gott (1972) approach would suggest.
We calculate the Rankine-Hugoniot condition for the actual Mach number
of each individual galaxy. Therefore this treatment is also correct for
supersonic galaxy motion in galaxy clusters with low Mach numbers.
The effect is most pronounced for very fast galaxies. In the case of
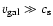 with
with
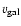 being the velocity of the galaxy relative to the ICM and
being the velocity of the galaxy relative to the ICM and 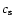 the
local sound velocity and treating the ICM as an ideal gas with
the
local sound velocity and treating the ICM as an ideal gas with
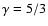 with
with 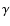 being
the ratio of specific heats, the ram pressure is lower by a factor of 4
behind the galactic bow shock than in front of the bow shock.
An additional effect in supersonic ram-pressure stripping could come from
the fact that the bow shock is bent according to the Mach number.
Since our simulations are performed on galaxy cluster scales we
cannot resolve individual galaxies and the form of their bow shocks.
But it is expected that for low Mach numbers the
opening angle of the bow shock is quite large.
Therefore we do not take into account the effect of
the bending of the bow shock. Roediger & Hensler (2005) also found a better agreement between analytic estimates and numerical simulations of ram-pressure stripping if a Rankine-Hugoniot correction is applied.
being
the ratio of specific heats, the ram pressure is lower by a factor of 4
behind the galactic bow shock than in front of the bow shock.
An additional effect in supersonic ram-pressure stripping could come from
the fact that the bow shock is bent according to the Mach number.
Since our simulations are performed on galaxy cluster scales we
cannot resolve individual galaxies and the form of their bow shocks.
But it is expected that for low Mach numbers the
opening angle of the bow shock is quite large.
Therefore we do not take into account the effect of
the bending of the bow shock. Roediger & Hensler (2005) also found a better agreement between analytic estimates and numerical simulations of ram-pressure stripping if a Rankine-Hugoniot correction is applied.
3 Simulation set up and model clusters
We run the hydrodynamic simulation on four levels of
nested grids centered on the cluster centers, the largest grid being
(20 Mpc)3 and the smallest (2.5 Mpc)3.
Each of the nested grids has a resolution of 1283 grid cells.
We start the hydrodynamic simulation at a redshift of z = 1
for numerical reasons and follow the
evolution of the ICM to a redshift of z = 0. This is the time
interval of interest as ram-pressure stripping is expected to be most
efficient after the galaxy clusters have formed.
In order to test the impact of ram-pressure stripping on different galaxy
clusters we chose model clusters that span a wide range of masses and
evolutionary histories. Our model clusters contain no cD galaxies and do not
feature cooling cores at their centers. The model clusters are as follows:
- Model cluster 1:
- this is the most massive cluster of our
sample. The final total cluster
mass at z=0 inside a radius of 3 Mpc is 1.3
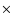
 .
This cluster experiences only small merger events after z = 1.
.
This cluster experiences only small merger events after z = 1.
- Model cluster 2:
- this is the least massive cluster
in our sample. The final total cluster mass at z=0 inside a radius of 3 Mpc is 7.4
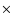
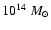 .
This cluster undergoes a major merger with a mass ratio
of 1:3 at a redshift of 0.5. Additionally it features the infall of several smaller
subsystems.
.
This cluster undergoes a major merger with a mass ratio
of 1:3 at a redshift of 0.5. Additionally it features the infall of several smaller
subsystems.
- Model cluster 3:
- this cluster has a mass of 8.7
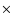
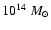 inside a radius of 3 Mpc at the final redshift of z = 0.
It undergoes two minor mergers.
inside a radius of 3 Mpc at the final redshift of z = 0.
It undergoes two minor mergers.
4 Results
The first quantity of interest is the total amount of material and metals
ejected into the ICM by ram-pressure stripping. As ram-pressure
stripping is a process dependent on the environment it is expected that the total
amount of material stripped from the affected cluster galaxies will
depend on the properties of the cluster. Galaxy clusters
with higher masses strip galaxies more efficiently than galaxy clusters
with lower masses. This is due to a higher ICM density
and to a higher velocity dispersion in high mass systems.
In our simulation we derive the total amount of metals stripped from
the cluster galaxies. By comparing
the total mass of metals stripped we
test the dependence of galactic metal loss on cluster mass.
We find that the total mass loss is
highest in the high mass cluster (model cluster 1) and lower in the low mass
clusters. We see that in the high mass cluster in our sample (model cluster 1) the total
amount of metals ejected into the ICM is about four times higher than in the
model clusters with lower mass.
Another interesting quantity is the fraction of the ICM that
originates from cluster galaxies and is lost by them due to ram-pressure stripping.
To investigate this question, we compare the mass of the hot ICM, which in our
simulations has never been inside any galaxy, to the amount of material that has
been lost by the galaxies (see Fig. 2).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.85cm,clip]{3921fig1.ps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg36.gif) |
Figure 1:
Temporal metallicity evolution
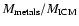 in the different model clusters. The values are given for all galaxies located inside
the central (2.5 Mpc)3 of our simulations. For an explanation of the different slopes
for the different model clusters see Sect. 4.2. in the different model clusters. The values are given for all galaxies located inside
the central (2.5 Mpc)3 of our simulations. For an explanation of the different slopes
for the different model clusters see Sect. 4.2. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.85cm,clip]{3921fig2.eps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg37.gif) |
Figure 2:
Fraction of the ICM that originates from cluster galaxies and is
lost by them due to ram-pressure stripping. The values are given for
the central (2.5 Mpc)3 of our simulations. For an explanation of the different slopes
for the different model clusters see Sect. 4.2. |
| Open with DEXTER |
We find that about 10% of the ICM in the central (2.5 Mpc)3 of
our simulation originates from ram-pressure affected galaxies.
The fraction of the ICM that originates from cluster galaxies is
comparable for all our model clusters (see Fig. 4.2). This result is
expected since in the high mass cluster the mass of the ICM is larger than
in the clusters with lower mass. Mixing then the ICM in the high mass cluster
with a larger amount of material
lost by the galaxies results in a comparable fraction of lost ICM
to primordial ICM as in the low mass clusters.
4.2 Mass loss rate due to ram-pressure stripping
We now investigate the combined mass loss rate of all cluster galaxies as a function of time. The time evolution of the mass and metal ejection is different for different model clusters
(see Figs. 1 and 2). With the analysis of the total mass loss rate of all cluster galaxies as a function of time, we further
explore this behavior. The mass loss of all cluster galaxies as a function
of time is shown in Figs. 3 and 4.
We find that in the first 3 Gyr the mass loss rate in the high mass
cluster (model cluster 1) is about an order of magnitude higher than the mass
loss rate in low mass clusters.
There is also a prominent peak at the start of the simulation in model
cluster 1. This first peak
originates from the mass loss of gas rich galaxies that experience
the effect of ram-pressure for the first time by switching on
the calculation.
After 3 Gyr the mass loss of the galaxies in the high mass cluster
drops significantly. We interpret this as an effect of cluster mass.
Stripping in the high mass cluster can reduce the
size of the gas disks of galaxies quite fast and then this mechanism
becomes less efficient (see Fig. 3).
The situation is very different for the merging cluster (model cluster 2).
In the case of a cluster experiencing mergers the prehistory of
ram-pressure is also followed within the infalling subsystems.
In this system, mass loss starts at a low rate but between 3 Gyr and 5 Gyr the rate rises by an order of magnitude. In this time interval the major cluster merger occurs. Here we see the
influence of the merger history on the evolution of the mass loss rate due to
ram-pressure stripping (see Fig. 4). At about 6 Gyr several galaxy groups fall towards the cluster center and the mass loss rate increases again.
Subcluster mergers can raise the stripping rate by an enhanced velocity
dispersion, increased ICM density and infall of gas-rich galaxies onto
the main cluster. The strongly enhanced mass loss rate during subcluster
mergers is also the reason for the quite different slopes for model cluster 1 and 3
and model cluster 2 in Figs. 1 and 2.
The influence of cluster mergers on ram-pressure stripping of cluster
galaxies is further analyzed in Mair et al. (in prep.).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.85cm,clip]{3921fig3.eps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg38.gif) |
Figure 3:
Combined mass loss rate of all galaxies as a function of time.
The values are given
for the central (2.5 Mpc)3 of our simulations. In this plot the
influence of cluster mass on the
combined stripping rate of all cluster galaxies can be seen.
Model cluster 1 is about twice as massive as model cluster 3. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.85cm,clip]{3921fig4.eps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg39.gif) |
Figure 4:
Combined mass loss rate of all galaxies as a function of time.
The values are given
for the central (2.5 Mpc)3 of our simulations. In this plot the influence of
the merger histories of the galaxy clusters on the combined stripping rate
can be seen. Model cluster 2 undergoes a major merger at t = 4 Gyr. |
| Open with DEXTER |
Model cluster 3 features a similar mass loss rate of its galaxies (with some scatter due to
small merger events) over the entire simulation
time of 8 Gyr. Hence on cluster scales ram-pressure stripping is a process that
can act over a quite long period of time. This supports the idea of some enrichment over the whole redshift range of cluster evolution
by ram-pressure stripping (Finoguenov et al. 2000).
Gas originating from cluster galaxies is enriched with heavy elements due to
feedback processes from stars and supernovae. If a large amount of this gas is
lost by the galaxies, the ICM into which this gas is mixed will also
be enriched
up to a certain level. In this section we investigate the contribution of
ram-pressure stripping on the
chemical evolution of the ICM. Tornatore et al. (2004)
have argued that some galactic mass loss and metal transport
at low redshifts is needed
to explain the overall chemical abundance of the ICM. Ram-pressure stripping
is a promising candidate that could account for the necessary mass transfer
away from the cluster galaxies.
We explore the ability of ram-pressure stripping to enrich at low
redshifts. The mean observed chemical abundance of the ICM is about 0.3 solar. For comparison with the observed values we derive the mean chemical abundance in the central (2.5 Mpc)3 of our simulation. The final level of enrichment
is 0.03 solar for model cluster 1, 0.05 solar for model cluster 2 and 0.04 solar for model cluster 3. This corresponds to a contribution of 10-15%
to the observed overall enrichment of the ICM, depending on cluster mass and
evolutionary history of the cluster.
For the galaxy cluster that experiences a major merger (Model cluster 2), the enrichment happens later in cluster evolution in comparison to the non-merging cluster (e.g. Model cluster 1).
The fraction
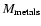 /
/
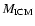 (see Fig. 1) rises faster than the fraction
(see Fig. 1) rises faster than the fraction
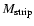 /
/
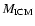 (see Fig. 2) for model cluster 2. This effect results from the internal metallicity evolution of the cluster galaxies. Material that is stripped later from galaxies is enriched to
a higher level since stellar feedback acts for a longer period of time on
this gas.
(see Fig. 2) for model cluster 2. This effect results from the internal metallicity evolution of the cluster galaxies. Material that is stripped later from galaxies is enriched to
a higher level since stellar feedback acts for a longer period of time on
this gas.
For a better comparison of the results of our simulations with X-ray observations
we derive emission weighted metallicity profiles.
These are shown for the three model clusters in Fig. 5. The profiles for all three model clusters are remarkably similar and do not show a strong signature of the different merger
histories of the different systems.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3921fig5.eps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg42.gif) |
Figure 5:
Emission weighted metallicity profiles of the three model clusters
at a redshift of z = 0. Ram-pressure stripping can account for the observed metallicity in the central 100 kpc in all simulations, but at larger radii processes other than ram-pressure
stripping have to contribute to the enrichment of the ICM. |
| Open with DEXTER |
In the calculated profiles we clearly see the highest level of chemical
enrichment of the ICM at the cluster center. At the cluster center the
environmental impact on the galaxies will be most important so it is expected that
the enrichment is most pronounced there. In the central 100 kpc ram-pressure
stripping can account
for an enrichment of about 0.2 solar which is close to the
observed value. At larger radii the chemical abundance drops very quickly and
processes other than ram-pressure stripping must contribute to the chemical evolution of the ICM.
Metallicity can be used as a tracer to identify the location of the gas
lost by cluster galaxies. To investigate the distribution of the
enriched material and to compare our simulations with observed galaxy clusters,
we obtain emission weighted metallicity maps. For a discussion on the effect of diffusion
on the metallicity distribution see Sect. 2.2.
In contrast to the full 3D distribution of the metal-rich areas, enriched
material located in high density regions is much more pronounced
in emission weighted metallicity maps. The emission weighted metallicity
maps clearly show a complex pattern of the chemically enriched material
(see Fig. 6). The nonuniform distribution of the enriched material is in good agreement with recent observations (e.g. Hayakawa et al. 2004).
![\begin{figure}
\par\includegraphics[width=15cm,clip]{3921fig6.ps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg43.gif) |
Figure 6:
Emission weighted metallicity maps of the model cluster. The size of
the boxes is 5 Mpc on a side. The level of enrichment is given in solar units. |
| Open with DEXTER |
In all the model clusters we see stripes of metal rich material that was left
behind by infalling galaxies. Some of them are even several
hundred kpc long. It is interesting to note the similarity of these stripes with the plume of stripped gas observed at the center of the Virgo cluster in HI (Oosterloo & van Gorkom
2005) and with the trails of ionized gas behind two galaxies
in Abell 1367 (Gavazzi et al. 2001). In contrast to these observations,
material in our computed enriched stripes is already mixed with the hot ICM.
Evaporation of stripped gas clouds at the center of our model cluster
(
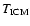
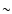 108 K,
108 K,
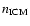
 10-3 cm-2) can occur within 107 yr (Vollmer et al. 2001), which is the typical time step of the hydrodynamic simulation.
Stripped gas from cluster galaxies is indeed seen in the hot (T = 108 K)
ICM of the Coma cluster (Finoguenov et al. 2004) in X-ray
observations.
10-3 cm-2) can occur within 107 yr (Vollmer et al. 2001), which is the typical time step of the hydrodynamic simulation.
Stripped gas from cluster galaxies is indeed seen in the hot (T = 108 K)
ICM of the Coma cluster (Finoguenov et al. 2004) in X-ray
observations.
The non-merging model cluster 1 shows metal maps with an almost
spherically symmetric appearance. There is only little evolution between 4.0 Gyr and 7.9 Gyr
in our simulation (see Fig. 6 two panels at the top).
This is in good agreement with the results of Sect. 4.2.
In contrast model cluster 2 shows a very complex distribution of the
enriched material and there is a lot of enrichment between a simulation time of 4.0 Gyr and 7.9 Gyr. The subcluster merger can
clearly be seen in the panel showing the situation at 4.0 Gyr. The emission
weighted metallicity maps for model cluster 2 are presented in Fig. 6
in the two central panels. Several stripes of enriched material can
be seen in the maps of model cluster 3 (see Fig. 6 lower two panels).
There is also some evolution up to the end of the simulation at 7.9 Gyr.
Thus, our simulations enable us to derive abundance maps of the ICM. With the
help of these maps we can identify the origin of highly enriched regions
that have recently been observed with X-ray observations (e.g. Hayakawa et al.
2004). Furthermore we can investigate the location and the fate
of the stripped material and compare this to up to date X-ray data
(e.g. Finoguenov et al. 2004).
5 Summary and discussion
In the present paper we investigate the chemical enrichment of the ICM
due to ram-pressure stripping of cluster galaxies from z = 1 to z = 0.
We find that ram-pressure
stripping plays a significant role in this stage of cluster evolution.
In particular we investigate
the efficiency, time dependence and spatial distribution of this process:
- More than 10% of the ICM originates from gas of cluster galaxies
which was removed from them by ram-pressure stripping.
- Enrichment by ram-pressure stripping contributes to the overall
metal enrichment of the ICM by about 10-15% within a radius of 1.3 Mpc.
It is more difficult to enrich high
mass clusters with high ICM densities than low mass clusters with lower
ICM densities. This effect is hardly compensated by the higher efficiency
of ram-pressure stripping in high mass systems.
- The total mass loss rate of all cluster galaxies depends on the cluster
mass. High mass clusters can reduce the gas disks of their galaxies very quickly
and enrichment of the ICM by ram-pressure stripping can take place within a few Gyr.
- Enrichment by ram-pressure stripping persists over the entire simulation
time and can therefore account for some late enrichment of the ICM. This
effect is more pronounced in low mass systems.
- Cluster mergers have an important impact on enrichment by ram-pressure
stripping. Subcluster mergers can raise the total mass loss of all cluster galaxies
significantly
- Ram-pressure stripping can account for the total observed level of enrichment
within the central 100 kpc but at larger radii other processes must contribute
to the chemical evolution of the ICM.
- Metallicity gradients are not very well suited to investigate the complex
distribution of metals in the ICM. Metal maps are much more useful to
investigate the present and past interactions between the ICM and the cluster
galaxies.
- We find an inhomogeneous distribution of the enriched material in the
ICM. This is in agreement with recent observations (e.g. Hayakawa et al.
2004)
- In our simulations we see stripes of metal rich material which were left
behind by ram-pressure affected galaxies. We note the remarkable similarity
of the shape of
these stripes with the plume of stripped material observed in the Virgo cluster
(see Oosterloo & van Gorkom 2005).
It seems that merger activity of the galaxy cluster has a large impact
on the enrichment of the ICM due to ram-pressure stripping of cluster
galaxies. Studying a larger sample of merging clusters will lead to a better
understanding of this problem. In the future we plan to investigate the effect
of various merger scenarios on the chemical evolution of the ICM.
In forthcoming, more refined studies we will also investigate the impact
of additional effects like abundance gradients in the galaxies, stripping due to
Kelvin-Helmholz instabilities, shapes of bow shocks of supersonic galaxies and
different galaxy evolution scenarios on the enrichment of the ICM due to
ram-pressure stripping.
Acknowledgements
The authors want to thank the anonymous referee for insightful and substantial comments
that greatly improved the clarity and content of this paper.
This work was supported by the Austrian Science Foundation FWF under
grant P15868, UniInfrastruktur 2004, Tiroler Wissenschaftsfonds,
the AUSTRIAN GRID, a graduate scholarship from the University of
Innsbruck, DFG grant Zi 663/6-1, the European Commission through
grant number HPRI-CT-1999-00026
(the TRACS Program at EPCC) and by the European
Commission's Research Infrastructures activity of the Stucturing the
European Research Area programme, contract number RII3-CT-2003-506079
(HPC-Europa). M.M. acknowledges the support of
a Doktoratsstipendium of the LFU Innsbruck. EvK is supported by the FWF
through grant P18416.
Edmund Bertschinger and Rien van de Weygaert are acknowledged
for providing their constrained random field code, Joshua Barnes and Piet Hut
are acknowledged for allowing use of their treecode.
- Abadi, M. G., Moore,
B., & Bower, R. G. 1999, MNRAS, 308, 947 [NASA ADS] [CrossRef] (In the text)
- Barnes, J. E.,
& Hut, P. 1986, Nature, 324, 446 [NASA ADS] [CrossRef] (In the text)
-
Bravo-Alfaro, H., Cayatte, V., van Gorkom, J. H., & Balkovsky,
C. 2000, AJ, 119, 580 [NASA ADS] [CrossRef] (In the text)
-
Bravo-Alfaro, H., Cayatte, V., van Gorkom, J. H., & Balkowski,
C. 2001, A&A, 379, 347 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Cayatte, V., van
Gorkom, J. H., Balkovsky, C., & Kotanyi, C. 1990, AJ, 100,
604 [NASA ADS] [CrossRef] (In the text)
- Collela, P.,
& Woodward, P. R. 1984, J. Comp. Phys., 54, 174 [NASA ADS] (In the text)
- De Lucia, G.,
Kauffmann, G., & White, S. D. M. 2004, MNRAS, 349, 1101 [NASA ADS] [CrossRef] (In the text)
- De Young, D. S.
1978, ApJ, 223, 47 [NASA ADS] [CrossRef] (In the text)
- Domainko, W.,
Gitti, M., Schindler, S., & Kapferer, W. 2004, A&A, 425,
L21 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Domainko, W.,
Kapferer, W., Schindler, S., et al. 2005, AdSpR, 36, 685 [NASA ADS] (In the text)
- Finoguenov,
A., David, L. P., & Ponman, T. J. 2000, ApJ, 544, 188 [NASA ADS] [CrossRef] (In the text)
- Finoguenov,
A., Briel, U. G., Henry, J. P., et al. 2004, A&A, 419, 47 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Fryxell, B.,
Müller, E., & Arnett, D. 1989, MPA Rep., 449
(In the text)
- Fukazawa, Y.,
Makishima, K., Tamura, T., et al. 1998, PASJ, 50, 187 [NASA ADS] (In the text)
- Fukazawa, Y.,
Kawano, N., & Kawashima, K. 2004, ApJ, 606, L109 [NASA ADS] [CrossRef] (In the text)
- Furusho, T.,
Yamasaki, N. Y., & Ohashi, T. 2003, ApJ, 596, 181 [NASA ADS] [CrossRef] (In the text)
- Gavazzi, G.,
Boselli, A., Mayer, L., et al. 2001, ApJ, 563, L23 [NASA ADS] [CrossRef] (In the text)
- Godunov, S. K.
1959, Mat. Sbornik, 47, 271 (In the text)
- Gunn, J. E., &
Gott, J. R. III 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] (In the text)
- Hayakawa, A.,
Furusho, T., Yamasaki, N. Y., Ishida, M., & Ohashi, T. 2004,
PASJ, 56, 743 [NASA ADS] (In the text)
- Henry, R. B. C.,
& Worthey, G. 1999, PASP, 111, 919 [NASA ADS] [CrossRef] (In the text)
- Hoffman, Y.,
& Ribak, E. 1991, ApJ, 380, L5 [NASA ADS] [CrossRef] (In the text)
- van Kampen,
E., Jimenez, R., & Peacock, J. A. 1999, MNRAS, 310, 43 [NASA ADS] [CrossRef] (In the text)
- Kapferer, W.,
Knapp, A., Schindler, S., Kimeswenger, S., & van Kampen, E.
2005a, A&A, 438, 87 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kapferer, W.,
Domainko, W., Schindler, S., et al. 2005b, AdSpR, 36, 682 [NASA ADS] (In the text)
- Kapferer, W.,
Ferrari, C., Domainko, W., et al. 2006, A&A, 447, 827 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kenney, J. D. P.,
van Gorkom, J. H., & Vollmer, B. 2004, AJ, 127, 3361 [NASA ADS] [CrossRef] (In the text)
- Kennicutt, R.
C. 1989, ApJ, 344, 685 [NASA ADS] [CrossRef] (In the text)
- Koopmann, R.
A., & Kenney, J. D. P. 2004, ApJ, 613, 851 [NASA ADS] [CrossRef] (In the text)
- Lang, K. R. 1999,
Astrophysical formulae, Third edition / K.R. Lang (New York:
Springer)
(In the text)
- Martin, C. L.,
& Kennicutt, R. C. 2001, ApJ, 555, 301 [NASA ADS] [CrossRef] (In the text)
- Mo, H. J., Mao, S., &
White, S. D. M. 1998, MNRAS, 295, 319 [NASA ADS] [CrossRef] (In the text)
- Mori, M., &
Burkert, A. 2000, ApJ, 538, 559 [NASA ADS] [CrossRef] (In the text)
- Nagashima,
M., Lacey, C. G., Baugh, C. M., Frenk, C. S., & Cole, S. 2005,
MNRAS, 358, 1247 [NASA ADS] [CrossRef] (In the text)
- Oosterloo,
T., & van Gorkom, J. 2005, A&A, 437, L19 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Quilis, V., Moore,
B., & Bower, R. 2000, Science, 288, 1617 [NASA ADS] [CrossRef] (In the text)
- Roediger, E.,
& Hensler, G. 2005, A&A, 433, 875 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Ruffert, M. 1992,
A&A, 265, 82 [NASA ADS] (In the text)
- Sanders, J. S.,
Fabian, A. C., Allen, S., & Schmidt, R. W. 2004, MNRAS, 349,
952 [NASA ADS] [CrossRef] (In the text)
- Schindler,
S., Kapferer, W., Domainko, W., et al. 2005, A&A, 435, L25 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Schmidt, R. W.,
Fabian, A. C., & Sanders, J. 2002, MNRAS, 337, 71 [NASA ADS] [CrossRef] (In the text)
- Sutherland,
R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] (In the text)
- Toniazzo, T.,
& Schindler, S. 2001, MNRAS, 325, 509 [NASA ADS] [CrossRef] (In the text)
- Tornatore, L.,
Borgani, S., Matteucci, F., Recchi, S., & Tozzi, P. 2004,
MNRAS, 349, L19 [NASA ADS] [CrossRef] (In the text)
- Vollmer, B.,
Cayatte, V., Balkowski, C., & Duschl, W. J. 2001, ApJ, 561,
708 [NASA ADS] [CrossRef] (In the text)
- Vollmer, B.,
Balkowski, C., Cayatte, V., van Driel, W., & Huchtmeier, W.
2004, A&A, 419, 35 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- van
de Weygaert, R., & Bertschinger, E. 1996, MNRAS, 281, 84 [NASA ADS] (In the text)
Copyright ESO 2006
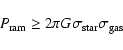
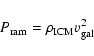
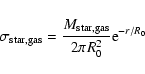

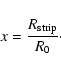
![\begin{displaymath}%
M(R_{\rm strip}) = M_{\rm gas}
\left[ 1- \left( x+1 \right)
{\rm e}^{-x} \right].
\end{displaymath}](/articles/aa/full/2006/24/aa3921-05/img22.gif)
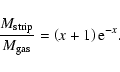
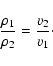
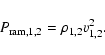
![\begin{figure}
\par\includegraphics[angle=-90,width=7.85cm,clip]{3921fig1.ps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg36.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.85cm,clip]{3921fig2.eps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg37.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.85cm,clip]{3921fig3.eps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg38.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.85cm,clip]{3921fig4.eps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3921fig5.eps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=15cm,clip]{3921fig6.ps}\end{figure}](/articles/aa/full/2006/24/aa3921-05/Timg43.gif)