A&A 452, 959-967 (2006)
DOI: 10.1051/0004-6361:20053270

V781 Tauri: a W Ursae Majoris binary with decreasing period

J. Kallrath^1,4 - E. F. Milone² - R. A. Breinhorst³ - R. E. Wilson^4,6 - A. Schnell⁵ - A. Purgathofer^5,

1 - BASF-AG, GVC/S-B009, 67056 Ludwigshafen, Germany
2 - Physics and Astronomy Department, The University of Calgary, 2500 University Drive, Calgary, Alberta, T2N 1N4, Canada
3 - Argelander-Institut für Astronomie der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
4 - Astronomy Department, University of Florida, Gainesville, 32611 FL, USA
5 - Institut für Astronomie, Universität Wien, Türkenschanzstraße 17, 1180 Wien, Austria
6 - Maria Mitchell Observatory, Nantucket, MA 02554

Received 20 April 2005 / Accepted 3 March 2006

Abstract
We analyze light curves of the W UMa type eclipsing binary V781 Tauri from three epochs and radial velocity curves from two epochs simultaneously, including previously unpublished B and V data. The overall time span is from 1983 to 2000 and the solution is done coherently in time (not phase) with five light curves and two sets of primary and secondary velocity curves. Minor systematic differences among the individual light curves are not large enough to undermine the value of a coherent solution that represents 18 years of observations. Times of minima confirm a period of $0\hbox{$.\!\!^{\rm d}$ }34491$ and the general solution finds a small period change, ${\rm d}P/P$, of $(5.08\pm{04})\times10^{-11}$ that represents recent behavior. The eclipse timings cover the last half-century and find ${\rm d}P/P$ about four times smaller, corresponding to a period change time scale, $P/({\rm d}P/{\rm d}t)$ of about 6 million years. The system is over-contact with a filling factor of 0.205. The solution produces a temperature difference of about 260 K between the components, an inclination of $65\hbox{$.\!\!^\circ$ }9$, and a mass ratio M₂/M₁=2.47. Separate solutions of the several light curves that incorporate dark spots find parameters that differ little from curve to curve. Absolute masses, luminosities, radii and the distance are derived, with luminosities and distance based on star 1 being of type G0V. The orbital angular momentum is compared with those of other W UMa type binaries and is normal. The star to star mass flow that one can infer from ${\rm d}P/{\rm d}t$ is opposite to that expected from TRO (Thermal Relaxation Oscillator) theory, but pertains to a time span that is very short compared to the time scale of TRO oscillations.

Key words: binaries: eclipsing - stars: individual: V781 Tauri

1 Introduction

V781 Tau [=BD +26$^{\circ }$971 = HD 248087 = SAO 077615 (spectral type G0)] was found to be variable by Harris (1979) while selecting comparison stars for asteroid photometry (Harris 1982), but he was unable to distinguish between periods of $0\hbox{$.\!\!^{\rm d}$ }3394$ and  $0\hbox{$.\!\!^{\rm d}$ }3449$. Limited numbers of photographic (Berthold 1981, 1983) and photoelectric measurements (Diethelm 1981) indicated the longer period to be more likely, but both data sets are very sparse. V781 Tau was originally classified as an A-type W UMa eclipsing binary (EB) by Rucinski (1974) but is now considered to be W-type. Cereda et al. (1988, hereafter CE88) produced the ephemeris: Min I = HelJD  $2443853\hbox{$.\!\!^{\rm d}$ }9096+0\hbox{$.\!\!^{\rm d}$ }3449094E$. They analyzed the light curves only by Fourier analysis and estimated an orbital inclination of  $68^{\circ }\pm 2^{\circ }$. To resolve the question of the period and achieve a light curve solution, three of us (RAB, AS, and AP) observed and carried out a preliminary analysis of the system in 1983. Since then Lu (1993) analyzed CE88 BV data along with his own radial velocities and Zwitter et al. (2003, hereafter ZW03) made a simultaneous photometric and spectroscopic solution based on Hipparcos and Tycho photometry and new radial velocity data. The binary underwent a continuous period decrease of about $1.6\pm 0.3\times 10^{-9}$ days/day after HJD 2 440 000 according to Liu & Yang (2000) and Donato et al. (2003). If one includes early photographic minima, there is evidence for a steady period decrease that goes back about 50 years.

2 Observations

We analyze the photometric and spectroscopic data specified in Table 1 simultaneously with time, not phase, as the independent variable. Previous approaches used only photometric data from one source and radial velocities if available. Using all these curves enhances consistency and enables us to use the WD modeling ability to find the ephemeris from whole light and RV curves over a time base of 50 years.

Table 1: Observational diary: the data sources, number of points in each curve, passband (effective central wavelength in nm), time interval in Julian date minus 2 400 000, and year of observation. Vienna V and B refer to the light curves obtained at Vienna Observatory, the Cereda B and V curves are by Cereda et al. (1988), $H_{{\rm p}}$ refers to the Hipparcos $H_{{\rm p}}$-band data centered $\approx$500 nm and the Tycho BV data described and analyzed by ZW03, DAO indicates the Lu (1993) radial velocity curves, and Asiago stands for the Asiago Observatory radial velocities from the Ca triplet region (ZW03).

 

2.1 Spectra and radial velocities

Lu's (1993) 38 radial velocity measurements produced a spectroscopic mass ratio ( $q_{\rm sp}$) and the first direct mass estimates. He used the Wilson-Devinney (hereafter, WD) program (1978 version) to analyze his radial velocities, and the CE88 light curves. Velocities of ZW03 have a resolution $\sim$17 000, which is similar to that planned for the radial velocity spectrometer onboard GAIA, an ESA cornerstone mission to be launched in December 2011 according to current plans. Munari et al. (2001) and Milone et al. (2003) discuss GAIA's prospects to obtain fundamental data from EB observations. ZW03 provided a description and reduction of V781 Tau data as a part of a series of GAIA tests (Munari et al. 2001); their velocities mimic the GAIA accuracy. Some velocities near the conjunctions depart from the expected proximity and eclipse effects, presumably because of line blending. We assigned zero weight to those points, as did ZW03, while all other points had weight 1.

2.2 Photometry

 

The previously published data are Johnson B and V light curves by Cereda et al. (1988) and the $H_{\rm P}$ and Tycho curves described in ZW03. One of us (AP) observed V781 Tau with Johnson BV filters on 13 nights in spring and autumn 1983 with a single channel photometer on the 60 cm RC telescope of the Leopold-Figl-Observatory of the University of Vienna. The photomultiplier was an unrefrigerated EMI 9844A and the integration time was 15 s. The comparison star, BD +26$^{\circ }$972, is 3 arcmin to the northeast and similar in color. No corrections for differential extinction were applied. Average magnitudes and color indices were determined by AP for the variable and comparison stars by observing photometric standards. For the variable the V magnitude and color index at phase 0.224 were:

$$V=8\hbox{$.\!\!^{\rm m}$ }{620}\pm {0\hbox{$.\!\!^{\rm m}$ }{005}}$$

$$B-V=0\hbox{$.\!\!^{\rm m}$ }{52}\pm 0{\hbox{$.\!\!^{\rm m}$ }{01}}$$

and for the comparison:

$$V=9\hbox{$.\!\!^{\rm m}$ }{630}\pm {0\hbox{$.\!\!^{\rm m}$ }{005}}$$

$$B-V=0\hbox{$.\!\!^{\rm m}$ }{44}\pm {0\hbox{$.\!\!^{\rm m}$ }{02}}.$$

The internal standard deviation of the V and B photometry is $\pm$ ${0\hbox{$.\!\!^{\rm m}$ }005}$ and $\pm$ ${0\hbox{$.\!\!^{\rm m}$ }009}$. The 1202 V and 267 B Vienna differential observations are available in electronic form at the CDS. The CE88 light curves reveal a sizable asymmetry (Davidge & Milone 1984) and a few hundredths of a magnitude difference between the primary and secondary minimum levels that are not obvious in the sparse Hipparcos light curves. The Tycho light curves are dominated by scatter.

The Vienna data allow more thorough modeling than do the Hipparcos, Tycho, or CE88 light curves. All Vienna BV and HIP observations are shown in Fig. 3 with computed curves for the solution discussed below. Both the primary minimum (Min I) and the maximum (Max II) preceding it are brighter in autumn 1983 than in spring 1983. Max II also shows substantial scatter. Note that this is due to lack of repetition as the V curve covers 881 cycles. Together with Cereda's light curve, this finding confirms variable light curve asymmetry. Data set properties are summarized in Table 1.

After the first submission of our paper Yakut et al. (2005) published 326 observations in B, 342 in V and 336 in R obtained on three nights. Their estimated standard deviations for each differential observation are $0\hbox{$.\!\!^{\rm m}$ }03$, $0\hbox{$.\!\!^{\rm m}$ }02$ and  $0\hbox{$.\!\!^{\rm m}$ }03$ for the B, V and R bands. These values appear consistent with the light curves in their Fig. 1. As these standard deviations appear relatively large, we did not include these data in our simultaneous analysis.

Figure 1: Residuals from a linear ephemeris versus HJD minus 2 445 000. The basis of this plot are 112 minima from the Kreiner, Kim and Nha database for V781 Tau with 13 Vienna and 5 Yakut et al. minimum times added. The parabola shows the fit to the residuals between the observed times of minima and the linear ephemeris (1). The Vienna minimum times near HJD 2 445 400 are well reproduced by this fit. The residuals with respect to this parabola are also displayed. 7 points with residuals smaller or larger than -0.015, or 0.015, respectively, are not displayed.

Open with DEXTER

2.2.1 Times of minima and orbital period

Previous information on the period and collections of minima are in Liu & Yang (2000), Donato et al. (2003), and the Kreiner, Kim, and Nha (KKN) website: www.as.ap.krakow.pl/o-c/index.php3. Seven primary and six secondary minima were observed in Vienna. The method of Kwee & van Woerden (1956) produced the epochs of minimum light in Table 2. Whenever possible the same interval and the same number of data points were used. A Least Squares solution of the Vienna timing data alone yielded the ephemeris

$${\rm MinI}_{\rm hel}=\rm JD~2~445~389\hbox{$.\!\!^{\rm d}$ }44622(19)+0\hbox{$.\!\!^{\rm d}$ }34490970(19)E.$$

In view of the low precision of early (photographic) minimum times, it is difficult to draw any conclusion about period changes from earlier minima and the Vienna minima alone. Therefore, we generate an EB timing diagram based on the minima included in the KKN database with linear ephemeris

$${\rm MinI}_{\rm hel}=\rm JD~2~443~853\hbox{$.\!\!^{\rm d}$ }911+0\hbox{$.\!\!^{\rm d}$ }344909292E$$ (1)

and include the Vienna minimum times. Residuals from minimum times are in Fig. 1. A (discontinuous) period decrease after JD 2 444 000 suspected by Berthold (1983) is possible, although Fig. 1 suggests a somewhat earlier date. The steady period change derived from the fit shown in Fig. 1 is ${\rm d}P/P=-(5.08\pm 0.04)\times 10^{-11}$ or $-\left( 5.38+0.42\right) \times 10^{-8}$ days/year. Solutions of the combined five photometric data sets with the WD program based on time as the independent variable, provided the ephemeris discussed in Sect. 4. Yakut et al. (2005) determined a value of $-5.32\times 10^{-8}$ days/year.

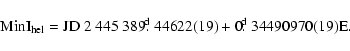
Table 2: Photoelectric minima observed at the Leopold-Figl-Observatory with $\rm O{-}C$ residuals (in days) computed from the linear ephemeris (1).

   
3 Modeling

We refer to the star eclipsed at the deeper (which we call primary) minimum at phase 0.0 as the primary component and label it star 1. Overall it has the weaker spectral lines and is the less massive star. JK used the light curve software package WD2006 based on the 1998 version of WD, to analyze the data. WD2006 is a successor of WD95 (Kallrath et al. 1998). The Least Squares parameter estimation problem is treated as described in Kallrath & Milone (1999, Chap. 4), which also covers the Simplex and Levenberg-Marquardt algorithms used in the Least Squares analysis. The simultaneous analysis included all data described in Table 1, i.e., 62 radial velocities from Lu (1993) and ZW03, and the Vienna and Cereda BV curves. Individual weights w_i are computed as

$$w=w_{{\rm flux}}w_{{\rm c}},$$ (2)

with the following meaning (viz. Wilson 1979):

• $w_{{\rm flux}}$ is a flux-dependent weight that is proportional to a power of the phase-dependent inverse flux (i.e. 1/l^2b) (see Wilson (1979) or Kallrath & Milone (1999, p. 103)), with b=1/2 as appropriate for counting statistics in the nomenclature of Linnell & Proctor 1970); and

• $w_{{\rm c}}$ is a curve-dependent weight that accounts for a given curve's scatter at a reference level.

Modes 1 and 3 (Wilson 1988) are intended for over-contact binaries, as they enforce the condition of a single equipotential for the star surfaces. Our solutions were in mode 3, i.e., the luminosity scaling factor L₂ used in the WD program is coupled to T₂ through the radiative prescription (stellar atmosphere or blackbody) with mutually independent temperatures T₁ and T₂. We also tried mode 2 (no geometrical constraints) to see whether over-contact is required. In WD2006 all Roche configurations (detached, semi-detached, over-contact) can be modeled within mode 2, which means that if one or both stars overfill a Roche lobe, the corresponding lobe-filling constraint is automatically applied. The primary temperature was estimated as 6000 K from its G0 spectral type. In other trials T₁ was 6390 K as in ZW03, based on the Tycho color indices at maximum light and an estimate of the contribution of star 1 to total light.

The strong correlation of limb darkening with other parameters is well-known (see, e.g., Wilson & Devinney 1971; or Twigg & Rafert 1980). Only under exceptional circumstances (e.g. high precision measures, eclipses that clearly are total-annular) will extraction of meaningful limb darkening coefficients be possible. Therefore, we trust coefficients derived from Kurucz (1979, 1993) model atmospheres and rather do not adjust limb darkening parameters. For all bands, including HIP and Tycho, we adopted limb darkening coefficients by Van Hamme (1993) for a logarithmic law, based on Kurucz atmospheres. Van Hamme's interpolation software (http://www.fiu.edu/~vanhamme/) was used to compute these values. If T₂ or log g changes in the course of the iterations, the limb darkening coefficients are altered accordingly. We used the model atmosphere passbands described in Kallrath et al. (1998): ca3flux for the radial velocities, Hpflux for the Hipparcos light curve, and Bflux and Vflux for the CE88 and Vienna B and V light curves.

Table 3: The logarithmic limb darkening coefficients used in the final stages of modeling for the various passbands, including the square passband centered on the calcium triplet region that was used for the radial velocity curves.

4 Solutions

Test runs converged toward contact geometry and also showed that light curves and solutions are insensitive to the albedos, which were fixed at values appropriate for convective envelopes, A₁=A₂=0.5 (Rucinski 1970). The gravity darkening exponents g₁=g₂=0.32 also correspond to convective envelopes (Lucy 1967).

Figure 2: Radial velocities from Lu (1993) and ZW03 and solution curves. The solid and dashed lines are for stars 1 and 2, respectively, with proximity and eclipse effects excluded ( top panel) and included ( bottom panel). The fit is not improved when proximity effects are included. The standard deviation even increased from 13.0 to 14.2 km s-1 as shown in Table 4. However q is different. We estimate the internal precision of a single measurement to be $\pm$5 km s-1 at quadrature and $\pm$10-15 km s-1near conjunction, based on comparison with other data from the same nights.

Open with DEXTER

We first analyzed the radial velocities separately and found a q that is not significantly different from that by Lu (1993). Only the semi-major axis, a=a₁+a₂, the system velocity, $\gamma$, and q were adjusted. Figure 2 shows the radial velocities and fitted curves without and with proximity and eclipse effects. The results are compared quantitatively in Table 4. Radial velocity solutions with proximity and eclipse effects require that the star shapes and surface flux distributions are known. This was achieved by adopting some of the parameters obtained in the simultaneous analysis. Note that the standard deviation of an observation of average weight increased when we included proximity effects. The proximity effects have been applied in all light and velocity simultaneous solutions.

Table 4: Radial velocity parameters without and with proximity and eclipse effects: Orbital semi-major axis, a, systemic velocity, $\protect\gamma$and q. Note that the q's differ by about $4.7\%$ while the a's and $\protect\gamma$'s are almost the same, within their uncertainties.

	Figure 3: Hp and the Vienna BV light curve fits and data versus phase. The lower panels show the residuals versus phase.
Open with DEXTER

	Figure 4: Same as Fig. 3 but for Cereda BV in the left and center columns. The right column shows the fit and residuals when Cereda B was fitted individually with one dark spot on each star.
Open with DEXTER

Table 5: Parameters and standard errors for the base light curve solution obtained by a simultaneous fit. B is polar surface brightness, f₁ and f₂ are the fill-out factors $f_{i}:=\frac{\Omega ^{{\rm I}}-\Omega _{i}}{\Omega ^{{\rm I}}-\Omega ^{{\rm O}}}$, with $\Omega ^{{\rm I}% }$ and $\Omega ^{{\rm O}}$ the Roche potentials of the inner and outer critical surfaces. S and V denote surface area and volume and <tex2html_comment_mark> k=R₂/R₁ is the ratio of the mean radii. a is the semimajor axis in solar radii, and $\protect\gamma$ is the systemic velocity in km s^-1.

Table 6: Solutions with standard errors. The last four rows give the standard deviations of the observed points from the solution curves that were used in curve-dependent weighting. The reference epoch, HJD₀, is given minus 2 440 000. The simultaneous fit column is the base for adding spots. The uncertainty specified for T₁ is based on personal judgment. The standard errors derived for T₂ were much smaller than the uncertainties assumed for T₁; therefore we added them to the uncertainties of T₁. All other uncertainties are standard errors.

Our analysis is summarized in Table 5 and the simultaneous fit (base solution) column of Table 6. We refer to this result as the base solution. It does not include spots but has adjusted the linear period change, $\dot{P}={\rm d}P/{\rm d}t$. We obtained the following ephemeris from simultaneous light and velocity fits covering 6267 days:

$${\rm HJD}_{0} 2~447~962.465720\pm 0.000183$$ = (3)

$$0.344907993\pm 0.000000059$$ P = (4)

$$\dot{P} -(6.45\pm 0.49)\times 10^{-10}~{\rm days/day}.$$ = (5)

This $\dot{P}$ corresponds to a mean period change of $-2.38\times 10^{-7}$ days/year over the years 1983-2000. Note that this $\left\vert \dot{P} \right\vert$ is larger by more than a factor of four than the value $% -\left( 5.38+0.42\right) \times 10^{-8}$ days/year derived from times of minima back to 1950 (see Sect. 2.2.1). The eclipse timings cover the last half-century and correspond to a period change time scale, $P/({\rm d}P/% {\rm d}t)$ of about 6 million years.

Table 7: Spot parameters for the Cereda and Vienna light curves: co-latitudes $\protect\theta_1$ and $\protect\theta_2$ of spots on star 1 and star 2, spot longitudes $\protect\lambda_1$ and $\protect\lambda_2$, spot angular radii $\protect\rho_1$ and $\protect\rho_2$, and dimensionless temperature factors $T^{\rm F}_1$ and $T^{\rm F}_2$. Angles are in radians. There are two spots on each star for Cereda BV while Vienna BV has two spots on star 1 and no spots on star 2. The second column has the standard deviation of the fit; $\protect\sigma = 1000 \protect\sigma_{{\rm fit}}$. In addition to the spot parameters those in the third column also were adjusted. We included i because it effects the amplitudes of light curves.

A similar solution follows when we assume T₁=6390 K. In that case, qis 2.46, the temperature difference T₁-T₂ is 250 K instead of 200 K, and the standard deviation is slightly larger. Distances from the T₁=6000 K and T₁=6390 K solutions are 83and 94 pc respectively, consistent with the Hipparcos distance of 81_-8⁺¹⁰ pc. Mode 2 solutions converged to over-contact. Forced solutions for slightly detached configurations gave different i, q and T₂ and slightly worse fits.

All of the simultaneous fits show systematic deviations. Observations over a few cycles in different years reveal substantial variability in the height of the secondary maximum. Magnetic spots are usually assumed to be responsible for such variability. Although spectroscopic evidence for spots is lacking for V781 Tau, they are common in W UMa binaries and are understood to be produced by magnetic dynamos caused by cell motions in convective envelopes. In any case, adoption of spots is unlikely to cause problems because, in cases where more than one method was used to deal with light curve asymmetries, the solutions were reasonably alike (see Milone et al. 1987, for an example). The issue of their reality may be resolved with stellar tomography and spectroscopy. For now, our strategy is to reach an optimal fit with a minimum number of spots.

The most problematic light curve is Cereda B, with discrepancies in both maxima and minima and even displacement of secondary minimum from 0.5 phase. A capability to solve for discontinuous period change events, as outlined in Wilson (2005), would have been helpful, but the associated version of the WD program is still under development and not yet ready for applications. Ephemeris parameters subject to Least Squares solution in the current WD program are: reference epoch, period, and (constant) dP/dt.

With the idea of refining the base solution by incorporation of dark spots, spot parameters were adjusted along with a few other parameters that are identified in Table 7. The CE88 and Vienna data were solved separately. Vienna V has secondary minimum slightly shifted from phase 0.5. Vienna B fits significantly less well than V and the simultaneous BV fit is clearly non-optimal. For that reason, and also because Vienna B covers only 3 cycles within the 864 cycles of Vienna V, we solved them separately. With other parameters taken from the base solution, one dark spot on each star sufficed to give a reasonable fit. Table 7 has the spot parameters. Addition of a few spots to the base solution did not help very much for Cereda B and V, where a simultaneous fit does not seem possible even when parameters such as i, T₂, or surface potentials, are allowed to vary. The fit improved only slightly with those parameters free, but adjustment of qimproved it more. However the revisions do not greatly change the derived masses and radii or the distance. For the Vienna BV simultaneous analysis the fit improved when we allowed i and T₂ to vary in addition to the spot parameters. We tried i because it affects light curves amplitudes.

Table 8: Absolute parameters for V781 Tau. All uncertainties are standard errors except for the temperatures as explained in the caption to Table 6. J is the orbital angular momentum in units of 10⁵² g cm² s^-1and j is the angular momentum per unit of reduced mass in units of 10¹⁸ cm² s^-1. Star 1 is eclipsed at primary minimum (phase 0 $.\!\!^{\scriptscriptstyle\rm p}$0).

	Figure 5: Intersections of V781 Tau's inner and outer critical equipotentials with the x-y-plane. The middle curve represents the (over-contact) surface. The left star is component 1.
Open with DEXTER

Our solution differs from that by Yakut et al. (2005) because they adopted a mass ratio of 2.278 instead of simultaneously fitting radial velocities and photometric data. They also adopted a different temperature of 6150 K for the primary component. Their fits (Fig. 1 of their publications) show systematic deviations close to the V and R secondary minima, and close to the secondary maximum in all bands. Only the inclination agrees within the standard errors. If we compare our light curve solution with the Yakut et al. observations we get fits of similar quality to theirs.

5 Absolute parameters and evolutionary status

Based on our analysis we derive the absolute parameters of Table 8:

Our T₁ of 6000 K comes from the G0V spectral type and is supported by the mean (B-V) of $\hbox{$.\!\!^{\rm m}$ }60$ (CE88) that closely agrees with the spectral type on the assumption of small interstellar reddening. V781 Tau's galactic coordinates are $l\approx 182^{\circ }$ and $b\approx 0\hbox{$.\!\!^\circ$ }8$. In this direction we find E(B-V)<0.1 (e.g., Paresce 1984) to more than 100 pc. Since a distance modulus  $m_{V}-M_{V}\approx 9.3 -4.6=4.7$ yields $r\approx 87$ pc as an upper limit, the assumption $E(B-V)\leq 0.05$ is realistic and leads to  $(B-V)_{0}\approx 0\hbox{$.\!\!^{\rm m}$ }55$ and type G0V. This approach differs from that by ZW03, which is based on a reasonable use of the Tycho passband data, but for which the temperature uncertainties may be underestimated. Aside from this issue our parameters are similar to those of ZW03, who used only Hipparcos/Tycho photometric data and radial velocities of similar quality to that expected for the GAIA space mission. The fact that the results based on limited data and quality of the data used by ZW03 produced results which were confirmed by our extended analysis increases the trust one might have towards GAIA and the expected results.

The absolute parameters in Table 8 include the orbital angular momentum, $J=2\pi \mu a^{2}/P$ (approximately the total system angular momentum); the reduced mass, $\mu =[m_{1}^{-1}+m_{2}^{-1}]^{-1}$; the semimajor axis, a; the period, P; and the specific angular momentum (per unit reduced mass), j. Angular momentum considerations are discussed, by, e.g., Mochnacki (1985), Duerbeck (1984) and Maceroni & Van't Veer (1996, MVV, hereafter). We included these data to compare V781 Tau's location with W UMa type binaries in Fig. 5 of MVV. The placement of V781 Tau (indicated by a circle) on a plot (Fig. 6) of angular momentum vs. reduced mass, shows it to be in the "middle of the pack'' of W UMa systems, the basic data for which were taken from MVV and enhanced with data from Maceroni's website http://mporzio.astro.it/~maceroni/wumacat.html.

Figure 6: System angular momentum vs. total mass. A circle marks V781 Tau, $\times$ marks CN And, and Maceroni's identification numbers indicate the following outliers in one or more of the plots: 70 = XY Boo, 79 = AK Her, 80 = AW UMa, 81 = TV Mus, 82 = TY Men, 84 = DK Cyg, 85 = XZ Leo, 86 = OO Aql, 87 = BU Vel, 88 = $\protect\epsilon$ Cra, 89 = AQ Tuc, 90 = RR Cen, 91 = V535 Ara, 92 = S Ant, 93 = RS Col, 94 = MW Pav, 95 = TY Pup, and 96 = UZ Oct. The dynamical and other properties of V781 Tau, CN And, and the outlier group are listed in Table 9 and are mostly taken from Maceroni & Van't Veer (1996).

Open with DEXTER

Table 9: Properties of V781 Tau compared to those of CN And and outlier stars of Fig. 5. CN And data are from Van Hamme et al. (2001). Data for the latter, except for J and j, were taken from Maceroni & Van't Veer (1996) and updated, and numbered, as per Maceroni's website compilation.

Although the over-contact parameter (0.205) of V781 Tau is larger than the medians and modes for W-types (see histograms in Fig. 7), it is not so large that a significant amount of matter is likely to be lost through the Lagrangian point L₂, as conjectured in ZW03. A more likely source of the period decrease in V781 Tau is, therefore, mass flow from the more massive to the less massive component.

Figure 7: Histograms of the frequency distribution of contact parameters (also called "fill out factors'') of over-contact systems, taken from the Maceroni & Van't Veer (1996) compilation, supplemented with newer data from Maceroni's website. The panels are for W-type, A-type, and for both types together. They demonstrate that V781 Tau's f of 0.205 is relatively large for W-type systems but is more consistent with W-type than A-type.

Open with DEXTER

In TRO theory (Lucy 1976; Flannery 1976; Robertson & Eggleton 1977) matter is transferred from the less to the more massive star, increasing the separation (and period) until the components are no longer in contact. In the broken contact stage, the more massive component overflows its lobe, causing matter to stream toward the secondary component, thus decreasing the orbit scale until contact is re-established. However V781 Tau is over-contact with mass flow ostensibly from the more to the less massive star, according to evidence of the decreasing orbit period. The mass flow should have reversed at this TRO stage unless contact was established too recently for reversal to have occurred, which seems unlikely, given the substantial over-contact. The period decrease is well established over the half-century of timing data, but TRO contact stages are predicted to last for $\approx$10⁷ years and W-types typically show random period jumps, so a half-century may not adequately represent long term behavior.

Qian (2001) concludes that a relation between the orbital period variation and the mass ratio of the W-type contact binaries exists. Using the KKN and MVV database, he found that those with $\dot{P}>0$ have mass ratios q>0.4, and those with $\dot{P}<0$ have mass ratio q<0.4; Qian seems to have defined the mass ratio such that it is always less than unity. V781 Tau, with its mass ratio 2.47, corresponding to <tex2html_comment_mark> q=0.40 in Qian's convention, has the apparently cross-over mass ratio 0.4. He asks why some systems show an orbital period increase while others decrease, and argues that if the secular period change is caused by conservative mass transfer, this relation may suggest that the evolution of W-type systems is oscillating around a "critical'' mass ratio ( $q\approx 0.4$). On the other hand, the relation may be potentially strong observational evidence for Rahunen's conclusion that angular momentum loss (AML) may enable the components to remain in good contact throughout the TRO cycle. This connection could be explained by the combination of the mass transfer and variable AML via changing contact depth. Qian also speculates that the secular period changes of binaries studied in his paper may be part of long-period variations. As an alternative, we propose that $q\approx 0.4$ may simply be a cross-over point for W-types at which AML balances mass transfer in regard to $\dot{P}$.

6 Summary and conclusions

Our analysis shows that V781 Tau is over-contact with $i=65\hbox{$.\!\!^\circ$ }6$, q=2.47, a contact parameter of 0.205, and a temperature difference of about 260 K. A steady period decrease over 50 years strongly suggests matter flow from the more to the less massive star, which is in the opposite sense to that expected in the over-contact stage of TRO oscillations. Contact could possibly have been re-established only recently, giving insufficient time for the flow to reverse. However the over-contact level argues against that interpretation, as it is typical of normal W-type W UMa's or even somewhat greater than average. Stellar structure theory has not explained why eclipses of the lower mass stars in W type systems are deeper than those of the other star. However study of V781 Tau and other W types with a polarizing spectrometer, such as CFHT's ESPaDOnS (Echelle Spectro-polarimetric Device for the Observation of Stars), could map magnetic fields and magnetic spots and thereby explore surface brightness distributions and their role in setting relative eclipse depths.

During the V781 Tau analysis it became clear to JK that further improvements in light curve analysis could be made by treating the following circumstances:

1.

discontinuous period changes; this is under development as outlined in Wilson (2005);

2.

several radial velocity curves for each component;

3.

(adjustable) curve-dependent phase shift $\it pshift$, epoch E_0c, period $P_{\rm c}$, period change $\dot{P}_{\rm c}$; and

4.

(adjustable) curve-dependent spot parameters, and allowance for differential stellar rotation and latitude migration of spot groups.

For systems such as V781 Tau these added capabilities would enhance the analysis significantly.

Acknowledgements

The authors are indebted to B.-C. Kämper for many helpful discussions and K. G. Strassmeier for valuable comments. J. Kreiner's help in providing the V781 Tau minimum times in electronic form is appreciated. We thank K. Yakut to make his BVR observations available to us. Later stages of this work were funded in part by grants from the Natural Sciences and Engineering Research Council of Canada to EFM. R. E. Wilson's participation was supported by US National Science Foundation grant No. 0307561.

References

• Berthold, T. 1981, Inf. Bull. Var. Stars No. 1942 (In the text)
• Berthold, T. 1983, Inf. Bull. Var. Stars No. 2443 (In the text)
• Cereda, L., Mist, A., Niarchos, P. G., & Poretti, E. 1988, A&AS, 76, 255 [NASA ADS] (In the text)
• Davidge, T. J., & Milone, E. F. 1984, ApJS, 55, 571 [NASA ADS] [CrossRef] (In the text)
• Diethelm, R. 1981, BBSAG No. 52, 71 (In the text)
• Donato, L., Lepardo, A., Santini, V., et al. 2003, Inf. Bull. Var. Stars No. 5391 (In the text)
• Duerbeck, H. W. 1984, Mitt. Astr. Gesell., 62, 87 [NASA ADS] (In the text)
• Flannery, B. P. 1976, ApJ, 205, 217 [NASA ADS] [CrossRef] (In the text)
• Harris, A. W. 1979, Inf. Bull. Var. Stars No. 1556 (In the text)
• Harris, A. W. 1982, IAPPP Comm No, 10, 44 (In the text)
• Kallrath, J., & Milone, E. F. 1999, Eclipsing Binaries - Modeling and Analysis (New York: Springer) (In the text)
• Kallrath, J., Milone, E. F., Terrell, D., & Young, A. T. 1998, ApJS, 508, 308 [NASA ADS] [CrossRef] (In the text)
• Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] (In the text)
• Kurucz, R. L. 1993, in Light Curve Modeling of Eclipsing Bianary Stars, ed. E. F. Milone (New York: Springer), 93 (In the text)
• Kwee, K. K., & van Woerden, H. 1956, Bull. Astron. Inst. Neth., 12, 327 [NASA ADS] (In the text)
• Linnell, A. P., & Proctor, D. D. 1970, ApJ, 162, 683 [NASA ADS] [CrossRef] (In the text)
• Liu, Q., & Yang, Y. 2000, A&AS, 142, 31 [EDP Sciences] [NASA ADS] (In the text)
• Lu, W. 1993, AJ, 105, 646 [NASA ADS] [CrossRef] (In the text)
• Lucy, L. B. 1967, ZfAp, 65, 89 [NASA ADS] (In the text)
• Maceroni, C., & Van't Veer, F. 1996, A&A, 311, 523 [NASA ADS] (In the text)
• Milone, E. F. 2003, in GAIA Spectroscopy, Science and Technology, ed. U. Munari, ASP Conf. Ser., 298, 303 (In the text)
• Milone, E. F., Wilson, R. E., & Hrivnak, B. J. 1987, ApJ, 318, 325 [NASA ADS] [CrossRef] M (In the text)
• Mochnacki, S. W. 1985, in Interacting Binaries, ed. P. P. Eggleton (In the text)
• Munari, U., Tomov, T., Zwitter, T., et al. 2001, A&A, 378, 477 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Paresce, F. 1984, AJ, 89, 1022 [NASA ADS] [CrossRef] (In the text)
• Qian, S. 2001, MNRAS, 328, 635 [NASA ADS] [CrossRef] (In the text)
• Robertson, J. A., & Eggleton, P. P. 1977, MNRAS, 179, 359 [NASA ADS] (In the text)
• Rucinski, S. M. 1974, Acta Astron., 24, 119 [NASA ADS] (In the text)
• Rucinski, S. M. 1985, in Interacting Binary Stars, ed. J. E. Pringle, & R. A. Wade (Cambridge University Press), 113
• Twigg, L. W., & Rafert, J. B. 1980, MNRAS, 193, 775 [NASA ADS] (In the text)
• Van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] (In the text)
• Van Hamme, W., Samec, R. G., Gothard, N. W., et al. 2001, AJ, 122, 3446 [NASA ADS] (In the text)
• Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] (In the text)
• Wilson, R. E. 1979, ApJ, 234, 1054 [NASA ADS] [CrossRef] (In the text)
• Wilson, R. E. 1988, Physical models for close binaries and logical constraints, in Critical Observations Versus Physical Models for Close Binary Systems, ed. K.-C. Leung (Montreux, Switzerland: Gordon and Breach), 193 (In the text)
• Wilson, R. E. 2005, Ap&SS, 299, 197-207 [NASA ADS] (In the text)
• Yakut, K., Ulas, B., Kalomeni, B., & Gülmen, Ö. 2005, MNRAS, 363, 1272 [NASA ADS] [CrossRef] (In the text)
• Zwitter, T., Munari, U., Marrese, P. M., et al. 2003, A&A, 404, 333 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)