A&A 452, 743-749 (2006)
DOI: 10.1051/0004-6361:20035604
C. Schuster 1 - I. Lerche1,2 - R. Schlickeiser1 - M. Pohl3
1 - Institut für Theoretische Physik, Lehrstuhl IV:
Weltraum- und Astrophysik, Ruhr-Universität Bochum, Germany
2 -
Institut für Geophysik und Geologie, Universität Leipzig, Germany
3 -
Department of Physics and Astronomy, Iowa State University, Ames, Iowa 50011
Received 31 October 2003 / Accepted 4 November 2005
Abstract
Context. Calculations of highly energetic neutrino and TeV ![]() -ray emission from relativistic jets of Active Galactic Nuclei (AGN) are often based on a model that involves a collimated relativistic blast wave, in which the spectral evolution of energetic particles is determined by the interplay between the particle injection by sweep up of the interstellar medium, energy losses by radiation and diffusive escape.
-ray emission from relativistic jets of Active Galactic Nuclei (AGN) are often based on a model that involves a collimated relativistic blast wave, in which the spectral evolution of energetic particles is determined by the interplay between the particle injection by sweep up of the interstellar medium, energy losses by radiation and diffusive escape.
Aims. To date such models only have been solved numerically because of the highly non-linear nature of the time-dependent equations describing particle spectra and bulk energy loss. However it is difficult to see how parameters and groupings of parameters influence the resulting numerical solutions, except through intensive investigations of many numerical simulations. Therefore analytic solutions are particularly helpful.
Methods. We provide exact mathematical solutions to a very broad class of AGN type models. By selecting different functional behaviors of parameter values, we cover a large compendium of possible situations. The comparison of the exact solutions with observational information can help to improve our understanding of the evolution of individual AGN. Exact solutions can also be used to provide controls on the appropropriateness and accuracy of numerical programs used to solve the equations.
Results. We provide an analytical description of the evolution of proton spectra according to the pick-up model. We analyze the behavior of the particle spectra in the plasma frame. The solutions are determined by two competing processes: the deceleration of the jet plasmoid and particle cooling via radiation.
Key words: methods: analytical - radiation mechanisms: non-thermal - galaxies: jets - galaxies: active - plasmas - gamma rays: theory
Active galactic nuclei (AGN) have been established as powerful emitters
of high-energy gamma-ray photons with energies from ![]() to
to ![]()
![]() -rays (for a recent review see Maraschi & Tavecchio 2005).
They are also prime candidates for sources of high-energy neutrino radiation
(Schuster et al. 2002; Waxman 2005) although no
detections have been reported yet (Ackermann et al. 2004).
-rays (for a recent review see Maraschi & Tavecchio 2005).
They are also prime candidates for sources of high-energy neutrino radiation
(Schuster et al. 2002; Waxman 2005) although no
detections have been reported yet (Ackermann et al. 2004).
The reported ![]() -ray emissions are highly variable on all time scales to
the observational limits of days at
-ray emissions are highly variable on all time scales to
the observational limits of days at ![]() energies and hours at
energies and hours at
![]() energies (von Montigny et al. 1995; Mukherjee et al.
1997; Catanese & Weekes 1999; Mattox et al. 1997;
Gaidos et al. 1996).
Combined with the huge luminosities these observations imply a relativistic
Doppler amplification of the high-energy photon radiation. In many cases the
relativistic bulk motion is directly observed as apparent super-luminal motion
of individual emission regions in the so-called jets of VLBI observations
of their radio emission (Pohl et al. 1995; Barthel et al. 1995;
Piner & Kingham 1997a,b).
It is therefore generally accepted that the high-energy photon (and neutrino)
emission of AGNs originates in the relativistic jets of these objects. The
Lorentz and Doppler factors derived from VLBI campaigns are of the order ten
for general samples of AGNs (Vermeulen & Cohen 1994), but may be
higher for AGNs showing prominent
energies (von Montigny et al. 1995; Mukherjee et al.
1997; Catanese & Weekes 1999; Mattox et al. 1997;
Gaidos et al. 1996).
Combined with the huge luminosities these observations imply a relativistic
Doppler amplification of the high-energy photon radiation. In many cases the
relativistic bulk motion is directly observed as apparent super-luminal motion
of individual emission regions in the so-called jets of VLBI observations
of their radio emission (Pohl et al. 1995; Barthel et al. 1995;
Piner & Kingham 1997a,b).
It is therefore generally accepted that the high-energy photon (and neutrino)
emission of AGNs originates in the relativistic jets of these objects. The
Lorentz and Doppler factors derived from VLBI campaigns are of the order ten
for general samples of AGNs (Vermeulen & Cohen 1994), but may be
higher for AGNs showing prominent ![]() -ray emission (Homan et al.
2002, 2003).
-ray emission (Homan et al.
2002, 2003).
The range of Lorentz factors present at the time of ![]() -ray emission,
which presumably occurs before the emission region becomes visible at radio
frequencies, is not known, but is likely considerably higher than ten,
especially as the bulk kinetic energy of the jets is the most probable
energy reservoir for particle acceleration. To accomodate all such
possibilities, this paper allows the initial bulk flow Lorentz factor
-ray emission,
which presumably occurs before the emission region becomes visible at radio
frequencies, is not known, but is likely considerably higher than ten,
especially as the bulk kinetic energy of the jets is the most probable
energy reservoir for particle acceleration. To accomodate all such
possibilities, this paper allows the initial bulk flow Lorentz factor ![]() to be up to several hundred, although the analysis is valid for all
to be up to several hundred, although the analysis is valid for all
![]() .
In particular, when graphical results are presented, high
initial bulk flow Lorentz factors are used to emphasize the relativistic
aspects. Lower initial Lorentz factors can also be used graphically, of course,
because the analytic solutions are valid as long as
.
In particular, when graphical results are presented, high
initial bulk flow Lorentz factors are used to emphasize the relativistic
aspects. Lower initial Lorentz factors can also be used graphically, of course,
because the analytic solutions are valid as long as
![]()
How the kinetic energies of such relativistic outflows is transferred to energetic particles, and subsequently converted into high-energy photon (and neutrino) radiation, is one of the most important issues in current AGN research. Many existing radiation models of AGNs (see e.g. Böttcher & Dermer 1998; Dermer & Schlickeiser 2002; Ghisellini 2002; Sikora 1997) are unspecific on the microphysical details of this crucial point. Without detailed discussion these models often assume that a significant fraction of the energy in nonthermal baryons of the relativistic outflow is injected into nonthermal ultrarelativistic pairs and/or hadrons with power-law energy distribution functions in the comoving jet frame. This significant conversion is attributed to the scenario that the outflowing relativistic jet plasma has produced a relativistic shock wave with fully developed hydromagnetic turbulence in order to allow for efficient nonthermal diffusive particle acceleration at the collisionless shock fronts.
In a series of papers (Pohl & Schlickeiser 2000; Pohl et al.
2002; Schlickeiser et al. 2002; Schlickeiser 2003;
Vainio 2004; Schlickeiser et al. 2003),
the microphysical details of this energy conversion process have been
investigated both for leptonic and hadronic relativistic outflows.
As described in Pohl & Schlickeiser (2000) the emission region in the AGN jet is assumed to be a cloud of dense plasma (hereafter called plasmoid),
which moves relativistically through the interstellar medium of the AGN host
galaxy. The swept-up ambient matter is quickly isotropized in the jet frame by
a relativistic two-stream instability, which provides relativistic particles in
the jet without invoking any further acceleration process. The typical primary
particles would be protons with an initial Lorentz factor of the order of one hundred, distributed isotropically in a jet also moving with an initial bulk
Lorentz factor of the order of one hundred. In the case of hadronic outflows,
inelastic proton-proton collisions with the outflow plasma would then lead to
the production of TeV ![]() -rays by
-rays by ![]() -decay and high energy neutrinos
via decay of charged pions (
-decay and high energy neutrinos
via decay of charged pions (![]() ), as well as synchrotron, inverse Compton
and bremsstrahlung emission produced by secondary electrons at lower energies.
Due to this efficient pick-up of interstellar particles, the outflowing cloud
is decelerated and mass-loaded, so that the Lorentz factor drops quickly to
the order of 10, as observed.
), as well as synchrotron, inverse Compton
and bremsstrahlung emission produced by secondary electrons at lower energies.
Due to this efficient pick-up of interstellar particles, the outflowing cloud
is decelerated and mass-loaded, so that the Lorentz factor drops quickly to
the order of 10, as observed.
The time-dependent numerical calculations of Pohl & Schlickeiser (2000)
indicate that the observed variability behavior and ![]() -ray spectra of
blazars may be accounted for especially if the outflowing cloud propagates
through a structured non-uniform ambient interstellar or intergalactic medium.
The observed variable light curves then reflect the spatial inhomogeneities of
the traversed medium because the varying ambient gas density regulates the
injection rate of primary protons, electrons and hydrogen neutrals into the
outflowing cloud.
-ray spectra of
blazars may be accounted for especially if the outflowing cloud propagates
through a structured non-uniform ambient interstellar or intergalactic medium.
The observed variable light curves then reflect the spatial inhomogeneities of
the traversed medium because the varying ambient gas density regulates the
injection rate of primary protons, electrons and hydrogen neutrals into the
outflowing cloud.
There are two aspects to the physics of radiation modeling. There are available detailed scenarios for radiation production from two flow leptonic models (Henri & Pelletier 1991), or from hadronic models (Mannheim et al. 1991; Rachen 2000), but these models do not include detailed descriptions of the primary particle (proton) spectra evolution in the evolving jets. Instead such particle spectra are assumed as input and then the radiation production is calculated. What is required is the second aspect: a detailed, time-dependent, self-consistent model of primary particle evolution that can then be coupled to radiation production. Precisely that problem is the focus of this paper.
The evolution of relativistic electrons and their associated radiation has already been discussed by Pohl & Schlickeiser (2000). Here we provide analytic results of the relevant equations rather than the purely numerical results reported earlier.
One can distinguish four main parts of the relativistic pick-up process:
Not only are TeV-emitting AGN highly variable but there is a correlation between the different emission bands in these AGN spectra (especially the two bumps shape of the blazars) with the correlation between the different bands beeing important in constraining the physics of the emission mechanism. A flow through non-uniform media may account for such conditions. However this paper is concerned dominantly with exploring and obtaining the self-consistent flow and associated primary particle spectra equations. A detailed comparison with observations of the resulting model behaviors is reserved for a future paper. Once one has a self-consistent structure, it is a matter of detailed determination of all parameters in the model based on a comparison with radiation from each jet to elucidate the "best fit'' to such data. This has already been done for a few jets (Schuster 2005) using the self-consistent model developed here, but considerably more work must be undertaken for more objects.
The organization of the paper is as follows:
after reviewing the basic physical features of the model for channelled
relativistic outflows in Sect. 2, we show the analytical solution for the
mass of the jet plasmoid in Sect. 3. This solution comes in useful for the
analytical description of the energy distribution of protons in an AGN jet,
derived in Sect. 4. In Sect. 5 we deal with an example of secondary
particle production the resulting ![]() -rays. In Sect. 6 we summarize
and discuss the results.
-rays. In Sect. 6 we summarize
and discuss the results.
As already stated, VLBI results indicate Lorentz factors of at least order ten.
The initial bulk flow models developed here allow for, but do not require,
initial outflow Lorentz factors of several hundred.
However a collimated flow (also called jet) can be produced by the
accretion disk surrounding the central black hole (the Blandford-Payne scenario)
or the central black hole itself (the Blandford-Znajek scenario).
Neither of these mechanisms are able to produce such relativistic outflow (the
extreme upper limit appears to be a Lorentz factor of the order of a few units. However a Lorentz factor of at least ten from radiation observations
(and surely higher for ![]() -ray emission) already stretches this to their
limits, if not beyond. Here we deal with what happens to a relativistically moving jet and its associated hadron (proton) particle
spectra. The high initial bulk Lorentz factor (of order of a few hundred) used
in the examples sharply emphasizes the consequences.
-ray emission) already stretches this to their
limits, if not beyond. Here we deal with what happens to a relativistically moving jet and its associated hadron (proton) particle
spectra. The high initial bulk Lorentz factor (of order of a few hundred) used
in the examples sharply emphasizes the consequences.
We briefly review the assumptions of the model for a collimated hadronic
outflow as given in Pohl & Schlickeiser (2000). An emission region
in the jet outflow is assumed to be a plasma cloud consisting of electrons
and protons with a cylindrical shape of thickness d, being small compared
to the radius R. The cloud is moving with a bulk Lorentz factor ![]() through the ambient medium. Viewed in the rest frame of the jet plasma cloud,
the interstellar medium forms an electron-proton beam of number
density
through the ambient medium. Viewed in the rest frame of the jet plasma cloud,
the interstellar medium forms an electron-proton beam of number
density![]()
![]() ,
which is low
compared with the plasma density
,
which is low
compared with the plasma density
![]() of the jet cloud.
of the jet cloud.
Pohl & Schlickeiser (2000) showed that the incoming particles of the
interstellar medium
quickly become isotropized by self-excited
![]() turbulence,
but retain their relative velocities with respect to the jet plasma.
The jet plasma thus becomes enriched with relativistic particles, of which
mainly the protons are of interest as secondary generators
(e.g.
turbulence,
but retain their relative velocities with respect to the jet plasma.
The jet plasma thus becomes enriched with relativistic particles, of which
mainly the protons are of interest as secondary generators
(e.g. ![]() -rays).
-rays).
So the relativistic protons are injected at a rate
As a main consequence of the sweeping up of interstellar matter we deal
with a system that is not stationary. Momentum conservation requires
that the bulk Lorentz factor ![]() of the plasmoid decreases at a rate:
of the plasmoid decreases at a rate:
Before the detailed discussion we comment on the physical parameters relevant for the emission regions of AGN jets:
1) from variability time scales ![]() corrected for beaming
corrected for beaming
![]() we estimate the size d to range from
we estimate the size d to range from
![]() (for sources variable on the scale of hours) to d=2.6
(for sources variable on the scale of hours) to d=2.6 ![]()
![]() (for sources variable on the scale of days) with
(for sources variable on the scale of days) with
![]() .
.
2) from Doppler-boosted ![]() -ray luminosity we estimate
the density
-ray luminosity we estimate
the density ![]() of the non-thermal particles:
of the non-thermal particles:
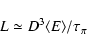 |
(4) |
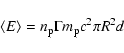 |
(5) |
![\begin{displaymath}%
{\rm d}E/{\rm d}t= - 0.65~c~ n_{\rm b}~ \sigma_{\rm pp} (E-m_{\rm p}c^2)~
\theta [E-E_{\rm th}] \;~ {\rm erg/s},
\end{displaymath}](/articles/aa/full/2006/24/aa0604-03/img40.gif) |
(6) |
| |
= | ||
| (7) |
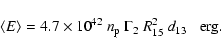 |
(8) |
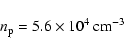 |
(9) |
Our detailed modelling is performed for these values of parameters and thus relevant for AGN jets.
Assuming the background magnetic field to be uniform and directed along the
x-axis and neglecting any expansion of the beam, the temporal evolution of
proton spectra
![]() obeys an enhanced continuity
equation
obeys an enhanced continuity
equation
The escape and diffusion of relativistic particles (protons, electrons and perhaps neutral hydrogen through charge exchange processes) is influenced by both the strength and orientation of any prevailing magnetic field in relation to the flow direction, as is known from many other astrophysical plasma kinetic situations. In particular, transverse and parallel diffusion are known to be different (Schlickeiser 2003). The influence of such a magnetic field orientation, particularly if non-uniform, on the self-consistent calculation reported here would be interesting to undertake, as would the influence of an energy-dependent diffusion tensor on the analytic solution. If, as suggested by Bogovalov & Tsinganos (1999), a non-relativistic MHD-jet is required for collimation, the assumption of a weak beam necessary for isotropisation would have to be abandoned. The latter assumption, however, appears to be corroborated by observation.
To achieve an analytical description of the particle spectrum
![]() consider first the behavior of the time dependent mass M of the jet plasma.
Transform Eq. (10) to:
consider first the behavior of the time dependent mass M of the jet plasma.
Transform Eq. (10) to:
| (16) |
Note especially that with the dependence of the parameters for
the time scale of diffusive escape
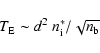 |
(17) |
As we will see in the next section, the temporal behavior of the mass function determines the particle distribution.
The main technical problem is to solve the partial differential Eq. (10) analytically for the particle spectrum
![]() .
After multiplication of Eq. (12) by
.
After multiplication of Eq. (12) by ![]() ,
integration and use of the standard method of characteristics we deduce
,
integration and use of the standard method of characteristics we deduce
The characteristic curves can be referred to as the paths of the particles
in a ![]() -
-![]() phase space because Eq. (18) completely
determines the cooling of the protons. For example a proton that starts at
t=0 with an initial bulk Lorentz factor
phase space because Eq. (18) completely
determines the cooling of the protons. For example a proton that starts at
t=0 with an initial bulk Lorentz factor
![]() can be found after
some time t with a reduced Lorentz factor
can be found after
some time t with a reduced Lorentz factor ![]() that coincides with the
value
that coincides with the
value ![]() of the characteristic curve labelled
of the characteristic curve labelled
![]() at the
corresponding Lorentz factor
at the
corresponding Lorentz factor ![]() .
Note also that, subject to the initial
condition
.
Note also that, subject to the initial
condition
![]() no particles populate particle paths at
t = 0. The characteristics may be therefore referred to as "virtual paths''
until they are enriched with particles subject to the sweep-up condition, which
is determined by Eq. (1).
no particles populate particle paths at
t = 0. The characteristics may be therefore referred to as "virtual paths''
until they are enriched with particles subject to the sweep-up condition, which
is determined by Eq. (1).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0604fig1.ps}\end{figure}](/articles/aa/full/2006/24/aa0604-03/Timg92.gif) |
Figure 1:
Example characteristic curves. Some particle paths
intersect the line of sweep-up (dashed line of
|
| Open with DEXTER | |
Figure 1 gives typical characteristic curves.
Additionally, the line of sweep-up of particles,
![]() ,
a diagonal line, is displayed.
With the appropriate approximations for small and large parameters Z,
the function
,
a diagonal line, is displayed.
With the appropriate approximations for small and large parameters Z,
the function
![]() ,
given by Eq. (18) can be
integrated in closed form. For very large values of the parameter Z the
function (18) reduces to:
,
given by Eq. (18) can be
integrated in closed form. For very large values of the parameter Z the
function (18) reduces to:
From Eq. (20) we can now see how the temporal behavior of
the particle spectrum is entirely determined by the interplay between
cooling and particle loss time scales. The particle injection by sweep-up
enters via the mass ![]() at the point when the relativistic particles
have joined the jet plasma.
at the point when the relativistic particles
have joined the jet plasma.
For a typical particle path (see Fig. 1) there are two zeros
of
![]() but some characteristic curves fail
completely to intersect the line of sweep-up. In between, there is one curve that will just touch this sweep-up line. In this case the particle path produces a singularity because the denominator of Eq. (20) vanishes
but some characteristic curves fail
completely to intersect the line of sweep-up. In between, there is one curve that will just touch this sweep-up line. In this case the particle path produces a singularity because the denominator of Eq. (20) vanishes
In Figs. 2 and 3 we display various particle distributions for some values of Z. The shape of the spectrum is altered in relation to the osculating point. So for calculations involving proton fluxes (as for example, generation of secondaries like GeV and TeV photons, due to decay of neutral pions), it is inappropriate to choose a simple power law for the injection spectra of protons.
At the osculation point of Eq. (22) ![]() we can write:
we can write:
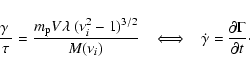 |
(23) |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0604fig2.ps}\end{figure}](/articles/aa/full/2006/24/aa0604-03/Timg110.gif) |
Figure 2: A typical evolution of a particle distribution calculated according to Eq. (20). One can clearly trace the alteration of the shape of the distribution due to the occurrence of the osculating curve. One can also trace the formation of the second peak that happens due to double zeros along some characteristic paths. Note the associated times refer to the jet plasma frame. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0604fig3.ps}\hspace*{4mm}
\includegraphics[width=7.5cm,clip]{0604fig4.ps}\end{figure}](/articles/aa/full/2006/24/aa0604-03/Timg111.gif) |
Figure 3: The left panel investigates the solution corresponding to a large value of Z, the right panel shows a typical solution for small values of Z. Because the osculating curve touches the line of sweep-up at a small Lorentz factor, no alteration of shape is seen in the right panel. |
| Open with DEXTER | |
The energetic protons in the jet plasma undergo inelastic collisions
and produce charged and neutral pions. The neutral pions decay into two ![]() -rays, while the charged pions produce high energy neutrinos.
-rays, while the charged pions produce high energy neutrinos.
![\begin{figure}
\par\includegraphics[width=6.35cm,clip]{0604fig5.ps}\includegraph...
...m,clip]{0604fig6.ps}\includegraphics[width=5.25cm,clip]{0604fig7.ps}\end{figure}](/articles/aa/full/2006/24/aa0604-03/Timg112.gif) |
Figure 4:
Comparison of the analytical solution (28)
with Monte Carlo results from Pohl & Schlickeiser (2000). Additionally,
we compute the results of a numerical integration, using Eq. (27).
The comparisons are nearly identical to the analytical solution, confirming
that the proton distribution determines the behavior of the |
| Open with DEXTER | |
From the the proton spectra derived in the previous section we now deal
with the secondary products, obtained as a folding with specific source
functions. The integrability depends on the form of the source function
and is not simple because of the zeros of Eq. (20), that are
dependent on ![]() via
via
![]() .
In this section
we provide an alternative method for the folding using the techniques already
derived.
.
In this section
we provide an alternative method for the folding using the techniques already
derived.
The number of photons produced per cubic centimetre per GeV and per
second can be calculated via the well-known source function:
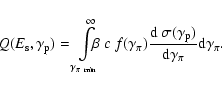 |
(25) |
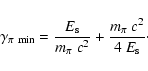 |
(26) |
Figure 4 displays an example of the temporal evolution
for the resulting photon spectra with a value of about Z=7.5 ![]() 106. This value has been calculated with physical parameters chosen
identical to those of Fig. 4 of Pohl & Schlickeiser (2000).
The number densities inside and outside the jet are
106. This value has been calculated with physical parameters chosen
identical to those of Fig. 4 of Pohl & Schlickeiser (2000).
The number densities inside and outside the jet are
![]()
![]()
![]() and
and
![]() ,
respectively, and the thickness of the disk is d = 3
,
respectively, and the thickness of the disk is d = 3 ![]()
![]() ,
whereas the initial Lorentz factor is
,
whereas the initial Lorentz factor is
![]() and the
red-shift z=0.5 enters with the luminosity distance of an Einstein-de Sitter model:
and the
red-shift z=0.5 enters with the luminosity distance of an Einstein-de Sitter model:
![\begin{displaymath}%
D_{\rm L} = {2~c~ (1+z)\over H_0}~
\left[ 1-{1\over \sqrt{1+z}}\right],
\end{displaymath}](/articles/aa/full/2006/24/aa0604-03/img126.gif) |
(29) |
Figure 4 also provides a comparison of the analytical
solution (28) with two numerical results, the first calculated
as the folding with a source function obtained directly from the Monte Carlo calculation of Pohl & Schlickeiser (2000) and the second being
the result of the same numerical routine but fed with the analytic
approximation to the source function
given by Eq. (27). Figure 4 shows that the solution (28) holds for all times and that all the deviations (which are
extremely minor, exept at the very highest energies abouve
![]() )
result from the approximation (27). It is, therefore, more than
adequate to use the analytic form of Eq. (20). The formalism
can be used for a wider class of source functions. The requirement is:
)
result from the approximation (27). It is, therefore, more than
adequate to use the analytic form of Eq. (20). The formalism
can be used for a wider class of source functions. The requirement is:
This paper has developed an analytical description of the evolution of proton spectra according to the pick-up model, in which a two-stream instability leads to sweep up of ambient matter. To trace the fate of the relativistically incoming particles, we first investigated the time dependent mass of the jet plasmoid. The accretion of mass was shown to depend crucially on the depth dof the jet disk as well as the outer and inner number densities. For quantitative investigation these parameters were combined into a single dimensionless parameter Z. Small values of Z correspond to solutions with a mass accretion lasting until the jet plasmoid decelerates to low bulk Lorentz factors. For very large Z the mass loading can be neglected.
For an analytical description of particle spectra we transformed the
variable ![]() (the Lorentz factor of the particles) into a new
variable
(the Lorentz factor of the particles) into a new
variable ![]() ,
labeling the characteristic path of a particle,
tracing the cooling of particles due to radiation losses.
,
labeling the characteristic path of a particle,
tracing the cooling of particles due to radiation losses.
This description further helped to analyze the behavior of the particle
spectra in the plasma frame. The solutions are determined by two competing
processes. When it takes a long time for the jet plasmoid to decelerate to
low bulk Lorentz factors, the particle cooling via radiation becomes more
effective.
Due to the fact that particles in the jet plasma are always swept up at
the Lorentz factor
![]() one can distinguish between "young''
spectra (the deceleration is so fast that the swept-up particles are
the ones with the lowest Lorentz factor
one can distinguish between "young''
spectra (the deceleration is so fast that the swept-up particles are
the ones with the lowest Lorentz factor ![]() )
and "old'' spectra
(the deceleration is now so slow that all particles are cooled to lower
energies than the swept-up particles). Between these two extreme
behaviors there is a point where both processes are equal, related to a integrable singularity in the solution. This description refers to the plasma frame only.
)
and "old'' spectra
(the deceleration is now so slow that all particles are cooled to lower
energies than the swept-up particles). Between these two extreme
behaviors there is a point where both processes are equal, related to a integrable singularity in the solution. This description refers to the plasma frame only.
This paper has dealt with the structure of solutions of the relativistic outflow model, the comparison with data is presented in Schuster & Schlickeiser (2005).
The relativistic particles in the jet plasma give rise to high energy radiation due to decay of neutral pions. To investigate the effects of the proton distribution on the resulting photon spectra, we analytically approximated the results from Monte Carlo claculations for the pion source function. We confirmed that all deviations in the resulting spectra are due to the analytically approximated source function and not to the proton spectrum itself.
Acknowledgements
Partial support by the Bundesministerium für Bildung und Forschung through the DESY, grant 05 CH1PCA 6, is gratefully acknowledged.
The procedure to obtain the mass function (14) is based
on transforming Eq. (12) into an ordinary
differential equation for the mass itself by multiplying
Eq. (12) by ![]() and subsequently performing an integration over
and subsequently performing an integration over
![]() where an integration by parts
of the second term on the left hand side of Eq. (12) gives:
where an integration by parts
of the second term on the left hand side of Eq. (12) gives:
Abbreviate
![]() with
with
![]() After dividing Eq. (10) by the deceleration
After dividing Eq. (10) by the deceleration
![]() and incorporating Eq. (2),
the equation for the particle spectrum reads
and incorporating Eq. (2),
the equation for the particle spectrum reads
| (A.10) |
Equation (28) is derived with a method similar to the derivation
for the mass function. Multiply Eq. (12) by
![]() to obtain (after an integration over
to obtain (after an integration over
![]() :
:
![$\displaystyle {\partial\Gamma \over \partial t} {\partial
\over \partial \Gamma...
...{1/ T_{\rm E}} + {1/ T_{\rm N}}\right] =
Q(\Gamma)~ \lambda~ \sqrt{\Gamma^2-1}.$](/articles/aa/full/2006/24/aa0604-03/img168.gif) |
(A.12) |
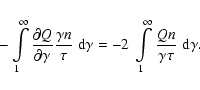 |
(A.14) |