A&A 452, 383-386 (2006)
DOI: 10.1051/0004-6361:20054432

Stochastic modeling of kHz quasi-periodic oscillation light curves[*]

R. Vio1 - P. Rebusco2 - P. Andreani3 - H. Madsen4 - R. V. Overgaard5


1 - Chip Computers Consulting s.r.l., Viale Don L. Sturzo 82, S. Liberale di Marcon, 30020 Venice, Italy
2 - Max Planck Institut für Astrophysik, K. Schwarzschild str. 1, 85748 Garching b. München, Germany
3 - INAF - Osservatorio Astronomico di Trieste via Tiepolo 11, 34131 Trieste, Italy
4 - Department of Informatics and Mathematical Modelling, Technical University of Denmark, Richard Petersens Plads, 2800 Kgs. Lyngby, Denmark
5 - Department of Informatics and Mathematical Modelling, Technical University of Denmark, Richard Petersens Plads, 2800 Kgs. Lyngby, Denmark

Received 28 October 2005 / Accepted 10 February 2006

Abstract
Aims. Kluzniak & Abramowicz explain the high frequency, double peak, "3:2'' QPOs observed in neutron star and black hole sources in terms of a non-linear parametric resonance between radial and vertical epicyclic oscillations of an almost Keplerian accretion disk. The 3:2 ratio of epicyclic frequencies occurs only in strong gravity. Recently, a simple model incorporating their suggestion was studied analytically: the result is that a small forcing may indeed excite the parametric 3:2 resonance. However, no explanation has been provided on the nature of the forcing which is given an "ad hoc'' deterministic form.
Methods. In the present paper the same model is considered. The equation are numerically integrated, dropping the ad hoc forcing and adding instead a stochastic term to mimic the action of the very complex processes that occur in accretion disks as, for example, MRI turbulence.
Results. We demonstrate that the presence of the stochastic term is able to trigger the resonance in epicyclic oscillations of nearly Keplerian disks, and it influences their pattern.

Key words: methods: data analysis - methods: statistical - X-rays: binaries - relativity - accretion, accretion disks

   
1 Introduction

Quasi Periodic Oscillations (QPOs) are a common phenomenon in nature. In the last few years many kHz QPOs have been detected in the light curves of about 20 neutron star and few black hole sources (for a recent review, see van der Klis 2004). The nature of these QPOs is one of the mysteries which still puzzle and intrigue astrophysicists: apart from giving important insights into the disk structure and the mass and spin of the central object (e.g. Török et al. 2005; Abramowicz & Kluzniak 2001; Aschenbach 2004), they offer an unprecedented chance to test Einstein's theory of General Relativity in strong fields.

High frequency QPOs lie in the range of orbital frequencies of geodesics just few Schwarzschild radii outside the central source. This feature inspired several models based directly on orbital motion (e.g. Stella & Vietri 1998; Lamb & Miller 2003), but there are also models that are based on accretion disk oscillations (Rezzolla et al. 2003; Wagoner et al. 2001; Li & Narayan 2004; Kato 2001). The Kluzniak & Abramowicz resonance model (see a collection of review articles in Abramowicz 2005) stresses the importance of the observed 3:2 ratio, pointing out that the commensurability of frequencies is a clear signature of a resonance. The relevance of the 3:2 ratio and its intimate bond with the QPOs fundamental nature is supported also by recent observations: Jeroen Homan of MIT reported at the AAS meeting on the 9th of January 2006 that the black hole candidate GRO J1655-40 showed in 2005 the same QPOs (at $\sim $300 Hz and $\sim $450 Hz) first detected by Strohmayer (2001).

The main limitation of the resonance model is that it does not yet explain the nature of the physical mechanism that excites the resonance. The idea that turbulence excites the resonance and feeds energy into it (e.g. Abramowicz 2005) is the most natural one, but it has never been explored in detail. The turbulence in accretion disks is most probably due to the Magneto-Rotational Instability (MRI, Balbus & Hawley 1991). At present, numerical simulations of turbulence in accretion disks do not fully control all the physics near the central source. For this reason, they cannot yet address the question of whether MRI turbulence does play a role in exciting and feeding the 3:2 parametric resonance. A situation like this is not specific of astronomy, but it is shared by other fields in applied research and engineering. The most common and, at the same time, effective, solution consists of modelling the unknown processes as stochastic ones. Such processes are characterized by a huge number of degrees of freedom and therefore they can be assumed to have a stochastic nature (e.g. Garcia-Okjalvo & Sancho 1999). Lacking any a priori knowledge, the most natural choice is represented by Gaussian white-noise processes. Of course, such an assumption is only an approximation. However, it can provide an idea of the consequences on the system of interest of the action of a large number of complex processes. This approach leads to the modelling of physical systems by means of stochastic differential equations (SDE) (Maybeck 1979; Vio et al. 2005; Ghanem & Spanos 1991; Maybeck 1982; Garcia-Okjalvo & Sancho 1999).

The present paper is a first qualitative step in this direction in the context of QPO modelling. In Sect. 2 we synthesize a stochastic version of the non-linear resonance model. Some experiments are presented and discussed in Sect. 3. The last section summarizes our findings. Since SDEs are not yet very well known in astronomy, Appendix A provides a brief description of the techniques for the numerical integration that are relevant for practical applications.

In all the experiments, we adopt the units $r_{\rm G}=2GM/c^2=1$ and c=1.

   
2 A simplified model for kHz QPOs

   
2.1 The Kluzniak-Abramowicz idea

The key point of the mechanism proposed by Abramowicz & Kluzniak (2001) is the observation that kHz QPOs often occur in pairs, and that the centroid frequencies of these pairs are in a rational ratio (e.g., Strohmayer 2001). This feature suggested to them that high frequency QPOs are a phenomenon due to non-linear resonance. The analogy of radial and vertical fluctuations in a Shakura-Sunyaev disk with the Mathieu equation pointed out that the smallest (and hence strongest) possible resonance is the 3:2. In all four micro-quasars which exhibit double peaks, the ratio of the two frequencies is 3:2, as well as in many neutron star sources. Moreover, combinations of frequencies and sub-harmonics have been detected: these are all signatures of non-linear resonance. A confirmation of the fact that kHz QPOs are due to orbital oscillations comes from the scaling of the frequencies with 1/M, where Mis the mass of the central object (McClintock & Remillard 2004).

   
2.2 Dynamics of a test particle

A simple mathematical approach to this idea was first developed by Rebusco (2004) and Horák (2004), in the context of isolated test particle dynamics.

The time evolution of perturbed nearly Keplerian geodesics is given by

  
$\displaystyle \ddot z(t) + \omega_{\theta}^2 z(t)$ = $\displaystyle f[\rho(t), z(t), r_0,\theta_0];$ (1)
$\displaystyle \ddot \rho(t) + \omega_r^2 \rho(t)$ = $\displaystyle g[\rho(t), z(t), r_0, \theta_0].$ (2)

Here $\rho (t)$ and z(t) denote small deviations from the circular orbit $r_0,\theta_0$(radial and the vertical coordinates respectively), f and g account for the coupling, and $\omega_{\theta}$ and $\omega_r$ are the epicyclic frequencies. In the case of the Schwarzschild metric, a Taylor expansion to third order leads to:
  
                   $\displaystyle f(\rho, z, r_0, \theta_0 )$ = $\displaystyle c_{11} z \rho + c_b \dot z \dot \rho + c_{21} \rho^2 z + c_{1b} \rho \dot z \dot \rho + c_{03} z^3;$ (3)
$\displaystyle g(\rho, z, r_0, \theta_0 )$ = $\displaystyle e_{02} z^2 + e_{20} \rho^2 + e_{z2} \dot z^2 + e_{30} \rho^3 + e_{1ze2} \rho \dot z^2$  
    $\displaystyle + e_{12} \rho z^2 + e_{r2} \dot \rho^2 + e_{1re2} \dot \rho^2 \rho.$ (4)

The functional form of the coefficients ci and ej can be found in Rebusco (2004). They are constants, which depend on r0, the distance of the unperturbed orbit from the centre. In previous studies these non-linear differential equations have been integrated numerically (Abramowicz et al. 2003) and analyzed through a perturbative method. These coupled harmonic oscillators display internal non-linear resonance, the strongest one occurs when $ \omega_\theta{:}\omega_r=3{:}2$ and the observed frequencies are close (but not equal) to the epicyclic ones.

2.3 Additional terms

As we have seen the perturbation of geodesics opens up the possibility of internal resonances. However these epicyclic oscillations would not be detectable without any source of energy to make their amplitudes grow. In Abramowicz et al. (2003) and Rebusco (2004) this source of energy was inserted by introducing a parameter $\alpha$. The effect of forcing (e.g., due to the neutron star spin), and its potential to produce new (external) resonances, have been addressed recently (e.g. Abramowicz 2005). The main limit in the approach proposed by Abramowicz et al. (2003) and Rebusco (2004) is that it represents an ad hoc solution. Moreover, as stressed in Sect. 1, it does not consider the many processes that take place in the central region of an accretion disk as, for example, MRI-driven turbulence (Balbus & Hawley 1991). For this reason, we propose the stochasticized version of Eqs. (1), (2)

  
$\displaystyle \ddot z(t) + \omega_{\theta}^2 z(t) - f[\rho(t), z(t), r_0, \theta_0]$ = $\displaystyle \sigma_z \beta(t);$ (5)
$\displaystyle \ddot \rho(t) + \omega_r^2 \rho(t) - g[\rho(t), z(t), r_0, \theta_0]$ = 0, (6)

with $\sigma_z$ a constant and $\beta(t)$ a continuous, zero mean, unit variance, Gaussian white-noise process.

There is no full understanding of turbulence in accretion disks. We know that the radial component is fundamental in producing the effective viscosity which allows accretion to occur, and that MRI-turbulence should be different in the vertical and radial direction. Here we make a first step by introducing a noise term only along the vertical direction: in the end this ansatz alone gives interesting results. In the Shakura & Sunyaev model (Shakura & Sunyaev 1973) the turbulent viscosity is parametrized via the famous $\alpha_{\rm SS}$. It is reasonable to assume that $\sigma_z$ is at maximum a fraction, smaller than $\alpha_{\rm SS}$, of the disk height. Hence for a geometrically thin disk one would expect a maximum $\sigma_z$ $\sim 10^{-4}$-10-3. As shown in Appendix A, the smallness of the stochastic perturbation permits the development of efficient integration schemes for the numerical integration of the system (5)-(6).

  
3 Results

We explored the dynamics of the test particle for different values of $\sigma_z$ and initial conditions z(0) and $\rho(0)$. All the integrations are performed by means of the scheme (A.13)-(A.17), with $h = 5 \times 10^{-4}$ and t=105, for r0=27/5 which is the value for which the unperturbed frequencies are in a 3:2 ratio. As a sample, three different starting values $[z(0),\dot z(0), \rho(0), \dot \rho(0)]$ have been used: [0.01, 0, 0.01, 0], [0.1, 0, 0.1, 0], and [0.2, 0, 0.2, 0], which we refer to as models 1, 2 and 3 respectively. For each of them we considered three values of $\sigma_z$: 0, 10-5 and 10-4. As pointed out in the previous section, a noise level stronger than these is unlike to occur, since it would destabilize the accretion flow. Moreover when the initial perturbations z(0) and $\rho(0)$ are greater than about 0.5 they diverge, even in absence of noise: this is the limit for which the system can be considered weakly non-linear and physically meaningful.

The lower panels of Figs. 1-3 show how the amplitudes reach greater values for greater noise dispersion. These plots are done for the initial conditions 2, but similar behavior is also obtained for different initial conditions: as expected, noise triggers the resonances. With regard to the frequencies at which the resonances are excited, the dominant one are always the epicyclic frequencies (the strongest peaks in the upper part of the plots). However, the sub- and super-harmonics also react (see Table 1), and their signal is stronger for greater noise dispersion. As predicted by means of the perturbative method of multiple scales, the dominant oscillations have frequencies ( $\omega_r^*$ and $\omega_\theta^*$), close to the epicyclic ones. The pattern of the other resonances (Table 1) is not interesting in itself, as it depends on the initial conditions and on the noise, but it is significant from a qualitative point of view, as it is a signature of the non-linear nature of the system.

When the noise is ${\sim} 10^{-3}$ or greater the solution diverges, whilst when it is too small ( ${\sim} 10^{-6}$) it does not differ too much from the results without noise. The exact limit of $\sigma_z$ over which the epicycles are swamped depends on the initial conditions: it is indeed lower for greater initial conditions, and vice versa.

  \begin{figure} \par\includegraphics[width=8.6cm,clip]{4432fig1.eps} \end{figure} Figure 1: Numerical simulation of the system (5)-(6). The upper panels show the power spectra of z(t) and $\rho (t)$, whereas the lower panels show the corresponding phase diagrams. Here $\sigma _z = 0$ (i.e. noise-free system). The displacements are in units of $r_{\rm g}$, the frequencies are scaled to kHz (e.g. assuming a central mass M of  $2~ M_\odot$).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{4432fig2.eps} \end{figure} Figure 2: The same as in Fig. 1 but with $\sigma _z=10^{-5}$.
Open with DEXTER

In the case where noise is assumed to be due to MRI turbulence, this simple experiment constrains its amplitude: turbulence that is too low does not supply enough energy to the growing resonant modes, whilst too much turbulence prevents the quasi-periodic behavior from occurring. From this oversimplified model we get an indication that the standard deviation of vertical MRI must be ${\sim} 10^{-5}{-}10^{-4}$, which is reasonable since it is comparable with a small fraction of the disk height.

In a yet unpublished work (private communication, Skinner 2005) considers how far the data from a QPO source can constrain the properties of a simple damped harmonic oscillator model - not only its resonant frequency and damping but also to some extent the excitation. Not unlike the present work, he adds random delta function shots to a simple harmonic oscillator equation, changing the amplitude and frequency of shots. He observes that the data constrain the allowed range of parameters for the excitation.

  \begin{figure} \par\includegraphics[width=8.6cm,clip]{4432fig3.eps} \end{figure} Figure 3: The same as in Fig. 1 but $\sigma _z=10^{-4}$. The comparison with the phase diagrams in the previous plots indicates how much the amplitudes grow under the effect of slightly stronger noise.
Open with DEXTER

Table 1: Resonant frequencies (apart from the epicyclic ones) for different initial conditions (1,2,3) and noise standard deviation ( $\sigma _z=0,10^{-5}, 10^{-4}$).

  
4 Conclusions

Up to now models for kHz QPOs have been based on deterministic differential equations. The main limits of these models is that they correspond to unrealistic physical scenarios where the many and complex processes that take place in the central regions of an accretion disk are not taken into account. In this paper, we have partially overcome this problem by adopting an approach based on stochastic differential equations. The assumption is that the above mentioned processes are characterized by a huge number of degrees of freedom, hence they can be assumed to have a stochastic nature. In particular, we have investigated a simplified model for the Kluzniak-Abramowicz non-linear theory and shown that a small amount of noise in the vertical direction can trigger coupled epicyclic oscillations. On the other hand too much noise would disrupt the quasi-periodic motion. This is similar to the stochastically excited p-modes in the Sun (Goldreich & Keeley 1977).

From our simple example we get an indication that the standard deviation of vertical noise cannot be greater than $10^{-5}{-}10^{-4}\:r_{\rm g}$, nor smaller than ${\sim} 10^{-6}\:r_{\rm g}$, but better modelling needs to be done. Nonetheless good estimates are still possible without detailed knowledge of all the mechanisms in accretion disks; this approach has the power to lead to a better understanding of both kHz QPOs and other astrophysical phenomena.

Acknowledgements
We thank Marek Abramowicz for his suggestions and support. The discussions with Omer Blaes and Axel Brandenburg made this work possible. P.R. acknowledges Marco Ajello and Anna Watts for their help and comments and Sir Franciszek Oborski for the unique hospitality in his Castle during the Wojnowice Workshop (2005).

References

 

  
Online Material

   
Appendix A: Some notes on the numerical integration of SDEs

A.1 General remarks

A generic system of SDEs can be written in the form

 \begin{displaymath} \vec{\dot x}= \vec{a}(t, \vec{x}) + {\bf\Sigma}(t, \vec{x}) \mbox{\boldmath$\beta$ }. \end{displaymath} (A.1)

Here $\vec{x}$, $\vec{a}$ are n-dimensional column vectors, $\mbox{\boldmath$\beta$ }$ is a m-dimensional column vector containing zero mean, unit variance, Gaussian white-noise processes and ${\bf\Sigma}$ is a $n \times m$ matrix. Typically, this equation is written in the more rigorous form

 \begin{displaymath} {\rm d} \vec{x}= \vec{a}(t, \vec{x}) {\rm d}t + {\bf\Sigma}(t, \vec{x}) {\rm d} \vec{w}, \end{displaymath} (A.2)

with solution

 \begin{displaymath} x_t = x_{t_0} + \int_{t_0}^t \vec{a}(s, x_s) {\rm d} s + \int_{t_0}^t {\bf\Sigma}(s, \vec{x}_s) {\rm d} \vec{w}_s. \end{displaymath} (A.3)

Here $\vec{w}$ is a m-dimensional Wiener process. The numerical integration of SDEs is quite a difficult problem. In fact, in the case of ordinary differential equations (ODEs)

 \begin{displaymath} {\rm d} \vec{x}= \vec{a}(t, \vec{x}) {\rm d}t \end{displaymath} (A.4)

numerical integration schemes are, either directly or indirectly, based on a Taylor expansion of the solution

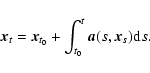\begin{displaymath}\vec{x}_t = \vec{x}_{t_0} + \int_{t_0}^t \vec{a}(s, \vec{x}_s) {\rm d} s. \end{displaymath} (A.5)

Something similar holds also for SDEs. However, the stochastic counterpart of the deterministic Taylor expansion is rather complex. In order to understand this point without entering into overly technical arguments, it is instructive to compare the expansions relative to a one-dimensional autonomous version of Eqs. (A.4) and (A.2) with m=1. In this case, for the ODE (A.4) the first-order integral form of the Taylor formula in the interval [t0, t] is

 \begin{displaymath} x_t = x_{t_0} + a(x_{t_0}) \int_{t_0}^t {\rm d} s + R_2, \end{displaymath} (A.6)

where R2 is the remainder. For the SDE (A.2) the corresponding expansion is
 
xt = $\displaystyle x_{t_0} + a(x_{t_0}) \int_{t_0}^t {\rm d} s + \sigma (x_{t_0}) \int_{t_0}^t {\rm d} w_s$ $\displaystyle + \sigma'(x_{t_0}) \sigma (x_{t_0}) \int_{t_0}^t \int_{t_0}^s {\rm d}w_z {\rm d} w_s + \bar R,$ (A.7)

where the symbol " ' '' denotes differentiation with respect to x, and $\bar R$ is the remainder. From Eq. (A.7) it is possible to see the presence of the additional terms

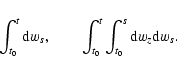\begin{displaymath}\int_{t_0}^t {\rm d}w_s, \qquad \int_{t_0}^t \int_{t_0}^s {\rm d}w_z {\rm d}w_s. \end{displaymath} (A.8)

When $n, m \neq 1$, it is possible to show that in the higher order expansions some quantities appear as

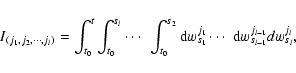\begin{displaymath}I_{(j_1, j_2, \cdots, j_l)} = \int_{t_0}^t \int_{t_0}^{s_l} \... ..._1}^{j_1} \cdots ~{\rm d}w_{s_{l-1}}^{j_{l-1}} dw_{s_l}^{j_l}, \end{displaymath} (A.9)

where $j_1, j_2, \cdots, j_l \in [0, 1, \ldots, m]$. Such quantities are termed multiple stochastic integrals. The main problem in dealing with them is that they cannot be computed exactly. Unfortunately, in its turn, numerical approximation is also a difficult affair.

The consequence of this situation is that, even in the case of simple systems, only integration schemes of very low order strong convergence[*] can be used. In fact, for the autonomous version of system (A.2) the most commonly used technique is the Euler scheme

\begin{displaymath}\vec{x}_{[k+1]} = \vec{x}_{[k]} + \vec{a}_{[k]} h_{[k]} + {\bf\Sigma}_{[k]} \Delta \vec{w}_{[k]}, \end{displaymath} (A.10)

where h[k] = t[k+1] - t[k] is the integration time step at the time t[k], and the elements of the vector

 \begin{displaymath} \Delta \vec{w}_{[k]} = \int_{t_k}^{t_{k+1}} {\rm d} \vec{w}_t = \vec{w}_{t_{[k+1]}} - \vec{w}_{t_{[k]}} \end{displaymath} (A.11)

are independent identically-distributed Gaussian random variables with mean equal to zero and variance equal to h[k].

A.2 Small noise approximation

If one takes into account that the order of strong convergence for the scheme (A.11) is only $\gamma = 0.5$, in contrast to $\gamma = 1$ for its deterministic counterpart, then it easy to understand why SDEs are not yet a standard tool in physical applications.

In order to improve this situation, Milstein & Tretýakov (1997) note that in many problems the random fluctuations that affect a physical system are small. This means that the system (A.2) can be written as

 \begin{displaymath} {\rm d} \vec{x}= \vec{a}(t, \vec{x}) {\rm d}t + \epsilon {\bf\Sigma}(t, \vec{x}) {\rm d} \vec{w}, \end{displaymath} (A.12)

where $\epsilon$ is a small positive parameter. This is an important observation since, for small noise, it is possible to construct special numerical methods that are more effective and easier to implement than in the general case. In fact, the term of the expansion depends not only on the time step hbut also on the parameter $\epsilon$. Typically, the mean-square global error of the schemes proposed by Milstein & Tretýakov (1997) is of order ${\cal{O}}(h^p + \epsilon^k h^q)$ with 0 < q < p. Although the strong order of these methods is given by q, typically not a large number, they are able to reach high exactness because of the factor $\epsilon^k$ at hq. For example, the simple scheme

 \begin{displaymath} \vec{x}_{[k+1]} = \vec{x}_{[k]} + \frac{1}{6} (\vec{K}_1 + 2... ...{K}_3 + \vec{K}_4) + \epsilon {\bf\Sigma}\Delta \vec{w}_{[k]} \end{displaymath} (A.13)

where
    
                            $\displaystyle \vec{K}_1$ = $\displaystyle h \vec{a}(t_{[k]}, \vec{x}_{[k]}),$ (A.14)
$\displaystyle \vec{K}_2$ = $\displaystyle h \vec{a}(t_{[k]} + h/2, \vec{x}_{[k]} + \vec{K}_1 /2),$ (A.15)
$\displaystyle \vec{K}_3$ = $\displaystyle h \vec{a}(t_{[k]} + h/2, \vec{x}_{[k]} + \vec{K}_2 /2),$ (A.16)
$\displaystyle \vec{K}_4$ = $\displaystyle h \vec{a}(t_{[k+1]}, \vec{x}_{[k]} + \vec{K}_3),$ (A.17)

is of order ${\cal{O}}(h^4 + \epsilon h + \epsilon^2 h^{1/2})$. In other words, the order of strong convergence is 0.5, as for the Euler scheme, but better results are to be expected because of the term  $\epsilon^2$that multiplies h1/2.


Copyright ESO 2006