A&A 452, 685-700 (2006)
DOI: 10.1051/0004-6361:20053716
M. Maris1 - C. Burigana2 - S. Fogliani1
1 - INAF - OATs, via G.B. Tiepolo 11, 34131 Trieste, Italy
2 -
INAF - IASF Bologna, via P. Gobetti, 101, 40129 Bologna, Italy
Received 28 June 2005 / Accepted 27 January 2006
Abstract
Context. The PLANCK satellite, scheduled for launch in 2007, will produce a set of all sky maps in nine frequency bands spanning from 30 GHz to 857 GHz, with an unprecedented sensitivity and resolution. Planets, minor bodies and diffuse interplanetary dust will contribute to the (sub)mm sky emission observed by PLANCK, representing a source of foreground contamination to be removed before extracting the cosmological information.
Aims. The aim of this paper is to assess the expected level of contamination in the survey of the forthcoming PLANCK mission.
Methods. Starting from existing far-infrared (far-IR) models of the Zodiacal Light Emission (ZLE), we present a new method to simulate the time-dependent level of contamination from ZLE at PLANCK frequencies.
Results. We studied the possibility of PLANCK to detect and separate the ZLE contribution from the other astrophysical signals.
Conclusions. We discuss the conditions in which PLANCK will be able to increase the existing information on the ZLE and IDP physical properties.
This work is done in the framework of the PLANCK/LFI activities.
Key words: interplanetary medium - infrared: solar system - submillimeter - methods: numerical - space vehicles: instruments - cosmology: cosmic microwave background
The ESA PLANCK satellite![]() (Tauber 2003), scheduled for launch in 2007
(Tauber 2003), scheduled for launch in 2007![]() , is a full-sky surveyor dedicated to
cosmic microwave background (CMB) and millimetric (mm) and sub-mm astronomy. It is a third
generation microwave mission, after the NASA COBE and WMAP missions.
The surveyor will observe the sky through a 1.5 m Gregorian aplanatic telescope carrying two instruments on the focal surface operating at the frequency bands centred at 30, 44, and 70 GHz (Low Frequency Instrument, LFI; Mandolesi et al. 1998)
and 100, 143, 217, 353, 545, and 857 GHz (High Frequency Instrument, HFI; Puget et al. 1998). PLANCK will be injected in a Lissajous orbit around the Sun-Earth Lagrangian point L2 of the Sun-Earth system at a distance of 1 507 683 km
, is a full-sky surveyor dedicated to
cosmic microwave background (CMB) and millimetric (mm) and sub-mm astronomy. It is a third
generation microwave mission, after the NASA COBE and WMAP missions.
The surveyor will observe the sky through a 1.5 m Gregorian aplanatic telescope carrying two instruments on the focal surface operating at the frequency bands centred at 30, 44, and 70 GHz (Low Frequency Instrument, LFI; Mandolesi et al. 1998)
and 100, 143, 217, 353, 545, and 857 GHz (High Frequency Instrument, HFI; Puget et al. 1998). PLANCK will be injected in a Lissajous orbit around the Sun-Earth Lagrangian point L2 of the Sun-Earth system at a distance of 1 507 683 km ![]() 0.01 AU from the Earth, from which it will observe the microwave sky for at least 15 months, necessary to complete two surveys of the whole sky with all the receivers.
The LFI beams are located on the PLANCK telescope field of view
in a ring with a radius of about 4
0.01 AU from the Earth, from which it will observe the microwave sky for at least 15 months, necessary to complete two surveys of the whole sky with all the receivers.
The LFI beams are located on the PLANCK telescope field of view
in a ring with a radius of about 4![]() around the telescope line of sight (LOS)
pointing at a scan angle
around the telescope line of sight (LOS)
pointing at a scan angle
![]() from the satellite spin
axis. The HFI beams, located closer to the centre, may be
also at few degrees from the LOS. In the simplest scanning strategy, the spin axis, chosen
pointed in the opposite direction from the Sun,
will be kept parallel to the Sun-spacecraft direction,
re-pointed by
from the satellite spin
axis. The HFI beams, located closer to the centre, may be
also at few degrees from the LOS. In the simplest scanning strategy, the spin axis, chosen
pointed in the opposite direction from the Sun,
will be kept parallel to the Sun-spacecraft direction,
re-pointed by
![]() once an hour
(
once an hour
(![]() per day) in order to follow the revolution of the L2 Lagrangian point, and will spin at 1 RPM. PLANCK will scan the sky in nearly great circles approximately orthogonal to the ecliptic plane at a rate of 24 circles per day, each
circle being scanned consecutively 60 times per hour. In this way
PLANCK will produce at least two full sky maps for each
frequency channel with an unprecedented resolution (FWHM from
per day) in order to follow the revolution of the L2 Lagrangian point, and will spin at 1 RPM. PLANCK will scan the sky in nearly great circles approximately orthogonal to the ecliptic plane at a rate of 24 circles per day, each
circle being scanned consecutively 60 times per hour. In this way
PLANCK will produce at least two full sky maps for each
frequency channel with an unprecedented resolution (FWHM from ![]() 33' to
33' to ![]() 5') and sensitivity (in the range of
5') and sensitivity (in the range of ![]() 10-49 mJy on a FWHM2 resolution element).
Although the detailed scanning strategy is currently
under study (Dupac & Tauber 2005), its general properties imply that
only objects located at
10-49 mJy on a FWHM2 resolution element).
Although the detailed scanning strategy is currently
under study (Dupac & Tauber 2005), its general properties imply that
only objects located at ![]()
![]() from the Sun will enter
the large circles traced in the sky by the main beams.
Solar System objects then will be observed nearly in quadrature with the
Sun i.e. within few degrees from a solar elongation of
from the Sun will enter
the large circles traced in the sky by the main beams.
Solar System objects then will be observed nearly in quadrature with the
Sun i.e. within few degrees from a solar elongation of ![]()
![]() .
.
Why would a cosmological mission like PLANCK consider the Solar System in its scientific program? How should Solar System studies take advantage from a mission like PLANCK? A valuable contribution has been provided by the COBE mission to solar system studies (Kelsall et al. 1998). The scanning strategy of PLANCK assures that all the Solar System components located outside the Earth Orbit, except Mars, will enter at least once into the field of view of the surveyor during the mission. In this way point-like Solar System objects (external planets; Burigana et al. 2001; Page et al. 2003; Schaefer et al. 2004, asteroids; Cremonese et al. 2002; Schaefer et al. 2004, comets) and the thermal emission of the diffuse interplanetary dust will represent foregrounds which have to be detected and properly removed in order to avoid the introduction of systematic errors in the cosmological measures (Maris et al. 2004a,2003).
The Zodiacal Light Emission (ZLE) due to thermal emission from the Interplanetary Dust Particles (IDPs) is the far-IR counterpart of the familiar Zodiacal Light due to scattering of the solar light by IDPs. Most of the properties of the ZLE below 300 ![]() m have been
studied by IRAS (Wheelock et al. 1994), COBE (Kelsall et al. 1998) and ISO
(Reach et al. 1996,2003). Peaking at
m have been
studied by IRAS (Wheelock et al. 1994), COBE (Kelsall et al. 1998) and ISO
(Reach et al. 1996,2003). Peaking at
![]()
![]() m, the ZLE is one of the major contributors to the sky background in the far-IR domain at
low ecliptic latitudes. A first detection in the
m, the ZLE is one of the major contributors to the sky background in the far-IR domain at
low ecliptic latitudes. A first detection in the
![]() band has been assessed by Fixsen & Dwek (2002) using yearly averaged
COBE/FIRAS data. Even a quick look at the data reported in Kelsall et al. (1998) and Fixsen & Dwek (2002) allows us to predict a contribution
of ZLE in the 857 GHz channel of PLANCK of
band has been assessed by Fixsen & Dwek (2002) using yearly averaged
COBE/FIRAS data. Even a quick look at the data reported in Kelsall et al. (1998) and Fixsen & Dwek (2002) allows us to predict a contribution
of ZLE in the 857 GHz channel of PLANCK of ![]() 0.6 MJy/sr.
It is evident that at the PLANCK lowest frequencies
its contribution is much weaker than the Galaxy emission. On the other hand,
at the PLANCK intermediate and high frequencies the ZLE is significantly weaker than
the Galactic emission only at low Galactic latitudes while it is
comparable to it outside the Galactic plane (for example, near the poles the Galactic emission
is
0.6 MJy/sr.
It is evident that at the PLANCK lowest frequencies
its contribution is much weaker than the Galaxy emission. On the other hand,
at the PLANCK intermediate and high frequencies the ZLE is significantly weaker than
the Galactic emission only at low Galactic latitudes while it is
comparable to it outside the Galactic plane (for example, near the poles the Galactic emission
is ![]() 1 MJy/sr at 857 GHz). The expected ZLE contribution is larger than the instrumental noise at the PLANCK highest frequencies. Therefore, a careful analysis of the ZLE in the PLANCK data
is required. Since the ZLE varies over angular scales
1 MJy/sr at 857 GHz). The expected ZLE contribution is larger than the instrumental noise at the PLANCK highest frequencies. Therefore, a careful analysis of the ZLE in the PLANCK data
is required. Since the ZLE varies over angular scales ![]()
![]() it can be properly studied by working at a resolution of
it can be properly studied by working at a resolution of ![]()
![]() .
At this scale the expected
.
At this scale the expected ![]() sensitivity per FWHM2 at 857 GHz at the end of the mission is
sensitivity per FWHM2 at 857 GHz at the end of the mission is ![]() 2
2 ![]() 10-3 MJy/sr (Lamarre et al. 2003). The extrapolated background from the Galaxy, representing the main large scale background component at this frequency, is
10-3 MJy/sr (Lamarre et al. 2003). The extrapolated background from the Galaxy, representing the main large scale background component at this frequency, is ![]() 1 MJy/sr. Because of the different tilt on the ecliptic of the Galactic plane and
of the IDP cloud, for most of the scan circles observed by PLANCK,
the sky position of the maximum of the ZLE will fall close to that of the
minimum of the Galactic emission. In this case the ZLE is extrapolated
to be about half of the Galactic emission. Of course one may wonder whether ground-based or balloon born CMB experiments may have been able to detect such a contribution.
Looking at some of the most recent balloon-borne experiments,
ARCHEOPS (Benoit et al. 2003) has constructed maps by bandpassing the
data between 0.3 and 45 Hz, corresponding to about 30
1 MJy/sr. Because of the different tilt on the ecliptic of the Galactic plane and
of the IDP cloud, for most of the scan circles observed by PLANCK,
the sky position of the maximum of the ZLE will fall close to that of the
minimum of the Galactic emission. In this case the ZLE is extrapolated
to be about half of the Galactic emission. Of course one may wonder whether ground-based or balloon born CMB experiments may have been able to detect such a contribution.
Looking at some of the most recent balloon-borne experiments,
ARCHEOPS (Benoit et al. 2003) has constructed maps by bandpassing the
data between 0.3 and 45 Hz, corresponding to about 30![]() and 15'
scales, respectively. MAXIMA (Lee et al. 2001) covered the multipole range
and 15'
scales, respectively. MAXIMA (Lee et al. 2001) covered the multipole range
![]() or angular scales smaller that
or angular scales smaller that ![]() .
The CMB power spectrum of BOOMERANG (Netterfield et al. 2002) covers
multipoles from
.
The CMB power spectrum of BOOMERANG (Netterfield et al. 2002) covers
multipoles from
![]() to
to
![]() ,
equivalent to angular scales
,
equivalent to angular scales
![]() .
From ground based experiments,
DASI (Pryke et al. 2002) measured the power spectrum for
.
From ground based experiments,
DASI (Pryke et al. 2002) measured the power spectrum for
![]() or angular scales less than
or angular scales less than ![]() .
Among these experiments it seems that only ARCHEOPS is able to
detect the large scale brightness variation connected with the ZLE.
We then expect that the ZLE will be observable as an excess of
signal superimposed on the Galaxy or it may be
considered as a source of systematics in studying the large scale Galactic emission.
.
Among these experiments it seems that only ARCHEOPS is able to
detect the large scale brightness variation connected with the ZLE.
We then expect that the ZLE will be observable as an excess of
signal superimposed on the Galaxy or it may be
considered as a source of systematics in studying the large scale Galactic emission.
Our strategy, in line with past studies, exploits the existing far-IR observations,
included in models, to derive the spatial distribution of the ZLE and to
extrapolate its Spectral Energy Distribution (SED) at PLANCK frequencies.
We take as a reference the yearly averaged values of Fixsen & Dwek (2002).
Our starting point to model the spatial distribution of the ZLE,
the work of Kelsall et al. (1998) for the ZLE based on
the COBE data (hereafter indicated as the COBE-model), has many
similarities with the IRAS model by Wheelock et al. (1994).
It describes in detail the emissivity of the IDP cloud, assumed to
extend up to ![]() 5.2 AU from the Sun, for wavelengths up to about 300
5.2 AU from the Sun, for wavelengths up to about 300 ![]() m. According to the COBE-model four components contribute to the ZLE: the dominating smooth component, the Earth orbit locked ring of dust (or circumsolar ring), the trailing blob, and three bands of dust.
m. According to the COBE-model four components contribute to the ZLE: the dominating smooth component, the Earth orbit locked ring of dust (or circumsolar ring), the trailing blob, and three bands of dust.
In this work only the standard IDP component has been considered. The analysis of the plausible, but not yet determined, contribution from the Kuiper Belt dust grains (Landgraf et al. 2002) will be the subject of another work.
With respect to other foregrounds usually considered in CMB studies, the ZLE (as the other Solar System objects) is peculiar, depending for its surface brightness not only on the pointing direction but also on the instantaneous position of the observer within the Solar System. Galactic and extragalactic foregrounds are generated by sources located so far from the observer that parallactic effects due to the motion of the observer within the Solar System are negligible compared to the instrumental resolution of CMB observatories. On the contrary, since the observer is located within the Solar System, the orbital motion about the Sun leads to changes in the ZLE brightness distribution as a function of the pointing direction. This underlines the relevance of studying the ZLE not only on maps but also on time ordered data streams (TODs). Moreover, the accurate simulation of observations for a satellite mission like PLANCK cannot be based on maps since the details of the orbit will have to be considered in addition to the usual scanning law.
The main aim of this work is to contribute to the following subjects: i) to define a representation method for the ZLE suitable for map based CMB mission simulators, with particular relevance for the PLANCK mission; ii) to determine suitable approximations (like scaling frequency laws) for the simulation of this component in the framework of the PLANCK simulation pipeline; iii) to determine to what extent the ZLE will impact the PLANCK survey; iv) to determine if it will be possible to separate the contribution of the ZLE from the data produced by the PLANCK mission in a self-consistent manner (i.e. reducing as much as possible the introduction of priors based on results from other missions in the PLANCK data processing pipeline); v) to explore the possibility of PLANCK to produce useful scientific results about the ZLE at frequencies barely explored in the past.
The paper is organised as follows. In Sect. 2 we briefly review the present knowledge about the ZLE. Section 3 describes the framework of our simulations, mainly based on the model of Kelsall et al. (1998), and the details of our numerical code discussing its main assumptions in the light of recent theoretical results. In Sect. 3.1 we present a series expansion of the ZLE spatial dependence that can be useful for many simulations and data analysis applications. In Sect. 4 we describe the main results of these simulations (mainly in form of TODs and maps) and compare the ZLE contribution to those expected from the Galactic emission. Section 5 is devoted to the separation of ZLE in the PLANCK data. Particular care is given to the analysis of the systematic effects in the differential approach for ZLE separation. Our main results and conclusions are summarised in Sect. 6.
To assess the expected errors in predicting the ZLE surface brightness at
PLANCK frequencies from a model based on far-IR and IR data
we review some theoretical concepts needed to link
the ZLE model, and in particular the COBE-model, to the optical properties
and the size distribution and other physical properties of the IDPs.
In sub-mm and mm bands the dominant emission mechanism from IDPs is thermal
emission of IR radiation driven by solar heating.
The most general expression for the brightness
averaged over the bandwidth and the beam,
detected in a radiometric channel of frequency f
on-board a space-bornexperiment produced
by a given population of IDP grains, representing a component c of the
IDPs cloud is
Table 1:
![]() estimated according to Eq. (4).
estimated according to Eq. (4).
We estimated Ef in the relevant range of frequencies comparing
the expected ZLE yearly averaged from the COBE model
with the existing surface brightness measures at PLANCK frequencies
from Fixsen & Dwek (2002) based on COBE/DIRBE and COBE/FIRAS data.
However, given the uncertainties in the interpretation of
these data, other extrapolation methods are possible.
According to the main result of Fixsen & Dwek (2002),
the SED of the ZLE Smooth component is approximately similar to
a blackbody with
![]() K scaled by an emissivity factor
nearly constant for
K scaled by an emissivity factor
nearly constant for
![]()
![]() m and scaling
as
m and scaling
as
![]() at longer wavelengths:
at longer wavelengths:
The colour correction Kf in Eq. (2) takes
into account the effect of the frequency instrumental response
within the bandwidth. At PLANCK frequencies, most of the ZLE is due to IDPs with
temperatures exceeding ![]() 200 K; within the bandwidth
of each PLANCK frequency channel, their emission integrated along the line of sight can be approximated by a power law with spectral index
200 K; within the bandwidth
of each PLANCK frequency channel, their emission integrated along the line of sight can be approximated by a power law with spectral index ![]() and normalisation
and normalisation
![]() (from here we will omit the pointing dependence to simplify the notation).
In addition, within a frequency band
(from here we will omit the pointing dependence to simplify the notation).
In addition, within a frequency band
![]() ,
where
,
where
![]() is the spectral emissivity correction and
is the spectral emissivity correction and
![]() accounts for the spatial distribution expected from grains emitting
as blackbodies and can be separated into a pure spatial dependence
accounts for the spatial distribution expected from grains emitting
as blackbodies and can be separated into a pure spatial dependence ![]() and a pure frequency scaling. Here normalisations are defined to match
the values of Ef and Zf for
and a pure frequency scaling. Here normalisations are defined to match
the values of Ef and Zf for ![]() and the overall
and the overall ![]() turns to be
turns to be
![]() .
Therefore, by imposing
.
Therefore, by imposing
We assess the value of Kf needed to compensate the fact that in Eq. (2) the integration over the bandwidth in Eq. (1) has been neglected. In addition we want to assess the level of uncertainty in the Kf correction induced by the uncertainty in the Ef prediction.
We restrict ourselves to the illustrative case of a simple top-hat window
![]() with relative bandwidth
with relative bandwidth
![]() .
For PLANCK rf = 0.2 for
.
For PLANCK rf = 0.2 for ![]() GHz and
rf = 0.25 for
GHz and
rf = 0.25 for
![]() GHz. We tested that for different reasonable shapes of
GHz. We tested that for different reasonable shapes of
![]() the results do not change significantly. Under these conditions, for
the results do not change significantly. Under these conditions, for
![]()
For numerical estimates, assuming
![]() and
and
![]() ,
we obtain
,
we obtain
![]() and
and
![]() .
For the case of a frequency-independent Ef,
.
For the case of a frequency-independent Ef,
![]() and
we find
and
we find
![]() and
and
![]() .
Leaving
.
Leaving ![]() to vary within
to vary within ![]() 1 unit Kf changes by only
1 unit Kf changes by only ![]() .
Thus it will be possible to avoid applying this small
correction in the numerical estimates presented in the remaining part of this paper.
.
Thus it will be possible to avoid applying this small
correction in the numerical estimates presented in the remaining part of this paper.
Note that in Kelsall et al. (1998) the colour correction
is defined as a correction for the instrumental response when a blackbody
is observed. For this reason the colour correction is parametrised
as a function of the blackbody temperature T which is a function of
the position along the line of sight, so that the argument of the
pointing direction
integral in Eq. (2) would have to be
scaled by the spatial dependent
![]() .
However, at our frequencies the bulk of the blackbody emissivity
comes from grains emitting not too far from the Rayleigh-Jeans limit, i.e. with a frequency power law scaling (within our rather limited bandwidth) with a power law index largely
independent of T. In this case the two definitions for Kf are equivalent.
.
However, at our frequencies the bulk of the blackbody emissivity
comes from grains emitting not too far from the Rayleigh-Jeans limit, i.e. with a frequency power law scaling (within our rather limited bandwidth) with a power law index largely
independent of T. In this case the two definitions for Kf are equivalent.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3716fig1.eps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg130.gif) |
Figure 1:
Relations between the heliocentric and cloud-centred frames used to
describe the Solar System scanning geometry for a mission like PLANCK.
The relations between Planck, Sun, Cloud Center and the observed portion of cloud are drawn,
the L2 point is not drawn to simplify the graph. The connection between the other two reference frames is shown in Fig. 2.
An example of scan circle and the related spin axis,
|
| Open with DEXTER | |
The surface brightness calculated for a given frequency band is
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{3716fig2a.eps}\par\includegraphics[width=7.8cm,clip]{3716fig2b.eps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg145.gif) |
Figure 2:
Relations between the cloud-centred ecliptic reference frame,
the cloud symmetry reference frame and the spacecraft
centred corotating reference frame.
Top panel: angles between the cloud-centred Ecliptical reference
frame (full yellow disc (light-gray in the bw version) - black arrows),
and the cloud cylindrical symmetry reference frame (dashed blue disc - red arrows).
Bottom panel: angles between the cloud cylindrical symmetry reference
frame, the cloud-centred corotating cylindrical reference frame,
the spacecraft - centred corotating reference frame.
The displacement of PLANCK (in this case above the symmetry plane),
|
| Open with DEXTER | |
We have implemented the COBE MODEL in a FORTRAN-90/95 program called FS_ZOD (F LIGHT S IMULATOR - Z ODIACAL L IGHT E MISSION) embedded in a supporting OCTAVE pipeline (Maris 2001). The code was originally designed as a module of the PLANCK Flight Simulator but can be used for any other experiment. Since the Ef scalings are largely uncertain it is left to the user to apply the proper one to the output of these programs. In this work we use the code to study the time dependence in the signal acquired by PLANCK for the nominal scanning strategy (Dupac & Tauber 2005) and a recently simulated spacecraft orbit (Hechler 2002) and to predict the ZLE induced perturbation in PLANCK data. We choose to express our results in terms of brightness (MJy/sr), as for IRAS and COBE data.
Simulators for CMB missions and the related data-reduction pipelines, such as those realized for PLANCK, are largely based on maps. A map allows a good representation of the sky brightness as a function of the pointing direction. This procedure neglects the time-dependent information on the PLANCK position within the Solar System, leading to a loss of information when Solar System components are considered. The ground segment of a mission like PLANCK would be able to handle and analyse TODs as well as maps obtained from them (Pasian & Sygnet 2002; Challinor et al. 2002; van Leeuwen et al. 2002). A TOD of ZLE would allow an exact representation of any seasonal dependence. However, TODs are large and their realization requires an effective scanning strategy and satellite orbit, possibly accommodated during the mission, so that the exchange of simulated data in the form of TODs is not practical for the data analysis of a multichannel, high-resolution mission like PLANCK. We implement a method able to 1. properly represent seasonal effects in a large set of mission configurations; 2. possibly be applied to other missions; 3. exploit the (cylindrical) symmetries in the components of the IDP cloud.
We propose to generalise the concept of pixelized map.
A pixelized map is usually defined as the values assumed by a given observable
on a set of pixels ordered according to the adopted pixelization scheme.
In this contest we can introduce a generalisation of this concept by
defining a pixelized "map'' as a list of values assumed by a given
observable on a set of pixels which are also functions of the positions of
the Sun
![]() and of the Spacecraft (PLANCK in our case)
and of the Spacecraft (PLANCK in our case)
![]() within the Solar System. In a reference frame (r.f.) in which the displacements of the Sun and spacecraft positions
are just small fractions of their averaged positions,
the pixelized "map'' can be replaced by the series expansion of
the observable about the average positions of the Sun and the Spacecraft.
within the Solar System. In a reference frame (r.f.) in which the displacements of the Sun and spacecraft positions
are just small fractions of their averaged positions,
the pixelized "map'' can be replaced by the series expansion of
the observable about the average positions of the Sun and the Spacecraft.
Then, denoting with
![]() ,
,
![]() the reference positions of
Spacecraft and Sun about which the series expansion is performed,
we have
the reference positions of
Spacecraft and Sun about which the series expansion is performed,
we have
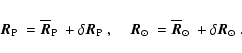 |
(10) |
We have tested that in the case of the ZLE it is preferable to expand
not the brightness spatial distribution but its logarithm in power series.
Then, denoting by
![]() the brightness
integral for a given frequency channel f, component c and
pixel index p (connected to the pointing direction
the brightness
integral for a given frequency channel f, component c and
pixel index p (connected to the pointing direction
![]() by the
mapping scheme) as a function of
by the
mapping scheme) as a function of
![]() and
and
![]() we adopt
the following decomposition
we adopt
the following decomposition
| (11) |
| (12) | |||
| (13) | |||
| (14) |
![\begin{figure}
\par\includegraphics[angle=90,width=8.6cm,clip]{3716fig3.eps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg175.gif) |
Figure 3:
Simulated contour plot of
|
| Open with DEXTER | |
The contour plot in Fig. 3 is an example
of
![]() for the Smooth component contribution
calculated for the 857 GHz frequency channel assuming
for the Smooth component contribution
calculated for the 857 GHz frequency channel assuming
![]() .
According to the discussion in Sect. 2,
.
According to the discussion in Sect. 2,
![]() and the expected observed surface brightnesses are about 2/3 the values reported in the plot.
The figure represents the variation of Zf as a function of the pointing direction
and the expected observed surface brightnesses are about 2/3 the values reported in the plot.
The figure represents the variation of Zf as a function of the pointing direction
![]() for a given combination of
for a given combination of
![]() ad
ad
![]() .
Contours
are drawn for
Zf = 0.21, 0.22, 0.23, 0.24, 0.25, 0.30,
.
Contours
are drawn for
Zf = 0.21, 0.22, 0.23, 0.24, 0.25, 0.30, ![]() ,
3.2 MJy/sr. Given the cylindrical symmetry of the IDPs, the pointing in the plot is
expressed as a function of the ecliptical latitude and of the relative ecliptical longitude,
i.e. the difference between the longitude of the pointing
direction and the longitude of the solar direction which is at
the centre of the plot. The blue dotted line represents the path described by a PLANCK beam at the centre of the field of view assuming the nominal scanning strategy
and the grey band represents the region observed by considering all the
PLANCK beams. Having the IDPs cloud a cylindrical symmetry, and the symmetry
reference frame being nearly equivalent to the PLANCK comoving reference
frame, for the nominal scanning strategy both the signal contour levels
and the region observed by PLANCK will shift approximately in
the same way when the spin axis is repointed.
Consequently, only a small fraction of the possible pointings in the
cloud reference frame will be observed by PLANCK.
In the case of more complicated scanning strategies, such as those including
slow spin axis precession about the Sun-Satellite direction or slow
oscillations above / below the ecliptic (Dupac & Tauber 2005),
the scanning path will be shifted normally and along the ecliptic plane.
Slow spin axis precession or oscillations with semi-amplitudes of
,
3.2 MJy/sr. Given the cylindrical symmetry of the IDPs, the pointing in the plot is
expressed as a function of the ecliptical latitude and of the relative ecliptical longitude,
i.e. the difference between the longitude of the pointing
direction and the longitude of the solar direction which is at
the centre of the plot. The blue dotted line represents the path described by a PLANCK beam at the centre of the field of view assuming the nominal scanning strategy
and the grey band represents the region observed by considering all the
PLANCK beams. Having the IDPs cloud a cylindrical symmetry, and the symmetry
reference frame being nearly equivalent to the PLANCK comoving reference
frame, for the nominal scanning strategy both the signal contour levels
and the region observed by PLANCK will shift approximately in
the same way when the spin axis is repointed.
Consequently, only a small fraction of the possible pointings in the
cloud reference frame will be observed by PLANCK.
In the case of more complicated scanning strategies, such as those including
slow spin axis precession about the Sun-Satellite direction or slow
oscillations above / below the ecliptic (Dupac & Tauber 2005),
the scanning path will be shifted normally and along the ecliptic plane.
Slow spin axis precession or oscillations with semi-amplitudes of
![]()
![]() ,
such as those considered
for the PLANCK scanning strategy, will change the path reported in the
plot by
,
such as those considered
for the PLANCK scanning strategy, will change the path reported in the
plot by ![]()
![]() with a resulting signal difference
more sensitive near the ecliptic plane (
with a resulting signal difference
more sensitive near the ecliptic plane (![]() 0.05-0.1 MJy/sr).
However for any reasonable scanning strategy the envelope of all the possible scanning path
will be only twice or three times wider than the grey band in the figure.
0.05-0.1 MJy/sr).
However for any reasonable scanning strategy the envelope of all the possible scanning path
will be only twice or three times wider than the grey band in the figure.
The tilt of the cloud with respect to the ecliptic plane and parallactic effects induced by the motion of the spacecraft with respect to the cloud introduce small modifications in the pattern of the contour lines and between the signal TODs from different scan circles.
TODs may be generated at any desired sampling rate, for example from that corresponding
to 1/3 of the instrumental FWHM resolution to
![]() resolution.
It is important to estimate the error in the computation of the signal in the TODs
when the true convolution with the beam about its centre direction is replaced by
the convolution with a "pencil beam''. Denoting with
resolution.
It is important to estimate the error in the computation of the signal in the TODs
when the true convolution with the beam about its centre direction is replaced by
the convolution with a "pencil beam''. Denoting with
![]() and
and
![]() the
displacements from the beam centre respectively
along the direction parallel to the scan circle oriented
in the scan direction and normal to it towards the Sun,
we compute the Zf derivatives along these directions.
They are displayed in Fig. 6, where
the
displacements from the beam centre respectively
along the direction parallel to the scan circle oriented
in the scan direction and normal to it towards the Sun,
we compute the Zf derivatives along these directions.
They are displayed in Fig. 6, where
![]() and
and
![]() are plotted for different positions along
the scan circle of Fig. 3 at 857 GHz and for the Smooth component.
For the Smooth component
are plotted for different positions along
the scan circle of Fig. 3 at 857 GHz and for the Smooth component.
For the Smooth component
![]()
![]() 10-3 deg-1 and
10-3 deg-1 and
![]()
![]() 10-3 deg-1 (here Zf is in MJy/sr). For displacements less than
10-3 deg-1 (here Zf is in MJy/sr). For displacements less than
![]() arcmin the error introduced by this approximation is at most 0.03% along
arcmin the error introduced by this approximation is at most 0.03% along
![]() and 0.05% along
and 0.05% along
![]() .
These error estimates can be linearly rescaled to larger displacements
.
These error estimates can be linearly rescaled to larger displacements
![]() and
and
![]() such as those associated with the sky pixelization.
such as those associated with the sky pixelization.
Figure 4 represents a portion of a TOD, with the associated uncertainty,
simulated at 857 GHz without noise and with a sampling at a resolution of 1![]() .
It is the generated sampling
.
It is the generated sampling
![]() from Fig. 3 scaled with
from Fig. 3 scaled with
![]() .
In the figure we report for comparison our preliminary estimate of
the sum of the other ZLE components.
Comparing the TOD with the corresponding contour map one sees
that maxima in ZLE (red lines in the figure) occur when the beam
crosses the plane of the IDPs cloud, slightly below the ecliptic plane
for the considered case. Minima instead occur when the beam is approximately orthogonal to it.
For PLANCK, the spin induced modulation of the ZLE signal has a main
period equivalent to 2 cycles per minute (for the nominal spin rate of 1 r.p.m.).
In a single scan circle, two maxima occur when the beam crosses the ascending node and the descending node between the scan plane and the IDPs cloud plane.
Since the plane is tilted on the ecliptic, Fig. 3
allows us to predict the occurrence of asymmetries between the two peaks even if the scan circle is centred at the antisolar direction.
The secondary components contribute
.
In the figure we report for comparison our preliminary estimate of
the sum of the other ZLE components.
Comparing the TOD with the corresponding contour map one sees
that maxima in ZLE (red lines in the figure) occur when the beam
crosses the plane of the IDPs cloud, slightly below the ecliptic plane
for the considered case. Minima instead occur when the beam is approximately orthogonal to it.
For PLANCK, the spin induced modulation of the ZLE signal has a main
period equivalent to 2 cycles per minute (for the nominal spin rate of 1 r.p.m.).
In a single scan circle, two maxima occur when the beam crosses the ascending node and the descending node between the scan plane and the IDPs cloud plane.
Since the plane is tilted on the ecliptic, Fig. 3
allows us to predict the occurrence of asymmetries between the two peaks even if the scan circle is centred at the antisolar direction.
The secondary components contribute ![]()
![]() to the bulk of the ZLE.
to the bulk of the ZLE.
![\begin{figure}
\par\includegraphics[angle=90,width=7cm,clip]{3716fig4.eps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg188.gif) |
Figure 4:
Simulated data stream of surface brightnesses (MJy/sr) measured at
857 GHz for the ZLE - smooth component (red), the Galaxy (green)
and the sum of the two (blue). The ordinate is the phase of the scan circle, assumed to be zero for the pointing direction nearest to the North ecliptic Pole. Two subsequent scan circles are displayed, the phase of the second being augmented of |
| Open with DEXTER | |
To compare the expected ZLE signal with the Galactic foreground,
TODs for the Galactic emission have been generated and averaged within a circle of ![]() radius. Galactic emission TODs are generated using Galactic maps obtained by
Schlegel et al. (1998) with the prescriptions in Finkbeiner et al. (1999) for the
scaling of the Galactic surface brightness as a function of frequency and
pointing direction. Due to the tilt of the ZLE symmetry plane over the Galactic plane,
the ZLE at 857 GHz is comparable to the Galactic emission at low
ecliptic latitudes where the Galaxy is weak, contributing a peak surface brightness of
radius. Galactic emission TODs are generated using Galactic maps obtained by
Schlegel et al. (1998) with the prescriptions in Finkbeiner et al. (1999) for the
scaling of the Galactic surface brightness as a function of frequency and
pointing direction. Due to the tilt of the ZLE symmetry plane over the Galactic plane,
the ZLE at 857 GHz is comparable to the Galactic emission at low
ecliptic latitudes where the Galaxy is weak, contributing a peak surface brightness of ![]() 0.7-0.2+0.4 MJy/sr, or approximately half of the weakest Galactic signal along that circle. Of course, the ecliptical longitude of the spin axis about which the scan circle
is drawn will affect the relative contribution of the ZLE with respect to
the Galaxy. For this reason, we report in Fig. 5
the variation of the ratio
0.7-0.2+0.4 MJy/sr, or approximately half of the weakest Galactic signal along that circle. Of course, the ecliptical longitude of the spin axis about which the scan circle
is drawn will affect the relative contribution of the ZLE with respect to
the Galaxy. For this reason, we report in Fig. 5
the variation of the ratio
![]() (where Gf denotes the Galactic surface brightness - we
consider here only the dominant dust emission) with the ecliptical longitude of the spin axis,
for three different PLANCK frequencies and for circular patches of
(where Gf denotes the Galactic surface brightness - we
consider here only the dominant dust emission) with the ecliptical longitude of the spin axis,
for three different PLANCK frequencies and for circular patches of ![]() radius.
The white-full line represents the ratio averaged over the given scan circle.
The black band is the
radius.
The white-full line represents the ratio averaged over the given scan circle.
The black band is the ![]()
![]() range of such variation, while the highest
ratios expected for each scan circle are represented by the gray-dashed line.
At 857 GHz for about half of the scan circles the
expected peak ZLE is roughly half of the Galactic dust emission.
Since the ZLE frequency scaling is not much different from that
of the Galactic dust emission, also at the lower
frequencies considered here its peak contribution to the sky emission is
still larger than some ten percent of the Galaxy for most of the circles.
This contribution is compared to the instrumental sensitivity.
The gray band at the bottom of each frame in the figure
represents the ratio between the
instrumental noise, Nf, and the Galactic dust Nf/Gf for
range of such variation, while the highest
ratios expected for each scan circle are represented by the gray-dashed line.
At 857 GHz for about half of the scan circles the
expected peak ZLE is roughly half of the Galactic dust emission.
Since the ZLE frequency scaling is not much different from that
of the Galactic dust emission, also at the lower
frequencies considered here its peak contribution to the sky emission is
still larger than some ten percent of the Galaxy for most of the circles.
This contribution is compared to the instrumental sensitivity.
The gray band at the bottom of each frame in the figure
represents the ratio between the
instrumental noise, Nf, and the Galactic dust Nf/Gf for ![]() circular patches, averaged over a scan circle. On average, the ZLE contribution is
largerly above the instrumental noise from 857 GHz to 353 GHz.
circular patches, averaged over a scan circle. On average, the ZLE contribution is
largerly above the instrumental noise from 857 GHz to 353 GHz.
![\begin{figure}
\par\hspace*{0.5mm}\includegraphics[angle=90,width=7.35cm,clip]{3...
...ce*{3mm}
\includegraphics[angle=90,width=7.45cm,clip]{3716fig5c.ps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg190.gif) |
Figure 5:
Relative contribution of ZLE, Galactic (dust) emission and noise as a function
of the pointing ecliptical longitude at three PLANCK frequency bands: 857 GHz ( top),
545 GHz ( middle), 343 GHz ( bottom).
For each pointing ecliptical longitude, the plots gaves the ratio of the
ZLE over the Galactic emission
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.4cm,clip]{3716fig6.eps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg193.gif) |
Figure 6:
Derivatives of
|
| Open with DEXTER | |
The time dependence in the ZLE signal is characterised by the short term modulation shown in Fig. 4 and by a long term modulation derived from the effective motion of the spacecraft within the IDP cloud determined by the L2 orbital motion around the Sun and the spacecraft Lissajous orbit around L2.
The effects of the spacecraft motion are better represented in the reference frame defined by the cylindrical symmetry of the cloud and corotating with L2. To understand the long term modulation we have to consider the followings:
Due to the ellipticity of the Earth orbit, the distance of L2 from the Sun varies
during the year by a 3%, i.e. of 0.03 AU ![]() 4.5
4.5 ![]() 106 km.
106 km.
Being on the ecliptic, the L2 point changes its distance from
the bulk component symmetry plane due to its tilt. This induces
at maximum a vertical oscillation of ![]() 5.2
5.2 ![]() 106 km.
In addition the Sun is off-centred with respect to the centre of IDP cloud
of the Smooth component
106 km.
In addition the Sun is off-centred with respect to the centre of IDP cloud
of the Smooth component ![]() 2
2 ![]() 106 km.
106 km.
The largest seasonal dependence is due to the tilt of the IDP fundamental plane.
It affects mainly the value of the minima of the surface brightness
observed by PLANCK. When the spacecraft is below the fundamental plane of the IDP cloud the optical depth towards the North ecliptic Pole is larger than that towards the South ecliptic Pole,
resulting in a North/South asymmetry in the minima. As PLANCK orbits about the Sun, the spacecraft goes toward the node between the ecliptic and the IDP cloud symmetry plane,
crosses it and enters a region where the symmetry plane is below the ecliptic. So, with time the North/South asymmetry goes to zero and then reverts its sign.
The tilt of the symmetry plane over the ecliptic does not significantly affect the
level of maximal ZLE surface brightness observed by PLANCK, while it affects the
location of the maxima and the shape about the peak. Figure 8 represents the modulation of the minima and the North/South asymmetry for a 857 GHz horn
supposed to be aligned with the telescope optical axis.
The full curve represents the surface brightnesses looking to the North
ecliptic Pole. The dashed curve represents the surface brightnesses looking towards
the South ecliptic Pole.
The relative seasonal modulation is about ![]() .
.
![\begin{figure}
\par\includegraphics[angle=90,width=7.9cm,clip]{3716fig7.ps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg201.gif) |
Figure 7:
Absolute and relative variation of the ZLE surface brightness during the
year at 857 GHz. The full-red line (light-gray in bw) is the yearly averaged ZLE surface brightness [MJy/sr] for a given eclipitical latitude.
The surrounding green band (dark-gray in bw) is the variation of ZLE surface brightness
during the year. Below (full black lines) the relative variation (with respect to the average)
of ZLE for a set of representative longitudes (from the left of the
black curves, from |
| Open with DEXTER | |
In Fig. 7 we compare the yearly averaged ZLE surface brightness with the daily surface brightness at 857 GHz. The variation of the PLANCK position with respect to the symmetry plane of the Smooth component introduces variations of up to ![]()
![]() in the
surface brightness with respect to the yearly average surface brightness,
almost independently of the considered frequency and Ef.
For typical Lissajous orbits, the variation of the PLANCK height with respect
to the cloud symmetry plane is
in the
surface brightness with respect to the yearly average surface brightness,
almost independently of the considered frequency and Ef.
For typical Lissajous orbits, the variation of the PLANCK height with respect
to the cloud symmetry plane is ![]()
![]() of the variation induced by
the tilt of the symmetry plane on the ecliptic but with a periodicity of
6 months and phase displacement with respect to the yearly periodicity related
to the exact launch date.
Therefore, about 10% of the above 10% variations of surface brightness
induced by the effective
PLANCK motion is introduced by the Lissajous orbit. Clearly, this is a second
order effect for studies of the yearly averaged properties of the Smooth
component, but it is still larger than the sensitivity of PLANCK TODs
averaged over
of the variation induced by
the tilt of the symmetry plane on the ecliptic but with a periodicity of
6 months and phase displacement with respect to the yearly periodicity related
to the exact launch date.
Therefore, about 10% of the above 10% variations of surface brightness
induced by the effective
PLANCK motion is introduced by the Lissajous orbit. Clearly, this is a second
order effect for studies of the yearly averaged properties of the Smooth
component, but it is still larger than the sensitivity of PLANCK TODs
averaged over ![]() or
or ![]() resolution, as it will be discussed in
Sect. 5. Secondary components contribute to about 10% of the global ZLE.
Therefore, neglecting the PLANCK orbit may significantly reduce the accuracy with which these components can be studied. Finally, the differential approach to ZLE separation that has several advantages with respect to other approaches (see Sect. 5.4)
exploits the variation of the ZLE during the mission. Neglecting the
Lissajous orbit effect will result in an error of
resolution, as it will be discussed in
Sect. 5. Secondary components contribute to about 10% of the global ZLE.
Therefore, neglecting the PLANCK orbit may significantly reduce the accuracy with which these components can be studied. Finally, the differential approach to ZLE separation that has several advantages with respect to other approaches (see Sect. 5.4)
exploits the variation of the ZLE during the mission. Neglecting the
Lissajous orbit effect will result in an error of ![]() in this kind of analysis.
Of course, the precise inclusion of the spacecraft position is not a concern from a computational nor practical point of view.
in this kind of analysis.
Of course, the precise inclusion of the spacecraft position is not a concern from a computational nor practical point of view.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{3716fig8.ps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg203.gif) |
Figure 8:
Seasonal modulation of the Smooth component of the ZLE at 857 GHz
for four selected pointing directions: the North ecliptic Pole (N),
the South eclitptic Pole (S), the Forward direction with respect to the PLANCK motion (FW) and
the Backward direction (BW). Longitudes are relative to the longitude of the ascending node.
Upper frame: the surface brightness variation looking to N (full line), S (long dashed line), FW (short dashed line), BW (dot-dashed line). The variation is the difference
between the surface brightness along the direction of choice and its yearly average. Here
|
| Open with DEXTER | |
The frequency scaling for
![]() is a theoretical outcome of the model and can be used to check
the extent by which it is possible to assume
is a theoretical outcome of the model and can be used to check
the extent by which it is possible to assume
![]() .
To study the frequency scaling for the spatial distribution of ZLE, sets of
.
To study the frequency scaling for the spatial distribution of ZLE, sets of
![]() have been generated for f covering all the PLANCK frequency channels up to f=1200 GHz, a fixed combination of
have been generated for f covering all the PLANCK frequency channels up to f=1200 GHz, a fixed combination of
![]() and
and
![]() positions,
positions,
![]() ,
and scanning the sky in circles of increasing angular radius from
,
and scanning the sky in circles of increasing angular radius from ![]() to
to ![]() centred in antisolar directions. The corresponding data are plotted in the upper frame of
Fig. 9, while the lower frame represents the spectral index obtained
by fitting a power law dependence for the surface brightnesses obtained for a given
pointing direction.
centred in antisolar directions. The corresponding data are plotted in the upper frame of
Fig. 9, while the lower frame represents the spectral index obtained
by fitting a power law dependence for the surface brightnesses obtained for a given
pointing direction.
![\begin{figure}
\par\includegraphics[angle=90,width=8.4cm,clip]{3716fig9.ps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg208.gif) |
Figure 9:
Deviation of the ZLE from an f2 scaling as a function of
the direction in the sky. Upper frame: the original data for f = 100, 143, 217,
353, 545, 857 GHz (from lower to upper surface brightness).
Lower frame: deviation from the f2 scaling in terms
of
|
| Open with DEXTER | |
Note that the average
![]() is
is ![]() 1.971, close to the expected
value
1.971, close to the expected
value
![]() .
In addition, the spectral index is modulated with the pointing and is anticorrelated
with the surface brightness, the higher spectral indices occurring for
lower surface brightnesses.
The amplitude of the modulation, however, is modest,
.
In addition, the spectral index is modulated with the pointing and is anticorrelated
with the surface brightness, the higher spectral indices occurring for
lower surface brightnesses.
The amplitude of the modulation, however, is modest,
![]()
![]() 10-3
in terms of peak-to-peak signal.
The colour correction would be then insignificantly affected.
The effect of a change of
10-3
in terms of peak-to-peak signal.
The colour correction would be then insignificantly affected.
The effect of a change of ![]() 0.07 AU in the position of PLANCK over the ecliptic results in a
0.07 AU in the position of PLANCK over the ecliptic results in a
![]() which has
negligible effects on Kf too. Smaller variations occur shifting the
PLANCK position in other directions. The same holds for a shift of the Sun position with respect to the centre of the cloud.
which has
negligible effects on Kf too. Smaller variations occur shifting the
PLANCK position in other directions. The same holds for a shift of the Sun position with respect to the centre of the cloud.
These results assure that a power law is an adequate
approximation within each frequency band, but this is only
approximately true considering the full range of PLANCK frequencies.
For example, in the range
![]() the mean spectral index is 1.990 while in the range
the mean spectral index is 1.990 while in the range
![]() the mean spectral index is 1.928.
the mean spectral index is 1.928.
Assuming at f = 100 GHz the same spectral index as at f=857 GHz, the relative error induced in the surface brightness prediction at 100 GHz would be ![]()
![]() .
Therefore, a set of spatial templates, one for each frequency channel, has to be produced in order to simulate the spatial dependence of the ZLE with an accuracy of
.
Therefore, a set of spatial templates, one for each frequency channel, has to be produced in order to simulate the spatial dependence of the ZLE with an accuracy of ![]() .
On the contrary, by relaxing the required accuracy to
.
On the contrary, by relaxing the required accuracy to ![]() ,
a spatial template at an appropriate reference frequency (for example at f = 1000 GHz)
followed by a spatially independent frequency scaling can be used.
,
a spatial template at an appropriate reference frequency (for example at f = 1000 GHz)
followed by a spatially independent frequency scaling can be used.
These effects, although very small, may be not negligible in CMB studies, that are
mainly carried out at
![]() GHz requiring foreground removal with an accuracy
better than
GHz requiring foreground removal with an accuracy
better than ![]()
![]() .
.
The ZLE represents a foreground contamination mainly relevant for the higher frequency channels of PLANCK. Its contribution has to be removed to accurately study the Galactic large scale structure and its frequency scaling. Given the weakness of the ZLE signal, the final separation quality will may rely on the prior information added to the system derived from other missions at IR bands, such as IRAS and COBE where the ZLE dominates the sky emissivity. We discuss here four different approaches to ZLE separation.
When ZLE is folded over a map, its histogram is strongly non-Gaussian, as for the Galaxy. In principle this suggests the possibility of obtaining a proper separation of the ZLE through blind component separation methods already used to analyze microwave maps.
We performed some numerical experiments with the FastICA code
(Maino et al. 2002) applied to full-sky maps obtained by adding the ZLE and
the Galactic emission. FastICA is a blind-separation
method which usually uses as input
![]() maps at
different frequencies that are linear combinations of
maps at
different frequencies that are linear combinations of
![]() signals, all non-Gaussian except for at most one.
The code gives as output maps of the various signals.
We exploited the two frequency channels at 857 GHz and 545 GHz
and, as a test case, neglected the noise. Although in principle this method could be investigated, possibly by applying it to PLANCK channels combined with IR data, this test gives discouraging results. Likely this is due to the weakness of the ZLE emission and the fact that this code does not use any prior information about the ZLE spatial distribution. In addition
part of this information is lost when passing from TODs to maps.
signals, all non-Gaussian except for at most one.
The code gives as output maps of the various signals.
We exploited the two frequency channels at 857 GHz and 545 GHz
and, as a test case, neglected the noise. Although in principle this method could be investigated, possibly by applying it to PLANCK channels combined with IR data, this test gives discouraging results. Likely this is due to the weakness of the ZLE emission and the fact that this code does not use any prior information about the ZLE spatial distribution. In addition
part of this information is lost when passing from TODs to maps.
An "ad hoc'' strategy for ZLE detection and separation can use a prior information,
derived from IR observations, on the spatial dependence of the ZLE.
We developed a model for ZLE detection and separation based on the extrapolation of the
geometrical information from COBE/DIRBE to PLANCK frequencies (or from any other
reliable model), leaving as free parameters the emissivity corrections,
![]() ,
at
PLANCK frequencies. The ability of PLANCK to measure the ZLE is then
translated into its accuracy in the determination of Ef at different
frequencies.
,
at
PLANCK frequencies. The ability of PLANCK to measure the ZLE is then
translated into its accuracy in the determination of Ef at different
frequencies.
A non-blind separation based on maps could be differently investigated
taking as prior information the ZLE spatial dependence and
the existing templates of the Galactic emission degraded to angular
resolutions comparable with the scales of significant ZLE variations (![]()
![]() ).
).
For example, denoting with
![]() the map obtained from the observed signal minus its
average,
the map obtained from the observed signal minus its
average,
![]() the Galactic emission template (or any other
relevant background signal) minus its average,
the Galactic emission template (or any other
relevant background signal) minus its average,
![]() the template for ZLE spatial distribution minus its average and
the template for ZLE spatial distribution minus its average and
![]() the template for noise spatial distribution minus its average for the considered scanning strategy and satellite orbit, then
the map for the signal (minus its average) may be approximated with
the template for noise spatial distribution minus its average for the considered scanning strategy and satellite orbit, then
the map for the signal (minus its average) may be approximated with
Assuming stationary noise equidistributed over the map,
the ![]() minimisation provides
the estimators for Ef and
minimisation provides
the estimators for Ef and
![]()
Table 2:
Correlation between Galaxy, ZLE and Differential ZLE at 857 GHz,
for
![]() ,
,
![]() ,
,
![]() .
.
In addition, it is possible that the true scaling factor is not constant over the sky.
To simulate this effect we replace a constant scaling
![]() with a normally
distributed variable, with expectation
with a normally
distributed variable, with expectation
![]() and rms
and rms
![]() .
.
We consider here an illustrative case with sensitivity per pixel
![]() MJy/sr,
where
MJy/sr,
where
![]() the effective number of observations
made during the mission which contributes to the pixel p,
the effective number of observations
made during the mission which contributes to the pixel p,
![]() ,
,
![]() ,
,
![]() at f=857 GHz, and a map sampled at
at f=857 GHz, and a map sampled at ![]()
![]() resolution,
and taking all the pixels in the map (i.e. including also
regions where the Galaxy largely dominates)
the rms for
resolution,
and taking all the pixels in the map (i.e. including also
regions where the Galaxy largely dominates)
the rms for
![]() is
is ![]() 2
2 ![]() 10-4
with a bias of the same order, while
10-4
with a bias of the same order, while
![]() is recovered with an rms accuracy of about 0.04 but an excess bias of about 0.06. On the other hand, removing all the pixels where the signal from the Galaxy does not greatly exceed that of ZLE reduces the bias.
Removing pixels for which the Galaxy exceeds the surface brightness of
4 MJy/sr,
is recovered with an rms accuracy of about 0.04 but an excess bias of about 0.06. On the other hand, removing all the pixels where the signal from the Galaxy does not greatly exceed that of ZLE reduces the bias.
Removing pixels for which the Galaxy exceeds the surface brightness of
4 MJy/sr,
![]() and
and
![]() are recovered with a rms accuracy
of about 0.01 for
are recovered with a rms accuracy
of about 0.01 for
![]() and 0.05 for
and 0.05 for
![]() .
Their expectations
are very close to their input values, with biases of a few
.
Their expectations
are very close to their input values, with biases of a few
![]() .
(In the remain we consider limits of surface brightness at values exceeding
1 MJy/sr). As can be seen, the accuracy of the method is very good.
.
(In the remain we consider limits of surface brightness at values exceeding
1 MJy/sr). As can be seen, the accuracy of the method is very good.
On the other hand, any (positive or negative)
residual contribution from the ZLE in the Galactic template from
the data analysis of the IR data will be scaled to
PLANCK frequencies and will introduce a systematic effect which
will be correlated with the spatial template adopted in
Eq. (16). This will result in biases in the recovered
![]() and
and
![]() values. An end-to-end evaluation of this
effect, beyond the scope of this paper,
would require to analyse in detail the mission and the
data reduction procedure used to obtain each IR data set used in
preparing the Galactic template.
However, the results of this approach can be compared with the
differential method described in Sect. 5.4
that automatically by-passes this problem.
values. An end-to-end evaluation of this
effect, beyond the scope of this paper,
would require to analyse in detail the mission and the
data reduction procedure used to obtain each IR data set used in
preparing the Galactic template.
However, the results of this approach can be compared with the
differential method described in Sect. 5.4
that automatically by-passes this problem.
The prior information derived from IR observations, discussed previously also can be applied to the time domain, taking also into account the time dependence of the spacecraft position within the IDP cloud.
In this approach the separation is based on the knowledge of the time dependence of the
ZLE signal in TODs derived from the spatial pattern
![]() .
Then, as before, we define an estimator
.
Then, as before, we define an estimator
![]() of
of
![]() starting from
the observed data and the known spatial pattern.
starting from
the observed data and the known spatial pattern.
Again, denoting with
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() the Galaxy, the ZLE, the noise and the signal (minus their average values over the mission), and neglecting systematic instrumental effects
the Galaxy, the ZLE, the noise and the signal (minus their average values over the mission), and neglecting systematic instrumental effects
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{3716fig10.eps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg275.gif) |
Figure 10:
Map of
|
| Open with DEXTER | |
Consider the case in which the Galactic contribution is neglected in the fitting,
as in Kelsall et al. (1998). Assuming stationary white noise, after
minimisation of
The bias is likely negligible for Kelsall et al. (1998)
since in their case the ZLE signal is much larger than the Galaxy
emissivity so that
![]() .
But at 857 GHz we obtain
.
But at 857 GHz we obtain
![]() MJy2/sr2, to be compared with
MJy2/sr2, to be compared with
![]() MJy2/sr2 and
MJy2/sr2 and
![]() MJy2/sr2,
leading to a bias
MJy2/sr2,
leading to a bias ![]() 3.4 in
3.4 in
![]() .
Such high bias such a small covariance comes from the fact that
.
Such high bias such a small covariance comes from the fact that
![]() is of the same order of magnitude as
is of the same order of magnitude as
![]() .
Selection of samples in order to reduce
.
Selection of samples in order to reduce
![]() does not mitigate the problem. For example, removing all the samples where the Galaxy is larger
than 1 MJy/sr leads to
does not mitigate the problem. For example, removing all the samples where the Galaxy is larger
than 1 MJy/sr leads to
![]()
![]() 10-3 MJy2/sr2,
10-3 MJy2/sr2,
![]() MJy2/sr2,
MJy2/sr2,
![]() MJy2/sr2,
with a bias
MJy2/sr2,
with a bias ![]() 0.23. Removing all samples where the Galaxy is larger than 0.4 MJy/sr leads to
0.23. Removing all samples where the Galaxy is larger than 0.4 MJy/sr leads to
![]()
![]() 10-4 MJy2/sr2,
10-4 MJy2/sr2,
![]()
![]() 10-3 MJy2/sr2,
10-3 MJy2/sr2,
![]()
![]() 10-3 MJy2/sr2,
with a bias
10-3 MJy2/sr2,
with a bias ![]() 0.14. As evident, the bias decreases when applying stronger cuts but it still remains significant (see Table 2, Cols. 1 to 6).
0.14. As evident, the bias decreases when applying stronger cuts but it still remains significant (see Table 2, Cols. 1 to 6).
PLANCK will scan the sky at least twice during the mission. Therefore, most of the sky directions will be observed at least twice with PLANCK in different positions within the IDP cloud. In the ideal case, the difference between these two measures will be due to the difference in the ZLE contribution that can be predicted from our model plus noise.
We denote with
![]() and
and
![]() the epochs of
the first and the second observation of a region seen in the direction
the epochs of
the first and the second observation of a region seen in the direction ![]() and with
and with
![]() ,
,
![]() (
(
![]() ,
,
![]() or
or
![]() ,
,
![]() or
or
![]() ,
,
![]() )
the corresponding observed surface brightness total signal variations (ZLE spatial distribution or Galactic emission or noise) with respect to the mean. With these definitions the differential surface brightnesses will be
)
the corresponding observed surface brightness total signal variations (ZLE spatial distribution or Galactic emission or noise) with respect to the mean. With these definitions the differential surface brightnesses will be
Applying the standard error propagation formula to Eq. (26)
and considering Eq. (24),
if the noise
![]() can be approximated as stationary,
independent and Gaussian with
variance
can be approximated as stationary,
independent and Gaussian with
variance
![]() ,
summing over all of the pairs we have
,
summing over all of the pairs we have
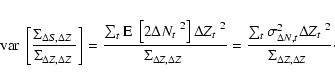
Figure 11 represents the expected
![]() for
for
![]() ,
the nominal scanning strategy of PLANCK at 857 GHz,
and a set of selected ecliptical longitudes of PLANCK
,
the nominal scanning strategy of PLANCK at 857 GHz,
and a set of selected ecliptical longitudes of PLANCK![]() .
Note that the peak differential signal is about
.
Note that the peak differential signal is about
![]() from the ecliptic plane.
The signal is calculated averaging over independent circular patches of
from the ecliptic plane.
The signal is calculated averaging over independent circular patches of ![]() in radius.
The difference between the first and the second scan never exceeds 0.06 MJy/sr,
then being a
in radius.
The difference between the first and the second scan never exceeds 0.06 MJy/sr,
then being a ![]()
![]() effect. However, when compared to the sensitivity
expected in this frequency channel (represented at
effect. However, when compared to the sensitivity
expected in this frequency channel (represented at ![]() by the gray band),
this signal is clearly detectable, particularly
when the spacecraft is located at ecliptical longitudes of
by the gray band),
this signal is clearly detectable, particularly
when the spacecraft is located at ecliptical longitudes of
![]()
![]() and
and ![]()
![]() ,
where a particularly good peak
,
where a particularly good peak
![]() is expected. For a S/N threshold
is expected. For a S/N threshold ![]() 5, a clear detection of
the differential signal is expected for
5, a clear detection of
the differential signal is expected for
![]() .
In case of
.
In case of
![]() ,
the S/N ratio is so good as to open the
possibility to also improve the parameters of the geometrical model, to study
possible spatial dependences in
,
the S/N ratio is so good as to open the
possibility to also improve the parameters of the geometrical model, to study
possible spatial dependences in
![]() ,
and to identify secondary components.
,
and to identify secondary components.
The noise statistics "per patch'' (rms and patch-to-patch correlation) depend on the
method used to assemble samples from TODs to form patches of sky.
To determine a simple statistic for the noise, we construct patches i) of fixed solid
angle (namely, circular patches with radius,
![]() ,
of
,
of ![]() or
or ![]() );
ii) observed in both surveys with a significantly large number of
samples coadded so as to avoid a significant difference
in the effective weight of each sky direction in the two surveys
(in order to assure a similar coverage of the same
patch in the two surveys and smooth out possible particularly bright
pixels - see also the discussion in Sect. 5.5.1);
iii) taken contiguously in time (
);
ii) observed in both surveys with a significantly large number of
samples coadded so as to avoid a significant difference
in the effective weight of each sky direction in the two surveys
(in order to assure a similar coverage of the same
patch in the two surveys and smooth out possible particularly bright
pixels - see also the discussion in Sect. 5.5.1);
iii) taken contiguously in time (
![]()
![]()
![]() )
in each survey; and iv) avoiding the presence of overlapping patches.
These constraints only slightly reduce the number of samples
used in the analysis. After two surveys the average instrumental noise rms on a single squared pixel with side equal to
)
in each survey; and iv) avoiding the presence of overlapping patches.
These constraints only slightly reduce the number of samples
used in the analysis. After two surveys the average instrumental noise rms on a single squared pixel with side equal to
![]() arcmin for the reference frequency channel at 857 GHz is 43 mJy.
Composing these pixels to form circular patches of
radius
arcmin for the reference frequency channel at 857 GHz is 43 mJy.
Composing these pixels to form circular patches of
radius
![]() ,
the noise per patch is
,
the noise per patch is
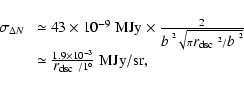
Columns 7 to 9 of Table 2 shows the statistics for the simulated scan
at 857 GHz. The last column gives the expected 1![]() error
on Ef determination according to Eq. (27) with the
expected level of noise.
error
on Ef determination according to Eq. (27) with the
expected level of noise.
Accepting all the sky samples at 857 GHz a rms accuracy
![]()
![]() 10-4
should be expected. The effect of cuts based on the Galactic surface brightness is shown in
Table 2. By considering regions where the Galactic signal is smaller than
10-4
should be expected. The effect of cuts based on the Galactic surface brightness is shown in
Table 2. By considering regions where the Galactic signal is smaller than
![]() MJy/sr (
MJy/sr (
![]() MJy/sr) the accuracy reduces to
MJy/sr) the accuracy reduces to
![]()
![]() 10-3 (
10-3 (
![]()
![]() 10-3).
On the other hand, for
10-3).
On the other hand, for
![]() MJy/sr
(relevant to reduce the impact of the relative calibration
uncertainty, see Sect. 5.5.3)
the number of independent pairs decreases from
MJy/sr
(relevant to reduce the impact of the relative calibration
uncertainty, see Sect. 5.5.3)
the number of independent pairs decreases from
![]() 8
8 ![]() 103 to
103 to ![]() 5.1
5.1 ![]() 103 with
103 with
![]() ,
only slightly degraded with respect to
the full sky analysis. The cut changes the sign of Col. 7 due to the
tilt of the ecliptic plane, so that the ZLE and its variation is
stronger where the Galaxy is weaker.
,
only slightly degraded with respect to
the full sky analysis. The cut changes the sign of Col. 7 due to the
tilt of the ecliptic plane, so that the ZLE and its variation is
stronger where the Galaxy is weaker.
A similar analysis carried out at 545 GHz and 353 GHz gives analogous
results on the scaling introduced by the surface brightness cut.
By considering the sky regions identified by the
![]() MJy/sr at 857 GHz, with the same kind of analysis we find
MJy/sr at 857 GHz, with the same kind of analysis we find
![]()
![]() 10-3 and
10-3 and
![]()
![]() 10-3 at 545 GHz and 353 GHz, respectively.
10-3 at 545 GHz and 353 GHz, respectively.
![\begin{figure}
\par\includegraphics[angle=90,width=8.65cm,clip]{3716fig11.ps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg347.gif) |
Figure 11:
Differential surface brightness of the ZLE from the Smooth component in
the 857 GHz channel,
|
| Open with DEXTER | |
The most important source of error in the determination of Ef
is the bias induced by
![]() when it is comparable to
when it is comparable to
![]() .
In this subsection the main sources of this bias are discussed.
.
In this subsection the main sources of this bias are discussed.
In the differential approach presented in the previous section we
cancel out the Galactic signal.
This is a good approximation provided that the patch
is equally sampled in each of the two surveys, implying
![]() .
In reality, uncertainties in the spacecraft attitude reconstruction
and in pointing maneuvers and, in particular, the displacements
between the positions of the various samples taken in the two surveys
will imply that the same patch is sampled in a different manner in each
survey. An estimate of the maximum displacement between the position of
a given sample in the first survey and the nearest sample taken in
the second survey is given by the maximum between half of the
spin axis displacement (1.25 arcmin) and half of the angular
sampling along the scan circle (
.
In reality, uncertainties in the spacecraft attitude reconstruction
and in pointing maneuvers and, in particular, the displacements
between the positions of the various samples taken in the two surveys
will imply that the same patch is sampled in a different manner in each
survey. An estimate of the maximum displacement between the position of
a given sample in the first survey and the nearest sample taken in
the second survey is given by the maximum between half of the
spin axis displacement (1.25 arcmin) and half of the angular
sampling along the scan circle (![]()
![]() ,
equivalent
to
,
equivalent
to ![]() 0.8 arcmin at 857 GHz).
The pointing accuracy for PLANCK is expected to be better
than 0.5 arcmin (
0.8 arcmin at 857 GHz).
The pointing accuracy for PLANCK is expected to be better
than 0.5 arcmin (![]() )
for each sample
(Puget et al. 2001; Burigana et al. 2001), a value smaller than
the above estimate
)
for each sample
(Puget et al. 2001; Burigana et al. 2001), a value smaller than
the above estimate![]() .
Denoting with
.
Denoting with ![]() the pointing direction neglecting the displacements discussed
above and with
the pointing direction neglecting the displacements discussed
above and with
![]() the effective pointing direction in the i-th survey, the displacement is
the effective pointing direction in the i-th survey, the displacement is
![]() .
We are interested in
.
We are interested in
![]() which depends on the combined displacements
which depends on the combined displacements
![]() .
Then
.
Then
![]() ,
leading to a bias in the determination of Ef of the order of
,
leading to a bias in the determination of Ef of the order of
![]() .
.
If we assume that
![]() does not correlate with the Galactic
emission or the ZLE, as is reasonable, no bias will be introduced.
On the other hand, this effect will degrade the sensitivity by
does not correlate with the Galactic
emission or the ZLE, as is reasonable, no bias will be introduced.
On the other hand, this effect will degrade the sensitivity by
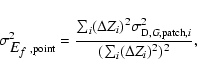 |
(28) |
Table 3:
Expected effect at 857 GHz of an isotropic, random pointing error on the Ef sensitivity as a function of
![]() .
Calculations are for a cut of 1 MJy/sr on the Galaxy and
.
Calculations are for a cut of 1 MJy/sr on the Galaxy and ![]() and
and ![]() patches.
patches.
We consider here the requirement ii) of Sect. 5.4.
We could have a different number of samples
![]() (
(![]()
![]() )
in the same patch
in the two surveys both because of the different samples at the boundary
of the patch and because of the result of the effective scanning
strategy. This implies a difference in the average Galactic
signals obtained in the two surveys, related to the fluctuations of the
Galaxy within the patch. With a simple algebra it is straightforward to derive that in this case
the variance of the induced
)
in the same patch
in the two surveys both because of the different samples at the boundary
of the patch and because of the result of the effective scanning
strategy. This implies a difference in the average Galactic
signals obtained in the two surveys, related to the fluctuations of the
Galaxy within the patch. With a simple algebra it is straightforward to derive that in this case
the variance of the induced
![]() in our differential
approach is
in our differential
approach is
The worst effect of systematic pointing errors would occur in sky regions with bright point-sources. It would then be preferable to remove pixels affected by bright sources before of the computation of the averages of the signals in each patch in order to manage only with signals dominated by the diffuse components.
An example of an intrinsic source of systematic pointing errors is the aberration of
light. When not accounted for, the aberration due to satellite motion about the Sun
may induce at most a pointing error of ![]() 2 v/c rad
2 v/c rad ![]() 0.7 arcmin, dominated
by the Earth motion about the Sun. The factor of 2 comes from the fact that patches
are acquired at most at about
0.7 arcmin, dominated
by the Earth motion about the Sun. The factor of 2 comes from the fact that patches
are acquired at most at about ![]() of longitude when the orbital motions
are toward opposed directions in the sky.
This effect may introduce an important bias; however since the spacecraft velocity is
known within 1 km s-1 or better, the effect may be removed by correcting the selected
pointings.
of longitude when the orbital motions
are toward opposed directions in the sky.
This effect may introduce an important bias; however since the spacecraft velocity is
known within 1 km s-1 or better, the effect may be removed by correcting the selected
pointings.
The relative motion of the satellite with respect to the Sun induces a Doppler shift in
the Galactic signal observed during each of the two scans.
The effect will be
![]()
![]() 10-4 and assuming
10-4 and assuming
![]() the surface brightness variation will be
the surface brightness variation will be
![]() .
Even for
.
Even for ![]() in the range 2-3,
in the range 2-3,
![]()
![]() 10-4.
Assuming
10-4.
Assuming
![]() and taking the statistics from the
signal correlations from Table 2, then
and taking the statistics from the
signal correlations from Table 2, then
![]()
![]() 10-5 MJy2/sr2 equivalent to a bias
10-5 MJy2/sr2 equivalent to a bias
![]()
![]() 10-2.
However the application of 4 MJy/sr cut will reduce this bias by an order
of magnitude. Of course, a further relevant reduction
(by a factor
10-2.
However the application of 4 MJy/sr cut will reduce this bias by an order
of magnitude. Of course, a further relevant reduction
(by a factor ![]() 10 or 100) of this effect
can be reached with a simple modelling of the Galatic emission spectral
index (for example at
10 or 100) of this effect
can be reached with a simple modelling of the Galatic emission spectral
index (for example at ![]() 10% or 1% accuracy).
10% or 1% accuracy).
In addition, assuming the IDP cloud to be at rest around the Sun (neither shifting, nor
rotating in time), the Doppler shift will affect the ZLE surface brightness too, so
that a
![]()
![]() 10-4 MJy/sr equivalent
to a bias in Ef of at most 10-4.
10-4 MJy/sr equivalent
to a bias in Ef of at most 10-4.
The impact of any absolute calibration error of PLANCK data uniform all over the
mission is of simple evaluation. In the differential approach, any calibration uncertainty of this kind produces a null effect in the Galactic signal.
The only final error will be a multiplicative uncertainty in the ZLE
and then in Ef given by
![]() ,
where
,
where ![]() is the relative uncertainty of the absolute
calibration (
is the relative uncertainty of the absolute
calibration (![]() according to FIRAS absolute calibration
accuracy from
according to FIRAS absolute calibration
accuracy from ![]() 300 GHz to
300 GHz to ![]() 900 GHz).
900 GHz).
The evaluation of the impact of calibration errors varying during the mission is more
difficult (i.e. relative calibration errors).
Clearly, the difference in the calibration errors in each patch in the
two considered surveys produces systematic effects in our differential
approach proportional to
![]() .
.
We evaluated the implications of random relative calibration errors.
The relative calibration accuracy of PLANCK/HFI highest frequency
channels is currently under definition.
Pajot et al. (2000) (Sect. 3.3.6.1) reported a preliminary
relative pixel-to-pixel calibration accuracy of ![]()
![]() .
Piat et al. (2002) investigated HFI calibration with a kinematic dipole at
frequencies at
.
Piat et al. (2002) investigated HFI calibration with a kinematic dipole at
frequencies at
![]() GHz and with Galactic templates at
GHz and with Galactic templates at
![]() GHz.
The authors reported a relative calibration accuracy on each scan circle of
GHz.
The authors reported a relative calibration accuracy on each scan circle of ![]()
![]() at
545 GHz and of
at
545 GHz and of ![]()
![]() at 353 GHz with suitable choices of the surface
brightness cut.
at 353 GHz with suitable choices of the surface
brightness cut.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{3716fig12.ps} \end{figure}](/articles/aa/full/2006/23/aa3716-05/Timg409.gif) |
Figure 12:
Effect of the random relative calibration error on the Ef determination
with the differential method at 857 GHz for 2 |
| Open with DEXTER | |
Rescaling the error estimate by Pajot et al. (2000) from ![]() 5 arcmin
pixels to circular patches of
5 arcmin
pixels to circular patches of ![]()
![]() radius, we find a relative accuracy,
radius, we find a relative accuracy,
![]() ,
of
,
of ![]() .
The results of Piat et al. (2002)
can be rescaled to the above circular patches considering that we have
about 102 scan circles per circular patch. In this way we estimate
.
The results of Piat et al. (2002)
can be rescaled to the above circular patches considering that we have
about 102 scan circles per circular patch. In this way we estimate
![]() at 545 GHz and
at 545 GHz and
![]() at 353 GHz.
at 353 GHz.
We then consider
![]() in the range
in the range
![]() ,
so perturbing the simulated
signal from each patch.
The comparison between the estimation of
Ef obtained in the absence of this
systematic error and by repeating the perturbed simulation described
above for many thousands of realizations and for various Galactic cuts
is shown in Fig. 12 for a particular case.
As evident, at 857 GHz, assuming
,
so perturbing the simulated
signal from each patch.
The comparison between the estimation of
Ef obtained in the absence of this
systematic error and by repeating the perturbed simulation described
above for many thousands of realizations and for various Galactic cuts
is shown in Fig. 12 for a particular case.
As evident, at 857 GHz, assuming
![]() and Galactic cuts in the range
and Galactic cuts in the range
![]() MJy/sr
we find a rms error on Ef of
MJy/sr
we find a rms error on Ef of ![]() 3
3 ![]() 10-2 (with an expectation value of the
residual bias of
10-2 (with an expectation value of the
residual bias of ![]() 10-4).
10-4).
For
![]() the rms errors on Ef
are
the rms errors on Ef
are ![]() 2.5
2.5 ![]() 10-2 or
10-2 or ![]() 1.5
1.5 ![]() 10-2respectively at 545 GHz or at 353 GHz
for suitable Galactic cuts. Table 4 summarizes our results.
The range of surface brightness cuts appropriate for each frequency
allowing the above sensitivity spans about one order of magnitude.
We verify that for
10-2respectively at 545 GHz or at 353 GHz
for suitable Galactic cuts. Table 4 summarizes our results.
The range of surface brightness cuts appropriate for each frequency
allowing the above sensitivity spans about one order of magnitude.
We verify that for
![]() the rms error on Ef scales linearly with
the rms error on Ef scales linearly with
![]() at all frequencies.
at all frequencies.
Table 4:
Effect of a random relative calibration error
![]() on the Ef determination at different PLANCK frequencies. Column 2 is the minimum rms error for the optimal surface brightness cut reported in Col. 3. Columns 4 and 5 give the range for which the rms error is
less than twice the value in Col. 2.
on the Ef determination at different PLANCK frequencies. Column 2 is the minimum rms error for the optimal surface brightness cut reported in Col. 3. Columns 4 and 5 give the range for which the rms error is
less than twice the value in Col. 2.
Of course, the optimal Galactic surface brightness cut should be identified a posteriori according to the recovered value of Ef and with a proper trade-off between the various systematic errors.
We presented an analysis to predict the level of contamination from the Zodiacal Light Emission (ZLE) in the survey of the forthcoming PLANCK mission and to evaluate the ability to extract the ZLE signal from the PLANCK data. This signal is used to gain more information about the ZLE physical properties.
Our starting point is the model of Kelsall et al. (1998) for the
ZLE based on the COBE data describing in detail the emissivity of the IDP cloud
for wavelengths up to about 300 ![]() m complemented by the recent
result of Fixsen & Dwek (2002) on the spectral behaviour of the ZLE.
According to the COBE model, four components contribute to the ZLE,
the dominating smooth components on which this paper is focussed,
the Earth orbit locked ring of dust (or circumsolar ring), the trailing blob,
and three bands of dust.
m complemented by the recent
result of Fixsen & Dwek (2002) on the spectral behaviour of the ZLE.
According to the COBE model, four components contribute to the ZLE,
the dominating smooth components on which this paper is focussed,
the Earth orbit locked ring of dust (or circumsolar ring), the trailing blob,
and three bands of dust.
With respect to other foregrounds usually considered in CMB studies,
the ZLE (as the other Solar System objects) is peculiar,
its surface brightness depending not only on the pointing direction but also on
the instantaneous position of the observer within the Solar System.
This underlines the relevance of a study of the ZLE not only on maps but also on time
ordered data streams.
Taking the average yearly position of PLANCK in the IDP dust cloud
will result in a ![]()
![]() error in the ZLE surface brightness estimate,
while neglecting the PLANCK orbit about L2 will imply a
error in the ZLE surface brightness estimate,
while neglecting the PLANCK orbit about L2 will imply a ![]()
![]() error in the ZLE surface brightness estimate.
Since the ZLE differential approach separation exploits the
error in the ZLE surface brightness estimate.
Since the ZLE differential approach separation exploits the ![]()
![]() variation of the
ZLE surface brightness between the two surveys, neglecting the PLANCK orbit will
introduce a non-negligible systematic
variation of the
ZLE surface brightness between the two surveys, neglecting the PLANCK orbit will
introduce a non-negligible systematic ![]()
![]() error in this method.
This will have a large impact on the study of secondary ZLE components, a natural
extension of this work.
error in this method.
This will have a large impact on the study of secondary ZLE components, a natural
extension of this work.
We have implemented the COBE model in a dedicated program that computes
![]() for a given list of values of
for a given list of values of ![]() ,
,
![]() ,
,
![]() and a set of parameters describing the properties of
the ZLE component for which the calculation has to be performed.
Of them, the emissivity correction Ef for each component and for each frequency
band is the hardest to extrapolate to PLANCK frequencies and it carries most of the
physical information on the IDP population producing the bulk emission at these
frequency bands. We then focused on the capability of PLANCK to recover Ef.
Since the Ef scalings are largely uncertain, the code separately generates the
surface brightnesses appropriate for each desired component. The outputs produced for
the various components then can be easily combined according to the user need.
and a set of parameters describing the properties of
the ZLE component for which the calculation has to be performed.
Of them, the emissivity correction Ef for each component and for each frequency
band is the hardest to extrapolate to PLANCK frequencies and it carries most of the
physical information on the IDP population producing the bulk emission at these
frequency bands. We then focused on the capability of PLANCK to recover Ef.
Since the Ef scalings are largely uncertain, the code separately generates the
surface brightnesses appropriate for each desired component. The outputs produced for
the various components then can be easily combined according to the user need.
Since the TODs are large and their realization is strictly related to the effective
scanning strategy and satellite orbit we also implemented an approximate, but accurate,
method able to compress the
![]() ,
,
![]() dependencies in TODs for the
desired pointings in matrices of appropriate series expansion coefficients.
dependencies in TODs for the
desired pointings in matrices of appropriate series expansion coefficients.
We investigated the possibility of obtaining a proper separation of the ZLE through a blind component separation method (FastICA) already used to analyse microwave maps, without obtaining encouraging results.
A non-blind separation based on maps has been investigated
taking as prior information the ZLE spatial dependence and
the existing templates of the Galactic emission degraded to angular
resolutions comparable with the scales of significant ZLE variations. We considered here in detail the case of the HFI 857 GHz channel. In this case the main foreground is the
dust Galactic emission.
For appropriate Galactic surface brightness cuts (![]() 1 MJy/sr) the value of Ef
recovered with this approach is in good agreement with the input one with an rms
absolute accuracy
1 MJy/sr) the value of Ef
recovered with this approach is in good agreement with the input one with an rms
absolute accuracy ![]() 0.05.
On the other hand, any possible residual contribution from the ZLE left in the IR Galactic template adopted from their original data analysis procedure will be scaled to
PLANCK frequencies and will introduce a systematic effect which will be correlated
with the spatial template adopted in ZLE estimates, possibly resulting in biases in the
recovered Ef. A total power approach on TOD has been also investigated, providing
similar results. These two methods require the use of low resolution Galactic
templates.
0.05.
On the other hand, any possible residual contribution from the ZLE left in the IR Galactic template adopted from their original data analysis procedure will be scaled to
PLANCK frequencies and will introduce a systematic effect which will be correlated
with the spatial template adopted in ZLE estimates, possibly resulting in biases in the
recovered Ef. A total power approach on TOD has been also investigated, providing
similar results. These two methods require the use of low resolution Galactic
templates.
To circumvent the need for Galactic templates and to better
take into account the effects introduced by the varying spacecraft
position, we have studied a differential approach exploiting the
fact that PLANCK will scan the sky at least twice during the mission,
staying in different positions within the IDP cloud.
In the ideal case, the difference between these two measures will be due to the
difference in the ZLE contribution that can be predicted from our model plus noise.
We find a typical absolute rms uncertainty on Ef induced by the limited instrumental
sensitivity of ![]() 10-3 (1
10-3 (1![]() )
at 857 GHz
for suitable choices of surface brightness cuts
(or 2.1
)
at 857 GHz
for suitable choices of surface brightness cuts
(or 2.1 ![]()
![]() and 2.6
and 2.6 ![]()
![]() at 545 GHz and 353 GHz, respectively).
For typical expected values of Ef
(
at 545 GHz and 353 GHz, respectively).
For typical expected values of Ef
(![]() 0.65, 0.26, 0.11 for 857 GHz, 545 GHz, 353 GHz)
the PLANCK sensitivity will allow an Ef recovery at 0.15%, 0.8% and 2.4%
(1
0.65, 0.26, 0.11 for 857 GHz, 545 GHz, 353 GHz)
the PLANCK sensitivity will allow an Ef recovery at 0.15%, 0.8% and 2.4%
(1![]() ) accuracy at 857 GHz, 545 GHz and 353 GHz, respectively.
) accuracy at 857 GHz, 545 GHz and 353 GHz, respectively.
We investigated the impact of the most relevant systematic effects, pointing and
sampling uncertainty, aberration of light, Doppler shift and relative calibration
uncertainty. While the first four effects are expected to be significantly below the
noise, the last effect is potentially the most critical one.
For a relative calibration error rms of ![]()
![]()
![]() on patches of
on patches of ![]() radius, we find an absolute rms error on Ef of
radius, we find an absolute rms error on Ef of ![]() 0.01-0.04
0.01-0.04
![]() 0.001-0.004) with only a weak dependence on the frequency in the range
0.001-0.004) with only a weak dependence on the frequency in the range
![]() 300-900 GHz, corresponding to relative errors on Ef
300-900 GHz, corresponding to relative errors on Ef ![]() ,
,
![]() ,
,
![]() (
(![]()
![]() ,
,
![]() ,
,
![]() )
respectively at 857 GHz, 545 GHz, 353 GHz for the most likely Ef values expected on the basis of COBE/FIRAS data.
This may ultimately determine the final accuracy of the
ZLE extraction from PLANCK data.
)
respectively at 857 GHz, 545 GHz, 353 GHz for the most likely Ef values expected on the basis of COBE/FIRAS data.
This may ultimately determine the final accuracy of the
ZLE extraction from PLANCK data.
A web page containing documentation, FITS files, and IDL routines to handle the series expansion for ZLE simulations is in preparation.
Acknowledgements
We warmly acknowledge the PLANCK collaboration teams for having provided us with instrument and mission details. We thank F. Boulanger and M. Juvela for constructive discussions and J. P. Bernard, G. Cremonese, M. Fulle, and G. De Zotti for encouraging and stimulating conversations. We acknowledge L. Abrami and C. Doz of the INAF/OAT for having supported the acquisition of bibliographic material. Some of the results in this paper have been derived using the HEALPix package (Górsky et al. 2005). We warmly thank the referee, W. T. Reach, for constructive comments and suggestions. M.M. acknowledges partial support by COFIN 2005 SubMM (prot. 2004028417_003) SISSA / Trieste / Italy.