A&A 452, 657-668 (2006)
DOI: 10.1051/0004-6361:20053273

Limb polarization of Uranus and Neptune

I. Imaging polarimetry and comparison with analytic models

H. M. Schmid¹ - F. Joos¹ - D. Tschan^1,2

1 - Institut für Astronomie, ETH Zürich, 8092 Zürich, Switzerland
2 - Alte Kantonsschule Aarau, Bahnhofstrasse 91, 5001 Aarau, Switzerland

Received 20 April 2005 / Accepted 10 January 2006

Abstract
Imaging polarimetry of Uranus and Neptune in the R, i, and z bands are presented. In all observations a radial limb polarization on the order of 1% was detected with a position angle perpendicular to the limb. The polarization is higher in both planets for the shorter wavelength bands. As a first approximation, the polarization seems to be equally strong along the entire limb. This is unlike Jupiter and Saturn, where significant limb polarization is only observed at the poles. We determined flux-weighted averages of the limb polarization and radial limb polarization profiles, and investigated the degradation and cancellation effects in the polarization signal due to the seeing-limited spatial resolution of our observations. Taking this into account we derived corrected values for the limb polarization in Uranus and Neptune. The results are compared with analytic models for Rayleigh scattering atmospheres for the semi-infinite case and finite layers with ground albedo. The comparison shows that the detected polarization is compatible with expectations. This indicates that limb-polarization measurements offer a powerful diagnostic tool for investigating the properties of scattering particles in the upper atmospheres of Uranus and Neptune, in particular if more sophisticated numerical modeling of the limb polarization becomes available. It is also concluded from the overall strength of the limb polarization that the disk-integrated polarization of Uranus and Neptune for large phase angles is high (p>20%). This is of interest for future polarimetric detections of extra-solar planets with atmospheric properties similar to Uranus and Neptune.

Key words: planets and satellites: individual: Uranus - planets and satellites: individual: Neptune - polarization - scattering

1 Introduction

Light reflected from planetary atmospheres is polarized. This basic property of planets provides a powerful diagnostic tool for the investigation of the atmospheric structure and the characterization of scattering particles as demonstrated e.g. for Venus, Jupiter, and Saturn.

Polarization studies of Venus are particularly powerful for constraining atmospheric particles, because a wide range of phase angles can be covered with observations from the ground (e.g. Dollfus & Coffeen 1970; Hansen & Hovenier 1974). For the outer planets the possible phase angles for ground based observations are very limited, and the disk-integrated polarization is close to zero due to the back-scattering situation. Nonetheless, the limb polarization effect can be used to constrain polarimetric properties of the atmosphere. Jupiter, for example, shows strong limb polarization at the poles reaching about $p=7\%$ and a low limb polarization $p<1\%$at the equator (e.g. Hall & Riley 1974, 1976; Gisler & Schmid 2003). The polarization is much higher at the poles because they are covered with a scattering layer consisting of highly polarizing haze particles and Rayleigh scattering molecules. At the equator, the radiation is predominately reflected by clouds and the resulting polarization is small. This interpretation is supported by polarimetric observations of Jupiter for large phase angles with space missions. The data show (e.g. in the R-band) a very high polarization of up to 50% at the poles as expected for a Rayleigh scattering atmosphere for phase angles near 90$^\circ$, and less than $5\%$ at the equator (Smith & Tomasko 1984; Braak et al. 2002). The polarization of Saturn is qualitatively similar but lower than for Jupiter (e.g. Tomasko & Doose 1984).

For Uranus and Neptune practically no polarimetric information has been available up to now. For Uranus, a disk-integrated polarization of $p<0.03\%$ has been measured with aperture polarimetry (Michalski & Stokes 1977). From this, only very limited information can be gained about the polarimetric properties of the atmosphere. To our knowledge space-based polarimetry of Uranus and Neptune has not been taken in the past, nor is such a mission planned for the coming decade. Thus, ground-based observations of the limb polarization of Uranus and Neptune seem to be the best way currently to investigate these planets polarimetrically. Up to now, such limb polarization data have not been reported in the literature.

In this work we present imaging polarimetry of Uranus and Neptune taken with the ESO 3.6 m Telescope at La Silla. Our data resolve the planetary disk and we detect the limb polarization effect clearly.

The limb polarization is a well-known second order scattering effect occurring in reflecting atmospheres where Rayleigh-type scattering processes are dominant (e.g. van de Hulst 1980). To understand this effect, one has to consider a back-scattering situation at the limb of a sphere, where we have locally a configuration of grazing incidence and grazing emergence (for a plane parallel atmosphere) for the incoming and the back-scattered photons, respectively. Photons reflected after one scattering are practically unpolarized, because the scattering angle is 180$^\circ$. Photons undergoing two scatterings travel after the first scattering predominantly parallel to the surface before being reflected towards us by the second scattering process. Photons going up will mostly escape without a second scattering, and photons going down have a low probability of being reflected towards us after the second scattering but a high probability to be absorbed or to undergo multiple scatterings. Because the polarization angle induced in a single dipole-type scattering process, like Rayleigh scattering, is perpendicular to the propagation direction of the incoming photon (which is often parallel to the limb), a polarization perpendicular to the limb is produced.

After the description of the observational data (Sects. 2-4) we derive the intrinsic limb polarization. The first step is to convert the measured polarization into a radial limb polarization and to determine a radial profile and a disk integrated average (Sects. 5-7), which is then corrected in a second step for the degradation of the polarization due to the limited resolution (seeing) of our measurements (Sect. 8). In Sect. 9 we compare our measurements with the analytic model results for Rayleigh scattering atmospheres from e.g. Chandrasekhar (1950), Coulson et al. (1960) and Abhyankar & Fymat (1971).

Already these simple models, together with our limb polarization measurements, provide important insight onto the global polarimetric properties of Uranus and Neptune, which are discussed in the final sections of this paper.

   
2 Observations and data reduction

Imaging polarimetry of Uranus and Neptune was taken on November 30, 2003 with EFOSC2 at the ESO 3.6 m telescope. EFOSC2 is a multi-mode imager and grism spectrograph that can be equipped with a Wollaston prism and a rotatable superachromatic half-wave plate for linear polarimetry and spectropolarimetry.

The Wollaston prism produces two images with opposite linear polarization $I_\parallel$ and $I_\perp$ (the ordinary and extraordinary beam) offset by 10'' on the CCD. In order to avoid confusion, a Wollaston mask was introduced at the telescope focus with alternating open and opaque strips. The open strips have a width of about 10'' corresponding to the splitting of the Wollaston prism. The strip period is 26.7''. Since the diameters of Uranus and Neptune are about 3.5'' and 2.2'', respectively, the whole planet is well contained in one 10''-strip. The data taken with different filters were recorded with a $2{\rm k} \times 2{\rm k}$ CCD (ESO CCD# 40) with a pixel scale of $0.157''~{\rm pixel}^{-1}$.

The linear polarization was measured in a standard way (e.g. Tinbergen & Rutten 1992) with one or several sets of four observations taken at half-wave position angles of $0^\circ$, $22.5^\circ$, $45^\circ$, and $67.5^\circ$, respectively. Three sets with 4 exposures each were taken for each broad-band filter in order to enhance the signal-to-noise. Only one set was taken for the narrow-band filter (plus mask) observations of Uranus (see Table 1).

Table 1: Parameters for the imaging polarimetry of Uranus and Neptune for November 30, 2003. The planet parameters were taken from the "The Astronomical Almanac 2003''. The South pole coordinates are given as distance from the disk center and position angle (see Fig. 1). For the filters the central wavelength $\lambda _{\rm c}$ and the band width $\Delta \lambda$ (FWHM) are given.

Exposures with the half-wave plate rotation angles at $0^\circ$ and $45^\circ$ yield Stokes $Q_{\rm inst}$ and the other two yield Stokes $U_{\rm inst}$ in the instrument coordinate system. Important in the data reduction procedure is that the different planetary images (e.g. $I_\parallel (0^\circ)$, $I_\perp (0^\circ)$, $I_\parallel (45^\circ)$ and $I_\perp (45^\circ)$), are centered in the same way and with an accuracy of about 1/10 of a pixel. One $Q_{\rm inst}/I$ frame results from the combination of 4 planet images according to

$${Q_{\rm inst}\over I} = {R-1\over R+1}\quad {\rm with} \quad ... ...erp(0^\circ)\over I_\parallel(45^\circ)/I_\perp(45^\circ)},$$

and equivalent for Stokes $U_{\rm inst}/I$ with the $I_\parallel$ and $I_\perp$images taken at half-wave plate angles $22.5^\circ$ and $67.5^\circ$.

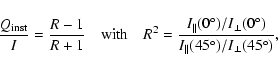
Unpolarized (HD 14069) and polarized (BD $+25^\circ 727$, HD 80558) standard stars were observed with the same instrumental set-up as for Uranus and Neptune in order to check the instrumental polarization and to rotate the $Q_{\rm inst}-U_{\rm inst}$polarization coordinate system into the celestial Q-U coordinate system. For this the wavelength dependence of the position angle of the optical axis of the superachromatic half wave plate has to be considered. The instrumental polarization was found to be less than 0.2%, and the polarization angle calibration should be accurate to about $\theta\approx 2^\circ$. During the same run spectropolarimetric observations of Uranus and Neptune were also made with the same instrument (see Joos et al. 2005). The calibration of the imaging polarimetry presented here was checked and verified with the spectropolarimetric data.

An effective seeing of about 0.8'' was estimated for the Uranus and Neptune observations. This value was derived from the stellar point spread functions measured in the standard star polarimetry taken during the same night.

Filters.

Central wavelengths and widths (FWHM) of the R, i, and z broad-band filters and the red narrow-band filters used for our polarimetry are given in Table 1. For the i and z filter observations the strong wavelength dependence of the CCD efficiency curve has to be considered, which drops from about 80% at 750 nm to 10% at 1 $\mu$m. The effective wavelengths and band widths for these filter observations are therefore added in the footnote of Table 1. The broad-band filters R, i, and z were used for Neptune and i, z for Uranus. Uranus was too bright to be observed in the R filter. For this reason we observed Uranus in two narrow band filters centered at 673 nm and 729 nm. These narrow filters were combined with an occulting mask, an opaque plate with a few dozen small holes allowing about 1% of the light through. The mask was installed in the filter wheel near the instrument pupil. This mask/filter setup was mainly used for observations of brighter planets such as Jupiter and Mars. It turned out that the throughput for Uranus was too low for high-quality polarimetric imaging. But the data can still be used for a rough estimate of the polarization level at these wavelengths.

3 Intensity images

Figure 1 shows intensity images of Uranus and Neptune taken in the i-band. Also indicated are the limb, the equator, and the south pole of the planets. The south pole of Uranus is near the east limb of the planet.

The Uranus image clearly shows the higher reflectivity of the southern high latitude regions compared to the northern latitudes. The same asymmetric intensity distribution is also visible in HST images of Uranus (e.g. Karkoschka 2001). In addition HST images of Uranus and Neptune from August 2003 are available (see press release STScI-PRC2004-05), which were taken just a few months before our observations. Of course the HST data show many more details due to the significantly higher spatial resolution when compared to our seeing-limited observations.

	Figure 1: Intensity image of Uranus ( left) and Neptune ( right) in the i-Band. North is up and East to the left. The size of the images is $6.1''\times 6.1''$.
Open with DEXTER

   
4 Stokes Q and U images for Uranus and Neptune

Stokes Q and U images of Uranus and Neptune are shown in Figs. 2 and 3, respectively. The Stokes parameters for the linear polarization are defined as Q=I₀-I₉₀ and U=I₄₅-I₁₃₅, where I_x is the intensity for a polarization angle x measured from North over East. The grey scale in the Stokes Q and U images is normalized to the peak intensity $I_{\rm peak}$ on the planetary disk and goes from $-0.005~I_{\rm peak}$ (black) to $+0.005~I_{\rm peak}$ (white).

The same quadrant pattern is visible in Q and U for Uranus and Neptune. Q is positive at the northern and southern limbs, negative at the eastern and western limbs, and essentially zero in the center of the planetary disk. For U the same pattern is visible but rotated by 45 degrees. In Neptune the polarization pattern is significantly stronger for the R-band when compared to the z-band (Fig. 3). This indicates that the polarization is lower for longer wavelengths. The same trend is seen for the i and z-band observations of Uranus.

The Stokes Q and U images of Uranus and Neptune indicate that in both planets the polarization is low near the disk center and high at the limb. The position angle of polarization is perpendicular to the limb everywhere. This basic polarization pattern is expected for backscattering from a Rayleigh-scattering atmosphere. The quadrant pattern in the Stokes Q and U images is highly symmetric. This indicates that the limb polarization has along the entire limb a similar strength.

	Figure 2: Stokes Q ( left) and U ( right) images for Uranus in the i-band. The grey scale in the Stokes Q and U images is normalized to the peak intensity $I_{\rm peak}$ and spans the range from $-0.5\%$ (black) to $+0.5\%$ (white).
Open with DEXTER

	Figure 3: Stokes Q and U images for Neptune taken in the R-filter ( top) and z-filter ( bottom). The grey scale is normalized to the peak intensity  $I_{\rm peak}$ and ranges from $-0.5\%$ (black) to $+0.5\%$ (white).
Open with DEXTER

It should be noted that, due to the very steep intensity gradients at the limb the resulting strength of the Q and U limb polarization features critically depend on an exact centering of the different planet images (e.g. $I_\parallel (0^\circ)$, $I_\perp (0^\circ)$, $I_\parallel (45^\circ)$, and $I_\perp (45^\circ)$ for the Q image). Experiments with the Q images of Uranus show that an artificial displacement of one of the four images by 0.2 pixel in the North-South direction reduces the positive Q-feature at the northern limb to almost zero, while the feature at the southern limb is strengthened. A displacement in the opposite direction reverses the effect at the northern and southern limbs. Standard star observations show that the relative position of the two star images on a given frame (the ordinary and extraordinary images from the Wollaston) is only stable to a precision of about 0.05 pixels for different half-wave plate positions and telescope pointings. From this limited stability of the instrument (and the lack of adequate calibration measurements), we have to conclude that small differences in the polarization level on opposite limbs should not be over-interpreted because of the limited resolution and alignment precision of our data. Despite this, we would however see extended polarization structures along the limb that deviate more than 50% from the average limb polarization. Such features are not seen in our data.

In any case the general quadrant pattern is present and real in all our Q and U images of Uranus and Neptune. It is practically impossible, with the applied observing and reduction technique, to obtain such a pattern artifically due to image misalignments, image distortions, or other spurious effects.

5 The radial polarization

The data are presented in the previous section as separate images of the Stokes Q and U flux instead of the polarized flux $p\times I=(Q^2+U^2)^{1/2}$. The square of Q and U in the formula for the polarized flux introduces large systematic errors, if the absolute value of the measured signals |Q| and |U| is not significantly higher than the measuring noise $\Delta Q$ and $\Delta U$. In our Uranus and Neptune data, there is $\Delta Q\approx \vert Q\vert$ (and $\Delta U\approx \vert U\vert$) in the middle of the planetary disk and between the positive and negative Q and U features. Therefore the use of the polarized flux $p\times I$ (or the normalized polarization p) as measuring parameter would lead to wrong results.

With radial Stokes parameters these problems can be avoided, and averaged (radial) polarization values for the limb polarization and the polarization as a function of radius can be derived without introducing systematic errors in the data reduction process. In particular, radial Stokes parameters are well-suited for characterizing a centro-symmetric polarization pattern.

The radial Stokes parameters $Q_{\rm r}$ and $U_{\rm r}$ describe the polarization in radial and tangential direction on the planetary disk. $Q_{\rm r}$ and $U_{\rm r}$ are given by

$$Q_{\rm r} +Q \cos 2\phi + U\sin 2\phi$$

$$U_{\rm r} -Q \sin 2\phi + U\cos 2\phi,$$

where $\phi$ is the polar angle of a given position (x,y)(equivalent to $(\alpha,\delta)$) on the apparent planetary disk (disk center (x₀,y₀)) with respect to the North direction:

$$\phi = \arctan {x-x_0\over y-y_0}\cdot$$

$Q_{\rm r}>0$ is equivalent to a radial polarization or a polarization perpendicular to the limb, while $Q_{\rm r}<0$ indicates a tangential polarization component. $U_{\rm r}$ describes the polarization in the directions ${\pm} 45^\circ$ with respect to the radial direction.

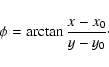
	Figure 4: Radial Stokes $Q_{\rm r}$ ( left) and $U_{\rm r}$ ( right) for Uranus in the i-band. The grey scale is normalized to the peak intensity $I_{\rm peak}$ and goes from $-0.5\%$ (black) to $+0.5\%$ (white).
Open with DEXTER

	Figure 5: Radial Stokes $Q_{\rm r}$ ( left) and $U_{\rm r}$ ( right) for Neptune in the R-band. The grey scale is normalized to the peak intensity $I_{\rm peak}$ and goes from $-0.5\%$ (black) to $+0.5\%$ (white).
Open with DEXTER

Figures 4 and 5 show the resulting radial polarization images $Q_{\rm r}$ and $U_{\rm r}$ for Uranus in the i-band and Neptune in the R-band. In both cases the limb polarization is clearly visible as a bright ring with positive $Q_{\rm r}$ polarization. The level of the ${\pm} U_{\rm r}$-polarization for an area of the size of the seeing disk is typically 5-10 times lower than the positive $Q_{\rm r}$ signal along the limb. The negative $U_{\rm r}$ patch (spurious signal due to two "hot'' pixels?) near the NE limb of Uranus in Fig. 4 or the negative $U_{\rm r}$ southern limb of Neptune in Fig. 5 are about 3-4 times weaker than the positive $Q_{\rm r}$ signal at these positions. We suspect that these localized $U_{\rm r}$ features are not real, and in any case they are significantly weaker than the positive (radial) $Q_{\rm r}$ polarization. From this we conclude that the radial polarization component (positive $Q_{\rm r}$) dominates. Observations in the other filters look similar, and the corresponding $Q_{\rm r}$-images are shown in Figs. 6 and 7.

For the z-filter observations of Uranus (Fig. 6), it may be suspected that the limb of the northern hemisphere (the limb to the west in sky coordinates) has a higher polarization than the limb near the South pole (limb to the east). Due to the strong dependence of such an asymmetry pattern on the image centering, as described in Sect. 4 it cannot be clarified that this feature is real. Higher resolution data are required to resolve this issue.

	Figure 6: Radial Stokes parameter $Q_{\rm r}$ for Uranus in the narrow $\lambda$ 673 nm filter ( left) and the z filter ( right); grey scale as in Fig. 5.
Open with DEXTER

	Figure 7: Radial Stokes parameter $Q_{\rm r}$ for Neptune in the i ( left) and z filters ( right); grey scale as in Fig. 5.
Open with DEXTER

6 Disk-integrated polarization

A first basic quantity to describe our polarimetry is the disk-integrated polarization. For this we sum up all counts in the I, Q, and U, respectively $Q_{\rm r}$ and $U_{\rm r}$ images. This yields $\Sigma Q$, $\Sigma U$, etc., from which we can calculate normalized polarization parameters $\langle Q/I\rangle$ ( $=\Sigma Q/\Sigma I$), $\langle U/I \rangle$ and $\langle Q_{\rm r}/I\rangle$, $\langle U_{\rm r}/I \rangle$, respectively (Table 2).

The $\langle Q/I\rangle$, $\langle U/I \rangle$ are disk-averaged values equivalent to a measurement with aperture polarimetry, where the aperture is larger than the planet. Our imaging polarimetry yields essentially null results ( $\vert\langle Q/I\rangle\vert$ and $\vert\langle U/I \rangle\vert \la0.05\%$) for the integrated polarization of Uranus and Neptune (Table 2). For Uranus, this agrees with previous full-disk polarimetry of Michalski & Stokes (1977) who obtained a polarization for their red filter consistent with <0.02%. This agreement indicates that systematic measuring errors in our disk-integrated polarization parameters given in Table 2 are smaller than 0.05%.

The absence of net polarization in the disk averages indicates that the sum of both negative $Q_{\rm E}$ and $Q_{\rm W}$ polarization features at the East and West limbs cancels the sum of the positive $Q_{\rm N}$ and $Q_{\rm S}$ features at the North and South limbs. For example, for the i-band polarimetry of Uranus, there is $Q_{\rm N}\approx Q_{\rm S}\approx -Q_{\rm E} \approx -Q_{\rm W} \approx 0.1\%$ of the total intensity of the entire planetary disk. Thus the limb polarization in one of these quadrants of the planetary disk is significantly higher than the resulting net polarization that is obtained by summing up all positive and negative components. The same can be said for the NE/SW and SE/NW polarization features in the U images. Note that the disk-integrated parameters $\langle Q/I\rangle$ and $\langle U/I \rangle$cannot be affected by inaccuracies in the image centering procedure.

A strong positive signal is obtained for the disk-integrated radial polarization $\langle Q_{\rm r}/I\rangle$(Table 2). The measured radial polarization is higher for Neptune compared to Uranus. The polarization decreases in both planets for longer wavelengths. The measuring error for $\langle Q_{\rm r}/I\rangle$ is <0.05% as estimated for the measuring error for $\langle Q/I\rangle$ and $\langle U/I \rangle$. This does not include the polarization cancellation due to the limited spatial resolution, which determined by the seeing conditions in our case. An assessment of the seeing effect and corresponding correction factors are given in Sect. 8.

Table 2: Normalized, disk-integrated polarization parameters $\langle Q/I\rangle$ and $\langle U/I \rangle$ in the celestial coordinate system and the radial polarization parameters $\langle Q_{\rm r}/I\rangle$ and $\langle U_{\rm r}/I \rangle$ for a centro-symmetric (radial) coordinate system centered on the planetary disk. The next column gives the radial polarization $\langle Q_{\rm r}/I\rangle^{\rm corr}$ corrected for the seeing-limited resolution according to Sect. 8. The chosen seeing-correction factors are 1.22 for Uranus and 1.54 for Neptune. The last column gives the effective geometric albedo $A_{\rm g}$ for Uranus and Neptune in the corresponding filter pass band.

The integrated radial polarization $\langle Q_{\rm r}/I\rangle$ is a good parameter for characterizing the overall limb polarization of a planet. Since $Q_{\rm r}$ is either positive or close to zero everywhere on the disk no polarization compensation effect is present. Furthermore, there is $\langle Q_{\rm r}/I\rangle\gg \langle U_{\rm r}/I \rangle\approx 0$, so that we can approximate

$$\langle p_{\rm r}\rangle= \sqrt{\langle Q_{\rm r}/I\rangle^2+... ...e U_{\rm r}/I\rangle^2} \approx \langle Q_{\rm r}/I \rangle .$$

Thus $Q_{\rm r}$ and $\Sigma Q_{\rm r}$ can be considered as the radially polarized flux and the disk integrated radially polarized flux, respectively. Then, $Q_{\rm r}/I$ and $\langle Q_{\rm r}/I\rangle$ are the corresponding normalized polarization values.

Effective albedos.

To characterize the scattering properties of a planet, it is important to know the effective geometric albedo $A_{\rm g}$ for a given filter observation. The evaluation of the effective albedo requires a flux weighting of the wavelength-dependent albedo, because the registered photons come predominantly from those spectral regions (in a given filter pass band) with the highest albedo, while only a few photons come from deep absorption bands where the albedo is low. Therefore we have given the effective (flux weighted) geometric albedo for the different filter observations in Table 2. For our evaluation we used the spectrophotometric observations of Karkoschka (1998) available from the Planetary Data System (PDS). They provide the geometric albedo as a function of wavelength for Uranus and Neptune. We had also to consider the wavelength-dependent instrument efficiency curves that were derived from the transmission curves of the filters employed (see Table 1) and the efficiency curve of the CCD (ESO CCD #40).

7 Polarization as function of radius

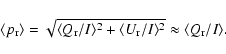
The observed polarization of Uranus and Neptune is essentially centro-symmetric. For this reason it is useful to construct rotationally averaged, radial profiles for the polarization, the normalized polarization, and the intensity. Of course, all intrinsic non-symmetric structures are neglected with this procedure. This is important to consider with respect to effects that could be related to the strong albedo asymmetry of Uranus, which has a brighter southern hemisphere (see e.g. Karkoschka 2001; Rages et al. 2004). However, assuming as a first approximation a rotational symmetry for the polarization structure seems to be reasonable considering the quality of our observations.

Non-symmetries introduced by alignment-inaccuracies in the reduction process hardly affect the resulting radial polarization profiles. A slight misalignment that produces a radial polarization too low on the one limb would at the same time cause too high a polarization on the opposite limb. The corresponding smearing effect in the rotationally averaged profile is small and certainly negligible with respect to the seeing resolution.

Figure 8: Uranus radial profile for intensity I and radial polarization $Q_{\rm r}$ ( upper panel) in the i and z filters. Both I and $Q_{\rm r}$ are normalized to the peak flux at r=0. The lower panel shows the corresponding normalized radial polarization $Q_{\rm r}/I$. The squares indicate the same curve for the narrow-band filter $\lambda =673$ nm. The error bars for the latter points are about twice the size of the broad-band filters. The radial distance is given in arcsec; $R_{\rm planet} = 1.75''$ for Uranus.

Open with DEXTER

	Figure 9: The radial profile of Neptune with intensity I and the radial polarization $Q_{\rm r}$ ( upper panel) and the corresponding normalized radial polarization $Q_{\rm r}/I$ ( lower panels) in the R, i, and z filters (as in Fig. 8). The radial distance is given in arcsec; $R_{\rm planet} = 1.12''$ for Neptune.
Open with DEXTER

Figures 8 and 9 show the radial polarization structure for Uranus and Neptune in the R, i, and z bands. The radial profiles are very similar for both planets and in all filters. The polarization $Q_{\rm r}$ in the disk center at r=0 is essentially zero. The normalized radial polarization $Q_{\rm r}/I$ increases steadily with radius and seems to reach a constant value in the seeing halo at $r>R_{\rm planet}$ before the photon noise starts to dominate the measurements. It is clearly visible that the normalized polarization is higher at shorter wavelengths. We measure for the last four data points in the $Q_{\rm r}/I$ curves in Figs. 8 and 9 the average polarization of 1.14%, 1.21%, and 0.68% in the $\lambda~673$, i, and z filters for Uranus and 1.56%, 1.14%, and 0.70% in the R, i, and z filters for Neptune.

Stokes $Q_{\rm r}$, the radial polarization flux, also increases with radius up to about $r\approx R_{\rm planet}$and decreases further out to zero in step with the intensity profile. It should be noted that the obtained radial profiles in Figs. 8 and 9 depend on the seeing conditions.

Figure 10: Modeling of the degradation of the polarization Q due to the cancellation of opposite polarization components +Q and -Qcaused by the seeing limited resolution; a) no seeing, b) seeing $0.3~R_{\rm planet}$, c) seeing $0.5~R_{\rm planet}$, and d) seeing $0.8~R_{\rm planet}$. The grey scale spans for all panels the range from $-1\%$ (black) to $+1\%$ (white) of the peak intensity of the initial (no seeing) intensity image.

Open with DEXTER

   
8 Seeing corrections

The seeing-limited resolution of our planet observations causes a polarization cancellation effect. This has to be taken into account for interpreting the polarization properties of Uranus and Neptune. Due to the seeing, the opposite polarization components +Q and -Q overlap and cause a reduction in the resulting net polarization. In the most extreme case of an unresolved centro-symmetric planetary disk, the polarization cancellation would be perfect and only a zero net polarization level could be measured. Of course the compensation effect is stronger for Neptune than for Uranus because of the smaller apparent diameter of the former planet.

For an estimate of the polarization cancellation, we adopted a "typical'' model for the expected polarization pattern (from Sect. 9). From this model we constructed 2-dimensional intensity maps for I₀, I₉₀, I₄₅, and I₁₃₅ and applied a folding with a Gaussian function (filter/Gauss task of the MIDAS package providing a Gaussian image smoothing). From the "smeared'' I-images, the corresponding Stokes Q and Stokes U maps can be constructed. Figure 10 illustrates the cancellation effect in the Stokes Q image due to the seeing for a semi-infinite, conservative Rayleigh scattering model atmosphere (see Sect. 9). The seeing, which is equivalent to the spatial resolution of the modeled observations, is characterized as full width at half maximum (FWHM) of the Gaussian filter function and given in units of the planet radius $R_{\rm planet}$.

The Q and U maps can be converted into maps for the radial polarization $Q_{\rm r}$ and $U_{\rm r}$, as for the observations. From $Q_{\rm r}$ the integrated radial polarization $\langle Q_{\rm r}/I\rangle_{\rm seeing}$ is calculated for different seeing parameters. The ratio between the $\langle Q_{\rm r}/I\rangle_{\rm seeing}/\langle Q_{\rm r}/I\rangle_0$ then yields the value for the expected seeing degradation of the disk-integrated radial polarization $\langle Q_{\rm r}/I\rangle$. The corresponding curve is shown in Fig. 11. The polarization cancellation described by the curve in Fig. 11 depends not on the strength, but on the geometric structure of the polarization pattern. As can be seen for the analytic Rayleigh scattering models (Sect. 9), the polarization pattern is very similar for the different model parameters. Thus the same seeing-correction curve (Fig. 11) can be applied to all our observations of Uranus and Neptune. The uncertainty of the correction factor in the end depends predominantly on the atmospheric seeing parameter that is not very accurately known.

	Figure 11: Measurable radial polarization $\langle Q_{\rm r}\rangle_{\rm seeing}$ relative to the initial radial polarization $\langle Q_{\rm r}\rangle_0$ as a function of the seeing for a planet with a (semi-infinite, conservative) Rayleigh-scattering atmosphere. The seeing (FWHM) is expressed in units of the radius of the planetary disk.
Open with DEXTER

In Sect. 2 we estimated a seeing of 0.8'' for our observations. The uncertainty in the estimated seeing is about $\pm 0.1''$. Thus the seeing degradation factor for the integrated radial polarization $\langle Q_{\rm r}\rangle_{\rm seeing}/\langle Q_{\rm r}\rangle_0$ is roughly 0.82 for Uranus (seeing $0.46~R_{\rm planet}$) and 0.65 for Neptune (seeing $0.71~R_{\rm planet}$). For an estimate of the intrinsic radial polarization $\langle Q_{\rm r}/I\rangle$, the values derived from the observations (Table 2) have to be multiplied by the inverse values, thus with 1.22 and 1.54 for Uranus and Neptune, respectively.

   
9 Results for scattering atmospheres models derived from the literature

Many papers describe the atmospheric structure of Uranus and Neptune (see review by Lunine 1993). Very important with respect to the limb polarization are the investigations of the atmospheric structure based on the reflected radiation as observed via the geometric albedo spectrum (e.g. Baines & Bergstralh 1986; Baines & Smith 1990; Sromovsky 2005a,b). The reflection models employed there are rather sophisticated and they can reproduce the observed geometric albedo spectra of Uranus and Neptune well. Important radiative transfer processes to be considered for the red to near-IR spectral region are Rayleigh scattering, high-altitude haze scattering, molecular absorption by methane, and the reflection from an optically thick cloud layer. Additional processes should also be considered, such as Raman scattering and absorption by other molecules.

Unfortunately, the existing radiative transfer models of Uranus and Neptune provide no model results for the limb polarization that might be compared with our observations. For this reason we consider the results from analytic calculations for the polarized light reflected by Rayleigh-scattering atmospheres from the seventies and earlier going back to the classical work of Chandrasekhar (1950). A comprehensive overview of the basic theory and many modeling results is given in van de Hulst (1980). However, not many results are available on the limb polarization effect for gaseous planets in opposition. In particular the disk integrated (averaged) radial polarization $\langle Q_{\rm r}/I\rangle$, the main parameter for characterizing the polarization of Uranus and Neptune in this work, cannot be found in the literature. We found only a short description in van de Hulst (1980, Sect. 18.3.2), which describes the limb polarization and its dependence on different model parameters. However, the resulting polarization is only presented in graphic form and then for only one particular point on the disk ( $r=0.91~R_{\rm planet}$). Therefore, this study is not suitable for comparison with our Uranus and Neptune data with seeing-limited spatial resolution.

For this reason we put together radial profiles for the intensity and polarization using formulas and tabulations based on analytic models given in the literature. From this the disk-integrated radial polarization $\langle Q_{\rm r}/I\rangle$ is calculated in order to compare the measurements with these models. It is emphasized that the results from these simple models of course allow only a qualitative comparison with our observations, but it does provide a useful first step. More sophisticated radiative transfer calculations, which actually do not exist for the limb polarization effect, would also require investigation of a huge model parameter space that is beyond the scope of this paper.

The model results are significantly simplified if only the case of exact opposition $\alpha =0^\circ$ is considered. Thus any position on the planetary surface can be approximated by the case of exact back-scattering from a plane-parallel atmosphere. Then the angle of incidence $\theta_0$ with respect to the surface normal ( $\mu_0=\cos\theta_0$) is equal to the angle of emergence $\theta$ (or $\mu$) with an azimuthal angle $\phi=180^\circ$. For this case the reflected intensity I(r) and the radial polarization flux $Q_{\rm r}(r)$are simply functions of the fractional disk radius r. In our calculations the reflected intensity is defined as

$$I(r) = I_0(r)~\mu (r)R(\mu_0(r),\mu (r)),$$

where the initial (iradiating) intensity I₀(r) is normalized to 1, $\mu(r)=(1-r^2)^{1/2}$, and $R(\mu_0(r),\mu (r))$ is the reflection function (R=1 for a perfect, diffusely reflection Lambertian surface). Integration of I(r) over the planetary disk yields the geometric albedo

$$A_{\rm g} = \int_0^1 I(r)~2\pi~ r~ {\rm d}r .$$

9.1 Semi-infinite Rayleigh-scattering atmospheres

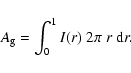
For semi-infinite Rayleigh-scattering atmospheres, the reflected intensity and polarization as function of radius (or $\mu$) can be calculated using the formulas and the tabulated functions given in Abhyankar & Fymat (1970,1971) and Chandrasekhar (1950). The resulting curves for intensity I, radial polarization $Q_{\rm r}$, and normalized polarization $Q_{\rm r}/I$ are shown in Fig. 12 for eight different values for the single-scattering albedo $\omega$. The $Q_{\rm r}/I$ curve for the conservative case ($\omega =1$) has already been discussed in detail in van de Hulst (1980). Note that our definition of the radial polarization $Q_{\rm r}$ yields positive values, while the definition for the radial polarization used in the literature is often negative.

Figure 12: Normalized reflected intensity I, radial polarization flux $Q_{\rm r}$ and normalized polarization $Q_{\rm r}/I$ as functions of disk radius r for a planet at exact opposition (phase angle $\alpha =0^\circ$) with a semi-infinite, Rayleigh-scattering atmosphere and single scattering albedos $\omega =1$ (thick solid), 0.99 (dash dotted), 0.95 (dashed), 0.90 (dotted), 0.80, 0.60, 0.40 and 0.20 (thin solid). Where space permits the curves are labeled with the corresponding $\omega$.

Open with DEXTER

The curves for the normalized radial polarization $Q_{\rm r}/I$ are strongly peaked at the limb for all scattering albedos $\omega$. The $Q_{\rm r}/I$-polarization does not strongly depend on $\omega$ for the range $\omega=0.9$ to 1.0 (see also Table 3). For lower $\omega$, the normalized limb polarization $\langle Q_{\rm r}/I\rangle$ decreases continuously. This occurs because a low single-scattering albedo strongly reduces the flux from photons undergoing two or more scatterings that are responsible for the limb-polarization effects. Much less reduced by the low scattering albedo are the photons that are reflected after one single (back)-scattering and that produce no limb polarization effect. For all scattering albedos the maximum polarization $Q_{\rm r}/I\vert _{\rm max}$ occurs around $r\approx 0.97$, very close to the limb.

Table 3: Model results for a planet at opposition (phase angle $\alpha =0^\circ$) with a semi-infinite Rayleigh-scattering atmosphere. The columns give the single-scattering albedo $\omega$, the geometric albedo $A_{\rm g}$, the disk-integrated radial polarization $\langle Q_{\rm r}/I\rangle$, the line-integrated radial polarization for a line through the disk center, and the maximum radial polarization $Q_{\rm r}(r)/I(r)\vert _{\rm max}$.

Table 3 summarizes key parameters for the different models. The geometric albedos $A_{\rm g}$, which are obtained with an interpolation and integration of the I(r) values are slightly, but systematically, lower by about 0.001-0.002 when compared to the results from Prather (1974). In that work $A_{\rm g}$ was obtained with a sophisticated numerical solution of the radiative transfer equations using a Feautrier technique. For example, the exact value for the maximum geometric albedo for a Rayleigh scattering atmosphere ($\omega =1$) is $A_{\rm g}=0.7975$(Prather 1974), while we obtain only $A_{\rm g}=0.796$. However, we consider the accuracy of our results as sufficient for comparing the measured radial polarization for Uranus and Neptune with simple model results.

The disk-integrated radial polarization $\langle Q_{\rm r}/I\rangle$given in Table 3 is useful for the comparison with our imaging polarimetry of Uranus and Neptune (Table 2). For this we use the I(r)and $Q_{\rm r}(r)$ curves to calculate for a given $\omega$ the ratio

$$\langle Q_{\rm r}/I\rangle = {\int Q_{\rm r}(r)~ r~{\rm d}r \over \int I(r)~ r~{\rm d}r}\cdot$$

The theoretical disk-integrated polarization stays at a high level of $\langle Q_{\rm r}/I\rangle\approx 2.5{-}3.5\%$ for geometric albedos from the maximum of $A_{\rm g}=0.796$ down to about $A_{\rm g}=0.25$.

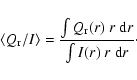
Table 3 also gives the polarization integrated along a radial line (or slit) through the disk center, thus

$$\langle Q_{\rm r}/I\rangle_{\rm line} = {\int Q_{\rm r}(r)~{\rm d}r\over \int I(r)~{\rm d}r}\cdot$$

These values will be useful for long-slit spectropolarimetric studies (see Joos et al. 2005). Likewise, the maximum polarization of the $Q_{\rm r}/I$-curves is given.

9.2 Finite Rayleigh scattering atmospheres with ground albedo

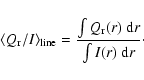
Results for the reflected intensity and polarization for finite Rayleigh scattering atmospheres are tabulated in Coulson et al. (1960). They give values for scattering atmospheres with an optical thickness of $b_\tau=0.02, 0.05, 0.10, 0.15, 0.50$, and 1.0 with ground reflectivity $A_{\rm ground}=0.0, 0.25$, and 0.80. For $A_{\rm ground}=0.25$ and 0.80, the ground behaves like a grey isotropically reflecting surface (according to Lambert's law), while the ground surface is black for $A_{\rm ground}=0.0$.

For a planet at opposition we need the reflected intensity $I(\mu_0,\mu,\phi)$ and polarization $Q(\mu_0,\mu,\phi)$ for $\mu_0=\mu$ and $\phi=180^\circ$. Values that fulfill these conditions are given or can be easily obtained by interpolation from the tables in Coulson et al. (1960) for $\mu=0.1,0.2,0.4,0.6,0.8,0.92$, and 1.0. In order to get well-sampled intensity I(r) and polarization curves $Q_{\rm r}(r)$, a spline interpolation was applied to generate I and Q values for 101 equidistant radius points. Examples of the initial data points and the final interpolation curves are given in Fig. 13, which shows the intensity I(r), the radially polarized flux Q(r), and the normalized polarization Q(r)/I(r) for $b_\tau = 1,0.15$ and $A_{\rm ground}=0.8,0.25,0.0$.

Figure 13: Intensity I ( top), radial polarization $Q_{\rm r}$ ( middle), and normalized polarization $Q_{\rm r}/I$ ( bottom) as functions of disk radius r for a planet at exact opposition (phase angle $\alpha =0^\circ$) with a finite Rayleigh scattering atmosphere. Models with an optical thickness of the Rayleigh-scattering layer of $b_\tau =1.0$ (thick lines) and $b_\tau =0.15$ (thin lines) are shown, each for three ground albedos $A_{\rm ground}=0.8,~0.25,$ or 0.0. The curves were constructed with a spline interpolation from the tabulated values from Coulson et al. (1960) indicated by $\diamond$ ( $A_{\rm ground}=0.8$), $\times$ ( $A_{\rm ground}=0.25$), and $\bigtriangleup$ ( $A_{\rm ground}=0.0$).

Open with DEXTER

It can be seen from the I(r) curves that the limb darkening for finite atmospheres with a high ground albedo $A_{\rm ground}=0.8$ behaves like a high-albedo, semi-infinite Rayleigh scattering atmosphere (see Fig. 12). A limb brightening is present for low ground albedos because relatively more photons are backscattered from the Rayleigh-scattering layer at the limb than at the center of the disk where a larger fraction of photons go down to the dark surface and are absorbed.

It is interesting to note that the polarized flux $Q_{\rm r}(r)$ only depends on the thickness of the Rayleigh scattering layer but not on the ground albedo. Of course the polarized flux is higher for planets with thicker Rayleigh scattering layers. The curve $Q_{\rm r}(r)$ reaches a maximum around r=0.90-0.95 for thick scattering layers and then decreases significantly at the extreme limb. For a thin Rayleigh scattering layer Q(r) shows a steady increase with radius up to at least r=0.995.

Table 4: Parameters for planets at opposition (phase angle $\alpha =0^\circ$) with finite Rayleigh scattering layer (optical thickness $b_\tau$) and ground albedo $A_{\rm ground}$. The tabulated values are the geometric albedo $A_{\rm g}$, the disk-integrated radial polarization $\langle Q_{\rm r}/I\rangle$, the line-integrated radial polarization for a line through the disk center, and the maximum radial polarization $Q_{\rm r}(r)/I(r)\vert _{\rm max}$.

Table 4 summarizes the calculated geometric albedo and polarization parameters for the finite Rayleigh scattering models as in Table 3 for the semi-infinite atmospheres. The values clearly indicate the main dependencies which are also visible in Fig. 13:

• The thickness of the Rayleigh scattering layer $b_\tau$ defines the amount of radially polarized flux $Q_{\rm r}$. In particular, the polarized flux $Q_{\rm r}$ or the product $A_{\rm g}\cdot \langle Q_{\rm r}/I \rangle$ does not depend essentially on the ground albedo.
• A low ground albedo reduces the amount of unpolarized reflected light for a given $b_\tau$. Thus for low $A_{\rm ground}$, the amount of reflected light (geometric albedo $A_{\rm g}$) is low, while the polarization degree $Q_{\rm r}/I$ is enhanced. This effect is particularly strong for planets with thin (small $b_\tau$) Rayleigh-scattering layers.

Table 4 can be supplemented with the limiting $A_{\rm g}$ and polarization values for the extreme cases $b_\tau =0$ and $\infty$. The case $b_\tau=\infty$ is equivalent to the semi-infinite, conservative $(\omega=1)$ Rayleigh scattering atmosphere discussed in the previous section. For $b_\tau =0$, the planet has no scattering atmosphere, and the geometric albedo of an isotropically reflecting surface (according to Lambert's law) is $A_{\rm g}=2/3\cdot A_{\rm ground}$, while the polarization of the reflected light is zero everywhere.

The accuracy of the calculated values given in Table 4 are not very high, since they are derived from curves that are interpolated from only seven tabulated points for I(r) and Q(r). The geometric albedos for $b_\tau=0.5,1$ and $A_{\rm ground}=0.8,0.0$ differ by up to $\pm$1% from those given in Kattawar & Adams (1971). The values for the maximum polarization $Q_{\rm r}/I\vert _{\rm max}$ are also not very accurate due to uncertainties in the interpolation procedure. We guess that the uncertainty is on the order of $Q_{\rm r}/I\vert _{\rm max}\pm 0.2\%$ for those cases where the maximum polarization occurs between r=0.9 and 0.98. For cases where the polarization increases steadily out to the extreme limb r=1, we had to extrapolate from r=0.995 ($\mu=0.1$) to r=1.0 ($\mu=0.0$).

10 Comparison between observations and models

From our observations of Uranus and Neptune, we derived the mean radial polarization $\langle Q_{\rm r}/I\rangle$ for various wavelength filters (Table 2). Furthermore we obtained the flux weighted geometric albedo $A_{\rm g}$ from the spectrophotometry of Karkoschka (1998) for the used filters pass bands (Table 2). In Fig. 14 the derived values $\langle Q_{\rm r}/I\rangle$ and $A_{\rm g}$ for Uranus and Neptune are compared with the semi-infinite and finite Rayleigh-scattering atmosphere models presented in the previous section.

The semi-infinite atmosphere models (Table 3) define points along a curve (solid) in the plot of the geometric albedo vs. averaged radial polarization. The finite atmosphere models from Table 4 produce a grid (diamonds) in this plot. Dashed lines are used to connect the grid points with the same ground albedo $A_{\rm ground}=0.8,0.25,0.0$. Models with the same $b_\tau$ (vertical optical thickness for the Rayleigh scattering layer) are connected with dotted curves defined by $A_{\rm g}\cdot \langle Q_{\rm r}/I\rangle=\rm const$. This product, the polarized flux, is essentially independent of $A_{\rm ground}$. The limiting case $b_\tau =0$ (filled circles) for a planet with a bare Lambert surface is given by $b_\tau=2/3\cdot A_{\rm ground}$ and $\langle Q_{\rm r}/I\rangle=0$.

Figure 14: Geometric albedo $A_{\rm g}$ versus averaged radial polarization for the observations of Uranus (squares) and Neptune ($\times$) and the Rayleigh scattering models. Broad band filters are indicated with R, i, and z, and narrow band filters for Uranus with CH4( $\lambda =729$ nm) and "c'' for continuum ( $\lambda =673$ nm). The semi-infinite Rayleigh scattering models are plotted as triangles connected by a solid line, while the finite models define a grid (diamonds). Grid points with the same ground albedo $A_{\rm ground}=0.8,0.25,0.0$ are connected with a dashed line, and points with the same optical thickness for the Rayleigh scattering layer $b_\tau$ with a dotted curve. From top to bottom the $b_\tau$-curves for 0.50, 0.25 (indicated), 0.15, 0.10, 0.05, and 0.02 are plotted. The limiting case $b_\tau =0$, i.e. a bare Lambert surface, is indicated with filled circles ($\bullet$).

Open with DEXTER

The finite and semi-infinite Rayleigh scattering models are now used as first approximations for the limb polarization of Uranus and Neptune. In addition we considered the constraints on the atmospheric structure from the modeling of the geometric albedo spectrum by Baines & Bergstralh (1986), Baines & Smith (1990), and Sromovsky (2005a,b). The following conclusions can be drawn from the observed limb polarization:

• A large fraction of photons are absorbed in the strong methane absorption bands in the red / near-IR before they can penetrate into deeper layers down to e.g. the cloud level. Only a small fraction of the photons are reflected in the high-altitude atmosphere by Rayleigh scattering, or by haze scattering (see Fig. 3 in Baines & Smith 1990 or Fig. 4 in Sromovsky 2005a). The effective geometric albedo in these bands is obviously low $A_{\rm g}<0.2$. This case can be roughly approximated with a semi-infinite Rayleigh scattering atmosphere with a low single-scattering albedo $\omega\la 0.5$. And indeed, the observations taken in the deepest methane absorptions (lowest effective albedos in Table 2 or Fig. 14), namely the $\lambda =729$ nm-filter and z-band for Uranus and the i- and z-bands for Neptune, are located in the $A_{\rm g}$ vs. $\langle Q_{\rm r}/I\rangle$ plot close to the solid line for the semi-infinite Rayleigh scattering models. The polarization derived from our measurements (Table 2 or Fig. 14) suggests a single-scattering albedo for Rayleigh scattering of about $\omega =0.2{-}0.3$ in the strong methane absorptions.
• In the red continuum, this means in the $\lambda =673$ nm narrow-band filter for Uranus and the R-band for Neptune, the stratosphere and upper troposphere are optically thin. The photons can penetrate deeply into the atmosphere and are reflected from clouds. This corresponds roughly to the Rayleigh-scattering case for a finite layer and an intermediate ground albedo. In the $A_{\rm g}$- $\langle Q_{\rm r}/I\rangle$ plot, the red filter points are not compatible with the semi-infinite Rayleigh-scattering models. The finite Rayleigh-scattering models are more appropriate and indicate an optical thickness of the Rayleigh scattering layer of $b_\tau\approx 0.15$ for Uranus and $b_\tau\approx 0.20$ for Neptune and a ground albedo of about $A_{\rm ground}=0.4$ for both planets.

From this comparison of the derived limb polarization $\langle Q_{\rm r}/I\rangle$with model calculations, it can be concluded that the limb polarization behaves as expected from the simple analytic models.

For the blue spectral region it is expected that Rayleigh scattering is very dominant, because the cross section behaves like $\sigma\propto 1/\lambda^4$. Thus for the blue an approximation with a semi-infinte scattering model again yields a reasonable first approximation; however, this time the single scattering albedo will be high. From this we predict that the limb polarization must be high in the blue for Uranus and Neptune.

11 Discussion and conclusions

11.1 Detection of the limb polarization

In this paper we present disk resolved imaging polarimetry of Uranus and Neptune in the red/near-IR spectral region. Our data show a limb polarization for the first time for both planets, as expected for a Rayleigh-scattering atmosphere. In the literature we found no previous imaging polarimetry which resolved these two planets. The limb polarization in Uranus and Neptune is high and measuring is straightforward with modern imaging polarimeters under sub-arcsecond seeing conditions.

The measured limb polarization for Uranus and Neptune is centro-symmetric at least to a first approximation. This is unlike Jupiter and Saturn where the limb polarization is essentially only present at the poles, but not at the equator (see Gisler & Schmid 2003). The resolution of our observations is not high enough to reveal details of the polarization structure along the limb. However, strong deviations from a centro-symmetric polarization pattern as in Jupiter and Saturn would be easily seen in our data.

Center-to-limb profiles are calculated for the radial Stokes parameter $Q_{\rm r}(r)$ and $Q_{\rm r}(r)/I(r)$. The profiles qualitatively agree with analytic models for Rayleigh-scattering atmospheres. The radial polarization is essentially zero in the disk center due to the symmetry of the scattering geometry. The normalized radial polarization increases outwards and in the seeing halo reaches a maximum between $+0.5\%$ and $+1.7\%$ depending on the planet and the wavelength band. Because a high polarization is only expected very close to the limb, the maximum limb polarization is averaged down by the seeing limited resolution of our observation of Uranus and Neptune.

We introduced the disk-averaged (flux-weighted) radial polarization $\langle Q_{\rm r}/I\rangle$, which characterizes well the strength of the measured limb polarization effect for the two planets. $\langle Q_{\rm r}/I\rangle$ depends on the effective resolution defined by the seeing. We have modeled the atmospheric seeing and derived seeing corrected values for the intrinsic $\langle Q_{\rm r}/I\rangle$ polarization of Uranus and Neptune.

The resulting (seeing corrected) values for the disk-averaged radial polarization $\langle Q_{\rm r}/I\rangle$are $+0.43\%$, $+0.74\%$, and $+0.84\%$ for Uranus in the z-, i- and narrow band $\lambda =673$ nm, respectively, and $+0.66\%$, $+1.08\%$, and $+1.48\%$ for Neptune in the z-, i-, and R-band. Thus, both planets show a higher limb polarization at shorter wavelengths. Overall, the limb polarization is roughly 50% higher in Neptune than in Uranus.

11.2 Comparison with model calculations

We compared our observations with analytic models for semi-infinite (non-conservative) Rayleigh scattering atmospheres and finite Rayleigh scattering atmospheres with ground albedo. These models can explain the measured polarization qualitatively in the different bands for Uranus and Neptune.

• The general tendency for the limb polarization to be higher at shorter wavelengths is caused by the wavelength dependence of the Rayleigh scattering cross section, which increases rapidly towards the blue (like ${\propto} 1/\lambda^4$).
• The polarization in the red continuum, i.e. in the $\lambda =673$ nm-filter for Uranus and R-band for Neptune, is significantly lower than expected for a semi-infinite atmosphere. The relatively low polarization can be explained by a Rayleigh scattering layer above a reflecting, optically thick cloud layer.
• In the strong methane absorption bands in the red and near-IR, the photons are absorbed predominantly before they reach the cloud tops. In this case the polarization can be roughly approximated with a semi-infinite Rayleigh-scattering atmosphere with a low single-scattering albedo $\omega\la 0.5$.

Our comparison with analytic models for the limb polarization provides a rough qualitative analysis. The models consider a strongly simplified atmospheric structure and neglect important processes, such as scattering by haze particles, absorption within a finite Rayleigh scattering layer, or Raman scattering. We expect that much more information will be extracted if the limb polarization measurements are analyzed using sophisticated model calculations for the limb polarization in Uranus and Neptune. Unfortunately, such model calculations do not exist yet. The diagnostic potential of the limb polarization measurements could be particularly high for the investigation of the scattering haze particles in the higher atmosphere.

Thus, we may conclude that limb polarization studies of Uranus and Neptune offer a powerful new tool for the investigation of the atmospheric structure of these two planets.

11.3 Polarization of extra-solar planets

Polarimetry may also provide an important tool for future investigations of extra-solar planets (Schmid et al. 2006; Stam et al. 2004). For planning future polarimetric instruments, we need estimates of the polarization expected in a "typical'' extra-solar planet. For this we have to consider that the best phase angles for extra-solar planet observations lie in the range $\alpha\approx 60^\circ{-}120^\circ$. For these phase angles the apparent separation will be largest, so a faint planet will be easier to detect in the glare of a bright, nearby star.

Currently, observational results on the polarization of planets are only available for solar-system targets. For the giant planets only for Jupiter and Saturn polarimetric data exist for large phase angles. Rough estimates of the disk-averaged (flux-weighted) polarization $\langle Q/I \rangle_{90^\circ}$ for phase angle $\alpha =90^\circ$ can be made from e.g. the R-band maps of Pioneer 10 and 11 (Smith & Tomasko 1984; Tomasko & Dose 1984). For Jupiter we estimate an R-band polarization of $\langle Q/I \rangle_{90^\circ} \approx 10$% for sight lines in the equatorial plane and somewhat higher $\langle Q/I \rangle_{90^\circ} \approx 15$% for polar sight lines, for which one Rayleigh scattering pole is the most visible. The polarization would be about 5% higher in the blue, thus roughly 15% to 20%, depending on the sight line. For Saturn, the polarization for large phase angles is significantly lower than for Jupiter, roughly of the order $\langle Q/I \rangle_{90^\circ} \approx 5$%.

For Uranus and Neptune, polarimetry for phase angles near $\alpha\approx 90^\circ$ is not available. But we can now estimate the polarization $\langle Q/I \rangle_{90^\circ}$ from our limb polarization measurement. For this we use the model results for the polarization of reflecting atmospheres for phase angle $\alpha =90^\circ$ for the scattering parameters derived for Uranus and Neptune from Fig. 14 (the comparison between observed limb polarization and the limb polarization models).

We calculated the disk integrated polarization $\langle Q/I \rangle_{90^\circ}$ for phase angle $\alpha =90^\circ$for the same parameters as for the limb polarization models ( $\alpha =0^\circ$) given in Tables 3 and 4. Our results, which were derived with the Monte Carlo code described in Schmid (1992), are given in Table 5. They are in good agreement with similar calculations by Kattawar & Adams (1971). More sophisticated models for the expected disk-integrated polarization from planetary atmospheres are given in Stam et al. (2004).

For the continuum in the red (R-band, $\lambda_{673}$-filter), the limb polarization for Uranus and Neptune suggest, according to Fig. 14, that a finite Rayleigh scattering atmosphere with a thickness of $b_\tau\approx 0.10 {-} 0.25$ and ground albedo $A_{\rm ground}\approx 0.4$ would be a reasonable first approximation. Kattawar & Adams (1971) have calculated the polarization for $A_{\rm ground}=0.4$ and $b_\tau=0.20$ and obtained a polarization of $\langle Q/I \rangle_{90^\circ}=27.6\%$.

The limb polarization in the strong methane bands of Uranus and Neptune (i- and z-band observations) suggest that a semi-infinite Rayleigh scattering atmosphere with a single scattering albedo of $\omega\approx 0.2{-}0.4$ is a good proxy (Fig. 14). According to Table 5 a very high polarization $\langle Q/I \rangle_{90^\circ}\geq 89\%$ is expected for $\omega\leq 0.4$.

The expectation that the polarization of Uranus and Neptune is high is also supported by a comparison with Jupiter. The limb polarization at a given limb position of Uranus and Neptune is comparable to the limb polarization at the poles of Jupiter. The R-band polarization map of Jupiter from Pioneer 11 for phase angle $\alpha=82^\circ$ shows that the polarization is around 50% for the polar regions (Smith & Tomasko 1984).

Table 5: Polarization at quadrature $\langle Q/I \rangle_{90^\circ}$ (phase angle $\alpha =90^\circ$) for model planets with semi-infinite Rayleigh scattering atmosperes (single scattering albedo $\omega$) and with finite Rayleigh scattering layer (optical thickness $b_\tau$) and ground albedo $A_{\rm ground}$. Results are based on Monte Carlo simulations.

Hence, based on our limb-polarization measurements, the expected polarization of Uranus and Neptune for phase angles $\alpha\approx 90^\circ$ is certainly high, on the order of 25% for the continuum in the R-band and higher in the strong methane absorptions. This suggests that extra-solar planets with atmospheric parameters similar to Uranus and Neptune are well suited for being searched and investigated in the future with polarimetric instruments.

Acknowledgements

We are indebted to the ESO La Silla support team at the 3.6 m telescope for their help with our very special EFOSC2 instrument setup. We are particularly grateful to Oliver Hainaut. We thank Harry Nussbaumer for carefully reading the manuscript. This work was supported by a grant from the Swiss National Science Foundation.

References

• Abhyankar, K. D., & Fymat, A. L. 1970, A&A, 4, 101 [NASA ADS] (In the text)
• Abhyankar, K. D., & Fymat, A. L. 1971, ApJS, 23, 35 [NASA ADS] [CrossRef] (In the text)
• Baines, K. H., & Bergstralh, J. T. 1986, Icarus, 65, 406 [NASA ADS] [CrossRef] (In the text)
• Baines, K. H., & Smith, W. H. 1990, Icarus, 85, 65 [NASA ADS] [CrossRef] (In the text)
• Braak, C. J., de Haan, J. F., Hovenier, J. W., & Travis, L. D. 2002, Icarus, 157, 401 [NASA ADS] [CrossRef] (In the text)
• Chandrasekhar, S. 1950, Radiative Transfer (Oxford: Clarendon Press) (In the text)
• Coulson, K. L., Dave, J. V., & Sekera, Z. 1960, Tables Related to Radiation Emerging from a Planetary Atmosphere with Rayleigh Scattering (Berkeley: Univ. of California Press) (In the text)
• Dollfus, A., & Coffeen, D. L. 1970, A&A, 8, 251 [NASA ADS] (In the text)
• Gisler, D., & Schmid, H. M. 2003, in Solar polarization 3, ed. J. Trujillo Bueno, & J. Sanchez Almeida, ASP Conf. Ser., 307, 58 (In the text)
• Hall, J. S., & Riley, L. A. 1974, in Planets, stars and nebulae studied with photopolarimetry, ed. T. Gehrels (Tucson: University of Arizona Press), 593 (In the text)
• Hall, J. S., & Riley, L. A. 1976, Icarus, 29, 231 [NASA ADS] [CrossRef] (In the text)
• Hansen, J. E., & Hovenier, J. W. 1974, J. Atm. Sci., 31, 1137 [NASA ADS] (In the text)
• Joos, F., Schmid, H. M., Gisler, D., et al. 2005, in Astronomical Polarimetry, ed. A. Adamson et al., ASP Conf. Ser., 343, 189 (In the text)
• Karkoschka, E. 1998, Icarus, 133, 134 [NASA ADS] [CrossRef] (In the text)
• Karkoschka, E. 2001, Icarus, 151, 84 [NASA ADS] [CrossRef] (In the text)
• Kattawar, G. W., & Adams, C. N. 1971, ApJ, 167, 183 [NASA ADS] [CrossRef] (In the text)
• Lunine, J. I. 1993, ARA&A, 31, 217 [NASA ADS] (In the text)
• Michalsky, J. J., & Stokes, R. A. 1977, ApJ, 213, L135 [NASA ADS] [CrossRef] (In the text)
• Prather, M. J. 1974, ApJ, 192, 787 [NASA ADS] [CrossRef] (In the text)
• Rages, K. A., Hammel, H. B., & Friedson, A. J. 2004, Icarus, 172, 548 [NASA ADS] [CrossRef] (In the text)
• Schmid, H. M. 1992, A&A, 254, 224 [NASA ADS] (In the text)
• Schmid, H. M., Beuzit, J.-L., Feldt, M., et al. 2006, in Direct Imaging of Exoplanets, ed. C. Aime, & F. Vakili, IAU Coll., 200 (in press) (In the text)
• Smith, P. H., & Tomasko, M. G. 1984, Icarus, 58, 35 [NASA ADS] [CrossRef] (In the text)
• Sromovsky, L. A. 2005, Icarus, 173, 254 [NASA ADS] [CrossRef] (In the text)
• Sromovsky, L. A. 2005, Icarus, 173, 284 [NASA ADS] [CrossRef]
• Stam, D. M., Hovenier, J. W., & Waters, L. B. F. M. 2004, A&A, 428, 663 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Tinbergen, J., & Rutten, R. 1992, Measuring polarization with ISIS, Users' manual, The Isaac Newton Group of Telescopes (http://www.ing.iac.es/) (In the text)
• Tomasko, M. G., & Doose, L. R. 1984, Icarus, 58, 1 [NASA ADS] [CrossRef] (In the text)
• van de Hulst, H. C. 1980, Multiple Light Scattering, 2nd Volume (New York: Academic Press) (In the text)