A&A 452, 481-485 (2006)
DOI: 10.1051/0004-6361:20052855
H. Hirashita1,2,![]() -
H. Shibai2
-
T. T. Takeuchi3,
-
H. Shibai2
-
T. T. Takeuchi3,![]()
1 - SISSA/International School of Advanced Studies,
via Beirut 4, 34014 Trieste, Italy
2 -
Graduate School of Science, Nagoya University, Furo-cho,
Chikusa-ku, Nagoya, 464-8602, Japan
3 -
Laboratoire d'Astrophysique de Marseille, Traverse du Siphon BP
8, 13376 Marseille Cedex 12, France
Received 10 February 2005 / Accepted 28 February 2006
Abstract
We investigate the possibility of searching for metal-poor
high column density (![]()
![]() )
clouds at
high redshift (z) by using gamma ray burst afterglows.
Such clouds could be related to primeval galaxies that may
cause a burst of star formation. We show that a large part
of hydrogen is in molecular form
in such a high column density environment. Therefore,
hydrogen molecules (H2) rather than hydrogen atoms should
be searched for. Then we show that infrared H2 lines are
detectable for metal-poor (
)
clouds at
high redshift (z) by using gamma ray burst afterglows.
Such clouds could be related to primeval galaxies that may
cause a burst of star formation. We show that a large part
of hydrogen is in molecular form
in such a high column density environment. Therefore,
hydrogen molecules (H2) rather than hydrogen atoms should
be searched for. Then we show that infrared H2 lines are
detectable for metal-poor (![]() 0.01 solar metallicity)
high column density (
0.01 solar metallicity)
high column density (
![]() )
systems at high-z without suffering dust extinction.
The optical properties of dust in infrared could also be
constrained by observations of high column density systems.
Some possible scenarios for
producing high column density systems are finally
discussed in the context of galaxy evolution.
)
systems at high-z without suffering dust extinction.
The optical properties of dust in infrared could also be
constrained by observations of high column density systems.
Some possible scenarios for
producing high column density systems are finally
discussed in the context of galaxy evolution.
Key words: galaxies: evolution - galaxies: ISM - infrared: ISM - ISM: dust, extinction - ISM: lines and bands - ISM: molecules
Intergalactic and interstellar gas is a main component of
baryonic matter, and it occupies most of the volume in
the Universe. Gas with various column densities has been
detected as line absorption of the background quasi-stellar
objects (QSOs). The strong
Ly![]() absorption feature is often
used to identify absorbing clouds, which are
called Ly
absorption feature is often
used to identify absorbing clouds, which are
called Ly![]() clouds. In particular,
if the H I column density is larger
than
clouds. In particular,
if the H I column density is larger
than
![]() ,
the
absorbing system is called damped Ly
,
the
absorbing system is called damped Ly![]() clouds (DLAs) because the continuum of background
QSOs is completely damped by the Ly
clouds (DLAs) because the continuum of background
QSOs is completely damped by the Ly![]() absorption
(e.g., Wolfe et al. 1986).
absorption
(e.g., Wolfe et al. 1986).
So far, the hydrogen column density has been sampled up
to
![]() (in this paper, we show all the
column densities in units of cm-2). It is
difficult to detect systems with higher column
density, since dust severely extinguishes the
background objects. Fall et al. (1989)
show that QSOs behind DLAs tend to be redder than
those without DLAs.
This result strongly suggests that the dust
contained in high
column density systems extinguishes the
background light (but see
Murphy & Liske 2004). If
(in this paper, we show all the
column densities in units of cm-2). It is
difficult to detect systems with higher column
density, since dust severely extinguishes the
background objects. Fall et al. (1989)
show that QSOs behind DLAs tend to be redder than
those without DLAs.
This result strongly suggests that the dust
contained in high
column density systems extinguishes the
background light (but see
Murphy & Liske 2004). If
![]() ,
the effects of extinction
become significant and a large fraction of
absorption systems can be missed
(e.g., Vladilo & Péroux 2005).
,
the effects of extinction
become significant and a large fraction of
absorption systems can be missed
(e.g., Vladilo & Péroux 2005).
Schaye (2001) proposes another possibility
for missing high column density systems. He shows
that a large fraction of hydrogen is in molecular
form if
![]() .
Such
molecular clouds may not be sampled by
Ly
.
Such
molecular clouds may not be sampled by
Ly![]() lines of H I, so it is
necessary to search for molecular hydrogen (H2).
Shibai et al. (2001, hereafter S01)
investigate the observability of H2 in absorption
for high column density systems. They focus on
near-infrared (NIR) vib-rotational lines, because
dust extinction is less severe in the NIR than
in the optical and ultraviolet (UV). Considering
typical QSOs as background sources, they show that
the high column density systems with
an H2 column density of
lines of H I, so it is
necessary to search for molecular hydrogen (H2).
Shibai et al. (2001, hereafter S01)
investigate the observability of H2 in absorption
for high column density systems. They focus on
near-infrared (NIR) vib-rotational lines, because
dust extinction is less severe in the NIR than
in the optical and ultraviolet (UV). Considering
typical QSOs as background sources, they show that
the high column density systems with
an H2 column density of
![]() could be
observed without being extinguished by dust if
the dust-to-gas ratio is less than 1 percent of
the Galactic value.
could be
observed without being extinguished by dust if
the dust-to-gas ratio is less than 1 percent of
the Galactic value.
However, QSOs are usually sampled in the optical wavelength, where dust extinction is severe. Ellison et al. (2001) investigated a sample of radio-selected QSOs and conclude that dust-induced bias in optical samples is small. Therefore, the significance of extinction bias is still being debated. In this paper, we consider the possibility of using gamma-ray burst (GRB) afterglows as background sources. Since GRB samples are defined in a wavelength not affected by dust extinction, we expect less extinction bias in GRB samples than in QSO samples. Indeed some DLAs are found to lie in the sightline of GRBs (e.g., Vreeswijk et al. 2004) and some GRBs are surrounded by high column density gas (e.g., Piro et al. 2005). Therefore, it may be possible to use NIR continua of GRB afterglows to detect NIR H2 lines.
Recently, Inoue et al. (2006) investigated the possibility of detecting the absorption lines originating from protostellar cores by using background GRB afterglows. They find that radio observations of some metal absorption lines of GRB afterglows are useful for detecting high-zprotostellar gas. However, it is still interesting to detect directly H2 because H2 is considered as playing a central role in star formation in metal-poor environments (e.g., Mizusawa et al. 2004). Therefore, in spite of its difficulty, the possibility of detecting IR H2 lines is worth investigating.
Since H2 vib-rotational lines are generally weak,
large infrared (IR) telescopes are necessary. The
strongest vib-rotational H2 lines are normally those
around the wavelength of
![]() m.
Those lines shift to the mid-IR (MIR) regime if we
observe high-z clouds. In MIR, it is essential to
avoid the emissions of both the atmosphere and
telescope. Thus, a cooled space telescope is
ideal. There are indeed suitable future missions planned
currently, such as the
Space Infrared Telescope for Cosmology and Astrophysics
(SPICA)
m.
Those lines shift to the mid-IR (MIR) regime if we
observe high-z clouds. In MIR, it is essential to
avoid the emissions of both the atmosphere and
telescope. Thus, a cooled space telescope is
ideal. There are indeed suitable future missions planned
currently, such as the
Space Infrared Telescope for Cosmology and Astrophysics
(SPICA)![]() .
Herschel
.
Herschel![]() is also a planned space mission in IR (but not cooled),
and the same kind of targets can be accessible if
the background sources are luminous enough.
In NIR (
is also a planned space mission in IR (but not cooled),
and the same kind of targets can be accessible if
the background sources are luminous enough.
In NIR (
![]() m), the
James Webb Space Telescope
(JWST)
m), the
James Webb Space Telescope
(JWST)![]() is more sensitive than the SPICA, and
is appropriate for H2 absorption at
is more sensitive than the SPICA, and
is appropriate for H2 absorption at ![]() .
.
First, in Sect. 2 we explain the method of calculating H2 absorption line luminosity. Our results are shown in Sect. 3, and some relevant physical and observational issues are discussed in Sect. 4. Our conclusions are given in Sect. 5.
We follow S01 for the formulation concerning IR H2 lines. We assume a uniform, cool gas cloud satisfying
![]() ,
where
,
where ![]() is the Boltzmann constant,
is the Boltzmann constant,
![]() the excitation
temperature, h the Planck constant, and
the excitation
temperature, h the Planck constant, and ![]() the
frequency of an H2 line.
the
frequency of an H2 line.
The optical depth of the line absorption,
![]() ,
is estimated as
,
is estimated as
Next, we consider extinction by dust grains,
whose optical depth at the wavelength ![]() is denoted as
is denoted as
![]() .
This
is estimated as
(Hirashita et al. 2005)
.
This
is estimated as
(Hirashita et al. 2005)
Finally, we obtain the absorption line flux with
extinction,
![]() ,
as
,
as
We assume that all the molecular hydrogens are in
the levels J=0, 1 of the vibrational ground
state (v=0), since we are interested in the
clouds whose excitation
temperature is much lower than the excitation
energy. The lines are summarized in S01.
The ortho vs. para ratio
is assumed to be 3:1; i.e.,
![]() and
and
![]() ,
where NJ is the column
density of H2 in the
level J and
,
where NJ is the column
density of H2 in the
level J and
![]() the total
hydrogen column density.
the total
hydrogen column density.
Observationally, it could be convenient to present
the equivalent width, since it is not
sensitive to the line width (or the spectral
resolution). The equivalent width ![]() given in wavelength units
is expressed as
given in wavelength units
is expressed as
![\begin{displaymath}W_\lambda = \frac{\lambda^2}{c}[1-\exp
(-\tau_{\rm line})]\Delta\nu .
\end{displaymath}](/articles/aa/full/2006/23/aa2855-05/img52.gif) |
(4) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2855fig1.eps}
\end{figure}](/articles/aa/full/2006/23/aa2855-05/Timg53.gif) |
Figure 1:
Equivalent width (EW) for various
H2 lines as a function of H2 column density.
The solid, dotted, dashed, and
dot-dashed lines represent the line wavelengths
of
|
| Open with DEXTER | |
The optical depth of dust,
![]() ,
is proportional to the dust-to-gas ratio and to
the hydrogen column density, if we fix
,
is proportional to the dust-to-gas ratio and to
the hydrogen column density, if we fix
![]() as a function of
as a function of ![]() (Eq. (2)), which is taken from
Hirashita et al. (2005).
We adopt the Galactic extinction curve,
which is consistent with
Mathis (1990), unless
otherwise stated. A different extinction curve
is examined in Sect. 4.2.
We assume that the Galactic
dust-to-gas ratio,
(Eq. (2)), which is taken from
Hirashita et al. (2005).
We adopt the Galactic extinction curve,
which is consistent with
Mathis (1990), unless
otherwise stated. A different extinction curve
is examined in Sect. 4.2.
We assume that the Galactic
dust-to-gas ratio,
![]() ,
is
,
is
![]() ,
since we should adopt the
values in Hirashita et al. (2005)
for consistency. We
define the normalized dust-to-gas ratio,
,
since we should adopt the
values in Hirashita et al. (2005)
for consistency. We
define the normalized dust-to-gas ratio,
![]() ,
as
,
as
| (5) |
We focus on GRB afterglows as one of the most
luminous sources in the Universe. If some dense
clouds lie in the line of sight of GRBs, we can
have a chance of detecting these
foreground clouds in absorption. For the flux
of GRB afterglows, we adopt a commonly used model
with synchrotron radiation from a relativistic
shock (Sari et al. 1998;
Ciardi & Loeb 2000). Here we
apply a set of values adopted by
Inoue et al. (2004): a magnetic energy
fraction of
![]() ,
an electron
energy fraction of
,
an electron
energy fraction of
![]() ,
a
spherical shock energy of E=1052 erg, an
ambient gas number density of
,
a
spherical shock energy of E=1052 erg, an
ambient gas number density of
![]() ,
and a power-law index of
the electron energy distribution of p=2.5.
For the timescale, we put t=1/24 day
(1 h), and the observational detection limits
are also calculated with 1-h integration.
,
and a power-law index of
the electron energy distribution of p=2.5.
For the timescale, we put t=1/24 day
(1 h), and the observational detection limits
are also calculated with 1-h integration.
We do not include the redshift dependence of GRB luminosity. GRBs may be brighter at high z than the local Universe (e.g., Lloyd-Ronning et al. 2002; Yonetoku et al. 2004). In this case, detection of high-z absorption lines becomes easier.
We consider a velocity width of
![]() km s-1, motivated by the
future cooled space telescopes, such as
SPICA with
km s-1, motivated by the
future cooled space telescopes, such as
SPICA with
![]() .
Accordingly,
the frequency resolution becomes
.
Accordingly,
the frequency resolution becomes
![]() .
Then,
.
Then,
![]() is
estimated as
is
estimated as
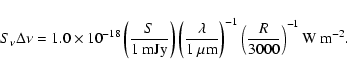 |
(6) |
We note that S01 scale the extinction by Z(metallicity normalized to the solar value). We have
confirmed that if we adopt ![]() ,
the
difference in
,
the
difference in
![]() is less than a factor
of 2. As shown by S01, the 2.12
is less than a factor
of 2. As shown by S01, the 2.12 ![]() m absorption
line is the strongest, and the dust obscuration does
not affect the line detection if
m absorption
line is the strongest, and the dust obscuration does
not affect the line detection if
![]() .
Therefore, we concentrate on
the 2.12
.
Therefore, we concentrate on
the 2.12 ![]() m line with
m line with
![]() in this
section.
in this
section.
As stated by S01, it is quite difficult to detect
absorption lines where optical depth is less than 0.01, since an extremely high signal-to-noise
ratio would be required to detect an absorption
with
![]() .
The H2 column
density that satisfies
.
The H2 column
density that satisfies
![]() is listed in S01 for various lines. For the
2.12
is listed in S01 for various lines. For the
2.12 ![]() m line,
m line,
![]() should be higher than
should be higher than
![]() to satisfy
to satisfy
![]() .
Therefore, if we use the
NIR H2 lines, we should target the absorption
systems with
.
Therefore, if we use the
NIR H2 lines, we should target the absorption
systems with
![]() .
However, we should
note that this condition is dependent on the
line width. The sound speed of H2-rich cold
clouds is generally much less than 100 km s-1. Therefore, if we had a
facility that is sensitive enough with a high
enough resolution,
we could observe an absorption system whose
H2 column density is lower than
.
However, we should
note that this condition is dependent on the
line width. The sound speed of H2-rich cold
clouds is generally much less than 100 km s-1. Therefore, if we had a
facility that is sensitive enough with a high
enough resolution,
we could observe an absorption system whose
H2 column density is lower than
![]() .
.
In Fig. 2, we show the
2.12 ![]() m absorption fluxes as a function of
m absorption fluxes as a function of
![]() for various background fluxes. The typical
detection limit expected for future IR cooled
telescopes such as SPICA is also shown
(
for various background fluxes. The typical
detection limit expected for future IR cooled
telescopes such as SPICA is also shown
(
![]() W m-2 for 5
W m-2 for 5![]() detection with an integration of
detection with an integration of ![]() 1 h;
Ueno et al. 2000; S01) as a
representative observability of future facilities.
With future space missions, high column density
systems with
1 h;
Ueno et al. 2000; S01) as a
representative observability of future facilities.
With future space missions, high column density
systems with
![]() can be
investigated if the background source
luminosity is
can be
investigated if the background source
luminosity is ![]() 10 mJy.
10 mJy.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{2855fig2.eps}\end{figure}](/articles/aa/full/2006/23/aa2855-05/Timg77.gif) |
Figure 2:
The 2.12 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2855fig3.eps}
\end{figure}](/articles/aa/full/2006/23/aa2855-05/Timg79.gif) |
Figure 3:
Observed flux of a gamma-ray burst
afterglow as a function of redshift. The
solid and dotted lines
correspond to the restframe wavelengths of
2.12 and 17 |
| Open with DEXTER | |
In order to show the flux level of GRB afterglows,
we present Fig. 3, which shows
the flux (![]() )
at the restframe wavelengths of
)
at the restframe wavelengths of
![]() m and 17
m and 17 ![]() m (i.e., the
observational wavelengths of
m (i.e., the
observational wavelengths of
![]() m and
m and
![]() m), respectively, where
m), respectively, where
![]() is the redshift of the GRB afterglow.
We observe that the afterglows are more luminous
at
is the redshift of the GRB afterglow.
We observe that the afterglows are more luminous
at
![]() m than at
m than at
![]() m. In reality, we should
observe at
m. In reality, we should
observe at
![]() m or
m or
![]() m, where
m, where
![]() is the redshift of a target absorption line system,
but if
is the redshift of a target absorption line system,
but if
![]() has the same order of
magnitude as
has the same order of
magnitude as
![]() ,
the absorption flux
does not change very much (the dependence on other
parameters assumed in Sect. 2.3 is
larger). Considering that the 2.1
,
the absorption flux
does not change very much (the dependence on other
parameters assumed in Sect. 2.3 is
larger). Considering that the 2.1 ![]() m
absorption line is
stronger than the other lines, observations at
m
absorption line is
stronger than the other lines, observations at
![]() m are effective of tracing
high column density
(
m are effective of tracing
high column density
(
![]() )
systems (see S01 for the other lines).
)
systems (see S01 for the other lines).
The dependence on the dust-to-gas ratio is also
shown for the background flux of 10 mJy
(Fig. 4). The absorption line
fluxes with
![]() ,
0.001, 0.01, and 1,
are examined. We see that if
,
0.001, 0.01, and 1,
are examined. We see that if
![]() ,
we
can detect the NIR H2 line if
,
we
can detect the NIR H2 line if
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{2855fig4.eps}
\end{figure}](/articles/aa/full/2006/23/aa2855-05/Timg89.gif) |
Figure 4:
Same as Fig. 2, but for
various dust-to-gas ratios
( |
| Open with DEXTER | |
Collapsed gas in a dark matter halo may form a disk
because of the initial angular momentum.
If we observe
a GRB in a nearly edge-on disk, we could identify the
disk as a high column density system.
If a galactic disk has a typical circular velocity of 100 km s-1, the typical mass (
![]() )
and radius (
)
and radius (
![]() )
of the disk should be
)
of the disk should be
![]() and
and
![]() kpc if it forms at
kpc if it forms at ![]() (Hirashita et al. 2003). With this
mass and size, the typical hydrogen column density
along the galactic disk is
(Hirashita et al. 2003). With this
mass and size, the typical hydrogen column density
along the galactic disk is
![]()
![]() .
Using the relation
.
Using the relation
![]() ,
where H is the disk thickness,
we obtain
,
where H is the disk thickness,
we obtain
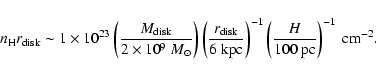 |
(7) |
As stated in Sect. 3, the dust-to-gas
ratio must be ![]() 10-2 times the Galactic value
(i.e.,
10-2 times the Galactic value
(i.e.,
![]() ).
With the typical disk mass
mentioned above (
).
With the typical disk mass
mentioned above (
![]() ), the corresponding
dust mass is
), the corresponding
dust mass is
![]() .
We estimate
the timescale of the dust enrichment up to
this level. Galactic disks observed as DLAs
can be considered as objects with a star formation rate
of
.
We estimate
the timescale of the dust enrichment up to
this level. Galactic disks observed as DLAs
can be considered as objects with a star formation rate
of ![]()
![]() (Hirashita & Ferrara 2005, hereafter HF05).
Using the Salpeter
initial mass function, we obtain the supernova rate of
(Hirashita & Ferrara 2005, hereafter HF05).
Using the Salpeter
initial mass function, we obtain the supernova rate of
![]() 10-3-10-2 yr-1. Assuming that
around 0.5
10-3-10-2 yr-1. Assuming that
around 0.5 ![]() of the dust is formed in a SN
(Todini & Ferrara 2001;
Nozawa et al. 2003), we obtain a typical
dust formation rate of
of the dust is formed in a SN
(Todini & Ferrara 2001;
Nozawa et al. 2003), we obtain a typical
dust formation rate of ![]()
![]() yr-1.
Thus, in
order to accumulate the dust mass estimated above, a
timescale
of
yr-1.
Thus, in
order to accumulate the dust mass estimated above, a
timescale
of
![]() yr is required, which
is much
larger than the lifetime of the GRB progenitors
(Heger et al. 2003).
yr is required, which
is much
larger than the lifetime of the GRB progenitors
(Heger et al. 2003).
It is observationally known that some DLAs have
dust-to-gas ratio of
![]() (Pettini et al. 1997;
Ledoux et al. 2003; HF05).
This observational evidence strongly suggests that
galactic disks with
(Pettini et al. 1997;
Ledoux et al. 2003; HF05).
This observational evidence strongly suggests that
galactic disks with
![]() exist
at high redshift.
exist
at high redshift.
In some starburst galaxies such as the Antennae
(Wilson et al. 2003) and Arp 229
(Casoli et al. 1999), supergiant
molecular complexes are observed. In those galaxies,
molecular gas of ![]()
![]() is concentrated
in a 1-kpc2area. This indicates an H2 column density that is
as high
as
is concentrated
in a 1-kpc2area. This indicates an H2 column density that is
as high
as ![]()
![]() (and a hydrogen
number density of
(and a hydrogen
number density of
![]() cm-3).
Arp 220 seems to have a comparable amount of gas in
more concentrated region
(Sakamoto et al. 1999). Thus, the
H2 column density in a starbursting region can exceed
several times
cm-3).
Arp 220 seems to have a comparable amount of gas in
more concentrated region
(Sakamoto et al. 1999). Thus, the
H2 column density in a starbursting region can exceed
several times
![]() .
This column density meets the requirement for
detecting H2 in absorption.
.
This column density meets the requirement for
detecting H2 in absorption.
HF05 have recently developed a method for calculating
a probable range of
![]() under a given range of
physical quantities concerning ISM. Their assumption
is that
under a given range of
physical quantities concerning ISM. Their assumption
is that
![]() is determined by the equilibrium
between formation on dust grains and destruction by
dissociating photons. The probability density
function of
is determined by the equilibrium
between formation on dust grains and destruction by
dissociating photons. The probability density
function of
![]() ,
,
![]() ,
is calculated by using the
method described in Appendix B of HF05.
As a first guess, we start from the ranges of
quantities derived for H2-detected
DLAs by HF05:
,
is calculated by using the
method described in Appendix B of HF05.
As a first guess, we start from the ranges of
quantities derived for H2-detected
DLAs by HF05:
![]() ,
,
![]() ,
and
,
and
![]() ,
where n is the
number density of gas particles, Tthe gas temperature, and
,
where n is the
number density of gas particles, Tthe gas temperature, and ![]() the
UV interstellar radiation field
intensity normalized to the Galactic value
taken from Habing (1968).
We adopt
the
UV interstellar radiation field
intensity normalized to the Galactic value
taken from Habing (1968).
We adopt
![]() for
the dust-to-gas ratio
(Sect. 3).
In Fig. 5, we
show
for
the dust-to-gas ratio
(Sect. 3).
In Fig. 5, we
show
![]() for various
for various ![]() .
From Fig. 5, we observe that
the gas becomes almost fully molecular for
.
From Fig. 5, we observe that
the gas becomes almost fully molecular for
![]() even if the dust-to-gas ratio
is only 1 percent of
the Galactic value (
even if the dust-to-gas ratio
is only 1 percent of
the Galactic value (
![]() ). This
is consistent with the conclusion
by Schaye (2001) that a large part
of hydrogen is in molecular form at
). This
is consistent with the conclusion
by Schaye (2001) that a large part
of hydrogen is in molecular form at
![]() .
We stress that at
.
We stress that at
![]() H2 formation is
accelerated and possibly leads to a burst of
star formation
(Hirashita & Ferrara 2002).
Therefore, our proposed observation is important
because we will trace the reservoir of gas
clouds that might cause a starburst.
Indeed Iliev et al. (2006) investigate
the fate of those clouds proposed by HF05
and conclude that they
can finally collapse even in the presence of
UV radiation.
H2 formation is
accelerated and possibly leads to a burst of
star formation
(Hirashita & Ferrara 2002).
Therefore, our proposed observation is important
because we will trace the reservoir of gas
clouds that might cause a starburst.
Indeed Iliev et al. (2006) investigate
the fate of those clouds proposed by HF05
and conclude that they
can finally collapse even in the presence of
UV radiation.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2855fig5.eps}
\end{figure}](/articles/aa/full/2006/23/aa2855-05/Timg118.gif) |
Figure 5:
Probability distribution function of the molecular
fraction (
|
| Open with DEXTER | |
Some observations show that the extinction curves of high-z galaxies are different from local ones (Maiolino et al. 2004). Therefore, it is interesting to examine the extinction curve derived for high-z galaxies. We adopt the theoretical curve of Hirashita et al. (2005), and adopt model b (based on the dust production in an unmixed SNe II; Nozawa et al. 2003) of Hirashita et al. (2005), which nearly reproduces the observational high-zextinction curve of Maiolino et al. (2004). This model is labeled as H05b (see Takeuchi et al. 2005 for the NIR part of the extinction curve).
We show the absorption
flux of the 2.12 ![]() m line
for the H05b extinction curve in
Fig. 4, assuming that
the dust-to-gas ratio is 0.01 times the Galactic value.
Comparing the upper and lower dotted lines
(corresponding to the Galactic and H05b
extinction curves, respectively), we observe that
the difference in the extinction curve does not
affect the absorption line flux for
m line
for the H05b extinction curve in
Fig. 4, assuming that
the dust-to-gas ratio is 0.01 times the Galactic value.
Comparing the upper and lower dotted lines
(corresponding to the Galactic and H05b
extinction curves, respectively), we observe that
the difference in the extinction curve does not
affect the absorption line flux for
![]() ,
since the
optical depth of dust is small. However,
the difference in the extinction becomes
significant for
,
since the
optical depth of dust is small. However,
the difference in the extinction becomes
significant for
![]() .
In H05b the system becomes more opaque for
.
In H05b the system becomes more opaque for
![]() than in the Galactic
extinction case.
This sensitive dependence on the extinction
could also be used to
constrain the IR extinction curves at
high z (see also
Vergani et al. 2004).
than in the Galactic
extinction case.
This sensitive dependence on the extinction
could also be used to
constrain the IR extinction curves at
high z (see also
Vergani et al. 2004).
There is no observational constraint on the
number of high column density systems with
![]() .
One simple way to
estimate the number is to extrapolate the
distribution of
.
One simple way to
estimate the number is to extrapolate the
distribution of ![]() sampled up to
sampled up to
![]() ,
although
Vladilo & Péroux (2005) argue
that the distribution should not be
extrapolated in the range of column densities
not sampled by the observation.
After correcting the
distribution for dust extinction,
Vladilo & Péroux (2005)
indicate that
,
although
Vladilo & Péroux (2005) argue
that the distribution should not be
extrapolated in the range of column densities
not sampled by the observation.
After correcting the
distribution for dust extinction,
Vladilo & Péroux (2005)
indicate that
![]() ,
where
,
where
![]() represents the number of absorbers along
a random line of sight with hydrogen column
densities between
represents the number of absorbers along
a random line of sight with hydrogen column
densities between ![]() and
and
![]() and redshift paths
between X and
and redshift paths
between X and
![]() (e.g., Péroux et al. 2003).
By assuming
(e.g., Péroux et al. 2003).
By assuming
![]() with
with
![]() (Vladilo & Péroux 2005),
we obtain
(Vladilo & Péroux 2005),
we obtain
![]() at
at
![]() .
At z=2,
.
At z=2,
![]() ,
and if we take the
interval of
,
and if we take the
interval of ![]() as
as ![]()
![]() ,
we obtain
the number of absorbers in a random line of
sight as
,
we obtain
the number of absorbers in a random line of
sight as ![]() 10-2.8. Therefore, around 600 lines of sight are needed to detect
a high column density object. If a large
part of those sources are favorable for
H2 formation as suggested in
Sect. 4.1,
we can detect H2 lines every
10-2.8. Therefore, around 600 lines of sight are needed to detect
a high column density object. If a large
part of those sources are favorable for
H2 formation as suggested in
Sect. 4.1,
we can detect H2 lines every ![]() 600 GRBs.
600 GRBs.
For example, the sample of
Schmidt (2001) consists of 1391 GRBs
in a period of 5.9 yr. Their analysis indicates
that about 500 GRBs are around
![]() .
Therefore,
it is possible that about 100 GRBs are
identified around
.
Therefore,
it is possible that about 100 GRBs are
identified around ![]() per year. Therefore,
we could find 0.2 GRBs
associated with high column density systems
per year. If we consider
an improvement of the sensitivity in the future,
we expect a larger number.
per year. Therefore,
we could find 0.2 GRBs
associated with high column density systems
per year. If we consider
an improvement of the sensitivity in the future,
we expect a larger number.
In this paper, we have investigated the possibility
of detecting IR H2 absorption lines from
dust-poor high column density (
![]() )
clouds at high-z. The H2 molecule is a unique
tracer of high column density clouds, because
hydrogen is considered to be in a molecular form
even at
extremely low dust-to-gas ratios (
)
clouds at high-z. The H2 molecule is a unique
tracer of high column density clouds, because
hydrogen is considered to be in a molecular form
even at
extremely low dust-to-gas ratios (
![]() ,
where
,
where ![]() is the dust-to-gas ratio normalized
to the Galactic value)
(Sect. 4.1). We have shown that if
is the dust-to-gas ratio normalized
to the Galactic value)
(Sect. 4.1). We have shown that if
![]() ,
we can observe H2 absorption lines
of gas whose column density is
,
we can observe H2 absorption lines
of gas whose column density is
![]() .
In particular,
if
.
In particular,
if
![]() ,
clouds with
,
clouds with
![]() are accessible
(Sect. 3; Fig. 4).
Since missions in the near future such as
SPICA will access GRB
afterglows up to
are accessible
(Sect. 3; Fig. 4).
Since missions in the near future such as
SPICA will access GRB
afterglows up to ![]() in the IR regime, the
search for metal-poor (or dust-poor) galaxies at
in the IR regime, the
search for metal-poor (or dust-poor) galaxies at
![]() is an important scientific target for
IR telescopes in the near future
(Sect. 4.3).
We should note that some bright GRBs at high-zcan be utilized to trace higher-z primeval galaxies.
is an important scientific target for
IR telescopes in the near future
(Sect. 4.3).
We should note that some bright GRBs at high-zcan be utilized to trace higher-z primeval galaxies.
Acknowledgements
We are grateful to A. Ferrara, C. Péroux, P. Petitjean, and T. Nakamura for stimulating discussions. We acknowledge several helpful comments of the anonymous referee. H.H. and T.T.T. have been supported by the Research Fellowship of the Japan Society for the Promotion of Science for Young Scientists.