A&A 452, L7-L10 (2006)
DOI: 10.1051/0004-6361:20065186
LETTER TO THE EDITOR
D. J. Wu1 - L. Yang1,2
1 - Purple Mountain Observatory, 2 West Beijing Road, Nanjing 210008, PR China
2 -
Graduate School of Chinese Academy of Sciences, Beijing 100039, PR China
Received 13 March 2006 / Accepted 13 April 2006
Abstract
Context. Some recent observations of the solar corona suggest that the heavy ions undergo an anisotropic (mainly across the magnetic field) and mass-dependent energization.
Aims. In this work, we investigate the nonlinear interaction of heavy ions with kinetic Alfvén waves, in particular, their energization in the nonlinear kinetic Alfvén waves.
Methods. Based on a three-component plasma model including electrons, protons, and heavy ions, a localized nonlinear structure of kinetic Alfvén wave is presented. In the nonlinear wave, the heavy ions are energized in the cross-field and field-aligned by the perpendicular polarization and the parallel acceleration of the wave electric field.
Results. It is found that the ion cross-field energization depends on its mass and abundance in the same way that the velocity is proportional to the mass-charge ratio and decreases with the abundance ratio. On the other hand, the ion field-aligned energy is proportional to the charge, but is free of the mass and abundance. In the low abundance case (<10%), in particular, the minor heavy ions have strongly anisotropic temperature as well as are hotter and flow faster than protons. The resulting ion-proton temperature ratio is proportional to the mass number and the square of the mass-charge ratio, and the ion perpendicular-parallel temperature ratio is proportional to the cube of the mass-charge ratio.
Conclusions. This anisotropic and mass-dependent energization mechanism by kinetic Alfvén waves for ions can be potentially important for understanding the microphysics of the energization of minor heavy ions observed in the solar corona.
Key words: acceleration of particles - plasmas - waves - Sun: corona
Remote observations with the UVCS (Ultraviolet Coronagraph Spectrometer) on board SOHO (Solar
and Heliospheric Observatory) show that heavy ions such as O5+ and Mg9+ have experienced
preferential cross-field heating, causing strong temperature anisotropy
![]() ,
and
are hotter and flow faster than protons in the inner heliosphere (Kohl et al. 1997; Li et al. 1998;
Esser et al. 1999; Cranmer et al. 1999; Marsch & Tu 2001).
A popular explanation for the ion energization across the ambient magnetic field is based on the
ion-cyclotron damping of high-frequency Alfvén waves injected into the base of the solar corona
(Marsch & Tu 2001; Ofman et al. 2002; Hong et al. 2004),
in which the wave dissipation range is formed by the high-frequency waves
with frequencies close to the local ion gyrofrequency (Hollweg & Isenberg 2002).
The ion-cyclotron heating scheme, however, is not free of difficulty (Voitenko & Goossens 2004a, 2005a,b). Recently, in situ observations
from the Cluster and FAST spacecrafts show that the low-frequency dispersive Alfvén waves with short
cross-field wavelengths, called Kinetic Alfvén Wave (KAW), can be responsible for the cross-field
energization of ions, as well as for the field-aligned energization of electrons that drive bright aurora
(Wygant et al. 2002; Chaston et al. 2003, 2004, 2005).
On the other hand, recently theoretical work also shows that KAWs can efficiently produce the both
electron heating in bright coronal loops (Wu & Fang 1999) and in dense coronal plumes (Wu & Fang 2003) and acceleration in auroral plasmas (Wu & Chao 2003, 2004a).
,
and
are hotter and flow faster than protons in the inner heliosphere (Kohl et al. 1997; Li et al. 1998;
Esser et al. 1999; Cranmer et al. 1999; Marsch & Tu 2001).
A popular explanation for the ion energization across the ambient magnetic field is based on the
ion-cyclotron damping of high-frequency Alfvén waves injected into the base of the solar corona
(Marsch & Tu 2001; Ofman et al. 2002; Hong et al. 2004),
in which the wave dissipation range is formed by the high-frequency waves
with frequencies close to the local ion gyrofrequency (Hollweg & Isenberg 2002).
The ion-cyclotron heating scheme, however, is not free of difficulty (Voitenko & Goossens 2004a, 2005a,b). Recently, in situ observations
from the Cluster and FAST spacecrafts show that the low-frequency dispersive Alfvén waves with short
cross-field wavelengths, called Kinetic Alfvén Wave (KAW), can be responsible for the cross-field
energization of ions, as well as for the field-aligned energization of electrons that drive bright aurora
(Wygant et al. 2002; Chaston et al. 2003, 2004, 2005).
On the other hand, recently theoretical work also shows that KAWs can efficiently produce the both
electron heating in bright coronal loops (Wu & Fang 1999) and in dense coronal plumes (Wu & Fang 2003) and acceleration in auroral plasmas (Wu & Chao 2003, 2004a).
This KAW can be created when an obliquely propagating Alfvén wave is affected by the electron
temperature (
![]() for
for ![]() )
and inertia (
)
and inertia (
![]() for
for ![]() ),
where
),
where
![]() is the wavenumber,
is the wavenumber,
![]() the ratio of the electron thermal
speed
the ratio of the electron thermal
speed
![]() to the Alfvén speed
to the Alfvén speed ![]() ,
,
![]() the ion
acoustic gyroradius,
the ion
acoustic gyroradius,
![]() the electron inertial length,
the electron inertial length,
![]() the mass ratio of electron to proton, and
the mass ratio of electron to proton, and
![]() the proton gyrofrequency (Hasegawa & Uberoi
1982). Since the pioneering theoretical work of Hasegawa & Chen (1975), KAW has been
an increasingly interesting topic in both experimental and theoretical studies. In the experimental, KAW
has been observed both in space (Louarn et al. 1994; Chaston et al. 1999) and the laboratory
(Leneman et al. 1999; Kletzing et al. 2003) plasmas. Also, theories of linear and nonlinear
KAW in electron-proton plasmas have been studied extensively and been applied to various fields from
laboratory to space and astrophysical plasmas, since the parallel component of its electric field
the proton gyrofrequency (Hasegawa & Uberoi
1982). Since the pioneering theoretical work of Hasegawa & Chen (1975), KAW has been
an increasingly interesting topic in both experimental and theoretical studies. In the experimental, KAW
has been observed both in space (Louarn et al. 1994; Chaston et al. 1999) and the laboratory
(Leneman et al. 1999; Kletzing et al. 2003) plasmas. Also, theories of linear and nonlinear
KAW in electron-proton plasmas have been studied extensively and been applied to various fields from
laboratory to space and astrophysical plasmas, since the parallel component of its electric field ![]() can
play an important role in the particle energization of magnetized plasmas (see e.g. Wu & Fang 1999,
2003; Wu & Chao 2003, 2004a,b; Stasiewicz et al. 2000).
can
play an important role in the particle energization of magnetized plasmas (see e.g. Wu & Fang 1999,
2003; Wu & Chao 2003, 2004a,b; Stasiewicz et al. 2000).
In a recent work based on a three-component (electrons, protons, and heavy ions) plasma model, we studied the interaction of heavy ions with linear KAWs (Yang & Wu 2005). In this letter, we go on to investigate the nonlinear interaction of heavy ions with KAWs based on the three-component model, in particular, the energization of minor heavy ions in nonlinear KAWs. The result shows that the ion cross-field energy (or i.e. temperature) is proportional to its mass number and the square of its mass-charge ratio and decreases with its background abundance ratio. On the other hand, the ion field-aligned energy is proportional to its charge, but free of its mass and abundance. In consequence, the heavy ions have strongly anisotropic temperature as well as are hotter and flow faster than protons. We anticipate that this novel energization mechanism is potentially important for explaining observations of the anisotropic and mass-dependent energization of minor heavy ions in the solar corona.
In a three-component plasma (electrons, protons, and heavy ions) magnetized by a magnetic field
![]() along the z axis, the equation set governing the dynamics of KAWs consists of
the following (Wu et al. 1995, 1996; Wu & Chao 2004b):
(i) the continuity equations of electrons, protons, and heavy ions
along the z axis, the equation set governing the dynamics of KAWs consists of
the following (Wu et al. 1995, 1996; Wu & Chao 2004b):
(i) the continuity equations of electrons, protons, and heavy ions
| (1) | |||
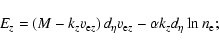 |
(2) |
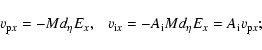 |
(3) |
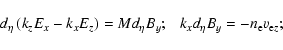 |
(4) |
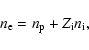 |
(5) |
Integrating the above equation set by using the localized boundary conditions for a solution with a localized
solitary structure:
![]() ,
,
![]() ,
,
![]() ,
,
![]() for
for
![]() ,
where
,
where
![]() is the ion abundance ratio in the background plasma (i.e. the unperturbed
ion number density in units of the unperturbed electron density). Limiting the attention on the low-
is the ion abundance ratio in the background plasma (i.e. the unperturbed
ion number density in units of the unperturbed electron density). Limiting the attention on the low-![]() case of
case of
![]() ,
one can obtain the nonlinear equation of the electron density in the nonlinear KAW as
follows (Wu et al. 1995; Wu & Chao 2004b):
,
one can obtain the nonlinear equation of the electron density in the nonlinear KAW as
follows (Wu et al. 1995; Wu & Chao 2004b):
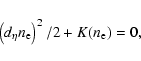 |
(6) |
![\begin{displaymath}K(n_{\rm e})={n_{\rm e}^6\over k_x^2 M_z^2} \left[{\left(n_{\...
...M_z^2n_{\rm e}\right)\over 6n_{\rm e}^3}
+I(n_{\rm e})\right],
\end{displaymath}](/articles/aa/full/2006/22/aa5186-06/img50.gif) |
(7) |
| (8) |
![$\displaystyle \displaystyle \frac{\sqrt{\left[\left(A_{\rm i}-1\right)n_{\rm e}...
...}-A_{\rm i}\right]^2+4N_{\rm i0}n_{\rm e}}}{2Z_{\rm i}\left(A_{\rm i}-1\right)}$](/articles/aa/full/2006/22/aa5186-06/img56.gif) |
(9) |
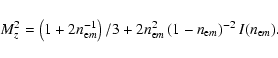 |
(10) |
Without loss of generality, we take one-time ionized oxygen ![]() as a special example of heavy ions.
For
as a special example of heavy ions.
For ![]() ,
the parameters
,
the parameters
![]() and
and
![]() and the Sagdeev potential
and the Sagdeev potential
![]() versus
versus ![]() is
plotted in Fig. 1 for the cases of the background ion abundance ratio
is
plotted in Fig. 1 for the cases of the background ion abundance ratio
![]() ,
0.5, and 0.8, and
the extremum
,
0.5, and 0.8, and
the extremum
![]() has been used. From Fig. 1, the wave also can be accompanied by a dip
density soliton in the three-component plasma with the low-
has been used. From Fig. 1, the wave also can be accompanied by a dip
density soliton in the three-component plasma with the low-![]() of
of
![]() ,
similar with that
in an electron-proton plasma (Wu et al. 1995, 1996). Figure 2 shows the
parallel phase speed Mz of the wave versus the density amplitude,
,
similar with that
in an electron-proton plasma (Wu et al. 1995, 1996). Figure 2 shows the
parallel phase speed Mz of the wave versus the density amplitude,
![]() for the cases of the perturbed ion abundance ratio
for the cases of the perturbed ion abundance ratio
![]() ,
0.5, and 0.8. From Fig. 2, one can
see that the higher ion abundance ratio causes the wave to propagate more slowly because the higher
ion abundance ratio implies that the plasma is more massive.
,
0.5, and 0.8. From Fig. 2, one can
see that the higher ion abundance ratio causes the wave to propagate more slowly because the higher
ion abundance ratio implies that the plasma is more massive.
![\begin{figure}\par\includegraphics[width=7.1cm,clip]{5186fig1.eps}\end{figure}](/articles/aa/full/2006/22/aa5186-06/Timg76.gif) |
Figure 1:
The Sagdeev potential
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=7.1cm,clip]{5186fig2.eps}\end{figure}](/articles/aa/full/2006/22/aa5186-06/Timg77.gif) |
Figure 2:
The parallel phase speed Mz: solid, dashed, and dotted lines represent
the cases of the background ion abundance
|
| Open with DEXTER | |
In the field-aligned direction, the energization of charged particles is caused simply by direct acceleration
of the parallel electric field Ez so that
![]() ;
that is, the field-aligned energization
depends on the field-aligned electric potential of the nonlinear KAW
;
that is, the field-aligned energization
depends on the field-aligned electric potential of the nonlinear KAW ![]() and on the particle charge
q, but free of its mass. On the other hand, in the cross-field, the particle cannot be accelerated directly
by the perpendicular field Ex because of its Lamor cyclotron motion. In consequence, the cross-field
energization depends on its gyrofrequency, hence on its mass. The
field-aligned and cross-field velocities
of particles in the KAW can be obtained from Eq. (1) as follows:
and on the particle charge
q, but free of its mass. On the other hand, in the cross-field, the particle cannot be accelerated directly
by the perpendicular field Ex because of its Lamor cyclotron motion. In consequence, the cross-field
energization depends on its gyrofrequency, hence on its mass. The
field-aligned and cross-field velocities
of particles in the KAW can be obtained from Eq. (1) as follows:
| (11) | |||
![\begin{figure}\par\includegraphics[width=6.9cm,clip]{5186fig3.eps}\end{figure}](/articles/aa/full/2006/22/aa5186-06/Timg95.gif) |
Figure 3:
Plots of the maximal velocities of electrons, protons, and ions in the wave versus the background
ion abundance ratio
|
| Open with DEXTER | |
From Fig. 3, one can find that the proton cross-field velocity is lower than the electron field-aligned velocity
by a factor of
![]() in the case of a low ion abundance ratio of
in the case of a low ion abundance ratio of
![]() ,
where
,
where ![]() is the
KAW propagating angle. As a qualitative estimation, let us consider the quasi-perpendicular propagating
case of the KAW in a low-
is the
KAW propagating angle. As a qualitative estimation, let us consider the quasi-perpendicular propagating
case of the KAW in a low-![]() plasma, where
plasma, where
![]() (Wu & Chao 2004b).
This gives us the following velocity relation:
(Wu & Chao 2004b).
This gives us the following velocity relation:
![]() .
In consideration of the smallness of the perpendicular scale of KAWs, we can imagine that these localized
nonlinear structures of KAWs distribute randomly in the magnetized plasma. In particular, their moving
directions in the perpendicular plane (i.e. the kx axis) are random such that the motion of the ions energized
by them manifests itself as a random motion or turbulence. This indicates that the heavy ions have an effective
perpendicular temperature
.
In consideration of the smallness of the perpendicular scale of KAWs, we can imagine that these localized
nonlinear structures of KAWs distribute randomly in the magnetized plasma. In particular, their moving
directions in the perpendicular plane (i.e. the kx axis) are random such that the motion of the ions energized
by them manifests itself as a random motion or turbulence. This indicates that the heavy ions have an effective
perpendicular temperature
![]() .
On the other hand, according to the above scenario for the particle energization in the KAW, the
ion parallel energy (or i.e. temperature)
.
On the other hand, according to the above scenario for the particle energization in the KAW, the
ion parallel energy (or i.e. temperature)
![]() .
In consequence, the ion-to-proton
temperature ratio and the ion temperature anisotropy can be estimated by, respectively,
.
In consequence, the ion-to-proton
temperature ratio and the ion temperature anisotropy can be estimated by, respectively,
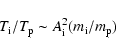 |
(12) |
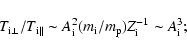 |
(13) |
The KAWs have been extensively observed by satellites (e.g. Freja, FAST, Polar, Cluster) in space plasmas (Louarn et al. 1994; Chaston et al. 1999; Stasiewicz et al. 2000) and have been shown to be in close relationship with the particle energization of the auroral plasma (Wygant et al. 2002; Chaston et al. 2003, 2005). Alfvén waves are one of most popular low-frequency electromagnetic fluctuations in the lower solar atmosphere and can be converted into KAWs when propagating outward due to the inhomogeneity, the parameter instability, or the nonlinear wave-wave coupling (see e.g. Shukla & Sharma 2001; Shukla et al. 2004; Voitenko et al. 2003; Voitenko & Goossens 2004b), although they cannot be observed directly in the current techniques of astronomic observations. We suggest they are what produce the preferential heating and temperature anisotropy of heavy ions observed by UVCS/SOHO in the corona (Kohl et al. 1997; Li et al. 1998; Esser et al. 1999; Cranmer et al. 1999; Marsch & Tu 2001).
In this letter we have investigated the nonlinear interaction of heavy ions with KAWs based on the three-component plasma model. It is shown that the ion energization is mass-dependent and anisotropic in which the ion cross-field energy is proportional to its mass and the square of its mass-charge ratio and the anisotropy (i.e. the perpendicular-parallel temperature ratio) to the cube of its mass-charge ratio.
As a special example, we took one-time ionized oxygen as the heavy ion species and estimated
the ion-to-proton temperature ratio and the ion temperature anisotropy. It is straightforward
to generalize these results to other cases including other ion species, such as He+,
O5+, Mg9+, and so on. For example, the temperature ratio of O5+ to
proton
![]() ,
that is, the O5+ temperature
,
that is, the O5+ temperature
![]() K for the proton
temperature of
K for the proton
temperature of
![]() K, and the temperature anisotropy of O5+,
K, and the temperature anisotropy of O5+,
![]() .
These showed satisfy the
requirement of the high ion cross-field temperatures (like O5+ and Mg9+) observed
by UVCS/SOHO in the corona.
.
These showed satisfy the
requirement of the high ion cross-field temperatures (like O5+ and Mg9+) observed
by UVCS/SOHO in the corona.
We anticipate that the results presented in this letter will help us understand the microphysics of the anisotropic and mass-dependent energization of the minor heavy ions observed recently in the corona.
Acknowledgements
This project has been supported by the NSFC under Grants No. 10425312, 10373026, 40574065, and 10333030.