A&A 452, 113-117 (2006)
DOI: 10.1051/0004-6361:20064811

GRB 030406 - an extremely hard burst outside of the INTEGRAL[*] field of view

R. Marcinkowski1,2 - M. Denis1 - T. Bulik3,4 - P. Goldoni5,6 - Ph. Laurent5,6 - A. Rau7,8


1 - Space Research Center, Bartycka 18a, 00716 Warsaw, Poland
2 - IPJ, 05-400 Swierk/Otwock, Poland
3 - Astronomical Observatory, Warsaw University, Aleje Ujazdowskie 4, 00478 Warsaw, Poland
4 - Nicolaus Copernicus Astronomical Center, Bartycka 18, 00716 Warsaw, Poland
5 - SAp CEA, 91911 Gif-sur-Yvette, France
6 - UMR 7164, 11 place M. Berthelot, 75231 Paris, France
7 - Max-Planck Institute for extraterrestrial Physics, Giessenbachstrasse, 85748 Garching, Germany
8 - Division of Physics, Mathematics, and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA

Received 8 August 2005 / Accepted 5 January 2006

Abstract
Using the IBIS Compton mode, the INTEGRAL satellite is able to detect and localize bright and hard GRBs, which happen outside of the nominal INTEGRAL field of view. We have developed a method of analyzing such INTEGRAL data to obtain the burst location and spectra. We present the results for the case of GRB 030406. The burst is localized with the Compton events, and the location is consistent with the previous Interplanetary Network position. A spectral analysis is possible by detailed modeling of the detector response for such a far off-axis source with an offset of 36.9 $^\circ$. The average spectrum of the burst is extremely hard: the photon index above 400 keV is -1.7, with no evidence of a break up to 1.1 MeV at a 90% confidence level.

Key words: gamma rays: burst

1 Introduction

The INTEGRAL satellite detects gamma-ray bursts (GRBs) in two different ways: for a small number of events that fall in the field of view (FoV) of the imager IBIS (Ubertini et al. 2003) and of the spectrometer SPI (Vedrenne et al. 2003), INTEGRAL provides accurate positions ($\sim $2 arcmin) for rapid ground- and space-based follow-up observations (Mereghetti et al. 2003). A significantly larger number of GRBs occurs outside of the FoV of the two instruments. These bursts can be monitored by the SPI anti-coincidence system: SPI-ACS (Rau et al. 2005; von Kienlin et al. 2003). Up to now, the localization of the bursts that happened outside of the field of view was only possible with the aid of the 3rd IPN (Hurley 1997).

In this paper we show that for some of these bursts it is also possible to perform a more detailed localization analysis using the Compton mode of IBIS, provided that the burst is sufficiently strong and spectrally hard.

We present the capabilities of the Compton mode using an example of GRB 030406, a burst that was detected outside of the INTEGRAL field of view. GRB 030406 has been detected by SPI-ACS on-board INTEGRAL as well as by Ulysses, Konus, and Mars Odyssey (Hurley et al. 2003). It was a long burst lasting $\sim $65 s. Ulysses reported the fluence of $1.3\times 10^{-5}$ erg cm-2 (25-100 keV). The observations by the three satellites yielded an estimate of the position centered on RA(2000 $) = \rm 19^h1^m43.0^s$, Dec(2000 $) = -68^\circ4'39.4''$, with the 3$\sigma$ error-box of 77 square arcminutes.

In Sect. 2 we describe the Compton mode of IBIS INTEGRAL and demonstrate its localization capabilities. In Sect. 2.2 we present the spectral analysis of GRB 030406 while Sect. 3 contains the discussion.

   
2 Observations and data analysis

The IBIS telescope is an imaging instrument on-board the INTEGRAL satellite with a coded mask (Goldwurm et al. 2003). There are two detection layers in the detector plane ISGRI (Lebrun et al. 2003) and PICsIT (Labanti et al. 2003). ISGRI is an array ( $128\times128$) of pixels made of semiconductive CdTe, sensitive to photons between 15 keV and $\sim $1 MeV. ISGRI works in photon-by-photon mode. PICsIT having the same detection area as ISGRI, is an array of  $64\times64$ CsI scintillators, sensitive between $\sim $170 keV and 15 MeV located 94 mm below ISGRI. PICsIT (usually) makes light curves of the whole detector by making histograms of all events (so called Spectral Timing Mode). ISGRI and PICsIT can act as a Compton telescope, registering photons that are scattered in one and absorbed in the other detector. The coincidence time window is a parameter programmable on-board and it was set to $\sim $4 microseconds at the time of GRB 030406. The Compton mode is sensitive between 200 keV and $\sim $5 MeV.

There is a 3 m long collimator on top of the detector unit. The walls of the collimator are made of lead and act as a shield to photons with energies up to $\approx$200 keV. For the geometrical reasons the optical depth of the shield is smaller for photons arriving at large angles. Thus hard photons from off-axis sources can pass through the shield and reach the detector. In particular off axis GRBs may be detectable in IBIS.

Thanks to the Compton mode data we were able to make successful, independent burst localization. Including information from the ISGRI data we have performed burst spectral analysis.


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{4811fig1.eps} \end{figure} Figure 1: Lightcurve of GRB 030406 seen by the INTEGRAL sub-systems: SPI-ACS, IBIS/ISGRI, IBIS Compton and IBIS/PICsIT. The gray areas: precursor, peak and tail correspond to the time regions chosen for spectral analysis. Time = 0 corresponds to the SPI-ACS trigger time at UTC 2003-04-06, 22:42:03.23.
Open with DEXTER

2.1 Compton imaging and localization

We have analyzed the Compton mode count rate during the GRB 030406. The burst profile in the Compton mode follows clearly the profiles seen by SPI-ACS, ISGRI and PICsIT (Fig. 1). The gamma ray burst was detected in the Compton mode at the level of 30$\sigma$ reaching $\sim $400 cts s-1 in the second peak (average background amount to $\sim $100 cts s-1). The Compton mode telemetry did not suffer the data gaps in contrast to ISGRI.

The Compton mode provides us with the following information:

-
energy deposits in ISGRI ($E_{\rm I}$) and PICsIT ($E_{\rm P}$);

-
position of the detection in ISGRI ( $x_{\rm I},y_{\rm I}$) and PICsIT ( $x_{\rm P},y_{\rm P}$);

-
timing of the event.

The two positions provide the information about the direction of the scattered photon. The two energies provide the Compton scatter angle $\theta_C$, which cosine, in case of the forward scatter, is given by:

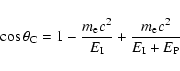
\begin{displaymath}\cos \theta_{\rm C} = 1 - \frac{m_{\rm e} c^2}{E_{\rm I}} + \frac{m_{\rm e} c^2}{E_{\rm I}+E_{\rm P}} \end{displaymath}

where $m_{\rm e} c^2$ is the electron rest energy. Given the angle  $\theta_{\rm C}$ and the direction after scattering we obtain a ring in the sky which contains the possible directions of the primary photon. In case of a point source all the rings cross at the location of the source. For a given observation a collection of such rings provides a Compton map of the sky S. In real observations the Compton map S consists of the source signal and the background B.

In the case of GRB 030406 we selected the Compton events from the begin of the peak up to the end of the tail, which consist of a 9.75 s time interval, see Fig. 1. For these events a Compton map Sij of the sky was calculated using the method described above with the angular resolution of one degree. In order to determine the background we used the pre-burst data divided into 200 intervals lasting 9.75 s each. For each interval we calculated the all-sky Compton map and we determined the mean background Bij and its variance Vij in each pixel.

The map $\sigma_{ij}$ was obtained by dividing the difference between the Compton map Sij and the background Bij by the map of the square root of variance of the noise in each pixel  $\sqrt{V_{ij}}$. We present the map of significance  $\sigma_{ij}$ in Fig. 2. The largest deviations from the noise are $\sim $20, and the position of the pixels with the strongest deviation is consistent with the IPN location.


  \begin{figure} \par\includegraphics[width=16cm,clip]{4811fig2.eps}\end{figure} Figure 2: All-sky Compton map taken during the second peak of the GRB 030406. The inset shows the dashed area around the GRB 030406 centered on the IPN position.
Open with DEXTER

In order to obtain an estimate of the accuracy of such positioning we used two approaches: the maximum likelihood and the Monte-Carlo. In the first approach we assumed that the probability density that the true position lies in a given pixel i,j is proportional to the likelihood function:

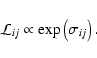
\begin{displaymath}{\cal L}_{ij} \propto \exp\left( {\sigma_{ij}} \right). \end{displaymath}

After normalizing such probability density we found the region containing 68% of the probability corresponding to the $\sim $$3.5^\circ$ radius.

In the second approach we used the IBIS mass model (Laurent et al. 2003) to extract the signal from simulated GRB events inserted into stretches of data with experimental background. We then performed the identical data analysis procedure and found the localization of such simulated bursts. We have analyzed 127 simulated bursts, and found the cumulative distribution of the distance between the actual burst position and the estimate obtained in our analysis. This distribution is presented in Fig. 3. The 1$\sigma$ region (containing 68% of the cases), corresponds to the accuracy of $\sim $4$^\circ$, and the 2$\sigma$ is constrained to $6.5^\circ$. The two methods lead to consistent results.

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{4811fig3.eps} \end{figure} Figure 3: The normalized cumulative distribution of the offset of best fit localizations of simulated bursts obtained in the Monte Carlo simulation: 68% of the events are localized within $\sim $$4^\circ $ of the actual position.
Open with DEXTER

   
2.2 Spectral analysis

In addition to the Compton mode GRB 030406 has been also detected by ISGRI and PICsIT. There are only two energy channels in the PICsIT data stream therefore we have decided to model together the Compton and ISGRI data, neglecting the PICsIT.

We have divided the data into three time intervals marked in gray in Fig. 1 as: precursor, peak and tail. The division of the main peak of the burst into the peak and tail was a consequence of the ISGRI data loss during the burst due to telemetry gap.

We first ran Monte Carlo simulations using the mass model of the INTEGRAL spacecraft to generate the detector response matrices (DRM) for a source located at the position of the burst. The DRM matrices were obtained for the ISGRI and Compton sub-systems. For all of them we have taken into account the influence of the IBIS VETO system, the energy thresholds in each ISGRI pixel and PICsIT crystal, the ISGRI noisy pixels, the failed ISGRI pixels and PICsIT crystals as well as the ISGRI and PICsIT energy resolution.

Table 1: Results of the spectrum fits for three time ranges of the GRB 030406. All the errors are at the $1\sigma $ level.


  \begin{figure} \mbox{\hspace*{2.5cm}{\em precursor}\hspace*{5cm}{\em peak}\hspac... ...4811fig9.eps}\hspace{0.7cm}\includegraphics[angle=0]{4811fig7.eps}} \end{figure} Figure 4: GRB 030406 spectrum fits to the combined ISGRI and Compton mode data. Upper panels show count spectra, while lower corresponding  $\nu {\rm F}_\nu $ spectra. Broken power law model was fitted in each case: to the precursor data ( left), to the peak part data ( center) and to the tail ( right). See text for details.
Open with DEXTER

The Compton data were binned into six energy channels covering the range from 200 to 2500 keV. The ISGRI data spans from 24 to  50 keV which partially overlaps the Compton energy range and were binned into seven channels. The analysis of the pre-burst data with the correction for the varying dead time effect and exposures provided an estimate of the background. This background was subtracted from the total count spectrum in each channel.

We used the standard XSPEC 11.2 (Arnaud 1996) to fit the data. For each time region we tried to fit several models: single power law, broken power law, and a non physical model of single black-body. The single power law model never fitted the combined ISGRI and Compton data. The broken power law fits the data very well in all analyzed regions: precursor, peak and tail. In additional fit we have allowed for different normalization of ISGRI and Compton components for peak region, taking to account two facts related with dead time influence:

-
during precursor and tail the count rate grows with factor about 1.5 for ISGRI and Compton mode, while during peak, these factors reach 2.5 for ISGRI and 4 for Compton mode,

-
the width of the burst peak, $\approx$1 s, is much shorter than the INTEGRAL dead time effect calculation bin, equal 8 s.
Except meaningful decreasing of the reduced $\chi ^2$ we have not found significant evidence of changing fitted parameters. Results of all fits are presented in Table 1. The broken power law fits and the residuals are presented in the top panels of Fig. 4.

We note that the precursor and the tail region can also be fitted with black body spectra with temperatures $\approx$100 keV. This is due to the fact that at high energies the count rates fall steeply. The lower panels of Fig. 4 show the deconvolved $\nu F_\nu$ spectra in each time interval. The precursor and tail spectra have peak power around 300-500 keV, while the $\nu F_\nu$ spectrum in the peak seems to rise all the way into high energies.

The high energy index of $\beta=-1.7 \pm 0.3$ for peak may imply the absence of a peak in the source power spectrum $\nu F_\nu$ in the range covered by our data, i.e. up to 2.5 MeV. In order to estimate the lower limit on such a break compatible with the data we conducted the following analysis. We fit the Compton data with a broken power law with fixed high energy index:

 \begin{displaymath}f(E) = N \left\{ \begin{array}{cl} E^\beta & E < E_{\rm br... ...eak}^{\beta+4} E^{-4} & E > E_{\rm break}. \end{array}\right. \end{displaymath} (1)

In this initial fit the break energy was constant $E_{\rm break}=3000$ keV. This value was chosen high enough not to influence the power law part of the fit. For this fit we obtained $\chi^2=0.55$ with 4 degrees of freedom. We used the standard model parameter estimation (Lampton et al. 1976) to calculate the values of $\chi ^2$ corresponding to 90% and 99% confidence regions, which are respectively $\Delta \chi^2=8.3$and $\Delta \chi^2=13.8$. Then keeping all the parameters but $E_{\rm break}$ constant we looked for the lowest value of  $E_{\rm break}$ for which $\chi ^2$ was equal to the above values. We present the results in Fig. 5. We obtained $E_{\rm break}>1110$ keV at 90% confidence level and $E_{\rm break}>880$ keV at 99% confidence level.


  \begin{figure} \par\includegraphics[width=8cm,clip]{4811fig0.eps} \end{figure} Figure 5: Confidence limits on $E_{\rm cutoff}$: the solid line represents the $\chi ^2$ as a function of $E_{\rm cutoff}$ using the model of Eq. (1). We present the $\chi ^2$ values corresponding to the 90% and 99% confidence levels.
Open with DEXTER

   
3 Discussion

We have shown that the IBIS Compton mode is able to detect and localize GRBs outside of the field of view of the INTEGRAL telescopes. We have found that the position of GRB 030406 obtained using the Compton mode technique is consistent with the IPN localization. The position accuracy has been estimated using the maximum likelihood and the Monte Carlo method. The results of both methods are consistent and the 1$\sigma$ errors are $\sim $$4^\circ $.

Given the position of the burst we computed the DRM for a source outside of the field of view of the satellite at this particular location. Using the DRM we analyzed the Compton data, along with the ISGRI detection and fitted the spectrum with a broken power law in the range from 50 keV to 3 MeV.

The peak spectrum is very hard; in the $\nu F_\nu$ the low energy index below 400 keV rises with the index $\approx$+3.5 and above this energy it is still positive $\approx$+0.3. We note that this spectrum is an average over the time interval of 2.8 s around the maximum, thus the spectrum of the maximum might have even been harder since the burst spectra usually evolve from hard in the peaks to soft in their tails. We do not see any evidence that the $\nu F_\nu$ spectrum peaks below 1.1 MeV. Thus, there is a hint of existence of bursts with the peak of $\nu F_\nu$ spectrum above the distribution shown by Mallozzi et al. (1995) which truncates at $\sim $1 MeV for the bright BATSE bursts.

Such hard spectra have already been seen by BATSE - Preece et al. (2000) present the distribution of the low and high energy spectral indexes for a sample of 156 bright bursts. Both, the low and the high energy spectral indexes of GRB 030406 lie in the upper tails of the distributions of the spectral indexes presented by Preece et al. (2000). It is therefore clear that the spectrum of this particular burst is in clear contradiction with the synchrotron model of GRBs (Katz 1994; Tavani 1995), which predicts that there is a strict upper limit on the low energy spectral index of $-{2\over 3}$ (Preece et al. 1998). The low energy spectral slope is consistent within the error bars with the jitter synchrotron model of GRBs (Medvedev 2000). We note that a detailed study of time resolved spectra (Ghirlanda et al. 2003) showed that the low energy spectral slopes are large $\sim $0.5-1 at the rising parts of several bursts.

The value of Ep of GRB 030406 - the peak of the $\nu F_\nu$ spectrum lies above 1.1 MeV. It should be noted that this is on the high end of the Amati and Ghirlanda relations (Amati et al. 2002; Ghirlanda et al. 2004). If this relation holds and we assume that the peak energy is larger than the 90% lower limit of 1100 keV, then the isotropic radiated energy for GRB 030406 is larger than  $(6{-}20)\times 10^{53}$ erg, where the uncertainty stems from the inaccuracy of the Amati relation. Hard bursts are therefore very energetic and may come from a population residing at high redshifts.

In summary, we confirm that the INTEGRAL in the Compton mode can detect hard GRBs. The localization accuracy is a few degrees. The GRB spectra can be studied in the range from $\sim $200 keV to $\sim $3 MeV depending on the location of the burst in the instrument coordinates. Further study of such hard bursts detectable in the INTEGRAL Compton mode may yield potential candidates of high redshift burst and also test the limits of validity if the Amati relation. Our rough estimations of the Compton mode capabilities give 2-3 detections of such bursts per year. They are consistent with BATSE results and seem to be confirmed by the other detections (Marcinkowski et al. in preparation). Finally, we note that analysis of Compton data in principle allows to determine the polarization. A study of of the polarization sensitivity of the IBIS Compton mode is currently under way (Laurent et al. in preparation).

Acknowledgements
This research was supported by the KBN grants 2 P03D 001 25, 1 P03D 003 27 and PBZ-KBN-054/P03/2001.

References

 
Copyright ESO 2006