A&A 452, 343-346 (2006)
DOI: 10.1051/0004-6361:20054608
Quasi-periodic modulation of solar and stellar flaring emission by magnetohydrodynamic oscillations in a nearby loop
V. M. Nakariakov - C. Foullon - E. Verwichte - N. P. Young
Physics Department, University of Warwick, Coventry,
CV4 7AL, UK
Received 30 November 2005 / Accepted 20 February 2006
Abstract
We propose a new model for quasi-periodic modulation of
solar and stellar flaring emission. Fast magnetoacoustic
oscillations of a non-flaring loop can interact with a nearby
flaring active region. This interaction occurs when part of the
oscillation situated outside the loop reaches the regions of steep
gradients in magnetic field within an active region and produces
periodic variations of electric current density. The modulation
depth of these variations is a few orders of magnitude greater than
the amplitude of the driving oscillation. The variations of the
current can induce current-driven plasma micro-instabilities and
thus anomalous resistivity. This can periodically trigger magnetic
reconnection, and hence acceleration of charged particles, producing
quasi-periodic pulsations of X-ray, optical and radio emission at
the arcade footpoints.
Key words: Sun: flares - Sun: oscillations - Sun: corona - stars: flare - stars: oscillations - stars: coronae
Quasi-periodic pulsations (QPP) in radio, optical, X-ray emission
generated in solar flares have been known for several decades (see,
Aschwanden 2004; Nakariakov & Verwichte 2005, for recent reviews).
QPP with similar parameters have been detected in stellar flares
(see, e.g. Mathioudakis et al. 2003; Mitra-Kraev et al. 2005, and references therein). Typical
periods of QPP are in the range of a few ms to several min. This
wide range of periods indicates that several different physical
processes may be responsible for the generation of QPP. Periods
longer than a few seconds are associated with magnetohydrodynamic
(MHD) oscillations of coronal loops (e.g. Rosenberg 1970; Zaitsev &
Stepanov 1975; Roberts et al. 1984; and the above cited reviews).
More precisely, periodicities in this range coincide with the
theoretical estimations of the transverse and longitudinal travel
times of acoustic and fast (or Alfvén) waves in coronal loops.
Recently, this interpretation has been supported by direct,
spatially resolved observations of various modes of MHD oscillations in the EUV and radio bands. The observational discoveries include standing kink, sausage and longitudinal modes.
Periods of the standing modes are determined by the ratios of the
loop lengths and characteristic speeds of the modes. Also, shorter
periods have been registered and shown to be associated with
propagating MHD waves guided by loops (Roberts et al. 1984;
Nakariakov et al. 2004).
Normally, the relative amplitudes of the coronal MHD waves observed
directly in the EUV and in the visible light bands are less than ten percent. On the other hand, QPP often detected in the microwave and
X-ray bands have much deeper modulation, sometimes of a hundred percent. A typical solar flare with QPP, observed in the hard X-ray
band, is shown in Fig. 1, demonstrating a periodicity of a few min and deep modulation of the emission. A question arises as to whether X-ray and microwave QPP are of the same nature as the MHD waves and oscillations directly observed in solar coronal structures
and, if the answer is positive, more questions follow, as to what is
responsible for the observed deep modulation and as whether it is
connected with the electron acceleration process.
There have been several mechanisms proposed for the explanation of
the X-ray and microwave QPP. In particular, dynamic models of
magnetic reconnection predict that the processes of tearing
instability and coalescence of magnetic islands occur iteratively,
leading to an intermittent or impulsive bursty energy release and
particle acceleration (e.g., Kliem et al. 2000). Tajima et al.
(1987) demonstrated the possibility of oscillatory regimes in
coalescence of current carrying loops. However, MHD oscillations
remain the most attractive paradigm for QPP, because of the simple
geometrical mechanisms (resonant or dispersive) for the creation
of the periodicity and because of the vast direct observational
evidence of these oscillations in coronal structures.
Brown & Hoyng (1975) developed a betatron mechanism for QPP: the
electron acceleration happens in a slowly vibrating magnetic
bottle and the spectrum of the non-thermal electrons varies
according to the vibrations. Zaitsev & Stepanov (1982) suggested
a model for flaring QPP, based upon the modulation of the mirror
ratio in a magnetic trap situated in the loop near the initial
flare energy release by sausage oscillations. This would lead to
the periodic escape of the particles from the trap downward toward
the loop footpoints and the subsequent precipitation of the
particles at the footpoints, causing QPP.
Asai et al. (2001) proposed another acceleration
modulation mechanism, based upon the periodic modulation of the
distance between two slow shocks at the magnetic reconnection site
by an MHD oscillation in a loop located under the site.
In some observed cases, it is possible to determine the spatial
structure of QPP and confirm that it is indeed connected with an MHD mode of the flaring coronal structure (e.g., the global sausage mode observed by Nakariakov et al. 2003). However, in
other cases, the geometrical sizes of X-ray and microwave loops
are very different from that required for the explanation of QPP
observed in them in terms of the MHD oscillations. Recently,
Foullon et al. (2005) analysed 10 min QPP in flares observed with
RHESSI (Reuven Ramaty High Energy Spectroscopic Imager) and other
instruments and suggested that, in the analysed case, QPP were
likely to be caused by kink mode oscillations in a magnetically-linked large loop.
Here, we present a model which can explain the coupling of
oscillations in nearby loops with QPP of flaring energy release. We
suggest that periods of X-ray and microwave QPP observed in a flaring loop or at its footpoints are produced by MHD oscillations
or propagating fast wave trains in another loop situated
nearby, which is not necessarily magnetically linked with the
flaring arcade. In the model, the MHD oscillations are not
considered to be responsible for the flaring energy release itself,
but play the role of periodic triggering, which modulates its
efficiency. Thus, we separate the process and location of the
flaring energy release on the one hand, from an MHD resonator which
is responsible for the generation of the periodicity on the other hand.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4608fig1.eps} \end{figure}](/articles/aa/full/2006/22/aa4608-05/Timg2.gif) |
Figure 1:
A typical hard X-ray (25-300 keV) solar flare with quasi-periodic
pulsations, observed in full disk measurements by RHESSI on the 19th of January,
2005. The event is associated with a flare of class X1.3 (peaking at 08:22 UT,
as seen by GOES 1-8 Å). |
| Open with DEXTER |
Coronal loops are known to support several MHD modes (e.g.
Nakariakov & Verwichte 2005):
e.g. kink, sausage and longitudinal modes, which have different
phase speeds, dispersion and symmetry of perturbations. As the
side boundaries of the loop
are open (the boundary conditions at the loop surface are the
continuity of the perturbation of the total pressure and transverse
displacement), MHD modes perturb the plasma not only inside the loop
but also in the external medium. In leaky modes this
external part of the mode propagates outside the loop, while the
external part of trapped modes is evanescent. The penetration depth
of a mode into the external medium is determined by physical
parameters in the loop and by its period. For example, in a typical
EUV loop (of length 200 Mm, with radius 1 Mm, Alfvén speed of 1000 km s-1 and density enhancement of a factor 2-3), the penetration
depth of kink modes, both standing (with a period of about 6 min)
and propagating (with a period of about, say, 10 s), is about 2 Mm.
For sausage modes this value is even larger and growing when the
longitudinal phase speed approaches the external Alfvén speed at a cut-off. These estimations demonstrate that an MHD mode of a loop can interact with other coronal structures which are situated at some distance from the oscillating loop.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{4608fig2.eps} \end{figure}](/articles/aa/full/2006/22/aa4608-05/Timg3.gif) |
Figure 2:
A sketch of the mechanism for the generation of
quasi-periodic pulsations of solar and stellar flaring emission. The cool (shaded)
loop experiences fast
magnetoacoustic oscillations (e.g., kink or sausage mode). A segment of the oscillating loop is situated nearby a flaring arcade. An external evanescent or leaking part of the
oscillation can reach magnetic null points in the arcade,
inducing quasi-periodic modulations of the electric current density.
The resulting current driven plasma micro-instabilities are known to cause anomalous resistivity, which triggers magnetic reconnection. This periodically accelerates
particles, which follow the field lines and precipitate in the
dense atmosphere, causing quasi-periodic emission in radio, optical and X-ray
bands. |
| Open with DEXTER |
In the following, we shall assume that there is a null-point
magnetic non-uniformity near the oscillating loop (see
Fig. 2), of much smaller size than the length of
the loop. In this case the properties of MHD modes of the loop, as a global phenomenon, are still determined by the whole loop and are
not significantly affected by the magnetic non-uniformity. The
external part of transverse oscillations looks, from the point of
view of the neutral point, as an incoming fast magnetoacoustic wave
with the period prescribed by parameters of the oscillating loop.
This effect can be produced by any fast mode - kink,
sausage or flute - as any of them produces a significant
perturbation of the loop boundary.
![\begin{figure}
\par\includegraphics[width=7.85cm,clip]{4608fig3.eps}\end{figure}](/articles/aa/full/2006/22/aa4608-05/Timg4.gif) |
Figure 3:
Time evolution of the maximum electric current density in the vicinity of a 2D magnetic neutral point. The current is generated by a harmonic fast magnetoacoustic wave with period of 5 time units, coming towards the neutral point. The initial relative amplitude of the wave is 1.5%. The plasma 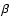 is finite. The normalising values are the magnetic field strength and the Alfvén speed at the domain boundary, and the characteristic spatial scale of the field
inhomogeneity.
is finite. The normalising values are the magnetic field strength and the Alfvén speed at the domain boundary, and the characteristic spatial scale of the field
inhomogeneity. |
| Open with DEXTER |
Recently, McLaughlin & Hood (2004, 2005) studied the interaction
of an aperiodic fast magnetoacoustic pulse with
two-dimensional single and double X-type neutral points and found
that, in the vicinity of a neutral point, the pulse amplitude
experiences amplification while its transverse wavelength
significantly decreases. This leads to an increase of the electric
current density associated with the pulse, which experiences an exponential growth up to a few orders of magnitude near the neutral point (see their Fig. 3).
Developing the studies of McLaughlin & Hood (2004, 2005) we have
performed a simple 2D numerical simulation of the interaction of a periodic fast magnetoacoustic wave with a magnetic neutral
point, with the use of Lare2d code (Arber et al. 2001). The plasma
temperature is taken to be uniform, the plasma-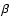 is equal to 0.02 at the domain boundary. The normalising values are the magnetic
field strength and the Alfvén speed at the domain boundary, and
the characteristic spatial scale of the field inhomogeneity. A
harmonic perturbation of the transverse component of the velocity is
generated at the boundary of the computational domain. The induced
fast magnetoacoustic wave propagates across the field, towards the
neutral point. Without the wave, the magnetic configuration is
force-free and the electric current is absent. The curl of the
magnetic field perturbations in the fast wave induces an electric
current. The decrease of the Alfvén speed in the vicinity of the
neutral point leads to the decrease of the wavelength, increasing
the current density. Because of the 2D structuring, the wave is
refracted towards the neutral point and hence focussed. For a single
fast pulse, this effect is described in detail by McLaughlin &
Hood (2004). Finite
is equal to 0.02 at the domain boundary. The normalising values are the magnetic
field strength and the Alfvén speed at the domain boundary, and
the characteristic spatial scale of the field inhomogeneity. A
harmonic perturbation of the transverse component of the velocity is
generated at the boundary of the computational domain. The induced
fast magnetoacoustic wave propagates across the field, towards the
neutral point. Without the wave, the magnetic configuration is
force-free and the electric current is absent. The curl of the
magnetic field perturbations in the fast wave induces an electric
current. The decrease of the Alfvén speed in the vicinity of the
neutral point leads to the decrease of the wavelength, increasing
the current density. Because of the 2D structuring, the wave is
refracted towards the neutral point and hence focussed. For a single
fast pulse, this effect is described in detail by McLaughlin &
Hood (2004). Finite 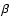 effects, included in our model, do not
change this effect qualitatively. The non-uniformity in the Alfvén speed and in the components of the magnetic field causes a complicated pattern of wave interference. In the vicinity of the
neutral point, there are steep gradients in the perturbations of the
magnetic field and, consequently, a build-up of high electric current.
effects, included in our model, do not
change this effect qualitatively. The non-uniformity in the Alfvén speed and in the components of the magnetic field causes a complicated pattern of wave interference. In the vicinity of the
neutral point, there are steep gradients in the perturbations of the
magnetic field and, consequently, a build-up of high electric current.
The time dependence of the maximum current density near the neutral
point, observed in the simulations, is shown in Fig. 3 (cf. Fig. 1). The periodicity of the curve is prescribed
by the driver, while the amplitude is much higher. For the
parameters used in the simulation, the modulation depth reaches 30%
for an initial wave amplitude of 1.5%.
The presence of a weak longitudinal magnetic field (perpendicular to
the plane of the neutral point) does not qualitatively change this
result. More detailed results on the fast wave interaction with a neutral point will be published elsewhere. Independent of these
results, our simulations clearly demonstrate that the periodicity in
the coming fast waves is efficiently transmitted into the periodic
modulation of the current, which builds up along the separatrices.
The energy of the incoming fast waves and hence the energy of the
built-up current is tiny, less than the energy of a nanoflare (e.g.,
a loop segment of length 10 Mm and radius 1 Mm, filled by a plasma
with the concentration 1010 cm-3, oscillating with the
amplitude 20 km s-1, has the energy of about 1024 erg). Thus, the
periodic modulation of the current cannot on its own explain
observed QPP. However, the electric current is known to induce
efficiently plasma micro-instabilities of various kinds, and hence
produce anomalous resistivity in the region of the current
concentration. Since the characteristic times of micro-instabilities
are normally shorter than the times of MHD processes (e.g. Benz
2002), the generation of the anomalously high resistivity follows
the variations of the current almost instantly. The anomalous
resistivity is a popular ingredient of the fast magnetic
reconnection theory, as it can efficiently trigger flaring energy
release (e.g. Yokoyama & Shibata 1994; see, also Priest & Forbes
2000 for a review). Consequently, the periodic variation of the
electric current at the vicinity of an X-point can cause periodic
triggering of reconnection, producing QPP.
The proposed model links QPP in flaring light curves with fast
magnetoacoustic oscillations in a coronal loop situated near the
flare site. We have demonstrated that the linkage can be carried out
by fast magnetoacoustic perturbations of the medium external to the
oscillating loop, in the form of an evanescent or leaky part of the
oscillating mode. Thus, QPP are prescribed by the period of the
oscillation, which can have periods from a few seconds (in the case
when the oscillation is caused by a propagating fast wave train) to
several minutes (in the case of the global kink mode, cf. Foullon
et al. 2005). For typical relative amplitudes of solar coronal
oscillations, of a few percent, the interaction of the evanescent or
leaky "tails'' of the oscillations with a magnetic neutral
point at the flare site is shown to produce quasi-periodic
variations of the electric current density, with relative amplitudes
reaching up to 30%. When the current variations exceed the
threshold of some current driven micro-instability, the
current-generated anomalous resistivity can trigger reconnection
energy release. As the current is periodically modulated, this can
generate quasi-periodic pulsations of electron acceleration. Hence,
the "external'' periodicity can be found in light curves of
flaring emission produced by precipitating electrons. Here, we do
not consider details of either the reconnection energy release or
particle acceleration at all, restricting our attention to the ideal
MHD part of the problem and to the qualitative discussion of the
proposed mechanism only.
Recent spatially resolved observations (e.g. Grigis & Benz 2005)
demonstrate that the 3D structure of hard X-ray QPP is quite
complicated. In particular, while the integral light curve contains
clear QPP, different bursts (or maxima of the QPP) are coming from
different loop footpoints of the flaring arcade. This finding can be
easily explained by the proposed model. The fast magnetoacoustic
wave front which triggers magnetic reconnection is necessarily
affected by local inhomogeneities of the Alfvén speed. As a result, the wave front becomes non-planar, possibly even filamented,
with one or several tongues stretched towards the regions of the
decreased Alfvén speed - e.g. the null points. The fast wave can
then reach only certain sites along the arcade. In turn, footpoints
of these sites, which are distributed parallel to the axis of the
arcade, become highlighted by the emission. The physical conditions
in the part of the arcade affected by the triggered reconnection
would not necessarily allow for another reconnection. But the next
reconnection event may be triggered by the next wave period
elsewhere along the arcade and will result in the observed spatial
structure of footpoint flaring.
Here, we have discussed only one possible mechanism
to link the incoming fast waves and the modulation of the flaring
X-ray and microwave emission: the periodic triggering of magnetic
reconnection by a fast wave through the periodic switching on of the
anomalous resistivity. The proposed mechanism does not exclude other
possible mechanisms for the modulation. In particular, the fast wave
can modulate the distance between the slow shocks in the model of
Asai et al. (2001). Moreover, nonlinear steepening of the fast wave
in the vicinity of a neutral-point (see, e.g. Landi et al. 2005) can
provide an efficient electron acceleration mechanism without
reconnection.
Acknowledgements
We would like to thank T.D. Arber, B. Dennis, V.F. Melnikov and L. Ofman for helpful discussions, and E. Kontar for attracting our
attention to the event on 19/01/2005. V.M.N. acknowledges support
of a Royal Society Leverhulme Trust Senior Research Fellowship;
V.M.N., E.V. and N.P.Y. acknowledge the support from PPARC.
- Arber, T. D.,
Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, J.
Comp. Phys., 171, 151 [NASA ADS] (In the text)
- Asai, A., et al. 2001,
ApJ, 562, L103 [NASA ADS] [CrossRef] (In the text)
- Aschwanden, M. J.
2004, Physics of the Solar Corona (Berlin: Springer Praxis
Books)
(In the text)
- Benz, A. O. 2002,
Plasma Astrophysics: Kinetic Processes in Solar and Stellar Coronae
(Dordrecht: Kluwer)
(In the text)
- Brown, J. C., &
Hoyng, P. 1975, ApJ, 200, 734 [NASA ADS] [CrossRef] (In the text)
- Foullon, C., Verwichte,
E., Nakariakov, V. M., & Fletcher, L. 2005, A&A, 440,
L59 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Grigis, P. C., &
Benz, A. O. 2005, ApJ, 625, L143 [NASA ADS] [CrossRef] (In the text)
- Kliem, B.,
Karlický, M., & Benz, A. O. 2000, A&A, 360, 715 [NASA ADS] (In the text)
- Landi, S., Velli, M.,
& Einaudi, G. 2005, ApJ, 624, 392 [NASA ADS] [CrossRef] (In the text)
- Mathioudakis, M.,
Seiradakis, J. H., Williams, D. R., et al. 2003, A&A, 403,
1101 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Mitra-Kraev, U.,
Harra, L. K., Williams, D. R., & Kraev, E. 2005, A&A, 436,
1041 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- McLaughlin, J. A.,
& Hood, A. W. 2004, A&A, 420, 1129 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- McLaughlin, J. A.,
& Hood, A. W. 2005, A&A, 435, 313 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Nakariakov, V. M.,
& Verwichte, E. 2005, Living Rev. Solar Phys., 2, 3 [NASA ADS].
URL(05/07/2005): http://www.livingreviews.org/lrsp-2005-3
(In the text)
- Nakariakov, V. M.,
Melnikov, V. F., & Reznikova, V. E. 2003, A&A, 412, L7 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Nakariakov, V. M.,
Arber, T. D., Ault, C. E., et al. 2004, MNRAS, 349, 705 [NASA ADS] [CrossRef] (In the text)
- Priest, E. R., &
Forbes, T. G. 2000, Magnetic Reconnection: MHD Theory and
Applications (Cambridge: Cambridge Univ. Press)
(In the text)
- Roberts, B., Edwin,
P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef] (In the text)
- Rosenberg, H. 1970,
A&A, 9, 159 [NASA ADS] (In the text)
- Tajima, T., Sakai, J.,
Nakajima, H., et al. 1987, ApJ, 321, 1031 [NASA ADS] [CrossRef] (In the text)
- Yokoyama, T., &
Shibata, K. 1994, ApJ, 436, L197 [NASA ADS] [CrossRef] (In the text)
- Zaitsev, V. V., &
Stepanov, A. V. 1975, Issled. Geomagn. Aeron. Fiz. Solntsa, 37,
3 (In the text)
- Zaitsev, V. V., &
Stepanov, A. V. 1982, Sov. Astron. Lett., 8, 132 [NASA ADS] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4608fig1.eps} \end{figure}](/articles/aa/full/2006/22/aa4608-05/Timg2.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{4608fig2.eps} \end{figure}](/articles/aa/full/2006/22/aa4608-05/Timg3.gif)
![\begin{figure}
\par\includegraphics[width=7.85cm,clip]{4608fig3.eps}\end{figure}](/articles/aa/full/2006/22/aa4608-05/Timg4.gif)