A&A 452, 51-61 (2006)
DOI: 10.1051/0004-6361:20054479
E. Semboloni1 - Y. Mellier1,2 - L. van Waerbeke3 - H. Hoekstra4 - I. Tereno1,6 - K. Benabed1,2 - S. D. J. Gwyn4 - L. Fu1 - M. J. Hudson7 - R. Maoli1,5 - L. C. Parker7
1 - Institut d'Astrophysique de Paris, UMR7095 CNRS, Université
Pierre & Marie Curie, 98bis boulevard Arago, 75014 Paris, France
2 - Observatoire de Paris, LERMA, 61 avenue de l'Observatoire,
75014 Paris, France
3 - University of British Columbia, Department of Physics and
Astronomy, 6224 Agricultural Road, Vancouver, B.C. V6T 1Z1, Canada
4 - Department of Physics and Astronomy, University of
Victoria, Victoria, B.C. V8P 5C2, Canada
5 - Department of Physics, University La Sapienza, Pl. A. Moro 2,
00185, Roma, Italy
6 - Departamento de Fisica, Universidade de Lisboa, 1749-016 Lisboa,
Portugal
7 - Department of Physics, University of Waterloo, Waterloo ON N2L 3G1, Canada
Received 5 November 2005 / Accepted 31 January 2006
Abstract
We present the first cosmic shear measurements obtained from
the T0001 release of the Canada-France-Hawaii Telescope Legacy
Survey. The data set covers three uncorrelated patches (D1, D3 and D4)
of one square degree each, observed in u*, g', r', i' and
z' bands, to a depth of i'=25.5. The deep, multi-colour
observations in these fields allow for several data-quality
controls. The lensing signal is detected in both r' and i' bands
and shows similar amplitude and slope in both filters. B-modes are
found to be statistically zero at all scales. Using multi-colour
information, we derived a photometric redshift for each galaxy and use
this to separate the background source sample into low-z and high-zsubsamples. A stronger shear signal is detected from the high-zsubsample than from the low-z subsample, as expected from weak lensing
tomography. While further work is needed to model the effects of
errors in the photometric redshifts, this result suggests that it will
be possible to obtain constraints on the growth of dark matter
fluctuations with lensing wide field surveys. The combined
Deep and Wide surveys give
![]() assuming the
Peacock & Dodds non-linear scheme (P&D), and
assuming the
Peacock & Dodds non-linear scheme (P&D), and
![]() for the halo model and
for the halo model and
![]() .
We assumed a Cold Dark
Matter model with flat geometry and have marginalized over the
systematics, the Hubble constant and redshift uncertainties. Using
data from the Deep survey, the
.
We assumed a Cold Dark
Matter model with flat geometry and have marginalized over the
systematics, the Hubble constant and redshift uncertainties. Using
data from the Deep survey, the ![]() upper bound for w0, the
constant equation of state parameter is
w0 < -0.8.
upper bound for w0, the
constant equation of state parameter is
w0 < -0.8.
Key words: cosmology: theory - cosmology: dark matter - cosmology: large-scale structure of universe - gravitational lensing
Cosmological weak lensing, also called cosmic shear, can be used to probe the dark matter distribution in the universe. Weak lensing observations complement other probes such as CMB anisotropies (Spergel et al. 2003), type Ia supernovae (Riess et al. 2004, 1998; Perlmutter et al. 1999), and redshift surveys (Lahav & Suto 2004). Weak lensing also has the advantage of being free of any assumption regarding the light versus matter distributions (Mellier 1999; Bartelmann & Schneider 2001; Van Waerbeke & Mellier 2003; Réfrégier 2003).
It has only recently been shown that cosmic shear measurement is
technically feasible (Bacon et al. 2000; Kaiser et al. 2000; Van Waerbeke et al. 2000; Wittman et al. 2000). Unfortunately, the
deepest weak lensing survey has a sky coverage limited to less than
one deg2 and the widest to ![]() 10 deg2. Moreover, most surveys
were performed in one colour only, and even rough redshift information
was not available. These limitations restricted the use of weak
lensing as a cosmological probe to a very small number of parameters.
Early weak lensing surveys were primarily focused on the measurements
of the normalization of the dark matter power spectrum,
10 deg2. Moreover, most surveys
were performed in one colour only, and even rough redshift information
was not available. These limitations restricted the use of weak
lensing as a cosmological probe to a very small number of parameters.
Early weak lensing surveys were primarily focused on the measurements
of the normalization of the dark matter power spectrum, ![]() ,
and the mass density parameter,
,
and the mass density parameter,
![]() .
The most recent cosmic
shear surveys reach a relative accuracy of about 10% on
.
The most recent cosmic
shear surveys reach a relative accuracy of about 10% on
![]() (Mellier 1999; Bartelmann & Schneider 2001; Van Waerbeke & Mellier 2003; Réfrégier 2003), but the
uncertainty on other parameters is still fairly large.
(Mellier 1999; Bartelmann & Schneider 2001; Van Waerbeke & Mellier 2003; Réfrégier 2003), but the
uncertainty on other parameters is still fairly large.
Second generation cosmic shear surveys are now under way and will
provide the community with multi-colour data of excellent image
quality, over a wide field of view. The Canada-France-Hawaii Telescope
Legacy Survey (CFHTLS)![]() , using the recently built M EGAP RIME/M EGACAM wide field camera, belongs to this generation. The
CFHTLS-Wide survey (the core of the CFHTLS cosmic shear survey)
will provide a large sky coverage of 170 deg2, and the deep four deg2 CFHTLS-Deep will provide shear information on smaller
scales and as a function of lookback time, out to higher redshift than
the CFHTLS-Wide.
, using the recently built M EGAP RIME/M EGACAM wide field camera, belongs to this generation. The
CFHTLS-Wide survey (the core of the CFHTLS cosmic shear survey)
will provide a large sky coverage of 170 deg2, and the deep four deg2 CFHTLS-Deep will provide shear information on smaller
scales and as a function of lookback time, out to higher redshift than
the CFHTLS-Wide.
Both surveys will ultimately consist of complete and homogeneous
panchromatic data in u*, g', r', i', z'. The data were taken
between June 1st, 2003 and July 22, 2004 as part of a preliminary
survey to provide detailed quality assessments and propose technical
or operational improvements, when necessary. The CFHTLS-Wide has the
same depth as V IRMOS-Descart, but so far, the available data is
only in one colour and covers ![]() 20 deg2. A cosmic shear
analysis with the wide data is performed in Hoekstra et al. (2005). The
CFHTLS-Deep has been observed in all five filters, therefore
photometric redshifts are available, and will be used in this
work. Moreover, the CFHTLS D1 Deep field is located in the V
IRMOS-VLT Deep Survey (VVDS) F02 field which has several thousand of
galaxy redshifts (Le Fèvre et al. 2005) and near infrared data (on a tiny
area). A combination of large and small scales from the Wide and the
Deep data will ultimately provide an excellent data set to probe the
nature of dark energy in the universe
(Cooray & Huterer 1999; Benabed & Bernardeau 2001; Linder & Jenkins 2003; Benabed & van Waerbeke 2004; Jarvis et al. 2005). In this work,
we describe the first CFHTLS cosmic shear studies based on Deep data,
and then combine the Wide and Deep data analysis to derive constraints
on
20 deg2. A cosmic shear
analysis with the wide data is performed in Hoekstra et al. (2005). The
CFHTLS-Deep has been observed in all five filters, therefore
photometric redshifts are available, and will be used in this
work. Moreover, the CFHTLS D1 Deep field is located in the V
IRMOS-VLT Deep Survey (VVDS) F02 field which has several thousand of
galaxy redshifts (Le Fèvre et al. 2005) and near infrared data (on a tiny
area). A combination of large and small scales from the Wide and the
Deep data will ultimately provide an excellent data set to probe the
nature of dark energy in the universe
(Cooray & Huterer 1999; Benabed & Bernardeau 2001; Linder & Jenkins 2003; Benabed & van Waerbeke 2004; Jarvis et al. 2005). In this work,
we describe the first CFHTLS cosmic shear studies based on Deep data,
and then combine the Wide and Deep data analysis to derive constraints
on
![]() and
and ![]() .
.
The organization of the paper is as follows. In Sect. 2 we introduce the notation and define the statistics we use. The data set is described in Sect. 3. In Sects. 4 and 5 we present results and residual systematics and we discuss them. Conclusions and perspectives are outlined in Sect. 6.
The theory of weak lensing has been previously been discussed in detail in the literature, including the physical motivations of various approximations (e.g. Bartelmann & Schneider 2001). Following Hoekstra (2004), Van Waerbeke et al. (2002), Van Waerbeke et al. (2005) we follow the notation of Schneider et al. (1998).
We introduce the power spectrum of the convergence ![]() as:
as:
Cosmic shear can be studied using three different 2-point statistics,
which differ only by their filtering schemes. These various statistics
have different wavelength sensitivities to the power spectrum and
therefore the effect of systematics on each is different. This enables
the comparison of multiple cross-checked solutions. Two-point
statistics are measured as a function of scale
![]() ,
which could
either be a galaxy pair separation or smoothing window radius. The
relation between each two-point statistics and the power spectrum of
the gravitational convergence (i.e. the projected dark matter
power spectrum) can be expressed as follows:
,
which could
either be a galaxy pair separation or smoothing window radius. The
relation between each two-point statistics and the power spectrum of
the gravitational convergence (i.e. the projected dark matter
power spectrum) can be expressed as follows:
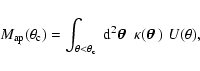 |
(5) |
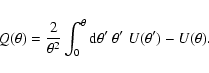 |
(9) |
Unfortunately, the
![]() statistic is sensitive to the smallest
accessible angular scales, where cosmic shear signal depends on the
poorly-known non-linear evolution of the dark matter power
spectrum. This shortcoming forces us to compute E- and B-modes on
larger angular scales in a different way. For this we use the top-hat
shear variance and the shear correlation functions. These functions
are usually derived from the
statistic is sensitive to the smallest
accessible angular scales, where cosmic shear signal depends on the
poorly-known non-linear evolution of the dark matter power
spectrum. This shortcoming forces us to compute E- and B-modes on
larger angular scales in a different way. For this we use the top-hat
shear variance and the shear correlation functions. These functions
are usually derived from the ![]() and
and ![]() shear correlation
functions:
shear correlation
functions:
Finally, the amplitude of the lensing signal depends on the galaxy
redshift distribution n(z) (see Eq. (1)). As in
previous works (see Van Waerbeke et al. 2002, 2005), we use the following
redshift distribution:
The Deep CFHTLS data used in this work consists of u*, g', r',
i' and z' stacked M EGACAM images that form the first CFHTLS
release (hereafter T0001). The release is composed of stacked images,
catalogues and relevant meta-data produced from observations in four
uncorrelated fields that were carried out at CFHT with the M
EGAPRIME instrument between June 1st 2003 and July 22, 2004.
Details regarding each field are listed on the CFHTLS web
pages![]() .
.
Each M EGACAM image consists of an array of 9 ![]() 4 EEV CCDs
of 2048
4 EEV CCDs
of 2048 ![]() 4612 pixel each (Boulade et al. 2003). The pixel scale is
0.186'' and the camera covers a total field of 1 degree
4612 pixel each (Boulade et al. 2003). The pixel scale is
0.186'' and the camera covers a total field of 1 degree ![]() 1 degree. There are two large gaps of 82 arcsec between rows of
CCDs. In order to produce complete fields, the gaps have been filled
by organizing observations in a series of exposure sequences with
large offsets. This results in an heterogeneous pixel illumination at
the borders of each CCD. This spatial flux variation induces a
varying pixel signal-to-noise ratio that is taken into account by
using pixel weight maps together with hand-made masks (see Sect. 4)
to discard noisy areas of each field.
1 degree. There are two large gaps of 82 arcsec between rows of
CCDs. In order to produce complete fields, the gaps have been filled
by organizing observations in a series of exposure sequences with
large offsets. This results in an heterogeneous pixel illumination at
the borders of each CCD. This spatial flux variation induces a
varying pixel signal-to-noise ratio that is taken into account by
using pixel weight maps together with hand-made masks (see Sect. 4)
to discard noisy areas of each field.
The stacks include only M EGACAM images with seeing better than
1.0''![]() and airmass below
1.4 have been selected. However, because there were fewer u*-band
images than for the other filters, we relaxed the selection criteria
for this filter and kept all u* images with seeing below 1.4''.
Only three of the four Deep fields have been selected for cosmic shear
studies. The D2 Deep field has been dropped from our sample because
it is significantly shallower than the other three fields.
and airmass below
1.4 have been selected. However, because there were fewer u*-band
images than for the other filters, we relaxed the selection criteria
for this filter and kept all u* images with seeing below 1.4''.
Only three of the four Deep fields have been selected for cosmic shear
studies. The D2 Deep field has been dropped from our sample because
it is significantly shallower than the other three fields.
Data were calibrated and processed at CFHT and the T ERAPIX data
center. The full T0001 release is archived at CADC![]() and available to any CFHTLS
registered user. A description of the data processing pipeline used
to produce the deep T0001 stacks is beyond the scope of the paper, but
the details can be found on the T ERAPIX web pages
and available to any CFHTLS
registered user. A description of the data processing pipeline used
to produce the deep T0001 stacks is beyond the scope of the paper, but
the details can be found on the T ERAPIX web pages![]() . Photometric and
astrometric methods and quality assessments done on these data are
explained in a short explanatory supplement
. Photometric and
astrometric methods and quality assessments done on these data are
explained in a short explanatory supplement![]() . The processing
(astrometric and photometric calibrations, pixel re sampling, image
warping and stacking, catalogue production) uses the current first
generation T ERAPIX software tools and closely follows the one
used for the V IRMOS-Descart survey that is described in
McCracken et al. (2003). We refer to this paper, and to the T ERAPIX and
CFHT
. The processing
(astrometric and photometric calibrations, pixel re sampling, image
warping and stacking, catalogue production) uses the current first
generation T ERAPIX software tools and closely follows the one
used for the V IRMOS-Descart survey that is described in
McCracken et al. (2003). We refer to this paper, and to the T ERAPIX and
CFHT![]() web pages for further details.
web pages for further details.
The accuracy of the photometric calibrations can be estimated from the
stellar colour-colour plots and the galaxy counts in all bands given
on the T ERAPIX T0001 pages and is also discussed in the more
detailed stellar analysis done by Schulteiss et al. (in
preparation). In all bands, the cumulative internal and systematic
photometric errors are 0.05 mag up to AB = 22.5, and never larger than
0.1 to the 80% completeness limit (![]() AB = 25.5). This
uncertainty is sufficient for the cosmic shear studies on this paper.
AB = 25.5). This
uncertainty is sufficient for the cosmic shear studies on this paper.
Table 1: Summary table of T0001 D1, D3 and D4 deep stacks used in this work. Magnitudes are instrumental AB. Details on magnitude, aperture, seeing and completeness definitions are given in the explanatory page http://terapix.iap.fr/article.php?id_article=383.
Table 1 summarizes the T0001 stacks used in this work.
The completeness limits have been computed by adding randomly
simulated stars (Moffat profiles) inside a
![]() area of
each Deep field and by running the detection and photometry again,
using the MAG_AUTO magnitude of SExtractor
area of
each Deep field and by running the detection and photometry again,
using the MAG_AUTO magnitude of SExtractor![]() software
(Bertin & Arnouts 1996). The completeness was also checked using
galaxy counts
software
(Bertin & Arnouts 1996). The completeness was also checked using
galaxy counts![]() .
.
The D4-z' data have not been released by T ERAPIX because the astrometric internal accuracy was below the scientific requirements. The large rms error found in the D4-z' data is not been fully understood, but it results in a large number of galaxy mismatches during the u*,g',r',i',z' catalogue cross-identification. This hampers reliable panchromatic studies for many galaxies detected in this field. A further investigation reveals that the D4-i' astrometric solution is also slightly off, while data quality in other filters are excellent. Although it has no impact on the D4- u*,g',r',i' photometric studies, a quick weak lensing analysis of the D4-i' field shows it has more systematic residuals than D1-i' and D3-i'. In contrast, the three Deep r' band data have similar quality and do not show systematics residual differences. We therefore used the r' band as the reference data set for all comparison between the fields, and only use the deep D1/D3 i' band data for colour comparisons, when needed.
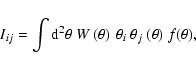 |
(14) |
The raw ellipticity is given by:
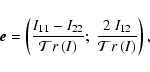 |
(15) |
Let us assume the shear-free intrinsic ellipticity of a galaxy is
![]() .
On the detector, its shape is eventually modified by the
distortions produced by gravitational lensing effects and systematics
that increase the smearing and the anisotropic component of the PSF
(atmosphere, optical aberrations). Assuming these distortions are
small, Kaiser et al. (1995) demonstrated the observed ellipticity,
.
On the detector, its shape is eventually modified by the
distortions produced by gravitational lensing effects and systematics
that increase the smearing and the anisotropic component of the PSF
(atmosphere, optical aberrations). Assuming these distortions are
small, Kaiser et al. (1995) demonstrated the observed ellipticity,
![]() ,
can be written:
,
can be written:
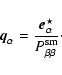 |
(17) |
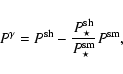 |
(18) |
Prior to cosmic shear analysis, all CFHTLS images are checked by eye
and masks are drawn by hand. These masks are designed to avoid
elongated defects, like saturated stars, as well as large foreground
galaxies with extended bright halo that may contaminate the shape of underlying faint galaxies (see Van Waerbeke et al. 2001, for details). We should
emphasize that masks are only drawn using criteria (z=0galaxies, bright stars, CCD defects) that are not correlated with the
lensing signal. In addition, we used the weight map images produced
by T ERAPIX for each stack to reject all pixels with a relative
weight amplitude less than of ![]() .
This rejection step reduces
significant spatial variation of the detection threshold and keeps the
averaged redshift distribution of lensed galaxies stable over the
field. The rejection scheme removes the CCD boundaries from all of
the fields, and is essentially equivalent to singling out each CCD
region, as was done earlier in V IRMOS-Descart survey. The gain
in homogeneity is however preserved at the expense of the sky
coverage. About
.
This rejection step reduces
significant spatial variation of the detection threshold and keeps the
averaged redshift distribution of lensed galaxies stable over the
field. The rejection scheme removes the CCD boundaries from all of
the fields, and is essentially equivalent to singling out each CCD
region, as was done earlier in V IRMOS-Descart survey. The gain
in homogeneity is however preserved at the expense of the sky
coverage. About ![]() of the initial area is lost after the masking
process.
of the initial area is lost after the masking
process.
Stars needed for the PSF correction are selected along the stellar
locus of the magnitude/size diagram (Fahlman et al. 1994), from the region
where stars are about one magnitude fainter than the saturation level
and where they cannot be confused with faint galaxies. The
![]() and
and
![]() values are derived at all M
EGACAM image positions from a PSF mapping that samples the PSF
smearing and PSF anisotropy at the position of each star, and by
interpolating their values between the stars. This operation is done
on each CCD separately, as suggested by Hoekstra (2004). The PSF is mapped
using a composite model of a second order polynomial and a rational
function,
values are derived at all M
EGACAM image positions from a PSF mapping that samples the PSF
smearing and PSF anisotropy at the position of each star, and by
interpolating their values between the stars. This operation is done
on each CCD separately, as suggested by Hoekstra (2004). The PSF is mapped
using a composite model of a second order polynomial and a rational
function,
![]() :
:
| (20) |
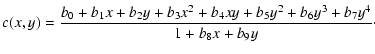 |
(21) |
The correction is made in two steps. First, the coefficients of the rational function are determined. Since the CFHTLS Deep fields are much deeper than the RCS (Hoekstra et al. 2002) and the V IRMOS-Descart (Van Waerbeke et al. 2000, 2001) surveys, the density of selected stars is higher and we do not need to map the PSF using external stellar fields. Each field has about 100 stars per CCD, so the high frequency PSF terms can be reasonably well sampled down to 0.5 arcmin, and all coefficients of the rational function can be constrained with sufficient accuracy. In a second step, the polynomial terms are determined.
We also compared the rational function solution against the second order polynomial interpolation. We found the results are not very different from our composite model, although the rational function improves the quality and stability of the PSF mapping.
Once ellipticity is corrected we keep in the sample all objects with angular size larger than the seeing disk and smaller than two arc-seconds. Following Van Waerbeke et al. (2000), we automatically reject one galaxy in every close pairs with angular separation less than 12 arcsec in order to avoid contamination of ellipticity measurements by overlapping isophotes of neighboring galaxies.
The magnitude distribution of the final object catalogue is shown in
Fig. 1. The limiting magnitude corresponding to a 80%
completeness limit is
r'AB=25.5.
![\begin{figure}
\par\includegraphics[width=6.5cm,height=6.1cm,clip]{4479F1.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg88.gif) |
Figure 1: Magnitude distribution of galaxies in the three fields in the rband. More detailed galaxy count plots, for each filter and for each Deep field, are available on the web at http://terapix.iap.fr/article.php?id_article=382. |
| Open with DEXTER | |
As proposed by Erben et al. (2001) we assign an ellipticity dispersion
![]() to each object corresponding to the ellipticity dispersion
in a box containing its 20 nearest neighbors in the
(
magnitude, size) space. Weighted 2-point statistics are computed
assigning to each galaxy a weight given by
to each object corresponding to the ellipticity dispersion
in a box containing its 20 nearest neighbors in the
(
magnitude, size) space. Weighted 2-point statistics are computed
assigning to each galaxy a weight given by
![]() where
where
![]() is the ellipticity dispersion of the unlensed
galaxies. A different noise estimation (Hoekstra et al. 2000) gives similar results.
is the ellipticity dispersion of the unlensed
galaxies. A different noise estimation (Hoekstra et al. 2000) gives similar results.
![\begin{figure}
\par\includegraphics[width=4.9cm,height=4.8cm,clip]{4479F2.ps}\in...
...cm]{4479F3.ps}\includegraphics[width=4.9cm,height=4.8cm]{4479F4.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg94.gif) |
Figure 2:
The mean ellipticity of the stars shows the behavior of the PSF anisotropy for the three fields D1, D3 and D4. For all of the three fields,
|
| Open with DEXTER | |
A visual inspection of the M EGAP RIME PSF (Fig. 2)
shows that the PSF anisotropy has significant variation over the field
and may also be very large at the boundaries![]() . The PSF correction is therefore a critical step and its
reliability demands careful verifications. In addition to the usual
B-mode analysis shown in the next section, in this section we carry
out several analyses of the systematics.
. The PSF correction is therefore a critical step and its
reliability demands careful verifications. In addition to the usual
B-mode analysis shown in the next section, in this section we carry
out several analyses of the systematics.
The quality of the PSF correction and its homogeneity over the M
EGACAM field camera can be assessed by comparing the mean star
ellipticity before and after PSF correction (Fig. 3). The
average stellar ellipticities
![]() and
and
![]() are plotted as a function of the radial distance from the
center of the field, r. It is interesting to note that the radial
ellipticity component degrades much more and much faster than the
tangential ellipticity. However, the PSF correction done by the PSF
mapping is very good, for each Deep field. After correction, the
dispersion of star ellipticities is about
are plotted as a function of the radial distance from the
center of the field, r. It is interesting to note that the radial
ellipticity component degrades much more and much faster than the
tangential ellipticity. However, the PSF correction done by the PSF
mapping is very good, for each Deep field. After correction, the
dispersion of star ellipticities is about
![]() at any
point of the camera. There is no significant change in the residual
error as function of position. The small increase in the fluctuation
of star shapes at very small distances is due to higher Poisson noise:
each radial bin has the same width, so the innermost circle
encompasses the smallest area and contains fewer stars than the
others.
at any
point of the camera. There is no significant change in the residual
error as function of position. The small increase in the fluctuation
of star shapes at very small distances is due to higher Poisson noise:
each radial bin has the same width, so the innermost circle
encompasses the smallest area and contains fewer stars than the
others.
Finally, we checked the residual amplitude of the shape correlation function between corrected stars. We found is to be two order of magnitude smaller than the expected lensing signal at all scales probed by this work (Fig. 4).
The tests discussed above only guarantee that the PSF correction is
excellent in the neighborhood of selected stars or on angular scales
larger than, or close to, the mean angular distance between stars. In
regions where no stars were selected or on small scales, the local PSF
correction residuals may be larger than the average. A useful test of
systematic residuals on small scales has been proposed by Bacon et al. (2003)
and Heymans et al. (2005b). Assuming the PSF model derived from stars and
applied to galaxies is unable to remove all systematic contributions,
the star-galaxy cross correlation will be non-zero and may vary as
a function of angular scale. If the residual is small, Bacon et al. (2003)
showed the systematic residual can be expressed as follows:
The Deep photometry provides a sample of the same galaxies detected in different filters, so the signal is expected to be the same. However, these filters have different depths, and the shallowest colours do not have enough galaxies to allow a comparison of the signal between all colours using the same galaxies. This limitation affects mainly the u* and g' bands. Furthermore, these bands are more sensitive to atmospheric dispersion than other filters. We expect their PSF anisotropy to be larger than for r', i' and z' bands and its correction may also depend more on the relative differences between the averaged spectral energy distributions of stars used for the PSF calibration and of galaxies. Hence, u* and g' are not well suited for weak lensing analysis. The comparison between the r' and the z' bands doesn't give many informations because of the limited size of the matched sample. We therefore decided only to focus on the comparison between r' and i' bands.
![\begin{figure}
\par\includegraphics[width=8.7cm,height=7.2cm,clip]{4479F5.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg101.gif) |
Figure 3: Bottom panels show the mean tangential ( left panel) and radial ( right panel) uncorrected stellar ellipticity as a function of the distance to the center of the camera for D1rT001 (filled triangles), D3rT001 (filled squares) and D4rT001 (filled circles) fields. Top panels show the same quantities after PSF correction. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,height=5.8cm,clip]{4479F6.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg102.gif) |
Figure 4: E-modes (red filled circles) and B-modes (black open circles) top-hat two point statistics of corrected stars show the smallness of residual PSF systematics. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.9cm,height=11cm,clip]{4479F7.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg103.gif) |
Figure 5:
Two-point signal statistics (red filled
circles): top-hat ( bottom) and
|
| Open with DEXTER | |
We computed the two-point statistics using the same objects in i'-band and r'-band in the D1 and D3 fields only. As reported before, D4 was discarded from this study because it shows higher systematic residuals in i' bands than the two other fields. It is worth noting that both r' and i' band images have been processed (flat fielding, astrometric and photometric calibrations, image selection, image stacking) in a totally independent way. The only correlations between the two samples are the software tools and the pipeline scheme used at T ERAPIX.
The r' and i' ellipticity catalogues have been computed and
PSF-corrected independently, starting from the r' and i' T0001
stacked images. The galaxy cross-identification is done at the very
end of the processing to compare the results. Figure 6 shows
the comparison of the E- and B-modes of the top-hat shear variance
for both the i' and r' data sets. The error bars are estimated as
the quadrature sum of the statistical and the systematic error
![]() defined by Eq. (22). The amplitude of the latter is
bigger in the r' band as shown by the residual B-modes in this
filter. The r' and i' bands results are remarkably similar, both
in shape and amplitude, they agree to within
defined by Eq. (22). The amplitude of the latter is
bigger in the r' band as shown by the residual B-modes in this
filter. The r' and i' bands results are remarkably similar, both
in shape and amplitude, they agree to within ![]() at all scales.
at all scales.
![\begin{figure}
\par\includegraphics[width=7.4cm,height=5.7cm,clip]{4479F8.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg104.gif) |
Figure 6: Top-hat variance of the E-modes in the i'-band (red filled circles) and in the r'-band (red filled triangles) for the same data set. Top-hat variance B-modes in the i'-band (black open circles) and in r'-band (black open triangles). |
| Open with DEXTER | |
The cosmic variance contribution is computed using the CFHTLS T0001
Deep survey properties: an effective density (after masking) of
![]() ,
an effective area of
,
an effective area of
![]() ,
and an ellipticity dispersion per
ellipticity component of 0.3 (the latter was measured from the
corrected ellipticity). However, the error calculation described in
Schneider et al. (2002) is only valid for a single connected field with a number
density of n equally-sized galaxies. We therefore replace the
statistical error component by the Poisson noise measured from the
data, using the weights (computed as described above) and positions of
each galaxy. For the top-hat variance and the correlation function,
the free integration constant is chosen so that the B-modes on scales
between 15 and 25 arcmin vanish. Although its amplitude is
meaningless, one can see that the B-mode is flat and stable over that
range of angular scales.
,
and an ellipticity dispersion per
ellipticity component of 0.3 (the latter was measured from the
corrected ellipticity). However, the error calculation described in
Schneider et al. (2002) is only valid for a single connected field with a number
density of n equally-sized galaxies. We therefore replace the
statistical error component by the Poisson noise measured from the
data, using the weights (computed as described above) and positions of
each galaxy. For the top-hat variance and the correlation function,
the free integration constant is chosen so that the B-modes on scales
between 15 and 25 arcmin vanish. Although its amplitude is
meaningless, one can see that the B-mode is flat and stable over that
range of angular scales.
In contrast, the
![]() statistic does not have an undetermined
integration constant (as explained previously), so the B-mode
amplitude is a physical property. Figure 7 shows the presence
of B-modes. Note that the
statistic does not have an undetermined
integration constant (as explained previously), so the B-mode
amplitude is a physical property. Figure 7 shows the presence
of B-modes. Note that the
![]() filter for a given size
filter for a given size
![]() is mostly sensitive to scales around
is mostly sensitive to scales around
![]() .
This
explains why the other two-point statistics do not show B-modes at the
same scales. The B-mode at such small scales may result from intrinsic
alignment of galaxies (King & Schneider 2002; Heymans & Heavens 2003) or from the correlation
between intrinsic ellipticity and shear (Hirata & Seljak 2004). If these
systematics are real, we expect to correct them in future work by
using the photometric redshifts. A further investigation confirms
that the B-modes come from weak objects (i.e.
25.0 < r'AB < 25.5), and that a magnitude cut that rejects objects with magnitude
fainter than 25.0 gives zero B-modes at all the scales, even for the
.
This
explains why the other two-point statistics do not show B-modes at the
same scales. The B-mode at such small scales may result from intrinsic
alignment of galaxies (King & Schneider 2002; Heymans & Heavens 2003) or from the correlation
between intrinsic ellipticity and shear (Hirata & Seljak 2004). If these
systematics are real, we expect to correct them in future work by
using the photometric redshifts. A further investigation confirms
that the B-modes come from weak objects (i.e.
25.0 < r'AB < 25.5), and that a magnitude cut that rejects objects with magnitude
fainter than 25.0 gives zero B-modes at all the scales, even for the
![]() statistic. However, we keep these objects in our catalogues
because a deep sample will be necessary to study the evolution of
signal with redshift. In addition, the presence of B-modes at small
scales will taken into account when we estimate cosmological
parameters.
statistic. However, we keep these objects in our catalogues
because a deep sample will be necessary to study the evolution of
signal with redshift. In addition, the presence of B-modes at small
scales will taken into account when we estimate cosmological
parameters.
![\begin{figure}
\par\includegraphics[width=5.9cm,height=11cm,clip]{4479F9.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg111.gif) |
Figure 7: Two-point statistics for all the three fields combined. Red filled circles show E-modes, black open circles show B-modes. E-mode error bars include the statistical error and the cosmic variance contribution, while B-modes are affected only by statistical error. |
| Open with DEXTER | |
The cosmological nature of the two-point statistical signal can be
established by comparing its amplitude as a function of source redshifts
with theoretical expectations of the gravitational instability
paradigm and the gravitational lensing theory (Bernardeau et al. 1997; Jain & Seljak 1997). To
first order, the signal should increase as
![]() (Bernardeau et al. 1997; Jain & Seljak 1997), so even a rough separation of galaxies into low- and
high-redshift populations should split the cosmological lensing signal
accordingly.
(Bernardeau et al. 1997; Jain & Seljak 1997), so even a rough separation of galaxies into low- and
high-redshift populations should split the cosmological lensing signal
accordingly.
The CFHTLS T0001 data sets are well suited for this analysis. The
observations can be used to sample the high redshift universe up to
![]() .
There are enough of galaxies to divide into two subsets
based on their estimated photometric redshifts.
.
There are enough of galaxies to divide into two subsets
based on their estimated photometric redshifts.
Photometric redshifts were measured using the hyper-z public
software![]() (Bolzonella et al. 2000). hyper-z uses the multi-band photometric
data of a galaxy to derive its most likely redshift and spectral
energy distribution (SED) based on the Bruzual & Charlot evolution
models (Bruzual & Charlot 1993).
(Bolzonella et al. 2000). hyper-z uses the multi-band photometric
data of a galaxy to derive its most likely redshift and spectral
energy distribution (SED) based on the Bruzual & Charlot evolution
models (Bruzual & Charlot 1993).
![\begin{figure}
\par\includegraphics[width=8.1cm,height=6.2cm,clip]{4479F10.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg114.gif) |
Figure 8: Density of galaxies of D1 field as a function of photometric redshift. |
| Open with DEXTER | |
We used the D1 and D3 u*, g', r', i' and z' images and the
D4 u*, g', r', i' images (the D4-z' stacked image is
missing in T0001). Photometric catalogues were produced by the SExtractor software. All galaxies were first detected in the r' band reference image. Magnitude and colours of galaxies are then
computed using the r'-center positions and inside an aperture scaled
according to the size of each galaxy in r'-band. The ![]() minimization was performed assuming magnitude errors derived from SExtractor, which range between
minimization was performed assuming magnitude errors derived from SExtractor, which range between
![]() and
and
![]() in all bands.
in all bands.
Table 2: Mean photometric redshift in magnitude bins.
Figure 8 shows the photometric redshift distribution of the galaxies in D1 field down to i'=24.0. This subsample can be compared with the VVDS spectroscopic redshift distribution obtained from 11000 spectra in the same region (Le Fèvre et al. 2005). There are no apparent discrepancies that would make the separation into photometric low- and high-redshift galaxies unreliable. Beyond i'=24.0, large spectroscopic redshift samples are not yet available, but we don't have any reason to believe that our photometric redshift accuracies will degrade significantly for the i'<24.0 sample.
The cosmic shear catalogue can therefore be split into two samples with equal numbers of galaxies at high and low redshifts with reasonable confidence and can be compared with cosmological predictions. Poisson noise is therefore similar in the two subsamples, but photometric redshift errors are expected to be larger in the high-redshift tail.
![\begin{figure}
\par\includegraphics[width=8.2cm,height=5.6cm,clip]{4479F11.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg140.gif) |
Figure 9:
Top-hat variance for "high-z'' subsample
(red filled triangles) and "low-z'' subsample'' (red filled
circles). B-modes for the two subsamples are also shown. Error bars
include statistical noise and cosmic variance. The data are compared
with theoretical fiducial model (
|
| Open with DEXTER | |
Figure 9 shows the top-hat shear variance measured for the
two populations. The low-z sample ranges in
![]() ,
while the high-z galaxies have
,
while the high-z galaxies have ![]() .
Error bars include
Poisson noise and cosmic variance (see Sect. 4.2). The difference
between the two samples demonstrates the cosmological nature of the
signal. An indicative comparison of signals with theoretical
predictions is also plotted.
.
Error bars include
Poisson noise and cosmic variance (see Sect. 4.2). The difference
between the two samples demonstrates the cosmological nature of the
signal. An indicative comparison of signals with theoretical
predictions is also plotted.
The relative lensing amplitude for the two source galaxy populations is less sensitive to cosmic variance fluctuations, and agrees with the predictions.
Contamination by galaxies with incorrect photometric redshifts is likely important, in particular for the faintest galaxies and the high-z tail (further informations about degeneracy of photometric redshifts in the case of missing infrared bands can be found on hyper-z user's guide).
In spite of potential contamination by incorrect photometric redshifts, the cosmological imprint of large-scale structure detected in the Deep CFHTLS data shows that M EGAP RIME is suitable for cosmic shear studies. Figure 9 also demonstrates that the CFHTLS Deep survey has promising potential for tomographic studies that explore the evolution of the dark matter power spectrum with look-back time.
In this section, we describe the estimation of cosmological
parameters. In a subsequent paper, we will perform a complete
parameter estimate, combining weak lensing with other cosmological
probes. Therefore, here we limit the analysis to the normalization of
the mass power spectrum (![]() )
and matter density (
)
and matter density (
![]() )
measurements. The shape parameter
)
measurements. The shape parameter ![]() is given by the Cold Dark
Matter paradigm
is given by the Cold Dark
Matter paradigm
![]() ,
where h is the reduced Hubble
constant.
We allow the characteristic redshift of the source distribution to
vary around the best fit that will be described in the next
subsection.
,
where h is the reduced Hubble
constant.
We allow the characteristic redshift of the source distribution to
vary around the best fit that will be described in the next
subsection.
To measure cosmological parameters, we adopt a maximum-likelihood
method. Let di be the input data vector (i.e. the top-hat shear
variance as a function of scale ![]() ), and
), and
![]() the prediction, function of the
parameters to be estimated. The likelihood function of the data is
then:
the prediction, function of the
parameters to be estimated. The likelihood function of the data is
then:
![\begin{displaymath}{\cal L}={1\over (2\pi)^n\vert{\vec C}\vert^{1/2}}
\exp\left[(d_i-m_i){\vec C}^{-1}(d_i-m_i)^{\rm T}\right],
\end{displaymath}](/articles/aa/full/2006/22/aa4479-05/img147.gif) |
(23) |
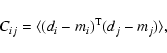 |
(24) |
As discussed above, the matrix
![]() is computed according to
Schneider et al. (2002), assuming an effective survey area of the CFHTLS Deep
fields: 2.1 square degrees, a number density of galaxies
is computed according to
Schneider et al. (2002), assuming an effective survey area of the CFHTLS Deep
fields: 2.1 square degrees, a number density of galaxies
![]() ,
and an intrinsic ellipticity dispersion of
,
and an intrinsic ellipticity dispersion of
![]() per component.
per component.
The cosmic variance is computed assuming Gaussian statistics. While
this assumption becomes inappropriate on small angular scales, errors
on such scales are dominated by the statistical noise contribution, so
the Gaussian approximation remains an excellent one (Van Waerbeke et al. 2002).
The covariance matrix components are derived for a fiducial
cosmological model corresponding to the best fit of WMAP data proposed
by Spergel et al. (2003):
![]() ,
,
![]() ,
,
![]() ,
,
![]() (the reduced Hubble constant is
h=0.7). The B-mode is calibrated by marginalizing around B=0within the 1
(the reduced Hubble constant is
h=0.7). The B-mode is calibrated by marginalizing around B=0within the 1![]() interval.
interval.
The source redshift distribution is calibrated using the Hubble Deep
Field (HDF) catalogues (Fernández-Soto et al. 1999), which provide a more accurate
estimate of redshift in absence of infrared data in CFHTLS fields. It
turns out that the F606 filter of WFPC2 is a good match to the M
EGACAM r' filter within our ![]() magnitude error. We select all galaxies with
21.5 < r'<
25.5. The Hubble Deep Fields provide a sample at
high redshifts that overlaps with the redshift range expected for the
CFHTLS Deep fields.
magnitude error. We select all galaxies with
21.5 < r'<
25.5. The Hubble Deep Fields provide a sample at
high redshifts that overlaps with the redshift range expected for the
CFHTLS Deep fields.
We use the source redshift distribution model of Eq. (12) and perform a
![]() fit, allowing the parameter
fit, allowing the parameter ![]() to vary. We then identify
the
to vary. We then identify
the
![]() and
and
![]() uncertainties, which we
marginalized over in the cosmological parameter estimation. We find
uncertainties, which we
marginalized over in the cosmological parameter estimation. We find
![]() ,
,
![]() ,
,
![]() .
Figure 10 shows the unnormalized weight in magnitude
slices in the Deep catalogues. The effect of down-weighting faint
galaxies is taken into account in the source redshift
estimation. Figure 11 shows the best fit model and the
underlying photometric redshifts from the Hubble Deep Fields (solid
line). Error bars are Poisson errors. The dashed-dotted line in Fig. 11 shows the redshift distribution one would have if we ignore
the weighting. The best fit redshift distribution model has a mean
source redshift of
.
Figure 10 shows the unnormalized weight in magnitude
slices in the Deep catalogues. The effect of down-weighting faint
galaxies is taken into account in the source redshift
estimation. Figure 11 shows the best fit model and the
underlying photometric redshifts from the Hubble Deep Fields (solid
line). Error bars are Poisson errors. The dashed-dotted line in Fig. 11 shows the redshift distribution one would have if we ignore
the weighting. The best fit redshift distribution model has a mean
source redshift of ![]() 1.01, nearly 0.2 higher in z than the
Wide survey (Hoekstra et al. 2005).
1.01, nearly 0.2 higher in z than the
Wide survey (Hoekstra et al. 2005).
![\begin{figure}
\par\includegraphics[width=7.8cm,height=6.1cm,clip]{4479F12.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg163.gif) |
Figure 10: Plot of mean weight per galaxy as a function of magnitude 21.5< r'AB < 25.5. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=6.1cm,clip]{4479F13.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg164.gif) |
Figure 11: The histogram shows the photometric redshift distribution of 21.5< r'AB < 25.5 galaxies of Hubble Deep Field North and South used in this work. The central solid line is the best fit model. The solid line histogram is that magnitude weighted redshift distribution. The dashed-dot histogram shows the redshift distribution if the galaxies were not magnitude weighted. |
| Open with DEXTER | |
The constraints on
![]() and
and ![]() are obtained after
marginalization of the reduced Hubble constant
are obtained after
marginalization of the reduced Hubble constant
![]() and
over the
and
over the
![]() limits of the source redshift parameter
limits of the source redshift parameter
![]() .
The resulting constraints in the
.
The resulting constraints in the
![]() -
-![]() plane
are given in Fig. 12. This figure shows
that the CFHTLS Deep field gives constraints as good as previous
lensing measurements, despite its small field of view. This is the
consequence of the larger fraction of high redshift galaxies, which
are more strongly lensed. Using the Peacock & Dodds (1996) non-linear
scheme, we obtain
plane
are given in Fig. 12. This figure shows
that the CFHTLS Deep field gives constraints as good as previous
lensing measurements, despite its small field of view. This is the
consequence of the larger fraction of high redshift galaxies, which
are more strongly lensed. Using the Peacock & Dodds (1996) non-linear
scheme, we obtain
![]() (
(
![]() )
for
)
for
![]() .
Error bars are the one
and two
.
Error bars are the one
and two ![]() errors respectively. The Smith et al. (2003) halo
model gives
errors respectively. The Smith et al. (2003) halo
model gives
![]() ,
which agrees with
previous normalization measurements. The similarity between
the result obtained using the Peacock & Dodds and that using the halo
fitted model is not surprising. Indeed, on scales
,
which agrees with
previous normalization measurements. The similarity between
the result obtained using the Peacock & Dodds and that using the halo
fitted model is not surprising. Indeed, on scales
![]() ,
which dominate our signal, the difference between the two models of
power spectrum is
,
which dominate our signal, the difference between the two models of
power spectrum is ![]() 5%. On smaller scales, we would expect an
increasing discrepancy between these different ways to estimate
5%. On smaller scales, we would expect an
increasing discrepancy between these different ways to estimate ![]() .
.
![\begin{figure}
\par\includegraphics[width=6.8cm,height=5.6cm,clip]{4479F14.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg170.gif) |
Figure 12:
|
| Open with DEXTER | |
We then measure ![]() by combining these constraints with those
obtained on the CFHTLS Wide survey (see Hoekstra et al. 2005, for the
details). The result of this joint analysis is shown in Fig. 13, and remarkably, the
by combining these constraints with those
obtained on the CFHTLS Wide survey (see Hoekstra et al. 2005, for the
details). The result of this joint analysis is shown in Fig. 13, and remarkably, the
![]() -
-![]() degeneracy is partially broken. This is the
consequence of measuring the large and small scales simultaneously, as
shown in Jain & Seljak 1997. For
degeneracy is partially broken. This is the
consequence of measuring the large and small scales simultaneously, as
shown in Jain & Seljak 1997. For
![]() ,
we get
,
we get
![]() using Peacock & Dodds (1996) for the non-linear scheme
and
using Peacock & Dodds (1996) for the non-linear scheme
and
![]() for the halo model (Smith et
al. 2003).
for the halo model (Smith et
al. 2003).
![\begin{figure}
\par\includegraphics[width=6.8cm,height=5.6cm,clip]{4479F15.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg173.gif) |
Figure 13:
Same as Fig. 12, combined with the CFHTLS Wide data
(Hoekstra et al. 2005). For
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.1cm,height=5.6cm,clip]{4479F16.ps}
\end{figure}](/articles/aa/full/2006/22/aa4479-05/Timg174.gif) |
Figure 14:
Dark energy constraints from the
Deep data only. Hidden parameters are marginalized using a flat prior
over
|
| Open with DEXTER | |
The power spectrum normalization is in very good agreement with
results from medium-redshift and low-source-redshift weak lensing
surveys (Hoekstra et al. 2002; Van Waerbeke & Mellier 2005). It is remarkable that the parameters
of the redshift distribution, which have been estimated from a
different survey, are such that the normalization ![]() lies
within the errors of previous measurements. This is strong evidence
that deep, medium and shallow lensing surveys are in cosmological
agreement, hence reinforcing the ability of cosmic shear to probe the
mass distribution at different redshifts and different scales.
lies
within the errors of previous measurements. This is strong evidence
that deep, medium and shallow lensing surveys are in cosmological
agreement, hence reinforcing the ability of cosmic shear to probe the
mass distribution at different redshifts and different scales.
Weak lensing can also be used to constrain dark energy. Figure 14 show the upper limit on w0, the constant
equation of state parameter derived from the Deep data only. Here we
used only the Peacock & Dodds non-linear prescription (a detailed
discussion on non-linear power spectrum correction in the context of
Dark Energy can be found in Hoekstra et al. (2005), which also includes a joint
analysis of the Wide and Deep data). We obtain
w0 < -0.8 at
![]() ,
and the contours show that this result is independent of
,
and the contours show that this result is independent of
![]() .
This is particularly interesting because lensing combined
with either cosmic microwave background (Jarvis et al. 2005) or
supernovae will provide a strong constraint on the dark energy
equation of state.
.
This is particularly interesting because lensing combined
with either cosmic microwave background (Jarvis et al. 2005) or
supernovae will provide a strong constraint on the dark energy
equation of state.
The T0001 data have been used to assess the capabilities of M EGAPRIME/M EGACAM and to clarify the potential and the science drivers of the CFHTLS Deep survey for weak lensing studies.
The correction for PSF anisotropy works very well, showing that residual systematics are almost zero at all scales probed by a M EGACAM field. This is confirmed by the star-galaxy cross-correlation analysis. This also demonstrates that the CFHT-E LIXIR-T ERAPIX calibration/reduction pipelines can deliver co-added images which have the required lensing quality. However, the presence of B-modes by weak objects at small scales should be further investigated.
The cosmic shear signal has been detected in the r'-band. Its consistency and achromaticity has been checked by independent r'- and i'-analysis of the same data sets. We have presented results for three standard two-point shear statistics.
Thanks to the depth of the CFHTLS Deep sample, and using the
photometric redshifts derived from the u*, g', r', i' and
z' images, the galaxy sample was split into low- and high-redshift
sources, and the cosmic shear signal was measured on the two
subsamples separately. Both subsamples show zero B-modes and the shear
amplitude of the high-z sample is clearly higher than the low-zone, with a ratio in agreement with the cosmic shear predictions. The
amplitude of the signals from the two subsamples are different from
each other at all scales with a significance level higher than 5-sigma
and their shapes follow theoretical expectations of ![]() -CDM
dominated universe. This strong evidence for the cosmological nature
of the signal shows that the CFHTLS Deep data will allow us to explore
the growth rate of cosmic shear signal with redshift, and hence the
evolution of the dark matter power spectrum as a function of lookback
time.
-CDM
dominated universe. This strong evidence for the cosmological nature
of the signal shows that the CFHTLS Deep data will allow us to explore
the growth rate of cosmic shear signal with redshift, and hence the
evolution of the dark matter power spectrum as a function of lookback
time.
Using only Deep data, and marginalizing over h and the redshift of
sources, we have derived constraints on ![]() and
and
![]() .
We
show that the degeneracy between these two parameters is partially
broken when the analysis is combined with data from Wide
survey. Assuming
.
We
show that the degeneracy between these two parameters is partially
broken when the analysis is combined with data from Wide
survey. Assuming
![]() ,
we found that
,
we found that
![]() for P&D and
for P&D and
![]() with the halo model, in
excellent agreement with Van Waerbeke et al. (2005,
with the halo model, in
excellent agreement with Van Waerbeke et al. (2005,
![]() )
and Hoekstra et al. (2002,
)
and Hoekstra et al. (2002,
![]() ). Likewise, we derive
w0<-0.8 using Deep data alone (see Hoekstra et al. 2005, for a deep+wide
analysis).
). Likewise, we derive
w0<-0.8 using Deep data alone (see Hoekstra et al. 2005, for a deep+wide
analysis).
Our results show that everything is in place to make a full scientific use the CFHTLS lensing data, and that soon with deeper Deep survey data and wider Wide survey data, we will able to provide the best cosmological constraints from weak lensing to date. In particular, we expect to explore the growth rate of structure from a tomographic cosmic shear measurement, and to better constrain cosmological models from the non-Gaussian features derived from a joint analysis of two-point and three-point statistics. The analysis of three-point statistics in CFHTLS data goes beyond the scope of this paper. Indeed, the Deep data used for this paper, is not wide enough for such a measurement. However, three-point statistics will be investigated using future samples both for the Deep and Wide survey.
Acknowledgements
We warmly thank the CFHT, T ERAPIX and CADC staff for their assistance and the considerable work they do to produce the CFHTLS data. We thank J. Benjamin, F. Bernardeau, T. Erben, B. Fort, C. Heymans, B. Ménard, P. Schneider, R. Pelló, C. Schimd, C. Shu, J.-P. Uzan for useful discussions. RM thanks the City of Paris and IAP for funding his research grants at IAP. YM, ES, IT and LF thanks the CNRS-INSU and the French Programme National de Cosmologie for their support to the CFHTLS cosmic shear program. E.S. thanks the University of British Columbia for hospitality. L.F. thanks the "European Association for Research in Astronomy'' training site (EARA) and the European Community for the Marie Curie doctoral fellowship MEST-CT-2004-504604. LVW, HH and MJH are supported by the Natural Sciences and Engineering Research Council (NSERC), the Canadian Institute for Advanced Research (CIAR) and the Canadian Foundation for Innovation (CFI).