A&A 452, 25-35 (2006)
DOI: 10.1051/0004-6361:20054283
Time delay of SBS 0909+532
A. Ullán1 - L. J. Goicoechea1 - A. P. Zheleznyak2 - E. Koptelova3 - V. V. Bruevich3 - T. Akhunov4 - O. Burkhonov4
1 - Departamento de Física Moderna, Universidad de Cantabria,
Avda. de Los Castros s/n, 39005 Santander, Spain
2 -
Institute of Astronomy of Kharkov National University,
Sumskaya 35, 61022 Kharkov, Ukraine
3 -
Sternberg Astronomical Institute, Universitetski Pr. 13,
119992 Moscow, Russia
4 -
Ulug Beg Astronomical Institute of Uzbek Academy of
Science, Astronomicheskaya. Str. 33, 700052 Tashkent, Republic
of Uzbekistan
Received 30 September 2005 / Accepted 12 January 2006
Abstract
Aims. The time delays between the components of a lensed quasar are basic tools for analysing the expansion of the Universe and the structure of the main lens galaxy halo. In this paper, we focus on the variability and time delay of the double system SBS 0909+532A,B as well as the time behaviour of the field stars.
Methods. We use VR optical observations of SBS 0909+532A, B and the field stars in 2003. The frames were taken at Calar Alto, Maidanak, and Wise observatories, and the VR light curves of the field stars and quasar components were derived from aperture and point-spread function fitting methods. We measured the R-band time delay of the system from the  and dispersion techniques and 1000 synthetic light curves based on the observed records.
and dispersion techniques and 1000 synthetic light curves based on the observed records.
Results. One nearby field star (SBS 0909+532c) was found to be variable, and the other two nearby field stars are non-variable sources. With respect to the quasar components, the R-band records seem more reliable and are more densely populated than the V-band ones. The observed R-band fluctuations permit a pre-conditioned measurement of the time delay. From the  minimization, if we assume that the quasar emission is observed first in B and afterwards in A (in agreement with basic observations of the system and the corresponding predictions), we obtain
minimization, if we assume that the quasar emission is observed first in B and afterwards in A (in agreement with basic observations of the system and the corresponding predictions), we obtain
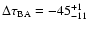 days (95% confidence interval). The dispersion technique leads to a similar delay range. A by-product of the analysis is the determination of a totally corrected flux ratio in the R band (corrected by the time delay and the contamination due to the galaxy light). Our 95% measurement
days (95% confidence interval). The dispersion technique leads to a similar delay range. A by-product of the analysis is the determination of a totally corrected flux ratio in the R band (corrected by the time delay and the contamination due to the galaxy light). Our 95% measurement
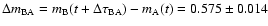 mag is in excellent agreement with previous results from contaminated fluxes at the same time of observation.
mag is in excellent agreement with previous results from contaminated fluxes at the same time of observation.
Key words: gravitational lensing - galaxies: quasars: general - galaxies: quasars: individual: SBS 0909+532
- stars: variables: general
The system SBS 0909+532 was discovered by Stepanyan et al. (1991). Some years later,
a collaboration between the Hamburger Sternwarte and the Harvard-Smithsonian Center
for Astrophysics resolved the system into a pair of quasars (A and B) with a direct
R-band flux ratio (at the same time of observation)
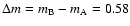 mag and a separation of about 1
mag and a separation of about 1
 1 (Kochanek et al. 1997). The direct R-band
flux ratio was not consistent with the direct flux ratios at other wavelengths:
1 (Kochanek et al. 1997). The direct R-band
flux ratio was not consistent with the direct flux ratios at other wavelengths:
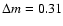 mag in the I band and
mag in the I band and
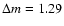 mag in the B band. From observations
with the 4.2 m William Herschel Telescope, a Spanish collaboration got spectra for each
component of the system. The data showed that the system consists of two quasars with
the same redshift (
mag in the B band. From observations
with the 4.2 m William Herschel Telescope, a Spanish collaboration got spectra for each
component of the system. The data showed that the system consists of two quasars with
the same redshift (
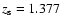 )
and identical spectral distribution, supporting the
gravitational lens interpretation of SBS 0909+532 (Oscoz et al. 1997). Oscoz et al. (1997)
detected an Mg II doublet in absorption at the same redshift (
)
and identical spectral distribution, supporting the
gravitational lens interpretation of SBS 0909+532 (Oscoz et al. 1997). Oscoz et al. (1997)
detected an Mg II doublet in absorption at the same redshift (
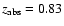 )
in
both components, and they suggested that the absorption features were associated with the
photometrically unidentified lensing galaxy. Through a singular isothermal sphere (SIS)
lens model, the authors also inferred the first constraint on the time delay between the
components:
)
in
both components, and they suggested that the absorption features were associated with the
photometrically unidentified lensing galaxy. Through a singular isothermal sphere (SIS)
lens model, the authors also inferred the first constraint on the time delay between the
components:
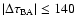 days, where
days, where
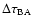 is the delay of B
with respect to A, and the Hubble constant is assumed to be H0 = 70 km s-1 Mpc-1.
is the delay of B
with respect to A, and the Hubble constant is assumed to be H0 = 70 km s-1 Mpc-1.
In recent years, Lubin et al. (2000) have indicated the possible nature of the main deflector
(early-type galaxy) and confirmed its redshift (
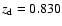 ). Lehár et al. (2000) reported
on a program including Hubble Space Telescope (HST) observations of SBS 0909+532. They
discovered the main lens galaxy between the components, which has a large effective radius,
with a correspondingly low surface brightness. This lens galaxy is closer to the brightest
component (A), which does not contradict SIS-like lens models when the farther and
fainter component (B) is more strongly affected by dust extinction (see below). The colours of
the lens are consistent with those of an early-type galaxy at redshift 0.83. Assuming a
singular isothermal ellipsoid (SIE) model, Lehár et al. predicted a time delay
). Lehár et al. (2000) reported
on a program including Hubble Space Telescope (HST) observations of SBS 0909+532. They
discovered the main lens galaxy between the components, which has a large effective radius,
with a correspondingly low surface brightness. This lens galaxy is closer to the brightest
component (A), which does not contradict SIS-like lens models when the farther and
fainter component (B) is more strongly affected by dust extinction (see below). The colours of
the lens are consistent with those of an early-type galaxy at redshift 0.83. Assuming a
singular isothermal ellipsoid (SIE) model, Lehár et al. predicted a time delay
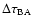 in the range [-10, -87] days (H0 = 70 km s-1 Mpc-1). At a given
emission time, the sign "-'' means that the corresponding signal is observed first in B and
later in A. The COSMOGRAIL collaboration has provided the distribution of predicted time delays of
the system (Saha et al. 2006). In their histogram (Fig. 10 of Saha et al.), there are two
features: the main feature is an asymmetric peak around - 80 days and the secondary one is
another asymmetric peak around -45 days. Therefore, if the COSMOGRAIL predictions are right,
the time delay is very probably 2-3 months (component B leading component A), but we
cannot rule out a delay of about one and a half months. On the other hand, the flux ratio
anomaly pointed by Kochanek et al. (1997) was confirmed and accurately studied by Motta et al.
(2002) and Mediavilla et al. (2005), who reported the existence of differential extinction in
the main lens galaxy. Chartas (2000) and Page et al. (2004) also studied the system in the
X-ray domain.
in the range [-10, -87] days (H0 = 70 km s-1 Mpc-1). At a given
emission time, the sign "-'' means that the corresponding signal is observed first in B and
later in A. The COSMOGRAIL collaboration has provided the distribution of predicted time delays of
the system (Saha et al. 2006). In their histogram (Fig. 10 of Saha et al.), there are two
features: the main feature is an asymmetric peak around - 80 days and the secondary one is
another asymmetric peak around -45 days. Therefore, if the COSMOGRAIL predictions are right,
the time delay is very probably 2-3 months (component B leading component A), but we
cannot rule out a delay of about one and a half months. On the other hand, the flux ratio
anomaly pointed by Kochanek et al. (1997) was confirmed and accurately studied by Motta et al.
(2002) and Mediavilla et al. (2005), who reported the existence of differential extinction in
the main lens galaxy. Chartas (2000) and Page et al. (2004) also studied the system in the
X-ray domain.
Time delays are basic tools for discussing the present expansion rate of the Universe and the
structure of the main lens galaxy haloes (e.g., Refsdal 1964; Kochanek et al.
2004), so that variability studies are crucial. While some time delays have been measured from
radio light curves (PKS 1830-211: Lovell et al. 1998; Q0957+561: Haarsma et al. 1999;
B0218+357: Biggs et al. 1999; B1600+434: Koopmans et al. 2000; B1422+231: Patnaik & Narasimha
2001; B1608+656: Fassnacht et al. 2002) or X-ray variability (e.g., Q2237+0305: Dai et al.
2003), an important set of delays is based on optical monitoring of gravitationally lensed
quasars. Optical frames taken at Apache Point Observatory, Fred Lawrence Whipple Observatory,
and Teide Observatory were used to estimate a 14-month delay for the double system Q0957+561
(e.g., Pelt et al. 1996; Kundic et al. 1997; Serra-Ricart et al. 1999; Ovaldsen et al. 2003).
Although the time delay of this first multiple quasar has been confirmed through independent
observations, the measurement is only 5% accurate, or equivalently, there is an uncertainty of
about 20 days (Goicoechea 2002). The Tel-Aviv University (TAU) group have recently determined
the time delay between the two components of HE 1104-1805 (Ofek & Maoz 2003). The TAU delay
of HE 1104-1805 disagrees with the earlier estimation by Gil-Merino et al.
(2002), but it is in excellent agreement with the determination by Wyrzykowski et al. (2003).
Schechter et al. (1997) measured two delays for the quadruply imaged quasar PG 1115+080. The
Belgian-Nordic collaboration were intensely active during the past five years.
They participated in several monitoring projects and measured several time delays at optical
wavelengths: B1600+434 (Burud et al. 2000), HE 2149-2745 (Burud et al. 2002a), RXJ 0911.4+0551
(Hjorth et al. 2002), SBS 1520+530 (Burud et al. 2002b), and FBQ 0951+2635 (Jakobsson et al.
2005). The formal accuracies of these 5 estimations range from 5 to 25% (the 1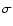 error
bars vary from 4 to 24 days). Kochanek et al. (2005) also measured the time delays between the
components of the quadruple quasar HE 0435-1223.
error
bars vary from 4 to 24 days). Kochanek et al. (2005) also measured the time delays between the
components of the quadruple quasar HE 0435-1223.
The aim of this paper is to present VR observations of SBS 0909+532 in 2003 conducted by
the University of Cantabria (UC, Spain), the Institute of Astronomy of Kharkov National
University (IAKhNU, Ukraine), the Sternberg Astronomical Institute (SAI, Russia), and the
Ulug Beg Astronomical Institute of Uzbek Academy of Science (UBAI, Uzbekistan). We also
present TAU observations of the field stars in 2003, which have been kindly made available to
us. This new optical monitoring campaign was carried out at the Calar Alto Observatory (Spain),
the Maidanak Observatory (Uzbekistan), and the Wise Observatory (Israel), and the frames were
taken with the 1.5 m Spanish telescope, the 1.5 m AZT-22 telescope at Mt. Maidanak, and the
Wise Observatory 1 m telescope (Sect. 2). In Sect. 3, we describe the methodology for
obtaining the fluxes of the quasar components and the field stars. The VR light curves are also
shown in Sect. 3. Section 4 is devoted to the time delay estimation from the light curves
of A and B (quasar components) in the R band. Finally, in Sect. 5 we summarise our
conclusions and discuss the feasibility of accurately determining the cosmic expansion
rate and the surface density in the main lensing galaxy.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{4283f1.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg50.gif) |
Figure 1:
Calar Alto image of SBS 0909+532, showing an FOV of 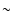
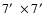 .
The field contains the gravitationally lensed quasar ("GL'') and six bright and non-saturated
stars ("a-c'', "s1-s2'' and "x''). The nearby ("a-c'') and relatively far ("s1-s2'') field stars
were introduced by Kochanek et al. (1997) and Nakos et al. (2003), respectively. A sixth field
star ("x'') is also included in the FOV. .
The field contains the gravitationally lensed quasar ("GL'') and six bright and non-saturated
stars ("a-c'', "s1-s2'' and "x''). The nearby ("a-c'') and relatively far ("s1-s2'') field stars
were introduced by Kochanek et al. (1997) and Nakos et al. (2003), respectively. A sixth field
star ("x'') is also included in the FOV. |
| Open with DEXTER |
We have three different sets of frames for SBS 0909+532. The first set of optical frames covers
the period between March 4 and June 2, 2003, and they are part of a UC project to test the
feasibility of quasar monitoring programs through 1-2 m telescopes in Spain (Ullán 2005).
These observations were made with the 1.52 m Spanish telescope at Calar Alto Observatory (EOCA),
Almeria, Spain (see Ziad et al. 2005, for a site-testing on Calar Alto). The EOCA is equipped
with a Tektronics
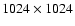 CCD detector, which has pixels with a physical size of 24
CCD detector, which has pixels with a physical size of 24 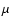 m, giving a 0.4 arcsec pixel-1 angular scale. The gain is 6.55 e-/ADU and the
readout noise is 6.384 e-. During this first monitoring, exposures in the V and R Johnson-Cousins filters were taken every night when clear, which makes a total of 20 observing
nights. Bad weather in March and April 2003 prevented us from achieving a very dense sampling.
For each monitoring night we had three consecutive frames on each filter, i.e., three 300 s
exposures in the V passband and three 180 s exposures in the R passband. Those were the
maximum exposure times to avoid saturation of selected stars in the field. In Fig. 1 we show
a typical frame. In this typical exposure, half a dozen bright and non-saturated stars were
fitted within the field of view (FOV). Following the notation of Kochanek et al. (1997), the
FOV included the gravitationally lensed quasar ("GL") and nearby field stars "a'' (South), "b'' (North), and "c'' (West). The FOV also included two stars that were introduced by Nakos et al.
(2003) and were labeled as "s1'' and "s2''. These two stars are placed relatively far from the
gravitational lens system, and they appear close to the NW edge of the frame (see Fig. 1). A sixth star ("x'') appears close to the SW edge of the typical frame.
m, giving a 0.4 arcsec pixel-1 angular scale. The gain is 6.55 e-/ADU and the
readout noise is 6.384 e-. During this first monitoring, exposures in the V and R Johnson-Cousins filters were taken every night when clear, which makes a total of 20 observing
nights. Bad weather in March and April 2003 prevented us from achieving a very dense sampling.
For each monitoring night we had three consecutive frames on each filter, i.e., three 300 s
exposures in the V passband and three 180 s exposures in the R passband. Those were the
maximum exposure times to avoid saturation of selected stars in the field. In Fig. 1 we show
a typical frame. In this typical exposure, half a dozen bright and non-saturated stars were
fitted within the field of view (FOV). Following the notation of Kochanek et al. (1997), the
FOV included the gravitationally lensed quasar ("GL") and nearby field stars "a'' (South), "b'' (North), and "c'' (West). The FOV also included two stars that were introduced by Nakos et al.
(2003) and were labeled as "s1'' and "s2''. These two stars are placed relatively far from the
gravitational lens system, and they appear close to the NW edge of the frame (see Fig. 1). A sixth star ("x'') appears close to the SW edge of the typical frame.
Table 1:
Observations of SBS 0909+532 in 2003.
![\begin{figure}
\par\includegraphics[width=4cm,clip]{4283f2.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg54.gif) |
Figure 2:
Maidanak zoomed-in image of SBS 0909+532 (about 8
 on a side). We chose one
of the frames taken with the best seeing conditions, and then expanded the portion occupied by
the two quasar components A (the brightest object) and B (the faintest object), i.e., the GL in
Fig. 1. To avoid the pixellation effect when a subframe is expanded, the brightness distribution
is also smoothed.
on a side). We chose one
of the frames taken with the best seeing conditions, and then expanded the portion occupied by
the two quasar components A (the brightest object) and B (the faintest object), i.e., the GL in
Fig. 1. To avoid the pixellation effect when a subframe is expanded, the brightness distribution
is also smoothed. |
| Open with DEXTER |
The second set of observations include frames in February 2003, as well as during April-May
and October-November 2003. The total number of nights is 18. In this second program the
images were taken with the 1.5 m AZT-22 telescope at Maidanak Observatory (Uzbekistan),
with near diffraction-limited optics and careful thermo-stabilization, which allowed for
high-angular-resolution imaging. The AZT-22 telescope has a LN-cooled (liquid nitrogen
cooled) CCD-camera, SITe-005 CCD, manufactured in Copenhagen (Denmark). For this camera, the
imaging area is split into
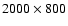 pixel, where the pixel size is 15
pixel, where the pixel size is 15 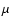 m and the
intrinsic angular scale is 0.26 arcsec pixel-1. The frames were taken in the R
Bessel filter, which corresponds approximately to the R Johnson-Cousins passband. The poor
tracking system of this telescope allows exposures only up to 3 min. To obtain sufficiently
high photometric accuracy, we took several frames each observation night. With respect to the
rectangular FOV of the telescope, the North/South coverage was 2.5 times smaller than the
East/West one, so the "s1'', "s2'', and "x'' stars were not included within the FOV. Figure 2 shows
a zoomed-in image made from one of the best frames in terms of seeing. There are two close
quasar components, but the very faint galaxy is not apparent. The observations at Mt. Maidanak
are part of IAKhNU, SAI, and UBAI projects to follow up on the variability of gravitationally
lensed quasars.
m and the
intrinsic angular scale is 0.26 arcsec pixel-1. The frames were taken in the R
Bessel filter, which corresponds approximately to the R Johnson-Cousins passband. The poor
tracking system of this telescope allows exposures only up to 3 min. To obtain sufficiently
high photometric accuracy, we took several frames each observation night. With respect to the
rectangular FOV of the telescope, the North/South coverage was 2.5 times smaller than the
East/West one, so the "s1'', "s2'', and "x'' stars were not included within the FOV. Figure 2 shows
a zoomed-in image made from one of the best frames in terms of seeing. There are two close
quasar components, but the very faint galaxy is not apparent. The observations at Mt. Maidanak
are part of IAKhNU, SAI, and UBAI projects to follow up on the variability of gravitationally
lensed quasars.
For the past six years, the TAU group has been monitoring several gravitationally lensed quasars
with the Wise Observatory 1 m telescope. The targets are mainly monitored in the Johnson-Cousins
R-band, and the frames obtained with a cryogenically cooled Tektronix
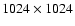 -pixel back-illuminated CCD. The angular scale is 0.7 arcsec per pixel. This
pixel scale and the median seeing (FWHM) of about 2
-pixel back-illuminated CCD. The angular scale is 0.7 arcsec per pixel. This
pixel scale and the median seeing (FWHM) of about 2
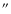 do not allow resolving most of the
lensed objects, e.g., SBS 0909+532. However, the frames of SBS 0909+532 in 2003 are characterized
by wide FOVs, which incorporate the "a-c'', "s1-s2'', and "x'' stars. This fact permits differential
photometry between several pairs of field stars to be done, and thus the reliability
of the Calar Alto and Maidanak records to be tested.
do not allow resolving most of the
lensed objects, e.g., SBS 0909+532. However, the frames of SBS 0909+532 in 2003 are characterized
by wide FOVs, which incorporate the "a-c'', "s1-s2'', and "x'' stars. This fact permits differential
photometry between several pairs of field stars to be done, and thus the reliability
of the Calar Alto and Maidanak records to be tested.
The pre-processing of the images included the usual bias subtraction, flat fielding using sky
flats, sky subtraction, and cosmic-ray removal by using the Image Reduction and Analysis
Facility (IRAF) and Munich Image Data Analysis System (MIDAS) environments. Some details about the
whole observational campaign are included in Table 1 (observatories, telescopes, frames/night,
filters, and observation periods).
Due to the small angular separation between the two lensed components, about 1
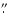 1 (Kochanek
et al. 1997), the photometry of SBS 0909+532 is a difficult task. This task is also complicated
by the presence of the main lensing galaxy between the components, which could make the
computation of individual fluxes even harder. In general, aperture photometry does not work, so
we must look for better approaches. An initial issue is to decide whether to include a
photometric model for the lensing galaxy. In principle, when computing the fluxes
of SBS 0909+532, we may use a galaxy model derived from the HST images of the system. The galaxy
model could also be inferred from the best images in terms of seeing. Once the relevant
information on the galaxy is known, we apply a PSF fitting method to all optical images,
setting the galaxy properties to those derived from the HST or the best-quality images, and
allowing the remaining parameters to vary (e.g., McLeod et al. 1998; Ullán et al. 2003).
1 (Kochanek
et al. 1997), the photometry of SBS 0909+532 is a difficult task. This task is also complicated
by the presence of the main lensing galaxy between the components, which could make the
computation of individual fluxes even harder. In general, aperture photometry does not work, so
we must look for better approaches. An initial issue is to decide whether to include a
photometric model for the lensing galaxy. In principle, when computing the fluxes
of SBS 0909+532, we may use a galaxy model derived from the HST images of the system. The galaxy
model could also be inferred from the best images in terms of seeing. Once the relevant
information on the galaxy is known, we apply a PSF fitting method to all optical images,
setting the galaxy properties to those derived from the HST or the best-quality images, and
allowing the remaining parameters to vary (e.g., McLeod et al. 1998; Ullán et al. 2003).
Magain et al. (1998) also presented an alternative task (deconvolution) that combines
all the frames obtained at different epochs to determine the numerical light distribution of the
lensing galaxy, as well as the positions of the point-like sources (quasar components), since
these parameters do not vary with time. The flux of the point-like sources are allowed to vary
from image to image, which produces the light curves. However, these and other procedures have a
reasonable limitation: they only work well when the galaxy light makes a significant contribution
to the crowded regions in the individual frames. For a very faint galaxy in a standard (i.e., not
superb) frame, there is confusion between galaxy signal and noise, so the use of a given galaxy
model could lead to biased fluxes of the components. The biases will depend on the quality of
the image (seeing, signal-to-noise ratio, etc.), which must produce artificial variability
superposed on the real one. On the other hand, the use of a direct PSF fitting method
(neglecting the galaxy brightness) leads to contaminated fluxes of the components. But if the
galaxy is very faint, the contaminations will be small. Moreover, the variation of the quasar
fluxes, seeing conditions, etc., will cause fluctuations in the contaminations, which are
expected to be below the typical contamination levels. For standard frames of a quasar lensed
by a very faint extended object, it is really difficult to choose between the approaches with
and without galaxy.
Most of the Calar Alto and Maidanak individual frames of SBS 0909+532 do not show evidence
of a galaxy brightness profile. This is due to the faintness of the galaxy, as we corroborate
below. If we consider a hypothetical astronomer who neglects the galaxy brightness and
does direct PSF fitting without taking the galaxy into account when computing the
fluxes, it is possible to roughly estimate the maximum contamination from the galaxy
to the closest component A (at 0
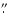 4 from the centre of the deflector). We take the paper about
10 lens systems by Lehár et al. (2000) into account, where, in Table 3, we can find the best
available photometric and astrometric (HST) data for SBS 0909+532. The authors were able to trace the
galaxy light in the H passband by measuring its position and brightness. If we use the colours in
the same table, we conclude that
4 from the centre of the deflector). We take the paper about
10 lens systems by Lehár et al. (2000) into account, where, in Table 3, we can find the best
available photometric and astrometric (HST) data for SBS 0909+532. The authors were able to trace the
galaxy light in the H passband by measuring its position and brightness. If we use the colours in
the same table, we conclude that
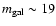 mag and
mag and
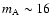 mag in the I band
(near-IR), and that
mag in the I band
(near-IR), and that
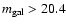 mag and
mag and
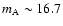 mag in the V optical band. Therefore, as
the R filter is placed just between the I filter and the V one, we may assume that
mag in the V optical band. Therefore, as
the R filter is placed just between the I filter and the V one, we may assume that
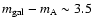 mag in the R band. The difference of 3.5 mag is consistent with a ratio of fluxes
mag in the R band. The difference of 3.5 mag is consistent with a ratio of fluxes
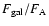 of about 1/25. Thus, in the case of QSO 0957+561, we found a R-band ratio of fluxes
of about 1/25. Thus, in the case of QSO 0957+561, we found a R-band ratio of fluxes
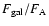 of about 1/2.5 (Ullán et al. 2003), and now we have
of about 1/2.5 (Ullán et al. 2003), and now we have
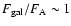 /25, which
explains our unsuccessful efforts when measuring the flux of the lens galaxy in standard frames.
/25, which
explains our unsuccessful efforts when measuring the flux of the lens galaxy in standard frames.
As a result of that, in an extreme case (when direct PSF fitting leads to a magnitude
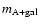 instead of
instead of 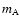 ,
i.e., all the galaxy light is included in the profile of the A component), we find
a relationship:
,
i.e., all the galaxy light is included in the profile of the A component), we find
a relationship:
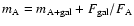 ,
where the true flux (in magnitudes)
,
where the true flux (in magnitudes) 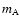 differs
from the contaminated flux through direct PSF fitting (
differs
from the contaminated flux through direct PSF fitting (
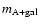 )
in a quantity
)
in a quantity
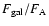 .
This maximum contamination of A would be only of 40 mmag, and the real contamination of both
components will be less than our upper limit. The artificial fluctuations (caused by variable
contamination) will be even smaller than the typical contamination levels, so we expect they will
not play an important role in analyses of quasar variability (e.g., time delay estimates).
.
This maximum contamination of A would be only of 40 mmag, and the real contamination of both
components will be less than our upper limit. The artificial fluctuations (caused by variable
contamination) will be even smaller than the typical contamination levels, so we expect they will
not play an important role in analyses of quasar variability (e.g., time delay estimates).
In order to derive the light curves of the components A and B, we decided to use a direct PSF fitting
method and do not consider the galaxy brightness in the fits. The key idea of this procedure was to
obtain the different fluxes we were interested in by using a PSF that comes from a bright star in the
field that is common to all frames. The point-like objects (quasar components and stars) are modelled by
means of the empirical PSF. Hence, we do not use a theoretical PSF (i.e., Gaussian distribution,
Lorentzian distribution, etc.), but the two-dimensional profile of a star in this field (a PSF star).
Apart from a PSF star, we also need a reference star to do differential photometry and to obtain
relative fluxes
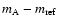 and
and
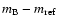 .
The good behaviour of the reference star is
usually checked by using a control star, so the fluxes
.
The good behaviour of the reference star is
usually checked by using a control star, so the fluxes
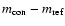 are expected to agree with
a constant level. Nevertheless, since the R-band flux ratio is discussed in Sect. 5, we also want
to obtain a rough estimation of the contaminations from this direct technique. With this aim, a
deconvolution technique (Koptelova et al. 2005) is also applied to a set of frames with good seeing
and signal. The selected frames are fitted to a model including the galaxy, and thus, we are able to
obtain a few clean fluxes of components A and B and compare them with the corresponding contaminated
fluxes (through a direct PSF fitting). The averaged contaminations are used in Sect. 5.
are expected to agree with
a constant level. Nevertheless, since the R-band flux ratio is discussed in Sect. 5, we also want
to obtain a rough estimation of the contaminations from this direct technique. With this aim, a
deconvolution technique (Koptelova et al. 2005) is also applied to a set of frames with good seeing
and signal. The selected frames are fitted to a model including the galaxy, and thus, we are able to
obtain a few clean fluxes of components A and B and compare them with the corresponding contaminated
fluxes (through a direct PSF fitting). The averaged contaminations are used in Sect. 5.
We adopt a model of the system including two point-like sources and a constant background. The
model is fitted to each image by adjusting its 7 free parameters (two-dimensional positions of A and B, instrumental fluxes of both components and background) to minimize the sum of the square residuals,
as described in McLeod et al. (1998) and Lehár et al. (2000). We use windows of
 pixel. Each empirical PSF is a subframe of
pixel. Each empirical PSF is a subframe of
 pixel around the PSF star (the "a'' star in
Fig. 1), while the lens system is analysed from a subframe of the same size, but centred on the
double quasar. The instrumental fluxes of the "b'', "c'', "s1'', and "s2'' stars are also inferred from
pixel around the PSF star (the "a'' star in
Fig. 1), while the lens system is analysed from a subframe of the same size, but centred on the
double quasar. The instrumental fluxes of the "b'', "c'', "s1'', and "s2'' stars are also inferred from
 pixel windows centred on them. We initially focus on the nearby field stars, and take the "b-c'' stars as the control-reference objects. The "a'' object is the brightest star in the "a-c'' triangle, and "b'' and "c'' were spectroscopically identified by Kochanek et al. (1997) and Zickgraf et al. (2003): "b'' is a FG star, whose spectrum includes the G-band and Ca II H-K lines, and "c'' is an M 3 star. The R - I and B - R colours of the brightest component (A) and the "a'' star are similar,
the colours of the faintest component (B) are close to the colours of the "b'' star, and the "c'' star has
colours different to those of the components and the "a-b'' stars (see Table 1 of Kochanek et al. 1997).
On the other hand, after checking the PSFs of the three nearby field stars ("a-c''), we do not find
significant differences between them. This suggests that the global shape of the PSFs around the lens
system does not depend on the position and colour of the point-like objects, so the PSF of the "a'' star
seems to be a reliable tracer of the PSF associated with any point-like object in the region of
interest.
pixel windows centred on them. We initially focus on the nearby field stars, and take the "b-c'' stars as the control-reference objects. The "a'' object is the brightest star in the "a-c'' triangle, and "b'' and "c'' were spectroscopically identified by Kochanek et al. (1997) and Zickgraf et al. (2003): "b'' is a FG star, whose spectrum includes the G-band and Ca II H-K lines, and "c'' is an M 3 star. The R - I and B - R colours of the brightest component (A) and the "a'' star are similar,
the colours of the faintest component (B) are close to the colours of the "b'' star, and the "c'' star has
colours different to those of the components and the "a-b'' stars (see Table 1 of Kochanek et al. 1997).
On the other hand, after checking the PSFs of the three nearby field stars ("a-c''), we do not find
significant differences between them. This suggests that the global shape of the PSFs around the lens
system does not depend on the position and colour of the point-like objects, so the PSF of the "a'' star
seems to be a reliable tracer of the PSF associated with any point-like object in the region of
interest.
As a first attempt to obtain light curves, we use the "b'' and "c'' stars as the control and reference
objects, respectively. Unfortunately, we find clear evidence of variability of the "c'' star,
since the three curves
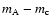 ,
,
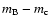 and
and
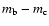 have a similar global behaviour. This
fact forces us to rule out the "c'' star as a reference-control object and, thus, to take the "a'' and "b'' nearby field stars as the control and reference point-like sources, respectively. In the next subsection,
we analyse the Maidanak-Wise fluxes
have a similar global behaviour. This
fact forces us to rule out the "c'' star as a reference-control object and, thus, to take the "a'' and "b'' nearby field stars as the control and reference point-like sources, respectively. In the next subsection,
we analyse the Maidanak-Wise fluxes
 and show that both stars ("a'' and "b'') are non-variable
objects. This result guaranties the good behaviour of "b''. The Calar Alto fluxes
and show that both stars ("a'' and "b'') are non-variable
objects. This result guaranties the good behaviour of "b''. The Calar Alto fluxes
 are not included in the analysis, since most Calar Alto data disagree with the Maidanak-Wise
common level of flux. We found an anomaly in the behaviour of the Calar Alto relative fluxes for widely
separate stars (see below), so only the relative fluxes for neighbouring point-like objects are reliable
photometric measurements. Fortunately, the comparison between the quasar components and the "b'' nearby
reference star seems to be a feasible approach.
are not included in the analysis, since most Calar Alto data disagree with the Maidanak-Wise
common level of flux. We found an anomaly in the behaviour of the Calar Alto relative fluxes for widely
separate stars (see below), so only the relative fluxes for neighbouring point-like objects are reliable
photometric measurements. Fortunately, the comparison between the quasar components and the "b'' nearby
reference star seems to be a feasible approach.
After applying the photometric method to the three individual frames for each filter and night (see
Table 1), we obtain three different measurements of
 and
and
 in the V and R passbands for each night. To test the reliability of the instrumental fluxes of A and B, we analyse
the residues in each residual frame. A residual frame is an image after subtracting the fitted background
and point-like objects (PSF fitting method). More properly, we focus on the residual subframe occupied by
the system, and then we estimate the residue-to-signal ratio (R/S) in each pixel of interest. An R/S value less than 10% is acceptable, so a subframe with at least 90% of the pixels having acceptable residues
is considered to be related to reliable photometric solutions. Thus, we classify the individual fits in
two categories: fits leading to <90% of pixels having acceptable residues (bad fits, unreliable
results) and good fits that are associated with reliable results (
in the V and R passbands for each night. To test the reliability of the instrumental fluxes of A and B, we analyse
the residues in each residual frame. A residual frame is an image after subtracting the fitted background
and point-like objects (PSF fitting method). More properly, we focus on the residual subframe occupied by
the system, and then we estimate the residue-to-signal ratio (R/S) in each pixel of interest. An R/S value less than 10% is acceptable, so a subframe with at least 90% of the pixels having acceptable residues
is considered to be related to reliable photometric solutions. Thus, we classify the individual fits in
two categories: fits leading to <90% of pixels having acceptable residues (bad fits, unreliable
results) and good fits that are associated with reliable results (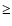 90% of pixels having acceptable
residues). As a complementary test, we study the relation between the quality of the fits (in terms of
post-fit residues) and two relevant parameters (image quality). The signal-to-noise at the brightest pixel of the lens system,
90% of pixels having acceptable
residues). As a complementary test, we study the relation between the quality of the fits (in terms of
post-fit residues) and two relevant parameters (image quality). The signal-to-noise at the brightest pixel of the lens system,
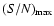 ,
and the seeing, FWHM (in
,
and the seeing, FWHM (in
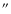 ), are the two parameters to
compare with the fit quality. Some kind of correlation between good fits and good images is expected. In
Fig. 3 we draw the
), are the two parameters to
compare with the fit quality. Some kind of correlation between good fits and good images is expected. In
Fig. 3 we draw the
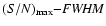 plots for frames in the R filter (top panel) and the V filter (bottom panel). Circles and triangles represent good and bad fits, respectively. The plots in
Fig. 3 indicate that the good fits correspond to images with high or moderate
plots for frames in the R filter (top panel) and the V filter (bottom panel). Circles and triangles represent good and bad fits, respectively. The plots in
Fig. 3 indicate that the good fits correspond to images with high or moderate
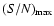 (
(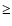 30).
Moreover, at moderate
30).
Moreover, at moderate
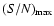 (
( 30-50), most of the good fits seem to be associated with a
relatively good seeing (<2
30-50), most of the good fits seem to be associated with a
relatively good seeing (<2
 ). To obtain robust photometry, we finally discard the frames
corresponding to the triangles in Fig. 3. For each filter and night, if there are two or three good
frames (good fits), then we get mean values of
). To obtain robust photometry, we finally discard the frames
corresponding to the triangles in Fig. 3. For each filter and night, if there are two or three good
frames (good fits), then we get mean values of 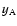 and
and 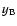 ,
and compute standard deviation of means
as errors. We only consider relative fluxes with uncertainties
,
and compute standard deviation of means
as errors. We only consider relative fluxes with uncertainties 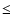 40 mmag.
40 mmag.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{4283f3.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg78.gif) |
Figure 3:
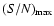 versus
versus
 for the Calar Alto frames in the R filter ( top panel) and
the V filter ( bottom panel). The circles and triangles represent the frames with good and bad
post-fit residues, respectively (see main text).
for the Calar Alto frames in the R filter ( top panel) and
the V filter ( bottom panel). The circles and triangles represent the frames with good and bad
post-fit residues, respectively (see main text). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{4283f4.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg79.gif) |
Figure 4:
Calar Alto light curves of the double quasar in the R filter. We use the "b'' star as the
reference object, because it is confirmed as a non-variable star in Fig. 7. The circles are the
fluxes 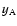 (
(
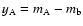 )
and the squares are the fluxes )
and the squares are the fluxes
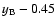 mag ( mag (
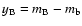 ).
The A light curve has a final decline, while the B light curve ends in a rise. ).
The A light curve has a final decline, while the B light curve ends in a rise. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{4283f5.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg80.gif) |
Figure 5:
Calar Alto light curves of the double quasar in the V filter. We use the non-variable
star "b'' as reference object (see Fig. 7). The circles are the fluxes 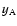 and the squares are the
fluxes
and the squares are the
fluxes
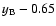 mag. mag. |
| Open with DEXTER |
Now we plot 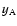 (circles) and
(circles) and
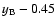 mag (squares) in Fig. 4 (R-band fluxes). If we
concentrate our attention on the period with the best sampling (after day 2755), the A light curve shows
a moderate decline and the B record shows a moderate rise. Indeed, it seems that the "b'' star is a good
reference object (constant flux), since there is no zero-lag global correlation between
mag (squares) in Fig. 4 (R-band fluxes). If we
concentrate our attention on the period with the best sampling (after day 2755), the A light curve shows
a moderate decline and the B record shows a moderate rise. Indeed, it seems that the "b'' star is a good
reference object (constant flux), since there is no zero-lag global correlation between 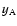 and
and 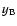 .
In Fig. 5 we show the light curves
.
In Fig. 5 we show the light curves 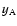 and
and
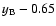 mag in the V passband. In this case we have
a total of 11 points for the A component (circles) and 10 points for the B component (squares). The
V-band and R-band light curves of the A component are consistent with each other. A final moderate
decline appears in both curves. The situation is more confused for the B component. The R-band final
rise is not clearly reproduced in the V band, and the V-band final measurements could have
underestimated formal errors. We note the relative faintness of B in the V band (
mag in the V passband. In this case we have
a total of 11 points for the A component (circles) and 10 points for the B component (squares). The
V-band and R-band light curves of the A component are consistent with each other. A final moderate
decline appears in both curves. The situation is more confused for the B component. The R-band final
rise is not clearly reproduced in the V band, and the V-band final measurements could have
underestimated formal errors. We note the relative faintness of B in the V band (
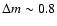 mag), and thus the possibility of systematic uncertainties when the PSF fitting method is applied at
some epochs. The data in both optical filters are available at http://grupos.unican.es/glendama/.
mag), and thus the possibility of systematic uncertainties when the PSF fitting method is applied at
some epochs. The data in both optical filters are available at http://grupos.unican.es/glendama/.
After presenting the records of the double quasar, we concentrate on the Calar Alto light curves of
the field stars that were previously introduced by Kochanek et al. (1997) and Nakos et al. (2003), i.e.,
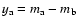 ,
,
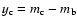 ,
,
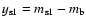 ,
and
,
and
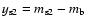 .
There are no
previous studies on the variability of the nearby field stars "a-c''. On the other hand, the farther
field stars ("s1-s2'') were verified as non-variable by using 76 Wise frames taken from December 24, 1999
to March 3, 2002 (Nakos et al. 2003). As Nakos et al. (2003) found that "s1'' and "s2'' seem
to be useful reference stars, we check the behaviour of "s1-s2'' in 2003. The PSF of the stars in the
surroundings of the double quasar could differ slightly from the PSF of the "s1-s2'' stars in a
relatively far region. Therefore, we must be careful when obtaining the instrumental fluxes of the
farther stars. To detect possible anomalies caused by a mismatch between the brightness profile of the
"a'' star and the PSF of "s1-s2'', the light curves
.
There are no
previous studies on the variability of the nearby field stars "a-c''. On the other hand, the farther
field stars ("s1-s2'') were verified as non-variable by using 76 Wise frames taken from December 24, 1999
to March 3, 2002 (Nakos et al. 2003). As Nakos et al. (2003) found that "s1'' and "s2'' seem
to be useful reference stars, we check the behaviour of "s1-s2'' in 2003. The PSF of the stars in the
surroundings of the double quasar could differ slightly from the PSF of the "s1-s2'' stars in a
relatively far region. Therefore, we must be careful when obtaining the instrumental fluxes of the
farther stars. To detect possible anomalies caused by a mismatch between the brightness profile of the
"a'' star and the PSF of "s1-s2'', the light curves
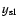 and
and
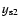 are derived from both PSF
fitting and aperture methods.
are derived from both PSF
fitting and aperture methods.
The records 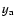 ,
,
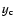 ,
,
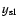 ,
and
,
and
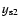 in the R filter are
depicted in Fig. 6. To guide the eyes, we use some offsets and dashed horizontal lines and put all
the relative records of each pair within a box. Filled and open symbols are associated with PSF fitting
and aperture, respectively. The top box includes the
in the R filter are
depicted in Fig. 6. To guide the eyes, we use some offsets and dashed horizontal lines and put all
the relative records of each pair within a box. Filled and open symbols are associated with PSF fitting
and aperture, respectively. The top box includes the
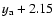 mag fluxes (open squares). The second,
third, and fourth boxes (under the top one) correspond to the
mag fluxes (open squares). The second,
third, and fourth boxes (under the top one) correspond to the 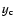 (filled squares),
(filled squares),
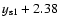 mag (filled and open triangles), and
mag (filled and open triangles), and
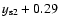 mag (filled and open circles) records, respectively.
As most of the stars are brighter than the quasar components (A and B) and they are far from other
objects, the typical formal errors in the stellar fluxes are clearly less than the typical uncertainties
in the fluxes of the components (usually fainter and are placed in a crowded region). The
stellar error bars in Fig. 6 are often smaller than the sizes of the associated symbols.
mag (filled and open circles) records, respectively.
As most of the stars are brighter than the quasar components (A and B) and they are far from other
objects, the typical formal errors in the stellar fluxes are clearly less than the typical uncertainties
in the fluxes of the components (usually fainter and are placed in a crowded region). The
stellar error bars in Fig. 6 are often smaller than the sizes of the associated symbols.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{4283f6.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg84.gif) |
Figure 6:
Calar Alto light curves of the stars in the R filter. The Calar Alto fluxes are checked from six Wise frames. Filled and open symbols are associated with PSF fitting and aperture, respectively.
First, the non-variable star "b'' (see Fig. 7) is taken as the reference object. The top box incorporates
the behaviour of
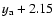 mag ( mag (
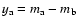 ): Calar Alto (open squares) and Wise (open triangles).
The second box (under the top box) contains the fluxes ): Calar Alto (open squares) and Wise (open triangles).
The second box (under the top box) contains the fluxes  (
(
 ): Calar Alto (filled
squares) and Wise (open circles). The third and fourth boxes include the ): Calar Alto (filled
squares) and Wise (open circles). The third and fourth boxes include the
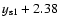 mag ( mag (
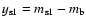 )
and )
and
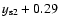 mag ( mag (
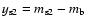 )
records, respectively. In the third box:
Calar Alto (filled and open triangles) and Wise (open astroids); in the fourth box: Calar Alto
(filled and open circles) and Wise (open rhombuses). Second, we plot the )
records, respectively. In the third box:
Calar Alto (filled and open triangles) and Wise (open astroids); in the fourth box: Calar Alto
(filled and open circles) and Wise (open rhombuses). Second, we plot the
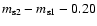 mag
records in the bottom box: Calar Alto (filled and open star symbols) and Wise (open crosses). mag
records in the bottom box: Calar Alto (filled and open star symbols) and Wise (open crosses). |
| Open with DEXTER |
When doing aperture photometry on six R-band Wise frames covering the first semester of 2003, we
obtain a
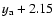 mag light curve (open triangles in the top box of Fig. 6) that disagrees with the
Calar Alto trend in the overlap period (between days 2710 and 2760). In the next subsection, we show
that the Wise and Maidanak brightnesses are constant and consistent with each other, so the Calar Alto
values of
mag light curve (open triangles in the top box of Fig. 6) that disagrees with the
Calar Alto trend in the overlap period (between days 2710 and 2760). In the next subsection, we show
that the Wise and Maidanak brightnesses are constant and consistent with each other, so the Calar Alto
values of  are not true fluxes, but anomalous results. On the contrary, the Wise light curve
are not true fluxes, but anomalous results. On the contrary, the Wise light curve 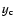 (open circles in the second box of Fig. 6) agrees with the Calar Alto curve in the overlap period. From
the Wise frames we confirm the flux level during the high-state of "c''. Unfortunately, the
small-amplitude variability of "c'' (rms fluctuation of
(open circles in the second box of Fig. 6) agrees with the Calar Alto curve in the overlap period. From
the Wise frames we confirm the flux level during the high-state of "c''. Unfortunately, the
small-amplitude variability of "c'' (rms fluctuation of 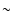 8 mmag) cannot be confirmed from the Wise
data. The rms fluctuation of the Wise fluxes (
8 mmag) cannot be confirmed from the Wise
data. The rms fluctuation of the Wise fluxes (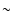 9 mmag) is very similar to the Calar Alto variation,
but the formal errors are relatively large (
9 mmag) is very similar to the Calar Alto variation,
but the formal errors are relatively large (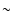 10 mmag). Moreover, there are no Wise frames in May 2003
(around the day 2780) and, thus, we cannot check (via Wise data) the reliability of the Calar Alto
dip in
10 mmag). Moreover, there are no Wise frames in May 2003
(around the day 2780) and, thus, we cannot check (via Wise data) the reliability of the Calar Alto
dip in 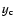 (80-100 mmag). However, the flux of the "c'' star at day 2793 in the V band confirms the
existence of a transition from the low-state to the high-state, which is finished at days 2800-2810
(see the last open circle in the second box of Fig. 6).
(80-100 mmag). However, the flux of the "c'' star at day 2793 in the V band confirms the
existence of a transition from the low-state to the high-state, which is finished at days 2800-2810
(see the last open circle in the second box of Fig. 6).
For the "s1-s2'' stars, which are as far from
star "b'' as star "a'' is, we again find a disagreement between the Calar Alto trends and the Wise records
(open astroids and rhombuses in the third and fourth boxes of Fig. 6). Although aperture curves are
closer to the Wise behaviours, we cannot reproduce the Wise data fairly. Some probes with the "x'' star (using
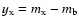 )
also indicate that the Calar Alto and Wise behaviours disagree. It seems
that the differential photometry between widely separate stars may lead to meaningless results, and only
the relative fluxes for neighbouring objects are reliable. To test this conclusion, apart from the
successful results through the neighbouring stars "b'' and "c'', we also analyse the differential
photometry between the pair "s1-s2'' (see Fig. 1). The curves
)
also indicate that the Calar Alto and Wise behaviours disagree. It seems
that the differential photometry between widely separate stars may lead to meaningless results, and only
the relative fluxes for neighbouring objects are reliable. To test this conclusion, apart from the
successful results through the neighbouring stars "b'' and "c'', we also analyse the differential
photometry between the pair "s1-s2'' (see Fig. 1). The curves
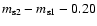 mag are depicted
in the bottom box of Fig. 6: Calar Alto (filled and open star symbols) and Wise (open crosses). In the
overlap period (from day 2710 to day 2760), there is reasonable agreement between the results from both
observatories, and the Calar Alto measurements seem to be quite reliable. From the Calar Alto frames,
both photometric techniques are consistent with each other, but a constant flux cannot explain the
observations. When we fit the data sets to a constant, our best solutions are characterised by
mag are depicted
in the bottom box of Fig. 6: Calar Alto (filled and open star symbols) and Wise (open crosses). In the
overlap period (from day 2710 to day 2760), there is reasonable agreement between the results from both
observatories, and the Calar Alto measurements seem to be quite reliable. From the Calar Alto frames,
both photometric techniques are consistent with each other, but a constant flux cannot explain the
observations. When we fit the data sets to a constant, our best solutions are characterised by
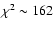 (PSF fitting) and
(PSF fitting) and
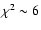 (aperture). It is a curious fact that aperture photometry on
only one frame per night leads to relative fluxes in rough agreement with a constant level. However, more
refined measurements (aperture or PSF fitting on several frames per night) reveal the variability of one
("s1'' or "s2'') or both stars.
(aperture). It is a curious fact that aperture photometry on
only one frame per night leads to relative fluxes in rough agreement with a constant level. However, more
refined measurements (aperture or PSF fitting on several frames per night) reveal the variability of one
("s1'' or "s2'') or both stars.
In the case of the R-band Maidanak observations, in order to derive the relative fluxes of the
components of SBS 0909+532, we also use a direct PSF fitting. For a given frame, after obtaining a first
estimate of the free parameters (initial solution), the fit is refined through an iterative procedure,
which works as the CLEAN algorithm (Østensen 1994). The iterative task is done with each individual
image, and the solutions converge after a few cycles. For each night, we take all the available images
and obtain the mean values of 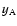 and
and 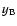 .
From the standard deviation of the means, we also derive
the errors in
.
From the standard deviation of the means, we also derive
the errors in 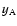 and
and 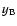 .
In agreement with the criteria in Sect. 3.1, only fluxes with errors
less than or equal to 40 mmag are considered. Apart from the analysis of the lens system, using aperture
photometry, we also measure
.
In agreement with the criteria in Sect. 3.1, only fluxes with errors
less than or equal to 40 mmag are considered. Apart from the analysis of the lens system, using aperture
photometry, we also measure 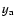 .
The relative fluxes
.
The relative fluxes 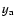 are depicted in Fig. 7 (open star symbols).
The Maidanak measurements in the first semester of 2003 and the six Wise data of
are depicted in Fig. 7 (open star symbols).
The Maidanak measurements in the first semester of 2003 and the six Wise data of 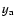 (open triangles;
see here above) are tightly distributed around -0.842 mag (solid line in Fig. 7). The rms fluctuation
of the data is only
(open triangles;
see here above) are tightly distributed around -0.842 mag (solid line in Fig. 7). The rms fluctuation
of the data is only 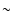 6 mmag (see the dashed lines in Fig. 7), which is consistent with the
typical error of the measurements. The
6 mmag (see the dashed lines in Fig. 7), which is consistent with the
typical error of the measurements. The 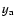 results in Fig. 7 suggest that both "a'' and "b'' are
non-variable objects. Through 2003 (first and second semesters), we did not find any evidence in favour
of variability of the "a-b'' stars.
results in Fig. 7 suggest that both "a'' and "b'' are
non-variable objects. Through 2003 (first and second semesters), we did not find any evidence in favour
of variability of the "a-b'' stars.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{4283f7.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg88.gif) |
Figure 7:
Maidanak (open star symbols) and Wise (open triangles) light curves 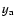 in the R filter (from late January to the middle of June 2003). The solid line represents the global mean value and
the two dashed lines describe the rms fluctuation of the measurements. This rms variation agrees with the
typical uncertainty, so "a'' and "b'' seem to be non-variable sources.
in the R filter (from late January to the middle of June 2003). The solid line represents the global mean value and
the two dashed lines describe the rms fluctuation of the measurements. This rms variation agrees with the
typical uncertainty, so "a'' and "b'' seem to be non-variable sources. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{4283f8.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg89.gif) |
Figure 8:
Global R-band fluxes of SBS 0909+532 in 2003. The open circles (Maidanak) and filled circles
(Calar Alto) are the fluxes 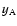 ,
whereas the open squares (Maidanak) and filled squares (Calar Alto) are
the relative fluxes ,
whereas the open squares (Maidanak) and filled squares (Calar Alto) are
the relative fluxes
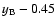 mag. The top panel contains the results from early February to late May 2003
and the bottom panel includes the results from the middle of October to late November 2003. mag. The top panel contains the results from early February to late May 2003
and the bottom panel includes the results from the middle of October to late November 2003. |
| Open with DEXTER |
We show our global R-band light curves of SBS 0909+532 in Fig. 8. The open circles (Maidanak) and
filled circles (Calar Alto) are the measurements of 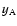 ,
while the open squares (Maidanak) and filled
squares (Calar Alto) are the values of
,
while the open squares (Maidanak) and filled
squares (Calar Alto) are the values of
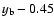 mag. We have 31 points for the A component (circles)
and 26 points for the B one (squares). The top panel of Fig. 8 contains the results from early February
to late May 2003 and the bottom panel of Fig. 8 includes the results from the middle of October to late
November 2003. For each component we
test the existence of a bias between the Calar Alto and Maidanak fluxes, e.g.,
mag. We have 31 points for the A component (circles)
and 26 points for the B one (squares). The top panel of Fig. 8 contains the results from early February
to late May 2003 and the bottom panel of Fig. 8 includes the results from the middle of October to late
November 2003. For each component we
test the existence of a bias between the Calar Alto and Maidanak fluxes, e.g.,
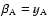 (Calar
Alto
(Calar
Alto
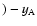 (Maidanak). Very small biases of
(Maidanak). Very small biases of
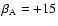 mmag and
mmag and
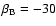 mmag are
found, and these corrections are taken into account to get the overall records in Fig. 8. The biases are
derived from the comparison between the Maidanak fluxes in a thirty day period (from day 2750 to day 2780) and the Calar Alto fluxes at equal or close dates (see the top panel of Fig. 8).
mmag are
found, and these corrections are taken into account to get the overall records in Fig. 8. The biases are
derived from the comparison between the Maidanak fluxes in a thirty day period (from day 2750 to day 2780) and the Calar Alto fluxes at equal or close dates (see the top panel of Fig. 8).
To roughly estimate contaminations from the direct PSF fitting technique, we take some of our best
Maidanak images (in terms of seeing conditions,
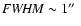 )
in the R band. A zoom-in of
one of these best frames is shown in Fig. 2. First, we combine the selected frames and derive a
numerical model of the galaxy from a regularizing algorithm. To produce a stabler reconstruction,
the real galaxy profile is assumed to be close to the Sersic profile (Koptelova et al. 2005). Our
deconvolution method differs only slightly from the former deconvolution techniques by Magain et al. (1998) and Burud et al. (1998). Figure 9 presents the galaxy reconstruction obtained from the
stack of the R-band selected frames. The box in Fig. 9 is 16
)
in the R band. A zoom-in of
one of these best frames is shown in Fig. 2. First, we combine the selected frames and derive a
numerical model of the galaxy from a regularizing algorithm. To produce a stabler reconstruction,
the real galaxy profile is assumed to be close to the Sersic profile (Koptelova et al. 2005). Our
deconvolution method differs only slightly from the former deconvolution techniques by Magain et al. (1998) and Burud et al. (1998). Figure 9 presents the galaxy reconstruction obtained from the
stack of the R-band selected frames. The box in Fig. 9 is 16
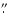 6 on a side. The positions of the
components are labeled with two crosses: A is on the left and B is on the right. The innermost contours
are circular-elliptical rings, whereas the outermost contours show a less definite shape. Secondly,
the selected frames are fitted to a photometric model that includes the galaxy brightness. Therefore,
we are able to infer clean relative fluxes of A and B (without contamination by galaxy light) and to compare them with the contaminated ones (from direct PSF fitting). As result of the comparison, we
report typical (averaged) contaminations of 18.8 mmag and 4 mmag for the A and B components,
respectively. These very weak contaminations are in reasonable agreement with our preliminary
considerations in the beginning of this section and are taken into account in the measurement of the R-band flux ratio in Sect. 5.
6 on a side. The positions of the
components are labeled with two crosses: A is on the left and B is on the right. The innermost contours
are circular-elliptical rings, whereas the outermost contours show a less definite shape. Secondly,
the selected frames are fitted to a photometric model that includes the galaxy brightness. Therefore,
we are able to infer clean relative fluxes of A and B (without contamination by galaxy light) and to compare them with the contaminated ones (from direct PSF fitting). As result of the comparison, we
report typical (averaged) contaminations of 18.8 mmag and 4 mmag for the A and B components,
respectively. These very weak contaminations are in reasonable agreement with our preliminary
considerations in the beginning of this section and are taken into account in the measurement of the R-band flux ratio in Sect. 5.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{4283f9.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg96.gif) |
Figure 9:
Galaxy reconstruction obtained from selected Maidanak frames. Although the double quasar has been
subtracted here, the positions of the components are labeled with two crosses: A is on the left and B is on
the right, and the separation between both crosses is of 1
 1-1 1-1
 2. The galaxy contours cover a
region of 2. The galaxy contours cover a
region of
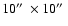 . . |
| Open with DEXTER |
To calculate the time delay between both components of SBS 0909+532, we use the R-band
brightness records from early February to late May 2003. The R-band records are more densely
populated than the V-band ones. Moreover, the R-band time coverage from early February
to late May 2003 (about 120 days) is longer than the time coverage from the middle of October to
late November 2003 (about 50 days). Thus we focus on the R-band data from day 2670 to day 2790, i.e., 22 points in the A component and 19 points in the B component (see the top panel
of Fig. 8). There are a different number of points for component A and component B because we only
consider fluxes with uncertainties below 40 mmag (see Sect. 3). As the B component is fainter,
its photometric uncertainties are larger and the number of final data is smaller. The new light
curves are characterized by a mean sampling rate of one point every six days.
Once we have the data set, a suitable cross-correlation technique is required. Here we mainly
use the  minimization (e.g., Kundic et al. 1997) and the minimum dispersion (D2) method
(Pelt et al. 1994, 1996). However, although other techniques are probably less robust than the
minimization (e.g., Kundic et al. 1997) and the minimum dispersion (D2) method
(Pelt et al. 1994, 1996). However, although other techniques are probably less robust than the
 and D2 ones (doing a first delay measurement without a previous empirical determination),
we also tentatively explore the modified cross-correlation function (MCCF) technique (Beskin &
Oknyanskij 1995; Oknyanskij 1997). The MCCF combines properties of both standard cross-correlation
functions: the CCF by Gaskell & Spark (1986) and the DCF by Edelson & Krolik (1988). We begin our
analysis using the
and D2 ones (doing a first delay measurement without a previous empirical determination),
we also tentatively explore the modified cross-correlation function (MCCF) technique (Beskin &
Oknyanskij 1995; Oknyanskij 1997). The MCCF combines properties of both standard cross-correlation
functions: the CCF by Gaskell & Spark (1986) and the DCF by Edelson & Krolik (1988). We begin our
analysis using the  method, which is based on a comparison between the light curve
method, which is based on a comparison between the light curve  (or
(or 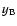 )
and the time shifted light curve
)
and the time shifted light curve 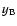 (or
(or 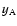 ). For a given lag, one can find the magnitude
offset that minimizes the
). For a given lag, one can find the magnitude
offset that minimizes the  difference. From a set of lags, a set of minima of
difference. From a set of lags, a set of minima of  can
be derived that permits us to make an
can
be derived that permits us to make an  spectrum:
spectrum:  vs. lag. The best solution to the
delay is the lag corresponding to the minimum of the
vs. lag. The best solution to the
delay is the lag corresponding to the minimum of the  spectrum. In general, the shifted epochs
spectrum. In general, the shifted epochs
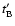 (or
(or
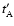 )
do not coincide with the unchanged epochs
)
do not coincide with the unchanged epochs 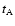 (or
(or 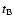 ), so we estimate the
values of
), so we estimate the
values of
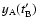 (or
(or
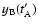 )
by averaging the A (or B) fluxes within bins centred on times
)
by averaging the A (or B) fluxes within bins centred on times
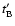 (or
(or
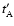 )
with a semiwidth
)
with a semiwidth 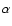 .
To average in each bin, the use of weights is
appropriate depending on the separation between the central time
.
To average in each bin, the use of weights is
appropriate depending on the separation between the central time
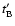 (or
(or
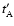 )
and the dates
)
and the dates 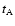 (or
(or 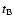 )
in the bin. In principle, we concentrate on the interval [-90, +90] days,
which includes the predicted negative delays (see Introduction), as well as a wide range of
unlikely positive delays (inconsistent with basic observations of the system).
)
in the bin. In principle, we concentrate on the interval [-90, +90] days,
which includes the predicted negative delays (see Introduction), as well as a wide range of
unlikely positive delays (inconsistent with basic observations of the system).
First, the curve 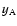 and the time-shifted curve
and the time-shifted curve 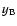 are compared (using bins in the A component).
In order to work with a reasonable time resolution, we use
are compared (using bins in the A component).
In order to work with a reasonable time resolution, we use
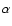 values less than or equal to two times the mean sampling time, i.e.,
values less than or equal to two times the mean sampling time, i.e.,
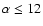 days. The
days. The  value roughly grows with the size of the bin, and
value roughly grows with the size of the bin, and
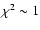 for
for
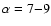 days. For
days. For
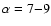 days, there are best solutions
days, there are best solutions
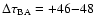 days (
days (
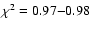 ), and we show the corresponding spectra in Fig. 10. We have drawn together the spectra for
), and we show the corresponding spectra in Fig. 10. We have drawn together the spectra for
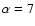 days,
days,
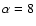 days, and
days, and
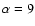 days. Apart from the main minima close to +50 days,
there are other secondary minima at negative and positive lags. In Fig. 10, two secondary
minima seem to stay significant for all the bin sizes: the minima close to -50 days and the
probable edge effects at +80-90 days. We also compare the curve
days. Apart from the main minima close to +50 days,
there are other secondary minima at negative and positive lags. In Fig. 10, two secondary
minima seem to stay significant for all the bin sizes: the minima close to -50 days and the
probable edge effects at +80-90 days. We also compare the curve 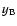 and the time shifted
curve
and the time shifted
curve 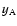 ,
using bins in the B component. For
,
using bins in the B component. For
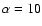 days, we obtain a best solution
days, we obtain a best solution
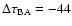 days (
days (
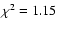 ). Smaller and larger bins lead to solutions
characterised by
). Smaller and larger bins lead to solutions
characterised by
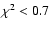 and
and
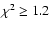 ,
respectively. In Fig. 11, the solid
line represents the spectrum for
,
respectively. In Fig. 11, the solid
line represents the spectrum for
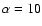 days, while the dashed line represents the
spectrum for
days, while the dashed line represents the
spectrum for
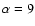 days, and the dotted line traces the spectrum for
days, and the dotted line traces the spectrum for
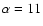 days.
Main minima in the interval of -40-50 days appear in all these cases. Unfortunately,
important signals at positive lags and probable border effects at +80-90 days are again
included in the complex spectra. The important structures at positive lags in Figs. 10, 11 are
probably caused by artifacts in the cross-correlation, so they have no physical origin, but
are due to the 10/20-day gaps and the moderate variability of the components. Therefore,
taking
days.
Main minima in the interval of -40-50 days appear in all these cases. Unfortunately,
important signals at positive lags and probable border effects at +80-90 days are again
included in the complex spectra. The important structures at positive lags in Figs. 10, 11 are
probably caused by artifacts in the cross-correlation, so they have no physical origin, but
are due to the 10/20-day gaps and the moderate variability of the components. Therefore,
taking
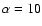 days (bins in the B component) and a negative range [-90, 0] days, we
try to determine a pre-conditioned time delay.
days (bins in the B component) and a negative range [-90, 0] days, we
try to determine a pre-conditioned time delay.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{4283f10.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg111.gif) |
Figure 10:
 spectra for
spectra for
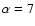 days (dashed line), days (dashed line),
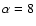 days (solid line), and days (solid line), and
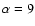 days (dotted line). The parameter days (dotted line). The parameter 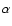 is the semiwidth of the bins in the A component, so the three spectra represent different results of a cross-correlation with reasonable
time-resolution (the mean sampling time is 6 days/point).
is the semiwidth of the bins in the A component, so the three spectra represent different results of a cross-correlation with reasonable
time-resolution (the mean sampling time is 6 days/point). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{4283f11.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg112.gif) |
Figure 11:
 spectra for
spectra for
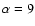 days (dashed line),
days (dashed line),
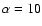 days (solid line), and
days (solid line), and
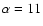 days (dotted line), where days (dotted line), where 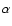 is the semiwidth of the bins in the B component.
is the semiwidth of the bins in the B component. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{4283f12.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg113.gif) |
Figure 12:
Histograms from 1000 repetitions and the  minimization (bins in B and
minimization (bins in B and
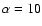 days). Top panel: best solutions of the time delay. Bottom panel: best solutions of the
magnitude offset (flux ratio). These distributions are consistent with a delay of about one and a half
months and a time-delay-corrected flux ratio of about 0.59 mag. days). Top panel: best solutions of the time delay. Bottom panel: best solutions of the
magnitude offset (flux ratio). These distributions are consistent with a delay of about one and a half
months and a time-delay-corrected flux ratio of about 0.59 mag. |
| Open with DEXTER |
In order to derive uncertainties, we follow a simple approach. We make one repetition
of the experiment by adding a random quantity to each original flux in the light curves. The
random quantities are realisations of normal distributions around zero, with standard
deviations equal to the errors of the fluxes. We can make a large number of repetitions,
and thus obtain a large number of
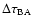 values. The true value will be included
in the whole distribution of measured delays. From the
values. The true value will be included
in the whole distribution of measured delays. From the  minimization (bins in B and
minimization (bins in B and
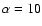 days) and 1000 repetitions, we obtain the histograms in Fig. 12. The main
features of the distributions in the top panel (delays) and bottom panel (flux ratios) of Fig. 12 lead to measurements
days) and 1000 repetitions, we obtain the histograms in Fig. 12. The main
features of the distributions in the top panel (delays) and bottom panel (flux ratios) of Fig. 12 lead to measurements
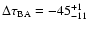 days and
days and
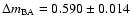 mag (95% confidence intervals). We note that the main delay peak
is asymmetric, so 55% of the repetitions correspond to -44-45 days, whereas 40% of the
repetitions correspond to values <- 45 days. The secondary delay peak (around -20 days)
represents about 5% of the repetitions and is associated with the secondary minima in the
negative region of Fig. 11. Therefore, the distribution in the top panel of Fig. 12 permits a
95% estimation of the time delay of SBS 0909+532.
mag (95% confidence intervals). We note that the main delay peak
is asymmetric, so 55% of the repetitions correspond to -44-45 days, whereas 40% of the
repetitions correspond to values <- 45 days. The secondary delay peak (around -20 days)
represents about 5% of the repetitions and is associated with the secondary minima in the
negative region of Fig. 11. Therefore, the distribution in the top panel of Fig. 12 permits a
95% estimation of the time delay of SBS 0909+532.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{4283f13.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg115.gif) |
Figure 13:
Comparison between the shifted A light curve (circles) and the B light curve (squares).
We use an  minimization, bins in B, and minimization, bins in B, and
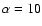 days. Top panel: best solution
( days. Top panel: best solution
(
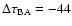 days, days,
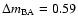 mag). Bottom panel: solution for mag). Bottom panel: solution for
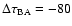 days ( days (
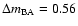 mag). mag). |
| Open with DEXTER |
In Fig. 13 (top panel), the A light curve, shifted by the optimal values of the
time delay and the magnitude offset (time-delay-corrected flux ratio), and the unchanged B light curve are plotted. The cross-correlation using bins in the B component
(
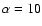 days) indicates that the initial variations in the brightness of B reasonably
agree with the final fluctuations in the brightness of A. The overlap for a delay of -80 days (e.g., Saha et al. 2006) also appears in the bottom panel of Fig. 13. However, this last
time delay is clearly rejected by the observations, since the
days) indicates that the initial variations in the brightness of B reasonably
agree with the final fluctuations in the brightness of A. The overlap for a delay of -80 days (e.g., Saha et al. 2006) also appears in the bottom panel of Fig. 13. However, this last
time delay is clearly rejected by the observations, since the  value is higher than 10 (
value is higher than 10 (
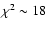 ).
).
To confirm the results from the  minimization, we also use the dispersion spectra
introduced by Pelt et al. (1994, 1996). The basic idea is a combination of
minimization, we also use the dispersion spectra
introduced by Pelt et al. (1994, 1996). The basic idea is a combination of 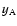 and
and 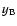 into one global record for every lag
into one global record for every lag 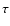 and magnitude offset m0 by taking all the
values of
and magnitude offset m0 by taking all the
values of 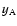 as they are and shifting the values of
as they are and shifting the values of
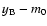 by
by 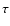 .
For each
.
For each 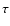 one can find the m0 value that minimizes a dispersion estimate
one can find the m0 value that minimizes a dispersion estimate
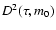 ,
so a
dispersion spectrum
,
so a
dispersion spectrum 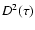 can be made in a direct way. We focus on the D24,2 spectra that are called D2 for simplicity (see Pelt et al. 1996, for details). This technique
incorporates a decorrelation length (
can be made in a direct way. We focus on the D24,2 spectra that are called D2 for simplicity (see Pelt et al. 1996, for details). This technique
incorporates a decorrelation length (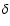 ), where
), where 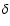 plays a role similar to that
of
plays a role similar to that
of 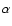 in the
in the  method. Considering reasonable values of
method. Considering reasonable values of 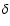 (from 7 to 11 days, see here above), we are able to make some interesting spectra. In Fig. 14 we have
plotted together the spectra for
(from 7 to 11 days, see here above), we are able to make some interesting spectra. In Fig. 14 we have
plotted together the spectra for
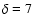 days,
days,
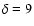 days, and
days, and
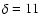 days.
Although there are main minima in the interval -40-50 days, there are also significant signals at positive lags and probable border
effects at +90 days. In the negative region of Fig. 14, a secondary minimum around -70 days
appears. Using
days.
Although there are main minima in the interval -40-50 days, there are also significant signals at positive lags and probable border
effects at +90 days. In the negative region of Fig. 14, a secondary minimum around -70 days
appears. Using
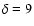 days and a negative range [-90, 0] days, we carry out a second
pre-conditioned measurement of the time delay. The uncertainties are deduced from 1000 repetitions of the experiment (see here above), and the relevant histograms are shown in
Fig. 15. While the top panel contains the distribution of delays, the bottom panel traces the
distribution of flux ratios. Through the distributions in Fig. 15, we obtain
days and a negative range [-90, 0] days, we carry out a second
pre-conditioned measurement of the time delay. The uncertainties are deduced from 1000 repetitions of the experiment (see here above), and the relevant histograms are shown in
Fig. 15. While the top panel contains the distribution of delays, the bottom panel traces the
distribution of flux ratios. Through the distributions in Fig. 15, we obtain
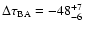 days and
days and
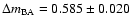 mag (90% confidence interval). These D2 results strengthen the conclusions from the
mag (90% confidence interval). These D2 results strengthen the conclusions from the  technique. A marginal measurement (10% confidence interval) of
technique. A marginal measurement (10% confidence interval) of
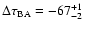 days and
days and
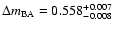 mag is also possible.
However, both this possibility and the
mag is also possible.
However, both this possibility and the  result of around -20 days are probably
related to the presence of gaps and the absence of strong variability in the light curves.
result of around -20 days are probably
related to the presence of gaps and the absence of strong variability in the light curves.
An MCCF technique (Beskin & Oknyanskij 1995; Oknyanskij 1997) is also explored. The MCCF is
a modification of the standard cross-correlation functions (CCF and DCF). When this MCFF is
applied to our data in the lag interval [-60, +60] days, the maximum correlation
coefficient (0.907) corresponds to a lag of -45 days. This last result basically agrees
with the  and dispersion spectra in Figs. 11 and 14.
and dispersion spectra in Figs. 11 and 14.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{4283f14.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg125.gif) |
Figure 14:
Dispersion spectra for
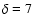 days (dashed line), days (dashed line),
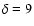 days (solid line), and days (solid line), and
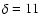 days (dotted line). The parameter days (dotted line). The parameter 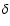 is the decorrelation length associated with the
D24,2 spectra (Pelt et al. 1996).
is the decorrelation length associated with the
D24,2 spectra (Pelt et al. 1996). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{4283f15.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg126.gif) |
Figure 15:
Histograms from 1000 repetitions and the D2 minimization (
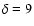 days).
Top panel: best solutions of the time delay. Bottom panel: best solutions of the
magnitude offset (flux ratio). These distributions are again consistent with a 1.5-month delay and
and a time-delay-corrected flux ratio of about 0.58-0.59 mag. days).
Top panel: best solutions of the time delay. Bottom panel: best solutions of the
magnitude offset (flux ratio). These distributions are again consistent with a 1.5-month delay and
and a time-delay-corrected flux ratio of about 0.58-0.59 mag. |
| Open with DEXTER |
Nowadays several groups are trying to coordinate the rich but scattered research potential
in the field of gravitationally lensed quasar monitoring. The goals are to rationalize the
astronomical work and to catalyze big scientific collaborations so that the astrophysics
community can make a significant progress towards understanding the central engine in
lensed quasars, the structure of the lensing galaxies, and the physical properties of the
Universe as a whole. Some examples are the Astrophysics Network for Galaxy
LEnsing Studies (ANGLES, http://www.angles.eu.org/), the Cosmic Lens All-Sky Survey (CLASS,
http://www.aoc.nrao.edu/~smyers/class.html), and the COSmological MOnitoring of
GRAvItational Lenses (COSMOGRAIL, http://www.cosmograil.org/).
The University of Cantabria group (Spain), three groups of the former Soviet Union
(Institute of Astronomy of Kharkov National University, Ukraine, Sternberg Astronomical
Institute, Russia, and Ulug Beg Astronomical Institute of Uzbek Academy of Science,
Uzbekistan), and the Tel-Aviv University group (Israel) are also carrying out a series of
initiatives to better exploit the recent individual monitoring campaigns, as well as to
solidify some future common project. In this paper we present the first collaborative
programme on the variability of the double quasar SBS 0909+532A,B. The VR observations of
the system and the field stars were made with three modern ground-based telescopes in the
year 2003.
The SBS 0909+532c star (N23210036195 in the GSC2.2 Catalogue) at (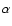 ,
,
 :12:53.59, +52:59:39.82) in J2000 coordinates is found to be variable, with two
different levels of flux. The VR gap between the low state and the high state is
80-100 mmag, and the low-state lasts about one month. In the high state the star also
seems to vary, but these small-amplitude variations are not as significant as the gap
between states. We want to emphasise the variability of this nearby star ("c'' star), and
to encourage colleagues to follow-up its fluctuations and identify the kind of variable
source. The "c'' star cannot be used as the reference object (differential photometry),
because it introduces a zero-lag global correlation between the light curves of the
quasar components A and B. However, the "a-b'' nearby stars are non-variable sources,
and we choose the "b'' star as the reference candle. On the other hand, the "s1'' and "s2''
stars are relatively far objects, which were proposed as good references in a previous
analysis (Nakos et al. 2003). However, the new R-band light curve
:12:53.59, +52:59:39.82) in J2000 coordinates is found to be variable, with two
different levels of flux. The VR gap between the low state and the high state is
80-100 mmag, and the low-state lasts about one month. In the high state the star also
seems to vary, but these small-amplitude variations are not as significant as the gap
between states. We want to emphasise the variability of this nearby star ("c'' star), and
to encourage colleagues to follow-up its fluctuations and identify the kind of variable
source. The "c'' star cannot be used as the reference object (differential photometry),
because it introduces a zero-lag global correlation between the light curves of the
quasar components A and B. However, the "a-b'' nearby stars are non-variable sources,
and we choose the "b'' star as the reference candle. On the other hand, the "s1'' and "s2''
stars are relatively far objects, which were proposed as good references in a previous
analysis (Nakos et al. 2003). However, the new R-band light curve
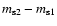 reveals the variability of one ("s1'' or "s2'') or both stars. This variability could be
either a very rare phenomenon or a consequence of doing more refined measurements
(aperture or PSF fitting on several frames per night). We warn about the possible
problems with this pair of stars and think it merits more attention. The point-spread
function (PSF) fitting methods permit the two components of the quasar to be resolved and
the VR light curves of each component to be derived. These new VR light curves represent
the first resolved brightness records of SBS 0909+532. Although the V-band curves are
interesting, the R-band records seem more reliable and are more densely populated.
The R-band curves show moderate variability through 2003, and the observed fluctuations
are promising for different kinds of future studies.
reveals the variability of one ("s1'' or "s2'') or both stars. This variability could be
either a very rare phenomenon or a consequence of doing more refined measurements
(aperture or PSF fitting on several frames per night). We warn about the possible
problems with this pair of stars and think it merits more attention. The point-spread
function (PSF) fitting methods permit the two components of the quasar to be resolved and
the VR light curves of each component to be derived. These new VR light curves represent
the first resolved brightness records of SBS 0909+532. Although the V-band curves are
interesting, the R-band records seem more reliable and are more densely populated.
The R-band curves show moderate variability through 2003, and the observed fluctuations
are promising for different kinds of future studies.
To estimate the time delay between the components of SBS 0909+532, we use a 120-day piece
of the R-band brightness records and  and dispersion (D2) techniques. The
cross-correlation of the two light curves (A and B) leads to complex
and dispersion (D2) techniques. The
cross-correlation of the two light curves (A and B) leads to complex  spectra.
However, assuming that the quasar emission is observed first in B and afterwards in A, or in
other words,
spectra.
However, assuming that the quasar emission is observed first in B and afterwards in A, or in
other words,
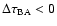 (in agreement with basic observations of the
system), 95% measurements
(in agreement with basic observations of the
system), 95% measurements
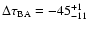 days and
days and
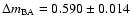 mag are inferred from 1000 repetitions of the
experiment (synthetic light curves based on the observed records). From the D2 minimization (Pelt et al. 1996) and 1000 repetitions, we also obtain 90% measurements
mag are inferred from 1000 repetitions of the
experiment (synthetic light curves based on the observed records). From the D2 minimization (Pelt et al. 1996) and 1000 repetitions, we also obtain 90% measurements
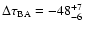 days and
days and
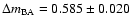 mag. The D2 uncertainties are derived under the assumption already mentioned that
mag. The D2 uncertainties are derived under the assumption already mentioned that
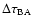 is negative. There is clear agreement between the results from both techniques, so
a delay value of about one and a half months is strongly favoured. Our light curves rule
out a delay close to three months, which has been claimed in a recent analysis (Saha et al. 2006). When we measure the time delay of the system, we simultaneously derive
the time-delay-corrected flux ratio (at the same emission time) in the R band. This
quantity,
is negative. There is clear agreement between the results from both techniques, so
a delay value of about one and a half months is strongly favoured. Our light curves rule
out a delay close to three months, which has been claimed in a recent analysis (Saha et al. 2006). When we measure the time delay of the system, we simultaneously derive
the time-delay-corrected flux ratio (at the same emission time) in the R band. This
quantity,
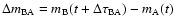 ,
is contaminated by light of
the lens galaxy; and taking the weak contaminations of A and B into account (see the end of
Sect. 3.2), the totally corrected R-band flux ratio is
,
is contaminated by light of
the lens galaxy; and taking the weak contaminations of A and B into account (see the end of
Sect. 3.2), the totally corrected R-band flux ratio is
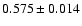 mag. Our
final R flux ratio is in total agreement with the rough (uncorrected by the
time delay and the contamination by galaxy light) measurement by Kochanek et al. (1997):
mag. Our
final R flux ratio is in total agreement with the rough (uncorrected by the
time delay and the contamination by galaxy light) measurement by Kochanek et al. (1997):
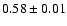 mag. To properly determine a flux ratio, one must use clean fluxes at the same
emission time, i.e., fluxes at different observation times and without contamination
(Goicoechea et al. 2005). Only for particular cases (e.g., faint lens galaxy,
short delay, and moderate variability) may it be reasonable to use direct fluxes.
mag. To properly determine a flux ratio, one must use clean fluxes at the same
emission time, i.e., fluxes at different observation times and without contamination
(Goicoechea et al. 2005). Only for particular cases (e.g., faint lens galaxy,
short delay, and moderate variability) may it be reasonable to use direct fluxes.
In order to get a reasonably good value of  ,
we do not need to introduce a time-dependent
magnitude offset or a complex iterative procedure (e.g., Burud et al. 2000; Hjorth
et al. 2002), i.e., only a delay and a constant offset are fitted. This is a strong point of
the analysis. The agreement between the results from different techniques is another strong
point. However, the new measurements have some weak points that we want to comment on here. The
weakest point is the relatively poor overlap between the A and B records, when the A light
curve is shifted by the best solutions of the time delay and the magnitude offset (e.g., see
the top panel of Fig. 13). Moreover, we carry out pre-conditioned measurements, since a
negative interval [-90, 0] days is considered in the estimation of uncertainties (component B leading component A). This second weak point is related to the presence of 10/20-day gaps
and the moderate variability of the components, which does not permit us to rule out positive
delays fairly. We nevertheless note that the negative interval agrees with
the predictions by Lehár et al. (2000) and Saha et al. (2006), and we find
,
we do not need to introduce a time-dependent
magnitude offset or a complex iterative procedure (e.g., Burud et al. 2000; Hjorth
et al. 2002), i.e., only a delay and a constant offset are fitted. This is a strong point of
the analysis. The agreement between the results from different techniques is another strong
point. However, the new measurements have some weak points that we want to comment on here. The
weakest point is the relatively poor overlap between the A and B records, when the A light
curve is shifted by the best solutions of the time delay and the magnitude offset (e.g., see
the top panel of Fig. 13). Moreover, we carry out pre-conditioned measurements, since a
negative interval [-90, 0] days is considered in the estimation of uncertainties (component B leading component A). This second weak point is related to the presence of 10/20-day gaps
and the moderate variability of the components, which does not permit us to rule out positive
delays fairly. We nevertheless note that the negative interval agrees with
the predictions by Lehár et al. (2000) and Saha et al. (2006), and we find  and D2 minima around -45 days when the observed data and both negative and positive lags are taken
into account (see Figs. 11 and 14). Of course, as for any another first determination of a time
delay, the 1.5-month value should be confirmed by future studies.
and D2 minima around -45 days when the observed data and both negative and positive lags are taken
into account (see Figs. 11 and 14). Of course, as for any another first determination of a time
delay, the 1.5-month value should be confirmed by future studies.
Forty years ago, Refsdal (1964) suggested the possibility of determining the current
expansion rate of the Universe (Hubble constant) and the masses of the galaxies from the
time delays associated with extragalactic gravitational mirages. More recently, for a
singular isothermal ellipsoid (SIE), Koopmans et al. (1998) found that
the time delay can be cast in a very simple form, depending on basic cosmological
parameters, redshifts and image positions. The relevant image positions are the
positions with respect to the centre of the main lens galaxy, and the SIE delay is
similar to the delay for a singular isothermal sphere (SIS). In principle, a singular
density distribution is justified because a small core radius changes the time delay
negligibly, and only a small core radius seems to be consistent with the absence of
a faint central image (e.g., Kochanek 1996). Moreover, individual lenses and lens
statistics are usually consistent with isothermal models (e.g., Witt et al.
2000, and references therein), so it is common to adopt an isothermal profile. Witt et al. (2000) show that an external shear changes the simple SIS time delay
in proportion to the shear strength. For two-image lenses that have a small shear and
images at different distances from the centre of the lens, the shear should have a
small effect on the time delay. Thus, when one has accurate measurements of image
positions, redshifts, and time delay, it is viable to accurately estimate H0
(using complementary information on the matter/energy content of the Universe).
Very recently, Kochanek (2002) also presented a new elegant approach to the subject.
He modelled the surface density locally as a circular power law, with a mean surface
density
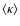 in the annulus between the images. Expanding the time delay as a
series in the ratio of the thickness of the annulus to its average radius, a delay is
derived that is proportional to the SIS time delay. The zero-order expansion
term consists of the SIS delay and a multiplicative factor
in the annulus between the images. Expanding the time delay as a
series in the ratio of the thickness of the annulus to its average radius, a delay is
derived that is proportional to the SIS time delay. The zero-order expansion
term consists of the SIS delay and a multiplicative factor
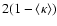 .
Kochanek
also incorporated the quadrupoles of an internal shear (ellipsoid) and an external
shear. However, for two-image lenses where the images lie on opposite sides of the
lens, the delay depends little on the quadrupoles. This novel perspective is useful
to infer
.
Kochanek
also incorporated the quadrupoles of an internal shear (ellipsoid) and an external
shear. However, for two-image lenses where the images lie on opposite sides of the
lens, the delay depends little on the quadrupoles. This novel perspective is useful
to infer
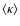 from observations of the lens system (time delay, image positions,
and redshifts) and complementary cosmological data (expansion and matter/energy
content of the Universe).
from observations of the lens system (time delay, image positions,
and redshifts) and complementary cosmological data (expansion and matter/energy
content of the Universe).
For SBS 0909+532, although the redshifts are very accurately known and the time delay
is now tightly constrained (or at least there is a first accurate estimation to be
independently confirmed), the inaccurate position of the main lens galaxy does not
permit an accurate measurement of the cosmic expansion rate and the surface density of the
main deflector. We have
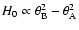 and
and
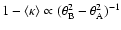 ,
where
,
where
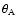 and
and
 are the image
angular positions with respect to the centre of the main lens galaxy. On the other
hand, using the astrometry in Table 3 of Lehár et al. (2000), it is easy to obtain
are the image
angular positions with respect to the centre of the main lens galaxy. On the other
hand, using the astrometry in Table 3 of Lehár et al. (2000), it is easy to obtain
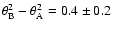 .
Thus we conclude that the accuracy in
.
Thus we conclude that the accuracy in
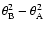 is only 50%, indicating the necessity of new accurate
astrometry for SBS 0909+532.
is only 50%, indicating the necessity of new accurate
astrometry for SBS 0909+532.
Acknowledgements
The UC members are indebted to J. Alcolea (Observatorio Astronómico Nacional, Spain) for
generously granting permission to operate the 1.52 m Spanish telescope at Calar Alto
Observatory (EOCA) in March-June 2003. This 4-month season was supported by Universidad de
Cantabria funds and the Spanish Department for Science and Technology grant AYA2001-1647-C02.
A.U. thanks the Departamento de Física Teórica y del Cosmos de la Universidad de Granada (E.
Battaner) for hospitality during the observational season. The post-observational work and the
dissemination of results are supported by the Department of Education and Science grants
AYA2002-11324-E, AYA2004-20437-E, and AYA2004-08243-C03-02. We acknowledge the use of data
obtained by the SAI group headed by B. Artamonov. We are also indebted to D. Maoz and E. Ofek
for providing the Wise frames of SBS 0909+532. A.P.Z. is grateful for the support of
the Science and Technology Center of Ukraine (STCU), grant U127k. The observational work by the
UBAI group (TA and OB) at Mt. Maidanak was supported by the German Research Foundation (DFG),
grant 436 UZB 113/5/0-1. We are also grateful to the referee for several helpful comments.
We acknowledge support by the European Community's Sixth Framework Marie Curie Research Training
Network Programme, Contract No. MRTN-CT-2004-505183 "ANGLES''. The GSC-II is a joint project of the
Space Telescope Science Institute (STScI) and the Osservatorio Astronomico di Torino (OAT). STScI
is operated by the Association of Universities for Research in Astronomy, for the NASA under
contract NAS5-26555. The participation of the OAT is supported by the Italian Council for
Research in Astronomy. Additional support is provided by ESO, Space Telescope European
Coordinating Facility, the International GEMINI project, and the ESA.
- Beskin, G. M.,
& Oknyanskij, V. L. 1995, A&A, 304, 341 [NASA ADS] (In the text)
- Biggs, A. D.,
Browne, I. W. A., Helbig, P., et al. 1999, MNRAS, 304, 349 [NASA ADS] [CrossRef] (In the text)
- Burud, I.,
Stabell, R., Magain, P., et al. 1998, A&A, 339, 701 [NASA ADS] (In the text)
- Burud, I.,
Hjorth, J., Jaunsen, A. O., et al. 2000, ApJ, 544, 117 [NASA ADS] [CrossRef] (In the text)
- Burud, I.,
Courbin, F., Magain, P., et al. 2002a, A&A, 383, 71 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Burud, I.,
Hjorth, J., Courbin, F., et al. 2002b, A&A, 391, 481 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Chartas, G.
2000, ApJ, 531, 81 [NASA ADS] [CrossRef] (In the text)
- Dai, X., Chartas, G.,
Agol, E., Bautz, M. W., & Garmire, G. P. 2003, ApJ, 589,
100 [NASA ADS] [CrossRef] (In the text)
- Edelson, R.
A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] (In the text)
-
Fassnacht, C. D., Xanthopoulos, E., Koopmans, L. V. E., et al.
2002, ApJ, 581, 823 [NASA ADS] [CrossRef] (In the text)
- Gaskell, C.
M., & Spark, L. S. 1986, ApJ, 305, 175 [NASA ADS] [CrossRef] (In the text)
- Gil-Merino, R.,
Wisotzki, L., & Wambsganss, J. 2002, A&A, 381, 428 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Goicoechea, L. J. 2002, MNRAS, 334, 905 [NASA ADS] [CrossRef] (In the text)
-
Goicoechea, L. J., Gil-Merino, R., & Ullán, A. 2005,
MNRAS, 360, L60 [NASA ADS] [CrossRef] (In the text)
- Haarsma, D.
B., Hewitt, J. N., Lehár, J., & Burke, B. F. 1999, ApJ,
510, 64 [NASA ADS] [CrossRef] (In the text)
- Hjorth, J.,
Burud, I., Jaunsen, A. O., et al. 2002, ApJ, 572, 11 [NASA ADS] [CrossRef] (In the text)
-
Jakobsson, P., Hjorth, J., Burud, I., et al. 2005, A&A, 431,
103 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kochanek,
C. S. 1996, ApJ, 466, 638 [NASA ADS] [CrossRef] (In the text)
- Kochanek,
C. S. 2002, ApJ, 578, 25 [NASA ADS] [CrossRef] (In the text)
- Kochanek,
C. S., Falco, E. E., Schild, R., et al. 1997, ApJ, 479, 678 [NASA ADS] [CrossRef] (In the text)
- Kochanek,
C. S., Schneider, P., & Wambsganss, J. 2004, Part 2 of
Gravitational Lensing: Strong, Weak & Micro, in Proc. of the
33rd Saas-Fee Advanced Course, ed. G. Meylan, P. Jetzer, & P.
North (Berlin: Springer-Verlag)
(In the text)
- Kochanek,
C. S., Morgan, N. D., Falco, E. E., et al. 2005
[arXiv:astro-ph/0508070]
(In the text)
- Koopmans,
L. V. E., de Bruyn, A. G., & Jackson, N. 1998, MNRAS, 295,
534 [NASA ADS] [CrossRef] (In the text)
- Koopmans,
L. V. E., de Bruyn, A. G., Xanthopoulos, E., & Fassnacht, C. D.
2000, A&A, 356, 391 [NASA ADS] (In the text)
-
Koptelova, E., Shimanovskaya, E., Artamonov, B., et al. 2005,
MNRAS, 356, 323 [NASA ADS] [CrossRef] (In the text)
- Kundic, T.,
Turner, E. L., Colley, W. N., et al. 1997, ApJ, 482, 75 [NASA ADS] [CrossRef] (In the text)
- Lehár, J.,
Falco, E. E., Kochanek, C. S., et al. 2000, ApJ, 536, 584 [NASA ADS] [CrossRef] (In the text)
- Lovell, J. E.
J., Jauncey, D. L., Reynolds, J. E., et al. 1998, ApJ, 508,
L51 [NASA ADS] [CrossRef] (In the text)
- Lubin, L. M.,
Fassnacht, C. D., Readhead, A. C. S., Blandford, R. D., &
Kundic, T. 2000, ApJ, 119, 451 [NASA ADS] (In the text)
- Magain, P.,
Courbin, F., & Sohy, S. 1998, ApJ, 494, 472 [NASA ADS] [CrossRef] (In the text)
- McLeod, B. A.,
Bernstein, G. M., Rieke, M. J., & Weedman, D. W. 1998, AJ, 115,
1377 [NASA ADS] [CrossRef] (In the text)
-
Mediavilla, E., Muñoz, J. A., Kochanek, C. S., et al. 2005,
ApJ, 619, 749 [NASA ADS] [CrossRef] (In the text)
- Motta, V.,
Mediavilla, E., Muñoz, J. A., et al. 2002, ApJ, 574, 719 [NASA ADS] [CrossRef] (In the text)
- Nakos, Th., Ofek,
E. O., Boumis, P., et al. 2003, A&A, 402, 1157 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Ofek, E. O., &
Maoz, D. 2003, ApJ, 594, 101 [NASA ADS] [CrossRef] (In the text)
-
Oknyanskij, V. L. 1997, In Astronomical Data Analysis Software and
Systems VI, ed. G. Hunt, & H. E. Payne, ASP Conf. Ser., 125,
162
(In the text)
- Oscoz, A.,
Serra-Ricart, M., Mediavilla, E., Buitrago, J., & Goicoechea,
L. J. 1997, ApJ, 491, L7 [NASA ADS] [CrossRef] (In the text)
-
Østensen, R. 1994, Ph.D. Thesis, University of
Tromsø
(In the text)
- Ovaldsen,
J. E., Teuber, J., Schild, R. E., & Stabell, R. 2003, A&A,
402, 891 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Page, K. L.,
Reeves, J. N., O'Brien, P. T., Turner, M. J. L., & Worrall, D.
M. 2004, MNRAS, 353, 133 [NASA ADS] [CrossRef] (In the text)
- Patnaik, A.
R., & Narasimha, D. 2001, MNRAS, 326, 1403 [NASA ADS] [CrossRef] (In the text)
- Pelt, J., Hoff, W.,
Kayser, R., Refsdal, S., & Schramm, T. 1994, A&A, 286,
775 [NASA ADS] (In the text)
- Pelt, J., Kayser,
R., Refsdal, S., & Schramm, T. 1996, A&A, 305, 97 [NASA ADS] (In the text)
- Refsdal, S.
1964, MNRAS, 128, 307 [NASA ADS] (In the text)
- Saha, P., Courbin,
F., Sluse, D., Dye, S., & Meylan, G. 2006, A&A, 450,
461 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Schechter, P. L., Bailyn, C. D., Barr, R., et al. 1997, ApJ, 475,
L85 [NASA ADS] [CrossRef] (In the text)
- Serra-Ricart, M.,
Oscoz, A., Sanchis, T., et al. 1999, ApJ, 526, 40 [NASA ADS] [CrossRef] (In the text)
-
Stepanyan, D. A., Lipovetskii, V. A., Chavushyan, V. O., Erastova,
L. K., & Shapovalova, A. I. 1991, Afz, 34, 1 [NASA ADS] (In the text)
- Ullán, A. 2005,
in e-Proceedings of the GLQ Workshop 25 Years After the Discovery:
Some Topics on Lensed QSOs,
http://grupos.unican.es/glendama/e-Proc.htm, C2
(In the text)
- Ullán, A.,
Goicoechea, L. J., Muñoz, J. A., et al. 2003, MNRAS, 346,
415 [NASA ADS] [CrossRef] (In the text)
- Witt, H. J., Mao,
S., & Keeton, C. R. 2000, ApJ, 544, 98 [NASA ADS] [CrossRef] (In the text)
-
Wyrzykowski, L., Udalski, A., Schechter, P. L., et al. 2003, Acta
Astron., 53, 229 [NASA ADS] (In the text)
- Ziad, A., Gredel,
R., Aceituno, J., et al. 2005, MNRAS, 362, 455 [NASA ADS] [CrossRef] (In the text)
- Zickgrof,
F.-J., Engels, D., Hagen, H.-J., Reimers, D., & Voges, W. 2003,
A&A, 406, 535 [EDP Sciences] [NASA ADS] [CrossRef]
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{4283f1.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg50.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{4283f3.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg78.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{4283f4.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg79.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{4283f5.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg80.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{4283f6.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg84.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{4283f7.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{4283f8.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg89.gif)
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{4283f9.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg96.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{4283f10.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg111.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{4283f11.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg112.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{4283f12.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg113.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{4283f13.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg115.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{4283f14.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg125.gif)
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{4283f15.eps}
\end{figure}](/articles/aa/full/2006/22/aa4283-05/Timg126.gif)