A&A 452, 339-342 (2006)
DOI: 10.1051/0004-6361:20053750
V. G. Ledenev1 - V. V. Tirsky2 - V. M. Tomozov1
1 - Institute of Solar-Terrestrial Physics, Russian Academy of Sciences,
PO Box 4026, Irkutsk, Russia
2 -
Institute of Laser Physics, Russian Academy of Sciences, Irkutsk Branch, Russia
Received 4 July 2005 / Accepted 8 February 2006
Abstract
We derived numerical solutions of a dispersion equation in order to analyze the effect of
finite plasma temperature on the high-frequency wave dispersion characteristics in conditions of hot
magnetized plasma in the solar corona. Spectra of the high-frequency eigen modes of these plasma
were determined in conditions when the electron gyrofrequency is lower than the plasma one and when the
eigen modes frequencies are higher than the electron gyrofrequency. The longitudinal wave mode is shown to
turn to the Z-mode at refractive index n < 1. At refractive index ![]() ,
the longitudinal wave frequency
increases when n grows, and these waves go to strongly damped ones with an anomalous dispersion. We interpret
some spectral features of type II and IV radio bursts in the solar corona.
,
the longitudinal wave frequency
increases when n grows, and these waves go to strongly damped ones with an anomalous dispersion. We interpret
some spectral features of type II and IV radio bursts in the solar corona.
Key words: Sun: activity - Sun: corona - plasmas
The solar corona is a high-temperature (>106 K) plasma that is filled with magnetic fields with structural forms on different scales. Numerous processes of energy release take place in the dynamical solar coronal plasma. These events cover wide spatial and temporal ranges (mainly in the form of nanoflares, microflares, flares, and coronal mass ejections), which are connected to magnetic field energy dissipation processes. The occurrence of fast plasma flows, beams of energetic particles, and shock waves accompany these processes. In turn, these energy release channels are connected with the appearance of radio emission in the form of different types of radio emission bursts owing to the development of plasma instabilities (Zheleznyakov 1970; Kaplan & Tsytovich 1973; Melrose 1980; Altyntsev et al. 1982). Similar bursts of much more intensive radio emission are observed in stars of late spectral classes (e.g., red dwarfs and close binary systems of F, G, K, M spectral classes) with high flare activity and high-temperature stretching coronae.
It is known that the analogy between the Sun and these classes of stars is usually used quite successfully to explain radio emission bursts from such stars (Gershberg & Pikelner 1972; Gershberg 2002; Stepanov 2003). Investigating the physical mechanisms of the radio emission generation in solar and stellar coronae is quite a significant problem for the diagnostics of the physical parameters of the coronal plasma. Though the energy release portion related to radio emission in the solar corona is relatively small, the physical parameters in the coronal plasma can be estimated from the basic characteristics of the radio emission (brightness temperature, polarization, radiation pulsations, and frequency drifts).
In our opinion, it is necessary to pay special attention to radio emission bursts with fine structure, because such burst structures are directly related to the radiation mechanism. A large number of varied solar and stellar radio emission bursts were interpreted on the basis of the plasma mechanism, including the excitation of high-frequency plasma waves by fast electron beams, with subsequent conversion of these waves into electromagnetic radiation. Besides, the plasma radiation mechanisms in coronal magnetic fields can be related to the instabilities of fast particle distribution functions in magnetic traps with a loss cone. These plasma instabilities are able to generate small-scale waves of different types, e.g., cyclotron harmonic waves, whistlers, and Langmuir waves.
In addition, (apart from the mechanisms mentioned above) to explain narrow band (
![]() ,
,
![]() is emission frequency), short-term (10-100 ms) solar events (radio spikes) in the
coronal plasma of the Sun, the electron-cyclotron maser mechanism is used successfully (Melrose & Dulk 1982;
Fleishman & Melnikov 1998), and this mechanism leads to different types of difficulty in high-temperature
stellar coronae: anomalously high Alfven velocities, the outcome problem of radio emission, etc. (Stepanov 2003).
is emission frequency), short-term (10-100 ms) solar events (radio spikes) in the
coronal plasma of the Sun, the electron-cyclotron maser mechanism is used successfully (Melrose & Dulk 1982;
Fleishman & Melnikov 1998), and this mechanism leads to different types of difficulty in high-temperature
stellar coronae: anomalously high Alfven velocities, the outcome problem of radio emission, etc. (Stepanov 2003).
Until now, interpretation of solar radio emission has been based on the spectra of eigen oscillations in approximating either isotropic or cold magnetized plasma. Usually, it is assumed that the effect of a plasma finite temperature could lead to some small corrections in results. Indeed, in many cases this approximation does lead to correct results, such as in the particular case of wave propagation at small angles to the magnetic field. For example, such a situation is realized in type III bursts when the energetic electron beam, which excites a beam instability, moves along the coronal magnetic field, and the direction to the observer coincides with a course of electron-beam motion. In this case, dispersion characteristics of transverse electromagnetic waves coincide with characteristics of the waves in the magnetized plasma.
However, this situation changes if the radiation is observed at an angle to a magnetic field. As angle ![]() between the magnetic field and wave propagation direction is not equal to zero, the dispersion curves for
ordinary and extraordinary waves approaching each other, and they almost merge in the weak magnetic field. The
calculations that were made in our paper show that, for longitudinal waves with refractive indexes n
> 10, dispersion characteristics change substantially. In this case, the effect of even a relatively weak
magnetic field (
between the magnetic field and wave propagation direction is not equal to zero, the dispersion curves for
ordinary and extraordinary waves approaching each other, and they almost merge in the weak magnetic field. The
calculations that were made in our paper show that, for longitudinal waves with refractive indexes n
> 10, dispersion characteristics change substantially. In this case, the effect of even a relatively weak
magnetic field (
![]() ,
where
,
where
![]() is the electron cyclotron frequency and
is the electron cyclotron frequency and
![]() the electron plasma frequency) essentially changes the dispersion characteristics of
high-temperature plasma. In particular, the longitudinal wave frequency increases as the refractive index grows,
and a branch appears corresponding to waves with negative (anomalous) dispersion, e.g. the waves whose frequency
decreases as the wave number increases. Besides, the longitudinal waves go to the Z-mode with the refractive
index n < 1, as it propagates at an angle to the magnetic field. This mode shifts into the frequency region
lower than
the electron plasma frequency) essentially changes the dispersion characteristics of
high-temperature plasma. In particular, the longitudinal wave frequency increases as the refractive index grows,
and a branch appears corresponding to waves with negative (anomalous) dispersion, e.g. the waves whose frequency
decreases as the wave number increases. Besides, the longitudinal waves go to the Z-mode with the refractive
index n < 1, as it propagates at an angle to the magnetic field. This mode shifts into the frequency region
lower than
![]() .
Since the solar corona is a hot plasma with a magnetic field, these results have to be
taken into account in many of the present and future models of sporadic radio emissions of the Sun.
.
Since the solar corona is a hot plasma with a magnetic field, these results have to be
taken into account in many of the present and future models of sporadic radio emissions of the Sun.
A considerable amount of papers and books are focussed on the study of different types of high-frequency waves
in the magnetized plasma (see, e.g., Baldwin et al. 1969; Ginzburg 1970; Akhiezer et al. 1975; Ginzburg &
Rukhadze 1975; Melrose 1980). For instance, the particular cases of wave propagation along and across the
magnetic field were considered in detail. In a review paper by Baldwin et al. (1969), the dispersion equations
for transverse (electromagnetic) and longitudinal (plasma) waves are quoted, which were derived in the
approximation of the weak magnetic field and relatively low temperature. From these equations one can conclude
that the characteristics of eigen plasma oscillations change even in this approximation. The finite temperature
plasma effect is considered on the basis of a quasi-hydrodynamic approximation (Ginzburg 1970), but this
approach does not allow the kinetic effects to be taken into account completely, although they do influence the
eigen oscillation parameters considerably. In Ginzburg (1970) the kinetic approach was realized in a frequency
range close to the electron plasma frequency without taking terms in the dispersion equation into account that
are proportional to
![]() (where
(where
![]() is the thermal velocity of electrons) and without the effects
of cyclotron harmonics above the second one. Willes & Cairns (2000) obtained an approximate solution for the
dispersion equation of a magnetized kinetic plasma for small
is the thermal velocity of electrons) and without the effects
of cyclotron harmonics above the second one. Willes & Cairns (2000) obtained an approximate solution for the
dispersion equation of a magnetized kinetic plasma for small ![]() by using an expansion of the dielectric
tensor longitudinal component in terms of the parameter
by using an expansion of the dielectric
tensor longitudinal component in terms of the parameter
![]() .
However, the cases
under consideration do not give a full notion of the eigen oscillation characteristics of a high-temperature
magnetized plasma, which can be used for correctly interpreting the characteristics of radio emission bursts in
solar and stellar coronae. To obtain these characteristics, an investigation of a full dispersion equation is
necessary. The solution of this equation can only be obtained by numerical methods.
.
However, the cases
under consideration do not give a full notion of the eigen oscillation characteristics of a high-temperature
magnetized plasma, which can be used for correctly interpreting the characteristics of radio emission bursts in
solar and stellar coronae. To obtain these characteristics, an investigation of a full dispersion equation is
necessary. The solution of this equation can only be obtained by numerical methods.
A paper by Andre (1985) and a review by R![]() nnmark (1985) both show the dispersion surfaces for
high-frequency plasma waves taking the effect of finite temperature plasma into account, which were determined
by numerical methods. These results, however, were obtained for parameters that are typical of the Earth's
magnetosphere and are essentially different from solar corona parameters. Furthermore, these results were
obtained with highly simplifying assumptions in the numerical computation procedure.
nnmark (1985) both show the dispersion surfaces for
high-frequency plasma waves taking the effect of finite temperature plasma into account, which were determined
by numerical methods. These results, however, were obtained for parameters that are typical of the Earth's
magnetosphere and are essentially different from solar corona parameters. Furthermore, these results were
obtained with highly simplifying assumptions in the numerical computation procedure.
In the present paper we investigate different types of high-frequency waves in a high-temperature magnetized
plasma at
![]() on the basis of a numerical solution of the dispersion equation. In Sect.
2 the dispersion equation describing high-frequency waves in a high-temperature magnetized plasma is presented
in its most general form, but unwieldy formulae are moved into the appendix. This section describes the results
of a numerical solution of the dispersion equation in detail and presents the high-frequency wave
characteristics by taking into account their propagation at different angles to the magnetic field. On the basis
of results for the characteristics of high-frequency waves in a high-temperature plasma, we provide a
qualitative interpretation of some features of type II and IV bursts in Sect. 3. In the conclusion, the main
results of this work are reported, followed by a brief discussion.
on the basis of a numerical solution of the dispersion equation. In Sect.
2 the dispersion equation describing high-frequency waves in a high-temperature magnetized plasma is presented
in its most general form, but unwieldy formulae are moved into the appendix. This section describes the results
of a numerical solution of the dispersion equation in detail and presents the high-frequency wave
characteristics by taking into account their propagation at different angles to the magnetic field. On the basis
of results for the characteristics of high-frequency waves in a high-temperature plasma, we provide a
qualitative interpretation of some features of type II and IV bursts in Sect. 3. In the conclusion, the main
results of this work are reported, followed by a brief discussion.
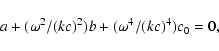 |
(1) |
Here, ![]() is the complex frequency, k the wave number, kz the longitudinal (with respect to
the magnetic field) wave vector component,
is the complex frequency, k the wave number, kz the longitudinal (with respect to
the magnetic field) wave vector component, ![]() the transverse wavevector component, and
the transverse wavevector component, and
![]() stands for the components of the dielectric tensor.
stands for the components of the dielectric tensor.
The waves in magnetized plasma, for which the refractive index
![]() ,
are customarily
considered as longitudinal (Ginzburg & Rukhadze 1975). It is assumed that their dispersion properties are
determined by the first term of Eq. (1). But it is correct for those values of the refractive index that are high
enough. For the oscillations with refractive indices
,
are customarily
considered as longitudinal (Ginzburg & Rukhadze 1975). It is assumed that their dispersion properties are
determined by the first term of Eq. (1). But it is correct for those values of the refractive index that are high
enough. For the oscillations with refractive indices ![]() ,
it is difficult to define the mode of the
high-frequency wave as purely transverse or purely longitudinal, so the contribution from the second and third
terms to the solution of Eq. (1) cannot be neglected any longer. As shown below, taking the second and third terms
in Eq. (1) for
,
it is difficult to define the mode of the
high-frequency wave as purely transverse or purely longitudinal, so the contribution from the second and third
terms to the solution of Eq. (1) cannot be neglected any longer. As shown below, taking the second and third terms
in Eq. (1) for ![]() into account leads to a substantial change in the dispersion characteristics of the waves
in a hot magnetized plasma as compared to the cold one.
into account leads to a substantial change in the dispersion characteristics of the waves
in a hot magnetized plasma as compared to the cold one.
Figures 1a-d present the results of calculations (by formulas A.1) for the dependence of the refractive index n
on the frequency of weakly damped modes for angles between the wave vector and the magnetic field ![]() = 0.0
and 1.0 for the parameters
= 0.0
and 1.0 for the parameters
![]() and 10, and
and 10, and
![]() .
These values are consistent with the parameters of the solar corona. The summation over cyclotron harmonics was
performed up to the fifteenth one. The contribution from higher harmonics does not alter the character of the
dispersion curves for the waves substantially. Landau-damping is not significant for
.
These values are consistent with the parameters of the solar corona. The summation over cyclotron harmonics was
performed up to the fifteenth one. The contribution from higher harmonics does not alter the character of the
dispersion curves for the waves substantially. Landau-damping is not significant for
![]() ,
which means that the refractive index of weakly damped waves is
,
which means that the refractive index of weakly damped waves is ![]() in this case. We also considered
the waves, which obey weaker inequality n < 70, since these waves can grow if the growth rate exceeds the
Landau-damping rate.
in this case. We also considered
the waves, which obey weaker inequality n < 70, since these waves can grow if the growth rate exceeds the
Landau-damping rate.
![\begin{figure}
\par\includegraphics[width=4cm,height=5cm,clip]{3750fig1.eps}\hsp...
...e*{4mm}
\includegraphics[width=4cm,height=5cm,clip]{3750fig4.eps}
\end{figure}](/articles/aa/full/2006/22/aa3750-05/Timg29.gif) |
Figure 1:
Frequency dependence of the refractive index for
|
| Open with DEXTER | |
The case of strict wave propagation along the magnetic field is a degenerated one, in the sense that the
solutions of the dispersion equation for longitudinal and transverse waves are independent. In this case
longitudinal waves are described by a well-known dispersion relation (Akhiezer et al. 1975; Ginzburg & Ruchadze
1975) that is defined by the equality to zero of the first term of Eq. (1) or via Re
![]() (see A.1). At
(see A.1). At
![]() there is an intersection of longitudinal and ordinary transverse wave branches (Figs. 1a and 1c)
and a transition of one type of wave into another. However, at
there is an intersection of longitudinal and ordinary transverse wave branches (Figs. 1a and 1c)
and a transition of one type of wave into another. However, at
![]() longitudinal wave turns to Z-mode
in the region n < 1, and the Z-mode branch goes to the frequency region lower than the plasma one. This result
agrees with Willes & Cairns (2000), who have found an approximate solution of the dispersion equation for the
Maxwellian magnetized plasma by means of the expansion in terms of the parameter
longitudinal wave turns to Z-mode
in the region n < 1, and the Z-mode branch goes to the frequency region lower than the plasma one. This result
agrees with Willes & Cairns (2000), who have found an approximate solution of the dispersion equation for the
Maxwellian magnetized plasma by means of the expansion in terms of the parameter
![]() .
Cutoff frequencies for ordinary and extraordinary waves are determined by the same relations as in the cold
magnetized plasma (Ginzburg 1970). As one can see from Figs. 1a-d, the distance between the cutoff frequencies
increases when the magnetic field grows. As the angle
.
Cutoff frequencies for ordinary and extraordinary waves are determined by the same relations as in the cold
magnetized plasma (Ginzburg 1970). As one can see from Figs. 1a-d, the distance between the cutoff frequencies
increases when the magnetic field grows. As the angle
![]() ,
the cutoff frequencies approach each
other and the frequency for ordinary waves shifts into the frequency region higher than
,
the cutoff frequencies approach each
other and the frequency for ordinary waves shifts into the frequency region higher than
![]() .
.
The most essential features of longitudinal wave-dispersion characteristics become apparent for refractive index
n > 10 (Figs. 1a-d). As n grows in this region, the longitudinal wave-frequency increases and reaches the
maximum value
![]() at
at ![]() .
At the same time, the Landau damping grows, since the
wave phase velocity approaches the electron thermal velocity. At
.
At the same time, the Landau damping grows, since the
wave phase velocity approaches the electron thermal velocity. At ![]() and
and
![]() ,
the damping achieves a value of about
,
the damping achieves a value of about ![]() .
Such waves can be excited only by strong instability. As the
refractive index rises further, the longitudinal wave frequency goes down, and the branch of anomalous
dispersion waves appears, i.e. the waves whose frequency decreases as the wave number increases. In Figs. 1a-d
this branch is marked by dotted lines. However, these waves strongly damp because, as the refractive index
grows, the wave phase velocity becomes equal to the electron thermal velocity.
.
Such waves can be excited only by strong instability. As the
refractive index rises further, the longitudinal wave frequency goes down, and the branch of anomalous
dispersion waves appears, i.e. the waves whose frequency decreases as the wave number increases. In Figs. 1a-d
this branch is marked by dotted lines. However, these waves strongly damp because, as the refractive index
grows, the wave phase velocity becomes equal to the electron thermal velocity.
The growth of the longitudinal wave frequency in the region ![]() is caused by the finite cyclotron radius
effect. This is a consequence of the fact that this growth is observed when the parameter
is caused by the finite cyclotron radius
effect. This is a consequence of the fact that this growth is observed when the parameter
![]() achieves unity in order of magnitude; i.e. the wave length is close to the cyclotron radius.
achieves unity in order of magnitude; i.e. the wave length is close to the cyclotron radius.
Our calculations show the weak angular dependence of the hot-plasma dispersion characteristics for longitudinal
waves. However, as ![]() approaches 900 (
approaches 900 (
![]() radian), the Bernstein longitudinal modes
become apparent in the spectrum of weakly damped plasma oscillations at the frequencies close to the cyclotron
harmonic frequencies. It is difficult to calculate the spectra in this case.
radian), the Bernstein longitudinal modes
become apparent in the spectrum of weakly damped plasma oscillations at the frequencies close to the cyclotron
harmonic frequencies. It is difficult to calculate the spectra in this case.
![\begin{figure}
\par\includegraphics[width=70mm,height=48mm,clip]{3750fig5.eps}
\end{figure}](/articles/aa/full/2006/22/aa3750-05/Timg40.gif) |
Figure 2: Type II solar radio burst with harmonic-component splitting. |
| Open with DEXTER | |
The characteristic feature of the type II bursts is the harmonic component splitting into two bands (Fig. 2)
with the distance between them about 10-20![]() of the emission frequency (Kundu 1965; Zheleznyakov 1970).
Ledenev & Urbarz (1993) explained the type II harmonic structure by the emission generation at the frequencies
corresponding to the cyclotron resonance
of the emission frequency (Kundu 1965; Zheleznyakov 1970).
Ledenev & Urbarz (1993) explained the type II harmonic structure by the emission generation at the frequencies
corresponding to the cyclotron resonance
![]() ,
where
,
where
![]() is the frequency of longitudinal waves that are excited by the beam-anisotropic instability
(Mikhailovsky 1974),
is the frequency of longitudinal waves that are excited by the beam-anisotropic instability
(Mikhailovsky 1974),
![]() is the longitudinal (with respect to the magnetic field) component of the
wave vector,
is the longitudinal (with respect to the magnetic field) component of the
wave vector,
![]() the longitudinal component of the electron velocity, and s the number of the
cyclotron harmonic. However, there was no convincing explanation of the origin of the harmonic component
splitting, while, as a rule, no more than two splitting bands are observed. Our calculations allow us to give a
more natural explanation for this event. As one can see from Figs. 1a-d, the frequency band of the waves excited
at high values of the refractive index (i.e. at the lowest energies of electrons, which excite longitudinal
waves) can achieve 30
the longitudinal component of the electron velocity, and s the number of the
cyclotron harmonic. However, there was no convincing explanation of the origin of the harmonic component
splitting, while, as a rule, no more than two splitting bands are observed. Our calculations allow us to give a
more natural explanation for this event. As one can see from Figs. 1a-d, the frequency band of the waves excited
at high values of the refractive index (i.e. at the lowest energies of electrons, which excite longitudinal
waves) can achieve 30![]() .
If the electron cyclotron frequency is about 10
.
If the electron cyclotron frequency is about 10![]() of the emission frequency, no
more than two cyclotron harmonics will most likely fall into the band of longitudinal wave generation. At that
point one should take into account that the distance between the splitting bands, generally speaking, is not
equal to the cyclotron frequency, because the resonance regions at the adjacent cyclotron harmonics are shifted
in the height due to the inhomogeneity of the solar corona. Different longitudinal wave frequencies and
cyclotron frequencies correspond to this resonance. Nevertheless, if the condition
of the emission frequency, no
more than two cyclotron harmonics will most likely fall into the band of longitudinal wave generation. At that
point one should take into account that the distance between the splitting bands, generally speaking, is not
equal to the cyclotron frequency, because the resonance regions at the adjacent cyclotron harmonics are shifted
in the height due to the inhomogeneity of the solar corona. Different longitudinal wave frequencies and
cyclotron frequencies correspond to this resonance. Nevertheless, if the condition
![]() is satisfied, the distance between the splitting bands can be used for estimating the magnetic
field in the region of type-II-burst generation. This condition is satisfied, if the emission is generated at
angles that are large enough to the magnetic field. Such estimation for the event in Fig. 2 is about 10 GHz for
the splitting frequency, which corresponds to 6 G for the magnetic field.
is satisfied, the distance between the splitting bands can be used for estimating the magnetic
field in the region of type-II-burst generation. This condition is satisfied, if the emission is generated at
angles that are large enough to the magnetic field. Such estimation for the event in Fig. 2 is about 10 GHz for
the splitting frequency, which corresponds to 6 G for the magnetic field.
The longitudinal wave excitation in a wide-frequency band allow us to explain the nature of the type IV
wide-band bursts (Kundu 1965; Zheleznyakov 1970) in greater detail. It has been suggested that type IV bursts are
generated by the plasma mechanism (Stepanov 1973; Ledenev 1982), and that wide-band emission is due to the
inhomogeneity of the coronal density. Our calculations show that the wide-band emission can be implemented
without taking this coronal density inhomogeneity into account. The wideband emission is generated due to the
excitation of longitudinal waves through the beam instability in the wide frequency band (up to 30![]() at the
fixed level in the corona). Though these waves strongly damp, electron beams with the velocities about the
thermal one can be so powerful that the wave's growth rate will be higher than the damping rate at the
background electrons. When taking the corona inhomogeneity and the electron velocity spread into account, the
emission band can achieve almost 100
at the
fixed level in the corona). Though these waves strongly damp, electron beams with the velocities about the
thermal one can be so powerful that the wave's growth rate will be higher than the damping rate at the
background electrons. When taking the corona inhomogeneity and the electron velocity spread into account, the
emission band can achieve almost 100![]() .
.
As is known, the sources of type III bursts (electron beams) move along the coronal magnetic field (Zheleznyakov & Zaitsev 1970; Dulk & Suzuki 1980). Ledenev & Messerotti (1999) suggested estimating the magnetic field in the corona by using the type III burst polarization. These bursts often show high polarization at the beginning of the burst. It was suggested that this effect is caused by generation of the emission in the region where only ordinary waves propagate. The frequency distance between the cutoff frequencies of ordinary and extraordinary waves determines the frequency bandwidth where high polarization is observed. In turn, the frequency bandwidth is proportional to the magnetic field. Our calculations show that the cutoff frequencies of these waves do not change. At this point, the magnetic field estimation offered by Ledenev & Messerotti (1999) can be used in the hot plasma of the solar corona.
It should be noted, moreover, that these effects must be appearing more distinctly in the characteristics of the radio emission of late spectral class stars owing to the high temperature of the star's coronae, but more specific investigations are still needed.
Acknowledgements
This work was carried out with support of RFBR grant 03-02-16229, Program of basic research RAS N30, and the Scientific School grants 477.2003.2 and RI-112/001/045. We acknowledge the IZMIRAN solar radio group who kindly provided the spectrographic radio data. The authors express appreciation to the referee for useful remarks and corrections that assisted them in improving the paper.
The dispersion Eq. (1) for waves in a hot magnetized plasma may be represented as
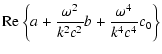 |
= | ![$\displaystyle {\rm Re}\{a\}+\frac{(\Omega ^2-\Gamma
^2){v}_{\rm Te}^2}{\rho ^2c...
...Re}\{Sp \varepsilon _{ij}\}+{\rm Im}\{a\}{\rm Im}\{Sp\varepsilon
_{ij}\}\right]$](/articles/aa/full/2006/22/aa3750-05/img49.gif) |
|
![$\displaystyle -\frac{2\Omega \Gamma {v}_{\rm Te}^2}{\rho ^2c^2}\left[\xi _2-{\r...
...varepsilon _{ij}\}\right]+{\rm Re}\left\{c_0\frac{\omega ^4}{k^4c^4}\right\}=0,$](/articles/aa/full/2006/22/aa3750-05/img50.gif) |
|||
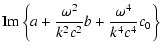 |
= | ![$\displaystyle {\rm Im}\{a\}+\frac{(2\Omega \Gamma
){v}_{\rm Te}^2}{\rho ^2c^2}\...
... Re}\{Sp\varepsilon _{ij}\}+{\rm Im}\{a\}{\rm Im}\{Sp\varepsilon
_{ij}\}\right]$](/articles/aa/full/2006/22/aa3750-05/img52.gif) |
|
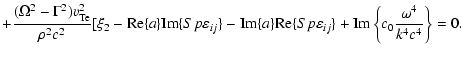 |
(A.1) |
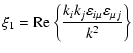 |
= | ||
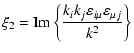 |
= | ||
![\begin{eqnarray*}{\rm Re}\left\{c_0\frac{\omega ^4}{k^4c^4}\right\}=\frac{{v}_{\...
...Gamma ^2]+{\rm Re}\{c_0\}4\Omega \Gamma (\Omega ^2-\Gamma ^2)\},
\end{eqnarray*}](/articles/aa/full/2006/22/aa3750-05/img65.gif)
![\begin{eqnarray*}{\rm Re}\{c_0\}&=&[{\rm Re}\{\varepsilon _{zz}\}{\rm Re}\{\vare...
...y}\}{\rm Re}\{\varepsilon _{xz}\}]{\rm Im}\{\varepsilon _{yz}\},
\end{eqnarray*}](/articles/aa/full/2006/22/aa3750-05/img66.gif)
![\begin{eqnarray*}{\rm Im}\{c_0\}&=&[{\rm Re}\{\varepsilon _{zz}\}{\rm Im}\{\vare...
...y}\}{\rm Re}\{\varepsilon _{xz}\}]{\rm Re}\{\varepsilon _{yz}\},
\end{eqnarray*}](/articles/aa/full/2006/22/aa3750-05/img67.gif)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
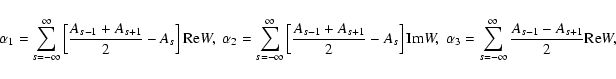
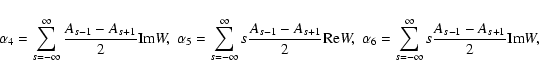
![\begin{displaymath}\alpha _7=\sum_{s=-\infty }^\infty
s\left[\frac{A_{s-1}+A_{s+...
...ty }^\infty s\left[\frac{A_{s-1}+A_{s+1}}2-A_s\right]{\rm Im}W.\end{displaymath}](/articles/aa/full/2006/22/aa3750-05/img76.gif)
![\begin{displaymath}{\rm Re}W(x_0+{\rm i}y_0)=[\exp (y_0^2-x_0^2)] [\cos (2x_0y_0...
...xp
(-y_0^2)\int_0^{x_0}\partial x[\exp (x^2)\sin [2(x_0-x)y_0],\end{displaymath}](/articles/aa/full/2006/22/aa3750-05/img79.gif)
![\begin{displaymath}{\rm Im}W(x_0+{\rm i}y_0)=[\exp (y_0^2-x_0^2)][-\sin (2x_0y_0...
...xp
(-y_0^2)\int_0^{x_0}\partial x[\exp (x^2)\cos [2(x_0-x)y_0].\end{displaymath}](/articles/aa/full/2006/22/aa3750-05/img80.gif)
![\begin{eqnarray*}\sqrt{\pi}{\rm Re}W(x_0+iy_0)&\approx& \frac{y_0}{x_0^2+y_0^2}-...
...y_0)
-2y_0x_0(x_0^5+5x_0y_0^4-10y_0^2x_0^3)]}{8(x_0^2+y_0^2)^7},
\end{eqnarray*}](/articles/aa/full/2006/22/aa3750-05/img82.gif)
![\begin{eqnarray*}\sqrt{\pi }{\rm Im}W(x_0+iy_0)&\approx&
\frac{x_0}{x_0^2+y_0^2}...
...^3)+2x_0y_0(y_0^5-10x_0^2y_0^3+5x_0^4y_0]}{8(x_0^2+y_0^2)^7}\cdot\end{eqnarray*}](/articles/aa/full/2006/22/aa3750-05/img83.gif)