A&A 452, 223-236 (2006)
DOI: 10.1051/0004-6361:20052754
Interstellar cloud structure: the statistics of centroid velocities
V. Ossenkopf1,2 - A. Esquivel3 - A. Lazarian3 -
J. Stutzki1
1 - I. Physikalisches Institut der Universität zu Köln,
Zülpicher Straße 77, 50937 Köln, Germany
2 -
SRON National Institute for Space Research, PO Box 800, 9700 AV Groningen, The Netherlands
3 -
Astronomy Department, University of Wisconsin-Madison, 475 N.
Charter St., Madison, WI 53706, USA
Received 24 January 2005 / Accepted 20 January 2006
Abstract
Context. The statistical properties of maps of line centroids have been used for almost 50 years, but there is still no general agreement on their interpretation.
Aims. We have tried to quantify which properties of underlying turbulent velocity fields can be derived from centroid velocity maps, and we tested conditions under which the scaling behaviour of the centroid velocities matches the scaling of the three-dimensional velocity field.
Methods. Using fractal cloud models we systematically studied the relation between three-dimensional density and velocity fields and the statistical properties of the resulting line centroid maps. We paid special attention to cases with large density fluctuations resembling supersonic interstellar turbulence. Starting from the  -variance analysis, we derived a new tool to compute the scaling behaviour of the three-dimensional velocity field from observed intensity and centroid velocity maps.
-variance analysis, we derived a new tool to compute the scaling behaviour of the three-dimensional velocity field from observed intensity and centroid velocity maps.
Results. We provide two criteria to decide whether the information from the centroid velocities directly reflects the properties of the underlying velocity field. Applying these criteria allows us to understand the different results found so far in the literature for interpreting the statistics of velocity centroids. The new iteration scheme can be used to derive the three-dimensional velocity scaling from centroid velocity maps for arbitrary density and velocity fields, but it requires accurate knowledge of the average density of the interstellar cloud under consideration.
Key words: ISM: clouds - ISM: kinematics and dynamics - ISM: structure - methods: statistical
Understanding the role and nature of interstellar turbulence
has been the subject of intensive studies for half a century now,
but many aspects still remain open (cf. Elmegreen & Scalo 2004).
Major questions concern the mechanisms by which turbulent
motions are driven and the role of the strong compressibility
of the interstellar medium for the structure of the turbulent
energy cascade. Both aspects are directly reflected on the
spectrum of velocity fluctuations in the turbulent motion.
It is frequently claimed that
driving mechanisms should create dominant motions at the
corresponding scales, and the power spectrum of velocities
in the turbulent cascade is known to change from a
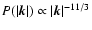 Kolmogorov spectrum for an incompressible medium to a
Kolmogorov spectrum for an incompressible medium to a
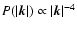 spectrum of Burger's turbulence in a highly compressible medium dominated by shocks
(Chappell & Scalo 1999). However, numerical simulations often
show a different behaviour (see Cho & Lazarian 2005),
which makes the issue of the observed spectrum very intriguing.
spectrum of Burger's turbulence in a highly compressible medium dominated by shocks
(Chappell & Scalo 1999). However, numerical simulations often
show a different behaviour (see Cho & Lazarian 2005),
which makes the issue of the observed spectrum very intriguing.
To support the theoretical understanding of the interstellar
turbulence, it is thus essential to actually measure the velocity
structure in the interstellar medium. Unfortunately, there
is no direct way to do this.
Observations of the profiles of atomic or molecular lines from
interstellar clouds allow information on the line-of-sight
velocity structure of the clouds to be deduced.
The problem of recovering the velocity information from lines
is far from being straightforward. Even in the simplest
case of thermally-excited, optically-thin lines from an isothermal
medium the line profiles originate from a convolution of the density
structure 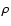 depending on the sky coordinates
depending on the sky coordinates
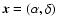 and the line-of-sight coordinate z with the velocity structure
and the line-of-sight coordinate z with the velocity structure
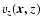 :
:
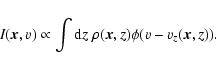 |
(1) |
In the limit of narrow lines, the line profile
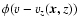 can be approximated by a
can be approximated by a 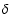 -function.
There are several complementary ways to use this information
(cf. Lazarian 2004). Here, we restrict ourselves to centroids, the first moment of the lines, but the centroids still provide no direct map of the velocity structure.
-function.
There are several complementary ways to use this information
(cf. Lazarian 2004). Here, we restrict ourselves to centroids, the first moment of the lines, but the centroids still provide no direct map of the velocity structure.
Models for the density structure and the relation between density
and velocity structure are needed to deduce the latter from the profiles
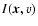 .
This is straightforward for simple geometries
like spherical clouds or thin disks but extremely difficult for
filamentary, turbulent cloud structures showing varying
substructures on all spatial scales. Hydrodynamic
or magneto-hydrodynamic numerical simulations can be used as physically
justified models for turbulent interstellar clouds within a limited
dynamic range. The nature of these can be described, however,
only in terms of statistical measures. Fractal cloud models provide
a reasonable phenomenological description of the clouds. We focus on measures
for the spatial scaling of the velocity structure. The ultimate
goal is to derive the three-dimensional (3D) power spectrum
of velocity fluctuations.
.
This is straightforward for simple geometries
like spherical clouds or thin disks but extremely difficult for
filamentary, turbulent cloud structures showing varying
substructures on all spatial scales. Hydrodynamic
or magneto-hydrodynamic numerical simulations can be used as physically
justified models for turbulent interstellar clouds within a limited
dynamic range. The nature of these can be described, however,
only in terms of statistical measures. Fractal cloud models provide
a reasonable phenomenological description of the clouds. We focus on measures
for the spatial scaling of the velocity structure. The ultimate
goal is to derive the three-dimensional (3D) power spectrum
of velocity fluctuations.
A recovery of 3D information from the available 2D data
requires, in general, an inversion, which may result in substantial noise
in the inverted data. To derive the turbulence statistics we can,
however, use its symmetries. Here, we restrict ourselves to statistically
isotropic turbulence. The derivation of properties of anisotropic, but
axisymmetric turbulence from observations was discussed by
Lazarian (1995). Anisotropies can be due to the magnetic
fields (Higdon 1984; Goldreich & Shridhar 1995; Zank & Matthaeus 1992). However, if, as both
theory and numerics suggest (see Cho & Lazarian 2003; Goldreich & Shridhar 1995), the
energy spectrum is dominated by fluctuations perpendicular
to the local direction of magnetic field, the effects of anisotropy
on the observed spectra can be neglected (Esquivel et al. 2003).
In order to derive the isotropic power spectrum, we use
an auxiliary quantity, the  -variance spectrum,
because of its practical advantages
when measuring the velocity scaling in observed data. Moreover,
we restrict the analysis here to the first moments of the lines, the
centroid velocity, as the most obvious tracer for measuring the
velocity structure in an interstellar cloud.
-variance spectrum,
because of its practical advantages
when measuring the velocity scaling in observed data. Moreover,
we restrict the analysis here to the first moments of the lines, the
centroid velocity, as the most obvious tracer for measuring the
velocity structure in an interstellar cloud.
Maps of observed line centroids have been systematically studied
to obtain the scaling behaviour of centroid velocity
differences as a function of lag for almost 50 years now
(e.g. Miesch & Bally 1994; Kleiner & Dickman 1985; Münch 1958; Miesch et al. 1999; Lis et al. 1996). However, there is still no agreement on the
theoretical relation between the observed scaling behaviour of the
centroid velocities and the scaling behaviour of the underlying
turbulent velocity structure.
Although it was clear from the very beginning that density structure
can influence the line centroids, until the recent past
there was no criterion for estimating the quantitative effect of
the density.
When investigating hydrodynamic turbulence simulations, Ossenkopf & Mac Low (2002) found
that the centroid maps show approximately the same Hurst index, i.e.
the same relative variation across a given scale, as the underlying
3D velocity structure. This means that the power spectral index in their
centroid maps was reduced by one compared to the power spectral index in
the 3D velocity structure. Studies of fractal clouds
by Miville-Deschênes et al. (2003a) showed in contrast that their centroid maps have
the same power spectral index as the 3D velocity structure![[*]](/icons/foot_motif.gif) . Lazarian & Esquivel (2003) provided an analytical treatment of the centroid statistics introducing a new, more robust definition of velocity centroids, and formulated
a criterion where the centroids represent the velocity
statistics, but this publication did not cover
the parameter space so as to be fairly compared with previous studies.
The problem was further elaborated in a subsequent study by
Levrier (2004), who pointed out that the statistical treatment
presented in the form of structure functions by Lazarian & Esquivel (2003) may
have some advantages if rewritten in terms of correlation functions.
By assuming that the fluctuations are small compared to the mean density,
he obtained analytic expressions for the correlation functions of centroids.
In combining structure and correlation functions Esquivel & Lazarian (2005) provided
a detailed study of centroid velocities for data obtained through
compressible MHD simulations.
Here, we compare the different centroid definitions and test their outcome
for a set of fractal cloud models.
. Lazarian & Esquivel (2003) provided an analytical treatment of the centroid statistics introducing a new, more robust definition of velocity centroids, and formulated
a criterion where the centroids represent the velocity
statistics, but this publication did not cover
the parameter space so as to be fairly compared with previous studies.
The problem was further elaborated in a subsequent study by
Levrier (2004), who pointed out that the statistical treatment
presented in the form of structure functions by Lazarian & Esquivel (2003) may
have some advantages if rewritten in terms of correlation functions.
By assuming that the fluctuations are small compared to the mean density,
he obtained analytic expressions for the correlation functions of centroids.
In combining structure and correlation functions Esquivel & Lazarian (2005) provided
a detailed study of centroid velocities for data obtained through
compressible MHD simulations.
Here, we compare the different centroid definitions and test their outcome
for a set of fractal cloud models.
Using the  -variance analysis, we show
that it is applicable to deriving the velocity power spectrum from
observed centroid maps but that the reliability of this derivation depends
critically on individual turbulence parameters. The centroid maps
reflect the actual velocity distribution only in a medium with an
average density that is large compared to the density dispersion.
Here, the
-variance analysis, we show
that it is applicable to deriving the velocity power spectrum from
observed centroid maps but that the reliability of this derivation depends
critically on individual turbulence parameters. The centroid maps
reflect the actual velocity distribution only in a medium with an
average density that is large compared to the density dispersion.
Here, the  -variance analysis
provides a direct measure for the power spectral index of the
velocity structure. Only when applied in an iterative process with
an a priori knowledge of the average density, the analysis of centroid
maps allows one to approximate the velocity structure in the general case.
The steeper the velocity spectrum and the better we know the average
density, the better the approximation.
-variance analysis
provides a direct measure for the power spectral index of the
velocity structure. Only when applied in an iterative process with
an a priori knowledge of the average density, the analysis of centroid
maps allows one to approximate the velocity structure in the general case.
The steeper the velocity spectrum and the better we know the average
density, the better the approximation.
In Sect. 2 we briefly repeat the formalism used to describe
the velocity centroids, and discuss the properties of the test data sets
and the ways to measure their spatial scaling behaviour in terms
of the  -variance.
In Sect. 3 we analyse the centroid maps using
the
-variance.
In Sect. 3 we analyse the centroid maps using
the  -variance, compare the results with the original test data,
and derive criteria when the centroid maps can be used to
directly measure the three-dimensional velocity structure.
In Sect. 4 we propose an iterative method to derive the
power spectrum of the velocity structure from the centroid maps
in cases without a direct matching.
Section 5 summarises our conclusions on the interpretation of observed data.
-variance, compare the results with the original test data,
and derive criteria when the centroid maps can be used to
directly measure the three-dimensional velocity structure.
In Sect. 4 we propose an iterative method to derive the
power spectrum of the velocity structure from the centroid maps
in cases without a direct matching.
Section 5 summarises our conclusions on the interpretation of observed data.
For the fluctuating density and velocity fields in a cloud, we can always
write
| |
|
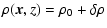 |
|
| |
|
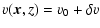 |
(2) |
where 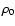 and v0 are averages over the whole cloud, and
and v0 are averages over the whole cloud, and
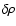 and
and 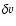 denote the variations across the cloud
denote the variations across the cloud![[*]](/icons/foot_motif.gif) .
.
When we assume that the emissivity is proportional to the density of the
cloud, the line intensity
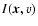 at velocity v is a measure for the total column density of emitters with this velocity at a given
line-of-sight
at velocity v is a measure for the total column density of emitters with this velocity at a given
line-of-sight 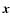 .
This condition is violated for optically
thick lines or media with strongly varying temperatures but it is
fulfilled well e.g. for the [C II] emission from the cold
neutral medium or the H I emission from the warm neutral medium.
The effect of self-absorption will be quantified in a subsequent paper.
For constant emissivity, the integrated line intensity is
.
This condition is violated for optically
thick lines or media with strongly varying temperatures but it is
fulfilled well e.g. for the [C II] emission from the cold
neutral medium or the H I emission from the warm neutral medium.
The effect of self-absorption will be quantified in a subsequent paper.
For constant emissivity, the integrated line intensity is
where X is the proportionality factor from Eq. (1)
translating the column density into a line intensity.
There are two different centroid definitions in common use.
Ordinary centroid velocities, also known as normalised centroids,
are obtained as
Unfortunately, this definition implies a complex combination of
density and velocity fluctuations, which makes it impossible to
disentangle the influence from both structures in the general
case. Only in case of very small fluctuations can a linearisation
technique be developed (Levrier 2004).
A better separation of density and velocity fluctuations in the
centroids is obtained when we apply the definition of weighted, i.e.
unnormalised, centroids as proposed by Lazarian & Esquivel (2003)![[*]](/icons/foot_motif.gif)
where
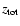 is the total thickness of the cloud. In
this definition the centroids do not have the dimension of a velocity but of velocity times column density. For a better comparison with the ordinary centroid velocities, it is useful to
normalise the weighted centroids by the average column density
is the total thickness of the cloud. In
this definition the centroids do not have the dimension of a velocity but of velocity times column density. For a better comparison with the ordinary centroid velocities, it is useful to
normalise the weighted centroids by the average column density
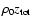 ,
but we omit this factor in the following to keep the equations shorter. The constant factor would
not change any of our conclusions on the scaling behaviour
of the velocity structure.
,
but we omit this factor in the following to keep the equations shorter. The constant factor would
not change any of our conclusions on the scaling behaviour
of the velocity structure.
We see that even in this definition the centroid velocities
are not simply determined by the projected velocities
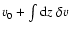 but also by two terms reflecting the density variations. The contribution
from the projected density variations
but also by two terms reflecting the density variations. The contribution
from the projected density variations
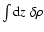 can be easily
obtained from the integrated line profiles, and it can be
eliminated by selecting a velocity scale with v0=0. However,
the term containing the product of the fluctuations in the density
and the velocity structure cannot be measured separately.
can be easily
obtained from the integrated line profiles, and it can be
eliminated by selecting a velocity scale with v0=0. However,
the term containing the product of the fluctuations in the density
and the velocity structure cannot be measured separately.
The scaling behaviour of the centroid velocities
depends on the combination of density and velocity
variations along the line of sight, which cannot be retrieved directly.
The relative contribution of the simple projection of the
velocity structure and the density variations
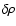 across
the line of sight
depends on the ratio between the density fluctuations
across
the line of sight
depends on the ratio between the density fluctuations
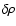 and the average density
and the average density 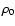 .
Equation (5) thus
shows already that the ratio between the density dispersion
.
Equation (5) thus
shows already that the ratio between the density dispersion
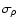 and the average density
and the average density 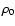 is a critical parameter for the relation between the 3D velocity scaling and
the centroid scaling.
is a critical parameter for the relation between the 3D velocity scaling and
the centroid scaling.
2.2 Test data sets
To study the general ability of different methods to extract
the underlying velocity structure from observed centroid velocities,
we constructed well defined test data sets for the density
and velocity structure that were used
to study the translation of their scaling properties
into centroid properties.
Interstellar cloud observations often reveal self-similar scaling
properties (e.g. Falgarone et al. 1995; Combes 2000) corresponding to power-law
power spectra of the intensity distribution. Such intensity
maps can be approximately modelled by
fractional Brownian motion (fBm) structures (see e.g. Stutzki et al. 1998; Bensch et al. 2001). They are defined by the single number 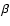 determining
the exponent of the power spectrum,
determining
the exponent of the power spectrum,
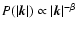 .
The phases of the Fourier spectrum are random.
.
The phases of the Fourier spectrum are random.
Thus fBm's represent one of the simplest possible representations of
interstellar cloud structures still allowing a parameter study
in terms of the spectral index 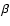 that determines the
actual appearance of the structures. The fBm's can be defined in
arbitrary dimensions and we used their essential property
that the projection of an fBm to lower dimensions results in
a new fBm with the same spectral index (Brunt & Mac Low 2004; Stutzki et al. 1998)
that determines the
actual appearance of the structures. The fBm's can be defined in
arbitrary dimensions and we used their essential property
that the projection of an fBm to lower dimensions results in
a new fBm with the same spectral index (Brunt & Mac Low 2004; Stutzki et al. 1998)![[*]](/icons/foot_motif.gif) . Thus the spectral index measured for the column density directly reflects
the index of the three-dimensional density structure.
. Thus the spectral index measured for the column density directly reflects
the index of the three-dimensional density structure.
Measured spectral indices for the column density structure of
interstellar
clouds range from 2.0 to 3.7 (Elmegreen & Scalo 2004; Falgarone et al. 2004).
Observations of large molecular clouds and molecular cloud complexes
and H I absorption line studies have provided typical values
between 2.4 and 2.9 (e.g. Langer et al. 1993; Stenholm 1984; Padoan et al. 2003; Bensch et al. 2001; Deshpande et al. 2000; Huber 2002), whereas
Bensch et al. (2001) found indications of somewhat larger indices at
the scales of cloud cores. Observations of the warm atomic gas provided
typical values between 3.3 (e.g. Stanimirovic & Lazarian 2001) and 3.6 (Miville-Deschênes et al. 2003b) with some indications of an even broader range
from 8/3 to 11/3 in the LMC (Elmegreen et al. 2001).
Due to a lack of direct measurements, as discussed in the introduction,
the index range of the velocity structure is still hardly known.
MHD simulations by Cho & Lazarian (2003) indicate that it should be close to
the Kolmogorov value of 11/3.
In contrast, Ossenkopf & Mac Low (2002) and Brunt & Heyer (2002) obtained
velocity spectral indices close to four from observations of
the Polaris Flare molecular cloud and of molecular clouds in the FCRAO survey
of the Outer Galaxy, respectively, consistent with the properties of a shock-dominated medium. In these cases, the velocity spectrum was
always steeper than the column density spectrum.
Here, we do not aim at reproducing the exact combination of spectral
indices for any particular interstellar cloud, but want to study the
general behaviour covering the full range of spectral indices observed so far.
Esquivel & Lazarian (2005) demonstrated that the centroid
structure function shows a qualitatively different behaviour for spectra
with an index above and below 3.0 (steep and shallow spectra).
Unfortunately, the observational data do not rule out
either of the two types. Thus we focus on two test data sets:
fBm's with a spectral index of 3.7 representing steep spectra and
with an index of 2.6 representing a shallow behaviour.
They sample both regimes and are close to some observed values
for the velocity and density structure.
We have studied a much larger parameter range covering spectral
indices between 2.0 and 4.0; but with the four possible mutual combinations of the two spectral indices mentioned, all major effects are covered so that we restrict ourselves
to these cases for all examples given in the following.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{2754fg1a.eps}\par\includegraphics[angle=90,width=8cm,clip]{2754fg1b.eps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg46.gif) |
Figure 1:
Projected maps of fBm structures with
spectral indices 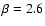 ( upper plot) and
( upper plot) and 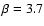 ( lower plot). Both data sets use the same random phases leading
to the apparent similarity of the overall distribution
in this example. ( lower plot). Both data sets use the same random phases leading
to the apparent similarity of the overall distribution
in this example. |
| Open with DEXTER |
In Fig. 1 we give a visual impression of
the difference in the actual projected structure between fBm's
of a different spectral index. The spectral index basically
determines the relative contribution of structures on different
size scales. The fBm with an index of 2.6 shows a large
amount of small-scale clumps and filaments, whereas the fBm
with 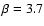 basically consists of one peak with fragmented
boundaries.
basically consists of one peak with fragmented
boundaries.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{2754fg2a.ps}\vspace*{3mm}
\includegraphics[angle=90,width=8cm,clip]{2754fg2b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg47.gif) |
Figure 2:
 -variance spectra of the projected structure of
exponentiated fBm's compared to the spectrum of the original fBm.
The upper plot represents -variance spectra of the projected structure of
exponentiated fBm's compared to the spectrum of the original fBm.
The upper plot represents 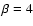 ,
the lower plot ,
the lower plot 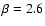 .
The different lines indicate different stretching factors aresulting in different logarithmic widths of the distributions.
The average logarithmic density is taken to be 2.0 in all cases. .
The different lines indicate different stretching factors aresulting in different logarithmic widths of the distributions.
The average logarithmic density is taken to be 2.0 in all cases. |
| Open with DEXTER |
The figure also reveals a general problem of fBm's when interpreted
as density structure. They show negative values. On average fBm's have
a Gaussian probability distribution with vanishing
mean so that negative values can only be avoided when adding a large
constant density offset. However, we drastically
change the ratio
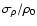 for the data set in this way.
Another method to create a density distribution containing only
positive values is to square or exponentiate the original fBm
as proposed by Stutzki et al. (1998). Miville-Deschênes et al. (2003a) have
claimed that exponentiation,
for the data set in this way.
Another method to create a density distribution containing only
positive values is to square or exponentiate the original fBm
as proposed by Stutzki et al. (1998). Miville-Deschênes et al. (2003a) have
claimed that exponentiation,
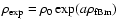 ,
does not affect the power-spectrum,
but it is mathematically obvious that it can potentially destroy
the power-law scaling. Thus we have tested the impact of exponentiation
for different spectral indices
,
does not affect the power-spectrum,
but it is mathematically obvious that it can potentially destroy
the power-law scaling. Thus we have tested the impact of exponentiation
for different spectral indices 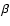 and different factors atranslating the standard deviation of the fBm into the logarithmic
standard deviation of the new density structure. The result is shown
in Fig. 2 for an fBm with
and different factors atranslating the standard deviation of the fBm into the logarithmic
standard deviation of the new density structure. The result is shown
in Fig. 2 for an fBm with 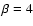 as used in Fig. 11 of Miville-Deschênes et al. (2003a) and for an fBm with
as used in Fig. 11 of Miville-Deschênes et al. (2003a) and for an fBm with 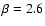 in terms of
in terms of  -variance spectra (see Sect. 2.3).
-variance spectra (see Sect. 2.3).
It is obvious, that for narrow distributions, the distortion of the
original spectrum by exponentiation is small, as the exponentiation
is then close to a linear transformation. In general, we have to
acknowledge, however, considerable distortions of the spectrum by
the exponentiation. When creating a very wide density distribution
from the 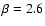 fBm, we
even find a completely different scaling behaviour that instead
resembles a structure with
fBm, we
even find a completely different scaling behaviour that instead
resembles a structure with 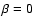 .
The example from
Miville-Deschênes et al. (2003a) corresponds approximately to the
.
The example from
Miville-Deschênes et al. (2003a) corresponds approximately to the 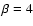 ,
,
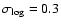 case shown in Fig. 2.
Here, the deviation from the original spectrum is small so that
it was not detectable. Moreover, we have found that
the
case shown in Fig. 2.
Here, the deviation from the original spectrum is small so that
it was not detectable. Moreover, we have found that
the  -variance reacts much more sensitively to the exponentiation
than does the azimuthally averaged power spectrum. Only for very wide
distributions and low spectral indices does the azimuthally averaged power
spectra show similar noticeable deviations. In general we have to
conclude that exponentiation leads to a change of
the scaling properties. Consequently, non-linear transformations
are not well suited to produce well defined test data for the
density structure. We will stick to the simple approach
of adding a constant to the fBm and ignoring the remaining
negative values for the construction of the density structure.
The implications for this approach are quantified in detail in
Sect. 3.1. In contrast to the density structure
that has to be positively defined and necessarily has a non zero mean
-variance reacts much more sensitively to the exponentiation
than does the azimuthally averaged power spectrum. Only for very wide
distributions and low spectral indices does the azimuthally averaged power
spectra show similar noticeable deviations. In general we have to
conclude that exponentiation leads to a change of
the scaling properties. Consequently, non-linear transformations
are not well suited to produce well defined test data for the
density structure. We will stick to the simple approach
of adding a constant to the fBm and ignoring the remaining
negative values for the construction of the density structure.
The implications for this approach are quantified in detail in
Sect. 3.1. In contrast to the density structure
that has to be positively defined and necessarily has a non zero mean 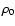 ,
the velocity structure can use fBm's directly thus guaranteeing a zero value for v0 so
that the simplifications discussed above apply.
,
the velocity structure can use fBm's directly thus guaranteeing a zero value for v0 so
that the simplifications discussed above apply.
When using independent fBm's to represent both the density
and the velocity structure of interstellar clouds, however, we neglect the
interrelation of both quantities in the interstellar medium
determined by the hydrodynamic equations, especially by the Poisson
equation. Comparisons with magneto-hydrodynamic simulations by Esquivel & Lazarian (2005) have
shown that the cross-correlation between the density
and velocity fields has a negligible effect
on the centroid velocities so that we can neglect its impact here.
We will further discuss the influence of cross-correlations between
density and velocity structure on different observational parameters
in a subsequent paper.
2.3 The  -variance
-variance
The  -variance analysis was introduced by Stutzki et al. (1998)
and improved and extended by Bensch et al. (2001) and Ossenkopf et al. (2005). Here, we
repeat only those definitions that are essential for
the centroid analysis.
-variance analysis was introduced by Stutzki et al. (1998)
and improved and extended by Bensch et al. (2001) and Ossenkopf et al. (2005). Here, we
repeat only those definitions that are essential for
the centroid analysis.
The  -variance in a structure
-variance in a structure
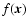 is computed
by filtering the data set with a spherically symmetric, normalised
wavelet of characteristic size l, consisting of a positive
inner part and a negative annulus, and computing the variance of the
filtered map. Ossenkopf et al. (2005) tested various wavelet shapes, but their
mutual differences are not significant for the analysis performed here
so that we stick to the ordinary French hat filter from Stutzki et al. (1998).
The
is computed
by filtering the data set with a spherically symmetric, normalised
wavelet of characteristic size l, consisting of a positive
inner part and a negative annulus, and computing the variance of the
filtered map. Ossenkopf et al. (2005) tested various wavelet shapes, but their
mutual differences are not significant for the analysis performed here
so that we stick to the ordinary French hat filter from Stutzki et al. (1998).
The  -variance is then the variance of the filtered map, as a function of the filter size, given by
-variance is then the variance of the filtered map, as a function of the filter size, given by
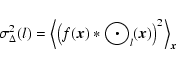 |
(6) |
where the symbol * stands for a convolution,
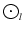 describes
the filter wavelet, and the average is taken over the whole data set.
If l is the average distance between two points in the core and the
annulus in the filter, the
describes
the filter wavelet, and the average is taken over the whole data set.
If l is the average distance between two points in the core and the
annulus in the filter, the  -variance spectrum
-variance spectrum
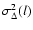 measures the amount of structure on the given scale l.
measures the amount of structure on the given scale l.
The  -variance is related to the power spectrum of a structure
-variance is related to the power spectrum of a structure
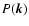 by
by
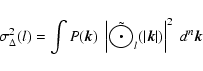 |
(7) |
where
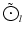 is the Fourier transform of the
filter function with the size l and
is the Fourier transform of the
filter function with the size l and  denotes the spatial frequency or wavenumber. In the case of
isotropic structures, the power spectrum is spherically
symmetric,
denotes the spatial frequency or wavenumber. In the case of
isotropic structures, the power spectrum is spherically
symmetric,
 .
This is also the case
for the Fourier-transformed filter function as long as it is
spherically symmetric in the spatial domain.
The power spectrum is given by the Fourier transform of the
autocorrelation function
.
This is also the case
for the Fourier-transformed filter function as long as it is
spherically symmetric in the spatial domain.
The power spectrum is given by the Fourier transform of the
autocorrelation function
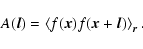 |
(8) |
For power-law power spectra, Stutzki et al. (1998) showed
that for 2D structures in the interval of spectral indices 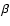 between 0 and 6, the
between 0 and 6, the  -variance spectrum is also
a power law with the exponent
-variance spectrum is also
a power law with the exponent
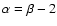 .
In three
dimensions the range is extended to
.
In three
dimensions the range is extended to
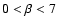 and the
exponent is
and the
exponent is
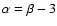 .
Equivalent slopes are obtained
locally in the case of non-power-law power spectra. However,
in this case there is no analytic relation for the normalisation
factor of the
.
Equivalent slopes are obtained
locally in the case of non-power-law power spectra. However,
in this case there is no analytic relation for the normalisation
factor of the  -variance spectrum so that it can only
be obtained by numeric integration.
-variance spectrum so that it can only
be obtained by numeric integration.
Thus the  -variance is basically a very robust method
of evaluating the power spectrum of a structure. The advantages of the
-variance is basically a very robust method
of evaluating the power spectrum of a structure. The advantages of the
 -variance compared to directly computing the power
spectrum result from the smooth filter shape, which provides
a very robust way for an angular average independent of gridding
effects, and from the insensitivity to edge effects as discussed
by Bensch et al. (2001). A possible disadvantage is the implicit
radial averaging, which does not allow for seeking signatures
of an anisotropy still contained in the 2D power spectrum
-variance compared to directly computing the power
spectrum result from the smooth filter shape, which provides
a very robust way for an angular average independent of gridding
effects, and from the insensitivity to edge effects as discussed
by Bensch et al. (2001). A possible disadvantage is the implicit
radial averaging, which does not allow for seeking signatures
of an anisotropy still contained in the 2D power spectrum
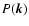 .
Such an anisotropy was considered by Esquivel & Lazarian (2005) but is irrelevant for our studies.
.
Such an anisotropy was considered by Esquivel & Lazarian (2005) but is irrelevant for our studies.
2.4 Comparing  -variance and structure function
-variance and structure function
Lazarian & Esquivel (2003) and Esquivel & Lazarian (2005) used the (second order)
structure function instead of the  -variance to characterise the
scaling of velocity centroids. The structure function is also related to
the autocorrelation function,
-variance to characterise the
scaling of velocity centroids. The structure function is also related to
the autocorrelation function,
![$D(\vec{l})=2\left[ A(0)-A(\vec{l}) \right]$](/articles/aa/full/2006/22/aa2754-05/img65.gif) (see e.g. Miesch & Bally 1994). With the power spectrum being the
Fourier transform of the autocorrelation
function, we also have a trivial relation between structure functions
and power spectra.
(see e.g. Miesch & Bally 1994). With the power spectrum being the
Fourier transform of the autocorrelation
function, we also have a trivial relation between structure functions
and power spectra.
For structures with a power-law power spectrum, Stutzki et al. (1998)
analytically studied the relation between the power spectrum, the
autocorrelation function and the  -variance. They find in the range
of spectral indices
-variance. They find in the range
of spectral indices
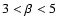 in 3D and for
in 3D and for
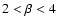 in 2D, and in the limit of infinitely large data sets,
power-law structure functions. Using the notation of Lazarian & Pogosyan (2000),
this is the range of steep spectra. Here, the spectral index of the
structure function agrees with the index of the
in 2D, and in the limit of infinitely large data sets,
power-law structure functions. Using the notation of Lazarian & Pogosyan (2000),
this is the range of steep spectra. Here, the spectral index of the
structure function agrees with the index of the  -variance
spectra discussed above.
In the range of shallow spectra with lower power spectral indices,
-variance
spectra discussed above.
In the range of shallow spectra with lower power spectral indices,
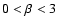 or
or
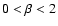 respectively,
the autocorrelation function is a power law
respectively,
the autocorrelation function is a power law![[*]](/icons/foot_motif.gif) so that the structure function must deviate from a power law
behaviour. The structure function is always increasing with lag towards
the maximum given by twice the total variance of the structure
so that the structure function must deviate from a power law
behaviour. The structure function is always increasing with lag towards
the maximum given by twice the total variance of the structure
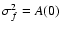 .
.
For MHD simulations producing basically steep velocity spectra
but with significant deviations from pure power laws Ossenkopf & Mac Low (2002)
compared the centroid velocity structure function
with the  -variance of the centroid map and showed that both
give a similar scaling behaviour, having comparable slopes within
a large part of the spectrum., The
-variance of the centroid map and showed that both
give a similar scaling behaviour, having comparable slopes within
a large part of the spectrum., The  -variance, however, is
advantageous with respect to the detection of pronounced scales in the map
and is more robust with respect to observational artifacts.
Altogether, the
-variance, however, is
advantageous with respect to the detection of pronounced scales in the map
and is more robust with respect to observational artifacts.
Altogether, the  -variance seems to be somewhat better suited
to determining the exponent of the power spectrum, as it shows
a wider range of power-law behaviour and is stabler with
respect to observational restrictions.
-variance seems to be somewhat better suited
to determining the exponent of the power spectrum, as it shows
a wider range of power-law behaviour and is stabler with
respect to observational restrictions.
On the other hand, Esquivel & Lazarian (2005) demonstrated that the
structure function of centroid velocities can be analytically
understood with respect to its composition from density and
velocity fluctuations. This represents a clear advantage
compared to the  -variance. Because of this, we actually performed
all tests of the centroid structures reported here both with the
-variance. Because of this, we actually performed
all tests of the centroid structures reported here both with the
 -variance analysis and with the structure
function. As a surprising result, we find very little difference
in the general behaviour. Therefore, we concentrate in the following
analysis on the
-variance analysis and with the structure
function. As a surprising result, we find very little difference
in the general behaviour. Therefore, we concentrate in the following
analysis on the  -variance spectra and discuss differences
to the structure functions only in Sect. 3.5.
-variance spectra and discuss differences
to the structure functions only in Sect. 3.5.
2.5 Projection effects
The relation between a 3D structure and projected
2D maps, obtained by integration along the line
of sight, has been studied in detail both in terms of the
 -variance (e.g. Stutzki et al. 1998; Mac Low & Ossenkopf 2000) and of
the structure function (Esquivel & Lazarian 2005). A projection
of the density structure
-variance (e.g. Stutzki et al. 1998; Mac Low & Ossenkopf 2000) and of
the structure function (Esquivel & Lazarian 2005). A projection
of the density structure
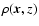 is inherently
performed when observing the intensity map
is inherently
performed when observing the intensity map
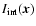 of
an optically thin tracer in a medium of constant excitation
temperature (Eq. (1)).
of
an optically thin tracer in a medium of constant excitation
temperature (Eq. (1)).
The projection effect on the  -variance spectrum can be easily
understood by realising that the
-variance spectrum can be easily
understood by realising that the  -variance is basically a robust method of deducing the power spectrum. In Fourier space, projection
corresponds to the selection of the zero-frequency component in the
considered direction. For isotropic structures the power spectral indices of
projected maps in any direction agree with the spectral index
of the 3D structure. This is fulfilled by definition for
the fB structures used here for testing. Thus the local slope of
the power spectrum
-variance is basically a robust method of deducing the power spectrum. In Fourier space, projection
corresponds to the selection of the zero-frequency component in the
considered direction. For isotropic structures the power spectral indices of
projected maps in any direction agree with the spectral index
of the 3D structure. This is fulfilled by definition for
the fB structures used here for testing. Thus the local slope of
the power spectrum 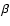 is retained, and all components with non-zero spatial frequencies
in the considered direction are dropped. Because the
is retained, and all components with non-zero spatial frequencies
in the considered direction are dropped. Because the  -variance
is obtained by convolving this power spectrum with the Fourier transform of
either a 3D or a 2D wavelet, the resulting spectrum
has a local slope
-variance
is obtained by convolving this power spectrum with the Fourier transform of
either a 3D or a 2D wavelet, the resulting spectrum
has a local slope
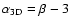 or
or
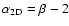 ,
respectively. The mutual translation is straightforward.
The exponent of the power spectrum is retained on projection, while the
index of the
,
respectively. The mutual translation is straightforward.
The exponent of the power spectrum is retained on projection, while the
index of the  -variance
-variance![[*]](/icons/foot_motif.gif) is increased by one.
This was confirmed in the application of the
is increased by one.
This was confirmed in the application of the  -variance
analysis to the 3D density structure of (magneto-)hydrodynamic simulations
and their projection onto maps by Mac Low & Ossenkopf (2000).
-variance
analysis to the 3D density structure of (magneto-)hydrodynamic simulations
and their projection onto maps by Mac Low & Ossenkopf (2000).
For power-law power spectra, the translation of the amplitudes can also
be performed analytically following the formalism provided in the Appendix of
Stutzki et al. (1998). As an approximation, we can also use the simple empirical
relation
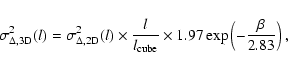 |
(9) |
which is accurate within a few percent for power spectral indices 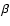 between 1 and 4 and cube sizes of at least 323 pixels. Even for sufficiently
smooth, but non-power-law
between 1 and 4 and cube sizes of at least 323 pixels. Even for sufficiently
smooth, but non-power-law  -variance spectra, Eq. (9)
can be applied by using an index
-variance spectra, Eq. (9)
can be applied by using an index 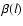 derived from the local slope.
derived from the local slope.
A general problem is, however, the actual loss of information
by projection. There is no way to recover the Fourier amplitudes that
are dropped by the projection. Thus the re-translation from the 2D
 -variance spectrum into the corresponding 3D spectrum
is only possible by assuming isotropy. Mac Low & Ossenkopf (2000) and Ossenkopf & Mac Low (2002) studied the
degree of anisotropy in hydrodynamic and magneto-hydrodynamic simulations
by comparing 2D and 3D
-variance spectrum into the corresponding 3D spectrum
is only possible by assuming isotropy. Mac Low & Ossenkopf (2000) and Ossenkopf & Mac Low (2002) studied the
degree of anisotropy in hydrodynamic and magneto-hydrodynamic simulations
by comparing 2D and 3D  -variance spectra and found
that the assumption is clearly violated for simulations with strong magnetic
fields but reasonably justified for most other simulations.
-variance spectra and found
that the assumption is clearly violated for simulations with strong magnetic
fields but reasonably justified for most other simulations.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{2754fg3a.ps}\vspace*{3mm}
\includegraphics[angle=90,width=8cm,clip]{2754fg3b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg77.gif) |
Figure 3:
 -variance spectra determined in
3D structures and their projection together with the translation
of the 3D -variance spectra determined in
3D structures and their projection together with the translation
of the 3D  -variance spectrum into the corresponding
2D spectrum using Eq. (9).
For the upper plot, an fBm with -variance spectrum into the corresponding
2D spectrum using Eq. (9).
For the upper plot, an fBm with 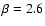 shifted by
shifted by 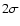 and
truncated at zero was used. The lower plot shows the result for an fBm with
and
truncated at zero was used. The lower plot shows the result for an fBm with 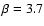 .
The solid lines mark slopes corresponding to the spectral indices .
The solid lines mark slopes corresponding to the spectral indices 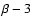 and
and 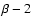 . . |
| Open with DEXTER |
Figure 3 demonstrates the influence of the projection
effects on the  -variance spectra of two fBm's. The upper graph
represents an fBm structure with a shallow index
-variance spectra of two fBm's. The upper graph
represents an fBm structure with a shallow index 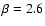 and the
lower graph a steep spectrum with
and the
lower graph a steep spectrum with 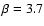 .
The
.
The  -variance
spectra measured in 3D and for the projected structure follow
the theoretical power-law relation almost exactly with the exponents
-variance
spectra measured in 3D and for the projected structure follow
the theoretical power-law relation almost exactly with the exponents
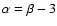 or
or
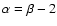 ,
respectively. The triangles
stand for the results from the
,
respectively. The triangles
stand for the results from the  -variance computed in 3D and
translated into a 2D spectrum using Eq. (9). We
find an excellent agreement with the spectra obtained directly
from the projected maps.
-variance computed in 3D and
translated into a 2D spectrum using Eq. (9). We
find an excellent agreement with the spectra obtained directly
from the projected maps.
Beyond the plotted range, the  -variance spectra show a turn-over at about half of the total size of the simulated
cube arising from the lack of larger structures due to the periodicity condition
in the construction of the data (see Bensch et al. 2001). Because of the
loss of significance at large lags, the spectra are only computed
up to lags of about a third of the cube size.
-variance spectra show a turn-over at about half of the total size of the simulated
cube arising from the lack of larger structures due to the periodicity condition
in the construction of the data (see Bensch et al. 2001). Because of the
loss of significance at large lags, the spectra are only computed
up to lags of about a third of the cube size.
When taking their relation to the autocorrelation function,
both the  -variance and the structure function of velocity
centroid maps will be given by
averages of the products
-variance and the structure function of velocity
centroid maps will be given by
averages of the products
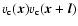 (see Eq. (8)). Using the decomposition
of the velocity centroids in Eq. (5) and assuming a zero
average velocity v0, we see that four terms characterise the scaling:
(see Eq. (8)). Using the decomposition
of the velocity centroids in Eq. (5) and assuming a zero
average velocity v0, we see that four terms characterise the scaling:
The first term is the autocorrelation function of the projected velocity
fluctuations.
If this term dominates, the scaling behaviour of the centroid velocities
reflects the scaling behaviour of the velocity structure exactly. In this case
it is easy to deduce the properties of the velocity structure from an observed
map of centroids. We find the simple projection of the velocity structure
onto a 2D map as in the case of the column density map reflecting the
3D density structure.
The second term describes a combination of the fluctuations of the density
and the velocity structure. The term also contains the
mutual correlation between density and velocity fluctuations along the
line of sight. The third and fourth terms
quantify the cross-correlation between velocity fluctuations at one point and density fluctuations at another point. In case of isotropic media,
both terms are identical. They should statistically vanish
in the case of independent density and velocity structures, but some
remainders due to accidental cross-correlations are expected for any
particular realisation. A similar decomposition in terms of the
structure function was provided by Lazarian & Esquivel (2003).
From the decomposition in Eq. (10), we see that the
ratio between the average density and the density fluctuations
should provide a criterion for deciding whether the centroid map is a good
measure of the scaling of the velocity field. In the following we test
the composition of centroid velocity maps from fBm structures by adjusting
their parameters in such a way that we cover the full range of
observed spectral indices for the density and velocity structure in the
interstellar medium.
3.1 The density zero level
A major problem with the artificial simulation of density structures
is the mutual incompatibility of Gaussian fluctuations and strictly
positive values for the density. As discussed in Sect. 2.2, fBm structures
always show a Gaussian distribution of values. Moreover, the analytic
expressions for the velocity centroids derived by Lazarian & Esquivel (2003) are also
based on the assumption of Gaussian fluctuations.
However, as long as the average of a Gaussian distribution is not large
compared its dispersion, negative values are unavoidable for sufficiently
large samples.
A common way to create positive densities is to add a constant
density until the minimum value in the cube falls to zero (Miville-Deschênes et al. 2003a; Esquivel et al. 2003). A major drawback of this method is, however, that
the minimum value of a Gaussian distribution depends on the
exact realisation of the random numbers used to generate the distribution,
and it is very sensitive to the size of the data cube. Thus
the added value, then providing the average density 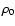 ,
may significantly vary from simulation to simulation. By renormalising
the average density to unity as proposed by Miville-Deschênes et al. (2003a)
and Esquivel et al. (2003), the variation is only transferred
to the standard deviation of the density distribution because
the ratio between standard deviation and mean is retained. Moreover,
the approach results typically in
,
may significantly vary from simulation to simulation. By renormalising
the average density to unity as proposed by Miville-Deschênes et al. (2003a)
and Esquivel et al. (2003), the variation is only transferred
to the standard deviation of the density distribution because
the ratio between standard deviation and mean is retained. Moreover,
the approach results typically in
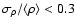 (Miville-Deschênes et al. 2003a). Such values
contradict many observational data (see e.g. Jenkins 2004).
Density fluctuations with
(Miville-Deschênes et al. 2003a). Such values
contradict many observational data (see e.g. Jenkins 2004).
Density fluctuations with
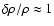 are expected for
Mach numbers approaching unity. Such Mach numbers characterise
warm media, while colder parts of the ISM tend to have supersonic
velocities (see Elmegreen & Scalo 2004) leading to
even larger density fluctuations (Padoan et al. 1997; Falgarone et al. 1998).
are expected for
Mach numbers approaching unity. Such Mach numbers characterise
warm media, while colder parts of the ISM tend to have supersonic
velocities (see Elmegreen & Scalo 2004) leading to
even larger density fluctuations (Padoan et al. 1997; Falgarone et al. 1998).
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{2754fg4.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg86.gif) |
Figure 4:
 -variance spectra of 3D density structures
obtained by shift-and-truncate from an fBm with -variance spectra of 3D density structures
obtained by shift-and-truncate from an fBm with 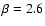 and different truncation levels. The spectrum for
the density cut at and different truncation levels. The spectrum for
the density cut at 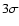 is partially indistinguishable
from the original spectrum.
is partially indistinguishable
from the original spectrum. |
| Open with DEXTER |
To a certain extent these problems can be circumvented by
combining the density shift with a truncation
of the residual negative tail.
When we shift the density distribution, e.g. by
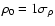 by adding this constant value, and discard all points falling below
zero, only 8% of the points from the original distribution
are set to a zero value so that the statistical properties of the
overall structure are hardly changed.
In this way we can obtain positive densities and a
by adding this constant value, and discard all points falling below
zero, only 8% of the points from the original distribution
are set to a zero value so that the statistical properties of the
overall structure are hardly changed.
In this way we can obtain positive densities and a
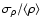 ratio of about one, avoiding all problems
from a dependency on the resolution and on the exact random numbers. One has to
keep in mind, however, that the truncation of the density structure
can have a noticeable influence on the scaling properties.
The pure addition of the constant density does not affect affect the spectrum
because it is scale-independent.
ratio of about one, avoiding all problems
from a dependency on the resolution and on the exact random numbers. One has to
keep in mind, however, that the truncation of the density structure
can have a noticeable influence on the scaling properties.
The pure addition of the constant density does not affect affect the spectrum
because it is scale-independent.
To test the possible error introduced by truncating
the distribution at a given density level, we analysed the
truncated fBm's and compared them to the original spectra. The result is shown
for a spectral index 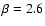 and different truncation levels
in Fig. 4. The actual shift of the
density by
and different truncation levels
in Fig. 4. The actual shift of the
density by 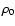 does not influence these spectra because
the
does not influence these spectra because
the  -variance is insensitive to any constant offset. We
see the pure truncation effect. For truncation levels of
-variance is insensitive to any constant offset. We
see the pure truncation effect. For truncation levels of
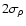 and above, the spectra are practically not changed. For truncation levels between
and above, the spectra are practically not changed. For truncation levels between
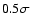 and
and 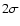 ,
the shape of the spectra is retained
but shifted to lower absolute values. This can be explained
by the reduction of the total variance in the data cubes, which
is visible in the scale-dependent
,
the shape of the spectra is retained
but shifted to lower absolute values. This can be explained
by the reduction of the total variance in the data cubes, which
is visible in the scale-dependent  -variance as well.
The original distribution was normalised to a variance of unity
in this example, whereas the truncation leads to reduced
variances of 0.96, 0.76, and 0.56 for the
-variance as well.
The original distribution was normalised to a variance of unity
in this example, whereas the truncation leads to reduced
variances of 0.96, 0.76, and 0.56 for the 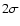 ,
,
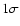 ,
and
,
and 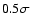 truncation levels, respectively. These are exactly the
numbers by which the
truncation levels, respectively. These are exactly the
numbers by which the  -variance spectra in Fig. 4
are shifted relative to the original spectrum. Only for a truncation level
at
-variance spectra in Fig. 4
are shifted relative to the original spectrum. Only for a truncation level
at 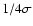 is the slope of the spectrum changed;
i.e. the scaling behaviour of the structure is modified. In this case
the absolute shift of the
is the slope of the spectrum changed;
i.e. the scaling behaviour of the structure is modified. In this case
the absolute shift of the  -variance spectrum also no longer
matches the corresponding reduction of the total variance of the
density distribution relative to the original value.
-variance spectrum also no longer
matches the corresponding reduction of the total variance of the
density distribution relative to the original value.
Examining the resulting projected maps shows that the relation between
the 3D scaling and the 2D scaling given in Eq. (9)
is also preserved down to truncation levels of 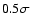 .
Corresponding studies for different spectral indices show that
the
.
Corresponding studies for different spectral indices show that
the  -variance spectra are least sensitive to truncations
at low spectral indices, between 2 and 2.5, where even truncation levels of
-variance spectra are least sensitive to truncations
at low spectral indices, between 2 and 2.5, where even truncation levels of
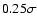 do not change the scaling behaviour and the
relation between total variance and
do not change the scaling behaviour and the
relation between total variance and  -variance.
At spectral indices close to four, in contrast, the
-variance.
At spectral indices close to four, in contrast, the 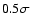 truncation plot shows already significant deviations,
so that we conclude that a negligible statistical impact on the
scaling behaviour is only guaranteed at truncation levels around
truncation plot shows already significant deviations,
so that we conclude that a negligible statistical impact on the
scaling behaviour is only guaranteed at truncation levels around 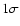 and above. The shift-and-truncate method to create positive densities is thus not perfect in terms of retaining
the original scaling properties of the structure, but the
introduced deviations are still small compared to those introduced
by the non-linear transformations discussed in Sect. 2.2. They would be hardly detectable in observed data, although we have to take them into account when
performing a detailed quantitative analysis.
and above. The shift-and-truncate method to create positive densities is thus not perfect in terms of retaining
the original scaling properties of the structure, but the
introduced deviations are still small compared to those introduced
by the non-linear transformations discussed in Sect. 2.2. They would be hardly detectable in observed data, although we have to take them into account when
performing a detailed quantitative analysis.
![\begin{figure}
\par\includegraphics[angle=90,width=7.9cm,clip]{2754fg5a.ps}\vspace*{3mm}
\includegraphics[angle=90,width=7.9cm,clip]{2754fg5b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg94.gif) |
Figure 5:
Comparison of the  -variance spectra of the
weighted centroid velocities with the spectra of the original
density and velocity structure for different truncation levels.
To plot equivalent quantities, the projected density is multiplied by -variance spectra of the
weighted centroid velocities with the spectra of the original
density and velocity structure for different truncation levels.
To plot equivalent quantities, the projected density is multiplied by
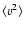 and the projected velocity by
and the projected velocity by
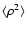 (see Esquivel & Lazarian 2005). The
(see Esquivel & Lazarian 2005). The
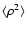 factor was computed for the factor was computed for the 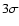 -cut density cube. The
corresponding plots for -cut density cube. The
corresponding plots for 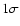 and
and
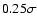 would be shifted
down by a factor 5.2 and 13.5, respectively. The upper plot
was computed from an fBm density structure with
would be shifted
down by a factor 5.2 and 13.5, respectively. The upper plot
was computed from an fBm density structure with
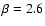 and a velocity structure with
and a velocity structure with 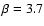 ,
while the lower
plot used the opposite spectral indices. ,
while the lower
plot used the opposite spectral indices. |
| Open with DEXTER |
Figure 5 shows two actual examples
for the influence of the density zero level definition on the
measured centroid velocity spectra. The scaling behaviour of the
centroids was computed in terms of the  -variance spectra
for three different shift-and-truncate levels of fBm generated
density structures. To judge how far they reflect the original
density or velocity structure, we have also plotted the
-variance spectra
for three different shift-and-truncate levels of fBm generated
density structures. To judge how far they reflect the original
density or velocity structure, we have also plotted the  -variance
spectra of these projected quantities multiplied with the mean square
of the complementary quantity to guarantee units equivalent
to the centroids.
-variance
spectra of these projected quantities multiplied with the mean square
of the complementary quantity to guarantee units equivalent
to the centroids.
The upper plot shows the combination of a shallow density spectrum with a steep velocity spectrum, matching a situation that is typically observed
in molecular clouds (see Sect. 2.2). The absolute shift of the
curves for weighted centroids is mainly determined by the different
values of
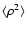 produced by different average
densities. However, this shift does not influence the characteristic
scaling behaviour within the structure. Looking at the slopes of the
centroid spectra, we find a confirmation of the general
considerations on the role of the density zero level
produced by different average
densities. However, this shift does not influence the characteristic
scaling behaviour within the structure. Looking at the slopes of the
centroid spectra, we find a confirmation of the general
considerations on the role of the density zero level 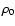 given
above. If the density structure is dominated by a large average, i.e.
in the case of
given
above. If the density structure is dominated by a large average, i.e.
in the case of
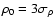 ,
the centroid velocities
are basically given by a projection of the velocity structure,
so that they reproduce the original velocity scaling behaviour.
For lower average densities, i.e. a lower relative contribution
of the pure velocity projection given by the first term in Eq. (10), the centroid scaling becomes shallower
with an exponent that is close to that of the velocity structure
on large scales and an exponent close to that of the density
structure on very small scales and the lowest values of
,
the centroid velocities
are basically given by a projection of the velocity structure,
so that they reproduce the original velocity scaling behaviour.
For lower average densities, i.e. a lower relative contribution
of the pure velocity projection given by the first term in Eq. (10), the centroid scaling becomes shallower
with an exponent that is close to that of the velocity structure
on large scales and an exponent close to that of the density
structure on very small scales and the lowest values of 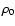 .
This plot seems to confirm the transition from purely velocity-dominated
centroids to density-dominated centroids as originally interpreted
by Lazarian & Esquivel (2003).
.
This plot seems to confirm the transition from purely velocity-dominated
centroids to density-dominated centroids as originally interpreted
by Lazarian & Esquivel (2003).
If we consider, however, the opposite situation of spectral
indices in the lower plot, we only find that the centroid
scaling becomes less and less representative for the actual
velocity structure when reducing the average density 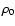 .
Their scaling does not tend towards the scaling
of the column density structure but becomes shallower as well. This fact
is confirmed in all simulations with other combinations of
spectral indices. At low values of
.
Their scaling does not tend towards the scaling
of the column density structure but becomes shallower as well. This fact
is confirmed in all simulations with other combinations of
spectral indices. At low values of
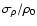 ,
the
centroids match the projected velocity structure, whereas
their scaling becomes shallower for lower average densities
irrespective of the actual spectral index of the density
structure. The spectral index of the density structure
determines, however, on which scales the deviations occur.
For density structures with a shallow spectral index, i.e. dominated
by many small-scale fluctuations, the main effect occurs on
small scales. In contrast, we find the main deviations at
large scales, when the density structure has a steep index,
representing a relative dominance of large-scale fluctuations.
When interpreting changes in the slope of the
,
the
centroids match the projected velocity structure, whereas
their scaling becomes shallower for lower average densities
irrespective of the actual spectral index of the density
structure. The spectral index of the density structure
determines, however, on which scales the deviations occur.
For density structures with a shallow spectral index, i.e. dominated
by many small-scale fluctuations, the main effect occurs on
small scales. In contrast, we find the main deviations at
large scales, when the density structure has a steep index,
representing a relative dominance of large-scale fluctuations.
When interpreting changes in the slope of the  -variance
spectrum of observed centroid maps, we can thus use the known
information on the projected density scaling to judge whether
they represent an actual deviation of the velocity structure
from self-similarity or whether they might be produced just by
the centroid composition effects. In general, we find a bigger
impact on the overall centroid spectrum as both spectra become
shallower. However, it is not clear that the a shallow velocity field is
physically motivated (Esquivel & Lazarian 2005).
-variance
spectrum of observed centroid maps, we can thus use the known
information on the projected density scaling to judge whether
they represent an actual deviation of the velocity structure
from self-similarity or whether they might be produced just by
the centroid composition effects. In general, we find a bigger
impact on the overall centroid spectrum as both spectra become
shallower. However, it is not clear that the a shallow velocity field is
physically motivated (Esquivel & Lazarian 2005).
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{2754fg6a.ps}\par\includegraphics[angle=90,width=8cm,clip]{2754fg6b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg96.gif) |
Figure 6:
Same as Fig. 5 but
for normalised centroids. They are rescaled by the factor
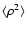 to obtain comparable dimensions.
to obtain comparable dimensions. |
| Open with DEXTER |
In Fig. 6 we show the same
effects for the ordinary, normalised centroids instead of the
weighted centroids used in Fig. 5.
We find the same general behaviour as for the weighted centroids
but differences in details. In all cases with high average
densities, i.e. for
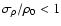 ,
the normalised
centroids provide a slightly better reproduction of the
original velocity structure than do the weighted centroids.
At lower densities, they are somewhat less changed for shallow
density spectra and somewhat more changed for steep density
spectra. The modifications correspond approximately to the
same effect that a change of
,
the normalised
centroids provide a slightly better reproduction of the
original velocity structure than do the weighted centroids.
At lower densities, they are somewhat less changed for shallow
density spectra and somewhat more changed for steep density
spectra. The modifications correspond approximately to the
same effect that a change of
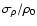 by a factor 1.5 would have for the weighted centroids. In general we can state, however, that either
both centroid definitions reveal the true velocity structure
or none of them do. The direct retrieval of the velocity scaling from
the
by a factor 1.5 would have for the weighted centroids. In general we can state, however, that either
both centroid definitions reveal the true velocity structure
or none of them do. The direct retrieval of the velocity scaling from
the  -variance spectra of the centroids will only succeed
when the average cloud density is significantly larger than
the density dispersion. In these cases the normalised centroids
are marginally better than the weighted centroids.
-variance spectra of the centroids will only succeed
when the average cloud density is significantly larger than
the density dispersion. In these cases the normalised centroids
are marginally better than the weighted centroids.
These results explain the differences and agreements between
the previous studies on velocity centroids discussed so far in the literature.
The studies of Miville-Deschênes et al. (2003a) and Lazarian & Esquivel (2003) used a relatively
large average density and they indicated a good match between centroid spectra
and projected velocity spectra. The mechanism of producing positive
densities from fBm's by adding large constant values used by
Miville-Deschênes et al. (2003a) and Esquivel et al. (2003) gave results
that correspond to our results for applying the
shift-and-truncate technique with a large average density, i.e. when
we add the 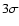 density offset. Both centroid definitions
follow the actual velocity scaling over a wide range of
scales, deviating at most at the very ends of the spectra
in this case. One has to emphasise that this matching is only
produced by adding a large
density offset. Both centroid definitions
follow the actual velocity scaling over a wide range of
scales, deviating at most at the very ends of the spectra
in this case. One has to emphasise that this matching is only
produced by adding a large 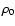 value, so that the general
conclusion that centroids are a good measure of the
velocity structure drawn by Miville-Deschênes et al. (2003a) and applied to interpreting
observational data by Miville-Deschênes et al. (2003b)
does not hold for the general case of interstellar gas
with substantial density fluctuations.
value, so that the general
conclusion that centroids are a good measure of the
velocity structure drawn by Miville-Deschênes et al. (2003a) and applied to interpreting
observational data by Miville-Deschênes et al. (2003b)
does not hold for the general case of interstellar gas
with substantial density fluctuations.
In cases with lower average densities, all using
a combination of steep velocity spectra with shallow density
spectra, Ossenkopf & Mac Low (2002), Lazarian & Esquivel (2003), and Brunt & Mac Low (2004)
found centroid spectra that were shallower than
the velocity spectrum. The hydrodynamic and magneto-hydrodynamic
turbulence models studied by Ossenkopf & Mac Low (2002) were characterised by
steep-velocity spectra with
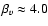 ,
shallow-density spectra with
,
shallow-density spectra with
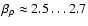 ,
and a high-density contrast with
,
and a high-density contrast with
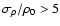 thus corresponding closely to the conditions for the
low-density curve in the upper plot of Fig. 6.
With a limited dynamic range for fitting the
thus corresponding closely to the conditions for the
low-density curve in the upper plot of Fig. 6.
With a limited dynamic range for fitting the  -variance
spectra, it is obvious that the flattening of the centroid
spectra relative to the original velocity spectrum seen in
the figure can be misinterpreted as a constant reduction of the slope by one.
-variance
spectra, it is obvious that the flattening of the centroid
spectra relative to the original velocity spectrum seen in
the figure can be misinterpreted as a constant reduction of the slope by one.
Our results can also explain the findings of Brunt & Mac Low (2004). They studied
the characteristics of velocity centroids of HD and MHD turbulence
simulations as a function of Mach number. With the known
relation between Mach number and density dispersion (Padoan et al. 1997),
their finding of a growing discrepancy between the average spectral
index of the velocity distribution and of the centroid map with
growing Mach number can be explained by the impact of an increasing
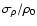 ratio, which reduces the relative
contribution of the projection term. This is most clearly
seen in the models of decaying turbulence where, e.g., for an initial
ratio, which reduces the relative
contribution of the projection term. This is most clearly
seen in the models of decaying turbulence where, e.g., for an initial
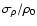 ratio of 1.1, the centroid spectrum is shallower by 0.8 than the velocity spectrum, whereas it is only
shallower by 0.1 for the final
ratio of 1.1, the centroid spectrum is shallower by 0.8 than the velocity spectrum, whereas it is only
shallower by 0.1 for the final
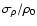 ratio of 0.5.
We have to emphasise, however, that this approach cannot explain the
differences in the spectral indices obtained by Brunt & Mac Low (2004) for MHD models
observed perpendicular or parallel to the main magnetic field
direction. In these cases, the isotropy assumption used in our
analysis is clearly violated.
ratio of 0.5.
We have to emphasise, however, that this approach cannot explain the
differences in the spectral indices obtained by Brunt & Mac Low (2004) for MHD models
observed perpendicular or parallel to the main magnetic field
direction. In these cases, the isotropy assumption used in our
analysis is clearly violated.
The composition of weighted centroids (Eq. (5))
is a priori symmetric with respect to density and velocity.
In the decomposition in Eq. (10),
we have assumed, however,
that the velocity scale is chosen in such way that v0=0 while
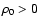 .
To better understand the centroid behaviour, it is useful
to perform an experiment using velocity fields with v0>0. From
the symmetry of the problem, we expect to find a centroid behaviour
matching the density scaling for large average velocities v0in the same way as we find centroids matching the velocity
scaling for large average densities
.
To better understand the centroid behaviour, it is useful
to perform an experiment using velocity fields with v0>0. From
the symmetry of the problem, we expect to find a centroid behaviour
matching the density scaling for large average velocities v0in the same way as we find centroids matching the velocity
scaling for large average densities 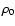 .
Indeed, we obtain
the new term
.
Indeed, we obtain
the new term
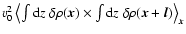 in Eq. (10) if
in Eq. (10) if 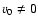 .
It
contains the spectrum of the projected density fluctuations.
In contrast to the density treatment, we do not apply any truncation
to the velocity structure when shifting it to v0>0. The experiment
thus provides an additional test for the significance of the truncation.
If the simple shift of the velocity structure behaves the same as
the shift-and-truncate of the density structure, we can be sure that
all effects result from the selection of the average values and not
from the truncation.
.
It
contains the spectrum of the projected density fluctuations.
In contrast to the density treatment, we do not apply any truncation
to the velocity structure when shifting it to v0>0. The experiment
thus provides an additional test for the significance of the truncation.
If the simple shift of the velocity structure behaves the same as
the shift-and-truncate of the density structure, we can be sure that
all effects result from the selection of the average values and not
from the truncation.
![\begin{figure}
\par\hspace*{1.5mm}\includegraphics[angle=90,width=7.9cm,clip]{27...
...\vspace*{3mm}
\includegraphics[angle=90,width=8cm,clip]{2754fg7b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg105.gif) |
Figure 7:
 -variance spectra of the centroid velocities computed using
the density and velocity structures from Fig. 5
and different v0 levels. A density structure
with -variance spectra of the centroid velocities computed using
the density and velocity structures from Fig. 5
and different v0 levels. A density structure
with
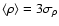 was used here.
was used here. |
| Open with DEXTER |
Figure 7 shows the impact of different velocity
offsets on the centroid  -variance spectra. A high average
density,
-variance spectra. A high average
density,
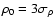 ,
was chosen to guarantee that the
centroid spectrum for v0=0 is dominated by the velocity
structure. The curves for v0=0 are identical to the
,
was chosen to guarantee that the
centroid spectrum for v0=0 is dominated by the velocity
structure. The curves for v0=0 are identical to the
 curves in Fig. 5.
When increasing the average velocity, we find a transition to shallower
spectra in the upper plot similar to the
effect of a reduced average density in Fig. 5.
The slope of the centroid spectrum remains close to the
slope of the velocity spectrum on large scales and on
small scales it takes the slope of the column density spectrum.
In the lower panel we also find that the centroid spectrum is more
and more similar to the column density spectrum when increasing the average
velocity. This is opposite to the effect of reducing the
average density in the lower panel of Fig. 5.
The adjustment of the average velocity reproduces the
transition from velocity-dominated spectra to density-dominated
spectra, as predicted by Lazarian & Esquivel (2003).
curves in Fig. 5.
When increasing the average velocity, we find a transition to shallower
spectra in the upper plot similar to the
effect of a reduced average density in Fig. 5.
The slope of the centroid spectrum remains close to the
slope of the velocity spectrum on large scales and on
small scales it takes the slope of the column density spectrum.
In the lower panel we also find that the centroid spectrum is more
and more similar to the column density spectrum when increasing the average
velocity. This is opposite to the effect of reducing the
average density in the lower panel of Fig. 5.
The adjustment of the average velocity reproduces the
transition from velocity-dominated spectra to density-dominated
spectra, as predicted by Lazarian & Esquivel (2003).
The equivalence in the impact of the velocity shift on the
centroid spectra to the impact of the shift-and-truncate method for
the density structures proves that the main change of the
centroid spectrum is due to the added offsets and not due to the
truncation of the density structure at its low density wing.
Unfortunately, the numerical experiment
cannot be exploited to derive the
true velocity scaling when the average density is so small that the
centroid spectra for v0=0 are "density-contaminated''.
By increasing v0 we will only increase the contribution from the
density scaling, which is already known from the projected intensity
maps, but we cannot remove the effect of the combination of
density and velocity fluctuations.
![\begin{figure}
\par\hspace*{-1.5mm}\includegraphics[angle=90,width=8cm,clip]{275...
...space*{3mm}
\includegraphics[angle=90,width=7.9cm,clip]{2754fg8b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg106.gif) |
Figure 8:
Decomposition of the  -variance spectra of the
weighted centroid velocities for the density and velocity structures
from Fig. 5 using shift-and-truncate by 1/4 of the original standard deviation for the density structure.
The solid line represents the contribution from the velocity structure
projected with a -variance spectra of the
weighted centroid velocities for the density and velocity structures
from Fig. 5 using shift-and-truncate by 1/4 of the original standard deviation for the density structure.
The solid line represents the contribution from the velocity structure
projected with a  weighting and the dash-dot line represents
the centroid contribution from the auxiliary density
fluctuation field. The sum of both terms (dash-dot-dot-dot) is very close to the measured centroid
spectrum (dashed). weighting and the dash-dot line represents
the centroid contribution from the auxiliary density
fluctuation field. The sum of both terms (dash-dot-dot-dot) is very close to the measured centroid
spectrum (dashed). |
| Open with DEXTER |
The results obtained so far show that the density zero level
basically changes the contribution from the first term in Eq. (10) representing the pure
projection of the velocity structure. In a next step we
investigate the relative contribution of the other three terms
to the deviation measured between the projected velocity spectra
and the centroid spectra.
The third and fourth terms vanish if there is no
cross-correlation between the density and velocity fields.
This should be the case for our independently generated fBm structures.
We expect, however, that in every realisation some
accidental correlations occur, so that the two terms
are only negligible in the ensemble average.
If the density field is known, we can obtain the second term,
i.e. the combination of density and velocity fluctuations,
by constructing an auxiliary density field
 and computing the weighted centroids for this auxiliary quantity.
As the average density of the auxiliary field vanishes, the derived
centroids directly match the second term in Eq. (10).
This procedure is illustrated in Fig. 8
where we plot the centroid spectrum for the auxiliary
field
and computing the weighted centroids for this auxiliary quantity.
As the average density of the auxiliary field vanishes, the derived
centroids directly match the second term in Eq. (10).
This procedure is illustrated in Fig. 8
where we plot the centroid spectrum for the auxiliary
field
 ,
and compare the full centroid spectrum obtained
from the original density structure with the sum of this second term
and the pure velocity scaling term.
For the sake of comparison we also plot the spectrum of the
projected density and velocity structure, where the velocity
spectrum is multiplied here by
,
and compare the full centroid spectrum obtained
from the original density structure with the sum of this second term
and the pure velocity scaling term.
For the sake of comparison we also plot the spectrum of the
projected density and velocity structure, where the velocity
spectrum is multiplied here by 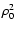 to represent
the first term in Eq. (10) exactly.
The same combination
of spectral indices as used in Fig. 5
was taken. A
to represent
the first term in Eq. (10) exactly.
The same combination
of spectral indices as used in Fig. 5
was taken. A
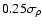 shift-and-truncate level was used for
the density structure, so that the centroid spectrum deviates
considerably from the spectrum of the velocity fluctuations.
shift-and-truncate level was used for
the density structure, so that the centroid spectrum deviates
considerably from the spectrum of the velocity fluctuations.
For all the combinations of spectral indices studied, we obtained a good match between the sum of the projected velocity spectrum
and the centroid spectrum from the auxiliary field of density
fluctuations with the full spectrum of the velocity centroids.
Nevertheless, we always found a non-negligible
difference between the two curves, resulting from the
accidental cross-correlations contributing to the third and
fourth term, which are not contained in the sum.
We also found that the second
term, giving the combination of all fluctuations, has a spectrum
which is always shallower than either of the projected spectra
involved. For a steep spectrum of density
fluctuations, its slope even turns negative at large scales.
This explains why the total spectrum of the weighted centroids
is always shallower than the projected velocity spectrum,
independent of the spectral index of the density spectrum.
The computations have confirmed the theoretical
expectation that the spectrum of velocity centroids consists
of only two main contributions: the pure projection of the velocity
structure determined by the average density 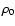 and a shallow term mainly determined by the density fluctuations.
In Sect. 4 we show how this
decomposition can be exploited to measure the actual velocity structure
from observed centroid maps if the
and a shallow term mainly determined by the density fluctuations.
In Sect. 4 we show how this
decomposition can be exploited to measure the actual velocity structure
from observed centroid maps if the
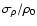 ratio
can be estimated independently.
ratio
can be estimated independently.
We have seen that the single quantity giving the ratio between the strength of the density fluctuations and the average density
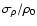 is able to discriminate between the different behaviours of the centroid spectra. For low values of this ratio,
the spectra are dominated by the actual velocity structure so that
the 3D velocity scaling is preserved in observed centroid maps.
For
is able to discriminate between the different behaviours of the centroid spectra. For low values of this ratio,
the spectra are dominated by the actual velocity structure so that
the 3D velocity scaling is preserved in observed centroid maps.
For
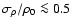 the
the  -variance spectrum of the centroid map directly measures the spectral index of the underlying velocity structure.
For higher values, the centroid spectra are always shallower than
the spectra from the projected velocity maps.
They are produced by a combination of density and velocity fluctuations.
-variance spectrum of the centroid map directly measures the spectral index of the underlying velocity structure.
For higher values, the centroid spectra are always shallower than
the spectra from the projected velocity maps.
They are produced by a combination of density and velocity fluctuations.
In contrast to the suggestion of a density-dominated regime by
Lazarian & Esquivel (2003), the systematic study of a wide range of combinations
of spectral indices with the  -variance spectra shows no
indications of a transition from velocity-dominated
centroids to density-dominated centroids, but rather a transition to
"density-contaminated'' spectra. Using a decomposition of structure
functions similar to Eq. (10), Lazarian & Esquivel (2003)
identified a term that indeed traces density fluctuations.
They showed that in general centroids
do not trace the velocity fluctuations directly.
However, in their numerical tests, they used a combination of steep velocity
and shallow density spectra, and disregard a cross term that is
equivalent to the convolution of velocity and density fluctuations
presented here. The shallow centroid spectrum was interpreted
as the density spectrum. We have demonstrated that for the
-variance spectra shows no
indications of a transition from velocity-dominated
centroids to density-dominated centroids, but rather a transition to
"density-contaminated'' spectra. Using a decomposition of structure
functions similar to Eq. (10), Lazarian & Esquivel (2003)
identified a term that indeed traces density fluctuations.
They showed that in general centroids
do not trace the velocity fluctuations directly.
However, in their numerical tests, they used a combination of steep velocity
and shallow density spectra, and disregard a cross term that is
equivalent to the convolution of velocity and density fluctuations
presented here. The shallow centroid spectrum was interpreted
as the density spectrum. We have demonstrated that for the  -variance spectra
a density-dominated regime arises only if we choose a velocity scale
with an offset so that
-variance spectra
a density-dominated regime arises only if we choose a velocity scale
with an offset so that 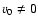 .
However, the combination
of the facts that the centroid spectrum is always shallower than the
velocity spectrum and that most observed density spectra are shallower
as well can give the false impression that
centroids trace the density scaling for large ratios
.
However, the combination
of the facts that the centroid spectrum is always shallower than the
velocity spectrum and that most observed density spectra are shallower
as well can give the false impression that
centroids trace the density scaling for large ratios
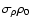 .
.
Esquivel & Lazarian (2005) presented another criterion for a match between
centroid and velocity scalings, namely,
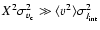 .
They stated, however, that it is not clear how large the ratio
.
They stated, however, that it is not clear how large the ratio
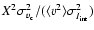 should eventually be to guarantee that the centroids reliably represent
the velocity structure.
When applied to the overall data cubes, we find that the distinctive
power of the criterion is limited.
In the examples plotted above, we obtain for instance a ratio
of 35 when using the
should eventually be to guarantee that the centroids reliably represent
the velocity structure.
When applied to the overall data cubes, we find that the distinctive
power of the criterion is limited.
In the examples plotted above, we obtain for instance a ratio
of 35 when using the 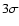 shift-and-truncate level of the density
distribution and a ratio of 3.0 for the
shift-and-truncate level of the density
distribution and a ratio of 3.0 for the
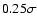 shift-and-truncate
level in the case of the shallow density and steep velocity spectrum.
In contrast, we obtain corresponding ratios of 2.6 and 0.32,
respectively, for the combination of steep density and shallow velocity
spectrum.
In both cases the
shift-and-truncate
level in the case of the shallow density and steep velocity spectrum.
In contrast, we obtain corresponding ratios of 2.6 and 0.32,
respectively, for the combination of steep density and shallow velocity
spectrum.
In both cases the 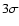 shift-and-truncate level
gives a good match between centroid and velocity scaling while
the
shift-and-truncate level
gives a good match between centroid and velocity scaling while
the
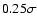 level results in very poor agreement.
Thus the global criterion is poorly quantified.
level results in very poor agreement.
Thus the global criterion is poorly quantified.
The criterion can be rewritten in a scale-dependent form
(Lazarian & Esquivel 2003):
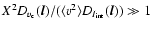 ,
when we consider the
structure function of the two maps at a given lag l.
One might assume that this criterion should
hold as well for
,
when we consider the
structure function of the two maps at a given lag l.
One might assume that this criterion should
hold as well for  -variance spectra because of their
similar scaling properties. Then a ratio
-variance spectra because of their
similar scaling properties. Then a ratio
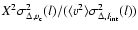 much larger than unity indicates a good match of the
centroid
much larger than unity indicates a good match of the
centroid  -variance spectrum with the true velocity spectrum.
The denominator grows compared to the numerator with
increasing scales when the density spectrum is steeper than the
velocity spectrum. In this case, matched by the lower panels
of Figs. 5-8,
the largest deviations in the centroid spectrum from the velocity
spectrum should occur on large scales, whereas the slopes
of the
-variance spectrum with the true velocity spectrum.
The denominator grows compared to the numerator with
increasing scales when the density spectrum is steeper than the
velocity spectrum. In this case, matched by the lower panels
of Figs. 5-8,
the largest deviations in the centroid spectrum from the velocity
spectrum should occur on large scales, whereas the slopes
of the  -variance spectra should match on small
scales. This is indeed the behaviour that we observe in
these figures. For the opposite relation of spectral
indices, where the velocity spectrum is steeper than the density spectrum,
as seen in the upper panels of the figures, the ratio is growing
towards larger scales, and in fact we find the
best matches of the scaling behaviour on large scales and the
main deviation on small scales.
-variance spectra should match on small
scales. This is indeed the behaviour that we observe in
these figures. For the opposite relation of spectral
indices, where the velocity spectrum is steeper than the density spectrum,
as seen in the upper panels of the figures, the ratio is growing
towards larger scales, and in fact we find the
best matches of the scaling behaviour on large scales and the
main deviation on small scales.
Using the  -variance
spectra in Fig. 5, we can evaluate
the criterion by eye from the plots. When the curves for
the centroids fall well above the dotted line giving the density spectrum,
the centroid spectrum should be a reliable tracer of the velocity structure.
The same test can be performed in the analysis
of observed data, because the
-variance
spectra in Fig. 5, we can evaluate
the criterion by eye from the plots. When the curves for
the centroids fall well above the dotted line giving the density spectrum,
the centroid spectrum should be a reliable tracer of the velocity structure.
The same test can be performed in the analysis
of observed data, because the  -variance spectra of
the intensity and the centroid velocity maps and the average velocity
dispersion are
easily measured in observed line data. However, we find that the
actual significance is also limited. In the upper panel of Fig. 5 with the shallow
density and steep velocity spectrum, we find that the velocity
spectrum is reproduced by the centroid spectrum when the
centroid
-variance spectra of
the intensity and the centroid velocity maps and the average velocity
dispersion are
easily measured in observed line data. However, we find that the
actual significance is also limited. In the upper panel of Fig. 5 with the shallow
density and steep velocity spectrum, we find that the velocity
spectrum is reproduced by the centroid spectrum when the
centroid  -variance exceeds the values from the column-density structure
by about a factor four, whereas for the steep density and shallow velocity
structure we get a good match even if the centroid curve falls just
above the column density spectrum.
For other combinations of spectral indices, we find
that a ratio of
two is sufficient to guarantee a match between centroid spectrum
and velocity spectrum, as long as the density spectrum is very steep
(
-variance exceeds the values from the column-density structure
by about a factor four, whereas for the steep density and shallow velocity
structure we get a good match even if the centroid curve falls just
above the column density spectrum.
For other combinations of spectral indices, we find
that a ratio of
two is sufficient to guarantee a match between centroid spectrum
and velocity spectrum, as long as the density spectrum is very steep
(
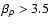 ), whereas ratios as high as 100 may be required
to guarantee a match when the density spectrum has an index shallower than 2.5. When using the normalised centroids in Fig. 6 we cannot derive an equivalent criterion to estimate the match between centroid scaling and velocity scaling
based on the measured map spectra. This is a clear practical
advantage of the weighted centroids.
), whereas ratios as high as 100 may be required
to guarantee a match when the density spectrum has an index shallower than 2.5. When using the normalised centroids in Fig. 6 we cannot derive an equivalent criterion to estimate the match between centroid scaling and velocity scaling
based on the measured map spectra. This is a clear practical
advantage of the weighted centroids.
Thus we can basically confirm the criterion, when applied in its
scale-dependent form to  -variance spectra, but have to emphasise that
there is no single value for the ratio where the transition between
velocity-dominated and "density-contaminated'' behaviour appears, but that
the exact shape of the density spectrum has to be taken into account.
-variance spectra, but have to emphasise that
there is no single value for the ratio where the transition between
velocity-dominated and "density-contaminated'' behaviour appears, but that
the exact shape of the density spectrum has to be taken into account.
3.5 Comparison of  -variance spectra and structure function
-variance spectra and structure function
As the structure function is related to the autocorrelation function,
the decomposition in Eq. (10) also applies
to the contributions to the structure function.
Lazarian & Esquivel (2003), however, showed that the second term representing the
combination of density and velocity fluctuations can be further split
into two separate
contributions in terms of the structure function. As one of them
represents the pure density fluctuations, they suggested that
the structure function can undergo a transition from a velocity-dominated
spectrum to a density-dominated spectrum.
To test this behaviour we repeated the experiments shown in
Figs. 5 to 7
for structure functions.
In general we expect to see clear deviations from power-laws as
the projection of structure functions results always in broken power laws.
Structure functions
of 2D projections can be represented by two asymptotic power laws:
one at small lags (
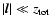 )
having a spectral index
)
having a spectral index 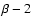 for both shallow and steep spectra, and another one at large lags
(
for both shallow and steep spectra, and another one at large lags
(
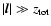 )
with a spectral index
)
with a spectral index 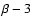 for steep spectra
and 0 (constant) for shallow spectra (Esquivel & Lazarian 2005).
Taking the general limitation of a restricted dynamic range of scales,
both in the fBm simulations and in most observed maps, the 2D structure
functions will always fall in the transition between the two asymptotes so that
their slope cannot be reconciled directly, preventing a direct recovery of
the underlying 3D statistics.
Hence, no simple inversion of the projection problem is possible.
Compared to the
for steep spectra
and 0 (constant) for shallow spectra (Esquivel & Lazarian 2005).
Taking the general limitation of a restricted dynamic range of scales,
both in the fBm simulations and in most observed maps, the 2D structure
functions will always fall in the transition between the two asymptotes so that
their slope cannot be reconciled directly, preventing a direct recovery of
the underlying 3D statistics.
Hence, no simple inversion of the projection problem is possible.
Compared to the  -variance spectra, the spectra of structure functions
are thus always somewhat more curved with steeper slopes at small lags
and shallower slopes at large lags, but in spite of the different analytic
decomposition of the structure function of centroid velocities
demonstrated by Esquivel & Lazarian (2005), the general behaviour is always
very similar to the
-variance spectra, the spectra of structure functions
are thus always somewhat more curved with steeper slopes at small lags
and shallower slopes at large lags, but in spite of the different analytic
decomposition of the structure function of centroid velocities
demonstrated by Esquivel & Lazarian (2005), the general behaviour is always
very similar to the  -variance spectra.
-variance spectra.
The measured changes due to variations in the density and velocity zero level
are also almost identical to the behaviour shown in Figs. 5
to 7. For the centroids obtained from
the density structure with the 3
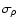 shift-and-truncate level,
we find a very good match between the structure functions of the centroids
and the projected velocity structure. The spectra flatten, however, if the
density dispersion is in the order of the average density.
Main deviations occur on large scales when the density spectrum is
steep and on small scales when it is shallow.
When comparing
shift-and-truncate level,
we find a very good match between the structure functions of the centroids
and the projected velocity structure. The spectra flatten, however, if the
density dispersion is in the order of the average density.
Main deviations occur on large scales when the density spectrum is
steep and on small scales when it is shallow.
When comparing  -variance spectra and structure functions in
detail, we find that the centroid structure functions
resemble the true velocity structure always slightly better than
the
-variance spectra and structure functions in
detail, we find that the centroid structure functions
resemble the true velocity structure always slightly better than
the  -variance spectra. This might be partially due
to the somewhat lower sensitivity of the structure function to
rapid changes in the power spectrum as found
by Ossenkopf & Mac Low (2002), but might also indicate a slight advantage of
the structure function compared to the
-variance spectra. This might be partially due
to the somewhat lower sensitivity of the structure function to
rapid changes in the power spectrum as found
by Ossenkopf & Mac Low (2002), but might also indicate a slight advantage of
the structure function compared to the  -variance spectra
when applied to centroid maps.
-variance spectra
when applied to centroid maps.
There is again no transition from velocity-matching
behaviour to density-matching behaviour, but rather a density-contaminated
structure with a spectrum that is shallower than the true velocity spectrum.
We also find a confirmation of the scale-dependent criterion
of Esquivel & Lazarian (2005) for a match between centroid
spectrum and true velocity spectrum.
Here, the critical ratio
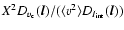 for a match between centroid structure function
and velocity structure function for a particular combination of spectral indices
is always somewhat smaller compared to the
for a match between centroid structure function
and velocity structure function for a particular combination of spectral indices
is always somewhat smaller compared to the  -variance spectra. For
steep density spectra, a ratio of one always seems to be sufficient, whereas
a ratio of 20 may be required for shallow density spectra to guarantee a velocity-dominated centroid behaviour.
-variance spectra. For
steep density spectra, a ratio of one always seems to be sufficient, whereas
a ratio of 20 may be required for shallow density spectra to guarantee a velocity-dominated centroid behaviour.
4 Derivation of the velocity structure from density-contaminated centroids
Whenever the average density of the medium is too small, such that
the centroid spectrum no longer reflects the underlying
velocity spectrum, we can deduce the true velocity spectrum from
measured centroids only when we find a way to compute the
second term in Eq. (10) and when the last
two terms produced by the accidental correlations are negligible.
Based on the results of the decomposition shown in Fig. 8, we propose an iteration scheme which computes the second term (the convolution of the two fluctuation
spectra) from the first term (the velocity projection weighted
with 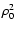 )
obtained in a previous iteration step, neglecting the
small contribution from the other two terms.
)
obtained in a previous iteration step, neglecting the
small contribution from the other two terms.
As a first step in computing the fluctuation term a 3D fluctuation structure has to be constructed that matches the
scaling behaviour of the measured column density structure. This can be done
in the following way. From the measured  -variance spectrum of
the density projection, i.e. the spectrum of the intensity map, we
can compute the 3D
-variance spectrum of
the density projection, i.e. the spectrum of the intensity map, we
can compute the 3D  -variance
spectrum by de-projecting it according to the results from Sect. 2.5. By translating this spectrum by
-variance
spectrum by de-projecting it according to the results from Sect. 2.5. By translating this spectrum by
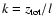 into a spherically symmetric power spectrum P(k), we create a new fBm-like structure using this power spectrum and random phases.
This new structure should match the scaling behaviour of the
input 2D
into a spherically symmetric power spectrum P(k), we create a new fBm-like structure using this power spectrum and random phases.
This new structure should match the scaling behaviour of the
input 2D  -variance spectrum.
-variance spectrum.
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{2754fg9.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg122.gif) |
Figure 9:
Two examples for the construction of fluctuation fields
from a projected  -variance spectrum. The figure compares the
input spectra with the spectra obtained from the -variance spectrum. The figure compares the
input spectra with the spectra obtained from the  -variance
analysis of the projection of the computed fluctuation fields. -variance
analysis of the projection of the computed fluctuation fields. |
| Open with DEXTER |
This is illustrated in Fig. 9, where we demonstrate
the quality of this construction for two examples. In the first case
we used the  -variance spectrum of the projection of a known fBm
with a spectral index
-variance spectrum of the projection of a known fBm
with a spectral index 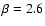 ,
while in the second we started
from an artificial spectrum given by a power law corresponding
to
,
while in the second we started
from an artificial spectrum given by a power law corresponding
to 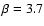 up to 17 pixels and an l-2 decay above. In both
cases we created the corresponding 3D fluctuation field, computed its
2D projection and the
up to 17 pixels and an l-2 decay above. In both
cases we created the corresponding 3D fluctuation field, computed its
2D projection and the  -variance spectrum of the projection.
Comparing this derived spectrum with the input spectrum in Fig. 9
gives an impression of the quality of the reconstruction.
-variance spectrum of the projection.
Comparing this derived spectrum with the input spectrum in Fig. 9
gives an impression of the quality of the reconstruction.
For the power-law input spectrum we find an almost perfect match with small
deviations due to the artificial gridding of the fluctuation field,
numerical uncertainties, and statistical fluctuations.
In contrast,
the spectrum composed of two power-laws is less accurately
reproduced. The  -variance spectrum of the fluctuation field
shows a broader peak and approaches the original spectrum only
at lags relatively far apart from the peak. This broadening is due to the
convolution of the power spectrum with the filter function in
Eq. (7), which was ignored in the simple
translation of the
-variance spectrum of the fluctuation field
shows a broader peak and approaches the original spectrum only
at lags relatively far apart from the peak. This broadening is due to the
convolution of the power spectrum with the filter function in
Eq. (7), which was ignored in the simple
translation of the  -variance spectrum back into the power spectrum
described above. In principle, we could try to include a corresponding
deconvolution to make the approach fully self-consistent, but
the reasonable agreement between the two curves, even in
this extreme case, shows that this additional refinement is not needed.
The example was chosen to be extreme in the sense that we have
a sharp turn from a steeply increasing spectrum into the steep
decay of the
-variance spectrum back into the power spectrum
described above. In principle, we could try to include a corresponding
deconvolution to make the approach fully self-consistent, but
the reasonable agreement between the two curves, even in
this extreme case, shows that this additional refinement is not needed.
The example was chosen to be extreme in the sense that we have
a sharp turn from a steeply increasing spectrum into the steep
decay of the  -variance representing completely uncorrelated structures.
In all cases with wider peaks, the agreement between
the original spectrum and the derived spectrum is better,
although the general tendency remains that the peak in the derived
fluctuation spectrum is always slightly too broad. The actual quality
of the construction of the fluctuation field
from the
-variance representing completely uncorrelated structures.
In all cases with wider peaks, the agreement between
the original spectrum and the derived spectrum is better,
although the general tendency remains that the peak in the derived
fluctuation spectrum is always slightly too broad. The actual quality
of the construction of the fluctuation field
from the  -variance spectrum will thus fall between the
two extremes shown in Fig. 9.
-variance spectrum will thus fall between the
two extremes shown in Fig. 9.
The fluctuation field constructed in this way has a zero average,
so that we can use it directly as the auxiliary field to compute
the centroids for
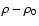 in Fig. 8,
i.e. the second term in Eq. (10).
Unfortunately, the unknown field of velocity fluctuations also enters
into this term, so that an iteration scheme is required; we start from the
measured centroid spectrum, assuming that it is determined purely by the
projection of the velocity field, then divide by
in Fig. 8,
i.e. the second term in Eq. (10).
Unfortunately, the unknown field of velocity fluctuations also enters
into this term, so that an iteration scheme is required; we start from the
measured centroid spectrum, assuming that it is determined purely by the
projection of the velocity field, then divide by 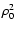 and construct
a fluctuation field for the velocities in the same way as
described above for the density fluctuation field. From the
convolution of the two fluctuation fields, we estimate the
and construct
a fluctuation field for the velocities in the same way as
described above for the density fluctuation field. From the
convolution of the two fluctuation fields, we estimate the
 -variance spectrum of the correction term. Subtracting this
spectrum from the measured centroid spectrum then provides
the next estimate of the pure projection of the velocity
field. This can be used again to determine the
pure fluctuation term in the centroids and so on.
The iteration is stopped when the velocity spectrum
obtained in subsequent steps remains constant within 1%
-variance spectrum of the correction term. Subtracting this
spectrum from the measured centroid spectrum then provides
the next estimate of the pure projection of the velocity
field. This can be used again to determine the
pure fluctuation term in the centroids and so on.
The iteration is stopped when the velocity spectrum
obtained in subsequent steps remains constant within 1%![[*]](/icons/foot_motif.gif) .
.
![\begin{figure}
\par\hspace*{-1.5mm}\includegraphics[angle=90,width=8cm,clip]{275...
...space*{3mm}
\includegraphics[angle=90,width=7.9cm,clip]{2754f10b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg124.gif) |
Figure 10:
 -variance spectra of the weighted centroid velocities
for the density and velocity structures from Fig. 8
(dotted lines). The solid line represents the projected velocity structure with
a -variance spectra of the weighted centroid velocities
for the density and velocity structures from Fig. 8
(dotted lines). The solid line represents the projected velocity structure with
a 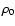 weighting. The dashed and the dash-dot lines represent the
correction term and the derived projected velocity contribution
at the end of the iteration. In the ideal case this converged solution
should agree with the spectrum from the original velocity structure. weighting. The dashed and the dash-dot lines represent the
correction term and the derived projected velocity contribution
at the end of the iteration. In the ideal case this converged solution
should agree with the spectrum from the original velocity structure. |
| Open with DEXTER |
An example of the result of this iteration is displayed in Fig. 10
for the centroid spectra obtained from the combination of shallow
density and steep velocity fields and vice versa, as shown in Fig. 8.
The general recovery of the projected velocity structure
is quite satisfactory. The absolute magnitude of the fluctuations is,
however, somewhat too small in both cases, and the derived overall
velocity spectrum is slightly steeper than the original spectrum
for the combination of the shallow density with the steep velocity spectrum.
These remaining deviations should stem from the accidental correlations
between density and velocity field, expressed in the higher
terms of Eq. (10).
Altogether, the
iteration scheme has proven to be a reliable method of recovering the
original velocity spectrum from a measured centroid spectrum, when
the projected density structure and the average density are known.
In all fBm combinations tested here, the overall slope of the derived velocity
spectrum agrees with that of the original spectrum within 0.1. This
is sufficient for distinguishing between different turbulence models
(Elmegreen & Scalo 2004).
A major drawback of this method is the need to accurately estimate
the average density in the considered interstellar cloud.
This is not easy to obtain from the projected density in
observational data because the line-of-sight extent of a cloud is
often not known. This can be overcome in clouds with a known
geometry or by excitation studies of molecular tracers sensitive to
particular densities. However, very accurate estimates will always be
difficult.
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{2754fg11.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg125.gif) |
Figure 11:
Derivation of the projected velocity spectrum from
a measured centroid spectrum when applying a 20% variation to the
density 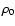 used in the iteration scheme.
used in the iteration scheme. |
| Open with DEXTER |
Thus we have studied the influence of an error in the
average density on the reconstruction of the velocity structure. In Fig. 11 we have repeated the experiment shown in the upper
plot of Fig. 10 when increasing and decreasing the
average density relative to its actual value by 20%. The result shows
the same tendencies as discussed in Sect. 3.1. When the
average density is overestimated, the centroids are thought to
resemble the scaling of the underlying velocity structure better. The velocity
fluctuations are underestimated because they are obtained by dividing
the spectrum by a 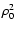 value that is too large. The
computed correction term is
too small and the derived velocity spectrum falls above the actual
spectrum and is too shallow. If the average density is underestimated,
we correct the centroid spectrum with an overestimated fluctuation
spectrum, so that the derived velocity spectrum is too small and too steep.
For steep velocity spectra a change in the average density by 20% corresponds
to a change in the average exponent of the spectrum by 0.25. For shallow
spectra, the influence is somewhat smaller.
value that is too large. The
computed correction term is
too small and the derived velocity spectrum falls above the actual
spectrum and is too shallow. If the average density is underestimated,
we correct the centroid spectrum with an overestimated fluctuation
spectrum, so that the derived velocity spectrum is too small and too steep.
For steep velocity spectra a change in the average density by 20% corresponds
to a change in the average exponent of the spectrum by 0.25. For shallow
spectra, the influence is somewhat smaller.
Thus we can conclude that it is possible to the retrieve
the actual velocity spectrum from measured centroids even if the centroid
spectrum is density-contaminated, but the accuracy of this retrieval depends
critically on knowing the average density in the cloud. Independent
measures of the
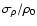 ratio are required. Methods
for accurately deriving the density from multi-line observations
have been successfully developed and applied e.g. by Schreyer et al. (1997); Sonnentrucker et al. (2003); Richter et al. (2003). They are based on a combination of information
from different species tracing a wide range of critical densities, but
the accurate determination of
ratio are required. Methods
for accurately deriving the density from multi-line observations
have been successfully developed and applied e.g. by Schreyer et al. (1997); Sonnentrucker et al. (2003); Richter et al. (2003). They are based on a combination of information
from different species tracing a wide range of critical densities, but
the accurate determination of 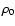 still remains a challenging task.
still remains a challenging task.
We have shown that the  -variance analysis is an appropriate tool
for characterising the scaling properties of both velocity centroid maps
and the underlying 3D velocity field. By directly
reflecting the power spectrum of fluctuations and preserving a power-law
behaviour through the projection, the
-variance analysis is an appropriate tool
for characterising the scaling properties of both velocity centroid maps
and the underlying 3D velocity field. By directly
reflecting the power spectrum of fluctuations and preserving a power-law
behaviour through the projection, the  -variance is well suited to
quantifying the properties of interstellar velocity fields.
The fact that velocity centroids may not reflect the
velocity statistics was always a concern for turbulence research. The
disagreement between the aforementioned statistics was already discussed
by Ossenkopf & Mac Low (2002) and Brunt & Mac Low (2004). We successfully tested the criterion
for the validity of centroids as measures of velocity statistics as
suggested by Lazarian & Esquivel (2003).
-variance is well suited to
quantifying the properties of interstellar velocity fields.
The fact that velocity centroids may not reflect the
velocity statistics was always a concern for turbulence research. The
disagreement between the aforementioned statistics was already discussed
by Ossenkopf & Mac Low (2002) and Brunt & Mac Low (2004). We successfully tested the criterion
for the validity of centroids as measures of velocity statistics as
suggested by Lazarian & Esquivel (2003).
We find that the most accurate criterion determining whether a centroid
spectrum reflects the velocity scaling properties is a small ratio between
the density dispersion and the mean density. The centroid spectra match
the underlying velocity structure for values below 0.5. Here,
the centroids are determined by the pure projection of the velocity
field. At higher
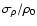 ratios, the mutual convolution
of density
and velocity fluctuation contributes a main term. Based on this knowledge,
we can qualitatively explain all the differences in the interpretation of
centroid spectra found in the literature.
ratios, the mutual convolution
of density
and velocity fluctuation contributes a main term. Based on this knowledge,
we can qualitatively explain all the differences in the interpretation of
centroid spectra found in the literature.
Without knowing the average density in the considered medium, we can
test whether a centroid spectrum reflects the true velocity structure
using the criterion by Lazarian & Esquivel (2003) that
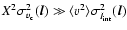 when
the centroid spectrum is velocity-dominated. Although derived for
the structure function, it holds for the
when
the centroid spectrum is velocity-dominated. Although derived for
the structure function, it holds for the  -variance as well.
However, there exists no unique factor by which the left hand side
has to exceed the right hand side.
We have confirmed the criterion by numerical experiments and found that factors
above two are sufficient in the case of steep density spectra, but factors
up to 100 may be required for extremely shallow density spectra.
Currently, observations and simulations of interstellar turbulence
show that both steep and shallow regimes may
occur with density spectral indices ranging from about 2.5 to 3.3
(see Sect. 2.2).
-variance as well.
However, there exists no unique factor by which the left hand side
has to exceed the right hand side.
We have confirmed the criterion by numerical experiments and found that factors
above two are sufficient in the case of steep density spectra, but factors
up to 100 may be required for extremely shallow density spectra.
Currently, observations and simulations of interstellar turbulence
show that both steep and shallow regimes may
occur with density spectral indices ranging from about 2.5 to 3.3
(see Sect. 2.2).
We do not see any transition from velocity-dominated to
density-dominated spectra at lower densities, but rather a transition to
"density-contaminated'' spectra that are systematically shallower.
The flattening of the centroid spectra relative to the true velocity
structure in the general case can be easily misinterpreted as a transition
from spectra reflecting the velocity structure to spectra
reflecting the density structure, because
the density spectra are often shallower
than the velocity spectra in interstellar turbulence. In any case, the density structure can be
obtained directly from column density maps. A density-dominated
spectrum occurs only if the velocity scale was chosen in an unfortunate way
so that the average velocity is not negligible compared to the velocity
dispersion. By adjusting the velocity frame such that the average
line is centred at zero, this term can always be eliminated.
Whenever the centroid spectrum is velocity-dominated, the  -variance
analysis is a simple and robust tool for directly inferring the velocity
scaling from the centroid map. The exponent of the
-variance
analysis is a simple and robust tool for directly inferring the velocity
scaling from the centroid map. The exponent of the  -variance
spectrum is the exponent of the power spectrum of the
velocity fluctuations reduced by two. Although, the second-order
structure function is connected to the power spectrum by a different
functional behaviour, we find very similar behaviour when applied to
centroid velocities. All general conclusions apply there as well. However,
the structure functions of projections of power-law power spectra are
always curved, so that a direct fit of the exponent is more difficult.
Moreover, we find that, although our analytical decomposition of the
velocity centroids is only valid for weighted centroids,
the normalised centroids behave qualitatively in the same way
so that they can also be used to derive the velocity structure
whenever the centroid spectrum is velocity-dominated.
-variance
spectrum is the exponent of the power spectrum of the
velocity fluctuations reduced by two. Although, the second-order
structure function is connected to the power spectrum by a different
functional behaviour, we find very similar behaviour when applied to
centroid velocities. All general conclusions apply there as well. However,
the structure functions of projections of power-law power spectra are
always curved, so that a direct fit of the exponent is more difficult.
Moreover, we find that, although our analytical decomposition of the
velocity centroids is only valid for weighted centroids,
the normalised centroids behave qualitatively in the same way
so that they can also be used to derive the velocity structure
whenever the centroid spectrum is velocity-dominated.
We provide an iteration scheme to derive the actual velocity structure
from the centroid maps in all cases where the average density is known,
even if the map is density-contaminated. An accurate determination
of the power spectrum of the velocity fluctuations depends on three
conditions: the correlation between density and velocity structure
can be neglected, the dynamic range of length scales covered by the
map is sufficient to compensate for statistical fluctuations at
particular lags, and the average density 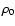 can be estimated with
high accuracy.
can be estimated with
high accuracy.
A different iteration scheme can be developed using the structure
function instead of the  -variance. In this case the decomposition
proposed by Esquivel & Lazarian (2005) can be used to obtain a scheme that is
less sensitive to the knowledge of the average density, but a considerably more complex approach is needed to evaluate the projection
effects. This will be the topic of a subsequent paper.
-variance. In this case the decomposition
proposed by Esquivel & Lazarian (2005) can be used to obtain a scheme that is
less sensitive to the knowledge of the average density, but a considerably more complex approach is needed to evaluate the projection
effects. This will be the topic of a subsequent paper.
Acknowledgements
V.O. was supported by the Deutsche Forschungsgemeinschaft
through grant 494A. A.E. acknowledges support from the NSF grant
AST-0307869 and the Center for Magnetic Self-Organization in Laboratory and Astrophysical Plasmas, and Mexico's Consejo Nacional de Ciencia y Tecnología. A.L. is supported by NSF grant AST0307869. We thank an anonymous
referee for comments helping to lay out many aspects in a clearer
and more precise way.
We have made use of NASA's Astrophysics Data System Abstract Service.
- Bensch, F., Stutzki,
J., & Ossenkopf, V. 2001, A&A, 366, 636 [EDP Sciences] [NASA ADS] [CrossRef]
- Brunt, C. M.,
& Heyer, M. H. 2002, ApJ, 566, 289 [NASA ADS] [CrossRef] (In the text)
- Brunt, C. M., & Mac
Low, M.-M. 2004, ApJ, 604, 196 [NASA ADS] [CrossRef]
- Chappell, D., &
Scalo, J. 1999, MNRAS, 310, 1 [NASA ADS] [CrossRef] (In the text)
- Cho, J., &
Lazarian, A. 2003, MNRAS, 345, 325 [NASA ADS] [CrossRef]
- Cho, J., &
Lazarian, A. 2005, Theor. and Comput. Fluid Dynamics, 19, 127 [NASA ADS] (In the text)
- Combes, F. 2000, in The
Chaotic Universe, ed. V. G. Gurzadyan, & R. Ruffini
(World Sci.), 143
- Deshpande, A. A.,
Dwarakanath, K. S., & Goss, W. M. 2000, ApJ, 543, 227 [NASA ADS] [CrossRef]
-
Elemgreen, B. G., Kim, S., & Staveley-Smith, L. 2001, ApJ, 548,
749 [NASA ADS] [CrossRef] (In the text)
- Elmegreen, B. G.,
& Scalo, J. 2004, ARA&A, 42, 211 [NASA ADS] (In the text)
- Esquivel, A., &
Lazarian, A. 2005, ApJ, 631, 320 [NASA ADS] [CrossRef] (In the text)
- Esquivel, A.,
Lazarian, A., Pogosyan, D., & Cho, J. 2003, MNRAS, 342,
325 [NASA ADS] [CrossRef] (In the text)
- Falgarone, E.,
Pineau Des Forêts, G., & Roueff, E. 1995, A&A, 300,
870 [NASA ADS]
- Falgarone,
E., Panis, J.-F., Heithausen, A., et al. 1998, A&A, 331,
669 [NASA ADS]
- Falgarone,
E., Hily-Blant, P., & Levrier, F. 2004, Ap&SS, 292, 89 [NASA ADS]
- Goldreich, P.,
& Shridhar, S. 1995, ApJ, 438, 763 [NASA ADS] [CrossRef]
- Higdon, J. C. 1984,
ApJ, 285, 109 [NASA ADS] [CrossRef]
- Huber, D. 2002,
Nonequilibrium, Self-Gravity and Fragmented Interstellar Medium,
Ph.D. Thesis No. 3348, Univ. Genève
- Jenkins, E. 2004,
Ap&SS, 289, 215 [NASA ADS] (In the text)
- Kleiner, S. C., &
Dickman, R. L. 1985, ApJ, 295, 466 [NASA ADS] [CrossRef]
- Kim, J., & Ryu, D. 2005,
ApJ, 630, L45 [NASA ADS] [CrossRef]
- Langer, W. D., Wilson,
R. W., & Anderson, C. H. 1993, ApJ, 408, L45 [NASA ADS] [CrossRef]
- Lazarian,
A. 1995, A&A, 293, 507 [NASA ADS] (In the text)
- Lazarian,
A. 2004, JKAS, 37, 563 [NASA ADS] (In the text)
- Lazarian, A.,
& Esquivel, A. 2003, ApJ, 592, L37 [NASA ADS] [CrossRef] (In the text)
- Lazarian, A., &
Pogosyan, D. 2000, ApJ, 537, 720 [NASA ADS] [CrossRef] (In the text)
- Levrier, F. 2004,
A&A, 421, 387 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Lis, D. C., Pety, J.,
Phillips, T. G., & Falgarone, E. 1996, ApJ, 463, 623 [NASA ADS] [CrossRef]
- Mac Low, M.-M., &
Ossenkopf, V. 2000, A&A, 353, 339 [NASA ADS]
- Miesch, M. S.,
& Bally, J. 1994, ApJ, 429, 645 [NASA ADS] [CrossRef]
- Miesch, M. S.,
& Scalo, J. M. 1995, ApJ, 450, L27 [NASA ADS] [CrossRef]
- Miesch, M. S.,
Scalo, J., & Bally, J. 1999, ApJ, 524, 895 [NASA ADS] [CrossRef]
-
Miville-Deschênes, M.-A., Levrier, F., & Falgarone, E.
2003a, ApJ, 593, 831 [NASA ADS] [CrossRef] (In the text)
-
Miville-Deschênes, M.-A., Joncas, G., Falgarone, E., &
Boulanger, F. 2003b, A&A, 411, 109 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Münch, G. 1958,
Rev. Mod. Phys., 30, 1035 [NASA ADS] [CrossRef]
- Ossenkopf, V.
2002, A&A, 391, 295 [EDP Sciences] [NASA ADS] [CrossRef]
- Ossenkopf, V., & Mac Low,
M.-M. 2002, A&A, 390, 307 [EDP Sciences] [NASA ADS] (In the text)
-
Ossenkopf, V., Bensch, F., & Stutzki, J. 2000, in The Chaotic
Universe, ed. V. G. Gurzadyan, & R. Ruffini, World
Sci., 394
- Ossenkopf, V., Krips, M.,
& Stutzki, J. 2005, A&A, submitted
(In the text)
- Padoan, P., Jones, J.
T., & Nordlund, A. P. 1997, ApJ, 474, 730 [NASA ADS]
- Padoan, P.,
Boldyrev, S., Langer, W., & Nordlund, A. P. 2003, ApJ,
583, 308 [NASA ADS] [CrossRef]
- Peitgen, H.-O., &
Saupe, D. 1988, The Science of Fractal Images (Berlin:
Springer)
- Richter, P., Sembach,
K. R., & Howk, J. C. 2003, A&A, 405, 1013 [EDP Sciences] [NASA ADS] [CrossRef]
- Schreyer, K.,
Helmich, F. P., van Dishoeck, E. F., & Henning, T. 1997,
A&A, 326, 347 [NASA ADS]
-
Sonnentrucker, P., Friedman, S. D., Welty, D. E., York,
D. G., & Snow, T. P. 2003, ApJ, 596, 350 [NASA ADS] [CrossRef]
- Stanimirovic, S.,
& Lazarian, A. 2001, ApJ, 551, L53 [NASA ADS] [CrossRef] (In the text)
- Stenholm, L. G.
1984, A&A, 137, 133 [NASA ADS]
- Stutzki, J.,
Bensch, F., Heithausen, A., Ossenkopf, V., & Zielinsky, M.
1998, A&A, 336, 697 [NASA ADS]
- Zank, G. P., &
Matthaeus, W. H. 1992, J. Plasma Phys., 48, 85
Copyright ESO 2006
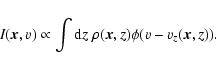
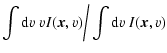
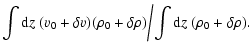
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{2754fg1a.eps}\par\includegraphics[angle=90,width=8cm,clip]{2754fg1b.eps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg46.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{2754fg2a.ps}\vspace*{3mm}
\includegraphics[angle=90,width=8cm,clip]{2754fg2b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg47.gif)
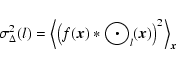
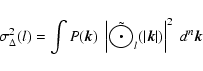
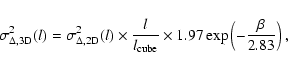
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{2754fg3a.ps}\vspace*{3mm}
\includegraphics[angle=90,width=8cm,clip]{2754fg3b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg77.gif)
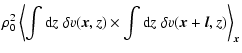
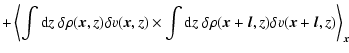
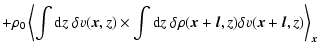
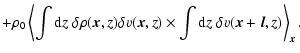
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{2754fg4.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg86.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=7.9cm,clip]{2754fg5a.ps}\vspace*{3mm}
\includegraphics[angle=90,width=7.9cm,clip]{2754fg5b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg94.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{2754fg6a.ps}\par\includegraphics[angle=90,width=8cm,clip]{2754fg6b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg96.gif)
![\begin{figure}
\par\hspace*{1.5mm}\includegraphics[angle=90,width=7.9cm,clip]{27...
...\vspace*{3mm}
\includegraphics[angle=90,width=8cm,clip]{2754fg7b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg105.gif)
![\begin{figure}
\par\hspace*{-1.5mm}\includegraphics[angle=90,width=8cm,clip]{275...
...space*{3mm}
\includegraphics[angle=90,width=7.9cm,clip]{2754fg8b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg106.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{2754fg9.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg122.gif)
![\begin{figure}
\par\hspace*{-1.5mm}\includegraphics[angle=90,width=8cm,clip]{275...
...space*{3mm}
\includegraphics[angle=90,width=7.9cm,clip]{2754f10b.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg124.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{2754fg11.ps}\end{figure}](/articles/aa/full/2006/22/aa2754-05/Timg125.gif)