Centre for Astrophysics Research, STRI, University of Hertfordshire, College Lane, Hatfield AL10 9AB, UK

Abstract
Aims. A recent spectroscopic analysis of central stars of planetary nebulae (CSPNe) claims that the sample studied includes five CSPNe with masses very close to the Chandrasekhar limit of white dwarfs. This claim is tested using available kinematical and chemical abundance information.
Methods. Kinematical parameters are extracted from Galactic orbits and compared with parameters expected for populations of different ages. The chemistry of the nebulae is compared with average values for different types.
Results. The reported high masses are not supported by our investigation. The claimed high central star masses are in contradiction with all other evidence. A more consistent picture emerges if CSPN masses close to the peak of the white dwarf mass distribution are assumed.

Key words: planetary nebulae: general - stars: AGB and post-AGB - stars: fundamental parameters - stars: kinematics

1 Introduction

Stellar masses are the most fundamental parameter of stars. However, they are notoriously difficult to derive by direct methods. The large majority of mass determinations make use of stellar models derived from computations of their evolution. Therefore it is of utmost importance that these models are checked against independent mass determinations.

In this respect the situation for planetary nebulae (PNe) and their central stars (CSPNe) is particularly dire. Napiwotzki (1999) performed an NLTE model atmosphere analysis of high gravity CSPNe and determined masses from the post-AGB tracks of Blöcker (1995) and Schönberner (1983). In a subsequent study Napiwotzki (2001) showed that the resulting distances are consistent with trigonometric parallax measurements and distances determined from companions in wide binaries, thus confirming the parameter and mass determination. However, this comparison was limited to high gravity central stars, which had already entered the white dwarf cooling sequence. No such test has been performed for low gravity CSPNe on the constant luminosity part of post-AGB evolution. "Statistical'' distance determinations using properties of the PN, like the famous Shklovsky method, exist, but they are notoriously unreliable (Napiwotzki 2001) and therefore cannot provide an independent test.

In a recent study Pauldrach et al. (2004, hereafter PHM) performed a model atmosphere analysis of UV spectra of nine luminous CSPNe. This analysis is based on spherically symmetric NLTE model atmospheres, which treat the hydrodynamics of the stellar wind in a self-consistent way. These and similar model atmospheres have been successfully applied to the spectra of hot massive main sequence stars (see discussion in Pauldrach et al. 2004). The usefulness of this method comes from the fact that it enables the determination of the absolute quantities stellar mass M and radius R without reference to stellar structure models. M and R are closely linked to the terminal wind velocity $v_\infty$ and the mass loss rate $\dot{M}$ , which can be determined from a fit of the spectral lines.

Table 1: Stellar parameters of the high mass CSPN from PHM, heliocentric radial velocities (from Durand et al. 1998) and proper motion measurements. The last column gives the source of the proper motion values.

The PHM analysis of the CSPNe sample produced a surprising result (Table 1): five out of the nine analysed stars have a mass very close to the Chandrasekhar limit for white dwarfs ( $1.40~M_\odot$ ; Hamada & Salpeter 1961) and a sixth one has a mass of $1.1~M_\odot$ . This result is surprising in at least two ways: 1) white dwarfs of such high mass are quite rare and thus we would not expect such a high fraction in a sample of CSPNe, and 2) the masses derived by PHM differ quite considerably from those derived from the comparison of effective temperature $\ensuremath{T_{{\rm eff}}}$ and gravity g with theoretical post-AGB tracks. If the results of PHM can be proven correct, this would indicate substantial flaws in the current theory of CSPNe evolution.

How can the PHM results be tested? One possible test is the comparison of the derived spectroscopic distances with other independent measurements. However, as already discussed in PHM there is a lack of reliable distance determinations for stars from the PHM sample in particular and for CSPNe of similar type in general.

Here, I use a different approach. The initial mass-final mass (IMFM) relation for white dwarfs is well established (Weidemann 2000). Some uncertainty exists at the high mass end, but we know from observations of white dwarfs in open clusters and binaries that high mass white dwarfs are produced by high mass progenitors. Even if one allows for some scatter in the IMFM relation and blue straggler scenarios it is hard to imagine that the progenitor of a ${>}1~M_\odot$ CSPNe is older than 1 Gyr, only slightly shorter than the main sequence lifetime of a $2~M_\odot$ star (Schaller et al. 1992). Therefore the high mass CSPNe should belong to the young thin disk population of the Milky Way. This population is characterised by small peculiar velocities (i.e. a small velocity dispersion) and small scale heights perpendicular to the Galactic disk. Progenitors of high mass CSPNe are associated with dredge-up of elements produced by nuclear burning, which can be detected by an analysis of the CSPNe or the surrounding PNe.

I use the kinematical properties and the PN chemistry of the PHM sample to check the results. In Sect. 2 the kinematics of this sample is compared to the expectation for a young population. Section 3 presents the evidence available from nebular abundance measurements. Section 4 concludes with a discussion of the combined evidence.

2 Kinematics

The kinematical state of a sample of stars contains information on the population membership and their age. The motion of stars in the Milky Way is usually described in the orthogonal coordinate system X, Y, Zand the corresponding velocities U, V, W. X points from the Sun in the direction of the Galactic centre, Y points in the direction of the galactic rotation at the position of the Sun and Z towards the north Galactic pole. Here I will assume an 8 kpc distance of the Sun from the Galactic centre, an orbital velocity of the local standard of rest (LSR) of 220 km s^-1 and $U_\odot=10.0$ km s^-1, $V_\odot=7.2$ km s^-1, $W_\odot=7.2$ km s^-1 relative to the LSR.

Older populations are characterised by larger scale heights in Zdirection and larger velocity dispersions in all directions. Investigations of solar neighbourhood stars often make use of diagrams plotting various combinations of the velocities U,V,W. However, this would produce misleading results if applied to stars several kpcs away from the Sun.

Insights into the kinematical state of stars can be gained from their orbits in the Milky Way. The orbits presented here are calculated with the programme ORBIT6 (Odenkirchen & Brosche 1992). The Galactic potential of Allen & Santillan (1991) is adopted. Radial velocities and proper motions were compiled from the literature and are presented in Table 1. Distances were taken from PHM. The results for IC 418 and IC 4593 are shown in Figs. 1 and 2, respectively. We use so-called meridional cuts with $\rho = \sqrt{X^2+Y^2}$ as the horizontal axis. Note that the orbit of a thin disk star without any peculiar velocity would appear as a dot in these plots. The orbit of IC 418 (Fig. 1) shows the characteristics of a disk star. The eccentricity ecc, defined as

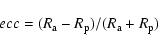
$\begin{displaymath}ecc = (R_{{\rm a}} - R_{{\rm p}})/ (R_{{\rm a}} + R_{{\rm p}}) \end{displaymath}$

Values of ecc and nze for the CSPNe sample are plotted in Fig. 3. The measurement errors were propagated via a Monte Carlo simulation (distance errors of 15% were assumed). For a discussion of these results we need to know where to find populations of different age in this diagram. We started with the velocity dispersions and asymmetric drifts given by Robin et al. (2003) for the young thin disk, the old thin disk and the thick disk (Table 2) and translated this into distributions in eccand nze via a Monte Carlo simulation with the ORBIT6 programme.

$\begin{figure} \par {\includegraphics[angle=-90,width=7.4cm,clip]{5103fig3.ps} } \end{figure}$	Figure 3: Kinematical properties of the CSPNe in the eccentricity-nzediagram. The distances computed by PHM and measured proper motions from Table 1 were used for this plot. The contour lines show the $3\sigma$ limits for young disk, old disk and thick disk stars (in order of increasing size). The error bars for individual objects indicate 68% confidence intervals.
Open with DEXTER

Table 2: Adopted velocity dispersions $\sigma _U$ , $\sigma _V$ , $\sigma _W$ and asymmetric drift $v_{{\rm ad}}$ for the young thin disk (YTD), the old thin disk (OTD) and for the thick disk (from Robin et al. 2003).

The results are shown in Fig. 3. They are inconsistent with what we expect for a young sample. Only one CSPNe (IC 418) is marginally consistent with membership of the old thin disk; Fig. 3 indicates even a halo nature of the supposedly young CSPNe of IC 4593. However, the error bars are large. The largest contribution comes from the uncertainties of the proper motion measurement. In principle the measurement of proper motions at this level of accuracy can be hampered by nebular structure close to the central star, which could cause offsets. If one wants to play devil's advocate one could argue that the proper motions may be completely unreliable. Although this is very likely over-pessimistic, it is possible that the error bars underestimate the real errors.

$\begin{figure} \par {\includegraphics[angle=-90,width=7.4cm,clip]{5103fig4.ps} } \end{figure}$	Figure 4: Kinematical properties of the CSPNe in the eccentricity-nzediagram with proper motions treated as free parameters (filled squares). The parameters resulting from the observed proper motions are indicated by open squares connected to the new results.
Open with DEXTER

As an experiment the proper motions were treated as free parameters. Distance and radial velocities were kept fixed at their values from Table 1 and an optimisation was performed to minimise the combined values of nze and eccentricity, $\sqrt{ecc^2 +nze^2}$ . The result is shown in Fig. 4. Even now only three CSPNe can be found close to the old thin disk contour, but not the young thin disk. Three stars (He 2-108, He 2-131, IC 4593) must be members of the thick disk or halo populations with a very high level of confidence. Thus we conclude that the kinematical evidence is in clear contradiction with the CSPNe being part of a young population.

3 Nebular abundances

High mass central stars with high mass progenitors are usually identified with PNe of type I in the classification scheme of Peimbert (1978). These show enhanced helium and nitrogen abundances ( ${\rm He/H} >0.125$ and ${\rm N/O} >0.50$ ; Peimbert & Torres-Peimbert 1983), which are explained by dredge-up processes in the progenitor. Although it is not clear whether all PN with high mass CSPN have enhanced abundances of helium and nitrogen, evidence for a type I nature of the PHM objects would strongly support their high mass nature.

Chemical abundances determined from the analysis of the surrounding nebulae are compiled in Table 3. These were taken from the compilation of Perinotto (1991) unless noted otherwise. Table 3 is supplemented by average abundances of type I and type II-III PNe from Perinotto (1991). PNe of type II and III are identified with lower mass CSPNe from the Galactic disc, probably including some objects from the thick disk.

Table 3 reveals that none of the PNe of the PHM sample qualifies as type I. The chemical abundances are well within the range expected for run of the mill PNe of type II and III. We conclude that again a high mass nature of the investigated objects is not supported.

4 What is the true nature of these objects?

I have presented two tests for the result of PHM that six of the CSPNe analysed by them have very high masses. The kinematical results of Sect. 2 are clearly at odds with these CSPN being young objects with massive progenitor stars. The PNe chemistry presented in Sect. 3 also points to lower mass progenitors of the PHM CSPNe. Thus I conclude that the PHM sample has failed this test and the high masses are not confirmed.

$\begin{figure} \par {\includegraphics[angle=-90,width=7.4cm,clip]{5103fig5.ps} } \end{figure}$	Figure 5: Kinematical properties of the CSPNe in the eccentricity-nzediagram resulting for assumed CSPNe masses of $0.565~M_\odot$ as discussed in the text.
Open with DEXTER

Are all these stars members of the old and metal poor thick disk and halo populations? This seems unlikely, given that the PN abundance determinations in Table 3 show that these are not very metal poor objects. However, the halo-like kinematics of the PHM sample are largely the result of the very large distances computed from the PHM parameters (Table 1). The picture becomes very different when we assume a low mass close to the peak of the white dwarf mass distribution ( $0.56\ldots0.59~M_\odot$ Napiwotzki et al. 1999; Liebert et al. 2005) and a radius consistent with standard stellar structure calculations. To demonstrate the effect I computed distances resulting from the $0.565~M_\odot$ post-AGB track of Schönberner (1983) and repeated the orbit calculations with these values. Note that I could have adopted the parameters of Kudritzki et al. (1997) instead, but this analysis has its own potential caveats, as discussed by the authors. The result is shown in Fig. 5. Now the parameters of five CSPNe are consistent with being members of the old thin disk. IC 4593 maybe member of the thick disk or halo. Interestingly, the oxygen abundance of this PN is lower than normal (Table 3), which would be consistent with such membership. However, the kinematical properties of single objects are not firm proof of their affiliation. For example, they could have suffered from unusually violent encounters with other stars.

Thus, neither the kinematical evidence nor the PNe chemistry supports the claim of high masses of the six CSPNe from the PHM sample. The findings are better explained if one assumes much lower CSPNe masses, which would correspond to lower progenitor masses. Unfortunately this would indicate that the model atmospheres applied by PHM are not yet able to produce reliable results for CSPNe, in contrast to their successful application to massive stars.

On near Chandrasekhar mass central stars of planetary nebulae

1 Introduction

2 Kinematics

3 Nebular abundances

4 What is the true nature of these objects?

References

$\begin{figure} \par {\includegraphics[angle=-90,width=7.4cm,clip]{5103fig1.ps} } \end{figure}$	Figure 1: Meridional cut of the Galactic orbit of IC 418. The orbit is integrated over 5 Gyr.
Open with DEXTER

$\begin{figure} \par {\includegraphics[angle=-90,width=7.4cm,clip]{5103fig2.ps} } \end{figure}$	Figure 2: Meridional cut of the Galactic orbit of IC 4593.
Open with DEXTER