A&A 451, 1125-1132 (2006)
DOI: 10.1051/0004-6361:20054363

Rotational excitation of carbon monosulfide by collisions with helium[*]

F. Lique1 - A. Spielfiedel1 - J. Cernicharo2


1 - LERMA and UMR 8112 of CNRS, Observatoire de Paris-Meudon, 92195 Meudon Cedex, France
2 - DAMIR. IEM-CSIC, c/ Serrano 121 28006 Madrid, Spain

Received 17 October 2005 / Accepted 15 January 2006

Abstract
Context. Over the next few years, Alma and Herschel missions will open the universe to high spatial and spectral resolution studies at infrared and sub-millimeter wavelengths. Modeling of the observed spectra will require accurate radiative and collisional rates on species of astrophysical interest.
Aims. The present paper focuses on the calculation of new rate coefficients among the 31 first rotational levels of the CS molecule in collision with He for temperatures ranging from 10 K to 300 K.
Methods. A new 2D potential energy surface for the CS-He system, calculated at a CS r-distance frozen at its experimental equilibrium distance was obtained with accurate quantum chemistry methods. Quantum close-coupling calculations lead to collisional cross sections and rate coefficients.
Results. The new rate coefficients are calculated up to 300 K. These new coefficients differ significantly from previously published ones. The consequences for astrophysical models are evaluated.

Key words: molecular processes - molecular data

1 Introduction

Observations of molecular emission at millimeter and infrared wavelengths, supplemented by careful and detailed modeling, are powerful tools for investigating the physical and chemical conditions of astrophysical objects. First detected by Penzias et al. (1971) in the interstellar gas, CS has been extensively observed. The modeling of line intensities requires excitation calculations using radiative as well as collisional rate coefficients with He and H2. Moreover, the Herschel satellite of the European Space Agency (ESA) will provide high spectral resolution observations of molecular emission in the submillimeter and far-IR domains. CS lines involving high-J levels will be observed with high signal to noise ratio given the expected sensitivity of the Herschel instruments. Hence, the interpretation of the Herschel data will require new rate coefficients involving high-J levels. It is thus important to provide accurate collisional rates for a large temperature range and also for high-J levels.

Presently, no collisional rates exist for the CS-He system. Calculations were done by Green & Chapman (1978) for the 13 lowest levels of the CS-para-H2(J=0) system. The collisional rate coefficients, calculated for temperatures ranging from 10 K to 100 K were obtained in the coupled states approach using a CS-H2 potential that was adapted from an electron gas model for the CS-He interaction. Turner et al. (1992) extended those calculations to the 21 first levels of CS and for temperatures up to 300 K using the same potential energy surface (PES) and the same approximate collisional method.

The goal of this work is to provide collisional rate coefficients of CS with He between the 31 first levels using the most accurate theoretical methods. We expected that these results will be also relevant for interpreting of the data that extremely powerful instruments, such as Herschel but also ALMA, will provide in the next few years.

In this paper, we will first describe the calculations of a new ab initio PES for the CS-He system. This accurate PES allows us to be confident that the dynamical calculations are accurate. Then, we describe the collisional method of calculations used. We present in Sect. 4 the cross sections and the collisional rate coefficients obtained for temperatures ranging from 10 K to 300 K, and we compare our results with those obtained by Turner et al. (1992) for the CS-para-H2(J=0) system. Finally, we analyze the effect of these new rate coefficients on the excitation of CS by modeling this excitation through a large velocity gradient code for different physical conditions that are representative of those of molecular clouds and star forming regions.

2 Potential energy surface

Table 1: PES of CS-He: first $V_{\lambda }(R)$ components in cm-1.


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{4363fig1.eps} \end{figure} Figure 1: Contour plot of the potential energy surface of CS-He as a function of R and theta with the C-S separation fixed at r= 2.90 a0. The energies are in cm-1 with a distance of 0.05 cm-1 between two adjacent contours, and the zero of energy is taken as that of the CS+He asymptote.
Open with DEXTER

The present work uses a Jacobi coordinate system, in which r is the CS distance, R the distance from the center of mass of CS to the He atom, and $\theta$ is the angle between the two distance vectors ($\theta=0$: He adjacent to carbon atom; $\theta=180$: He adjacent to sulfur atom). For rotational excitation calculations, the potential energy surface (PES) was calculated in the supermolecular approach based on the single and double excitation coupled cluster method (Hampel et al. 1993) (CCSD) with perturbative contributions from connected triple excitations computed as defined by Watts et al. (1993) (CCSD(T)). The CS r-distance was frozen at its experimental equilibrium distance $r_{\rm e}=2.90~a_{0}$ (Huber & Herzberg 1979). The ab initio surface was calculated using the MOLPRO package (2002). The three atoms were described by the standard correlation consistent polarized valence quadruple zeta set of Dunning (1989) (cc-pVQZ) augmented with the diffuse functions of s,p,d,f, and g symmetries by Kendall (1992) (aug-cc-pVQZ). This basis set was further augmented by the [3s3p2d2f1g] bond functions optimized by Cybulski & Toczylowski (1999) and placed at mid-distance between the He atom and the CS center of mass. The basis set superposition error (BSSE) was corrected at all geometries with the Boys & Bernardi (1970) counterpoise procedure. For a van der Waals system, where the ground state is described well by a predominant configuration at all computed geometries, this level of theory was expected to yield reliable results.

The radial scattering coordinate R was assigned values from 3.5 a0 to 16.0 a0 by steps of 0.25 a0, the angular grid was uniform with a 15 degree spacing from 0 to 180 degrees.

A contour plot of the potential is shown in Fig. 1. For this van der Waals system, the global minimum of the interaction energy was found to be -99.35175 $\mu$hartree i.e. -21.8051 cm-1 ( R=7.26 a0, $\theta=75$ degree).

Finally the fitting procedure described by Werner et al. (1988) for the CN-He system was adapted in order to obtain the $V(r=r_{\rm e},R,\theta)$ numerical expansion required as input by MOLSCAT (Hutson & Green 1995) to perform the dynamical calculation. Deviations between the fitted potential values and the ab initio points are concentrated in the repulsive part of the PES. Over the entire grid, the mean difference between the analytic fit and the ab initio calculations is 1.5%.

In terms of the Legendre polynomials, the interaction energy surface can be expressed as:

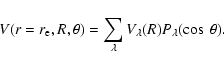\begin{displaymath}V(r=r_{\rm e},R,\theta)=\sum_{\lambda}V_{\lambda}(R)P_{\lambda}(\cos~\theta). \end{displaymath} (1)

The first $V_{\lambda }(R)$ components are given in Table 1.

Table 2: Parameters of the MOLSCAT calculations.

Comparison, made with the $V_{\lambda}$ components of the PES used by Green & Chapman (1978), shows that large differences exist for all distances (up to a factor 2 for some geometries). The PES used by Green & Chapman (1978) and Turner et al. (1992) is in fact a CS-He surface, calculated with an electron gas model and simply modified at long range ( $R \ge 8~a_{0}$) to smoothly join the asymptotic interaction of CS-H2(J=0). We used the CCSD(T) method here, which is well known for giving accurate PES for non reactive van der Waals systems, so we are confident in the quality of our approach.

By comparing this PES with the PES calculated recently for the system SO-He (Lique et al. 2005), we observe significant differences in the position and in the depth of the minimum. In particular, the global well of the SO-He system is deeper by a factor two. As a consequence, the energy range of the resonances in the cross sections is expected to be less for the CS-He collisions.

3 Collision dynamics

The ground electronic state of the CS molecule is a $^{1}\Sigma$ state with a rotational constant equal to 0.817 cm-1 (Bustreel et al. 1979).

The exact close coupling approach (CC hereafter), introduced by Arthurs & Dalgarno (1960), was used. The collision equations in the space-fixed reference frame are:

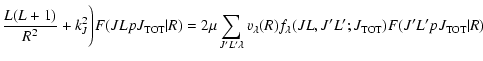$\displaystyle \Bigg( \frac{{\rm d}^{2}}{{\rm d}R^{2}}$ - $\displaystyle \frac{L(L+1)}{R^{2}}+k_{J}^{2} \Bigg)F(JLpJ_{\rm TOT}\vert R) = 2... ...lambda}v_{\lambda}(R)f_{\lambda}(JL,J'L';J_{\rm TOT})F(J'L'pJ_{\rm TOT}\vert R)$ (2)

with:
                                        $\displaystyle f_{\lambda}(JL,J'L';J_{\rm TOT})=$  
    $\displaystyle (-1)^{J+J'-J_{\rm TOT}}[(2J+1)(2J'+1)(2L+1)(2L'+1)]^{\frac{1}{2}}$  
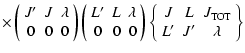    $\displaystyle \times \left( \begin{array}{ccc} J' & J & \lambda \\ 0 & 0 & 0 \... ...begin{array}{ccc} J & L & J_{\rm TOT} \\ L' & J' & \lambda \end{array}\right\}$ (3)

where $\left( 3j \right)$ and $\left\{ 6j \right\}$ are respectively the "3-j'' and "6-j'' symbols likewise $\mu$ is the reduced mass of the system, E the total energy of the collision and J, L, p and $J_{\rm TOT}$ refer, respectively to the rotational quantum number, the relative orbital angular momentum, the parity and the total angular momentum. The integral cross sections are obtained by summing the partial cross sections over  $J_{\rm TOT}$ until convergence is reached.

All the calculations were performed with the MOLSCAT code (Hutson & Green 1995). For this system, terms up to $\lambda =11$ were retained in the potential expansion. The calculations were carried out using the propagator of Manolopoulos (1986). The reduced mass of the system is 3.669. The propagation parameters were tested in order to obtain convergence of the cross sections for energies up to 2000 cm-1. Typically, the minimum and maximum integration distances are, respectively  $R_{\rm min}=2.75~a_{0}$ and $R_{\rm max}= 40~a_{0}$. The calculations included at each energy value all the open channels corresponding to energetically accessible levels. Several energetically inaccessible levels were added in order to obtain convergence of the collisional cross sections (see Table 2). At 2000 cm-1, the 31 first rotational levels were thus considered and 33 levels included in the calculation.

   
4 Results

4.1 Cross sections

Figure 2 shows the excitation cross sections from the first two rotational levels as a function of the barycentric collision energy. The cross sections decrease with increasing $\Delta$J and present resonances for energy below 30 cm-1 (see first two columns of Fig. 2). These resonances correspond to the presence at 7.26 a0 of a well whose depth is about 22 cm-1. Such behavior is typical of all the cross sections. It is interesting to note that resonances disappear at higher kinetic energies, and do not exist for cross sections involving levels with large $\Delta J$ due to the large threshold energy value (see third column of Fig. 2).


  \begin{figure} \par\includegraphics[width=12cm,clip]{4363fig2.eps}\end{figure} Figure 2: Collisional excitation cross sections of CS by He from the first two levels.
Open with DEXTER

4.2 Rate coefficients

The rate coefficients are the Boltzmann thermal average at temperature T of collision cross sections $\sigma_{J_{i} \to J_{f}}$:

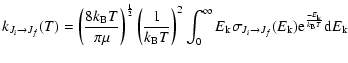$\displaystyle k_{J_{i} \to J_{f}}(T) = \left(\frac{8k_{\rm B}T}{\pi\mu}\right)^... ...} \to J_{f}}(E_{\rm k}) {\rm e}^{\frac{-E_{\rm k}}{k_{\rm B}T}}{\rm d}E_{\rm k}$     (4)

where Ji and Jf are, respectively, the initial and final states of the transition, $E_{\rm k}$ is the kinetic energy and $k_{\rm B}$ is the Boltzmann constant.

We performed CC calculations of cross sections from an energy value corresponding to the opening of the lowest inelastic channel to a total energy of 2000 cm-1. We carefully spanned the energy ranges to take the presence of resonances into account. The energy steps are 0.1 cm-1 below 50 cm-1, 0.2 cm-1 from 50 to 100 cm-1, 0.5 cm-1 from 100 to 200 cm-1, 1 from 200 to 800 cm-1, 2 from 800 to 900 cm-1, 5 from 900 to 1000 cm-1, 10 from 1000 to 1200 cm-1, and 50 from 1200 to 2000 cm-1 . Convergence of the integration was tested. Calculations up to 2000 cm-1 allow us to determine rates up to 300 K. Results were obtained for the first 31 levels (up to J=30). Collisional rate coefficients between the nine first levels are given in Tables 4-9 for temperatures equal to 10, 20, 50, 100, 200, 300 K, respectively. The complete set of rate coefficients are published in the electronic version of the paper and on our WEB site (Basecol).


  \begin{figure} \par\includegraphics[width=12cm,clip]{4363fig3.eps} \end{figure} Figure 3: Calculated CS-He rate coefficients (this work: filled circles) at 20 K ( up left), 40 K ( up right), 100 K ( down left) and 300 K ( down right) compared with CS-para-H2(J=0) rate coefficients calculated by Turner et al. (1992) (empty diamonds).
Open with DEXTER

Table 3: Comparison between cross sections obtained by Close Coupling and Coupled States approach.


  \begin{figure} \par\includegraphics[width=15cm,clip]{4363fig4.eps} \end{figure} Figure 4: Excitation temperature, $T_{\rm EX}$, and brightness temperature ratios ($T_{\rm B}$(Green rate coefficients)/$T_{\rm B}$(present rate coefficients)) for the 1-0, 2-1, 3-2, and 4-3 lines of CS ( from top to bottom) using our rate coefficients (solid lines) and those of Green & Chapman (1978) (dashed lines). The H2 volume density varies between 10 and 109 cm-3 and the CS column density from  $3\times 10^{12}$ and  $3\times 10^{15}$ cm-2 by a step factor of 10 (blue, green, red and black lines, respectively). From left to right the kinetic temperature corresponds to 10, 15, and 20 K, respectively.
Open with DEXTER

It is generally assumed that rate coefficients with para-H2(J=0) should be larger than He rate coefficients owing to the smaller collisional reduced mass and the larger size of H2, the scaling factor being 1.4 (Schöier et al. 2005). We have compared our upward CS-He rate coefficients for $\Delta J=J_{f}-J_{i}=1$, 2, and 5 with the CS-para-H2(J=0) rate coefficients obtained by Turner et al. (1992) for temperatures ranging from 20 to 300 K. As seen in Fig. 3, the ratio between the two sets of rate coefficients varies strongly with Ji and with temperature. In particular, at low temperatures, the CS-He rate coefficients are higher or lower than the CS-para-H2(J=0) rate coefficients according to the Ji value. Several factors may contribute to these differences:

(i)
the two PES used in the dynamics calculations differ at all distances: in the repulsive part, in the depth of the well, and in long range part, too. The PES used in Turner et al. (1992) was calculated for the CS-He system with an electron gas model, modified at long-range to smoothly join with the asymptotic electrostatic interaction of CS and H2(J=0). The electron gas model may induce large inaccuracies in the dynamics calculations, as pointed out by Thomas et al. (1980). Due to this approach, Turner et al. (1992) indicate that their rate coefficients may be in error by a factor up to 2-3;
(ii)
the collisional rates in Turner et al. (1992) were calculated in the coupled states approach that neglects the exact coupling of angular momenta. To analyze the effect of this approximation, we have calculated cross sections with our ab initio PES in the Coupled states approximation (McGuire & Kouri 1974). As expected, we have found that the Coupled states approach leads to some errors, compared to CC results, for calculated cross sections at low kinetic energies (<50 cm-1), this mostly affects the rates at very low kinetic temperatures (T < 50 K). Table 3 shows a comparison between CC and CS cross sections at different kinetic energies. The energies are chosen far from the resonance area to avoid differences due to resonance shifts. A global agreement is obtained between these two methods ($\sim$10-15%) but we can see that for small cross sections ( $\Delta J \ge 5$) the difference can be important, up to a factor 2.
From this comparison, it clearly appears that the differences between the two sets of rate coefficients cannot be explained only by the difference of mass of the perturbers and that the PES plays a major role. Considering the expected good accuracy of the CCSD(T) method used for the present CS-He PES and of the CC approach for dynamics calculations, it appears to us that the CS-He rate coefficients (multiplied by a factor 1.4 to take into account the ratio of the reduced mass between CS-He and CS-H2 systems) could presently be the most appropriate for interpreting observations of CS in astrophysical environments. In addition, our calculations extend the previous collisional rates for high-J levels of CS.

Table 4: Collisional rate coefficients in cm3 s-1 at T=10 K.

Table 5: Collisional rate coefficients in cm3 s-1 at T=20 K.

Table 6: Collisional rate coefficients in cm3 s-1 at T=50 K.

Table 7: Collisional rate coefficients in cm3 s-1 at T=100 K.

Table 8: Collisional rate coefficients in cm3 s-1 at T=200 K.

Table 9: Collisional rate coefficients in cm3 s-1 at T=300 K.


  \begin{figure} \par\includegraphics[width=14cm,clip]{4363fig5.eps} \end{figure} Figure 5: Excitation temperature, $T_{\rm EX}$, and brightness temperature ratios ($T_{\rm B}$(Turner et al. rate coefficients)/$T_{\rm B}$(present rate coefficients)) for the 1-0, 2-1, 3-2, and 4-3 lines of CS ( from top to bottom) using our rate coefficients (solid lines) and those of Turner et al. (1992) (dashed lines). The H2 volume density varies between 10 and 109 cm-3 and the CS column density from  $3\times 10^{12}$ and  $3\times 10^{15}$ cm-2 by a step factor of 10 (blue, green, red and black lines, respectively). From left to right the kinetic temperature corresponds to 40, 60, and 150 K, respectively.
Open with DEXTER

5 Astrophysical implications

In order to check the impact of the new rates on the interpretation of astrophysical observations, we have made astrophysical modeling using the large velocity gradient (LVG) approach, using our rate coefficients scaled to take into account both the reduced mass difference and those of Green & Chapman (1978) for T=10,15, and 20 K and Turner et al. (1992) for T=40, 60, and 150 K.

Figure 4 shows the comparison between the excitation temperatures and the brightness temperature ratios obtained with our rate coefficients and those of Green & Chapman (1978) for the typical physical conditions found in cold dark clouds. The excitation temperatures, $T_{\rm EX}$, for the Ji-Jf=1-0 to 4-3 lines have a similar behavior although ours are slightly higher than those obtained with the Green & Chapman (1978) rate coefficients. This can be easily seen in the brightness temperature ratios shown in the same figures, which indicate differences as large as 20-30% for the four lines. These differences become slightly smaller for TK=20 K. The effect of suprathermal excitation for low opacity in the 1-0 line is essentially the same for both sets of rate coefficients.

Considering that future observations with ALMA and Herschel should have calibration errors below 5%, these differences in the predicted line intensities will lead to an overestimation of the volume density, if Green & Chapman's rate coefficients are used. Figure 5 shows the same calculations but using Turner et al. (1992) rate coefficients and for higher kinetic temperatures. The effects become very large as Ji and $T_{\rm K}$ increase (see for example the right bottom panel). While the comparison with the Green & Chapman (1978) (low temperatures) rate coefficients indicates a systematic trend in the computed brightness temperature ratio, the calculations with Turner et al. (1992) rate coefficients (higher temperatures) show an underestimation of the volume density for n(H 2) < 105 cm-3 for low-J lines and an overestimation for higher densities. However, the situation is the opposite for the high-J lines (see the 4-3 line compared with the 1-0 line). The differences are even more evident for high-J lines not shown in this figure.

6 Conclusion

In this work, we report new calculations of rate coefficients for rotational excitation of CS induced by collisions with He. Cross sections were computed for the first 31 levels of CS using a new ab initio potential energy surface and quantum mechanical coupled-channel method for collision energies up to 2000 cm-1. From the cross sections, thermally averaged rate coefficients were calculated for kinetic energies ranging from 10 to 300 K. All the rate coefficients are available on the Basecol site http://boum.obspm.fr/basecol/.

These rate coefficients, scaled to take the reduced mass ratio into account, were used as surrogates for CS-para-H2(J=0) rate coefficients to calculate the excitation temperature and the brightness temperature in the various physical conditions typical of molecular clouds. The comparison with the same quantities calculated by using the rate coefficients of Green & Chapman (1978) and Turner et al. (1992) pointed out systematic differences that have an important impact on the diagnostic of the densities of molecular clouds. We will now extend this work to higher temperatures (300-1500 K), in order to interpret observations in high mass star forming regions, shocks, and the circumstellar envelopes of evolved stars. Although what is really needed for accurately interpreting the astronomical observations of CS are the rate coefficients for the CS-H2 system, we provide, for the first time, in this paper the results for the collisional excitation of high energy levels of CS by He. The rotational transitions between these high-J CS levels will be observed with the Herschel satellite and our calculations will permit to interpret these data. We would like to stress again that the available CS-H2 rates up to J=21 were obtained from a modified CS-He PES using an electron gas model that provides limited accuracy, and also using less precise methods than those used in this paper for calculating the collisional rates.

Acknowledgements
We would like to acknowledge N. Feautrier for her continuing interest in this work and for the fruitful discussions. We also acknowledge M.-L. Dubernet for helpful discussions and for help in the numerical dynamics calculations and G. Dhont for making his fitting code of the potential energy surface available to us. The calculations of ab initio potential energy surfaces were performed on the parallel machine MPOPM of Paris Observatory, and all the scattering calculations were performed at the IDRIS-CNRS center (Institut de Développement et des Ressources en Informatique Scientifique du Centre National de la Recherche Scientifique) under project 050883. We acknowledge the financial support of the PAI PICASSO and of the Spanish MEC grants AYA2003-2785, AYA2002-10113-E, and ESP2004-00665. We would also like to thank the UE FP6 program "The Molecular Universe'' for funding support. Finally, the fruitful comments by the referee are gratefully acknowledged.

References

 
Copyright ESO 2006