A&A 451, 917-924 (2006)
DOI: 10.1051/0004-6361:20053845
M. Röllig1 - V. Ossenkopf1,2 - S. Jeyakumar - J. Stutzki1 - A. Sternberg3
1 - I. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
2 - SRON National Institute for Space Research, PO Box 800, 9700 AV Groningen, The Netherlands
3 - School of Physics and Astronomy, Tel Aviv University, Ramat Aviv 69978, Israel
Received 18 July 2005 / Accepted 14 November 2005
Abstract
We study the effects of a metallicity variation on
the thermal balance and [CII] fine-structure line
strengths in
interstellar photon dominated regions (PDRs).
We find that a reduction in the dust-to-gas ratio and
the abundance of heavy elements in the gas phase
changes the heat balance of the gas in PDRs.
The surface temperature of PDRs decreases as
the metallicity decreases except for high density
(n>106 cm-3) clouds exposed to weak (![]() )
FUV fields where
vibrational
H2-deexcitation heating dominates over photoelectric heating of the gas.
We incorporate the metallicity dependence in our KOSMA-
)
FUV fields where
vibrational
H2-deexcitation heating dominates over photoelectric heating of the gas.
We incorporate the metallicity dependence in our KOSMA-![]() PDR model
to study the metallicity dependence of [CII]/CO line ratios
in low metallicity galaxies. We find that the main trend in the variation
of the observed CII/CO ratio with metallicity is well reproduced
by a single spherical clump, and does not necessarily require
an ensemble of clumps as in the semi-analytical model presented
by Bolatto et al. (1999).
PDR model
to study the metallicity dependence of [CII]/CO line ratios
in low metallicity galaxies. We find that the main trend in the variation
of the observed CII/CO ratio with metallicity is well reproduced
by a single spherical clump, and does not necessarily require
an ensemble of clumps as in the semi-analytical model presented
by Bolatto et al. (1999).
Key words: ISM: abundances - ISM: structure - ISM: clouds - ISM: general - galaxies: ISM - galaxies: abundances
In PDRs the molecular gas
is heated by the far-ultraviolet (FUV) radiation field, either
the strong FUV radiation in the vicinity of hot young stars, or weak average
FUV fields in the Galaxy.
The gas cools through the spectral line radiation of atomic and
molecular species (Hollenbach & Tielens 1999; Sternberg 2004).
The gas-phase chemistry together with a depth dependent FUV intensity
lead to the formation of atomic and molecular species at different depths through
the cloud. This typical stratification of PDRs is for example reflected by the the
H/H2 and C+/C/CO transitions (Boger & Sternberg 2005; Sternberg & Dalgarno 1995).
At low visual extinctions the gas
is cooled by emission of atomic fine-structure lines, mainly [CII] 158 ![]() m and
[OI] 63
m and
[OI] 63 ![]() m. At larger depths,
millimeter, sub-millimeter and far-infrared
molecular rotational-line cooling (CO, OH, H2O) becomes important together
with the interaction of dust and gas.
Physical conditions such as temperature and density
can be derived, by comparing the observed line emissions with model predictions
(Zielinsky et al. 2000; Le Bourlot et al. 1993; Warin et al. 1996; Störzer et al. 1996; Kaufman et al. 1999; Gorti & Hollenbach 2002; Wolfire et al. 1995; Störzer et al. 2000).
m. At larger depths,
millimeter, sub-millimeter and far-infrared
molecular rotational-line cooling (CO, OH, H2O) becomes important together
with the interaction of dust and gas.
Physical conditions such as temperature and density
can be derived, by comparing the observed line emissions with model predictions
(Zielinsky et al. 2000; Le Bourlot et al. 1993; Warin et al. 1996; Störzer et al. 1996; Kaufman et al. 1999; Gorti & Hollenbach 2002; Wolfire et al. 1995; Störzer et al. 2000).
[CII] emission is a widely used diagnostic
indicator of star formation (Stacey et al. 1991; Malhotra et al. 2000; Kramer et al. 2004; Pierini et al. 1999; Boselli et al. 2002b; Pierini et al. 2003).
Observations suggest that low metallicity systems have
higher [CII] to CO rotational line ratios
compared to the Galactic value. In particular, the intensity ratio
![]() may vary from
may vary from ![]() 1000 in the inner Milky Way, up to
1000 in the inner Milky Way, up to ![]() 105 in extremely low metallicity systems
(e.g. Madden et al. 1997; Bolatto et al. 1999; Hunter et al. 2001; Madden 2000; Mochizuki et al. 1998).
Several studies have suggested that a lower abundance
of heavy elements affects the chemical structure
of PDRs and the cooling line emission, and
that estimates of molecular gas masses from the
observed CO(J=1-0) line intensities using the standard conversion factor may
underestimate the true masses
in such objects (Rubio et al. 2004; Wilson 1995; Israel 1997; Israel et al. 2003).
105 in extremely low metallicity systems
(e.g. Madden et al. 1997; Bolatto et al. 1999; Hunter et al. 2001; Madden 2000; Mochizuki et al. 1998).
Several studies have suggested that a lower abundance
of heavy elements affects the chemical structure
of PDRs and the cooling line emission, and
that estimates of molecular gas masses from the
observed CO(J=1-0) line intensities using the standard conversion factor may
underestimate the true masses
in such objects (Rubio et al. 2004; Wilson 1995; Israel 1997; Israel et al. 2003).
Bolatto et al. (1999) modelled the metallicity variation of the line ratio [CII]/CO(1-0), for an ensemble of spherical "clumps'', assuming an inverse relation between the size of the C+ region and the metallicity. However the sizes of the C+, C and CO regions also depend on the chemistry in PDRs and the chemical network is modified at low metallicities (Lequeux et al. 1994). Additionally it has been suggested that the size of the C+, C and CO regions may also significantly depend on the overall cloud morphology, e.g. density variations (Hegmann & Kegel 2003) and velocity fluctuations (Röllig et al. 2002). Moreover the temperature of the molecular gas might depend on the metallicity which affects the observable line intensities (Wolfire et al. 1995).
We study the effects of metallicity changes on the temperature and chemical structure
of PDRs.
In Sect. 2 we consider the dependence of the PDR gas
temperature on the metallicity using a simplified semi-analytic model
and compare it with numerical results from full
PDR model calculations. Our computations were carried out
using an updated version of our spherical
KOSMA-![]() model (Störzer et al. 1996) which was originally adapted from
the plane-parallel model presented by Sternberg & Dalgarno (1995). In Sect. 3 we examine the
predicted size of the C+ zones as a function of metallicity.
We then model the strength of the [CII] emission and investigate
the dependence of the [CII]/CO(J=1-0) line ratio on the metallicity.
Finally we compare the results with observational data in Sect. 4.
model (Störzer et al. 1996) which was originally adapted from
the plane-parallel model presented by Sternberg & Dalgarno (1995). In Sect. 3 we examine the
predicted size of the C+ zones as a function of metallicity.
We then model the strength of the [CII] emission and investigate
the dependence of the [CII]/CO(J=1-0) line ratio on the metallicity.
Finally we compare the results with observational data in Sect. 4.
The basic cooling and heating processes in PDRs, are affected
by the abundances of elements as well as the content and the composition of dust grains
(Kaufman et al. 1999; Wolfire et al. 1995).
The dust-to-gas ratio (D/G) and the optical properties of the dust
may depend on the metallicity, Z. Fits to observations suggest that
the ratio depends almost linearly on the metallicity,
![]() (Boselli et al. 2002a). There are other studies that find deviations from linearity
for higher values of D/G (Lisenfeld & Ferrara 1998). Li & Draine (2002) suggested that
the mixture of PAHs in the metal-poor SMC differs from the Milky Way.
There are a few observations indicating that PAHs could have
been destroyed by intense UV fields at low metallicities (Bolatto et al. 2000; Thuan et al. 1999),
but the detailed composition of dust in low metallicity
environments and the influence on its optical properties is not yet understood.
Because of the insufficient knowledge we assume in our model that
the composition of the grains does not change with
metallicity and that the dust-to-gas ratio and the gas-phase abundance
of heavy elements scale linearly with Z.
(Boselli et al. 2002a). There are other studies that find deviations from linearity
for higher values of D/G (Lisenfeld & Ferrara 1998). Li & Draine (2002) suggested that
the mixture of PAHs in the metal-poor SMC differs from the Milky Way.
There are a few observations indicating that PAHs could have
been destroyed by intense UV fields at low metallicities (Bolatto et al. 2000; Thuan et al. 1999),
but the detailed composition of dust in low metallicity
environments and the influence on its optical properties is not yet understood.
Because of the insufficient knowledge we assume in our model that
the composition of the grains does not change with
metallicity and that the dust-to-gas ratio and the gas-phase abundance
of heavy elements scale linearly with Z.
Changes in Z affect the abundances of major coolants as well as the electron densities in PDRs. Additionally, a reduction in the dust abundance diminishes the UV opacity, the photo electric heating rate, and the H2 formation rate. These changes affect the temperature and chemistry in the surface layers where C+ is most abundant.
The dependence of the surface gas temperature on Z can be
estimated considering the balance of cooling and heating.
The dominant cooling processes depend predominantly on the total hydrogen
gas density n.
[OI]63 ![]() m, [CII]158
m, [CII]158 ![]() m emission, and gas-grain collisions
are important cooling processes (Störzer et al. 1996; Burke & Hollenbach 1983). Their relative importance
in the different regimes is discussed in Sect. 2.2.1.
The dominant heating process depends on the far-ultraviolet (FUV; 6-13.6 eV)
field and the density. Grain photo-electric emission
(PE) (Lepp & Dalgarno 1988; d'Hendecourt & Léger 1987; Verstrate et al. 1990; Bakes & Tielens 1994), collision deexcitation
of FUV pumped molecular hydrogen H
m emission, and gas-grain collisions
are important cooling processes (Störzer et al. 1996; Burke & Hollenbach 1983). Their relative importance
in the different regimes is discussed in Sect. 2.2.1.
The dominant heating process depends on the far-ultraviolet (FUV; 6-13.6 eV)
field and the density. Grain photo-electric emission
(PE) (Lepp & Dalgarno 1988; d'Hendecourt & Léger 1987; Verstrate et al. 1990; Bakes & Tielens 1994), collision deexcitation
of FUV pumped molecular hydrogen H![]() (Burton et al. 1990; Sternberg & Dalgarno 1989) and
heating from H2 formation play important roles. They are discussed in
detail in Sect. 2.2.2. By explicitly considering the
metallicity dependence of each of these cooling and heating
processes and identifying the dominant processes in the different
parameter regimes we will show how the energy balance
in PDRs depends on Z for a quantitative
understanding of the PDR surface temperature.
(Burton et al. 1990; Sternberg & Dalgarno 1989) and
heating from H2 formation play important roles. They are discussed in
detail in Sect. 2.2.2. By explicitly considering the
metallicity dependence of each of these cooling and heating
processes and identifying the dominant processes in the different
parameter regimes we will show how the energy balance
in PDRs depends on Z for a quantitative
understanding of the PDR surface temperature.
In our study
we use an updated version of the spherical PDR code described
in detail by Störzer et al. (1996).
Briefly, this model solves the coupled equations of energy balance
(heating and cooling), chemical equilibrium, and radiative transfer
in spherical geometry.
The PDR-clumps are characterized by a) the incident FUV field
intensity ![]() ,
given in units of the mean interstellar radiation
field of Draine (1978);
b) the clump mass; and c) the average density of the clump, for a
radial power-law density distribution with index
,
given in units of the mean interstellar radiation
field of Draine (1978);
b) the clump mass; and c) the average density of the clump, for a
radial power-law density distribution with index ![]() .
We incorporate the effects of varying metallicity by varying the
assumed abundance of dust grains and
heavy elements. The following parameters are multiplied by the
metallicity factor Z: (a) the total effective FUV dust absorption cross section
per hydrogen nucleus
.
We incorporate the effects of varying metallicity by varying the
assumed abundance of dust grains and
heavy elements. The following parameters are multiplied by the
metallicity factor Z: (a) the total effective FUV dust absorption cross section
per hydrogen nucleus ![]() ;
(b) the photo-electric heating rate;
(c) the H2 formation rate;
(d) the metal abundance. We consider a range of Z from 0.2 to 1.
For Z=1 we use
;
(b) the photo-electric heating rate;
(c) the H2 formation rate;
(d) the metal abundance. We consider a range of Z from 0.2 to 1.
For Z=1 we use
![]() cm2,
cm2,
![]() ,
and
,
and
![]() as standard values for the
local ISM (Hollenbach & Tielens 1999). These values are slightly lower than recent
solar values of
as standard values for the
local ISM (Hollenbach & Tielens 1999). These values are slightly lower than recent
solar values of
![]() by Asplund et al. (2004). For a
detailed discussion see Baumgartner & Mushotzky (2005). We do not
consider gas depletion on grains.
by Asplund et al. (2004). For a
detailed discussion see Baumgartner & Mushotzky (2005). We do not
consider gas depletion on grains.
In the simplified model we
include the three main cooling processes: [CII] and [OI] line cooling
and gas-grain collisional cooling (Störzer et al. 1996; Burke & Hollenbach 1983).
Gas cooling is generally
dominated by fine structure emission of [CII] and [OI]. Gas-grain
cooling starts to contribute significantly for high densities.
At ![]() cm-3 the coupling between gas and dust is strong
enough so that the efficient cooling of the dust by infrared radiation
also provides a major coolant to the gas.
The total cooling rate per unit volume by these radiative processes
is the sum
cm-3 the coupling between gas and dust is strong
enough so that the efficient cooling of the dust by infrared radiation
also provides a major coolant to the gas.
The total cooling rate per unit volume by these radiative processes
is the sum
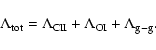 |
(1) |
Analytic expressions for the three cooling processes are
derived
in Appendix A. In Fig. 1 we show the
relation between the fine-structure line cooling contributions
as a function of n and ![]() for two different values of Z.
The region in parameter space where [CII] cooling
dominates over [OI] is shaded in gray. For densities above 104.5 cm-3[CII] cooling is quenched and [OI] cooling
dominates. At all lower densities [CII] cooling dominates.
Every point in Fig. 1 corresponds to a different
equilibrium temperature and resulting ratio
for two different values of Z.
The region in parameter space where [CII] cooling
dominates over [OI] is shaded in gray. For densities above 104.5 cm-3[CII] cooling is quenched and [OI] cooling
dominates. At all lower densities [CII] cooling dominates.
Every point in Fig. 1 corresponds to a different
equilibrium temperature and resulting ratio
![]() .
The dependence on
.
The dependence on ![]() in Fig. 1 results from
the implicit temperature dependence of the fine-structure cooling rates.
Grain cooling dominates
only for densities greater than 106 cm-3.
in Fig. 1 results from
the implicit temperature dependence of the fine-structure cooling rates.
Grain cooling dominates
only for densities greater than 106 cm-3.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{3845fig1.eps}
\end{figure}](/articles/aa/full/2006/21/aa3845-05/Timg38.gif) |
Figure 1:
The solid and dashed line represent the points in |
| Open with DEXTER | |
The dominant heating process depends on the FUV
field intensity and density. For high intensities grain photo-electric heating
dominates. The rate for this process, given by Bakes & Tielens (1994), is
![]() erg s-1 cm-3 where
erg s-1 cm-3 where ![]() is the photoelectric
heating efficiency and G0 is the UV intensity in units of the
Habing field. Following Bakes & Tielens (1994) the photoelectric heating
efficiency is given by:
is the photoelectric
heating efficiency and G0 is the UV intensity in units of the
Habing field. Following Bakes & Tielens (1994) the photoelectric heating
efficiency is given by:
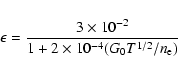 |
(2) |
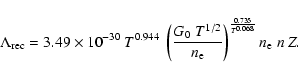 |
(4) |
The density of atomic and molecular hydrogen
is determined by Eq. (6) and can be written as
From
Eqs. (5)-(7) it follows that
This is in good agreement with the results from the numerical PDR model shown in Fig. C.1 in Appendix C.
The assumption of a constant formation rate R0 is valid for
![]() .
A higher UV field the dust temperature increases
leading to a rapid reduction of the accommodation coefficient
.
A higher UV field the dust temperature increases
leading to a rapid reduction of the accommodation coefficient ![]() .
Hence in our calculations the maximum H2 heating rate drops for
.
Hence in our calculations the maximum H2 heating rate drops for
![]() as shown in the bottom plot in Fig. C.1 in Appendix C.
as shown in the bottom plot in Fig. C.1 in Appendix C.
H2 not only contributes to the heating, but
cools the gas at higher temperatures (Sternberg & Dalgarno 1989). To account for the cooling we
define the net heating rate
![]() .
Using the analytic approximations
to the molecular level structure of H2 derived in Appendix C we obtain
.
Using the analytic approximations
to the molecular level structure of H2 derived in Appendix C we obtain
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{3845fig2.eps}
\end{figure}](/articles/aa/full/2006/21/aa3845-05/Timg80.gif) |
Figure 2:
The solid and dashed line represent the points in |
| Open with DEXTER | |
The relative reduction of the H2 heating at high radiation fields
is demonstrated in Fig. 2
comparing the PE heating and the H2 de-excitation heating
for the different parameter regimes. We see that at any given density
![]() exceeds
exceeds
![]() beyond a
certain
beyond a
certain ![]() value, but that this limit increases with the gas
density.
value, but that this limit increases with the gas
density.
Although
![]() and
and
![]() are
the two main heating terms it is necessary to account for a third
process in order to achieve a reasonable approximation of the full
energy balance. For UV fields
are
the two main heating terms it is necessary to account for a third
process in order to achieve a reasonable approximation of the full
energy balance. For UV fields
![]() ,
and densities
n<104 cm-3, H2 formation heating may contribute significantly. Assuming that each formation process
releases 1/3 of its binding energy to heat the gas (Sternberg & Dalgarno 1989), the corresponding
heating rate is:
,
and densities
n<104 cm-3, H2 formation heating may contribute significantly. Assuming that each formation process
releases 1/3 of its binding energy to heat the gas (Sternberg & Dalgarno 1989), the corresponding
heating rate is:
Table 1: Metallicity dependence of the individual heating processes.
An inspection of the heating and cooling functions described above
reveals their metallicity dependence. Table 1 summarizes the
scaling relations.
The radiative cooling functions are
linear in Z. The photoelectric
heating depends on the metallicity via
![]() .
The influence of
.
The influence of
![]() can be neglected as long as
can be neglected as long as
![]() .
Thus,
for low UV fields
.
Thus,
for low UV fields
![]() .
For higher values of
.
For higher values of ![]() the efficiency accounts for an additional influence due to the electron density
which is proportional to Z for high densities, and independent of Z
for very low densities. The metallicity dependence for densities between
103...105 cm-3 is not trivial. Equation (3) shows that the electron
density is linear in Z for very high n. In the intermediate range this dependence
roughly shifts from Z0 to Z1.
This leads to
the efficiency accounts for an additional influence due to the electron density
which is proportional to Z for high densities, and independent of Z
for very low densities. The metallicity dependence for densities between
103...105 cm-3 is not trivial. Equation (3) shows that the electron
density is linear in Z for very high n. In the intermediate range this dependence
roughly shifts from Z0 to Z1.
This leads to
![]() for high values of n and
for high values of n and
![]() for very low densities.
for very low densities.
The recombination cooling depends on the metallicity
through the electron density, resulting in
![]() and Z1.5for low and high densities respectively.
The Z-dependence in the hydrogen heating (Eqs. (10) and (11))
comes from the hydrogen density
which depends on the metallicity as Z/(1+2 Z) for high densities and low
values of
and Z1.5for low and high densities respectively.
The Z-dependence in the hydrogen heating (Eqs. (10) and (11))
comes from the hydrogen density
which depends on the metallicity as Z/(1+2 Z) for high densities and low
values of ![]() ,
and as Z otherwise.
,
and as Z otherwise.
As a result we show in Fig. 3 the surface temperature of model clouds
for a variety of different UV field strengths and densities computed from
the analytic approximation and from the full KOSMA-![]() PDR model.
We covered a parameter space ranging from
PDR model.
We covered a parameter space ranging from
![]() cm-3 and
cm-3 and
![]() .
It is obvious that the metallicity dependence varies
strongly over the parameter space. We obtain a good agreement for low and high UV fields. Even in the intermediate UV and density range, where the quantitative
accord is weaker, the qualitative dependence of
.
It is obvious that the metallicity dependence varies
strongly over the parameter space. We obtain a good agreement for low and high UV fields. Even in the intermediate UV and density range, where the quantitative
accord is weaker, the qualitative dependence of
![]() on Z is well
reproduced
by the semi-analytical model.
on Z is well
reproduced
by the semi-analytical model.
The Z-dependence of the temperature can be understood by comparing the
dominant net rates of heating ![]() and cooling
and cooling ![]() .
At high
UV fields, where the PE heating dominates, the heating is proportional
to Z2 at high densities. For a density of n=103 the PE heating is
.
At high
UV fields, where the PE heating dominates, the heating is proportional
to Z2 at high densities. For a density of n=103 the PE heating is ![]()
![]() .
Due to the high UV field
.
Due to the high UV field
![]() for all given densities thus the electron density
influences the heating also for small values of n. If the density increases the term
14.4 T0.75/n vanishes and
for all given densities thus the electron density
influences the heating also for small values of n. If the density increases the term
14.4 T0.75/n vanishes and
![]() .
This is reflected
in the slopes of the surface temperature in Fig. 3(top).
For intermediate FUV fields we find a similar behavior with the addition that
.
This is reflected
in the slopes of the surface temperature in Fig. 3(top).
For intermediate FUV fields we find a similar behavior with the addition that ![]() is <100 for high densities and
is <100 for high densities and ![]() 100 for low densities, thus the metallicity dependence
shifts from Z2 to Z with increasing density. This shift can be seen in the middle
plot in Fig. 3.
100 for low densities, thus the metallicity dependence
shifts from Z2 to Z with increasing density. This shift can be seen in the middle
plot in Fig. 3.
When H2 vibrational de-excitation heating dominates (compare Fig. 2),
the corresponding rate varies as
Z/(1+2 Z), hence the surface temperature drops as
1/(1+2 Z). This is shown for n=106 cm-3in Fig. 3(middle) and for ![]() cm-3in the bottom panel of Fig. 3 which gives the temperatures for a FUV field strength of
cm-3in the bottom panel of Fig. 3 which gives the temperatures for a FUV field strength of ![]() .
For
low FUV fields and low densities the temperature is proportional to Z due to the PE heating as seen
in Fig. 3(bottom).
.
For
low FUV fields and low densities the temperature is proportional to Z due to the PE heating as seen
in Fig. 3(bottom).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3845fig3}\par\includegraph...
...4cm,clip]{3845fig4}\par\includegraphics[width=8.4cm,clip]{3845fig5}
\end{figure}](/articles/aa/full/2006/21/aa3845-05/Timg114.gif) |
Figure 3:
Comparison of the KOSMA- |
| Open with DEXTER | |
The offset between the semi-analytical approximation and numerical result
for ![]() is due to a small contribution of additional cooling processes in that
parameter range. This increases the total cooling efficiency and hence the temperatures in
the full numerical calculations are smaller. This
also holds for n=106 cm-3 and
is due to a small contribution of additional cooling processes in that
parameter range. This increases the total cooling efficiency and hence the temperatures in
the full numerical calculations are smaller. This
also holds for n=106 cm-3 and ![]() .
In that case the cooling is dominated by CO line
cooling which is stronger than [OI] 63
.
In that case the cooling is dominated by CO line
cooling which is stronger than [OI] 63 ![]() m and also by H2O cooling which
is comparable to [OI] 63
m and also by H2O cooling which
is comparable to [OI] 63 ![]() m. Here our initial assumptions are clearly underestimating the
overall cooling. Even so this does not change the behavior with Z which is well reproduced.
m. Here our initial assumptions are clearly underestimating the
overall cooling. Even so this does not change the behavior with Z which is well reproduced.
As there is some debate on D/G we tested as an extreme example
![]() instead of linearity. This mainly changes the
behavior of the heating rates. The dominant surface cooling processes do not depend on D/G, but only on the elemental abundances, while the heating processes are affected by
an altered D/G. This leads to a decreased heating efficiency for Z<1, hence the
surface temperature is significantly lower if we assume
instead of linearity. This mainly changes the
behavior of the heating rates. The dominant surface cooling processes do not depend on D/G, but only on the elemental abundances, while the heating processes are affected by
an altered D/G. This leads to a decreased heating efficiency for Z<1, hence the
surface temperature is significantly lower if we assume
![]() .
In the
extreme example of
.
In the
extreme example of ![]() ,
n=106 cm-3, and Z=0.2 we find
,
n=106 cm-3, and Z=0.2 we find
![]() K, a factor of 4 smaller than for
K, a factor of 4 smaller than for
![]() .
The cooling inside the cloud also depends somewhat on D/G, since
the escape probability of cooling lines
depends on the dust attenuation.
.
The cooling inside the cloud also depends somewhat on D/G, since
the escape probability of cooling lines
depends on the dust attenuation.
At the surface of the PDR the FUV radiation ionizes almost all of the carbon atoms. At larger depths the FUV intensity decreases and carbon recombines and is eventually incorporated into CO molecules. Thus, a PDR clump can be subdivided into a CO core surrounded by an atomic carbon shell and an outer C+ envelope. We examine here, the thickness of the C+ envelope as a function of metallicity Z. We define the C+ envelope thickness as the distance from the cloud surface to the depth where the abundances of C and C+ are equal.
The dominant reaction channels for the formation and destruction of C+ are
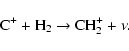
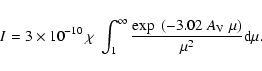 |
(15) |
We have defined the radial point
![]() as the location where the abundances
of C+ and C are equal,
as the location where the abundances
of C+ and C are equal,
![]() .
If we neglect the contribution of CO
at
.
If we neglect the contribution of CO
at
![]() then
then
![]() there.
Results from the PDR model suggest, that the electron density,
there.
Results from the PDR model suggest, that the electron density,
![]() ,
thus
,
thus
![]() .
For the sake of simplicity we chose this expression for
.
For the sake of simplicity we chose this expression for ![]() rather than the one introduced in
Eq. (3) which would introduce an additional temperature dependence.
With
rather than the one introduced in
Eq. (3) which would introduce an additional temperature dependence.
With
![]() and molecular hydrogen dominating the gas
density,
and molecular hydrogen dominating the gas
density,
![]() ,
we can resolve Eq. (14) for
the density at
,
we can resolve Eq. (14) for
the density at
![]()
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3845fig6.eps}
\end{figure}](/articles/aa/full/2006/21/aa3845-05/Timg146.gif) |
Figure 4:
The width of the C+ layer is plotted against the metallicity.
The open circles represent spherical clump of mass
|
| Open with DEXTER | |
The squares representing the constant density model show that the C+layer width depends approximately as Z-1.1 on the metallicity which
closely matches with the assumption of an inverse proportionality by Bolatto et al. (1999).
The circles in Fig. 4 represent the model by the
![]() .
They can be numerically fitted with
function,
.
They can be numerically fitted with
function,
![]() pc. Figure 4 shows that our results using
Eq. (16) agrees well with the model calculations. However the estimated
widths are slightly higher than the model calculations, which reflects the fact that
there are more reactions which quantitatively influence the chemistry of C+.
pc. Figure 4 shows that our results using
Eq. (16) agrees well with the model calculations. However the estimated
widths are slightly higher than the model calculations, which reflects the fact that
there are more reactions which quantitatively influence the chemistry of C+.
Table 2: Metallicities and observed [CII]/CO(1-0) line ratios of nearby galaxies and Galactic star forming regions.
The [CII] emission as well as the [CII]/CO(1-0) line ratio is typically considered to
be a good tracer of star formation (Stacey et al. 1991).
The intensity ratio
![]() /
/
![]() ,
observed in many nearby
low metal galaxies, is higher than for sources with solar and super-solar metallicities
(Madden et al. 1997; Bolatto et al. 1999; Hunter et al. 2001; Madden 2000; Mochizuki et al. 1998). Table 2 summarizes
available line ratios and metallicities of nearby galaxies. The corresponding numbers
for Orion are also given as a Galactic reference.
,
observed in many nearby
low metal galaxies, is higher than for sources with solar and super-solar metallicities
(Madden et al. 1997; Bolatto et al. 1999; Hunter et al. 2001; Madden 2000; Mochizuki et al. 1998). Table 2 summarizes
available line ratios and metallicities of nearby galaxies. The corresponding numbers
for Orion are also given as a Galactic reference.
This dependence has been modelled by Bolatto et al. (1999) assuming that the size of the C+ region scales inversely with metallicity, and assuming a constant temperature for the gas.
For our spherical PDR model we compute the surface brightness as function of
clump mass/radius and metallicity. The surface brightness is the projected average intensity
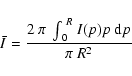 |
(17) |
In the prior sections we derived approximate expressions for the surface temperature of a PDR as well as
for the expected depth of the C+ envelope. We can use these approximations to estimate the total [CII] surface
brightness of the PDR. The local emissivity
![]() from Eq. (A.2)
can be used to calculate the line integrated
intensity of the PDR in the optically thin case
from Eq. (A.2)
can be used to calculate the line integrated
intensity of the PDR in the optically thin case
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3845fig7.eps}
\end{figure}](/articles/aa/full/2006/21/aa3845-05/Timg158.gif) |
Figure 5:
The surface brightnesses of the [CII] 158 |
| Open with DEXTER | |
Importantly, the total surface brightness does not scale linearly with the surface density of the clouds. Rather it peaks for intermediate values of n, depending on Z.
This is mainly a geometrical effect, which can be understood by some qualitative arguments. If we assume that [CII] is optically thin, we see all ![]() atoms. In the low density case, where ionized carbon fills the whole cloud, the surface brightness is then proportional to n (V/A), with the volume of the cloud V and the projected area A, hence
atoms. In the low density case, where ionized carbon fills the whole cloud, the surface brightness is then proportional to n (V/A), with the volume of the cloud V and the projected area A, hence
![]() .
But
.
But
![]() ,
since we kept the cloud mass constant, and thus we find
,
since we kept the cloud mass constant, and thus we find
![]() .
For higher densities the width of the
.
For higher densities the width of the ![]() layer decreases faster than it is compensated by the growing n. The relative thickness of the
layer decreases faster than it is compensated by the growing n. The relative thickness of the ![]() layer becomes very small for higher densities (i.e. if
layer becomes very small for higher densities (i.e. if
![]() ). The surface brightness then is proportional to
). The surface brightness then is proportional to
![]() ,
hence
,
hence
![]() .
We observe a reduced surface brightness caused by the geometry of the cloud. This is inverse to the common area filling effect for optically thick lines, like e.g. CO (1-0), where the projected area of the CO core decreases with decreasing density as demonstrated in Fig. 5. This was also mentioned by Störzer et al. (1996). This means, that even though the local emissivity
.
We observe a reduced surface brightness caused by the geometry of the cloud. This is inverse to the common area filling effect for optically thick lines, like e.g. CO (1-0), where the projected area of the CO core decreases with decreasing density as demonstrated in Fig. 5. This was also mentioned by Störzer et al. (1996). This means, that even though the local emissivity
![]() scales linearly with n (see Eq. (A.2)), this is not true for the total surface brightness. As a second order effect we also notice a temperature dependence of the local emissivity. The differences between our analytical model and the detailed temperature structures from the PDR calculations are responsible for most of the deviations shown in Fig. 5.
scales linearly with n (see Eq. (A.2)), this is not true for the total surface brightness. As a second order effect we also notice a temperature dependence of the local emissivity. The differences between our analytical model and the detailed temperature structures from the PDR calculations are responsible for most of the deviations shown in Fig. 5.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3845fig8.eps}
\end{figure}](/articles/aa/full/2006/21/aa3845-05/Timg166.gif) |
Figure 6:
The surface brightnesses of the [CII] 158 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3845fig9.eps}
\end{figure}](/articles/aa/full/2006/21/aa3845-05/Timg168.gif) |
Figure 7:
The intensity ratio
|
| Open with DEXTER | |
We use our PDR model calculations to study the
metallicity dependence of the [CII]/CO(1-0) line ratio. We adopt a density of 104 cm-3, a
![]() ,
and a UV field,
,
and a UV field,
![]() similar to the values assumed by Bolatto et al. (1999).
Their prediction is an average over a clump
ensemble as a model for the large scale emission from the ISM. In
contrast, we start here
by investigating the metallicity dependence for a single, typical
clump. The discussion below shows that this is already sufficient to reproduce
the observed trends versus metallicity. The detailed investigation of the
effects of averaging over a clump ensemble are left to a subsequent paper.
Figure 6 summarizes the results for this typical clump.
The dominance of the geometrical effect
is reflected in the almost constant [CII] surface brightnesses in Fig. 6.
Hence the line ratio [CII]/CO decreases for increasing metallicities and tends to be constant for very
high values of Z.
similar to the values assumed by Bolatto et al. (1999).
Their prediction is an average over a clump
ensemble as a model for the large scale emission from the ISM. In
contrast, we start here
by investigating the metallicity dependence for a single, typical
clump. The discussion below shows that this is already sufficient to reproduce
the observed trends versus metallicity. The detailed investigation of the
effects of averaging over a clump ensemble are left to a subsequent paper.
Figure 6 summarizes the results for this typical clump.
The dominance of the geometrical effect
is reflected in the almost constant [CII] surface brightnesses in Fig. 6.
Hence the line ratio [CII]/CO decreases for increasing metallicities and tends to be constant for very
high values of Z.
Figure 7 shows that
the trend in the observed ratios in normal galaxies can be represented by a single-clump model with
![]() ,
shown as solid and dotted lines in Fig. 7. We also plotted model results
for different cloud parameters to demonstrate how different observations may
be explained by different local physical conditions, e.g. the higher observed
ratio for the 30 Doradus region can be explained by a similar model,
but exposed to an UV field of
,
shown as solid and dotted lines in Fig. 7. We also plotted model results
for different cloud parameters to demonstrate how different observations may
be explained by different local physical conditions, e.g. the higher observed
ratio for the 30 Doradus region can be explained by a similar model,
but exposed to an UV field of ![]() (or alternatively by a clump of less mass). This is consistent
with derived FUV strengths for 30 Doradus (Kaufman et al. 1999).
The peculiar source IZw 36, with a very low [CII]/CO ratio at extremely low
metallicity can be approximated by a model with a lower FUV field of
(or alternatively by a clump of less mass). This is consistent
with derived FUV strengths for 30 Doradus (Kaufman et al. 1999).
The peculiar source IZw 36, with a very low [CII]/CO ratio at extremely low
metallicity can be approximated by a model with a lower FUV field of
![]() ,
consistent
with estimations by Mochizuki et al. (1998).
,
consistent
with estimations by Mochizuki et al. (1998).
Our model results for single clumps reproduce qualitatively the results shown by the semi-analytical clumpy model of (Bolatto et al. 1999) for a clump ensemble in reproducing the trends versus metallicity. Thus we can confirm Bolatto's findings whan taking the detailed physical and chemical structure of the clumps into account.
From a practical point of view it is obvious that a clumpy ensemble of different clouds should be closer to the true local conditions than a single spherical clump, but we find that a clumpy approach is not necessary to explain the observerved trend with Z. To model the [CII]/CO line ratio of a particular source in detail it may of course be necessary to apply a clumpy approach. But to understand the general behavior for different metallicities it is sufficient to consider a single, typical clump.
We study the effects of metallicity variations on the gas temperature and [CII] emission line properties of spherical PDRs. We find that the surface temperature of PDRs at high UV fields varies linearly with metallicity. For low UV fields and high densities this metallicity behavior of the surface temperature is converse, showing an inverse dependence with metallicity due to the dominant H2 heating. We introduce a new two level FUV H2 heating and cooling function that properly accounts for energy losses via vibrational collisional excitations.
We examine the dependence of the C+ envelope on metallicity and find that
its geometrical depth scales
inversely with Z.
This produces
a higher [CII]/CO(J=1-0)
line ratio at lower metallicities. We used the numerical results from the
KOSMA-![]() model to study the dependence of PDR emission lines with
metallicity. The observed variation of [CII]/CO(J=1-0) with metallicity can
be explained
well by a single-clump model and
it is not necessary to refere to an average over a clump ensemble.
We conclude that the [CII]/CO(J=1-0) line ratios for sources with
differing metallicities do not provide a strong constraint on the clumpy
morphology of a molecular clouds.
model to study the dependence of PDR emission lines with
metallicity. The observed variation of [CII]/CO(J=1-0) with metallicity can
be explained
well by a single-clump model and
it is not necessary to refere to an average over a clump ensemble.
We conclude that the [CII]/CO(J=1-0) line ratios for sources with
differing metallicities do not provide a strong constraint on the clumpy
morphology of a molecular clouds.
Acknowledgements
This work is supported by the Deutsche Forschungs Gemeinschaft (DFG) via Grant SFB 494. A.S. thanks the Israel Science Foundation for support. We thank the anonymous referee for her/his helpful comments.
The cooling of the gas is dominated by fine structure line
emission of [CII] and [OI]. The line cooling rate can always be written as
![]() erg s-1 cm-3 where
erg s-1 cm-3 where ![]() is the escape probability,
is the escape probability,
![]() is the
transition probability and
is the
transition probability and ![]() the number of atoms in the upper
state u and
the number of atoms in the upper
state u and
![]() is the corresponding transition energy
(Hollenbach & McKee 1979). Below the critical density for the [OI] emission
is the corresponding transition energy
(Hollenbach & McKee 1979). Below the critical density for the [OI] emission
![]() cm-3, the
main cooling is provided by the 158
cm-3, the
main cooling is provided by the 158 ![]() m [CII] line. The general
cooling rate of a two-level system S can be expressed as:
m [CII] line. The general
cooling rate of a two-level system S can be expressed as:
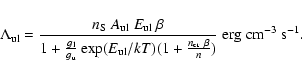 |
(A.1) |
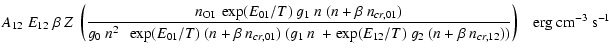 |
(A.3) |
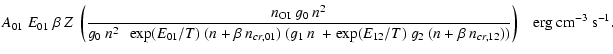 |
(A.4) |
| |
= | ||
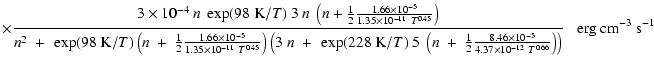 |
(A.5) | ||
| = | |||
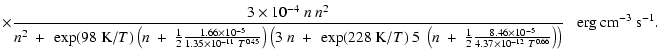 |
(A.6) |
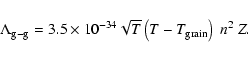 |
(A.7) |
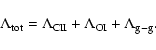 |
(A.8) |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{3845fi12.eps}
\end{figure}](/articles/aa/full/2006/21/aa3845-05/Timg203.gif) |
Figure B.2:
A comparison of numerically obtained electron densities (symbols) with
the analytical expression (lines) in Eq. (B.4),
at
|
An important heating processes in dense PDRs is collisional deexcitation of FUV-pumped H2 molecules (Sternberg & Dalgarno 1995). Here we present a two level approximation for the H2 vibrational heating and cooling valid in the parameter range where the process plays a major role (see Sect. 2.2.2). The approximation reproduces the net heating rate computed by SD95 assuming transitions among all 15 vibrational levels in the ground electronic state, but neglecting the rotational structure.
Vibrational cooling reduces the net heating
at large gas temperatures (see Fig. C.1, bottom).
The vibrational cooling is most effective at low ![]() for which a large H2 density is maintained. With PDR temperatures
of typically less than 2000 K (see Sect. 2)
and the energy gap between the two lowest vibrational
levels
for which a large H2 density is maintained. With PDR temperatures
of typically less than 2000 K (see Sect. 2)
and the energy gap between the two lowest vibrational
levels
![]() K, we can assume that most of the H2is always in the ground (v=0) level in this regime. Vibrational cooling
is thus basically given by collisional excitation to v=1 followed
by either radiative decay or photodissociation.
Using the molecular constants for the lowest vibrational transition
we obtain the collisional cooling rate
K, we can assume that most of the H2is always in the ground (v=0) level in this regime. Vibrational cooling
is thus basically given by collisional excitation to v=1 followed
by either radiative decay or photodissociation.
Using the molecular constants for the lowest vibrational transition
we obtain the collisional cooling rate
In contrast vibrational heating is important when the FUV radiation
field provides a significant pumping to higher vibrational states.
Thus we define a separate equivalent two-level system for the
heating. It is characterized by the effective coefficients
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() providing the same heating rate as the full 15 level system
providing the same heating rate as the full 15 level system
With the simple analytic two-level approximation, we can easily understand the quantitative behavior of the H2 vibrational energy balance from basic principles thus providing a handy tool for estimates of temperature structures. Burton et al. (1990) also introduced a two-level approximation for the H2 heating. However, they considered only a single pseudo excited level with an energy corresponding to v=6 and hence did not properly account for cooling via rapid excitation to v=1, or heating via pumping and collisional deexcitation from all 15 levels.