A&A 451, 999-1008 (2006)
DOI: 10.1051/0004-6361:20053841
A comprehensive study of the SX Phoenicis star BL Camelopardalis
S. Fauvaud1 - E. Rodríguez2 - A. Y. Zhou3,4 -
J. P. Sareyan5 - I. Ribas6,7 - M. D. Reed4 -
G. Klingenberg8 - J. Farrell9 - J. Michelet10 -
S. E. Robinson11 - G. Santacana1 - J. J. Rives1
1 - Association AstroQueyras, Le bois de Bardon, Taponnat, 16110 La
Rochefoucauld, France
2 -
Instituto de Astrofísica de Andalucía, CSIC,
PO Box 3004, 18080 Granada, Spain
3 -
National Astronomical Observatories, Chinese Academy of Sciences,
Beijing 100012, PR China
4 -
Department of Physics, Astronomy, and Materials Science, Missouri
State University, 901 S. National, Springfield, MO 65897, USA
5 -
Observatoire de la Côte d'Azur, BP 4229, 06304 Nice Cedex 4, France
6 -
Institut de Ciéncies de l'Espai, CSIC, Facultat de Ciéncies, Campus UAB,
Torre C5-parell, 2a planta, 08193 Bellaterra, Spain
7 -
Institut d'Estudis Espacials de Catalunya (IEEC), C/Gran Capitá 2-4, 08034
Barcelona, Spain
8 -
Norwegian Astronomical Society, Engeshaugen 15, 8616 Mo i Rana, Norway
9 -
Sulphur Flats Observatory, 449 Sulphur Creek Road, Jemez Springs,
NM 87025, USA
10 -
Club d'Astronomie Lyon Ampère, 37 rue Paul Cazeneuve, 69008 Lyon, France
11 -
American Association of Variable Star Observers, 25 Birch Street, Cambridge,
MA 02138, USA
Received 18 July 2005 / Accepted 5 January 2006
Abstract
Context. BL Cam is an extreme field multiperiodic short-period low-metallicity high-amplitude SX Phe-type variable where its probably complex pulsational content is subject of controversies.
Aims. A comprehensive study has been carried out to investigate the nature and pulsational properties of this object.
Methods. The analysis is based on new photometric data collected during the last few years at different sites, as well as on all available previously published data. Frequency analyses have been performed on a number of reliable data sets to analyse the pulsational content. In addition, the classical O-C method was used to study the behaviour of the main period.
Results. Our frequency analysis confirms some aspects on the multiperiodicity of BL Cam, previously found by other authors, showing a number of secondary modes close to the main frequency
f0=25.5769 cd-1. The secondary modes present eventual amplitude variations. However, the main frequency exhibits no significant changes in its amplitude and seems to correspond to the fundamental mode of radial pulsation. Abrupt changes sometimes observed in the light curves could be due to spurious activity on or close to the star's photosphere. We confirm the existence of a secondary frequency at 31.6 or 32.6 cd-1, with variable amplitude, and with the possibility of both frequencies being intrinsic to the star. More than one hundred of new times of light maxima have been determined in the present work. These together with those available in the literature allow us a more discriminating analysis of the O-C diagram. This shows that the observed variations of the main period can be described by two terms: (i) a secular increase of the main period at a rate of
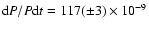 yr-1; and (ii) a perturbation from a companion star in a rather eccentric orbit with a period of 10.5(
yr-1; and (ii) a perturbation from a companion star in a rather eccentric orbit with a period of 10.5(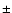 0.2) yr causing a light time semi-amplitude of 148(
0.2) yr causing a light time semi-amplitude of 148(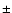 12) s.
12) s.
Key words: stars: variables: delta Sct - stars: individual: BL Cam -
stars: oscillations - techniques: photometric
BL Cam (=GD 428,
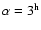 47
47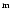 19
19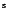 ,
,
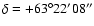 ,
J2000.0,
,
J2000.0,
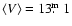 ,
,
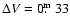 )
is classified among the dozen
field SX Phe-type pulsators known to date (Rodríguez & Breger 2001).
SX Phe stars are detected among field stars, globular clusters and nearby
dwarf galaxies (Rodríguez & López-González 2000).
Most display visual peak-to-peak amplitudes larger than
)
is classified among the dozen
field SX Phe-type pulsators known to date (Rodríguez & Breger 2001).
SX Phe stars are detected among field stars, globular clusters and nearby
dwarf galaxies (Rodríguez & López-González 2000).
Most display visual peak-to-peak amplitudes larger than  0
0
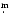 3
with short periods (
3
with short periods (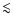 0
0
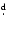 08) and some belong to double or multiple
systems. SX Phe stars have typical Population II characteristics, i.e. they
belong to the halo and old disk populations of the Galaxy
with low metallicities and high
spatial motions. However, they show surprisingly large masses
(
08) and some belong to double or multiple
systems. SX Phe stars have typical Population II characteristics, i.e. they
belong to the halo and old disk populations of the Galaxy
with low metallicities and high
spatial motions. However, they show surprisingly large masses
(
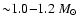 )
and relatively young ages (
)
and relatively young ages ( 2-5 Gyr)
(see e.g., Nemec & Mateo 1990), characteristics which
are still not fully explained by stellar evolution theory.
The field SX Phe stars are pulsating variables located in the Lower
Instability Strip, mixed with
Population I
2-5 Gyr)
(see e.g., Nemec & Mateo 1990), characteristics which
are still not fully explained by stellar evolution theory.
The field SX Phe stars are pulsating variables located in the Lower
Instability Strip, mixed with
Population I 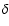 Sct-type variables. Recent reviews for the
high-amplitude members of this class can be found in
Rodríguez (2003, 2004).
Sct-type variables. Recent reviews for the
high-amplitude members of this class can be found in
Rodríguez (2003, 2004).
The discovery in the 1980's of three SX Phe variables in the globular
cluster 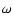 Cen (Rodríguez & López-González 2000) confirmed
that SX Phe and Population I
Cen (Rodríguez & López-González 2000) confirmed
that SX Phe and Population I 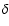 Sct variables
are different. At present, we know that the majority of the SX Phe variables
located in globular clusters belong to their blue straggler (BS) population.
These stars are bluer and brighter than the main sequence turn-off of the
cluster (e.g., Mateo 1993) and their origin is still unclear
with various hypotheses having been proposed in the literature:
internal mixing
in the atmosphere of single stars or mergers of two stars via mass
transfer or direct collisions (Livio 1993; Stryker 1993).
The connection between SX Phe stars and the BS phenomenon has been analysed
by several authors (e.g. Eggen & Iben 1989; Nemec & Mateo 1990).
Indeed, the investigation of the SX Phe-type variability can provide
valuable advances in understanding the BS phenomenon and the history of
the globular clusters themselves.
Sct variables
are different. At present, we know that the majority of the SX Phe variables
located in globular clusters belong to their blue straggler (BS) population.
These stars are bluer and brighter than the main sequence turn-off of the
cluster (e.g., Mateo 1993) and their origin is still unclear
with various hypotheses having been proposed in the literature:
internal mixing
in the atmosphere of single stars or mergers of two stars via mass
transfer or direct collisions (Livio 1993; Stryker 1993).
The connection between SX Phe stars and the BS phenomenon has been analysed
by several authors (e.g. Eggen & Iben 1989; Nemec & Mateo 1990).
Indeed, the investigation of the SX Phe-type variability can provide
valuable advances in understanding the BS phenomenon and the history of
the globular clusters themselves.
Additionally,
as field high-amplitude SX Phe and 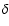 Sct stars are known to be
mostly monoperiodic or double-mode
pulsators, their simple frequency spectra allow reliable mode identifications
allowing the opportunity to use these pulsators to check
the evolutionary tracks predicted by stellar evolution models (e.g.,
Høg & Petersen 1997). Period-luminosity relations (Nemec et al. 1994;
McNamara 1995) provide new distance scales independent of those derived
from other methods, e.g., classical Cepheids or RR Lyr stars. This is of
particular interest in globular clusters when a significant number of SX Phe
variables are detected in the same cluster allowing precise period-luminosity
relations to be determined and used as distance indicators (e.g., Pych et al.
2001; Mazur et al. 2003; Jeon et al. 2003, 2004).
Sct stars are known to be
mostly monoperiodic or double-mode
pulsators, their simple frequency spectra allow reliable mode identifications
allowing the opportunity to use these pulsators to check
the evolutionary tracks predicted by stellar evolution models (e.g.,
Høg & Petersen 1997). Period-luminosity relations (Nemec et al. 1994;
McNamara 1995) provide new distance scales independent of those derived
from other methods, e.g., classical Cepheids or RR Lyr stars. This is of
particular interest in globular clusters when a significant number of SX Phe
variables are detected in the same cluster allowing precise period-luminosity
relations to be determined and used as distance indicators (e.g., Pych et al.
2001; Mazur et al. 2003; Jeon et al. 2003, 2004).
BL Cam presents the
second shortest period (
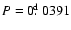 )
among the known field SX Phe variables
(the shortest one corresponds to PL43 = CS22966-043 (Preston & Landolt 1998)
with
)
among the known field SX Phe variables
(the shortest one corresponds to PL43 = CS22966-043 (Preston & Landolt 1998)
with
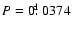 )
and the shortest one
among the high-amplitude objects of this type.
BL Cam was originally reported by Giclas et al. (1970) as a possible white
dwarf star. The variability of this object was discovered during a series of
observations of white dwarf stars by Berg & Duthie (1977). These authors also
noted a recurrence of the light curve during 6 cycles over 5 days, a
configuration that later turned out to be more complex than suggested by those
preliminary results. An investigation of the basic parameters of BL Cam
was carried out by McNamara & Feltz (1978). In particular, their
spectroscopic observations showed "an extreme weakness of the K line and
the absence of other metal lines''. The extreme metal-poor nature of this
star (
)
and the shortest one
among the high-amplitude objects of this type.
BL Cam was originally reported by Giclas et al. (1970) as a possible white
dwarf star. The variability of this object was discovered during a series of
observations of white dwarf stars by Berg & Duthie (1977). These authors also
noted a recurrence of the light curve during 6 cycles over 5 days, a
configuration that later turned out to be more complex than suggested by those
preliminary results. An investigation of the basic parameters of BL Cam
was carried out by McNamara & Feltz (1978). In particular, their
spectroscopic observations showed "an extreme weakness of the K line and
the absence of other metal lines''. The extreme metal-poor nature of this
star (
![$\rm [Fe/H]=-2.4$](/articles/aa/full/2006/21/aa3841-05/img24.gif) )
was later confirmed by McNamara (1997).
)
was later confirmed by McNamara (1997).
Besides the main pulsation, a secondary periodicity was first identified
by Hintz et al. (1997). Their
photometric data suggested a radial double-mode pulsation nature with a
primary
(f0) to secondary (
f1=32.6443 cd-1) frequency ratio of
f0/f1=0.783. This ratio fits the
observed period-ratio versus metallicity relation established for the
known fundamental/first-overtone double-mode
high-amplitude radial pulsators in the Lower Instability Strip.
However, different values for f1 were
determined by different authors using subsequent observations
(
f1=31.5912 cd-1 by Zhou et al. (1999) and
f1=32.3182 cd-1
by Kim et al. (2003) which lead to frequency ratios of f0/f1=0.810 and
0.791, respectively).
The reason of such different values for f1 is
still unknown and may be due to observational errors or to true changes in the
pulsational content of BL Cam. Hence, it is important to solve this
question as different frequency ratios have
consequences in interpreting its double-mode nature. Furthermore,
the data set collected by Zhou et al. (1999) revealed some additional modes
of non-radial
nature close to the main frequency f0. If confirmed by new
observations, BL Cam would have the most complex pulsation spectra
among the field high-amplitude SX Phe-type variables, and one of the most
complex among the general population of SX Phe variables.
Hintz et al. (1997) were the first to detect a
secular increase in BL Cam's primary frequency
using the classical O-C method. A more detailed analysis
of their O-C diagram, by Breger & Pamyatnykh (1998), revealed a 0.02 s
increase over the last 20 years. This gives
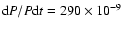 y-1, which is the largest period change
detected in
any high-amplitude
y-1, which is the largest period change
detected in
any high-amplitude 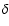 Sct or SX Phe variable and cannot be explained by
stellar evolutionary models. Nevertheless, Kim et al. (2003) pointed out a
reversed trend
of the O-C diagram since 1999, leading to a possible sinusoidal behaviour,
suggesting that BL Cam might be part of a binary system (with an orbital
period of
Sct or SX Phe variable and cannot be explained by
stellar evolutionary models. Nevertheless, Kim et al. (2003) pointed out a
reversed trend
of the O-C diagram since 1999, leading to a possible sinusoidal behaviour,
suggesting that BL Cam might be part of a binary system (with an orbital
period of  25 yr, Rodríguez 2003). These controversies make
the study of BL Cam even more compelling.
25 yr, Rodríguez 2003). These controversies make
the study of BL Cam even more compelling.
In this paper, new photometric observations of BL Cam have been carried out
in order to perform a comprehensive study the behaviour of the main period,
making use of the classical O-C method, as well as investigating the nature
and pulsation properties of this extreme object.
The new photometric observations of BL Cam presented in this work were
carried out at six observatories in 1996 and from 2003 to 2005.
The summary and journal of new observations are given in Table 1. All
observations were obtained with
CCDs using various filters, including some observations
without any filter.
Most of the data have been obtained with the 0.62 m telescope at the
Château-Renard Observatory (2930 m altitude, Saint-Véran, French Alps), a
facility operated by the Paris-Meudon Observatory and AstroQueyras, an
amateur association, and also with the 0.85 m telescope at the Xinglong
Station, Beijing Astronomical Observatory (China). Some additional
observations have been
collected at Mo i Rana Observatory (Norway) with a 0.20 m
telescope, at McDonald Observatory (USA) using the 2.10 m Otto Struve
telescope, and at Sulphur Flats and Rockville observatories (USA) with 0.40
and 0.45 m telescopes, respectively. In total, more than 100 h of useful
data were obtained on 28 nights.
Table 1:
Journal of new observations. Observatory code: ChR = Château-Renard
Observatory (France), XL = Xinglong Station (China), SFO = Sulphur Flats
Observatory (USA), RO = Rockville Observatory (USA), McD = McDonald Observatory
(USA), MR = Mo i Rana Observatory (Norway).
Notes: a) 5 nights in filter B (5 h of data and 7 times of maximum) and
4 nights in R (4 h and 4 maxima), b) no filter was used on 2 of the 5
nights, c) filter S is Schott BG40, centred at
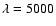 Å (Zhou et al. 2005),
d) one night without filter and one night using Johnson V filter.
Å (Zhou et al. 2005),
d) one night without filter and one night using Johnson V filter.
Each CCD frame has been corrected for dark, bias and flat-field. All light
measurements were made by synthetic aperture photometry. Atmospheric
and differential colour extinction were also calculated and corrected.
The typical photometric uncertainties (standard deviation)
estimated from the differences between comparison stars are about 0
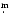 01 to
0
01 to
0
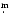 03. The comparison stars have not shown any variability at this
precision level during our observing runs.
03. The comparison stars have not shown any variability at this
precision level during our observing runs.
Apart from their variable amplitude, possibly due to multiple periodic
modulation (Zhou et al. 1999, and this work), the light curves of this
variable star are strongly asymmetric, with sharp light maxima, and rather
round-shaped light minima, occuring at phase 0.58(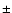 0.04) after the maxima.
Figure 1 shows an example of a single night's light-curve of BL Cam.
0.04) after the maxima.
Figure 1 shows an example of a single night's light-curve of BL Cam.
The light curves of BL Cam can follow uncommon behaviours, with very abrupt
decreases/increases of the apparent amplitudes from one cycle to another.
For example, our October 2003 and February 2004
observations show that the amplitudes can vary widely ( 25% at
HJD 2 452 925.5 or 2 453 053.3, or
25% at
HJD 2 452 925.5 or 2 453 053.3, or  35% at HJD 2 453 051.3) on close
successive cycles.
35% at HJD 2 453 051.3) on close
successive cycles.
Our B and R observations obtained in 1996 at Château-Renard Observatory show
that the colour index (B-R) has a total amplitude of about 0
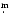 15, the colour
index mimima lag at phase
15, the colour
index mimima lag at phase  0.43 after the maxima, i.e. significantly
before phase 0.58 mentioned above for the light minima. The light curve
decrease is quicker in blue than in red colour (or viceversa, the blue light
increase starts before the red light increase), i.e. the light minima in R filter occurs later than in B.
0.43 after the maxima, i.e. significantly
before phase 0.58 mentioned above for the light minima. The light curve
decrease is quicker in blue than in red colour (or viceversa, the blue light
increase starts before the red light increase), i.e. the light minima in R filter occurs later than in B.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{3841fig1.eps}\end{figure}](/articles/aa/full/2006/21/aa3841-05/Timg27.gif) |
Figure 1:
R light curve of BL Cam observed on October 13, 2003 at
Château-Renard Observatory. 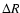 means magnitude differences variable
minus comparison star.
means magnitude differences variable
minus comparison star. |
| Open with DEXTER |
In all cases the data were used to determine new times of
(the sharper) light maximum, by fitting a third degree polynomial on each
observed peak. As such, we included 105 new timings of light maximum
(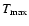 )
in our ephemeris.
The typical error on the time of the individual maxima, is estimated at around
0
)
in our ephemeris.
The typical error on the time of the individual maxima, is estimated at around
0
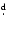 0004, i.e. less than 1% of the main period of this variable. Table 2
displays the new observed times of light maximum.
0004, i.e. less than 1% of the main period of this variable. Table 2
displays the new observed times of light maximum.
Frequency analysis was carried out on each of the new data sets presented in
this work and on those available in the literature
that we considered as reliable enough for
this purpose.
The followed procedure is described in Rodríguez et al. (1998),
where single-frequency and multiple-frequency techniques are combined using
both Fourier and multiple least squares algorithms. The multiple-frequency
least squares technique always calculates the best fit with all
frequencies considered simultaneously.
The purpose of this analysis is to study
the multiperiodic content of the light curves in order
(i) to confirm the existence of the secondary frequency around 31-32 cd-1
detected by other authors, and determine its real value;
(ii) to investigate the existence of eventual additional frequencies detected
by Zhou et al. (1999); (iii) to study the multiperiodic
behaviour over time (i.e. the number of observed frequencies and possible
amplitude variations); and (iv) to investigate the behaviour of the main
frequency f0 with time (i.e. its possible amplitude variations).
In our analysis, we assume that the value of the main frequency is already
known as
f0=25.5769 cd-1, which corresponds to the period
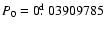 derived by Zhou et al. (1999, Eq. (2)).
The mentioned strong asymmetry in the shape of the light curve obviously
generates the harmonics 2f0 and 3f0 in the Fourier analysis, their
amplitudes and phases giving a mathematical representation of the asymmetry
itself, an asymmetry common to most large amplitude variables (i.e. undergoing
nonlinear physical processes). In order to make our analysis as homogeneous as
possible, in each data set we first extracted the frequencies f0, 2f0
and 3f0 and then analysed the residuals.
A peak of frequency has been considered as significant as soon as it
fulfils the criterion given by
Breger et al. (1993, 1996), i.e. an amplitude signal/noise (S/N) ratio
derived by Zhou et al. (1999, Eq. (2)).
The mentioned strong asymmetry in the shape of the light curve obviously
generates the harmonics 2f0 and 3f0 in the Fourier analysis, their
amplitudes and phases giving a mathematical representation of the asymmetry
itself, an asymmetry common to most large amplitude variables (i.e. undergoing
nonlinear physical processes). In order to make our analysis as homogeneous as
possible, in each data set we first extracted the frequencies f0, 2f0
and 3f0 and then analysed the residuals.
A peak of frequency has been considered as significant as soon as it
fulfils the criterion given by
Breger et al. (1993, 1996), i.e. an amplitude signal/noise (S/N) ratio
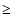 4.0
for independent peaks and 3.5 for peaks corresponding to frequency
combinations (Breger et al. 1999).
4.0
for independent peaks and 3.5 for peaks corresponding to frequency
combinations (Breger et al. 1999).
In order to compare amplitudes obtained in different filters,
all of them have been converted
to equivalent amplitudes in the Johnson's V filter. When observations
were collected in B or R filters, the corresponding amplitudes can be
transformed to V equivalent amplitudes following
Balona & Evers (1999, Fig. 2), assuming a typical 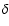 Sct regime.
The following transformation equations were determined:
Sct regime.
The following transformation equations were determined:
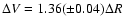 and
and
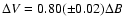 .
Data collected at McDonald Observatory in 2004 were obtained in filter S (i.e.
Schott BG 40), which has a peak transmission around
.
Data collected at McDonald Observatory in 2004 were obtained in filter S (i.e.
Schott BG 40), which has a peak transmission around
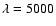 Å (Zhou et al. 2005). The
corresponding equivalent V amplitudes were obtained following the procedure
described in Rodríguez (1999), which yields
Å (Zhou et al. 2005). The
corresponding equivalent V amplitudes were obtained following the procedure
described in Rodríguez (1999), which yields
 .
.
Table 2:
New times of light maximum of BL Cam. 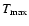 is in HJD-2 400 000.
Observatory code as in Table 1. Whenever quoted B, R it means that the
corresponding
is in HJD-2 400 000.
Observatory code as in Table 1. Whenever quoted B, R it means that the
corresponding 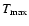 was determined as the mean value.
was determined as the mean value.
We first investigated the possibility of amplitude changes in
the main frequency f0 on the time scale of years.
Table 3 lists the amplitudes of f0 along with the
secondary frequency f1, when detected in the range
31-32 cd-1. No significant changes are detected in the amplitude of f0
which is stable at 146 mmag within  10 mmag.
It must be noted that the error bars listed in this table are
the "formal'' error bars as a result of the Fourier fitting,
but the "true'' ones are slightly larger. Also, some data sets are not
long enough, which can induce scatter in the solution of the fits.
The amplitudes of f0 can also be disturbed by the existence
of secondary peaks close to f0 which are not obviously discerned
in short data sets (see Sect. 4.1.3).
10 mmag.
It must be noted that the error bars listed in this table are
the "formal'' error bars as a result of the Fourier fitting,
but the "true'' ones are slightly larger. Also, some data sets are not
long enough, which can induce scatter in the solution of the fits.
The amplitudes of f0 can also be disturbed by the existence
of secondary peaks close to f0 which are not obviously discerned
in short data sets (see Sect. 4.1.3).
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{3841fig2.ps}\end{figure}](/articles/aa/full/2006/21/aa3841-05/Timg33.gif) |
Figure 2:
Power spectra of BL Cam corresponding to the 1999 data set
collected by Zhou et al. (2001). Panels: 1) residuals after removing f0,
2f0 and 3f0, 2) same after removing f0-f3, 3) same after removing
f0-f5 and 4) same after removing f0-f7. |
| Open with DEXTER |
Table 3:
Amplitudes,
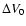 and
and
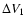 ,
of
f0=25.5769 cd-1 and f1, respectively, determined from
different data sets by Fourier analysis.
,
of
f0=25.5769 cd-1 and f1, respectively, determined from
different data sets by Fourier analysis.
In exploring the multiperiodic nature of BL Cam,
the first aim is to determine
the existence and true value of the secondary peak f1 claimed by some
authors in the region 31-32 cd-1. Previously published results give values
of 32.6443 cd-1 (Hintz et al. 1997), 31.5912 cd-1 (Zhou et al.
1999), 32.3182 cd-1 (Kim et al. 2003), and 32.517 cd-1
(Delaney et al.
2000, unpublished). These differing results for f1
can be caused by too short or not
reliable enough data sets (high noise levels as compared with the low
amplitude commonly found for f1).
The results in Table 3 confirm that f1 reliably exists and that
its value is
close to 31.6 cd-1 or 32.6 cd-1. At least one of these frequencies
is present in each data set, although not
always detected, and with amplitudes that
show a rather large dispersion.
A summary of the frequencies detected in the range 31-32 cd-1 is given in
Table 4. They cluster around the mean values 31.64(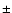 0.05)
and 32.64(
0.05)
and 32.64(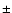 0.10) cd-1.
The difference between these two frequencies
might be due to the well-known 1 cd-1 alias problem, inherent in
single-site data.
The frequencies around 32.6 cd-1 show a higher dispersion and,
if we consider the two better data sets (i.e. those collected
in 1996 and 1999 by Zhou et al. 1999, 2001),
f1 should be 31.6 cd-1.
0.10) cd-1.
The difference between these two frequencies
might be due to the well-known 1 cd-1 alias problem, inherent in
single-site data.
The frequencies around 32.6 cd-1 show a higher dispersion and,
if we consider the two better data sets (i.e. those collected
in 1996 and 1999 by Zhou et al. 1999, 2001),
f1 should be 31.6 cd-1.
Is f1 really a one peak solution
with a 1 cd-1 aliasing problem? When analysing the 1999 data set of
Zhou et al. (2001), the best published photometric run for BL Cam, we
find the frequency 31.6759 cd-1 along with another peak
at 32.5456 cd-1 (Tables 4 and 6).
This suggests that, at least in some data sets,
the peaks detected around 31.6 cd-1 and those around 32.6 cd-1
are intrinsic rather than produced by the 1 cd-1 alias. Possible
explanations could be that (i) in some data sets only one frequency is
detected because the spectrum resolution is not sufficient
to resolve the two frequencies;
and/or (ii) amplitude changes lead to sometimes detecting one frequency
rather than the other.
Table 4:
Summary of frequencies in the range 31-32 cd-1. (*) Possible
alias (see Note e) in Table 3).
In addition to f0 and its two first harmonics (2f0, 3f0) and f1
(in the region 31-32 cd-1), some other
peaks have been detected in the power spectra of BL Cam by Zhou et al. (1999),
in the region close to the main frequency f0. Some frequency
combinations of the new peaks with f0 were also found by the same authors.
This suggests the existence of microvariability in this star, with additional
peaks corresponding to nonradial modes.
Sometimes these new peaks have amplitudes larger than
f1. Similar microvariability has been previously found in some other
high-amplitude 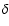 Sct and SX Phe-type variables (SX Phe itself and
DY Peg by Garrido & Rodríguez 1996; AI Vel by Walraven et al. 1992;
RV Ari by Pócs et al. 2002; RY Lep by Rodríguez et al. 2003).
Sct and SX Phe-type variables (SX Phe itself and
DY Peg by Garrido & Rodríguez 1996; AI Vel by Walraven et al. 1992;
RV Ari by Pócs et al. 2002; RY Lep by Rodríguez et al. 2003).
In order to investigate microvariability in BL Cam, we have re-analysed
the data sets available in the bibliography which are reliable for this
task: those of Hintz et al. (1997), Kim et al. (2003),
Wolf et al. (2002) and Zhou et al. (1999, 2001). In addition, our best
observation runs were also investigated: those obtained
at Xinglong Station (in the period
November-December 2003) and Château-Renard Observatory (October 2003).
We first extracted the set of frequencies
f0=25.5769 cd-1, 2f0 and 3f0 and then analysed the residuals,
as described above.
The new significant peaks detected have then been simultaneously optimized
and removed from the data according to Rodríguez et al. (1998).
We will discuss in some detail the results obtained
for the data sets of Zhou et al. (1999, 2001) which are listed in Tables 5 and 6 together with the corresponding S/N values.
For simplicity, the same names are assigned to the same peaks in both
tables, whatever their amplitudes.
Our results are in very good agreement with those
published in Zhou et al. (1999).
In addition to
f1=31.5927 cd-1, other additional independent
frequencies f2, f5 and f7 are detected together with the
combinations
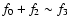 and
and
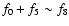 ,
and
the amplitudes of f2 and f5 are larger than f1.
We do not detect at a significant level
the linear combination f0+f1 reported by Zhou et al. (1999).
On the other hand, a new significant peak at
f7=25.6441 cd-1
and with
,
and
the amplitudes of f2 and f5 are larger than f1.
We do not detect at a significant level
the linear combination f0+f1 reported by Zhou et al. (1999).
On the other hand, a new significant peak at
f7=25.6441 cd-1
and with
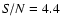 is
detected in our analysis. This is very close to
f7=25.6653 cd-1 that
we find in our re-analysis of Zhou et al.'s (2001) data.
is
detected in our analysis. This is very close to
f7=25.6653 cd-1 that
we find in our re-analysis of Zhou et al.'s (2001) data.
Table 6 and Fig. 2 show the results obtained for the data set
collected in 1999 by Zhou et al. (2001). This is the best run available in the
bibliography with about 50 h of observations and 2700 measurements
collected during
17 nights spanning 67 days. The majority of these nights are
of excellent photometric quality. The results of our analysis confirm
the majority of the modes detected by Zhou et al. (1999).
In particular, the
independent modes
f2=25.2469 cd-1,
f5=25.9122 cd-1 and
f7=25.6653 cd-1 are confirmed. However, their amplitudes
are much smaller here and the combination f0+f5 is not detected;
only the combination f0+f2 is significantly detected. Interestingly,
in addition to the frequency
f1=31.6759 cd-1, another peak is clearly
detected at
f4=32.5456 cd-1, as discussed in the previous
section.
Table 7 summarizes the frequencies detected close to the main pulsation f0
from different sets.
We confirm the independent modes at
 25.24 cd-1,
25.24 cd-1,  25.92 cd-1 and
25.92 cd-1 and
 25.65 cd-1, values very close to those already found by Zhou et al. (1999). From our data sets,
the best is that collected in 2003 at Xinglong Station,
although only 3 nights were devoted to observations in the Johnson V filter.
One secondary peak was detected at 24.220 cd-1 with low amplitude
(7.5 mmag) and
S/N ratio
25.65 cd-1, values very close to those already found by Zhou et al. (1999). From our data sets,
the best is that collected in 2003 at Xinglong Station,
although only 3 nights were devoted to observations in the Johnson V filter.
One secondary peak was detected at 24.220 cd-1 with low amplitude
(7.5 mmag) and
S/N ratio
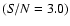 .
Moreover, when the 2003 data set collected at
Château-Renard Observatory is investigated, a secondary significant peak is
found at 23.904 cd-1 with
.
Moreover, when the 2003 data set collected at
Château-Renard Observatory is investigated, a secondary significant peak is
found at 23.904 cd-1 with
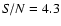 .
.
As shown in Table 7, changes in amplitude are evident for the secondary
peaks detected in the region of 25 cd-1. Moreover,
most of them present quite low amplitudes and low S/N ratio, which means that
they can appear at the extreme limit of, or beyond, reliability.
Table 5:
Results of Fourier analysis applied to the 1996 data set of
Zhou et al. (1999). The sigma of the residuals is 28.6 mmag.
Table 6:
Results of Fourier analysis applied to the 1999 data set of
Zhou et al. (2001). The sigma of the residuals is 13.7 mmag.
Table 7:
Frequencies detected close to the main pulsation f0. Sources
as in Table 3.
In Sect. 4.1.1, we have seen that the amplitude of the main frequency f0
seems to be stable (Table 3), within our errors with
the light curves appearing
rather regular "on the average'' (e.g. most of Zhou et
al.'s 1999 observations). However,
a puzzling problem in the pulsation analysis comes from the fact that, from
time to time, amplitude variations can appear in the form of progressive
decreases or increases on the height of the maximum (e.g. at
HJD 2 449 750,
Hintz et al. 1997, Fig. 2; or at HJD 2 452 925, Fig. 1 of this paper),
as well as on the minima (e.g. at HJD 2 449 748.7, d=6799.0 in Fig. 6 in
Zhou et al. 1999).
In our runs, we observed
amplitude variations of  25-35% on very close successive cycles (see
Sect. 3), and an extreme case of such sudden amplitude variation from cycle
to cycle is found in Blake et al. (2000), with amplitude variations reaching
25-35% on very close successive cycles (see
Sect. 3), and an extreme case of such sudden amplitude variation from cycle
to cycle is found in Blake et al. (2000), with amplitude variations reaching
 40% (increase/decrease) at half cycle distances
(their Fig. 3). Blake et al. (2000) emphasized that such amplitude modulations
seem to be more pronounced in their I bandpass filter.
40% (increase/decrease) at half cycle distances
(their Fig. 3). Blake et al. (2000) emphasized that such amplitude modulations
seem to be more pronounced in their I bandpass filter.
The existence of multiperiodicity can cause modulations
of the light curve. However, such rapid
and large amplitude variations, as those mentioned above, are difficult to
understand in terms of simple close additional frequencies (the energy
available in the pulsation should vary by a factor  3 according to Blake
et al.'s (2000) observations). These abrupt variations can in no way
be related to the frequencies determined here,
nor can they be the product of a beat/superposition of multiple
frequencies at their detected amplitudes. Thus, we suggest that
non-pulsation phenomena are superimposed on the multifrequency solution. These
perturbations could be due to strong stellar activity appearing at the level
of the star's photosphere, bound to the inner
layers of the star, or brought by the rather violent pulsation, into the
star's atmosphere.
3 according to Blake
et al.'s (2000) observations). These abrupt variations can in no way
be related to the frequencies determined here,
nor can they be the product of a beat/superposition of multiple
frequencies at their detected amplitudes. Thus, we suggest that
non-pulsation phenomena are superimposed on the multifrequency solution. These
perturbations could be due to strong stellar activity appearing at the level
of the star's photosphere, bound to the inner
layers of the star, or brought by the rather violent pulsation, into the
star's atmosphere.
According to Sect. 4.1.2, the existence of a secondary frequency f1 in
the 31-32 cd-1 range is confirmed, with a most-likely value of
 31.6 cd-1, though another independent frequency at
31.6 cd-1, though another independent frequency at
 32.6 cd-1 could also exist. However, the question of these
being independent frequencies remains open as long
as we do not have multi-longitude coordinated data.
32.6 cd-1 could also exist. However, the question of these
being independent frequencies remains open as long
as we do not have multi-longitude coordinated data.
Although Nemec et al. (1994) have initially assigned a first overtone status
to the principal frequency of BL Cam, one can argue that it corresponds to the
fundamental mode f0 of radial pulsation, on the following bases:
(i) the atmospheric parameters
derived, e.g. in Zhou et al. (1999), lead to a pulsation constant Q of about
0
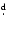 031; (ii) McNamara (1995, 1997) pointed out that the pulsating stars
of this type with V amplitudes larger than
031; (ii) McNamara (1995, 1997) pointed out that the pulsating stars
of this type with V amplitudes larger than  0.25 mag and
asymmetric light curves are fundamental mode pulsators; (iii) as discussed
in (Sect. 3), for 1996 B and R data, the R maxima lag the B ones.
Taking into account f0, 2f0 and 3f0, the Fourier analysis of
these data leads to a positive phase-shift of 0.014(
0.25 mag and
asymmetric light curves are fundamental mode pulsators; (iii) as discussed
in (Sect. 3), for 1996 B and R data, the R maxima lag the B ones.
Taking into account f0, 2f0 and 3f0, the Fourier analysis of
these data leads to a positive phase-shift of 0.014(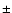 0.003), which
suggests a radial nature for the f0 mode (Balona & Evers 1999).
0.003), which
suggests a radial nature for the f0 mode (Balona & Evers 1999).
We will now examine the real frequency and nature of f1.
If the frequency of
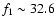 cd-1 is assumed, the ratio f0/
cd-1 is assumed, the ratio f0/
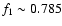 is
compatible with a radial first overtone identification for f1.
Given the extreme low metallicity of BL Cam, this period ratio is in agreement
with the relations "period ratio versus metallicity'' established for
double-mode high-amplitude
is
compatible with a radial first overtone identification for f1.
Given the extreme low metallicity of BL Cam, this period ratio is in agreement
with the relations "period ratio versus metallicity'' established for
double-mode high-amplitude 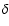 Sct and SX Phe pulsators (Hintz et al. 1997; Kim et al. 2003). This f1 value is also consistent with Petersen
diagrams for period ratio versus period
(Petersen & Christensen-Dalsgaard 1996; Olech et al. 2005): the theoretically
predicted period ratios
Sct and SX Phe pulsators (Hintz et al. 1997; Kim et al. 2003). This f1 value is also consistent with Petersen
diagrams for period ratio versus period
(Petersen & Christensen-Dalsgaard 1996; Olech et al. 2005): the theoretically
predicted period ratios 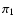 /
/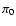 increase quickly towards shorter
periods, with differences for stars in the 0
increase quickly towards shorter
periods, with differences for stars in the 0
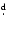 04-0
04-0
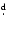 125 range arrising
mainly from differences in metallicity. BL Cam should also fit the Petersen
diagrams shown in Poretti et al. (2005) where it can be compared with a sample
of Population I and II double-mode high-amplitude pulsators. It can be seen
in these diagrams that the main differences in the period ratios come from
differences in mass for the longer periods (
125 range arrising
mainly from differences in metallicity. BL Cam should also fit the Petersen
diagrams shown in Poretti et al. (2005) where it can be compared with a sample
of Population I and II double-mode high-amplitude pulsators. It can be seen
in these diagrams that the main differences in the period ratios come from
differences in mass for the longer periods (
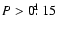 ).
).
However, if we assign
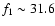 cd-1 and thus a ratio of
f0/
cd-1 and thus a ratio of
f0/
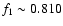 ,
our actual period ratio is too high at any metallicity
for Petersen's
,
our actual period ratio is too high at any metallicity
for Petersen's 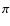 1/
1/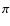 0 diagrams, and is too low at low
metallicities for
0 diagrams, and is too low at low
metallicities for 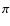 2/
2/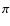 1 diagrams (Olech et al. 2005).
The 0.810 value could only be identified with
that derived from first and second overtones for radial pulsation at solar
abundances (Stellingwerf 1979). As this is unrealistic for BL Cam,
the nonradial interpretation is best suited for f1.
1 diagrams (Olech et al. 2005).
The 0.810 value could only be identified with
that derived from first and second overtones for radial pulsation at solar
abundances (Stellingwerf 1979). As this is unrealistic for BL Cam,
the nonradial interpretation is best suited for f1.
Furthermore, if we consider the four best data
sets in Table 3, i.e. those of Hintz et al. (1997), Zhou et al. (1999),
Zhou et al. (2001) and the present work (2003 data set collected at Xinglong
Station), the corresponding amplitudes for f0 are 146.5, 146.8, 145.7 and
146.9 mmag, and those for f1 are 9.0, 11.5, 7.0 and 9.6 mmag.
It suggests that, although the amplitude of f0 seems to be very
stable, there could be some real variation in the amplitude of f1.
If this is true, it could be an indication of nonradial pulsation for this
mode, although one has to examine very carefully the corresponding
amplitude S/N ratio at the level of millimagnitudes.
Nevertheless, it might also be that
the amplitudes listed
for f1 correspond to a mixture of modes at  31.6 and
31.6 and
 32.6 cd-1 with both peaks being real pulsation modes.
Hence, new and precise photometric observations should be crucial
to discern if both peaks are real. Moreover, multicolour
observations should also be very useful to discriminate their radial or
nonradial nature.
32.6 cd-1 with both peaks being real pulsation modes.
Hence, new and precise photometric observations should be crucial
to discern if both peaks are real. Moreover, multicolour
observations should also be very useful to discriminate their radial or
nonradial nature.
The frequencies detected near f0 (Table 7) seem to
cluster in three groups around 25.25(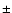 0.03), 25.65(
0.03), 25.65(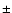 0.02), and
25.92(
0.02), and
25.92(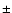 0.02) cd-1.
Their occurrence was found as significant in 4,
3 and 3 times, respectively, if we include the two detected aliases
at a 1 or 2 cd-1 "distance'' (Table 8).
Some other frequency peaks have
been detected at 24.22 cd-1 in 2003 and at 25.93 cd-1 in 2001,
although both with S/N values under 4.0.
0.02) cd-1.
Their occurrence was found as significant in 4,
3 and 3 times, respectively, if we include the two detected aliases
at a 1 or 2 cd-1 "distance'' (Table 8).
Some other frequency peaks have
been detected at 24.22 cd-1 in 2003 and at 25.93 cd-1 in 2001,
although both with S/N values under 4.0.
The amplitudes of peaks near f0 are relatively
small and undergo large variations inside each of the three groups.
The two most significant ones (i.e.  25.25 cd-1
and
25.25 cd-1
and  25.92 cd-1 groups) are nearly symmetric on each
side of the main frequency f0=25.58 cd-1. We cannot distinguish
whether it is a physical splitting of this frequency f0
(if the star rotates in a few days) or if it is a pure mathematical
artefact, but it is likely not a coincidence.
A small distorsion of the light curve or a simple modulation of
the main frequency and/or of its amplitude during short observation sessions
could create, in the Fourier analysis, some spurious frequencies
quite close to the principal peak.
Considering that it has been reported by several authors using various
data sets with differing alias issues, we believe they are most likely
intrinsic pulsations within the star.
25.92 cd-1 groups) are nearly symmetric on each
side of the main frequency f0=25.58 cd-1. We cannot distinguish
whether it is a physical splitting of this frequency f0
(if the star rotates in a few days) or if it is a pure mathematical
artefact, but it is likely not a coincidence.
A small distorsion of the light curve or a simple modulation of
the main frequency and/or of its amplitude during short observation sessions
could create, in the Fourier analysis, some spurious frequencies
quite close to the principal peak.
Considering that it has been reported by several authors using various
data sets with differing alias issues, we believe they are most likely
intrinsic pulsations within the star.
According to our analysis, performed with old and new
data sets in a homogeneous framework, multiperiodicity probably exists around 25.25, 25.65 and 25.92 cd-1. However, these secondary frequencies should
be checked and confirmed from longer-duration observations and/or
multi-site photometric campaigns.
Table 8:
Frequencies detected close to f0. Only peaks with
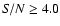 are listed.
are listed.
Figure 3 shows the evolution of the O-C values with Heliocentric Julian Dates,
calculated for the main frequency f0,
using 415 available times of light maximum of Berg & Duthie (1977),
Blake et al. (2000),
Hintz et al. (1997), Kim et al. (2003), McNamara & Feltz (1978),
Rodríguez et al. (1990), Van Cauteren & Wils (2000), Wolf et
al. (2002) and Zhou et al. (1999, 2001), and our new maxima (Table 2). In
this diagram we converted the light minima given by Van Cauteren & Wils
(2000) to maxima by adding 0.58 of a period,
according to the phase lag determined above (Sect. 3).
Due to the very large discrepancy with the rest of their
data, five light maxima of Zhou et al. (1999) were not taken into account,
at HJD 2 448 297.3617 and .3958, 2 448 298.1000 and .1397, 2 448 299.0367.
The O-C values were calculated using the linear ephemeris given by Zhou et al.
(1999, Eq. (2)): HJDmax(d) =
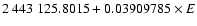 ,
where E is the cycle
number. The resulting O-C diagram (Fig. 3) shows three main regions:
,
where E is the cycle
number. The resulting O-C diagram (Fig. 3) shows three main regions:
- (i)
- A clear parabolic zone (HJD 2 443 125 to 2 450 852 or 21 years) displaying a
steady period increase (0.02 s in the last 20 years; see Hintz et al. (1997)
corrected by Breger & Pamyatnykh 1998). We confirm this
0.020(
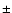 0.004) s/20 years (i.e.
0.004) s/20 years (i.e.
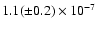 sc-1 or
sc-1 or
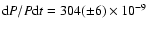 yr-1) average period increase.
yr-1) average period increase.
- (ii)
- A more confused zone (HJD 2 451 416 to 2 452 530, i.e. 3 years)
that was first interpreted as a period decrease caused by binarity (reversed
trend, Kim et al. 2003). More recent observations (Wolf et al. 2002)
showed that this was indeed an almost horizontal feature in the O-C
diagram, with a rather large vertical dispersion.
- (iii)
- The third part of the diagram (our 2003 to 2005 observations) shows that
BL Cam has resumed its period increase (if we only consider the last
2.6 years, i.e about HJD 2 452 520 to 2 453 478, the mean period should have
increased at least by
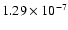 dc-1 or
dc-1 or  0.0003% per cycle).
0.0003% per cycle).
The variable shape/amplitude of the star light variations could account for a
large part of the typical  0
0
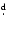 002 vertical dispersion in the O-C
diagrams. As already pointed out by Hintz et al. (1997), the combination of the two f0 and f1 frequencies with their
respective amplitudes can explain part of the intrinsic dispersion
of the light maxima plotted in the O-C diagrams, around the mean value
given by the f0 frequency (e.g., in our 2003 data, it leads to a
002 vertical dispersion in the O-C
diagrams. As already pointed out by Hintz et al. (1997), the combination of the two f0 and f1 frequencies with their
respective amplitudes can explain part of the intrinsic dispersion
of the light maxima plotted in the O-C diagrams, around the mean value
given by the f0 frequency (e.g., in our 2003 data, it leads to a
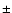 0
0
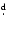 0005 to 0
0005 to 0
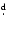 0006 dispersion in the O-C diagram plotted for
frequency f0).
0006 dispersion in the O-C diagram plotted for
frequency f0).
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{3841fig3.eps}\end{figure}](/articles/aa/full/2006/21/aa3841-05/Timg59.gif) |
Figure 3:
O-C diagram for BL Cam using the ephemeris of Zhou et al. (1999,
Eq. (2)). |
| Open with DEXTER |
The last 4500 days of the O-C diagram display significant deviations from the
mean parabola of a linear period increase. These deviations
could be either abrupt changes (revealing adjustments of the principal
pulsation period) as suggested by Koen (2000), or cyclic variations due to
light travel time effect in a binary. Indeed, when the parabolic fit
is removed from the O-C diagram an almost cyclic variation remains.
An explanation could be small transitory readjustments of the internal
structure of the star (around the mean secular trend shown by the parabolic
O-C behaviour), generating small discontinuous "jumps'' between stable but
transient periods. Given the dispersion in the observed O-C diagram,
this could mimic an oscillation. However, a
hybrid adjustment using a parabola and two
straight-line segments respectively for the first and last two parts of the
O-C diagram does not give a satisfactory fit: an oscillatory trend
remains. As such, discontinuous period jumps are not completely excluded,
although we do not favour this hypothesis.
Accordingly, we have carried out a binary analysis of the O-C diagram.
The expressions that describe the light-travel time (LTT) effect as
a function of the orbital properties were first provided by Irwin (1952).
In our work, we used Eq. (1) of Ribas et al. (2002), which is similar
to Eq. (2) of Irwin (1952). The O-C timings obtained after HJD 2 449 000 were
selected to cover about one cycle of the possible secondary body. With
the full set of timings (and their corresponding uncertainties) given by the
different authors, fits were run with given
weights proportional to 1/(sigma2). When no uncertainty
was available, we adopted a median uncertainty value of 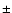 0
0
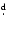 0005.
0005.
The following parameters were considered in our fits: semi-amplitude,
eccentricity, argument of periastron, orbital period, date of periastron
passage. Solutions with free eccentricity were found to be unstable.
This is because the
fit quality is degenerate with respect to this parameter and the fits can
attain arbitrarily large values. So fits were run by fixing eccentricity
to values between 0 and 1 at regular steps. The fits clearly prefer highly
eccentric values, greater than 0.5. When the eccentricity changes from
0.5 to 0.7 and then to 0.9, the improvement is hardly perceptible.
As such,
a value of 0.7(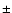 0.2) was adopted. We obtained a tentative period of
10.5(
0.2) was adopted. We obtained a tentative period of
10.5(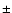 0.2) yr with a semi-amplitude of 148(
0.2) yr with a semi-amplitude of 148(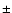 12) s in O-C. The set of
orbital elements of the binary system are presented in Table 9.
12) s in O-C. The set of
orbital elements of the binary system are presented in Table 9.
Figure 4 (bottom) shows the O-C diagram fitted with the parameters of
Table 9. The root mean square residual (top of Fig. 4) is 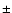 0
0
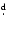 001,
and residuals do not show any systematic trends.
001,
and residuals do not show any systematic trends.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{3841fig4.eps}\end{figure}](/articles/aa/full/2006/21/aa3841-05/Timg60.gif) |
Figure 4:
O-C diagram for BL Cam. Bottom: O-C values (dots) together with
the synthetic curve (solid line) using the parameters of the
binary system given in Table 9. Top: residuals from the fitting. |
| Open with DEXTER |
Table 9:
Orbital elements of the possible BL Cam binary system.
Based on analysis of the O-C residuals,
some high-amplitude pulsators in the Lower Instability Strip
have been reported as or suspected to be members of binary systems
(Rodríguez 2003), BL Cam being one of the candidates.
Previous authors have estimated the increasing rate of the main period
of BL Cam with a parabolic fit. Hintz et al. (1997) and Zhou et al. (1999)
found respectively
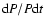 values of
values of
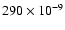 yr-1 and
yr-1 and
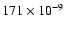 yr-1.
In the same way, with all available and new O-C data, we find
yr-1.
In the same way, with all available and new O-C data, we find
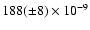 yr-1. However, in the case of the binarity
hypothesis, the O-C diagram can be better described by a secular increase of
the period at a rate of
yr-1. However, in the case of the binarity
hypothesis, the O-C diagram can be better described by a secular increase of
the period at a rate of
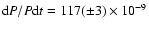 yr-1 (i.e.
yr-1 (i.e.
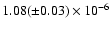 s d-1),
in addition to the 10.5(
s d-1),
in addition to the 10.5(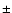 0.2) yr orbital
period of the system.
0.2) yr orbital
period of the system.
We can draw up a tentative representation of the system of
BL Cam. Using Kepler's Third Law, and adopting a mass of  1
1 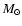 for BL Cam (McNamara 1997), Table 9 indicates a range in mass of
0.1 to 0.5
for BL Cam (McNamara 1997), Table 9 indicates a range in mass of
0.1 to 0.5 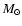 (with a minimum of
(with a minimum of  0.1
0.1 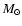 )
for the
secondary body with a semi-major axis of
)
for the
secondary body with a semi-major axis of  5-6 AU.
As we did not find any eclipse in the light curves, the
inclination of this possible high eccentricity binary system cannot be
determined.
5-6 AU.
As we did not find any eclipse in the light curves, the
inclination of this possible high eccentricity binary system cannot be
determined.
However, some observational evidence is opposed to the binary hypothesis.
Though there is no obvious
systematic trend in the scatter of the residuals in Fig. 4 (top panel),
we note that the latest O-C values (HJD 2 453 264 to 2 453 478) have residuals
larger than expected
from the LTT effect model based on our previous values (Fig. 4).
As already mentioned in Sect. 5.1, there is a large dispersion
( 0
0
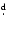 002) in the O-C diagram, so the times of last light maxima are
not, up to now, sufficient to discard the binarity hypothesis. Indeed, very
recent O-C data (Simonetti, private communication) confirm the plausibility
of the binary hypothesis. Finally, as the interpretation of the O-C diagram
requires observations over a long time base, new observations during several
years are necessary to definitively conclude on the existence of a
binary perturbation.
002) in the O-C diagram, so the times of last light maxima are
not, up to now, sufficient to discard the binarity hypothesis. Indeed, very
recent O-C data (Simonetti, private communication) confirm the plausibility
of the binary hypothesis. Finally, as the interpretation of the O-C diagram
requires observations over a long time base, new observations during several
years are necessary to definitively conclude on the existence of a
binary perturbation.
This should be of crucial importance in our understanding of the
processes
taking place in BL Cam and stars of similar evolutionary status. As discussed
in previous reviews (Breger & Pamyatnykh 1998; Rodríguez 2003), the large
and
positive rate of period change determined in BL Cam is not predicted by
the evolutionary tracks. The observed rate is much larger than
predicted by the models. On the one hand, the binary hypothesis could be
a partial explanation of this discrepancy. Binarity could also be the cause of
similar disagreements found for other high-amplitude 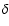 Sct and SX Phe
variables (Rodríguez & Breger 2001).
On the other hand, the existence of
jumps in the O-C diagram of BL Cam should not be completely ruled out.
Possible sudden jumps could occur in a number
of these variables, although they are commonly shown as an alternative to
parabolic fits and the choice between the two options is not an easy
task.
Sct and SX Phe
variables (Rodríguez & Breger 2001).
On the other hand, the existence of
jumps in the O-C diagram of BL Cam should not be completely ruled out.
Possible sudden jumps could occur in a number
of these variables, although they are commonly shown as an alternative to
parabolic fits and the choice between the two options is not an easy
task.
Our observed period variation in BL Cam is also positive, which
is consistent with all the previous determinations.
However, such period variation is opposite to that
observed in the rest of the high-amplitude SX Phe pulsators with reliable
determinations, with the possible exception of XX Cyg (Zhou et al. 2002; and
Blake et al. 2003 find
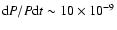 yr-1 for this star). This makes BL Cam a very
interesting object: the precise determination of its O-C behaviour will give
us insights on what part of the period change rate can be explained by
standard stellar evolution and what part explained by non-evolutionary
effects. It could also give us some insight on the role of
the non-evolutionary effects in the O-C diagrams.
yr-1 for this star). This makes BL Cam a very
interesting object: the precise determination of its O-C behaviour will give
us insights on what part of the period change rate can be explained by
standard stellar evolution and what part explained by non-evolutionary
effects. It could also give us some insight on the role of
the non-evolutionary effects in the O-C diagrams.
A comprehensive study of the high-amplitude SX Phe-type pulsator BL Cam is
presented. An
investigation of the pulsation content of this variable has been performed,
using both previously published data and our new observations obtained in 1996,
and during the years 2003 to 2005.
Our frequency analysis confirms the existence of multiperiodicity in this
star, as pointed out by previous authors. Independent peaks have been
significantly detected
in the region close to the main frequency
f0=25.5769 cd-1;
in particular at around
25.25, 25.65 and 25.92 cd-1, and which also show signs of amplitude
variability. Nevertheless, the main frequency does not
exhibit significant amplitude changes and probably corresponds to the
fundamental mode of radial pulsation.
We also confirm the existence of at least one frequency in the of region
31-32 cd-1.
Our results suggest the existence
of two independent frequencies in this region at about 31.6 and
32.6 cd-1, but the frequency at 31.64(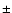 0.05) cd-1 is the
most reliably detected.
Sudden amplitude variations in the light curves, within a very few
pulsation cycles, suggest that strong stellar activity can occasionally
occur and is superimposed upon the pulsation.
0.05) cd-1 is the
most reliably detected.
Sudden amplitude variations in the light curves, within a very few
pulsation cycles, suggest that strong stellar activity can occasionally
occur and is superimposed upon the pulsation.
These topics make BL Cam a very good and unique target among the field
high-amplitude SX Phe-type variables for further studies from an
asteroseismological point of view in order to constraint its pulsation
parameters.
Furthermore, multicolour photometric observations, in at least two filters,
will be very important to prove the radial nature of f0 and discern
the true nature of the intrinsic peaks in the region
31-32 cd-1. If confirmed, the radial double-mode nature of this star
would be a significant find as it would add constraints to the
period-luminosity and/or period-metallicity relations for high-amplitude
pulsators
in the Lower Instability Strip because of its extreme short period and
low metallicity. Improved precision in the period ratios of BL Cam
will also improve the Petersen diagrams.
We also studied the behaviour of the main period making
use of the classical O-C method. The new O-C diagram, completed by our
2003 to 2005 measurements, suggests that a sinusoidal behaviour
is superimposed to
the classical parabolic one since the first half of the 1990's, when the star
has been more frequently observed.
Although we do
not definitely discard discontinuous variations of the main pulsation period,
we have shown that the observed variations of the period can be described by
two terms: (i) a secular increase of the main period at a rate of
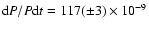 yr-1, and (ii) a perturbation from a
companion star in a rather eccentric orbit
with a period of 10.5(
yr-1, and (ii) a perturbation from a
companion star in a rather eccentric orbit
with a period of 10.5(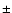 0.2) yr causing a light time semi-amplitude of
148(
0.2) yr causing a light time semi-amplitude of
148(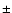 12) s.
To gain insights on the true behaviour on the main period in
the O-C diagram, it will be of great interest to locate this variable in the
observational framework among the high-amplitude pulsators in the Lower
Instability Strip.
This would place direct (and likely opposing) constraints on
stellar evolution models, and could provide
insight on the possible secondary effects taking place at this stage of
stellar evolution (see e.g., Rodríguez et al. 1995; Breger & Pamyatnykh 1998).
12) s.
To gain insights on the true behaviour on the main period in
the O-C diagram, it will be of great interest to locate this variable in the
observational framework among the high-amplitude pulsators in the Lower
Instability Strip.
This would place direct (and likely opposing) constraints on
stellar evolution models, and could provide
insight on the possible secondary effects taking place at this stage of
stellar evolution (see e.g., Rodríguez et al. 1995; Breger & Pamyatnykh 1998).
BL Cam obviously deserves continued photometric monitoring in the coming
years. Remaining observational issues are
to confirm our detected frequency content, pulsation
behaviour and checking our O-C binary hypothesis. To shed some
light on these issues, the organization of a coordinated multisite
photometric campaign with observations from several observatories at
different longitudes would be of a great importance. We are
already working in this direction for the near future.
Acknowledgements
We would like to give our most sincere thanks to P. Van Cauteren, E. Hintz,
C. Kim, M. Wolf, P. Delaney, R. Robb and J. Simonetti for making available
different data sets used in this work.
Also thanks to M. Newberry (Axiom Research, Inc.),
P. Lampens (Koninklijke Sterreanwacht van België),
E. Michel (observatoire de
Paris-Meudon), C. Sterken (Vrije Universiteit Brussel) and R. Pellock (AAVSO).
E.R. thanks for the support by the Junta de Andalucía and the Dirección
General de Investigación (DGI) under project AYA2003-04651. J.M. especially
acknowledges R. Behrend (observatoire de Genève) who provided the Courbrot
software. S.F. is grateful to M. Fauvaud, D. Pommier, J. Vandenbroere, A. Bruno,
C. Fournou, Y. Pothier, D. and F. Béziat for their help and technical
assistance during observing runs. This research has made use of both the
Simbad database, operated at CDS, Strasbourg, France, and the Astrophysics
Data System, provided by NASA, USA. MDR and A.-Y. Zhou were supported by
the National Science Foundation grant AST007480.
- Balona, L. A.,
& Evers, E. A. 1999, MNRAS, 302, 349 [NASA ADS] [CrossRef] (In the text)
- Berg, R. A., &
Duthie, J. G. 1977, AJ, 215, L25 [NASA ADS] [CrossRef] (In the text)
- Blake, R. M.,
Khosravani, H., & Delaney, P. A. 2000, JRASC, 94, 124 [NASA ADS] (In the text)
- Blake, R. M.,
Delaney, P. A., Khosravani, H., Tome, J., & Lightman, M. 2003,
PASP, 115, 212 [NASA ADS] [CrossRef] (In the text)
- Breger, M., &
Pamyatnykh, A. A. 1998, A&A, 332, 958 [NASA ADS] (In the text)
- Breger, M., Stich,
J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] (In the text)
- Breger, M.,
Handler, G., Serkowitsch, E., et al. 1996, A&A, 309, 197 [NASA ADS] (In the text)
- Breger, M.,
Handler, G., Garrido, R., et al. 1999, A&A, 349, 225 [NASA ADS] (In the text)
- Eggen, O. J., &
Iben, I. Jr. 1989, AJ, 97, 431 [NASA ADS] [CrossRef] (In the text)
- Garrido, R.,
& Rodríguez, E. 1996, MNRAS, 281, 696 [NASA ADS] (In the text)
- Giclas, H. L.,
Burnham, R. Jr., & Thomas, N. G. 1970, Lowell Obs. Bull., 7,
183 [NASA ADS] (In the text)
- Hintz, E. G., Joner,
M. D., McNamara, D. H., Nelson, K. A., & Moody, J. W. 1997,
PASP, 109, 15 [NASA ADS] [CrossRef] (In the text)
- Høg, E., &
Petersen, J. O. 1997, A&A, 323, 827 [NASA ADS] (In the text)
- Irwin, J. B. 1952,
ApJ, 116, 211 [NASA ADS] [CrossRef] (In the text)
- Jeon, Y. B., Lee, M.
G., Kim, S. L., & Lee, H. 2003, AJ, 125, 3165 [NASA ADS] [CrossRef] (In the text)
- Jeon, Y. B., Lee, M.
G., Kim, S. L., & Lee, H. 2004, AJ, 128, 287 [NASA ADS] [CrossRef] (In the text)
- Kim, C., Jeon, Y. B.,
& Kim, S. L. 2003, PASP, 115, 755 [NASA ADS] [CrossRef] (In the text)
- Koen, C. 2000, PASPC,
210, 448 [NASA ADS] (In the text)
- Livio, M. 1993,
PASPC, 53, 3 [NASA ADS] (In the text)
- Mateo, M. 1993,
PASPC, 53, 74 [NASA ADS] (In the text)
- Mazur, B.,
Krzeminski, W., & Thompson, I. B. 2003, MNRAS, 340, 1205 [NASA ADS] [CrossRef] (In the text)
- McNamara, D. H.
1995, AJ, 109, 1751 [NASA ADS] [CrossRef] (In the text)
- McNamara, D. H.
1997, PASP, 109, 1221 [NASA ADS] [CrossRef] (In the text)
- McNamara, D.
H., & Feltz, K. A. 1978, PASP, 90, 275 [NASA ADS] [CrossRef] (In the text)
- Nemec, J. M., &
Mateo, M. 1990, PASPC, 11, 64 [NASA ADS] (In the text)
- Nemec, J. M., Nemec,
A. F. L., & Lutz, T. E. 1994, AJ, 108, 222 [NASA ADS] [CrossRef] (In the text)
- Olech, A.,
Dziembowski, W. A., Pamyatnykh, A. A., et al. 2005, MNRAS, 363,
40 [NASA ADS] [CrossRef] (In the text)
- Petersen, J.
O., & Christensen-Dalsgaard, J. 1996, A&A, 312, 463 [NASA ADS] (In the text)
- Pócs, M. D.,
Szeidl, B., & Viraghalmy, G. 2002, A&A, 393, 555 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Poretti, E.,
Suárez, J. C., Niarchos, P. G., et al. 2005, A&A, 440,
1097 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Preston, G. W.,
& Landolt, A. U. 1998, AJ, 115, 2515 [NASA ADS] [CrossRef] (In the text)
- Pych, W., Kaluzny, J.,
Krzeminski, W., et al. 2001, A&A, 367, 148 [EDP Sciences] [NASA ADS] [CrossRef]
- Ribas, I., Arenou,
F., & Guinan, E. F. 2002, AJ, 123, 2033 [NASA ADS] [CrossRef] (In the text)
- Rodríguez, E.
1999, PASP, 111, 709 [NASA ADS] [CrossRef] (In the text)
- Rodríguez, E.
2003, Recent Res. Devel. Astron. Astroph., 1, 881 (In the text)
- Rodríguez, E.
2004, Comm. Asteroseismology, 145, 40 [NASA ADS] (In the text)
- Rodríguez, E.,
& Breger, M. 2001, A&A, 366, 178 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Rodríguez, E.,
& López-González, M. J. 2000, A&A, 359, 597 [NASA ADS] (In the text)
- Rodríguez, E.,
Rolland, A., & López de Coca, P. 1990, IBVS, 3428
(In the text)
- Rodríguez, E.,
López de Coca, P., Costa, V., & Martín, S. 1995,
A&A, 299, 108 [NASA ADS] (In the text)
- Rodríguez, E.,
Rolland, A., López-González, M. J., & Costa, V. 1998,
A&A, 338, 905 [NASA ADS] (In the text)
- Rodríguez, E.,
Arellano-Ferro, A., Costa, V., López-González, M. J.,
& Sareyan, J. P. 2003, A&A, 407, 1059 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Stellingwerf, R. F. 1979, ApJ, 227, 935 [NASA ADS] [CrossRef] (In the text)
- Stryker, L. L.
1993, PASP, 105, 1081 [NASA ADS] [CrossRef] (In the text)
- Van Cauteren,
P., & Wils, P. 2000, IBVS, 4872
(In the text)
- Walraven, T.,
Walraven, J., & Balona, L. A. 1992, MNRAS, 254, 59 [NASA ADS] (In the text)
- Wolf, M., Crlikova, M.,
Basta, M., et al. 2002, IBVS, 5317
(In the text)
- Zhou, A. Y.,
Rodríguez, E., Jiang, S. Y., Rolland, A., & Costa, V.
1999, MNRAS, 308, 631 [NASA ADS] [CrossRef] (In the text)
- Zhou, A. Y., Du, B. T.,
Zhang, X. B., & Zhang, R. X. 2001, IBVS, 5061
(In the text)
- Zhou, A. Y., Jiang, S.
Y., Chayan, B., & Du, B. T. 2002, Ap&SS, 281, 699 [NASA ADS] (In the text)
- Zhou, A. Y., An, D.,
Eggen, J. R., et al. 2006, Ap&SS, submitted
(In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{3841fig1.eps}\end{figure}](/articles/aa/full/2006/21/aa3841-05/Timg27.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{3841fig2.ps}\end{figure}](/articles/aa/full/2006/21/aa3841-05/Timg33.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{3841fig3.eps}\end{figure}](/articles/aa/full/2006/21/aa3841-05/Timg59.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{3841fig4.eps}\end{figure}](/articles/aa/full/2006/21/aa3841-05/Timg60.gif)