A&A 451, 417-429 (2006)
DOI: 10.1051/0004-6361:20054446

The cosmic infrared background resolved by Spitzer

Contributions of mid-infrared galaxies to the far-infrared background

H. Dole1 - G. Lagache1 - J.-L. Puget1 - K. I. Caputi1 - N. Fernández-Conde1 - E. Le Floc'h2,3 - C. Papovich2 - P. G. Pérez-González2 - G. H. Rieke2 - M. Blaylock2


1 - Institut d'Astrophysique Spatiale (IAS), bât. 121, 91405 Orsay Cedex, France; Université Paris-Sud 11 and CNRS (UMR 8617), France
2 - Steward Observatory, University of Arizona, 933 N Cherry Ave, Tucson, AZ, 85721, USA
3 - Associated with Observatoire de Paris, GEPI, 92195 Meudon, France

Received 31 October 2005 / Accepted 18 February 2006

Abstract
Aims. We quantify the contributions of 24 $\mu $m galaxies to the Far-Infrared (FIR) Background at 70 and 160 $\mu $m. We provide new estimates of the Cosmic Infrared Background (CIB), and compare it with the Cosmic Optical Background (COB).
Methods. Using Spitzer data at 24, 70 and 160 $\mu $m in three deep fields, we stacked more than 19000 MIPS 24 $\mu $m sources with $S_{24} \ge 60~\mu$Jy at 70 and 160 $\mu $m, and measured the resulting FIR flux densities.
Results. This method allows a gain up to one order of magnitude in depth in the FIR. We find that the Mid-Infrared (MIR) 24 $\mu $m selected sources contribute to more than 70% of the Cosmic Infrared Background (CIB) at 70 and 160 $\mu $m. This is the first direct measurement of the contribution of MIR-selected galaxies to the FIR CIB. Galaxies contributing the most to the total CIB are thus $z \sim 1$ luminous infrared galaxies, which have intermediate stellar masses. We estimate that the CIB will be resolved at 0.9 mJy at 70 and 3 mJy at 160 $\mu $m. By combining the extrapolation of the 24 $\mu $m source counts below Conclusions. The MIPS surveys have resolved more than three quarters of the MIR and FIR CIB. By carefully integrating the Extragalactic Background Light (EBL) SED, we also find that the CIB has the same brightness as the COB, around 24 nW m-2 sr-1. The EBL is produced on average by 115 infrared photons for one visible photon. Finally, the galaxy formation and evolution processes emitted a brightness equivalent to 5% of the primordial electromagnetic background (CMB).

Key words: cosmology: observations - cosmology: diffuse radiation - galaxies: evolution - galaxies: starburst - galaxies: infrared

1 Introduction

The Cosmic Infrared Background (CIB) is the relic emission at wavelengths larger than a few microns of the formation and evolution of the galaxies of all types, including Active Galactic Nuclei (AGN) and star-forming systems (Lagache et al. 1999; Gispert et al. 2000; Hauser et al. 1998; Puget et al. 1996; Hauser & Dwek 2001; Kashlinsky 2005). Characterizing the statistical behavior of galaxies responsible for the CIB - such as the number counts, redshift distribution, mean Spectral Energy Distribution (SED), luminosity function, clustering - and their physical properties - such as the roles of star-forming vs. accreting systems, the density of star formation, and the number of very hot stars - has thus been an important goal (Partridge & Peebles 1967). The SED of the CIB peaks near 150 $\mu $m. It accounts for roughly half of the total energy in the optical/infrared Extragalactic Background Light (EBL) (Hauser & Dwek 2001), although still with some uncertainty (Aharonian et al. 2005; Wright 2004). Since locally the infrared output of galaxies is only a third of the optical one (Soifer & Neugebauer 1991), there must have been a strong evolution of galaxy properties towards enhanced Far-Infrared (FIR) output in the past. Understanding this evolution requires interpretation of cosmological surveys conducted not only in the infrared and submillimeter spectral ranges, but also at other wavelengths (Lagache et al. 2005).

The cryogenic infrared space missions IRAS (Infrared Astronomical Satellite) and ISO (Infrared Space Observatory) provided us with valuable insights to the IR-dominated galaxies in the Mid-Infrared (MIR) and FIR (Sanders & Mirabel 1996; Genzel & Cesarsky 2000; Elbaz 2005; Lagache et al. 2005; Dole 2003, for reviews). ISO MIR surveys were able to resolve a significant fraction of the 15 $\mu $m CIB (Elbaz et al. 1999, counts close to convergence). Using model SEDs of galaxies (Chary & Elbaz 2001; Lagache et al. 2003; Xu et al. 2001, for instance), the contribution of MIR-selected galaxies to the peak of the CIB (around 140 to 170 $\mu $m) can be inferred. Elbaz et al. (2002) derived that $64\pm 38$% ($16 \pm 5$ over $25 \pm 7$ nW m-2 sr-1) of the 140 $\mu $m background is due to ISOCAM 15 $\mu $m galaxies, whose median redshift is $z \sim 0.8$.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{4446f01.ps}\end{figure} Figure 1: Sensitivity to the bolometric luminosity (and star formation rate, assuming star forming galaxies) of various infrared and submillimeter experiments. Detections of at least 10 sources in the surveys can be made in the areas above the curves. We assumed the scenario of a typical deep survey. ISOCAM 15 $\mu $m ( $S_{\nu} > 250~\mu$Jy, 2 Sq. Deg.); ISOPHOT 170 $\mu $m ( $S_{\nu } > 180 $ mJy, 5 Sq. Deg.); Spitzer/MIPS 24 $\mu $m ( $S_{\nu} > 80~\mu$Jy, 5 Sq. Deg.); Spitzer/MIPS 70 $\mu $m ( $S_{\nu } > 25 $ mJy, 5 Sq. Deg.); Spitzer/MIPS 160 $\mu $m ( $S_{\nu } > 50 $ mJy, 5 Sq. Deg.); SCUBA 850 $\mu $m ( $S_{\nu } > 1 $ mJy, 1 Sq. Deg.); This plot makes use of the Lagache et al. (2004) model and their starburst SED for the conversion to $L_{\rm bol}$. At $z \sim 1$, MIPS detects only ULIRGs in the FIR, and detects LIRGs in the MIR. The stacking analysis allows to gain an order of magnitude and to probe LIRGs in the FIR.
Open with DEXTER

The Spitzer Observatory (Werner et al. 2004) is performing much deeper and wider-area surveys, in particular at 24, 70 to 160 $\mu $m using the Multiband Imaging Photometer for Spitzer (MIPS) (Rieke et al. 2004). However, because of the limited angular resolution ("smoothing'' the high spatial frequency signal in the FIR maps), deep MIPS 70 and 160 $\mu $m maps are confusion limited (Dole et al. 2003,2004b) - the source surface density corresponds to 20 beams per source or less e.g. in the GTO fields. The FIR images do not allow us to directly probe the same galaxy population as that detected at 24 $\mu $m, where the extragalactic source confusion is less important. Figure 1 shows the typical sensitivity of MIPS surveys to the bolometric luminosity of galaxies as a function of redshift, using the modeled starburst SED of Lagache et al. (2004). At a redshift $z \sim 1$, MIPS FIR surveys are sensitive to ultraluminous IR galaxies (ULIRGs, $L \ge 10^{12}~ L_{\odot}$) where MIPS 24 $\mu $m surveys can probe luminous IR galaxies (LIRGs, $L \ge 10^{11}~ L_{\odot}$). It is therefore impossible to derive MIR and FIR SEDs of individual LIRGs at $z \sim 1$ and above.

MIPS can detect high redshift sources at 24 $\mu $m: about 25 to 30% of the population of galaxies lie at $z \ge 1.5$, at faint flux densities (down to few tens of $\mu $Jy) (Le Floc'h et al. 2004; Lonsdale et al. 2004; Pérez-González et al. 2005; Caputi et al. 2006; Chary et al. 2004; Houck et al. 2005; Egami et al. 2004). Papovich et al. (2004) showed that MIPS surveys resolve about 70% of the 24 $\mu $m IR galaxy CIB for $S_{24} \ge 60~\mu$Jy. In comparison, MIPS 70 and 160 $\mu $m (Dole et al. 2004a) surveys detect only about 20% and less than 10% of the CIB at 70 and 160 $\mu $m, respectively. Programs of very deep 70 $\mu $m imaging on small fields (e.g. D. Frayer, private communication) are likely to resolve a larger fraction, but due to confusion noise the FIR CIB will still not be significantly resolved into individual sources, while the MIR CIB at 24 $\mu $m is well resolved.

In this paper, we use a stacking analysis method that takes advantage of the good sensitivity of the MIPS 24 $\mu $m MIR channel, to fill the sensitivity gap between the MIR and the FIR surveys. By stacking the FIR data at the locations of MIR sources, we statistically investigate the FIR properties of 24 $\mu $m-selected galaxies. In particular, we quantify the contribution of the 24 $\mu $m resolved galaxies to the 70 and 160 $\mu $m background, put strong lower limits to the CIB, and give new estimates of the 70 and 160 $\mu $m background.

Throughout this paper, we adopt a cosmology with h=0.65, $\Omega_{\rm M} = 0.3$ and $\Omega_{\Lambda} = 0.7$. The surface brightnesses (e.g. of the CIB) are usually expressed in units of MJy/sr or nW m-2 sr-1. For a given frequency $\nu$ in GHz and wavelength $\lambda$ in microns, the conversion between the two is given by:

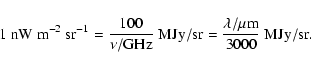\begin{displaymath}1 ~\rm nW ~ m^{-2} ~ sr^{-1} = \frac{100}{\nu / GHz}~MJy/sr = \frac{\lambda / \mu m}{3000}~MJy/sr. \end{displaymath} (1)

   
2 Data and sample

The data for our analysis are from the Spitzer MIPS Guaranteed Time Observations (GTO) cosmological surveys performed in three fields: the Chandra Deep Field South (CDFS), the Hubble Deep Field North (HDFN) and the Lockman Hole (LH). The MIPS observations at 24 $\mu $m are detailed in Papovich et al. (2004) and at 70 and 160 $\mu $m in Dole et al. (2004a). Each field covers about 0.4 square degrees, and the integration times per sky pixel are 1200 s, 600 s and 120 s at 24, 70 and 160 $\mu $m, respectively. The data were reduced and mosaicked using the Data Analysis Tool (Gordon et al. 2005). We make use of a recent new analysis of the calibration by the instrument team and the instrument support team that will soon be adopted officially. The uncertainty is now 4%, 7% and 12% at 24, 70 and 160 $\mu $m, respectively, and the calibration level has been changed by less than 10% compared with the previous determinations (see the Spitzer Science Center calibration pages[*]).

Papovich et al. (2004) showed that the 80% completeness level at 24 $\mu $m in the GTO deep fields is reached at $S_{24} = 80~ \mu$Jy. Nevertheless, Papovich et al. (2004) and Chary et al. (2004) show that the detection of very faint 24 $\mu $m sources, down to $S_{24} \sim 30~ \mu$Jy, is possible, but with increased photometric uncertainties and reduced completeness (to lower than 5% at the GTO depth and 20% at the GOODS depth).

Dole et al. (2004a) showed that at 70 and 160 $\mu $m sources can be safely extracted down to 15 mJy and 50 mJy, respectively. The Frayer et al. (2006) results go deeper. However, confusion limits the extraction of sources fainter than typically 56 $\mu $Jy at 24 $\mu $m, 3.2 mJy at 70 $\mu $m, and 36 mJy at 160 $\mu $m (Dole et al. 2004b). A priori information on the existence of a source deduced from shorter wavelength and less confusion-limited observations can extend the reliable detection threshold below this nominal confusion limit.

To implement this approach, we build a sample as follows:

$\bullet$
We select the central part of each field where all 3 MIPS wavelengths have a common sky coverage and maximum redundancy. This area covers 0.29 Sq. Deg in the CDFS and LH, and 0.27 Sq. Deg. in HDFN, for a total of 0.85 Sq. Deg. in these three fields.
$\bullet$
In these selected areas, we identify every MIPS 24 $\mu $m source with $S_{24} \ge 60~\mu$Jy. This flux density limit corresponds to 50% completeness (Papovich et al. 2004). There are 6543 galaxies above this limit in CDFS, 6039 in the HDFN, and 6599 in the LH. The total number of sources considered in the three fields is thus 19181.
To analyze this sample, we proceed as follows:
$\bullet$
In each field, we sort the 24 $\mu $m sources by decreasing flux density S24.
$\bullet$
We put the sources in 20 bins of flux density for $S_{24} \ge 60~\mu$Jy. These bins have equal logarithmic width $\Delta S_{24} / S_{24} \sim 0.15$, except for the bin corresponding to the brightest flux, which includes all the bright sources (0.92 mJy to 1 Jy).
$\bullet$
We correct the average flux obtained by stacking each S24 bin for incompleteness, following the correction of Papovich et al. (2004) (their Fig. 1). Since the bins between 60 and 80 $\mu $Jy are complete to the 50-80% level, only the weakest fluxes bins are significantly corrected.

   
3 Stacking analysis

The process of stacking the sources based on the 24 $\mu $m detections allows us to measure more of the total contribution of 70 and 160 $\mu $m sources to the CIB.

   
3.1 Processing

At 24 $\mu $m, the detector pixel size is 2.5 arcsec, the FWHM of the point spread function (PSF) is 6 arcsec, and the plate scale of the mosaic is chosen to be 1.25 arcsec. At 70 $\mu $m, the detector pixel size is 9.9 arcsec, the FWHM of the PSF is 18 arcsec, and the plate scale of the mosaic is chosen to be 4.5 arcsec. At 160 $\mu $m the detector pixel size is 18 arcsec, the FWHM of the PSF is 40 arcsec, and the plate scale of the mosaic is chosen to be 18 arcsec (Rieke et al. 2004; Gordon et al. 2005, for more details). The 70 and 160 $\mu $m mosaics have been resampled to the scale of the 24 $\mu $m mosaic (1.25 arcsec per pixel) using a bilinear interpolation. This last step greatly facilitates the weight management of the three maps, since each has different coverage, and it allows easy extraction of the signal at the three wavelengths for the same sky position.


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{4446f02.ps} \end{figure} Figure 2: Images at 24, 70 and 160 $\mu $m ( left to right) of stacked sources in the brightest bin of 24 $\mu $m flux density, with a random position offset added before each sum. Color coding: dark is high flux, light is low flux. This allows us to check that the stacking method does not introduce any artifacts, i.e. a false source detection in the center.
Open with DEXTER

For each S24 flux density bin we select every 24 $\mu $m source, extract a square image about 440 arcsec on a side centered on the source, and store it. We proceed similarly on the mosaics at 70 and 160 $\mu $m, extracting images at the position of each 24 $\mu $m source regardless of the presence of a detected FIR source. The products at this stage are thus three cubes of data at 24, 70 and 160 $\mu $m with the same dimensions (same number of source images and same box size) for each of the 24 $\mu $m flux density bins.

We then add the images in each cube at each wavelength, to generate a stacked image of sources at 24, 70 and 160 $\mu $m for a given S24flux bin. This operation is a simple sum, without any outlier rejection. When stacking, we rotate each image by $+\pi/2$ with respect to the previous one (and so on), to cancel out the large-scale background gradients such as the prominent zodiacal background at 24 $\mu $m. This processing is done both in each field separately as well as using all the data at once. Unless otherwise stated, we use the stacked data of all the fields together in the rest of this paper. We checked that no significant signal was detected when we added a random or systematic artificial offset to each 24 $\mu $m position and then performed exactly the same sub-image extraction and stacking as we did for the real 24 $\mu $m source list. Figure 2 shows the results of stacking the sources (only from the brightest bin), with a random position offset added prior to the sum. No source appears in the center, as expected. This guarantees that the stacking method does not introduce an artifact that mimics a source.

Since the stacking analysis aims at statistically detecting faint unresolved sources at 70 and 160 $\mu $m, in principle there is no need to also stack data at 24 $\mu $m, where all sources are resolved. However, doing so allows us to double-check the method, since we know by design what the stacked photometry should be.


  \begin{figure} \par\includegraphics[width=6.6cm,clip]{4446f03.ps} \end{figure} Figure 3: Images at 24 $\mu $m of stacked sources in bins of 24 $\mu $m flux density ( $S_{24} \ge 60~\mu$Jy) in the three MIPS GTO Fields: CDFS, HDFN, and LH covering about 0.85 Sq. Deg. A total number of 19181 sources has been used. The number of sources used in the sum in each S24 bin is reported. Each image has $350 \times 350$ pixels of 1.25 arcsec, thus covering about $7.3 \times 7.3$ Sq. Arcmin. Since no outlier rejection has been made, other sources can be seen in the surroundings of the stacked sources.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.6cm,clip]{4446f04.ps} \end{figure} Figure 4: Images at 70 $\mu $m of stacked sources in bins of 24 $\mu $m flux density. See caption of Fig. 3 for details.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.6cm,clip]{4446f05.ps} \end{figure} Figure 5: Images at 160 $\mu $m of stacked sources in bins of 24 $\mu $m flux density. See caption of Fig. 3 for details.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4446f06a.ps}\vspace*{2mm} \includegraphics[width=7.7cm,clip]{4446f06b.ps} \end{figure} Figure 6: Normalized radial profiles of the stacked images. The crosses represent the data, and the solid line the empirical PSF. The vertical dotted lines show the radii of the aperture used for photometry. From top to bottom: faintest S24 bin at 70 $\mu $m; brightest S24 bin at 70 $\mu $m; faintest S24 bin at 160 $\mu $m; brightest S24 bin at 160 $\mu $m.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{4446f07.ps} \end{figure} Figure 7: Top: confidence Level of the detections at 70 (dash) and 160 $\mu $m (solid) on stacked images (Figs. 4 and 5), as a function of the S24 bin. Middle: Signal-to-Noise ratio, as computed from a Gaussian fit to the flux distribution measured on about 2000 positions; this S/N is not relevant at low flux (see Sect. 3.2). Bottom: average flux in mJy per stacked source. Note that a different number of sources have been stacked in each bin.
Open with DEXTER

   
3.2 Stacked images and photometry

The final stacked images at 24, 70 and 160 $\mu $m as a function of the 24 $\mu $m flux density S24 are presented in Figs. 3-5, respectively. We report also in these figures the number of sources stacked in each of the S24 bins. The figures show clear detections of stacked sources at 70 and 160 $\mu $m for every S24 bin, even the faintest corresponding to $60 \le S_{24} < 69 ~\mu $Jy. Given the surface density of the 24 $\mu $m sources at 60 $\mu $Jy of $(9.6 \pm 0.04) \times 10^7$ sr-1(Papovich et al. 2004), this translates to 1.04 and 0.2 beams per source at respectively 70 and 160 $\mu $m (Dole et al. 2003, using beams from their Table 1). This is well beyond the confusion limits at these FIR wavelengths (Dole et al. 2004b). This statistical detection of FIR sources already demonstrates the great potential of this technique to probe FIR galaxies down to levels below the confusion, thanks to the excellent quality of the pointing and the stability of the effective PSF (see below).

We check that the radial profile of the stacked sources is in agreement with the PSF profile, at each wavelength and for each flux bin. We show in Fig. 6 two profiles at each wavelength corresponding to the extreme cases: the brightest and faintest S24 flux bins. We used both the empirical PSF (from bright sources) and the modeled STinyTim MIPS PSF (Rieke et al. 2004; Gordon et al. 2005; Krist 1993). At large S24, the stacked radial profiles at 70 and 160 $\mu $m (bottom plots in Fig. 6) agree well with the PSF in the central part. At the faintest fluxes (top plots), the agreement is good down to about 10% of the peak brightness. Since the stacked images visually represent the 2-dimensional correlation function of galaxies, the potential presence of many neighboring sources at small scales (source clustering) might have widened the radial profile, which is not observed; thus source clustering does not contribute significantly to the noise budget.

We measure the flux density of the stacked sources with aperture photometry and correct for aperture size. The radii of the apertures and reference annulus are, in arcseconds: ( $r_{\rm aper}$, $r_{\rm int}$, $r_{\rm ext}$) = (12.2, 17, 24), (30, 49, 79) and (54, 90, 126) for 24, 70 and 160 $\mu $m, respectively. These radii correspond to approximatively 3, 5 and 7 times the FWHM in the FIR and 2, 3, 4 times the FWHM in the MIR. We measured the noise in each image by using about 2000 measurements on random positions. We compute the confidence level (C.L.) of each detection (top of Fig. 7) using the cumulative distribution of the noise measurements. The deviation from 100% of the C.L. is the probability that the noise creates a spurious source. For the faintest bin, the C.L. is around 80%, and it rises to 97% for the next four bins, and stays at 100% for the brighter S24 bins. We fitted a Gaussian function to the distribution of noise to get the standard deviation in order to estimate the S/N ratio. This method works for the brighter bins (middle panel in Fig. 7), where the flux distribution is indeed nearly a Gaussian distribution. In this range, the S/N values have a median of 8 at 70 $\mu $m and 7 at 160 $\mu $m. In the three faintest bins, the noise distribution is not Gaussian, because of the presence of slightly brighter sources; the Gaussian fit is therefore not relevant and we opt for the C.L. technique. The bottom plot in Fig. 7 shows the average FIR flux per stacked galaxy. A set of $\sim$100 $\mu $Jy MIR-selected galaxies would have a typical average FIR flux of $\sim$0.5 and 3 mJy if taken individually at 70 and 160 $\mu $m, respectively. Since the confusion limits are at about 3 and 40 mJy at these wavelengths (Dole et al. 2004b), the gain of the stacking analysis technique is one order of magnitude in flux compared to individual detection. Finally, it is not necessary to remove the brightest sources for the goals of this paper, because we stack typically 1000 to 2000 galaxies per flux bin, so their influence is negligible except maybe in the 3 faintest bins.


  \begin{figure} \par\includegraphics[width=7.9cm,clip]{4446f08.ps}\end{figure} Figure 8: Contributions to the CIB: brightness of stacked sources at 160 and 70 $\mu $m per logarithmic bin $\frac{{\rm d}B_{\lambda}}{{\rm d}\log(S_{24})}$ (solid symbols), as a function of the 24 $\mu $m flux, in all three MIPS GTO Fields. A completeness correction has been applied. The highest flux bin goes up to 1 Jy. Open symbols: published differential source counts multiplied by S24-0.5 and a color ratio of bright galaxies (160/24 = 60 and 70/24 = 20, cf. the brightest bin in the lower panel of Fig. 7); Square: Dole et al. (2004a); Circle: Frayer et al. (2006). There is a good agreement between the source counts, the brightest stacked bin, and the fainter stacked bins.
Open with DEXTER

The brightness of the stacked sources at 70 and 160 per logarithmic flux density bin, or $\frac{{\rm d}B_{\lambda}}{{\rm d}\log(S)}$, as a function of the 24 $\mu $m flux bin, is presented in Fig. 8. $B_{\lambda}$ in MJy/sr is defined as the total stacked flux density divided by the survey area. Using a logarithmic flux density bin allows direct comparison of the contribution in energy of each bin to the CIB, and is directly related to the differential source counts with a scaling factor $S_{\nu}^{-0.5}$. In the range $100 \le S_{24} \le 300 ~ \mu$Jy, both contributions to the CIB present a maximum, which shows that the contributions have reached convergence. Converting S70 and S160 into S24 using the color ratios of 9 and 30 (see Table 2 below), this means the FIR CIB will be mainly resolved at $S_{70} \sim 0.1 \times 9 = 0.9$ mJy and at $S_{160} \sim 0.1 \times 30 = 3$ mJy. We have also plotted the source counts of Dole et al. (2004a) and Frayer et al. (2006); we used the conversion to S24 as given by color ratios relevant for bright galaxies of 20 and 60 at 70 and 160 $\mu $m, measured on the very bright end of the bottom plot in Fig. 7. Despite this simplifying assumption of a single color ratio, there is excellent agreement between the brightness derived from the stacking analysis and the source counts. This plot can be used to constrain models of galaxy evolution.

Sample variance plays a role in these results. To probe its effects, we split each of our three fields (CDFS, HDFN, LH) into four subfields of about 250 square arcmin each, and performed an independent analysis on each of these twelve subfields. We obtain contributions varying in some cases by as much as a factor of two (peak-to-peak). For instance, computing the standard deviation of the distribution of the cumulative 160 $\mu $m flux (the faintest points in Fig. 10) measured over these 12 subfields gives $\sigma=0.3$ MJy/sr and a mean and median both of 0.53 MJy/sr. Renormalizing by the twelve sub-fields gives $\sigma=0.09$: the uncertainty induced by the Large Scale Structure variations across the fields is of order 15%.

From here on in this paper, our error budget takes into account: 1) the calibration uncertainties; 2) the photometric uncertainty; 3) the large-scale structure (sample variance).

   
4 Contributions of mid-infrared galaxies to the cosmic infrared background

   
4.1 Value of the cosmic infrared background brightness

To compute the fraction of background resolved with the stacking analysis of the MIPS data, we first need to review the measurements of the total CIB, in particular at 24, 70 and 160 $\mu $m. It should be remembered that the total cosmic background contains the contribution of all extragalactic sources but also more diffuse emissions, e.g. from dust in galaxy clusters (Montier & Giard 2005). Furthermore the extragalactic sources are expected to be mostly galaxies but it cannot be excluded that other lower luminosity sources, population III stars for instance, contribute significantly but will not be detected directly in the present deep surveys.

Measuring the CIB directly by photometry is particularly difficult because one needs 1) an absolute photometer and 2) a proper estimate of the foreground. The two FIR channels of MIPS are not absolute photometers for the very extended spatial scales, since no internal calibrated reference can be observed to calibrate absolutely the slow response. A better knowledge of the instrument in the future may allow a proper absolute calibration, using its "Total Power'' mode, similarly to what has been done successfully in the past, e.g. with ISOPHOT at 170 $\mu $m on some selected low surface brightness fields (Lagache & Dole 2001). However, MIPS is by design well calibrated for small spatial scales, e.g., point sources, because the frequent stimulator flashes and the scanning strategy (acting like a chopping mode) properly track the fast response of the photoconductors (Gordon et al. 2005,2006, for instance). For these reasons, we do not use MIPS as an absolute photometer to estimate the level of the CIB and the foregrounds, but as a detector of small scale fluctuations to resolve the CIB based on 24 $\mu $m source observations. Our approach has the important advantage that it is not biased by the foregrounds and their modeling, which can lead to significant errors.

We therefore start by reviewing the direct measurements, using absolute photometry in large beams, provided mainly by the COBE FIRAS and DIRBE experiments and also the IRTS and rocket experiments in the near infrared (${<} 3~\mu$m). These measurements can be combined with indirect upper limits derived from observations of gamma rays from distant Blazars at TeV energies.

To use the FIRAS and DIRBE data to provide CIB absolute measurements requires an accurate component separation. Local extended emission from interplanetary and interstellar dust can be removed using their specific SEDs and anisotropic spatial distributions traced independently, as well as time variability for the zodiacal emission and scattering (Hauser & Dwek 2001, for instance). Early gamma ray data from Blazars from the CAT experiment led to upper limits on the CIB intensity significantly lower than the DIRBE residuals as pointed out by Renault et al. (2001) and Wright (2004). Recent results on more distant Blazars (Aharonian et al. 2005; Schroedter 2005) constrain the CIB even more in the near and thermal infrared. Together with lower limits obtained by integrating the galaxy counts from HST, ISO, and Spitzer, these measurements tightly constrain the Extragalactic Background Light between $\sim$0.8 to ${\sim} 20~\mu$m.

At 160 $\mu $m, the CIB can be interpolated from the DIRBE/COBE measurements at 100 $\mu $m (Lagache et al. 2000) and 140 and 240 $\mu $m (Hauser et al. 1998): $0.78\pm0.21$, $1.17\pm0.32$, $1.09\pm0.20$ MJy/sr, respectively. If the FIRAS photometric scale is used in the calibration (rather than the DIRBE photometric calibration), lower values are obtained at 140 and 240 $\mu $m: 0.7 MJy/sr and 1.02 MJy/sr (Hauser et al. 1998). A large uncertainty in the determinations at 100 and 140 $\mu $m comes from the zodiacal emission removal, as is also true at 60 $\mu $m. The DIRBE zodiacal emission model was obtained by Kelsall et al. (1998) relying on the variability with viewing geometry. Its accuracy can be estimated a posteriori using the residuals observed at wavelengths where the zodiacal emission is at a maximum (12 and 25 $\mu $m). The residual emission, obtained by Hauser et al. (1998), has in fact a spectrum very similar to the zodiacal one. The residuals are about $4.7 \times 10^{-7}$ Wm-2 sr-1 at 12 and 25 $\mu $m, far above the upper limit derived by high-energy experiments like HESS (Aharonian et al. 2005), but not very much larger than the uncertainties of the Kelsall et al. (1998) zodiacal emission model. A conservative estimate of the amount of zodiacal emission not removed in this model at 12 and 25 $\mu $m is therefore about $4 \times 10^{-7}$ Wm-2 sr-1. Using the Kelsall et al. (1998) smooth high latitude zodiacal cloud colors, the amount not removed at 100, 140 and 240 $\mu $m translates to 0.30, 0.14, 0.045 MJy/sr, respectively. This reduces the CIB from 0.78 to 0.48 MJy/sr at 100 $\mu $m, from 1.17 to 1.03 at 140 $\mu $m and from 1.09 to 1.05 at 240 $\mu $m. Adopting the FIRAS photometric scale gives at 140 and 240 $\mu $m, 0.56 and 0.98 MJy/sr respectively. From the above discussion, we see that the CIB at 140  $\mu $m - the closest in wavelength to the 160 $\mu $m MIPS bandpass - is still uncertain by a factor of about 2 because of the uncertainty in the zodiacal level. The DIRBE/FIRAS measurement of the CIB at 240 $\mu $m suffers less from zodiacal residuals and photometric calibration uncertainty.


  \begin{figure} \par\includegraphics[width=14.4cm,clip]{4446f09.ps} \end{figure} Figure 9: Current measurements of the Extragalactic Background Light Spectral Energy Distribution from 0.1 $\mu $m to 1 mm, showing the Cosmic Optical Background (COB, with $\lambda \le 8~\mu$m) and the Cosmic Infrared Background (CIB, with $\lambda > 8~\mu$m). Black arrows represent lower limits. Purple arrows and lines represent upper limits. The EBL observational constraints come from: Edelstein et al. (2000) at 0.1 $\mu $m using Voyager UVS; Brown et al. (2000) and Gardner et al. (2000) with HST/STIS (lower limits); Madau & Pozzetti (2000) with HST (incl. NICMOS) and Thompson (2003); Bernstein et al. (2002) corrected by Mattila (2003) (filled circles); Matsumoto et al. (2005) between 2.2 and 4 $\mu $m using the IRTS (thin plus); Gorjian et al. (2000) at 2.2 and 3.3 $\mu $m using DIRBE and Lick; Wright (2001) and Cambresy et al. (2001) at 1.25 and 2.2 $\mu $m using DIRBE and 2MASS (five branch star); DIRBE values from Wright (2004) from 1.25 to 240 $\mu $m (gray circles); Spitzer IRAC 3.6, 4.5, 5.8 and 8.0 $\mu $m lower limits from number counts by Fazio et al. (2004); fluctuation analysis with IRAC by Savage & Oliver (2005) (open triangles); Schroedter (2005) using Very High Energy Blazars, 98% confidence upper limit (gray region); HESS upper limit from Aharonian et al. (2005) using P0.55 (solid line between 0.8 and 4 $\mu $m); Renault et al. (2001) upper limits from 5 to 15 $\mu $m using the CAT in the $\gamma $-rays on Mkn501; Elbaz et al. (1999) lower limit at 15 $\mu $m using galaxy counts with ISOCAM; upper limit at 20 $\mu $m by Stecker & De Jager (1997) on Mkn421; lower limit from galaxy counts at 24 $\mu $m with MIPS by Papovich et al. (2004); an indirect evaluation at 60 $\mu $m using fluctuations in IRAS data from Miville-Deschênes et al. (2002) (open gray square); lower limits at 70 and 160 $\mu $m using galaxy counts with MIPS by Dole et al. (2004a); an estimate of the CIB at 100 $\mu $m using CAT and DIRBE Renault et al. (2001) (four branch star); Lagache et al. (2000) at 100, 140 and 240 $\mu $m using DIRBE and WHAM, updated in the present work (diamond); Hauser et al. (1998) at 140 and 240 $\mu $m using DIRBE (open square); Smail et al. (2002) lower limit at 850 $\mu $m using galaxy counts with SCUBA; Lagache et al. (2000) spectrum between 200 $\mu $m and 1.2mm using FIRAS (solid line above 200 $\mu $m). The IDL script to generate this figure is available on the web: http://www.ias.u-psud.fr/irgalaxies.
Open with DEXTER

A firm upper limit of 0.3 MJy/sr at 60 $\mu $m has been derived by Dwek & Krennrich (2005) using observations of TeV gamma ray emission from distant AGNs. Miville-Deschênes et al. (2002) uses a fluctuation analysis of IRAS maps to set an upper limit of 0.27 MJy/sr and give an estimate of 0.18 MJy/sr, on the assumption that the level of fluctuations-to-total intensity ratio is not strongly wavelength dependent.

At 24 $\mu $m we use for the contribution of IR galaxies to the CIB the estimate of Papovich et al. (2004) of 2.7+1.1-0.7 nW m-2 sr-1. This value comes from 1) integration of the source counts down to 60 $\mu $Jy giving $1.9 \pm 0.6$ nW m-2 sr-1; 2) extrapolation of the source counts to lower fluxes, giving a contribution of 0.8+0.9-0.4 nW m-2 sr-1; and 3) upper limits from Stecker & De Jager (1997) and from CAT (Renault et al. 2001).

The most constraining measurements and lower and upper limits on the Cosmic Optical Background (COB) and the CIB from 0.1 $\mu $m to 1 mm are all reported in Fig. 9. The Lagache et al. (2004) model predicts a CIB at 240 $\mu $m of 0.98 MJy/sr, which is in very good agreement with the estimate from combined measurements discussed above. Furthermore this model agrees with the observational constraints (e.g. number counts, CIB intensity and fluctuations). We can thus take the CIB values from this model as a reasonable interpolation between the better constrained CIB values at shorter and longer wavelengths: 0.82 MJy/sr at 160 $\mu $m, and 0.15 MJy/sr at 70 $\mu $m.

   
4.2 Contributions from MIR sources with $S_{24} \ge 60~\mu$Jy

To estimate the contribution of MIR sources to the background, we add up the brightnesses of all the S24 bins to get the integrated light at 24, 70 and 160 of all the resolved 24 $\mu $m sources. Each S24 bin is corrected for incompleteness. The results are presented Table 1, and Fig. 10 shows the cumulative integrated light from galaxies in the FIR as a function of S24. For a sanity check, we obtain that at 24 microns the percentage of the CIB that is resolved is 79%, which is in agreement with Papovich et al. (2004) within the error bars. At 70 and 160 micron we resolve 92% and 69% of the background, respectively.

Half of the 24 $\mu $m CIB is resolved by sources with $S_{24} \ge 190~ \mu$Jy. In the FIR, half of the 70 $\mu $m CIB is resolved by 24 $\mu $m sources brighter than $S_{24} \sim 220~\mu$Jy, and half of the 160 $\mu $m CIB is resolved by 24 $\mu $m sources brighter than $S_{24} \sim 130~\mu$Jy. This difference between 70 and 160 suggests that the CIB at 160 $\mu $m is dominated by galaxies at slightly higher redshift than at 70 $\mu $m, a consequence of the spectral shape of LIRGs and ULIRGs or, equivalently, the effect of k-correction. This point is illustrated in Figs. 5 and 6 of the review by Lagache et al. (2005).

To put in perspective the problem of resolving the CIB and what the stacking analysis accomplishes, we plot in Fig. 11 the new observed constraints on the extragalactic background SED. The fraction of the CIB resolved at MIPS wavelengths by unbiased surveys was 79%, 20% and 7% at respectively 24, 70 and 160 $\mu $m (Papovich et al. 2004; Dole et al. 2004a). When using the present stacking analysis, this fraction rises to 92% and 69% at 70 and 160 $\mu $m respectively, and is represented by the red lower limits (see also Table 1).

Based purely on observations without modeling of galaxy SEDs, we find that most of the FIR background is resolved into MIR galaxies. This confirms the model-dependent result of Elbaz et al. (2002). This analysis is the first direct resolution of the CIB simultaneously in the MIR and the FIR.

Table 1: Contribution to the CIB of $S_{24} \ge 60~\mu$Jy galaxies. Sources of uncertainty come from photometry, calibration, and large scale structure. The CIB column gives the best estimate from the discussion in Sect. 4.1.

Table 2: Mean observed colors in $I_{\nu }$ of $S_{24} \ge 60~\mu$Jy galaxies contributing to the CIB.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{4446f10.ps} \end{figure} Figure 10: Cumulative brightness ( left axis, in MJy/sr) and fraction of the background resolved ( right axis) at 160, 70 and 24 $\mu $m ( from top to bottom), as a function of the 24 $\mu $m flux in the three combined MIPS GTO Fields. A completeness correction has been applied based on the incompleteness level of the 24 $\mu $m sample. The horizontal dashed line represents 50% of the CIB at each wavelength.
Open with DEXTER

Moreover, we can now securely establish the physical parameters of the typical galaxies responsible for most of the CIB near its peak. Previous studies based on ISO already characterized the 15 $\mu $m population (Flores et al. 1999; Franceschini et al. 2003; Elbaz & Cesarsky 2003, for instance); see Lagache et al. (2005) for a review. Our 24 $\mu $m sample is almost complete in flux (80% completeness down to $S_{24} = 80~ \mu$Jy and 50% at $60~\mu$Jy), and the physical properties of $S_{24} \ge 80~ \mu$Jy galaxies have been extensively studied (Le Floc'h et al. 2004; Pérez-González et al. 2005; Caputi et al. 2006; Le Floc'h et al. 2005). These works, mainly targeting the CDFS field, show that 25-30% of the 24 $\mu $m galaxies lie at redshifts $z \ge 1.5$, and that the redshift distribution peaks around $z \sim 1$ (between 0.7 and 1.1). Assuming the CDFS is a representative field, the MIR and FIR CIB is thus mainly composed of galaxies with typical redshifts of unity, with a contribution from z >1.5 galaxies. At these redshifts, the galaxies are mostly LIRGs with typical bolometric luminosities of about $3 \times 10^{11}~ L_{\odot}$ (between 1011 and $10^{12} ~ L_{\odot}$) forming about $50~ M_{\odot} ~\rm yr^{-1}$ (20-130). They have intermediate stellar masses of about 1010 to $10^{11} ~ M_{\odot}$ (Pérez-González et al. 2005; Caputi et al. 2006). From this latter work we can also estimate the specific star formation rates of these galaxies to be between 0.1 and 1 Gyr-1.

   
4.3 Mean colors of the galaxies contributing to the CIB

Looking at the 24 $\mu $m number counts of Papovich et al. (2004), one can see that the bulk of 24 $\mu $m CIB is mainly due to sources with $130 \le S_{24} \le 400~\mu$Jy. We select three cuts in S24 to investigate the colors of the contributions to the CIB by different galaxy populations. In the following, redshifts come from Caputi et al. (2006) (see their Fig. 5), and the relative contributions come from the integration of the Papovich et al. (2004) source counts and the Lagache et al. (2004) model. The cuts are:

$\bullet$
Above 400 $\mu $Jy: bright galaxies contributing about 25% to the 24 $\mu $m CIB. The redshift distribution has a mean of 0.53 and a median of 0.44.
$\bullet$
$130 \le S_{24} \le 400~\mu$Jy: galaxies contributing the most to the 24 $\mu $m CIB, about 30%. The redshift distribution has a mean of 1.18 and a median of 1.03.
$\bullet$
$60 \le S_{24} \le 130~\mu$Jy: fainter galaxies with relatively low contributions to the 24 $\mu $m CIB (about 15%). The redshift distribution has a mean of 1.27 and a median of 1.11. The sample becomes incomplete at $60 \le S_{24} \le 80~\mu$Jy, so the mean redshift may be underestimated.
The observed colors change systematically with S24, as can be seen in the bottom of Fig. 7: S70 vs. S24 shows a slope larger than one, when S160 vs. S24shows an average slope of the order of unity. Table 2 gives the colors and their associated $1\sigma$ uncertainties in the three bins. The 160/24 color is compatible with a constant of 33. The 70/24 color increases with the flux from 6.3 to 9.6. Finally, the 160/70 color steadily decreases with flux.

These colors can be interpreted as the SED of a LIRG being redshifted, since fainter 24 $\mu $m sources lie at larger redshifts: the 160/70 ratio increases (with decreasing flux) because the peak of the big grains' FIR spectrum is shifted longwards of 160 $\mu $m. The color ratios involving the 24 $\mu $m band are less obvious to interpret, since the Polycyclic Aromatic Hydrocarbon (PAH) (Puget & Leger 1989) features (especially between 6.2 and 8.6 $\mu $m) and the silicate absorption feature are redshifted into and then out of this band. The 70/24 ratio evolution might have for its origin a mix of PAH (increasing the 24) and very small grains continuum (decreasing the 70) being redshifted, that cancel out each other.

If one wants to extrapolate the contribution of fainter ( $S_{24} \le 60~\mu$Jy) MIR galaxies to the FIR CIB, a conservative approach is to use a constant 160/24 and 70/24 color ratio for the unresolved population. To set these ratios, we take the colors from the faintest population ( $60 \le S_{24} \le 130~\mu$Jy); this faint population presumably has the closest characteristics to the unresolved one. We will therefore use $I_{160}/I_{24} = 32.7 \pm 6.8$, and $I_{70}/I_{24} = 6.3 \pm 1.1$ (from Table 2). Since the contribution to the CIB of these faint galaxies is modest (30% at most), the large uncertainties in these color ratios will not dominate the total background estimate.

   
5 New estimates of the cosmic far-infrared background

5.1 New lower limits at 70 and 160 $\mu $m

The present stacking analysis performed on detected galaxies $S_{24} \ge 60~\mu$Jy gives strong measured lower limits to the CIB due to galaxies at 70 and 160 $\mu $m, without requiring any modeling. To determine upper limits to the FIR CIB requires a different approach. There are many difficulties at 70 $\mu $m in extracting an accurate value of the CIB, mostly due to the problems in the removal of the zodiacal component (Renault et al. 2001; Finkbeiner et al. 2000, for instance). At 160 $\mu $m the CIB estimate is more robust, but still with a significant uncertainty (factor of $\sim$3, see Sect. 4.1).

Another way to get a good estimate of the FIR galaxy CIB brightness is to estimate the unresolved 24 $\mu $m background fraction, use the 160/24 and 70/24 colors measured for the weakest sources, and then apply these colors to the unresolved part to get the 70 and 160 $\mu $m background estimates. Thus, we extrapolate the colors of galaxies with $S_{24} \le 60~\mu$Jy using the colors of the $60 \le S_{24} \le 130~\mu$Jy galaxies derived in the previous section. To estimate the unresolved 24 $\mu $m background, Papovich et al. (2004) used a simple extrapolation of the differential number counts. Since the slope of the counts below 100 $\mu $Jy is strongly decreasing ( $-1.5 \pm 0.1$ in ${\rm d}N/{\rm d}S$), the integral is dominated by the largest fluxes S24. The estimate is robust, unless a hypothetical faint population exists. The remaining unresolved 24 $\mu $m background created by $S_{24} < 60~\mu$Jy sources is therefore 0.54 $\rm nW~ m^{-2}~ sr^{-1}$, (to be compared to 2.16  $\rm nW~ m^{-2}~ sr^{-1}$ for $S_{24}>60~\mu$Jy sources).


  \begin{figure} \par\includegraphics[width=14.4cm,clip]{4446f11.ps} \end{figure} Figure 11: Extragalactic background light spectral energy distribution from 0.1 $\mu $m to 1 mm, with new constraints from MIPS. The lowest lower limits (red) represent the fraction of the CIB resolved at 70 and 160 $\mu $m using the stacking analysis for sources with $S_{24} \ge 60~\mu$Jy. The large (blue) square represents the contribution of all the unresolved 24 $\mu $m sources (extrapolation from number counts), and the highest lower limits arrows (blue) represent the contribution of all 24 $\mu $m sources to the FIR background, using a simple color extrapolation for 70 and 160 $\mu $m (Sect. 5). See Fig. 9 for the other symbols.
Open with DEXTER

We derive the extrapolated FIR CIB level due to IR galaxies using:

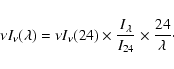\begin{displaymath}\nu I_{\nu}(\lambda) = \nu I_{\nu}(24) \times \frac{I_{\lambda}}{I_{24}} \times \frac{24}{\lambda}\cdot \end{displaymath} (2)

The results of the extrapolation are presented in Table 3. We obtain $7.1 \pm 1.0$ and $ 13.4 \pm 1.7~\rm nW~ m^{-2}~ sr^{-1}$, at 70 and 160 $\mu $m respectively. Our new estimate, based on the integration of all the 24 $\mu $m IR galaxies, is in principle a lower limit because it does not account for any diffuse emission unrelated to the IR galaxies, nor for a small fraction of IR galaxies that might have been missed. Indeed, the extrapolation in color of the unresolved 24 $\mu $m population accounts for the faint-end of the luminosity function, but not for the hypothetical very high-redshift sources, or faint local galaxies with high FIR output, like a hypothetical population of elliptical galaxies with large 160/24 colors. However, if this population exists, its contribution to the FIR background is constrained by the upper limits to be less than $\sim$20%.

Our estimate at 70 $\mu $m is higher than the Lagache et al. (2004) model estimate by 11%, and lower by about 13% at 160 $\mu $m. About 25% of the CIB brightness at 70 and 160 $\mu $m comes from faint MIR sources ( $S_{24} \le 60~\mu$Jy). Assuming our new FIR CIB values represent the actual CIB values, we estimate that our stacking analysis of $S_{24} \ge 60~\mu$Jy galaxies finally resolves 80% of the background at 70 and 160 $\mu $m. We also show that the population dominating the CIB is made of galaxies seen at 24 $\mu $m and their simplest extrapolation to lower fluxes.

5.2 Spectral energy distribution of the extragalactic background

In the near and mid-IR, upper and lower limits tightly constrain the EBL SED: 1) with HST+Spitzer and HESS between 0.8 and 4 $\mu $m, and 2) with ISO, Spitzer and CAT between 5 and 24 $\mu $m. In this range, the EBL SED is constrained to better than 50% (and to the 20% level in several wavelength ranges). The EBL is now also well constrained in the FIR; direct measurements of the diffuse emission and our new lower limits constrain the CIB SED to the 50% level.

The permitted zone for the EBL SED is presented in Fig. 12. This zone is defined as the area between current upper and lower limits. In this zone, the COB brightness ranges from 19.5 to 35.5 nW m-2 sr-1, and the CIB from 24 to 27.5 nW m-2 sr-1. The ratio COB/CIB thus ranges from 0.7 to 1.5.

Table 3: Contributions of the 24$~\mu$m galaxies to the FIR CIB in nW m-2 sr-1. For the $S_{24} \le 60~\mu$Jy galaxies, a simple color extrapolation has been used, as described in Sect. 5.

From these constraints, we may derive a conservative estimate of the EBL SED, that typically lies between the upper and lower limits and that makes use of well known physical processes. The CIB estimate, based on the Lagache et al. (2004) model, agrees with the data and is strongly constrained in the MIR and the 240-400 $\mu $m range. It strongly decreases with increasing frequency below 8 $\mu $m because of the main PAH features at 6.2 to 8.6 $\mu $m being redshifted. The COB estimate also decreases with increasing wavelength above 2 $\mu $m because of the old stellar population SED. This simple SED behavior is in agreement with the model of Primack et al. (1999). Our reasonable guess is that the COB and CIB have equal contributions around 8 $\mu $m.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{4446f12.ps} \end{figure} Figure 12: Cosmic Optical Background and Cosmic Infrared Background due to galaxies permitted zone estimate (shaded area), using upper and lower values. See Fig. 9 for the other symbols.
Open with DEXTER

Figure 13 shows our smooth EBL SED estimate (thick line), as well as our best estimate of the COB (blue shaded) and the CIB (red shaded). The overlap region where both COB and CIB contribute significantly and the resulting total EBL is shown as the gray-shaded area around 8 $\mu $m. We find that the brightness of the COB is 23 nW m-2 sr-1, and 24 nW m-2 sr-1 for the CIB. The ratio between the COB and CIB is thus of the order of unity for this EBL SED.

Our results are in contradiction with Wright (2004) who finds a COB/CIB ratio of 1.7, and values at least 50% higher than ours: 59 nW m-2 sr-1 (COB) and 34 nW m-2 sr-1 (CIB). However, the Wright (2004) estimate came before the strong upper limits of HESS (Aharonian et al. 2005) below 4 $\mu $m. This limit puts the COB much closer to the integrated light from galaxy counts than to the diffuse measurements. From the galaxy counts and stacking analysis (lower limits), and high-energy experiments (upper limits), the EBL is now very well constrained. In particular, we can now securely state that the contributions to the EBL of faint diffuse emissions outside identified galaxy populations - too weak to be detected in current surveys, like population III stars relic emission, galaxy clusters, hypothetical faint IR galaxy populations - can represent only a small fraction of the integrated energy output in the universe.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{4446f13.ps} \end{figure} Figure 13: Our best Cosmic Optical Background (blue-shaded, left) and Cosmic Infrared Background (red-shaded, right) estimates. The gray-shaded area represents the region of overlap. See Fig. 9 for the other symbols.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{4446f14.ps} \end{figure} Figure 14: Schematic Spectral Energy Distributions of the most important (by intensity) backgrounds in the universe, and their approximate brightness in nW m-2 sr-1 written in the boxes. From right to left: the Cosmic Microwave Background (CMB), the Cosmic Infrared Background (CIB) and the Cosmic Optical Background (COB).
Open with DEXTER

5.3 The extragalactic background vs. the cosmic microwave background

It is interesting to update the contributions of the most intensive electromagnetic backgrounds in the universe, as has been done for instance by Scott (2000) or Wright (2004), and we schematically represent these in Fig. 14. Obviously, the Cosmic Microwave Background (CMB) dominates the universe's SED, and accounts for about 960 nW m-2 sr-1. We showed that the CIB and COB each account for 23 and 24 nW m-2 sr-1, respectively. With a total of 47 nW m-2 sr-1 in the optical and the Far-Infrared, the EBL represents about 5% of the brightness of the CMB. Taking into account the complete SED of the EBL will not change this picture, since the contributions to the total EBL brightness of the radio, UV, X-ray (Hasinger et al. 2001; Mushotzky et al. 2000) and $\gamma $ ray (Strong et al. 2004) extragalactic backgrounds are smaller by one to three orders of magnitude than the COB and CIB (Scott 2000).

The galaxy formation and evolution processes provide 5% in brightness of the electromagnetic content of the Universe. Half of the energy comes in the form of starlight (COB) and half as dust-reprocessed starlight (CIB). The maximum of the power distribution is at ${\sim} 1.3~\mu$m for the COB and ${\sim} 150~\mu$m for the CIB (Fig. 14). There are therefore on average 115 infrared photons for 1 visible photon emitted in these processes.

   
6 Conclusions

Our key points and results for the resolution and characterization of the FIR CIB and the EBL are:

$\bullet$
A stacking analysis in three fields covering 0.85 square degrees including a sample of 19 181 MIPS 24 $\mu $m sources with $S_{24} \ge 60~\mu$Jy lets us probe faint 70 and 160 $\mu $m galaxies one order of magnitude below the confusion level and with a high signal-to-noise ratio. We take into account in our noise budget uncertainties coming from: photometry, calibration systematics, and large-scale structure.
$\bullet$
24 $\mu $m galaxies down to $S_{24} = 60 ~ \mu$Jy contribute 79%, 92%, 69% of the CIB at respectively 24, 70 and 160 $\mu $m (using 2.7, 6.4 and 15.4 nW m-2 sr-1 as the total CIB values at 24, 70 and 160 $\mu $m, respectively). This is the first direct measurement of the contribution of MIR-selected galaxies to the FIR background.
$\bullet$
We derive the contributions to the CIB by flux density bin, and show good agreement between our stacking analysis and the published source counts. This is a strong constraint for models. Moreover, we show that the CIB will be mainly resolved at flux densities of about $S_{70} \sim 0.9$ mJy and $S_{160} \sim 3$ mJy at 70 and 160 $\mu $m, respectively.
$\bullet$
We directly measure that the total CIB, peaking near 150 $\mu $m, is largely resolved into MIR galaxies. Other works (Pérez-González et al. 2005; Caputi et al. 2006; Le Floc'h et al. 2005, especially) show that these MIPS 24 $\mu $m sources are ${\sim} 3 \times 10^{11} ~ L_{\odot}$ LIRGs distributed at redshifts $z \sim 1$, with stellar masses of about $3 \times 10^{10}$ to $3 \times 10^{11} ~ M_{\odot}$and specific star formation rates in the range 0.1 to 1 Gyr-1.
$\bullet$
Using constant color ratios 160/24 and 70/24 for MIR galaxies fainter than 60 $\mu $Jy, we derive new conservative lower limits to the CIB at 70 and 160 $\mu $m including the faint IR galaxies undetected at 24 $\mu $m: $7.1 \pm 1.0$ and $ 13.4 \pm 1.7$ nW m-2 sr-1, respectively. These new estimates agree within 13% with the Lagache et al. (2004) model.
$\bullet$
Using these new estimates for the 70 and 160 $\mu $m CIB, we show that our stacking analysis down to $S_{24} \ge 60~\mu$Jy resolves 80% of the 70 and 160 $\mu $m CIB.
$\bullet$
Upper limits from high-energy experiments and direct detections together with lower limits from galaxy counts and stacking analysis give strong constraints on the EBL SED.
$\bullet$
We estimate the Extragalactic Background Light (EBL) Spectral Energy Distribution (SED) permitted zone (between lower and upper limits), and measure the optical background (COB) to be in the range 19.5-35.5 nW m-2 sr-1, and the IR background (CIB) in the range 24 to 27.5 nW m-2 sr-1. The ratio COB/CIB thus lies between 0.7 and 1.5.
$\bullet$
We integrate our best estimate of the COB and the CIB, and obtain respectively 23 and 24 nW m-2 sr-1; We find a COB/CIB ratio close to unity.
$\bullet$
The galaxy formation and evolution processes have produced photons equivalent in brightness to 5% of the CMB, with equal amounts from direct starlight (COB) and from dust-reprocessed starlight (CIB). We compute that the EBL produces on average 115 infrared photons per visible photon.

Acknowledgements
This work is based on observations made with the Spitzer Observatory, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under NASA contract 1407. We thank the funding from the MIPS project, which is supported by NASA through the Jet Propulsion Laboratory, subcontract #1255094. This work also benefited from funding from the CNES (Centre National d'Etudes Spatiales) and the PNC (Programme National de Cosmologie). We thank Jim Cadien for the great help in the data processing. We thank Nabila Aghanim, Hervé Aussel, Noel Coron, Daniel Eisenstein, David Elbaz, Charles Engelbracht, Dave Frayer, Karl Gordon, Nicolas Ponthieu, Martin Schroedter, and Xianzhong Zheng for fruitful discussions.

References

 
Copyright ESO 2006