A&A 451, 515-538 (2006)
DOI: 10.1051/0004-6361:20054081
Outer structure of the Galactic warp and flare: explaining the Canis Major over-density
Y. Momany1,2 -
S. Zaggia3
-
G. Gilmore4
-
G. Piotto2
-
G. Carraro2,5 -
L. R. Bedin6 -
F. De Angeli4
1 - INAF- Oss. Astronomico di Padova, Vicolo
dell'Osservatorio 5, 35122 Padova,
Italy
2 - Dip. di Astronomia, Università di Padova, Vicolo
dell'Osservatorio 2, 35122 Padova, Italy
3 - INAF - Oss. Astronomico di Trieste, Via Tiepolo 11, 34131
Trieste, Italy
4 - Institute of Astronomy, University of Cambridge, Cambridge, CB3 OHA, UK
5 - Andes Fellow, Departamento de Astronomía, Universidad de Chile, Casilla 36-D,
Santiago, Chile Astronomy Department, Yale University, New Haven,
CT 06511, USA
6 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748
Garching b. München, Germany
Received 21 August 2005 / Accepted 28 February 2006
Abstract
Aims. In this paper we derive the structure of the Galactic stellar warp and flare.
Methods. We use 2MASS red clump and red giant stars, selected at mean and fixed heliocentric distances of
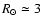 ,
7 and 17 kpc.
,
7 and 17 kpc.
Results. Our results can be summarized as follows: (i) a clear stellar warp signature is derived for the 3 selected rings, proving that the warp starts already within the solar circle; (ii) the derived stellar warp is consistent (both in amplitude and phase-angle) with that for the Galactic interstellar dust and neutral atomic hydrogen; (iii) the consistency and regularity of the stellar-gaseous warp is traced out to about
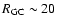 kpc; (iv) the Sun seems not to fall on the line of nodes. The stellar warp phase-angle orientation (
kpc; (iv) the Sun seems not to fall on the line of nodes. The stellar warp phase-angle orientation (
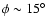 )
is close to the orientation angle of the Galactic bar and this, most importantly, produces an asymmetric warp for the inner
)
is close to the orientation angle of the Galactic bar and this, most importantly, produces an asymmetric warp for the inner
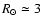 and 7 kpc rings; (v) a Northern/Southern warp symmetry is observed only for the ring at
and 7 kpc rings; (v) a Northern/Southern warp symmetry is observed only for the ring at
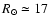 kpc, at which the dependency on
kpc, at which the dependency on 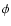 is weakened; (vi) treating a mixture of thin and thick disk stellar populations, we trace the variation with
is weakened; (vi) treating a mixture of thin and thick disk stellar populations, we trace the variation with
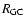 of the disk thickness (flaring) and derive an almost constant scale-height (
of the disk thickness (flaring) and derive an almost constant scale-height ( 0.65 kpc) within
0.65 kpc) within
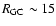 kpc. Further out, the disk flaring increase gradually reaching a mean scale-height of
kpc. Further out, the disk flaring increase gradually reaching a mean scale-height of  1.5 kpc at
1.5 kpc at
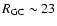 kpc; (vii) the derived outer disk warping and flaring provide further robust evidence that there is no disk radial truncation at
kpc; (vii) the derived outer disk warping and flaring provide further robust evidence that there is no disk radial truncation at
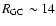 kpc.
kpc.
Conclusions. In the particular case of the Canis Major (CMa) over-density we confirm its coincidence with the Southern stellar maximum warp occurring near
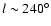 (for
(for
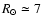 kpc) which brings down the Milky Way mid-plane by
kpc) which brings down the Milky Way mid-plane by 
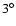 in this direction. The regularity and consistency of the stellar, gaseous and dust warp argues strongly against a recent merger scenario for Canis Major. We present evidence to conclude that all observed parameters (e.g. number density, radial velocities, proper motion etc) of CMa are consistent with it being a normal Milky Way outer-disk population, thereby leaving no justification for more complex interpretations of its origin. The present analysis or outer disk structure does not provide a conclusive test of the structure or origin of the Monoceros Ring. Nevertheless, we show that a warped flared Milky Way contributes significantly at the locations of the Monoceros Ring. Comparison of outer Milky Way H I and CO properties with those of other galaxies favors the suggestion that complex structures close to planar in outer disks are common, and are a natural aspect of warped and flaring disks.
in this direction. The regularity and consistency of the stellar, gaseous and dust warp argues strongly against a recent merger scenario for Canis Major. We present evidence to conclude that all observed parameters (e.g. number density, radial velocities, proper motion etc) of CMa are consistent with it being a normal Milky Way outer-disk population, thereby leaving no justification for more complex interpretations of its origin. The present analysis or outer disk structure does not provide a conclusive test of the structure or origin of the Monoceros Ring. Nevertheless, we show that a warped flared Milky Way contributes significantly at the locations of the Monoceros Ring. Comparison of outer Milky Way H I and CO properties with those of other galaxies favors the suggestion that complex structures close to planar in outer disks are common, and are a natural aspect of warped and flaring disks.
Key words: Galaxy: structure - Galaxy: formation - galaxies:
interactions - galaxies: individual: Canis Major
There was a revitalisation of interest in the outer disk of the
Milky Way with the photometric discovery of significant
over-densities of F stars in the Sloan Digital Sky Survey by Newberg
et al. (2002) towards the Galactic anti-center.
The reported over-densities defined a type of stellar Ring
structure, relatively confined to the Galactic plane
(
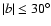 ), and stretching over the sky for
), and stretching over the sky for 
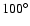 in longitude centered in Monoceros.
A kinematic and spectroscopic study of the Ring structure by
Yanny et al. (2003) confirmed (i) a Galactocentric distance
of 18 and 20 kpc (respectively above and below the Galactic plane);
(ii) an inconsistency of its velocity dispersion with typical Galactic
halo and thick disk structures; and (iii) a metallicity of
[Fe/H
in longitude centered in Monoceros.
A kinematic and spectroscopic study of the Ring structure by
Yanny et al. (2003) confirmed (i) a Galactocentric distance
of 18 and 20 kpc (respectively above and below the Galactic plane);
(ii) an inconsistency of its velocity dispersion with typical Galactic
halo and thick disk structures; and (iii) a metallicity of
[Fe/H
![$]\simeq-1.6$](/articles/aa/full/2006/20/aa4081-05/img50.gif) consistent with halo populations.
In the context of continuing searches for outer structure
related to the Sgr dwarf, and other possible accretion events the
most natural scenario proposed by Yanny etal for the Monoceros Ring
(Mon. Ring) was that it traced a remnant dwarf satellite galaxy in the
late process of disruption (if not already dissolved).
Accumulating evidence supporting the existence of the Mon. Ring
(Rocha-Pinto et al. 2003; Crane et al. 2003;
Frinchaboy et al. 2004) soon triggered a search for a progenitor, obviously carried out near the Galactic plane.
consistent with halo populations.
In the context of continuing searches for outer structure
related to the Sgr dwarf, and other possible accretion events the
most natural scenario proposed by Yanny etal for the Monoceros Ring
(Mon. Ring) was that it traced a remnant dwarf satellite galaxy in the
late process of disruption (if not already dissolved).
Accumulating evidence supporting the existence of the Mon. Ring
(Rocha-Pinto et al. 2003; Crane et al. 2003;
Frinchaboy et al. 2004) soon triggered a search for a progenitor, obviously carried out near the Galactic plane.
At the same time, in an alternative, more conservative
scenario, the existence of the Mon. Ring was seen as the
consequence of perturbations in the outer disk caused by ancient
warps (Ibata et al. 2003).
Indeed, the Mon. Ring rotates in a prograde orbit that is almost
circularized, strongly suggestive of a disk origin.
Nevertheless, simulations by Helmi (2003) showed that
accretion models, where co-planar streams can follow
circular orbits, were indeed feasible.
This encouraged a search for a progenitor of the Ring: if there is
one (the Sagittarius dwarf) why not another.
In an analysis of 2MASS data, Martin et al. (2004a)
assumed a symmetric Galactic vertical stellar distribution around
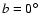 and searched for asymmetrical differences between
Northern and Southern star-counts.
Among other features, they pointed to an elliptical-shaped stellar
over-density centered at
and searched for asymmetrical differences between
Northern and Southern star-counts.
Among other features, they pointed to an elliptical-shaped stellar
over-density centered at
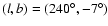 .
They
interpreted this over-density as the core of a satellite galaxy
currently undergoing in-plane accretion, namely the Canis Major (CMa)
dwarf spheroidal galaxy, the best Ring progenitor candidate.
.
They
interpreted this over-density as the core of a satellite galaxy
currently undergoing in-plane accretion, namely the Canis Major (CMa)
dwarf spheroidal galaxy, the best Ring progenitor candidate.
In Momany et al. (2004b), we highlighted the fact that in
the analyses in Martin et al. (2004a) and Bellazzini et al. (2004, first astro-ph version) the possible influence of
a Galactic stellar warp on the detection of a vertically asymmetric
distribution so close to the Galactic plane was not considered.
Observationally, the warp is a bending of the Galactic plane
upwards in the first and second Galactic longitude quadrants
(
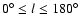 )
and downward in the third and fourth
quadrants (
)
and downward in the third and fourth
quadrants (
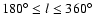 ).
We emphasise that the suggested reality of an outer stellar warp
was not a new proposal by us. Among other earlier studies, one of
particular relevance is that of Carney & Seitzer (1993)
who analysed the "Galaxy's own structure to obtain at
least a peak at the outer disk'', i.e. using certain lines of
sights, one can look away from the plane, reducing the foreground disk
signal as well as reddening-absorption-crowding and derive the age and
metallicity of the outer warped disk.
Analyzing the color-magnitude diagrams of fields very near to the CMa
center [
).
We emphasise that the suggested reality of an outer stellar warp
was not a new proposal by us. Among other earlier studies, one of
particular relevance is that of Carney & Seitzer (1993)
who analysed the "Galaxy's own structure to obtain at
least a peak at the outer disk'', i.e. using certain lines of
sights, one can look away from the plane, reducing the foreground disk
signal as well as reddening-absorption-crowding and derive the age and
metallicity of the outer warped disk.
Analyzing the color-magnitude diagrams of fields very near to the CMa
center [
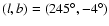 ]
Carney & Seitzer claimed to
have detected the main sequence and turnoff region of the outer
Galactic disk.
On the other hand, the analysis of Martin et al. (2004a) and
Bellazzini et al. (2004) discounted the Galactic warp
in this zone, so that the stellar populations previously
identified as outer disk main sequence, were now proposed as an
un-expected stellar population. Further hints of a
star-count anomaly at
]
Carney & Seitzer claimed to
have detected the main sequence and turnoff region of the outer
Galactic disk.
On the other hand, the analysis of Martin et al. (2004a) and
Bellazzini et al. (2004) discounted the Galactic warp
in this zone, so that the stellar populations previously
identified as outer disk main sequence, were now proposed as an
un-expected stellar population. Further hints of a
star-count anomaly at
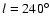 are found in Alard
(2000) who, again, associated the "strong asymmetry''
in this region with the Galactic stellar warp.
are found in Alard
(2000) who, again, associated the "strong asymmetry''
in this region with the Galactic stellar warp.
In Momany et al. (2004b) we concluded that the CMa
over-density can be fully accounted for if the Galactic disk (at
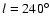 )
is
)
is 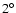 displaced/warped below the mid-plane;
i.e. the symmetry axis for this region is at
displaced/warped below the mid-plane;
i.e. the symmetry axis for this region is at
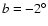 and not
and not
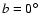 .
In response to our analysis, Martin et al. (2004b)
presented radial velocities and argued that the Galactic stellar warp
(location and amplitude), cannot explain the CMa over-density. In
particular, they argued that (i) a warp angle of
.
In response to our analysis, Martin et al. (2004b)
presented radial velocities and argued that the Galactic stellar warp
(location and amplitude), cannot explain the CMa over-density. In
particular, they argued that (i) a warp angle of
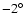 is not
enough to erase the CMa over-density; and (ii) the CMa over-density
is stronger in amplitude and located too far from the Southern
hemisphere warp at
is not
enough to erase the CMa over-density; and (ii) the CMa over-density
is stronger in amplitude and located too far from the Southern
hemisphere warp at
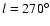 .
More recently, Rocha-Pinto et al. (2005) proposed that the
amplitude of the CMa over-density is small with respect to another
over-density, this time located in Argo (
.
More recently, Rocha-Pinto et al. (2005) proposed that the
amplitude of the CMa over-density is small with respect to another
over-density, this time located in Argo (
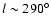 ). In this
later analysis, Rocha-Pinto et al. view the CMa over-density as the
consequence of a dust extinction window aligned with a maximum warp
location at
). In this
later analysis, Rocha-Pinto et al. view the CMa over-density as the
consequence of a dust extinction window aligned with a maximum warp
location at
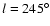 (as seen in López-Corredoira et al.
2002). Confusingly, Martin et al. (2004b) and
Bellazzini et al. (2006) use the same source (López-Corredoira et al. 2002) to argue that the maximum
warp location is at
(as seen in López-Corredoira et al.
2002). Confusingly, Martin et al. (2004b) and
Bellazzini et al. (2006) use the same source (López-Corredoira et al. 2002) to argue that the maximum
warp location is at
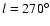 .
.
In order to clarify this situation, it is timely to re-evaluate the
detailed properties of the Galactic stellar warp, specifically the
location and amplitude of its maximum.
Most recently, Conn et al. (2005) presented a wide-field
survey of the Mon. Ring and emphasised that the presence of Ring
streams above and below the Galactic plane argue against a Galactic
origin of the Mon. Ring. Moreover, they suggested that positive
detections of the Mon. Ring below the plane may also be correlated
with the Triangulum-Andromeda (TriAnd) structure (Majewski et al.
2004; Rocha-Pinto et al. 2005). In this
scenario, although the Mon. Ring and TriAnd structure are located at
different distances, the TriAnd structure could be the distant arm of
a multiply-wrapped tidal stream.
In the main part of this paper we use 2MASS data to derive
and trace the signature of the Galactic stellar warp as a function of
Galactic longitude.
Our working hypothesis is simple: had the CMa over-density been due to
an extra-Galactic accretion, one would expect it to appear as a
distortion on top of a large-scale structure, that is the Galactic
stellar warp. As we shall demonstrate, CMa as an over-density is
easily accounted for as being the maximum Southern stellar warp. This,
in our opinion, allows Occam's Razor to indicate a clear preference
for a Galactic structural origin of the CMa over-density. We then
discuss evidence which we believe associates the Mon. stream with the
warped and flaring Galactic disk.
In several Appendices we briefly review and comment on important
aspects of the observational properties of CMa and the Mon Ring.
In Bellazzini et al. (2006) the authors commented on
how the different adopted parametrization of the warp may lead
to some confusion. Indeed, the warp has been derived from: (1) the mean
latitude of the adopted tracer as a function of longitude (Djorgovski
& Sosin 1989); (2) the ratio of star counts in Northern and
Southern hemispheres as a function of longitude (López-Corredoira
et al. 2002); and (3) the latitude of peak brightness as a
function of longitude (Freudenreich et al. 1994). There has
been some disagreement about these determinations. Bellazzini et al.
(2006) argued that the Momany et al. parametrization of the
warp was "not a fair description'' of the South/North
over-densities. In the following we will firstly expand on our method
of tracing the Galactic warp and then secondly we will compare our
results with those derived by other methods. This comparison show
excellent consistency.
In Momany et al. (2004b, Fig. 2) we extracted dereddened
2MASS M-giants (
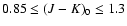 )
within an oblique box
surrounding the CMa red giant branch in the CMD, and falling in
a strip between
)
within an oblique box
surrounding the CMa red giant branch in the CMD, and falling in
a strip between
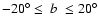 and
and
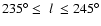 .
Initially assuming reflection symmetry around
.
Initially assuming reflection symmetry around
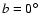 (warp angle
(warp angle
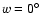 )
we performed Northern and Southern star
counts, binned in
)
we performed Northern and Southern star
counts, binned in
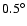 .
This showed clearly (upper panels of the same figure) that
by assuming a symmetry around
.
This showed clearly (upper panels of the same figure) that
by assuming a symmetry around
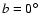 ,
as done in Martin
et al. (2004a), one can recover the identified (CMa)
over-density.
Successively the symmetry axis was varied within
the range
,
as done in Martin
et al. (2004a), one can recover the identified (CMa)
over-density.
Successively the symmetry axis was varied within
the range
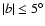 ,
in steps of
,
in steps of
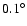 .
For each step (i.e. each warp angle) the Northern and Southern
latitude profiles were folded and a reduced
.
For each step (i.e. each warp angle) the Northern and Southern
latitude profiles were folded and a reduced 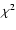 defined as:
defined as:
![\begin{displaymath}\chi^2 = \sum \left[(y_{\rm North}-y_{\rm South})^2/(y_{\rm North}+y_{\rm South})\right]
\end{displaymath}](/articles/aa/full/2006/20/aa4081-05/img70.gif) |
(1) |
was employed to determine the warp angle which minimized the
differences between the two profiles (y is the Log(N) of star counts
computed in the latitude profiles, see Fig. 4).
A symmetry of around
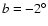 (i.e warp angle
(i.e warp angle
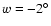 )
almost completely canceled the (CMa)
over-density. This warp angle has been derived (not modeled
as argued in Martin et al. (2004a) and Bellazzini et al.
(2004)) and agrees with the angle derived for the
gas warp by Freudenreich (1994).
It is important to note that this result is obtained independently of
the adopted dereddening method: (i) pure Schlegel et al.
(1998) values; or (ii) modified with the Bonifacio et al.
(2000) correction (see Amôres & Lépine
(2005) for recent confirmation of errors in the Schlegel et al. values).
)
almost completely canceled the (CMa)
over-density. This warp angle has been derived (not modeled
as argued in Martin et al. (2004a) and Bellazzini et al.
(2004)) and agrees with the angle derived for the
gas warp by Freudenreich (1994).
It is important to note that this result is obtained independently of
the adopted dereddening method: (i) pure Schlegel et al.
(1998) values; or (ii) modified with the Bonifacio et al.
(2000) correction (see Amôres & Lépine
(2005) for recent confirmation of errors in the Schlegel et al. values).
Thus, we are able to measure the latitude angle at which the latitude
profiles crossing the Galactic disk are symmetric; i.e. the warp-angle
or the mid-plane of the warped disk. In this section we apply this
method for the entire 2MASS catalog within
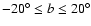 ,
and derive the global Galactic warp
as a function of longitude. Most importantly, the warp signature is
traced by means of different stellar sources (red clump (RC) and red
giants (RGB)) at different distances. This is particularly important
because we want to investigate the impact of the tracer contamination
and its distance on the derived warp signature.
,
and derive the global Galactic warp
as a function of longitude. Most importantly, the warp signature is
traced by means of different stellar sources (red clump (RC) and red
giants (RGB)) at different distances. This is particularly important
because we want to investigate the impact of the tracer contamination
and its distance on the derived warp signature.
To emphasize the particular importance of the contamination and
distance properties of the assumed tracer (and the intrinsic
difficulty for similar investigations) we will briefly comment
on two recent studies probing the Galactic warp, namely
Yusifov (2004) and López-Corredoira et al.
(2002).
2.1 The Yusifov stellar warp model
![\begin{figure}
\par\includegraphics[width=7.5cm,height=5.2cm,clip]{4081fig1.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg73.gif) |
Figure 1:
The distribution pulsars in the Manchester et al. (2005) catalog. Filled squares and
open circles are pulsars with Galactocentric distances between 1 and 5 kpc, and 5 and 10 kpc respectively. Open triangles are pulsars at
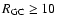 kpc. kpc. |
| Open with DEXTER |
In his analysis, Yusifov used the asymmetric distribution of 1412
Galactic pulsars (from the Manchester et al.
2005 catalog) to trace the Galactic stellar warp
and flare (the increase in scale-height as a function of
Galactocentric distance). Yusifov limited his analysis to pulsars
within
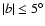 whose distances are
whose distances are 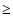 1 kpc. He
calculated the ratio of the cumulative number of pulsars above and
below the Galactic plane as a function of Galactic longitude, and
so derived a warp model.
However, as seen in Fig. 1, the Manchester et al.
(2005) catalog has only 1 pulsar at R>5 kpc
between
1 kpc. He
calculated the ratio of the cumulative number of pulsars above and
below the Galactic plane as a function of Galactic longitude, and
so derived a warp model.
However, as seen in Fig. 1, the Manchester et al.
(2005) catalog has only 1 pulsar at R>5 kpc
between
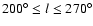 .
Clearly, the pulsar catalog is already strongly incomplete at
.
Clearly, the pulsar catalog is already strongly incomplete at 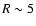 kpc in the outer Milky Way. Although one might doubt how these data
can reliably predict the number density of stars at CMa distances, it
is true that the Yusifov warp model predictions have turned out to be
comparable with other studies based on more complete samples, and we
therefore will compare our results with this model.
kpc in the outer Milky Way. Although one might doubt how these data
can reliably predict the number density of stars at CMa distances, it
is true that the Yusifov warp model predictions have turned out to be
comparable with other studies based on more complete samples, and we
therefore will compare our results with this model.
The López-Corredoira et al. 2MASS-based investigation was a
major attempt at studying the Galactic stellar warp and flare. There
are, however, a few points that must be kept in mind regarding their
analysis. Firstly, 2MASS was not complete at the time that their
analysis was concluded, so that they were able to analyse only 820 lines of sight, each of area between 0.5 and 1.0 square degrees,
restricted to
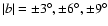 .
This is particularly important in understanding the determination (cf.
Martin et al. 2004b; Bellazzini et al. 2004,
2006) of the maximum of the stellar warp at
.
This is particularly important in understanding the determination (cf.
Martin et al. 2004b; Bellazzini et al. 2004,
2006) of the maximum of the stellar warp at
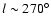 ,
a result often cited from the López-Corredoira
et al. paper.
Indeed, the area around
,
a result often cited from the López-Corredoira
et al. paper.
Indeed, the area around
 was missing in the López-Corredoira et al. study, and nowhere in that article is it
stated that the stellar warp maximum is at
was missing in the López-Corredoira et al. study, and nowhere in that article is it
stated that the stellar warp maximum is at
 .
Indeed the formula describing the López-Corredoira et al. warp
model at CMa distances shows that the maximum stellar warp is near to
.
Indeed the formula describing the López-Corredoira et al. warp
model at CMa distances shows that the maximum stellar warp is near to
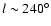 (see Sect. 4).
The value of
(see Sect. 4).
The value of
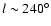 for the maximum Galactic warp is in
fact found in other studies, e.g. Freudenreich (1994, their
Fig. 3) studying the gaseous warp, and Djorgovski & Sosin
(1989, their Fig. 1) analyzing IRAS sources
for the maximum Galactic warp is in
fact found in other studies, e.g. Freudenreich (1994, their
Fig. 3) studying the gaseous warp, and Djorgovski & Sosin
(1989, their Fig. 1) analyzing IRAS sources![[*]](/icons/foot_motif.gif) .
.
![\begin{figure}
\par\includegraphics[width=7.7cm,height=10cm,clip]{4081fig2.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg80.gif) |
Figure 2:
The upper 4 panels display a Besançon  square
area simulated color-magnitude diagram around CMa
(
square
area simulated color-magnitude diagram around CMa
(
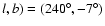 .
These show the expected
different contributions of stars as a function of their distance. The
lowest panel displays data from 2MASS between .
These show the expected
different contributions of stars as a function of their distance. The
lowest panel displays data from 2MASS between
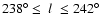 and
and
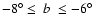 .
The outlined vertical boxes mark 4 distance intervals as selected from
the red clump distribution in simulated diagrams.
The 3 oblique boxes trace 3 samples of red giant stars extracted
at three different heliocentric distances.
The thick line is the Majewski et al. calibration of the
Sagittarius dwarf RGB, shifted to 2.8, 7.3 and 16.6 kpc. .
The outlined vertical boxes mark 4 distance intervals as selected from
the red clump distribution in simulated diagrams.
The 3 oblique boxes trace 3 samples of red giant stars extracted
at three different heliocentric distances.
The thick line is the Majewski et al. calibration of the
Sagittarius dwarf RGB, shifted to 2.8, 7.3 and 16.6 kpc. |
| Open with DEXTER |
Second, López-Corredoira et al. derive the ratio of Northern to
Southern star-counts,
 for red clump stars with
for red clump stars with
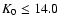 (see their Fig. 15).
To help us evaluate the impact of contamination when using RC stars as warp-tracers, in Fig. 2 we use Besançon (Robin
et al. 2003) simulated color-magnitude diagrams around CMa
and plot the data as a function of their distance.
Focusing our attention around (J-K)
(see their Fig. 15).
To help us evaluate the impact of contamination when using RC stars as warp-tracers, in Fig. 2 we use Besançon (Robin
et al. 2003) simulated color-magnitude diagrams around CMa
and plot the data as a function of their distance.
Focusing our attention around (J-K)
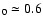 ,
one sees
that the stellar populations at
,
one sees
that the stellar populations at 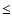 2 kpc which will contribute
to the final
2 kpc which will contribute
to the final
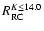 ratio include: (i) RC stars at
ratio include: (i) RC stars at
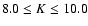 ,
and most importantly, (ii) dwarfs at the
fainter magnitudes
,
and most importantly, (ii) dwarfs at the
fainter magnitudes
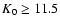 .
At magnitudes around the RC of CMa (
.
At magnitudes around the RC of CMa (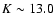 ), we estimate a
contamination by local foreground dwarfs of about 25-30%.
Thus, if one is interested in the
), we estimate a
contamination by local foreground dwarfs of about 25-30%.
Thus, if one is interested in the
 ratio at say, the CMa
distance, one must bear in mind that this ratio is subject to
potentially serious contamination by RC and dwarf stars at distances
closer than the CMa over-density.
ratio at say, the CMa
distance, one must bear in mind that this ratio is subject to
potentially serious contamination by RC and dwarf stars at distances
closer than the CMa over-density.
2.3 Tracing the stellar warp and flare with RC and RGB stars
We employ our method in tracing the Galactic warp and flare using two
stellar tracers: red clump and red giant stars. For both tracers we
repeat the analysis for different mean distances.
The advantage in using two stellar tracers derives from their
different contamination status.
With respect to RC stars, red giants are an ideal instrument in
probing the Galactic warp and flare since these suffer less external contamination by nearby dwarfs. At the same time red giants
projected at different distances do not overlap in the color-magnitude
diagram (i.e. no internal contamination) and this guarantees a
better distance separation. Indeed, being the bright and evolved part
of the faint and un-detected main sequence stars, red giants allow us
(already in the not so deep 2MASS catalog) to probe the most
distant, and almost entire, Milky Way disk populations.
The vertical boxes in Fig. 2 set 4 heliocentric
distance intervals ( 2,
2, 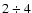 ,
,
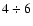 and
and 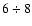 kpc)
from which we extract RC stars and use their star-counts to derive
the warp and flare.
kpc)
from which we extract RC stars and use their star-counts to derive
the warp and flare.
Similarly, the 3 oblique boxes trace red giant stars at fixed
heliocentric distances between
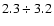 ,
,
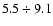 ,
and
,
and
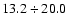 kpc. Thus, the mean assumed distances of the RGB samples are 2.8, 7.3 and 16.6 kpc, with the intermediate sample
being centered on the CMa RGB.
To estimate the distances to Milky Way M-giants we apply the
same method as in Martin et al. (2004a), that first led to
the identification of the CMa over-density.
This is done by using the Sagittarius dwarf RGB as a reference. Assuming a distance modulus of 16.9 and a mean [Fe/H] of
kpc. Thus, the mean assumed distances of the RGB samples are 2.8, 7.3 and 16.6 kpc, with the intermediate sample
being centered on the CMa RGB.
To estimate the distances to Milky Way M-giants we apply the
same method as in Martin et al. (2004a), that first led to
the identification of the CMa over-density.
This is done by using the Sagittarius dwarf RGB as a reference. Assuming a distance modulus of 16.9 and a mean [Fe/H] of  -0.5
-0.5![[*]](/icons/foot_motif.gif) Majewski et al. (2003) derived
the following calibration of the Sagittarius RGB:
Majewski et al. (2003) derived
the following calibration of the Sagittarius RGB:
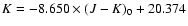 (see the thick line in
Fig. 2).
The mean metallicity of Sagittarius can be considered intermediate
between inner (more metal-rich) and outer (more metal-poor) Milky Way
disk stars. Indeed, the mean abundance of the disk stars is known to
vary between
(see the thick line in
Fig. 2).
The mean metallicity of Sagittarius can be considered intermediate
between inner (more metal-rich) and outer (more metal-poor) Milky Way
disk stars. Indeed, the mean abundance of the disk stars is known to
vary between 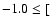 Fe/H
Fe/H![$]\le+0.3$](/articles/aa/full/2006/20/aa4081-05/img99.gif) (see Bensby et al. (2004) for differences between thin and thick
disk populations)
(see Bensby et al. (2004) for differences between thin and thick
disk populations)
![\begin{figure}
\par\includegraphics[width=8.7cm,height=8.2cm,clip]{4081fig3.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg100.gif) |
Figure 3:
A schematic view (from Drimmel & Spergel 2001) of
the Milky Way as seen from its North pole showing the 4 spiral
arms as mapped by H II regions and dust (see also Vallée
2005; and Russeil
2003).
The Galactic center, the Sun and the names of the spiral arms are
plotted. Note the presence of the Local arm (Orion-Cygnus) close to
the Sun's position and the outer arm that is also called
Norma-Cygnus.
The 3 heliocentric circles define the regions at fixed 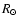 where we extract RGB samples to trace the Galactic warp and flare.
The direction of the warp phase angle where we extract RGB samples to trace the Galactic warp and flare.
The direction of the warp phase angle 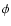 ,
and longitude directions
are also plotted.
We have also added the Galactic bar at an orientation angle of ,
and longitude directions
are also plotted.
We have also added the Galactic bar at an orientation angle of
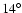 (following Freudenreich 1998) with length
3 kpc (following Vallée 2005). Note however
that a recent Galactic Legacy Mid-Plane Survey Extraordinaire
(GLIMPSE) study by Benjamin et al. (2005) report on a linear
Galactic bar with half-length of
(following Freudenreich 1998) with length
3 kpc (following Vallée 2005). Note however
that a recent Galactic Legacy Mid-Plane Survey Extraordinaire
(GLIMPSE) study by Benjamin et al. (2005) report on a linear
Galactic bar with half-length of 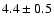 kpc. kpc. |
| Open with DEXTER |
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=7.2cm,height=4.8cm,clip]{...
...{2mm}
\includegraphics[width=7.5cm,height=8.1cm,clip]{4081fig5.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg101.gif) |
Figure 4:
The upper panels display two examples of the derivation of best
warp angles and their relative error by means of a reduced 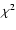 .
The lower panels show the latitude profiles for a third field: (i) assuming no warp ( upper panel) and; (ii) having derived the best warp
angle ( lower panel). The dashed and solid lines refer to the Northern and
Southern latitude profiles, respectively. All panels refer to the RGB sample at .
The lower panels show the latitude profiles for a third field: (i) assuming no warp ( upper panel) and; (ii) having derived the best warp
angle ( lower panel). The dashed and solid lines refer to the Northern and
Southern latitude profiles, respectively. All panels refer to the RGB sample at
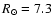 kpc. kpc. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.1cm,height=5.2cm]{4081fig6.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg102.gif) |
Figure 5:
An example of deriving the scale height (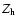 )
from the RGB sample
at )
from the RGB sample
at
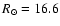 kpc. The filled circles show the Northern
hemisphere latitude profile while the open circles show the
Southern profile. Vertical lines delimit the region where we apply a
linear fit (dotted line) to the data. kpc. The filled circles show the Northern
hemisphere latitude profile while the open circles show the
Southern profile. Vertical lines delimit the region where we apply a
linear fit (dotted line) to the data. |
| Open with DEXTER |
At the same time we note that the Majewski et al. RGB calibration
would reproduce the entire range of disk metallicities if age is
allowed to vary. For example the Sagittarius RGB would overlap with a 10 Gyr and [Fe/H]=-0.7 theoretical isochrone (appropriate for outer
disk populations?) as well as one with 4 Gyr and [Fe/H]=-0.4(appropriate for inner disk populations?).
A systematic uncertainty in estimating the distances of the Galactic
M-giants is therefore un-avoidable. Similarly, contamination between
different populations and uncertainties in reddening corrections will
cloud our analysis.
A schematic view of the Milky Way and of the regions where we probe
the stellar warp and flare are shown in Fig. 3.
Examples of the application of our method are shown in the upper
horizontal panels of Fig. 4, reporting the derivation of
the best warp angle for two fields extracted from the
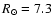 kpc RGB sample. We show two cases: the first field
kpc RGB sample. We show two cases: the first field
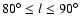 and
and
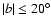 is more
populated and the warp angle (minimum
is more
populated and the warp angle (minimum 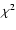 ,
as reported in
Eq. (1)) is easier to determine, having a relatively
small
,
as reported in
Eq. (1)) is easier to determine, having a relatively
small
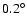 error. The second field,
error. The second field,
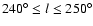 ,
is less populated and the error is
higher reaching
,
is less populated and the error is
higher reaching
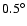 .
.
The lower panels of Fig. 4, show an example of deriving the
best warp angle for latitude profiles between
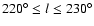 from the
from the
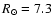 kpc RGB sample.
The upper panel shows the Northern and Southern latitude profile
assuming no warp, i.e. a symmetry axis around
kpc RGB sample.
The upper panel shows the Northern and Southern latitude profile
assuming no warp, i.e. a symmetry axis around
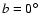 .
The lower
panel shows the same two profiles assuming a symmetry axis around
.
The lower
panel shows the same two profiles assuming a symmetry axis around
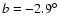 ,
as derived when the differences between the folded
profiles are minimized and the symmetry angle is allowed
to vary within
,
as derived when the differences between the folded
profiles are minimized and the symmetry angle is allowed
to vary within
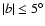 .
One may note that for large warp angles the Southern latitude profile
becomes shorter than the Northern one. This is due to the
warp angle becoming significant compared to the imposed angular
limit in the extraction; i.e.
.
One may note that for large warp angles the Southern latitude profile
becomes shorter than the Northern one. This is due to the
warp angle becoming significant compared to the imposed angular
limit in the extraction; i.e.
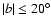 .
.
Once the warp angle has been derived for each line of sight we
proceed in estimating the vertical density profile of the stellar
disk: the scale-height (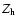 ). Our intent is to characterize the
radial trend of the stellar disk scale-height. A disk
flaring is usually seen as an increasing scale-height towards the
outer parts of the disk.
An example of the adopted procedure is shown in Fig. 5.
Having derived the warp angle, the b angles were transformed in
linear Z height according to the distance from the Sun of the
sample. Then the Northern and Southern profiles were overlapped and
the star density profile was fitted by a power law, thus deriving
). Our intent is to characterize the
radial trend of the stellar disk scale-height. A disk
flaring is usually seen as an increasing scale-height towards the
outer parts of the disk.
An example of the adopted procedure is shown in Fig. 5.
Having derived the warp angle, the b angles were transformed in
linear Z height according to the distance from the Sun of the
sample. Then the Northern and Southern profiles were overlapped and
the star density profile was fitted by a power law, thus deriving 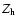 .
The fitting of the vertical density profile was made within 2 limits
in Z, so as to exclude: (i) the highly obscured inner regions
within
.
The fitting of the vertical density profile was made within 2 limits
in Z, so as to exclude: (i) the highly obscured inner regions
within 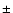
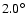 from the mid-plane and; (ii) the very outer regions where in cases of high warp angles the latitude profile
of one hemisphere is short with respect to the other
hemisphere (cf. the latitude profiles in lower panel of
Fig. 4).
from the mid-plane and; (ii) the very outer regions where in cases of high warp angles the latitude profile
of one hemisphere is short with respect to the other
hemisphere (cf. the latitude profiles in lower panel of
Fig. 4).
The vertical Z scale-height was fitted by a single exponential. We
have not tried to use a more complicated formula like the sech or
double exponential (see for example the analysis by Alard
2000).
Thus, our analysis is aimed at measuring the order of magnitude of the
flare in the outer disk. A detailed parametrization of the flare (in
terms of thin-thick disk separation), although very interesting, is
beyond the scope of this paper.
In particular, we note that for the regions of most interest (the
outer disk) any thin disk flaring would act in a way that increases the
confusion between the thin and thick disk components.
This in-ability in separating thin-thick disk components in the outer
regions is exacerbated by the unavailability of kinematic
all-sky data, which might allow a separation of the two
components. Thus, for the outer disk, one is left with determining
only an approximate amplitude of any flare.
Figure 5 shows an example of the vertical density profile fit
for the RGB sample at a heliocentric distance of 16.6 kpc
(
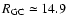 kpc).
The abscissa, |Z-w|, indicates the linear Z height folded around
the mid-plane of the disk as determined by the warp angle analysis.
The analysis of the radial trend of the vertical scale height,
kpc).
The abscissa, |Z-w|, indicates the linear Z height folded around
the mid-plane of the disk as determined by the warp angle analysis.
The analysis of the radial trend of the vertical scale height, 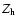 ,
for the RGB sample will be discussed in Sect. 5.
,
for the RGB sample will be discussed in Sect. 5.
2.4 Comparing DIRBE integrated surface photometry with
2MASS star counts
In this paper we compare the derived stellar
warp with that obtained for other Galactic components, including
integrated light, neutral gas and the interstellar dust.
In regards to this, we mainly make use of the Freudenreich et al.
(1994) study where the warp due to dust and integrated light
has been derived using the Diffuse Infrared Background Experiment
(DIRBE) mapping of the Galactic plane (see also Vig et al. 2005).
The results of DIRBE however come from integrated light surface
photometry which sum contributions from composite stellar populations
at different distances and luminosities, and therefore these can
be correctly compared with the 2MASS results only after a discussion
of their relative weight.
The DIRBE 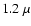 m and
m and 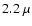 m spectral bands correspond roughly
to the infrared J and K pass-bands. It is important to note that
the DIRBE near-infrared (
m spectral bands correspond roughly
to the infrared J and K pass-bands. It is important to note that
the DIRBE near-infrared (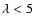
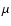 m) emission is dominated by
stellar disk stars [whereas in far-infrared bands (e.g.
m) emission is dominated by
stellar disk stars [whereas in far-infrared bands (e.g.
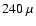 m) the emission by interstellar dust dominates].
m) the emission by interstellar dust dominates].
To better understand which stellar populations contribute most in the
DIRBE emission maps, we used the 2MASS star counts to integrate the
light coming from specific stellar populations. We limit this analysis
to only one line of sight (the 2MASS color-magnitude diagram presented
in the lowest panel of Fig. 2), and expect this to be
representative of any other line of sight.
We roughly disentangle three main populations in this 2MASS color
magnitude diagram: (i) MS objects with
(J-K)<0.45, mainly main
sequence and blue super-giants stars; (ii) RC stars with
0.45<(J-K)<0.65; and (iii) RGB, red super-giant and asymptotic
branch stars with
(J-K)>0.65.
For each of these three stellar populations we summed up the light
contribution coming from the single point sources (stars) falling
within the above color intervals.
![\begin{figure}
\includegraphics[width=8.3cm,height=8.2cm,clip]{4081fig7.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg116.gif) |
Figure 6:
The relative luminosity contribution of the
three stellar populations in the J band ( upper panel) and K band
( middle panel). The lower figure shows the cumulative distributions of
the distances of RGB stars without any luminosity-weighting along the
line of sight (dark line). The grey line shows instead the
distance-weighted distribution. |
| Open with DEXTER |
In Fig. 6 we show the relative luminosity contribution of
the three stellar populations in the J band (upper panel) and K band (middle panel). A limiting magnitude of K=14.0 has been applied
in estimating the cumulative and relative luminosity of the three
different stellar populations.
The middle panel, displaying the relative luminosity contribution of
the three populations to the total luminosity, shows clearly that in
the case of the K band the total light contribution of MS stars is
almost negligible in DIRBE, contributing only 15% of the total light.
On the other hand, RGB stars contribute up to 60% of the total light,
a level that goes up to 82% once also the RC are summed together with
RGB stars.
Thus we conclude that the level of contamination by MS stars in 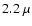 m (
m ( K) DIRBE emission maps is fairly low and that red
populations dominate the integrated light. Similar conclusions can be
drawn for the shortest DIRBE wavelength band at
K) DIRBE emission maps is fairly low and that red
populations dominate the integrated light. Similar conclusions can be
drawn for the shortest DIRBE wavelength band at 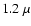 m (
m ( J,
upper panel): the RGB and RC populations dominate the DIRBE light,
contributing up to 75% of the total light.
J,
upper panel): the RGB and RC populations dominate the DIRBE light,
contributing up to 75% of the total light.
We also checked the weighted distance range at which DIRBE is more
sensitive. Considering that the RGB population is the dominant
population in both J and K bands we calculated their distance
distribution using the Majewski calibration of the Sagittarius red
giant branch (see Sect. 2.3).
The dark line in the lowest plot of Fig. 6 shows the
cumulative distributions of the distances of RGB stars without any
luminosity weighting along the line of sight. The grey line shows the
cumulative distance distribution once we weight the stellar distance
with the stars light.
Clearly, the DIRBE integrated light is linearly sensitive to distances
within  9 kpc (at least in this direction
9 kpc (at least in this direction
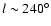 )
where the light contribution reaches
)
where the light contribution reaches 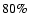 of the total.
This result, based on RGB stars, should not change considerably once
we add the contribution of (i) the RC stars which weight more to
larger distances; and (ii) the MS stars which weight more to shorter
distances. Thus, being of the same size, the two opposite
contributions of the MS and RC stars will to first order cancel out.
of the total.
This result, based on RGB stars, should not change considerably once
we add the contribution of (i) the RC stars which weight more to
larger distances; and (ii) the MS stars which weight more to shorter
distances. Thus, being of the same size, the two opposite
contributions of the MS and RC stars will to first order cancel out.
In conclusion, with the help of the 2MASS star counts we have
identified which stellar populations are the main contributers to the
DIRBE luminosity, and at what distances these contribute the most.
The results are that the RGB stars are the dominant contributors of
the J and K DIRBE integrated light, within  9 kpc. This
allows us to perform a fruitful comparison of the DIRBE warp results
with those obtained from our 2MASS analysis.
9 kpc. This
allows us to perform a fruitful comparison of the DIRBE warp results
with those obtained from our 2MASS analysis.
3 The stellar warp as traced by RC stars
In this section we present the derived stellar warp as traced by RC stars. We anticipate two obvious points: (i) the warp amplitude
depends on the employed wavelength; shorter wavelength investigations
probe nearer areas and therefore may underestimate the warp amplitude
if it increases with distance; and (ii) the warp amplitude derived
depends on the contamination of the employed stellar tracer: inclusion
of nearby stars in samples of more distant stars will underestimate
the warp amplitude at larger distances. Overall, red clump stars are
not the ideal tracers of the warp at larger distances, and we will
show this using Figs. 7 and 8.
The upper left panel of Fig. 7 displays the stellar warp
as derived using RC stars at
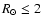 kpc. At first sight,
the presence of a global stellar warp can be debatable, as it contrasts
with the neat sinusoidal function seen in Djorgovski & Sosin
(1989) for IRAS sources.
It remains true however that the Southern stellar warp is distinguishable
between
kpc. At first sight,
the presence of a global stellar warp can be debatable, as it contrasts
with the neat sinusoidal function seen in Djorgovski & Sosin
(1989) for IRAS sources.
It remains true however that the Southern stellar warp is distinguishable
between
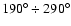 .
This brings the Galactic
mid-plane
.
This brings the Galactic
mid-plane 
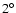 down at around
down at around
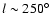 ,
and
demonstrates that the stellar warp is detectable already in the solar
circle.
Problems arise when searching for a global stellar warp in the
Northern hemisphere. A sudden drop at around
,
and
demonstrates that the stellar warp is detectable already in the solar
circle.
Problems arise when searching for a global stellar warp in the
Northern hemisphere. A sudden drop at around
 seems
to interrupt a global warp signature.
To understand the absence of a clear stellar warp in the Northern
hemisphere we make a comparison with the latitude of peak
brightness as derived in Freudenreich et al. (1994) using
DIRBE mapping of the Galactic plane.
Overall, the DIRBE data-points at 1.2
seems
to interrupt a global warp signature.
To understand the absence of a clear stellar warp in the Northern
hemisphere we make a comparison with the latitude of peak
brightness as derived in Freudenreich et al. (1994) using
DIRBE mapping of the Galactic plane.
Overall, the DIRBE data-points at 1.2 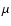 m reproduce the global
features derived from nearby
m reproduce the global
features derived from nearby
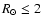 kpc RC stars.
In particular both data-sets show an early drop at
kpc RC stars.
In particular both data-sets show an early drop at
 demonstrating: (i) the consistency of the DIRBE-2MASS comparison; and (ii) the presence of a localized nearby structure.
Indeed, the drop in 2MASS and DIRBE traces the presence of the
Orion-Cygnus segment (called Local Arm in Russeil
2003).
demonstrating: (i) the consistency of the DIRBE-2MASS comparison; and (ii) the presence of a localized nearby structure.
Indeed, the drop in 2MASS and DIRBE traces the presence of the
Orion-Cygnus segment (called Local Arm in Russeil
2003).
![\begin{figure}
\includegraphics[width=8cm,height=8.2cm,clip]{4081fig8.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg121.gif) |
Figure 7:
The stellar warp as derived from RC stars at
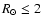 kpc (filled squares). The results are compared with the latitude of peak brightness obtained from
DIRBE at wavelengths 1.2, 3.5 and 240 kpc (filled squares). The results are compared with the latitude of peak brightness obtained from
DIRBE at wavelengths 1.2, 3.5 and 240 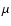 m by Freudenreich et al.
(1994, grey open triangles). m by Freudenreich et al.
(1994, grey open triangles). |
| Open with DEXTER |
![\begin{figure}
\includegraphics[width=8cm,height=8.2cm,clip]{4081fig9.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg122.gif) |
Figure 8:
The stellar warp as derived from RC stars for 4 distance
intervals (dark filled squares). The results are compared with
the latitude of peak brightness obtained from DIRBE at
wavelengths 3.5 and 240 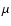 m by Freudenreich et al.
(1994, grey open triangles). m by Freudenreich et al.
(1994, grey open triangles). |
| Open with DEXTER |
The lower left panel of Fig. 7 over-plots the DIRBE
data-points at 3.5 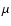 m. As anticipated before, at
m. As anticipated before, at
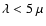 m
DIRBE emission is still dominated by disk stars. However, as one moves
to longer wavelengths DIRBE data-points sample more distant structures
that were obscured at shorter wavelengths. This explains why at
3.5
m
DIRBE emission is still dominated by disk stars. However, as one moves
to longer wavelengths DIRBE data-points sample more distant structures
that were obscured at shorter wavelengths. This explains why at
3.5 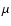 m we do not observe the strong drop at
m we do not observe the strong drop at
 (seen at 1.2
(seen at 1.2 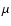 m and in RC stars at
m and in RC stars at
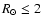 kpc) and this
is replaced by a global, and smooth warp signature.
This effect is further demonstrated when comparing the warp obtained
for RC stars at
kpc) and this
is replaced by a global, and smooth warp signature.
This effect is further demonstrated when comparing the warp obtained
for RC stars at
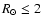 kpc with that due to the dust (traced
at
kpc with that due to the dust (traced
at 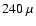 m). The dust warp does not show the drop at
m). The dust warp does not show the drop at
 anymore, and although still fluctuating, overall a
global and large-scale structure (the warp) is identified.
We emphasize however that a simple comparison between the warp of RC
stars at
anymore, and although still fluctuating, overall a
global and large-scale structure (the warp) is identified.
We emphasize however that a simple comparison between the warp of RC
stars at
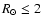 kpc with that at
kpc with that at 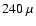 m is rather improper, since the DIRBE dust warp is sensitive to more distant
regions.
The comparison has been meant to show how increasing the adopted
wavelength unveils more distant regions and a larger warp amplitude.
m is rather improper, since the DIRBE dust warp is sensitive to more distant
regions.
The comparison has been meant to show how increasing the adopted
wavelength unveils more distant regions and a larger warp amplitude.
Before drawing our conclusions on the RC stars as a stellar warp
tracer, we analyze the impact of their contamination status on the
global warp properties.
This is illustrated in Fig. 8, which displays the stellar
warp as derived from RC stars at heliocentric distances between
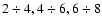 and
and 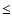 8 kpc.
The upper panels of Fig. 8 prove again how the presence of
a global warp can be debatable for the "nearest'' RC samples.
Things change considerably for RC stars between
8 kpc.
The upper panels of Fig. 8 prove again how the presence of
a global warp can be debatable for the "nearest'' RC samples.
Things change considerably for RC stars between
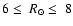 .
At this distance a global warp signature is evident in both
hemispheres.
The warp is regular and shows a strong asymmetry in the maximum warp
amplitude. At
.
At this distance a global warp signature is evident in both
hemispheres.
The warp is regular and shows a strong asymmetry in the maximum warp
amplitude. At
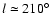 the warp brings the Galactic
mid-plane
the warp brings the Galactic
mid-plane 
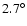 below the nominal
below the nominal
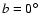 ,
whereas
in the Northern hemisphere the maximum warp amplitude stops at
,
whereas
in the Northern hemisphere the maximum warp amplitude stops at
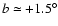 .
Comparing the warp obtained for the
.
Comparing the warp obtained for the
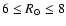 kpc RC sample with DIRBE data shows excellent agreement with that obtained at 240
kpc RC sample with DIRBE data shows excellent agreement with that obtained at 240 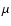 m tracing the dust.
This indicates that the RC star sample between
m tracing the dust.
This indicates that the RC star sample between
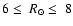 kpc (although it includes up to 30% contamination by local dwarfs)
still enables sufficient isolation of distant stars, those whose warp
signature matches that of DIRBE at 240
kpc (although it includes up to 30% contamination by local dwarfs)
still enables sufficient isolation of distant stars, those whose warp
signature matches that of DIRBE at 240 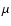 m.
m.
The impact of contamination on the retrieved warp amplitude is best
illustrated in the lower right panel of Fig. 8.
With respect to the warp derived from RC stars between
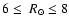 kpc, those between
kpc, those between
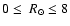 kpc
show a significant change in the amplitude of the warp maximum
and location.
In particular, the maximum warp amplitude passes from
kpc
show a significant change in the amplitude of the warp maximum
and location.
In particular, the maximum warp amplitude passes from 
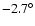 (for RC between
(for RC between
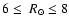 kpc) to
kpc) to 
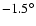 (for RC at
(for RC at
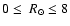 kpc).
A comparison with DIRBE data now shows a better agreement with the
kpc).
A comparison with DIRBE data now shows a better agreement with the 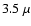 m data and this is again the expected result.
Indeed, both the 2MASS
m data and this is again the expected result.
Indeed, both the 2MASS
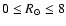 kpc star counts and the
DIRBE
kpc star counts and the
DIRBE 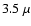 m surface photometry are sensitive all along the line of
sight up to
m surface photometry are sensitive all along the line of
sight up to  8 kpc.
8 kpc.
In conclusion, the plots presented in
Figs. 7, 8 highlight the fact that a thorough
characterization of the Galactic stellar warp, in particular its
maximum amplitude and maximum location, sensitively depend on the
distance and contamination-status of the employed tracer.
The lower panels of Fig. 8 are the most significant in
demonstrating how the maximum stellar warp can shift its location by 
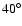 in longitude and can halve its amplitude depending on
the contamination degree of the adopted tracer.
In addition, the lower right panel of Fig. 8 proves the
validity of our method in tracing the stellar warp, and the
consistency of the comparison between DIRBE and 2MASS.
in longitude and can halve its amplitude depending on
the contamination degree of the adopted tracer.
In addition, the lower right panel of Fig. 8 proves the
validity of our method in tracing the stellar warp, and the
consistency of the comparison between DIRBE and 2MASS.
This being established we will now focus our discussion on the stellar
warp as derived using red giants. As anticipated in
Sect. 2.3, the red giant samples include less contamination
by local dwarfs and enable a better and more reliable separation of
more distant stars.
![\begin{figure}
\par\includegraphics[width=14cm,height=14cm,clip]{4081fig10.ps}\p...
...{2mm}
\includegraphics[width=14.5cm,height=7.5cm,clip]{4081fig11.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg137.gif) |
Figure 9:
The upper left panel displays the stellar warp as derived
from red giants at
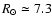 kpc.
In the lower left panel we compare the derived warp with those based
on two RC samples between: (i) kpc.
In the lower left panel we compare the derived warp with those based
on two RC samples between: (i)
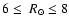 ,
and (ii) ,
and (ii)
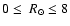 kpc.
The upper right panel over-plots the dust warp as derived from DIRBE at kpc.
The upper right panel over-plots the dust warp as derived from DIRBE at 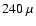 m data, whereas the lower right panel over-plots the
Galactic warp as derived from neutral H I gas (also from Freudenreich
et al. 1994).
The lower panel shows the density maps and contours of the m data, whereas the lower right panel over-plots the
Galactic warp as derived from neutral H I gas (also from Freudenreich
et al. 1994).
The lower panel shows the density maps and contours of the
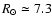 RGB sample. One can trace by eye the warp
signature (a colored version is more appropriate). Over-plotted is
also the location of the mean mid-plane warped disk as a function of
longitude.
RGB sample. One can trace by eye the warp
signature (a colored version is more appropriate). Over-plotted is
also the location of the mean mid-plane warped disk as a function of
longitude. |
| Open with DEXTER |
4 The stellar warp as traced by RGB stars
Figures 9 and 10 display the stellar warp as
derived from RGB samples at
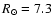 and
and
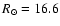 kpc.
A global regular warp signature is clearly evident in both samples,
reflecting large-scale Galactic structure (see
Sect. 4.2).
The most striking feature for the RGB
kpc.
A global regular warp signature is clearly evident in both samples,
reflecting large-scale Galactic structure (see
Sect. 4.2).
The most striking feature for the RGB
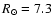 kpc sample is
the amplitude of the Southern maximum warp, which lowers the Galactic
mid-plane by almost
kpc sample is
the amplitude of the Southern maximum warp, which lowers the Galactic
mid-plane by almost  .
By applying a Gaussian fit to the
data-points between
.
By applying a Gaussian fit to the
data-points between
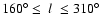 ,
we estimate a
mean warp maximum at
,
we estimate a
mean warp maximum at
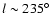 .
Similarly, for the
.
Similarly, for the
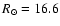 kpc RGB sample the warp maximum is estimated at
kpc RGB sample the warp maximum is estimated at
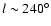 .
.
The lower left panel of Fig. 9 shows a comparison between
the stellar warp as derived from the RC star samples
(
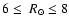 and
and
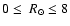 kpc) with the RGB sample at
kpc) with the RGB sample at
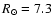 kpc. This comparison is an excellent
demonstration of how (i) the distance and (ii) the contamination
status of the adopted stellar tracer affect the discussion on the
location and amplitude of the maximum stellar warp.
The RC sample between
kpc. This comparison is an excellent
demonstration of how (i) the distance and (ii) the contamination
status of the adopted stellar tracer affect the discussion on the
location and amplitude of the maximum stellar warp.
The RC sample between
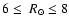 kpc shows a comparable
Southern warp maximum amplitude with the RGB sample at
kpc shows a comparable
Southern warp maximum amplitude with the RGB sample at
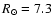 kpc, and this reflects the fact that both samples refer to the
same distance range. Yet, the location of the warp maximum for the RC sample between
kpc, and this reflects the fact that both samples refer to the
same distance range. Yet, the location of the warp maximum for the RC sample between
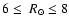 kpc is
kpc is 
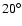 shifted
with respect to that for the RGB sample at
shifted
with respect to that for the RGB sample at
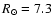 kpc.
On the other hand, the more contaminated RC sample between
kpc.
On the other hand, the more contaminated RC sample between
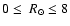 kpc shows a better agreement with the RGB sample
at
kpc shows a better agreement with the RGB sample
at
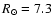 kpc in the mean location of the warp maximum around
kpc in the mean location of the warp maximum around
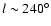 .
However, the maximum amplitude of the RC sample
between
.
However, the maximum amplitude of the RC sample
between
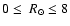 kpc has clearly decreased, a reminder of
how the inclusion of nearby stars leads to an under-estimated warp
amplitude.
kpc has clearly decreased, a reminder of
how the inclusion of nearby stars leads to an under-estimated warp
amplitude.
We now turn our attention to the comparison of the stellar warp
(derived from the RGB sample at
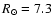 kpc) with that
obtained for the interstellar dust and neutral atomic hydrogen
components. The upper right panel shows the comparison with the DIRBE
data at
kpc) with that
obtained for the interstellar dust and neutral atomic hydrogen
components. The upper right panel shows the comparison with the DIRBE
data at 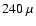 m. The agreement between the stellar and dust warp is
evident. The two share the same warp phase-angle and show only small
differences in the Southern maximum amplitude.
m. The agreement between the stellar and dust warp is
evident. The two share the same warp phase-angle and show only small
differences in the Southern maximum amplitude.
A recent upgrade of the Drimmel & Spergel (2001) Galactic
dust model, using DIRBE 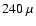 m data, shows the presence of an
extended spiral arm entering the third quadrant and intersecting the
suggested location of CMa.
The reconstruction of the Galactic dust distribution is always model
dependent. However, the new model (Drimmel 2005) indicates
that the far infrared DIRBE
m data, shows the presence of an
extended spiral arm entering the third quadrant and intersecting the
suggested location of CMa.
The reconstruction of the Galactic dust distribution is always model
dependent. However, the new model (Drimmel 2005) indicates
that the far infrared DIRBE 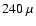 m data, are sensitive to at least
m data, are sensitive to at least  7 kpc from the Sun, and possibly beyond.
The distance consistency of the far infrared DIRBE
7 kpc from the Sun, and possibly beyond.
The distance consistency of the far infrared DIRBE 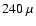 m data with
the RGB star sample at
m data with
the RGB star sample at
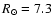 kpc (and given the excellent
agreement presented in the upper right panel of Fig. 9)
allows us to ascertain that the dust and stars at CMa distances are
similarly warped.
kpc (and given the excellent
agreement presented in the upper right panel of Fig. 9)
allows us to ascertain that the dust and stars at CMa distances are
similarly warped.
Besides the excellent agreement between the dust and stellar warp, a
similar conclusion is also obtained for the gaseous and stellar warp.
The H I latitude of peak brightness as derived by Freudenreich et al.
(1994![[*]](/icons/foot_motif.gif) )
follows the same warp signature we have obtained from the RGB sample
at CMa distance. The only obvious difference is related to the maximum
Southern warp amplitude of H I that seems to saturate; showing
an almost constant w warp-angle of
)
follows the same warp signature we have obtained from the RGB sample
at CMa distance. The only obvious difference is related to the maximum
Southern warp amplitude of H I that seems to saturate; showing
an almost constant w warp-angle of
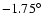 for longitudes between
for longitudes between
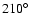 and
and
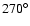 .
Might this observed difference between the amplitude of the stellar
and gaseous warp suggest an "accretion-perturbation'' on top of the
large-scale warp structure derived in this paper?. In regard to the
reality of this effect, one must keep in mind that over the last few
years there has been alternating evidence on warp amplitude
differences between stars and gas.
Indeed, we remind the reader that the disk radial truncation
hypothesis at
.
Might this observed difference between the amplitude of the stellar
and gaseous warp suggest an "accretion-perturbation'' on top of the
large-scale warp structure derived in this paper?. In regard to the
reality of this effect, one must keep in mind that over the last few
years there has been alternating evidence on warp amplitude
differences between stars and gas.
Indeed, we remind the reader that the disk radial truncation
hypothesis at
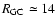 kpc was first proposed (Freudenreich et al. 1994; Porcel et al.
1997) in order to explain "why the stellar warp
seemed half the amplitude of the gaseous warp''. Thus, our results
which go in the opposite direction (stellar RGB warp at
kpc was first proposed (Freudenreich et al. 1994; Porcel et al.
1997) in order to explain "why the stellar warp
seemed half the amplitude of the gaseous warp''. Thus, our results
which go in the opposite direction (stellar RGB warp at
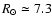 kpc showing twice the H I warp amplitude) should
only be read in terms of the different confusion status, and therefore
of the mean probed distances, of the gas.
kpc showing twice the H I warp amplitude) should
only be read in terms of the different confusion status, and therefore
of the mean probed distances, of the gas.
![\begin{figure}
\includegraphics[width=8cm,height=8cm,clip]{4081fig12.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg145.gif) |
Figure 10:
Same as Fig. 9, but for RGB stars at
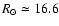 kpc. Note the structure ("swelling'') around kpc. Note the structure ("swelling'') around
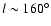 and how the the agreement with H I is better with
respect to the
and how the the agreement with H I is better with
respect to the
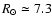 kpc sample. kpc sample. |
| Open with DEXTER |
Indeed, whereas we are able to isolate the warp signature due only
to the stellar populations at
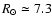 kpc, the gaseous
warp derived by Freudenreich et al. (1994) is that due to
the summing of different warp signatures by gas distributed
along the line of sight, at different distances.
This is a direct consequence of the inability to recover gas
distribution distances in lines of sight without clear kinematical
signatures.
Thus the saturation effect seen in the H I warp may reflect
that seen for the stellar warp (cf. the lower panels in
Fig. 8 and the lower left panel in Fig. 9) when
including nearby stars in distant star samples.
More fundamentally, leaving apart the flattening of the gas warp
in the range
kpc, the gaseous
warp derived by Freudenreich et al. (1994) is that due to
the summing of different warp signatures by gas distributed
along the line of sight, at different distances.
This is a direct consequence of the inability to recover gas
distribution distances in lines of sight without clear kinematical
signatures.
Thus the saturation effect seen in the H I warp may reflect
that seen for the stellar warp (cf. the lower panels in
Fig. 8 and the lower left panel in Fig. 9) when
including nearby stars in distant star samples.
More fundamentally, leaving apart the flattening of the gas warp
in the range
 ,
one notes excellent
agreement between of the gas and stellar warp profiles at all
the other viewing angles.
,
one notes excellent
agreement between of the gas and stellar warp profiles at all
the other viewing angles.
Moving to the stellar warp derived by RGB stars at
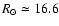 kpc (Fig. 12) one notes structure
("swelling'') between
kpc (Fig. 12) one notes structure
("swelling'') between
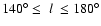 .
Is this a
deviation from a smooth global warp signature?. We suggest that this
is the same effect seen for nearby RC samples, and it is due to the
Orion-Cygnus Local Arm (short dashed line in Fig. 3).
This "swelling'' is not seen in the
.
Is this a
deviation from a smooth global warp signature?. We suggest that this
is the same effect seen for nearby RC samples, and it is due to the
Orion-Cygnus Local Arm (short dashed line in Fig. 3).
This "swelling'' is not seen in the
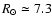 kpc sample
because the selected RGB stars are bright enough to avoid the faintest
regions of the diagrams (mostly populated by nearby dwarfs).
On the contrary, the RGB sample at
kpc sample
because the selected RGB stars are bright enough to avoid the faintest
regions of the diagrams (mostly populated by nearby dwarfs).
On the contrary, the RGB sample at
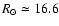 kpc can be
easily contaminated by nearby
kpc can be
easily contaminated by nearby
 kpc dwarf stars (compare
the upper and lower panels of Fig. 2) which would enter our
selection box if subject to high reddening or photometric error.
In turn, the structure appears in the
kpc dwarf stars (compare
the upper and lower panels of Fig. 2) which would enter our
selection box if subject to high reddening or photometric error.
In turn, the structure appears in the
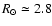 kpc RGB sample (Fig. 12) supporting our interpretation that the
"swelling'' is due to nearby dwarf stars that contaminate
primarily the
kpc RGB sample (Fig. 12) supporting our interpretation that the
"swelling'' is due to nearby dwarf stars that contaminate
primarily the
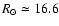 kpc RGB sample.
Given the similarities between the
kpc RGB sample.
Given the similarities between the
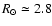 and 16.6 kpc
warps, to what extent might the
and 16.6 kpc
warps, to what extent might the
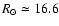 kpc warp
signature be in fact a signature of nearby contamination in the
kpc warp
signature be in fact a signature of nearby contamination in the
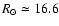 kpc RGB sample? The amplitude difference in the
Northern warp of the
kpc RGB sample? The amplitude difference in the
Northern warp of the
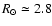 and 16.6 kpc samples
however argues against this possibility (compare Figs. 12 and 13).
and 16.6 kpc samples
however argues against this possibility (compare Figs. 12 and 13).
Recently McClure-Griffiths et al. (2004) presented an H I study from the Southern Galactic Plane Survey (SGPS), and pointed to
the possible presence of a distant spiral arm in the fourth quadrant
of the Milky Way. The distinct and cohesive feature has been traced over
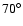 and is located between
and is located between
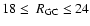 kpc.
In regards to this, it is interesting to note that our detection of a
stellar warp in the RGB sample at
kpc.
In regards to this, it is interesting to note that our detection of a
stellar warp in the RGB sample at
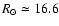 kpc might
represent the stellar counter-part of this distant H I spiral arm.
Indeed, the RGB sample at a mean distance of
kpc might
represent the stellar counter-part of this distant H I spiral arm.
Indeed, the RGB sample at a mean distance of
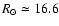 kpc
probes the stellar populations between
kpc
probes the stellar populations between
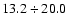 kpc from the Sun
(Fig. 3) and this is compatible with the mean position of
this H I arm being within
kpc from the Sun
(Fig. 3) and this is compatible with the mean position of
this H I arm being within  20 kpc from the Galactic center
(cf. Fig. 3a of McClure-Griffiths et al. 2004).
20 kpc from the Galactic center
(cf. Fig. 3a of McClure-Griffiths et al. 2004).
Interestingly, McClure-Griffiths et al. find that this distant arm is
well-confined to the Galactic plane, dropping at most by  1 kpc
below the Galactic equator. This again is in agreement with our
result (Fig. 13) that the Galactic mid-plane (at these
distances and lines of sight) is located at
1 kpc
below the Galactic equator. This again is in agreement with our
result (Fig. 13) that the Galactic mid-plane (at these
distances and lines of sight) is located at  0.5 kpc below
latitudes of
0.5 kpc below
latitudes of
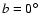 .
The SGPS H I survey analysis however remains limited to
.
The SGPS H I survey analysis however remains limited to
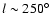 (McClure-Griffiths et al. 2005), so
that a detailed comparison of the stellar-gaseous warp and the
interpretation of this part of the outer disk awaits the completion of
the third quadrant.
In conclusion, and as we shall argue in Sect. 5, the
detection of the warp in the
(McClure-Griffiths et al. 2005), so
that a detailed comparison of the stellar-gaseous warp and the
interpretation of this part of the outer disk awaits the completion of
the third quadrant.
In conclusion, and as we shall argue in Sect. 5, the
detection of the warp in the
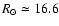 kpc sample proves
that the MW stellar disk is not truncated at
kpc sample proves
that the MW stellar disk is not truncated at
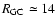 kpc, and
that a more extended stellar component is present.
kpc, and
that a more extended stellar component is present.
![\begin{figure}
\includegraphics[width=8cm,clip]{4081fig13.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg151.gif) |
Figure 11:
A comparison of our Galactic stellar disk warp height
 (kpc), as obtained from the RGB sample at heliocentric
distances of 7.3 kpc points with error bars, with models based
on stellar tracers lines. Note the excellent agreement between
data and models for the Southern warp. The disagreement for the
Northern warp is explained in the text. (kpc), as obtained from the RGB sample at heliocentric
distances of 7.3 kpc points with error bars, with models based
on stellar tracers lines. Note the excellent agreement between
data and models for the Southern warp. The disagreement for the
Northern warp is explained in the text. |
| Open with DEXTER |
Before discussing the possible implications of the warp as determined
empirically here on the CMa over-density, we first compare our results
with other available models.
In Fig. 11 we show a comparison of our derived Z-warp at
the proposed distance of CMa (
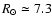 kpc) with
available models based on stellar tracers, namely Drimmel & Spergel
(2001)
kpc) with
available models based on stellar tracers, namely Drimmel & Spergel
(2001)![[*]](/icons/foot_motif.gif) , López-Corredoira et al. (2002) and
Yusifov (2004).
The 3 models used the distribution of integrated star light, red clump
and pulsar stars, respectively. In the following all models were
converted to
, López-Corredoira et al. (2002) and
Yusifov (2004).
The 3 models used the distribution of integrated star light, red clump
and pulsar stars, respectively. In the following all models were
converted to
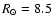 kpc.
At first sight, one sees how all three models converge on showing a
warp maximum near
kpc.
At first sight, one sees how all three models converge on showing a
warp maximum near
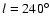 rather than
rather than
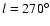 ,
a clear
hint of the association of CMa with the warp maximum amplitude. Most
importantly, at a heliocentric distance of 7.3 kpc the 3 models show
excellent agreement with our observed warp
amplitude around
,
a clear
hint of the association of CMa with the warp maximum amplitude. Most
importantly, at a heliocentric distance of 7.3 kpc the 3 models show
excellent agreement with our observed warp
amplitude around
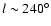 .
.
One also notes that there exists: (i) an overall good agreement
between the López-Corredoira et al. (2002) and
Drimmel & Spergel (2001) models; (ii) a significant
dis-agreement between these two models and the Yusifov
(2004) model; and (iii) significant agreement between
our observed stellar warp and the Yusifov (2004) model.
In Sect. 2.1 we showed that the Yusifov (2004)
model is based on a rather incomplete catalog, thus the closer
agreement of our retrieved warp with this model was an un-expected
result. To solve this confusion however, one must go into the details
of the models.
The 3 models describe the warp as a series of concentric rings which
intersect the Galactic plane along a line of nodes (usually measured
as the Galactocentric angle from the sun to the Galactic center 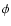 ,
see Fig. 3 and Fig. 1A of Evans et al. 1998).
The models of López-Corredoira et al. (2002) and
Drimmel & Spergel (2001) report
,
see Fig. 3 and Fig. 1A of Evans et al. 1998).
The models of López-Corredoira et al. (2002) and
Drimmel & Spergel (2001) report
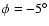 and
and 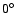 respectively. On the other hand, the Yusifov
(2004) model derives a rather higher
respectively. On the other hand, the Yusifov
(2004) model derives a rather higher
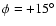 .
.
 different than zero means that the Sun is not located on
the line of nodes, instead it is already inside one of the
two oppositely warped regions.
As a consequence, when viewed from the Sun, geometrically the warp
maximum is nearer to us in one hemisphere than it is in the
other.
Thus, if the warp is traced at fixed distances from the Sun and
different than zero means that the Sun is not located on
the line of nodes, instead it is already inside one of the
two oppositely warped regions.
As a consequence, when viewed from the Sun, geometrically the warp
maximum is nearer to us in one hemisphere than it is in the
other.
Thus, if the warp is traced at fixed distances from the Sun and
 ,
then the observed warp is asymmetric.
Yusifov (2004) derives a positive
,
then the observed warp is asymmetric.
Yusifov (2004) derives a positive  value and
therefore predicts a significantly asymmetric warp, with a relatively
stronger Southern warp maximum amplitude.
On the contrary, López-Corredoira et al. (2002) derive
a negative
value and
therefore predicts a significantly asymmetric warp, with a relatively
stronger Southern warp maximum amplitude.
On the contrary, López-Corredoira et al. (2002) derive
a negative 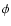 value which produces an observable asymmetric
warp, with a relatively stronger Northern warp maximum amplitude.
Lastly, Drimmel & Spergel (2001) derive
value which produces an observable asymmetric
warp, with a relatively stronger Northern warp maximum amplitude.
Lastly, Drimmel & Spergel (2001) derive
 and therefore their model predicts a symmetric warp; equivalent
Northern/Southern warp maximum amplitudes.
and therefore their model predicts a symmetric warp; equivalent
Northern/Southern warp maximum amplitudes.
Another factor that contributes to the appearance of an asymmetric
warp is due to the chance location of the Northern warp just behind
the Norma-Cygnus arm (labeled outer in Fig. 3).
Thus, extinction in the Norma-Cygnus arm and possible variations of
the extinction curve (due to the penetration of gaseous or dusty
regions), coupled with the possibility that the Sun may not lie on the
line of nodes are all factors that conspire in producing a less
pronounced apparent Northern warp at heliocentric distances of 2.8 and 7.3 kpc.
To develop further the particular issue of a symmetric and asymmetric
stellar warp, we now compare the stellar warp as traced by the 3 RGB samples at different heliocentric distances. Since our
results favor rather high and positive  values
we will continue the comparison with the Yusifov model as this has
shown the best fit to our RGB sample at heliocentric distance 7.3 kpc.
Figure 12 shows clearly that the Yusifov model
provides a satisfactory match with the stellar warp as
derived by the
values
we will continue the comparison with the Yusifov model as this has
shown the best fit to our RGB sample at heliocentric distance 7.3 kpc.
Figure 12 shows clearly that the Yusifov model
provides a satisfactory match with the stellar warp as
derived by the
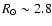 and
and  7.3 kpc RGB samples.
Figure 12 also shows how the Northern warp amplitude is almost
half that of the Southern warp, for the two distances.
7.3 kpc RGB samples.
Figure 12 also shows how the Northern warp amplitude is almost
half that of the Southern warp, for the two distances.
In principle, the warp derived at
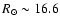 kpc should not
be compared with the Yusifov model (Fig. 13) since that model
is not applicable at
kpc should not
be compared with the Yusifov model (Fig. 13) since that model
is not applicable at
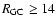 kpc. Nevertheless, for the
derived warp at
kpc. Nevertheless, for the
derived warp at
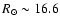 kpc we find that the Yusifov model
predicts maximum warp amplitudes that are not very far from our
derived values; with amplitude differences of 0.25 and 0.15 kpc
above and below the mid-plane, respectively. Moreover, the location
of the warp maxima are still close to those of the derived
data-points, indicating that the warp phase angle is still in
agreement with observations.
Figure 13, also shows another important finding: only at
distances of
kpc we find that the Yusifov model
predicts maximum warp amplitudes that are not very far from our
derived values; with amplitude differences of 0.25 and 0.15 kpc
above and below the mid-plane, respectively. Moreover, the location
of the warp maxima are still close to those of the derived
data-points, indicating that the warp phase angle is still in
agreement with observations.
Figure 13, also shows another important finding: only at
distances of
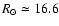 kpc can we obtain a good
symmetry between Northern and Southern warp maximum amplitudes;
both being around
kpc can we obtain a good
symmetry between Northern and Southern warp maximum amplitudes;
both being around  0.6 kpc above and below the mid-plane.
The fact that we obtain a symmetric warp at
0.6 kpc above and below the mid-plane.
The fact that we obtain a symmetric warp at
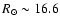 kpc
also indicates that probing the warp at such large distances is
affected less by the dependence on
kpc
also indicates that probing the warp at such large distances is
affected less by the dependence on  .
.
The passage from the stellar warp at
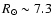 kpc to that at 16.6 kpc shows an out-break in the Northern warp maximum by almost 0.45 kpc. This confirms how probing distant regions (which are less
affected by grand-design structures like the Norma-Cygnus arm) reveals
the real entity of the Northern warp amplitude.
On the other hand, the passage to the stellar warp at
kpc to that at 16.6 kpc shows an out-break in the Northern warp maximum by almost 0.45 kpc. This confirms how probing distant regions (which are less
affected by grand-design structures like the Norma-Cygnus arm) reveals
the real entity of the Northern warp amplitude.
On the other hand, the passage to the stellar warp at
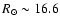 kpc shows a limited increase in the Southern
warp maximum amplitude by
kpc shows a limited increase in the Southern
warp maximum amplitude by  0.2 kpc.
This limited increase probably reflects the way the Southern
gaseous warp shows a saturation effect at
0.2 kpc.
This limited increase probably reflects the way the Southern
gaseous warp shows a saturation effect at  0.75 kpc below
the plane, that induced previous investigations to consider it
constant after
0.75 kpc below
the plane, that induced previous investigations to consider it
constant after
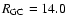 kpc (Burton 1998).
kpc (Burton 1998).
![\begin{figure}
\par\includegraphics[width=7.8cm,height=7.8cm,clip]{4081fig14.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg163.gif) |
Figure 12:
The Galactic stellar disk warp height as derived from
the RGB samples at
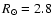 and 7.3 kpc compared
with the Yusifov (2004) model.
and 7.3 kpc compared
with the Yusifov (2004) model. |
| Open with DEXTER |
![\begin{figure}
\includegraphics[width=7.8cm,height=7.8cm,clip]{4081fig15.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg164.gif) |
Figure 13:
The Galactic stellar disk warp height as derived from
the RGB sample at
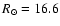 kpc improperly compared with
the Yusifov (2004) model (not applicable at these
distances). Note that for Galactocentric distances greater than 14
kpc the model imposes a constant Southern stellar warp so as to be
consistent with the derived parameters of the gaseous warp. kpc improperly compared with
the Yusifov (2004) model (not applicable at these
distances). Note that for Galactocentric distances greater than 14
kpc the model imposes a constant Southern stellar warp so as to be
consistent with the derived parameters of the gaseous warp. |
| Open with DEXTER |
4.2 Significance of the retrieved stellar warp
Figures 9-13 allow us to conclude the following:
- The correspondance of the CMa over-density with the Southern
warp maximum at
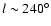 :
this conclusion is based on both our derivation of the stellar warp
(at different distances) and independently derived models. This
establishes that the warp maximum is significantly displaced from
:
this conclusion is based on both our derivation of the stellar warp
(at different distances) and independently derived models. This
establishes that the warp maximum is significantly displaced from
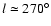 at CMa distances.
at CMa distances.
Now that our results indicate that the Galactic warp at
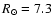 kpc can bring the mid-plane
kpc can bring the mid-plane 
 below the
nominal
below the
nominal
 ,
star-count comparisons above and below the
plane should be made as follows: in the Canis Major direction
(
,
star-count comparisons above and below the
plane should be made as follows: in the Canis Major direction
(
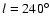 )
star counts at CMa core (
)
star counts at CMa core (
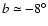 )
should
be compared with those at
)
should
be compared with those at
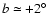 .
This explains the consistent detection of a CMa over-density or
peculiar signature when comparison fields are taken at
.
This explains the consistent detection of a CMa over-density or
peculiar signature when comparison fields are taken at
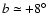 (Martin et al. 2005; Bellazzini et al. 2004).
One further piece of evidence which indicates that the CMa detection
is the recovery of the Galactic warp Southern hemisphere maximum is
found in the so-called structure A.
Along with the CMa over-density, structure A is the second
over-density found in the Martin et al. (2004a)
analysis. Its location (in the Northern hemisphere) makes it fully
compatible with being the Northern warp maximum, as also found in this
paper.
(Martin et al. 2005; Bellazzini et al. 2004).
One further piece of evidence which indicates that the CMa detection
is the recovery of the Galactic warp Southern hemisphere maximum is
found in the so-called structure A.
Along with the CMa over-density, structure A is the second
over-density found in the Martin et al. (2004a)
analysis. Its location (in the Northern hemisphere) makes it fully
compatible with being the Northern warp maximum, as also found in this
paper.
Yet another overdensity (in Argo) has recently been announced
(Rocha-Pinto et al. 2005). Our results suggest that this
over-density cannot be directly correlated to the Galactic warp
maximum (as suggested in Bellazzini et al. 2006).
Indeed, at
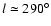 (
( Argo center) the Galactic warp
amplitude is less pronounced than that at
Argo center) the Galactic warp
amplitude is less pronounced than that at
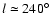 .
To consider a possible origin of this over-density, we
briefly reconsider the analysis of Rocha-Pinto et al. (2005).
In order to increase their accessibility to low latitude sky areas and
reduce the dependency on foreground reddening Rocha-Pinto et al.
(2005) use a Galactic model to remove the foreground
density. The model is idealised in that it assumes a cylindrically
symmetric density distribution about the Galactic center.
Figure 9 shows that the Galactic warp amplitude at
.
To consider a possible origin of this over-density, we
briefly reconsider the analysis of Rocha-Pinto et al. (2005).
In order to increase their accessibility to low latitude sky areas and
reduce the dependency on foreground reddening Rocha-Pinto et al.
(2005) use a Galactic model to remove the foreground
density. The model is idealised in that it assumes a cylindrically
symmetric density distribution about the Galactic center.
Figure 9 shows that the Galactic warp amplitude at
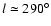 is not zero, inconsistent with the assumptions of
the Rocha-Pinto Galactic model.
Although this effect remains to be quantified, and although the warp
amplitude is not extreme at
is not zero, inconsistent with the assumptions of
the Rocha-Pinto Galactic model.
Although this effect remains to be quantified, and although the warp
amplitude is not extreme at
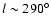 ,
the high star density
this close to the Galactic disk will amplify the residual Galactic
component when Galactic populations are removed, necessarily affecting
the quantification of the Argo over-density.
,
the high star density
this close to the Galactic disk will amplify the residual Galactic
component when Galactic populations are removed, necessarily affecting
the quantification of the Argo over-density.
- The regularity of the Galactic stellar warp out to
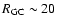 kpc:
We have measured the stellar warp at 3 different distances and argued
that the only visible perturbation away from regularity (a
"swelling'' in the
kpc:
We have measured the stellar warp at 3 different distances and argued
that the only visible perturbation away from regularity (a
"swelling'' in the
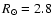 and 16.6 kpc rings) can be
explained as being due to the presence of the Orion-Cygnus arm in
lines of sight towards the Northern warp and between
and 16.6 kpc rings) can be
explained as being due to the presence of the Orion-Cygnus arm in
lines of sight towards the Northern warp and between
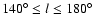 .
That is, we conclude that a global and regular warp signature is
traced to Galactocentric distances of at least
.
That is, we conclude that a global and regular warp signature is
traced to Galactocentric distances of at least  20 kpc in the
anti-center direction. We emphasise this finding, since it is a clear
conclusion even though there are two factors that could have masked
such a signature: 1) the Galactic flare (see next section) and 2) the
decreasing stellar density in the Galaxy's outskirts.
20 kpc in the
anti-center direction. We emphasise this finding, since it is a clear
conclusion even though there are two factors that could have masked
such a signature: 1) the Galactic flare (see next section) and 2) the
decreasing stellar density in the Galaxy's outskirts.
- The consistency of the stellar warp with the dust and gaseous
warp:
In addition to being a regular large-scale structure, the stellar warp
is consistent with that of the interstellar dust and neutral atomic
hydrogen.
The consistency might have been expected given the close physical
correlation between these 3 components. However, it is when
considering accretion scenarios that this finding acquires more
significance.
Accretion of companions can be responsible for generating a
short-lived warp, and can modify differentially the stars-dust-gas
warp properties (cf. Binney 1992).
In regards to this, it is interesting to recall that the numerical
simulations by Helmi et al. (2003), cited to explain
the almost circular orbits of CMa and Mon. Ring, suggest that the
accretion event must be relatively young (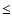 1 Gyr) otherwise any
coherent structure would be dissolved.
Developing consistency between dynamically young events - a few
rotation periods - and global regularity remains to be investigated in
detail.
1 Gyr) otherwise any
coherent structure would be dissolved.
Developing consistency between dynamically young events - a few
rotation periods - and global regularity remains to be investigated in
detail.
- The orientation of the Galactic bar and warp:
The results presented in this paper define a stellar warp
with a rather high and positive phase-angle.
Interestingly, we note that a positive warp phase-angle follows the
orientation of the Galactic bar. The amplitude of the warp
phase-angle (
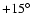 )
in Yusifov's model is very similar to
recent determinations of the Galactic bar orientation: Freudenreich
(1998) derive
)
in Yusifov's model is very similar to
recent determinations of the Galactic bar orientation: Freudenreich
(1998) derive
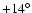 ,
while Babusiaux & Gilmore
(2005) derive
,
while Babusiaux & Gilmore
(2005) derive
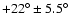 .
We have shown that the pulsar catalog used by Yusifov is biased
towards the Galactic inner regions (
.
We have shown that the pulsar catalog used by Yusifov is biased
towards the Galactic inner regions (
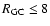 kpc, see
Fig. 1). Whereas this could have been a shortcoming in his
model, it turns out that this inner regions weighted catalog may
have led to a better determination of an important warp parameter; its
phase-angle at least in the inner Galaxy.
Thus, it may be that the Milky Way bar and the inner warp-rings share
the same orientation angle. This point will be further investigated
in Momany et al. (in prep.). For the time being, we note that our
determination of a non-zero phase angle frees us from the
uncomfortable assumption of a fortuitous location of the Sun
along the line of nodes.
kpc, see
Fig. 1). Whereas this could have been a shortcoming in his
model, it turns out that this inner regions weighted catalog may
have led to a better determination of an important warp parameter; its
phase-angle at least in the inner Galaxy.
Thus, it may be that the Milky Way bar and the inner warp-rings share
the same orientation angle. This point will be further investigated
in Momany et al. (in prep.). For the time being, we note that our
determination of a non-zero phase angle frees us from the
uncomfortable assumption of a fortuitous location of the Sun
along the line of nodes.
5 The Galactic flare
In the present section, and before extending our discussion on
the Mon. Ring, we derive another necessary Galactic ingredient,
flaring of the Galactic disk.
For this analysis we use the 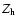 values of the scale height as
determined in Sect. 2.3 for the 3 M-giants samples at
values of the scale height as
determined in Sect. 2.3 for the 3 M-giants samples at
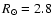 ,
7.3 and 16.6 kpc.
The flaring of the Galactic disk (viewed as an increase of the
scale-height with increasing Galactocentric distance) is evident in
Fig. 14, where we trace the radial trend of
,
7.3 and 16.6 kpc.
The flaring of the Galactic disk (viewed as an increase of the
scale-height with increasing Galactocentric distance) is evident in
Fig. 14, where we trace the radial trend of 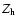 .
Before discussing the details of Fig. 14, we remind the
reader that: (i) we used a single exponential in fitting the vertical
density profile, defining a scale-height; (ii) in the fitting process
we excluded regions at low latitudes so as to avoid regions of high
reddening corrections around the Galactic mid-plane; and most
importantly (iii) our three 2MASS M-giants samples have an upper
vertical limit in latitude of
.
Before discussing the details of Fig. 14, we remind the
reader that: (i) we used a single exponential in fitting the vertical
density profile, defining a scale-height; (ii) in the fitting process
we excluded regions at low latitudes so as to avoid regions of high
reddening corrections around the Galactic mid-plane; and most
importantly (iii) our three 2MASS M-giants samples have an upper
vertical limit in latitude of
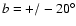 ,
and this corresponds
to different upper Z probing once the distances of the 3 samples is
accounted for.
This also means that we have a different weighting of the thin and
thick disk stellar populations for the three M-giant samples.
Table 1 reports the adopted limits in the vertical density
profile fitting, for the three samples.
Considering that at the solar distance the scale-height of the thin
disk is
,
and this corresponds
to different upper Z probing once the distances of the 3 samples is
accounted for.
This also means that we have a different weighting of the thin and
thick disk stellar populations for the three M-giant samples.
Table 1 reports the adopted limits in the vertical density
profile fitting, for the three samples.
Considering that at the solar distance the scale-height of the thin
disk is  0.3 kpc while that of the thick disk is
0.3 kpc while that of the thick disk is  1 kpc (Wyse
& Gilmore 2005), it is clear that the sample at
1 kpc (Wyse
& Gilmore 2005), it is clear that the sample at
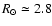 kpc is weighted more by thin disk populations. On
the contrary the
kpc is weighted more by thin disk populations. On
the contrary the
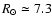 and 16.6 kpc are weighted more
by thick disk populations.
and 16.6 kpc are weighted more
by thick disk populations.
Thanks to the use of different lines of sight at fixed heliocentric
distances, our data-points cover a wide range of Galactocentric
distances and thus are reliable in tracing the flare all over the
Galactic stellar disk (inner and outer).
In particular we note the following:
![\begin{figure}
\includegraphics[width=8cm,clip]{4081fig16.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg177.gif) |
Figure 14:
Variation of the scale-height (derived from the
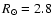 ,
7.3 and 16.6 kpc RGB samples) as a function of
Galactocentric distances. We also show a comparison of our results
with two models and data-points from Alard (2000). ,
7.3 and 16.6 kpc RGB samples) as a function of
Galactocentric distances. We also show a comparison of our results
with two models and data-points from Alard (2000). |
| Open with DEXTER |
- For Galactocentric distances in the range
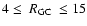 kpc, the
kpc, the
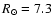 kpc M-giants sample (filled
squares), shows only small variations and in general displays an
almost constant scale-height.
Interestingly, the last data-points clustering around
kpc M-giants sample (filled
squares), shows only small variations and in general displays an
almost constant scale-height.
Interestingly, the last data-points clustering around
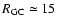 kpc show a saturation of the scale-height at
kpc show a saturation of the scale-height at  0.75 kpc;
0.75 kpc;
- For Galactocentric distances in the range
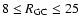 kpc, the
kpc, the
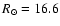 kpc M-giants sample
(open squares), shows a bimodal behavior with an: (i) almost constant
scale-height within
kpc M-giants sample
(open squares), shows a bimodal behavior with an: (i) almost constant
scale-height within
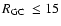 kpc; and (ii) increasing
scale-height for
kpc; and (ii) increasing
scale-height for
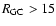 kpc.
The inner radii with the
kpc.
The inner radii with the  constant trend show a mean
scale-height of the same order as that derived from the
constant trend show a mean
scale-height of the same order as that derived from the
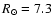 kpc M-giants sample.
By contrast, at large Galactocentric distances with an increasing
scale-height we note that the data-points do not converge to a single
value, but show a gradual increase with distance out to at least
kpc M-giants sample.
By contrast, at large Galactocentric distances with an increasing
scale-height we note that the data-points do not converge to a single
value, but show a gradual increase with distance out to at least
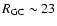 kpc.
The general trends reflect that seen in Alard (2000, starred
symbols) and show fair agreement with the Yusifov model.
A quantitative parametrization of the observed flare and warp will be
subject of a future paper (Momany et al. in prep.).
kpc.
The general trends reflect that seen in Alard (2000, starred
symbols) and show fair agreement with the Yusifov model.
A quantitative parametrization of the observed flare and warp will be
subject of a future paper (Momany et al. in prep.).
- In contrast to the almost constant scale-height derived from the
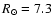 and 16.6 kpc M-giants samples for the inner regions,
the sample at
and 16.6 kpc M-giants samples for the inner regions,
the sample at
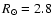 kpc (open triangles) shows some differences.
Between
kpc (open triangles) shows some differences.
Between
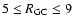 kpc, the
kpc, the
 kpc shows a mean
scale-height of 0.35 kpc, almost half that found for the
kpc shows a mean
scale-height of 0.35 kpc, almost half that found for the
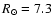 and 16.6 kpc M-giants samples (0.65 kpc).
and 16.6 kpc M-giants samples (0.65 kpc).
This difference in scale-height is mainly due to the different
weighting of the thin and thick disk populations when extracting the
M-giants samples at different distances between
 .
This translates into different
limits when performing the scale-height fitting (cf.
Table 1). For the
.
This translates into different
limits when performing the scale-height fitting (cf.
Table 1). For the
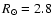 kpc sample the profile
fitting was made between 0.15 and 0.85 kpc, clearly more weighted
towards the thin disk regime. Reassuringly, the overall mean
scale-height of the
kpc sample the profile
fitting was made between 0.15 and 0.85 kpc, clearly more weighted
towards the thin disk regime. Reassuringly, the overall mean
scale-height of the
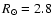 kpc sample (
kpc sample ( 0.35) is close
to typical values for that of the thin disk.
On the other hand, for the
0.35) is close
to typical values for that of the thin disk.
On the other hand, for the
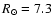 and 16.6 kpc samples the
profile fitting starts at
and 16.6 kpc samples the
profile fitting starts at  1.5 times the thin disk
scale-height. Therefore, the overall mean scale-height of the
1.5 times the thin disk
scale-height. Therefore, the overall mean scale-height of the
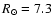 and 16.6 kpc samples is an intermediate value
(0.65 kpc) that reflects the mixing of the thin and the thick disk
populations and respective scale-heights.
Lastly, besides the small difference in mean scale-height, one notes that
the sample at
and 16.6 kpc samples is an intermediate value
(0.65 kpc) that reflects the mixing of the thin and the thick disk
populations and respective scale-heights.
Lastly, besides the small difference in mean scale-height, one notes that
the sample at
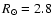 kpc shows a similar trend with
Galactocentric distance as does the flare
model derived by López-Corredoira et al. (2002).
kpc shows a similar trend with
Galactocentric distance as does the flare
model derived by López-Corredoira et al. (2002).
In general, our data-points reflect the fact that the scale-height
increases with increasing Galactocentric radii.
For the inner Galaxy the scale-height is rather similar to the that in
the solar neighborhood, a consistency that continues to about
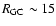 kpc.
Further out the scale-height grows relatively rapidly, with a
smooth increase until about
kpc.
Further out the scale-height grows relatively rapidly, with a
smooth increase until about  23 kpc.
23 kpc.
Table 1:
The limits within which we fit the vertical scale-height for
the three M-giants samples. All values are in kpc.
The thickening of the stellar disk is the re-distribution of stars
from lower to higher latitudes. A disk thickening or flaring is a
phenomenon that requires a reduction below single exponential
extrapolation in the stellar density near the Galactic plane for the
outer disk.
Thus, our detection of (i) a large-scale warp signature out to
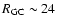 kpc; and (ii) a disk flaring out to
kpc; and (ii) a disk flaring out to
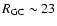 kpc
provides new evidence of a rather extended Milky Way stellar disk.
Therefore, our results add to earlier suggestions by López-Corredoira et al. (2002) and Alard (2000)
that the thin disk cut-off at
kpc
provides new evidence of a rather extended Milky Way stellar disk.
Therefore, our results add to earlier suggestions by López-Corredoira et al. (2002) and Alard (2000)
that the thin disk cut-off at
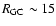 kpc (Ruphy et al.
1996) "is not only unnecessary but also inconsistent
with the data''.
kpc (Ruphy et al.
1996) "is not only unnecessary but also inconsistent
with the data''.
In Fig. 15 we compare the thickening/flaring of the
stellar disk (as obtained from the RGB samples at
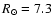 and 16.6 kpc) with that found for the neutral hydrogen gas layer and
molecular clouds ensemble (Wouterloot et al. 1990).
On the one hand, the observations by Wouterloot et al. (1990) are a reminder of the presence of molecular
clouds with embedded star formation out to
and 16.6 kpc) with that found for the neutral hydrogen gas layer and
molecular clouds ensemble (Wouterloot et al. 1990).
On the one hand, the observations by Wouterloot et al. (1990) are a reminder of the presence of molecular
clouds with embedded star formation out to
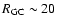 kpc. The
authors argue that the lack of CO emission at
kpc. The
authors argue that the lack of CO emission at
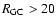 kpc is not
to be attributed to the sensitivity of the IRAS survey, rather it
shows the absence of recent star formation at these distances.
On the other hand, the figure proves the compatibility of the stellar
and gaseous flaring for the outer Milky Way. We remind the reader
that the filled squares refer to a mixture of thin/thick disk stellar
populations, and this explains the gas-stars differences in relative
scale-heights. The different populations shown have different vertical
velocity dispersions, hence their different scale heights.
The only unexpected aspect of this comparison is the very high outer
gas scale height, apparently exceeding that of the stars beyond
kpc is not
to be attributed to the sensitivity of the IRAS survey, rather it
shows the absence of recent star formation at these distances.
On the other hand, the figure proves the compatibility of the stellar
and gaseous flaring for the outer Milky Way. We remind the reader
that the filled squares refer to a mixture of thin/thick disk stellar
populations, and this explains the gas-stars differences in relative
scale-heights. The different populations shown have different vertical
velocity dispersions, hence their different scale heights.
The only unexpected aspect of this comparison is the very high outer
gas scale height, apparently exceeding that of the stars beyond
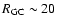 kpc. This is not understood.
kpc. This is not understood.
![\begin{figure}
\includegraphics[width=7.2cm,height=4.2cm,clip]{4081fig17.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg187.gif) |
Figure 15:
A comparison of the thickness of the stellar disk, neutral
hydrogen gas layer and molecular clouds ensemble for the outer Milky
Way. Filled squares show the flaring for the RGB samples at
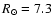 and 16.6 kpc, whereas the open squares plot the RGB samples at
and 16.6 kpc, whereas the open squares plot the RGB samples at
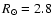 kpc. kpc. |
| Open with DEXTER |
Having demonstrated the existence and determined the properties of the
stellar warp and flare, we now apply this description of a deformed stellar disk to investigate its impact on reported stellar
over-densities at low Galactic latitudes.
In the previous sections we showed that the warp and flare are fairly
well described by the Yusifov model. We therefore will continue
using this model. We remind the reader that the model describes rather
well the inner
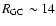 kpc, but represents only a
qualitative description of the outer Milky Way warped and flared
regions.
kpc, but represents only a
qualitative description of the outer Milky Way warped and flared
regions.
6.1 The Canis Major over-density
To show tangibly the importance of allowing for deviations away from
symmetry around
 for studies of the Milky Way stellar
disk, in Fig. 16 we show a cut in the YZ plane of the warped
and flared Galaxy
for studies of the Milky Way stellar
disk, in Fig. 16 we show a cut in the YZ plane of the warped
and flared Galaxy![[*]](/icons/foot_motif.gif) using the Yusifov warp model in the direction
[(
using the Yusifov warp model in the direction
[(
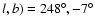 ]
and distance [
]
and distance [
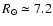 kpc] of CMa (as most recently derived by Bellazzini et al. 2006).
kpc] of CMa (as most recently derived by Bellazzini et al. 2006).
The solid line traces the mean warped stellar disk, whereas the grey
dashed lines follow the three scale heights of the Galactic disk. The
figure shows clearly that the CMa over-density falls at less than  500 pc from the Galactic warped mid-plane, that is
500 pc from the Galactic warped mid-plane, that is 
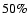 the maximum density of the stellar disk at that distance.
the maximum density of the stellar disk at that distance.
This figure clarifies how important is the Galactic warp to any
analysis of the CMa over-density. Specifically, comparing star counts
at  kpc with those at
kpc with those at 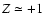 kpc one ends up comparing
a region falling within
kpc one ends up comparing
a region falling within 
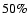 of the stellar disk density with
another having only
of the stellar disk density with
another having only 
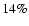 .
.
![\begin{figure}
\includegraphics[width=8cm,height=4.8cm,clip]{4081fig18.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg194.gif) |
Figure 16:
A cut in the YZ plane of the warped and flared Galaxy using the
Yusifov warp model in the direction and at the distance of CMa. The
thick line marks the mean warped stellar disk whereas the grey dashed
lines trace the density at  , ,
 and
and  the scale-height of the
disk. the scale-height of the
disk. |
| Open with DEXTER |
6.2 The Monocerous Ring over-densities
The knowledge of the outer structure of the Galactic disk derived in
this analysis does not provide an explanation for the Monocerous
Ring. However, we show that the Galactic flare can account for
some aspects of some positive detections of the Mon. Ring in various
surveys and therefore, needs to be taken into account in
investigations of the relative importances of accretion or Galactic
structure for the origin for the Mon. Ring.
![\begin{figure}
\includegraphics[width=7.5cm,height=7cm,clip]{4081fig19.ps}\par\...
...*{2mm}
\includegraphics[width=7.5cm,height=7cm,clip]{4081fig20.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg195.gif) |
Figure 17:
The same as in Fig. 16 but for fields where positive detections of
the Mon. Ring have been reported. For the Sloan detections ( upper
three panels) we plot detections at heliocentric distances of 7, 8, 9
and 10 kpc. Similarly, the lower three panels show INT
detections (Conn et al. 2005; Ibata et al. 2003) plotted at the distances given in Table 3 of Conn
et al. |
| Open with DEXTER |
In Fig. 17 we show the location of positive Mon. Ring
detections with respect to the warped and flared Milky Way disk. For
the Sloan fields (Newberg et al. 2002), we plot
detections at heliocentric distances of 7, 8, 9 and 10 kpc, whereas
for the INT fields (Conn et al. 2005; and Ibata et al. 2003) we plot the detections at the specific distances
given in Table 3 of Conn et al.
Figure 17 shows that all reported Mon. Ring detections are at
locations where the structure of the outer warp and flare contribute
to the analysis, and must be carefully considered, and at locations
where the dynamical interaction between Monocerous and the outer disk
will be very important.
The Mon. Ring has attributed properties (a radius of 15-20 kpc, a
radial thickness of 2 kpc and a vertical scale-height of 0.75 kpc,
Ibata et al. 2003) which place it well within the outer
disk defined earlier in this paper.
Of all the Mon. Ring fields, the one at
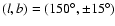 is perhaps the most important.
In their INT survey, Conn et al. (2005) argued that the
detection of Mon. Ring structures on both sides of the Galactic plane,
at similar Galactic longitudes, is the strongest evidence that the
Mon. Ring is not an artefact of Galactic warp effects on star counts.
We agree with Conn et al. (2005) that inadequate
substraction of the warp is not a valid explanation for Mon. Ring
detections above and below the mid-plane. We consider here if disk
flaring provides a valid explanation for the Mon. Ring detections in
both hemispheres at
is perhaps the most important.
In their INT survey, Conn et al. (2005) argued that the
detection of Mon. Ring structures on both sides of the Galactic plane,
at similar Galactic longitudes, is the strongest evidence that the
Mon. Ring is not an artefact of Galactic warp effects on star counts.
We agree with Conn et al. (2005) that inadequate
substraction of the warp is not a valid explanation for Mon. Ring
detections above and below the mid-plane. We consider here if disk
flaring provides a valid explanation for the Mon. Ring detections in
both hemispheres at
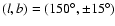 .
.
A hint that Mon. Ring detections are related to disk flaring comes
from the field at
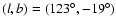 ,
first studied by
Ibata et al. (2003), who reported a positive Mon. Ring
detection at
,
first studied by
Ibata et al. (2003), who reported a positive Mon. Ring
detection at
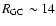 kpc. This field was re-examined by Conn et al. (2005) who reported a possible new detection at
kpc. This field was re-examined by Conn et al. (2005) who reported a possible new detection at
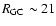 kpc. Figure 17 shows that the earlier and this
new tentative detection of Mon. Ring features follow the expected Z height of the flared MW disk.
kpc. Figure 17 shows that the earlier and this
new tentative detection of Mon. Ring features follow the expected Z height of the flared MW disk.
We are clearly far from performing a quantitative analysis of the
impact of a flared disk on positive detections of Mon. Ring.
On the one hand, we should do our best to decrease the rather
large uncertainties in the distances of Mon. Ring detections.
On the other hand, it would be interesting to have new Galactic models
in which, for example, the radial truncation of the stellar disk at
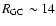 kpc is dropped, the orientation of the warp phase-angle
is updated, and new flare modeling is included.
Note for example that the extensive comparison between observed and
Besançon simulated diagrams in Mon. Ring fields (Conn et al. 2005) implicitly assume a stellar disk truncation at
kpc is dropped, the orientation of the warp phase-angle
is updated, and new flare modeling is included.
Note for example that the extensive comparison between observed and
Besançon simulated diagrams in Mon. Ring fields (Conn et al. 2005) implicitly assume a stellar disk truncation at
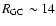 kpc.
Since most of the Mon. Ring detections are at Galactocentric >14 kpc it follows that the comparison with the Galactic model is
inconsistent.
kpc.
Since most of the Mon. Ring detections are at Galactocentric >14 kpc it follows that the comparison with the Galactic model is
inconsistent.
7 Galactic structure to
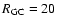 kpc in the outer Galaxy: what
do we expect?
kpc in the outer Galaxy: what
do we expect?
In the previous sections we have shown how complex the outer (beyond
the Solar circle) stellar disk of our Galaxy is, and how many intrinsic
structures can be identified in it. We have also critically discussed
the difficulties in determining the stellar disk main parameters
(warp, flare, scale height) by studying its main stellar
components. Despite these unavoidable difficulties, we have shown that
the parameters inferred from the stellar distribution compare well
with what has been obtained from a number of investigations on the
distribution of the gas, dust, and neutral Hydrogen. In order to
complete our discussion, in this section we add additional information
on what we know about the outer Galactic disk, and some information of
the properties of the stellar disk in other galaxies.
The outer structure of galactic disks, and the Galactic disk, has been
extensively studied for very many years, prior to the current
re-discovery of its intrinsic interest. A considerable amount of
direct information on the outer Galaxy is available, as is further
information by analogy from studies of other galaxies.
A superb review by Burton (1988) summarizes and explains
the subject and data, while presenting the observed basic features
and results which remain valid in the light of new data. The most
extensively studied major component is the H I.
This H I extends approximately smoothly and continuously to 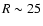 kpc (Burton 1988 Figs. 7.19, 7.20). The distribution is
significantly warped and flared (Figs. 7.18 to 7.23), there are
significant non-circular motions, and the gas is distributed
asymmetrically in azimuth (Fig. 7.21), implying a very significantly
lop-sided gas distribution.
The results from Burton (1988) were updated and extended by
Hartmann & Burton (1997), and most recently in a very
extensive new study of the whole sky H I distribution, using
significantly improved calibrations and stray-light corrections, by
Kalberla et al. (2005).
Inspection of the Hartmann/Burton maps for velocities corresponding to
the far outer Galaxy (
kpc (Burton 1988 Figs. 7.19, 7.20). The distribution is
significantly warped and flared (Figs. 7.18 to 7.23), there are
significant non-circular motions, and the gas is distributed
asymmetrically in azimuth (Fig. 7.21), implying a very significantly
lop-sided gas distribution.
The results from Burton (1988) were updated and extended by
Hartmann & Burton (1997), and most recently in a very
extensive new study of the whole sky H I distribution, using
significantly improved calibrations and stray-light corrections, by
Kalberla et al. (2005).
Inspection of the Hartmann/Burton maps for velocities corresponding to
the far outer Galaxy (
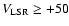 km s-1) shows extremely clearly
that the outer gas layer exists, is smooth in velocity space (i.e.
distance), is centered significantly below the Galactic plane, is
lop-sided and warped, and is thick. By contrast, until the present
resurgence of interest, there have been rather few large angular-scale
studies of the stellar distribution.
km s-1) shows extremely clearly
that the outer gas layer exists, is smooth in velocity space (i.e.
distance), is centered significantly below the Galactic plane, is
lop-sided and warped, and is thick. By contrast, until the present
resurgence of interest, there have been rather few large angular-scale
studies of the stellar distribution.
A very important point to note in anti-center sight-lines is the
considerable "foreground'' complexity associated with the spiral arm
structure, which extends well beyond the solar circle: in particular,
there is the Perseus spiral arm just outside the solar orbit, clearly
visible in CO l-v maps extending across the entire anti-center
region from
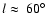 through
through
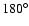 to
to
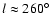 .
In the anti-center foreground, up to 2 kpc distant, especially in the
directions towards
.
In the anti-center foreground, up to 2 kpc distant, especially in the
directions towards
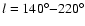 ,
there are large
angular-scale star-forming regions, with their associated dust,
including Monoceros, Orion, the Taurus-Perseus-Auriga complex, and UMa
and Cam OB-star regions. Some of these large-angle structures are
physically large in space (e.g. Gould's belt) and are distributed highly
asymmetrically with respect to the main Galactic Plane.
,
there are large
angular-scale star-forming regions, with their associated dust,
including Monoceros, Orion, the Taurus-Perseus-Auriga complex, and UMa
and Cam OB-star regions. Some of these large-angle structures are
physically large in space (e.g. Gould's belt) and are distributed highly
asymmetrically with respect to the main Galactic Plane.
Thus the simplest and most robust conclusion from a direct examination
of the sky is that one does not expect any simple symmetric
distribution of sources on the sky to be an adequate description of
the outer Galaxy. One must select tracers by distance, and appreciate
complex foregrounds, and expect the outward continuation of normal
spiral structure.
Diplas & Savage (1991), in an early extensive study of
outer-Galaxy gas which remains valid and topical, conclude: for
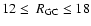 kpc the z-distribution of the H I is
complicated, and reveals the existence of a confined component and an
extended component. The confined component exists only within a
Galactocentric radius
kpc the z-distribution of the H I is
complicated, and reveals the existence of a confined component and an
extended component. The confined component exists only within a
Galactocentric radius
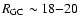 kpc, while the extended
component can be followed in some directions to
kpc, while the extended
component can be followed in some directions to
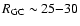 kpc.
In the directions of maximum warp
(
kpc.
In the directions of maximum warp
(
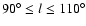 )
the average distance of the gas
away from the the Galactic plane is found to reach
)
the average distance of the gas
away from the the Galactic plane is found to reach  4 kpc at
4 kpc at
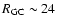 kpc, and the flaring of the layer as measured by
kpc, and the flaring of the layer as measured by
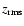 increases to
increases to  3 kpc. In these directions the warping
outer layer appears to be reliably traced over a region at least 10 kpc thick in z. When viewing from the position of the Sun, this
implies that the warped and flaring outer Galaxy extends to Galactic
latitudes as large as
3 kpc. In these directions the warping
outer layer appears to be reliably traced over a region at least 10 kpc thick in z. When viewing from the position of the Sun, this
implies that the warped and flaring outer Galaxy extends to Galactic
latitudes as large as
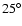 .
.
This raises the interesting question: is the "confined component''
what has been re-discovered recently, the Mon. Ring?
Nakanishi & Sofue (2004) completed a global analysis of
Galactic H I: they show extensions of H I in the outer Galaxy well
beyond 20 kpc, with evidence of very large scale rotational
asymmetry (lop-sided), so much so that the Galaxy extends farther in
the first and fourth quadrants. An important point relevant to
current discussions is that the general outer distribution of the H I is connected but is not simply smooth. Since the distances are derived
from a kinematic model (flat rotation curve), there is a direct
degeneracy between kinematic asymmetries - i.e. elliptical orbits, and
spatial inhomogeneities. Outer spiral structure is evident, as is
vertical warping.
We emphasize that from all these and the many other H I and CO studies there is no evidence for a significant
perturbation from a major satellite accretion event currently
underway: quite the opposite in fact, the global approximate smoothness of
the H I distribution is very difficult to reconcile with such a
model.
There are many molecular studies of the outer Galaxy indicating that
the gas undergoes "normal'' outer galaxy rates and distributions of
star formation, again supportive of a largely steady-state system.
An example is the Brand & Wouterloot (1995) study of outer
IRAS sources, which are star-forming molecular clouds out to
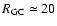 kpc. They collect data from several earlier
studies. Snell et al. (2002) provide a valuable overview of
both the Galactic data and studies of other galaxies, concluding
that outer Galaxy molecular cloud properties and star formation is a
natural extension of the inner Galaxy properties.
kpc. They collect data from several earlier
studies. Snell et al. (2002) provide a valuable overview of
both the Galactic data and studies of other galaxies, concluding
that outer Galaxy molecular cloud properties and star formation is a
natural extension of the inner Galaxy properties.
We note a study by Freudenreich (1996) of the DIRBE
observations of outer galaxy dust, which reports a detection only to
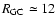 kpc. It is unclear why this study fails to detect
the farther Galactic molecular material, but this paper is the
anomaly, all the other studies agree rather well.
kpc. It is unclear why this study fails to detect
the farther Galactic molecular material, but this paper is the
anomaly, all the other studies agree rather well.
A major CO study by Dame et al. (2001) and
recent extension to higher latitudes by Dame & Thaddeus
(2004) shows extended CO emission at latitudes up to
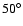 in the anti-center region, with this gas probably being
associated with star formation in Taurus-Auriga. Their Fig. 3 shows
very well the outer molecular gas at velocities up to +100 km s-1,
corresponding to very large Galactocentric distances.
in the anti-center region, with this gas probably being
associated with star formation in Taurus-Auriga. Their Fig. 3 shows
very well the outer molecular gas at velocities up to +100 km s-1,
corresponding to very large Galactocentric distances.
The most recent high-sensitivity southern H I survey, Dickey et al.
(2004) shows that the H I warp continues to more-negative
z-distance as distance increases to a minimum between
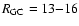 kpc, with the location a function of longitude through this distance
range, and then returns to near Z=0 by
kpc, with the location a function of longitude through this distance
range, and then returns to near Z=0 by
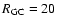 kpc. Beyond 20 kpc and out to 30 kpc the H I distribution "is dominated'' by a
density enhancement which extends coherently over very wide angles,
and may be a coherent extension of the Perseus spiral arm for
longitudes
kpc. Beyond 20 kpc and out to 30 kpc the H I distribution "is dominated'' by a
density enhancement which extends coherently over very wide angles,
and may be a coherent extension of the Perseus spiral arm for
longitudes
 .
This very large structure, if indeed it is coherent, may be similar to
the spiral-like structures in H I extending well beyond the visible
optical disk seen in several other galaxies, with associated star
formation and apparently normal structures, by Ferguson et al. (1998) and the several other examples recently
observed by UV analysis.
.
This very large structure, if indeed it is coherent, may be similar to
the spiral-like structures in H I extending well beyond the visible
optical disk seen in several other galaxies, with associated star
formation and apparently normal structures, by Ferguson et al. (1998) and the several other examples recently
observed by UV analysis.
As an example of studies of external spirals, we note the complex,
asymmetrical, inflowing H I seen in NGC 2403. Fraternelli et al.
(2002) show this is a normal, non-interacting spiral
galaxy, suggesting that such H I features may be common among spiral
galaxies and that, perhaps, they have not been detected yet because of
the low sensitivity of previous surveys.
Bailin & Steinmetz (2003) note that warps are very common,
so much so that perhaps 50% of galaxies have them (Reshetnikov &
Combes (1998). But, warps are not long-lived (e.g.
Binney 1992), so they must be generated in some way.
Hence, if a warp is kinematically driven, there is no reason to expect
simple geometry or kinematics. The actual kinematic pattern will
depend on what is the cause, which is not clear. Possible causes
include the cumulative effects of many satellites (not necessarily on
decaying orbits), though in the case of the Galaxy it may just be the
LMC which induces a large-scale reaction from the DM halo (Weinberg
1998; Tsuchiya 2002; but see
García-Ruiz et al. 2002) or maybe by
Sagittarius (Bailin & Steinmetz 2003).
Bailin & Steinmetz emphasize that a warp generated by interaction
with a satellite is a dynamical warp, so that one does not expect to
see stationary or uniformly precessing kinematics. A transient
induced warp moves outward at the group velocity of bending waves in a
stellar disk, which scales as
 ,
for
surface density
,
for
surface density 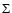 and rotational velocity
and rotational velocity 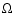 (Hofner &
Sparke 1994) or
(Hofner &
Sparke 1994) or  30 kpc/Gyr near the Sun.
30 kpc/Gyr near the Sun.
Newberg & Yanny (2005) suggest significant triaxiality in
the large scale structure of the outer galaxy star counts. This is for
distances of 3-16 kpc exterior to the Sun. This follows earlier
suggestions by Roberta Humphreys.
Note that they see similar triaxiality and coherent radial motions in
the local old disk, a pattern perhaps consistent with the combined
perturbations on circular orbits due to spiral structure (cf. de Simone et al. 2004) and effects due to a
bar-shaped perturbation in the disk/bulge potential (cf. Babusiaux &
Gilmore 2005). In any event, simple circular orbits are
neither natural nor expected.
Star formation in very outer disks, beyond two R25, has been
detected from H-alpha imaging in several galaxies (e.g. NGC 628,
NGC 1058, NGC 6946 Ferguson et al. 1998). Thilker et al.
(2005) GALEX imaging the outer disk of M 83, shows current
star formation at up to three
 in the warped outer disk
of M 83. The extreme patchiness of the very outer disk is evident in
Fig. 1 of Thilker et al., yet there is no suggestion that what is
observed is anything other than star formation in a disk, albeit at
very large Galactocentric distances.
The GALEX images show star formation, and the existence of both young
and intermediate-age open clusters, well beyond an apparent disk
"edge''. The authors note the location of the young star-forming
regions "preferentially on local maxima or filaments in the structure
of the warped H I disk'', with these complexes superimposed on an
extended field stellar population.
in the warped outer disk
of M 83. The extreme patchiness of the very outer disk is evident in
Fig. 1 of Thilker et al., yet there is no suggestion that what is
observed is anything other than star formation in a disk, albeit at
very large Galactocentric distances.
The GALEX images show star formation, and the existence of both young
and intermediate-age open clusters, well beyond an apparent disk
"edge''. The authors note the location of the young star-forming
regions "preferentially on local maxima or filaments in the structure
of the warped H I disk'', with these complexes superimposed on an
extended field stellar population.
Gentile et al. (2003) looked at ESO123-G23, an apparently
thin edge-on galaxy with a warp in the optical, and saw H I warped gas
up to 15 kpc from the optical major axis, implying a warp through
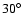 .
.
An interesting specific study, which reminds us that the dynamics of
outer galaxies may not always require current active mergers, is that
by Fraternali et al. (2002) of NGC 2403. They studied
the spiral galaxy NGC 2403 with the VLA, and discussed the properties
of the extended, differentially rotating H I layer with its H I holes,
spiral structure, and outer warp.
In addition, their new data reveal the presence of a faint, extended,
and kinematically anomalous component. This shows up in the H I line
profiles as extended wings of emission toward the systemic velocity.
In the central regions these wings are very broad (up to 150 km s-1) and
indicate large deviations from circular motion. They separated the
anomalous gas component from the cold disk and obtained a
separate velocity field and a separate rotation curve for each. The mass of
the anomalous component is 1/10 of the total H I mass. The rotation
velocity of the anomalous gas is 25-50 km s-1 lower than that of the
disk. Its velocity field has non-orthogonal major and minor axes that
they interpret as due to an overall inflow motion of 10-20 km s-1toward the center of the galaxy. The picture emerging from these
observations is that of a cold H I disk surrounded by a thick and
clumpy H I layer characterized by slower rotation and inflow motion
toward the center. The origin of this anomalous gas layer is
unclear. It is likely, however, that it is related to the high rate of
star formation in the disk of NGC 2403 and that its kinematics is the
result of a galactic fountain-type of mechanism.
In a related study, Fraternali et al. (2004) show that
thin "cold'' H I disks are often surrounded by thick layers (halos) of
neutral gas with anomalous kinematics. They present results for three
galaxies viewed at different inclination angles: NGC 891 (edge-on),
NGC 2403 (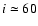 ), and NGC 6946 (almost face-on). These studies
show the presence of halo gas up to distances of 10-15 kpc from the
plane. Such gas has a mean rotation 25-50 km s-1 lower than that of
the gas in the plane, and some complexes are detected at very high
velocities, up to 200-300 km s-1. The nature and origin of this halo
gas are poorly understood. It can either be the result of a galactic
fountain or of accretion from the intergalactic medium. It is
probably analogous to some of the High Velocity Clouds (HVCs) of the
Milky Way.
), and NGC 6946 (almost face-on). These studies
show the presence of halo gas up to distances of 10-15 kpc from the
plane. Such gas has a mean rotation 25-50 km s-1 lower than that of
the gas in the plane, and some complexes are detected at very high
velocities, up to 200-300 km s-1. The nature and origin of this halo
gas are poorly understood. It can either be the result of a galactic
fountain or of accretion from the intergalactic medium. It is
probably analogous to some of the High Velocity Clouds (HVCs) of the
Milky Way.
The overall picture from these many studies is that the outer parts of
galaxies are complex, asymmetric and time-dependent. While not
understood, ongoing mergers of significant companions seem not to be
the primary explanation or cause at work.
We have used the 2MASS all-sky catalog to probe two important outer
Milky Way parameters; the Galactic warp and flare.
We show that the Galactic warp can fully explain the detection of the
Canis Major over-density. We also show that the Galactic flare of the
outer disk will be apparent at those places where there are detection
of Monocerous Ring over-densities.
Thus, the results presented in this paper provide a reminder
that disentangling the accretion history of the outer disk from its
complex and time-dependent dynamics remains a challenge.
Our results add to the well-known evidence of the complexity of outer
Milky Way structure.
The Galactic warp: using 2MASS red clump and red giant stars
we first demonstrated the dependency of the warp parametrization
(amplitude and phase-angle) on the contamination status of the adopted
stellar tracer. Red giants are proved excellent tools in probing the
outer most parts of the Milky Way.
The detection of a global warp signature by RGB stars at mean
heliocentric distances of
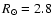 ,
7.3 and 16.6 kpc, has
helped us understand the following:
,
7.3 and 16.6 kpc, has
helped us understand the following:
- The warp phase-angle is oriented in such a way that at fixed
distances from the Sun we observe an asymmetric warp (relatively stronger
maximum amplitude in one hemisphere with respect to the other
hemisphere). For the
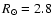 ,
7.3 kpc RGB samples, the
Southern hemisphere warp maximum shows twice the amplitude of
that in the Northern hemisphere. A symmetry of the warp
maximum is obtained only for the
,
7.3 kpc RGB samples, the
Southern hemisphere warp maximum shows twice the amplitude of
that in the Northern hemisphere. A symmetry of the warp
maximum is obtained only for the
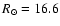 kpc, at which the
dependency on the phase-angle is weakened;
kpc, at which the
dependency on the phase-angle is weakened;
- The warp phase-angle (
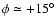 )
is close to the
orientation of the Galactic bar;
)
is close to the
orientation of the Galactic bar;
- The detection of the stellar warp in the RGB sample at a mean
distance
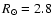 kpc proves that the warp starts within the
solar circle;
kpc proves that the warp starts within the
solar circle;
- The detection of the stellar warp in the RGB sample at a mean
distance
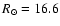 kpc proves the presence of an extended Milky
Way stellar population out to
kpc proves the presence of an extended Milky
Way stellar population out to
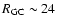 kpc. This is in clear
contradiction with the assumption of a radial truncation of the
stellar disk at
kpc. This is in clear
contradiction with the assumption of a radial truncation of the
stellar disk at
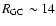 kpc.
The detection of an extended stellar disk is confirmed by parallel,
and independent studies reporting: (i) recent star formation, traced
by molecular clouds, out to
kpc.
The detection of an extended stellar disk is confirmed by parallel,
and independent studies reporting: (i) recent star formation, traced
by molecular clouds, out to
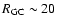 kpc; and (ii) an extended
H I spiral arm in the Third and Fourth quadrants;
kpc; and (ii) an extended
H I spiral arm in the Third and Fourth quadrants;
- For the 3 RGB samples, the Southern hemisphere warp maximum
is found around
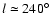 ,
we therefore establish the identity of the CMa center with the warp maximum.
,
we therefore establish the identity of the CMa center with the warp maximum.
- The derived stellar warp shows excellent agreement (in both
the phase-angle and amplitude of the maximum) with that of the gaseous
and interstellar dust distribution. This resolves
conflicting evidence of amplitude differences between the 3 Galactic
components. The origin of the different warp signatures is due
to foreground contamination and distance resolution of the adopted tracer;
These results do not answer the fundamental question of what is
the driving mechanism of the warp? There is no general agreement on
which process, or processes, generate warps (see
Castro-Rodríguez et al. 2002).
Satellite accretion remains one among many scenarios put forward to
explain warps. Other possibilities include: cosmic infall, bending
instabilities, intergalactic magnetic field, accretion of
intergalactic medium (see also Olano 2004, for a possible
warp-HVCs-Magellanic Clouds connection).
Any proposed scenario in a special case should also account for the
fact that warps are a ubiquitous property of most, perhaps all, disk
galaxies (Sánchez-Saavedra et al. 2003).
The Canis Major Overdensity: we have shown here that CMa is
the southern hemisphere maximum stellar warp. We also note that all
CMa properties (measured so far) point to the over-density reflecting
a normal warped disk population rather than that of a cannibalized
dwarf galaxy. Among these we note:
- the absence of any peculiar radial velocity signature (see
Appendix A);
- a possible shortage of an old (
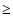 9 Gyr) and metal poor stellar
population (see Appendix B);
9 Gyr) and metal poor stellar
population (see Appendix B);
- the absence of any peculiar proper motion signature (see
Appendix C) and a rather problematic orbital motion
![[*]](/icons/foot_motif.gif) ; and
; and
- a rather high line-of-sight extent (see Appendix D).
The Galactic flare: having characterized the warp, we also
derived the Galactic flare for the 3 RGB samples.
Unable to kinematically discern thick from thin disk populations, the
retrieved variation with
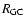 of the disk thickness shows a rather
constant scale-height (
of the disk thickness shows a rather
constant scale-height ( 0.65 kpc) within
0.65 kpc) within
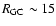 kpc.
Further out, the mean scale-height increases gradually reaching
kpc.
Further out, the mean scale-height increases gradually reaching  1.5 kpc at
1.5 kpc at
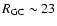 kpc.
Whereas this trend refers to a mixture of thin-thick disk populations,
for the RGB sample at
kpc.
Whereas this trend refers to a mixture of thin-thick disk populations,
for the RGB sample at
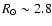 kpc (dominated by thin disk
populations) we derive a mean scale-height of
kpc (dominated by thin disk
populations) we derive a mean scale-height of  0.35 kpc that is
consistent with typical values for the thin disk.
0.35 kpc that is
consistent with typical values for the thin disk.
Overall, we trace the stellar disk flaring out to
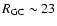 kpc. Thus, we add further and final evidence on the inconsistency of
the disk radial truncation hypothesis, at
kpc. Thus, we add further and final evidence on the inconsistency of
the disk radial truncation hypothesis, at
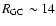 kpc.
Indeed, the detection of stellar disk warping and flaring out to
kpc.
Indeed, the detection of stellar disk warping and flaring out to
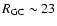 kpc is the key answer to the observed drop in stellar
density near the Galactic plane.
kpc is the key answer to the observed drop in stellar
density near the Galactic plane.
Acknowledgements
We are indebted to the anymous referee the useful suggestions that
improved the overall quality of the paper. YM, GP, LRB and FdA
acknowledge the support by the Italian MIUR under the program PRIN03.
YM thanks Marcel Clemens and Melissa Evans for a careful reading of
the manuscript, and H.I.N.A.S for all the support.
This publication makes use of data products from the Two Micron All
Sky Survey, which is a joint project of the University of
Massachusetts and the Infrared Processing and Analysis
Center/California Institute of Technology, funded by the National
Aeronautics and Space Administration and the National Science
Foundation. We also make use of the WEBDA database and NASA
ExtraGalactic Database.
In "Why the Canis Major over-density is not due to the Warp'', Martin
et al. (2004b) presented radial velocities of M-giants at
the center of CMa. The overall distribution of radial velocities was
strongly characterized by a double-peak morphology. Martin et al. used this distribution to argue that the peak at
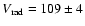 km s-1 is to be attributed to an extra population, CMa, that is
distinguishable from typical disk stars peaking at
km s-1 is to be attributed to an extra population, CMa, that is
distinguishable from typical disk stars peaking at
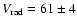 km s-1.
km s-1.
A recent analysis by the same group (Martin et al. 2005)
of more than 1500 RGB and RC stars, showed that the bimodal radial
velocity distribution was artificially produced by template
issues. The new
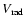 distribution is now broad; there is no
peculiar signature of CMa stars and these are indistinguishable from
surrounding disk stars.
Nevertheless, Martin et al. proceeded and have identified
a "peculiar distance-radial velocity relation that is unlike
that expected from thin or thick disk stars''. That is, while CMa
stars show a mean radial velocity of
distribution is now broad; there is no
peculiar signature of CMa stars and these are indistinguishable from
surrounding disk stars.
Nevertheless, Martin et al. proceeded and have identified
a "peculiar distance-radial velocity relation that is unlike
that expected from thin or thick disk stars''. That is, while CMa
stars show a mean radial velocity of 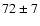 km s-1 at
km s-1 at
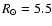 kpc, the mean
kpc, the mean
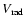 increases to about
increases to about 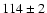 km s-1 at
km s-1 at
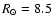 kpc.
kpc.
To date, this "peculiar''
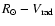 relation is considered
the strongest kinematic evidence standing in favor of an accretion
scenario. However, as we shall demonstrate below, this relation
reflects nothing more than the Galactic differential rotation.
relation is considered
the strongest kinematic evidence standing in favor of an accretion
scenario. However, as we shall demonstrate below, this relation
reflects nothing more than the Galactic differential rotation.
![\begin{figure}
\includegraphics[width=10.3cm,height=10.3cm,clip]{4081fig21.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg228.gif) |
Figure A.1:
Explaining the "peculiar''
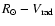 relation found for CMa stars as due to Galactic differential rotation.
The left panel shows a Besançon simulated relation found for CMa stars as due to Galactic differential rotation.
The left panel shows a Besançon simulated
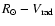 distribution for stars at the CMa center.
Grey dots highlight the modeled Thin Disk truncation at distribution for stars at the CMa center.
Grey dots highlight the modeled Thin Disk truncation at
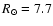 kpc (marked by a horizontal line). Black dots plot
the Thick Disk and Halo stars.
Open triangles show the kpc (marked by a horizontal line). Black dots plot
the Thick Disk and Halo stars.
Open triangles show the
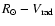 distribuition for
simulated stars extracted from the synthetic color-magnitude diagram
(upper right panel), and falling within a box delimiting the RC region
between
distribuition for
simulated stars extracted from the synthetic color-magnitude diagram
(upper right panel), and falling within a box delimiting the RC region
between
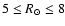 kpc.
The open squares are the observed-RC sample from Martin et al.
(their Fig. 6).
Right middle panel shows the distribution of radial velocities of the
Martin et al. observed-RC sample (dashed histogram), and the
scaled distribution of simulated-RC stars (continuous
histogram).
The right lower panel shows the mean kpc.
The open squares are the observed-RC sample from Martin et al.
(their Fig. 6).
Right middle panel shows the distribution of radial velocities of the
Martin et al. observed-RC sample (dashed histogram), and the
scaled distribution of simulated-RC stars (continuous
histogram).
The right lower panel shows the mean
 of the
dwarfs-decontaminated and RC-simulated sample (open triangles)
estimated in three distance intervals.
The open squares plot the observed mean
of the
dwarfs-decontaminated and RC-simulated sample (open triangles)
estimated in three distance intervals.
The open squares plot the observed mean
 values for CMa RC stars (see Table 2 of Martin et al.) in the same distance
intervals. The error bars are from the same table.
The Dashed line is a linear fit to the Martin et al.
mean values; which is fully compatible with recent estimates of the A Oort constant being
values for CMa RC stars (see Table 2 of Martin et al.) in the same distance
intervals. The error bars are from the same table.
The Dashed line is a linear fit to the Martin et al.
mean values; which is fully compatible with recent estimates of the A Oort constant being
 . .
|
To shed more light on this "peculiar''
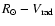 relation,
we combine the results obtained by Martin et al. (their Table 2) with
a kinematic simulation from the Besançon Galactic model.
In the left panel of Fig. A.1 we show the
relation,
we combine the results obtained by Martin et al. (their Table 2) with
a kinematic simulation from the Besançon Galactic model.
In the left panel of Fig. A.1 we show the
 distribution for all simulated stars in the
simulated field centered at (
distribution for all simulated stars in the
simulated field centered at (
 ,
,
 ).
We remind the reader that the Besançon model imposes a stellar disk
truncation already at
).
We remind the reader that the Besançon model imposes a stellar disk
truncation already at
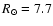 kpc (
kpc (
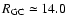 kpc)
kpc)![[*]](/icons/foot_motif.gif) , more or less at the CMa distance.
Thus, at about
, more or less at the CMa distance.
Thus, at about
 kpc and beyond, one cannot
quantitatively compare the observed kinematics with the incomplete
Besançon simulation.
To highlight the abrupt truncation of the simulated Galactic disk,
Thin Disk stars within
kpc and beyond, one cannot
quantitatively compare the observed kinematics with the incomplete
Besançon simulation.
To highlight the abrupt truncation of the simulated Galactic disk,
Thin Disk stars within
 kpc are plotted as grey
dots, while those further out (Thick Disk and Halo) are
plotted as black dots.
Before going into more detail, and prior to any selection or
analysis, one already sees that there is an intuitable
kpc are plotted as grey
dots, while those further out (Thick Disk and Halo) are
plotted as black dots.
Before going into more detail, and prior to any selection or
analysis, one already sees that there is an intuitable
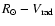 trend in the simulated data, similar to that found
in the Martin et al. analysis for CMa stars.
trend in the simulated data, similar to that found
in the Martin et al. analysis for CMa stars.
The RC sample of Martin et al. (their Fig. 6) is presented in the
left panel (open squares).
In order to compare this observed-RC sample with an appropriate
counterpart from the Besançon simulation (a simulated-RC
sample), we extract RC stars from the one square degree, dereddened K0, (J-K)0 diagram.
The simulated color-magnitude diagram is displayed in the upper
right panel.
In grey symbols we highlight all simulated stellar populations
between
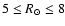 kpc.
The selection box, where we extract simulated-RC stars between
kpc.
The selection box, where we extract simulated-RC stars between
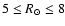 kpc is shown as grey rectangle area.
We emphasize that this simulated-RC sample, as that studied by
Martin et al., is subject to foreground contamination.
kpc is shown as grey rectangle area.
We emphasize that this simulated-RC sample, as that studied by
Martin et al., is subject to foreground contamination.
The advantage of using simulated data is that one can easily isolate
the foreground dwarf contamination from the simulated-RC sample,
by means of the simulated stars distance entries.
All stars included in the simulated-RC sample are plotted in the
left panel (open triangles), showing clearly the contamination by
local dwarfs within  1 kpc.
Between 5.5 and 8.0 kpc simulated-RC stars overlap with the
Martin et al. observed sample (a colored version of the figure is
more appropriate for the disentangling).
1 kpc.
Between 5.5 and 8.0 kpc simulated-RC stars overlap with the
Martin et al. observed sample (a colored version of the figure is
more appropriate for the disentangling).
The middle right panel shows the radial velocities distribution
of the Martin et al. observed-RC sample (dashed histogram).
The distribution of simulated-RC stars as extracted from the
Besançon simulation is plotted as a continuous histogram.
We make use of the Martin et al. (2005) estimate of the
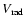 intrinsic dispersion of disk stars at the CMa distance and
add this value (via a Gaussian distribution) to the simulated-RC
stars.
The model histogram has been scaled to fit the observed histogram:
other appropriate scaling is not possible since the Martin et al. (2005) selection function of RC stars is unknown.
The similarity of the two distributions is remarkable, we note however
that the histogram of simulated-RC stars shows a slightly higher
distribution (with respect to the observed sample) for stars
with
intrinsic dispersion of disk stars at the CMa distance and
add this value (via a Gaussian distribution) to the simulated-RC
stars.
The model histogram has been scaled to fit the observed histogram:
other appropriate scaling is not possible since the Martin et al. (2005) selection function of RC stars is unknown.
The similarity of the two distributions is remarkable, we note however
that the histogram of simulated-RC stars shows a slightly higher
distribution (with respect to the observed sample) for stars
with
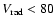 km s-1, and a lower distribution for
km s-1, and a lower distribution for
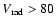 km s-1.
The later feature can be explained as being due to the truncation of
disk population in the Besançon model at
km s-1.
The later feature can be explained as being due to the truncation of
disk population in the Besançon model at
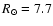 kpc:
simulating more distant populations will result in more stars only
having
kpc:
simulating more distant populations will result in more stars only
having
 higher than 80 km s-1. On the other hand, the higher
distribution of simulated-RC stars at
higher than 80 km s-1. On the other hand, the higher
distribution of simulated-RC stars at
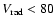 km s-1 can be
due to a stronger foreground dwarf contamination in the input model
(note in fact the discrete and distinguishable distribution of local
dwarfs within 1 kpc).
The two distributions remain, however, very similar and this is
further demonstrated in the lower right panel where we (i) exclude nearby dwarfs from the simulated-RC sample, (ii) use
this cleaned simulated-RC sample to estimate the mean
km s-1 can be
due to a stronger foreground dwarf contamination in the input model
(note in fact the discrete and distinguishable distribution of local
dwarfs within 1 kpc).
The two distributions remain, however, very similar and this is
further demonstrated in the lower right panel where we (i) exclude nearby dwarfs from the simulated-RC sample, (ii) use
this cleaned simulated-RC sample to estimate the mean
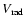 in 3 distances intervals (
in 3 distances intervals (
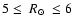 ,
,
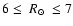 and
and
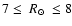 kpc); and (iii) compare the cleaned and simulated
kpc); and (iii) compare the cleaned and simulated
 values with those
derived by Martin et al. (2005), in the 3 distance
intervals.
values with those
derived by Martin et al. (2005), in the 3 distance
intervals.
We emphasize the fact that the mean CMa
 values derived in the 3 distance intervals (Martin et al 2005, open squares in the
lower right panel) are based on what they call "CMa RC sample'',
which they disentangle from the "contaminating population''.
Keeping in mind all the uncertainties associated with the
Besançon model, one clearly sees that the cleaned simulated-RC
sample (open triangles in the lower right panel) shows, within 1
values derived in the 3 distance intervals (Martin et al 2005, open squares in the
lower right panel) are based on what they call "CMa RC sample'',
which they disentangle from the "contaminating population''.
Keeping in mind all the uncertainties associated with the
Besançon model, one clearly sees that the cleaned simulated-RC
sample (open triangles in the lower right panel) shows, within 1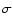 ,
the same
,
the same
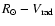 trend found by Martin et al. for a cleaned CMa RC sample.
trend found by Martin et al. for a cleaned CMa RC sample.
One last piece of evidence which demonstrates that the "peculiar
CMa observed
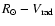 trend'' is nothing but the imprint
of Galactic differential rotation of normal disk stars is shown in the
lower panel of Fig. A.1.
Indeed, a linear fit of the three points reported by Martin et al.
(2005) yields
trend'' is nothing but the imprint
of Galactic differential rotation of normal disk stars is shown in the
lower panel of Fig. A.1.
Indeed, a linear fit of the three points reported by Martin et al.
(2005) yields
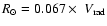 .
Using the
Oort equation:
.
Using the
Oort equation:
one easily gets
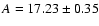 ,
fully compatible with recent
estimates of the A Oort constant (see Dehnen 1998).
Obviously, one has to consider the CMa large heliocentric distance and
location with respect to the Galactic disk, however, the linear
relation is really surprising, and does not leave room for any other
easy interpretation.
,
fully compatible with recent
estimates of the A Oort constant (see Dehnen 1998).
Obviously, one has to consider the CMa large heliocentric distance and
location with respect to the Galactic disk, however, the linear
relation is really surprising, and does not leave room for any other
easy interpretation.
Given that (i) the bimodal
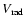 distribution (Martin et al.
2004b) was due to an artifact in their
reduction procedure, and (ii) that the claimed peculiar
distribution (Martin et al.
2004b) was due to an artifact in their
reduction procedure, and (ii) that the claimed peculiar
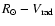 relation (Martin et al. 2005) is well
reproduced by a self-consistent kinematical model, and most
importantly, seems to be nothing more than the imprint of differential
Galactic rotation.
We therefore conclude that the stellar populations of CMa do not
show any peculiar or distinguishable
relation (Martin et al. 2005) is well
reproduced by a self-consistent kinematical model, and most
importantly, seems to be nothing more than the imprint of differential
Galactic rotation.
We therefore conclude that the stellar populations of CMa do not
show any peculiar or distinguishable
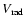 signature with respect
to normal disk stars.
signature with respect
to normal disk stars.
All studied dwarf galaxies are known to possess an ancient stellar
population that is traced by the detection of either 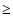 9 Gyr RR Lyrae variables and/or red/blue horizontal branch stars of similar
age. Dwarf galaxies in the Local Group show no exception to this rule
(Mateo 1998; Tolstoy 2000; Grebel
2001)
9 Gyr RR Lyrae variables and/or red/blue horizontal branch stars of similar
age. Dwarf galaxies in the Local Group show no exception to this rule
(Mateo 1998; Tolstoy 2000; Grebel
2001)![[*]](/icons/foot_motif.gif) . To this adds the most recent entry, Ursa Major (Willman et al. 2005), which shows a clear clump of blue horizontal
branch stars.
Those in favor of an extra-Galactic accretion scenario of CMa often
highlight the similarities (e.g. mean metallicity, mean mass, MVetc.) between the CMa stellar populations and the Sagittarius dwarf
spheroidal. As a consequence, it is particularly important to
investigate the presence of an old (
. To this adds the most recent entry, Ursa Major (Willman et al. 2005), which shows a clear clump of blue horizontal
branch stars.
Those in favor of an extra-Galactic accretion scenario of CMa often
highlight the similarities (e.g. mean metallicity, mean mass, MVetc.) between the CMa stellar populations and the Sagittarius dwarf
spheroidal. As a consequence, it is particularly important to
investigate the presence of an old (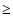 9 Gyr) and metal-poor
population of CMa.
9 Gyr) and metal-poor
population of CMa.
Needless to say, an old and metal-poor population is necessary to
metal enrich successive generations of stars, otherwise one cannot
explain how a metal-rich galaxy ([Fe/H![$]\ge-1$](/articles/aa/full/2006/20/aa4081-05/img242.gif) )
could have built
metal-poor clusters.
The Sagittarius dwarf fulfills this requirement; i.e. besides being on
average a metal-rich galaxy, it possesses a metal-poor component that
is traced by RR Lyraes and blue horizontal branch stars (see Monaco et al. 2003 and references therein), and possibly extreme horizontal
branch stars (Momany et al. 2004a). This explains the
progeny of metal-poor clusters like Terzan 8 and M 54.
Studying the Sagittarius stellar populations outside the tidal radius
of M 54, Monaco et al. (2003) proved that the group of blue
horizontal branch stars identified in S341+57-22.5 by Newberg et al.
(2002), are fully compatible with the blue horizontal
branch of Sagittarius. This shows that a stream, narrow by
definition, originating from a disrupting dwarf is likely to leave a
footprint of all its stellar populations (both red and blue).
)
could have built
metal-poor clusters.
The Sagittarius dwarf fulfills this requirement; i.e. besides being on
average a metal-rich galaxy, it possesses a metal-poor component that
is traced by RR Lyraes and blue horizontal branch stars (see Monaco et al. 2003 and references therein), and possibly extreme horizontal
branch stars (Momany et al. 2004a). This explains the
progeny of metal-poor clusters like Terzan 8 and M 54.
Studying the Sagittarius stellar populations outside the tidal radius
of M 54, Monaco et al. (2003) proved that the group of blue
horizontal branch stars identified in S341+57-22.5 by Newberg et al.
(2002), are fully compatible with the blue horizontal
branch of Sagittarius. This shows that a stream, narrow by
definition, originating from a disrupting dwarf is likely to leave a
footprint of all its stellar populations (both red and blue).
![\begin{figure}
\includegraphics[width=7.5cm,height=7.5cm,clip]{4081fig22.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg243.gif) |
Figure B.1:
A 1 dereddened color-magnitude diagrams of the
core of CMa. Over-plotted is a 6.3 Gyr Z=0.004 ([Fe/H
dereddened color-magnitude diagrams of the
core of CMa. Over-plotted is a 6.3 Gyr Z=0.004 ([Fe/H
![$]\simeq -0.76$](/articles/aa/full/2006/20/aa4081-05/img35.gif) )
isochrone from The Girardi et al. (2002) library. The
assumed distance modulus is (m-M)0=14.5. Each star was
dereddened according to its position in the Schlegel et al. (1998) reddening maps. Also plotted are the red clump and
blue horizontal branch location of the Sagittarius, as derived by
Monaco et al. (2003). )
isochrone from The Girardi et al. (2002) library. The
assumed distance modulus is (m-M)0=14.5. Each star was
dereddened according to its position in the Schlegel et al. (1998) reddening maps. Also plotted are the red clump and
blue horizontal branch location of the Sagittarius, as derived by
Monaco et al. (2003). |
Despite the fact that contamination can seriously hamper the
identification of old blue horizontal branch stars near the Galactic
plane, we note that the CMa over-density has not been associated with
a clear identification, or even a hint, of old blue horizontal branch
stars.
Figure B.1 displays a wide-field color-magnitude diagram
of the CMa center, based on archival ESO/2.2 m telescope data. The data
has been reduced and calibrated following the standard techniques
presented in (Momany et al. 2001).
Upon this color-magnitude diagram we over-plot the mean location of
red clump and blue horizontal branch stars in the Sagittarius dwarf
(as derived in Monaco et al. 2003), shifted to match the
CMa red clump population. No hint of an over-density of stars at the
expected blue horizontal branch location can be seen.
Instead, the distribution of stars between
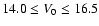 and
and
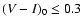 smoothly increases towards fainter
magnitudes.
We remind the reader that at
smoothly increases towards fainter
magnitudes.
We remind the reader that at
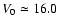 ,
and in between
,
and in between
 there lies a population of young
there lies a population of young  100 Myr main sequences stars which belong to the Norma-Cygnus spiral
arm, as demonstrated by Carraro et al. (2005) by means of
100 Myr main sequences stars which belong to the Norma-Cygnus spiral
arm, as demonstrated by Carraro et al. (2005) by means of  two-color diagrams. This population is intermediate between the
disk MS stars (oblique sequence extending from
two-color diagrams. This population is intermediate between the
disk MS stars (oblique sequence extending from
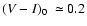 at
at
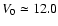 to
to
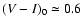 at
at
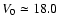 )
and the blue plume population at bluer colors.
An eventual over-density due to the presence of blue horizontal branch
star (
)
and the blue plume population at bluer colors.
An eventual over-density due to the presence of blue horizontal branch
star (
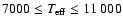 K) should take place in between
the disk main sequence and blue plume, but this region lacks any
significant over-density.
A similar indication is found in the optical color-magnitude diagrams
of Martínez-Delgado (2005) and Bellazzini
(2006).
K) should take place in between
the disk main sequence and blue plume, but this region lacks any
significant over-density.
A similar indication is found in the optical color-magnitude diagrams
of Martínez-Delgado (2005) and Bellazzini
(2006).
Recently, Mateu et al. (2004) reported on a preliminary RR Lyrae search in an area of 8.3 square degrees at the center of the
CMa. Five RR Lyraes were found at heliocentric distances of less than
6.5 kpc. Assuming the most recent CMa distance range (6.2-8.2 kpc by Bellazzini et al. 2006) the 5 variables with a mean distance of 5.6 kpc are outside the main body of the CMa over-density.
Yet, as noted by the Mateu et al., the detection of 5 variables is
higher than what would be expected in the same volume of the Galactic Halo ( 1 variable).
Unfortunately, a direct comparison with the expected number of Disk RR Lyrae is difficult since the distribution (and density) of RR
Lyrae stars in the thick disk is not known. Moreover, one
should add the current uncertainty in (i) disentangling Disk and Halo
RR Lyrae at low Galactic latitudes, and (ii) the disk density profile
as a function of
1 variable).
Unfortunately, a direct comparison with the expected number of Disk RR Lyrae is difficult since the distribution (and density) of RR
Lyrae stars in the thick disk is not known. Moreover, one
should add the current uncertainty in (i) disentangling Disk and Halo
RR Lyrae at low Galactic latitudes, and (ii) the disk density profile
as a function of
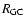 .
As demonstrated thoroughly in this paper,
the disk radial extension does not show an abrupt truncation at
.
As demonstrated thoroughly in this paper,
the disk radial extension does not show an abrupt truncation at
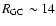 kpc, and this might increase the number of expected
variable stars.
kpc, and this might increase the number of expected
variable stars.
We therefore conclude that there is no evidence which demonstrates the
presence of an old, blue horizontal branch population CMa. At the same
time, RR Lyrae surveys leave this issue rather 2open, highlighting
intrinsic difficulties (expected Galactic contamination and relative
vicinity of CMa) of similar studies.
More data is needed to draw a firmer conclusion.
Dinescu et al. (2005) have recently re-measured the
absolute proper motion at the center of the Canis Major over-density,
which was first determined by Momany et al. (2004b using
UCAC2 catalogs![[*]](/icons/foot_motif.gif) ).
The authors find that while CMa has an in-plane rotation (similar to
the mean of thick disk stars) it shows significant 3
).
The authors find that while CMa has an in-plane rotation (similar to
the mean of thick disk stars) it shows significant 3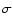 motion
perpendicular to the disk. In turn, they find this inconsistent (at a
7
motion
perpendicular to the disk. In turn, they find this inconsistent (at a
7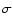 level) with the expected motion of the warp at these
Galactic locations (estimated in Drimmel et al.
2000).
This incompatibility lead Dinescu et al. (2005) to
conclude that CMa is part of a satellite galaxy remnant.
level) with the expected motion of the warp at these
Galactic locations (estimated in Drimmel et al.
2000).
This incompatibility lead Dinescu et al. (2005) to
conclude that CMa is part of a satellite galaxy remnant.
To resolve the claimed incompatibility we note that the Dinescu et al.
(2005) conclusions rely on two points. The first is the
assumption that their selected sample [used to measure the proper
motion and consisting of "likely main sequence stars'' or blue
plume stars] is a photometrically clean sample of genuine CMa stars,
un-contaminated by Galactic disk stars.
This assumption however is in complete contradiction with the recent
finding of Carraro et al. (2005), who have shown that the
distribution of the blue plume population in the background of 30 open
clusters (in the Third quadrant and at
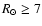 kpc) follows
the expected pattern of the Norma-Cygnus (outer) spiral arm remarkably
well.
Thus the CMa over-density resides on an outer spiral arm, and the
young blue plume population (seen in various CMa diagrams) is simply
not associated with it.
This is a particularly important issue because it explains the
difference in the proper motion at the CMa-center obtained by Dinescu
et al. (2005, using MS stars) and Momany et al.
(2004b, using RGB stars) which in turn brings us back to
the situation where the proper motion of CMa is indistinguishable from
surrounding disk stars
kpc) follows
the expected pattern of the Norma-Cygnus (outer) spiral arm remarkably
well.
Thus the CMa over-density resides on an outer spiral arm, and the
young blue plume population (seen in various CMa diagrams) is simply
not associated with it.
This is a particularly important issue because it explains the
difference in the proper motion at the CMa-center obtained by Dinescu
et al. (2005, using MS stars) and Momany et al.
(2004b, using RGB stars) which in turn brings us back to
the situation where the proper motion of CMa is indistinguishable from
surrounding disk stars![[*]](/icons/foot_motif.gif) .
.
Secondly, the fact that the negative W of CMa is irreconcilable with
the expected signature of the Galactic warp (positive W) is simply
not true, since these expectations are model-dependent. We will
demonstrate this by using the same cited article of Drimmel et al.
(2000), paying more attention to what these authors report
at the end of their article.
We first remind the reader that Drimmel et al. (2000)
used Hipparcos OB stars as tracers of the Galactic warp. Therefore,
it is particularly important to recall recent problems in the inferred
Hipparcos parallaxes of O stars. Schröder et al.
(2004) using a sample of 153 stars, conclude that their
absolute magnitude (calculated from their apparent magnitude and the
Hipparcos parallax) appear to be much fainter than expected, by
up to 5 mag. Such huge differences were found to arise from
the distances at which O stars were located, and the level of
precision of the parallax measurements achieved by Hipparcos. Their
Fig. 2 clearly shows that large magnitude differences are expected
when using the relatively uncertain Hipparcos parallaxes at distances
of already  1 kpc.
1 kpc.
Accounting for this fact, we reconsider the work of Drimmel et al. (2000). In their Fig. 11, they report a comparison
of the measured vertical velocity component (W) vs.
Galactocentric distances. At
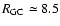 kpc, a
divergence between measured W values of distant OB stars
(increasingly negative W values) and the expected observable
signature of the warp (increasingly positive W values) occurs.
It remains, however, that Drimmel et al. (2000, their
Sect. 7) investigate the effect of bias, amplitude and precision on
the inconsistency between the observed and the expected warp W values. In their Fig. 12, the authors unambiguously show that
"negative vertical motions are finally achieved'', if they
allow for: (i) a warp that has half the amplitude with respect to the
one they derive; (2) a warp precessing at -25 km s-1 kpc-1; and (iii) a 0.5 mag error is added.
kpc, a
divergence between measured W values of distant OB stars
(increasingly negative W values) and the expected observable
signature of the warp (increasingly positive W values) occurs.
It remains, however, that Drimmel et al. (2000, their
Sect. 7) investigate the effect of bias, amplitude and precision on
the inconsistency between the observed and the expected warp W values. In their Fig. 12, the authors unambiguously show that
"negative vertical motions are finally achieved'', if they
allow for: (i) a warp that has half the amplitude with respect to the
one they derive; (2) a warp precessing at -25 km s-1 kpc-1; and (iii) a 0.5 mag error is added.
Now, leaving aside the excessively high precision rates which
Drimmel et al. (2000) also find questionable, it is a matter of
fact that the remaining two bias strongly contribute in reproducing
negative vertical velocities.
On the one hand, the results presented in this paper (see in
particular Fig. 2 of Yusifov 2004) show that the warp
amplitude as derived by Drimmel et al. (2000) is very
high.
Indeed, at a Galactocentric distance of 10 kpc, Drimmel et al. note
that their warp amplitude is more than twice the gas warp amplitude,
and not surprisingly they halve it. In particular, the authors
note that the effect of misplacement of a star to larger distances is
that its measured relative vertical motion will be smaller than its
true relative vertical motion.
On the other hand, there is now enough evidence to suggest that the
Hipparcos data can have significantly higher errors as suggested by
Schröder et al. (see also Soderblom et al. (2005)
on a recent confirmation of errors in the Hipparcos parallaxes already
at the Pleiades distance).
Thus, introducing a 0.5 mag (as done by Drimmel et al.
2000) could have been seen as extreme at that time.
Nowadays, however, with confirmed errors of more than 2 mag
(for the same sample of hot stars) at much closer distances, the
evidence suggests that the expected warp signature can be and is
compatible with negative vertical velocity.
Since Dinescu et al. mistake main sequence stars belonging to a
Galactic spiral arm for genuine CMa population, and given the above
discussion on the compatibility of negative W values with the warp
at CMa location, we conclude that the proper motion of CMa does not
show any peculiar signature with respect to Galactic disk stars.
Recently Martínez-Delgado et al. (2005) presented
a deep wide-field B, (B-R) color-magnitude diagram of the CMa
center and derived the line-of-sight extent (or depth) of CMa.
For this task, Martínez-Delgado et al. estimated the observed
width of the CMa main sequence (
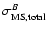 )
by
selecting stars in a narrow color range,
)
by
selecting stars in a narrow color range,
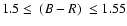 ,
at
,
at
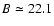 .
Their best fitting of
.
Their best fitting of
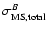 (converted into
kilo-parsec) yielded
(converted into
kilo-parsec) yielded
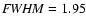 kpc. Moreover, and for a proper
comparison with other studied Local Group dwarf spheroidals, they also
estimated the line-of-sight half-brightness radius (r1/2),
obtaining
kpc. Moreover, and for a proper
comparison with other studied Local Group dwarf spheroidals, they also
estimated the line-of-sight half-brightness radius (r1/2),
obtaining  1 kpc.
1 kpc.
Martínez-Delgado et al. (2005) noted that this size
is "significantly bigger than that of several dwarf galaxies in
the Local Group'', e.g. the r1/2 of the Fornax dwarf
spheroidal is 0.33 kpc (see Table 4 of Irwin & Hatzidimitriou
1995).
Nevertheless, one finds that this rather large value found by
Martínez-Delgado et al. (2005) is often cited in
support of a "narrow extent line-of-sight'' of CMa (Martin et al. 2005; Conn et al. 2005) or even evidence of a
"typical size of a dwarf spheroidal galaxy'' (Bellazzini et al. 2006).
In regards to this, and in light of recent finding of the presence of the
Norma-Cygnus (outer) spiral arm in the third quadrant (Carraro et al. 2005), we compare the FWHM of CMa as obtained by
Martínez-Delgado et al. (2005) with typical values
for Galactic spiral arms.
Following Bronfman et al. (2000), we estimate the FWHM of
the most distant spiral arm at
R/R0=1.3, where R0=8.5 kpc. Relying on their Fig. 8, we estimate a FWHM of  1.7 kpc, very much in accordance with the Martínez-Delgado et al.
(2005) 1.95 kpc value for CMa. Indeed, one must also bear
in mind that an outer spiral arm would also be more flared,
thereby a FWHM of
1.7 kpc, very much in accordance with the Martínez-Delgado et al.
(2005) 1.95 kpc value for CMa. Indeed, one must also bear
in mind that an outer spiral arm would also be more flared,
thereby a FWHM of  1.7 kpc sets only a lower limit.
One last piece of evidence that the reported CMa FWHM is compatible
with a spiral arm feature comes from the study by McClure-Griffiths et al. (2005). The detected H I arm in the Fourth and
Third quadrants appeared to be approximately 1 to 2 kpc thick along
the line of sight.
1.7 kpc sets only a lower limit.
One last piece of evidence that the reported CMa FWHM is compatible
with a spiral arm feature comes from the study by McClure-Griffiths et al. (2005). The detected H I arm in the Fourth and
Third quadrants appeared to be approximately 1 to 2 kpc thick along
the line of sight.
We therefore conclude that the CMa depth as measured by
Martínez-Delgado et al. (2005) is more compatible
with a distant spiral arm rather than a dwarf spheroidal.
Note added in proof
Recently, Moitinho et al. (2006) used young ( 100 Myr) open clusters and field "blue plume'' population to reconstruct
the spiral structure in the Third Galactic quadrant. They confirmed
the detection of a structure interpreted as a natural extension of the
Norma-Cygnus spiral arm. Their conclusion (based on
100 Myr) open clusters and field "blue plume'' population to reconstruct
the spiral structure in the Third Galactic quadrant. They confirmed
the detection of a structure interpreted as a natural extension of the
Norma-Cygnus spiral arm. Their conclusion (based on  photometry of OB objects) is consistent with our finding of an
extended MW disk (using 2MASS M-giants). Moitinho et al. went a step
further and proposed that the CMa M-giant over-density is simply the
result of looking along the extension of the local Orion arm in the
Third quadrant.
photometry of OB objects) is consistent with our finding of an
extended MW disk (using 2MASS M-giants). Moitinho et al. went a step
further and proposed that the CMa M-giant over-density is simply the
result of looking along the extension of the local Orion arm in the
Third quadrant.
In regards to this, we note that the Moitinho et al. (2006) and Carraro et al. (2005) papers
have been valuable in clearing the connection between the blue plume
population (erroneously attributed to CMa by Martínez-Delgado
et al. 2005; Bellazzini et al. 2004; and Dinescu
et al. 2005) and both the red clump and red giant
populations (that first brought to the detection of the CMa
over-density).
Nevertheless, the Moitinho et al. analysis does not address, nor
preclude, the very occurrence of the CMa over-density at
 .
Indeed, the detection of a spiral arm composed by young blue
objects (best identified in
.
Indeed, the detection of a spiral arm composed by young blue
objects (best identified in  photometry) is not sufficient to
affirm/conclude a Galactic nature for the un-ambiguous presence of the
older (2-10 Gyr) CMa M-giant over-density (best seen in the
2MASS infrared photometry).
The asymmetry in the distribution of the MW disk stars (Galactic warp)
remains the explanation for the observed asymmetric number
density at
photometry) is not sufficient to
affirm/conclude a Galactic nature for the un-ambiguous presence of the
older (2-10 Gyr) CMa M-giant over-density (best seen in the
2MASS infrared photometry).
The asymmetry in the distribution of the MW disk stars (Galactic warp)
remains the explanation for the observed asymmetric number
density at
 and
and
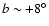 .
The warp
signature is evident in Fig. 2 of Moitinho et al.
(2006).
.
The warp
signature is evident in Fig. 2 of Moitinho et al.
(2006).
- Alard, C. 2000
[arXiv:astro-ph/0007013]
(In the text)
- Amôres, E. B.,
& Lépine, J. R. D. 2005, AJ, 130, 659 [NASA ADS] [CrossRef] (In the text)
- Bailin, J., &
Steinmetz, M. 2003, Proceedings of the conference, Satellites and
Tidal Streams [arXiv:astro-ph/0310199]
(In the text)
- Babusiaux, C., &
Gilmore, G. 2005, MNRAS, 358, 1309 [NASA ADS] [CrossRef] (In the text)
- Benjamin, R. A.,
Churchwell, E., Babler, B. L., et al. 2005, ApJ, 630, L149 [NASA ADS] [CrossRef] (In the text)
- Bensby, T.,
Feltzing, S., & Lundström, I. 2004, A&A, 421, 969 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Bellazzini, M., Ibata,
R., Monaco, L., et al. 2004, MNRAS, 354, 1263 [NASA ADS] [CrossRef] [B04]
(In the text)
- Bellazzini, M., Ibata,
R., Martin, N., et al. 2006, MNRAS, 155
[arXiv:astro-ph/0504494]
(In the text)
- Binney, J. 1992,
ARA&A, 30, 51 [NASA ADS] (In the text)
- Bonifacio, P., Monai,
S., & Beers, T. C. 2000, AJ, 120, 2065 [NASA ADS] [CrossRef] (In the text)
- Brand, J., &
Wouterloot, J. G. A. 1995, A&A, 303, 851 [NASA ADS] (In the text)
- Bronfman, L.,
Casassus, S., May, J., & Nyman, L.-Å. 2000, A&A, 358,
521 [NASA ADS] (In the text)
- Burton, W. B. 1988,
in Galactic and Extragalactic Radio astronomy, ed. G. L. Verscuur,
& K. I. kellermann (Springer)
(In the text)
- Carney, B. W.,
& Seitzer, P. 1993, AJ, 105, 212 [NASA ADS] (In the text)
- Carraro, G.,
Vázquez, R. A., Moitinho, A., & Baume, G. 2005, ApJ, 630,
L153 [NASA ADS] [CrossRef] (In the text)
- Carraro, G.,
Bresolin, F., Villanova, S., et al. 2004, AJ, 128, 1676 [NASA ADS] [CrossRef]
-
Castro-Rodríguez, N., López-Corredoira, M.,
Sánchez-Saavedra, M. L., & Battaner, E. 2002, A&A,
391, 519 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Conn, B. C., Lewis, G.
F., Irwin, M. J., et al. 2005, MNRAS, 362, 475 [NASA ADS] [CrossRef] (In the text)
- Crane, J. D.,
Majewski, S. R., Rocha-Pinto, H. J., et al. 2003, ApJ, 594,
L119 [NASA ADS] [CrossRef] (In the text)
- Cutri, R. M., et al.
2003, VizieR Online Data Catalog, 2246
- Dame, T. M., Hartmann,
D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] (In the text)
- Dame, T. M., &
Thaddeus, P. 2004, Milky Way Surveys: The Structure and Evolution
of our Galaxy, ASP Conf. Ser., 317, 66
(In the text)
- De Simone, R., Wu,
X., & Tremaine, S. 2004, MNRAS, 350, 627 [NASA ADS] [CrossRef] (In the text)
- Dehnen, W. 1998,
AJ, 115, 2384 [NASA ADS] [CrossRef] (In the text)
- Dickey, J. M.,
McClure-Griffiths, N. M., Gaensler, B. M., & Green, A. J. 2004,
Milky Way Surveys: The Structure and Evolution of our Galaxy, ASP
Conf. Ser., 317, 26
(In the text)
- Dinescu, D. I.,
Martínez-Delgado, D., Girard, T. M., et al. 2005, ApJ, 631,
L49 [NASA ADS] [CrossRef] (In the text)
- Diplas, A., &
Savage, B. D. 1991, ApJ, 377, 126 [NASA ADS] [CrossRef] (In the text)
- Djorgovski, S., &
Sosin, C. 1989, ApJ, 341, L13 [NASA ADS] [CrossRef] (In the text)
- Drimmel, R.,
Smart, R. L., & Lattanzi, M. G. 2000, A&A, 354, 67 [NASA ADS] (In the text)
- Drimmel, R.,
& Spergel, D. N. 2001, ApJ, 556, 181 [NASA ADS] [CrossRef] (In the text)
- Drimmel, R. 2005,
The Three-Dimensional Universe with Gaia, ESA SP-576, 167
(In the text)
- Evans, N., Gyuk, G.,
Turner, M., & Binney, J. 1998, ApJ, 501, L45 [NASA ADS] [CrossRef] (In the text)
- Ferguson, A. M.
N., Wyse, R. F. G., Gallagher, J. S., & Hunter, D. A. 1998,
ApJ, 506, L19 [NASA ADS] [CrossRef] (In the text)
- Fraternali,
F., van Moorsel, G., Sancisi, R., & Oosterloo, T. 2002, AJ,
123, 3124 [NASA ADS] [CrossRef] (In the text)
- Fraternali,
F., Oosterloo, T., Boomsma, R., Swaters, R., & Sancisi, R.
2004, IAU Symp., 217, 136 [NASA ADS] (In the text)
- Freudenreich, H. T.,
et al. 1994, ApJ, 429, L69 [NASA ADS] [CrossRef] (In the text)
- Freudenreich, H. T.
1996, ApJ, 468, 663 [NASA ADS] [CrossRef] (In the text)
- Freudenreich, H. T.
1998, ApJ, 492, 495 [NASA ADS] [CrossRef] (In the text)
- Frinchaboy, P. M.,
Majewski, S. R., Crane, J. D., et al. 2004, ApJ, 602, L21 [NASA ADS] [CrossRef] (In the text)
- García-Ruiz,
I., Kuijken, K., & Dubinski, J. 2002, MNRAS, 337, 459 [NASA ADS] [CrossRef] (In the text)
- Gentile, G.,
Fraternali, K. U., & Salucci, P. 2003, A&A, 405, 969 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Girardi, L., Bertelli,
G., Bressan, A., et al. 2002, A&A, 391, 195 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Grebel, E. 2001,
Ap&SS, 277, 231 (In the text)
- Hartmann, Dap,
& Burton, W. B. 1997 in Atlas of galactic neutral hydrogen
(Cambridge, New York: Cambridge University Press)
(In the text)
- Helmi, A., Navarro,
J. F., Meza, A., Steinmetz, M., & Eke, V. R. 2003, ApJ, 592,
L25 [NASA ADS] [CrossRef] (In the text)
- Hofner, P., &
Sparke, L. S. 1994, ApJ, 428, 466 [NASA ADS] [CrossRef] (In the text)
- Ibata, R. A., Irwin,
M. J., Lewis, G. F., Ferguson, A. M. N., & Tanvir, N. 2003,
MNRAS, 340, L21 [NASA ADS] [CrossRef] (In the text)
- Irwin, M., &
Hatzidimitriou, D. 1995, MNRAS, 277, 1354 [NASA ADS] (In the text)
- Izotov, Y. I.,
& Thuan, T. X. 2004, ApJ, 616, 768 [NASA ADS] [CrossRef]
- Kalberla, P. M.
W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440,
775 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
López-Corredoira, M., Cabrera-Lavers, A., Garzón, F.,
& Hammersley, P. L. 2002, A&A, 394, 883 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Majewski, S.
R., Skrutskie, M. F., Weinberg, M. D., & Ostheimer, J. C. 2003,
ApJ, 599, 1082 [NASA ADS] [CrossRef] (In the text)
- Majewski, S.
R., Ostheimer, J. C., Rocha-Pinto, H. J., et al. 2004, ApJ, 615,
738 [NASA ADS] [CrossRef] (In the text)
- Manchester,
R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129,
1993 [NASA ADS] [CrossRef] (In the text)
- Martin, N.,
Ibata, R., Bellazzini, M., et al. 2004a, MNRAS, 348, 12 [NASA ADS] [CrossRef] [M04a]
(In the text)
- Martin, N. F.,
Ibata, R., Conn, B., et al. 2004b, MNRAS, 355, L33 [NASA ADS] [CrossRef] [M04b]
(In the text)
- Martin, N. F.,
Ibata, R. A., Conn, B. C., et al. 2005, MNRAS, 362, 906 [NASA ADS] [CrossRef] (In the text)
-
Martínez-Delgado, D., Butler, D. J., Rix, H.-W., et al. 2005,
ApJ, 633, 205 [NASA ADS] [CrossRef] (In the text)
- Mateo, M. L. 1998,
ARA&A, 36, 435 [NASA ADS] (In the text)
- Mateu, C. E., Vivas,
A. K., Zinn, R., & Miller, L. 2004
[arXiv:astro-ph/0504333]
(In the text)
-
McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., &
Green, A. J. 2004, ApJ, 607, L127 [NASA ADS] [CrossRef] (In the text)
-
McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., et al.
2005, ApJS, 158, 178 [NASA ADS] [CrossRef] (In the text)
- Moitinho, A.,
Vázquez, R. A., Carraro, G., et al. 2005, MNRAS
[arXiv:astro-ph/0602493]
(In the text)
- Momany, Y.,
Vandame, B., Zaggia, S., et al. 2001, A&A, 379, 436 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Momany, Y.,
Bedin, L. R., Cassisi, S., et al. 2004a, A&A, 420, 605 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Momany, Y.,
Zaggia, S. R., Bonifacio, P., et al. 2004b, A&A, 421, L29 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Momany, Y., &
Zaggia, S. 2005, A&A, 437, 339 [EDP Sciences] [NASA ADS] [CrossRef]
- Momany, Y., Held,
E. V., Saviane, I., et al. 2005, A&A, 439, 111 [EDP Sciences] [NASA ADS] [CrossRef]
- Monaco, L.,
Bellazzini, M., Ferraro, F. R., & Pancino, E. 2003, ApJ, 597,
L25 [NASA ADS] [CrossRef] (In the text)
- Monaco, L.,
Bellazzini, M., Bonifacio, P., et al. 2005, A&A, 441, 141 [EDP Sciences] [NASA ADS] [CrossRef]
- Nakanishi,
H., & Sofue, Y. 2004, Milky Way Surveys: The Structure and
Evolution of our Galaxy, ASP Conf. Ser., 317, 32
(In the text)
- Newberg, H. J.,
Yanny, B., Rockosi, C., et al. 2002, ApJ, 569, 245 [NASA ADS] [CrossRef] (In the text)
- Newberg, H.,
& Yanny, B., ASP Conf. Ser., Astrometry in the Age of the Next
Generation of Large Telescopes 2005, ed. A. Monet, & K.
Seidelmann [arXiv:astro-ph/0502386]
(In the text)
- Olano, C. A. 2004,
A&A, 423, 895 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Oort, J. H., Kerr, F.
J., & Westerhout, G. 1958, MNRAS, 118, 379 [NASA ADS]
-
Peñarrubia, J., Martínez-Delgado, D., Rix, H. W., et al.
2005, ApJ, 626, 128 [NASA ADS] [CrossRef]
- Porcel, C.,
Battaner, E., & Jimenez-Vicente, J. 1997, A&A, 322,
103 [NASA ADS] (In the text)
-
Reshetnikov, V., & Combes, F. 1998, A&A, 337, 9 [NASA ADS] (In the text)
- Robin, A.,
Reylé, C., Derrière, & Picaud, S. 2003, A&A, 409,
523 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Rocha-Pinto, H.,
Majewski, S., Skrutskie, M., & Crane, J. 2003, ApJ, 594,
L115 [NASA ADS] [CrossRef] (In the text)
- Rocha-Pinto, H. J.,
Majewski, S. R., Skrutskie, M. F., Crane, J. D., & Patterson,
R. J. 2004, ApJ, 615, 732 [NASA ADS] [CrossRef]
- Rocha-Pinto, H.,
Majewski, S. R., Skrutskie, M. F., & Patterson, R. J. 2005, ApJ
[arXiv:astro-ph/0504122]
(In the text)
- Russeil, D. 2003,
A&A, 397, 133 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Ruphy, S., Robin, A.
C., Epchtein, N., et al. 1996, A&A, 313, L21 [NASA ADS] (In the text)
-
Sánchez-Saavedra, M. L., Battaner, E., Guijarro, A.,
López-Corredoira, M., & Castro-Rodríguez, N. 2003,
A&A, 399, 457 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Sbordone, L.,
Bonifacio, P., Marconi, G., Zaggia, S., & Buonanno, R. 2005,
A&A, 430, L13 [EDP Sciences] [NASA ADS] [CrossRef]
- Schlegel, D. J.,
Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [CrossRef] (In the text)
- Schröder,
S. E., Kaper, L., Lamers, H. J. G. L. M., & Brown, A. G. A.
2004, A&A, 428, 149 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Snell, R. L.,
Carpenter, J. M., & Heyer, M. H. 2002, ApJ, 578, 229 [NASA ADS] [CrossRef] (In the text)
- Soderblom, D.
R., Nelan, E., Benedict, G. F., et al. 2005, AJ, 129, 1616 [NASA ADS] [CrossRef] (In the text)
- Taffoni, G.,
Mayer, L., Colpi, M., & Governato, F. 2003, MNRAS, 341,
434 [NASA ADS] [CrossRef]
- Thilker, D. A.,
Bianchi, L., Boissier, S., et al. 2005, ApJ, 619, L79 [NASA ADS] [CrossRef] (In the text)
- Tsuchiya, T.
2002, New Astronomy, 7, 293 [NASA ADS] [CrossRef] (In the text)
- Tolstoy, E. 2000
[arXiv:astro-ph/0010028]
(In the text)
- Tolstoy, E. 2005
[arXiv:astro-ph/0506481]
- Vallée, J. P.
2005, AJ, 130, 569 [NASA ADS] [CrossRef] (In the text)
- Vig, S., Ghosh, S. K.,
& Ojha, D. K. 2005, A&A, 436, 867 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Weinberg, M. D.
1998, MNRAS, 299, 499 [NASA ADS] [CrossRef] (In the text)
- Weaver, H., &
Williams, D. R. W. 1973, A&AS, 8, 1 [NASA ADS]
- Willman, B.,
Dalcanton, J. J., Martinez-Delgado, D., et al. 2005, ApJ, 626,
L85 [NASA ADS] [CrossRef] (In the text)
- Wouterloot, J.,
Brand, Burton, W., & Kwee, K. 1990, A&A, 230, 21 [NASA ADS] (In the text)
- Wyse, R. F. G., &
Gilmore, G. 2005 [arXiv:astro-ph/0510025]
(In the text)
- Yanny, B., Newberg,
H. J., Grebel, E. K., et al. 2003, ApJ, 588, 824 [NASA ADS] [CrossRef] (In the text)
- Yusifov, I. 2004
[arXiv:astro-ph/0405517]
(In the text)
Copyright ESO 2006
![\begin{displaymath}\chi^2 = \sum \left[(y_{\rm North}-y_{\rm South})^2/(y_{\rm North}+y_{\rm South})\right]
\end{displaymath}](/articles/aa/full/2006/20/aa4081-05/img70.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,height=5.2cm,clip]{4081fig1.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg73.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,height=10cm,clip]{4081fig2.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg80.gif)
![\begin{figure}
\par\includegraphics[width=8.7cm,height=8.2cm,clip]{4081fig3.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg100.gif)
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=7.2cm,height=4.8cm,clip]{...
...{2mm}
\includegraphics[width=7.5cm,height=8.1cm,clip]{4081fig5.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=7.1cm,height=5.2cm]{4081fig6.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg102.gif)
![\begin{figure}
\includegraphics[width=8.3cm,height=8.2cm,clip]{4081fig7.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg116.gif)
![\begin{figure}
\includegraphics[width=8cm,height=8.2cm,clip]{4081fig8.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg121.gif)
![\begin{figure}
\includegraphics[width=8cm,height=8.2cm,clip]{4081fig9.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg122.gif)
![\begin{figure}
\par\includegraphics[width=14cm,height=14cm,clip]{4081fig10.ps}\p...
...{2mm}
\includegraphics[width=14.5cm,height=7.5cm,clip]{4081fig11.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg137.gif)
![\begin{figure}
\includegraphics[width=8cm,height=8cm,clip]{4081fig12.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg145.gif)
![\begin{figure}
\includegraphics[width=8cm,clip]{4081fig13.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg151.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,height=7.8cm,clip]{4081fig14.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg163.gif)
![\begin{figure}
\includegraphics[width=7.8cm,height=7.8cm,clip]{4081fig15.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg164.gif)
![\begin{figure}
\includegraphics[width=8cm,clip]{4081fig16.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg177.gif)
![\begin{figure}
\includegraphics[width=8cm,height=4.8cm,clip]{4081fig18.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg194.gif)
![\begin{figure}
\includegraphics[width=7.5cm,height=7cm,clip]{4081fig19.ps}\par\...
...*{2mm}
\includegraphics[width=7.5cm,height=7cm,clip]{4081fig20.ps}
\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg195.gif)
![\begin{figure}
\includegraphics[width=10.3cm,height=10.3cm,clip]{4081fig21.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg228.gif)
![\begin{figure}
\includegraphics[width=7.5cm,height=7.5cm,clip]{4081fig22.ps}\end{figure}](/articles/aa/full/2006/20/aa4081-05/Timg243.gif)