A&A 451, 457-474 (2006)
DOI: 10.1051/0004-6361:20042592
P. Tozzi1 - R. Gilli2 - V. Mainieri3 - C. Norman4,5 - G. Risaliti2,6 - P. Rosati7 - J. Bergeron8 - S. Borgani9 - R. Giacconi4 - G. Hasinger3 - M. Nonino1 - A. Streblyanska3 - G. Szokoly3 - J. X. Wang10 - W. Zheng4
1 - INAF Osservatorio Astronomico di Trieste, via G.B. Tiepolo
11, 34131 Trieste, Italy
2 -
INAF Osservatorio Astrofisico di
Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
3 -
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstraße, PF 1312, 85741 Garching, Germany
4 - Dept. of
Physics and Astronomy, The Johns Hopkins University, Baltimore, MD
21218, USA
5 -
Space Telescope Science Institute, 3700 S. Martin
Drive, Baltimore, MD 21210, USA
6 -
Harvard-Smithsonian Center for
Astrophysics, 60 Garden Street Cambridge, MA 02138
7 -
European
Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching,
Germany
8 -
Institut d'Astrophysique de Paris, 98bis bd Arago,
75014 Paris France
9 -
Università di Trieste, Dip. Astronomia, via
Tiepolo 11, 34131 Trieste, Italy
10 -
Center for Astrophysics,
University of Science and Technology of China, Hefei, Anhui 230026,
PR China
Received 22 December 2004 / Accepted 7 February 2006
Abstract
We present a detailed X-ray spectral analysis of the
sources in the 1Ms catalog of the Chandra Deep Field South (CDFS)
taking advantage of optical spectroscopy and photometric redshifts for
321 extragalactic sources out of the total sample of 347 sources. As
a default spectral model, we adopt a power law with slope ![]() with an intrinsic redshifted absorption
with an intrinsic redshifted absorption ![]() ,
a fixed Galactic
absorption and an unresolved Fe emission line. For 82 X-ray bright
sources, we are able to perform the X-ray spectral analysis leaving
both
,
a fixed Galactic
absorption and an unresolved Fe emission line. For 82 X-ray bright
sources, we are able to perform the X-ray spectral analysis leaving
both ![]() and
and ![]() free. The weighted mean value for the slope
of the power law is
free. The weighted mean value for the slope
of the power law is
![]() ,
and
the distribution of best fit values shows an intrinsic dispersion of
,
and
the distribution of best fit values shows an intrinsic dispersion of
![]() .
We do not find hints of a correlation
between the spectral index
.
We do not find hints of a correlation
between the spectral index ![]() and the intrinsic absorption
column density
and the intrinsic absorption
column density ![]() .
.
We then investigate the absorption distribution for the whole sample,
deriving the ![]() values in faint sources by fixing
values in faint sources by fixing
![]() .
We also allow for the presence of a scattered component at soft
energies with the same slope of the main power law, and for a pure
reflection spectrum typical of Compton-thick AGN. We detect the
presence of a scattered soft component in 8 sources; we also identify
14 sources showing a reflection-dominated spectrum. The latter are
referred to as Compton-thick AGN candidates.
.
We also allow for the presence of a scattered component at soft
energies with the same slope of the main power law, and for a pure
reflection spectrum typical of Compton-thick AGN. We detect the
presence of a scattered soft component in 8 sources; we also identify
14 sources showing a reflection-dominated spectrum. The latter are
referred to as Compton-thick AGN candidates.
By correcting for both incompleteness and sampling-volume effects, we
recover the intrinsic ![]() distribution representative of the whole
AGN population,
distribution representative of the whole
AGN population,
![]() ,
from the observed one.
,
from the observed one.
![]() shows
a lognormal shape, peaking around
shows
a lognormal shape, peaking around
![]() and with
and with
![]() .
Interestingly, such a distribution shows
continuity between the population of Compton-thin and that of
Compton-thick AGN.
.
Interestingly, such a distribution shows
continuity between the population of Compton-thin and that of
Compton-thick AGN.
We find that the fraction of absorbed sources (with
![]() cm-2) in the sample is constant (at the level of about 75%) or
moderately increasing with redshift.
Finally, we compare the optical classification to the X-ray
spectral properties, confirming that the correspondence of unabsorbed
(absorbed) X-ray sources to optical type I (type II) AGN is accurate
for at least 80% of the sources with spectral identification (1/3 of
the total X-ray sample).
cm-2) in the sample is constant (at the level of about 75%) or
moderately increasing with redshift.
Finally, we compare the optical classification to the X-ray
spectral properties, confirming that the correspondence of unabsorbed
(absorbed) X-ray sources to optical type I (type II) AGN is accurate
for at least 80% of the sources with spectral identification (1/3 of
the total X-ray sample).
Key words: X-rays: diffuse background - surveys - cosmology: observations - X-rays: galaxies - galaxies: active
Deep X-ray surveys with Chandra (Brandt et al. 2001; Rosati et al. 2002; Cowie et al. 2002; Alexander et al. 2003; Barger et al. 2003) and XMM (Hasinger et al. 2001) showed that the so called
X-ray background (XRB) is mainly provided by Active Galactic Nuclei
(AGN) both in the soft (0.5-2 keV) and in the hard (2-10 keV)
band. In particular, major progress has been made in the hard band,
for which the sources known before Chandra were providing only ![]() 30% of the XRB (Cagnoni et al. 1998; Ueda et al. 1999a). While some
evidence of spectral hardening was found towards faint fluxes
(e.g. Della Ceca et al. 1999), most of the X-ray sources were
identified with Broad Line AGN with a typical X-ray spectral slope of
30% of the XRB (Cagnoni et al. 1998; Ueda et al. 1999a). While some
evidence of spectral hardening was found towards faint fluxes
(e.g. Della Ceca et al. 1999), most of the X-ray sources were
identified with Broad Line AGN with a typical X-ray spectral slope of
![]() ,
steeper than that of the XRB (
,
steeper than that of the XRB (
![]() ).
On the contrary, the source population discovered by Chandra and XMM at fluxes below
).
On the contrary, the source population discovered by Chandra and XMM at fluxes below ![]() 10-13-10-14 erg cm-2 s-1 in the
hard band, is constituted mostly by obscured AGN with a hard spectrum,
and provides the solution to the "spectral paradox'' as predicted by
the XRB synthesis models (Setti & Woltjer 1989; Madau et al. 1993; Comastri et al. 1995; Gilli et al. 2001). The detection limit reached in the hard
band in the 2Ms exposure of the Chandra Deep Field North is
10-13-10-14 erg cm-2 s-1 in the
hard band, is constituted mostly by obscured AGN with a hard spectrum,
and provides the solution to the "spectral paradox'' as predicted by
the XRB synthesis models (Setti & Woltjer 1989; Madau et al. 1993; Comastri et al. 1995; Gilli et al. 2001). The detection limit reached in the hard
band in the 2Ms exposure of the Chandra Deep Field North is
![]() erg s-1 cm-2 (Alexander et al. 2003) and
a factor 2 higher in the 1Ms exposure of the Chandra Deep Field South
(CDFS, Rosati et al. 2002; Giacconi et al. 2002). The XRB is now
resolved at the level of
erg s-1 cm-2 (Alexander et al. 2003) and
a factor 2 higher in the 1Ms exposure of the Chandra Deep Field South
(CDFS, Rosati et al. 2002; Giacconi et al. 2002). The XRB is now
resolved at the level of ![]() 80% in the 1-2 and 2-8 keV bands
(see Hickox & Markevitch 2005), with the AGN providing the large
majority of the resolved fraction. While a non-negligible part of
the unresolved fraction in the soft band is expected to be contributed
by a diffuse warm intergalactic medium (e.g., Cen & Ostriker 1999),
Worsley et al. (2004, 2005) pointed out that at E> 6 keV less and
less of the hard XRB is resolved, showing that a significant
population of strongly absorbed, possibly Compton-thick sources,
preferentially at z<1, is still not observed (see also Comastri
2004; Brandt & Hasinger 2005).
80% in the 1-2 and 2-8 keV bands
(see Hickox & Markevitch 2005), with the AGN providing the large
majority of the resolved fraction. While a non-negligible part of
the unresolved fraction in the soft band is expected to be contributed
by a diffuse warm intergalactic medium (e.g., Cen & Ostriker 1999),
Worsley et al. (2004, 2005) pointed out that at E> 6 keV less and
less of the hard XRB is resolved, showing that a significant
population of strongly absorbed, possibly Compton-thick sources,
preferentially at z<1, is still not observed (see also Comastri
2004; Brandt & Hasinger 2005).
The two Chandra Deep Field Surveys lead to the detection of several
populations of X-ray extragalactic sources: unabsorbed AGN (defined
as sources with absorbing column densities
![]() cm-2),
usually identified with optical Broad Line (type I) AGN and QSO;
absorbed AGN (with column densities
cm-2),
usually identified with optical Broad Line (type I) AGN and QSO;
absorbed AGN (with column densities
![]() cm-2),
optically identified mostly as narrow line (type II) AGN, distributed
around moderate redshifts
cm-2),
optically identified mostly as narrow line (type II) AGN, distributed
around moderate redshifts ![]() (see Barger et al. 2002; Szokoly
et al. 2004); X-ray bright, optically normal galaxies (XBONG, see
Comastri et al. 2001) which generally harbor obscured AGNs; high
redshift type II QSO (see Norman et al. 2002; Stern et al. 2002;
Mainieri et al. 2005b; Ptak et al. 2005); starburst and quiescent
galaxies at z<1 (Bauer et al. 2002; Hornschemeier et al. 2003;
Norman et al. 2004), which contribute to the XRB only 2-3% in
energy, but they are expected to outnumber the AGN at fluxes below
(see Barger et al. 2002; Szokoly
et al. 2004); X-ray bright, optically normal galaxies (XBONG, see
Comastri et al. 2001) which generally harbor obscured AGNs; high
redshift type II QSO (see Norman et al. 2002; Stern et al. 2002;
Mainieri et al. 2005b; Ptak et al. 2005); starburst and quiescent
galaxies at z<1 (Bauer et al. 2002; Hornschemeier et al. 2003;
Norman et al. 2004), which contribute to the XRB only 2-3% in
energy, but they are expected to outnumber the AGN at fluxes below
![]() erg cm-2 s-1 (Bauer et al. 2004a). In
this paper we will focus on the X-ray properties of the AGN population, in order to provide a baseline for possible models of the
AGN formation and evolution.
erg cm-2 s-1 (Bauer et al. 2004a). In
this paper we will focus on the X-ray properties of the AGN population, in order to provide a baseline for possible models of the
AGN formation and evolution.
Tentatively, the different classes of AGN-powered X-ray sources can
be associated to three phases: a first phase of strong accretion onto
the massive black hole, characterized by high intrinsic absorption and
intense star formation (for recent evidence in the submm range see
Alexander et al. 2005a), followed by an unobscured phase, and
subsequent fading (see Fabian 1999; Granato et al. 2004). A test of
this or other possible scenarios for the accretion history and galaxy
formation in the Universe, requires a good knowledge of the
distribution of the X-ray properties of the AGN population, in
particular intrinsic luminosity and intrinsic absorption as a function
of cosmic epoch, as well as their relation with the optical
properties. The distribution of the intrinsic absorption, ![]() ,
is
known only for local, optically selected Seyfert II galaxies (Risaliti
et al. 1999). These local samples, selected to be complete as a
function of intrinsic luminosity, typically include medium or low
luminosity sources, and about 50% of them are Compton-thick.
Difficulty of assembling large unbiased AGN sample as a function of
intrinsic luminosity, has hampered attempts to measure the
,
is
known only for local, optically selected Seyfert II galaxies (Risaliti
et al. 1999). These local samples, selected to be complete as a
function of intrinsic luminosity, typically include medium or low
luminosity sources, and about 50% of them are Compton-thick.
Difficulty of assembling large unbiased AGN sample as a function of
intrinsic luminosity, has hampered attempts to measure the ![]() distribution. The
distribution. The ![]() distribution and the evolution of the
fraction of absorbed sources, has been investigated recently by Ueda
et al. (2003) from a combination of surveys from HEAO1, ASCA and
Chandra. Their sample is dominated by bright, low absorption AGN, and
their
distribution and the evolution of the
fraction of absorbed sources, has been investigated recently by Ueda
et al. (2003) from a combination of surveys from HEAO1, ASCA and
Chandra. Their sample is dominated by bright, low absorption AGN, and
their ![]() distribution is broadly peaked above
distribution is broadly peaked above
![]() cm-2. Except for a few objects with good photon statistics, Ueda
et al. use the redshift and the hardness ratio to derive the intrinsic
luminosity distribution in the 2-10 keV band as a function of
redshift, without performing a single-source analysis. Similar
results have been recently obtained by La Franca et al. (2005) on the
basis of the HELLAS2XMM sample combined with other catalogs. At
brighter fluxes, other investigations are under way both with Chandra
and XMM in wide, shallower surveys (ChaMP, Green et al. 2004;
Silverman et al. 2005; XMM-BSS, Della Ceca et al. 2004; CLASXS, Yang
et al. 2004; Steffen et al. 2004; HELLAS2XMM, Baldi et al. 2002;
Perola et al. 2004). We believe that these X-ray surveys, designed
to bridge the gap between the pencil beam, deepest surveys and the
wide shallow ones from previous missions, are probably biased against
heavily absorbed faint AGN, whose fraction is expected to increase
towards fainter fluxes. On the other hand, optical surveys can
actually discover heavily obscured AGNs at moderate redshift (z<1.3)
but only through extensive optical spectroscopy of large sample of
galaxies, such as the SDSS, among which type II AGNs can be identified
from the strong narrow emission lines (for example,
[OII]
cm-2. Except for a few objects with good photon statistics, Ueda
et al. use the redshift and the hardness ratio to derive the intrinsic
luminosity distribution in the 2-10 keV band as a function of
redshift, without performing a single-source analysis. Similar
results have been recently obtained by La Franca et al. (2005) on the
basis of the HELLAS2XMM sample combined with other catalogs. At
brighter fluxes, other investigations are under way both with Chandra
and XMM in wide, shallower surveys (ChaMP, Green et al. 2004;
Silverman et al. 2005; XMM-BSS, Della Ceca et al. 2004; CLASXS, Yang
et al. 2004; Steffen et al. 2004; HELLAS2XMM, Baldi et al. 2002;
Perola et al. 2004). We believe that these X-ray surveys, designed
to bridge the gap between the pencil beam, deepest surveys and the
wide shallow ones from previous missions, are probably biased against
heavily absorbed faint AGN, whose fraction is expected to increase
towards fainter fluxes. On the other hand, optical surveys can
actually discover heavily obscured AGNs at moderate redshift (z<1.3)
but only through extensive optical spectroscopy of large sample of
galaxies, such as the SDSS, among which type II AGNs can be identified
from the strong narrow emission lines (for example,
[OII]![]() 3727 Å or [OIII]
3727 Å or [OIII]![]() 5007 Å). In the absence
of high-sensitivity X-ray surveys above 10 keV, we propose that the
search for the still missing strongly absorbed AGN population can be
best performed through a detailed spectral analysis of faint sources
detected in very deep X-ray surveys.
5007 Å). In the absence
of high-sensitivity X-ray surveys above 10 keV, we propose that the
search for the still missing strongly absorbed AGN population can be
best performed through a detailed spectral analysis of faint sources
detected in very deep X-ray surveys.
In this paper, we present a systematic study of the X-ray spectra of
all the sources in the CDFS, taking advantage of spectroscopic
(Szokoly et al. 2004) and photometric (Zheng et al. 2004; Mainieri et al. 2005a) redshifts from the optical follow-up program with the
ESO-VLT. Given the flux limits in the CDFS (
![]() and
and
![]() erg cm-2 s-1 in the soft and hard
band respectively), the 347 sources detected (346 from the catalog of
Giacconi et al. 2002 plus one added in Szokoly et al. 2004) are mostly
AGN, with a fewer number of normal or star forming galaxies with
respect to CDFN, where, thanks to the lower flux limits, normal
galaxies start to be a significant fraction of the faint source
population. The paper is structured as follows. In Sect. 2 we briefly
describe the X-ray and the Optical data. In Sect. 3 we describe our
X-ray spectral analysis procedure, after dividing the sample into two
subsamples based on the counts statistics. In Sect. 4 we present the
X-ray spectral analysis of the X-ray bright sample, focusing on the
slope of the power law component. In Sect. 5 we present the X-ray
spectral analysis for the whole sample of 321 sources with measured
redshift and total luminosity
erg cm-2 s-1 in the soft and hard
band respectively), the 347 sources detected (346 from the catalog of
Giacconi et al. 2002 plus one added in Szokoly et al. 2004) are mostly
AGN, with a fewer number of normal or star forming galaxies with
respect to CDFN, where, thanks to the lower flux limits, normal
galaxies start to be a significant fraction of the faint source
population. The paper is structured as follows. In Sect. 2 we briefly
describe the X-ray and the Optical data. In Sect. 3 we describe our
X-ray spectral analysis procedure, after dividing the sample into two
subsamples based on the counts statistics. In Sect. 4 we present the
X-ray spectral analysis of the X-ray bright sample, focusing on the
slope of the power law component. In Sect. 5 we present the X-ray
spectral analysis for the whole sample of 321 sources with measured
redshift and total luminosity
![]() erg s-1 (we exclude
the faintest luminosity bin which is dominated by normal galaxies),
focusing on the intrinsic absorption. In Sect. 6 we discuss the
distributions of the X-ray spectral properties after correcting for
incompleteness and sampling-volume effects, deriving in particular
the intrinsic absorption distribution. This allows us to estimate the
fraction of absorbed sources in our sample as a function of epoch.
Finally, in Sect. 7 we compare the X-ray and optical properties,
revisiting the comparison of the Optical vs. X-ray classification
scheme proposed by Szokoly et al. (2004). Our conclusions are
summarized in Sect. 8. Luminosities are quoted for a flat cosmology with
erg s-1 (we exclude
the faintest luminosity bin which is dominated by normal galaxies),
focusing on the intrinsic absorption. In Sect. 6 we discuss the
distributions of the X-ray spectral properties after correcting for
incompleteness and sampling-volume effects, deriving in particular
the intrinsic absorption distribution. This allows us to estimate the
fraction of absorbed sources in our sample as a function of epoch.
Finally, in Sect. 7 we compare the X-ray and optical properties,
revisiting the comparison of the Optical vs. X-ray classification
scheme proposed by Szokoly et al. (2004). Our conclusions are
summarized in Sect. 8. Luminosities are quoted for a flat cosmology with
![]() and H0=70 km s-1 Mpc-1 (see Spergel et al. 2003).
and H0=70 km s-1 Mpc-1 (see Spergel et al. 2003).
The 1Ms dataset of the CDFS is the result of the coaddition of 11 individual Chandra ACIS-I (Garmire et al. 1992; Bautz et al. 1998) exposures with aimpoints only a few arcsec from each other.
The nominal aim point of the CDFS is ![]() :32:28.0,
:32:28.0,
![]() :48:30 (J2000). The reduction and analysis of the X-ray
data are described in Giacconi et al. (2001), Tozzi et al. (2001) and
Rosati et al. (2002). The final image covers 0.108 deg2, where 347 X-ray sources are identified (the catalog is presented in Giacconi et al. 2002). Here we use an updated X-ray data reduction, where we used
Ciao 3.0.1 and CALDB2.26, therefore including the correction for the
degraded effective area of ACIS-I chips due to material accumulated
on the ACIS optical blocking filter at the epoch of the observation.
We also apply the recently released, time-dependent gain
correction
:48:30 (J2000). The reduction and analysis of the X-ray
data are described in Giacconi et al. (2001), Tozzi et al. (2001) and
Rosati et al. (2002). The final image covers 0.108 deg2, where 347 X-ray sources are identified (the catalog is presented in Giacconi et al. 2002). Here we use an updated X-ray data reduction, where we used
Ciao 3.0.1 and CALDB2.26, therefore including the correction for the
degraded effective area of ACIS-I chips due to material accumulated
on the ACIS optical blocking filter at the epoch of the observation.
We also apply the recently released, time-dependent gain
correction![]() .
.
We briefly recall the main steps of the spectral analysis of the
reduced data. First we extract the photon files and the spectrum
(pha file) for every source in our catalog, along with the
corresponding background. The area of extraction of each source, as
described in Giacconi et al. (2001), is defined as a circle of radius
![]() (with a minimum radius of 5 arcsec). The FWHM is
modeled as a function of the off-axis angle to reproduce the
broadening of the PSF. The background is extracted from an annulus
with outer radius
(with a minimum radius of 5 arcsec). The FWHM is
modeled as a function of the off-axis angle to reproduce the
broadening of the PSF. The background is extracted from an annulus
with outer radius
![]() and an inner radius of
and an inner radius of
![]() ,
after
masking out other sources. Each background spectrum samples more than
400 photons in the 0.5-7 keV range. We create a response matrix and
an ancillary response matrix for each source. To do that, we first
create the two matrices in the source position in each of the 11 observations of the CDFS (therefore the effect of the degraded
effective area of ACIS-I chips is applied individually to each
pointing). Finally we sum the 11 files weighting them for the
exposure time of each exposure. We notice that most of the sources
show variability (see Paolillo et al. 2004), therefore our measured
fluxes and luminosities are time-averaged on the observation
epochs. We also stress that, assuming there is no significant changes
in the spectra, we correctly measure the spectral shape of each
source, since the response matrices are time-averaged on the same
epochs, keeping track in the most detailed way of the characteristics
of the different regions and the different conditions of the detector
at the time of the observations.
,
after
masking out other sources. Each background spectrum samples more than
400 photons in the 0.5-7 keV range. We create a response matrix and
an ancillary response matrix for each source. To do that, we first
create the two matrices in the source position in each of the 11 observations of the CDFS (therefore the effect of the degraded
effective area of ACIS-I chips is applied individually to each
pointing). Finally we sum the 11 files weighting them for the
exposure time of each exposure. We notice that most of the sources
show variability (see Paolillo et al. 2004), therefore our measured
fluxes and luminosities are time-averaged on the observation
epochs. We also stress that, assuming there is no significant changes
in the spectra, we correctly measure the spectral shape of each
source, since the response matrices are time-averaged on the same
epochs, keeping track in the most detailed way of the characteristics
of the different regions and the different conditions of the detector
at the time of the observations.
The spectroscopic identification program carried out with the ESO-VLT
is presented in Szokoly et al. (2004). The optical classification is
based on the detection of high ionization emission lines. The
presence of broad emission lines (FWHM larger than 2000 km s-1) like
Mg![]() ,
C
,
C
![]() ,
and, at large redshifts, C
,
and, at large redshifts, C![]() and
Ly
and
Ly![]() ,
identifies the source as a Broad Line AGN (BLAGN), type-1
AGN or QSO in the simple unification model (Antonucci 1993). The
presence of unresolved high ionization emission lines (like O
,
identifies the source as a Broad Line AGN (BLAGN), type-1
AGN or QSO in the simple unification model (Antonucci 1993). The
presence of unresolved high ionization emission lines (like O
![]() ,
Ne
,
Ne![]() ,
Ne
,
Ne
![]() or He
or He![]() )
identifies the source as a High
Excitation line galaxy (HEX), often implying an optical type-2
classification. Objects with unresolved emission lines consistent
with an H
)
identifies the source as a High
Excitation line galaxy (HEX), often implying an optical type-2
classification. Objects with unresolved emission lines consistent
with an H![]() region spectrum are classified as Low Excitation Line
galaxies (LEX), implying sources without signs of nuclear activity in
the optical (however, discriminating between a Seyfert II galaxy and
an H II region galaxy involves the measure of line ratio as shown in
Veilleux & Osterbrock (1987), which is not used here as a
classification scheme, considering also that their classification
scheme relies on lines which are not visible in optical spectra from
the ground at z>0.7). Objects with typical galaxy spectrum showing
only absorption lines are classified as ABS; among the last two
classes we expect to find star-forming galaxies or Narrow Line
Emission Galaxies, but also hidden AGN. The optical identification is
flagged according to the quality of the optical information. Quality
flags
region spectrum are classified as Low Excitation Line
galaxies (LEX), implying sources without signs of nuclear activity in
the optical (however, discriminating between a Seyfert II galaxy and
an H II region galaxy involves the measure of line ratio as shown in
Veilleux & Osterbrock (1987), which is not used here as a
classification scheme, considering also that their classification
scheme relies on lines which are not visible in optical spectra from
the ground at z>0.7). Objects with typical galaxy spectrum showing
only absorption lines are classified as ABS; among the last two
classes we expect to find star-forming galaxies or Narrow Line
Emission Galaxies, but also hidden AGN. The optical identification is
flagged according to the quality of the optical information. Quality
flags ![]() indicates spectroscopic redshifts (see Table 1). In several cases, the optical spectral properties do
not allow us to obtain a secure determination of the spectral type.
As shown in Szokoly et al. (2004), the optical classification scheme
is failing in identifying an AGN in about 40% of the X-ray sources
optically classified as LEX or ABS. Therefore, an X-ray
classification scheme, based on the source hardness ratio and observed
X-ray luminosity, was worked out by Szokoly et al. (2004) and
compared with the optical one (see their Fig. 13). In Sect. 7 we
will reconsider this X-ray classification scheme using the intrinsic
luminosities (as opposed to observed ones) and intrinsic absorption
(as opposed to the hardness ratio).
indicates spectroscopic redshifts (see Table 1). In several cases, the optical spectral properties do
not allow us to obtain a secure determination of the spectral type.
As shown in Szokoly et al. (2004), the optical classification scheme
is failing in identifying an AGN in about 40% of the X-ray sources
optically classified as LEX or ABS. Therefore, an X-ray
classification scheme, based on the source hardness ratio and observed
X-ray luminosity, was worked out by Szokoly et al. (2004) and
compared with the optical one (see their Fig. 13). In Sect. 7 we
will reconsider this X-ray classification scheme using the intrinsic
luminosities (as opposed to observed ones) and intrinsic absorption
(as opposed to the hardness ratio).
Optical and near-IR images of the CDFS are also used to derive photometric redshifts for all the remaining X-ray sources. Using the widest multiwavelength photometry available today, Zheng et al. (2004) and Mainieri et al. (2005a) derived photo-z for the whole sample of sources but four. Photometric redshifts are obtained from different methods labelled with different quality flags (see Zheng et al. 2004 for details). When we have consistent redshift from more than one method, the corresponding quality flag is the sum of the single Q(always less than 1 for photometric redshift). Given the good agreement of photometric redshifts with spectroscopic ones (see Zheng et al. 2004), we do not divide our sample according to the optical spectra quality. Indeed, our statistical analysis is not expected to be significantly affected by uncertainties in the photometric redshifts. Uncertainties in the redshift estimate may instead significantly affect the search for the Fe line, as we discuss later.
The total number of sources with spectral or photometric redshift
z>0 is 336 over a total of 347 X-ray detections. Besides the 4
X-ray sources without any redshift estimate, we indeed identify 7
stars with good optical spectra. Therefore the spectral completeness
of our sample of extragalactic sources is ![]() 99%. Since we want
to focus on AGN, we adopt a conservative criterion and exclude 15 sources with total luminosity in the 0.5-10 keV band
99%. Since we want
to focus on AGN, we adopt a conservative criterion and exclude 15 sources with total luminosity in the 0.5-10 keV band
![]() erg s-1, a luminosity range which is expected to be dominated by
normal or star forming galaxies. We note that the higher
luminosiy range
erg s-1, a luminosity range which is expected to be dominated by
normal or star forming galaxies. We note that the higher
luminosiy range
![]() erg s-1 may include
several star forming galaxies as well, with star formation rate of the
order of
erg s-1 may include
several star forming galaxies as well, with star formation rate of the
order of
![]() /yr. However, we keep all the sources in the
luminosiy range
/yr. However, we keep all the sources in the
luminosiy range
![]() erg s-1 to include any
possible low-luminosity AGN in the sample. The final sample amounts
to 321 sources. The redshifts with the corresponding spectral quality
are shown along with the results from the X-ray spectral fits in
Table 1.
erg s-1 to include any
possible low-luminosity AGN in the sample. The final sample amounts
to 321 sources. The redshifts with the corresponding spectral quality
are shown along with the results from the X-ray spectral fits in
Table 1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig01.ps}\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg64.gif) |
Figure 1: Distribution of the net detected counts for all the sources in the sample (solid line: 0.5-2 keV band counts; dashed line: 2-7 keV band counts). |
| Open with DEXTER | |
We use XSPEC v11.3.1 (see Arnaud 1996) to perform the spectral fits.
The ability of obtaining a reliable fit depends on the X-ray spectral
quality, or, in simpler terms, on the signal to noise of the spectrum
under analysis. The distribution of the net counts in the 0.5-7 keV band
for all the sources in our sample, peaks below ![]() 100 (see
Fig. 1). The mean value of the net detected
counts in the total 0.5-7 keV band for all the sources in our sample
(including the two X-ray brightest sources in the sample, with about
10 000 counts each) is
100 (see
Fig. 1). The mean value of the net detected
counts in the total 0.5-7 keV band for all the sources in our sample
(including the two X-ray brightest sources in the sample, with about
10 000 counts each) is ![]() 240 counts, while the median is much
lower
240 counts, while the median is much
lower ![]() 70 counts.
70 counts.
Therefore, the strategy for the X-ray spectral analysis must be
appropriate for the low counts regime. In performing the spectral
fits we used an extension of the Cash statistics which makes use of
both the source and background spectral files![]() .
Cash statistics is applied to unbinned data, and therefore exploit the
full spectral resolution of the ACIS-I instrument, allowing better
performance with respect to the canonical
.
Cash statistics is applied to unbinned data, and therefore exploit the
full spectral resolution of the ACIS-I instrument, allowing better
performance with respect to the canonical ![]() analysis,
particularly for low signal-to-noise spectra (Nousek & Shue
1989). In order to assess the ability of our fitting procedure in a
typical case (a source with
analysis,
particularly for low signal-to-noise spectra (Nousek & Shue
1989). In order to assess the ability of our fitting procedure in a
typical case (a source with
![]() and
and
![]() cm-2 at z=1) we run several simulations for different input
fluxes, in which we try to recover the input parameters with two
different fitting procedures: Cash statistics (unbinned) and the
classic
cm-2 at z=1) we run several simulations for different input
fluxes, in which we try to recover the input parameters with two
different fitting procedures: Cash statistics (unbinned) and the
classic ![]() statistics with a binning of 10 photons per bin. The
results are summarized in Fig. 2. Note that we are
forced to use a binning of 10 photons (as opposed to the commonly used
binning of 20 photons) in order have a reasonable number of bins to
perform the
statistics with a binning of 10 photons per bin. The
results are summarized in Fig. 2. Note that we are
forced to use a binning of 10 photons (as opposed to the commonly used
binning of 20 photons) in order have a reasonable number of bins to
perform the ![]() fits in the low-counts regime. Such a small
binning is known to give inappropriate weights for the
fits in the low-counts regime. Such a small
binning is known to give inappropriate weights for the ![]() analysis, therefore we do not mean to present a detailed comparison of
the two methods. Indeed, here we just explore the effects that their
use would have in the spectral analysis of our sample. For the
analysis, therefore we do not mean to present a detailed comparison of
the two methods. Indeed, here we just explore the effects that their
use would have in the spectral analysis of our sample. For the
![]() statistics, we find that for sources with a number of net
counts equal or larger than 50, the input parameters are recovered
with very good accuracy, while for lower values, the peak of the
distribution of the best-fit-values starts to depart from the input
value. The shift in the distribution of the best-fit values is a
consequence of the binning, which, especially in the case of
low-counts statistics, acts as an effective smoothing on the
spectrum. On the other hand, the distribution of the best-fit values
with Cash-statistics appears to be closer to the input values. In
addition, the rms dispersion of best-fit values is
significantly lower with respect to the
statistics, we find that for sources with a number of net
counts equal or larger than 50, the input parameters are recovered
with very good accuracy, while for lower values, the peak of the
distribution of the best-fit-values starts to depart from the input
value. The shift in the distribution of the best-fit values is a
consequence of the binning, which, especially in the case of
low-counts statistics, acts as an effective smoothing on the
spectrum. On the other hand, the distribution of the best-fit values
with Cash-statistics appears to be closer to the input values. In
addition, the rms dispersion of best-fit values is
significantly lower with respect to the ![]() statistics. We also
checked that the confidence levels for the Cash-statistics can be
defined as in the
statistics. We also
checked that the confidence levels for the Cash-statistics can be
defined as in the ![]() -statistics (i.e.,
-statistics (i.e.,
![]() corresponds to 1
corresponds to 1 ![]() ,
,
![]() corresponds to 90% c.l. for one interesting parameter). Therefore we choose to quote
only the best fit values obtained with the Cash statistics.
corresponds to 90% c.l. for one interesting parameter). Therefore we choose to quote
only the best fit values obtained with the Cash statistics.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2592fig02.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg67.gif) |
Figure 2:
The average best-fit parameters (with rms dispersion) for a
source with intrinsic
|
| Open with DEXTER | |
Of course, the weak signal of our faintest sources limits the ability
to perform a fit keeping all the spectral parameters free. To
determine the validity of our approach, we first run the fit for our
default model with three free parameters (![]() ,
,
![]() and
normalization) on all the sources with more than 40 net detected
counts in the total 0.5-7 keV band
and
normalization) on all the sources with more than 40 net detected
counts in the total 0.5-7 keV band![]() . First we focus on the
distribution of the best-fit values for
. First we focus on the
distribution of the best-fit values for ![]() as a function of the
net counts (see Fig. 3, left). We notice that for sources
detected with a large number of counts (larger than
as a function of the
net counts (see Fig. 3, left). We notice that for sources
detected with a large number of counts (larger than ![]() 200) the
spectral slope is almost constant. On the other hand, at low counts,
the best fit spectral slope
200) the
spectral slope is almost constant. On the other hand, at low counts,
the best fit spectral slope ![]() shows an apparent trend
associated with a significant increase in the dispersion on
shows an apparent trend
associated with a significant increase in the dispersion on ![]() (see Fig. 3, right): lower values at lower soft counts,
higher values at lower hard counts. In principle this is expected,
since most of the sources with few soft counts are among the hardest
sources, and they can be fitted with a flat power law, and viceversa
the softest sources can be fitted with a very steep power
law. However, we argue that this behaviour may be affected by the poor
statistics. To avoid any possible bias induced by the low statistics,
we conservatively define an X-ray bright sample by considering those
sources exceeding at least one of these thesholds: 170 total counts,
120 soft counts, 80 hard counts. As we can see in Fig. 3b, the threshold on the soft counts is particularly
efficient in selecting sources for which the statistical error on
(see Fig. 3, right): lower values at lower soft counts,
higher values at lower hard counts. In principle this is expected,
since most of the sources with few soft counts are among the hardest
sources, and they can be fitted with a flat power law, and viceversa
the softest sources can be fitted with a very steep power
law. However, we argue that this behaviour may be affected by the poor
statistics. To avoid any possible bias induced by the low statistics,
we conservatively define an X-ray bright sample by considering those
sources exceeding at least one of these thesholds: 170 total counts,
120 soft counts, 80 hard counts. As we can see in Fig. 3b, the threshold on the soft counts is particularly
efficient in selecting sources for which the statistical error on ![]() is smaller than 20% (about 10% in average). The bright
sample, constituted by 82 sources, will be used to investigate both
the intrinsic spectral slope
is smaller than 20% (about 10% in average). The bright
sample, constituted by 82 sources, will be used to investigate both
the intrinsic spectral slope ![]() and the intrinsic absorption
and the intrinsic absorption ![]() .
We remark here that the bright sources are selected on the
basis of the net detected counts, and not on the basis of the energy
flux; among the brigth sample, we find sources with fluxes larger than
.
We remark here that the bright sources are selected on the
basis of the net detected counts, and not on the basis of the energy
flux; among the brigth sample, we find sources with fluxes larger than
![]() erg s-1 cm-2 in the soft and
erg s-1 cm-2 in the soft and
![]() erg s-1 cm-2 in the hard band. As for the
remaining 3/4 of the sample, we decide to fix the slope to the
canonical value of
erg s-1 cm-2 in the hard band. As for the
remaining 3/4 of the sample, we decide to fix the slope to the
canonical value of
![]() (see Turner et al. 1997), which
is, in turn, very close to the average value measured for our bright
sample (as shown in Sect. 4), and focus on the intrinsic absorption.
(see Turner et al. 1997), which
is, in turn, very close to the average value measured for our bright
sample (as shown in Sect. 4), and focus on the intrinsic absorption.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig03a.ps}\hspace*{4mm}
\includegraphics[width=8cm,clip]{2592fig03b.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg71.gif) |
Figure 3:
Left: best fit values of the spectral slope |
| Open with DEXTER | |
We assume a default spectral model based on a power law (XSPEC model
pow) and intrinsic absorption at the source redshift (XSPEC
model zwabs) with redshift frozen to the spectroscopic or
photometric value. Also, we search for the Fe K![]() line at 6.4 keV rest-frame, which is one of the most common features of AGN X-ray spectra. To investigate the presence of such a line, we added
a redshifted unresolved Gaussian line at 6.4/(1+z) keV (Nandra &
Pounds 1994). We also take into account the local Galactic absorption
(XSPEC model tbabs) with a column density frozen to
line at 6.4 keV rest-frame, which is one of the most common features of AGN X-ray spectra. To investigate the presence of such a line, we added
a redshifted unresolved Gaussian line at 6.4/(1+z) keV (Nandra &
Pounds 1994). We also take into account the local Galactic absorption
(XSPEC model tbabs) with a column density frozen to
![]() cm-2 (from Dickey & Lockman 1990). The fits are
performed on the energy range 0.6-7 keV. We cut below 0.6 keV to
avoid uncertainties in the ACIS calibration in an energy range which
anyway offers a small effective area. At high energies, the
efficiency of Chandra is rapidly decreasing, and the energy bins at
more than 7 keV are dominated by the noise for the large majority of
the sources in our flux range. It has recently been shown that a
methylen layer on the Chandra mirrors increases the effective area at
energies larger than 2 keV (see Marshall et al. 2003)
cm-2 (from Dickey & Lockman 1990). The fits are
performed on the energy range 0.6-7 keV. We cut below 0.6 keV to
avoid uncertainties in the ACIS calibration in an energy range which
anyway offers a small effective area. At high energies, the
efficiency of Chandra is rapidly decreasing, and the energy bins at
more than 7 keV are dominated by the noise for the large majority of
the sources in our flux range. It has recently been shown that a
methylen layer on the Chandra mirrors increases the effective area at
energies larger than 2 keV (see Marshall et al. 2003)![]() .
This has a small effect on the total measured fluxes, but it can have
a non-negligible effect on the spectral parameters. To correct for
this, we include in the fitting model a "positive absorption edge''
(XSPEC model edge) at an energy of 2.07 keV and with
.
This has a small effect on the total measured fluxes, but it can have
a non-negligible effect on the spectral parameters. To correct for
this, we include in the fitting model a "positive absorption edge''
(XSPEC model edge) at an energy of 2.07 keV and with
![]() (Vikhlinin et al. 2005). This multiplicative component
artificially increases the hard fluxes by
(Vikhlinin et al. 2005). This multiplicative component
artificially increases the hard fluxes by ![]() 3.5%, therefore
the final hard fluxes and luminosities computed from the fit are
corrected downwards by the same amount.
3.5%, therefore
the final hard fluxes and luminosities computed from the fit are
corrected downwards by the same amount.
In some cases, the fit with a simple absorbed power law may not be a
good description of the X-ray spectrum. On the other hand, our
limited counts statistics does not allow us to investigate for complex
spectral shapes as often observed in AGN. However, we identify two
possible additional spectral models. A first spectral model we
investigate is the presence of a soft component in addition to the
absorbed power law, as often found in the X-ray spectra of Seyfert 2
galaxies (e.g. Turner et al. 1997). Such a soft component can arise
from several physical processes, like nuclear radiation scattered by a
warm medium (the so-called "warm mirror'', e.g. Matt et al. 1996), or
nuclear radiation leaking through the absorber. In this cases, the
soft component is expected to have the same spectral slope of the main
power law. Here we do not consider the soft excess possibly due to
thermal emission or comptonization of soft photons, as found in bright
quasars (see Porquet et al. 2004). Thus, we repeated the fits simply
adding to the Compton-thin model an unabsorbed power law component
with slope equal to that of the main power law, requiring the
intrinsic normalization of the soft component to be always less than 10% of the intrinsic normalization of the main power law. This last
requirement embraces typical values both for a scattered component and
for leaky absorbers (see Turner et al. 1997). This upper limit may
exclude some leaky absorber with a low covering fraction, but at the
same time helps us in avoiding false detections of high-normalization
soft components implying spuriously high values of ![]() relative to
the absorbed component. With this procedure, a soft component is
detected with
relative to
the absorbed component. With this procedure, a soft component is
detected with
![]() in 8 sources.
in 8 sources.
Moreover, when the intrinsic absorption is as high as
![]() cm-2, the Compton optical depth is equal to
unity and the directly transmitted nuclear emission is strongly
suppressed in the Chandra soft and hard bands. In particular, for an
intrinsic power-law spectrum with
cm-2, the Compton optical depth is equal to
unity and the directly transmitted nuclear emission is strongly
suppressed in the Chandra soft and hard bands. In particular, for an
intrinsic power-law spectrum with
![]() ,
the fraction of
transmitted photons is less than
,
the fraction of
transmitted photons is less than ![]() in the soft band up to redshift
z=2. Absorption is less severe in the hard band, where for z>1already a fraction of
in the soft band up to redshift
z=2. Absorption is less severe in the hard band, where for z>1already a fraction of ![]() of the emitted photons are recovered. It
is clear that only the intrinsically brightest, heavily absorbed
high-redshift AGN can be detected by their transmitted nuclear
emission. In this regime, a radiation component reflected by a cold
medium, expected to be in average
of the emitted photons are recovered. It
is clear that only the intrinsically brightest, heavily absorbed
high-redshift AGN can be detected by their transmitted nuclear
emission. In this regime, a radiation component reflected by a cold
medium, expected to be in average ![]() of the intrinsic power in the
2-10 keV band, starts to be important. For these Compton-thick
sources, the most commonly observed spectrum is dominated by a
Compton-reflection continuum from cold medium, usually assumed to be
produced by the far inner side of the putative obscuring torus. This
can be modeled with the XSPEC model pexrav (Magdziarz &
Zdziarski 1995) plus the redshifted Fe K line.
of the intrinsic power in the
2-10 keV band, starts to be important. For these Compton-thick
sources, the most commonly observed spectrum is dominated by a
Compton-reflection continuum from cold medium, usually assumed to be
produced by the far inner side of the putative obscuring torus. This
can be modeled with the XSPEC model pexrav (Magdziarz &
Zdziarski 1995) plus the redshifted Fe K line.
The pexrav model often provides a better fit for the sources in
our sample with a flat spectrum. For simplicity, we fix all the
parameters to the default, typical values (
![]() ,
reflection
relative normalization = 0, element and Fe abundance set to 1, cosine of
inclination angle set to 0.45) but the normalization of the intrinsic
power law spectrum. Our selection of Compton-thick candidates, then,
is based on the comparison of the Cash-statistics obtained in the
best fits with the zwabs pow model (with two free parameters,
,
reflection
relative normalization = 0, element and Fe abundance set to 1, cosine of
inclination angle set to 0.45) but the normalization of the intrinsic
power law spectrum. Our selection of Compton-thick candidates, then,
is based on the comparison of the Cash-statistics obtained in the
best fits with the zwabs pow model (with two free parameters,
![]() and normalization) with that obtained with the pure reflection
model (with only one free parameter, the normalization). The
difference
and normalization) with that obtained with the pure reflection
model (with only one free parameter, the normalization). The
difference ![]() is an indication of the goodness of the pexrav model with respect to the standard absorbed power law. Due to
the different number of free parameters and the low signal-to-noise
typical of our sources, we choose a threshold
is an indication of the goodness of the pexrav model with respect to the standard absorbed power law. Due to
the different number of free parameters and the low signal-to-noise
typical of our sources, we choose a threshold
![]() to
select Compton-thick candidates after extensive simulations. The
simulations procedure is described in Appendix B. We find that a
threshold
to
select Compton-thick candidates after extensive simulations. The
simulations procedure is described in Appendix B. We find that a
threshold
![]() allows us to select a sample of
Compton-thick candidates with a contamination fraction of about 20%.
On the other hand, we also find that with our selection criteria, we
may miss a fraction as high as 40% of the total Compton-thick
population. Indeed, we find that, given the typical signal-to-noise
of our sample, it is extremely difficult to efficiently select
Compton-thick sources on the basis of the shape of the X-ray
spectrum. We recognize that, in order to perform a careful search for
Compton-thick candidates, other spectral features, like the Fe K line, or other wavelengths (like the submillimeter range of SCUBA)
should be explored (see Alexander et al. 2005b). This goes beyond the
goal of this paper.
allows us to select a sample of
Compton-thick candidates with a contamination fraction of about 20%.
On the other hand, we also find that with our selection criteria, we
may miss a fraction as high as 40% of the total Compton-thick
population. Indeed, we find that, given the typical signal-to-noise
of our sample, it is extremely difficult to efficiently select
Compton-thick sources on the basis of the shape of the X-ray
spectrum. We recognize that, in order to perform a careful search for
Compton-thick candidates, other spectral features, like the Fe K line, or other wavelengths (like the submillimeter range of SCUBA)
should be explored (see Alexander et al. 2005b). This goes beyond the
goal of this paper.
To summarize, we label as C-thin the sources for which the best fit model is a power law with intrinsic absorption; C-thick the sources for which the best fit is given by a pexrav model; finally Soft-C for sources whose best fit model includes a soft component with the same slope of the main power law. Finally, we always add a Gaussian component to model the Fe K line, which, in case of no detection, gives a null or negligible contribution to the spectral shape.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig04.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg82.gif) |
Figure 4:
Distribution of the spectral slope |
| Open with DEXTER | |
First, we consider only the X-ray bright sample of 82 sources with
more than 120 net detected counts in the soft band or more than 80 in
the hard band, and more than 170 net counts overall. Among them, only
two sources with soft component are found, and no Compton thick
candidates. We note that the low fraction of sources with significant
soft component, lower than that in the local sample of Turner et al. (1997), may be ascribed to the high redshifts in our sample, for
which the soft component is often shifted below 0.6 keV. We use this
subsample (1/4 of the total sample) to investigate the behaviour of
the spectral slope ![]() .
The normalized distribution of spectral
slopes for the X-ray bright sample is shown in Fig. 4.
The distribution has been obtained by extracting the value of
.
The normalized distribution of spectral
slopes for the X-ray bright sample is shown in Fig. 4.
The distribution has been obtained by extracting the value of ![]() of each source 104 times from the range allowed by the statistical
error bars, assuming a Gaussian error distribution. With this
procedure, we weight each source in the histogram according to the
statistical errors on
of each source 104 times from the range allowed by the statistical
error bars, assuming a Gaussian error distribution. With this
procedure, we weight each source in the histogram according to the
statistical errors on ![]() .
Before computing the weighted mean
value, we exclude the two brightest sources in the sample (about 104 net counts each) which otherwise would dominate the statistics.
We find that the weighted mean value for the spectral slope of the
bright sample is
.
Before computing the weighted mean
value, we exclude the two brightest sources in the sample (about 104 net counts each) which otherwise would dominate the statistics.
We find that the weighted mean value for the spectral slope of the
bright sample is
![]() (error bar
refers to 1
(error bar
refers to 1 ![]() uncertainty on the mean value). While the
typical error on a single measure is about
uncertainty on the mean value). While the
typical error on a single measure is about
![]() ,
the dispersion of the distribution of the best fit values is
,
the dispersion of the distribution of the best fit values is
![]() .
Assuming that both statistical errors and the intrinsic
dispersion in
.
Assuming that both statistical errors and the intrinsic
dispersion in ![]() are distributed as a Gaussian, the intrinsic
scatter is of the order of
are distributed as a Gaussian, the intrinsic
scatter is of the order of
![]() .
If we focus on
the 30 brightest sources to decrease the statistical errors (still
excluding the two sources with
.
If we focus on
the 30 brightest sources to decrease the statistical errors (still
excluding the two sources with ![]() 104 counts), the estimate of
the intrinsic scatter decrease to
104 counts), the estimate of
the intrinsic scatter decrease to
![]() ,
and the
weighted mean value is
,
and the
weighted mean value is
![]() .
.
In Fig. 5, we plot the best fit values of ![]() versus the best fit values of the intrinsic absorption
versus the best fit values of the intrinsic absorption ![]() .
We do
not detect any correlation between
.
We do
not detect any correlation between ![]() and
and ![]() (Spearman Rank
coefficient
(Spearman Rank
coefficient
![]() ). Note that if the intrinsic absorption is
close to the Galactic value for the CDFS field (
). Note that if the intrinsic absorption is
close to the Galactic value for the CDFS field (
![]() cm-2) we are not able to derive any meaningful
value, due to the low-energy limit of our spectral range (E >0.6 keV). We considered these sources to be unabsorbed, plotting them at
cm-2) we are not able to derive any meaningful
value, due to the low-energy limit of our spectral range (E >0.6 keV). We considered these sources to be unabsorbed, plotting them at
![]() cm-2 in our figures. We detect no correlation
between
cm-2 in our figures. We detect no correlation
between ![]() and the hard rest-frame intrinsic (unabsorbed)
luminosity (see Fig. 6). The Spearman Rank correlation
is null also between
and the hard rest-frame intrinsic (unabsorbed)
luminosity (see Fig. 6). The Spearman Rank correlation
is null also between ![]() and the redshift (see Fig. 7).
and the redshift (see Fig. 7).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig05.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg92.gif) |
Figure 5:
Scatter plot of the best fit values of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig06.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg93.gif) |
Figure 6:
Scatter plot of the best fit values of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig07.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg94.gif) |
Figure 7:
Scatter plot of the best fit values of |
| Open with DEXTER | |
From the analysis of the bright sample, we conclude that among our
sources the intrinsic continuum is well approximated by a power law
with
![]() (typical of Seyfert galaxies and AGN, as known
also from ASCA studies of AGN, see Turner et al. 1997) at any epoch.
On the other hand, it is well known that the flattening of the average
spectrum of the sources at low fluxes in deep X-ray survey is due
mainly to increasing intrinsic absorption (see Ueda et al. 1999b;
Tozzi et al. 2001; Piconcelli et al. 2003; La Franca et al. 2005). In
addition, previous studies found no hints for a change in the slope of
the intrinsic power law as a function of epoch or luminosity (see also
Mainieri et al. 2002; Piconcelli et al. 2003; Vignali et al. 2003).
We conclude that the slope of the intrinsic power law can be assumed
to be constant for all the AGN population, and, therefore, we choose
to fix the spectral slope to
(typical of Seyfert galaxies and AGN, as known
also from ASCA studies of AGN, see Turner et al. 1997) at any epoch.
On the other hand, it is well known that the flattening of the average
spectrum of the sources at low fluxes in deep X-ray survey is due
mainly to increasing intrinsic absorption (see Ueda et al. 1999b;
Tozzi et al. 2001; Piconcelli et al. 2003; La Franca et al. 2005). In
addition, previous studies found no hints for a change in the slope of
the intrinsic power law as a function of epoch or luminosity (see also
Mainieri et al. 2002; Piconcelli et al. 2003; Vignali et al. 2003).
We conclude that the slope of the intrinsic power law can be assumed
to be constant for all the AGN population, and, therefore, we choose
to fix the spectral slope to
![]() when fitting the remaining
fainter sources, focusing on the
when fitting the remaining
fainter sources, focusing on the ![]() distribution for the whole
sample.
distribution for the whole
sample.
We complete the analysis of the total sample fixing
![]() and
deriving
and
deriving ![]() for the remaining faint sources (239/321). We remark
that our division in a bright and a faint subsample does not
correspond to a dramatic selection in redshift. Indeed, the X-ray
bright and the X-ray faint subsamples have a similar distribution in
redshift (see Fig. 8). The results of the fits, along
with the redshifts and the quality of the optical spectra, are shown
in Table 1.
for the remaining faint sources (239/321). We remark
that our division in a bright and a faint subsample does not
correspond to a dramatic selection in redshift. Indeed, the X-ray
bright and the X-ray faint subsamples have a similar distribution in
redshift (see Fig. 8). The results of the fits, along
with the redshifts and the quality of the optical spectra, are shown
in Table 1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig08.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg95.gif) |
Figure 8: Normalized redshift distribution for the X-ray bright (solid line, 82 sources) and the X-ray faint (dashed line, 239 sources) subsamples. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig09.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg96.gif) |
Figure 9:
The solid line shows the observed |
| Open with DEXTER | |
The distribution of the absorbing column densities is shown for the
whole sample in Fig. 9. Our results are in good
agreement with preliminary results from the CDFN (Bauer et al. 2004a).
The distribution has been obtained by extracting the value of ![]() of
each source 104 times from the range allowed by the statistical
error bars, assuming Gaussian errors. When the lower
of
each source 104 times from the range allowed by the statistical
error bars, assuming Gaussian errors. When the lower ![]() error
bars hit zero, we adopt the upper error bar to allow the
error
bars hit zero, we adopt the upper error bar to allow the ![]() resampled value to go below zero; in this case, the resampled values
are included in the lowest bin. The lowest bin shown is the value of
the Galactic absorption,
resampled value to go below zero; in this case, the resampled values
are included in the lowest bin. The lowest bin shown is the value of
the Galactic absorption,
![]() cm-2, below which
we cannot measure the intrinsic absorption, especially at high
redshifts. This bin includes all the sources with nominal
cm-2, below which
we cannot measure the intrinsic absorption, especially at high
redshifts. This bin includes all the sources with nominal ![]() best
fit value lower than 1020 cm-2. Among these sources we
expect both redshifted AGN with low absorbing columns and normal
X-ray galaxies. Note that here
best
fit value lower than 1020 cm-2. Among these sources we
expect both redshifted AGN with low absorbing columns and normal
X-ray galaxies. Note that here ![]() is an equivalent hydrogen
column measured assuming the photo-electric cross-sections by
Morrison & McCammon (1983), with metal abundances relative to
Hydrogen by Anders & Ebihara (1982). The last bin at
is an equivalent hydrogen
column measured assuming the photo-electric cross-sections by
Morrison & McCammon (1983), with metal abundances relative to
Hydrogen by Anders & Ebihara (1982). The last bin at
![]() cm-2 includes the few sources with measured
cm-2 includes the few sources with measured
![]() cm-2 and the Compton-thick candidates.
cm-2 and the Compton-thick candidates.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig10.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg99.gif) |
Figure 10:
Significance of the Fe line (measured with simulations, see
text) plotted versus the observed |
| Open with DEXTER | |
We look for the Fe line only in those sources having at least 10 net
counts in both bands, to have an acceptable estimate of the continuum
and avoid spurious measures of high equivalent widths. Adopting a
threshold
![]() with respect to the fit without the
line, corresponding to a minimum 90% c.l. for one interesting
parameter, we find evidence for a significant Fe line in 20 sources
with at least 10 net counts in both bands. The corresponding
equivalent widths span the 100-3000 eV range. We carefully checked
that our criterion
with respect to the fit without the
line, corresponding to a minimum 90% c.l. for one interesting
parameter, we find evidence for a significant Fe line in 20 sources
with at least 10 net counts in both bands. The corresponding
equivalent widths span the 100-3000 eV range. We carefully checked
that our criterion
![]() actually corresponds to more than 90% c.l. also in the case of a line detection (for which the
canonical confidence level criterion cannot be applied, see Protassov
et al. 2002). For each X-ray source we simulated 500 spectra starting
from the observed best fit model without the line. We then fitted each
simulated spectrum and looked for any variation in the C-stat when
adding a Fe line at 6.4/(1+z). The frequency of occurrence of
actually corresponds to more than 90% c.l. also in the case of a line detection (for which the
canonical confidence level criterion cannot be applied, see Protassov
et al. 2002). For each X-ray source we simulated 500 spectra starting
from the observed best fit model without the line. We then fitted each
simulated spectrum and looked for any variation in the C-stat when
adding a Fe line at 6.4/(1+z). The frequency of occurrence of
![]() gives the probability P that the
detected line is a statistical fluctuation. In Fig. 10 we show the significance (1-P) of the Fe line
versus the measured
gives the probability P that the
detected line is a statistical fluctuation. In Fig. 10 we show the significance (1-P) of the Fe line
versus the measured ![]() .
We conclude that in the large
majority of the cases the criterion
.
We conclude that in the large
majority of the cases the criterion
![]() corresponds to a
confidence level greater than 95%. Among the sources with more than 10 counts in both bands and a significant Fe line, 14/116 (
corresponds to a
confidence level greater than 95%. Among the sources with more than 10 counts in both bands and a significant Fe line, 14/116 (![]() 12%) are found among the sources with spectroscopic redshift, and
only 6/125 (
12%) are found among the sources with spectroscopic redshift, and
only 6/125 (![]() 5%) are found in the subsample with photometric
redshift. This shows that, given our X-ray spectral resolution, the
uncertainties in the photometric redshifts are likely to negatively
affect the detection of the Fe line with our method, i.e., fixing the
expected observing-frame energy of the line. Indeed, we notice that
some sources do show strong hints of a Fe line at a redshift different
from the photometric one (see Mainieri et al. 2005a), or peculiar
lines (see Wang et al. 2003); finally, source variability could hide
the emission line (see Braito et al. 2005). Therefore, we conclude
that the fraction of sources with significant emission line is
slightly larger than that found in an X-ray bright subsample in the CDFN (7%, see Bauer et al. 2004b). In principle, if the Fe line were
produced only by the interaction of photons with the absorbing medium,
a positive correlation between
5%) are found in the subsample with photometric
redshift. This shows that, given our X-ray spectral resolution, the
uncertainties in the photometric redshifts are likely to negatively
affect the detection of the Fe line with our method, i.e., fixing the
expected observing-frame energy of the line. Indeed, we notice that
some sources do show strong hints of a Fe line at a redshift different
from the photometric one (see Mainieri et al. 2005a), or peculiar
lines (see Wang et al. 2003); finally, source variability could hide
the emission line (see Braito et al. 2005). Therefore, we conclude
that the fraction of sources with significant emission line is
slightly larger than that found in an X-ray bright subsample in the CDFN (7%, see Bauer et al. 2004b). In principle, if the Fe line were
produced only by the interaction of photons with the absorbing medium,
a positive correlation between ![]() and equivalent width might be
expected in obscured sources (Leahy & Creighton 1993; Ghisellini et al. 1994). As shown in Fig. 11, we do not find strong
evidence of a correlation given the scatter of our data points, as
already observed (see Mushotzky et al. 1993). The Fe lines
measured with low intrinsic absorption (
and equivalent width might be
expected in obscured sources (Leahy & Creighton 1993; Ghisellini et al. 1994). As shown in Fig. 11, we do not find strong
evidence of a correlation given the scatter of our data points, as
already observed (see Mushotzky et al. 1993). The Fe lines
measured with low intrinsic absorption (
![]() cm-2), may
be produced by the accretion disk, therefore breaking the expected
correlation.
cm-2), may
be produced by the accretion disk, therefore breaking the expected
correlation.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig11.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg102.gif) |
Figure 11:
Equivalent width of the Fe line plotted versus the intrinsic
absorption |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig12.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg103.gif) |
Figure 12:
Intrinsic absorption versus redshift for the complete sample.
Upper limits (1 |
| Open with DEXTER | |
In Fig. 12 we show the scatter plot of intrinsic
absorption as a function of redshift for the whole sample. We note
the lack of sources with high absorption (
![]() cm-2)
at z<1. This is due to the fact that the low-luminosity, low-zsources with high absorption show a strongly suppressed flux, and only
the intrinsically more luminous, rarer sources can be detected for a
given threshold in count rate; the detection probability, then,
decreases due to the small volume probed at low-z. We also note a
lack of sources with low absorption (around
cm-2)
at z<1. This is due to the fact that the low-luminosity, low-zsources with high absorption show a strongly suppressed flux, and only
the intrinsically more luminous, rarer sources can be detected for a
given threshold in count rate; the detection probability, then,
decreases due to the small volume probed at low-z. We also note a
lack of sources with low absorption (around
![]() cm-2) at high z. This effect may be due to the difficulty in
measuring
cm-2) at high z. This effect may be due to the difficulty in
measuring ![]() at z>2, since the absorption cutoff is redshifted
below the lower limit of the Chandra energy band we use (0.6 keV). This effect could result in spuriously high values of
at z>2, since the absorption cutoff is redshifted
below the lower limit of the Chandra energy band we use (0.6 keV). This effect could result in spuriously high values of ![]() with
large error bars. Note, however, that some of the points are just 1
with
large error bars. Note, however, that some of the points are just 1![]() upper limits, implying the presence of sources with low
upper limits, implying the presence of sources with low ![]() value at high redshift as well. It is clear that the
value at high redshift as well. It is clear that the
![]() scatter plot shows the effects of the incompleteness and partial
sampling of the AGN population. Before investigating the shape and
evolution of the intrinsic
scatter plot shows the effects of the incompleteness and partial
sampling of the AGN population. Before investigating the shape and
evolution of the intrinsic ![]() distribution, we must correct for the
number of sources with a given
distribution, we must correct for the
number of sources with a given ![]() ,
,
![]() and z that fall outside
our detection criteria. We will do this in the next section.
and z that fall outside
our detection criteria. We will do this in the next section.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig13.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg107.gif) |
Figure 13:
Unabsorbed rest-frame luminosities in the soft ( upper panel)
and in the hard ( lower panel) band plotted versus the intrinsic
absorption. Upper limits (1 |
| Open with DEXTER | |
In Fig. 13 we show the scatter plot of ![]() versus the
intrinsic, unabsorbed luminosities in the soft and in the hard band.
We remark that the intrinsic luminosities are computed in the
rest-frame soft and hard bands setting to zero the intrinsic
absorption in the XSPEC best fit model; for the Compton-thick
candidates we measure the intrinsic luminosities using a power law
model with
versus the
intrinsic, unabsorbed luminosities in the soft and in the hard band.
We remark that the intrinsic luminosities are computed in the
rest-frame soft and hard bands setting to zero the intrinsic
absorption in the XSPEC best fit model; for the Compton-thick
candidates we measure the intrinsic luminosities using a power law
model with
![]() and normalization fixed to that of the best
fit pexrav model. With this assumption the emitted (reflected)
luminosity of the C-thick sources is always about 6% of the
intrinsic one in the hard band (while only 0.2% in the soft). We
also note that this model may give a lower limit to the intrinsic
luminosity, since its assumes a maximally efficient reflection; the
intrinsic luminosity can be higher for lower refelection efficiency
(Ghisellini et al. 1994). The envelope at low luminosity and
high
and normalization fixed to that of the best
fit pexrav model. With this assumption the emitted (reflected)
luminosity of the C-thick sources is always about 6% of the
intrinsic one in the hard band (while only 0.2% in the soft). We
also note that this model may give a lower limit to the intrinsic
luminosity, since its assumes a maximally efficient reflection; the
intrinsic luminosity can be higher for lower refelection efficiency
(Ghisellini et al. 1994). The envelope at low luminosity and
high ![]() is due to the fact that our survey is flux limited. The
luminosity lower limit at a given redshift is not sharp, for two
reasons: first, our survey is count-rate limited, and different
spectral shapes may correspond to different fluxes and luminosities
for the same count rates; second, the unabsorbed luminosities are
related to the observed fluxes by a correction that depends on the
measured
is due to the fact that our survey is flux limited. The
luminosity lower limit at a given redshift is not sharp, for two
reasons: first, our survey is count-rate limited, and different
spectral shapes may correspond to different fluxes and luminosities
for the same count rates; second, the unabsorbed luminosities are
related to the observed fluxes by a correction that depends on the
measured ![]() .
For a preliminary investigation of a correlation
between
.
For a preliminary investigation of a correlation
between ![]() and intrinsic luminosity, we select two regions in
Fig. 13: i)
and intrinsic luminosity, we select two regions in
Fig. 13: i)
![]() erg s-1 and
erg s-1 and
![]() cm-2; ii)
cm-2; ii)
![]() erg s-1 and
erg s-1 and
![]() cm-2. In this way we try to minimize the effects due to the
flux-limited nature of our sample. In the first case, we do not find
significant correlation between
cm-2. In this way we try to minimize the effects due to the
flux-limited nature of our sample. In the first case, we do not find
significant correlation between ![]() and hard luminosity (Spearmann
Rank coefficient SR = 0.06 for 154 sources). In the second case as
well, we do not detect significant correlation between
and hard luminosity (Spearmann
Rank coefficient SR = 0.06 for 154 sources). In the second case as
well, we do not detect significant correlation between ![]() and hard
luminosity (Spearmann Rank coefficient SR = 0.08 from 184 sources). This result is not in disagreement with results obtained
from larger samples. Indeed, in flux-limited samples, the dependence
of the absorbed fraction on luminosity tends to be much weaker, as
discussed by Perola et al. (2004). In the following, we will not
introduce by hand the correlation between the absorbed fraction and
luminosity found in larger sample spanning more than six decades in
flux. The inability of retrieving in our sample such a correlation,
will not affect our main results, like the intrinsic distribution of
and hard
luminosity (Spearmann Rank coefficient SR = 0.08 from 184 sources). This result is not in disagreement with results obtained
from larger samples. Indeed, in flux-limited samples, the dependence
of the absorbed fraction on luminosity tends to be much weaker, as
discussed by Perola et al. (2004). In the following, we will not
introduce by hand the correlation between the absorbed fraction and
luminosity found in larger sample spanning more than six decades in
flux. The inability of retrieving in our sample such a correlation,
will not affect our main results, like the intrinsic distribution of ![]() ,
with the caveat that we are probing the luminosity range up to few
,
with the caveat that we are probing the luminosity range up to few
![]() erg s-1.
erg s-1.
In Fig. 13 we also show the locus of type II QSO, which is
the upper right corner marked with the dashed lines. The criterion is
![]() erg s-1 and
erg s-1 and
![]() cm-2. For a
spectral slope of
cm-2. For a
spectral slope of
![]() ,
a total luminosity of 1044 erg s-1 in the 0.5-10 keV band corresponds to
,
a total luminosity of 1044 erg s-1 in the 0.5-10 keV band corresponds to
![]() erg s-1 in the 0.5-2 keV band and
erg s-1 in the 0.5-2 keV band and
![]() erg s-1 in the 2-10 keV band. With these criteria, using X-ray
spectral parameters and, most importantly, unabsorbed luminosities,
the number of QSOII in the CDFS sample is 54. This corresponds to a
surface density of X-ray selected QSO equal to
erg s-1 in the 2-10 keV band. With these criteria, using X-ray
spectral parameters and, most importantly, unabsorbed luminosities,
the number of QSOII in the CDFS sample is 54. This corresponds to a
surface density of X-ray selected QSO equal to
![]() sq deg-2 at the flux limit of
sq deg-2 at the flux limit of
![]() erg cm-2 s-1. This is higher than the value found by Padovani et al. (2004), but the difference is due to their selection based on the
condition
L2-10> 1044 erg s-1. Applying the same
criteria, we find a surface density of
erg cm-2 s-1. This is higher than the value found by Padovani et al. (2004), but the difference is due to their selection based on the
condition
L2-10> 1044 erg s-1. Applying the same
criteria, we find a surface density of
![]() sq deg-2 in
very good agreement with Padovani et al. (2004; see also La Franca et al. 2005). We note, however, that the density of type II QSO depends
sensitively on the luminosity cut in the intrinsic power used in the
analysis.
sq deg-2 in
very good agreement with Padovani et al. (2004; see also La Franca et al. 2005). We note, however, that the density of type II QSO depends
sensitively on the luminosity cut in the intrinsic power used in the
analysis.
Finally, we present a sample of 14 Compton-thick candidates selected
only on the basis of the X-ray spectral shape with the selection
thresholds described in Sect. 3.2. Two of them were already identified as
Compton-thick sources on the basis of multiwavelength data (source ID 202 and 263, see Norman et al. 2002; Mainieri et al. 2005b). We
assign a value
![]() cm-2 to our
Compton-thick candidates. Among them, 2 sources (out of 7 with
secure spectroscopic redshift) show a Fe K emission line, while no
Compton thick candidate source with photometric redshift does show a
statistically significant line. We believe that the uncertainties in
the photometric redshift prevent us from recovering the line. We also
note that some high column density sources at low redshift may not
have strong Fe K lines (see Fruscione et al. 2005). We checked that
the distribution of the net detected counts of the C-thick candidates
is not different from that of the whole sample, indicating that there
are no evident bias due to the low signal-to-noise. The
net-detected counts for the C-thick sample ranges from 170 to 40,
with an average of 65. We notice that for these sources the detection
probability is low, due to their hard spectra. Consequently, their
associated sky-coverage is low, and their surface density
correspondingly higher, close to
cm-2 to our
Compton-thick candidates. Among them, 2 sources (out of 7 with
secure spectroscopic redshift) show a Fe K emission line, while no
Compton thick candidate source with photometric redshift does show a
statistically significant line. We believe that the uncertainties in
the photometric redshift prevent us from recovering the line. We also
note that some high column density sources at low redshift may not
have strong Fe K lines (see Fruscione et al. 2005). We checked that
the distribution of the net detected counts of the C-thick candidates
is not different from that of the whole sample, indicating that there
are no evident bias due to the low signal-to-noise. The
net-detected counts for the C-thick sample ranges from 170 to 40,
with an average of 65. We notice that for these sources the detection
probability is low, due to their hard spectra. Consequently, their
associated sky-coverage is low, and their surface density
correspondingly higher, close to
![]() deg-2. The
actual surface density of C-thick sources may be 20% higher if
including selection effects (see Appendix C). We notice also that the
fraction of C-thick sources predicted by updated models for the
synthesis of the XRB is in very good agreement with that found in the
CDFS (Gilli et al. 2006, in preparation).
deg-2. The
actual surface density of C-thick sources may be 20% higher if
including selection effects (see Appendix C). We notice also that the
fraction of C-thick sources predicted by updated models for the
synthesis of the XRB is in very good agreement with that found in the
CDFS (Gilli et al. 2006, in preparation).
In this section, we estimate the intrinsic absorption distribution
(the ![]() function) for the AGN population in our sample. The
distribution of
function) for the AGN population in our sample. The
distribution of ![]() that we showed in Fig. 9, does
not include any correction for incompleteness, and it refers only to
the sources observed in the region of the
that we showed in Fig. 9, does
not include any correction for incompleteness, and it refers only to
the sources observed in the region of the
![]() space
which is delimited by the count-rate detection thresholds of the
survey. To go from this distribution to a distribution which is
representative of the whole AGN population, we must apply two
independent corrections. The first is the completeness correction and
it is given by the effective solid angle under which a source of a
given intrinsic luminosity, absorbing column density and redshift, is
detected in the CDFS with our criteria. The second correction takes
into account the sources which are outside the detectability region in
the
space
which is delimited by the count-rate detection thresholds of the
survey. To go from this distribution to a distribution which is
representative of the whole AGN population, we must apply two
independent corrections. The first is the completeness correction and
it is given by the effective solid angle under which a source of a
given intrinsic luminosity, absorbing column density and redshift, is
detected in the CDFS with our criteria. The second correction takes
into account the sources which are outside the detectability region in
the
![]() space, and therefore it must be based on a
specific model of the luminosity function of AGN. We remind that a
reliable luminosity function cannot be obtained from CDFS data alone,
but should rather be derived from a combination of wider surveys, in
order to sample the bright end of the luminosity distribution, which
is poorly represented in our pencil beam survey (see Brandt &
Hasinger 2005). We describe these two corrections below.
space, and therefore it must be based on a
specific model of the luminosity function of AGN. We remind that a
reliable luminosity function cannot be obtained from CDFS data alone,
but should rather be derived from a combination of wider surveys, in
order to sample the bright end of the luminosity distribution, which
is poorly represented in our pencil beam survey (see Brandt &
Hasinger 2005). We describe these two corrections below.
To correct for incompleteness, we simply weight each source for the
inverse of the solid angle under which the source can be detected in
the CDFS. To measure this quantity, first we compute the net count
rate in the soft and hard band that would be measured in the aimpoint
of the CDFS for each source in the sample, using its best-fit model.
Then, we measure the solid angle ![]() where the ith source can
be detected in the CDFS, including the vignetting correction and the
background evaluated locally. Since the detection threshold is
applied separately in the hard and the soft image, the effective solid
angle is the largest between the two. We recall that our survey is
limited in count rate, not in flux, and for a given intrinsic
luminosity and redshift, the count rate is strongly dependent on the
intrinsic absorption, especially in the soft band, where the
sensitivity of our survey is the highest. Most of the sources have
the largest detectability angle in the soft band, while the fewer,
strongly absorbed, hard sources have the largest detectability solid
angle in the hard image. The a priori probability of having a
given source included in the CDFS sample is simply the ratio of the
solid angle
where the ith source can
be detected in the CDFS, including the vignetting correction and the
background evaluated locally. Since the detection threshold is
applied separately in the hard and the soft image, the effective solid
angle is the largest between the two. We recall that our survey is
limited in count rate, not in flux, and for a given intrinsic
luminosity and redshift, the count rate is strongly dependent on the
intrinsic absorption, especially in the soft band, where the
sensitivity of our survey is the highest. Most of the sources have
the largest detectability angle in the soft band, while the fewer,
strongly absorbed, hard sources have the largest detectability solid
angle in the hard image. The a priori probability of having a
given source included in the CDFS sample is simply the ratio of the
solid angle ![]() to the total solid angle covered by the 11
exposures of the CDFS (
to the total solid angle covered by the 11
exposures of the CDFS (
![]() deg2). Then, when
binning our sample as a function of the measured
deg2). Then, when
binning our sample as a function of the measured ![]() ,
we weight each
source for the inverse of its detection probability:
,
we weight each
source for the inverse of its detection probability:
Then, we compute the second correction, to account for the sources
which are outside the detectability region in the
![]() space in the CDFS survey. This correction is relevant for strongly
absorbed sources, since our limit in count-rate allows us to sample a
smaller range of intrinsic luminosity for increasing
space in the CDFS survey. This correction is relevant for strongly
absorbed sources, since our limit in count-rate allows us to sample a
smaller range of intrinsic luminosity for increasing ![]() at a given
redshift. This effect is mitigated at high redshift due to the
positive X-ray K-correction. Therefore, for any given redshift and
luminosity, we are measuring a different fraction of unabsorbed and
absorbed sources with respect to the total AGN population. As a
consequence, the directly observed fraction of sources with a given
at a given
redshift. This effect is mitigated at high redshift due to the
positive X-ray K-correction. Therefore, for any given redshift and
luminosity, we are measuring a different fraction of unabsorbed and
absorbed sources with respect to the total AGN population. As a
consequence, the directly observed fraction of sources with a given ![]() is affected by the shape of the actual AGN luminosity function
and by its cosmic evolution.
is affected by the shape of the actual AGN luminosity function
and by its cosmic evolution.
To correct for this effect, we must assume a model for the AGN
luminosity function. One of the most recent is the Luminosity
Dependent Density Evolution model obtained by Ueda et al. (2003; but
see Barger et al. 2005 for another determination of the AGN X-ray
luminosity function consistent with pure luminosity evolution), in
which low-luminosity sources peak at lower redshift than
high-luminosity AGN. Such a luminosity function is measured from a
combination of surveys with HEAO-1, ASCA and Chandra including part
of the CDFN sample (see also Hasinger et al. 2005 for the
most recent measure of the type I AGN luminosity function). In
particular, we use Eqs. (11), (15)-(17) of Ueda et al. (2003) to
write the comoving density of AGN per hard-band luminosity interval
![]() .
.
After assuming a luminosity function for the whole AGN population, we
can write the number of AGN in a given interval of ![]() ,
,
![]() and z as
and z as
| = | |||
| (2) |
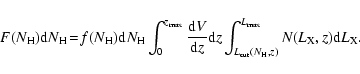 |
(3) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig14.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg136.gif) |
Figure 14:
Intrinsic minimum rest-frame luminosity in the 2-10 keV
band (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig15.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg137.gif) |
Figure 15:
Total fraction of all the AGN detected in the CDFS survey as
a function of the intrinsic |
| Open with DEXTER | |
Since
![]() (computed with Eq. (1)) is the directly observed
(computed with Eq. (1)) is the directly observed ![]() distribution (after correcting for incompleteness), the
probability function
distribution (after correcting for incompleteness), the
probability function
![]() can be obtained after Eq. (3)
(discretizing the integral over
can be obtained after Eq. (3)
(discretizing the integral over ![]() ). The resulting fraction of AGN
visible in the CDFS as a function of
). The resulting fraction of AGN
visible in the CDFS as a function of ![]() is shown in Fig. 15 for three different redshift intervals (solid lines),
and for the whole explored redshift range (thick dashed line). This
fraction is computed as the ratio of the detectable AGN over the total
number of AGN predicted by the Ueda et al. luminosity function in the
range
is shown in Fig. 15 for three different redshift intervals (solid lines),
and for the whole explored redshift range (thick dashed line). This
fraction is computed as the ratio of the detectable AGN over the total
number of AGN predicted by the Ueda et al. luminosity function in the
range
![]() erg s-1,
erg s-1,
![]() erg s-1, and
erg s-1, and
![]() .
Note that the low values of this
fraction does not imply that the majority of the AGN are not detected
in the CDFS; in fact, such low values are mostly due to the
conservatively low minimum luminosity adopted here (
.
Note that the low values of this
fraction does not imply that the majority of the AGN are not detected
in the CDFS; in fact, such low values are mostly due to the
conservatively low minimum luminosity adopted here (
![]() erg s-1) and depend on the faint end slope of the
luminosity function. These aspects, in turn, weakly affects the
dependence of the fraction on
erg s-1) and depend on the faint end slope of the
luminosity function. These aspects, in turn, weakly affects the
dependence of the fraction on ![]() ,
which is our main concern here.
Here we do not discuss the effects of the shape of the underlying
luminosity function, postponing this to a subsequent paper.
Therefore, we estimate in a robust way the dependence of the total
fraction of visible AGN on the redshift (given the flux limit in the
CDFS) and on
,
which is our main concern here.
Here we do not discuss the effects of the shape of the underlying
luminosity function, postponing this to a subsequent paper.
Therefore, we estimate in a robust way the dependence of the total
fraction of visible AGN on the redshift (given the flux limit in the
CDFS) and on ![]() .
The fraction decreases towards higher values of
.
The fraction decreases towards higher values of ![]() due to the reduced emission in the soft band, but it flattens
again in the Compton-thick regime, where the emitted luminosity is
roughly a constant fraction of the intrinsic one.
due to the reduced emission in the soft band, but it flattens
again in the Compton-thick regime, where the emitted luminosity is
roughly a constant fraction of the intrinsic one.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig16.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg142.gif) |
Figure 16:
Intrinsic |
| Open with DEXTER | |
The corrected, normalized distribution of the intrinsic absorption for
the whole sample is shown in Fig. 16. Errors are
obtained from the poissonian uncertainties on the number of detected
sources in each bin. The distribution that we measured is bimodal, in
the sense that 10% of sources have
![]() cm-2 and
appear separated from the distribution of the bulk of the sources.
However, we remark that the fraction of sources with negligible
absorption in our sample may include normal galaxies with high star
formation rate. The distribution of the bulk of the sources can be
roughly approximated with a lognormal distribution centered on
cm-2 and
appear separated from the distribution of the bulk of the sources.
However, we remark that the fraction of sources with negligible
absorption in our sample may include normal galaxies with high star
formation rate. The distribution of the bulk of the sources can be
roughly approximated with a lognormal distribution centered on
![]() and with a dispersion
and with a dispersion
![]() .
We remark that in the Compton-thin regime, where our estimates
are more robust, the number of obscured sources is steeply increasing
with
.
We remark that in the Compton-thin regime, where our estimates
are more robust, the number of obscured sources is steeply increasing
with ![]() in agreement with Risaliti et al. (1999) and Dwelly et al. (2005).
in agreement with Risaliti et al. (1999) and Dwelly et al. (2005).
This distribution accounts for the Compton-thin sources with
intrinsic absorption up to
![]() cm-2, and for
Compton-thick sources at higher absorption, bridging the bulk of the AGN to the Compton-thick population. This is the main difference
with the distribution presented in Treister et al. (2004), where the
fraction of sources with
cm-2, and for
Compton-thick sources at higher absorption, bridging the bulk of the AGN to the Compton-thick population. This is the main difference
with the distribution presented in Treister et al. (2004), where the
fraction of sources with
![]() cm-2 is dropping.
Indeed, strongly absorbed AGN are expected to be missed by surveys
that rely on optical spectroscopy. Here we show that part of the
population of Compton-thick sources can be detected in present deep
X-ray Surveys via a careful spectral analysis of all the X-ray
detected sources, avoiding selection based on optical spectroscopy.
Our results are consistent with the preliminary results on the
cm-2 is dropping.
Indeed, strongly absorbed AGN are expected to be missed by surveys
that rely on optical spectroscopy. Here we show that part of the
population of Compton-thick sources can be detected in present deep
X-ray Surveys via a careful spectral analysis of all the X-ray
detected sources, avoiding selection based on optical spectroscopy.
Our results are consistent with the preliminary results on the ![]() distribution found in the CDFN (Bauer et al. 2004a), which already
shows a peak at larger
distribution found in the CDFN (Bauer et al. 2004a), which already
shows a peak at larger ![]() values with respect to the results of
Ueda et al. (2003). We remark that this result is not affected by
small variations with respect to the luminosity function proposed by
Ueda et al. (2003), which indeed is consistent with the present data
on the AGN luminosity distribution. To summarize, we conclude that at
least part of the expected population of strongly absorbed AGN (expected to be observed in the submillimiter with the Spitzer
satellite) is already present in the deep X-ray Survey such as the
CDFS.
values with respect to the results of
Ueda et al. (2003). We remark that this result is not affected by
small variations with respect to the luminosity function proposed by
Ueda et al. (2003), which indeed is consistent with the present data
on the AGN luminosity distribution. To summarize, we conclude that at
least part of the expected population of strongly absorbed AGN (expected to be observed in the submillimiter with the Spitzer
satellite) is already present in the deep X-ray Survey such as the
CDFS.
The ![]() function is derived under the assumption of no strong
intrinsic correlation between L and
function is derived under the assumption of no strong
intrinsic correlation between L and ![]() or z and
or z and ![]() in our
sample, so that we can obtain
in our
sample, so that we can obtain
![]() without binning our sample as a
function of
without binning our sample as a
function of ![]() or z. However, here we investigate for possible
evolution with redshift of the absorbed fraction of sources. Due to
the limited statistics, we focus on the cosmic evolution of the ratio
of absorbed sources (
or z. However, here we investigate for possible
evolution with redshift of the absorbed fraction of sources. Due to
the limited statistics, we focus on the cosmic evolution of the ratio
of absorbed sources (
![]() cm-2) to all the AGNs in three
bins of redshift. The redshift bins are z=0-0.7, 0.7-1.5,
1.5-5, including 76, 125 and 109 sources with
cm-2) to all the AGNs in three
bins of redshift. The redshift bins are z=0-0.7, 0.7-1.5,
1.5-5, including 76, 125 and 109 sources with
![]() erg s-1 respectively (the first two bins include the two most
prominent spikes in the CDFS redshift distribution at z=0.67 and
z=0.73, as shown in Gilli et al. 2003). The correction for the
absorbed sources that are missed is larger at low redshift, as can be
seen in Fig. 15 (upper curve for the redshift range z=0-0.7), while at high z is almost flat up to log(
erg s-1 respectively (the first two bins include the two most
prominent spikes in the CDFS redshift distribution at z=0.67 and
z=0.73, as shown in Gilli et al. 2003). The correction for the
absorbed sources that are missed is larger at low redshift, as can be
seen in Fig. 15 (upper curve for the redshift range z=0-0.7), while at high z is almost flat up to log(![]() )=23.5(lower curve for the redshift range z=1.5-5). In Fig. 17 we show that the absorbed fraction is consistent with
a moderate increase, in agreement with the model of Gilli et al. (2001; see also Civano et al. 2005). We remark that
the absorbed fraction in the first bin at z<0.8, including the low
luminosity sources, may be underestimated due to the presence of star
forming galaxies in the luminosity range
1041-1042 erg s-1.
)=23.5(lower curve for the redshift range z=1.5-5). In Fig. 17 we show that the absorbed fraction is consistent with
a moderate increase, in agreement with the model of Gilli et al. (2001; see also Civano et al. 2005). We remark that
the absorbed fraction in the first bin at z<0.8, including the low
luminosity sources, may be underestimated due to the presence of star
forming galaxies in the luminosity range
1041-1042 erg s-1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig17.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg147.gif) |
Figure 17:
Fraction of absorbed AGNs with
|
| Open with DEXTER | |
We note that the overall value of the fraction of absorbed sources is
larger than that found by Ueda et al. (2003). However, the points of
Ueda et al. (2003) include only sources with
![]() erg s-1, and therefore are expected to be significantly higher when
including lower luminosities. The global fraction of absorbed sources
is in agreement with that estimated in the CDFN by Perola et al. (2004), and with a ratio of absorbed over unabsorbed sources in
the sample of about 4, as observed in the local Universe (e.g. Maiolino
& Rieke 1995). This value is also consistent with the theoretical
expectation of 3/4 of all the AGN being absorbed as in the standard
unification scenario (Antonucci 1993). While in the CDFS and CDFN the fraction of obscured sources seems to be in agreement with the
expectations of the standard unification scenario and popular
synthesis models of the X-ray background, in shallower serendipitous
surveys like those performed with XMM by Piconcelli et al. (2003) and
Mateos et al. (2005) obscured sources seem to be a factor of
erg s-1, and therefore are expected to be significantly higher when
including lower luminosities. The global fraction of absorbed sources
is in agreement with that estimated in the CDFN by Perola et al. (2004), and with a ratio of absorbed over unabsorbed sources in
the sample of about 4, as observed in the local Universe (e.g. Maiolino
& Rieke 1995). This value is also consistent with the theoretical
expectation of 3/4 of all the AGN being absorbed as in the standard
unification scenario (Antonucci 1993). While in the CDFS and CDFN the fraction of obscured sources seems to be in agreement with the
expectations of the standard unification scenario and popular
synthesis models of the X-ray background, in shallower serendipitous
surveys like those performed with XMM by Piconcelli et al. (2003) and
Mateos et al. (2005) obscured sources seem to be a factor of ![]() 2 less abundant. At typical X-ray fluxes of a few 10-14 erg s-1 cm-2, XMM serendipitous sources have a median luminosity
of a few 1044 erg s-1. It is therefore possible that the
intrinsic fraction of obscured sources is decreasing at luminosities
higher than that observed in the Chandra Msec fields, which would
point towards a paucity of obscured QSOs as found by Ueda et al. (2003; see also La Franca et al. 2005). Alternatively, one could
argue about the large spectroscopic incompleteness of XMM samples
(more than 60% of the sources are as yet unidentified) before drawing
solid conclusions.
2 less abundant. At typical X-ray fluxes of a few 10-14 erg s-1 cm-2, XMM serendipitous sources have a median luminosity
of a few 1044 erg s-1. It is therefore possible that the
intrinsic fraction of obscured sources is decreasing at luminosities
higher than that observed in the Chandra Msec fields, which would
point towards a paucity of obscured QSOs as found by Ueda et al. (2003; see also La Franca et al. 2005). Alternatively, one could
argue about the large spectroscopic incompleteness of XMM samples
(more than 60% of the sources are as yet unidentified) before drawing
solid conclusions.
If we classify the whole sample of 321 sources with
![]() erg s-1, according only to the optical spectra, we obtain the
following:
erg s-1, according only to the optical spectra, we obtain the
following:
Table 2: Comparison of the optical and X-ray classification.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{2592fig18.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg152.gif) |
Figure 18:
Normalized |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{2592fig19.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg153.gif) |
Figure 19: Normalized distribution of the intrinsic rest-frame luminosity in the hard band for the four different optical classes (see text). |
| Open with DEXTER | |
We also plot the normalized distribution of the intrinsic absorption
and hard luminosities for the four optical classes in Figs. 18 and 19. Here we account for the statistical
errors by resampling each value according to its error bars, but we do
not introduce any correction for selection effects, since here we are
dominated by optical selection criteria. We find that, as expected,
the BLAGN class mostly includes AGN with low absorbing column
densities: among the 34 BLAGN, only 7 sources have
![]() cm-2; they give a fraction of 0.18 of BLAGN with
cm-2; they give a fraction of 0.18 of BLAGN with
![]() cm-2, after accounting for statistical errors. This fraction is
somewhat larger than that found in shallower surveys by Perola et al. (2004) and in the ChaMP survey by Silverman et al. (2005).
However, we notice that most of the absorbed BLAGN are at
cm-2, after accounting for statistical errors. This fraction is
somewhat larger than that found in shallower surveys by Perola et al. (2004) and in the ChaMP survey by Silverman et al. (2005).
However, we notice that most of the absorbed BLAGN are at ![]() .
Due to the large errors expected when measuring
.
Due to the large errors expected when measuring ![]() in high redshift
sources, we do expect a scatter towards high values increasing with
redshift. A spurious trend
in high redshift
sources, we do expect a scatter towards high values increasing with
redshift. A spurious trend
![]() may be visible if we
simply plot the best fit values for
may be visible if we
simply plot the best fit values for ![]() .
We carefully checked with
simulations with XSPEC that the error bars keep track of this effect,
being larger at higher z. In these simulations, described in Appendix
C, we show that in the hypothesis of
.
We carefully checked with
simulations with XSPEC that the error bars keep track of this effect,
being larger at higher z. In these simulations, described in Appendix
C, we show that in the hypothesis of
![]() for all the BLAGN
sources, we should expect none of them to have
for all the BLAGN
sources, we should expect none of them to have
![]() at 2
at 2![]() c.l. Instead, we find five of them to have
c.l. Instead, we find five of them to have
![]() cm-2 at 2
cm-2 at 2![]() .
Using the better count statistics and the larger energy
range (E>0.2 keV) of XMM (see Streblyanska et al. 2004), the
spectral analysis of 5 of these sources gives absorption in the range
.
Using the better count statistics and the larger energy
range (E>0.2 keV) of XMM (see Streblyanska et al. 2004), the
spectral analysis of 5 of these sources gives absorption in the range
![]() cm-2, confirming that these BLAGN have a
non-negligible absorption, but that the Chandra best-fit values are
somewhat higher, possibly due to the limited energy range used which
may hamper the measure of low column densities at high z.
To summarize, we put a strict upper limit of 18% for absorbed sources
(
cm-2, confirming that these BLAGN have a
non-negligible absorption, but that the Chandra best-fit values are
somewhat higher, possibly due to the limited energy range used which
may hamper the measure of low column densities at high z.
To summarize, we put a strict upper limit of 18% for absorbed sources
(
![]() cm-2) within BLAGN.
cm-2) within BLAGN.
Absorbed AGNs with
![]() cm-2 are found mostly in the HEX and LEX classes (80% and 60% respectively). They are also found
in the ABS class, where, however few sources have
cm-2 are found mostly in the HEX and LEX classes (80% and 60% respectively). They are also found
in the ABS class, where, however few sources have
![]() cm-2. We find less evidence for Narrow Line AGN (here classified
as HEX) with low absorption. We observe only about
cm-2. We find less evidence for Narrow Line AGN (here classified
as HEX) with low absorption. We observe only about ![]() 10% of
such sources, for which the most likely scenario is severe dilution of
the AGN optical emission by the underlying galaxy. Therefore, the
simple identification scheme of unabsorbed AGN with optical type I
(BLAGN) and absorbed AGN with optical type II (HEX and LEX) is roughly
correct, with uncertainties of less than 20%.
10% of
such sources, for which the most likely scenario is severe dilution of
the AGN optical emission by the underlying galaxy. Therefore, the
simple identification scheme of unabsorbed AGN with optical type I
(BLAGN) and absorbed AGN with optical type II (HEX and LEX) is roughly
correct, with uncertainties of less than 20%.
As for the hard luminosities (Fig. 19), we show that the
BLAGN and HEX classes have X-ray luminosities in the range
1042-1044 erg s-1 typical of AGN, with very few
sources below 1042 erg s-1. The value 1042 erg s-1 can be considered as an effective luminosity threshold
dividing AGN and normal or star forming galaxies, except for few cases
of galaxies with a strong starburst, which can reach
![]() erg s-1 for a star formation rate of about 100
erg s-1 for a star formation rate of about 100 ![]() /yr (Ranalli et al. 2003). This luminosity range, where the
presence of normal galaxies is expected to be significant, starts to
be progressively populated in the LEX and ABS classes. However, also
for the HEX class the majority of the sources have luminosities
/yr (Ranalli et al. 2003). This luminosity range, where the
presence of normal galaxies is expected to be significant, starts to
be progressively populated in the LEX and ABS classes. However, also
for the HEX class the majority of the sources have luminosities
![]() erg s-1, and only the ABS class is consistent with
being an equal mix of galaxies and AGN. The distribution of the
intrinsic rest-frame luminosities in the hard bands shows that broad
line AGN have larger intrinsic luminosities than narrow line AGN, as
noted by Barger et al. (2005). In particular, the fraction of BLAGN in
our sample among the sources with optical spectra, is strongly
increasing with luminosity, while their average luminosity is
increasing with redshift, in agreement with the findings of Steffen et al. (2003), as shown in Fig. 20.
However, due to our small sampling volume at low redshift, to the low
optical spectral completeness of our sample (
erg s-1, and only the ABS class is consistent with
being an equal mix of galaxies and AGN. The distribution of the
intrinsic rest-frame luminosities in the hard bands shows that broad
line AGN have larger intrinsic luminosities than narrow line AGN, as
noted by Barger et al. (2005). In particular, the fraction of BLAGN in
our sample among the sources with optical spectra, is strongly
increasing with luminosity, while their average luminosity is
increasing with redshift, in agreement with the findings of Steffen et al. (2003), as shown in Fig. 20.
However, due to our small sampling volume at low redshift, to the low
optical spectral completeness of our sample (![]() 1/3), and,
finally, to the possible effect of the stellar dilution that may
hinder the presence of broad lines (see, e.g., Moran et al. 2002) we
do not draw strong conclusion on this aspect.
1/3), and,
finally, to the possible effect of the stellar dilution that may
hinder the presence of broad lines (see, e.g., Moran et al. 2002) we
do not draw strong conclusion on this aspect.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2592fig20.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg160.gif) |
Figure 20:
Upper panel: fraction of BLAGN among the sample of sources
with optical redshift as a function of the 0.5-10 keV luminosity bin.
Lower panel: average 0.5-10 keV luminosity of BLAGN as a function of
the redshift bin. Only sources with
|
| Open with DEXTER | |
We presented the detailed spectral analysis of 321 sources in the
CDFS, taking advantage of spectroscopic and photometric redshifts. We
fitted the source X-ray spectra assuming a default model consisting
in a single power law with intrinsic redshifted absorption (plus a
local absorption frozen to the Galactic value in the direction of the
CDFS) and a Gaussian line at the redshifted energy of the Fe K line
complex. We look for sources with a spectrum dominated by a
reflection component (Compton-thick candidates) and for sources
showing an unabsorbed scattered component at soft energies. We are
able to derive the spectral slope distribution for the 82 brightest
sources in the sample and intrinsic absorbing column density for the
whole sample. Then, from the observed ![]() distribution, we derive
the intrinsic
distribution, we derive
the intrinsic ![]() distribution for the whole AGN population, after
correcting for incompleteness and for the differential sampling of the
AGN population as a function of intrinsic luminosity and
distribution for the whole AGN population, after
correcting for incompleteness and for the differential sampling of the
AGN population as a function of intrinsic luminosity and ![]() (modelling the luminosity function of AGN after Ueda et al. 2003). We
accounted for statistical errors in our measures by convolving the
distributions according to the error bars associated to each
measurement. We also look for evolution in the fraction of absorbed
sources as a function of the redshift. Our main results are
summarized as follows:
(modelling the luminosity function of AGN after Ueda et al. 2003). We
accounted for statistical errors in our measures by convolving the
distributions according to the error bars associated to each
measurement. We also look for evolution in the fraction of absorbed
sources as a function of the redshift. Our main results are
summarized as follows:
Acknowledgements
The Authors thank Keith Arnaud for help in the use of XSPEC; Alexei Vikhlinin and Nico Cappelluti for discussion on the reduction of Chandra data. We also thank Marcella Brusa, Andrea Comastri, Fabrizio Fiore, Fabio La Franca, Maurizio Paolillo, Andrew Ptak and Tahir Yaqoob for discussion. P. Tozzi acknowledges support under the ESO visitor program in Garching and the visitor scholarship program the John Hopkins University during the completion of this work. We thank the entire Chandra Team for the high degree of support.
Table 1:
Best fit parameters for the whole sample of
sources in the CDFS with a measured spectroscopic or photometric
redshift. Error bars correspond to 1 ![]() c.l. Luminosities are
computed for a flat
c.l. Luminosities are
computed for a flat
![]() cosmology and H0 = 70km s-1/Mpc. ID are from Giacconi et al. (2002). Quality flags with
cosmology and H0 = 70km s-1/Mpc. ID are from Giacconi et al. (2002). Quality flags with
![]() indicate optical spectral quality: Q=1 corresponds to
spectra with a single optical line identified; Q=2 indicates secure
spectra but uncertain counterpart; Q=3 indicates secure redshift.
Photometric redshifts are obtained from different methods described in
Zheng et al. (2004): HyperZ (Q=0.2), BPZ (Q=0.3), COMBO-17
(Q=0.4 Wolf et al. 2001; 2003; 2004). When we have consistent
redshift from more than one method, the corresponding quality flag is
the sum of the single Q.
indicate optical spectral quality: Q=1 corresponds to
spectra with a single optical line identified; Q=2 indicates secure
spectra but uncertain counterpart; Q=3 indicates secure redshift.
Photometric redshifts are obtained from different methods described in
Zheng et al. (2004): HyperZ (Q=0.2), BPZ (Q=0.3), COMBO-17
(Q=0.4 Wolf et al. 2001; 2003; 2004). When we have consistent
redshift from more than one method, the corresponding quality flag is
the sum of the single Q.
The background-subtracted, unfolded spectra of the sources analyzed in this paper, along with the best fit models, are shown in Figs. A.1-A.22. Spectra are binned for display purpose only, with the simple criterion of having at least 20 counts or a signal-to-noise of 3 in each bin for sources with more than 100 net detected counts. Weaker sources spectra are binned with at least 10 counts or a signal-to-noise of 2 in each bin. We recall that the binning is used only to plotting purpose, while the unbinned spectra are used when performing the fit, as described in the text. Each source is fitted with the best-fit model, which is the canonical Compton-thin plus Gaussian line model for the large majority of the sources (Figs. A.1-A.22). For 14 Compton-thick candidates we show the reflection model plus the Gaussian line (Figs. A.20), while in 8 cases we add a soft component (Fig. A.21). We remind that a reversed edge at 2.07 keV is added to each spectrum to take into account a small increase in the efficiency of the ACIS detectors which is not yet included in the ACIS response functions in CALDB2.26. Such a feature, visible as a small step just above 2 keV, should not be considered intrinsic to the sources.
![\begin{figure}
\par\resizebox{17cm}{!}{\includegraphics[angle=270]{src_1_uf_l.ps...
...gle=270]{src_17_uf_l.ps}\includegraphics[angle=270]{src_18_uf_l.ps}}\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg1643.gif) |
Figure A.1:
Unfolded spectra and best fit model for the 299 C-thin
sources (fitted with a zwabs pow model with
|
![\begin{figure}
\resizebox{18cm}{!}{\includegraphics[angle=270]{src_153_uf_cthick...
...gle=270]{src_610_uf_cthick.ps}\includegraphics[angle=270]{blank.ps}}\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg1663.gif) |
Figure A.21: Unfolded spectra and best fit model for the 14 C-thick sources (fitted with a pexrav model). |
![\begin{figure}
\resizebox{18cm}{!}{\includegraphics[angle=270]{src_29_uf_sc.ps}\...
...s[angle=270]{src_268_uf_sc.ps}\includegraphics[angle=270]{blank.ps}}\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg1664.gif) |
Figure A.22: Unfolded spectra and best fit model for the 8 Soft-C sources (fitted with a pow + zwabs pow model). |
We also assume for simplicity, that all the sources can be described
by two possible spectral shape: an absorbed power law for Compton thin
sources, and a pure reflection for Compton thick sources. With the
command fakeit within XSPEC, we simulated 1000 sources with a
pure cold reflection spectrum, pexrav in XSPEC, with ![]() fixed to 1.8 and all the other parameters set to the default values
(Simulation 1). Each simulated source is assigned a redshift and a
normalization according to the distribution of the redshifts and the
net detected counts of the subsample of real sources. Then, we
simulated another 1000 sources with an absorbed power law (zwabs
pow model), with a similar redshift and net detected counts
distributions (Simulation 2). In Fig. B.1 we compare the
redshift and net detected counts distributions of the simulated
sources with that of the parent sample of real sources. The values of
fixed to 1.8 and all the other parameters set to the default values
(Simulation 1). Each simulated source is assigned a redshift and a
normalization according to the distribution of the redshifts and the
net detected counts of the subsample of real sources. Then, we
simulated another 1000 sources with an absorbed power law (zwabs
pow model), with a similar redshift and net detected counts
distributions (Simulation 2). In Fig. B.1 we compare the
redshift and net detected counts distributions of the simulated
sources with that of the parent sample of real sources. The values of ![]() for the sources simulated with the model zwabs pow, are
consistently extracted from the distribution we found in the paper
(but only for
for the sources simulated with the model zwabs pow, are
consistently extracted from the distribution we found in the paper
(but only for
![]() cm-2 to exclude Compton thick
sources).
cm-2 to exclude Compton thick
sources).
Then, we analyzed the two sets of simulation both with the pexrav (appropriate only for Simulation 1) and zwabs pow
(appropriate only for Simulation 2) model. We verified that in the
the first case we succesfully recover the input values for the
normalization of the pexrav spectra, and in the second case the
input values for ![]() ,
within the errors. Finally, we compute the
difference between the Cash-statistics obtained with the zwabs
pow model and that obtained with the pexrav model:
,
within the errors. Finally, we compute the
difference between the Cash-statistics obtained with the zwabs
pow model and that obtained with the pexrav model:
![]() .
The normalized distributions of the values of
.
The normalized distributions of the values of ![]() are shown in Fig. B.2. We recall that we have
two free parameters for the zwabs pow model and only one for the
pexrav model; this explains why the distribution of Simulation 2
has a much larger tail at negative values of
are shown in Fig. B.2. We recall that we have
two free parameters for the zwabs pow model and only one for the
pexrav model; this explains why the distribution of Simulation 2
has a much larger tail at negative values of ![]() .
Our goal is
to use these distributions to choose a fixed threshold
.
Our goal is
to use these distributions to choose a fixed threshold
![]() that allows us to select Compton thick candidates among the parent
sample. The optimal choice would minimize the number of Compton thin
sources mistakenly included in the C-thick sample, at the same time
recovering the largest fraction of the Compton thick population.
that allows us to select Compton thick candidates among the parent
sample. The optimal choice would minimize the number of Compton thin
sources mistakenly included in the C-thick sample, at the same time
recovering the largest fraction of the Compton thick population.
The distribution of ![]() for Simulation 1 is skewed towards
large positive values, as expected since the pexrav model is the
correct one. The tail at low values of
for Simulation 1 is skewed towards
large positive values, as expected since the pexrav model is the
correct one. The tail at low values of ![]() is a measure of how
many Compton thick sources may be missed when choosing a fixed
threshold in
is a measure of how
many Compton thick sources may be missed when choosing a fixed
threshold in ![]() .
The distribution of
.
The distribution of ![]() for
Simulation 2 is centered around negative values, since here the pexrav model is not appropriate. Therefore, the tail at high values
of
for
Simulation 2 is centered around negative values, since here the pexrav model is not appropriate. Therefore, the tail at high values
of ![]() is a measure of how many sources with an actual zwabs pow spectrum are mistakenly selected as C-thick candidates for
a fixed threshold in
is a measure of how many sources with an actual zwabs pow spectrum are mistakenly selected as C-thick candidates for
a fixed threshold in ![]() .
.
The simplifying assumption that our subsample of real sources includes
only C-thin and C-thick sources, reads
![]() where
where
![]() is the total number of sources
in the subsample (here 110). We collect NC sources as C-thick
candidates by selecting the sources from the parent sample for which
is the total number of sources
in the subsample (here 110). We collect NC sources as C-thick
candidates by selecting the sources from the parent sample for which
![]() .
The expected value for NC is:
.
The expected value for NC is:
| (B.1) |
Therefore, the actual fraction of the C-thick sources in the parent
sample
![]() can be estimated as:
can be estimated as:
Obviously, for higher values of ![]() ,
the quality of the
C-cthick condidates sample is increasing, while the fraction of true
C-thick sources actually recovered drops. Assuming
,
the quality of the
C-cthick condidates sample is increasing, while the fraction of true
C-thick sources actually recovered drops. Assuming
![]() ,
we plot in Fig. B.4 the following quantities as a
function of
,
we plot in Fig. B.4 the following quantities as a
function of ![]() :
the expected fraction of true C-thick sources
among the candidates (
:
the expected fraction of true C-thick sources
among the candidates (
![]() ); the expected fraction of spurious
sources among the candidates (
); the expected fraction of spurious
sources among the candidates (
![]() ); the fraction of the total
C-thick source population actually recovered (
); the fraction of the total
C-thick source population actually recovered (
![]() ). We notice
that for
). We notice
that for
![]() more than 50% of the total C-thick source
population is recovered. Therefore we assume
more than 50% of the total C-thick source
population is recovered. Therefore we assume
![]() .
.
The number of C-thick candidates we find for
![]() is
14 (see text). The number of spurious sources among the C-thick
candidates turns out to be still significant, between 3 and 5. To
summarize, we demonstrated here that a selection of C-thick sources
on the basis of the X-ray spectrum is feasible. We also show that we
can quantify the completeness and the contamination of our C-thick
candidate sample. We also notice that the level of contamination is
not negligible, pointing towards the need of a more sophisticated
X-ray spectral analysis, including, for example, the systematic
search for the Fe line expected more frequently in
reflection-dominated spectra, or considering the presence of a soft
component that can mimick a flat spectrum (see Weaver et al. 1996).
Overall, we believe that a refined version of this approach can
constitute a valuable tool to look for Compton thick sources on the
basis of the X-ray data only.
is
14 (see text). The number of spurious sources among the C-thick
candidates turns out to be still significant, between 3 and 5. To
summarize, we demonstrated here that a selection of C-thick sources
on the basis of the X-ray spectrum is feasible. We also show that we
can quantify the completeness and the contamination of our C-thick
candidate sample. We also notice that the level of contamination is
not negligible, pointing towards the need of a more sophisticated
X-ray spectral analysis, including, for example, the systematic
search for the Fe line expected more frequently in
reflection-dominated spectra, or considering the presence of a soft
component that can mimick a flat spectrum (see Weaver et al. 1996).
Overall, we believe that a refined version of this approach can
constitute a valuable tool to look for Compton thick sources on the
basis of the X-ray data only.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{deltac_histo2.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg1679.gif) |
Figure B.1:
Normalized distribution of |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fct_vs_dc.ps}
\end{figure}](/articles/aa/full/2006/20/aa2592-04/Timg1680.gif) |
Figure B.2:
Estimated value of the fraction of C-thick sources among
the parent sample (110 sources) as a function of |
The best fit values of ![]() may show a spurious trend with redshift,
due to the increasing difficulty of measuring
may show a spurious trend with redshift,
due to the increasing difficulty of measuring ![]() when the
rest-frame soft band, which is most sensible to the intrinsic
absorption, is shifted out of the Chandra energy range. What happens
typically is that the error bars are so large that, while the upper
limits to
when the
rest-frame soft band, which is most sensible to the intrinsic
absorption, is shifted out of the Chandra energy range. What happens
typically is that the error bars are so large that, while the upper
limits to ![]() increase with redshift, the best fit values may
fluctuate at large positive values also when the source has a
negligible intrinsic absorption. We take into account part of this
effect by resampling the value of
increase with redshift, the best fit values may
fluctuate at large positive values also when the source has a
negligible intrinsic absorption. We take into account part of this
effect by resampling the value of ![]() according to the error bars,
however since
according to the error bars,
however since ![]() is always defined as positive, it is hard to avoid
an average trend of increasing intrinsic absorption with redshift. In
particular, we asked ourselves if the absorbed BLAGN found at z>2may be spurious (see Sect. 7).
is always defined as positive, it is hard to avoid
an average trend of increasing intrinsic absorption with redshift. In
particular, we asked ourselves if the absorbed BLAGN found at z>2may be spurious (see Sect. 7).
To investigate this effect, we performed three sets of simulations
(100 spectra each) of sources with negligible absorption (equal to the
galactic value
![]() cm-2) with redshift distributed
uniformly in the range z=0-4. The average number of net detected
counts in each set of simulations is 490, 150 and 80. In Fig. C.1 we show the best fit values of
cm-2) with redshift distributed
uniformly in the range z=0-4. The average number of net detected
counts in each set of simulations is 490, 150 and 80. In Fig. C.1 we show the best fit values of ![]() (with 1
(with 1![]() error bars) plotted versus redshift. We also plot separately the
cases in which
error bars) plotted versus redshift. We also plot separately the
cases in which
![]() at more than 1
at more than 1![]() .
We notice that,
while the upper limits increases following approximately the (1+z)3 law, the number of false detections of a non-negligible intrinsic
absorption (
.
We notice that,
while the upper limits increases following approximately the (1+z)3 law, the number of false detections of a non-negligible intrinsic
absorption (
![]() at more than 1
at more than 1![]() )
is not increasing
significantly with redshift. In addition, we find that at 2
)
is not increasing
significantly with redshift. In addition, we find that at 2![]() confidence level, all the values of
confidence level, all the values of ![]() are consistent with
negligible absorption.
are consistent with
negligible absorption.
Therefore, the sample of BLAGN we discuss is consistent with no
absorption in average (since
![]() for all the BLAGN at 2
for all the BLAGN at 2![]() c.l.). However the number of sources with best fit value
c.l.). However the number of sources with best fit value
![]() cm-2 among the BLAGN is 7, and it is larger than that
expected for negligible absorption on the basis of the simulations
(which is about 3). We conclude that some of the high-z BLAGN do
have absorption at the level of
cm-2 among the BLAGN is 7, and it is larger than that
expected for negligible absorption on the basis of the simulations
(which is about 3). We conclude that some of the high-z BLAGN do
have absorption at the level of
![]() cm-2, still
consistent with that found in type I AGN. Values typical of type II
AGN, larger than 1022 cm-2, would have been detected, while
values around 1021 cm-2 are compatible with what we found in
the data (see Fig. C.2). This picture is confirmed by the
analysis of the XMM data for these sources (see discussion in Sect. 7).
cm-2, still
consistent with that found in type I AGN. Values typical of type II
AGN, larger than 1022 cm-2, would have been detected, while
values around 1021 cm-2 are compatible with what we found in
the data (see Fig. C.2). This picture is confirmed by the
analysis of the XMM data for these sources (see discussion in Sect. 7).
To summarize, we find that the effect of an artificially increasing
measure of intrinsic absorption with redshift is under control in our
sample. A complete removal of the spurious trend would need extensive
simulations and several iterations, since the effect depends on the
actual behaviour of ![]() with redshift. Such an approach goes beyond
the scope of this paper, but it should be adopted for larger AGN samples.
with redshift. Such an approach goes beyond
the scope of this paper, but it should be adopted for larger AGN samples.