A&A 451, 141-146 (2006)
DOI: 10.1051/0004-6361:20054634
A dynamical model for the dusty ring in the Coalsack
P. Hennebelle1 - A. P. Whitworth2 - S. P. Goodwin3
1 - École Normale Supérieure, Laboratoire de Radioastronomie Millimétrique,
24 rue Lhomond, 75231 Paris Cedex 05, France
2 -
School of Physics & Astronomy, Cardiff University,
5 The Parade, Cardiff CF24 3YB, Wales, UK
3 -
Department of Physics & Astronomy, University of Sheffield, Hicks Building,
Housfield Road, Sheffield S3 7RH, UK
Received 18 July 2005 / Accepted 2 February 2006
Abstract
Lada et al. recently presented a detailed near-infrared extinction map
of Globule G2 in the Coalsack molecular cloud complex, showing that this starless core has a
well-defined central extinction minimum. We propose a model for G2 in which a rapid increase
in external pressure is driving an approximately symmetric compression wave into the core.
The rapid increase in external pressure could arise because the core has recently been
assimilated by the Coalsack cloud complex, or because the Coalsack has recently been created by
two large-scale converging flows. The resulting compression wave has not yet converged on the centre
of the core, so there is a central rarefaction. The compression wave has increased the density
in the swept-up gas by about a factor of ten, and accelerated it inwards to speeds of order
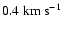 .
It is shown that even a low initial level of turbulence completely
destroys the coherence of the ring, as seen in projection. In the
scenario of strong external compression that we are proposing this
implies that the initial turbulent energy in the globule was low,
.
It is shown that even a low initial level of turbulence completely
destroys the coherence of the ring, as seen in projection. In the
scenario of strong external compression that we are proposing this
implies that the initial turbulent energy in the globule was low,
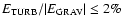 .
Protostar formation
should occur in about 40 000 years.
.
Protostar formation
should occur in about 40 000 years.
Key words: ISM: clouds - stars: formation - hydrodynamics - instabilities - shock waves
In the current paradigm for star formation, single stars, binary and multiple stars, and even
small-N clusters, are presumed to form following the collapse and fragmentation of a dense
molecular core (e.g. André et al. 2000). However, many details of this paradigm
remain to be understood, in particular the processes which form dense molecular cores in the
first place, and thereby determine the initial conditions for collapse and fragmentation.
In an attempt to understand these processes, Lada and colleagues have explored the structures
of several cores, using the NICE technique (Alves et al. 1998). These include B68 (Alves et al. (2001), where there is evidence that the core is oscillating, in accordance with the
predictions of Matsumoto & Hanawa (2003) and Hennebelle (2003), and B335 (Harvey et al. 2001),
where the density profile suggests that the core has already become unstable against collapse.
In a more recent application of the NICE technique, Lada et al. (2004) have mapped Tapia's
Globule 2 in the Coalsack (Tapia 1973).
The Coalsack is an extended cloud complex at a distance
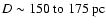 (Cambresy 1999; Rodgers 1960). If we adopt the smaller distance, the angular extent of the
complex (
(Cambresy 1999; Rodgers 1960). If we adopt the smaller distance, the angular extent of the
complex (
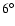 )
corresponds to a linear extent of
)
corresponds to a linear extent of 
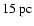 ,
and the mass
of molecular gas is
,
and the mass
of molecular gas is 
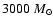 (Nyman et al. 1989). The
highly structured molecular gas mapped by Nyman et al. is probably accompanied by an
envelope and/or infill of somewhat more diffuse HI, providing shielding from the ambient
H2-dissociating UV radiation field. This HI would be very hard to detect unambiguously,
since the systemic velocity of the Coalsack is very low (
(Nyman et al. 1989). The
highly structured molecular gas mapped by Nyman et al. is probably accompanied by an
envelope and/or infill of somewhat more diffuse HI, providing shielding from the ambient
H2-dissociating UV radiation field. This HI would be very hard to detect unambiguously,
since the systemic velocity of the Coalsack is very low (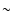
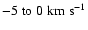 )
and there would therefore be confusion with local
)
and there would therefore be confusion with local
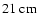 emitting gas.
emitting gas.
Despite its molecular content, and therefore presumably relatively high density, the Coalsack
cloud complex shows no unambiguous evidence for ongoing star formation. There are no flare
stars (Weaver 1973); no T Tauri stars (Weaver 1974a,b); no H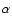 emission stars (Schwartz
1977); and no IRAS sources associated with either the extinction peaks or CO emission peaks
(Nyman et al. 1989). Reipurth detected a single HH object, R10, in the
direction of the Coalsack, and Eaton et al. (1990) showed it to be a bipolar nebula with a
heavily obscured illuminating star. However, Kato et al. (1999) question whether R10 is
really associated with the Coalsack, and it is certainly a long way from Globule 2 (hereafter G2).
emission stars (Schwartz
1977); and no IRAS sources associated with either the extinction peaks or CO emission peaks
(Nyman et al. 1989). Reipurth detected a single HH object, R10, in the
direction of the Coalsack, and Eaton et al. (1990) showed it to be a bipolar nebula with a
heavily obscured illuminating star. However, Kato et al. (1999) question whether R10 is
really associated with the Coalsack, and it is certainly a long way from Globule 2 (hereafter G2).
It is therefore possible that G2, which appears to be the densest core in the Coalsack, is
in an early stage of condensing to form a protostar (or protostars) and, if so, its detailed
structure could contain important clues about how cores form. To this end, Lada et al.
(2004) have obtained deep near-IR photometry of 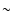 24 000 stars seen through G2, and
have used this data to construct an extinction map of the core with unprecedented resolution.
24 000 stars seen through G2, and
have used this data to construct an extinction map of the core with unprecedented resolution.
The most remarkable feature of this map is that the core has a local extinction minimum in
the middle, and the maximum extinction is in a ring-like structure around this minimum. Lada
et al. discuss some possible explanations for this structure, under the general headings:
"flattened geometry and magnetic fields'' and "spherical geometry: a core in transition''.
We here present a detailed model under the second heading, in which G2 is a core responding
to a sudden increase in external pressure as investigated in Hennebelle et al. (2003, 2004).
This increase in external pressure is driving
a compression wave into the cloud, producing a dense shell which - seen in projection
- is visible as a ring of enhanced extinction. The broad 12C18O (
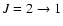 )
emission line observed by Lada et al. along a single line of sight through
the core is then attributable to the extra trans-sonic velocity generated by the
inward-propagating compression wave.
)
emission line observed by Lada et al. along a single line of sight through
the core is then attributable to the extra trans-sonic velocity generated by the
inward-propagating compression wave.
In Sect. 2 we describe briefly the code used to simulate this model, and the initial
conditions adopted. In Sect. 3 we present the results obtained and compare them to the
observations; it should be emphasised at the outset that we do not perform an extensive
parameter search to obtain the best fit to the observational data, since this does not, at
the present time, seem justified by the scope of the observations. In Sect. 4 we discuss
the results, attempt to justify key aspects of the model, and summarise our main conclusions.
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{4634fig1.ps}
\end{figure}](/articles/aa/full/2006/19/aa4634-05/Timg32.gif) |
Figure 1:
The lefthand column shows volume-density profiles, n(r) (where n is in
H
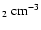 and r is in pc. The middle column sows radial velocity profiles,
u(r) (where u is in
and r is in pc. The middle column sows radial velocity profiles,
u(r) (where u is in
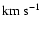 and r is in pc). The righthand
column shows column-density profiles N(b) (where N is is H
and r is in pc). The righthand
column shows column-density profiles N(b) (where N is is H
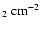 and
b is in pc. The simulation results are represented by solid lines, and the
column-density profile derived from the observed extinction is represented by a dashed
line. The top row is at time
and
b is in pc. The simulation results are represented by solid lines, and the
column-density profile derived from the observed extinction is represented by a dashed
line. The top row is at time
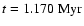 ;
the middle row is at time ;
the middle row is at time
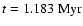 ;
and the bottom row is at time ;
and the bottom row is at time
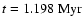 . . |
| Open with DEXTER |
The simulations were performed using the SPH code DRAGON, with 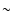 500 000 particles.
This code invokes an oct-tree to find neighbours and calculate gravitational accelerations.
The particle smoothing lengths are adjusted so that each particle has
500 000 particles.
This code invokes an oct-tree to find neighbours and calculate gravitational accelerations.
The particle smoothing lengths are adjusted so that each particle has
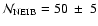 neighbours. A second-order Runge-Kutta integration scheme is used, with
multiple particle time-steps. Other details of the code are given in Goodwin et al. (2004).
neighbours. A second-order Runge-Kutta integration scheme is used, with
multiple particle time-steps. Other details of the code are given in Goodwin et al. (2004).
In the first instance we present a simulation with zero turbulence, since this seems to
capture well the azimuthally averaged features of the ring-like structure reported by
Lada et al. (2005). The initial conditions for this simulation are a truncated Bonnor-Ebert
sphere with boundary
at radius
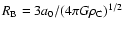 ,
where a0 is the
isothermal sound speed and
,
where a0 is the
isothermal sound speed and
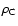 is the central density. We set
is the central density. We set
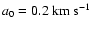 (corresponding to molecular gas at
(corresponding to molecular gas at
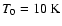 )
and
)
and
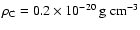 (corresponding to
(corresponding to
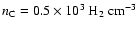 ). This gives a core radius
). This gives a core radius
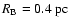 and a total core mass
and a total core mass
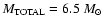 .
The cloud is in stable equilibrium with external pressure
.
The cloud is in stable equilibrium with external pressure
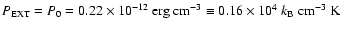 .
The initial conditions are set up with a random but settled (i.e.
non-crystalline) distribution of particles in detailed hydrostatic equilibrium, and the subsequent
evolution is isothermal (i.e.
.
The initial conditions are set up with a random but settled (i.e.
non-crystalline) distribution of particles in detailed hydrostatic equilibrium, and the subsequent
evolution is isothermal (i.e.
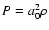 ,
with uniform and constant a0).
At t = 0, we increase
,
with uniform and constant a0).
At t = 0, we increase
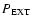 at a constant rate, by a factor of 10, over a thirtieth
of a crossing time, i.e.
at a constant rate, by a factor of 10, over a thirtieth
of a crossing time, i.e.
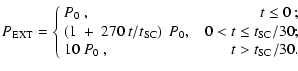 |
|
|
(1) |
The sound-crossing time is given by
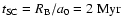 ,
and so the new increased external pressure is reached after
,
and so the new increased external pressure is reached after 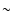
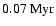 .
.
We then explore how the evolution of the core is modified if it has a modest level of internal
turbulence. This is motivated by the fact that the ring-like structure observed by Lada et al. presents
significant departures from an ideal axisymmetric ring.
We therefore explore what level of turbulence is compatible with the
observed ring pattern.
The turbulence is characterised by two parameters: (i) the ratio of turbulent energy,
 ,
to self-gravitational potential energy,
,
to self-gravitational potential energy,
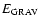 ,
i.e.
,
i.e.
 ;
and (ii) the exponent n in the turbulent power spectrum,
;
and (ii) the exponent n in the turbulent power spectrum,
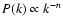 .
The turbulent parameters in the different simulations are given in Table 1.
.
The turbulent parameters in the different simulations are given in Table 1.
Table 1:
Parameters of the initial turbulence in the different simulations.
Figure 1 shows the profiles of volume-density, n(r), inflow velocity, u(r),
and column-density, N(b), generated by the non-turbulent simulation (simulation 1 in Table 2) at three times,
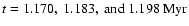 (i.e. well after the external pressure has reached its new increased value, 10P0). Here r is distance from the centre of the core and b is the impact parameter of the line of sight
relative to the centre of the core.
The density in the swept-up shell has been increased from
(i.e. well after the external pressure has reached its new increased value, 10P0). Here r is distance from the centre of the core and b is the impact parameter of the line of sight
relative to the centre of the core.
The density in the swept-up shell has been increased from
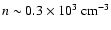 to
to
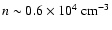 ,
and the swept-up shell is travelling inwards at
,
and the swept-up shell is travelling inwards at
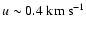 (i.e. Mach-2).
(i.e. Mach-2).
If we adopt the relation
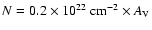 (where N
is the column-density of hydrogen nuclei in all forms, and
(where N
is the column-density of hydrogen nuclei in all forms, and
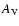 is the visual extinction
in magnitudes), we can convert the azimuthally averaged
extinction profile obtained by Lada et al. (2004) from their near-IR measurements through G2 (their
Fig. 3) into a column-density profile. The result of this conversion is shown as a dashed line
in the righthand panels of Fig. 1. We see that the observed column-density profile
is fitted best by the simulated column-density profile at
is the visual extinction
in magnitudes), we can convert the azimuthally averaged
extinction profile obtained by Lada et al. (2004) from their near-IR measurements through G2 (their
Fig. 3) into a column-density profile. The result of this conversion is shown as a dashed line
in the righthand panels of Fig. 1. We see that the observed column-density profile
is fitted best by the simulated column-density profile at
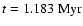 .
The
simulated profile has a minimum of
.
The
simulated profile has a minimum of
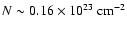 in the centre,
and a maximum of
in the centre,
and a maximum of
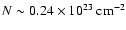 at radii
at radii
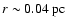 ,
close to the maximum of the observed profile. We note that, with a spherically symmetric model,
it requires a very deep - approximately tenfold - drop in the volume density n at the centre
to produce a
,
close to the maximum of the observed profile. We note that, with a spherically symmetric model,
it requires a very deep - approximately tenfold - drop in the volume density n at the centre
to produce a 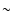
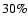 dip in the column-density N; it is very unlikely that the subsonic
velocities involved in an oscillating core could reproduce this feature.
dip in the column-density N; it is very unlikely that the subsonic
velocities involved in an oscillating core could reproduce this feature.
It is worth stressing that our model predicts a column density in the external part of
the cloud (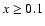 pc) which is roughly two times lower than the observed column-density.
This discrepancy could be due to unrelated gas along the line of
sight, or additional gas which has been accreted by the core.
pc) which is roughly two times lower than the observed column-density.
This discrepancy could be due to unrelated gas along the line of
sight, or additional gas which has been accreted by the core.
Lada et al. (2004) also report a single line profile for the 12C18O (
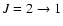 )
transition from a line of sight which is displaced from the notional centre
of symmetry of the core by
)
transition from a line of sight which is displaced from the notional centre
of symmetry of the core by
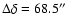 and
and
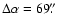 ,
giving a
net angular displacement of
,
giving a
net angular displacement of 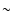 100''. At a distance of
100''. At a distance of
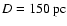 ,
this
corresponds to an impact parameter
,
this
corresponds to an impact parameter
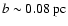 .
We can therefore predict the
line profile expected from the simulation, using
.
We can therefore predict the
line profile expected from the simulation, using
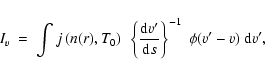 |
(2) |
where v is the radial velocity (i.e. frequency) observed,
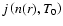 is the integrated volume emissivity
in the line, s is distance along the line of sight (measured from the tangent point),
is the integrated volume emissivity
in the line, s is distance along the line of sight (measured from the tangent point),
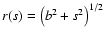 ,
,
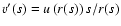 is the inflow velocity
projected along the line of sight, and
is the inflow velocity
projected along the line of sight, and
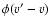 is the profile function (reflecting thermal,
turbulent and natural broadening of the line).
is the profile function (reflecting thermal,
turbulent and natural broadening of the line).
Figure 2 shows emission line profiles for 12C18O (
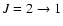 )
on lines of sight with impact parameters b = 0, 0.04, 0.08 and 0.12 pc. The
simulated line profile at
)
on lines of sight with impact parameters b = 0, 0.04, 0.08 and 0.12 pc. The
simulated line profile at
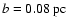 matches the width of the broad line component
observed by Lada et al. (2004) quite well. We concur with their interpretation of the narrow
line component as due to a small-scale turbulent fluctuation, and we would not expect the present
model to reproduce this. From the profiles presented in Fig. 2, it
should be straightforward to test the model proposed here by measuring 12C18O (
matches the width of the broad line component
observed by Lada et al. (2004) quite well. We concur with their interpretation of the narrow
line component as due to a small-scale turbulent fluctuation, and we would not expect the present
model to reproduce this. From the profiles presented in Fig. 2, it
should be straightforward to test the model proposed here by measuring 12C18O (
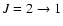 )
line profiles at different positions within the G2 core. Positions within
)
line profiles at different positions within the G2 core. Positions within 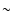 50'' of the centre should present double-peaked line profiles, due to the receding and
approaching sides of the compression wave.
50'' of the centre should present double-peaked line profiles, due to the receding and
approaching sides of the compression wave.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4634fig2.ps}
\end{figure}](/articles/aa/full/2006/19/aa4634-05/Timg75.gif) |
Figure 2:
12C18O (
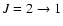 )
line profiles at time )
line profiles at time
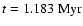 ,
from lines of sight at different impact parameters b, relative to the
centre of the simulated core. The impact parameters are ,
from lines of sight at different impact parameters b, relative to the
centre of the simulated core. The impact parameters are
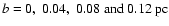 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4634fig3.eps}\par\vspace*{2mm}
\hspace*{-2mm}\includegraphics[width=6.8cm,clip]{4634fig4.eps}
\end{figure}](/articles/aa/full/2006/19/aa4634-05/Timg78.gif) |
Figure 3:
Column density maps from simulations with initial turbulence.
Parameters are:
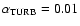 ,
n = 5/3.
Top panel is for time equal to ,
n = 5/3.
Top panel is for time equal to
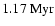 whereas second panel is for
whereas second panel is for
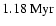 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4634fig5.eps}\par\vspace*{4mm}
\includegraphics[width=7cm,clip]{4634fig6.eps}
\end{figure}](/articles/aa/full/2006/19/aa4634-05/Timg80.gif) |
Figure 4:
Same as Fig. 3 for
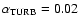 ,
n = 5/3.
Top panel is for time equal to ,
n = 5/3.
Top panel is for time equal to
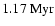 whereas second panel is for
whereas second panel is for
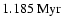 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4634fig7.eps}\par\vspace*{4mm}
\includegraphics[width=7cm,clip]{4634fig8.eps}\end{figure}](/articles/aa/full/2006/19/aa4634-05/Timg83.gif) |
Figure 5:
Same as Fig. 3 for
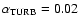 ,
n = 0.
Top panel is for time equal to ,
n = 0.
Top panel is for time equal to
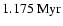 whereas second panel is for
whereas second panel is for
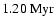 . . |
| Open with DEXTER |
Here we present the results of three simulations in which the initial conditions
are the same as in Simulation 1, except that a turbulent velocity field is superimposed at
the outset. The figures all show column density maps.
The different turbulence parameter
combinations are given in Table 1. We note that the levels of turbulence
invoked are very low
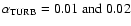 .
The turbulent
power spectra have exponents n = 5/3 (corresponding to Kolmogorov) and 0 (i.e.
more power on small scales).
.
The turbulent
power spectra have exponents n = 5/3 (corresponding to Kolmogorov) and 0 (i.e.
more power on small scales).
Figure 3 displays the column densities at two times steps close to t=1.18 Myr which
matches best the observation. It shows that even with
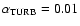 and n=5/3 (simulation 2) the ring is significantly distorted. It is still roundish but
is fragmented in denser clumps. We note that this is actually the case for the ring
observed by Lada et al.
and n=5/3 (simulation 2) the ring is significantly distorted. It is still roundish but
is fragmented in denser clumps. We note that this is actually the case for the ring
observed by Lada et al.
Figure 4 shows that with
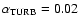 and n=5/3 (simulation 3) the ring is lost rapidly and completely.
The gas rapidly concentrates in one single dense clump.
and n=5/3 (simulation 3) the ring is lost rapidly and completely.
The gas rapidly concentrates in one single dense clump.
The only way to
retrieve the ring with
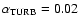 is to concentrate turbulent energy at short wavelengths by decreasing n. This is illustrated in Fig. 5, where
is to concentrate turbulent energy at short wavelengths by decreasing n. This is illustrated in Fig. 5, where
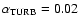 and n=0
(simulation 4), and the ring stays almost axisymmetric during a longer amount of time.
However, such a flat power spectrum is unrealistic since usually Kolmogorov-like power spectra
are found in observations and in numerical simulations. We note that for large values of
and n=0
(simulation 4), and the ring stays almost axisymmetric during a longer amount of time.
However, such a flat power spectrum is unrealistic since usually Kolmogorov-like power spectra
are found in observations and in numerical simulations. We note that for large values of
 (
(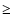
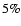 ), the ring is destroyed even with n=0.
), the ring is destroyed even with n=0.
We conclude that, within the scope of our model, the ring-like structure observed by
Lada et al. (2005) requires the initial core to have a very low level of turbulence.
This suggests that the initial core has been very settled before it was
subjected to an increase in external pressure, and consequently there
was enough time for the turbulence to decay almost completely.
We have modelled Tapia's Globule G2 in the Coalsack as a core which is responding to a rapid
increase in external pressure. The resulting compression wave has not yet reached the centre,
and therefore there is a central rarefaction which manifests itself as a dip in the extinction
towards the centre, as observed by Lada et al. (2004). This model requires that the core was
already in existence as a coherent entity with relatively low mean density,
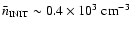 ,
and large extent,
,
and large extent,
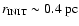 ,
and
that the external pressure acting on it increased by a factor
,
and
that the external pressure acting on it increased by a factor 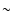 10 (from
10 (from 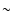
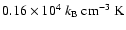 to
to 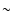
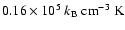 )
in a small fraction of a sound-crossing time,
)
in a small fraction of a sound-crossing time,
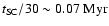 .
The advantages of such external triggers for synchronising the formation of stars in
clusters and generating high multiplicity have been emphasised by Whitworth et al. (1996).
.
The advantages of such external triggers for synchronising the formation of stars in
clusters and generating high multiplicity have been emphasised by Whitworth et al. (1996).
One possibility is that the Coalsack has been involved in, or even created by, a collision
between two large-scale turbulent flows. To deliver the required large pressure increase in
the required short time requires a flow with minimum density
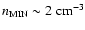 and minimum speed
and minimum speed
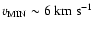 .
Neither
requirement is extreme. Indeed the models of Audit & Hennebelle (2005) show that pressure
increases of the magnitude invoked by our model are very common in the atomic gas from which
molecular complexes like the Coalsack are presumed to form.
.
Neither
requirement is extreme. Indeed the models of Audit & Hennebelle (2005) show that pressure
increases of the magnitude invoked by our model are very common in the atomic gas from which
molecular complexes like the Coalsack are presumed to form.
A second possibility is that the core has fallen into a denser environment and been compressed by
the increased ambient pressure. The local cloud within which G2 resides is Region II in the
scheme of Nyman et al. (1989); see also Kato et al. (1999). This cloud has mass
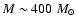 and cross-sectional area
and cross-sectional area
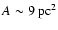 ,
so its mean surface density
is
,
so its mean surface density
is
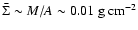 ,
and therefore, assuming that
it is self-gravitating, its central pressure must be
,
and therefore, assuming that
it is self-gravitating, its central pressure must be
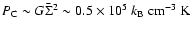 .
It follows that the core only needs to
travel about one third of the cloud radius, i.e.
.
It follows that the core only needs to
travel about one third of the cloud radius, i.e. 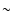
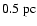 ,
to experience the
required increase in external pressure, and it can do this in
,
to experience the
required increase in external pressure, and it can do this in
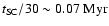 by travelling at
by travelling at 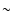
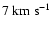 ,
which is a typical bulk velocity
for a cool cloud in the local interstellar medium. Since the measured radial velocity of G2 is
,
which is a typical bulk velocity
for a cool cloud in the local interstellar medium. Since the measured radial velocity of G2 is
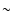
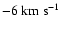 ,
and the measured radial velocity of the Coalsack is
,
and the measured radial velocity of the Coalsack is
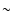
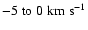 (Nyman et al. 1989), the relative radial
velocity is in the range
(Nyman et al. 1989), the relative radial
velocity is in the range 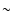
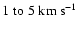 .
Thus if the net
velocity of G2 relative to the Coalsack is
.
Thus if the net
velocity of G2 relative to the Coalsack is 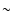
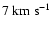 ,
the chance of
its radial component being in this range is
,
the chance of
its radial component being in this range is 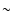
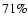 .
Given that we have only one
case, we cannot take statistical arguments any further, but this at least illustrates
that the model is not based on a highly unlikely coincidence. We note that this estimate is based
on the assumption that the main effect of the globule falling into a denser region is a
pressure increase. However other processes like accretion of more material into the
original globule could certainly have a significant impact and promote the formation of a core
out of equilibrium.
.
Given that we have only one
case, we cannot take statistical arguments any further, but this at least illustrates
that the model is not based on a highly unlikely coincidence. We note that this estimate is based
on the assumption that the main effect of the globule falling into a denser region is a
pressure increase. However other processes like accretion of more material into the
original globule could certainly have a significant impact and promote the formation of a core
out of equilibrium.
We have also shown that within the scope of our model
the initial level of turbulence in the core (before t = 0) must
have been very low (
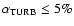 )
in order for the ring-like structure to develop in a coherent manner.
Turbulence promotes fragmentation of the ringlike structure, and
generates dense clumps resembling those observed by Lada et al. in
the dusty ring in the Coalsack.
)
in order for the ring-like structure to develop in a coherent manner.
Turbulence promotes fragmentation of the ringlike structure, and
generates dense clumps resembling those observed by Lada et al. in
the dusty ring in the Coalsack.
However we note that unlike in our simulations,
in the observations these overdensities seem to protrude from the ring. We do not know at
this stage the reason of this. It may be due to the setting up of turbulent fluctuations
with random phases or to incomplete treatment of the physics of the core, since
we have ignored the effects of magnetic fields and large-scale
anisotropy. Our numerical resolution could also be insufficient to
describe accurately such small scale structures.
We reiterate that we have not performed an extensive parameter search to obtain a best-fit model.
The observational constraints (the azimuthally averaged, radial extinction profile; and a single,
off-centre, approximately pencil-beam, line-profile) do not justify detailed modelling, so we are
here only attempting a feasibility study. The next step in testing the model should be to perform
further line observations to test the kinematic predictions of the model (see Fig. 2). We hope to
obtain these observations soon. Another line of investigation which should be pursued is to explore
numerically the departures from spherical symmetry which can be expected because the
pressure increase acting on the core is likely to be anisotropic.
In the meantime, it is appropriate to contrast the predictions of our model with those of the
magnetic model developed by Li & Nakamura (2002).
- (i)
- The magnetic model requires that the core be viewed from close to the axis of symmetry. In
contrast, our model can be viewed from any angle, since it is spherically symmetric.
- (ii)
- The magnetic model requires the magnetic field to be mainly along the line of sight. Lada
et al. (2004) show that the field component in the plane of the sky (estimated from the dispersion
in polarisation angles of background stars, using the Chandraskhar-Fermi equation) is rather close
to the equipartition value, and they point out that this rather large field component in the plane
of the sky is hard to reconcile with the idea that the main component is along the line of sight.
- (iii)
- G2 is located towards the edge of the cloud complex, so it is difficult to see how it can
evolve quasistatically in the ordered way described by Li & Nakamura (2002). This presumably
requires the field to be anchored in some larger-scale structure, but no such structure is evident
on the CO maps of Nyman et al. (1989) and Kato et al. (1999).
The model proposed here falls naturally within the category "spherical geometry: a core
in transition'' defined by Lada et al. (2004). The question then arises as to whether the core
will eventually settle into an equilibrium state (a Bonnor-Ebert sphere) or whether it will
continue contracting to form a star (or stars) at the centre.
Our simulation shows that when the compression
wave converges on the centre of the core it creates a primary
protostar (cf. Hennebelle et al. 2003, 2004). This is expected to
happen in about 40 000 years.
Acknowledgements
We thank Maryvonne Gerin for drawing the Lada et al. paper to our attention, and Charlie Lada
for useful discussions. This paper was written while APW was a visitor at the École Normale
Supérieure, and he is very grateful for the support and hospitality he received during his visit.
SPG is supported by a UKAFF Fellowship. We thank Ian Bonnell, the referee, for his comments which have
significantly improved the original manuscript.
- Alves, J., Lada,
C. J., Lada, E. A., Kenyon, S. J., & Phelps, R. 1998, ApJ, 506,
292 [NASA ADS] [CrossRef] (In the text)
- Alves, J., Lada,
C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] (In the text)
- André, Ph.,
Ward-Thompson, D., & Barsony, M. 2000, in Protostars and
Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russell
(Tucson: Univ. Arizona Press), 59
(In the text)
- Audit, E., &
Hennebelle, P. 2005, A&A, 433, 1 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Cambresy, L.
1999, A&A, 345, 965 [NASA ADS] (In the text)
- Eaton, N., Rolph,
C. D., Scarrott, S. M., & Wolstencroft, R. D. 1990, MN, 244,
527 [NASA ADS] (In the text)
- Goodwin, S.
P., Whitworth, A. P., & Ward-Thompson, D. 2004, A&A, 414,
633 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Harvey, D. W.
A., Wilner, D., Alves, J., et al. 2001, ApJ, 563, 903 [NASA ADS] [CrossRef] (In the text)
- Hennebelle, P. 2003, A&A, 411,
9 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Hennebelle, P., Whitworth, A. P.,
Gladwin, P. P., & André, Ph. 2003, MN, 340, 870 [NASA ADS] [CrossRef] (In the text)
- Hennebelle, P., Whitworth, A. P., Cha,
S.-H., & Goodwin, S. P. 2004, MN, 348, 687 [NASA ADS] [CrossRef] (In the text)
- Kato, S., Mizuno,
N., Asayama, S.-I., et al. 1999, PASJ, 51, 883 [NASA ADS] (In the text)
- Lada, C. J., Huard,
T. L., Crews, L. J., & Alves, J. F. 2004, ApJ, 610, 303 [NASA ADS] [CrossRef] (In the text)
- Li, Z.-Y., &
Nakamura, F. 2002, ApJ, 578, 256 [NASA ADS] [CrossRef] (In the text)
- Matsumoto,
T., & Hanawa, T. 2003, ApJ, 595, 913 [NASA ADS] [CrossRef] (In the text)
- Nyman, L.-Å.,
Bronfman, L., & Thaddeus, P. 1989, A&A, 216, 185 [NASA ADS] (In the text)
- Reipurth, B.
1981, A&ASS, 44, 379 [NASA ADS]
- Rodgers, A. W.
1960, MN, 120, 163 [NASA ADS] (In the text)
- Schwartz, R.
D. 1977, ApJSS, 35, 161 [NASA ADS] (In the text)
- Tapia, S. 1973, in
Interstellar Dust and Related Topics, ed. J. M. Greenberg, & H.
C. van de Hulst (Dordrecht: Reidel), IAU Symp., 52, 43
(In the text)
- Weaver, W. B.
1973, ApJ, 184, 881 [NASA ADS] [CrossRef] (In the text)
- Weaver, W. B.
1974a, ApJ, 189, 81 [NASA ADS] [CrossRef] (In the text)
- Weaver, W. B.
1974b, ApJ, 189, 263 [NASA ADS] [CrossRef]
- Whitworth,
A. P., Bhattal, A. S., Francis, N., & Watkins, S. J. 1996,
MNRAS, 283, 1061 [NASA ADS] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{4634fig1.ps}
\end{figure}](/articles/aa/full/2006/19/aa4634-05/Timg32.gif)
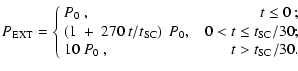
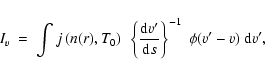
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4634fig2.ps}
\end{figure}](/articles/aa/full/2006/19/aa4634-05/Timg75.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4634fig3.eps}\par\vspace*{2mm}
\hspace*{-2mm}\includegraphics[width=6.8cm,clip]{4634fig4.eps}
\end{figure}](/articles/aa/full/2006/19/aa4634-05/Timg78.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4634fig5.eps}\par\vspace*{4mm}
\includegraphics[width=7cm,clip]{4634fig6.eps}
\end{figure}](/articles/aa/full/2006/19/aa4634-05/Timg80.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4634fig7.eps}\par\vspace*{4mm}
\includegraphics[width=7cm,clip]{4634fig8.eps}\end{figure}](/articles/aa/full/2006/19/aa4634-05/Timg83.gif)